Skip to main content
PMC home page
RSC Advances logoLink to RSC Advances
. 2018 Aug 6;8(49):27979–27987. doi: 10.1039/c8ra04264k

Theoretical investigation of the effects of various substituents on the large energy gap between triplet excited-states of anthracene†

Yu Dawei 1, Zhang Xiaojuan 1, Wang Zhiming 3, Yang Bing 2, Ma Yuguang 3, Pan Yuyu 1,✉
PMCID: PMC9083491  PMID: 35542694

Abstract

The utilization of excitons is key to the effectiveness of organic electroluminescent materials. Recently, HLCT state materials were shown to use triplet excitons to achieve ultra-high electroluminescence efficiency. The large energy gap between triplet states (ΔET1–T2) is key for these materials. In the current computational work, we used the anthracene structure with its large ΔET1–T2 as a template, and to this skeleton we connected various substituents at different sites to explore the effects of these substituents on the excited states of the full molecule. We focused on the change of the ΔET1–T2. Based on our analysis, we concluded the strongly electron-withdrawing substituents and those groups containing oxygen atoms to have the greater influence on the excited state, and to yield anthracene derivatives no longer having the large triplet energy difference characteristic of the unsubstituted anthracene molecule.

The utilization of excitons is key to the effectiveness of organic electroluminescent materials.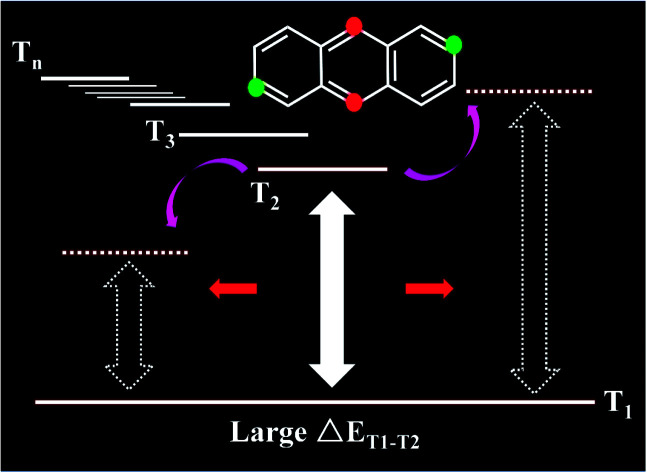graphic file with name c8ra04264k-ga.jpg

Introduction

In electroluminescence processes, electrons and holes are injected into an emitting layer with random spin orientations from a cathode and anode, respectively. Driven by an electric field, the electrons and holes then migrate through the emitting layer, becoming captured quickly by each other to generate singlet and triplet excitons or polaron pairs. However, most organic materials can only use the 25% of the excitons that are singlet excitons, and the remaining excitons, i.e., the triplet excitons, are wasted as a result of the internal conversion (IC) rate being much higher than the intersystem crossing (ISC) rate.1–8 In this process, the use of triplet excitons is the most effective way to improve the luminous efficiency of organic electroluminescent materials.9–14 Recently, the laboratory of Professor Ma found a new way to increase the utilization rate of triplet excitons, with this new way involving reverse intersystem crossing (RISC) through a specific exciton channel to the singlet state. However, to ensure that this channel is clearly open, there should be a large energy gap in the triplet state (ΔET1–T2), which blocks the relaxation of triplet excitons.15–20 Of the molecules with very large values of ΔET1–T2, anthracene is most representative and is widely used in blue luminescent and charge-conductive materials.21–24 In our previous work, we systematically studied what leads to large ΔET1–T2 values in a series of acene molecules.25

In the current work, we instead used the anthracene molecule and carried out a theoretical study of its triplet energy level. Specifically, the molecular configurations and excited state properties of anthracene derivatives were investigated. We focussed on deriving the effects of substituents and substitution sites on the triplet energy level. The purpose of this study was to attain an in-depth understanding of the factors influencing the triplet energy level of these anthracene derivatives. We expect the results of this study to provide experimental researchers with much useful information for designing and synthesizing new efficient OLED materials.

Methodology and computational details

Density-functional theory (DFT) is widely used in the study of the ground and excited states of small molecules, and the accuracy of the energy levels of these states as determined using DFT has been widely recognized.26–29 In our previous work, we showed that the description of the ground-state configuration hardly depended at all on which method or functionals were used. In order to accurately describe the excited-state molecules, we used the EOM-CCSD and TD-DFT method with 11 functionals, including 2 local functionals (SVWN and PBE), 7 hybrid functionals (BLYP, B3LYP, PBE0, BMK, BH and HLYP, M06-2X, M06HF), and 2 long-range-corrected functionals (CAM-B3LYP and ωB97X), with these 11 functionals used in combination with the 6-31+G(d,p) basis sets.30,31 The anthracene and its derivatives, which geometries and emission maxima used as fluorescent materials in OLED have been compared to the available experimental data. Of these methods, those using the RSH functionals TD-DFT/ωB97X provided the results closest to the corresponding data from EOM-CCSD and the experimental values. All quantum chemical calculations were carried out using the Gaussian 09 (version D.01) package on a PowerLeader cluster.32 Multiwfn software was used to calculate the centroids of the charges for the excited state and the transition density matrix for the quantitative composition of the HLCT state.33

If the character of the triplet excited state can be accurately described by means of theoretical calculations, and the influences on the triplet energy gap can be ascertained on this basis, the molecular design can be targeted and the molecules synthesized more accurately.

Results and discussions

All compounds in the present work are displayed in Scheme 1. For this anthracene (AN) series, the methylene (–CH3), aldehyde (–CHO), cyano (–CN), nitro (–NO2), methoxy (–OCH3), hydroxyl (–OH) and bromine (–Br) functional groups, each attached to the AN core through a single bond, served as electron-withdrawing and electron-donating groups. In the current work, we investigated two single-site substitutions, specifically of sites 2 and 9, as well as two double-site substitutions, specifically of 2,6 and 9,10. These substitutions were chosen to investigate the influence of peripheral groups (acceptors and donors) and substitution sites on the optical properties of the molecule.

Scheme 1. Representations of anthracene and its derivatives investigated herein.

Scheme 1

Open in a new tab

Molecular geometries

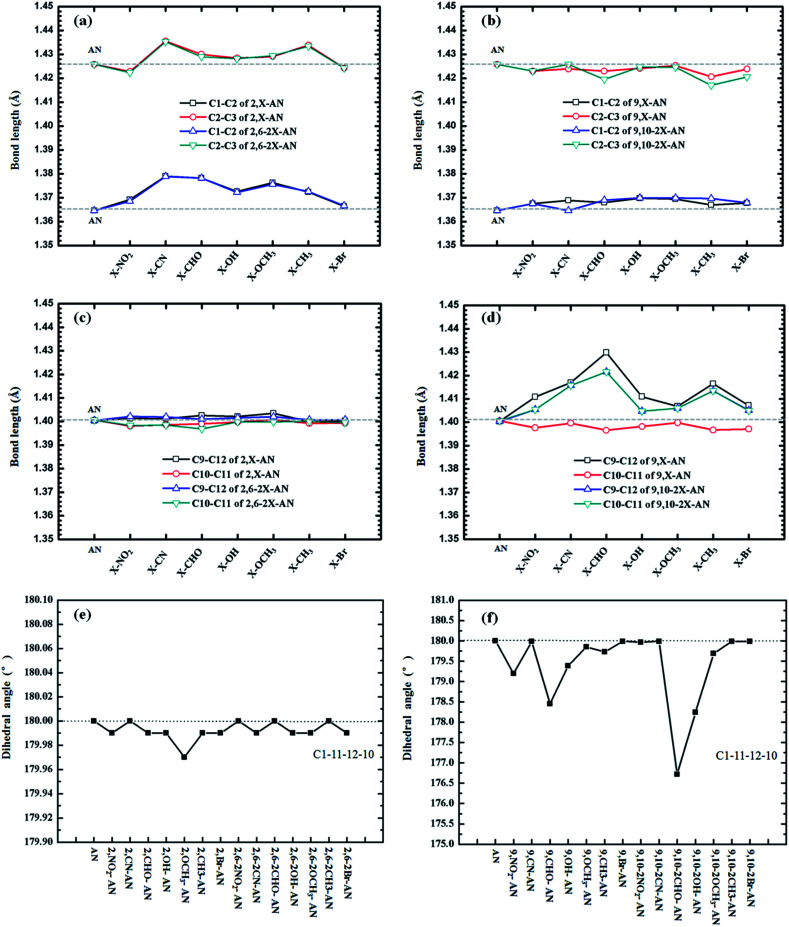
The molecular structures of our investigated AN system are shown in Scheme 1. We optimized ground (S0)-state structures of these compounds, and the vibrational frequencies were computed to verify whether these structures are the stationary points on their potential energy surfaces by checking the imaginary frequency with the lower-energy structures. The frequency calculations of the ground state of each of the above AN molecules showed no imaginary frequency. Selected important bond lengths and the dihedral angle of each of these molecules in the S0 states, including those of the anthracene molecule, are shown in Fig. 1 and Table S1.†

Fig. 1. The important bond lengths and dihedral angle of anthracene and its derivatives in the ground-state geometries.

Fig. 1

Open in a new tab

First, we analyzed the relevant bond length and dihedral angle. In general, the distance of the substituents, quantities, and electron-withdrawing abilities of the substituents were found according to our calculations to have little effect on the bond length, but some trends were observed, such as a relationship between the change in bond length and the distance of the substituents. The closer the substituents, the greater the influence on the bond length changes they would be expected to have. To more clearly observe, we measured the lengths of the C1–C2, C2–C3, C9–C12 and C10–C11 bonds, i.e., those relatively close to the 2,6,9 and 10 substituents, respectively (see Fig. 1). As shown in Fig. 1(b) and (c), the C1–C2, C2–C3, C9–C12 and C10–C11 bonds are farther from the substituents, so the bond lengths are almost unchanged. The differences between the results shown in Fig. 1(a) and (d) are greater, with the C9–C12 of 9,–CHO–AN bond lengths being most prominent, lengthening to about 3 Å. At the same time, the results showed the mono-substitution and double-substitution to have no effect on the corresponding bond lengths.

In addition, we compared the related dihedral angles. The substituents were found to not have much influence on the dihedral angle, and this lack of dependence was attributed to the high rigidity of the anthracene molecule. The single-site substitution at site 2 and the double-site substitution at 2,6 showed especially little effect on the dihedral angle, but the substitutions of positions 9 and 9,10 resulted in some differences. As shown in the Fig. 1(f), substituting a –CHO group at position 9 was calculated to result in the plane becoming bent by nearly 2°. Increasing the number of substitutions, specifically having both positions 9 and 10 substituted at the same time, resulted in a nearly 4° change in the dihedral angle.

Frontier molecular orbitals (FMO)

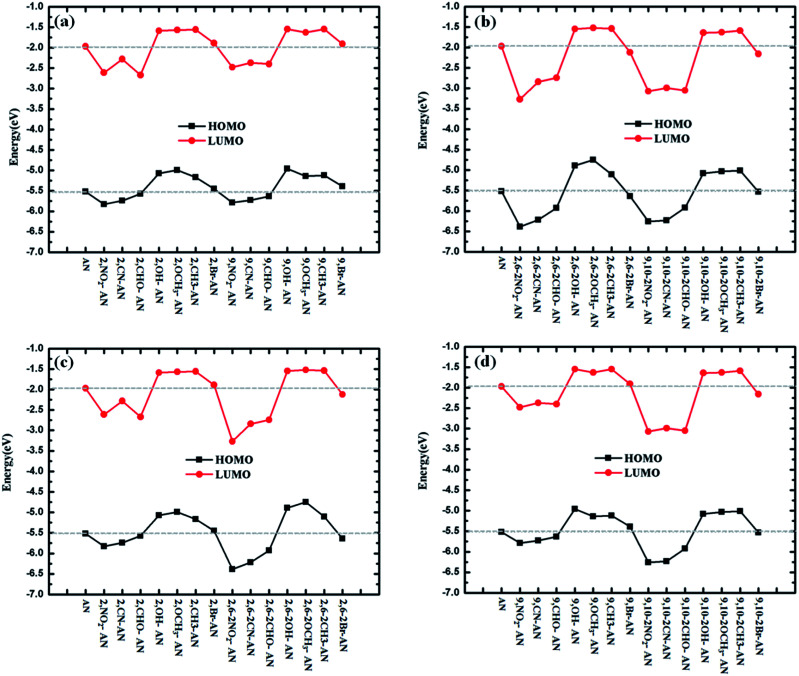
We also expected to find it useful to examine the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital LUMO levels of the studied molecules.34–36 The relative ordering of the occupied and virtual orbitals provides a reasonable qualitative indication of the excitation properties of the anthracene and its derivatives and the ability of these molecular to inject electrons and holes into the light-emitting layer. Since the first dipole-allowed electron transitions and the strongest electron transitions with largest oscillator strength usually correspond almost exclusively to the promotion of an electron from the HOMO to LUMO, the HOMO and LUMO energies of ΔEH–L were calculated by using the ωB97X functional; these energies are listed in Table S1.† To more clearly understand the dependence of the energies on the HOMO and LUMO, we plotted this relationship, as shown in Fig. 2. The electronic density contours of FMOs are plotted in Fig. S2.†

Fig. 2. The highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) energy (eV) levels of the substituents and AN molecules calculated using DFT//ωB97X/6-31+G(d,p).

Fig. 2

Open in a new tab

The substituents were found to have a great influence on the energy levels of the molecules. In general, electron-withdrawing groups reduce energy, while electron-withdrawing groups cause energy to rise. First, from the perspective of the type of substituents, the substitutions of –NO2, –CN–CHO caused in each case the energy of the frontier orbital to decrease, and the substitutions in each case of –OCH3, –CH3 and –OH increased the frontier orbital energy of the molecule. The –Br substituent showed the least influence on the energy. Second, from the perspective of the number of substituents, the magnitude of the increase and decrease of the frontier orbital energies were calculated to become greater as the number of substituents was increased.

Properties of the excited state

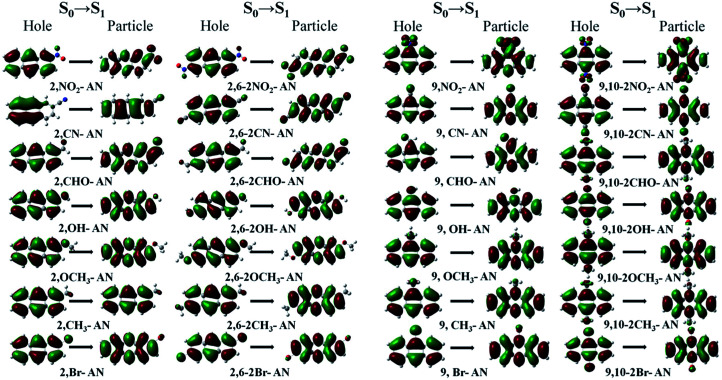
In theory, the transition properties of the excited states are usually determined by the magnitude of the transition dipole moment, the distribution of the electron cloud of NTOs and the transition density matrix. First, we illustrated the dominant “hole”–“particle” contributions of the NTOs of the first excited state in anthracene and its derivatives, as shown in Fig. 3.37

Fig. 3. The dominant “hole”–“particle” contributions of the NTOs of the first excited state of anthracene and its derivatives determined using DFT//ωB97X/6-31+G(d,p).

Fig. 3

Open in a new tab

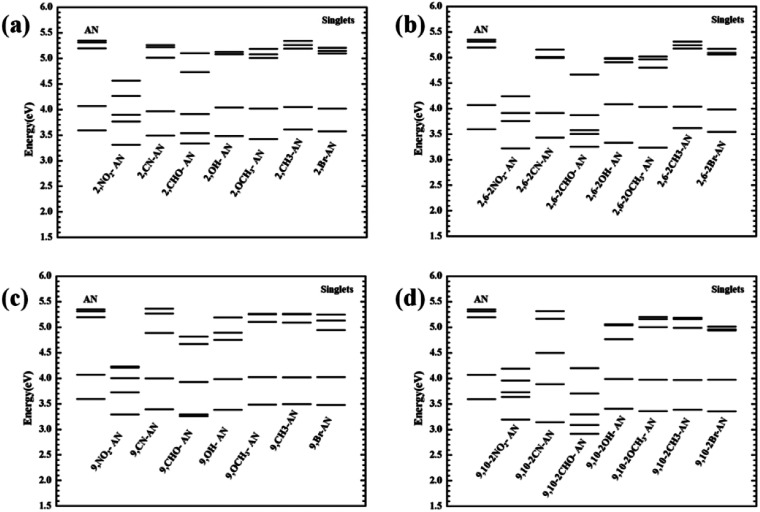
From the transition electron cloud distribution of the S1 state, whether an electron-withdrawing or electron-donating group was connected, the main transition was determined to occur uniformly in the entire skeleton of the molecule. The substitution position and number showed little effect on the transition. As shown in Fig. 4, the singlet state of each of the substituted anthracenes showed a higher energy than did that of anthracene. Except for the –CH3 and –Br groups, introducing substituents at position 2 or 2,6 did not result in any noticeable change in the energy, and the other groups caused the vertical excitation energy to decrease, but by an insignificant amount (<0.3 eV). Introducing a substituent at position 9 or substituents at the 9,10 positions resulted in an overall decrease in the vertical excitation energy. This decrease was most prominent for –NO2 and –CHO, and especially so for –CHO at positions 9 and 10 and for which the vertical excitation energy decreased by about 0.7 eV. Therefore, as a whole, the 9- and 10-position substitutions were calculated to have a greater influence on the excited-state energy, and the effect increased as the number of substitutions was increased.

Fig. 4. The vertical transition energy of the singlet excited states of anthracene and its derivatives.

Fig. 4

Open in a new tab

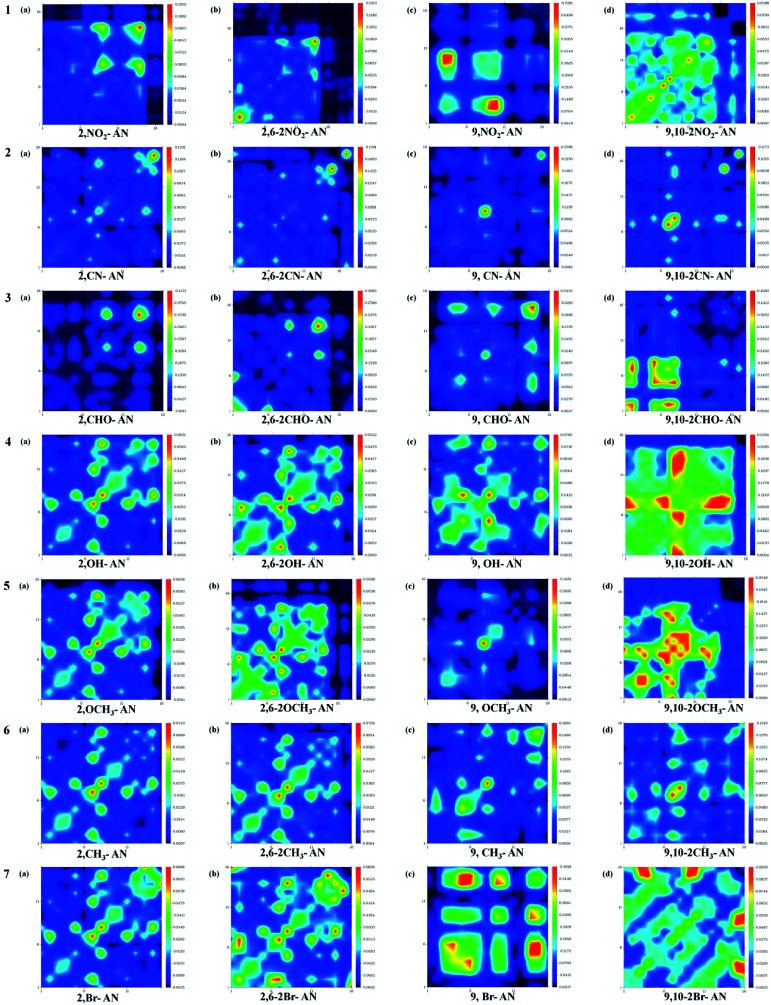
In order to observe the influence of different substituents on the anthracene molecule in the excited state more intuitively, we used the Multiwfn software version 3.3.9 to calculate the wave function of electron–hole pairs of the S1 state from the transition density matrix, and plot the transition density matrix of the S1 state in the anthracene and its derivatives in a two-dimensional (2D) color-coded map, as shown in the Fig. 5. The transition density matrix could quantify the composition of the excited state and from this map we can understand which atoms are mainly affected by the electron transition and which atom pairs are strongly coherent when an electron transits. A stronger effect during the transition is represented by a brighter value in the map. The diagonal part represents the locally-excited (LE) state component, while the off-diagonal region denotes the charge-transfer (CT) state component. As shown in Fig. 4, the highlights are mainly concentrated in the diagonal direction, so the local state is predominant. However, when an electron-withdrawing group was substituted on the anthracene molecular skeleton, transitions of electrons were determined to occur mainly on the atoms attached to the electron-withdrawing group, while when an electron-donating group was substituted instead, a wide range of electronic transitions were found throughout the anthracene molecular skeleton.

Fig. 5. Color-coded maps of the transition density matrix for anthracene and its derivatives. The maps were produced using Multiwfn software.

Fig. 5

Open in a new tab

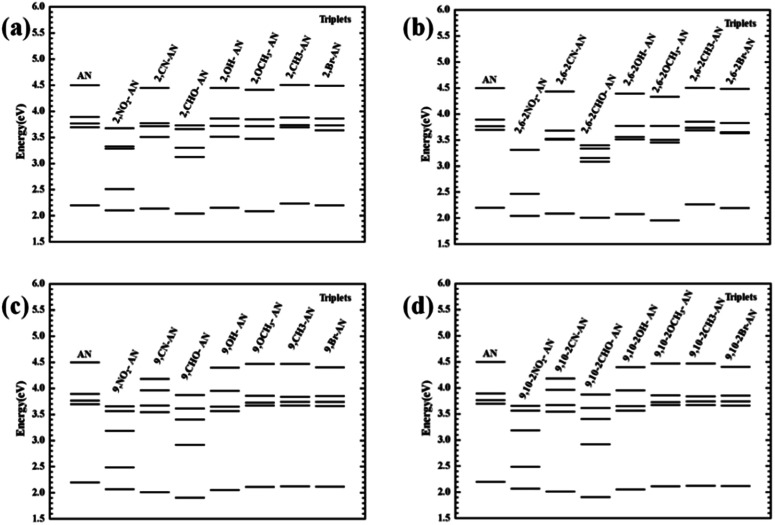
For the triplet state, the anthracene molecule displays a remarkable feature: its T1 and T2 states have a very large energy gap ΔET1–T2 (about 1.5 eV). This feature allows for anthracene to find use in many fields requiring electroluminescence. The focus of the current work involved determining the influence of the substituents on the triplet energy level of anthracene. We first analyzed the energy level distribution of its triplet. As shown in Fig. 6, our analyses indicated the position and number of substituents on anthracene to have little effect on the energy of the T1 state, but to have an effect on ΔET1–T2. Inspection of the energy level diagram clearly showed the large ΔET1–T2 of the derivatives of anthracene molecules to still be maintained, except for the –NO2 and –CHO substituents, which were broken by other energy levels. In order to more clearly analyze the nature of the triplet transitions, we further developed the NTO diagram for this series of molecules, as shown in Fig. 7. It can be seen that there are certain differences between the T1 and T2 transitions in molecules with energy gaps and those without energy gaps. For the molecules substituted with –NO2 and –CHO, and regardless of the position and number of substitutions, we found the T1 state transitions to occur throughout the molecule, but the T2 state transitions to be localized in the substituents. This feature results in the intercalation of the energy levels of the substituents into the region of the energy level of the anthracene molecule. As a result, the large range of energy levels no longer occurs, and the T1 and T2 transitions of other molecules both occur on the anthracene molecular skeleton, so the large energy difference unique to anthracene molecules is maintained.

Fig. 6. The vertical transition energy levels of the triplet excited states of anthracene and its derivatives.

Fig. 6

Open in a new tab

Fig. 7. The dominant “hole”–“particle” contributions of the NTOs of the T1 and T2 excited states in anthracene and its derivatives determined using DFT//ωB97X/6-31+G(d,p).

Fig. 7

Open in a new tab

Conclusions

The large ΔET1–T2 is a special property of anthracenes, and can prevent the rapid internal conversion of the triplet excitons to the T1 state during the electroluminescence process, thereby utilizing the exciton channel to reverse intersystem crossing to the singlet state. This feature increases the utilization of excitons. In the current work, anthracene structures were used as templates to connect to different substituents at different sites, and then the influences of such substitutions on their excited states and large triplet energy ranges were explored. By studying the configuration, frontier molecular orbitals, and NTOs of the singlet and triplet excited states, and the transition matrix of this series of molecules, we found the substituent sites to have little effect on the excited state, especially the single-line excited state. However, as the number of substituents was increased, the excited state energy level decreased. Regarding the triplet energy level, we found that electron-withdrawing and oxygen-containing substituents may generate energy levels in the middle of a large triplet energy gap, thereby eliminating the large energy gaps. We expect this finding to provide an approach for the design of molecules with adjustable energy levels and to provide a reference for the application of energy levels of triplet excited states.

Conflicts of interest

There are no conflicts to declare.

Supplementary Material

RA-008-C8RA04264K-s001

Acknowledgments

We are grateful for financial support from National Science Foundation of China (grant number 51603127, 91233113, 51273078, 51473063, 51203091) and National Basic Research Program of China (973 Program grant number 2013CB834705, 2013CB834801, 2015CB655003).

†

Electronic supplementary information (ESI) available: The optimised geometries of ground. See DOI: 10.1039/c8ra04264k

References

  1. Kasha M. Discuss. Faraday Soc. 1950;9:14. doi: 10.1039/DF9500900014. [DOI] [Google Scholar]
  2. Damm M. Deckert F. Hippler H. Troe J. J. Phys. Chem. 1991;95:2005. doi: 10.1021/j100158a022. [DOI] [Google Scholar]
  3. Foggi P. Neuwahl F. V. R. Moroni L. Salvi P. R. J. Phys. Chem. A. 2003;107:1689. doi: 10.1021/jp021313e. [DOI] [Google Scholar]
  4. Tang C. W. VanSlyke S. A. Appl. Phys. Lett. 1987;51:913. doi: 10.1063/1.98799. [DOI] [Google Scholar]
  5. Grabowski Z. R. Rotkiewicz K. Rettig W. Chem. Rev. 2003;103:3899. doi: 10.1021/cr940745l. [DOI] [PubMed] [Google Scholar]
  6. Shirota Y. Kinoshita M. Noda T. Okumoto K. Ohara T. J. Am. Chem. Soc. 2000;122:11021. doi: 10.1021/ja0023332. [DOI] [Google Scholar]
  7. Doi H. Kinoshita M. Okumoto K. Shirota Y. Chem. Mater. 2003;15:1080. doi: 10.1021/cm020948n. [DOI] [Google Scholar]
  8. Uoyama H. Goushi K. Shizu K. Nomura H. Adachi C. Nature. 2012;492:234. doi: 10.1038/nature11687. [DOI] [PubMed] [Google Scholar]
  9. Zhang Q. Li B. Huang S. Nomura H. Tanaka H. Adachi C. Nat. Photonics. 2014;8:326. doi: 10.1038/nphoton.2014.12. [DOI] [Google Scholar]
  10. Tanaka H. Shizu K. Miyazaki H. Adachi C. Chem. Commun. 2012;48:11392. doi: 10.1039/C2CC36237F. [DOI] [PubMed] [Google Scholar]
  11. Duan C. Li J. Han C. Ding D. Yang H. Wei Y. Xu H. Chem. Mater. 2016;28:5667. doi: 10.1021/acs.chemmater.6b01691. [DOI] [Google Scholar]
  12. Eichelbaum M. Rademann K. Adv. Funct. Mater. 2009;19:560. doi: 10.1002/adfm.200801892. [DOI] [Google Scholar]
  13. Liang Q. Han C. Duan C. Xu H. Adv. Opt. Mater. 2018;6:1800020. doi: 10.1002/adom.201800020. [DOI] [Google Scholar]
  14. Lv X. Zhang W. Ding D. Han C. Huang Z. Xiang S. Zhang Q. Xu H. Wang L. Adv. Opt. Mater. 2018;6:1800165. doi: 10.1002/adom.201800165. [DOI] [Google Scholar]
  15. Zhang S. Li W. Yao L. Pan Y. Shen F. Xiao R. Yang B. Ma Y. Chem. Commun. 2013;49:11302. doi: 10.1039/C3CC47130F. [DOI] [PubMed] [Google Scholar]
  16. Li W. Liu D. Shen F. Ma D. Wang Z. Feng T. Xu Y. Yang B. Ma Y. Adv. Funct. Mater. 2012;22:2797. doi: 10.1002/adfm.201200116. [DOI] [Google Scholar]
  17. Yao L. Zhang S. Wang R. Li W. Shen F. Yang B. Ma Y. Angew. Chem., Int. Ed. 2014;53:2119. doi: 10.1002/anie.201308486. [DOI] [PubMed] [Google Scholar]
  18. Yang B. Ma Y. Sci. China, Ser. B: Chem. 2013;43:1457. [Google Scholar]
  19. Pan Y. Li W. Zhang S. Yao L. Gu C. Xu H. Yang B. Ma Y. Adv. Opt. Mater. 2014:510. doi: 10.1002/adom.201300467. [DOI] [Google Scholar]
  20. W. Li Pan Y. Yao L. Liu H. Zhang S. Wang C. Shen F. Lu P. Yang B. Ma Y. Adv. Opt. Mater. 2014:892. doi: 10.1002/adom.201400154. [DOI] [Google Scholar]
  21. T. Zeng Hoffmann R. Ananth N. J. Am. Chem. Soc. 2014:1365755. doi: 10.1021/ja505275m. [DOI] [PubMed] [Google Scholar]
  22. Nelson S. F. Lin Y. Y. Gundlach D. J. Jackson T. N. Appl. Phys. Lett. 1998;72:1854. doi: 10.1063/1.121205. [DOI] [Google Scholar]
  23. Skotheim A. and Reynolds J. E., Conjugated Polymers: Theory, Synthesis, Properties, and Characterization, CRC Press, 2006 [Google Scholar]
  24. Müullen K. and Wegner G., Electronic Materials: The Oligomer Approach, Wiley-VCH, 1998 [Google Scholar]
  25. Pan Y. Y. Huang J. Wang Z. M. Yu D. W. Yang B. Ma Y. G. RSC Adv. 2017;7:26697. doi: 10.1039/C7RA02559A. [DOI] [Google Scholar]
  26. Van Caillie C. Amos R. D. Chem. Phys. Lett. 2000;317:159. doi: 10.1016/S0009-2614(99)01346-9. [DOI] [Google Scholar]
  27. Furche F. Ahlrichs R. J. Chem. Phys. 2002;117:7433. doi: 10.1063/1.1508368. [DOI] [Google Scholar]
  28. Scalmani G. Frisch M. J. Mennucci B. Tomasi J. Cammi R. Barone V. J. Chem. Phys. 2006;124:094107. doi: 10.1063/1.2173258. [DOI] [PubMed] [Google Scholar]
  29. Vosko S. H. Wilk L. Nusair M. Can. J. Phys. 1980;58:1200. doi: 10.1139/p80-159. [DOI] [Google Scholar]
  30. Pan Y. Y. Huang J. Zhang S. T. Yu D. W. Yang B. Ma Y. G. RSC Adv. 2016;6:108404. doi: 10.1039/C6RA22267F. [DOI] [Google Scholar]
  31. Pan Y. Y. Huang J. Wang Z. M. Yu D. W. Yang B. Ma Y. G. RSC Adv. 2017;7:19576. doi: 10.1039/C7RA01270E. [DOI] [Google Scholar]
  32. Frisch M. J., Trucks G. W., Schlegel H. B., Scuseria G. E., Robb M. A., Cheeseman J. R., Scalmani G., Barone V., Mennucci B., Petersson G. A., Nakatsuji H., Caricato M., Li X., Hratchian H. P., Izmaylov A. F., Bloino J., Zheng G., Sonnenberg J. L., Hada M., Ehara M., Toyota K., Fukuda R., Hasegawa J., Ishida M., Nakajima T., Honda Y., Kitao O., Nakai H., Vreven T., Montgomery Jr J. A., Peralta J. E., Ogliaro F., Bearpark M., Heyd J. J., Brothers E., Kudin K. N., Staroverov V. N., Kobayashi R., Normand J., Raghavachari K., Rendell A., Burant J. C., Iyengar S. S., Tomasi J., Cossi M., Rega N., Millam J. M., Klene M., Knox J. E., Cross J. B., Bakken V., Adamo C., Jaramillo J., Gomperts R., Stratmann R. E., Yazyev O., Austin A. J., Cammi R., Pomelli C., Ochterski J. W., Martin R. L., Morokuma K., Zakrzewski V. G., Voth G. A., Salvador P., Dannenberg J. J., Dapprich S., Daniels A. D., Farkas Ö., Foresman J. B., Ortiz J. V., Cioslowski J., and Fox D. J., Gaussian 09, Version D.1, Gaussian, Inc., Wallingford CT, 2009 [Google Scholar]
  33. Lu T. Chen F. J. Comput. Chem. 2012;33:580. doi: 10.1002/jcc.22885. [DOI] [PubMed] [Google Scholar]
  34. Friend R. H. Gymer R. W. Holmes A. B. Burroughes J. H. Marks R. N. Taliani C. Bradley D. D. C. dos Santos D. A. Bredas J. L. Lögdlund M. Salaneck W. R. Nature. 1999;397:121. doi: 10.1038/16393. [DOI] [Google Scholar]
  35. Coropceanu V. Cornil J. Demetrio A. S. F. Yoann O. Robert S. Brédas J. L. Chem. Rev. 2007;107:926. doi: 10.1021/cr050140x. [DOI] [PubMed] [Google Scholar]
  36. Bredas J. L. Beljonne D. Coropceanu V. Cornil J. Chem. Rev. 2004;104:4971. doi: 10.1021/cr040084k. [DOI] [PubMed] [Google Scholar]
  37. Martin R. L. J. Chem. Phys. 2003;118:477. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

RA-008-C8RA04264K-s001
RA-008-C8RA04264K-s001.pdf (852.2KB, pdf)

Articles from RSC Advances are provided here courtesy of Royal Society of Chemistry

RESOURCES