Daily longitudinal sampling of SARS-CoV-2 infection reveals substantial heterogeneity in infectiousness

Abstract

The dynamics of SARS-CoV-2 replication and shedding in humans remain poorly understood. We captured the dynamics of infectious virus and viral RNA shedding during acute infection through daily longitudinal sampling of 60 individuals for up to 14 days. By fitting mechanistic models, we directly estimated viral expansion and clearance rates, and overall infectiousness for each individual. Significant person-to-person variation in infectious virus shedding suggests that individual-level heterogeneity in viral dynamics contributes to superspreading. Viral genome loads often peaked days earlier in saliva than in nasal swabs, indicating strong tissue compartmentalization and suggesting that saliva may serve as a superior sampling site for early detection of infection. Viral loads and clearance kinetics of Alpha (B.1.1.7) and previously circulating non-variant of concern viruses were mostly indistinguishable, indicating that the enhanced transmissibility of this variant cannot be simply explained by higher viral loads or delayed clearance. These results provide a high-resolution portrait of SARS-CoV-2 infection dynamics and implicate individual-level heterogeneity in infectiousness in superspreading.

Transmission of SARS-CoV-2 by pre-symptomatic and asymptomatic individuals has been a major contributor to the explosive spread of this virus ^1–5. Recent epidemiological investigations of community outbreaks have indicated that transmission of SARS-CoV-2 is highly heterogeneous, with a small fraction of infected individuals (often referred to as “superspreaders”) contributing a disproportionate share of forward transmission ^6–8. Transmission heterogeneity has also been implicated in the epidemic spread of several other important viral pathogens, including measles and smallpox ⁹. Numerous behavioral and environmental explanations have been offered to explain transmission heterogeneity, but the extent to which the underlying features of the infection process within individual hosts contribute towards the superspreading phenomenon remains unclear. Addressing this gap in knowledge will inform the design of more targeted and effective strategies for controlling community spread.

Viral infection is a highly complex process in which viral replication and shedding dynamics are shaped by the complex interplay between host and viral factors. Recent studies have suggested that the magnitude and/or duration of viral shedding in both nasal and saliva samples correlate with disease severity, highlighting the potential importance of viral dynamics in influencing infection outcomes ^10–13. Variation in viral load has also been suggested to correlate with transmission risk ¹⁴. In addition to implications for pathogenesis and transmission, defining the contours of viral shedding dynamics is also critical for designing effective surveillance, screening, and testing strategies ¹⁵. To date, studies aimed at describing the longitudinal dynamics of SARS-CoV-2 shedding have been limited by (a) sparse sampling frequency, (b) failure to capture the early stages of infection when transmission is most likely, (c) absence of individual-level data on infectious virus shedding kinetics, and (d) biasing towards the most severe clinical outcomes ^16–21. This is also true for viruses beyond SARS-CoV-2, as the dynamics of natural infection in humans have not been described in detail for any acute viral pathogen.

Here, we capture the longitudinal viral dynamics of mild and asymptomatic early acute SARS-CoV-2 infection in 60 people by recording daily measurements of both viral RNA shedding (from mid-turbinate nasal swabs and saliva samples) and infectious virus shedding (from mid-turbinate nasal swabs) for up to 14 days. We reveal a striking degree of individual-level heterogeneity in infectious virus shedding between individuals, thus providing a partial explanation for the central role of superspreaders in community transmission of SARS-CoV-2. We also directly compare the shedding dynamics of Alpha (B.1.1.7) and previously circulating, non-Alpha viruses, revealing no significant differences in nasal or saliva shedding. Altogether, these results provide a high-resolution, multi-parameter empirical profile of acute SARS-CoV-2 infection in humans and implicate person-to-person variation in infectious virus shedding in driving patterns of epidemiological spread of the pandemic.

Description of cohort and study design

During the Fall of 2020 and Spring of 2021, all faculty, staff, and students at the University of Illinois at Urbana-Champaign were required to undergo at least twice weekly RTqPCR testing for SARS-CoV-2 ²². We leveraged this large-scale, high-frequency screening program to enroll symptomatic, pre-symptomatic, and asymptomatic SARS-CoV-2-infected individuals. We enrolled university faculty, staff, and students who reported a negative RTqPCR test result in the past seven days and were either (a) within 24 hours of a positive RTqPCR result, or (b) within five days of exposure to someone with a confirmed positive RTqPCR result. These criteria ensured that we only enrolled people within the first days of infection.

We collected both nasal and saliva samples daily for up to 14 days to generate a high-resolution portrait of viral dynamics during the early stages of SARS-CoV-2 infection. Participants also completed a daily online symptom survey. Our study cohort was primarily young (median age: 28; range: 19–73), non-Hispanic white, and skewed slightly towards males (Table S1). All infections were either mild or asymptomatic, and none of the participants were ever hospitalized for COVID-19. All participants in this cohort reported that they had never been previously infected with SARS-CoV-2, and none were vaccinated against SARS-CoV-2 at the time of enrollment.

Early SARS-CoV-2 viral dynamics vary significantly between individuals

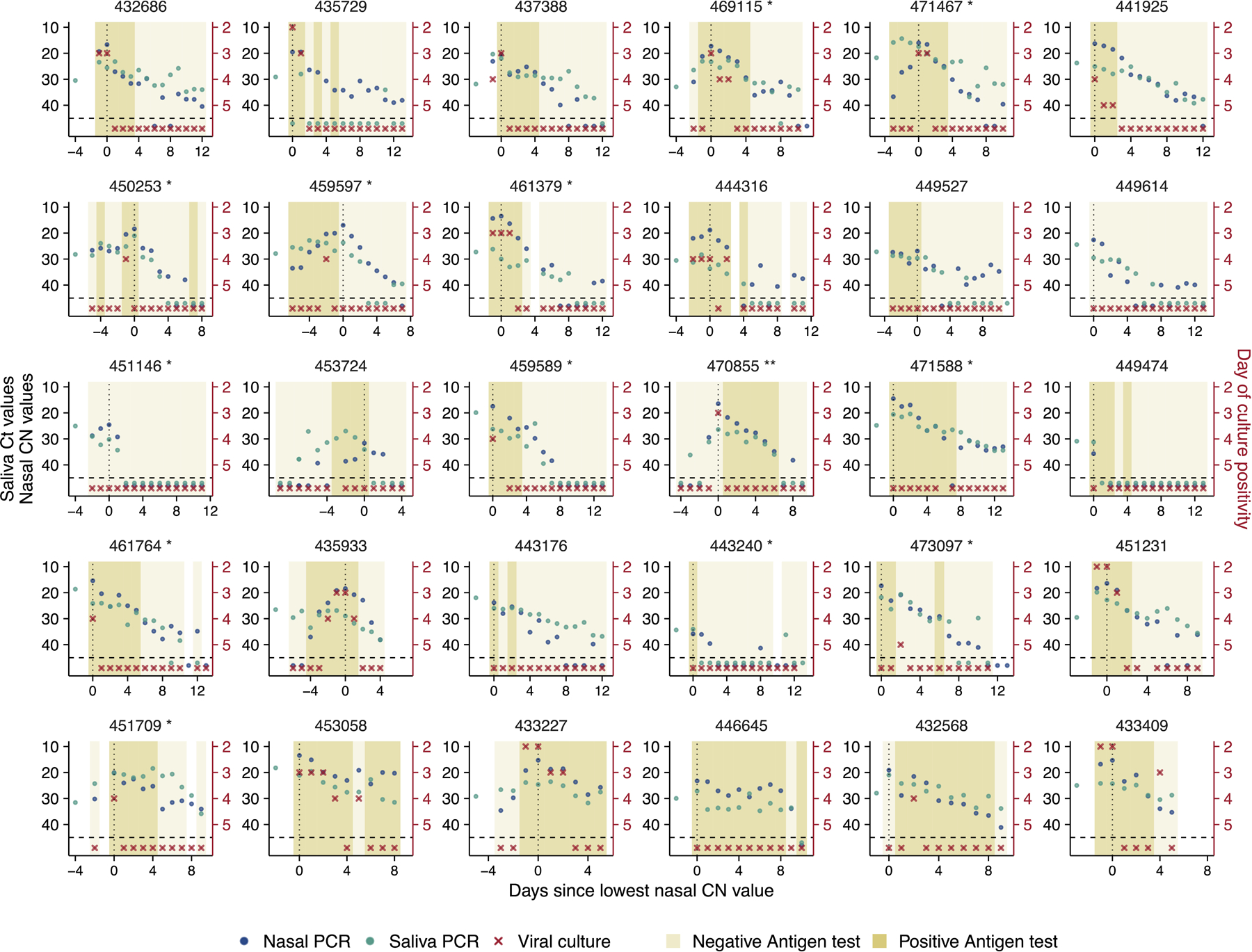
To examine viral dynamics at the individual level, we plotted Ct/CN values from both saliva and nasal swab samples (the RTqPCR assay used for nasal swab samples reports CN values, an objective measure of the cycle number of the maximal rate of PCR signal increase, rather than Ct values. CN values and Ct values are equivalent in suitability for quantitative estimates ²³), Quidel SARS Sofia 2 antigen fluorescent immunoassay (FIA) results, and viral culture data from nasal swabs, as a function of time relative to the lowest observed CN values (Fig 1A, Extended data Fig 1). In many cases, we captured both the rise and fall of viral genome shedding in nasal and/or saliva samples. A comparison between individuals revealed substantial heterogeneity in shedding dynamics, with obvious differences in the duration of detectable infectious virus shedding, clearance kinetics, and the temporal relationship between shedding in nasal and saliva compartments. Further, 9 out of 60 individuals had no detectable infectious virus in nasal samples (Fig 1A, Extended data Fig 1).

Figure 1: SARS-CoV-2 viral dynamics captured through daily sampling.

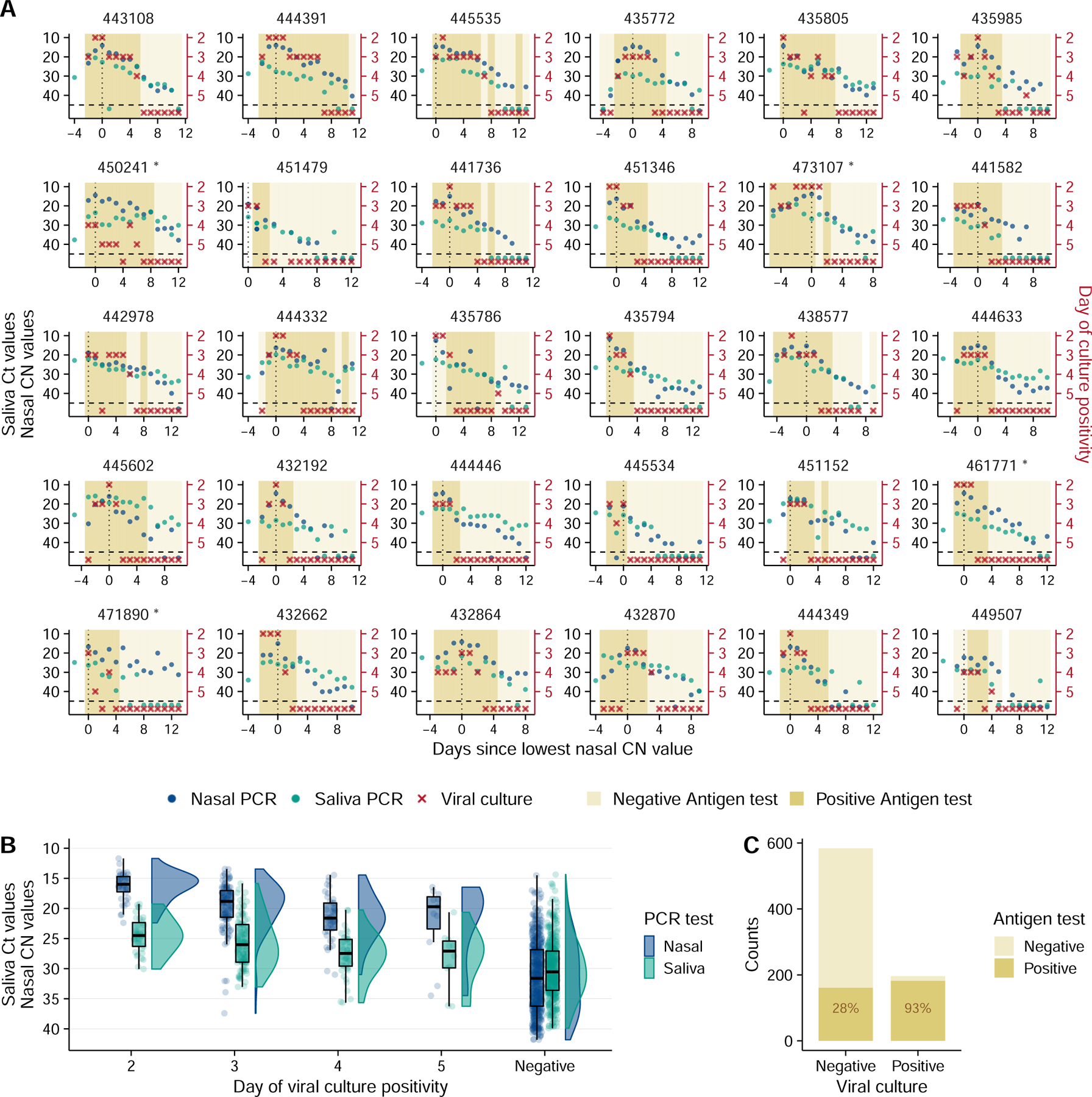
(A) Temporal trends for the saliva RTqPCR (teal dots), nasal swab RTqPCR (navy blue dots), nasal swab viral culture (red crosses), and positive nasal swab antigen test results (dark mustard shaded area). The left Y axis indicates Ct values for saliva RTqPCR assay (covidSHIELD) and CN values for nasal swab RTqPCR assay (Abbott Alinity). The right Y axis indicates results of viral culture assays, where day of culture positivity indicates the day of incubation at which > 50% of Vero-TMPRSS2 cells infected with the sample were positive for cytopathic effect. The vertical dotted line shows the day at which the lowest nasal CN value is observed. Horizontal dashed line indicates limit of detection of RTqPCR and viral culture assays. The title of each plot corresponds to the participant ID for the top 30 individuals with the most data points (the remaining 30 participants are shown in figure S1). Single and double asterisks next to the participant ID indicates B.1.1.7 and P.1 variants respectively. (B) Individual Ct (for saliva) and CN (for nasal swabs) values from samples plotted based on concurrent results from the viral culture assay. Negative indicates samples for which viral culture assay showed no viral growth after 5 days. The boxplot shows first and third quartiles (interquartile range IQR), where the horizontal line is the median value, and the whiskers are 1.5 times the IQR. (C) Plot showing antigen FIA results from days where participants tested either positive or negative by viral culture. The text inside the bars indicates the percentage of antigen FIA results that were positive when concurrent viral culture sample was positive or negative.

Generally, earlier positivity results in the viral culture assay (which suggests higher infectious viral loads) were associated with lower CN values in nasal samples (Fig 1B). This is unsurprising, as both nasal viral genome load and viral infectivity were assayed using the same sample. Saliva Ct values tended to be higher than matched nasal samples, likely due in part to the lower molecular sensitivity of the specific saliva RTqPCR assay used which does not include an RNA extraction step ²⁴. For both sample types, the relationship between viral culture results and Ct/CN values was not absolute, as several nasal swab samples with CN values greater than 30 also tested positive for infectious virus. These data indicate that caution must be exercised when using a simple Ct/CN value cutoff as a surrogate for infectious status.

We also assessed the relationship between antigen FIA and viral culture results and found that participants tested positive by antigen FIA on 93% of the days on which they also tested positive by viral culture (Fig 1C). This finding is consistent with earlier cross-sectional studies examining the relationship between antigen tests positivity and infectious virus shedding ^25,26.

While the symptom profiles self-reported by study participants varied widely across individuals, all cases were mild and did not require medical treatment (Extended data Fig 2). To determine whether any specific symptoms correlated with viral culture positivity, we compared the reported frequencies for each symptom on days where individuals tested viral culture positive or negative (Extended data Fig 3). Muscle aches, runny nose, and scratchy throat were significantly more likely to be reported on days when participants were viral culture positive, suggesting these specific symptoms as potential indicators of infectious status. No other symptoms examined exhibited a clear association with viral culture status. Self-reported symptom data from this study may be partially skewed by having been collected after participants were notified of their initial positive test result or potential exposure.

Within-host mechanistic models capture viral dynamics in nasal and saliva samples

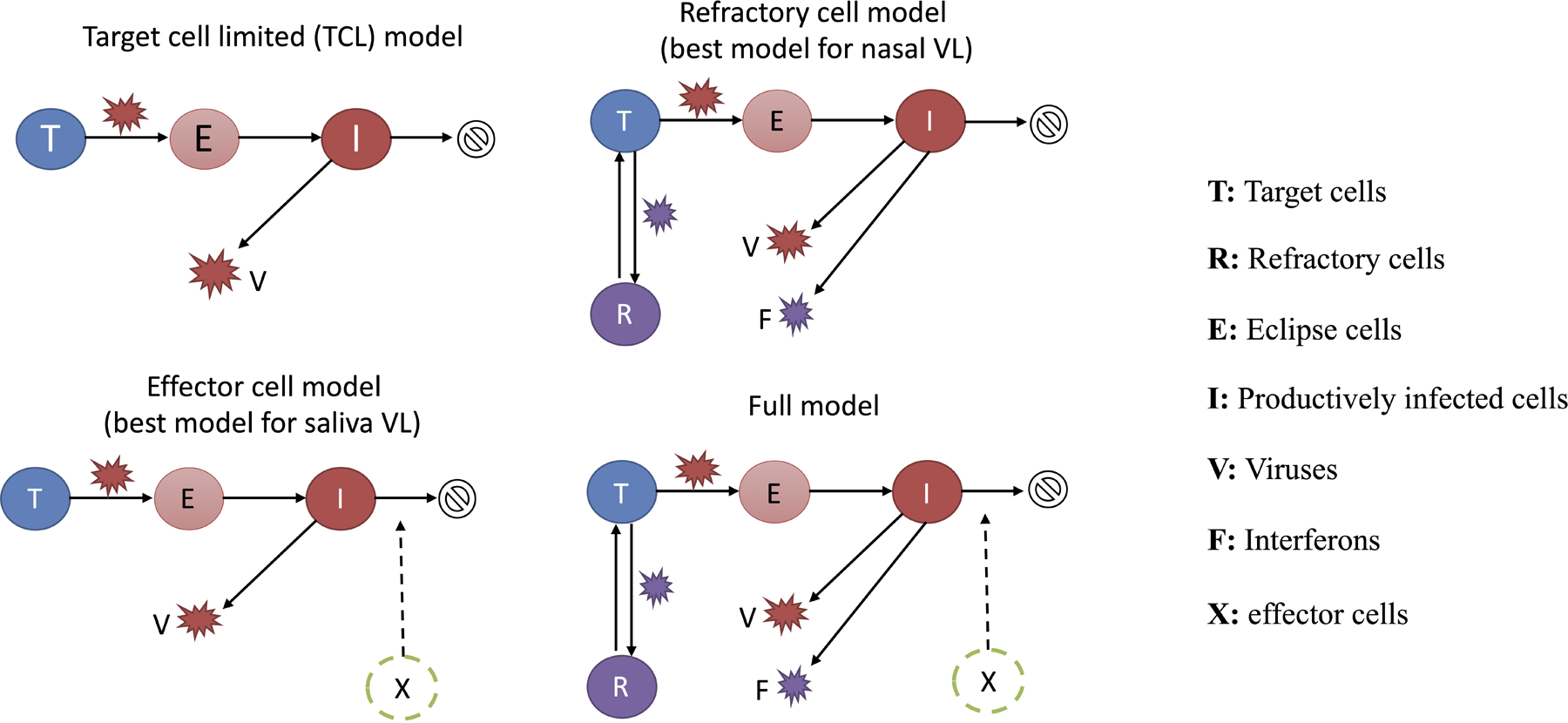
To better quantify the specific features of viral dynamics within individuals, we implemented five within-host mechanistic models based on models developed previously for SARS-CoV-2 and influenza infection (see Supporting Text for details) (Figs 2A, Extended data Fig 4) ^27–29. We fit these models to viral genome loads derived from the observed Ct/CN values using a population mixed effect modeling approach (see Supporting Text for details). The viral dynamics in nasal and saliva samples were distinct from each other in most individuals, indicating strong compartmentalization of the oral and nasal cavities. We thus fit the models to data from nasal and saliva samples separately. For each sample type, viral genome loads from 4 individuals remained very low or undetectable throughout the sampling period (Extended data Fig 1), suggesting that these individuals either (a) were enrolled late during infection despite having a recent negative test result, or (b) exhibited highly irregular shedding dynamics. Because we were primarily interested in early infection dynamics, data from these individuals were excluded. Altogether, we selected data from 56 out of 60 individuals for each sample type for model fitting. Adding the excluded individuals did not change the main conclusions (analysis not shown).

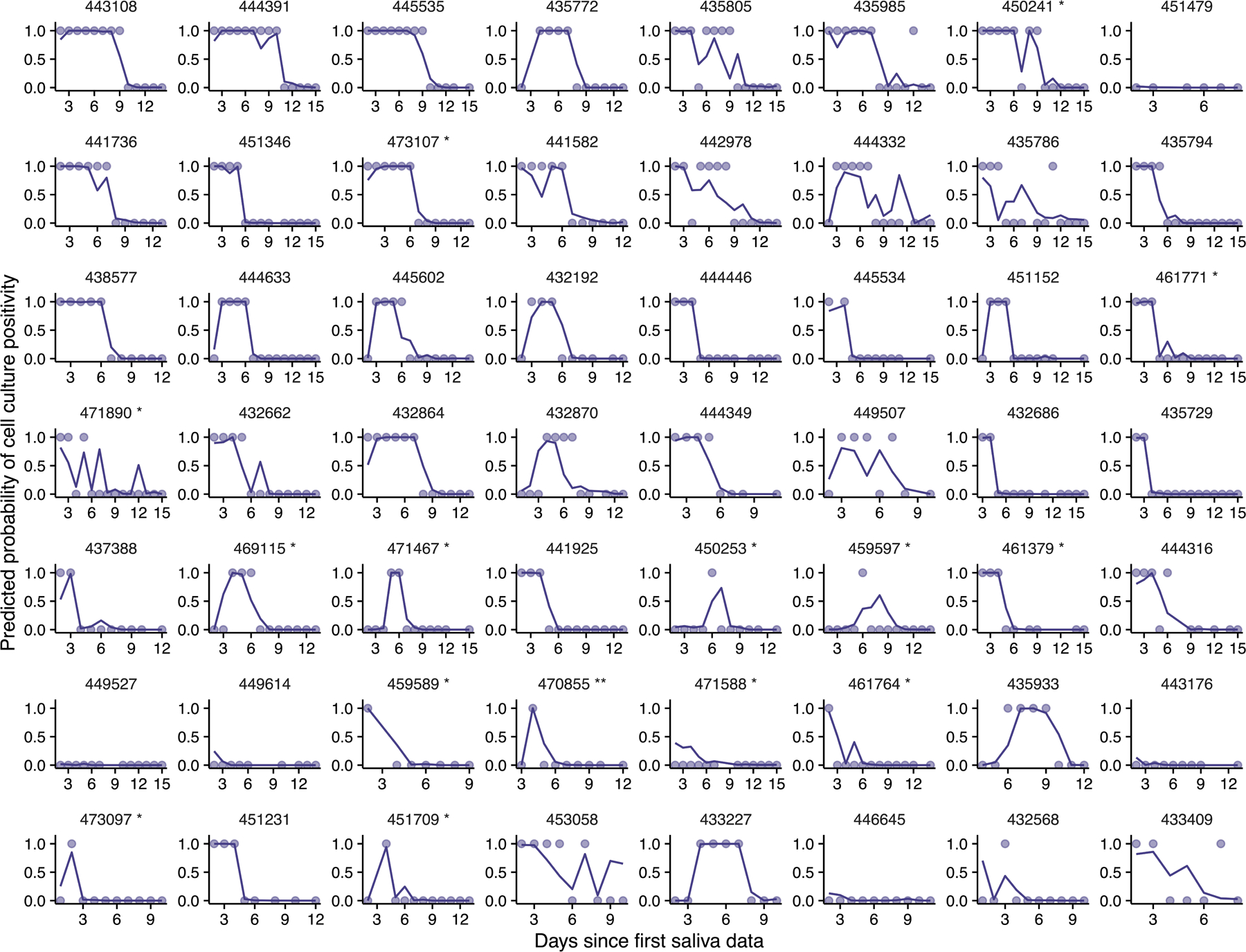
Figure 2: Model fits quantify heterogeneity in viral dynamics and discordance in genome shedding between nasal and saliva samples.

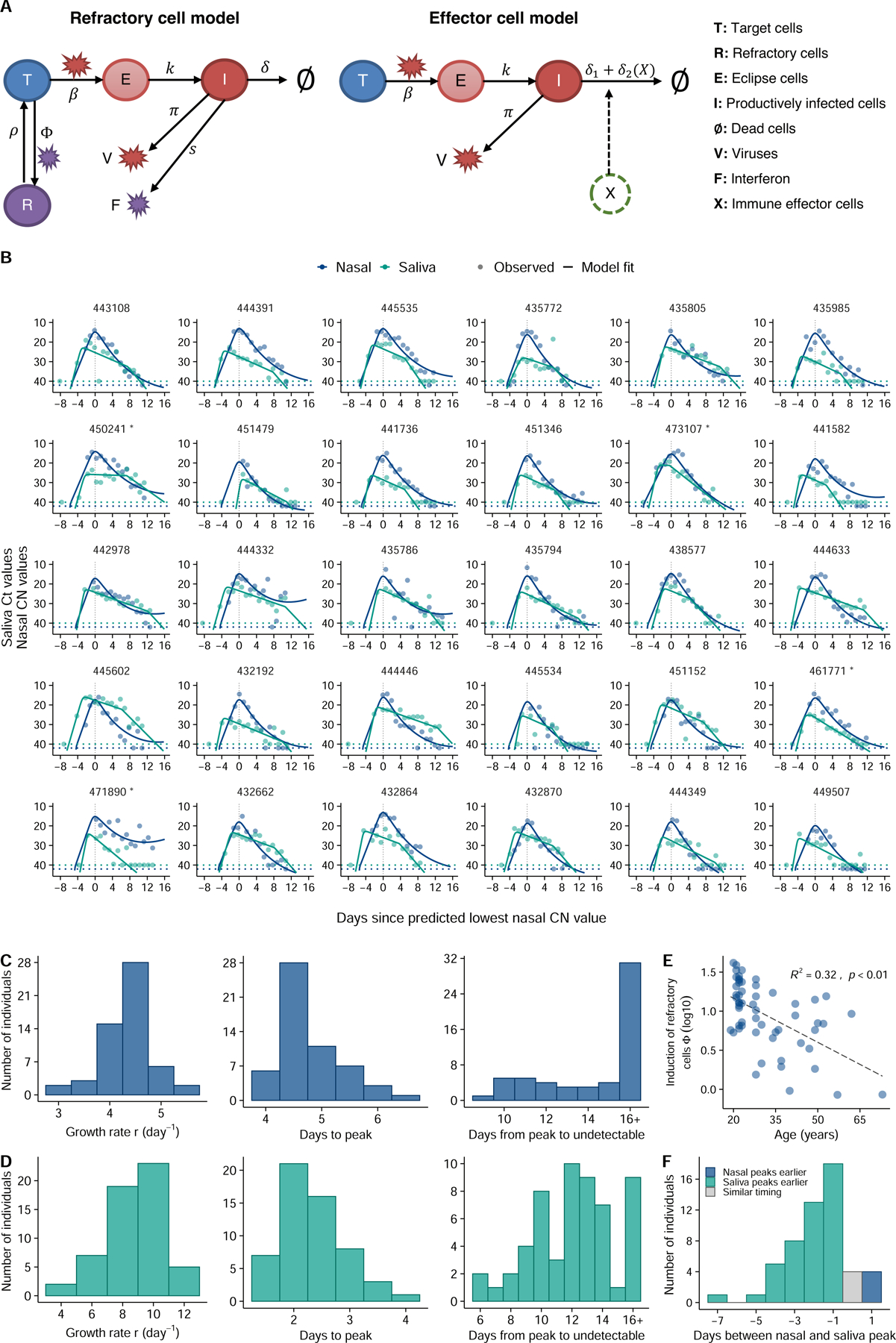
(A) Diagrams outlining structures of the refractory cell model and the immune effector cell model that best fit the nasal swab and saliva RTqPCR data, respectively. In the refractory cell model, target cells (T) are infected by viruses (V) at rate $\text{β}$. Infected cells first become eclipse cells (E) and do not produce viruses; at rate $\text{k}$, eclipse cells become productively infected cells (I) producing both viruses and interferon (F) at rate $\text{π}$ and $\text{s}$, respectively. They die at rate $\text{δ}$. Binding of interferons with target cells induces an antiviral response that turns target cells into cells refractory to infection (R). The rate of induction of the antiviral response is $\Phi$. Refractory cells can revert to target cells at rate $\text{ρ}$. In the effector cell model, we assume that over the course of infection, immune effector cells (X) that clear infected cells are activated and recruited. This leads to an increase in infected cell death rate from ${\text{δ}}_1$ to ${\text{δ}}_1+{\text{δ}}_2$. (B) Model fits to nasal sample (navy blue) and saliva (teal) RTqPCR results from the same subset of individuals shown in figure 1A. Includes last recorded negative saliva RTqPCR result prior to study enrollment. Dotted lines represent the limit of detection (LoD) for the RTqPCR assays. Dots on the dotted lines denote measurements under the LoD. (C, D) Distributions of the exponential viral growth rates, days from infection to peak viral genome load, and days from peak to undetectable viral genome loads predicted by the refractory cell model (nasal data; panel C) and the immune effector model (saliva data; panel D) across 56 individuals in this cohort. (E) Association between age and the estimated strength of the antiviral immune response (Φ) based on nasal sample data. The Y axis is shown on a log 10 scale. Associations are examined using a standard linear regression analysis. The R-squared value and the p-value are reported. (F) Distribution of the differences in the estimated times of peak viral genome loads between the saliva and nasal samples. Bars colored teal and navy blue represent estimated saliva peaks that occur at least 0.5 day earlier and later than nasal samples, respectively. The gray bar indicates the number of individuals that have similar timing in the peaks.

To identify factors that might partially explain the observed variation in individual-level dynamics, for each model we tested whether the age of the participants or the infecting viral genotype (i.e. non-B.1.1.7 vs. B.1.1.7) co-vary with any of the estimated model parameters in the model fitting. A total of 114 model variations were tested (see Supporting text for the testing strategy). We compared the relative abilities of these model variations to capture the RTqPCR data using the corrected Akaike Information Criterion (AICc) and found that in general, the refractory model and the effector cell model best describe data from nasal and saliva samples, respectively (Table S2, S3). In the refractory model (Fig 2A), we assumed that target cells can be rendered refractory to infection through the activity of soluble immune mediators released by infected cells, such as interferon ³⁰. In the best-fit immune effector cell model (Fig 2A), we assumed that innate and adaptive immune cells are activated and recruited to eliminate infected cells, leading to increased viral clearance ²⁸. See Tables S4, S5 and S6 for estimated values of the population and individual parameters and the fixed parameter values, respectively. Overall, these models described the observed Ct/CN values in both nasal and saliva samples very well (Fig 2B).

The frequent longitudinal sampling of participants during early infection provided a unique opportunity to precisely quantify viral load kinetics during the viral expansion phase, prior to the peak in genome shedding. We estimated the mean early exponential expansion rate r before peak viral load (growth rate, for short) to be 4.4/day (SD: ±0.5/day) in the nasal compartment. The growth rate is 8.8/day (SD: ±1.8/day) in the saliva compartment, i.e. much higher than in the nasal compartment (Fig 2C-D).

Viral clearance kinetics clearly differed between nasal and saliva samples (Fig 2B-D). For nasal samples, viral genome loads decreased relatively quickly after peak. This decrease is mostly driven by lose of productively infected cells, and we estimated an average death rate of productively infected cells at 2.5/day (SD: ±0.4/day); however, the viral decline slowed down over time. In saliva, post-peak viral genome loads declined initially at a slower rate than the decline in nasal samples. Consequently, we estimated a much smaller average death rate of productively infected cells in saliva during this phase, at 0.4/day (SD: ±0.3/day). However, our model suggested the existence of a second clearance phase with a more rapid decline occurring 1–2 weeks after infection, potentially due to the onset of effector cell and/or neutralizing antibody responses. Overall, we estimate that it takes on average 4.9/day (SD: ±0.5/day) and 3.9/day (SD: ±0.8/day) from infection to peak viral loads, in the nasal and the saliva compartments, respectively (Fig 2C-D). The average period from peak to undetectable genome viral load is 22.3 days (SD: ±8.3 days) and 14.9 days (SD: ±3.2 days) in the nasal and the saliva compartments, respectively.

Interestingly, the model predicts a significant correlation (p<0.01) in nasal samples between age and the Φ parameter which describes the effectiveness of the anti-viral immune response in rendering target cells refractory to infection (Fig 2E). This suggests that innate immune responses are less effective at limiting SARS-CoV-2 in the nasal compartment of older individuals within our cohort, consistent with prior studies describing dysregulation of innate immunity to viral infection in aged individuals ^31–33. There was no significant correlation between age and either growth rate or clearance rate in nasal samples (Extended data Fig 5).

Overall, we noted a surprising degree of discordance in viral dynamics between nasal and saliva samples for many participants. In most individuals (46 out of 54 analyzed), viral genome shedding peaked at least 1 day earlier in saliva than in nasal samples (Fig 2F). In contrast, the peak in nasal shedding only preceded the saliva peak by at least 1 day in 4 individuals.

Significant heterogeneity in the infectious potential of individuals

We next examined the duration of infectious virus shedding in nasal samples, as a surrogate for the infectious potential of an individual. There exists a large variation in the number of days for which an individual tested positive for cell culture on nasal swabs (Fig 3A). 9 out of 60 individuals tested negative by viral culture throughout the sampling period, whereas 1 individual tested positive for 9 days (Fig 3A). We found a weak positive correlation between the duration of viral culture positivity and participant age (Fig 3B). Of note, many study participants were viral culture positive on the first day of sample collection, suggesting that we failed to capture the onset of viral culture positivity for these individuals and thus may be underestimating the duration of infectious virus shedding for a subset of study participants.

Figure 3: Substantial heterogeneity in infectious virus shedding between individuals.

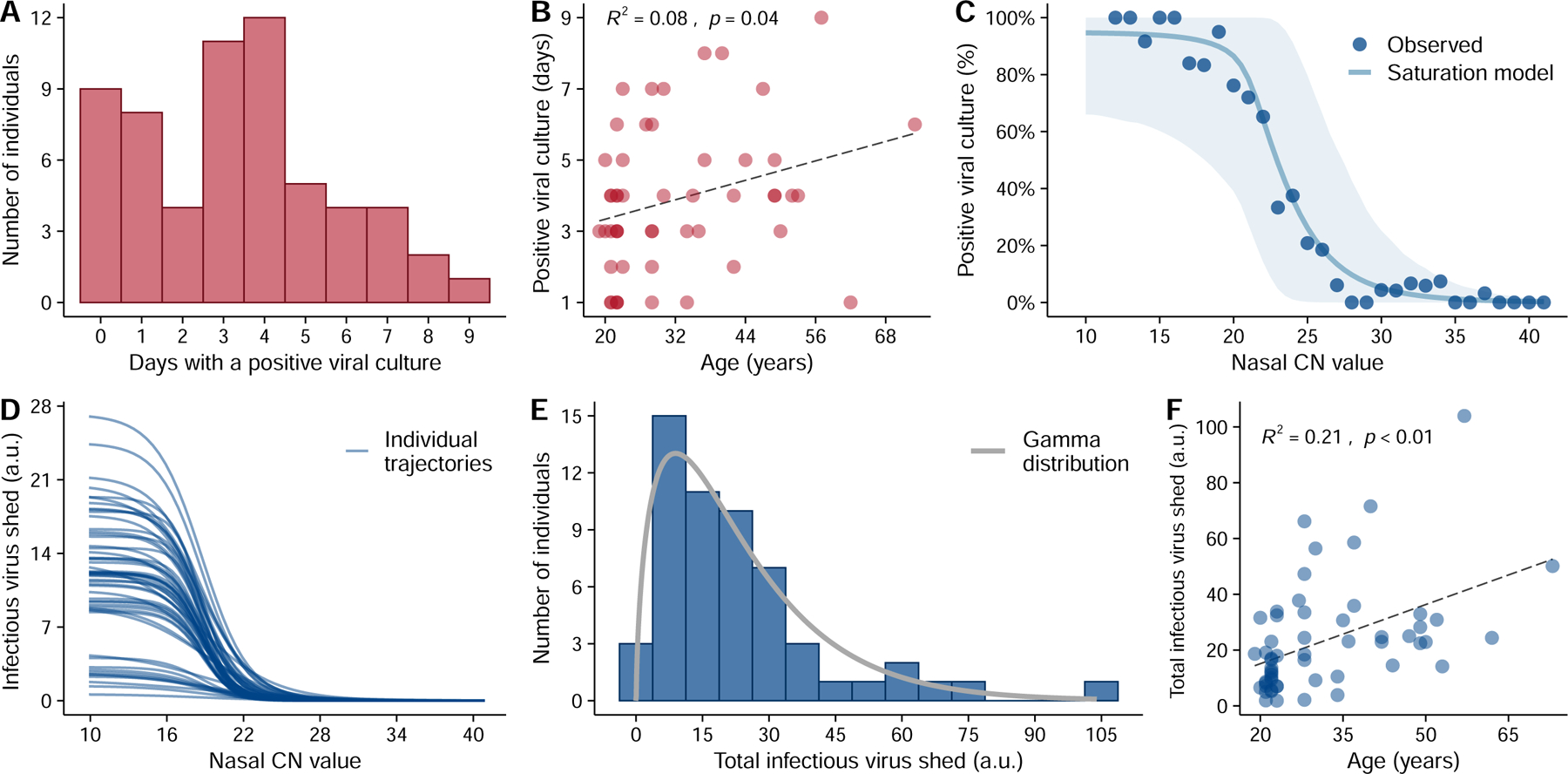
(A) The distribution in the numbers of days in which participants tested positive by viral culture on nasal swabs following study enrollment. (B) Association between age of study participants and the number of days of positive viral culture using a standard linear regression analysis. The R-squared value and the p-value are reported. (C) Relationship between the CN value in nasal samples and the probability of the sample being viral culture positive, summarized across all individuals. Individual samples were binned based on their CN values. Dots indicate the observed percentage of positive samples within a bin that were viral culture positive. The solid line and the shaded area are the mean and the 90% confidence intervals, respectively, of the trajectories generated using the best-fit parameters of the saturation model (see extended data Fig 7 for individual fits). (D) The relationship between infectious virus shed (in arbitrary units or a.u.) and CN values by the saturation model for 56 individuals in our analysis. (E) Distribution of the estimated total cumulative level of infectious virus (in arbitrary units) shed from the nasal passage by each participant over the course of infection. Solid line shows the best-fit gamma distribution with a shape parameter of 1.6. (F) Association between age and the estimated total infectious virus (in arbitrary units) shed by each individual. The R² value and the p-value from a linear regression (dashed line) are shown in panels (B) and (F).

To better quantify the infectious potential of each individual, we first used the viral culture data as a measure for intrinsic infectiousness (infectiousness for short below) to characterize how infectiousness depends on the viral genome load. We fitted three alternative models as proposed before ²⁷ to the paired nasal RTqPCR and viral culture data collected from each individual using a non-linear mixed effect modeling approach (see Extended data Fig. 6 for a workflow and Supporting Text for more details). Comparing models using the AIC scores, we found that the relationship is best described by a saturation model where the infectious virus load is a Hill-type function of the viral genome load (Fig 3C, Extended data Fig 7, and Table S7). See Table S8 for the best-fit parameter values.

Using the best-fit model, we estimated the infectiousness of each individual over the course of infection (Extended data Fig 8). Note that the dataset only allows us to estimate a quantity that is a constant proportion of the infectious virus load (rather than its absolute value) across time and between individuals, thus we report the predicted values in arbitrary units (a.u.) as a relative measure of infectiousness. Our model predicts that infectious virus shedding increases sharply when nasal CN values fall below 22, and that the average amount of infectious virus shed is zero for CN values above 29 (Fig. 3D). Importantly, there exists a high level of heterogeneity in infectiousness across different individuals that is not fully explained by differences in viral genome load (Fig. 3D). For example, at nasal CN values around 13, infectious virus shedding reaches values higher than 20 a.u. in 3 individuals; while in 11 individuals it is below 4 a.u. This suggests that viral Ct/CN values are not precisely predictive of infectiousness.

We next estimated the total infectiousness of each individual by integrating the area under the infectious virus load curve over the course of infection. This approach again revealed a large degree of heterogeneity in individual-level infectiousness, with a more than 57-fold difference between the highest and lowest estimated infectiousness (104.0 and 1.8 a.u., respectively) (Fig 3E). We found that a Gamma distribution with a shape parameter of 1.6 describes the distribution of individual infectiousness well (Fig 3E). These data suggest that the previously reported heterogeneity in secondary transmission rates ^6,7 is likely to arise from a combination of heterogeneity in contact structure and heterogeneity in intrinsic infectiousness³⁴. This emphasizes the potential for a small subset of individuals that exhibit high intrinsic infectiousness to function as ‘superspreaders’ if they have frequent and/or high-risk contacts during the infectious period. Finally, we observed a significant correlation between age and total infectiousness (p<0.01; R² = 0.21, Fig 3F).

Analysis of B.1.1.7 (Alpha) viral dynamics

Finally, we asked whether infection with the B.1.1.7 (Alpha) variant of concern (VOC) was associated with any significant differences in viral dynamics that could potentially explain the enhanced transmissibility of this genotype ^35–37. Previous studies have suggested that B.1.1.7 infection may result in higher peak viral loads or prolonged shedding compared with previously circulating genotypes ^38–40. Within our cohort, 16 out of 60 individuals were infected with B.1.1.7.

Both the empirical data and our model analysis (Fig 4A, C) suggest that the overall viral genome shedding dynamics in both nasal and saliva samples are indistinguishable between B.1.1.7 and non-B.1.1.7 infections (none of the latter were VOC genotypes except for a single P.1 (Gamma) infection; see Table S9). Comparison of parameter estimates in nasal samples suggested a slightly slower growth rate and time to peak for B.1.1.7 versus non-B.1.1.7 (Fig 4B), however it is not clear whether this difference is biologically meaningful (Fig 4A). Most importantly, we estimate that there is no significant difference between B.1.1.7 and non-B.1.1.7 viruses in total infectiousness in the nasal compartment (Fig 4B). Previously, we have shown that the area under the logarithm of genome viral loads, denoted as AUC(log), may serve as a surrogate for infectiousness ²⁷. Here, we calculated AUC(log) from predicted viral load trajectories in the saliva compartment in each individual, and found no difference between B.1.1.7 and non-B.1.1.7 viruses (Fig 4D). These data indicate that other mechanisms not reflected in viral shedding dynamics drive the increased transmissibility of the B.1.1.7 (Alpha) variant.

Figure 4: Comparison of viral dynamics between B.1.1.7 and non-B.1.1.7 viruses.

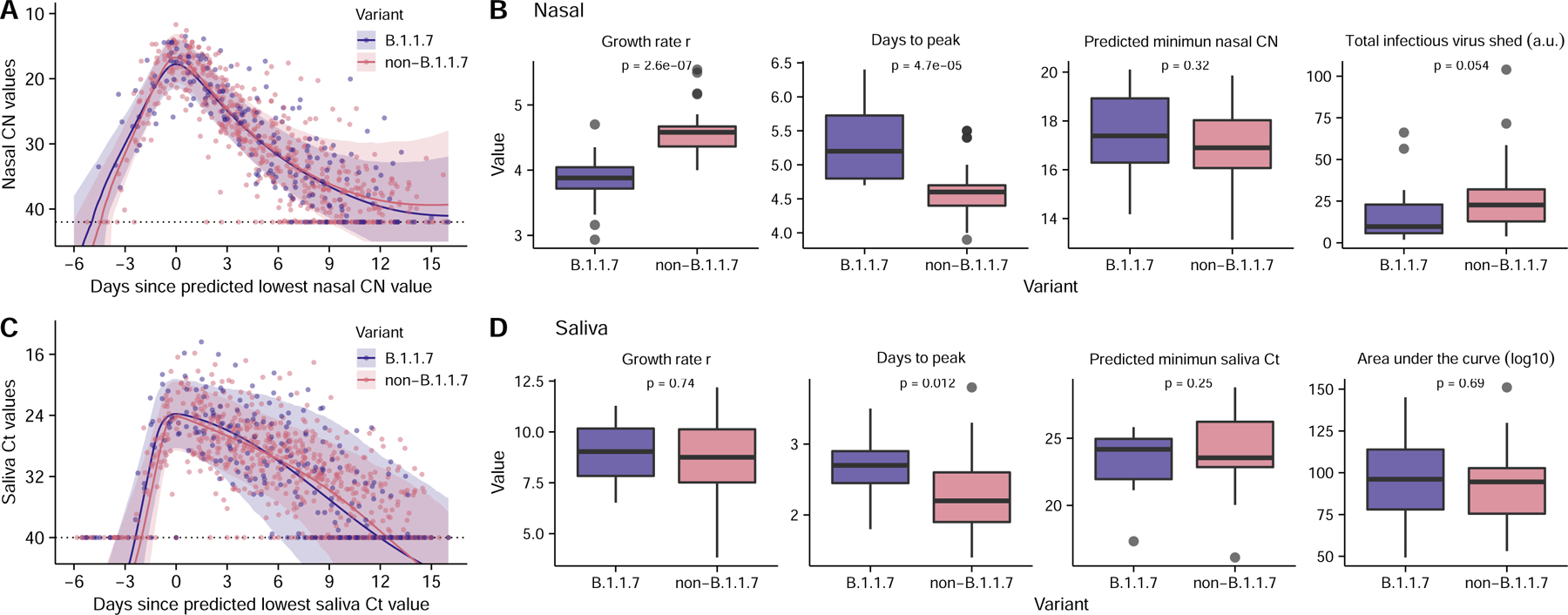
(A, C) Viral genome load of B.1.1.7 infections (purple) and non-B.1.1.7 infections (pink) over time in (A) nasal and (C) saliva samples, as measured by RTqPCR (Dots). Ribbons indicate 90% confidence intervals of predicted CN and Ct value trajectories respectively using population parameters estimated from modeling analysis (Table S4). (B, D) Comparison of estimated values for the indicated summary statistics of viral dynamics between individual B.1.1.7 and non-B.1.1.7 infections. (n=14 and 42 for B.1.1.7 and non-B.1.1.7 infections, respectively). The boxes of the boxplots start in the first quartile and ends in the third quartile of the data (e.g., interquartile range IQR), and the line inside the box represents the median. The whiskers represent 1.5 x the IQR, and the closed circles represent outliers. The p-values for the Wilcoxon rank-sum test are reported. Note that because age covaries with the total infectious virus shed (Fig. 3F), comparison of the total infectious virus shed after adjusting for age is shown in panel (B) (see Methods).

Discussion:

This study describes the results of daily multi-compartment sampling of viral dynamics within dozens of individuals newly infected with SARS-CoV-2 and provides a comprehensive, high-resolution description of viral shedding and clearance dynamics in humans.

Superspreading, in which a small subset of infected individuals are responsible for a disproportionately large share of transmission events, has been identified as a major driver of community spread of SARS-CoV-2, SARS-CoV, and many other acute viral pathogens ^6,7,9. Superspreading is believed to arise from heterogeneity in both (1) contact structure between individuals arising from behavioral and environmental factors, and (2) the intrinsic infectiousness of individuals ^9,34,41. While heterogeneity in contact structure has been studied extensively ^42–45, the extent of heterogeneity in infectiousness arising from individual-level viral dynamics remains unknown. Although several studies attempted to quantify this ^20,34, the lack of empirical measure of viral genome load and infectious virus shedding dynamics during early infection, i.e. a critical period for SARS-CoV-2 transmission, prevents precise estimation.

To address this question, we empirically quantified infectious virus shedding through daily longitudinal sampling of individuals infected with SARS-CoV-2. The substantial heterogeneity in infectious virus shedding that we observed among individuals indicates that superspreading is likely driven by individual-level variation in specific features of the infection process, in addition to behavioral and environmental factors. We also found that heterogeneity in infectious virus shedding was only partly explained by individual-level heterogeneity in viral genome load dynamics, suggesting that additional factors such as variation in the timing and magnitude of the neutralizing antibody response might contribute ⁴⁶. Our results here suggest caution in assessing the infectiousness of an individual using viral genome load data alone. Further, the absence of clear viral genetic correlates of infectiousness within this dataset suggests the existence of specific host determinants of superspreading potential. While we identified age as a significant correlate of infectiousness, additional determinants likely exist. Defining these correlates could aid future efforts to mitigate community spread of the virus by helping identify individuals with elevated risk of becoming superspreaders.

Our finding that viral shedding often peaks earlier in saliva versus the nasal compartment, sometimes by several days, corroborates a recent study of four individuals ⁴⁷ and has several important implications. First, saliva screening may be a more effective sample type than nasal swabs for detecting infected individuals prior to or early in the infectious period ⁴⁸. Early detection and isolation of infected individuals is absolutely critical for breaking transmission chains ¹⁵. Moreover, early viral shedding from the oral cavity may contribute to the high prevalence of pre-symptomatic SARS-CoV-2 transmission. We were unable to directly assess viral infectivity in saliva, so it remains unclear whether the earlier peaks in viral RNA shedding that we observed in saliva reflect earlier shedding of transmission-competent virus. The earlier detection of virus in saliva also raises questions about the initial site of SARS-CoV-2 infection. A recent study demonstrated that both salivary glands and oral mucosal epithelium can support SARS-CoV-2 replication, suggesting that infection could be initiated within the oral cavity ⁴⁹. Alternatively, if infection is initiated in the nasopharynx or soft palette, viral RNA might be detectable in saliva prior to detection in the mid-turbinate swabs used in this study. The discordance in shedding dynamics between oral and nasal samples that we observed in many participants is consistent with a significant degree of compartmentalization between these adjacent but distinct tissue sites, as has been observed in animal models of influenza virus infection ^50,51.

The specific mechanisms driving the enhanced transmissibility of the B.1.1.7 variant remain poorly understood. Recent studies have identified alterations in the structural conformation of the spike protein and enhanced antagonism of innate immunity by B.1.1.7 as potential contributors ^52,53. Contrary to previous clinical studies, we observed no significant differences in either peak viral loads or clearance kinetics between B.1.1.7 and non-B.1.1.7 viruses as measured in either nasal swabs or saliva. Our results are consistent with studies demonstrating the absence of a growth advantage for B.1.1.7 in primary human respiratory epithelial cells ^54,55. Similarly, a recent longitudinal study of RNA shedding observed no significant differences in mean peak viral RNA loads, clearance kinetics, or infection duration of the Alpha and Delta variants compared with non VOCs ³⁹. If the timing of symptom onset differs between B.1.1.7 and non-B.1.1.7 infections, it could potentially explain why cross-sectional analyses of viral loads might register lower Ct values for B.1.1.7 samples. These data suggest that the enhanced transmissibility of the B.1.1.7 variant may also be driven by features not reflected in shedding dynamics, e.g., enhanced environmental stability or a lower infectious dose threshold.

This study has several limitations that must be considered. First, our study cohort was limited to faculty, students, and staff of the University of Illinois at Urbana-Champaign and did not include anyone who was hospitalized for COVID-19. The limited demographic and clinical profile of this cohort means that our results may not reflect the dynamics that occur during severe and lethal infections and/or in populations not well represented in our study. Second, there are multiple potential sources of technical variation that could contribute to noise in our experimental measurements. These include variability in sample collection quality and the potential for sub-genomic viral RNA to be detected in our RTqPCR assays. While we took steps to minimize variation in sample collection quality, including having all sample collections remotely observed by trained study staff, it is possible that some of the sample-to-sample variation we observe is due to differences in sample quality. Finally, it must be noted that the results of viral culture assays performed on nasal swabs may not perfectly correlate with the actual transmission potential of an individual.

Altogether, our data provide a high-resolution view of the longitudinal viral dynamics of SARS-CoV-2 infection in humans and implicate individual-level heterogeneity in viral shedding as playing a critical role in community spread of this virus.

Methods:

This study was approved by the Western Institutional Review Board, and all participants provided informed consent.

Participants

All on-campus students and employees of the University of Illinois at Urbana-Champaign are required to submit saliva for RTqPCR testing every 2–4 days as part of the SHIELD campus surveillance testing program. Individuals testing positive were instructed to isolate and were eligible to enroll in this study for a period of 24 hours following receipt of their positive test result. Close contacts of individuals who test positive (particularly those co-housed with them) are instructed to quarantine and were eligible to enroll for up to 5 days after their last known exposure to an infected individual. All participants were also required to have received a negative saliva RTqPCR result 7 days prior to enrollment.

Individuals were recruited via either a link shared in an automated text message providing isolation information sent within 30 minutes of a positive test result, a call from a study recruiter, or a link shared by an enrolled study participant or included in information provided to all quarantining close contacts. In addition, signs were used at each testing location and a website was available to inform the community about the study.

Participants were required to be at least 18 years of age, have a valid university ID, speak English, have internet access, and live within 8 miles of the university campus. After enrollment and consent, participants completed an initial survey to collect information on demographics and health history and were provided with sample collection supplies. Participants who tested positive prior to enrollment or during quarantine were followed for up to 14 days. Quarantining participants who continued to test negative by saliva RTqPCR were followed for up to 7 days after their last exposure. All participants’ data and survey responses were collected in the Eureka digital study platform. All study participants were asked if they had previously tested positive for SARS-CoV-2 or vaccinated against SARS-CoV-2. All participants included in this cohort reported no prior SARS-CoV-2 infection and were unvaccinated at time of enrollment.

Sample collection

Each day, participants were remotely observed by trained study staff collecting:

1. 2 mL of saliva into a 50mL conical tube.

2. 1 nasal swab from a single nostril using a foam-tipped swab that was placed within a dry collection tube.

3. 1 nasal swab from the other nostril using a flocked swab that was subsequently placed in a collection vial containing 3mL of viral transport media (VTM). Swab and VTM manufacturer were same throughout study.

The order of nostrils (left vs. right) used for the two different swabs was randomized. For nasal swabs, participants were instructed to insert the soft tip of the swab at least 1 cm into the indicated nostril until they encountered mild resistance, rotate the swab around the nostril 5 times, leaving it in place for 10–15 seconds. After daily sample collection, participants completed a symptom survey. A courier collected all participant samples within 1 hour of collection using a no-contact pickup protocol designed to minimize courier exposure to infected participants.

Saliva RTqPCR

After collection, saliva samples were stored at room temperature and RTqPCR was run within 12 hours of initial collection in a CLIA-certified diagnostic laboratory. The protocol for the covidSHIELD direct saliva-to-RTqPCR assay used has been detailed previously ²⁴. In brief, saliva samples were heated at 95°C for 30 minutes, followed by the addition of 2X Tris/Borate/EDTA buffer (TBE) at a 1:1 ratio (final concentration 1X TBE) and Tween-20 to a final concentration of 0.5%. Samples were assayed using the Thermo Taqpath COVID-19 assay.

Antigen testing

Foam-tipped nasal swabs were placed in collection tubes, transported with cold packs, and stored at 4°C overnight based on guidance from the manufacturer. The morning after collection, swabs were run through the Sofia SARS antigen FIA on Sofia 2 devices according to the manufacturer’s protocol.

Nasal swab RTqPCR

Collection tubes containing VTM and flocked nasal swabs were stored at −80°C after collection and were subsequently shipped to Johns Hopkins University for RTqPCR and virus culture testing. After thawing, VTM was aliquoted for RTqPCR and infectivity assays. One ml of VTM from the nasal swab was assayed on the Abbott Alinity per manufacturer’s instructions in a College of American Pathologist and CLIA-certified laboratory.

Calibration curve for nasal swab RTqPCR assay

Calibration curve for Alinity assay was determined using digital droplet PCR (ddPCR) as previously described ⁵⁶. Nasal swab samples previously quantified using the Alinity assay were stored in a −80°C freezer between initial quantification and extraction for calibration curve. Samples were extracted simultaneously using the Perkin Elmer Chemagic 360 automated extraction platform with a sample input and eluate volumes of 300 uL and 60 uL respectively. RNA eluates were stored at −80°C. Digital droplet RT-PCR was performed following the BIO-RAD EUA assay package insert (https://www.fda.gov/media/137579/download). A master mix was prepared per sample using the reagents provided in the ddPCR Supermix for Probes kit as follows: 5.5 uL SuperMix (BIO-RAD), 2.2 uL reverse transcriptase (BIO-RAD), 1.1 uL dithiothreitol (BIO-RAD), 1.1 uL of CDC triplex SARS-CoV-2 primer and probe mix (IDT), and 7.1 uL of nuclease-free water. 17 uL of master mix was transferred to a 96-well PCR plate and combined with 5 uL of RNA in eluate. The plate was then loaded on to the QX-200 automated droplet generator (BIO-RAD). The droplet-containing plate was then heat-sealed with foil in a plate sealer (BIO-RAD) and placed on a C1000 Touch thermal cycler (BIO-RAD) to perform reverse-transcription and amplification. Droplet were read by the QX-200 droplet reader (BIO-RAD). Data were analyzed using the QuantaSoft Analysis Pro 1.0 software.

Virus culture from nasal swabs

Vero-TMPRSS2 cells were grown in complete medium (CM) consisting of DMEM with 10% fetal bovine serum (Gibco), 1 mM glutamine (Invitrogen), 1 mM sodium pyruvate (Invitrogen), 100 U/ml of penicillin (Invitrogen), and 100 μg/ml of streptomycin (Invitrogen) ⁵⁷. Viral infectivity was assessed on Vero-TMPRSS2 cells as previously described using infection media (IM; identical to CM except the FBS is reduced to 2.5%) ²⁶. When a cytopathic effect was visible in >50% of cells in a given well, the supernatant was harvested. The presence of SARS-CoV-2 was confirmed through RTqPCR as described previously by extracting RNA from the cell culture supernatant using the Qiagen viral RNA isolation kit and performing RTqPCR using the N1 (and N2 SARS-CoV-2-specific primers and probes in addition to primers and probes for human RNaseP gene (Using the CDC research use only 2019-Novel Coronavirus (2019-nCoV) Real-time RT-PCR primer and probes sequences) using synthetic RNA target sequences to establish a standard curve ⁵⁸.

Viral genome sequencing and analysis

Viral RNA was extracted from 140 uL of heat inactivated (30 minutes at 95°C, as part of protocol detailed in ²⁴) saliva samples using the QIAamp viral RNA mini kit (QIAGEN). 100ng of viral RNA was used to generate cDNA using the SuperScript IV first strand synthesis kit (Invitrogen). Viral cDNA was then used to generate sequencing libraries using the Swift SNAP Amplicon SARS CoV2 kit with additional coverage panel and unique dual indexing (Swift Biosciences) which were sequenced on an Illumina Novaseq SP lane. Data were run through the nf-core/viralrecon workflow (https://nf-co.re/viralrecon/1.1.0), using the Wuhan-Hu-1 reference genome (NCBI accession NC_045512.2). Swift v2 primer sequences were trimmed prior to variant analysis from iVar version 1.3.1 (https://genomebiology.biomedcentral.com/articles/10.1186/s13059-018-1618-7) retaining all calls with a minimum allele frequency of 0.01 and higher. Viral lineages were called using the Pangolin tool (https://github.com/cov-lineages/pangolin) version 2.4.2, pango version 1.2.6, and the 5/19/21 version of the pangoLEARN model; based on the nomenclature system described in ⁵⁹.

Statistics & Reproducibility

Details of statistical analysis methods are below. No statistical method was used to predetermine sample size. For some analyses, a small number of individuals were excluded for reasons detailed in the results section where relevant. The experiments were not randomized and the investigators were not blinded to allocation during experiments and outcome assessment.

Statistical analyses

The difference in the distribution of a parameter of interest between the non-B.1.1.7 infection group and the B.1.1.7 infection group is assessed using a univariate analysis and the p-value is calculated using the Wilcoxon rank-sum test. The comparison of infectious virus shedding between the non-B.1.1.7 infection group and the B.1.1.7 infection group is performed using a multivariate analysis with age as an additional variate. The predicted levels of infectious viral shedding after adjusting for age by assuming age is at 28, i.e. the median age of the cohort, are shown in Fig. 4C.

Figure generation

All figures except for 2A were generated using r studio. Figure 2A was generated using Microsoft Powerpoint.

Overview of model construction and parameter estimation

The goal of the quantitative analyses is to use mathematical models to characterize viral shedding dynamics based on both viral genome loads (as measured by RTqPCR) and the presence or absence of infectious virus (as measured by viral culture assay). Analyzing the model results, we quantify the individual-level heterogeneity in both viral genome shedding dynamics and individual infectiousness. See Extended data Fig 6 for an overview of the analysis workflow.

First, we performed experiments to derive the calibration curves for transforming the Ct/CN values from RTqPCR to viral genome loads (“Viral genome load calibration from Ct/CN values” section below). Note that due to the nature of the RTqPCR assays and the noise in sampling, the viral genome loads derived using the calibration curves represent a proxy for the actual quantities. Nonetheless, this approach is the best approach available to derive viral genome loads for the purpose of viral dynamic modeling and is widely used in understanding SARS-CoV-2 dynamics^21,60.

Second, we constructed viral dynamic models and fit these models to viral genome loads (“Viral dynamics models” section below). We estimated key parameters governing infection processes in the nasal and the saliva-associated compartments, such as the viral exponential growth rate before peak viral genome load and the viral clearance rate. This allows us to characterize the individual level heterogeneity in infection kinetics.

Third, we constructed mathematical models to describe how the amount of infectious virus shed relates to changes in the viral genome load, as measured by RTqPCR (“Modeling infectiousness of an individual” section below). We fit the models to viral culture assay data. Using the best model and the predicted viral genome load kinetics from the viral dynamic model, we predicted the extent of infectious virus shedding, i.e. the infectiousness, for each individual, and thus quantified the individual-level heterogeneity in infectiousness.

Viral genome load calibration from Ct/CN values

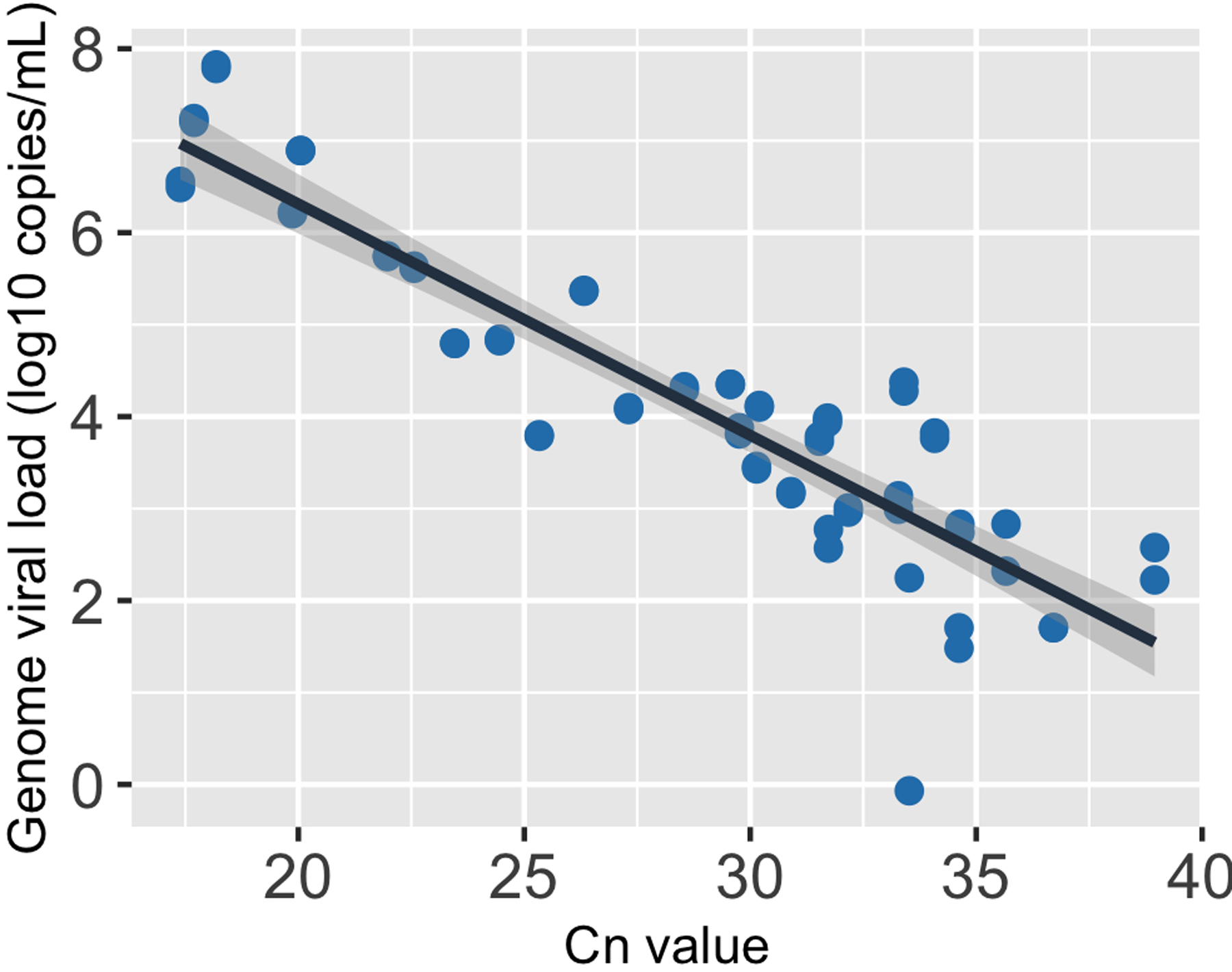
Viral genome load calibration – nasal samples

To calculate viral genome loads from CN values reported for the nasal samples, we performed calibration curve experiments to empirically define the relationship between CN values obtained from the RTqPCR assay used on nasal swab samples, and absolute viral genome loads within samples, as quantified by digital droplet PCR. We quantified viral genome loads for 62 nasal samples with CN values ranging between 17 and 38. For each sample, absolute copy numbers of viral genomes were measured using two different N-gene-specific primer sets (N1 and N2). To account for technical noise between samples, we also determined the concentration of the host RNAse P (RP) transcript as a control (see Table S10). We then normalized the copy numbers of N1 and N2 targets by dividing by their corresponding RP target numbers, and then multiplied the mean of the RP concentration across all samples. Note that the unit of these measurement is /mL. This is because nasal swab samples were each collected in 3mL of viral transport media (VTM).

Plotting the logarithm of the normalized viral genome loads against the associated CN values shows a clear linear relationship, justifying the use of a linear regression below. Linear regression lines with similar coefficients were used as calibration curves in other studies^21,60. We also note that the noise in genome viral loads is high when CN values are high (e.g. >33), likely a reflection of increased noise when signal is low²⁶. However, this high level of variation at high CN values will not impact on the conclusion of our study, because the range of viral loads relevant to transmission is much higher (>10⁶ copies/mL; see Fig 3D in the main text).

We then performed a linear regression on the measured CN values and the log₁₀ viral genome loads (Extended data Fig 9). This leads to the following formula for the relationship between CN values and viral genome load:

$${\log }_{10}V=11.35-0.25CN$$

where V and $CN$ denote the viral genome load and the CN value, respectively. Note that, because of the high number of data points we measured, the level of uncertainty in the regression line is minimal (Extended data Fig 9).

Viral genome load calibration – saliva samples

Unlike the nasal samples, we were not able to measure the calibration curve using saliva samples taken from participants. To quantify the efficiency of the RTqPCR assay used on saliva samples, we used data from calibration experiments in which saliva samples obtained from healthy donors were spiked with SARS-CoV-2 genomic RNA. More specifically, 0.9 mL of saliva from a healthy donor were spiked with 0.1mL of 1.8×10^8, 5.4×10^5 or 6.0×10^4 RNA copies/mL. For samples spiked with 1.8×10^8 RNA copies/mL, 10-fold serial dilutions were performed until the final concentration was 1.8×10^4 RNA copies/mL. A total of 24 samples were collected and Ct values of the N gene were then measured (Table S11).

As above, we plotted the logarithm of the viral loads against the Ct values (Extended data Fig 10). The plot shows a clear linear relationship, justifying the use of a linear regression below. We then performed a linear regression on the measured CN values and the log₁₀ viral genome loads (Extended data Fig 10). This leads to the following formular for the relationship between CN values and viral genome load:

$${\log }_{10}V=14.24-0.28Ct$$

where $V$ and $Ct$ denote the viral genome load and the Ct value, respectively. As for the nasal calibration curve, the level of uncertainties in the regression line is minimal (Extended data Fig 10).

Note that a major difference between samples spiked with viral genomes with samples taken from infected individuals is that the latter is likely to be noisier because of variation in the sample collection process. However, the two approaches should not differ substantially in assessing the efficiency of the RT-PCR protocol. The impact of the noise in the nasal sample can be minimized by taking a large number of samples over a wide range of CN values, as we have done for the nasal samples. Therefore, the calibration curves we derived above represent an accurate translation of Ct/CN values to viral load.

Viral dynamic models

We constructed viral dynamic models to describe the dynamic changes in viral genome load. The viral genome load patterns in nasal and saliva samples are distinct from each other in many individuals, suggesting compartmentalization of infection dynamics in these two sample sites. Therefore, we use the models below to describe data collected from these two compartments separately. See Fig 2A and Extended data Fig 4 for schematics of these models.

The target cell limited (TCL) model

We first constructed a within-host model based on the target cell limited (TCL) model used for other respiratory viruses, such as influenza⁶¹ and recently SARS-CoV-2^27,29,62. We keep track of the total numbers of target cells (T), cells in the eclipse phase of infection (E), i.e. infected cells not yet producing virus, productively infected cells (I) and viruses (V). The ordinary differential equations are:

$$\begin{gathered} \frac{dT}{dt}=-\beta VT \\ \frac{dE}{dt}=\beta VT-kE \\ \frac{dI}{dt}=kE-\delta I \\ \frac{dV}{dt}=\pi I-cV \end{gathered}$$ [S1]

In this model, target cells are infected by virus with rate constant $\beta$. Cells in the eclipse phase become productively infected cells at per capita rate $k$. Productively infected cells die at per capita rate $\delta$. We use V to describe viruses measured in nasal or saliva samples and it is a proportion of the total virus in the compartment under consideration. Therefore, the rate $\pi$ is the product of the viral production rate per infected cell and the proportion of virus that is sampled. See Ke et al.²⁷ for a detailed derivation. Viruses are cleared at per capita rate c.

Refractory cell model

We extend the TCL model by including an early innate response, i.e. the type-I/III interferon response, where interferons are secreted from infected cells and bind to receptors on uninfected target cells, stimulating an antiviral response that renders them refractory to viral infection. Note that this is the best model to describe the viral genome load dynamics as measured by RTqPCR from nasal samples.

We keep track of interferon (F) and cells refractory to infection (R), in addition to other quantities in the TCL model. The full ODEs for target cells, refractory cells and interferon are

$$\begin{gathered} \frac{dT}{dt}=-\beta VT-\varphi FT+\rho R \\ \frac{dR}{dt}=\varphi FT-\rho R \\ \frac{dE}{dt}=\beta VT-kE \\ \frac{dI}{dt}=kE-\delta I \\ \frac{dV}{dt}=\pi I-cV \\ \frac{dF}{dt}=sI-\mu F \end{gathered}$$ [S2]

In this model, the impact of the innate immune response is to convert target cells into refractory cells at rate $\varphi FT$, where $\varphi$ is a rate constant. Refractory cells can become target cells again at rate $\rho$. Interferon is produced and cleared at rates $s$ and $\mu$, respectively.

For simplicity and due to a lack of empirical data on interferon responses in our study, we simplify the model by making the quasi-steady-state assumption that the interferon dynamics are much faster than the dynamics of infected cells and assume that $\frac{dF}{dt}=0$. Thus $sI=\mu F$ or $F=\frac{s}{\mu }I$.

Let $\Phi =\varphi \frac{s}{\mu }$, so that the ODEs for the innate immunity model become:

$$\begin{gathered} \frac{dT}{dt}=-\beta VT-\Phi IT+\rho R \\ \frac{dR}{dt}=\Phi IT-\rho R \\ \frac{dE}{dt}=\beta VT-kE \\ \frac{dI}{dt}=kE-\delta I \\ \frac{dV}{dt}=\pi I-cV \end{gathered}$$ [S3]

Viral production reduction model

In addition to making target cells refractory to infection, the impact of interferons may include reducing virus production from infected cells. We include this action of interferons in the viral production reduction model. As above, we make the quasi-steady-state assumption that the interferon dynamics are much faster than the dynamics of infected cells and assume that $F$ is proportional to $I$. The ODEs for the model are:

$$\begin{gathered} \frac{dT}{dt}=-\beta VT \\ \frac{dE}{dt}=\beta VT-kE \\ \frac{dI}{dt}=kE-\delta I \\ \frac{dV}{dt}=\frac{\pi }{1+\gamma I}I-cV \end{gathered}$$ [S4]

where $\gamma$ is a constant representing the effect of interferon in reducing viral production.

Immune effector cell model

Over the course of infection, immune effector cells are activated and recruited to kill infected cells. These immune effector cells include innate immune cells such as macrophages and natural killer cells, as well as cells developed during the adaptive immune response, such as cytotoxic T lymphocytes and antibody-secreting B cells. To consider the impact of these immune effector cells, we develop a model, i.e. the effector cell model, based on a previous model for influenza infection²⁸. In this model, we assume that the death rate of infected cells is ${\delta }_1$ at the beginning of the infection. This may reflect the cytotoxic effects of viral infection. After time $t_1$, the death rate of infected cells increases by ${\delta }_2$, where ${\delta }_2$ models the killing of infected cells by immune effector cells. The ODEs for the model are:

$$\begin{gathered} \frac{dT}{dt}=-\beta VT \\ \frac{dE}{dt}=\beta VT-kE \\ \frac{dI}{dt}=kE-\delta \left(t\right)I \\ \frac{dV}{dt}=\pi I-cV \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\delta \left(t\right)=\left\{\begin{array}{cc}{\delta }_1& t<t_1\\ {\delta }_1+{\delta }_2& t\ge t_1\end{array}\right. \end{gathered}$$ [S5]

Note that this is the best model to describe the viral genome load dynamics as measured by RTqPCR from saliva samples.

Combined model

In the full model, we combine the refractory cell model and the immune effector cell model to consider both the immediate interferon response and the immune effector response. The ODEs for the model are:

$$\begin{gathered} \frac{dT}{dt}=-\beta VT-\Phi IT+\rho R \\ \frac{dR}{dt}=\Phi IT-\rho R \\ \frac{dE}{dt}=\beta VT-kE \\ \frac{dI}{dt}=kE-\delta \left(t\right)I \\ \frac{dV}{dt}=\pi I-cV \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\delta \left(t\right)=\left\{\begin{array}{cc}{\delta }_1& t<t_1\\ {\delta }_1+{\delta }_2& t\ge t_1\end{array}\right. \end{gathered}$$ [S6]

Choice parameter values:

Total target cell numbers $\left(T_0\right)$

We calculate the total numbers of target cells in the nasal and saliva compartments by multiplying the total number of epithelial cells in these two compartments by the fraction of epithelial cells expected to be targets for SARS-CoV-2 infection.

For the total number of epithelial cells in the nasal compartment, we use the estimate from Baccam et al., i.e. 4×10⁸ cells⁶¹. This is calculated from the estimate that the surface area of nasal turbinates is 160 cm^{2 63}, and the surface area per epithelial cell is 2 × 10⁻¹¹ to 4 × 10⁻¹¹ m²/cell⁶¹. For the saliva compartment, the total surface area of the mouth was estimated to be 214.7 cm^{2 64}. Therefore, we estimate that the total number of epithelial cells in the mouth is approximately 4×10⁸×214.7/160=5.4×10⁸ cells.

Hou et al. estimated that the fraction of cells that express angiotensin-converting enzyme 2 (ACE2), i.e. the receptor for SARS-CoV-2 entry, on cell surface is approximately 20% in the upper respiratory tract (URT)⁶⁵. Therefore, in our model, the initial numbers of target cells are calculated as 4×10⁸×20%=8×10⁷ cells and 5.4×10⁸×20%=1.08×10⁸ cells, in the nasal and the saliva compartment, respectively.

Note that these estimates are approximations using available best-estimates in the literature. For a standard viral dynamics model, the number of initial target cells and the virus production rate are unidentifiable and only their product is identifiable⁶⁶. Thus, if the actual number of target cells differs from what we estimated here, an increase in the initial number of target cells will lead to corresponding decrease in the estimate of the virus production rate, and vice versa.

The initial number of infected cells (E₀)

We assume that one cell in the compartment of interest is infected at the start of infection, $E_0=1$ cell, consistent with Refs. ²⁷ and ⁶⁷. The small number of infected cells is also consistent with a recent work that estimated from sequencing data that the transmission bottleneck is small for SARS-CoV-2 and there are likely 1–3 infected cells at the initiation of infection^68–70. Note that, in an earlier work, we showed that changes in the number of initially infected cells between 1–5 in the model do not substaintially change the inference results²⁷.

The initial viral growth rate, r

For all the models above, the initial growth of the viral population before peak viral genome load is dominated by viral infection. This means that the immune responses considered in our models act to change the viral growth trajectory substantially only at later time points⁷¹. Thus, we derive an approximation to the initial viral growth rate using the TCL model only (Eqn. S1). This approximation also represents a good approximation for other models.

We first make two simplifying assumptions commonly used in analyzing initial dynamics of the viral dynamic models^72,73. First, because at the initial stage of infection, the number of infected cells is orders of magnitude lower than the number of target cells, we assume that the number of target cells is at a constant level, T₀. Second, the dynamics of viruses are much quicker than the dynamics of infected cells. For example, the rate of viral clearance is in the time scale of minutes and hours, whereas the death of productively infected cells is in days. Therefore, we make the quasi-steady state assumption, $\frac{dV}{dt}\approx 0$, such that the concentrations of viruses are always in proportion to the concentration of productively infected cells, i.e.$\pi I\approx cV$. This gives $V\approx \frac{\pi }{c}I$.

With these two assumptions, Eqn. S1 becomes a system of linear ODEs with 2 variables, $E$ and $I$:

$$\begin{gathered} \frac{dE}{dt}=\beta \frac{\pi }{c}I{T}_0-kE \\ \frac{dI}{dt}=kE-\delta I \end{gathered}$$ [S7]

The Jacobian matrix, $J$, for this system of ODEs is:

$$J=\left[\begin{array}{cc}-k& \beta \frac{\pi }{c}{T}_0\\ k& -\delta \end{array}\right]$$

The initial growth rate r is the leading eigenvalue of the Jacobian matrix of the ODE system. We calculate the eigenvalues, $\lambda$, for the Jacobian matrix above from $\left|J-\lambda \text{I}\right|=0$, where $\text{I}$ is the identity matrix, and get:

$\lambda =\frac{1}{2}\left[-\left(k+\delta \right)\pm \sqrt{{\left(k+\delta \right)}^2+4k\delta \left(R_0-1\right)}\right]$, where $R_0=\frac{\beta \pi }{\delta c}{T}_0$.

Then, the leading eigenvalue, i.e. the initial growth rate r, is:

$$r=\frac{1}{2}\left[-\left(k+\delta \right)+\sqrt{{\left(k+\delta \right)}^2+4k\delta \left(R_0-1\right)}\right]$$ [S8]

Model fitting strategy

Fitting viral dynamic models to the viral genome load data

We took a non-linear mixed effect modeling approach to fit the viral dynamic models to viral genome load data from all individuals simultaneously. All estimations were performed using Monolix (Monolix Suite 2019R2, Antony, France: Lixoft SAS, 2019. lixoft.com/products/monolix/). We allowed random effects on the fitted parameters (unless specified otherwise). All population parameters except for the starting time of simulation, t₀, are positive and therefore, we assume that they follow log-normal distributions. For t₀, we assume a normal distribution because t₀ can be positive or negative.

The parameters $\beta$ and $\pi$ in the viral dynamic models strongly correlate with each other when the models are fitted to viral genome load data⁶⁶. We tested three choices in handling this correlation in fitting all 5 viral dynamic models: 1) a correlation is assumed between parameter $\beta$ and $\pi$ in Monolix, 2) parameter $\beta$ has fixed effect only (i.e. its value is set to be the same across all individuals), and 3) parameter $\pi$ has fixed effect only.

To test if the age of the individuals and/or the infecting viral genotype (categorized as either non-B.1.1.7 or B.1.1.7) explains the heterogenous patterns in the viral genome load trajectories across the cohort, we tested whether they covary with any of the fitted parameters in the model by setting the two variables as a continuous and a categorical covariate, respectively, in Monolix.

The assumptions on parameters $\beta$ and $\pi$ and the choice of parameters that covariate with age or viral strain of infection led to a large number of model choices for fitting. Therefore, we took the following strategy to ensure that we identified the best model and parameter combinations to describe the data:

• First, we tested the three assumptions about parameters $\beta$ and $\pi$ in the five viral dynamic models without any covariate and selected the best assumption for further analysis based on their AICc scores.

• Second, using the best assumption, we tested the model by including the age of the individuals as a continuous covariate of all fitted parameter values with a random effect first. We then took an iterative approach to test whether if the covariate should be removed from any of the parameters in the model using the Pearson’s correlation test in Monolix. The parameter(s) that has a non-significant p-value (p-value>0.05) or with the lowest p-value is removed from next round of parameter fitting. We iterated the process until all parameters were removed.

• Then, the best model variant with the lowest AICc score was selected for analysis on whether parameter estimates differed in individuals infected by different viral strains. As before, we take an iterative approach. We first set the viral strain, i.e. non-B.1.1.7 or B.1.1.7 as a categorical covariate of all fitted parameter values with a random effect in the model. We then tested whether the covariate should be removed from any of the parameters in the model using the Analysis of Variance (ANOVA) in Monolix. The parameter(s) that has a non-significant p-value (p-value>0.05) or with the lowest p-value is removed from next round of parameter fitting. We iterated the process until all parameters were removed.

• Finally, the model variant with the lowest AICc score was selected as the best model.

Predicting viral genome load trajectories for non-B.1.1.7 and B.1.1.7 strains

We randomly sampled 5000 sets of parameter combinations from the distribution specified by the best-fit population parameters (Table S4). For the effector cell model for the saliva compartment, $\beta$ and $\pi$ are strongly correlated. We thus applied formulations such that the correlations between the two parameter values are preserved in the random sampling in accordance with the estimated correlation coefficient. We simulated the best-fit model using the 5000 sets of parameter combinations for each of the strain. The median and the 5^th and 95^th quantile of viral genome loads at each time points are reported.

Modeling infectiousness of an individual

We model how infectiousness depends on the viral genome load in an individual similar to the framework proposed in Ke et al.²⁷. Specifically, we first use the viral culture data collected in this study to infer how the level of infectious virus shed relates to viral genome loads as measured by RTqPCR. From this model, we predict how the level of infectious virus shedding changes over time in each individual and how the overall infectiousness of the infection varies among the participants.

Relationship between viral genome load and infectious viruses

We first consider three alternative models describing how the amount of infectious virus in a sample is related to viral genome load (derived from the CN values): the ‘linear’ model, ‘power-law’ model and the ‘saturation’ model. In these models, due to the nature of stochasticity in sampling, we assume the number of infectious viruses that was in the sample for cell culture experiment to be a random variable, Y, that follows a Poisson distribution, and $V_{inf}$ represents the expected number of infectious viruses, i.e.$V_{inf}=E\left(Y\right)$.

1. The linear model

   We assume that $V_{inf}$, is proportional to the viral genome load, V, in the sample:

   $$V_{inf}=E\left(Y\right)=AV$$ [S9]

   where A is a constant.

2. The power-law model

   We assume that $V_{inf}$, is related to the viral genome load, V, by a power function:

   $$V_{inf}=E\left(Y\right)=B{V}^h$$ [S10]

   where B and h are constants.

3. 3. The saturation model

   We assume that $V_{inf}$, is related to the viral genome load, V, by a Hill function

   $$V_{inf}=E\left(Y\right)=V_m\frac{V^h}{V^h+K_m^h}$$ [S11]

   where $V_m$ and $K_m$ are constants and h is the Hill-coefficient.

Probability of cell culture being positive

If each infectious virus has a probability $\varrho$ to establish infection such that the cell culture becomes positive, the number of viruses that successfully establish an infection in cell culture is Poisson distributed with parameter $\lambda =E\left(Y\right)\varrho =V_{inf}\varrho$. Thus, the probability of one or more viruses successfully infecting the culture so that it tests positive is

$$p_{positive}=1-\exp \left(-\lambda \right)=1-\exp \left(-V_{inf}\varrho \right)$$ [S12]

Substituting the expressions of $V_{inf}$ from the three models above, we get the following expressions for $p_{positive}$ from the three models (note that we use the subscripts ‘1’, ‘2’ and ‘3’ to denote the three models for $V_{inf}$):

$$p_{positive,1}=1-\exp \left(-V_{inf}\varrho \right)=1-\exp \left(-DV\right)$$ [S13]

where $D=A\varrho$.

$$p_{positive,2}=1-\exp \left(-V_{inf}\varrho \right)=1-\exp \left(-G{V}^h\right)$$ [S14]

where $G=B\varrho$.

$$p_{positive,3}=1-\exp \left(-V_{inf}\varrho \right)=1-\exp \left(-J\frac{V^h}{V^h+K_m^h}\right)$$ [S15]

where $J=V_m\varrho$.

Note that from the expressions above, it becomes clear that we will not be able to estimate parameters A, B and $V_m$ in the three models, because they appear as products with the unknown parameter $\varrho$ in the equations. This means that the viral culture data does not allow us to estimate the absolute number of infectious viruses in a sample or given a viral genome load; instead, we are able to estimate a quantity that is a constant proportion of the actual number of infectious viruses over time and across individuals. Therefore, we report estimations of infectious viruses in an arbitrary unit (a.u.). These estimates represent relative measure of infectiousness. Two estimates measured at different time points and/or from different individuals can be compared with each other using this method.

Model fitting using a population effect modeling approach

For each sample, the viral genome load and the cell culture positivity were measured. Using this data, we estimate parameter values in the three models by minimizing the negative log-likelihood of the data.

More specifically, the likelihood of the m^th observation being positive or negative in cell culture is calculated as:

$$p_{i,m}=\left\{\begin{array}{cc}{p}_{positive,i}\left(V_m\right),& if\hspace{0.33em}the\hspace{0.33em}kth\hspace{0.33em}observation\hspace{0.33em}is\hspace{0.33em}positive\\ 1-p_{positive,i}\left(V_m\right),& if\hspace{0.33em}the\hspace{0.33em}kth\hspace{0.33em}observation\hspace{0.33em}is\hspace{0.33em}negative\end{array}\right.$$ [S16]

where $V_m$ is the viral genome load of the m^th observation.

Because we have the paired nasal RTqPCR and viral culture data for each individual, we fit the three mathematical models using a non-linear mixed effect modeling approach. Again, all estimations were performed using Monolix (lixoft.com/products/monolix/). We allowed random effects on the fitted parameters (unless specified otherwise). All population parameters with a random effect are assumed to follow log-normal distributions.

To find the best-model explaining the data, we tested models with different combination of parameters with either a random effect or without a random effect (Table S7). The model with the lowest AIC score is selected as the best model.

Note that for each of the three models, we tested a model variation where all parameters in the models have fixed effects only, i.e. a single set of parameters is used to explain viral culture data from every individual. In this case, there is no heterogeneity in parameter values across individuals. The resulting AIC scores are significantly worse than the best-fit model assuming random effects on parameters (see Table S7). This indicates that there is a substantial level of individual heterogeneity in the relationship between infectious viruses shedding and viral genome loads (as shown in Fig 3D).

Calculating confidence intervals of the cell-culture-positivity curve (in Fig 3C)

Similar as the procedures performed for predicting the confidence intervals of viral genome load trajectories, we randomly sampled 5000 sets of parameter combinations from the distribution specified by the best-fit population parameters of the best model, i.e. the saturation model assuming $K_m$ only has a fixed effect (Table S8). More specifically, we sampled parameters from a log-normal distribution for $J$ and $h$, with their means and standard deviations at the best-fit values. Using the parameter combinations, we generated curves of probability of cell-culture positivity at CN values ranging between 10 and 40. The median and the 5^th and 95^th quantile of viral genome loads at each CN values are reported.

Extended Data

Extended Data Fig. 1. Remainder of individual plots.

Plots of longitudinal assay results from study participants not shown in Figure 1A. Single asterisk next to the participant ID indicates B.1.1.7 variant infection, while double asterisks indicate P1 variant infection.

Extended Data Fig. 2. Individual-level symptom data.

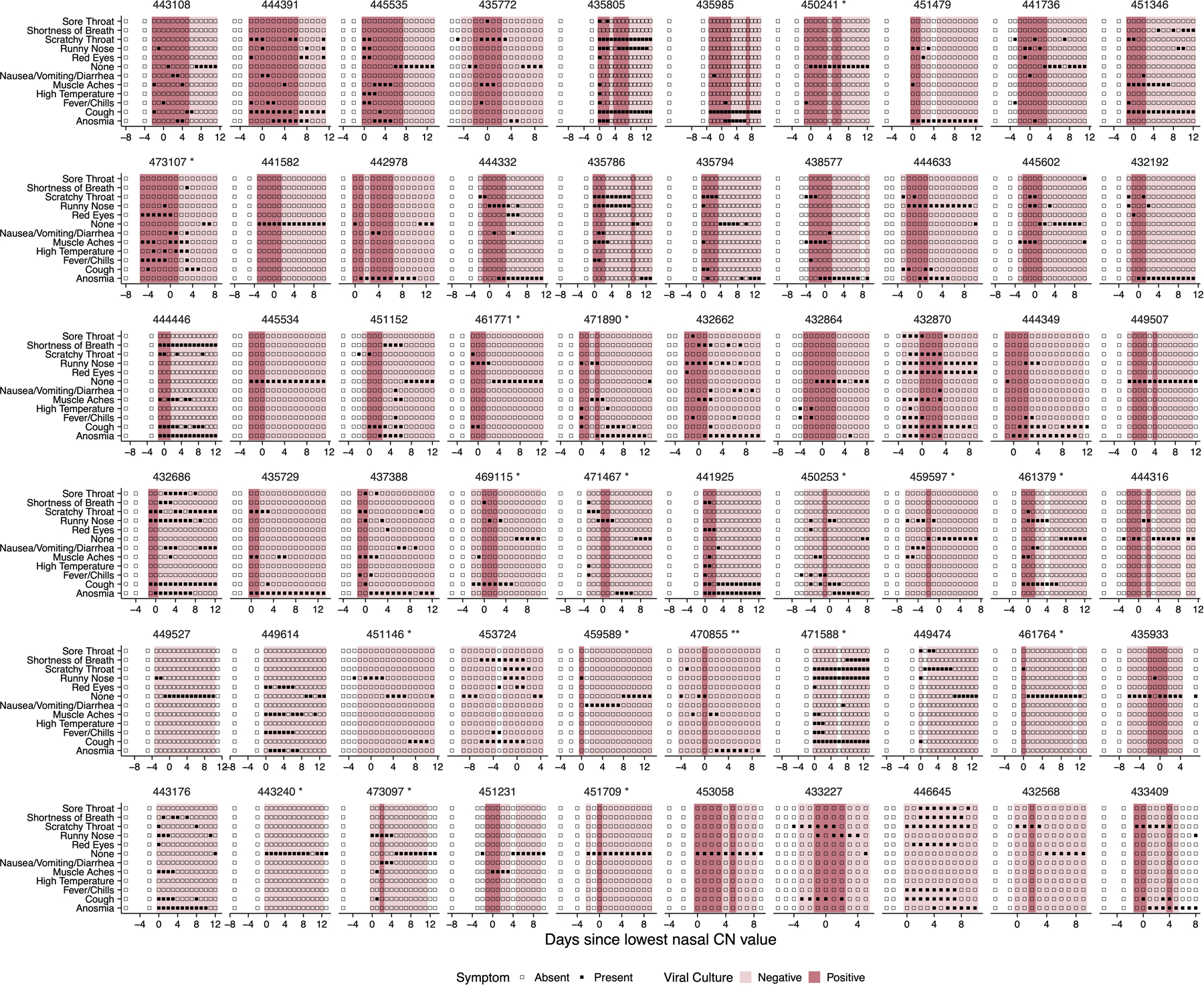
Self-reported symptom data from study participants, overlaid with viral culture status. Participants were asked to complete a survey through the Eureka digital study platform inquiring about the presence or absence of the indicated set of symptoms each day after sample collection.

Extended Data Fig. 3. Comparison of symptoms and viral culture status.

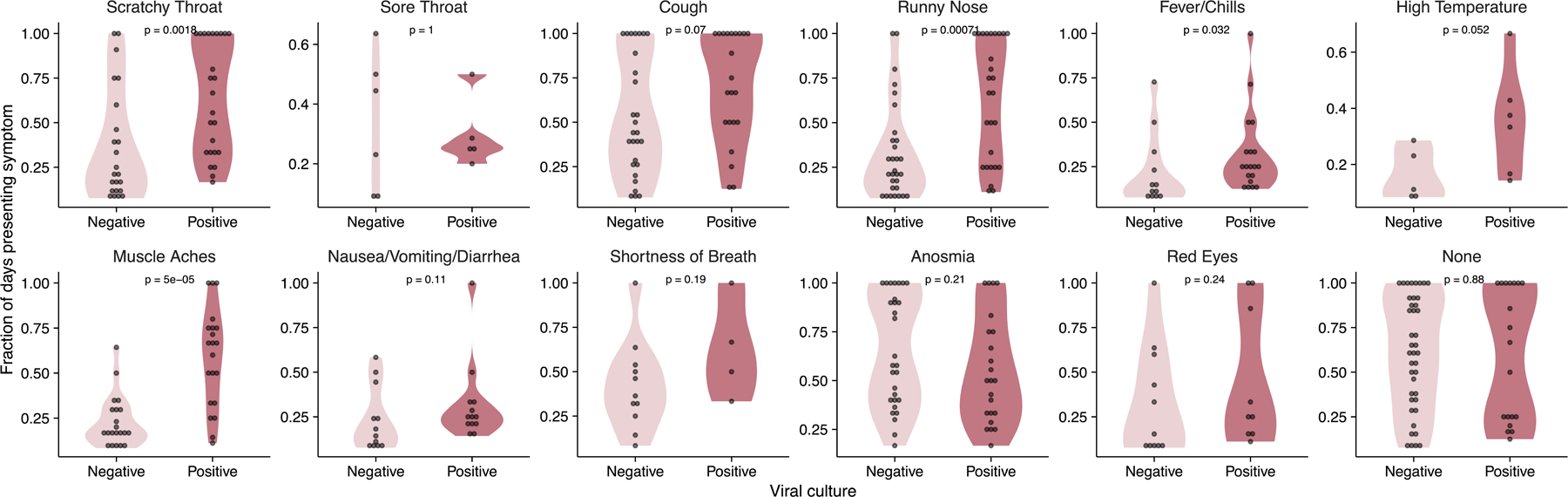
Plots show the proportions of either viral culture negative or viral culture positive days for which participants reported the indicated symptoms. The p-values for the Wilcoxon rank-sum test are reported. Data are only shown for individuals who reported the indicated symptom at least once.

Extended Data Fig. 4. Model structures.

Diagrams showing the structures of the additional three models (not shown in Figure 2A) considered for describing viral load data. See Supporting Text for descriptions of the models.

Extended Data Fig. 5. Model parameter estimates as a function of age.

Plots showing the relationship between age and the indicated model parameter estimates for (A) the refractory cell model (nasal data) and the (B) the immune effector cell model (saliva data). Linear regressions were performed on the data. R² values and p-values are shown.

Extended Data Fig. 6. Analysis workflow.

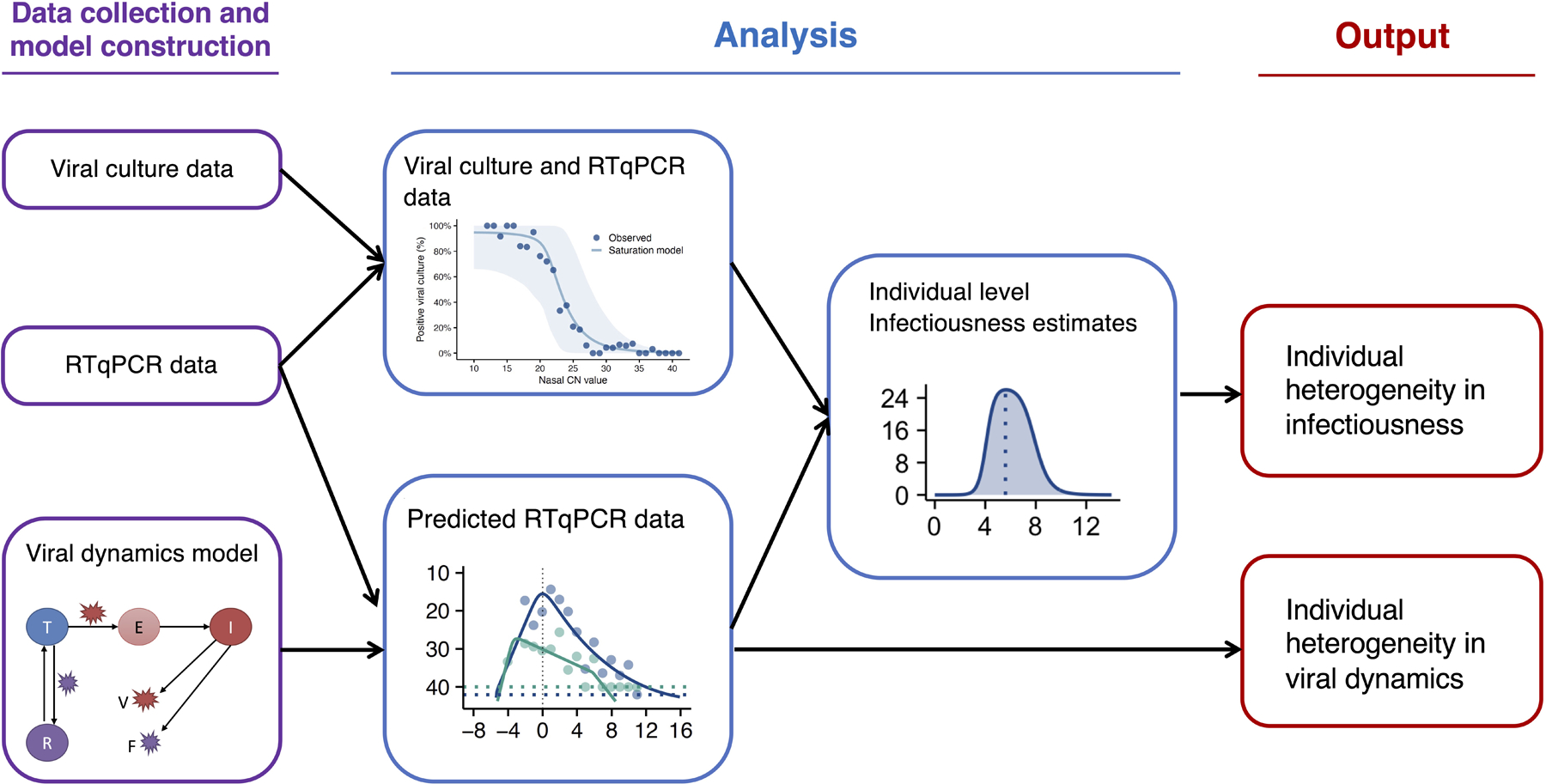
Diagram indicating how empirical RTqPCR and viral culture data were used to generate estimations of individual level viral dynamics and infectiousness.

Extended Data Fig. 7. The saturation model accurately predicts the cell culture positivity data.

Lines denote the predicted probability of cell culture being positive. Dots denotes cell culture positivity data, where a dot is at 1 or 0 when the cell culture is positive or negative, respectively.

Extended Data Fig. 8. Individual infectiousness plots.

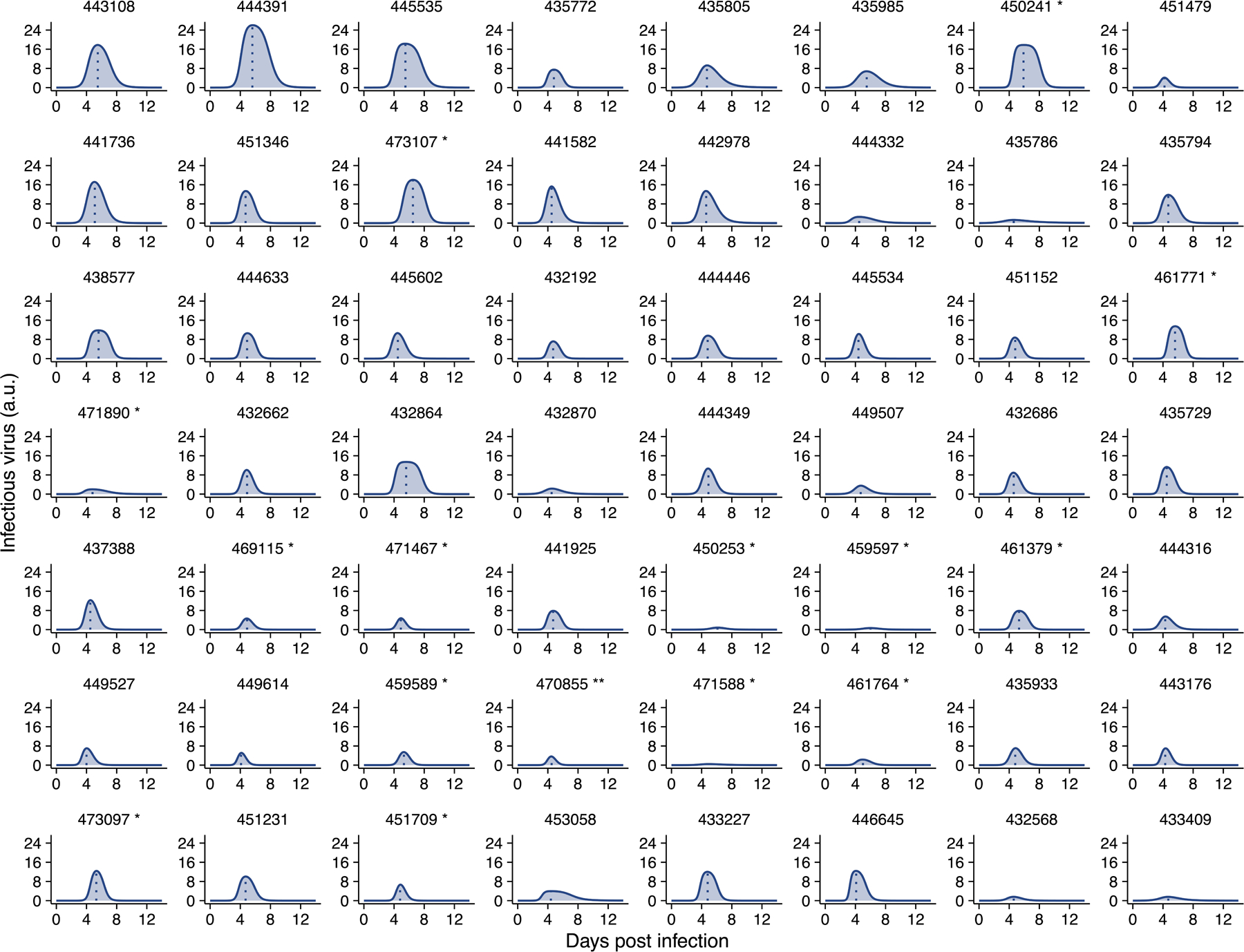
Estimated infectiousness over time plotted for individual study participants. Dashed lines indicate inferred peak in infectiousness.

Extended Data Fig. 9. The relationship between genome viral load (y-axis; on a log₁₀ scale) and CN value of the nasal samples.

The black line, i.e. the center of the error band, represents the linear regression calibration curve. The shading around the black line shows the standard error for the regression.

Extended Data Fig. 10. The relationship between genome viral load (y-axis; on a log₁₀ scale) and Ct value of the saliva samples.

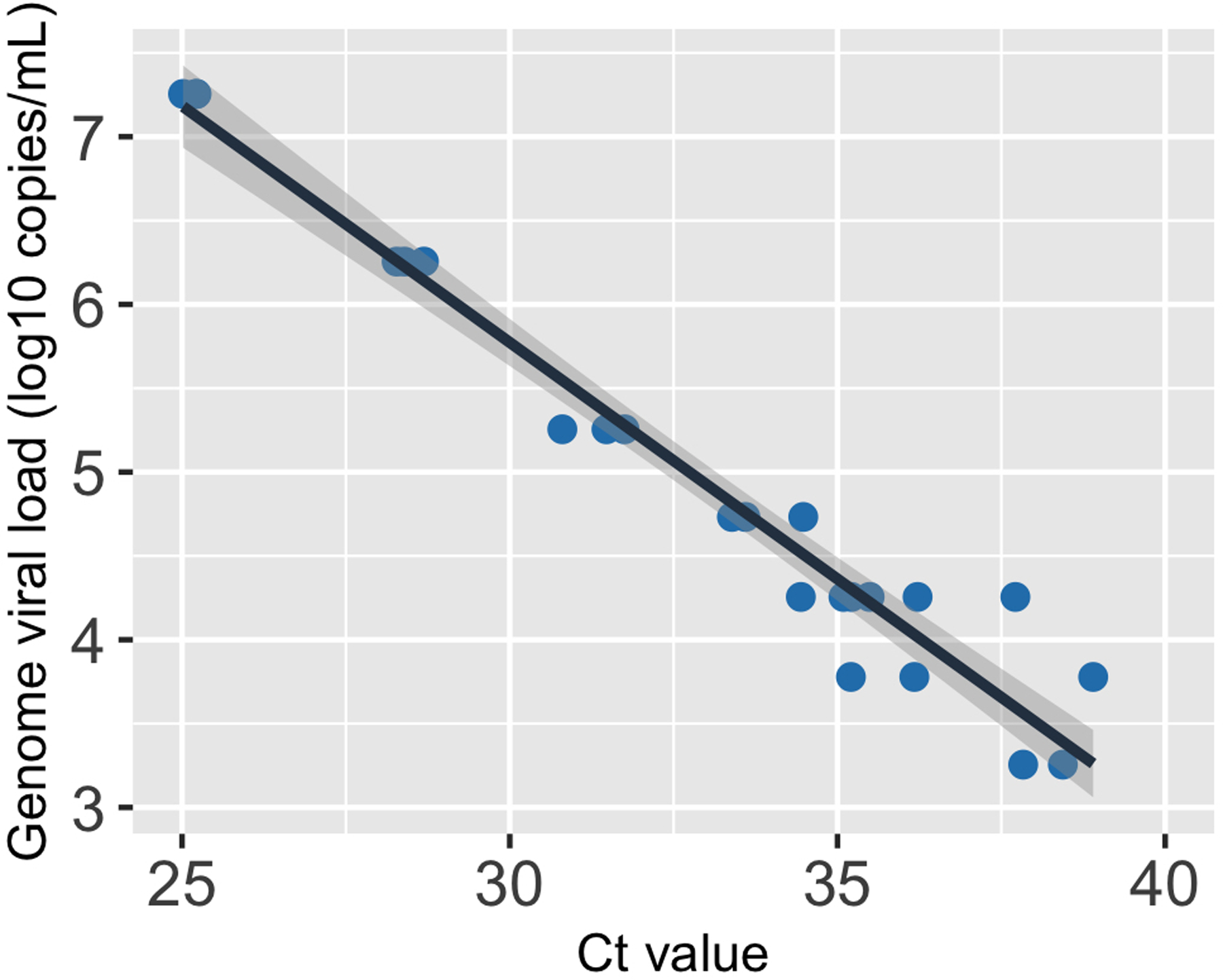
The black line, i.e. the center of the error band, represents the linear regression calibration curve. The shading around the black line shows the standard error for the regression.

Data availability:

All raw data used is included as a supplemental table. Raw sequence data files can be found under BioProject ID PRJNA809434.