Molecularly imprinted polymers for selective adsorption of quinoline: theoretical and experimental studies

Abstract

The effects of solvent on the synthesis of molecularly imprinted polymers (MIPs) for the selective adsorption of quinoline were evaluated in this work. The MIPs were synthesized by the “bulk” method using the quinoline molecule (IQ) as a template in different solvents, such as toluene (MIPT) and chloroform (MIPC). The adsorbents were characterized by thermogravimetric analysis (TGA), Fourier transform infrared (FT-IR) spectroscopy, scanning electron microscopy (SEM), and N₂ adsorption/desorption measurements. The influences of time, adsorbate concentration, and temperature on the adsorption of quinoline by MIPT and MIPC were evaluated. Maximum adsorption capacities (q_e) of 35.23 and 24.10 mg g⁻¹ were obtained for MIPT and MIPC, respectively. Thermodynamic studies indicate that occur physisorption and a spontaneous process (Δ_adsG° < 0) entropically directed. Finally, the highest selectivity and reusability of MIPC for quinoline adsorption was ascribed to the better interaction between the chloroform and monomer, which favors the formation of porous adsorbents with higher numbers of adsorption sites.

Molecularly imprinted polymers synthesized by a one-pot synthesis absorb quinoline efficiently and selectively.

1. Introduction

The fuel oils widely used by modern society contain contaminants, including nitrogen (N) and sulfur (S). The burning of these fuels leads to the formation of N and S oxides when in contact with water, producing acid rain.¹ These emissions can cause various health problems for humans, such as respiratory problems, skin irritation, birth defects, and various types of cancer. Due to this, technologies based on hydrodenitrification (HDN) and hydrodesulfurization (HDS) for the removal of these compounds have been developed. The conventional methods of hydrotreatment have been satisfactory for the removal of nitrogen and sulphur; however, they are less efficient for treating heterocyclic compounds such as benzothiophene (BTs), dibenzothiophene (DBTs), indole, quinoline, carbazole, and acridine.² Moreover, the HDN and HDS methods have the disadvantages of high cost, difficult operating conditions, and poor selectivity. Therefore, it is necessary to develop new techniques and more efficient methods for the removal of these contaminants of fuels.³

The low removal rates of sulfide compounds in these processes are attributed to the presence of nitrogen compounds, which can strongly inhibit the reactions of the hydroprocessing by competitive adsorption. This occurs because the nitrogen atoms in the contaminants strongly adsorb on the active sites of the catalyst. Quinoline is one of the most powerful inhibitors of the HDT process due to poisoning of the catalysts.^4,5 Adsorption treatments using porous materials, such as zeolites, activated carbon, activated alumina, silica gel, kaolinite, and montmorillonite, are the preferred alternatives for the removal of these contaminants; however, they are not selective.^4,5 On the other hand, molecularly imprinted polymers (MIPs) are highly selective adsorbents because they are capable of forming complementary sites with the target molecule on their surfaces, which leads to the formation of specific cavities in the polymer network. Because of their benefits, such as selectivity, stability and relatively easy synthesis, the use of MIPs to remove specific compounds from environmental samples has attracted attention in recent years.^6,7 Extensive efforts have been directed at the synthesis of these materials, as well as adsorption studies in organic phase^8–11 and aqueous phase.¹² It is important to note that the selective adsorption of quinoline favors its recovery and, consequently, its use as a molecular platform for the synthesis of other compounds of interest, such as quinolinic acid. The primary parameter studied during the synthesis of MIPs is the solvent. The ideal solvent should ensure selective interaction between the monomer and the target molecule. Thus, careful choice of solvent is required, with adequate polarity to favor the interactions between the monomer and the template molecule. The synthesis of the adsorbent must be performed in solvents with polarities similar to the medium in which the material will be used. Another characteristic that must be evaluated in a solvent for the synthesis of MIPs is its vapor pressure; solvents with higher vapor pressures are more readily volatilized, favoring pore formation during the synthesis and resulting in adsorbents with greater surface areas. Thus, it is fundamental to study the solvent that will be used during the synthesis when the aim is the production of a MIP with high selectivity and adsorption capacity.

In view of the above, the present study aims to evaluate the influence of the solvent in obtaining selective and efficient MIPs for the adsorption of quinoline in an organic matrix.

2. Materials and methods

2.1. Reagents

Dibenzothiophene (98%), carbazole (≥95%), quinoline (98%), methacrylic acid (MAA), ethylene glycol dimethylacrylate (EGDMA) and azobisisobutyronitrile (AIBN) were purchased from Sigma Chemical Company (U.S.A.). Toluene (Quimex), chloroform, methanol, and NaOH were purchased from Synth (Brazil), while n-heptane was obtained from Neon Ltda (Brazil). Glacial acetic acid (100%) was produced by Merck KGaA (Germany). All chemicals were used as received without further purification.

2.2. Equipment

Quinoline was quantified using a UV-VIS (Hewlett Packard 8453) spectrophotometer at a wavelength of 314 nm and a SHIMADZU BID2010 Plus gas chromatograph (GC) with a plasma detector and SH-Rtx-5 column using the following parameters: detector temperature of 553 K, injection opening temperature of 623 K, furnace temperature of 493 K. The agitation in the adsorption studies was maintained in a Shaker Tecnal (TE-421) instrument at 200 rpm.

The infrared spectra were obtained in the 400 to 4000 cm⁻¹ range with an ABB Bomem brand instrument coupled with accessories for attenuated total reflectance (ATR) and diffuse reflectance (DRIFT) analysis. The thermogravimetric analyses were performed on SDT2960 Simultaneous TGA-DTA equipment, model 2960, TA Instruments, with temperature variation from 25 °C to 1000 °C and a heating rate of 10 °C per minute in an inert atmosphere using N₂. The micrographs were produced at different magnification levels using a JEOL/EO scanning electron microscope (SEM), model JSM-5500, version 1.0, with a coupled reflex photo capture system. The specific surface areas and porosities of the materials were measured using AutosorbIQ equipment.

2.3. Synthesis of MIPs

The polymer adsorbents were synthesized by the Bulk method. The pre-polymerization mixture was formed by the template (quinoline) at a concentration of 1 mmol (0.13 mL) and 3 mmol (0.26 mL) of the functional monomer (MAA) dissolved in 20.00 mL of toluene (for MIPT) and 20.00 mL of chloroform (for MIPC) in a closed 50.00 mL amber flask with magnetic stirring for 24 hours. After the solubilization time, 22.5 mmol (4.25 mL) of the cross-linking agent (EGDMA) and 1.00 mL of the radical initiator (AIBN) were added. In order to ensure an inert atmosphere, the reaction medium was purged with N₂ flow for 8 min. Each polymerization was carried out at 60 °C with constant mechanical stirring for 24 hours. Synthesis under the same conditions was performed in the absence of the toluene template (NIPT) and chloroform (NIPC) to evaluate the effectiveness of the molecular imprinting.

Removal of the template after the polymerization was performed in a Soxhlet extractor by washing the material with a methanol/acetic acid (9 : 1 v/v) mixture. The final time of extraction was considered to be that at which the presence of residual template in the final extraction solution was not observed. After maximum removal of the target molecule, the polymer was dried at 40 °C for 24 hours and stored at room temperature.

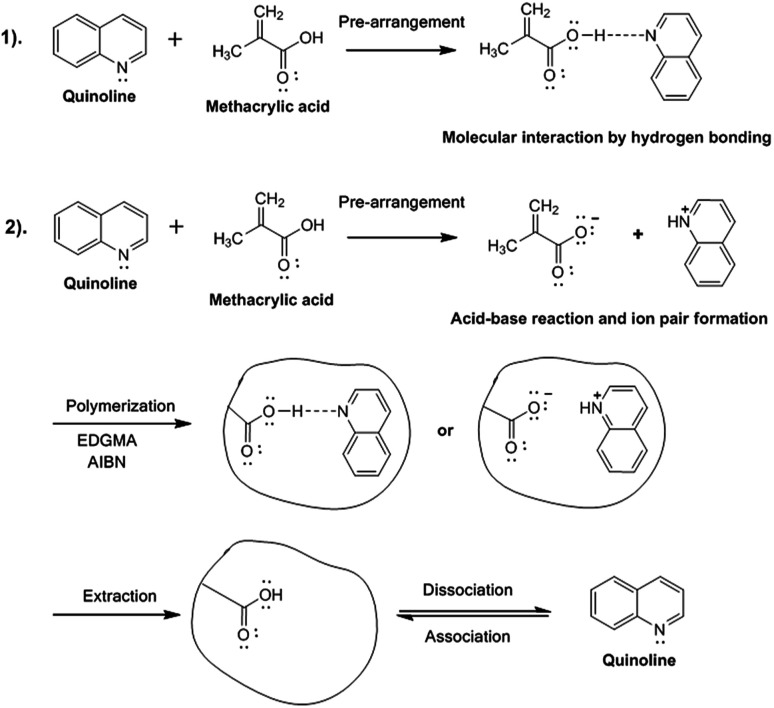
Fig. 1 schematically illustrates the two possible molecular imprinting procedures in MIPs, i.e. molecular interaction through hydrogen bonding or electrostatic interaction with ion pair formation.

Fig. 1. Synthesis and imprinting processes for the formation of MIPs.

2.4. Adsorption isotherms

In the adsorption studies, n-heptane was used as a solvent to simulate an apolar environment similar to those found in petrochemical systems where quinoline is present. Batch adsorption studies were performed on a Tecnal Shaker (TE-421) with a temperature control device adjusted for different temperatures (288.15, 298.15, 308.15 and 318.15 K). Quinoline solutions of 5.00 mL prepared at different concentrations (4, 12, 20, 28, 36, 44, 52, 60, 68, 76 and 82 mg L⁻¹) were placed in contact with 10.00 mg of MIPC or MIPT adsorbent in amber flasks under constant stirring at 180 rpm for four hours.

The quantification of quinoline was performed in triplicate before and after the adsorption assays to determine the capacity of adsorption, q_e (mg g⁻¹), of the adsorbent in equilibrium. The Langmuir, Freundlich, Sips, and Temkin models were used to fit the adsorption isotherms.

2.5. Kinetic studies

5.00 mL of quinoline solution with a defined concentration of 20 mg L⁻¹ was placed in contact with 10.00 mg of the different polymeric materials and maintained under shaking at 180 rpm in a Shaker Tecnal incubator (TE-421) at 288.15, 298.15, 308.15 and 318.15 K. At predetermined time intervals (5, 15, 30, 60, 90, 120, 180, 240 and 300 min), aliquots of 2.00 mL were taken from the centrifuged solutions and analyzed in the UV-VIS spectrophotometer at a wavelength of 314 nm.

The results of the kinetic studies were evaluated by adjusting the data to the order n (PON) model, expressing the adsorption rate and the number of active sites per adsorbent particle.¹³ The pseudo-second order model was also evaluated as described by Ho and Mckay (1999), and the rate constant k_2ads (g mg⁻¹ min⁻¹) was determined. In addition, the Elovich model was evaluated according to equations proposed by Roginsky and Zeldovich in 1934; the constant a (mg g⁻¹ min⁻¹) is considered to be the initial rate of the adsorption process, and b (g mg⁻¹) is a parameter related to the covered surface and the energy activation. The intraparticle diffusion model was tested according to Weber and Morris (1963) by determining K_pi (g mg⁻¹ min^−1/2), which is the diffusion rate constant between the particles of step i, where C_i is the intersection of step i. The best model was determined by analysis of the error functions X², Adj. R² and RMSE.

The Freundlich model suggests that the binding sites are not independent and assumes that the surface is energetically heterogeneous, allowing interactions between the adsorbed molecules²⁰ (eqn (1)):

q = KC_f^1/n 1

where K ((mg g⁻¹) (L g⁻¹)^1/n) is the Freundlich constant, which indicates the adsorbed capacity, and 1/n is a constant that represents the intensity of the adsorption.¹⁴

The Sips model is a versatile expression that can simulate behaviors of the Langmuir and Freundlich models. It is a model of three parameters, deduced for the prediction of heterogeneous adsorption systems, and avoids limiting the concentration of adsorbate output in the Freundlich model.¹⁵Eqn (2) represents the mathematical model:

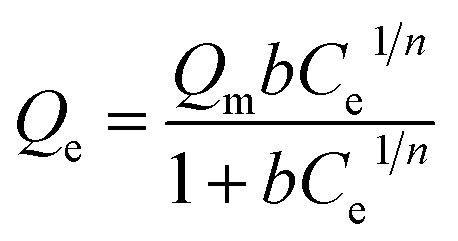2

where b is the affinity constant of adsorption (L mg⁻¹) and n is a heterogeneity index. The Temkin model assumes that the decrease in the adsorption heat is linear in all the adsorbent layers; this is due to possible adsorbate/adsorbent interactions. Thus, the adsorption is characterized as being uniform over the entire contact surface.¹⁶eqn (3) represents the model:

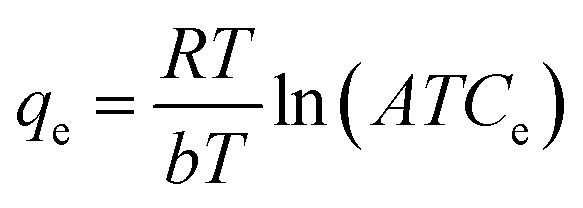3

where R is the gas constant, T is the temperature in kelvin, and A_T and b are Temkin constants.

2.6. Energy aspects

The parameters of the changes in Gibbs free energy (Δ_adsG°), enthalpy (Δ_adsH°) and entropy (Δ_adsS°) were determined by the equation

ΔG° = −RT ln K_p 4

where K_p is the thermodynamic constant of equilibrium, T (K) is the absolute temperature, and R (8.314 J mol⁻¹ K⁻¹) is the universal gas constant. The thermodynamic equilibrium constant is obtained from the Langmuir equation, with dimensionless conversion. The graphical representation of ln K_pvs. 1/T from eqn (5) results in a straight line. The values of ΔH° and ΔS° can be calculated from the slope and intercept of the line obtained by linear regression.

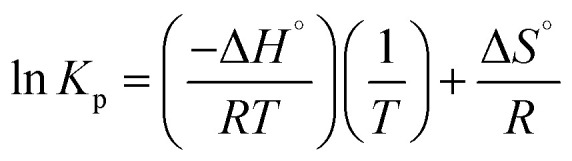5

The Van't Hoff equation shows the dependence between the adsorption equilibrium constant and the temperature.¹⁷

2.7. Selectivity studies

A solution containing 50 mg L⁻¹ carbazole, dibenzothiophene, and quinoline in n-heptane was prepared. The experiment was performed by adding 10.00 mg of MIPT or MIPC to flasks containing 5.00 mL of the simulated mixed solution. The flasks were subjected to constant stirring at 180 rpm and a temperature of 298.15 K for 4 hours. After adsorption, the supernatant was separated and analyzed in a GC BID2010 Plus Gas Chromatograph (SHIMADZU) with a plasma detector and SH-Rtx-5 column using the following parameters: detector temperature of 553 K, injection opening temperature of 623 K, furnace temperature of 493 K.

Through the parameters outlined in eqn (6)–(8), specific coefficients were determined to evaluate the selectivities of the imprinted adsorbents.

The distribution coefficient K_d (L g⁻¹) for each compound was calculated by the equation

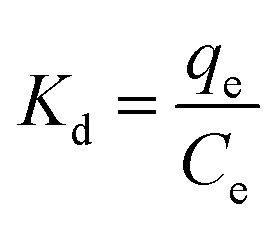6

The selectivity coefficient k of quinoline concerning the analogous molecule (identified as X) was calculated by eqn (7), as follows:

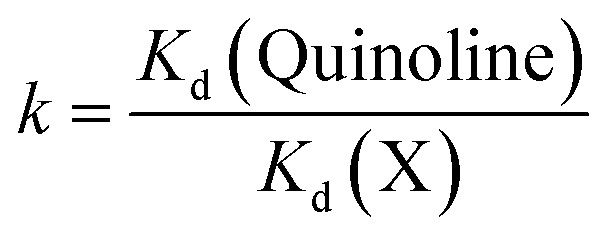7

The relative selectivity coefficient k′ in relation to MIP and NIP was calculated as follows:

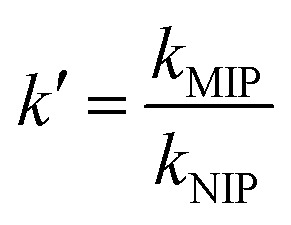8

2.8. Regeneration studies of MIPs

In this study, after adsorption of the quinoline (50 mg L⁻¹) in the organic phase (10.00 mL) over 10.00 mg of MIPs, the adsorbents were collected and separated from the solution. The polymers were vacuum filtrated and washed with methanol/acetic acid (9 : 1 v/v). Then, the adsorbents were regenerated in 10.00 mL methanol/acetic acid solution on a thermostatic shaker at 25 °C for 1 hour, or until quinoline could not be determined in the eluate. The regenerated MIPs were used to adsorb quinoline again (50 mg L⁻¹) at 298.15 K over a contact time of 4 hours. In total, five regeneration cycles were performed.

2.9. Computational methods

To understand the interaction between the adsorbate and the MAA (X⋯MAA) described in Fig. 1, where X = quinoline, DBT or carbazole, optimization and frequency calculations were performed at the M06-2X/6-311++g (d,p) level using Gaussian 09 software.¹⁸ The solvation environment was implicitly simulated by the PCM method¹⁹ using chloroform as the solvent at a temperature of 333.15 K and toluene at a temperature of 343.15 K. The characterization of the X⋯MAA interaction was confirmed by topological analysis using the AIMALL software.²⁰

3. Results and discussion

3.1. Synthesis of MIPs

The synthesis process was carried out with the purpose of evaluating the difference between the use of toluene and chloroform in the synthesis of a MIP with good selective adsorptive capacity. Toluene was used because it is an apolar solvent with a lower dielectric constant than chloroform, which is a less apolar solvent with a much higher dielectric constant. Hydrogen bonding is the predominant interaction with toluene, while electrostatic interactions are formed with chloroform. Also, the solvent exerts a wide influence on the synthesis of MIPs in general because it allows the creation of selective porosity on the surface of the polymer; this depends on the specific interactions formed with the template.

3.2. Characterization of MIPs

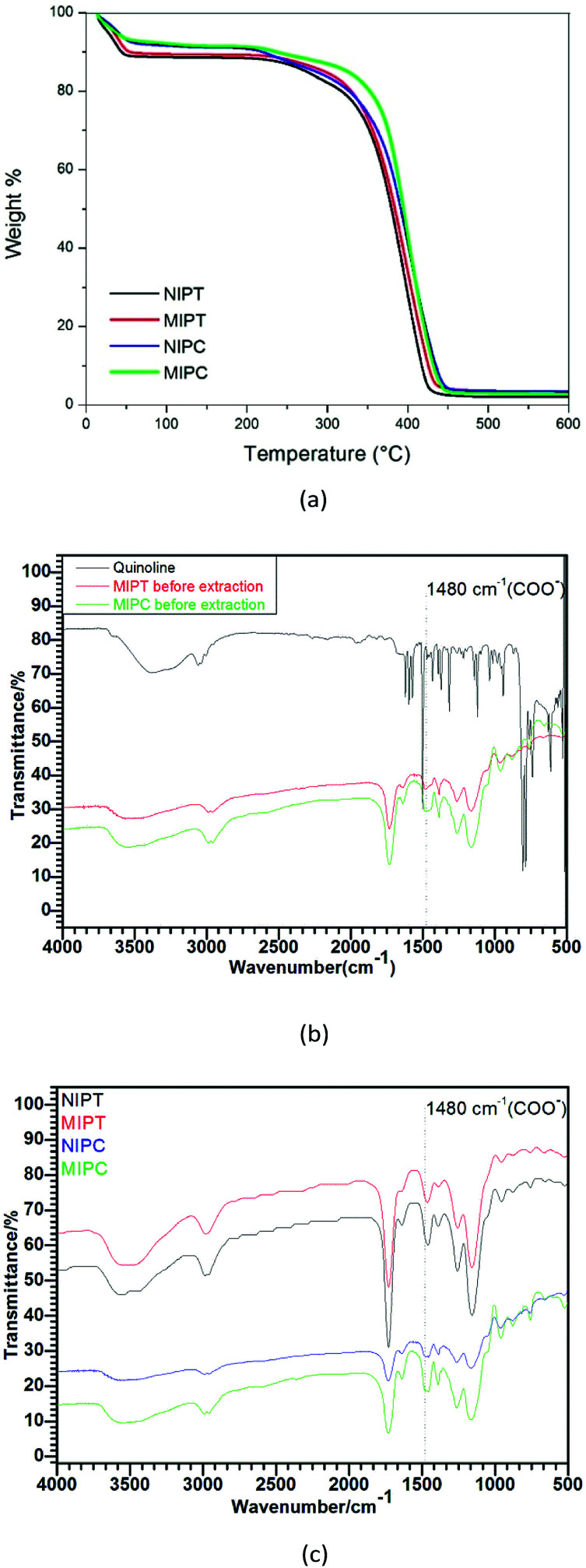
The corresponding TGA and FTIR analyses of the imprinted and non-imprinted polymers can be seen in Fig. 2. The TGA profiles (Fig. 2a) show estimated mass losses of 8% to 12% for the polymers up to 50 °C. This may occur due to traces of volatile organic compounds trapped inside the wells which were absorbed in the synthesis process.²¹ The polymers undergo thermal degradation in the temperature range of 250 °C to 450 °C, with loss percentages of 93% and 97% for MIPT and MIPC, respectively. Small amounts of remaining inert residue exist, with respective percentages of 7% and 3%. The polymer decomposition kinetics are faster for the NIPT and NIPC non-imprinted polymers than for the corresponding MIPT and MIPC, indicating the higher thermal resistance of the imprinted polymers.

Fig. 2. (a) TGA profiles and (b) FTIR spectra of quinoline and MIPs before extraction, and (c) FTIR spectra of MIPs and NIPs after extraction.

Fig. 2b and c show the FTIR spectra of the polymers. For all polymers, similarity was observed in the bands. A wide band at 3170 to 3672 cm⁻¹ with a maximum of 3500 cm⁻¹, attributed to the stretching (O–H) mode of the hydroxyl groups of the MAA functional monomer,²² was observed. Bands at 2900 cm⁻¹, resulting from (C–H) stretching, and at 1384 cm⁻¹, resulting from (CH₂) stretching/distortion, were observed.²³ Strong bands appeared at 1750 (C O), 1230, and 1125 cm⁻¹ (C–O–C), which are characteristic of MAA and ester groups (EGDMA), respectively.²⁴ At 1480 cm⁻¹, a band originating from the stretching (–COO) of the MAA was observed. In Fig. 2b, it can be observed that the band at 1480 cm⁻¹ attributed to the vibration of the COO group of the monomer has a lower intensity than the same band shown in Fig. 2c. This may occur due to the interaction of quinoline with the COO group of the monomer, as suggested in Fig. 1. It is worth emphasizing that variation in the intensity of a band is not enough to confirm the presence or absence of the template. However, for these types of materials, the mass fraction of the template (quinolone) in the MIP is very low because all other compounds were added in excess during the synthesis of the material. Therefore, the specific vibrations of the monomers, radical initiators and cross-link agents are more intense, which makes it difficult to see specific vibrations between the monomer and template. However, a change in the chemical environment of the system with the insertion of a new interaction between the monomer and the template may decrease the intensity of the –COO vibration frequencies because as shown by theoretical calculations, the interaction between the template and the monomer occurs at the carboxylic acid function of methacrylic acid. The bands at 937, 875 and 750 cm⁻¹ are due to out-of-plane deformation of (C–H) on different substituted benzene rings. The spectra initially indicate that the quinoline extraction was successful because the spectra of the MIPs with quinoline molecular imprinting are similar to the spectra of the non-molecular imprinted NIPs.

Table 1 shows the specific areas (BET), pore sizes, and volume data for the adsorbents. According to the results, the MIP that developed the largest specific area was the MIPC (205.90 m² g⁻¹, which is twice the value obtained for the MIPT). The lower boiling point of chloroform (61.2 °C) compared to toluene (110.6 °C) can explain this result. Solvents with higher vapor pressures are responsible for increasing the surface area of the adsorbent during synthesis, contributing to better performance.

Surface characterization of MIPs and NIPs.

Polymer	Specific area – BET (m2 g−1)	Average pore sizes (Å)		Pore volume (cm3 g−1)
		Micro	Meso	Micro	Meso	Total
NIPT	81.8	17.7	131.15	6.5 × 10−2	1.12	1.18
MIPT	100.0	17.2	132.35	7.0 × 10−3	2.14	2.13
NIPC	161.1	17.7	105.59	5.9 × 10−2	1.17	1.23
MIPC	205.9	17.8	133.29	7.3 × 10−2	1.06	1.13

In both MIPs, there was greater development in the amount of mesopores (20 to 500 Å) compared to micropores (<20 Å). The mean micropore size for all the materials was 17 Å, and that of the mesopores was 120 to 130 Å. Note that the specific areas of the NIPs were smaller than those obtained for the corresponding MIPs, indicating that the porogenic solvent in the presence of the template probably develops a better porous structure. Thus, it is possible to infer that the imprinted polymers are mesoporous adsorbents, which have exciting characteristics for use in adsorption processes (Table 1).

The SEM images obtained for the materials are shown in Fig. 3. The different micrometric scales of 10 μm to 20 μm allow us to determine the external morphology of each of the materials with increases of 800 up to 1000 times, showing the macroporous cavities. The macropores indicate uniformity and similarity between the NIPs and MIPs. The general surfaces of all the polymers are exhibited, showing spherical particles of different sizes. For the materials synthesized with toluene, the surfaces appear to be wider, whereas for the materials synthesized with chloroform, the surfaces appear to be more complex and narrow.

Fig. 3. SEM images of the different synthesized polymers: (a) NIPT, (b) MIPT, (c) NIPC and (d) MIPC.

3.3. Adsorption studies

3.3.1. Kinetic study

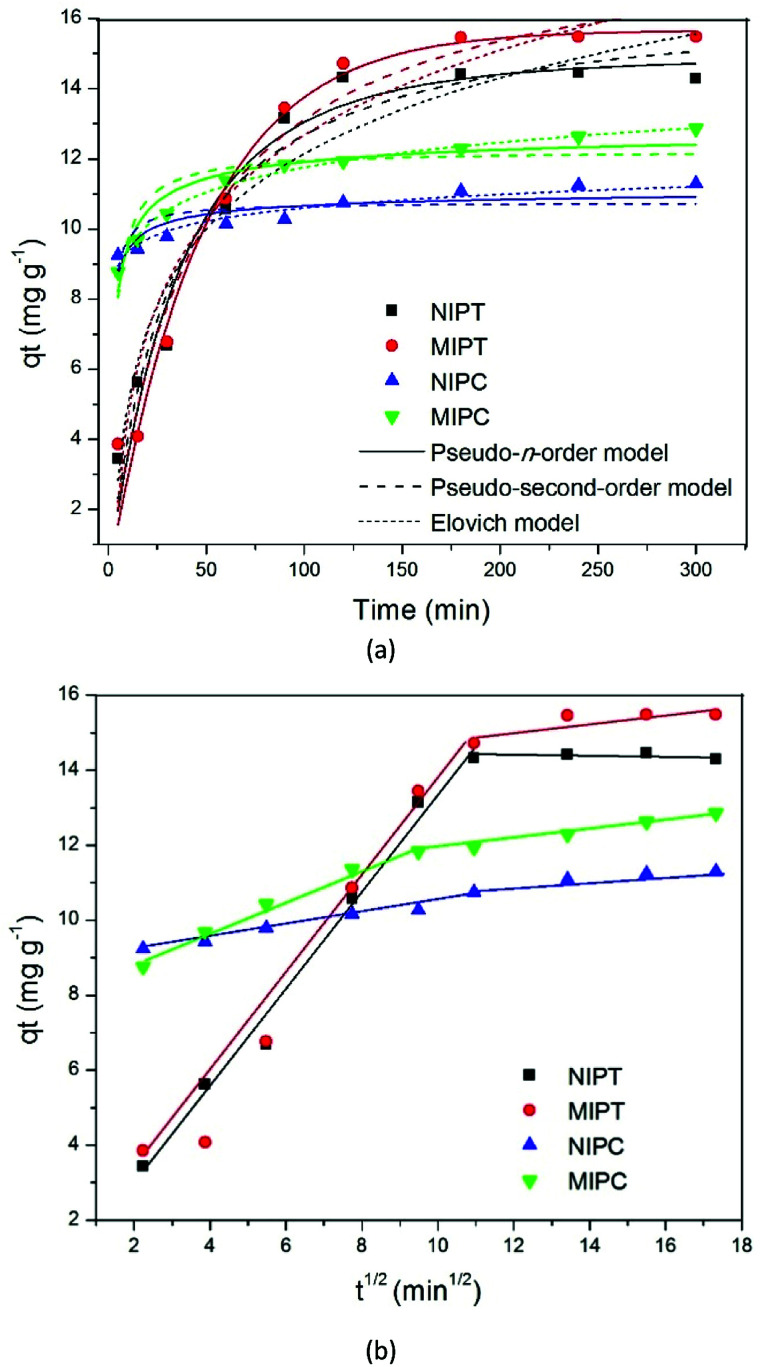
Fig. 4a shows the adsorption data fitted by the pseudo-order n (PON), pseudo-second-order (PSO), and Elovich kinetic models. The plots of q_t as a function of time indicate that for all adsorbents, the quantities of adsorbed quinoline increase with time until a steady state is reached. The adsorption rate was high in the first minutes (0 min to 25 min), with initial adsorbed amounts of 2 to 8 mg g⁻¹ for MIPT and MIPC, respectively; maximum adsorption amounts were reached in approximately 100 min for MIPT and 125 min for MIPC, with respective values of 15.484 and 12.857 mg g⁻¹. It should be noted that the largest difference between the adsorbed amounts of NIPs with the MIPs was observed for MIPC, confirming the superior ability of chloroform to develop cavities with better specific recognition capacity compared to toluene. The plots of q_tversus t^1/2 (Fig. 4b) indicate multilinearity, revealing the presence of two steps in the adsorption processes. The first step indicates adsorption on the outer surface or instant adsorption, which is considered to be the fastest step. The second step indicates gradual adsorption, where intraparticle diffusion is the rate-limiting step.^25–28

Fig. 4. Kinetic models (a) and intraparticle diffusion (b) of the polymers.

Table 2 shows the parameters obtained for each model. It can be observed that the pseudo-order model n (PON) best fit the adsorption process of MIPT. The parameter n is responsible for measuring the order of the reaction; the value of this variable for MIPT was close to 1, which indicates that the pseudo-first order equation could also fit the experimental data. The adjustment of this model may indicate that the adsorption process for materials synthesized with toluene occurs with the occupation of a single active site on a solid and energetically homogeneous surface.²⁸

Adsorption kinetic parameters of MIPs and NIPs.

Model	Polymer	NIPT	MIPT	NIPC	MIPC
	q e,exp (mg g−1)	14.28	15.48	11.29	12.85
Pseudo second order	q e,calc (mg g−1)	16.62	18.52	10.70	12.24
	K 2 (min−1)	1.9 × 10−3	1.3 × 10−3	0.08	0.03
	X 2	0.90	1.38	0.19	0.26
	Adj. R2	0.95	0.95	0.53	0.79
	R 2	0.97	0.98	0.59	0.82
	RMSE	0.31	0.39	0.14	0.17
Pseudo order n	q e,calc (mg g−1)	14.91	15.66	11.25	13.08
	k n (min−1)	0.01	0.02	0.01	3.6 × 10−3
	n	1.27	0.98	2.85	2.51
	X 2	0.51	0.45	4.8 × 10−3	3.8 × 10−3
	Adj. R2	0.95	0.96	0.68	0.90
	R 2	0.98	0.98	0.75	0.92
	RMSE	0.24	0.38	0.02	0.02
Elovich	a (mg g−1 min−1)	1.38	1.20	1.4 × 106	989.53
	b (g mg−1)	0.32	0.28	1.83	0.97
	X 2	1.05	2.34	0.03	8.3 × 10−3
	Adj. R2	0.92	0.91	0.96	0.99
	R 2	0.96	0.96	0.97	0.99
	RMSE	0.34	0.51	0.05	0.02
Intraparticle diffusion	K 1p	1.33	1.68	0.16	0.06
	K 2p	0.001	0.11	0.31	0.13

When comparing the values of the kinetic constant k_n of NIPT (0.015 min⁻¹) and MIPT (0.023 min⁻¹), it is possible to note that for MIPT, adsorption occurred more rapidly; this behavior may be related to the lower limit of mass transfer of the quinoline molecules to the selective sites compared to non-specific sites generated in the NIPT polymer synthesized without molecular imprinting.

The model that best fit the adsorption process for MIPC was the Elovich model. This model suggests that the active sites of the respective adsorbents are of a heterogeneous nature and, therefore, exhibit different activation energies in the adsorption process.²⁹ The constant a is related to the adsorption rate, and the constant b is related to the surface coverage.³⁰ For NIPC, the reaction rate was faster and the surface coverage was higher, which indicates an increase of the adsorption surface available to the adsorbent with increasing adsorption. The opposite occurred for MIPC, which indicates a decrease in available sites for quinoline with increasing time in the adsorption process.

The values of the K_p diffusion rates for the corresponding adsorption systems were higher for the constant k₁ than for k₂, indicating that the quinoline adsorption was generally fast at the beginning and decreased with time. This explains why these materials have wide external surfaces.

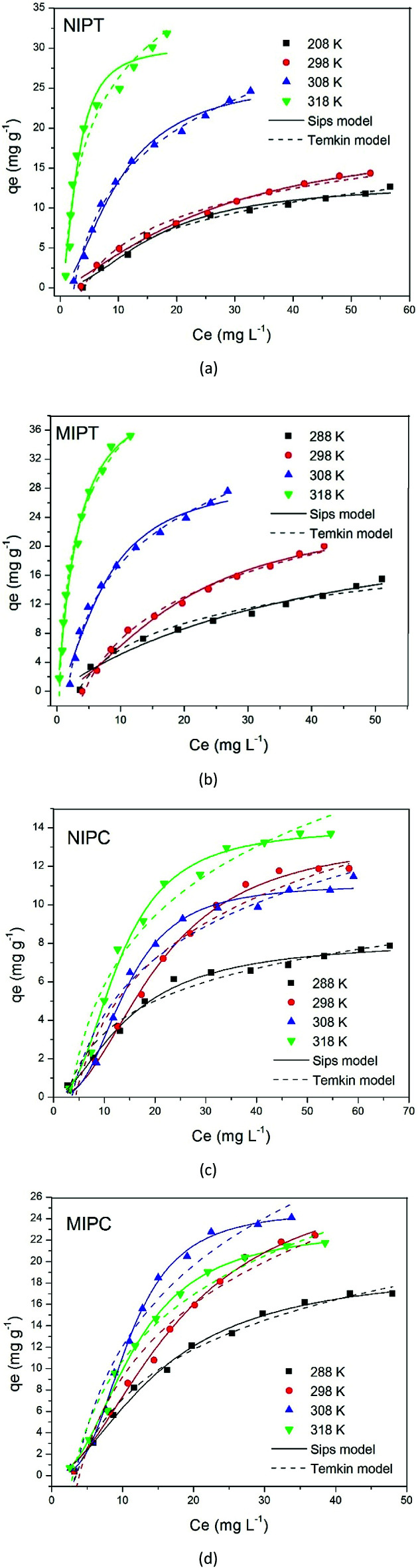
3.3.2. Adsorption isotherms

The quinoline amounts (q_e) adsorbed against C_e are shown in Fig. 5. The parameters obtained from the nonlinear equations of each model are presented in Tables 3 and 5. The differences in the q_e values of the MIPs and NIPs give a notion of the selective recognition ability of the MIPs for quinoline. For the adsorption systems of NIPT and MIPT, the results shown in Fig. 5a and b indicate better specific recognition at a temperature of 298.15 K, with a difference in the adsorption capacity q_e of ∼6 mg g⁻. The Temkin model was the one that best fit the data when evaluating the heat adsorption of all the molecules in the interaction layer/adsorbate–adsorbent on the adsorbent surface. It can be seen in Table 3 that the heat of adsorption (b_T) decreases linearly with the coverage due to adsorbent–adsorbate interactions, where adsorption is mainly characterized by the uniform distribution of binding energies.^31,32 This model also evaluates the adsorption potentials, which correspond to an increase in the free energy experienced by the adsorbate. The A_T parameter is the equilibrium binding constant, corresponding to the maximum binding energy. The values obtained for MIPT and NIPT increase with increasing temperature, showing more favorable adsorptions at high temperatures. The values of the Temkin constant A_T (L mg⁻¹) can be compared with the results of the Langmuir constant b (L mg⁻¹), which also increases with increasing temperature.

Fig. 5. Non-linear Sips and Temkin models obtained at different temperatures for each of the MIPT and MIPC adsorption isotherms.

Parameters obtained from the non-linear equations for the NIPC and MIPC polymers.

Polymer		NIPC				MIPC
Model	Parameters	Temperature (K)
		288.15	298.15	308.15	318.15	288.15	298.15	308.15	318.15
	q exp (mg g−1)	7.86	11.88	11.46	13.69	16.99	22.43	24.10	21.73
Freundlich	K f (mg g−1) (L g−1)1/n	1.01	0.70	1.11	1.48	1.44	1.08	1.91	2.00
	n (L mg−1)	1.98	1.37	1.69	1.70	1.50	1.15	1.32	1.45
	X 2	0.42	1.02	1.59	2.30	1.91	2.03	7.34	4.45
	Adj. R2	0.91	0.92	0.86	0.87	0.93	0.95	0.87	0.90
	R 2	0.95	0.96	0.93	0.94	0.96	0.98	0.94	0.95
	RMSE	0.64	1.01	1.26	1.51	1.38	1.42	2.70	2.11
Langmuir	Q max (mg g−1)	10.90	27.51	18.34	22.62	32.48	44.79	29.78	44.25
	b (L mg−1)	0.01	0.02	0.03	0.04	0.01	0.01	0.02	0.02
	X 2	0.15	0.61	0.92	1.23	0.93	1.04	5.35	2.62
	Adj. R2	0.96	0.95	0.92	0.93	0.96	0.96	0.90	0.94
	R 2	0.98	0.98	0.96	0.96	0.98	0.98	0.95	0.97
	RMSE	0.39	0.78	0.96	1.11	0.96	1.20	2.31	1.61
Sips	Q max (mg g−1)	8.16	13.53	11.0	14.00	19.34	28.46	24.77	23.12
	b (L mg−1)	0.06	0.04	0.07	0.07	0.06	0.05	0.09	0.08
	n	0.57	0.46	0.36	0.41	0.56	0.53	0.33	0.43
	X 2	0.05	0.05	0.10	0.16	0.18	0.20	0.13	0.18
	Adj. R2	0.98	0.99	0.99	0.99	0.99	0.99	0.99	0.99
	R 2	0.99	0.99	0.99	0.99	0.99	0.99	0.99	0.99
	RMSE	0.23	0.23	0.32	0.40	0.43	0.45	0.37	0.43
Temkin	b T (kJ mol−1)	0.98	0.53	0.61	0.50	0.35	0.25	0.23	0.29
	A T (L mg−1)	0.39	0.23	0.27	0.30	0.29	0.25	0.30	0.33
	X 2	0.15	0.92	0.66	0.78	0.28	1.60	3.57	1.62
	Adj. R2	0.96	0.93	0.94	0.95	0.98	0.96	0.93	0.96
	R 2	0.97	0.97	0.97	0.98	0.99	0.98	0.97	0.98
	RMSE	0.38	0.96	0.81	0.83	0.53	1.26	1.89	1.27

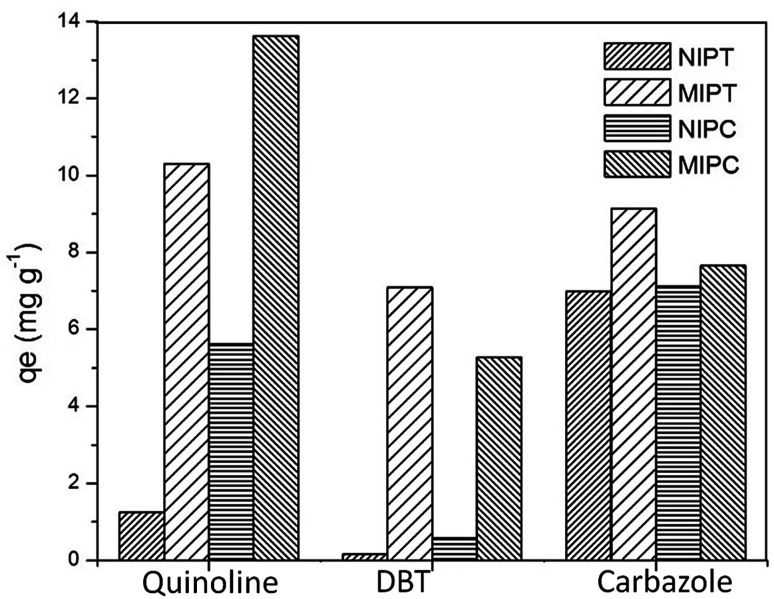
Adsorption parameters of MIPT and MIPC obtained in the selectivity tests.

Polymer	Selectivity parameters	Target and analogous molecules
		Quinoline	DBT	Carbazole
NIPT	q exp (mg g−1)	1.25	0.16	6.99
	K d (L g−1)	0.02	0.003	0.19
	K	—	7.90	0.13
MIPT	q exp (mg g−1)	10.29	7.09	9.13
	K d (L g−1)	0.34	0.19	0.28
	k	—	1.76	1.21
	k′	—	0.22	8.91
NIPC	q exp (mg g−1)	5.62	0.57	7.12
	K d (L g−1)	0.14	0.01	0.19
	K	—	12.36	0.72
MIPC	q exp (mg g−1)	13.61	5.26	7.65
	K d (L g−1)	0.59	0.13	0.22
	k	—	4.47	2.70
	k′	—	0.36	3.72

From Fig. 5c and d, an increase in adsorption for MIPC was observed at 298.15 and 308.15 K, with q_e values of 22.43 and 24.10 mg g⁻¹, respectively. The difference in the q_e values of MIPC and NIPC was ∼13 mg g⁻¹, indicating better specific recognition at 308.15 K. This shows that the synthesis conditions for these materials favored the formation of a more selective polymer, resulting in greater recognition capacity. Considering the results presented so far, it is worth pointing out that the use of chloroform as a porogenic solvent in the MIPC preparation favored the formation of specific interactions between the template and the monomer during the monomer/template active complex formation step. The model that best fit the MIPC data adsorption isotherm is the Sips model. The values of the parameter n presented in Table 3 are all lower than 1, which shows that the surfaces of these materials have an energetically heterogeneous distribution of active sites. The values of the Sips (n) parameter were compared with those obtained from the Freundlich (1/n) parameter; they were lower than 1, reinforcing the positive cooperation phenomenon between the adsorbent and the adsorbate presented on the heterogeneous surfaces resulting from the corresponding polymers. In addition, if the n values of the Freundlich model are greater than 1, favorable adsorption is predicted.³³

3.4. Energy aspects

The thermodynamic parameters of Gibbs free energy (Δ_adsG°), enthalpy (Δ_adsH°), and entropy (Δ_adsS°) are the real indicators of potential practical applications of the adsorption process. Table 4 shows the obtained thermodynamic parameters; the Gibbs free energy, Δ_adsG°, was negative for the adsorption isotherms, indicating spontaneity in the process, where more negative values represent more energetically favorable adsorption.³⁴ For all the studied systems, it is possible to observe an increase of spontaneity with increasing temperature.

Thermodynamic parameters of MIPT and MIPC.

Polymer	ΔadsG (kJ mol−1)				TΔadsS° (kJ mol−1)	ΔadsH° (kJ mol−1)
	Temperature (K)
	288.15	298.15	308.15	318.15
NIPT	−18.43	−19.92	−22.85	−26.56	80.59	59.99
MIPT	−17.79	−19.71	−23.02	−27.21	93.35	72.95
NIPC	−18.13	−20.02	−21.84	−23.09	50.05	30.11
MIPC	−17.39	−18.59	−20.48	−21.76	44.75	25.93

Adsorption processes can be classified as physical or chemical according to the enthalpy change of adsorption Δ_adsH°; if the resulting value is less than 80 kJ mol⁻¹, the phenomenon that occurs in the mechanism of adsorption is physical, but if the value is in the range between 80 and 400 kJ mol⁻¹, the phenomenon that occurs is chemisorption. Thus, the obtained adsorption enthalpy values (Δ_adsH°) are in the range in which the adsorption process occurs by the physisorption phenomenon; this indicates the presence of stronger electrostatic interactions, probably ion-dipole, for the materials synthesized with toluene. In addition, the positive value obtained from the parameter Δ_adsH° shows that the adsorption of the quinoline was endothermally directed. Due to the results obtained up to the present moment, it is possible to point out that the interaction process between the template/monomer can be better explained by electrostatic interaction. One hypothesis is that during the formation of the active complex, methacrylic acid transfers H⁺ to the basic functional group of the quinoline molecule. This action results in a positive electrostatic interaction between the carboxylate anion and the protonated amino group of the quinoline.

The positive result of TΔ_adsS° indicates an increase in the number of degrees of freedom in the system; this phenomenon is a consequence of desolvation between quinoline and n-heptane after adsorption, where for a process to be spontaneous, the following condition must be fulfilled: Δ_adsG° = Δ_adsH° − TΔ_adsS° < 0. In this study, the relation TΔ_adsS° > Δ_adsH° was obtained; it can be said that the increase in the degree of freedom at the adsorbent interface is due to an entropically directed process.

3.5. Selectivity studies

Selectivity studies (Fig. 6) were performed to compare the quinoline adsorption in relation to different analogous molecules (dibenzothiophene-DBT and carbazole). The adsorption capacities of quinoline q_exp that developed in the MIPs (MIPT = 10.296 mg g⁻¹ and MIPC = 13.613 mg g⁻¹) are remarkable. Unfavorable selective adsorption of MIPT by quinoline is presented in relation to the amount of adsorbed carbazole; this indicates that the template imprinting in the MIPT cavities was not effective. The removal of quinoline by MIPC was superior to that observed for MIPT; this suggests the presence of specific imprinted sites in MIPC, favoring the adsorption of the target molecules and decreasing the number of interfering bonds.

Fig. 6. Adsorption selectivities of quinoline and its analogues on different adsorbents.

Table 5 shows the obtained parameters. The K_d values with quinoline were higher for the MIPs compared to the NIPs. Similar results were obtained with the values of k. For the MIPs, the values of k were >1; these values indicate that the adsorption of quinoline occurred preferentially. MIPC obtained the highest k values for both interferences (carbazole and DBT), showing that the synthesis conditions utilized favored higher specificity between the monomer and the template molecule; this indicates that the synthesis with chloroform provides a greater interaction with quinoline.

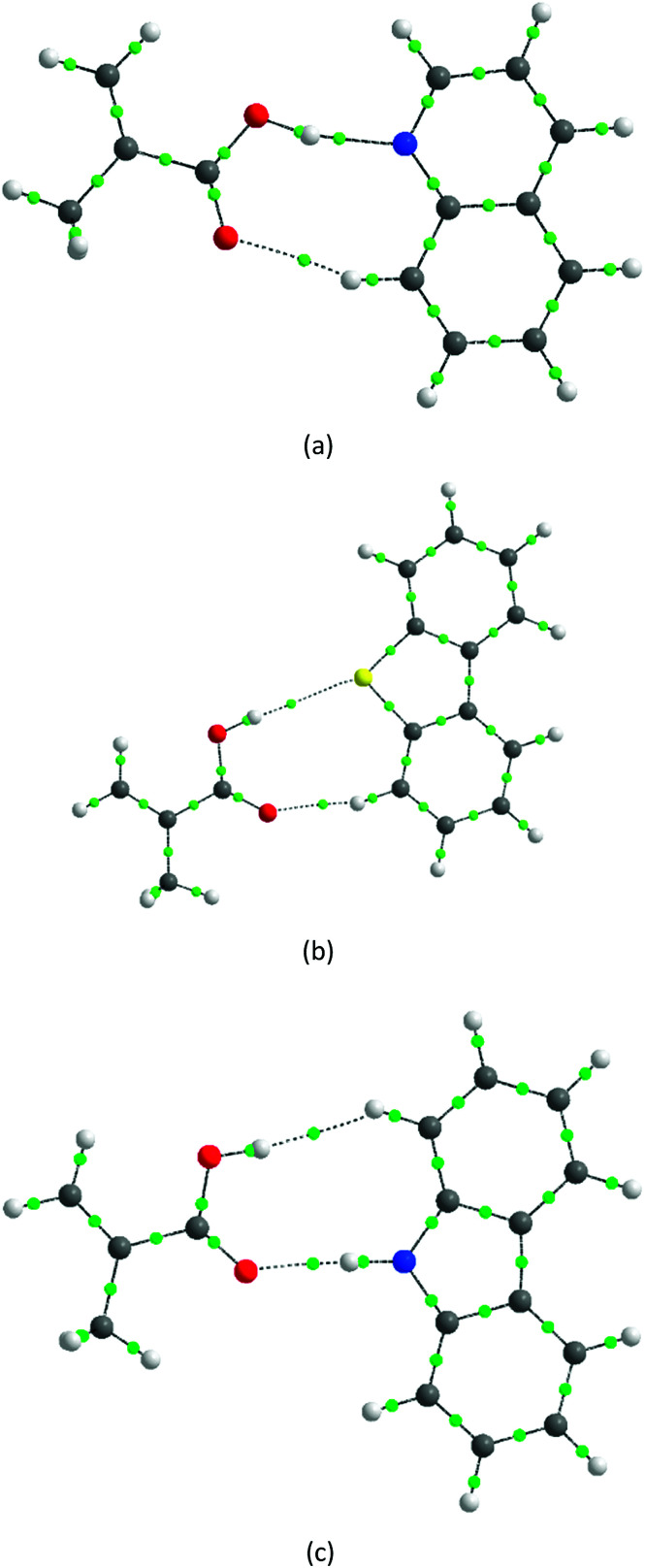
Fig. 7 illustrates the interactions of different adsorbates with MAA using theoretical calculations. Initially, it was not possible to distinguish the interactions between ion pairs and hydrogen bonds because all calculations converged to this last scenario. However, the results for the relative free energy of interaction provide interesting evidence. The values of ΔΔG, shown in Table 6, confirm that the adsorption selectivity (Fig. 6) is directly proportional to the free energy interaction, which increases in the order A > C > B. In addition, the volume factor is also relevant and directly proportional to the adsorption selectivity, maintaining the order A > C > B. Furthermore, according to our theoretical results, the differences in volume units between quinoline and its analogues are greater in chloroform than in toluene. For example, DBT is 273.95 bohr mol⁻³ greater and carbazole is 106.85 bohr mol⁻³ greater than quinoline in chloroform, but is only 266.02 bohr mol⁻³ and 4.55 bohr mol⁻³ greater in toluene, respectively.

Fig. 7. Optimized structures of the interactions between the adsorbates and MAA (X⋯MAA): (a) quinoline, (b) dbt and (c) carbazole. Carbon is represented in gray, hydrogen in white, oxygen in red, nitrogen in blue, and sulfur in yellow; critical binding sites (BCP) are represented by green spheres. The critical points 1 and 2 are highlighted as those referring to the interaction X⋯MAA.

Relative Gibbs free energies (kJ mol⁻¹) of the interaction between the target/analogous molecules and MAA, and the molar volumes of the target and analogous molecules (bohr³ mol⁻¹). Clo = chloroform and Tol = toluene.

	ΔΔG		Volume
	Clo	Tol	Clo	Tol
Quinoline	0.00	0.00	1335.92	1320.61
DBT	68.07	66.61	1609.87	1586.63
Carbazole	36.72	46.32	1442.77	1325.16

Using topological electron density analysis, it is possible to define the covalent or ionic character of the interactions between atoms. In order to understand the specific interaction X⋯MAA, we will analyze the critical points (BCP) 1 and 2 appearing between X and MAA (Fig. 7). In this sense, it is important to infer two magnitudes: ∇²ρ and |G/V|. ∇²ρ indicates whether the electronic density converges (negative values) or diverges (positive values) in the BCP. Therefore, covalent interactions present negative values for this magnitude, while electrostatic interactions have positive values.^35–37 In |G/V|, the proportion between the kinetic energy (G) and the potential (V) is given. If |G/V| > 1, in BCP, V has a smaller modulus than G. Thus, the electronic density tends to position itself around the nuclei, which is typical behavior of electrostatic interactions. Meanwhile, for covalent interactions, |G/V| < 1.^36–38

Table 7 shows the values of |G/V| and ∇²ρ for the BCPs 1 and 2 in Fig. 7. Note that for all cases, ∇²ρ is positive, which characterizes electrostatic interactions. The values of |G/V| converge to this same conclusion, except for the critical point 1 for dimer A. At this point, |G/V| is 0.754 in chloroform and 0.769 in toluene; this proportion is usually found for hydrogen bonds.³⁸ However, BCPs in hydrogen bonds with covalent character must have ∇²ρ < 0, which is not observed in this case.³⁷ Therefore, the interactions between X and MAA should be predominantly electrostatic, which may explain the selectivity difference.

Kinetic energies (G), potential energies (V) and electronic density Laplacians (∇²ρ) at the critical points (BCP) 1 and 2 of the molecules illustrated in Fig. 7. Clo = chloroform and Tol = toluene^a.

BCP	G		V		|G/V|		∇2ρ
	Clo	Tol	Clo	Tol	Clo	Tol	Clo	Tol
1-A	0.039	0.037	−0.051	−0.049	0.754	0.769	0.105	0.104
2-A	0.008	0.009	−0.007	−0.007	1.201	1.206	0.039	0.041
1-B	0.004	0.005	−0.003	−0.003	1.446	1.422	0.021	0.024
2-B	0.013	0.013	−0.010	−0.010	1.255	1.256	0.062	0.062
1-C	0.022	0.017	−0.019	−0.014	1.154	1.215	0.099	0.081
2-C	0.003	0.001	−0.002	−0.001	1.314	1.477	0.013	0.005

^aValues are truncated at the third decimal place.

Because it is an electrostatic phenomenon, the interaction between X and MAA will compete for interactions with the solvent. In fact, solvents with high polarity will weaken the electrostatic interactions between X and MAA through new electrostatic interactions between solvent⋯X and solvent⋯MAA; thus, the MAA carboxyl groups will be organized outside the pores to maximize the solvent⋯MAA interactions.^38–40 For this reason, the pores of MIPC will have less availability to form hydrogen bonds than the pores of MIPT. In consequence, only the strongest X⋯MAA interactions will prevail, giving more selectivity to the MIP. For our DFT calculations, the hydrogen bond interaction between quinoline⋯MAA was by far the strongest among the tested analogs. Thus, quinoline is preferred over DBT and carbazole.

3.6. Regeneration study of MIPs

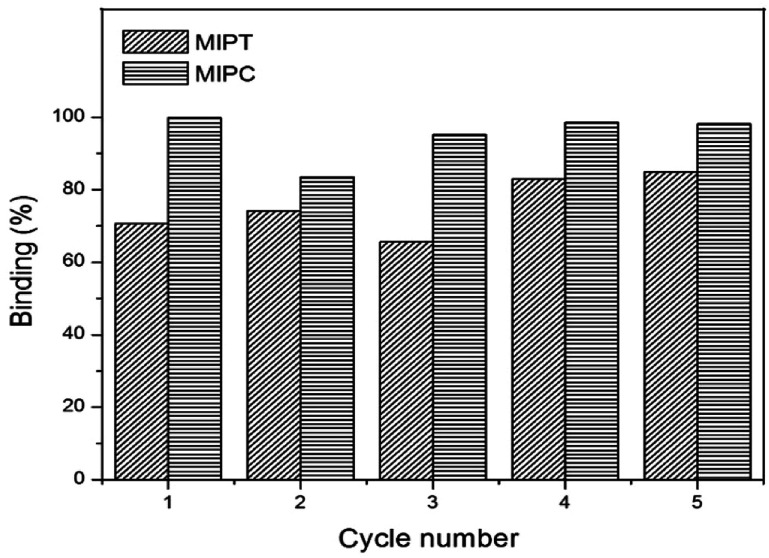
Desorption and regeneration studies express the importance of the reutilization capacity of MIPs. Fig. 8 shows the results of our study.

Fig. 8. Re-use of MIPs after five cycles.

After five adsorption/desorption cycles, the adsorption capacities of the MIPs were retained. For MIPT, the percentage of regeneration of 70% in the first cycle increased as the number of cycles increased, ending with regeneration of 82% in cycle 5. In the MIPC, the percentage decreased from 100% to 83% in cycle 2; however, as the number of cycles increased, the regeneration percentage also increased, with 100% recovery of the material at the end. These data show that the material can be used for several cycles without losing its capacity; in addition, the quinoline can be recovered after the process using a solid–liquid extraction system. This possibility guarantees greater sustainability for the process; thus, the application of this material is more attractive.

4. Conclusions

The present work demonstrated that the polymer synthesis method using chloroform (MIPC) may be more suitable for the synthesis of a selective adsorbent for quinoline, developing more efficient specific recognition and high adsorption capacity (24.10 mg g⁻¹). The chloroform favors the interaction ion pair compared to toluene because chloroform has a higher dielectric constant. Solvents with higher dielectric constants consequently increase the diffusional effect of the ionic species in the reaction medium, increasing the specificity between the template and the monomer. In addition, the higher vapor pressure and polarity of chloroform helped to provide a material with a greater surface area; during the synthesis, this property contributes to a higher porogenic capacity compared to toluene, increasing its selectivity, adsorption capacity and efficiency.

The computational calculations indicate that electrostatic interactions are predominant between the monomer and the template. The produced adsorbent materials presented high thermal stability, which enables their use in petrochemical industries. MIPC demonstrated the capability to regenerate itself and to be reused with good efficiency in different cycles, which facilitates the recovery of quinoline after the process.

Conflicts of interest

There are no conflicts to declare.