Insights into the role of electrostatics in temperature adaptation: a comparative study of psychrophilic, mesophilic, and thermophilic subtilisin-like serine proteases

Abstract

To investigate the role of electrostatics in different temperature adaptations, we performed a comparative study on subtilisin-like serine proteases from psychrophilic Vibrio sp. PA-44 (VPR), mesophilic Engyodontium album (Tritirachium album) (PRK), and thermophilic Thermus aquaticus (AQN) using multiple-replica molecular dynamics (MD) simulations combined with continuum electrostatics calculations. The results reveal that although salt bridges are not a crucial factor in determining the overall thermostability of these three proteases, they on average provide the greatest, moderate, and least electrostatic stabilization to AQN, PRK, and VPR, respectively, at the respective organism growth temperatures. Most salt bridges in AQN are effectively stabilizing and thus contribute to maintaining the overall structural stability at 343 K, while nearly half of the salt bridges in VPR interconvert between being stabilizing and being destabilizing, likely aiding in enhancing the local conformational flexibility at 283 K. The individual salt bridges, salt-bridge networks, and calcium ions contribute differentially to local stability and flexibility of these three enzyme structures, depending on their spatial distributions and electrostatic strengths. The shared negatively charged surface potential at the active center of the three enzymes may provide the active-center flexibility necessary for nucleophilic attack and proton transfer. The differences in distributions of the electro-negative, electro-positive, and electro-neutral potentials, particularly over the back surfaces of the three proteases, may modulate/affect not only protein solubility and thermostability but also structural stability and flexibility/rigidity. These results demonstrate that electrostatics contributes to both heat and cold adaptation of subtilisin-like serine proteases through fine-tuning, either globally or locally, the structural stability and conformational flexibility/rigidity, thus providing a foundation for further engineering and mutagenesis studies.

Differently charged surface patches contribute to temperature adaptation of subtilisin-like serine proteases through affecting/modulating the protein solubility and thermostability and the structural flexibility/rigidity/stability.

Introduction

Microorganisms can generally be classified into three categories, psychrophiles, mesophiles, and thermophiles according to the temperature of their living environment. The production of enzymes that function optimally at extreme temperatures is critically important for the survival of extremophiles. Generally, the structures of thermophilic enzymes exhibit a tightly packed hydrophobic core and abundant stabilizing interactions to ensure sufficient stability at high temperatures,^1,2 whereas those of psychrophilic enzymes exhibit a less compact packing, reduced stability, and enhanced flexibility to compensate for the low thermal energy provided by low-temperature habitats and to maintain sufficient catalytic activity at low temperatures.^3–6 Determining the molecular determinants and/or structural factors governing the relationships among stability, flexibility, and activity in extremophilic enzymes is essential for understanding the molecular mechanisms of enzyme temperature adaptation.

Optimization of electrostatics appears to be one of the simplest ways used in nature to manipulate biophysical properties central to enzyme structural stability, conformational flexibility, and catalytic activity.^7–10 Protein electrostatic properties are modulated by the proportion and distribution of charged and polar residues and their interactions.¹¹ The so-called ion pair refers to a pair of oppositely charged residues in the protein structure. If the two side-chain charged groups of an ion pair are sufficiently close, the interaction can be regarded as a salt bridge. Theoretical and experimental studies have demonstrated that ion pairs/salt bridges contribute either favorably or unfavorably to protein thermostability,^12–15 depending on the buried/exposed location and distance/geometrical orientation of the side-chain charged groups and the spatial distribution of all other charges in the protein structure.^16,17 Furthermore, it has also been shown that ion pairs/salt bridges can interconvert between being stabilizing and destabilizing to the structure in an ensemble; therefore, the stabilizing or destabilizing contribution of an ion pair/salt bridge depends on the conformational population/flexibility.^18–20

Through a comprehensive statistical comparison of a variety of structural properties such as hydrogen bonds, cavities, secondary structure, surface polarity, and ion pairs between homologous proteins from the mesophilic, moderately thermophilic, and extremely thermophilic organisms in a constructed non-redundant structural data set, Szilágyi and Závodszky revealed that the most significant difference is the number of ion pairs, which increases significantly with increasing habitat temperature of the source organisms.⁹ A similar study by Kumar et al. showed that the salt bridges and side chain-side chain hydrogen bonds are more prevalent in most thermophilic proteins than in their mesophilic counterparts.²¹ A comparative study of the electrostatic strengths (i.e., electrostatic free energy contribution to protein stability) of salt bridges in the thermophilic and mesophilic glutamate dehydrogenase monomers revealed that most salt bridges in the thermophilic enzyme are highly stabilizing, whereas those in the mesophilic enzyme are only marginally stabilizing.²² Therefore, salt bridges likely play an important role in maintaining the structural stability of proteins at high temperatures.

An interesting question is whether electrostatics contributes to cold adaptation of psychrophilic proteins. This issue has been investigated by Kumar and Nussinov⁷ by comparing the electrostatic properties of the psychrophilic, mesophilic, and thermophilic citrate synthases. They found that thermophilic enzyme salt bridges and their networks largely cluster in the active-site regions and are more electrostatically stabilizing at high temperatures, whereas in the psychrophilic enzyme, the charged residues in the active-site regions are more destabilizing and thus ensure proper active-site flexibility at low temperatures. Other studies also showed that the optimization of electrostatics can contribute to temperature adaptation by modulating stability and flexibility of cold- and warm-active enzymes.^8,10 However, it is important to note that differently temperature-adapted homologues in different enzyme families likely differ in number, spatial distribution, and electrostatic strength of charged residues, salt bridges and salt-bridge networks. Therefore, the role of electrostatics in modulating the stability and flexibility, and in contributing to temperature adaptation of specific enzyme families requires investigation.

To improve the understanding of the role of electrostatics in temperature adaptation, we used three subtilisin-like serine proteases from the proteinase K family as a comparative model system: the cold-adapted protease from the psychrophilic marine bacterium Vibrio sp. PA-44 (VPR),^23,24 mesophilic proteinase K from the fungus Engyodontium album (Tritirachium album) (PRK),²⁵ and thermophilic aqualysin I from the Gram-negative thermophilic bacterium Thermus aquaticus YT-1 (AQN).^26,27 The psychrophilic VPR was shown to be nearly two-fold more catalytically efficient than the mesophilic PRK and dozens of times more efficient than the thermophilic AQN towards the synthetic substrate succinyl-AAPF-p-nitroanilide at temperatures of 15–55 °C.²⁴ The stability of the three enzymes, measured as the sensitivity to both heat and denaturants, is in the order of VPR < PRK < AQN,^23,24 while their flexibility, measured as the accessibility of cysteine side chains, is in the order of VPR > PRK > AQN.²⁴ Our molecular dynamics (MD) simulation studies of VPR and PRK also revealed that VPR has a lower structural stability and higher conformational flexibility than PRK.^6,28 In this study, the three enzyme structures were subjected to multiple-replica MD simulations followed by continuum electrostatics calculations and comparison of electrostatic surface potentials to evaluate the possible role of electrostatics in their respective temperature adaptation. The results from our comparative analyses indicate that electrostatics contributes to both heat and cold adaptation of subtilisin-like serine proteases via affecting and modulating structural stability and conformational flexibility/rigidity.

Materials and methods

Structural and sequence comparison

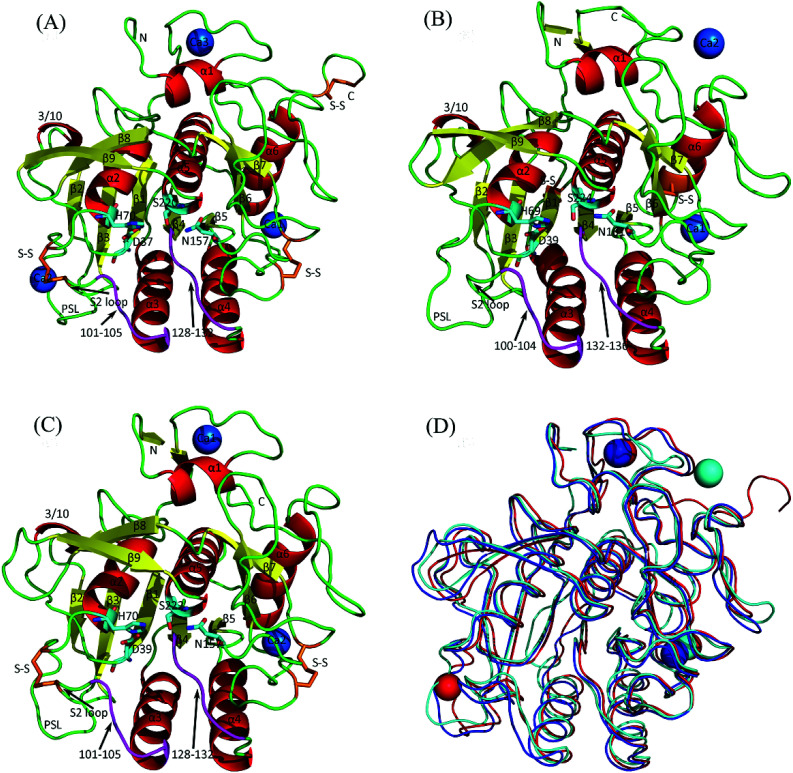
The X-ray crystallographic structures of VPR, PRK, and AQN were retrieved from the Protein Data Bank (PDB; http://www.rcsb.org) with PDB IDs of 1SH7 (resolution 1.84 Å),²⁹1IC6 (0.98 Å),³⁰ and 4DZT (1.95 Å),³¹ respectively. 3D structural superposition (Fig. 1D) and structure-based multiple sequence alignment (ESI Fig. S1†) were obtained using the all-against-all structural comparison module of the Dali server (http://ekhidna2.biocenter.helsinki.fi/dali/).³² The amino acid residue numbering used corresponds to that of PRK unless otherwise specified. Salt bridges in the crystal structures were identified using the tool Salt Bridges Plugin within VMD,³³ with the cut-off distance between any side-chain oxygen atom of Asp or Glu and any side-chain nitrogen atom of Arg or Lys set to 4.0 Å.

Fig. 1. Cartoon representations of the crystal structures of the three serine proteases and their backbone superposition. (A) Psychrophilic VPR. (B) Mesophilic PRK. (C) Thermophilic AQN. (D) Backbone superposition of the three structures. In (A), (B), and (C), α-helices, β-strands, loops, substrate-binding segments (residues 100–104 and 132–136) are colored red, yellow, green, and purple, respectively; catalytic triads (D37-H70-S220, D39-H69-S224, and D39-H70-S222 in VPR, PRK, and AQN, respectively) and oxyanion holes (N157, N161, and N157 in VPR, PRK, and AQN, respectively) are represented as stick models, with carbon, oxygen, and nitrogen atoms colored cyan, red, and blue, respectively; disulfide bridges (S–S) are shown as stick models in orange; calcium ions are represented as blue spheres and numbered Ca1, Ca2, or Ca3 according to their numbering order in the crystal structures. In (D), the backbones of VPR, PRK, and AQN, as well as their contained calcium ions, are colored red, cyan, and blue, respectively.

MD simulations

MD simulations were performed using GROMACS 5.1.2 (ref. 34) with CHARMM36 force field.³⁵ Before simulation, the ionization state of charged residues was modeled using the GROMACS tool ‘gmx pdb2gmx’ to mimic a neutral pH environment. All histidines were treated as neutral residues because their pK_a values predicted by DelPhiPKa³⁶ were less than 7.0 (ESI Table S1†). Histidines outside the catalytic triad were protonated automatically on either N_δ1 or N_ε2 atom based on the optimal hydrogen-bonding conformation followed by visual inspections, while histidines within the catalytic triad were protonated only on N_δ1 to guarantee the correct hydrogen bonds (His69–N_δ1–H⋯O_δ2–Asp39 and Ser224–O_γ–H⋯N_ε2–His69) for charge relay.^37,38

After protonation, each structure was soaked in a dodecahedral box of TIPS3P water molecules,³⁹ with the minimum distance between any solute atom and box edges set to 1.0 nm and periodic boundary conditions applied in all directions. To neutralize the system and add an additional concentration of 100 mM NaCl, 19 Cl⁻ and 23 Na⁺, 22 Cl⁻ and 17 Na⁺, and 20 Cl⁻ and 15 Na⁺ were introduced into the systems of VPR, PRK, and AQN, respectively. The total numbers of atoms in the final systems of VPR, PRK, and AQN were 32 088, 27 335, and 24 741, respectively.

Each system was subjected to 1000 steps of steepest-descent energy minimization followed by 1000 steps of conjugate-gradient minimization. The last minimization was followed by four successive 100 ps position-restrained MD simulations in the isochoric–isothermal (NVT) ensemble, with protein heavy atoms and Ca²⁺ restrained by the harmonic potential with reduced force constants (i.e., Kposres = 1000, 100, 10, and 0 kJ mol⁻¹ nm⁻²)^38,40 and temperature maintained at 300 K using a velocity rescaling thermostat.⁴¹ Finally, at each of the three temperatures (i.e., 283, 300, and 343 K, which are the approximate habitat temperatures of the source organisms of VPR, PRK, and AQN, respectively), five 30 ns production MD runs were performed in the NPT ensemble. To improve conformational sampling, each of the five MD runs was initialized with different initial atomic velocities. Temperature and pressure were maintained using the velocity rescaling thermostat (with a coupling time constant of 0.1 ps) and Parrinello–Rahman barostat (with a coupling time constant of 0.5 ps),⁴² respectively. All bonds involving hydrogen atoms were constrained with the LINCS algorithm,⁴³ allowing an integration time step of 2 fs. The short-range non-bonded cut-off distance was set to 12 Å and van der Waals forces were smoothly switched to zero from 10 to 12 Å. The particle-mesh Ewald method⁴⁴ was used for treatment of long-range electrostatic interactions. System coordinates were saved every 2 ps. For all simulations, the last 24 ns trajectory was selected as the equilibrium portion based on the time evolution of the C_α root mean square deviation (RMSD) values with respect to the starting structure. For each simulation system at each temperature, the five equilibrium portions were concatenated into a single 120 ns trajectory for subsequent analyses.

Relative solvent accessibility and persistence degree of salt bridges

The residue solvent-accessible surface area (SASA) was computed using the GROMACS tool ‘gmx sasa’ with a solvent probe radius of 1.4 Å. The relative SASA (R-SASA) of a residue X was calculated as the ratio of SASA in each frame to its maximum SASA in the tripeptide Gly-X-Gly,⁴⁵ and then averaged over all frames. The R-SASA of a salt bridge/salt-bridge network was calculated as the average of R-SASAs of the participating residues. Salt bridges in the equilibrium trajectories were identified using an in-house Tcl/Tk script executed by the Tk console of VMD. The persistence degree (P-degree) of a salt bridge was calculated as the percentage of frames in which the salt bridge was detected. Only those with P-degree > 20% were considered as stable salt bridges,⁸ for which the electrostatic strengths were estimated by continuum electrostatics calculations.

Continuum electrostatics calculations

The continuum electrostatics calculation method⁴⁶ implemented in DelPhi 6.2 (ref. 47) was used to assess the electrostatic strengths of salt bridges. In this method, the electrostatic free energy contribution to protein stability (ΔΔG_tot-sb; also known as electrostatic strength) by a salt bridge can be dissected into contributions from three energy terms:¹⁴

ΔΔG_tot-sb = ΔΔG_dslv-sb + ΔΔG_brd-sb + ΔΔG_prt-sb 1

where ΔΔG_dslv-sb is the unfavorable free energy penalty due to the desolvation of charged side chains of salt-bridging residues upon protein folding (desolvation energy penalty term), ΔΔG_brd-sb is the change in free energy due to the favorable electrostatic interaction between the two oppositely charged side chains within a salt bridge (bridge energy term), and ΔΔG_prt-sb represents the change in free energy due to interactions of charged side chains of salt-bridging residues with charges in the rest of the folded protein (protein energy term).

Similarly, the electrostatic strength of a salt-bridge network (ΔΔG_tot-ntwk) was calculated as the sum of the three energy terms: desolvation (ΔΔG_dslv-ntwk), bridge (ΔΔG_brd-ntwk), and protein (ΔΔG_prt-ntwk). The electrostatic strength of a calcium ion (ΔΔG_tot-Ca) was the sum of the desolvation (ΔΔG_dslv-Ca) and protein energy terms (ΔΔG_prt-Ca).

For each system at each temperature, continuum electrostatics calculations were performed on 300 frames collected evenly over the 120 ns concatenated equilibrium MD trajectory (i.e., every 400 ps a snapshot was collected). Of note is that a salt bridge with P-degree > 20% does not necessarily exist in each of the 300 frames. The atomic radii and partial charges from the PARSE⁴⁸ parameter set were used because this parameter set has been shown to perform best in continuum electrostatics calculations⁴⁹ and reproduce the experimental data for amino acid side chain and peptide backbone analogs with an average error of only 0.1 kcal mol⁻¹.⁴⁸ In all calculations, a 1.4 Å solvent probe radius was used to evaluate the SASA of the protein; water dielectric constants were set to those corresponding to specified temperatures: 83.96 at 283 K, 77.87 at 300 K, and 63.73 at 343 K;⁵⁰ the protein internal dielectric constant was set to 4;¹⁴ ionic strength was set to 100 mM. The linearized Poisson–Boltzmann equation was solved using the iterative finite difference method. Each calculation consisted of an initial rough run followed by two high-resolution focusing runs. In the initial run, the full coulombic boundary (Debye–Huckel) condition was applied,⁵¹ and the grid spacing was set to 0.6 grid units per Å so that the protein filled ∼23% of the cubic grid. The focusing boundary condition obtained from the previous run was used in the focusing run. In the second and final runs, the protein filled ∼70% (1.6 grid units per Å) and ∼92% (2.0 grid units per Å) of the cubic grid, respectively. Therefore, only the results from the final run are shown.

The energy value outputted by DelPhi is in units of kT, where k and T are the Boltzmann constant and temperature, respectively. The conversion factors between kT and kcal mol⁻¹ are temperature-dependent: 0.5624, 0.5962, and 0.6816 kcal mol⁻¹ at 283, 300, and 343 K, respectively.

Results

Salt bridges/salt-bridge networks identified in the crystal structures and MD simulations

Fig. 1 shows the crystal structures of VPR, PRK, and AQN, all of which present a well-defined globular fold composed primarily of one seven-stranded parallel central β-sheet, six α-helices, and two two-stranded antiparallel β-sheets. The sequence identity and structural similarity (measured as the C_α RMSD) of VPR vs. PRK, VPR vs. AQN, and PRK vs. AQN are 45% and 1.3 Å, 62% and 0.7 Å, and 48% and 1.2 Å, respectively, indicating that the psychrophilic VPR and thermophilic AQN are more similar to each other than to the mesophilic PRK.

The numbers of salt bridges/salt-bridge networks identified in the crystal structures (referred to as the crystal salt bridges/salt-bridge networks hereafter) of VPR, PRK, and AQN are 7/1, 8/1, and 6/0, respectively (ESI Tables S2 and S3†). The three crystal structures share only one common salt bridge (Arg12-Asp187); the two extremophilic enzyme crystal structures (VPR and AQN) share two salt bridges (Asp58-Arg94 and Asp142-Arg173); and the numbers of unique salt bridges in the crystal structures of VPR, PRK, and AQN are 4, 7, and 3, respectively (ESI Table S3†).

Table 1 lists the salt bridges with P-degrees greater than 20% in the concatenated equilibrium MD trajectories of the three proteases. All crystal salt bridges were retained during MD simulations at temperatures of 283, 300 and 343 K, with the conserved ones exhibiting P-degrees greater than 84% while only a few unique ones exhibiting relatively low P-degrees (lower than 50%). This indicates that the crystal salt bridges, especially the conserved ones, remained highly stable during simulations, regardless of the simulation temperatures.

P-degrees of salt bridges in the concatenated equilibrium MD trajectories of the psychrophilic VPR, mesophilic PRK, and thermophilic AQN at temperatures of 283, 300, and 343 K.

Salt bridgea	VPRb (%)			PRKb (%)			AQNb (%)
	283 K	300 K	343 K	283 K	300 K	343 K	283 K	300 K	343 K
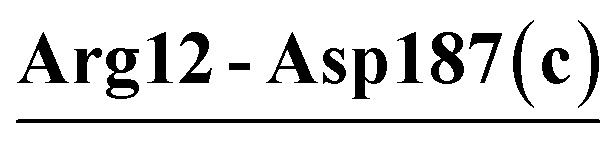
	100	100	100	100	100	100	100	100	100
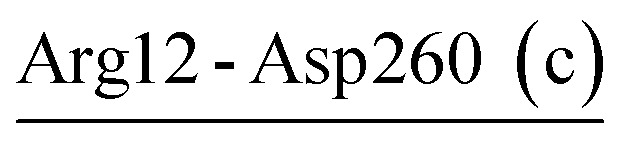
	—	—	—	100	100	100	—	—	—
Arg16-Asp278 (c)	25	34	45	—	—	—	—	—	—
Asp17-Arg260 (c)	—	—	—	—	—	—	100	99	99
Asp29-Lys86	19	0	27	—	—	—	—	—	—
Arg31-Glu239 (c)	—	—	—	—	—	—	78	57	66
Glu43-Arg64	—	—	—	68	40	73	—	—	—
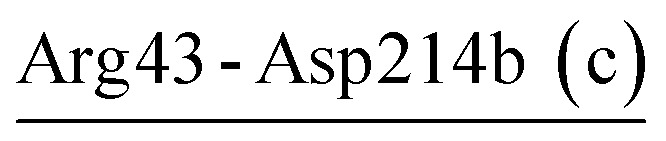
	—	—	—	—	—	—	86	65	28
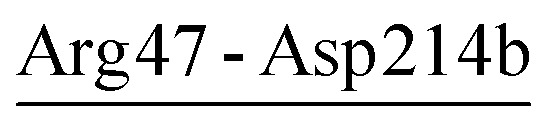
	—	—	—	—	—	—	0	8	20
Glu48-Arg80 (c)	—	—	—	98	95	74	—	—	—
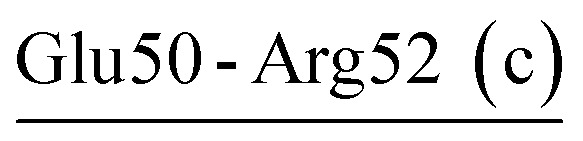
	—	—	—	93	90	93	—	—	—
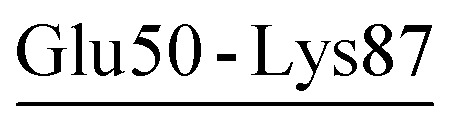
	—	—	—	34	47	59	—	—	—
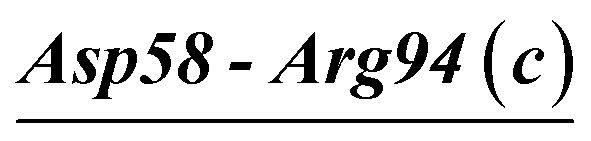
	100	100	100	—	—	—	84	100	100
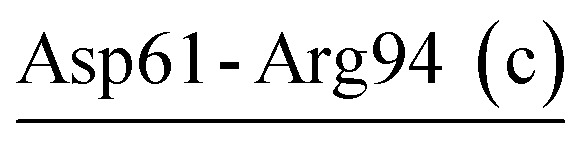
	99	98	99	—	—	—	—	—	—
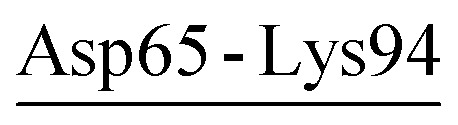
	—	—	—	0	40	6	—	—	—
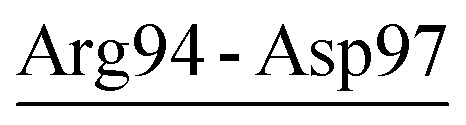
	—	—	—	—	—	—	7	31	37
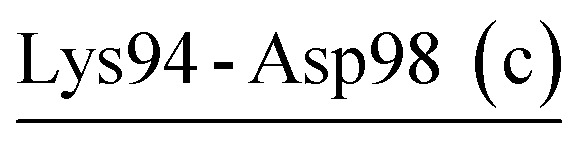
	—	—	—	96	68	90	—	—	—
Asp112-Arg116	—	—	—	—	—	—	79	61	81
Asp112-Arg147 (c)	—	—	—	38	50	62	—	—	—
Asp117-Arg121 (c)	—	—	—	100	100	99	—	—	—
Asp142-Arg173 (c)	95	99	100	—	—	—	100	100	94
Lys146-Glu176	—	—	—	—	—	—	65	34	62
Asp165-Arg167	—	—	—	36	41	85	—	—	—
Asp184-Arg188 (c)	—	—	—	93	87	74	—	—	—
Arg185-Asp207	—	—	—	37	21	13	—	—	—
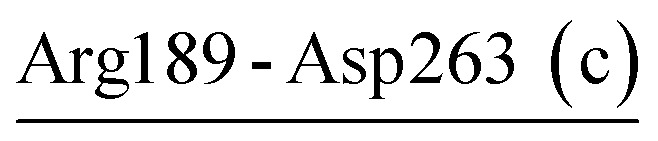
	34	85	90	—	—	—	—	—	—
Glu240-Arg255 (c)	100	99	98	—	—	—	—	—	—
Arg250-Asp254	—	—	—	19	47	40	—	—	—
Glu258-Lys271	62	75	79	—	—	—	—	—	—
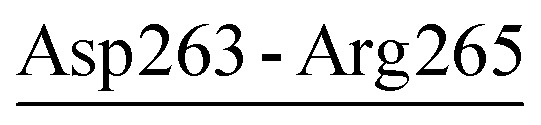
	22	55	78	—	—	—	—	—	—

^aSalt bridges identified in the crystal structures are followed by ‘c’ in parentheses; salt bridges common to the three proteases (absolutely conserved) are in bold; salt bridges shared between VPR and AQN (conserved) are bolded and italicized; salt bridges participating in the salt-bridge network are underlined.

^b P-degree is the percentage of the frames in which a given salt bridge exists. If a salt bridge does not exist at any temperature, it is indicated as ‘—’; if the P-degree of a salt bridge at any of the three temperatures is greater than 20%, its P-degrees at all three temperatures are also shown.

During the MD simulations at the respective habitat temperatures of the source organisms, two, six, and four newly formed salt bridges were found in VPR (283 K), PRK (300 K), and AQN (343 K), respectively, giving total numbers of 9, 14, and 10 salt bridges in VPR, PRK, and AQN, respectively (Table 1). Fig. 2 shows these salt bridges in the respective 3D structures of the three proteases. All the newly formed salt bridges are non-conserved among the three proteases and generally show lower P-degrees than the retained crystal salt bridges. With a few exceptions, the newly formed salt bridges exhibit higher P-degrees at 343 K than at 283 K. The enhanced atomic fluctuations caused by elevated temperatures, in combination with the long-range characteristics of electrostatic forces, may have increased the opportunity for spatially distant, oppositely charged side chains to get close enough to be within the salt-bridging distance.

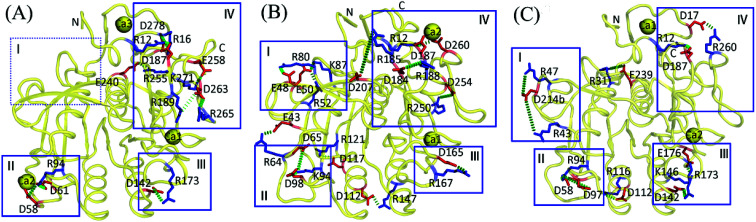
Fig. 2. Salt bridges with P-degree greater than 20% in the concatenated equilibrium MD trajectories of the three proteases at the respective habitat temperatures of the source organisms. (A) Psychrophilic VPR at 283 K. (B) Mesophilic PRK at 300 K. (C) Thermophilic AQN at 343 K. The representative 3D structures are shown as backbone traces (yellow). The salt-bridging residues are shown as stick models, with the negatively and positively charged residues colored red and blue, respectively. Salt bridges are shown as green dashes. The boxed regions (i.e., I–IV) are those where salt bridges are relatively enriched (for details, see text in Discussion section).

The salt-bridge networks present in the crystal structures of VPR (Asp58-Arg94-Asp61) and PRK (Asp187-Arg12-Asp260) were well retained during MD simulations at the three temperatures (Table 1). There were one and two newly formed networks in the simulations of VPR (Arg189-Asp263-Arg265 at the three temperatures) and PRK (Arg52-Glu50-Lys87 at the three temperatures and Asp65-Lys94-Asp98 at 300 K), respectively. Although the thermophilic AQN contains no crystal salt-bridge network, two low-persistence networks, Arg43-Asp214b-Arg47 (at 343 K) and Asp58-Arg94-Asp97 (at 300 and 343 K), were observed in simulations. As a result, the total numbers of salt-bridge networks observed in MD simulations of VPR, PRK, and AQN are 2, 3, and 2, respectively.

Effect of temperature on the overall properties of salt bridges

Table 2 lists the average values of the geometrical and energetic properties of all salt bridges calculated over the concatenated equilibrium MD trajectory at each temperature. The large standard deviations (SDs) around the energy averages indicate wide scatter in the data because of the diversity/variability in the distance between side-chain charged groups and in the buried/exposed location and spatial distribution/structural environment of individual salt bridges in the MD trajectory. Nevertheless, because the average value reflects the mean level of the whole data, the difference in the average can still provide valuable information regarding the trend in temperature-dependent changes in the “average behavior” of a salt-bridge property. Similarly, comparison of the averages among the three proteases is useful for detecting differences in the “average behavior” of a salt-bridge property.

Average values (SDs are in parentheses) of geometrical properties and electrostatic energy terms of all salt bridges calculated over the concatenated equilibrium MD trajectories of the psychrophilic VPR, mesophilic PRK, and thermophilic AQN at the three simulation temperatures.

Protein	Tempa (K)	P-degreeb (%)	R-SASAc (%)	ΔΔGdslv-sbd (kcal mol−1)	ΔΔGbrd-sbe (kcal mol−1)	ΔΔGprt-sbf (kcal mol−1)	ΔΔGtot-sbg (kcal mol−1)
VPR	283	71 (33)	27.8 (16.6)	10.3 (5.3)	−5.1 (3.8)	−8.2 (6.3)	−3.0 (3.7)
VPR	300	83 (23)	25.4 (15.1)	11.4 (5.0)	−6.1 (3.5)	−9.2 (6.6)	−3.8 (3.9)
VPR	343	81 (25)	26.6 (14.2)	12.4 (5.3)	−6.9 (3.8)	−10.2 (6.8)	−4.7 (4.2)
PRK	283	74 (28)	32.6 (13.6)	8.6 (4.2)	−4.7 (2.7)	−7.1 (4.9)	−3.2 (2.7)
PRK	300	66 (27)	33.7 (15.9)	9.1 (5.0)	−4.6 (2.4)	−8.5 (7.9)	−3.9 (4.4)
PRK	343	79 (18)	34.2 (15.2)	10.6 (4.6)	−6.3 (2.5)	−8.9 (6.7)	−4.6 (3.7)
AQN	283	87 (12)	32.4 (17.9)	10.6 (5.4)	−6.9 (3.0)	−6.5 (5.6)	−2.8 (3.0)
AQN	300	72 (27)	32.5 (18.6)	10.9 (5.9)	−6.1 (3.7)	−8.2 (7.0)	−3.4 (3.5)
AQN	343	69 (29)	35.2 (18.3)	11.4 (6.1)	−6.5 (4.2)	−9.1 (6.8)	−4.2 (3.4)

^aMD simulation temperature.

^bPersistence degree of the salt bridge.

^cRelative solvent-accessible surface area of the salt bridge.

^dDesolvation free energy penalty paid by the salt bridge.

^eInteraction free energy between the two charged side chains within the salt bridge.

^fInteraction free energy of the salt-bridging side chains with the remainder of the protein.

^gTotal electrostatic free energy (or electrostatic strength) of the salt bridge, which is the sum of the above three energy terms.

As shown in Table 2, the average values of salt-bridge P-degrees vary between 66% and 87% and either increase or decrease as temperature increases. The psychrophilic VPR has a smaller average value of salt-bridge R-SASA than its warm-adapted counterparts at each temperature, indicating more salt-bridge burial in VPR. This explains the relatively higher desolvation energy penalties (ΔΔG_dslv-sb) paid by the salt bridge in VPR than in PRK and AQN. Increasing the temperature from 283 to 300 K either increases (for PRK and AQN) or decreases (for VPR) the average value of R-SASA, while a further increase to 343 K increases the R-SASA average values of all three proteases, which can be attributed to greater relaxation of the protein structures in the 343 K simulations.

For all three proteases, the average values of desolvation energy penalty (ΔΔG_dslv-sb) increase slightly on average as temperature increases. Similar results were observed in the thermophilic and mesophilic glutamate dehydrogenase monomers (Tables III(A)–III(C) in ref. 22). The observed increase in the desolvation penalty with increasing temperature in the continuum electrostatics calculations can be attributed to the increased energy conversion factor (see the Materials and methods section), which over-amplifies the reduced desolvation penalty (in units of kT) resulting from the decreased dielectric constant of water and thus gives a higher final value (in units of kcal mol⁻¹) at a higher temperature.

Nevertheless, as temperature increases, the decreased water dielectric constant reduces the solvent screening for electrostatic interactions between the two salt-bridging side chains and between the salt bridge and its surroundings. This leads to a larger increase in the magnitude of the summed bridge (ΔΔG_brd-sb) and protein (ΔΔG_prt-sb) energy terms than that of the desolvation penalty term, ultimately resulting in a more negative total electrostatic free energy value (ΔΔG_tot-sb) at a higher temperature. For instance, when the temperature increases from 283 to 300 K and from 300 to 343 K, the average values of ΔΔG_tot-sb are reduced by −0.8 and −0.9 kcal mol⁻¹ for VPR, −0.7 and −0.7 kcal mol⁻¹ for PRK, and −0.6 and −0.8 kcal mol⁻¹ for AQN, respectively (Table 2). These results agree with those of previous studies,^7,10,22 collectively indicating that an increase in temperature enhances the average electrostatic strength of the salt bridge.

At 300 K, the average salt-bridge electrostatic strengths of PRK (−3.9 kcal mol⁻¹) and VPR (−3.8 kcal mol⁻¹) are comparable to each other and stronger than that of AQN (−3.4 kcal mol⁻¹), suggesting that salt bridges on average provide greater stabilization to PRK and VPR than to AQN at this temperature. However, the salt bridge is strongest and weakest in the thermophilic AQN (−4.2 kcal mol⁻¹) and psychrophilic VPR (−3.0 kcal mol⁻¹) at their respective habit temperatures, respectively. Compared to the VPR salt bridge at 283 K, the average electrostatic strength of the AQN salt bridge at 343 K is stronger because of differences in the bridge and protein energy terms, which are more favorable by −1.4 and −0.9 kcal mol⁻¹, respectively, although the desolvation penalty is more unfavorable by 1.1 kcal mol⁻¹. In addition, at each temperature, VPR exhibits a greater variability (i.e., a higher SD value) in the average salt-bridge electrostatic strength than AQN.

Electrostatic free energy contribution of individual salt bridges

Tables 3–5 present the P-degree, R-SASA, and average energy values of individual salt bridges calculated over the concatenated equilibrium MD trajectories of VPR, PRK, and AQN at the respective habitat temperatures (i.e., 283, 300, and 343 K), respectively. For the three proteases, most salt bridges show R-SASA values greater than 20%, while only a few have values smaller than 10%. A clear trend is that as the R-SASA value decreases, the desolvation energy penalty paid by the salt bridge increases. Another trend is that salt bridges with high P-degree values (>80%) typically show more favorable values of bridge energy terms than those with low P-degree values (<50%).

Persistence degree (P-degree), relative solvent-accessible surface area (R-SASA), and average energy values of individual salt bridges during MD simulations of VPR at 283 K.

Salt bridgea	P-degree (%)	R-SASA (%)	ΔΔGdslv-sbb (kcal mol−1)	ΔΔGbrd-sbc (kcal mol−1)	ΔΔGprt-sbd (kcal mol−1)	ΔΔGtot-sbe (kcal mol−1)
Arg12-Asp187 (c)	100	4.5	19.5 (1.4)	−13.7 (1.3)	−6.6 (1.0)	−0.8 (1.0)
Arg16-Asp278 (c)	25	43.3	6.0 (1.4)	−1.1 (1.2)	−7.1 (2.2)	−2.3 (1.8)
Asp58-Arg94 (c)	100	4.6	18.6 (0.9)	−7.5 (0.7)	−23.5 (2.0)	−12.4 (1.7)
Asp61-Arg94 (c)	99	31.3	9.5 (0.8)	−2.8 (0.7)	−11.9 (2.9)	−5.1 (2.6)
Asp142-Arg173 (c)	95	20.7	12.3 (2.7)	−7.9 (2.2)	−5.7 (2.1)	−1.2 (1.4)
Arg189-Asp263 (c)	34	34.2	8.7 (1.8)	−1.9 (1.9)	−11.0 (2.5)	−4.2 (2.0)
Glu240-Arg255 (c)	100	24.8	8.4 (0.7)	−5.7 (0.7)	−2.6 (0.6)	0.1 (0.7)
Glu258-Lys271	62	26.7	6.2 (2.0)	−3.8 (2.4)	−3.0 (1.7)	−0.7 (1.5)
Asp263-Arg265	22	60.1	3.3 (1.6)	−1.5 (2.0)	−2.1 (1.9)	−0.4 (1.5)

^aCrystal salt bridges retained during MD simulations are followed by ‘c’ in parentheses.

^bThe desolvation penalty term. SD is in parentheses.

^cThe bridge energy term. SD is in parentheses.

^dThe protein energy term. SD is in parentheses.

^eThe total electrostatic free energy (or electrostatic strength). SD is in parentheses.

Persistence degree (P-degree), relative solvent-accessible surface area (R-SASA), and average energy values of individual salt bridges during MD simulations of PRK at 300 K.

Salt bridgea	P-degree (%)	R-SASA (%)	ΔΔGdslv-sbb (kcal mol−1)	ΔΔGbrd-sbc (kcal mol−1)	ΔΔGprt-sbd (kcal mol−1)	ΔΔGtot-sbe (kcal mol−1)
Arg12-Asp187 (c)	100	10.3	14.8 (1.8)	−7.3 (1.3)	−12.2 (1.5)	−4.6 (1.5)
Arg12-Asp260 (c)	100	21.4	12.3 (1.0)	−3.4 (0.6)	−19.0 (1.8)	−10.1 (1.8)
Glu43-Arg64	40	43.8	4.6 (1.7)	−1.9 (1.8)	−6.8 (2.7)	−4.1 (1.9)
Glu48-Arg80 (c)	95	32.0	7.5 (1.3)	−6.6 (1.6)	−2.9 (2.9)	−2.0 (2.2)
Glu50-Arg52 (c)	90	28.6	12.1 (2.4)	−5.7 (2.0)	−11.6 (2.8)	−5.2 (2.0)
Glu50-Lys87	47	46.0	5.2 (2.0)	−3.4 (2.8)	−4.4 (1.3)	−2.7 (1.4)
Asp65-Lys94	40	5.6	20.7 (4.7)	−6.2 (4.8)	−30.4 (7.9)	−15.9 (6.0)
Lys94-Asp98 (c)	68	27.4	12.1 (3.3)	−5.7 (3.2)	−11.3 (4.1)	−4.8 (3.2)
Asp112-Arg147 (c)	50	53.5	4.4 (3.0)	−3.3 (2.9)	−0.4 (0.2)	0.7 (0.7)
Asp117-Arg121 (c)	100	21.8	13.1 (0.9)	−9.8 (1.2)	−4.2 (0.7)	−0.9 (0.9)
Asp165-Arg167	41	45.0	6.4 (1.9)	−2.8 (2.5)	−5.1 (2.1)	−1.6 (1.4)
Asp184-Arg188 (c)	87	27.7	7.9 (1.7)	−4.3 (2.0)	−8.3 (2.4)	−4.8 (1.9)
Arg185-Asp207	21	44.7	3.6 (1.1)	−1.0 (0.9)	−2.0 (1.7)	0.6 (1.2)
Arg250-Asp254	47	64.0	3.1 (1.5)	−2.0 (1.9)	−0.2 (0.5)	0.8 (0.8)

^aCrystal salt bridges retained during MD simulations are followed by ‘c’ in parentheses.

^bThe desolvation penalty term. SD is in parentheses.

^cThe bridge energy term. SD is in parentheses.

^dThe protein energy term. SD is in parentheses.

^eThe total electrostatic free energy (or electrostatic strength). SD is in parentheses.

Persistence degree (P-degree), relative solvent-accessible surface area (R-SASA), and average energy values of individual salt bridges during MD simulations of AQN at 343 K.

Salt bridgea	P-degree (%)	R-SASA (%)	ΔΔGdslv-sbb (kcal mol−1)	ΔΔGbrd-sbc (kcal mol−1)	ΔΔGprt-sbd (kcal mol−1)	ΔΔGtot-sbe (kcal mol−1)
Arg12-Asp187 (c)	100	2.7	21.5 (1.9)	−15.5 (1.6)	−8.8 (1.4)	−2.8 (1.5)
Asp17-Arg260 (c)	99	42.9	8.4 (0.9)	−7.6 (1.3)	−2.0 (0.7)	−1.2 (0.9)
Arg31-Glu239 (c)	66	45.6	10.6 (2.5)	−5.6 (3.7)	−15.1 (3.2)	−10.1 (2.7)
Arg43-Asp214b (c)	28	40.6	7.4 (3.2)	−2.9 (3.9)	−6.2 (3.1)	−1.7 (2.4)
Arg47-Asp214b	20	59.7	5.1 (2.4)	−1.4 (1.5)	−7.1 (6.2)	−3.4 (4.2)
Asp58-Arg94 (c)	100	11.6	21.7 (1.6)	−9.8 (2.0)	−22.2 (3.0)	−10.3 (2.5)
Arg94-Asp97	37	21.0	12.5 (2.4)	−1.8 (1.2)	−17.7 (6.5)	−7.0 (4.3)
Asp112-Arg116	81	56.6	5.3 (1.7)	−5.2 (2.5)	−0.7 (0.5)	−0.6 (1.0)
Asp142-Arg173 (c)	94	23.8	16.0 (2.4)	−10.5 (2.7)	−8.6 (1.8)	−3.2 (1.9)
Lys146-Glu176	62	47.9	5.3 (3.0)	−4.8 (3.5)	−2.5 (1.9)	−2.0 (1.9)

^aCrystal salt bridges retained during MD simulations are followed by ‘c’ in parentheses.

^bThe desolvation penalty term. SD is in parentheses.

^cThe bridge energy term. SD is in parentheses.

^dThe protein energy term. SD is in parentheses.

^eThe total electrostatic free energy (or electrostatic strength). SD is in parentheses.

In VPR, PRK, and AQN, the percentages of highly stabilizing salt bridges (i.e., those with ΔΔG_tot-sb ≤ −5 kcal mol⁻¹) are 22.2% (2 out of 9), 21.4% (3 out of 14), and 30% (3 out of 10), respectively, and those of moderately stabilizing salt bridges (−5 kcal mol⁻¹ < ΔΔG_tot-sb ≤ −1 kcal mol⁻¹) are 33.3% (3 out of 9), 50.0% (7 out of 14), and 60.0% (6 out of 10), respectively. Consequently, the percentage of effectively stabilizing salt bridges is in the order of AQN (90.0%) > PRK (71.4%) > VPR (55.6%).

Marginally stabilizing/destabilizing salt bridges are defined as those with |ΔΔG_tot-sb| < 1 kcal mol⁻¹. The thermophilic AQN has only one marginally stabilizing salt bridge (10.0%) and contains no destabilizing salt bridge; the numbers of marginally stabilizing/destabilizing salt bridges in VPR and PRK are 3 (33.3%)/1 (11.1%) and 1 (7.1%)/3 (21.4%), respectively. Notably, each of the marginally stabilizing/destabilizing salt bridges has a SD equal to or greater than the corresponding |ΔΔG_tot-sb| value, indicating that these salt bridges can interconvert between being stabilizing and destabilizing during MD simulations.

In summary, the thermophilic AQN shows the highest percentage of effectively stabilizing salt bridges and lowest percentage of marginally stabilizing/destabilizing salt bridges, and the opposite results were observed in the psychrophilic VPR. This explains why the averaged salt-bridge electrostatic strength is stronger in AQN (−4.2 kcal mol⁻¹) than in VPR (−3.0 kcal mol⁻¹). Additionally, because the marginally stabilizing/destabilizing salt bridges can interconvert between being stabilizing and destabilizing, the high proportion of these salt bridges in VPR may indicate their role in cold adaptation.

Electrostatic free energy contribution of salt-bridge networks

The electrostatic strengths of individual salt-bridge networks were calculated along the concatenated equilibrium MD trajectories of the three proteases to quantify their effect on protein thermostability. As observed for the salt bridges, most salt-bridge networks show increased electrostatic strengths as temperature increases; this is because of a larger increase in the magnitude of summed bridge and protein energy terms than that of the desolvation penalty when the temperature is elevated (Table S4†).

Table 6 lists the average values of electrostatic strengths and energy terms of individual salt-bridge networks during MD simulations of the three proteases at the respective habitat temperatures of the source organisms. All salt-bridge networks are, on average, stabilizing. Only one network, Arg43-Asp214b-Arg47 in AQN, is marginally stabilizing and shows a larger SD than the corresponding |ΔΔG_tot-ntwk| value, implying its strong capability to interconvert between being stabilizing and destabilizing during simulations.

Relative solvent-accessible surface area (R-SASA) and average energy values of individual salt-bridge networks during MD simulations of VPR (283 K), PRK (300 K), and AQN (343 K) at the respective habitat temperatures of the source organisms.

Salt-bridge networka	Protein	R-SASAb (%)	ΔΔGdslv-ntwkc (kcal mol−1)	ΔΔGbrd-ntwkd (kcal mol−1)	ΔΔGprt-ntwke (kcal mol−1)	ΔΔGtot-ntwkf (kcal mol−1)
Asp58-Arg94-Asp61 (c)	VPR	21.0	21.2 (1.0)	−6.5 (1.4)	−33.8 (4.2)	−19.2 (3.4)
Arg189-Asp263-Arg265	VPR	43.3	10.1 (2.3)	−2.2 (2.9)	−11.9 (2.5)	−4.0 (1.9)
Arg52-Glu50-Lys87	PRK	34.1	13.4 (2.9)	−7.6 (3.6)	−10.4 (1.4)	−4.6 (1.6)
Asp65-Lys94-Asp98	PRK	21.6	24.1 (5.8)	−9.6 (5.8)	−29.5 (7.5)	−15.0 (5.9)
Asp187-Arg12-Asp260 (c)	PRK	20.8	19.3 (2.0)	−7.4 (1.4)	−30.2 (2.4)	−18.4 (2.1)
Arg43-Asp214b-Arg47	AQN	50.4	9.1 (3.3)	−4.0 (3.8)	−5.5 (2.7)	−0.4 (2.5)
Asp58-Arg94-Asp97	AQN	18.6	25.8 (2.7)	−10.9 (1.9)	−29.8 (7.3)	−15.0 (5.0)

^aCrystal salt-bridge networks retained during MD simulations are followed by ‘c’ in parentheses.

^bR-SASA was calculated as the average of relative solvent-accessible surface areas of the network-participating residues.

^cThe desolvation energy penalty term. SD is in parentheses.

^dThe bridge energy term. SD is in parentheses.

^eThe protein energy term. SD is in parentheses.

^fThe total electrostatic free energy (or electrostatic strength). SD is in parentheses.

Interestingly, the two crystal salt-bridge networks (Asp58-Arg94-Asp61 in VPR and Asp187-Arg12-Asp260 in PRK) retained during MD simulations are most stabilizing among the networks listed in Table 6. Notably, the ΔΔG_tot-ntwk values of these two networks are more negative than the summed ΔΔG_tot-sb values of the individual network-participating salt bridges, indicating that they improve the electrostatic strength overall compared to the network participants (cooperative effect of salt-bridge network). Comparison between the corresponding energy terms of the network and individual network-participating salt bridges reveals a significant increase in the magnitude of the protein energy term (ΔΔG_prt-ntwk), which gives rise to the enhanced electrostatic strength of the network.

The newly formed salt-bridge networks observed in simulations can be very highly stabilizing (ΔΔG_tot-ntwk ≤ −10 kcal mol⁻¹), moderately stabilizing (−5 kcal mol⁻¹ < ΔΔG_tot-ntwk ≤ −1 kcal mol⁻¹), or even only marginally stabilizing (−1 kcal mol⁻¹ < ΔΔG_tot-ntwk < 0 kcal mol⁻¹). Furthermore, the electrostatic strengths of these networks were observed to be either stronger or weaker than those of the individual network-participating salt bridges, depending on the differences in the protein energy term between a network (ΔΔG_prt-ntwk) and its participates (ΔΔG_prt-sb). Therefore, the electrostatic environment surrounding the salt-bridge network appears to be an important factor in determining the cooperative effect of the salt-bridge network.

Electrostatic free energy contribution of calcium ions

The crystal structures of VPR, PRK, and AQN contain three, two, and two calcium ions, respectively (Fig. 1). Similar to the results observed for the salt bridges and salt-bridge networks, all calcium ions show increased electrostatic strength as the simulation temperature increases (Tables S5 and S6†). Table 7 lists the average values of the SASA and energy terms of individual calcium ions during MD simulations of the three proteases at the respective habitat temperatures of the source organisms. All three proteases share a common Ca²⁺-binding site, to which VPR-Ca1, PRK-Ca1, and AQN-Ca2 bind (Table 7 and Fig. 1). Although PRK-Ca1 and AQN-Ca2 show larger SASA average values than VPR-Ca1, the two formers have slightly higher desolvation penalty average values than the latter. Furthermore, the two formers, especially AQN-Ca2, have larger magnitudes of average values of the protein energy term than VPR-Ca1, thus resulting in stronger electrostatic strengths.

Average values of solvent-accessible surface area (SASA) and energy terms of individual calcium ions during MD simulations of VPR (283 K), PRK (300 K), and AQN (343 K) at the respective habitat temperatures of the source organisms.

No.	Protein	Ca2+-binding site	SASA (Å2)	ΔΔGdslv-Caa (kcal mol−1)	ΔΔGprt-Cab (kcal mol−1)	ΔΔGtot-Cac (kcal mol−1)
Ca1	VPR	P175, G177, D200	10.5 (3.8)	28.6 (3.2)	−32.7 (3.5)	−4.1 (1.9)
Ca2	VPR	D58, D61b, D62	4.9 (3.3)	42.4 (2.9)	−68.5 (5.2)	−26.1 (3.1)
Ca3	VPR	D11, D14, Q15, D20, N22	0.2 (0.8)	59.6 (5.3)	−91.4 (9.1)	−31.8 (4.6)
Ca1	PRK	P175, V177, D200	14.6 (8.2)	30.3 (6.9)	−34.9 (7.0)	−4.6 (1.9)
Ca2	PRK	T16, D260	35.7 (4.9)	19.6 (1.9)	−27.8 (2.1)	−8.2 (1.3)
Ca1	AQN	D11, D14, Q15, S20, S22	2.5 (3.0)	63.2 (6.4)	−90.7 (8.4)	−27.4 (4.6)
Ca2	AQN	V174, A177, T179, D200	13.8 (5.1)	31.7 (3.6)	−39.5 (5.5)	−7.7 (3.3)

^aThe desolvation penalty term. SD is in parentheses.

^bThe protein energy term. SD is in parentheses.

^cThe total electrostatic free energy (or electrostatic strength). SD is in parentheses.

The two extremophilic proteases share a common Ca²⁺-binding site, to which VPR-Ca3 and AQN-Ca1 bind (Table 7, Fig. 1A and C). VPR-Ca3 is almost completely buried within its binding site, while AQN-Ca1 shows a relatively larger exposure to the solvent. Although these two calcium ions show comparable average values of the protein energy term, VPR-Ca3 needs to overcome a smaller desolvation penalty than AQN-Ca1 and thus yields a stronger electrostatic strength (−31.8 vs. −27.4 kcal mol⁻¹).

VPR-Ca2 and PRK-Ca2 are unique to the respective crystal structures of VPR and PRK (Table 7, Fig. 1A and B). VPR-Ca2, which is coordinated by residues Asp58, Asp61b, and Asp62, has an average electrostatic strength value of −26.1 kcal mol⁻¹. Such an ultra-high stability can be ascribed to the high concentration of negative charges at the Ca2 site (three aspartates), which results in a protein energy term (−68.5 kcal mol⁻¹) with a much larger magnitude than the desolvation energy term (42.4 kcal mol⁻¹). PRK-Ca2 is coordinated by only two residues (Thr16 and Asp260), and hence is most exposed to the solvent and suffers the smallest desolvation penalty among all calcium ions; nevertheless, PRK-Ca2 also shows the lowest magnitude for the protein energy term, ultimately yielding a moderately favorable electrostatic strength (−8.2 kcal mol⁻¹).

Taken together, despite the differences in electrostatic strengths, all calcium ions in the three proteases contribute favorably to the protein thermostability because of their larger magnitudes for the protein energy term than for the desolvation penalty term. The three structurally equivalent calcium ions (VPR-Ca1, PRK-Ca1, and AQN-Ca2) show electrostatic stability in the expected order of VPR < PRK < AQN. However, unexpectedly, Ca3 in the psychrophilic VPR is more stabilizing than its equivalent, Ca1 in the thermophilic AQN, and Ca2 unique to VPR is also highly stabilizing, making it difficult to determine how the differences in the electrostatic strengths of these calcium ions contribute to temperature adaptation of serine proteases.

Electrostatic potential surface

Among the three proteases, the psychrophilic VPR has the highest numbers of charged acidic residues (24) and polar uncharged residues (141), while the lowest numbers of charged basic residues (14) and hydrophobic/nonpolar residues (98) (Table S2†). Therefore, VPR has the highest ratios of acidic to basic residues (1.71) and polar uncharged to hydrophobic residues (1.44), respectively. These two ratios are lowest in the thermophilic AQN (0.94 and 1.13) and moderate in the mesophilic PRK (0.95 and 1.38). These differences are expected to cause differences in the electrostatic surface potential and hydrophobicity among the three proteases.

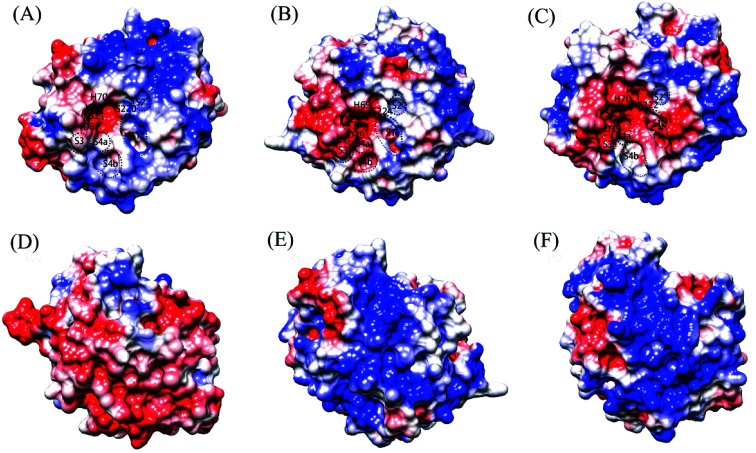
Fig. 3 shows the electrostatic potential surface representations of the three proteases obtained by continuum electrostatics calculations on the representative structures of the concatenated equilibrium trajectories at the respective habitat temperatures of the source organisms. A common feature is that the substrate-binding site S2 and catalytic active center are characterized by the electro-negative potential, although the negatively charged surface is more extended around the active centers of the warm-active proteases, covering the substrate-binding sites S3 and S4 (composed of S4a and S4b) in PRK (Fig. 3B) and S1, S3, and S4a in AQN (Fig. 3C). In PRK and AQN, the other regions of the front surfaces are largely interspersed by both electro-positive and electro-neutral/hydrophobic patches, while there is a large electro-positive patch on the upper half of VPR front surface (Fig. 3A). The most pronounced differences occur among the back surfaces of the three proteases. VPR shows a predominant distribution of electro-negative potential over the back surface (Fig. 3D). Despite the sporadic distributions of electro-negative and electro-neutral patches on the back surfaces of PRK (Fig. 3E) and AQN (Fig. 3F), electro-positive patches are dominant; notably, the positively charged potential appears to be larger, denser, and more continuous on the back surface of AQN than on that of PRK. The differential electrostatic surface potential distributions in relation to temperature adaptation of the three proteases will be discussed in the Discussion section.

Fig. 3. Molecular surface representations showing the electrostatic surface potentials of the three proteases. (A), (B), and (C) are the front surfaces of VPR (at 283 K), PRK (at 300 K), and AQN (at 343 K), respectively; (D), (E), and (F) are their respective back surfaces. Front surface is the surface containing the catalytic active center/catalytic triad; back surface is opposite to the front surface. The positively and negatively charged surfaces are colored blue and red, respectively, and the electro-neutral (or nonpolar/hydrophobic) surface is colored white. The catalytic triad residues and approximate locations of the substrate-binding sites/pockets, i.e., S2′, S1, S2, S3, and S4a and S4b (which are sub-sites of S4), are labeled on the front surface.

Discussion

According to the spatial distribution of salt bridges, the enzyme structure can be approximately divided into four distinct regions where salt bridges are relatively enriched (Fig. 2). Region I is in the neighborhood of the N-terminus and primarily comprises a 3/10 helix and several surface-exposed loops. Region II is composed of two loops, i.e., the well-exposed polar surface loop (PSL, residues 58–68) and S2-loop (residues 95–101), which are parts of, or in close vicinity to, the S2 substrate-binding site⁵² (see Fig. 1 and 3A–C). Region III is located at the bottom of the substrate-binding site S1 and comprises a part of α4, a 3/10 helix (residues 166–168; see Fig. S1†), and two loops connected by the 3/10 helix. Region IV, which is composed of several surface-exposed loops and parts of α1 and α6, is relative large and lies near both the N- and C-termini.

In the AQN crystal structure, the proportion of salt-bridging residues out of the total number of charged residues is 36.4%, which is comparable to that in VPR (36.8%) but lower than that in PRK (41.0%) (Table S2†). However, during MD simulations, AQN gained more newly formed salt bridges (four) than VPR (two), thus increasing the proportion to 60.6%, higher than that in VPR (47.4%). In VPR, the two newly formed salt bridges (Glu258-Lys271 and Asp263-Arg265) are located at the C-terminus (region IV; see Fig. 2A) and only marginally stabilizing (Table 3). In AQN, the four newly formed salt bridges (Arg47-Asp214b, Arg94-Asp97, Asp112-Arg116, and Lys146-Glu176) are distributed in different regions of the enzyme structure (Fig. 2C), with three being highly or moderately stabilizing and only one marginally stabilizing (Table 5). Interestingly, in a study by Jónsdóttir et al.,⁵³ three (Arg47-Asp214b, Asp112-Arg116, and Lys146-Glu176) of the four newly formed salt bridges were also detected by MD simulations; furthermore, through site-directed mutagenesis of the salt-bridging residues followed by stability measurement, they found that these three salt bridges had little effect on the overall thermostability of AQN. This is likely because other factors (e.g., structural/electrostatic environments surrounding the salt-bridge site and remaining interactions) can compensate for the lost stability.⁵³ However, in this section we only focus on the possible effects of individual salt bridges on the stability and flexibility of the local regions connected by salt bridges based on the calculated electrostatic strength. Specifically, the newly formed Arg94-Asp97 with a calculated electrostatic strength of −7.0 kcal mol⁻¹ links the C-terminus of β3 to the S2-loop (region II); therefore, this salt bridge may help to enhance S2 site stability at high temperatures. The newly formed Lys146-Glu176 shows an electrostatic strength of −2.0 kcal mol⁻¹ and connects α4 and a loop near the S1 site (region III), thus likely aiding in stabilizing the S1 site of AQN. The newly formed Arg47-Asp214b, which connects two surface-exposed regions, a 3/10 helix and the loop located between β8 and β9 (region I), contributes −3.4 kcal mol⁻¹ to their stability. Asp112-Arg116 is within α3 and has a marginal stabilizing effect (−0.6 kcal mol⁻¹) on this helix. The mesophilic PRK has six newly formed salt bridges (Fig. 2B and Table 4), of which three lie close to the substrate-binding sites (i.e., Glu43-Arg64 and Asp65-Lys94 lie around the S2 site, and Asp165-Arg167 is near the S1 site) and contribute to stabilizing these sites, while the other three are dispersed in peripheral regions and are either moderately stabilizing or even marginally destabilizing.

As shown in Fig. 2A, all nine salt bridges in VPR are localized in three distinct regions (i.e., regions II–IV) but region I contains no salt bridge. However, in PRK (14 salt bridges) and AQN (10 salt bridges), salt bridges are scattered throughout the structure (Fig. 2B and C, respectively), with relative enrichment observed in regions I–IV. It is possible that the scattered salt-bridge distribution is advantageous for improving the overall protein stability, while the relatively concentrated distribution may play a role in modulating the balance between local rigidity and local flexibility. Interestingly, region III contains two salt bridges in AQN (Asp142-Arg173 and Lys146-Glu176) but only one salt bridge in PRK (Asp165-Arg167) and VPR (Asp142-Arg173), and those in AQN are more electrostatically stabilizing than in PRK and VPR. Therefore, the AQN region-III salt bridges are likely more conducive for maintaining S1 site stability at high temperatures. Comparison of flexibility using the C_α root mean square fluctuation (RMSF) calculated from our MD trajectories as index (ESI Table S7†) reveals that the AQN S1 site is indeed most stable among the three proteases because of its lowest average C_α RMSF values at all three simulation temperatures.

For PRK and AQN, region I contains three (Glu48-Arg80, Glu50-Arg52, and Glu50-Lys87) and two salt bridges (Arg43-Asp214b and Arg47-Asp214b), respectively. These salt bridges collectively contribute favorably to region I stability with electrostatic strength ranging from −1.7 to −5.2 kcal mol⁻¹ (Tables 4 and 5). Notably, in the thermophilic AQN, Arg43 and Arg47 are next to the catalytic-triad residue Asp39, and Asp214b is in a loop connected to the nucleophilic residue Ser224 via β9; therefore, salt bridges involving these residues may contribute to improving the stability of the catalytic triad via the neighborhood effect and/or hinge-bending mechanism.^38,54–56 The AQN mutants R47E and D214bN have been shown to have higher K_cat values (K_m values are comparable to that of the wild type) and hence higher catalytic efficiencies than the wild type at 313 K,⁵³ suggesting that local destabilization of salt-bridge sites that are relatively distant from the catalytic triad can facilitate catalysis-associated conformational changes via the hinge-bending mechanism.

Additionally, the two salt bridges, Arg31-Glu239 and Glu240-Arg255, which may affect stability of the catalytic triad via the hinge-bending mechanism, were also observed in AQN and VPR, respectively. For Arg31-Glu239, Arg31 is in a loop preceding β1 at whose C-terminus the catalytic triad residue Asp39 lies, and Glu239 resides at the C-terminus of α5 whose N-terminus carries the nucleophilic residue Ser224 (Fig. 2C); moreover, this salt bridge was evaluated to be highly stabilizing (−10.1 kcal mol⁻¹) in the present study; therefore, it may aid in improving the AQN catalytic triad stability at high temperatures. However, Jónsdóttir et al. showed that the disruption of this salt bridge by R31F mutation had nearly no effect on the overall thermostability of AQN.⁵³ This may be because the intact Glu239 still interacts favorably with its surrounding (with the protein energy term and electrostatic strength of −23.0 and −14.6 kcal mol⁻¹, respectively), and this compensates for the lost stability arising from the R31F mutation. For Glu240-Arg255 (Fig. 2A), only Glu240 is connected to Ser224 via α5; furthermore, this salt bridge is marginally destabilizing (0.1 kcal mol⁻¹). Therefore, it may facilitate fluctuations in Ser224, thus benefiting to the nucleophilic attack at low temperatures. In addition, comparison of the average C_α RMSF values of the catalytic triad among the three proteases (ESI Table S7†) shows that the catalytic triad is most mobile and stable in VPR and AQN, respectively, thus implying the possibility for the hinge-bending-mediated stabilizing/destabilizing effect of the above salt bridges.

Although the thermophilic AQN contains no salt-bridge network in the crystal structure, two newly formed networks were observed in MD simulations (Table 6 and Fig. 2C). One of them, Asp58-Arg94-Asp97, connects PSL to S2-loop (region II) and may have contributed to enhancing the stability of these two loops because of its strong electrostatic strength (−15.0 kcal mol⁻¹). Interestingly, the newly formed network Asp65-Lys94-Asp98 (−15.0 kcal mol⁻¹), which shows a similar stabilizing effect on PSL and S2-loop, was observed in MD simulations of PRK (Table 6 and Fig. 2B). For the psychrophilic VPR, the retained crystal salt-bridge network, Asp58-Arg94-Asp61 (−19.2 kcal mol⁻¹), links the C-terminus of β3 to the PSL and thus stabilizes these two substructures (Tables 3 and 6, Fig. 2A). This network appears to indirectly stabilize the S2-loop as the C-terminus of β3 precedes the S2-loop, but directly stabilizes the PSL because the two network-participating residues (Asp58 and Asp61) are within the PSL. In fact, the average RMSF values of the S2-loop at all three temperatures are indeed relatively higher in VPR than in PRK and AQN (ESI Table S7†), implying a weak stabilizing effect of Asp58-Arg94-Asp61 on the VPR S2-loop. Interestingly, the calcium ion Ca2, which is unique to VPR, also contributes greatly to the PSL stability by −26.1 kcal mol⁻¹ (Table 7). For all three proteases, most residues in the PSL are polar and highly exposed to the solvent. Notably, the PSL of VPR has a three-residue insertion relative to that of the other two proteases (Fig. S1†). Therefore, the PSL is potentially more unstable in the psychrophilic VPR than in its warm-active counterparts. In VPR, additional stabilizing factors such as calcium (Ca2) binding, disulfide bridge (Cys66-Cys98; see Fig. 1A), and salt bridges/salt-bridge network may act together to enhance the stability of this loop. Actually, at 300 K, the average RMSF value of the PSL of VPR (0.81 Å) is comparable to that of AQN (0.82 Å) and lower than that of PRK (1.02 Å).

The other salt-bridge networks in the three proteases are far away from the substrate-binding sites and contribute to stabilizing several surface-exposed regions connected by these networks. For instance, in PRK, the retained crystal salt-bridge network Asp187-Arg12-Asp260 (region IV) links together a long loop (residues 184–200) located between β6 and β7, α1 near the N-terminus, and a loop near the C-terminus. This network (−18.4 kcal mol⁻¹), in conjunction with Ca2 (−8.2 kcal mol⁻¹) coordinated by Thr16 and Asp260 (Table 7 and Fig. 2B), contributes greatly to stabilizing the N- and C-termini and the long loop of PRK. In VPR, the newly formed salt-bridge network Arg189-Asp263-Arg265 (Table 6 and Fig. 2A) functions similarly to Asp187-Arg12-Asp260 in PRK, but stabilizes only the long loop and C-terminus with weaker electrostatic strength (−4.0 kcal mol⁻¹).

The protein surface constitutes an interface through which a protein directly interacts with the solvent.^57,58 However, the differently charged surface patches (i.e., negatively charged, positively charged, and neutral/hydrophobic patches) interact in different manners with water molecules and thus exhibit different hydration properties, which in turn can affect/modulate protein biophysical properties such as solubility, thermostability, and structural flexibility/rigidity/stability. It has been shown that increased negative surface charge correlates strongly with increased protein solubility,⁵⁹ and that the positively charged surface associates with protein insolubility to a much larger extent than the nonpolar surface.⁶⁰ This is because of the protic nature of water, which makes water molecules interact more favorably with the electro-negative surface with less loss of the solvent entropy than with the electro-positive surface.⁶¹ Moreover, the structure of hydration water around differently charged amino acids is very different: water molecules around the negatively charged and polar uncharged residues (whose side-chain polar atoms carry partial negative charges) form a high-density, collapsed structure (CS) and those around nonpolar and positively charged residues form a low-density, expanded structure (ES).^62,63 Because the CS water is characterized by weak hydrogen-bonding strength and fast dynamics, and the ES water is characterized by strong hydrogen-bonding strength and slow dynamics, the CS and ES water environments likely facilitate and restrict protein conformational fluctuations, respectively.^58,63–66

Indeed, it has been shown that increased anionic surface (and thus increased CS water environment) can increase the flexibility of rat trypsinogen,⁶⁷ and that the position of ES ⇆ CS equilibrium around the enzymes is important for their activity with the enzyme balanced between flexibility (CS environment) and rigidity (ES environment).⁶⁸ In our previous study,⁶⁹ we found that, when compared to the nematode cuticle-degrading serine protease Ver112 with predominant distributions of electro-positive and electro-neutral potentials on the protein surface, the cuticle-degrading protease PII characterized by the heavily negatively charged surface potential exhibited higher structural flexibility and catalytic activity at room temperature and decreased thermostability. In the present study, we choose the mesophilic PRK as an example to illustrate the correlation of the differently charged surfaces with the surface flexibility. For the solvent-exposed residues that are covered by the electro-negative, electro-positive, and electro-neutral potentials, their average C_α RMSF values calculated at 300 K are 1.16 ± 0.76, 0.61 ± 0.31, and 0.73 ± 0.39 Å, respectively, and the percentages of them with RMSFs > 0.61 Å (i.e., the average RMSF value of all residues in PRK) are 68.8%, 30.0%, and 58.8%, respectively. These indicate that the negatively charged surface tends to be more flexible than the neutral/nonpolar surface, which in turn tends to be more flexible than the positively charged surface. Additionally, the increased exposure of the hydrophobic surface area in the warm-active enzymes compared to their cold-adapted counterparts has been suggested to be related to the enhanced thermostability of warm-active enzymes.^28,70 To this end, it is reasonable to consider that the negatively charged surface potential contributes to increasing enzyme solubility, structural flexibility, and catalytic activity, while the electro-neutral/hydrophobic and electro-positive surface potentials contribute to increasing insolubility, thermostability, and structural rigidity/stability.

For the psychrophilic VPR, it appears likely that the dominant electro-negative potential on the back surface (Fig. 3D) ensures the low-temperature solubility, which is considered important for the enzyme's catalytic function at low temperatures.⁷ Interestingly, it has been shown that the origin of cold adaptation in trypsin is not localized to the active site but is related to the increased surface flexibility/softness of the psychrophilic trypsin compared to its mesophilic counterpart.⁷¹ For VPR, the dominant electro-negative surface potential may ensure sufficient surface or even global flexibility at low temperatures, thus likely contributing to maintaining the catalytic activity at low temperatures. At 283 K, the average C_α RMSF values of all residues in VPR, PRK, and AQN are 0.70, 0.52, and 0.51 Å, respectively (ESI Table S7†), indicating that VPR has the highest global flexibility.

The distribution range of the electro-negative surface potential around the active-site region in the three proteases shows unexpected results. In VPR, only the S2 site and active center exhibit a strong electro-negative potential (Fig. 3A), whereas in PRK and AQN, the strong electro-negative potential extends from the active center to the other substrate-binding sites (Fig. 3B and C). For all three proteases, the electro-negative character at the active center is helpful in enhancing its local conformational flexibility, which in turn is beneficial to the catalytic reaction by facilitating nucleophilic attack and proton transfer. However, for the thermophilic AQN, the potential high flexibility of the substrate-binding sites S1 and S2 (because of their strong electro-negativity) is detrimental to substrate stability at high temperatures. Nevertheless, the disulfide bridges (Cys66-Cys98 and Cys167-Cys198, which are close to the substrate sites S2 and S1, respectively), and particularly Ca2 (which resides near the S2 site) and several nearby salt bridges substantially enhance the stability of these two sites at high temperatures.

For the warm-active PRK and AQN, the predominant distributions of the electro-positive and electro-neutral surface patches may contribute to increasing their thermostability and structural rigidity. Notably, when compared to PRK, the back surface of AQN shows a larger and denser electro-positive potential, which may lower the solubility of AQN to a certain extent, but may also help increase the structural rigidity and thus the stability of AQN at high temperatures (for details of global stability/flexibility comparison, see ESI Table S7†). Additional studies are required to investigate the relationships between the electrostatic surface potentials and flexibility/rigidity/stability of the protein structure.

Conclusions

Here we have investigated the role of electrostatics in temperature adaptation of subtilisin-like serine proteases by performing a comparative study on the psychrophilic VPR, mesophilic PRK, and thermophilic AQN using multiple-replica MD simulations combined with continuum electrostatics calculations. During the MD simulations at the respective habitat temperatures of the source organisms, more new salt bridges were formed in the warm-active PRK and AQN than in the cold-adapted VPR, suggesting that care should be taken when performing comparative statistical analysis of salt-bridge numbers based on the crystal structures of homologous proteins. At the same temperatures, salt bridges on average are more stabilizing in VPR and PRK than in AQN, indicating that the salt bridge may not be a crucial factor in determining the overall thermostability of subtilisin-like serine proteases. Nevertheless, because the salt-bridge electrostatic strength increases as the simulation temperature increases, salt bridges on average provide greater stabilization to the thermophilic AQN at 343 K than to the psychrophilic VPR at 283 K. Actually, most salt bridges in AQN are effectively stabilizing at 343 K but in VPR nearly half of them exhibit the capability to interconvert between being stabilizing and destabilizing at 283 K, implying different roles of salt bridges in temperature adaptation of serine proteases.

For all three proteases at all three simulation temperatures, salt-bridge networks and calcium ions contribute on average more significantly to protein thermostability than salt bridges, although the cumulative contributions of salt bridges are comparable or even greater than those of salt-bridge networks or calcium ions because of the significantly higher number of salt bridges (ESI Table S6†). Nevertheless, there still exist some individual salt-bridges/salt-bridge networks capable of interconverting between being stabilizing and destabilizing, suggesting that they do not necessarily make a positive contribution to protein thermostability but could destabilize the local structural regions involved. Therefore, care must be taken when correlating a salt bridge to the local structural stability. Notably, all calcium ions in the three proteases make positive contributions to protein thermostability, supporting the proposal that the Ca²⁺ binding is an important factor in enhancing the thermostability of subtilisin-like proteases.⁷²

In the psychrophilic VPR, salt bridges and their networks are localized to three discrete regions (i.e., regions II–IV), whereas in the warm-active PRK and AQN, they are more dispersed throughout the structure, with relative enrichment in regions I–IV. Electrostatic interactions appear to contribute to both heat and cold adaptation of serine proteases via modulating the local structural stability and flexibility. Compared to PRK and VPR, AQN's region III (near the substrate-binding site S1) contains more salt bridges with stronger electrostatic strengths, which, together with the nearby Ca2 exhibiting the strongest electrostatic strength among the three structurally equivalent calcium ions (VPR-Ca1, PRK-Ca1, and AQN-Ca2), contribute more favorably to enhancing the S1 site stability of AQN at high temperatures. Compared to AQN and PRK, VPR's PSL seems to be potentially more unstable due to a three-residue insertion; however, the calcium ion Ca2 (which is unique to VPR), in conjunction with a salt-bridge network possessing a high stabilizing effect, may aid in enhancing the PSL stability of VPR even at low temperatures. In addition, some salt bridges, despite being relatively distant from the catalytic triad, were identified to affect the stability and flexibility of the catalytic center via the hinge-bending mechanism. For instance, in the thermophilic AQN, the three salt bridges, Arg43-Asp214b, Arg47-Asp214b, and Arg31-Glu239, likely enhance the active-center stability and hence oppose disorder at high temperatures, whereas in the psychrophilic VPR, a marginally stabilizing salt bridge, Glu240-Arg255, likely facilitates fluctuations in the nucleophilic residue and hence benefits to nucleophilic attack at low temperatures.

Compared to the electrostatic interactions involving salt bridges/salt-bridge networks and calcium ions, electrostatic surface potentials likely play an more important role in temperature adaptation of subtilisin-like serine proteases because differently charged surface patches can affect/modulate, via distinct interactions with water molecules, the protein solubility and thermostability and the structural flexibility/rigidity/stability. For all three proteases, the common negatively charged surface potential at the active center may provide the active-center flexibility necessary for nucleophilic attack and proton transfer. For the psychrophilic VPR, the predominant distribution of the electro-negative potential over the back surface may ensure sufficient low-temperature solubility and surface flexibility of VPR, which are crucial for the maintenance of catalytic activity at low temperatures. For the warm-active PRK and AQN, the predominant distributions of the electro-positive and electro-neutral potentials may contribute to enhancing the surface rigidity and structural stability. Compared to PRK, the larger and denser electro-positive potential on the backside surface of the thermophilic AQN may be more advantageous in maintaining the rigidity and stability of the AQN structure at high temperatures.

It should be noted, however, that temperature adaptation of enzymes is a complicated mechanism involving other factors (e.g., entropic effects such as hydrophobicity, entropy-increasing nature of the natively folded state, and desolvation in protein folding; and enthalpic forces such as hydrogen bonds, van der Waals contacts, and other favorable interactions^73,74) in addition to electrostatics, all of which act together to regulate the balance between stability and flexibility of the enzyme structure to maintain sufficient catalytic activity at extreme temperatures. Nevertheless, our results reveal that the differences in electrostatics among the three differently temperature-adapted subtilisins can contribute to their temperature adaptation, thus providing a foundation for further engineering and mutagenesis studies.

Conflicts of interest

There are no conflicts to declare.