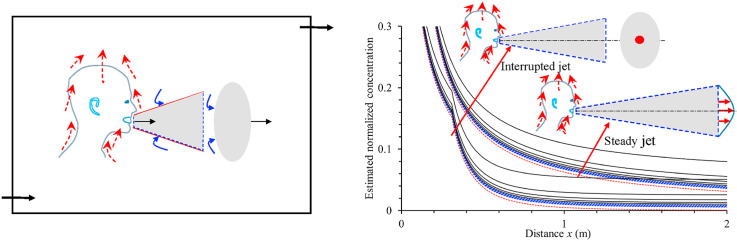
Abstract
Leading health authorities have suggested short-range airborne transmission as a major route of severe acute respiratory syndrome coronavirus-2 (SARS-CoV-2). However, there is no simple method to assess the short-range airborne infection risk or identify its governing parameters. We proposed a short-range airborne infection risk assessment model based on the continuum model and two-stage jet model. The effects of ventilation, physical distance and activity intensity on the short-range airborne exposure were studied systematically. The results suggested that increasing physical distance and ventilation reduced short-range airborne exposure and infection risk. However, a diminishing return phenomenon was observed when the ventilation rate or physical distance was beyond a certain threshold. When the infectious quantum concentration was less than 1 quantum/L at the mouth, our newly defined threshold distance and threshold ventilation rate were independent of quantum concentration. We estimated threshold distances of 0.59, 1.1, 1.7 and 2.6 m for sedentary/passive, light, moderate and intense activities, respectively. At these distances, the threshold ventilation was estimated to be 8, 20, 43, and 83 L/s per person, respectively. The findings show that both physical distancing and adequate ventilation are essential for minimising infection risk, especially in high-intensity activity or densely populated spaces.
Keywords: Short-range airborne transmission, Wells-riley model, Ventilation rate, Physical distance, Interrupted jet, COVID-19
Graphical abstract
Practical implications
This study provides, for the first time, a simple approach for assessing the infection risk via the short-range airborne route. The minimum requirements for ventilation and physical distance to minimise short-range infection risk were determined for different activities. To help prevent respiratory infections by predominantly short-range airborne transmission, both adequate physical distancing and sufficient ventilation/filtration to remove expired infectious aerosols must be maintained, especially in spaces with high-intensity activity. If a less-than-threshold physical distance is maintained, relying on ventilation dilution alone is not sufficient to prevent infection.
1. Introduction
As the coronavirus disease 2019 (COVID-19) pandemic continues, major health authorities, including the World Health Organization (WHO) and the US Centers for Disease Control and Prevention, have at least partially recognised the importance of airborne transmission of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) since October 2020 [1] and of short-range airborne transmission since late April 2021 [2]. Recognising the short-range airborne route is important for determining appropriate interventions, as wearing N95 masks has become necessary for healthcare workers working in the presence of COVID-19 patients in healthcare settings and improved building ventilation has become an important infection control measure in the community. Here, we define airborne transmission as exposure to exhaled fine aerosols or droplet nuclei with diameters less than 5 μm that contain infectious viruses and eventually lead to infection. Short-range airborne transmission is defined as direct inhalation exposure of a susceptible person, through the mouth or nose, to expired virus-containing droplets or aerosols smaller than 50 μm in the expired jet of an infected person. Large droplet transmission has been shown to be insignificant or less important compared to short-range airborne transmission [3]. The concept of airborne transmission traditionally implies long-range airborne transmission. Identifying the presence of a short-range airborne transmission route by health authorities is a major milestone in determining appropriate interventions for respiratory infections.
The Wells-Riley equation has been widely used to describe the infection risk via the long-range airborne route in indoor spaces [4]. presented the first model, assuming fully mixed room air with a uniform distribution of infectious pathogens. At a steady state, the probability of infection is
| (1) |
where n is the number of infectors, is the infectious quantum generation rate by one infector (quanta/min), p is the average pulmonary ventilation rate or inhalation rate of a susceptible individual (m3/min), is the exposure duration (min), and is the room ventilation flow rate or strictly speaking, the effective ventilation rate including filtration (m3/min).
The definition of an infectious quantum arises from the need to resolve the challenge of not knowing the number of infectious virus particles. A quantum is defined as the number of virus particles needed to produce a probability of 63.2% (or exactly, 1-1/e) of infecting a susceptible individual [5]. Once an outbreak is detected, the infectious quantum generation rate may be determined using Equation (1) or its variants if the ventilation rate at the time of infection can be determined. A transient version of the equation was derived by Rudnick and Milton [6] and others. For cases of non-uniform distribution, Qian et al. [7] developed an approach using computational fluid dynamics and the infectious quantum concept.
There are at least two challenges in analysing short-range infection risk. First, the infectious quantum generation rates are expected to differ for short- and long-range airborne transmission. Compared with the long-range airborne transmission, the airborne aerosols involved in the short-range airborne route can be larger within the expired jet of any individual, and more viable virus particles may exist in these aerosols expired by an infected individual [8,9]. People are constantly in close contact with others in their daily life [10]. The exposure duration and physical distance during close contact are difficult to determine. The conventional approach for determining the quantum generation rate for long-range transmission using Equation (1) cannot be directly applied to short-range transmission.
Second, the dilution factors in the expired jet zone and in the rest of the room are governed by different mechanisms. The key mechanism for controlling long-range airborne transmission is the dilution by ventilation, filtration and settling, as described by the term in the Wells-Riley equation (1). The dilution factor for a jet at distance from jet origin may be defined as , i.e., the ratio of the jet flow rate at distance to the jet flow rate at the jet origin. Alternatively, , which is the ratio of the average concentrations of the infectious quanta at the origin and at distance , can be used to calculate the dilution factor. In general, infectious droplets evaporate, with larger droplets settling, and infectious viruses may be deactivated while traveling in the expired jet. Hence, may not equal . Dilution in the expired jet differs based on whether the surrounding air is clean or polluted. The cleanliness of surrounding air is controlled by room air ventilation (dilution) when the source of the pollution is fixed. A continuum model has recently been developed by Li et al. [11], in which short- and long-range airborne exposure are integrated.
Li et al. [11] described a steady expired air jet theory that provides the dilution factor of the expired infectious aerosols in the expired jet as a function of distance. However, the accuracy of such a steady jet model for estimating dilution factors during different expiration activities remains unknown. Expired air flows may be better described as a two-stage jet during most respiratory activities (normal breathing, speaking, coughing, and sneezing) [12]. Such a two-stage jet consists of a jet-like stage, when an expired jet is released from the source for a finite duration, and a puff-like stage after the source supply is terminated, after which, the cycle repeats. The jet-like stage may be characterised by a starting jet, and the puff-like stage by a puff [[12], [13], [14]]. Fierce et al. [15] and Wagner et al. [16] utilized a size-dependent aerosol release model with turbulent dispersion to assess aerosol deposition in the nasal cavity and initiate infection. Cortellessa et al. [17] investigated short-range transmission risk at proximity using a three-dimensional computational numerical model. Fu et al. [18] measured inhalation fraction with different interpersonal distances using thermal manikins to simulate source and susceptible individuals. Bazant et al. [19] and Li et al. [11] combined a simple steady jet into the short-range airborne plume transmission. Although experimental data exist for the starting jet and puff theories [20], to the best of our knowledge, there are no data on the dilution factor of such a two-stage jet, which is essential for estimating the short-range inhalation exposure of expired aerosols.
In this study, a dilution factor of the two-stage expired jet was derived for the first time. We integrated the continuum model described by Li et al. [11] and the newly derived dilution factor formula using the two-stage jet model to estimate short-range airborne exposure. The term ‘continuum’ recognises the connection between short- and long-range airborne exposure. The new continuum model was used to propose a short-range Wells-Riley model to assess infection risk.
2. Methods
2.1. A two-stage jet model for estimating the dilution factor
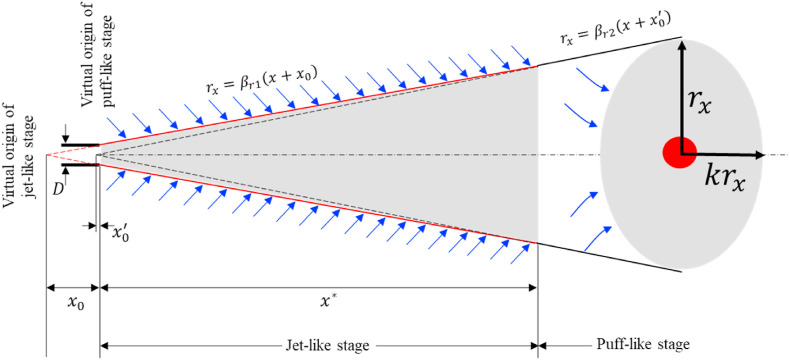
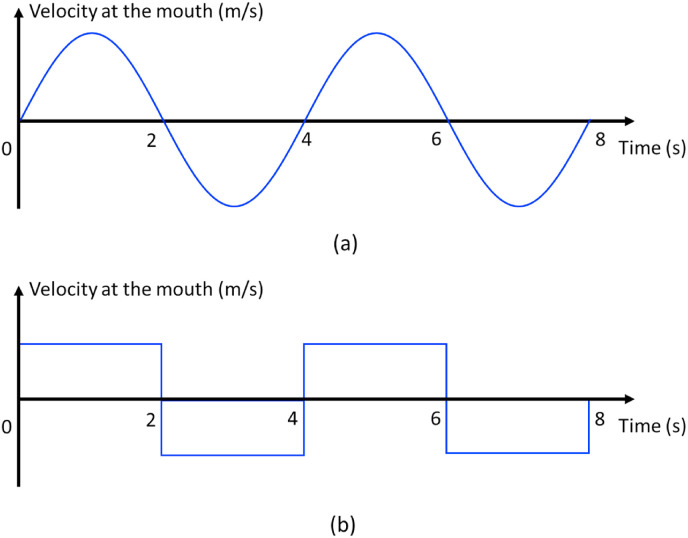
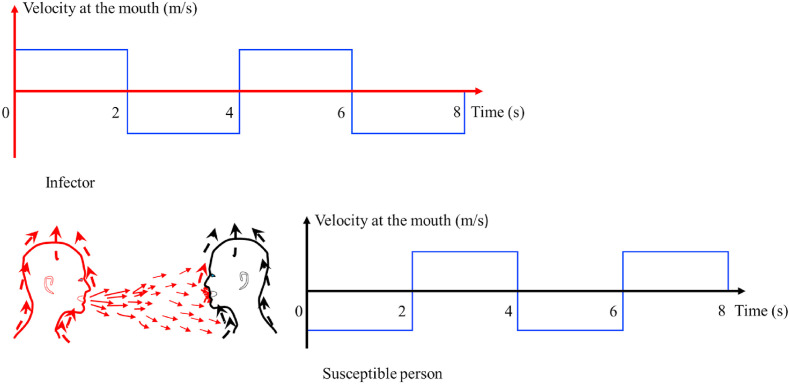
We focus on inhalation transmission here. Particles with a diameter of smaller than 50 μm follow the expired jet streamline [3]. Hence the spatial variation of virus-containing airborne particle concentration can be characterized by the two-stage jet dilution model. We assumed that the mouth opening was a nozzle with a diameter (m) (Fig. 1 ). The expired airflow rate at the mouth of an infected individual for the duration of exhalation is (m3/s or L/s), where the exhalation rate is the exhaled/inhaled flow rate during a period (e.g., a minute or a day) as defined by the US Environmental Protection Agency (US EPA) [21], rather than during the exhalation period. For a breathing cycle with a period , the exhalation duration is , the inhalation duration is , and the coefficient is defined as . When exhalation and inhalation durations are equal (Fig. 2 ), = 2. In the calculations here, a coefficient of was used.
Fig. 1.
Schematic diagram of the expired jet using a two-stage jet model.
Fig. 2.
Idealised breathing cycles. (a) Sinusoidal cycles; (b) square cycles. We considered an ideal 4-s breathing cycle in this idealised model.
The jet flow rate increases to (m3/s or L/s) at a streamwise penetration distance due to entrainment of the surrounding air. We aimed to estimate the jet dilution factor at any distance . The dilution factor in this study is the average dilution factor of the cross-section at distance . Knowledge of the dilution factor allowed us to estimate the short-range exposure of a susceptible individual by direct inhalation of the expired airflows of an infected individual. Dilution occurs due to continuous turbulent entrainment as an expired jet develops.
For a steady jet originating from a round opening, the dilution factor is
| (2) |
where is the diameter of the mouth opening. Equation (2) is valid at distances of [22]. For a typical mouth diameter of 20 mm, m. Buoyancy, stratification, and cross flows are known to affect the jet dilution factor [22].
An interrupted jet is driven by an intermittent momentum source. Buoyancy forces can also exist but were ignored here for simplicity. A sudden instantaneous release of the momentum produces a puff. In the case of an expired flow, instead of instantaneous release, a release with a finite duration occurs, followed by a short duration of inspiration, after which, the cycle repeats. The inspiration flow has a potential flow pattern, drawing air from all directions.
Recall that the steady-jet dilution ratio is obtained using the basic mass and momentum conservation principle, with an additional assumption that the radial penetration distance grows linearly with the streamwise penetration distance [22]. A similar approach was used here to derive the dilution formula for the interrupted jet.
We first approximated a realistic inhalation/exhalation profile to a square cycle (Fig. 2b). The specification of uniform velocity at the mouth allowed us to use existing jet data [20]. Jets with an irregular velocity profile (e.g., Fig. 2a) have also been studied by Wei et al. [12]. For an ideal square breathing cycle, the expired flow velocity is calculated as , where is the mouth opening area.
We assumed calm surrounding air and used the experimental data of Sangras et al. [20] and Diez et al. [23], including both starting jets and puffs. The exhalation phase (t = 0–2 s in Fig. 2) is the jet-like stage, which is dominated by conservation of the momentum flux. After the exhalation phase (t > 2 s), the exhaled flow enters a puff-like stage, which is dominated by conservation of the momentum force.
At the jet-like stage, the streamwise penetration distance is proportional to the square root of the lapsed time , and the radial penetration distance is proportional to the streamwise penetration distance . Note that the radial penetration distance here was not the Gaussian width described by Lee and Chu (2012, page 37) [22], but the visible radii, i.e., the top-hat width. Including the correction of the jet virtual origin, we have
| (3) |
and
| (4) |
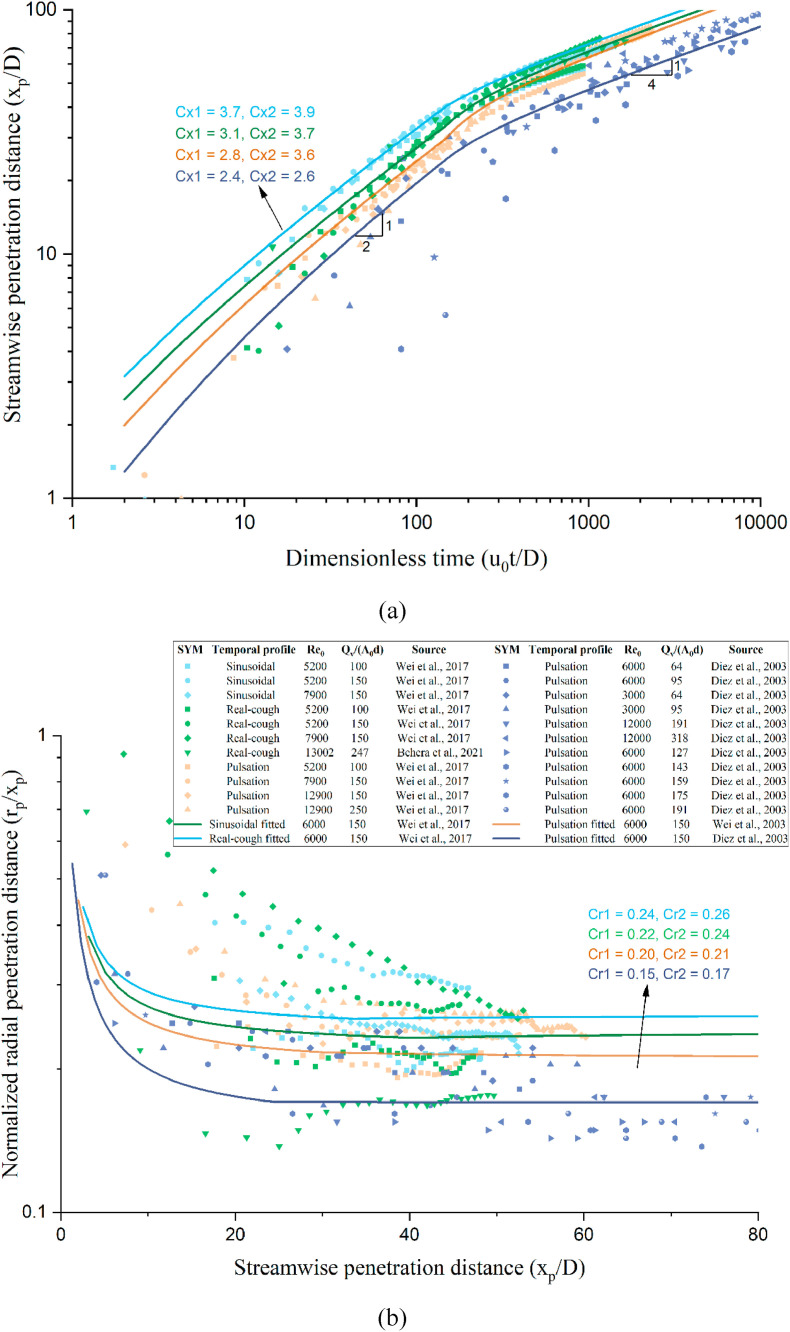
where is the streamwise penetration distance of the expired jet geometric centre from the mouth; is the radial penetration distance at distance ; is the distance from the virtual origin of the jet-like stage to the mouth (); and is the corresponding virtual time of (). The two empirical parameters and are the radial penetration coefficient and the streamwise penetration coefficient in the jet-like stage, respectively, and and , according to Diez et al. [23]. Note that and are not constants for the expired jet tip, but for the expired jet geometric centre or centroid (Supplementary Information C1).
Momentum fluxes of the expired jet are at the mouth and at distance in the jet-like stage, where the mouth opening area was calculated as and the cross-sectional area of the expired jet was calculated as .
Following momentum flux conservation in the jet-like stage (), we derived .
We then obtained ; hence, the dilution factor in the jet-like stage becomes
| (5) |
as .
Alternatively, by taking the derivative with respect to time in Equation (3), we obtained , and subsequently,
| (6) |
The dilution factor in the jet-like stage then becomes
| (7) |
The detailed derivation process is shown in Supplementary Information C2.
The transition point from the jet-like stage to the puff-like stage was determined using Equation (3) at transition time (e.g., 2 s in Fig. 2).
| (8) |
where is the streamwise penetration distance at the transition point. The dilution factor at transition point was estimated using Equation (5) as .
At the puff-like stage, the streamwise penetration distance is proportional to the fourth root of the lapsed time , and the radial penetration distance is proportional to the streamwise penetration distance .
| (9) |
| (10) |
| (11) |
| (12) |
where is the distance from the virtual origin of the puff-like stage to the mouth; is the corresponding virtual time of ; and are the radial penetration coefficient and the streamwise penetration coefficient in the puff-like stage, respectively, for the two coefficients, and [23]. Note that and are not constants for the expired jet tip, but for the expired jet geometric centre (Supplementary Information C1). is the expired air volume (m3 or L) during one breathing cycle, i.e., . For the ideal breathing cycle depicted in Fig. 2, .
A puff cloud may be best described as an ellipsoid with a radius and a height where [24]. The cloud volume is estimated as .
In the puff-like stage, the dilution factor at distance is calculated as the product of the dilution factor at transition point and the volume ratio of the puff cloud at distance to the puff cloud at distance , i.e., .
| (13) |
The dilution factor in the jet-like stage is, thus, similar to the dilution factor in a steady jet, but the dilution factor in the puff-like stage is different from that in a steady jet. The dilution factor during the puff-like stage depends on the released volume of air during the exhalation period of one breathing cycle.
2.2. An improved continuum model
If the surrounding air is clean, the dilution factor described above can be used directly to evaluate short-range inhalation exposure. In an enclosed environment, aerosols in the surrounding air may be simultaneously entrained into the expired airflows.
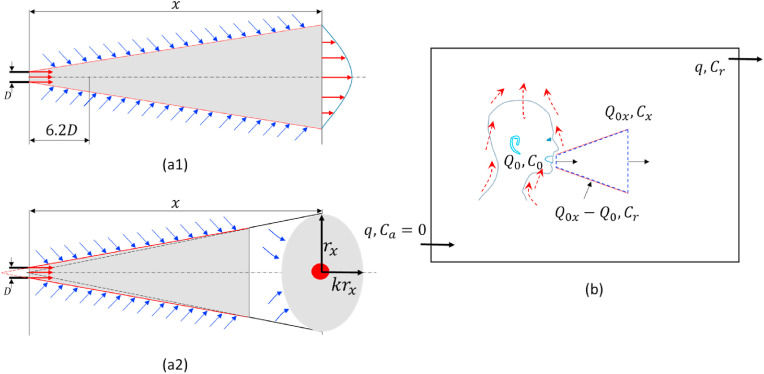
Such an entrainment effect is considered in the continuum model derived by Li et al. [11]. This continuum model may be improved using the newly derived dilution factor described above for a two-stage jet. We divided a room space into two zones (Fig. 3): the jet zone (e.g., m for certain respiratory activities) and the room zone (i.e., the rest of the room). The volume of the jet zone (typically 0.15 m3 for a 2-m expired jet cone) is much smaller than the volume of the room zone (>30 m3).
Fig. 3.
A simple model of the continuum from short-range to long-range inhalation routes. (a) A simple jet model assuming the expired jet is steady (a1) or interrupted (a2); (b) The jet zone with a variable distance x in (a), and the room zone. The jet model may be modelled using the ideal steady jet model of (a1) and the two-stage jet model of (a2).
Consider exhaled virus-containing aerosols with an average concentration of at the jet origin (the mouth), an average concentration of at distance , and an average concentration of in the room zone. When the infectious quantum is used, the concentration is measured in quanta/m3 or quanta/L, the room ventilation rate is (L/s), and the ambient (outdoor) concentration is zero.
The steady-state and time-averaged macroscopic mass balance equations for the exhaled virus-containing aerosol concentrations in the room zone and the jet zone, respectively, become
| (14) |
and
| (15) |
where , is the equivalent ventilation rate due to particle settling, is the deposition rate (h−1) (Supplementary Information B), V is the room air volume (m3), is the equivalent ventilation rate due to filtration, is the equivalent ventilation rate due to virus deactivation, and is the fraction of infectious aerosols in suspended aerosols in the expired jet that remain suspended in the room zone. Note that the exhaled flow rate during a period (e.g., a minute or a day) as defined by the US EPA [21] was used here, not . Correspondingly, the jet flow rate at distance should also be understood as the corresponding jet flow rate when the exhaled flow rate is at the mouth. Hence, the dilution factor here is calculated as . Note that the effects of particle deposition and virus deactivation were not considered in the jet zone in Equation (15), but were considered in the room zone in Equation (14).
The size range of suspended aerosols is less in the room zone than in the jet zone due to air speed differences between the two zones [8,9]. Infectious pathogens may also be more likely to survive in the jet region. Differences in both size and survival characteristics suggest . Although we were interested in the short-range airborne infection risk here, as there is entrained air from the room zone into the expired jet, we needed to assign a value to . However, an accurate determination of the value is not yet available. Using a larger value may over-estimate the long-range exposure. Here, we used , following Li et al. [11].
Solving Equations (14) and (15), we obtained
| (16) |
where the ratio is the rebreathed fraction [6]. For example, with a typical exhalation rate, , of 0.1 L/s and a ventilation rate of 10 L/s per person,. Equation (16) shows a simple dilution process of both the quantum concentration at the mouth and the average room quantum concentration .
When ventilation is infinite (), Equation (16) can be simplified to:
| (17) |
In the room zone, when is infinite, the average concentration at distance becomes
| (18) |
This reflects the nature of the continuity of exposure to respiratory droplets from a close range to a long range.
2.3. A short-range Wells-Riley equation
We considered the worst situation in which breathing patterns of the infector and the susceptible individual involved in a conversation are synchronic (Fig. 4 ). In such a situation, the susceptible individual is in close proximity, and his/her inhalation occurs at the same time that the exhaled puff arrives.
Fig. 4.
The assumed worst condition in which a susceptible person inhales exactly when the exhaled air of the infected person arrives at his/her mouth.
We can directly integrate the newly obtained dilution factors with the quantum concentration equations.
The short-range Wells-Riley equation for one infector in a room is:
| (19) |
In outdoor situations or when ventilation is infinite,
| (20) |
The long-range equation for one infector in the room zone is:
| (21) |
We assumed that all individuals in a room can be presented by an average person, i.e., the exhalation rate of the infected individual equals the inhalation rate of the susceptible individual ( ). The short- and long-range equations can be further simplified, such that Equation (19) becomes
| (22) |
The long-range equation then becomes
| (23) |
The difference between the long- and short-range infection risk can be seen in Equations (22) and (23). When the infection risk is low, we can simplify Equation (22) by Taylor series expansion to . For this simplified formula, the first term refers to the direct inhalation of the expired air with a concentration of , which is now diluted by a factor of . The direct inhalation exposure at a close range is approximately proportional to the inhalation/exhalation flow rate , although the dilution factor is somewhat affected by (see later discussion of Fig. 8). The indirect inhalation at a close range is approximately proportional to . The significance of this re-entrained ‘long-range’ term is determined by the effective ventilation rate . The ‘long-range’ exposure, calculated using Equation (23), is approximately proportional to , as the dilution factor is somewhat affected by .
Fig. 8.
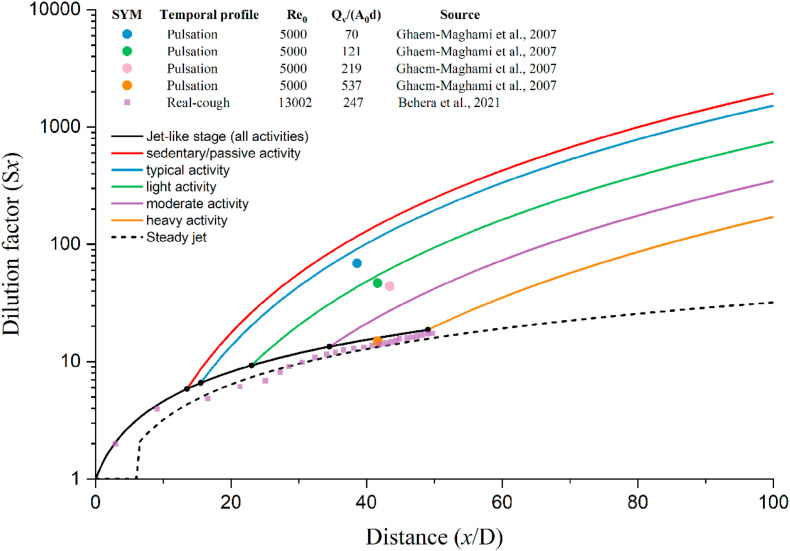
The measured and predicted dilution factors vary with the distance from the discharge orifice. Prediction using the steady and two-stage jet models was made with five activity intensities and the discharge orifice as 0.02 m. The representative inhalation/exhalation rates listed in Table 1 were used. Note that for the steady jet model, the dilution factor is 1 when the distance is less than 0.12 m. The jet or puff flow in Ghaem-Maghami and Johari [29] and Behera et al. [28] was injected into an isothermal and isobaric chamber. The former was accompanied by a weak co-flow (a 0.5% of jet velocity) while the latter had no co-flow.
In theory, we can use the long-range Wells-Riley equation (21) to determine the long-range quantum generation rate from long-range exposure data and use the short-range Wells-Riley equation (19) to determine the short-range quantum generation rate from short-range exposure data if an outbreak existed with data for both short- and long-range airborne transmission. The value of can then be determined. However, complexities arise. The close-contact duration and distance from an infector may differ for different susceptible individuals. The short-range infection risk cannot be simply estimated by dividing the observed number of newly infected individuals in close contact with the infector by the total number of susceptible individuals in close contact with the infector, as the close-contact period and distance may not be the same for all susceptible individuals. Individual exposure periods and distances need to be estimated. To the best of our knowledge, there are no adequate data from previous outbreaks to estimate the value. For example, for the restaurant outbreak of COVID-19 in Guangzhou, close-contact data are available, but no secondary infections were found to be associated with these close-contact events [25].
From another perspective, if the short-range infection risk is known for a certain distance, activity intensity, close-range exposure duration, and ventilation rate, the short-range infectious quantum concentration can also be determined. However, such data do not exist. The infectious quantum concentration of initial expired air was estimated as 0.1 quanta/L using the closest dataset in Chu et al. [26] (see Fig. S4 in Supplementary Information D), which was further applied in demonstrating short-range airborne exposure risk assessment.
2.4. Activity and breathing mode
It remains unknown how the number of expired droplets or the virus concentration varies due to different activity intensities. The exhaled droplet generation mechanism is likely mechanical, such as due to shear stress along the respiratory epithelium surface. Thus, we may assume that the number of generated droplets or the viral emission rate increases linearly as the expired flow rate increases. Such an assumption remains to be investigated. We used the exhaled/inhaled flow rate recommended by the US EPA [21]. The quantum concentration of exhaled air of the infected individual is assumed to be identical for a particular infector and all activity intensities.
Table 1 shows that the rebreathed fraction varies with different activities, as the exhalation rate changes. When the ventilation rate is kept as a constant at 10 L/s per person, the rebreathed fraction becomes larger for higher-intensity activities. If the rebreathed fraction is kept at a constant value of 0.01, the required ventilation rates also increase for higher-intensity activities.
Table 1.
Summary of the combined exhalation/inhalation rates of men and women of all ages from birth (lowest value) to 81 years or older during various activity intensities [21].
| Activity intensity | The exhalation rate or the inhalation rate |
when L/s per person | L/s per person when | ||
|---|---|---|---|---|---|
| L/min | L/s | Representativea L/s | |||
| Sleep or nap | 3–5.2 | 0.05–0.09 | 0.06 | 0.006 | 6 |
| Sedentary/passive activity | 3.1–5.4 | 0.05–0.09 | 0.08 | 0.008 | 8 |
| Standard activity | 6 | 0.1 | 0.1 | 0.01 | 10 |
| Light activity | 7.6–13 | 0.13–0.22 | 0.20 | 0.02 | 20 |
| Moderate activity | 14–29 | 0.23–0.48 | 0.43 | 0.043 | 43 |
| Intense activity | 26–53 | 0.43–0.88 | 0.83 | 0.083 | 83 |
The representative value is the median inhalation rate for all ages for the specific activity intensity. The highest value is for young people. A standard-intensity activity with an exhalation flow rate of 0.1 L/s is also included.
3. Results
3.1. Development and validation of the expired two-stage jet model
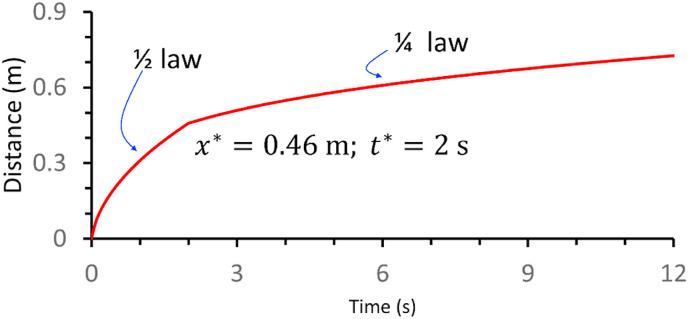
Each ideal breathing cycle (Fig. 4) consists of a 2-s exhalation phase and a 2-s inhalation phase. The time-varying streamwise penetration distance of the geometric centre of the expired jet is shown for a light activity in Fig. 5 . The forward movement of the expired jet decreased much faster in the puff-like stage than in the jet-like stage. During the 2-s exhalation phase, the expired flow satisfied the conservation of the momentum flux () and the self-preserving growth of the jet (. These conditions resulted in a relationship between the streamwise penetration distance of the initial jet and time, represented as . After the 2-s exhalation phase, the puff cloud satisfied the conservation of the momentum force ( and the self-preserving growth of the puff cloud (, leading to a relationship between the streamwise penetration distance of the puff and time, represented as .
Fig. 5.
The time-varying streamwise penetration distance of the geometric centre of the expired jet estimated using the two-stage model for light activity (exhalation/inhalation rate, 0.2 L/s). The streamwise penetration distance of the starting jet and the streamwise penetration distance of the puff after the 2-s exhalation phase.
In our standard two-stage jet model, we used , , and following Sangras et al. [20] and Diez et al. [23]. As shown in Fig. 6 , we compared the predicted and measured streamwise and radial penetration distances for an interrupted jet including three types of exhalation profiles, i.e., square/pulsation, sinusoidal and real coughing. The measured data included those reported by [[12], [23], [27], [28]]. A reasonable agreement was observed between the predicted and measured data, although differences of streamwise and radial penetration coefficients in three exhalation profiles and different studies exist.
Fig. 6.
Comparison of the measured and predicted streamwise and radial penetration distances for an interrupted jet. (a) Streamwise penetration distance as a function of dimensionless time; (b) normalised radial penetration distance as a function of the streamwise penetration distance.
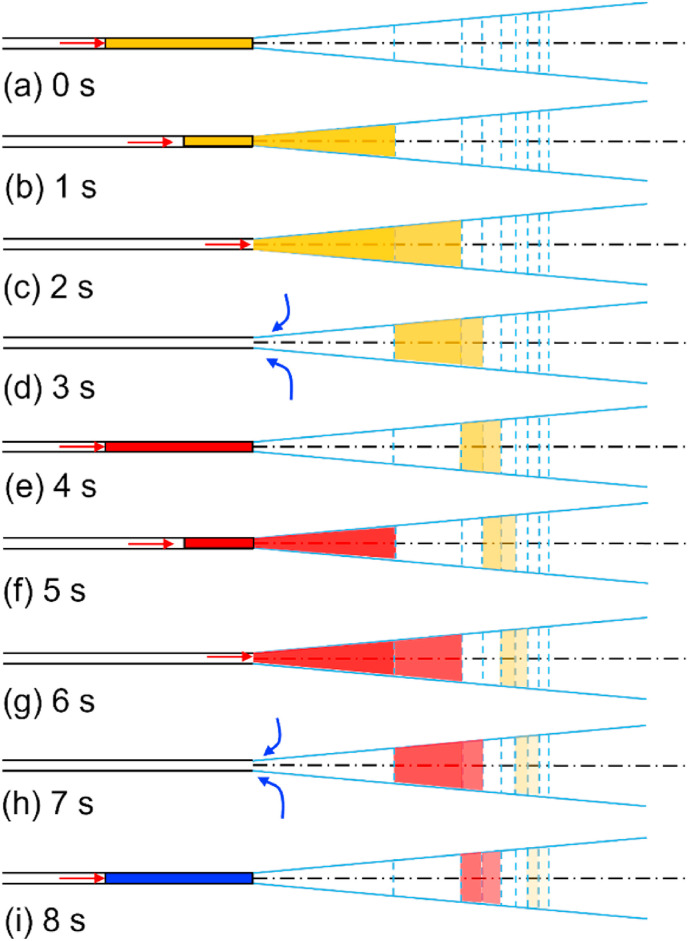
Fig. 7 shows the idealised puff trains of the expired air flows, using the data presented in Fig. 5. As each train reaches a distance (a stop) downstream, the volume of air increases, and the concentration of the discharge at the origin is diluted. Only two complete breathing cycles (duration of 8 s) are shown in Fig. 7. The expired air volume reduces as it travels for more than 2 s (Fig. 7b). As shown in Fig. 7i, the two sequential air volumes are closer at 8 s after the first discharge. When these two air volumes are sufficiently close, the two vortices may merge. This is identical to the observed jet-like flow in the numerical simulation for speech presented by Abkarian et al. [14], in which the inhalation duration was 1 s, while the exhalation duration was 3 s. With this simple analysis, it is possible to describe jet-like physics.
Fig. 7.
An ideal model of the development of expiratory interrupted jet flows for 8 s during light activity (exhalation/inhalation rate, 0.2 L/s). The transparent level of yellow and red colours illustrates flow dilution. The jet tip was estimated using Equations (3) and (9). (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)
3.2. Comparing estimated dilution factors between the steady jet and two-stage jet models
As expected, both the steady jet and the two-stage jet models predicted that the dilution factor always increases with an increase in the streamwise penetration distance. The dilution factor of a steady jet increased linearly with the streamwise penetration distance, with a slope that was independent of activity intensity. The steady-jet-estimated dilution factor was less than the dilution factor predicted by the two-stage jet model (Fig. 8). This is an important observation, as it suggested that the steady-state model used by Li et al. [11] is inadequate for describing the dilution factor. An underestimated dilution factor may lead to an overestimation of the threshold distance for minimising infection risk during close contact.
With the two-stage jet model, the dilution factor also increases linearly with the streamwise penetration distance in the jet-like stage, but in contrast, it increases with the cubic of the streamwise penetration distance in the puff-like stage. The transition point from the jet-like to the puff-like stage increases with increasing expired flow rate at the mouth (activity intensity). The transition points were 0.28 m for sedentary/passive activity, 0.31 m for standard activity, 0.47 m for light activity, 0.7 m for moderate activity, and 0.99 m for intense activity. A shorter jet-like stage length resulted in greater puff-like dilution factors at any streamwise penetration distance. Hence, the dilution factor at any streamwise penetration distance for the puff-like stage decreases as the activity intensifies. For example, the dilution factors at 2 m are 1,928-fold for sedentary/passive activity, 1,520-fold for standard activity, 747-fold for light activity, 345-fold for moderate activity, and 171-fold for intense activity. Moreover, the average dilution ratios of isolated puffs with stroke ratio () of 70, 121, 219, and 537 at distances to are 70, 48, 45, and 16 in the experimental data of Ghaem-Maghami and Johari [29]. In our study, the injection parameters of standard, light, moderate, and intense activities were 64, 127, 273, and 528, and the corresponding average dilution factors at 0.5–1.1 m were 116, 55, 26, and 16, respectively (Fig. 8). Our predicted dilution factors are somewhat in agreement with those reported by Ghaem-Maghami and Johari [29] and Behera et al. [28].
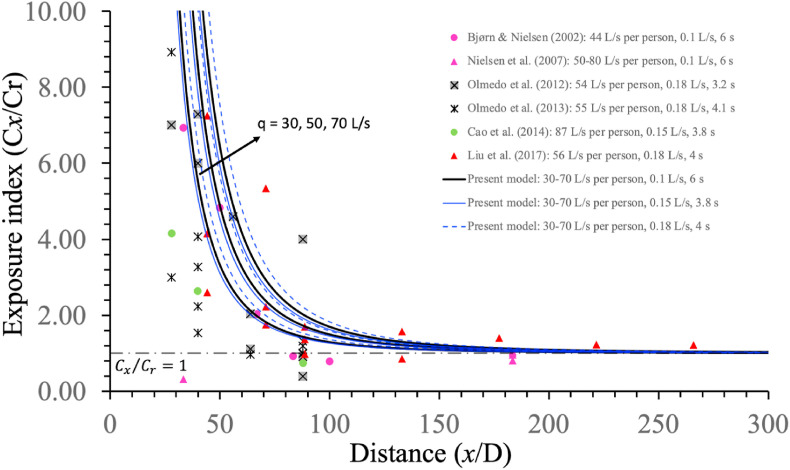
To further verify the developed dilution model, we predicted the exposure index and compared it with the measured data from the literature (Fig. 9 ). As our room zone model was based on a fully mixing assumption, we chose only those data with mixing ventilation or with manikin heads in the mixing zone when displacement ventilation was used. In these experiments, one can assume . A reasonable agreement was observed, suggesting that the developed dilution factor formula and its integration with the continuum model reasonably predicted short-range exposure.
Fig. 9.
The measured and predicted exposure index varies with the distance from source manikin. Prediction using the two-stage jet model was made with three ventilation rates: 30, 50, and 70 L/s per person. In the legend, each case is shown with [#L/s per person, & L/s, $ s], in which # refers to the ventilation rate, & refers to the exhalation rate, and $ refers to the breathing duration. The air distribution design was displacement ventilation in the studies [30,[31], [32]]; downward ventilation in the studies [33,34]; and mixing ventilation in the study [35]. In data of displacement ventilation, the heads of the source and the target manikins are suspected to be within the upper mixing zone. These measurement data were first summarised by Chen et al. [36].
3.3. Predicted normalised concentrations of the expired aerosols at various distances and activity intensities
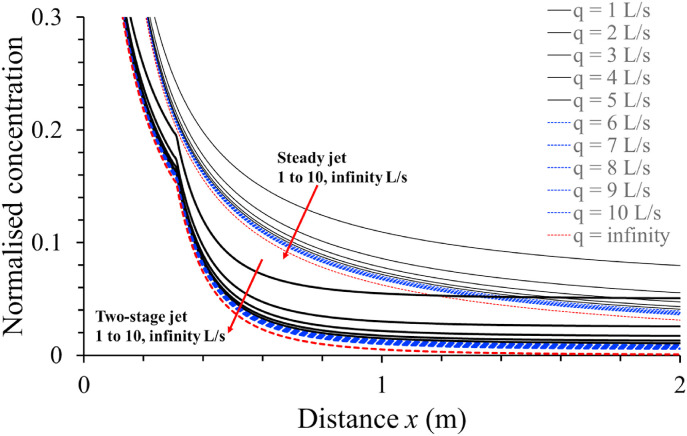
We compared the estimated normalised concentrations of the expired aerosols at any streamwise penetration distance and various ventilation rates using the new two-stage jet model and the steady-state jet model for standard activity (exhalation rate, 0.1 L/s) in Fig. 10 .
Fig. 10.
The predicted normalised concentrations of the expired flow at different distances and ventilation rates of 1–10 L/s per person and infinity for standard activity (exhalation rate, 0.1 L/s). The results of the new two-stage jet model and the steady-state jet model are shown and compared.
Two major observations can be made. First, the normalised concentration of the expired aerosols predicted by the steady jet model (thin lines in Fig. 10) is higher than the corresponding concentration predicted by the two-stage jet model for all conditions (thick lines in Fig. 10). This can be explained by an underestimate of the dilution factor by the steady jet model. In contrast to the steady jet model, the normalised concentration profile predicted by the two-stage jet model was not smooth, with a transition point at approximately 0.3 m for standard activity with an exhalation rate of 0.1 L/s. A ventilation rate less than 5 L/s per person gave a significantly higher concentration than outdoor conditions (with an infinite ventilation rate as shown by the red dashed curves), whereas a ventilation rate higher than 5 L/s per person did not. To be safe, we suggest a threshold ventilation rate of 10 L/s per person for standard activity with an exhalation/inhalation rate of 0.1 L/s so that the indoor infection risk at a short range is similar to the risk outdoors where the ventilation rate is infinite. This suggestion was also made in our previous study [11].
The short-range normalised concentration profiles when the exhalation rate changes from 0.1 L/s are shown in Fig. S3. The short-range normalised concentrations are determined by the exhalation rate, ventilation rate, and dilution factor. Unlike the steady jet model, the dilution factor estimated by the two-stage jet model depends on the exhalation rate of the infector. A higher activity intensity results in a lower dilution factor in the puff-region (Fig. 8). Simultaneously, a higher activity intensity results in a greater rebreathed fraction () if the ventilation rates are kept constant. Thus, a higher short-range normalised concentration, (), is predicted for heavier activities than for standard activities if the ventilation rates are kept constant (Fig. S3).
3.4. Infection risk via the short-range airborne route using the two-stage jet model
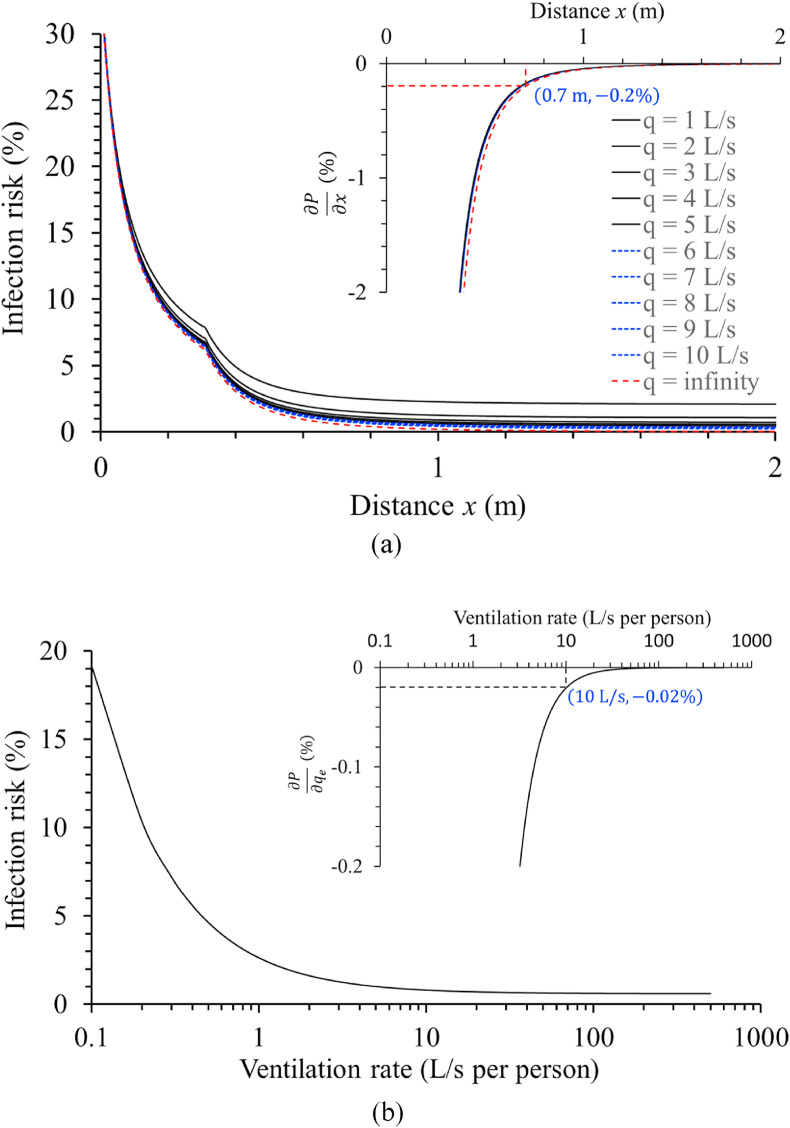
The short-range airborne infection risk was estimated using a quantum concentration of 0.1 quantum/L and an exposure duration of 42 s as an example. Fig. 11 shows the predicted profiles of the short-range airborne infection risk for standard activity (inhalation rate, 0.1 L/s). The data clearly show that a ventilation rate less than 5 L/s per person introduces a significantly higher infection risk than outdoor conditions. This conclusion is consistent with the exposure estimates presented in Fig. 10.
Fig. 11.
Estimated short-range airborne infection risk varies with distance and ventilation rate, and the partial derivatives of infection risk against distance and ventilation rate. (a) Estimated short-range airborne infection risk, , as a function of the distances and ventilation rates for standard activity (infectious quantum concentration, 0.1 quanta/L and exposure time, 42 s, assuming a 2-h total exposure period with four close-contact events per hour and 5.4 s/per close-contact event). In the inserted figure, the partial derivative of infection risk is shown against distance . (b) The estimated short-range airborne infection risk at threshold distance m and, in the inset figure, the partial derivative of infection risk against the ventilation rate are shown.
We examined whether it was possible to estimate a threshold distance and threshold ventilation rate when the quantum concentration at the mouth was unknown. Answering this question is complicated by two factors, namely, the distance and ventilation rate, which jointly affect the short-range airborne infection risk. When we evaluated the partial derivative as a function of distance, the curves for different ventilation rates collapsed into almost one curve. We attempted to identify a relatively flat region by determining when has a small value. Outdoor infection risk is known to be low at a typical close-contact distance, which is approximately 0.7 m. At m, we found that , which may be located in a relatively flat region of the curve (Fig. 11a). This corresponds to an infection risk of 0.82% for a ventilation rate of 10 L/s per person. At m and L/s per person, we also found that , which may also be located in a relatively flat region of the curve (Fig. 11b). Thus, we determined a threshold distance of 0.7 m and a threshold ventilation rate of 10 L/s per person for standard activity (inhalation rate, 0.1 L/s). Further, two parameters, namely, with an infinite ventilation rate and at the corresponding threshold distance, were regarded as the benchmarks for determining the threshold distance and threshold ventilation rates for other activities.
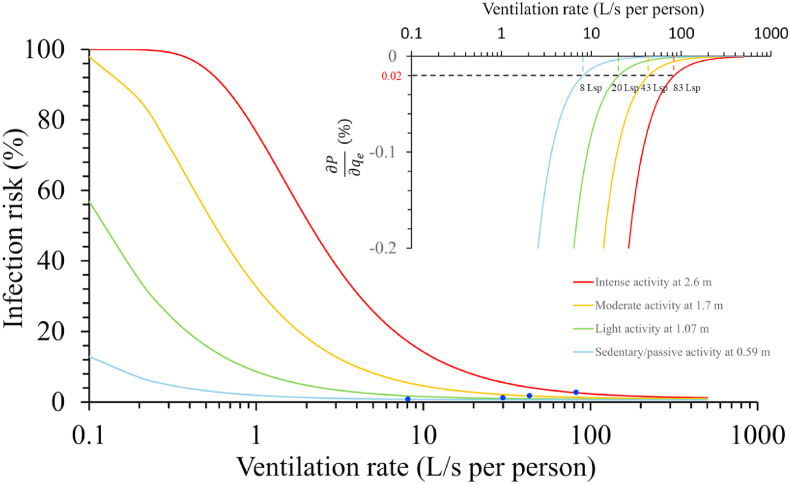
We further estimated the short-range infection risk for different activity intensities using the infectious quantum concentration of 0.1 quanta/L and exposure time of 42 s as an example (Fig. S6). In all settings, we determined the threshold distance for with an infinite ventilation rate. The threshold distance was then found to be 0.59 m for sedentary/passive activity, 1.1 m for light activity, 1.7 m for moderate activity, and 2.6 m for intense activity. Once a threshold distance was found, the corresponding threshold ventilation rate was determined using at the corresponding threshold distance. The threshold ventilation rate was 8 L/s per person for sedentary activity, 20 L/s per person for light activity, 43 L/s per person for moderate activity, and 83 L/s per person for intense activity (Fig. 12 ). It was clear that the threshold ventilation rate that we identified was proportional to the inhalation rate. The partial derivative approach predicted a threshold ventilation rate that was identical to the ventilation rate that gives a constant rebreathed fraction of 0.01 (Table 1).
Fig. 12.
Estimated short-range infection risk for four activity intensities and the corresponding physical distance threshold, with ventilation rates ranging from 0.1 to 500 L/s per person, and a partial derivative of infection risk against the ventilation rate using the equations presented in Supplementary Information C3.
Note that the partial derivative method we used to determine the threshold distance and threshold ventilation rate did not lead to a constant infection risk under threshold conditions. The risk of infection under threshold conditions was 0.79% for sedentary/passive activity, 0.82% for standard activity (inhalation rate, 0.1 L/s), 1.14% for light activity, 1.74% for moderate activity, and 2.61% for intense activity. The explanation for this finding is that the obtained threshold ventilation rates for all activity intensities led to a constant rebreathed fraction, , of 0.01, i.e., the concentration of the expired aerosols was the same after dilution. When the infection risk is low, Equation (20) can be simplified by Taylor series expansion to . From this simplified formula, the short-range airborne infection risk is approximately proportional to the inhalation volume if ventilation rates for different activity intensities are kept at threshold ventilation rates (i.e., a constant rebreathed fraction, ). However, higher-intensity activity had a larger dilution factor at the corresponding threshold distance, i.e., 54-fold at 0.59 m for sedentary/passive activity, 69-fold at 0.7 m for standard activity, 115-fold at 1.1 m for light activity, 211-fold at 1.7 m for moderate activity, and 383-fold at 2.6 m for intense activity. This led to a decrease in short-range exposure for higher-intensity activity at the threshold distance and ventilation rate compared to the proportional relationship with the inhalation volume . In contrast, the long-range exposure was proportional to the inhalation volume at the threshold ventilation rate.
4. Discussion
4.1. A new short-range Wells-Riley model with challenges
Our study is the first to present a dilution factor formula for a two-stage jet, and our estimated dilution factor was in reasonable agreement with measured or simulated data from the literature (Fig. 8). The dilution factor formula was further confirmed by comparing the predicted short-range exposure with measured data from the literature (Fig. 9). To the best of our knowledge, such a formula has not previously been reported, but it is required to assess the short-range exposure and infection risk of respiratory infections. The traditional steady jet model [11] does not consider the effect of respiratory activity on the dilution factor. In the steady jet model, the dilution factor is not a function of activity intensity, but is constant, and the predicted dilution factors are 8, 16, and 32 at distances of 0.5, 1, and 2 m, respectively. The two-stage jet model predicted a dilution factor that depends on activity intensity (exhalation rate, Fig. 8). For light activity, the predicted dilution factors were 12, 94, and 748 at distances of 0.5, 1, and 2 m, respectively (Fig. 5). The dilution factors for intense activity were smaller than those for light activity, but still significantly higher than those predicted by the steady jet model. For the rest scenarios, the dilution factor predicted in the puff-like stage at 2 m was up to 79 times higher with the two-stage jet model than with the steady jet model.
Using an existing continuum model of short- and long-range airborne transmission of SARS-CoV-2 [11], we derived a new, simple short-range Wells-Riley model. This model promises to provide a simple formula for the estimation of infection risk without wearing a mask based on physical distance, activity intensity, and ventilation rate. Our short-range Wells-Riley model is based on the single-hit assumption, which can be further expanded to a general short-range dose-response model using the multiple-hit assumption if the minimum infection dose is known [37,38]. Wearing a mask by infector decreases expired virus-containing aerosol concentration () at mouth. Wearing a mask by the susceptible individual reduces the inhaled aerosols. Mask wearing also changes the jet geometry and reduce the streamwise penetration distance and short-range airborne exposure risk. Hence, wearing a mask is one of the most important strategies to reducing short-range inhalation exposure [15,16].
Most SARS-CoV-2 infections have occurred indoors [39]. The original continuum model described by Li et al. [11] aimed to explain the low outdoor infection risk phenomenon. The revised continuum model using the new dilution factor also explained the low outdoor infection risk phenomenon, as the ventilation rate may be assumed to be infinite outdoors (Figs. 10 and 11). The new continuum model predicted a more dramatic decrease in infection risk as the distance changed from 0.5 m to 1 m, while the steady jet model predicted a smoother profile of the normalised concentration (Fig. 10).
The new model predictions suggest that the short-range infection risk with intense activity is significantly high when the ventilation rate and physical distance requirements cannot be satisfied. This is expected, as high infection rates have been observed in gyms, fitness centres, and dance floors during the on-going COVID-19 pandemic. Our new model predicted that outdoor infection may also occur with intense activity at close range, such as during sports activities or heavy labour. The data suggested that for light activities, the outdoor infection risk due to short-range inhalation was low; however, during intense activity, short-range inhalation transmission is possible. This has implications for intervention measures at outdoor events. The observed high infection risk among Hong Kong construction workers may support this observation, although their lounge room was also poorly ventilated [40,41], such that infection may have occurred indoors. A greater physical distance of 2.6 m is required for people engaging in intense activities outdoors. However, for indoor settings, even at this distance, a minimum ventilation rate of 83 L/s per person is needed according to our simple model.
Various approaches have been used to determine the threshold physical distance for infection control [42]. Different countries have also adopted different physical distances from 1 to 2 m [43]. Our data support the use of a threshold distance of 1 m for light activities in the presence of sufficient ventilation, but a higher threshold distance for higher-intensity activities. A much higher ventilation rate is also needed to reduce the short-range airborne infection risk associated with high-intensity activities.
Different close-contact distances between people are chosen for various social purposes. The average distance between people is approximately 0.7 m. One commonly cited, but informal, explanation for keeping a minimum distance is to avoid body odour or expired gas odour from other people. The provision of sufficient ventilation is also known to minimise body odour. If this is correct, then the commonly used minimum ventilation standard of 10 L/s per person is sufficient. At a standard activity intensity, with an exhalation flow rate of 0.1 L/s, a ventilation rate of 10 L/s per person results in a 100-fold dilution for the room average odour concentration. Thus, a dilution of 100-fold may lead to sufficient dilution of expired air to avoid odour problems. In the steady jet model, the normalised concentration was estimated to be 0.03, or a dilution of only 33-fold, at a physical distance of 2 m in outdoor conditions. If a 100-fold dilution is required to avoid body odour, and body odour can be avoided at a standard distance of 0.7 m, then the estimate by the steady jet model is markedly out of scale. This is expected, as a realistic expired jet is not a steady jet. In contrast, the two-stage jet model offers a reasonable prediction. To achieve a 100-fold dilution or a normalised concentration of 0.01, the estimated physical distance was 0.73 m for sedentary/passive activity, 0.8 m for standard activity, 1.02 m for light activity, 1.33 m for moderate activity, and 1.68 m for intense activity. The predicted distance of 0.8 m is relatively close to the 0.7 m predicted for standard activity, suggesting that the two-stage jet model dilution formula offers a reasonable prediction of the expired jet dilution.
One striking observation with the two-stage jet model was that increasing ventilation was much less effective at reducing short-range airborne infection risk than increasing physical distance, when the physical distance was less than the threshold distance. At a closer distance, any further increase in ventilation rate was no longer effective. For example, for intense activity, the short-range airborne infection risk is 16.5% at 1 m when the ventilation rate is 100 L/s per person, but becomes 3.6% at 2 m with the same ventilation. When the ventilation is infinite, the infection risk is still 15.4% at 1 m.
4.2. Explanation of some observed transmission phenomena
Short-range airborne infection risk increases as activity intensifies at any physical distance and ventilation rate. For example, when the infectious quantum concentration is 0.1 quanta/L at the mouth, at a physical distance of 1.5 m and a ventilation rate of 5 L/s per person, the 42-s short-range infection risk is 0.3% for sedentary/passive activity, 1.9% for light activity, 8.6% for moderate activity, and 28.4% for intense activity. Physical distancing or a high ventilation rate alone is not sufficient to reduce the infection risk at close range in indoor spaces. Physical distancing and ventilation need to be combined.
Our partial derivative method suggested a threshold distance of 0.59 m for sedentary/passive activity, 1.1 m for light activity, 1.7 m for moderate activity, and 2.6 m for intense activity. The corresponding threshold ventilation rate was 8 L/s per person for sedentary/passive activity, 20 L/s per person for light activity, 43 L/s per person for moderate activity, and 83 L/s per person for intense activity (Fig. 12). The 42-s short-range airborne infection risk at the threshold conditions was 0.79% for sedentary/passive activity, 0.82% for standard activity, 1.14% for light activity, 1.74% for moderate activity, and 2.61% for intense activity. Thus, if the threshold physical distance and ventilation rate are achieved, the short-range airborne infection risk can be theoretically low [44]. However, some existing building ventilation systems may not satisfy the high ventilation rate required for moderate and intense activities [45]. Thus, a high risk of close-contact transmission may be expected due to intense activities in such settings, as previously observed [46,47].
For sedentary/passive or light activities in indoor spaces (e.g., residential buildings or offices), the current minimum ventilation rate can easily satisfy our estimated ventilation rate requirement of 10 L/s per person. For example, the current ventilation standard is 8.5 L/s per person in office spaces and 7 L/s per person in residential spaces [45]. The required physical distance thresholds of 0.59 and 1.1 m may also be easily satisfied in offices, but not in homes. This may explain why there have been more household outbreaks than office outbreaks [[39], [48]].
In contrast, for moderate or intense activities (e.g., in fitness centres or gyms), the threshold physical distance may be easily satisfied. However, the existing ventilation standards (e.g. ASHRAE 62.1-2019 [45]) are far from meeting the required ventilation rates for moderate and intense activities. For example, in a fitness centre with a ventilation rate of 10 and 240 L/s per person, the 42-s short-range airborne infection risks at a physical distance of 2 m are 15.2% and 2.4%, respectively. This explains the difference in attack rate caused by ventilation difference between super-spreading events in fitness centres and gyms [44,47,[49], [50]].
In addition to physical activity intensity, the exhalation and inhalation rate also depend on respiratory activity (e.g., breathing, speaking, singing) [[21], [51]]. Speaking or singing activities increase exhalation and inhalation rates and thus, increase the infection risk via both short-range and long-range airborne routes, which may explain why there are higher infection risks in restaurants and at choir rehearsals than in other indoor spaces with activities of equal intensity [[52], [53], [54]]. Moreover, some indoor spaces (e.g., bars and karaoke clubs) with both intense activity and speaking or singing activity meet neither the physical distance requirements nor the ventilation rate requirements, which has led to a high infection risk and super-spreading events in bars and karaoke clubs [55,[56], [57], [58]].
4.3. Infectious quantum emission rate for short- and long-range airborne routes
Two methods are currently available for estimating the infectious quantum generation rate. The commonly used method is to use infection and ventilation data from a super-spreading event [54]. Only long-range quantum generation rates have been estimated thus far, due to difficulties in isolating short-range infection data from long-range infection, as close-contact scenarios are mostly unknown at the time of exposure. The viral load and droplet release rate may also be used to estimate the quantum generation rate [59]. This method has the potential to be developed for estimating both short- and long-range quantum generation rates. However, additional data, such as the survival of the virus in the short-range expired jet, are needed. This is a difficult problem to solve, as the residence time of the aerosols in the expired jet is less than 1 or only a few seconds. Virus survival characteristics within such a short duration are difficult to obtain. There are no data for virus survival in aerosols within the first few seconds of their release. In addition, the long-range quantum generation rate should be much less than the short-range quantum generation rate, given that the size range of suspended aerosols within a close range may be larger than the size range of suspended aerosols in the rest of the room [8,9]. The fraction values remain to be determined.
In this study, we made a crude estimate of the short-range infectious quantum generation rate using data reported by Chu et al. [26]. However, complexities exist when using these data. The observed infection at close range reported by Chu et al. [26] may have been due to the lack of adherence to the threshold distance, such that at least some infections may have occurred at a close distance. In such situations, our estimated short-range quantum generation rate may have been over-estimated. It is also possible that the average close-contact exposure period may be longer or shorter than our assumed values. A secondary infection may also be the result of both short- and long-range exposure. A Monte Carlo method may be used in future studies to perform such estimates, but more reliable data are needed. However, no reliable short-range quantum generation rate exists. Thus, a reliable approach to estimate short- and long-range quantum generation rates is needed.
4.4. Limitations of the study
There are several major limitations of this study. The short-range Wells-Riley model assumes that the emission rate of bioeffluents or the number of exhaled droplets is proportional to the exhalation rates for different activity intensities, and that the infectious quantum concentration at the mouth is constant. For subjects infected with the human rhinovirus, the exhaled particle concentration (<10 μm) is likely to be proportional to minute ventilation at a close range [60]; however, it remains unknown how the number and size distribution of droplets exhaled by healthy subjects or subjects infected with a respiratory virus vary when physical activity intensity and respiratory activity change. It is also unknown how the virus concentration is distributed in different sizes of particles, even though Milton et al. [61] found that, for influenza virus, fine particles may contain a much higher number of viral copies than coarse particles. Hence, data are needed on how the number and size distribution of exhaled droplets change with activity intensity/mode, and how the infectious quantum concentration at the mouth changes with exhaled droplet size. The dilution analysis of short-range airborne infection risk in Section 3.4 was based on ventilation rate per infector only, without considering effective dilution due to aerosols settling, filtration and virus deactivation as suggested in Equation (14). Our model (Equation (22)) is appliable to the situation with multiple infectors, and in such situations, the overall room dilution air flow rate should be used as in Equation (14).
Several physical and biological assumptions were made in this study. Our model did not consider particle settling or virus deactivation at a close range. A more accurate model needs to consider dispersion of individual droplets in the expired jet. Evaporation or dehydration is known to occur at a close range. Virus deactivation over a short range may need to be considered. The jet trajectory changes due to buoyancy, but being ignored here, but the dilution factor formula may still be applied along the trajectory. Our model simplified the breathing profile as a square cycle, which may lead to an underestimation of the streamwise penetration distance of the jet-like stage and an overestimation of the dilution factor at any distance in the puff-like stage. Hence, the required physical distance and ventilation rate may be underestimated. A calm air surrounding was assumed to avoid considering ambient turbulent dispersion; however, in reality, room air is not usually calm. Once the jet is destroyed by the surrounding air flows, the short-range transmission merges into long-range transmission. The change in streamlines when approaching the exposed individual affect the inhalation exposure [3].
5. Concluding remarks
Using the newly developed dilution factor formula, we estimated a dilution factor that depends on the exhalation flow rate. In the jet-like stage, the newly estimated dilution factor was similar to the dilution factor predicted by the steady jet model. However, the dilution factor markedly increased in the puff-like stage for all activity intensities, with light activity corresponding to a higher dilution than intense activity for a simple reason, i.e., more intense activity has a later transition point from jet-like to puff-like stages. The higher estimated dilution factor indicates a more rapid decrease of the normalised concentration of virus-containing particles within expired flows of the corresponding short-range exposure.
The newly developed dilution factor using the two-stage expired jet model has enabled the development of a simple short-range infection risk model. The infectious quantum generation rate differs between short-range and long-range airborne infection. The short-range quantum generation rate remains to be determined. Following this uncertainty, we propose to use a partial derivative approach to estimate the threshold distance and threshold ventilation rate. The partial derivative approach has been shown to be valid when the infectious quantum concentration is less than 1 quantum/L at the mouth, or when the equivalent quantum generation rate is less than 360 quanta/h at an exhaled flow rate of 0.1 L/s. The newly defined threshold distance and threshold ventilation rate are independent of the quantum concentration.
The insights gained from this model are meaningful. For example, the model showed that physical distancing or ventilation alone is generally not sufficient to reduce the infection risk in indoor spaces. Poor ventilation leads to long-range airborne infection and increases the risk of short-range airborne infection. Physical distancing is essential for minimising infection risk at a close distance, and adequate ventilation may also reduce short-range infection risk, especially in spaces used for high-intensity activity. However, a significant infection risk is associated with a less-than-threshold physical distance. In such a situation, ventilation is no longer effective, even if the ventilation rate is very high. The work will be useful for developing ventilation standards for infection control.
CRediT authorship contribution statement
Wei Jia: Writing – original draft, Visualization, Methodology, Investigation, Formal analysis, Data curation. Jianjian Wei: Writing – review & editing, Methodology. Pan Cheng: Writing – review & editing, Investigation, Data curation. Qun Wang: Writing – review & editing, Investigation. Yuguo Li: Writing – review & editing, Writing – original draft, Methodology, Investigation, Conceptualization.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work was supported by a General Research Fund grant (grant number 17202719) provided by the Research Grants Council of Hong Kong. We are grateful to Professor Chen Chun of Chinese University of Hong Kong for providing original datasets in Chen et al. [36].
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.buildenv.2022.109166.
Appendix A. Supplementary data
The following is the Supplementary data to this article:
References
- 1.World Health Organization (WHO) World Health Organization; 2020. Transmission of SARS-CoV-2: Implications for Infection Prevention Precautions: Scientific Brief, 09 July 2020 (No. WHO/2019-nCoV/Sci_Brief/Transmission_modes/2020.3) [Google Scholar]
- 2.World Health Organization (WHO) Coronavirus disease (COVID-19): how is it transmitted? 2021. https://www.who.int/news-room/q-a-detail/coronavirus-disease-covid-19-how-is-it-transmitted Updated on 30 April 2021.
- 3.Chen W., Zhang N., Wei J., Yen H.L., Li Y. Short-range airborne route dominates exposure of respiratory infection during close contact. Build. Environ. 2020;176 doi: 10.1016/j.buildenv.2022.109166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Riley E.C., Murphy G., Riley R.L. Airborne spread of measles in a suburban elementary school. Am. J. Epidemiol. 1978;107(5):421–432. doi: 10.1093/oxfordjournals.aje.a112560. [DOI] [PubMed] [Google Scholar]
- 5.Wells W.F. Harvard University Press; Cambridge, MA: 1955. Airborne Contagion and Air Hygiene. An Ecological Study of Droplet Infections. [Google Scholar]
- 6.Rudnick S.N., Milton D.K. Risk of indoor airborne infection transmission estimated from carbon dioxide concentration. Indoor Air. 2003;13(3):237–245. doi: 10.1034/j.1600-0668.2003.00189.x. [DOI] [PubMed] [Google Scholar]
- 7.Qian H., Li Y., Nielsen P.V., Huang X. Spatial distribution of infection risk of SARS transmission in a hospital ward. Build. Environ. 2009;44(8):1651–1658. [Google Scholar]
- 8.Xie X., Li Y., Chwang A.T., Ho P.L., Seto W.H. How far droplets can move in indoor environments--revisiting the Wells evaporation-falling curve. Indoor Air. 2007;17(3):211–225. doi: 10.1111/j.1600-0668.2007.00469.x. [DOI] [PubMed] [Google Scholar]
- 9.Gralton J., Tovey E., McLaws M.L., Rawlinson W.D. The role of particle size in aerosolised pathogen transmission: a review. J. Infect. 2011;62(1):1–13. doi: 10.1016/j.jinf.2010.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zhang N., Chen W., Chan P.T., Yen H.L., Tang J.W.T., Li Y. Close contact behavior in indoor environment and transmission of respiratory infection. Indoor Air. 2020;30(4):645–661. doi: 10.1111/ina.12673. [DOI] [PubMed] [Google Scholar]
- 11.Li Y., Cheng P., Jia W. Poor ventilation worsens short-range airborne transmission of respiratory infection. Indoor Air. 2022;32(1) doi: 10.1111/ina.12946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wei J., Li Y. Human cough as a two-stage jet and its role in particle transport. PLoS One. 2017;12(1) doi: 10.1371/journal.pone.0169235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bourouiba L., Dehandschoewercker E., Bush J.W. Violent expiratory events: on coughing and sneezing. J. Fluid Mech. 2014;745:537–563. [Google Scholar]
- 14.Abkarian M., Mendez S., Xue N., Yang F., Stone H.A. Speech can produce jet-like transport relevant to asymptomatic spreading of virus. Proc. Natl. Acad. Sci. Unit. States Am. 2020;117(41):25237–25245. doi: 10.1073/pnas.2012156117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fierce L., Robey A.J., Hamilton C. Simulating near - field enhancement in transmission of airborne viruses with a quadrature-based model. Indoor Air. 2021;31(6):1843–1859. doi: 10.1111/ina.12900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wagner J., Sparks T.L., Miller S., Chen W., Macher J.M., Waldman J.M. Modeling the impacts of physical distancing and other exposure determinants on aerosol transmission. J. Occup. Environ. Hyg. 2021;18(10–11):495–509. doi: 10.1080/15459624.2021.1963445. [DOI] [PubMed] [Google Scholar]
- 17.Cortellessa G., Stabile L., Arpino F., Faleiros D.E., Van Den Bos W., Morawska L., Buonanno G. Close proximity risk assessment for SARS-CoV-2 infection. Sci. Total Environ. 2021;794 doi: 10.1016/j.scitotenv.2021.148749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Fu L., Nielsen P.V., Wang Y., Liu L. Indoor and Built Environment; 2021. Measuring Interpersonal Transmission of Expiratory Droplet Nuclei in Close Proximity. 1420326X211029689. [Google Scholar]
- 19.Bazant M.Z., Bush J.W. A guideline to limit indoor airborne transmission of COVID-19. Proc. Natl. Acad. Sci. Unit. States Am. 2021;118(17) doi: 10.1073/pnas.2018995118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Sangras R., Kwon O.C., Faeth G.M. Self-preserving properties of unsteady round nonbuoyant turbulent starting jets and puffs in still fluids. J. Heat Tran. 2002;124(3):460–469. [Google Scholar]
- 21.U.S. EPA . U.S. Environmental Protection Agency; Washington, DC: 2011. (Exposure Factors Handbook 2011 Edition (Final Report)). EPA/600/R-09/052F. [Google Scholar]
- 22.Lee J.H.W., Chu V.H. Kluwer Academic; Boston: 2003. Turbulent Jets and Plumes: A Lagrangian Approach. [Google Scholar]
- 23.Diez F.J., Sangras R., Kwon O.C., Faeth G.M. Erratum: self-preserving properties of unsteady round nonbuoyant turbulent starting jets and puffs in still fluids [ASME Journal of Heat Transfer, 124(3). 460-469 (2002)] J. Heat Tran. 2003;125(1):204–205. [Google Scholar]
- 24.Scorer R.S. Experiments on convection of isolated masses of buoyant fluid. J. Fluid Mech. 1957;2(6):583–594. [Google Scholar]
- 25.Zhang N., Chen X., Jia W., Jin T., Xiao S., Chen W.…Kang M. Evidence for lack of transmission by close contact and surface touch in a restaurant outbreak of COVID-19. J. Infect. 2021;83(2):207–216. doi: 10.1016/j.jinf.2021.05.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Chu D.K., Akl E.A., Duda S., Solo K., Yaacoub S., Schünemann H.J.…Reinap M. Physical distancing, face masks, and eye protection to prevent person-to-person transmission of SARS-CoV-2 and COVID-19: a systematic review and meta-analysis. Lancet. 2020;395(10242):1973–1987. doi: 10.1016/S0140-6736(20)31142-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Agrawal A, Bhardwaj R. Reducing chances of COVID-19 infection by a cough cloud in a closed space. Phys. Fluids. 2020;32(10) doi: 10.1063/5.0029186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Behera S, Bhardwaj R, Agrawal A. Effect of co-flow on fluid dynamics of a cough jet with implications in spread of COVID-19. Phys. Fluids. 2021;33(10) doi: 10.1063/5.0064104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ghaem-Maghami E., Johari H. Concentration field measurements within isolated turbulent puffs. J. Fluid Eng. 2007;129(2):194–199. [Google Scholar]
- 30.Bjørn E., Nielsen P.V. Dispersal of exhaled air and personal exposure in displacement ventilated rooms. Indoor Air. 2002;12(3):147–164. doi: 10.1034/j.1600-0668.2002.08126.x. [DOI] [PubMed] [Google Scholar]
- 31.Olmedo I., Nielsen P.V., Ruiz de Adana M., Jensen R.L., Grzelecki P. Distribution of exhaled contaminants and personal exposure in a room using three different air distribution strategies. Indoor Air. 2012;22(1):64–76. doi: 10.1111/j.1600-0668.2011.00736.x. [DOI] [PubMed] [Google Scholar]
- 32.Liu L., Li Y., Nielsen P.V., Wei J., Jensen R.L. Short-range airborne transmission of expiratory droplets between two people. Indoor Air. 2017;27(2):452–462. doi: 10.1111/ina.12314. [DOI] [PubMed] [Google Scholar]
- 33.Nielsen P.V., Hyldgaard C.E., Melikov A., Andersen H., Soennichsen M. Personal exposure between people in a room ventilated by textile terminals—with and without personalized ventilation. HVAC R Res. 2007;13(4):635–643. [Google Scholar]
- 34.Olmedo I., Nielsen P.V., Ruiz de Adana M., Jensen R.L. The risk of airborne cross -infection in a room with vertical low - velocity ventilation. Indoor Air. 2013;23(1):62–73. doi: 10.1111/j.1600-0668.2012.00794.x. [DOI] [PubMed] [Google Scholar]
- 35.Cao G., Nielsen P.V., Jensen R.L., Heiselberg P., Liu L., Heikkinen J. Protected zone ventilation and reduced personal exposure to airborne cross - infection. Indoor Air. 2015;25(3):307–319. doi: 10.1111/ina.12142. [DOI] [PubMed] [Google Scholar]
- 36.Chen C., Zhao B., Lai D., Liu W. A simple method for differentiating direct and indirect exposure to exhaled contaminants in mechanically ventilated rooms. Build. Simulat. 2018;11(5):1039–1051. doi: 10.1007/s12273-018-0441-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Haas C.N. Estimation of risk due to low doses of microorganisms: a comparison of alternative methodologies. Am. J. Epidemiol. 1983;118(4):573–582. doi: 10.1093/oxfordjournals.aje.a113662. [DOI] [PubMed] [Google Scholar]
- 38.Sze To G.N., Chao C.Y.H. Review and comparison between the Wells-Riley and dose-response approaches to risk assessment of infectious respiratory diseases. Indoor Air. 2010;20(1):2–16. doi: 10.1111/j.1600-0668.2009.00621.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Qian H., Miao T., Liu L., Zheng X., Luo D., Li Y. Indoor transmission of SARS-CoV-2. Indoor Air. 2021;31(3):639–645. doi: 10.1111/ina.12766. [DOI] [PubMed] [Google Scholar]
- 40.Low Z. Hong Kong's construction sites could be Covid-19 transmission hotspots, experts say, but blanket work stoppages are unlikely to help. South China Morning Post. 2020. https://sg.news.yahoo.com/hong-kong-construction-sites-could-150500126.html
- 41.GCR Staff 3000 workers tested as Covid outbreak disrupts Hong Kong's 3rd runway mega project. Glob. Construct. Rev. 2021 https://www.globalconstructionreview.com/3000-workers-tested-covid-outbreak-disrupts-hong-k/ [Google Scholar]
- 42.Liu F., Luo Z., Li Y., Zheng X., Zhang C., Qian H. Revisiting physical distancing threshold in indoor environment using infection-risk-based modeling. Environ. Int. 2021;153:106542. doi: 10.1016/j.envint.2021.106542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Shulman D. Coronavirus: could social distancing of less than two metres work? BBC. 2020. https://www.bbc.co.uk/news/science-environment-52522460
- 44.Marr L.C. SARS-CoV-2 Superspread in fitness center, Hong Kong, China, March 2021. Emerg. Infect. Dis. 2021;27(9):2507. doi: 10.3201/eid2709.211177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.ASHRAE 62.1-2019 . American Society of Heating, Refrigerating and Air-Conditioning Engineers; 2019. Ventilation for Acceptable Indoor Air Quality. [Google Scholar]
- 46.Bae S., Kim H., Jung T.Y., Lim J.A., Jo D.H., Kang G.S.…Kwon H.J. Epidemiological characteristics of COVID-19 outbreak at fitness centers in Cheonan, Korea. J. Kor. Med. Sci. 2020;35(31) doi: 10.3346/jkms.2020.35.e288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Chu D.K., Gu H., Chang L.D., Cheuk S.S., Gurung S., Krishnan P.…Poon L.L. SARS-CoV-2 superspread in fitness center, Hong Kong, China, March 2021. Emerg. Infect. Dis. 2021;27(8):2230. doi: 10.3201/eid2708.210833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Chan J.F.W., Yuan S., Kok K.H., To K.K.W., Chu H., Yang J.…Yuen K.Y. A familial cluster of pneumonia associated with the 2019 novel coronavirus indicating person-to-person transmission: a study of a family cluster. Lancet. 2020;395(10223):514–523. doi: 10.1016/S0140-6736(20)30154-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Jang S., Han S.H., Rhee J.Y. Cluster of coronavirus disease associated with fitness dance classes, South Korea. Emerg. Infect. Dis. 2020;26(8):1917. doi: 10.3201/eid2608.200633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Groves L.M., Usagawa L., Elm J., Low E., Manuzak A., Quint J.…Kemble S.K. Community transmission of SARS-CoV-2 at three fitness facilities—Hawaii, June–July 2020. MMWR (Morb. Mortal. Wkly. Rep.) 2021;70(9):316. doi: 10.15585/mmwr.mm7009e1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Adams W.C. California Air Resources Board; Sacramento, CA: 1993. Measurement of Breathing Rate and Volume in Routinely Performed Daily Activities. Final Report, Contract No. A033-205. [Google Scholar]
- 52.Li Y., Qian H., Hang J., Chen X., Cheng P., Ling H.…Kang M. Probable airborne transmission of SARS-CoV-2 in a poorly ventilated restaurant. Build. Environ. 2021;196 doi: 10.1016/j.buildenv.2021.107788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Lakha F., Rudge J.W., Holt H. Rapid synthesis of evidence on settings which have been associated with SARS-CoV-2 transmission clusters. 2020. https://superspreadingdatabase.github.io/Evidence_on_clusters_final.pdf
- 54.Miller S.L., Nazaroff W.W., Jimenez J.L., Boerstra A., Buonanno G., Dancer S.J.…Noakes C. Transmission of SARS-CoV-2 by inhalation of respiratory aerosol in the Skagit Valley Chorale superspreading event. Indoor Air. 2021;31(2):314–323. doi: 10.1111/ina.12751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Adam D.C., Wu P., Wong J.Y., Lau E.H., Tsang T.K., Cauchemez S.…Cowling B.J. Clustering and superspreading potential of SARS-CoV-2 infections in Hong Kong. Nat. Med. 2020;26(11):1714–1719. doi: 10.1038/s41591-020-1092-0. [DOI] [PubMed] [Google Scholar]
- 56.Furuse Y., Sando E., Tsuchiya N., Miyahara R., Yasuda I., Ko Y.K.…Oshitani H. Clusters of coronavirus disease in communities, Japan, January–April 2020. Emerg. Infect. Dis. 2020;26(9):2176. doi: 10.3201/eid2609.202272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Chau N.V.V., Hong N.T.T., Ngoc N.M., Thanh T.T., Khanh P.N.Q., Nguyet L.A.…Van Tan L. Superspreading event of SARS-CoV-2 infection at a bar, Ho Chi Minh city, Vietnam. Emerg. Infect. Dis. 2021;27(1):310. doi: 10.3201/eid2701.203480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Gu Y., Lu J., Su W., Liu Y., Xie C., Yuan J. Transmission of SARS-CoV-2 in the karaoke room: an outbreak of COVID-19 in Guangzhou, China, 2020. J. Epidemiol. Glob. Health. 2021;11(1):6. doi: 10.2991/jegh.k.201007.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Buonanno G., Stabile L., Morawska L. Estimation of airborne viral emission: quanta emission rate of SARS-CoV-2 for infection risk assessment. Environ. Int. 2020;141 doi: 10.1016/j.envint.2020.105794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Fabian P., Brain J., Houseman E.A., Gern J., Milton D.K. Origin of exhaled breath particles from healthy and human rhinovirus-infected subjects. J. Aerosol Med. Pulm. Drug Deliv. 2011;24(3):137–147. doi: 10.1089/jamp.2010.0815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Milton D.K., Fabian M.P., Cowling B.J., Grantham M.L., McDevitt J.J. Influenza virus aerosols in human exhaled breath: particle size, culturability, and effect of surgical masks. PLoS Pathog. 2013;9(3) doi: 10.1371/journal.ppat.1003205. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.