New 3D graphical representation for RNA structure analysis and its application in the pre-miRNA identification of plants

Abstract

MicroRNAs (miRNAs) are a family of short non-coding RNAs that play significant roles as post-transcriptional regulators. Consequently, various methods have been proposed to identify precursor miRNAs (pre-miRNAs), among which the comparative studies of miRNA structures are the most important. To measure and classify the structural similarity of miRNAs, we propose a new three-dimensional (3D) graphical representation of the secondary structure of miRNAs, in which an miRNA secondary structure is initially transformed into a characteristic sequence based on physicochemical properties and frequency of base. A numerical characterization of the 3D graph is used to represent the miRNA secondary structure. We then utilize a novel Euclidean distance method based on this expression to compute the distance of different miRNA sequences for the sequence similarity analysis. Finally, we use this sequence similarity analysis method to identify plant pre-miRNAs among three commonly used datasets. Results show that the method is reasonable and effective.

MicroRNAs (miRNAs) are a family of short non-coding RNAs that play significant roles as post-transcriptional regulators.

Introduction

MicroRNAs (miRNAs) are a family of short noncoding RNAs that play significant roles as post-transcriptional regulators.¹ With extracellular miRNAs, hypothalamic stem cells partially control the aging rate.² As such, miRNA is an important noncoding RNA involved in many important biological processes, including plant development, signal transduction, and protein degradation.^3,4 miRNA prediction has constantly been an important issue in the miRNA research domain. The bases of single-stranded miRNAs in live cells are constantly folded to form an miRNA secondary structure rather than a linear form. The three-dimensional (3D) structure and function of miRNAs are determined by their secondary structures,³ and their functions are mainly determined by their structures.⁵ Thus, studies on RNA sequences and their secondary structures are essential for identifying and understanding the functional similarities between plant miRNAs. Precursor miRNAs (pre-miRNAs) of plants generally have a more complex secondary structure than those of animals, and existing prediction methods on animal pre-miRNA classification cannot be effectively applied to predict plant pre-miRNAs.⁶ Experimental methods, such as ChIP-sequencing for pre-miRNA identification, are expensive and time consuming, thereby presenting the need for computational methods. Computational methods, including machine learning (ML) and sequence analysis methods, should be developed to predict, analyze, and provide reliable miRNA candidates for subsequent biological experiments.⁷

ML-based methods have been widely applied to identify plant miRNAs.^1,8–15 ML-based methods have treated pre-miRNA identification as a binary classification task to discriminate between real and pseudo-pre-miRNAs. However, the performance of ML-based predictors mainly depends on ML algorithms or operation engines. Numerous classification prediction algorithms, which yield different results, have been utilized to recognize pre-miRNA. ML-based algorithms include support vector machines (SVM),^1,8,16–26 back-propagation and self-organizing map (SOM) neural networks,^27–29 and random forest (RF).^30–32 Difficulties in using ML-based methods are attributed to the selection of representative samples that adequately describe the sample space of an entire positive dataset (pre-miRNA) and negative dataset counterexamples (pseudo pre-miRNA). Computational complexity in predicting large genome mass data is also high. These approaches involve a large number of false positive candidates. Therefore, miRNA classification prediction should be investigated and solved on the basis of ML prediction methods to improve sensitivity and specificity.

Sequence-based methods, including sequence alignment and distance analysis, are mainly used to analyze the similarities between miRNA sequences. T. Dezulian et al.³³ used BLAST for sequence alignment to search for homologous sequences that are similar to known plant pre-miRNAs. The similarity of sequence distance is mainly transformed into the similarity between analysis sequences and secondary structures by graphical representation. Graphical representation has been widely applied to RNA sequence representation, especially for the analysis of RNA secondary structures. Y. H. Yao et al.^34,35 proposed a graphical representation based on two-dimensionality (2D) to analyze the similarity of RNA secondary structures. On the basis of sequence and base physicochemical information, Jeffrey et al.^36,37 proposed a 3D representation of RNA secondary structures. Liao et al.^38,39 proposed four- to seven-dimensional graphical representation method for RNA secondary structures. This method can solve the problem of structural degradation and information loss of 2D graphical representation, but it is not conducive to graphic visualization. Zhang et al.^40–42 developed a graphical representation for ncRNA secondary structures. To validate the aforementioned methods, researchers usually build phylogenetic trees based on the similarity between sequences to compare the reliability of the methods. In contrast to ML or other complex computing techniques, a graphical representation is an effective analysis method that can provide an intuitive and unique perspective in analyzing sequence similarity.

In this study, we propose a new 3D graphical representation of miRNA secondary structures. In this representation, an miRNA secondary structure is initially transformed into a characteristic sequence based on the frequency and physicochemical properties of nucleic acids. A numerical characterization of the 3D graph is then used to represent the miRNA secondary structure. On the basis of the proposed 3D graphical representation method, we utilize a novel Euclidean distance method to compute the distance of different miRNA secondary structures for similarity analysis. A small distance indicates a high similarity and vice versa. We use this similarity analysis method to identify plant pre-miRNAs among three commonly used datasets. Our results show that our method is reasonable, effective, simple to operate without training parameters, and more intuitive than several ML-methods.

Methods

Framework of the proposed method

Fig. 1 illustrates the overall framework of our method, which consists of two main phases, namely, pre-miRNA similarity analysis and prediction. In the similarity analysis phase, the initial pre-miRNA sequences are extracted from the raw data. Then, homology bias is avoided by using the CD-HIT software⁴³ (threshold set to 0.8) to filter samples with a similarity greater than the threshold in the initial dataset, and the secondary structure of the given benchmark dataset is predicted with the RNAfold software.⁴⁴ We design a new 3D graphical representation to represent the miRNA secondary structure. On the basis of the proposed method, we utilize a novel Euclidean distance method to compute the distance of different miRNA secondary structures for similarity analysis. In the pre-miRNA prediction phase, the distance between any two sequences in the benchmark datasets is calculated using the proposed method. The smaller the distance is, the more similar the two pre-miRNA sequences will be. The jackknife method is applied to traverse the entire benchmark datasets and to predict whether a given sequence is a plant pre-miRNA.

Fig. 1. Overall framework of the proposed method.

New 3D graphical representation of miRNA structure

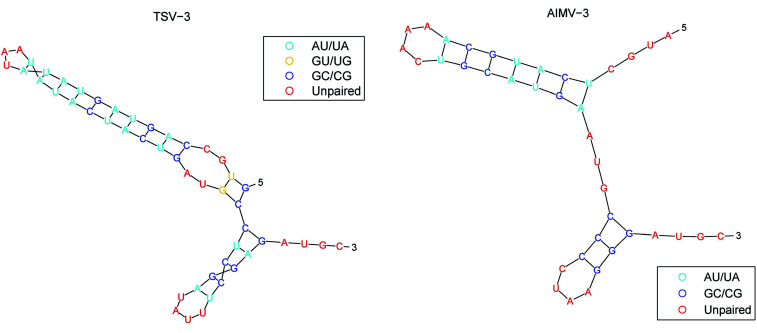
The secondary structure of RNAs consists of a number of free bases (i.e., A, G, C, and U) and paired bases (i.e., A–U, G–C, and G–U). A total of 9 viral RNA base sequences are obtained from ref. 45. Fig. 2 shows the secondary structure of the RNA sequence of the obtained TSV-3 and AIMV-3 using the algorithm in ref. 46.

Fig. 2. The secondary structure of the RNA sequence of the TSV-3 and AIMV-3.

For research convenience, the base and unpaired bases should be distinguished. The bases of A, G, C, and U located in base pairs A–U, G–C, and G–U are denoted as a, g, c, and u, respectively. The RNA sequences of the 9 obtained viruses from ref. 45 are processed by RNAfold,⁴⁴ and the RNA secondary structure sequence is shown in Table 1.

Information about the secondary structure of RNA sequences of 9 viruses.

Species	RNA secondary structure	Length
AIMV-3	AUGCucaugcaAAACugcaugaAUGCcccUAAgggAUGC	39
APMV-3	AAUGCccacaacGUGAAguuguggAUGCcccGUUAgggAAGC	42
AVII	AUGCcuaaUacucucucuCAGggagagaguuuagAUGCcuccAAAggagAUGC	53
CILRV	AUGCcuauauuuucucUCCUgagaaaauauagAUGCcuccAAAggagAUGC	51
CVV-3	AUGCccaAAcucucucuCAUggagagagAAuggAUGCcuccGAAggagAUGC	52
EMV-3	CcuaauUcucucucuCACggagagagauuagAUGCcucCAAGgagAUGC	49
LRMV-3	UUCcuauucucucucUCAGgagagGagaauagAUGCcuccAAAggagUCGC	51
PDV-3	AUGCccucaccGUAAggugaggAUGCcccuUAAagggAUGC	41
TSV-3	GUGCcaguaguauaUAAuauacuacugAUGCcuccuUUAUaggagAUGC	49

Let s = s₁, s₂, s₃, …, s_n represent an RNA secondary structure sequence, where n is the length of the sequence. Let point coordinates s_i(x_i, y_i, z_i) be the i-th base of the secondary structure sequence of miRNA, which corresponds to the eqn (1).

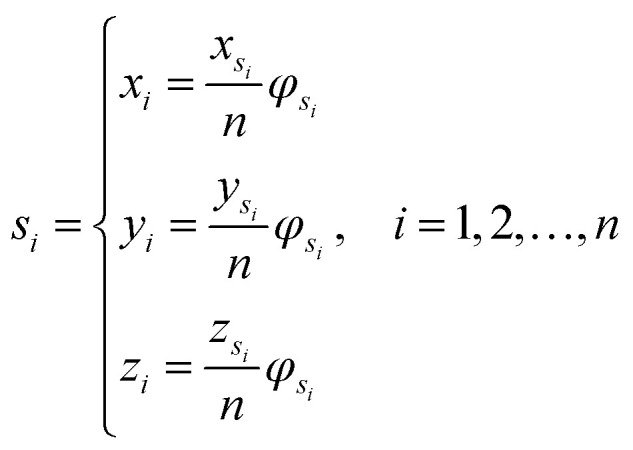1

where φ_si represents the accumulative occurrence frequency of the base at position i, and n is the length of the sequence. Ref. 35, 41 and 47 divided the bases in the pre-miRNA secondary structure sequence into three categories based on the physicochemical properties and obtained three representing graphs. Inspired by previous studies,^35,41,47 in this study, x_si, y_si and z_si are represented as eqn (2)–(4).

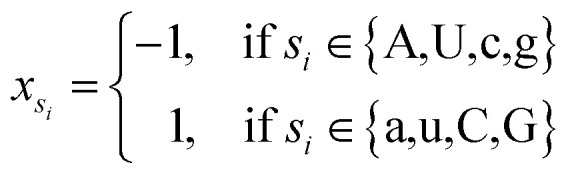2

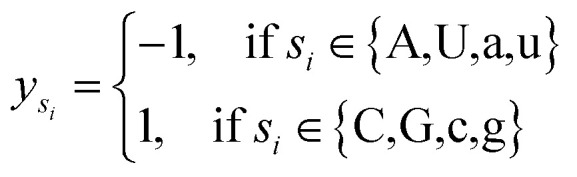3

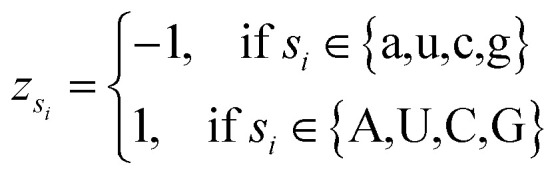4

For every base in the RNA secondary structure, a new accumulative coordinate S_i(X_i, Y_i, Z_i) can be obtained, which can be expressed as follows:

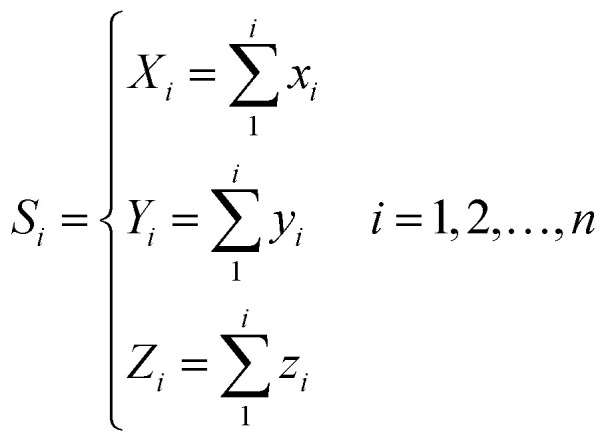5

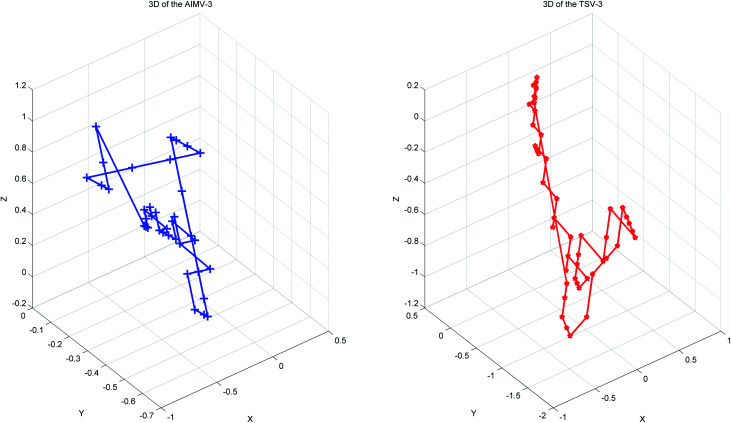
Thus, every base can obtain another point S_i(X_i, Y_i, Z_i). The advantages of the accumulative coordinate depend on the calculation where it contains a large amount of information, and the accuracy is good and computing the distance between sequences with different lengths is convenient. The RNA secondary structure sequences of TSV-3 and AIMV-3 are used as examples. Table 2 shows the accumulative coordinates of the 20 bases in front of the RNA secondary structures of TSV-3 and AIMV-3. Fig. 3 shows the 3D graphical representation of the RNA secondary structures of TSV-3 and AIMV-3.

The cumulative coordinates of the first 20 bases in the RNA secondary structures of TSV-3 and AIMV-3. X, Y, and Z denote the cumulative coordinates of the X, Y, and Z coordinate axes of the base, respectively.

TSV-3	X	Y	Z	AIMV-3	X	Y	Z
G	0.02	0.02	0.02	A	−0.03	−0.03	0.03
U	0	0	0.04	U	−0.05	−0.05	0.05
G	0.04	0.04	0.08	G	−0.03	−0.03	0.08
C	0.06	0.06	0.1	C	0	0	0.1
c	0.08	0.08	0.12	u	0.03	−0.03	0.08
a	0.06	0.06	0.1	c	0.05	0	0.1
g	0.04	0.08	0.08	a	0.03	−0.03	0.08
u	0.06	0.06	0.06	u	0.08	−0.08	0.03
a	0.02	0.02	0.02	g	0.05	−0.05	0
g	−0.02	0.06	−0.02	c	0.1	0	0.05
u	0.02	0.02	−0.06	a	0.05	−0.05	0
a	−0.04	−0.04	−0.12	A	0	−0.1	0.05
u	0.02	−0.1	−0.18	A	−0.08	−0.18	0.13
a	−0.06	−0.18	−0.27	A	−0.18	−0.28	0.23
U	−0.1	−0.22	−0.22	C	−0.13	−0.23	0.28
A	−0.12	−0.24	−0.2	u	−0.05	−0.31	0.21
A	−0.16	−0.29	−0.16	g	−0.1	−0.26	0.15
u	−0.08	−0.37	−0.24	c	−0.03	−0.18	0.23
a	−0.18	−0.47	−0.35	a	−0.1	−0.26	0.15
u	−0.08	−0.57	−0.45	u	0	−0.36	0.05

Fig. 3. The 3D graphical representation of the RNA secondary structure of viruses TSV-3 and AIMV-3.

Cumulative coordinates or cumulative distances are widely used in many research areas because they show many advantages.⁴⁸ However, the first residue may also be important, and the sequence space may be unbalanced. This study is different from the result of a previous cumulative coordinate study because the effects of sequence space imbalance are reduced in terms of the following aspects:

(1) The values of the cumulative coordinates are not monotonically increasing or decreasing. The coordinate value of each base may be positive or negative, and its positive and negative values depend on eqn (1)–(4). The cumulative coordinates are calculated by using eqn (5).

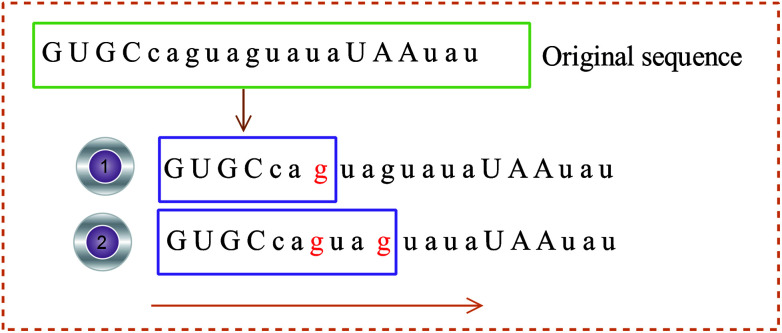
(2) The 3D coordinates of the constructed base are dynamically changed with the frequency of the base, reflecting the local characteristics of the sequence. For example, the initial sequence in Fig. 4 represents the first 20 bases of RNA “TSV-3”, which contains two g bases, and the coordinates of the two g bases are calculated using eqn (1). Re-routing from the beginning to the position of the base g is necessary to calculate the g base coordinate. Therefore, the coordinates of the base dynamically change with the position and number of bases, and the cumulative coordinates reflect the local characteristics of the pre-miRNA sequence to the base.

Fig. 4. Example of the base coordinate calculation.

(3) Table 2 shows that the coordinate values of the bases were not much different from the initial values, and the values gradually differed until the base position was about 10. Therefore, the cumulative coordinate values in this paper did not depend primarily on the first residue.

In summary, the cumulative coordinates are not monotonous, and they reflect the local characteristics of the sequence as the position and number of bases change dynamically. Therefore, the imbalance caused by the first residue in the sequence space has a slight effect.

A novel method for computing the distance of two sequences

To analyze the similarity between RNA sequences, a novel similarity calculation method for RNA secondary structure is proposed based on Euclidean distance. A smaller distance indicates more similarity, and vice versa.

Let the secondary structures of two arbitrary RNA sequences be represented by S_a and S_b, where N_a and N_b denote the lengths of the two sequences. The distance between S_a and S_b is calculated as follows:

(1) If the lengths of two sequences S_a and S_b are equal, that is, N_a = N_b, then D(S_a, S_b) represents the distance between sequences S_a and S_b, and is defined as eqn (6)

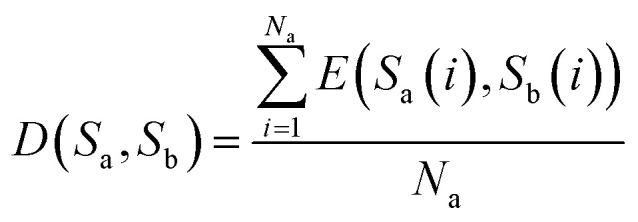6

Here, E(S_a(i), S_b(i)) represents the Euclidean distance between the i-th bases of sequences S_a and S_b.

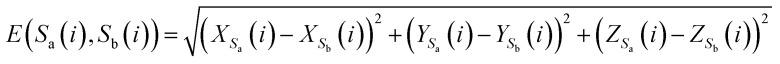7

(2) If the lengths of two sequences are not equal, then the distance between sequences S_a and S_b are computed as follows to obtain considerable information of the sequences:

Pattern 1

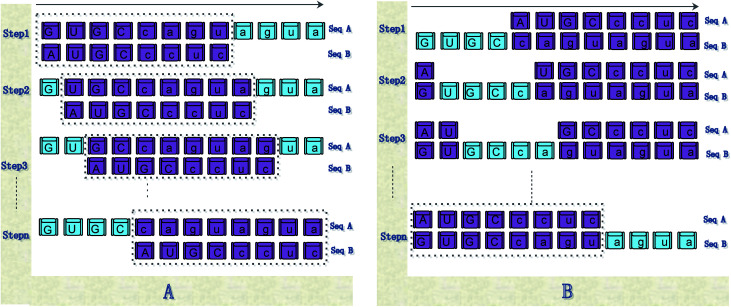
If N_a > N_b, sequence S_b moves one base to the right each time, and the total times of sequences S_b needs to moves to the right is (N_a − N_b). Eqn (6) is used to calculate the accumulative distance between subsequences S_a(1:N_b), S_a(2:N_b + 1), …, S_a(N_a − N_b + 1:N_a), and S_b successively, as shown in Fig. 5(a).

Fig. 5. Illustration of the steps of our method for calculating the distance between sequences. (A) shows the calculation steps for Pattern 1; (B) shows the calculation steps for Pattern 2.

Step 1: use eqn (6) to calculate the distance between sequence S_a(1:N_b) or sequence “GUGCcagu” and sequence S_b;

Step 2: sequence S_b moves on the right by a base character. Use eqn (6) to calculate the distance between sequences S_a(2:N_b) and S_b, as shown in Step 2 of Fig. 5(a).

…

Step (N_a − N_b + 1): sequence S_b moves on the right by a base character. Use eqn (6) to calculate the distance between sequences S_a((N_a − N_b + 1):N_a) and S_b.

Then, the average distance of every step is calculated (by dividing N_a − N_b) as shown in eqn (8).

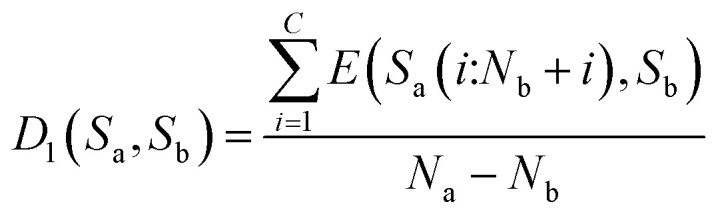8

Pattern 2

If N_a > N_b, then the subsequence whose length (N_a − N_b) is used, and sequence S_a moves one base character to the right each time successively. Then, eqn (10) is used to calculate the accumulative distance between subsequences S_a − S_a(1:N_a − N_b), S_a − S_a(2:N_a − N_b + 1), …, S_a − S_a(N_b:N_a), and S_b, and the average distance is calculated (by dividing N_a), as shown in Fig. 5(b).

Step 1: exclude sequence S_a(1:N_a − N_b), that is, sequence “GUGC”, and use eqn (6) to calculate the distance between S_a − S_a(1:N_a − N_b) or sequence “caguagua” and sequence S_b, as shown in Step 1 of Fig. 5(b).

Step 2: use the sequence whose length is N_a − N_b in sequence S_a, which moves one base character to the right. Use eqn (6) to calculate the distance between the remaining bases of sequences S_a and S_b, as shown in Step 2 of Fig. 5(b).

…

Step B: use eqn (6) to calculate the distance between S_a − S_a(N_b:N_a) and S_b.

Then, calculate the average distance of each Step (B). The computational formula is demonstrated by eqn (9).

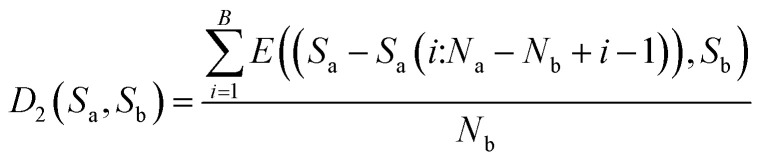9

After synthesizing the aforementioned scenarios, the distance between sequences S_a and S_b is expressed as shown in eqn (10).

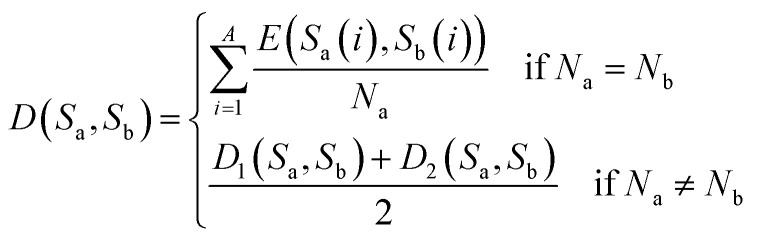10

where, N_a, N_b represent the lengths of the sequences S_a, S_b. E, D₁ and D₂ refer to eqn (7), (8) and (9), respectively.

We use the sequence similarity analysis method to compute the distances among 9 viruses.⁴⁵Table 3 shows the distance matrix of 9 RNA virus sequences. From the table, the three smallest values correspond to the RNA sequence pairs, namely, (AVII, LRMV-3), (LRMV-3, EMV-3), and (AVII, EMV-3), which indicate that they are the most similar. In addition, the large values in the table appear in the rows of APMV-3, AIMV-3, and PDV-3, which indicates that obvious differences exist between APMV-3, AIMV-3, and PDV-3 and other RNA sequences. In addition, the distances between APMV-3, AIMV-3, and PDV-3 22 are small, which indicate that the similarity among them is higher than the similarity among the other sequences. These results show that our method successfully captures the apparent similarity among the 9 RNA sequences. The results are similar to those of Liao et al.^37,38,40,41 Our 3D graphical representation and sequence similarity analysis method extract some essential information on RNA secondary structure and can effectively analyze the similarity of RNA sequences.

The distance matrix of the secondary structure of the 9 RNA virus sequences.

	APMV-3	AVII	CILRV	CVV-3	EMV-3	LRMV-3	PDV-3	TSV-3
AIMV-3	0.97	1.64	2.70	1.17	2.16	1.75	1.42	1.89
APMV-3	0.00	2.14	3.33	1.09	2.58	2.18	0.76	2.69
AVII		0.00	1.57	1.64	0.69	0.58	2.31	1.40
CILRV			0.00	2.92	1.47	1.89	3.62	1.14
CVV-3				0.00	2.01	1.53	1.21	2.45
EMV-3					0.00	0.70	2.67	1.79
LRMV-3						0.00	2.32	1.49
PDV-3							0.00	3.01

Results and discussions

MiRNAs are involved in a large number of biological processes, such as plant development and metabolism by either translational repression, RNA degradation, or through an RNA-induced silencing complex. Here, we apply our method to predict plant pre-miRNAs based on the similarity of pre-miRNA sequences.

We divide the datasets of plant pre-miRNA sequences into sample and test datasets. In the test dataset, a test sequence can be classified as the category of the sequence in the sample dataset that has the smallest distance with the test sequence. For example, the sequence with the smallest distance from the sample dataset is the pseudo pre-miRNA (negative data), and this test sequence is also the pseudo pre-miRNA, and vice versa. We use the jackknife method to calculate the accuracy of our method.

Datasets

In this section, we use three datasets to evaluate the performance of the proposed method.

Dataset 1

A total of 1906 plant pre-miRNAs were obtained as positive samples from ref. 6. A total of 2122 pseudo pre-miRNA were used negative samples. The dataset processing using the same method of Liu et al.^8,24–26,49 is expressed as follows. (1) To avoid redundancy and homologous bias, the threshold of CD-HIT software⁴³ was set to 80% to filter those other similarity sequences of more than 80% samples in the same sample dataset. (2) Then, the sequences that contained non-U, -A, -G, and -C character bases were excluded. (3) The secondary structure of pre-miRNAs was predicted by RNAfold,⁴⁴ and the pre-miRNAs that did not form a single-hairpin structure were removed. A total of 1204 plant pre-miRNAs were obtained as positive samples, and 1975 pseudo pre-miRNAs were obtained as negative samples. To avoid the imbalance between positive and negative samples, 1204 samples were selected from 1975 pseudo pre-miRNAs from front to back, and negative sample sets were constructed. Finally, 1204 plant pre-miRNAs were obtained as positive samples, and 1204 negative samples were obtained as dataset 1.

Dataset 2

In this study, we selected miRBase (19th edition),^50,51 which has been proved by experiments as a positive sample dataset for pre-miRNA sequences. A similar screening process with that of dataset 1 was conducted, and a total of 1848 non-redundant pre-miRNAs with single-hairpin structure were obtained. The pseudo pre-miRNAs obtained from ref. 14 were subjected to a similar screening process with that of dataset 1, and 1848 samples were selected from front to back to construct the negative dataset 2.

Dataset 3

Arabidopsis thaliana, Oryza sativa, Populus trichocarpa, Physcomitrella patens, and Medicago truncatula are typical model plants. Sorghum bicolor, Zea mays, and Glycine max are important crops. Ten sets of species datasets were obtained from ref. 6 through the screening process of the above data. A total of 153 A. thaliana (ATH dataset), 256 O. sativa (OSA dataset), 133 P. trichocarpa (PTC dataset), 184 P. patens (PPT dataset), 67 M. truncatula (MTR dataset), S. bicolor (105 SBI dataset), 74 Z. mays (ZMA dataset), 69 G. max (GMA dataset), 167 A. lyrata (updated ALY dataset), and 105 G. max (updated GMA dataset) pre-miRNAs were obtained, as well as 1095 pseudo pre-miRNA negative samples. The negative sample set was selected from the 1095 pseudo pre-miRNAs to maintain the consistency between the positive and negative samples, thereby avoiding the imbalance between positive and negative samples. For example, the ATH dataset containing 153 pre-miRNAs selected 153 pseudo pre-miRNAs from the 1095 pseudo pre-miRNAs as the negative sample set.

Comparison of state-of-the-art algorithms

The following measures were used to assess the performance of the classifiers used in this study.

To measure the effectiveness of identifying plant pre-miRNAs, the following equations are used to measure the experiment results, including the overall accuracy (ACC), sensitivity (SE), specificity (SP), and Mathews coefficient (MCC). The expressions are shown as follows:

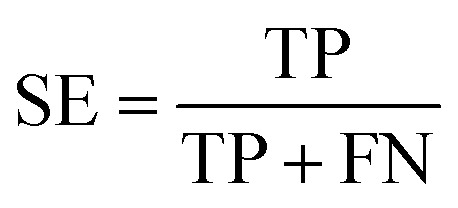11

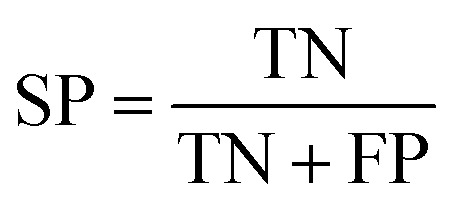12

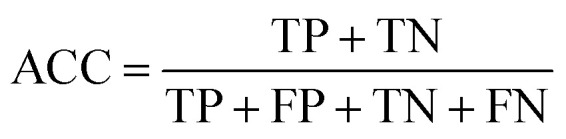13

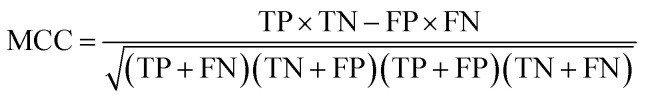14

The results of the jackknife test for dataset 1, dataset 2, and dataset 3 are listed in Tables 4, 5, and 6, respectively. Table 4 shows the results of our method and of microPred 52, iMcRNA 24, TripletSVM 53, and miPlantPre 14 methods applied to dataset 1. From the table, the ACC and MCC achieve 89.74% and 79.67% using our method, respectively, which are higher than others. Table 5 shows that the accuracy of our method is lower than the miPlantPre 14 method in dataset 2.

Comparison of prediction performance for different methods on the dataset 1 with a jackknife test.

Methods	ACC	SE	SP	MCC
iMcRNAa	85.88	87.83	83.31	71.86
miPlantPreb	82.68	97.59	75.18	68.48
microPredc	73.96	74.92	73.51	47.93
TripletSVMd	75.72	63.34	84.54	53.24
Our method	89.74	86.3	92.69	79.67

^aThe result based on the iMcRNA method.²⁴

^bThe result based on the miPlantPre method.¹⁴

^cThe result based on the microPred method.⁵²

^dThe result based on the TripletSVM method.⁵³

Comparison of prediction performance for different methods on the dataset 2 with a jackknife test.

Methods	Sensitivity	Specificity	MCC	ACC
miPlantPrea	96.21	93.24	89.28	94.62
TripletSVMb	62.98	78.33	36.25	67.39
Our method	88.26	91.48	80.08	90.02

^aThe result based on the miPlantPre method.¹⁴

^bThe result based on the TripletSVM method.⁵³

Comparison of prediction performance for different methods on the dataset 3 with a jackknife test.

Datasets	iMcRNAa	microPredb	miPlantPrec	Our method
mtr_67	89.5	76.1	86.6	95.52
osa_256	86.1	73.8	83.4	93.6
ppt_184	76.9	68.8	84.5	96.5
ath_153	86.2	67.6	85	96.1
updated_aly_167	86.5	69.5	85	98.2
ptc_133	78.6	72.2	82.7	91.4
sbi_105	85.2	76.7	83.8	92.9
updated_gma_105	88.1	82.4	83.8	92.4
zma_74	85.8	74.3	85.1	96
gma_69	88.4	71	85.5	92.8

^aThe result based on the iMcRNA method.²⁴

^bThe result based on the microPred method.⁵²

^cThe result based on the miPlantPre method.¹⁴

In addition, our method did not use any machine learning classifiers, which can improve the accuracy by training and complicated computing. Thus, our method is easy to implement and requires a small amount of time. Table 6 shows the results of our method and of microPred 52, iMcRNA-PseSSC 24, and miPlantPre 14 methods applied to dataset 3. From the table, our method has the best ACC and MCC among the 10 plant pre-miRNA datasets (i.e., mtr, osa, ppt, ath, ptc, sbi, zma, gma, updated_aly, and updated_gma). This result indicates the effectiveness of our method.

In summary, our method obtains a good accuracy in identifying plant pre-miRNAs and has excellent stability based on the analysis of the aforementioned experiments. In comparison with existing machine learning algorithms, the proposed method is simple to operate and does not require training parameters.

Conclusions

Graphical representations based on sequences (e.g., DNA, RNA, and proteins) have been the focus of research.^{41,42,54–57} In this study, we proposed a 3D graphical representation of the secondary structure of the pre-miRNA in combination with the frequency and physicochemical properties of the base. We then subjected the pre-miRNA secondary structure to similarity analysis by calculating their Euclidean distance. The smaller the distance was, the higher the similarity between the two sequences would be and vice versa. Finally, the sequence similarity method proposed in this paper was used to identify plant pre-miRNA. The experimental results showed that the proposed method was reasonable and effective in the three common benchmark datasets.

In future work, we will develop an enhanced representation of the pre-miRNA secondary structure by merging additional information and designing a more complete graphical model and more efficient similarity analysis methods to improve the performance of pre-miRNA prediction. In addition, our method for predicting and classifying other noncoding RNAs, such as Piwi-interacting RNA and long-noncoding RNA, is a key issue that should be further investigated.

Conflicts of interest

There are no conflicts to declare.