Characterization and analysis of the aspect ratio of carbide grains in WC–Co composites

Abstract

To study the aspect ratio distribution of carbide grains in WC–Co composites, two novel approaches, namely grain shape ellipse calculation and five parameter analysis (FPA) methods, are reported in this work. According to grain shape ellipse calculation, carbide grains that have a grain shape aspect ratio of 0.62 demarcate the more anisotropic grains with a larger size and the less anisotropic grains with a smaller size. Moreover, these grains remained predominantly populous under different cases of structural parameters and processing factors. According to five parameter analysis, the interface area aspect ratio can be derived from the relative area of prevalent (0001) basal planes and (10−10) prismatic planes, and can then be set relevance with the measured mechanical properties. The present work therefore offers new alternatives to establish the connection between the aspect ratio measurement and the property optimization of WC–Co composites.

To study the aspect ratio distribution of carbide grains in WC–Co composites, two novel approaches, namely grain shape ellipse calculation and five parameter analysis (FPA) methods, are reported in this work.

1. Introduction

WC–Co composites have outstanding mechanical properties and are widely used in machining, mining, cutting, and many other industrial applications. The mechanical properties of WC–Co composites are strongly influenced by their microstructures, which can be described as WC grains embedded in a cobalt phase. Such dense polycrystalline materials consist of irregularly shaped, approximately polygonal, single carbide crystals joined at internal interfaces referred to as grain boundaries.¹ An increasing number of studies have shown that the shape of WC crystals affects the mechanical properties of the composite; for example, the formation of plate-like WC crystals was reported to increase the fracture toughness of WC–Co composites.^2,3 These developments precipitate the necessity to fully characterize the appearance features of carbide grains, and such characterization should be put into the context of fabricating routines, which is significant to optimize the properties of the final products.

The aspect ratio is an important parameter to characterize the appearance of carbide grains because it takes both the size and shape into account. There are various aspect ratio definitions of tungsten carbide grains. The conventional definition refers to the aspect ratio as the longest axis divided by the shortest axis of the studied carbide grain.^4,5 As a typical example, two aspect ratio definitions were used to describe the equilibrium carbide shape in ref. 6: one was the ratio between the lengths of the short and long prismatic facets, the other was the ratio between the thickness along the 〈0001〉 direction and the width of the basal plane. As another example, in some other commercial software, there is an application of grain shape aspect ratio defined as the length of the minor axis divided by the length of the major axis of the ellipse fitting to a certain grain (the value of the grain shape aspect ratio hence ranges from 0 to 1), and the ellipse fitted to the grain is calculated by the least squares method.⁷ These examples are all based on the measured plane and therefore belong to the two-dimensional (2D) case. More recently, the development of stereology has made the characterization of the aspect ratio in a three-dimensional (3D) sense possible; in more detail, it has been demonstrated that the average 3D crystal habits can be determined by combining the geometric information found in conventional micrographs with the crystal orientation data,⁸ and the stereological approach named “five parameter analysis (FPA)” was thus developed.⁹ The five macroscopic crystallographic parameters comprise three for lattice misorientation and two for grain boundary plane orientation. If without considering any misorientations, the 2D calculation in the FPA method determines the aspect ratio by the ratio of the length along the edge of the (0001) basal facet of carbide crystal pyramid to its height along the (10−10) facet.¹⁰

Accordingly, the main aim of the current work was to systematically study the grain shape aspect ratio of WC–Co composites via the aforementioned methods, namely, the grain shape ellipse calculation and five parameter analysis methods. The two methods both closely correlate to the grain orientation: for grain shape ellipse calculation, the so-called grain shape orientation can be defined as the angle between the major axis and the horizontal direction;⁷ for five parameter analysis, the original data, the crystal orientation data are routinely determined from electron backscattered diffraction (EBSD) patterns.¹⁰ Meantime, both methods are based on the data in batches and therefore, their outcome would show the aspect ratio distribution with a statistical meaning. In this regard, the major novelty of the current work is the study of the aspect ratio distribution by these novel approaches. In particular, by checking the grain shape aspect ratio under different structural parameters and processing factors, the current work significantly establishes a connection between the aspect ratio measurement and the property optimization of WC–Co composites.

2. Materials and methods

Six WC–Co samples prepared by the correspondence author were studied in this work, with the related information of each sample listed in Table 1, and where the preparation processes are similar with that descripted in ref. 11. The samples were divided into four groups, with each group corresponding to the diversification of a certain structural parameter or processing factor while other parameters and factors were kept nominally the same. The purpose for doing this was to check the effect of each parameter and factor on the aspect ratio distribution in the studied samples. Thus, group A concerned the effect of the cobalt fraction, group B concerned the effect of the carbide grain size, group C concerned the effect of the densification mechanism, and group D concerned the effect of plastic deformation.

Information on the WC–Co samples used in the present study.

Sample	Carbide grain size (μm)	Cobalt fraction (wt%)	Densification method11	Plastic deformation	Group
1	1.0	6	Sinter-HIP	No	A
2	1.0	8	Sinter-HIP	No	A B C D
3	1.0	10	Sinter-HIP	No	A
4	2.0	8	Sinter-HIP	No	B
5	0.5	8	SPS	No	C
6	1.0	8	Sinter-HIP	Yes	D

The samples were treated for EBSD analysis by polishing with a diamond abrasive and etching in Murakami's reagent (1 g potassium + 1 g sodium + 10 ml distilled water) for no more than 5 s. This treatment yielded WC surfaces suitable for EBSD mapping and ensured the quality of the diffraction patterns. For specimens other than sample 4, the EBSD measurements were performed by a high-speed Hikari camera (EDAX, Inc., USA) incorporated in a Quanta 200 field emission environmental scanning electron microscope (FESEM) (FEI Company, USA). For sample 4, the EBSD measurement was performed by a Nordlys camera (Oxford Instruments, UK) incorporated in a Quanta 250 FESEM (FEI Company, USA).

The grain shape aspect ratio was derived from TSL OIM Analysis 5.3 software (EDAX Inc., USA) by selecting the grain shape ellipses option in the map properties dialog. Each point was shaded according to the aspect ratio of the grain to which it belongs, and the grain shape aspect ratio was given by the length of the minor axis divided by the length of the major axis of an ellipse fitted to the grain, with the least squares approach along with a linear solver adapted for grain shape ellipse calculation.

The interface area aspect ratio was based on the relative areas of the different types of interfaces that were determined by stereological techniques described in ref. 8. The observations needed for the stereological analysis were line segments, which were extracted from the orientation maps and were associated with the crystal orientations. Note that in ref. 10, the interface area aspect ratio was derived from the WC/Co phase boundary plane distributions at the (0001) (basal) and (10−10) (prismatic) positions. However, in this work, most cobalt phases in the EBSD scan planar section were removed by Murakami's reagent, so the interface area aspect ratio was calculated based on the intact WC/WC grain boundary plane distributions instead, and defined as the relative area of the (0001) basal facet to the relative area of the (10−10) prism facet, where such a basal-to-prism aspect ratio could describe the average form for a batch of studied carbide grains, and was calculated using stereological programs developed at Carnegie Mellon University.

In the current work, the transverse rupture strength was selected as a typical mechanical parameter of WC–Co composites. For samples 1–5, their transverse rupture strength values were measured by a MTS System 810 material test machine, with a test span of 14.5 ± 0.5 mm and a loading speed of 200 N min⁻¹.

3. Results and discussion

3.1. Grain shape aspect ratio analysis

The microstructures of the samples were illustrated by the image quality (IQ) maps combined with grain shape ellipses highlighted in red imposed on, with one example (one scan region of sample 2) illustrated in Fig. 1(a). Here, IQ maps can represent variations in the quality of EBSD patterns in a given area, and the image quality is lower for diffraction patterns obtained near grain boundaries. One can easily see from the figure that carbide grains are in randomly crystallographic orientations because the major axes have random inclinations with the horizontal direction. Moreover, inversed pole figure (IPF) maps can also represent the randomness of carbide crystal orientations by referring to the color coding scheme in a stereographic unit triangle.¹² Accordingly, there should be a limited number of {0001} or {10−10} crystal planes within the scan region. In Fig. 1(a), the grain shape ellipses were calculated and imposed on the corresponding carbide grains, thus each carbide grain has its own grain shape aspect ratio value. A very interesting result obtained in the present work is that the carbide grains in various WC–Co composites have a typical grain shape aspect ratio of about 0.62 (between 0.61 and 0.63 and similarly hereinafter), whereby this specific value occupies a predominant fraction in each studied specimen. Take the similar region of sample 2 as an example, the carbide grains are highlighted in different colors according to their grain shape aspect ratios, as illustrated in Fig. 1(b). It can be observed from the figure that grains with aspect ratios lower than 0.61 (highlighted in green) have larger grain sizes, where their longer major axes and shorter minor axes correspond to the average bulky bar shapes of carbide grains. While the grains with aspect ratios above 0.63 (highlighted in yellow) have smaller grain sizes and average equal-axied platelet morphologies. The grains with aspect ratios between 0.61 and 0.63 (highlighted in blue), therefore, correspond to medium grain sizes and a shape configuration between bar-like and plate-like.

Fig. 1. The microstructures of sample 2 are illustrated in (a) with the image quality maps with grain shape ellipses highlighted in red imposed on; and (b) with the grains highlighted in different colors according to their grain shape aspect ratios, where grains with aspect ratios beneath 0.61 are highlighted in green, grains with aspect ratios between 0.61 and 0.63 are highlighted in blue, and grains with an aspect ratio above 0.63 are highlighted in yellow.

The aforementioned phenomena represent the size evolution and equilibrium morphology of WC crystals during heating and sintering processes (samples 1 to 5) and the deformation procedure (sample 6). With respect to the sintering process, the shape of a crystal during growth close to or far from an equilibrium shape of that crystal depends on whether the crystal growth is controlled by the energy balance or kinetic factors.⁶ The 1500 °C sintering temperature in the sinter-HIP process in this work is just above the melting point of cobalt (1450 °C), so during such liquid-phase sintering, WC grain growth occurs by dissolution of the small grains and precipitation on the larger; thus the morphologies of the large grains and of the small grains are not completely similar,¹³ since the large WC grains are well developed with a shape close to the equilibrium. The SPS process has a sintering temperature of 1200 °C and generally a very short holding time, and is mainly a solid-phase sintering process. In this case, the WC grains cannot develop sufficiently, which may result in a shape far from the equilibrium. With respect to the procedure of plastic deformation, the grain size evolution was reported in.¹⁴ Considering these, the values and ranges of the grain shape aspect ratio can be taken as a critical proxy for the carbide shape development. Take sample 2 as an example; here, grains with an aspect ratio above 0.63 have smaller grain sizes and more equal-axied plate-like shapes, and thus can serve as a proxy of the earlier sintering stage, in which the grain shape anisotropy has not been fully developed (or in other words, the grain shape is closer to equiaxed). On the other hand, grains with an aspect ratio below 0.61 have larger grain sizes and more rod-like shapes, and can serve as a proxy of the later sintering stage, in which the anisotropy of the crystal and crystallographic orientations have fully developed. The population of grains with an aspect ratio of about 0.62 can thereby represent the intermediate state between the less anisotropic stage and the more anisotropic stage, whereby the deviation of this stage in two directions may help to determine the development degree of the shape anisotropy in the microstructure of the WC–Co composites.

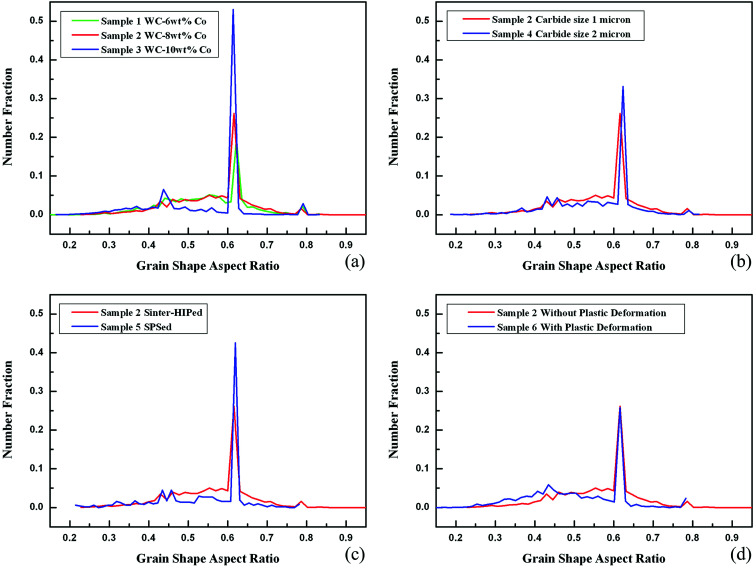
To describe the effects of various structural parameters and processing factors on the grain shape aspect ratio distributions, the number fraction as a function of the grain shape aspect ratio of specimens divided into different groups were calculated and the results are illustrated in Fig. 2. Meanwhile, for each sample, the grain shape aspect ratio was divided into three sections and the number fraction summations in each section were calculated and the results are listed in Table 2. In Fig. 2, we selected sample 2 to represent the procedure to calculate the grain shape aspect ratio. Note that for a single sample, after the EBSD data was collected, the corresponding grain orientation map (namely the inverse pole figure map, or IPF map, not shown here) and image quality map (IQ map) could be obtained. In turn, the size and shape of carbide grains could be counted. We should also note that the size and shape of carbide grains can be affected by various structural parameters and processing factors, see the authors' recent reports¹¹ as an example.

Fig. 2. The number fraction as a function of the grain shape aspect ratio of specimens divided into different groups: (a) corresponding to group A, which concerns the effect of the cobalt fraction; (b) corresponding to group B, which concerns the effect of carbide grain size; (c) corresponding to group C, which concerns the effect of densification mechanism; (d) corresponding to group D, which concerns the effect of plastic deformation on the grain shape aspect ratio distribution.

Number fractions of grain shape aspect ratio.

Sample	Grain shape aspect ratio ranges
	<0.61	0.61–0.63	>0.63
1	0.626	0.264	0.109
2	0.511	0.347	0.143
3	0.410	0.551	0.040
4	0.525	0.385	0.090
5	0.480	0.460	0.060
6	0.662	0.289	0.048

As mentioned before, samples in group A concerned the effect of the cobalt fraction on the distribution of the grain shape aspect ratios. From Fig. 2(a), it can be observed that grains with an aspect ratio of about 0.62 maintain a predominant fraction with various cobalt contents. Table 2 shows that with increasing the cobalt fraction, the population fractions of carbide grains with the 0.62 aspect ratio have an obvious growing trend, causing the population reduction of carbide grains with an aspect ratio either below 0.61 or above 0.63. One plausible interpretation of this phenomenon could be that with the increasing cobalt fraction, the dissolution and precipitation of smaller WC grains during liquid-phase sintering are reinforced, so the grain shape can therefore be fully developed¹⁵ and during this procedure, the grain shape aspect ratio with a value of 0.62 is remarkably populous.

Samples in group B concerned the effect of the carbide grain size on the distribution of the grain shape aspect ratios. Fig. 2(b) illustrates that grains with an aspect ratio of about 0.62 are still prevalent in the samples with different carbide grain sizes. Note, however, that the extreme values for the grain shape aspect ratio in sample 2 were 0.228 (minimum) and 0.988 (maximum), while the values in sample 4 were 0.187 and 0.816, respectively, indicating that average smaller grains are more prone to be equal-axied, while average larger grains are prone to have more anisotropic shapes, which is consistent with the results in Table 2 showing that there is a more distinct population difference of carbide grains with aspect ratios above 0.63. One possible cause for the average larger carbide grain size promoting the shape anisotropy could be that the driving force of liquid cobalt migration as an obstacle to the carbide grain growth is inversely proportional to solid carbide particle size.¹⁶

Samples in group C were used in our earlier report,¹¹ and were reused in this work to study the effect of densification methods on the distribution of grain shape aspect ratios. As elaborated in ref. 11, compared with sample 2 that was prepared by the sinter-HIP process, in which there was rapid grain growth accomplished by the coalescence of WC grains, sample 5 prepared by the SPS process with a reduced sintering temperature and a much shorter holding time showed a finer grain structure because the grain growth was effectively inhibited. One can easily observe through Fig. 2(c) that sample 5 has more grains inhibited at the 0.62 stage than sample 2, while a further check of Table 2 shows that the population fraction of carbide grains in sample 5 with an aspect ratio either below 0.61 or above 0.63 is lower than that in sample 2. Based on these experimental results, we regard that the aspect ratio retention at the 0.62 position could be used as a proxy of grain shape development adequacy.

Samples in group D concerned the effect of plastic deformation on the distribution of grain shape aspect ratios and the results are illustrated in Fig. 2(d). It can be seen that the samples have quite similar carbide grain population fraction at the position of the 0.62 aspect ratio; nevertheless, there are more carbide grains within the scope of aspect ratios from 0.3 to 0.5 in the deformed sample, illustrating that plastic deformation exacerbates the grain shape anisotropy. The mechanism of shape factor transformation in plastic deformation is still an open issue, although an earlier report¹⁷ considered that the movement of strong interfaces, like Σ2 grain boundaries,¹⁸ might be crucial in the deformation procedure. Our more recent study found that in the plastic deformation, the Σ2 grain boundary plane orientations are altered more than the misorientation.

3.2. Interface area aspect ratio analysis

As aforementioned, in this work, we focus on the carbide/carbide grain boundary planes that are formed by the intersection of the carbide crystal's habit planes. Note that when a certain boundary plane intersects the plane of EBSD observation, a boundary trace segment can be observed. With reference to a crystal's orientation, the line segment can be transformed to the crystal reference frame. Also note that each segment belongs to a set of possible planes whose normals are perpendicular to the segment, and these planes lie on a great circle perpendicular to the line segment on a stereographic projection. The premier principle for FPA analysis is that correct habit planes are correlated with a high probability, and there is at least one habit plane in each set of possible planes. After observing enough segments from a batch of grains, the great circles arising from each observed line segment must intersect at the positions of the habit planes; in other words, the true habit planes must appear far more frequently than the non-habit planes. With this information, each observed segment can be assigned a habit plane of origin; moreover, based on the total length of the segments associated with each facet, the relative areas of the habit planes can be estimated and the average shape can thus be defined. More detailed descriptions can be found in ref. 1 and 9.

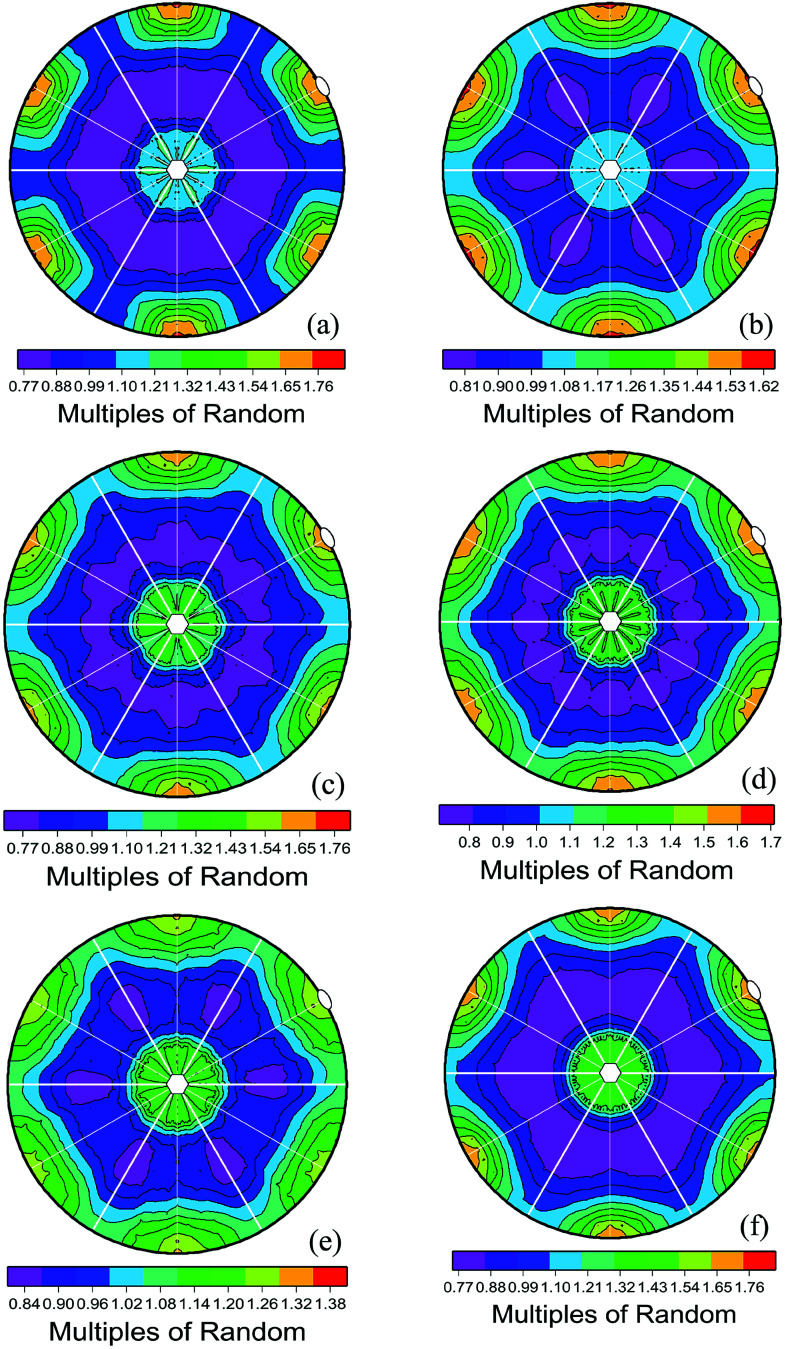
Turning to the specimens in this work, the distributions of the habit plane of carbide grains averaged over all the misorientations (in other words, regardless of the misorientation) are shown in Fig. 3. The major steps to obtain Fig. 3 are as follows: first, the EBSD data are collected; then, after the clean-up procedure, the crystallographic information of carbide/carbide boundary traces can be obtained; and then, for a single boundary trace, five spherical parameters are needed to give a complete description about the orientation of the boundary plane that contains that boundary trace: three for lattice misorientation across the boundary plane and two for boundary plane orientation; and then, the misorientation are averaged over all the boundaries, and the boundary plane orientation are statistically counted for all the boundaries; finally, the outcomes are plotted in a crystallographic frame (in this work, the frame is a hexagonal one). See ref. 8 and 9 for more detail. Note that the distributions are plotted in unit of multiples of a random distribution (MRD). Values greater than unity (refers to one in this work) indicate that the total area associated with a specific type of plane is larger than would be expected in a random distribution, while values less than one are associated with specific planes, whose total areas are less than expected in a random distribution. Taking the stereograms of sample 2 as an example (see Fig. 3(b)), as it is characteristic of all the other specimens, the basal orientation is in the center, marked by a hexagon, while the prismatic orientation is on the periphery, marked by an oval. The peaks in the distributions are at the (0001) (basal) and (10−10) (prismatic) positions, indicating that in the case of Fig. 3(b), habit planes with the (0001) orientation are observed more than 1.26 times as frequently and those with (10−10) orientation are observed more than 1.62 times as frequently as expected in a random distribution.

Fig. 3. Distribution of WC/WC grain boundary orientations without consideration of misorientation, in (a) sample 1, (b) sample 2, (c) sample 3, (d) sample 4, (e) sample 5, and (f) sample 6. The stereograms show distribution peaks at the positions of the basal and prismatic facets, which are indicated by hexagons and ovals.

Fig. 3 overall illustrates that the (0001) basal and (10−10) prismatic planes are the most common habit planes, which is consistent with many earlier reports (see ref. 3, 6, 10, and 19) that the carbide crystals have a trigonal prismatic shape. Also note that for each specimen studied in this work, the peaks at the prismatic orientation and at the basal position differ, and the basal orientations has a relatively smaller peak compared with the prismatic orientations, indicating that the basal orientation makes up a smaller fraction of the total bounding surface, which is consistent with the interface energy study in ref. 19. Our previous work¹¹ also supported this via the fact that the Σ2 twist boundaries (where the interface consists of prismatic planes in both grains) are prevalent and there are very few Σ2 tilt boundaries (where the interface consists of a basal plane in one grain against a prismatic plane in the other). To quantify the difference between the distribution intensity of the basal and prismatic orientations, the line segments that give rise to these peaks were used to evaluate the relative areas using a previously described procedure. In this work, the interface area aspect ratio was used to describe the relative basal-to-prism area ratio for a batch of studied carbide grains by calculating the ratio of the relative area of the (0001) basal facet to the relative area of the (10−10) prism facet, or in other words, the ratios of basal grain boundary area to prismatic grain boundary area, and thus the aspect ratio describes the average shape for several carbide grains in a 3D sense. (A similar definition can be found in recent work,²⁰ however, it was merely based on a single crystal.) The outcomes are listed in Table 3, while the average grain shape aspect ratios calculated by the weighted mean method and representing a 2D sense are also listed as a reference.

Interface area and average grain shape aspect ratios of the samples.

Sample	Basal MRD	Prismatic MRD	Interface area aspect ratio	Average grain shape aspect ratio
1	1.32	1.76	0.750	0.542
2	1.26	1.62	0.778	0.547
3	1.43	1.76	0.813	0.556
4	1.50	1.70	0.882	0.547
5	1.26	1.38	0.913	0.563
6	1.54	1.76	0.867	0.506

In Table 3, it can be observed that compared with the interface area aspect ratios, the average grain shape aspect ratios in each sample group have no conspicuous trend. This is because the calculations are weighted on the population fractions, so if we calculate the average grain shape aspect ratio of a certain sample by the ratio of its average minor axis to its average major axis that are achieved both by weighting on population fractions, we merely get similar results. The interface area aspect ratios, however, show evident tendencies in each sample group. Note that the samples in group A and group B were sintered with the same 1500 °C sintering temperature in the sinter-HIP process, so the temperature should not play a dominant role in determining the shape variation. The variation trend of the interface area aspect ratios in group A and group B validate the aforementioned consequence that changes in the average aspect ratio were found to be dependent on the cobalt volume fraction and carbide grain size. One recent theory for the development of anisotropic grain boundary plane distributions (GBPDs) suggests that in the late stages of microstructural development, the relative areas will reach a steady state.²¹ According to this, samples in group C can be taken as a proxy of typical sintering courses. Here, sample 5 has minor MRD values at both the basal and prismatic positions compared with sample 2, however, it has an obvious larger interface area aspect ratio than sample 2, indicating that anisotropic shape development is more restrained in the SPS process than in the sinter-HIP process. The samples in group D demonstrated that the remaining anisotropy of the plastic deformation is more centralized at basal boundary positions than at prismatic boundary positions.

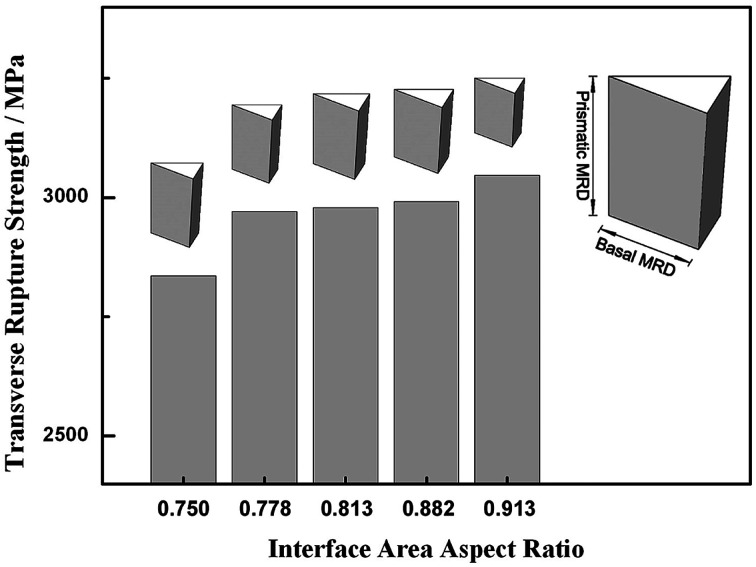
Although Table 3 indicates that the crystals may have a consistent habit plane area (see the prismatic MRD values of samples 1, 3, and 6), they may vary in size. In this work, idealized polygons were used to represent the average polygonal shape of the carbide grains, and the approach to do this involved plotting a triangular prism, where the side length of the equilateral triangle basal equals the basal MRD value, and the height of the triangular prism equals the prismatic MRD value; therefore, the relative basal and prism areas can be represented by the side length and the height respectively, while the relative basal-to-prism area ratio can be represented by the ratio of the side length to the height of the polygon, and the average grain size in the 3D sense can be represented by the volume of the polygon. The idealized polygons of specimens are illustrated in Fig. 4 in the sequence of the interface area aspect ratio increasing, and the polygon of sample 6 is amplified to explain the drawing geometry of polygons. One can imagine that if carbide grains have on average more equal-axied and less anisotropic shapes, the interface area ratio will approach 1 and the polygon will have a more uniformed shape and with more vertices; conversely, if the carbide grains have on average less equal-axied and more anisotropic shapes, the interface area ratio will deviate to a minor value and the polygon will have a more pockety shape. Furthermore, if the carbide grains have a relatively larger basal area, the polygon will look more plate-like, while if carbide grains have a relatively larger prismatic area, the polygon will look more bar-like. Take sample 1 and sample 3 as examples, the specimens have the same prismatic area, where the variation of the interface area aspect ratio can be clearly seen by virtue of the basal area discrepancy. Take sample 2 and sample 5 of group C as other examples, the average grain shape diversity brought by typical densification methods can be distinctly revealed by the disparity of the polygon volumes. Furthermore, many ref. 4–6 and 13 report the close correlation between the grain shape factors and mechanical properties, whereby the possible origins of such connection could be that most common grain boundaries favor low index habit planes,¹⁰ and boundaries with low energy and large area are more easily preserved; therefore, the (0001) basal and (10−10) prismatic orientations clearly distinguished in present study provide the evidence of the interface energy distribution that determines the mechanical properties both geometrically and energetically. To verify this, the transverse rupture strength of each specimen (excluding sample 6 because it relates to a failed specimen) is also shown below the corresponding stereograms in Fig. 4. The outcome is that the strength of the samples is slightly geared up as a function of the interface area aspect ratio increasing. It should be pointed out that such a correlation is a nominal one and the principal controlling factors are the subject of future investigations. Despite this, the current results provide reasonable relevance between the aspect ratio measurement and the mechanical properties.

Fig. 4. The idealized polygons of specimens in the sequence of the interface area aspect ratio increasing; note, the polygon of sample 6 is amplified to explain the drawing geometry of polygons, and the transverse rupture strength of each specimen, excluding sample 6, are shown below the corresponding stereograms.

4. Conclusions

To characterize the aspect ratio of carbide grains in WC–Co composites, two kinds of methods were used in this paper. The grain shape ellipse calculation is a 2D approach that calculates the grain shape aspect ratio via the least squares method and presents the outcome in the form of a grain shape ellipse. In the current work, it was found that carbide grains that have a grain shape aspect ratio of 0.62 occupy a predominant number fraction under various structural parameters and processing factors; moreover, these grains can be used to distinguish between the more anisotropic carbide grains that have a larger size and the less anisotropic carbide grains that have a smaller size. The five parameter analysis is a 3D approach that defines the interface area aspect ratio as the ratio of the relative (0001) basal to the (10−10) prismatic area of carbide grains. By using the FPA method, the WC/WC grain boundary plane distributions that ignore the misorientations can be obtained, which can in turn present the outcome of the FPA method as idealized polygons that represent the average spatial shapes of carbide grains. In the current work, such an aspect ratio has been effectively correlated with the measured mechanical properties. The two methods as a whole suggest a valid way to link the aspect ratio measurement with the property optimization of WC–Co composites.

Conflicts of interest

There are no conflicts to declare.