Quantitative analysis of cell shape and the cytoskeleton in developmental biology

Abstract

Computational approaches that enable quantification of microscopy data have revolutionized the field of developmental biology. Due to its inherent complexity, elucidating mechanisms of development requires sophisticated analysis of the structure, shape, and kinetics of cellular processes. This need has prompted the creation of numerous techniques to visualize, quantify, and merge microscopy data. These approaches have defined the order and structure of developmental events, thus, providing insight into the mechanisms that drive them. This review describes current computational approaches that are being used to answer developmental questions related to morphogenesis and describe how these approaches have impacted the field. Our intent is not to comprehensively review techniques, but to highlight examples of how different approaches have impacted our understanding of development. Specifically, we focus on methods to quantify cell shape and cytoskeleton structure and dynamics in developing tissues. Finally, we speculate on where the future of computational analysis in developmental biology might be headed.

Introduction

Never before have developmental biologists been able to generate such rich, multidimensional imaging data sets. For example, the large repertoire of genetically encoded fluorescent proteins available to label cells in developing embryos or specific proteins within these cells has enabled the visualization of cell size, cell shape, and subcellular protein localization in both live and fixed tissues (Rodriguez et al., 2017). Advances in gene editing techniques such as CRISPR/Cas9 are enabling developmental biologists to more effectively fuse these fluorescent proteins to endogenous proteins of interest (Dickinson, Ward, Reiner, & Goldstein, 2013; Hisano et al., 2015; Port, Chen, Lee, & Bullock, 2014; Zhang, Koolhaas, & Schnorrer, 2014). Currently, standard confocal microscopes can readily obtain images of embryos with subcellular resolution. In addition, the advances in microscopic techniques such as light-sheet microscopy can capture the entirety of embryonic development with unprecedented spatial and temporal resolution (Keller, Schmidt, Wittbrodt, & Stelzer, 2008; Krzic, Gunther, Saunders, Streichan, & Hufnagel, 2012; Tomer, Khairy, Amat, & Keller, 2012). However, with this ability comes a hurdle: being able to process and find the salient information that is present large and complex data sets.

Quantitative approaches that analyze microscopy data are increasingly enabling fundamental discoveries about development. While this review will focus on methods to analyze cell shape and the cytoskeleton, quantitative measurements are also being used in many other aspects of developmental biology. For example, our understanding of pattern formation as a result of a graded signal (a morphogen) has been greatly enhanced by the application of quantitative techniques to measuring these gradients (Gregor, Wieschaus, McGregor, Bialek, & Tank, 2007). Quantitative analysis of morphogen gradients has been useful to define their spatial precision, mechanism of diffusion, and function. Advances have also allowed for a more complete view of expression patterns in embryos. An experimental limitation is that the expression patterns of only a few genes can be marked in a single sample. However, learning algorithms and other computational approaches have spatio-temporally registered and averaged embryos, forming a more comprehensive view of development (Dsilva et al., 2015; Faure et al., 2016; Fowlkes et al., 2008; Villoutreix et al., 2017; Yuan et al., 2014). Composite maps of gene expression patterns from high-throughput screens can inform our understanding of gene regulatory interactions. Automated classification has also opened new possibilities for amassing a global view of precise temporal changes during development not attainable using human visual classification.

One of the most beautiful aspects of development is the establishment of organism and organ shape. Classic studies showed that changes in tissue shape, such as tissue bending, are associated with changes in the morphology of individual cells (Holtfreter, 1943). A branch of developmental biology has therefore been devoted to understanding how cells change their shape and how cell shape change is coordinated across a field of cells to change tissue form. Traditionally, cell shape was analyzed qualitatively or by quantifying manual traces (Costa, Wilson, & Wieschaus, 1994; Hardin & Keller, 1988). However, with improved computing systems and commercially available and home-made software for cell segmentation and tracking, the analysis of cell shape and movement in tissues has become much more quantitative. Quantitative analysis is also being used to correlate properties of intracellular structures, such as the cytoskeleton, with cell shape and even mechanical force. This has resulted in mechanistic models for how cells generate force and change their own shape and that of the tissue (Fernandez-Gonzalez & Zallen, 2009; Heisenberg & Bellaiche, 2013; Lecuit, Lenne, & Munro, 2011).

Analysis of cell shape in tissues

Two-dimensional analysis of cell shape

Epithelial tissues are composed of sheets of polarized, adherent cells. During development, many epithelia undergo diverse morphogenetic movements such as folding and extension or extensive growth (Heer & Martin, 2017; Irvine & Shraiman, 2017). Analyzing the shapes of epithelial cells during these morphogenetic events has helped uncover what drives shape change at the tissue level. Epithelial cells are polarized along the axis that is perpendicular to the epithelial sheet, which is referred to as the apical-basal axis. The shapes of epithelial cells with respect to this axis, such as at the apical or basal surface, is commonly quantified. In samples where the membrane or surface of the cell is labeled, approaches as simple as a watershed algorithm have been useful for reconstructing cell boundary outlines and subsequently measuring epithelial cell deformation (Vincent, Vincent, & Soille, 1991). Watershed approaches rely on identifying seed points, which correspond to regional minima in pixel intensity, each of which represents a single cell to be segmented. These topological minima can be thought of as catchment basins. Starting at seed points, the watershed algorithm simulates a flooding process whereby the basins are filled with water and a boundary is defined at locations of spillover from one seed region to another. Thus, the watershed algorithm identifies regions of high intensity that separate cell bodies, delineating the cell boundaries.

The success of watershed approaches is sensitive to image noise because the watershed line depends on identifying the correct number of seeds or cell bodies. Challenges arise when cell division occurs because a single seed point turns into two. Temporal tracking of seeds can help identify errors for correction. Watershed techniques often allow for user intervention to correct errors in segmentation. Segmentation errors can be corrected by manually altering the edges of the automatically outlined cells (Gelbart et al., 2012), or by adding seed points (Heller et al., 2016; M. F. Wang et al., 2017). Advances in machine learning are now being used to cut out direct user intervention, for example, to track cells in a dividing tissue (M. F. Z. Wang & Fernandez-Gonzalez, 2017).

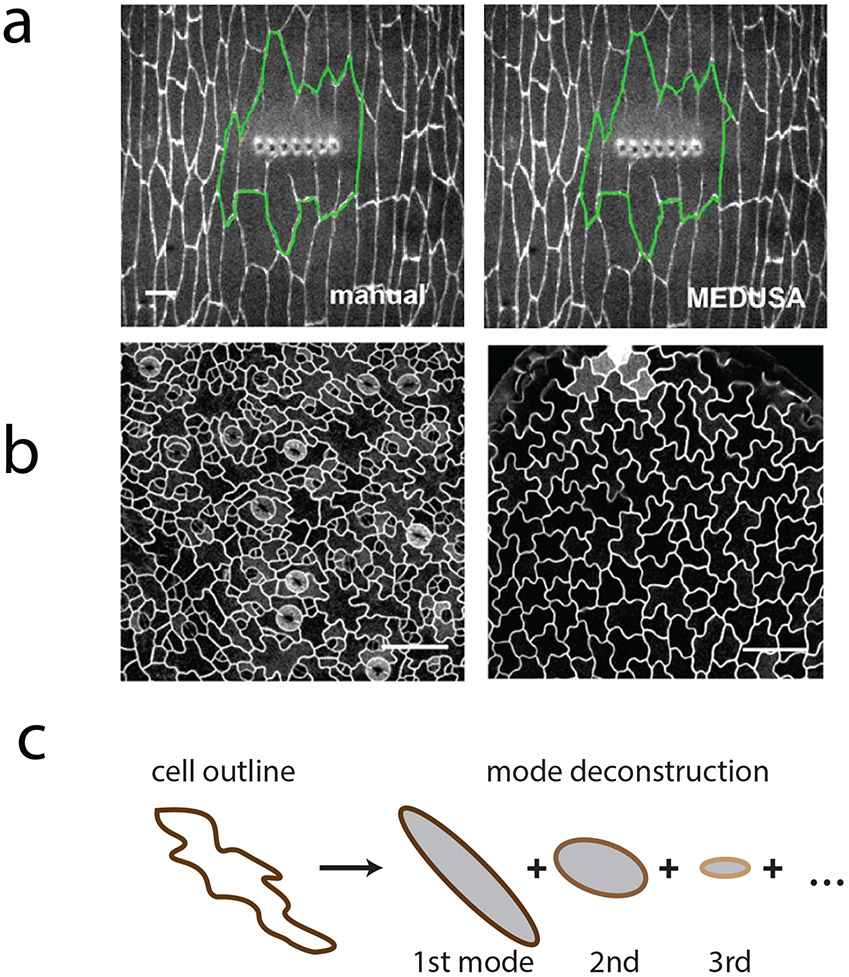
In addition to watersheds, there are more sophisticated approaches that are designed to trace complex contours. Complex shapes can arise from wounding a group of cells in a tissue (Figure 1a). An approach that was employed to segment the wound margin in a tissue used an active contour method in which a polygon is moved on the image to search for the lowest energy configuration, where polygon energy is related to its length, edge smoothness, and the image intensity that it overlaps (Zulueta-Coarasa, Tamada, Lee, & Fernandez-Gonzalez, 2014) (Figure 1a). In addition, certain cell types exhibit more complicated shapes than the hexagonal packing of cells in epithelia. For example, pavement cells in plant leaves exhibit shapes that resemble the pieces of a jigsaw puzzle (Figure 1b) (Bergmann, Lukowitz, & Somerville, 2004). A method using elliptical Fourier analysis in which a cell’s contours are decomposed into a series of ellipses has been developed to analyze the shape of complicated plant and animal cells (Sanchez-Corrales, Hartley, van Rooij, Maree, & Grieneisen, 2018) (Figure 1c).

Figure 1:

Analyzing complex cell shapes.

a) A wounded region in the Drosophila embryo expressing β-catenin::GFP. The automated tracing algorithm, MEDUSA, employs an active contour algorithm where the delineation of the wound evolves to minimize its energy (green). Figure is adapted from (Zulueta-Coarasa et al., 2014).

b) Pavement cells in Arabidopsis thaliana exhibit complex shapes. Figure is adapted from (Sanchez-Corrales et al., 2018)

c) Complex cell outlines can be approximated using Elliptic Fourier analysis (LOCO-EFA), which deconstructs cell shape into an infinite sum of elliptical modes. Figure is adapted from (Sanchez-Corrales et al., 2018). Scale bars: 20 μm.

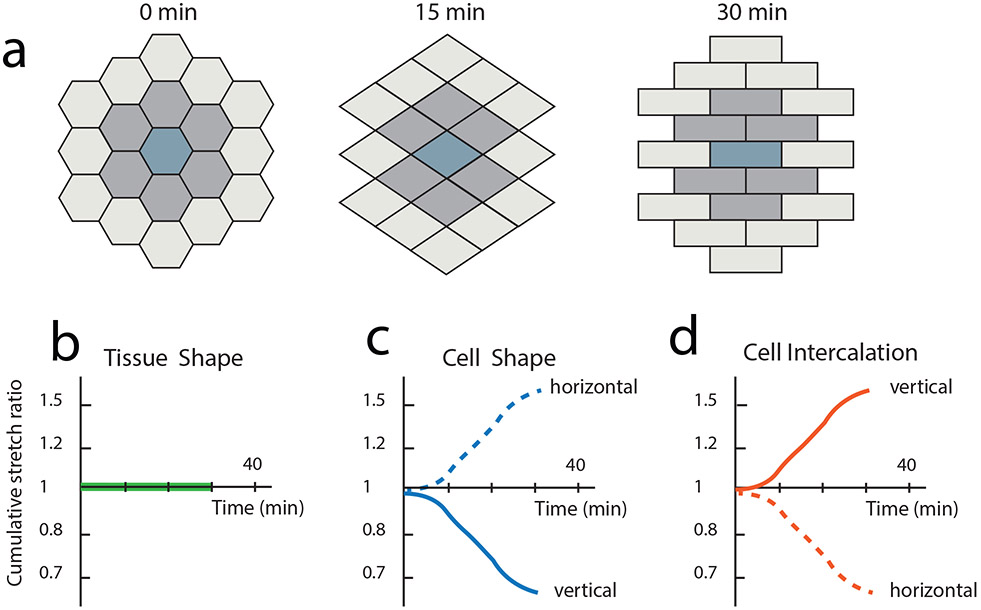
Cell segmentation and subsequent cell tracking can be used to determine how tissue shape emerges from the collective behavior of constituent cells. For example, measuring the strain rates of both the tissue and individual cells enables researchers to discern the contributions of cell shape change (i.e., elongation) and cell intercalation (i.e., sliding) to tissue deformation (Blanchard et al., 2009). Strain from cell shape deformations (Figure 2c) can cancel strain from cell intercalation (Figure 2d) conserving overall tissue shape (Figure 2a,b). Cell shape analysis can therefore reveal important cellular rearrangements that either change or preserve tissue shape. This approach was used to define the contributions of cell intercalation and cell shape change to tissue extension in the Drosophila embryo and identified an anterior-posterior tensile force that is relaxed by cell intercalation (Butler et al., 2009). More recent studies have impressively decomposed complex morphogenetic movements into contributions of cell division, intercalation, shape change, and delamination (Etournay et al., 2016; Etournay et al., 2015; Guirao et al., 2015). In addition, quantification of the dynamics of cell shape change has defined mechanisms of apical or basal constriction, which can occur in a pulsatile or oscillating manner (He, Wang, Tang, & Montell, 2010; Martin, Kaschube, & Wieschaus, 2009; Solon, Kaya-Copur, Colombelli, & Brunner, 2009). Thus, two-dimensional segmentation has provided significant insight into how different cell processes contribute to tissue growth and morphogenesis.

Figure 2:

Analyzing how cell shape change and rearrangement contribute to tissue shape. a) Simulation of one possible cellular scenario during tissue morphogenesis. Strain from cell shape changes counteract strain due to cell intercalations to result in no overall tissue shape change. Cumulative stretch ratios are plotted on a log scale vs time for vertical (solid line) and horizontal orientation (dotted line) for b) tissue shape c) cell shape and d) cell intercalation. Figure is adapted from (Blanchard et al., 2009).

It is important to consider the 3D shape of a tissue when extracting the relevant plane for segmenting in 2D. Maximum intensity projections of confocal stacks are often used to extract in-focus features from a curved tissue. However, maximum projections can result in pixel discontinuity with neighboring pixels in the projection originating from very different z heights in the tissue. Smooth manifold extraction techniques consider the overall tissue shape and the spatial position of each pixel when forming an index map of what z height to include in the projection. Manifold methods reduce background signal and increase accuracy of the 2D image used for analysis (Shihavuddin et al., 2017).

An important limitation in restricting segmentation to a 2D surface, even with accurate z projections, is that it provides a more limited view of the cell’s entire shape. In the case of epithelia, focusing analysis on the apical domain of a cell can miss important processes that are happening on the basal side of the cell and vice versa. For example, recent 3D analysis of cell intercalation in the Drosophila embryo revealed that intercalating cells exhibit basal cell protrusions that are involved in intercalation (Sun et al., 2017). This suggests that epithelial extension in Drosophila may be mechanistically more similar to convergent extension in vertebrate cells than was previously thought (Shih & Keller, 1992).

Three-dimensional analysis of cell shape.

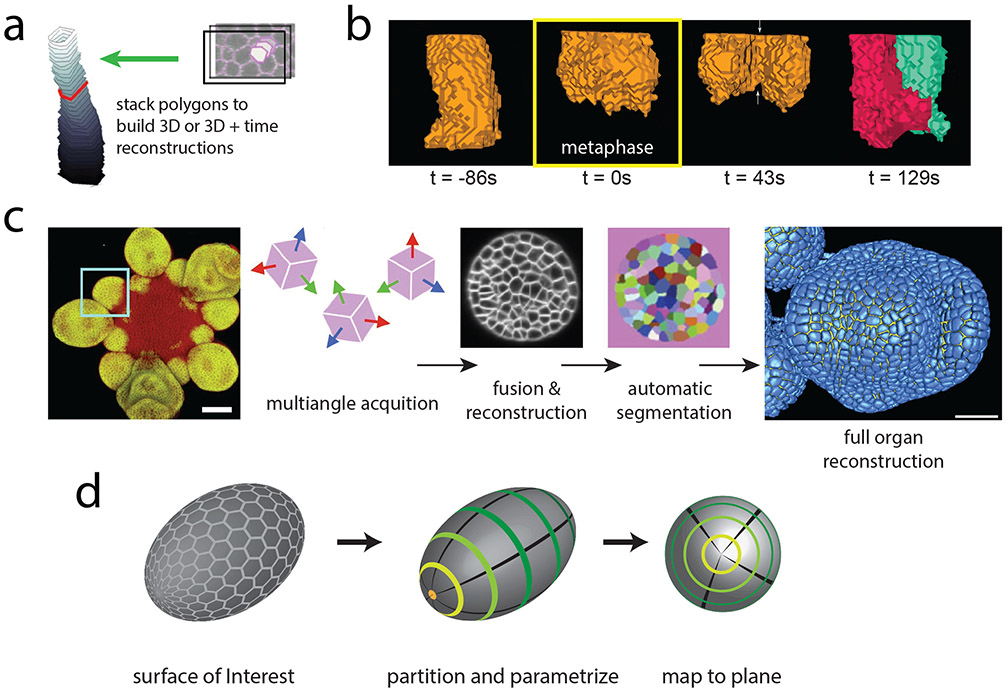
In cases where data sets consist of a stack of optical slices, measurements from 2D segmentation in multiple slices of the stack have been used to approximate 3D cell shape. For example, 3D measurements of cell volume have been made for epithelial cells undergoing apical constriction in developmental contexts by stacking together segmented cell boundaries at all z heights to recreate the 3D shape of each cell (Gelbart et al., 2012; Saias et al., 2015) (Figure 3a). Analysis revealed that in the early Drosophila embryo, cell volume is conserved during apical constriction, which could explain concurrent cell shape changes in the basal portion of the cell (Gelbart et al., 2012). In contrast, at the later stage of dorsal closure, when the embryo seals the gap in the epidermis on the dorsal side of the embryo (Kiehart, Crawford, Aristotelous, Venakides, & Edwards, 2017), apical constriction is associated with a decrease in cell volume, suggesting a possible role for volume decrease in contraction (Saias et al., 2015). Thus, 3D segmentation has revealed different modes whereby epithelial cells change shape: changes in volume explain some cell shape changes, whereas in other cases volume is conserved and changes in cross-sectional area in one part of the cell can impact the shape of the rest of the cell.

Figure 3:

Analyzing the three-dimensional shapes of cells in developing tissues.

a) 3D reconstruction of cell shape can be approximated by stacking the polygons obtained in each z frame from 2D cell segmentation algorithms. Tracking these stacks over time yields a 4D mapping of each cell in the tissue. Figure is adapted from (Gelbart et al., 2012).

b) Reconstruction of cell shape using EDGE4D during the first mitotic division of the Drosophila embryo. 3D cell shape is followed before mitotic entry, at metaphase (yellow box, 0 s), during cytokinesis, and after abscission. Images are taken from (Chanet, Sharan, et al., 2017).

c) Multiangle acquisition of Arabidopsis thaliana flower expressing a flower-specific GFP marker are fused into a single reconstruction. Each cell is automatically segmented and the full 3D organ reconstruction is represented in blue. By fusing acquisitions from different angles, the limitations of microscope resolution anisotropy on cell segmentation are avoided Figure is adapted from (Fernandez et al., 2010) Scale bars: 25 μm.

d) Tissue cartography reduces the 3D shape of a tissue by identifying a Surface of Interest. The surface of Drosophila embryo is parameterized to map signal measured on its surface to a single plane for analysis. Figure is adapted from (Heemskerk & Streichan, 2015).

An alternative to simply segmenting and tracking cell cross-sections at multiple z heights is to use the image information in all dimensions to identify the 3D surface of a cell’s membrane. The resolution of a point object is impacted by the point spread function of a microscope, a 3D function that defines the extent to which diffraction deforms a fluorescent point in a given direction with respect to the imaging axis (i.e., parallel to the light path). The strength of a membrane signal is therefore dependent on its relative alignment to the point spread function of the microscope. In contrast to the sharp signal that results from membranes aligned with the imaging axis, membrane signal that is not aligned becomes diffuse. Several approaches have been adopted to overcome this limitation. Techniques have been developed to identify the cell membrane in 3D , which correct for intensity inhomogeneity of sheet-like regions of the cell surface, which are off axis. These advances have enabled 3D cell segmentation of cells during zebrafish somite formation (Mosaliganti, Noche, Xiong, Swinburne, & Megason, 2012). In addition, studies of plant and animal development have relied on a package, MorphoGraphX, which is tailored to curved 3D structures and has been used for cell segmentation to link cell shape to growth, tissue mechanics, protein localization and gene expression (Barbier de Reuille et al., 2015; Kierzkowski et al., 2012). Geometric strategies and combining information from nuclear and membrane channels have also been used for robust 3D segmentation (Khan, Wang, Wieschaus, & Kaschube, 2014). In Drosophila, this method has been useful in reconstructing epithelial cell shape in tissues undergoing morphogenesis and in cells undergoing cell division (Chanet, Sharan, Khan, & Martin, 2017; Y. C. Wang, Khan, Kaschube, & Wieschaus, 2012) (Figure 3b). Commercial software available for 3D image processing, such as Imaris (Bitplane, Oxford Instruments), facilitates extracting 3D surfaces from confocal stacks with an interface to visualize and rotate reconstructions. Tracing the apical outline of follicle cells in 3D of Drosophilid eggs appendages in Imaris, for example, uncovered diverse strategies of morphogenesis in related species relying on varying amounts of cell shape changes and rearrangements (Osterfield, Schupbach, Wieschaus, & Shvartsman, 2015). Alternatively, to alleviate the challenges associated with signal alignment with the point spread function of a microscope, the specimen can be imaged at multiple angles to reconstruct a volumetric image (Figure 3c). Image reconstruction for example has enabled cell segmentation of plant meristem cells during flower development (Fernandez et al., 2010). Nuclear segmentation and tracking has also been useful to trace cell lineage during C. elegans embryonic development (Du, Santella, He, Tiongson, & Bao, 2014; Santella et al., 2015).

Embryo-wide analysis of a cell shape.

Reconstructing cell shapes and movements in an entire developing embryo (i.e. in toto imaging) is important for a holistic understanding of organism shape. One early example of this was the reconstruction of the early development of Caenorhabditis elegans (Heid, Voss, & Soll, 2002). This computer-assisted approach identified the edges of cells in differential interference contrast (DIC) microscopy images and converted these to a β-spline model of cell surfaces. This approach generated a reconstruction of the C. elegans embryo through the 28-cell stage (Heid et al., 2002). A similar approach was used in to model cell shape and movement in the Ascidian, Ciona intestinalis, through the 44-cell stage (Tassy, Daian, Hudson, Bertrand, & Lemaire, 2006).

Advanced imaging techniques such as multiview light-sheet microscopy enable imaging that encompasses an organ or organism containing hundreds and thousands of cells (Krzic et al., 2012; Tomer et al., 2012). The enormous size of the resulting data sets is a limiting factor for both visualizing the data and for extracting useful information. This is especially the case when considering a property as complicated as cell shape. Therefore, methods have been developed to aid in the analysis of cell shape in embryo scale data sets.

One method called Image Surface Analysis Environment (ImSAnE) changes the data structure of such images. The method takes surfaces of interest and maps them onto planes that can then be stored in an atlas (Heemskerk & Streichan, 2015) (Figure 3d). Such a technique reduces the dimensionality of the data, providing a data structure that is amenable to analysis by techniques used for 2D image segmentation described above. This approach has been applied to the Drosophila embryo as well as to entire vertebrate organs such as the zebrafish heart.

Analysis of the cytoskeleton in tissues

Static measurement of the cytoskeleton: orientation

Cells embedded in a tissue respond to mechanical force (Chanet & Martin, 2014; Fernandez-Gonzalez & Zallen, 2009). During development, actin filaments and microtubules are dynamically assembled and disassembled and can align under external force. Cytoskeletal alignment often correlates with the principal direction of stress in a tissue (Chanet, Miller, et al., 2017; Hamant et al., 2008). Therefore, measuring the cytoskeleton’s orientation can provide insight into the forces that are exerted on individual cells within a tissue.

In cases where multiple fibers are highly aligned, a one-dimensional Fourier transform can measure spatial frequency patterns in cytoskeletal structure by calculating it along a line perpendicular to the fibers (Chen, Lipari, Dehghan, Streichan, & Bilder, 2016; Hannezo, Dong, Recho, Joanny, & Hayashi, 2015). To quantify two-dimensional cytoskeletal orientation, individual fibers within a cell can be traced using edge detection algorithms and the orientation of each fiber can be separately extracted. For example, edge detection algorithms quantified actin filament alignment in the C. elegans spermatheca, a reproductive organ that houses the oocyte during fertilization. Oocyte entry stretches spermathecal cells, activating myosin. Quantification revealed how the strength cytoskeletal alignment with stretch is dependent on myosin II activity (Wirshing & Cram, 2017).

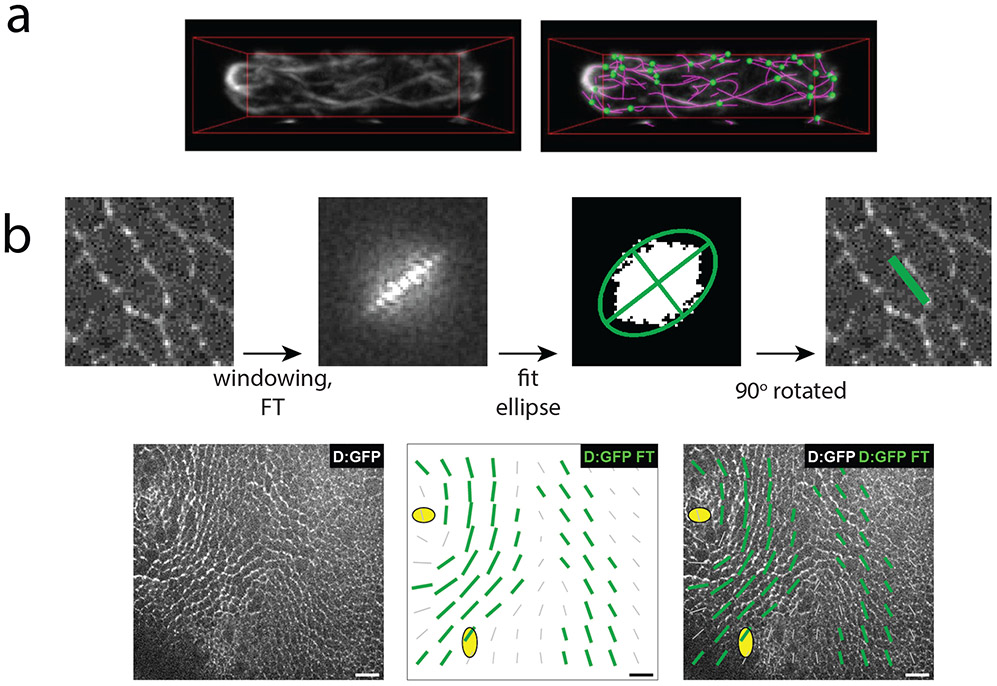
Rudimentary edge detection algorithms compute the pixel coordinates of fibers in an image, however, information about the connectivity of the fibers (i.e. the position of nodes or fiber branch points) is unaccounted for. Recently, more complex edge detection packages have been made available to not only trace network structure but also to quantify network connectivity in 3D for highly curved filaments. For example, SOAX, an algorithm which first identifies fibers by extracting ridges in intensity but then evolves the fiber contours over time, stretching and merging them can localize both the position and connectivity of all the actin cables in fission yeast. Such a map of network connectivity can inform our understanding of how cell polarity is established (Xu et al., 2015) (Figure 4a).

Figure 4:

Analyzing cytoskeletal orientation at single time points.

a) Actin cables in fission yeast marked via GFP-CHD. Actin is traced by SOAX analysis which also infers the topology of the network to identify network junctions (green). Figure is adapted from (Xu et al., 2015). b) A Fourier transform is employed to calculate the local orientation of Dachs:GFP (D:GFP) in the Drosophila dorsal thorax. First the 2D discrete Fourier transform is calculated on the original image (after multiplication by a square cosine function, ‘windowing’, to minimize edge effects). Pixels above the 80^th percentile are retained and fitted by an ellipse. From the ellipse the anisotropy and orientation of the original image can be extracted. Green bars plotted over the tissue represent local D:GFP anisotropy. Figure is adapted from (Bosveld et al., 2012). Scale bar: 10 μm.

In images with high noise or in dense networks, direct filament tracing is often too cumbersome. Additionally, segmentation is computationally intensive and therefore slow for processing large data sets. An alternative is to calculate the course-grained orientation map of the cytoskeleton on subcellular windows in order to capture changes in local orientation of the image. A two-dimensional Fourier transform can be applied to each window to identify the principal orientation of the contained fibers (Bosveld et al., 2012; Cetera et al., 2014) (Figure 4b). Other techniques employ structure tensors, which are matrices that encode information about the local intensity gradients of each subwindow calculated for each subwindow over an entire image (Puspoki, Storath, Sage, & Unser, 2016) or on a manually selected subwindow (Boudaoud et al., 2014). The first eigenvector of the structure tensor defines the main orientation of the entire subregion, namely, the direction where the directional derivative is maximized. The anisotropy, or coherence extracted from the tensor quantifies the strength of the orientation ordering within the subwindow. This measure can differentiate between the case where there is one principal direction in the subwindow from one where there is an isotropic distribution of fibers. Tensor analysis has been employed to quantify microtubule orientation in Arabidopsis shoot apical meristem (Louveaux, Rochette, Beauzamy, Boudaoud, & Hamant, 2016) and basal actin alignment in the Drosophila egg chamber (Isabella & Horne-Badovinac, 2015). In each of these cases cytoskeletal alignment has been an important readout of the mechanics of the tissue.

Tensor description has also been useful to quantify non-filamentous structure. For example, it was employed to quantify the gradient of the apical and basal myosin II intensity across the entire early Drosophila embryo (Streichan, Lefebvre, Noll, Wieschaus, & Shraiman, 2018). The anisotropy of the ‘myosin tensor’ across the entire tissue was able to predict the global morphogenetic flow in the Drosophila embryo. This is consistent with the fact that in at least some of these morphogenetic processes myosin II functions as a motor that generates tension and movement (Vasquez, Heissler, Billington, Sellers, & Martin, 2016).

Kinetics of the cytoskeleton: oscillations

Imaging tagged cytoskeletal proteins with high temporal resolution and measuring the intensity of these proteins over time has uncovered new mechanisms for processes that drive tissue morphogenesis. For example, measuring myosin II accumulation during Drosophila ventral furrow formation (Martin et al., 2009), Drosophila dorsal closure (Blanchard, Murugesu, Adams, Martinez-Arias, & Gorfinkiel, 2010; David, Tishkina, & Harris, 2010), and tissue extension (Fernandez-Gonzalez & Zallen, 2011; Rauzi, Lenne, & Lecuit, 2010; Sawyer et al., 2011) identified cycles of myosin II assembly and disassembly, called myosin II pulses. The cyclical nature of cytoskeletal contractions has now been observed in vertebrate development (Christodoulou & Skourides, 2015; Kim & Davidson, 2011; Maitre, Niwayama, Turlier, Nedelec, & Hiiragi, 2015). The cyclical nature of myosin II pulses represents myosin’s repeated activation and filament assembly and inactivation (Munjal, Philippe, Munro, & Lecuit, 2015; Vasquez, Tworoger, & Martin, 2014). To understand the interplay between the cytoskeleton and cell shape, relevant changes in the myosin II signal must be identified and their amplitude and period quantified.

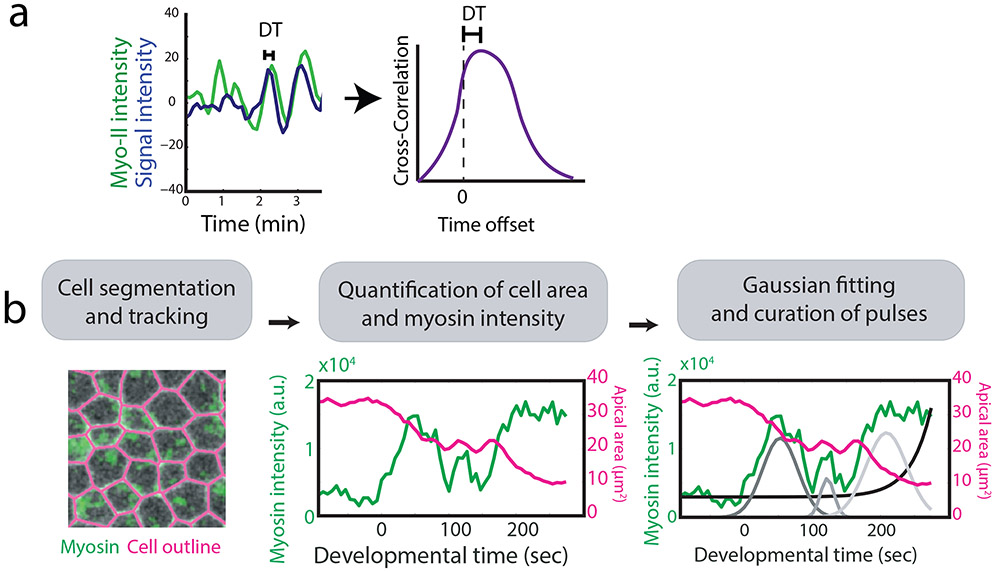
An important measurement that suggested that myosin II pulses were driving cell constriction was the cross-correlation between the myosin II signal and cell constriction (Blanchard et al., 2010; Martin et al., 2009). Demonstrating a cross-correlation between a tagged protein signal and cell shape has been extremely useful in cell biology to define mechanisms of movement (Machacek et al., 2009). This approach measures the similarity of one signal (i.e., myosin intensity) with respect to shifted copies of a second signal (i.e., apical area) as a function of lag time between them. An offset in the correlation defines how much one signal must be shifted with respect to the other for the two to have the highest degree of similarity. The cross correlation therefore can quantify the lag between the peak of the protein intensity signal and the resulting change in cell shape (Figure 5a). One useful method to determine whether pulsing is affected by a perturbation is to measure a cross correlation between the two signals. Perturbations that disrupt pulsing often result in a loss of cross correlation between the myosin signal and corresponding cell shape change (Mason, Tworoger, & Martin, 2013; Vasquez et al., 2014).

Figure 5:

Analyzing cytoskeletal dynamics. a) Cross-correlation between two signals identifies the time shift of one relative to the other. Here the time offset quantifies the delay between the time when the signal of interest peaks and the time when myosin is at local maximum.

b) To quantitatively identify a sequence of myosin pulses in the Drosophila ventral furrow, first cells were segmented and tracked. Myosin intensity was then quantified inside each cell and a multiple Gaussian fitting to the myosin intensity identified pulse sequences which were confirmed via manual curation. Figure is adapted from (Xie & Martin, 2015).

Currently, there is no standard for defining pulses and measuring their properties. For example, perturbations that in our hands abrogate pulsing, such as Cytochalasin D injection (Mason et al., 2013), have been used to quantify pulse characteristics in other studies (Clement, Dehapiot, Collinet, Lecuit, & Lenne, 2017). This discrepancy could reflect different mechanisms for pulsing in different cell types or could reflect the lack of a standard for defining a myosin II pulse. Techniques to identify the timing of a myosin pulse (i.e., the location of the pulse’s maxima) vary depending on the regularity in which they occur. Fourier analysis can identify the location and frequency of periodic pulses (Sokolow, Toyama, Kiehart, & Edwards, 2012). Autocorrelation of the myosin signal can be used to identify the time between subsequent peaks (Rauzi et al., 2010). If pulsing is non-periodic or if there is insufficient time to clearly observe the period, it is a challenge to identify what constitutes a significant peak of myosin and what constitutes a signal fluctuation due to noise. One strategy to detect a sequences of relevant pulses employs an iterative multiple-Gaussian fitting algorithm to localize pulses from the myosin intensity signal evolution (Xie & Martin, 2015) (Figure 5b). In other cases, amplitude change of the myosin signal can be thresholded above a chosen value to remove minor local maxima and minima in the signal. It is important to note that in some systems a fluorescence signal increases faster than it is lost, a property that is not captured with a symmetrical pulse fitting (Blanchard et al., 2010).

Kinetics of cell cytoskeleton: flows

While pulse measurements consider changes in concentration over a defined spatial region, one can also consider how a fixed amount of a cytoskeletal protein moves through each point in space in a cell or tissue. For example, shortly after anaphase initiation in Xenopus oocytes and embryos, cortical waves of filamentous actin (F-actin) and RhoA GTPase activity propagate across the surface (Bement et al., 2015). Measurements of location, timing, and interplay between waves are important to gain insight into how they are excited and involved in the cell cycle. Kymographs are an effective method to visualize wave behavior: a line is selected through an image and pixels at the same location in subsequent time frames are concatenated to create a 2D image, which visualizes the change at that spatial position over time. Overlapping kymographs of RhoA activity and F-actin indicated the timing of one wave with respect to the other, revealing an antagonistic behavior between Rho and F-actin. RhoA activity triggers F-actin assembly, but F-actin assembly acts to inactivate RhoA (Bement et al., 2015). However, kymographs are a 1D measure and they can mask movement perpendicular to the subwindow. Kymocubes employ a similar method, but instead of a line, a 2D region is defined and stacked together with subsequent time frames to yield a 3D representation, which can be rotated to view how tagged markers change over time through the window. Kymocubes illustrated complex spatial patterns of RhoA activity in starfish oocytes, such as spiral waves (Bement et al., 2015).

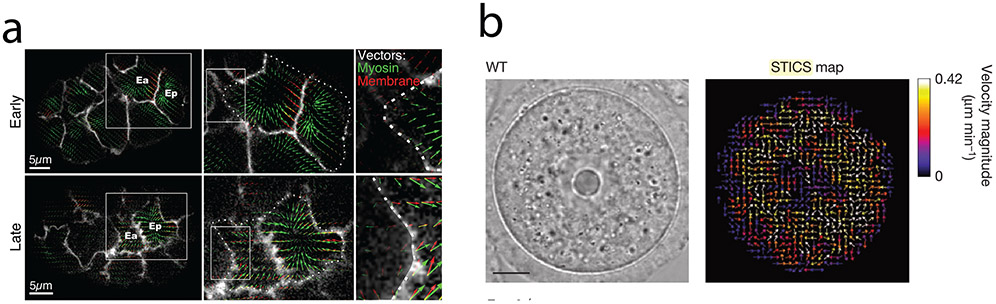
Particle Image Velocometry (PIV) is another method of quantifying global flow fields. This technique was originally developed to visualize and measure fluid flow, by using tracer particles, whose position could be correlated between subsequent images (Raffel, Willert, Wereley, & Kompenhans, 2013). In contrast to injected tracer particles, PIV can measure flow in living systems by correlating the positions of image features in subsequent frames. An image is divided into a mesh of overlapping subwindows. Each subwindow at time t is correlated with the subwindow at the same location at time t+1 and a displacement vector is calculated using the movement of local features in the subwindow. For example, PIV has been used in Drosophila to quantify the movement of yolk granules and identify how microtubule flows set up the anterior posterior axis in the Drosophila oocyte (Khuc Trong, Doerflinger, Dunkel, St Johnston, & Goldstein, 2015). PIV was also instrumental in showing a mechanism whereby the attachment between the actomyosin cytoskeleton and an intercellular junction is regulated during C. elegans gastrulation (Roh-Johnson et al., 2012). In this case the authors compared myosin II flow inside a cell to the movement of the surrounding membrane. They identified an early phase where cytoskeletal flow occurs before the membrane is successfully pulled in (Figure 6a). Subsequently, cytoskeletal flow is accompanied by membrane movement revealing a mechanism that promotes apical constriction (Figure 6a) (Roh-Johnson et al., 2012).

Figure 6:

Image correlation analysis and measuring cytoskeletal flow. a) Analysis on the C. elegans embryo illustrates how PIV can be used to detect protein movement during gastrulation. Images show PIV vectors tracking the movement of myosin clusters (green arrows) and the cell membrane (red arrows). Note that cell membrane movement becomes aligned with centripetal myosin movement at the late stages of gastrulation. Images are taken from (Roh-Johnson et al., 2012). Scale bar: 5μm.

b) STICS analysis performed on a transmitted-light video (left) quantifies the local velocities of yolk granules to measure cytoplasmic activity. Images are taken from (Almonacid et al., 2015). Scale bars: 15μm.

PIV, commonly calculated for two-dimensional images, fails to capture flows out of the plane. Attention also needs to be given to separate tissue drift or global tissue flows that are separate from the movement of subcellular features of interest. PIV is sensitive to window size and if it is too small the feature one is trying to follow can displace beyond the window size between time steps. A window that is too large will result in excessive averaging of disparate feature movement. One way to minimize this problem is with multipass PIV methods where PIV is first calculated using large subwindows for a rough measurement of displacements in the image. Then, PIV is recalculated on smaller windows to refine the flow. As PIV is a coarse grain measurement, the window can capture deformation of cell junctions and flows in neighboring cells, which needs to be separated from flow occurring inside the cell of interest. Spatiotemporal Image Correlation Spectroscopy (STICS) (Hebert, Costantino, & Wiseman, 2005) is a method similar to PIV, which is better suited to measuring diffusion in addition to flow fields. An additional step filters in the Fourier space to remove stationary objects within the field of view. Also, STICS accounts for rotation of the image while PIV only tracks translational movements. For example, the STICS method has been used to visualize active diffusion in the mouse oocyte mediated by a cytoplasmic actin meshwork (Yi et al., 2011) (Figure 6b).

Defining the trajectories of cytoskeletal proteins is important to understand how they are recruited to specific locations. Particle tracking can measure individual protein movement at low protein concentration or the movement of concentrated protein clusters (Ponti, Machacek, Gupton, Waterman-Storer, & Danuser, 2004). Manual tracking plugins to ImageJ allow a user to define the position of a feature in time ensuring that the correct particle is being followed (Meijering, Dzyubachyk, & Smal, 2012; Tinevez et al., 2017). However, tracking by user input lacks precision in identifying the feature’s centroid and is highly time consuming. Automated feature tracking is an alternative to process larger data sets. Successive images are compared and a cost function is used to optimize the mapping of particles from one frame to the next. Automated tracking relies on clearly distinguishable features and particles that are close, can be mislabeled or defined as a single object. When direct tracking of fluorescent molecules is not possible, the use of tracer particles that tag a molecule/structure of interest is a useful substitute. Single-walled carbon nanotubes (SWNT), first validated in cell culture, can be attached to molecular motors and tracked over time (Fakhri et al., 2014). SWNTs have the advantage that they emit in the near-infrared to avoid overlap with other color channels. In addition, unlike fluorescent proteins they do not bleach, permitting long-term tracking. SWNTs have been employed to identify the role of myosin II in driving random cytoskeletal stirring which acts as an intermediate method of transportation in the cell between slow thermally driven diffusion and fast kinesin driven directed transport (Fakhri et al., 2014).

Passive tracers that do not link directly to any cytoskeletal component can reveal information about the functioning of the molecular motors in a developing system. Passive tracers larger than the typical cytoskeletal mesh size are big enough to get trapped in it. Therefore, tracking the fluctuations in their position is a read-out for the fluctuations in the cytoplasm. Calculating a mean squared displacement (MSD) from the trajectories of these passive tracers is commonly used to reveal the degree of activity of the system and identify whether it is out of equilibrium (Almonacid et al., 2015; Guo et al., 2014). If motors in the system are inactive, diffusion (to a first approximation) should depend on the size of the tracer particle. If the system is active, however, movement of the tracer particles captures not just thermal Brownian motion, but also motion due to an ensemble of forces resulting from overall activity in the cytoplasm (Guo et al., 2014).

Future directions:

Advances in quantitative analysis of imaging data have enhanced our understanding of developmental biology, but many imaging technologies are still in their nascent stages. Super-resolution microscopy techniques, such as structured illumination, PALM, and STORM, are changing the way we visualize cells and their components, creating the need to develop methods to process new types of data sets and interpret the biological phenomena they uncover (Betzig et al., 2006; Gustafsson, 2005; Rust, Bates, & Zhuang, 2006). Single molecule localization methods have the power to quantify not just the location and orientation of the proteins in developing tissues, but go further to elucidate the ultrastructure of cells. Currently, many of the advances in this area are limited to single cells and have not yet been extrapolated to developing tissues. For example, structured illumination can detect individual myosin II minifilaments, defining how different isoforms of mammalian myosin II can form heterotypic oligomers in different cellular contexts (Beach et al., 2014). In cell culture, it has been proposed that isoforms may be playing both unique and redundant functions, however, little is known about how myosin isoforms work together during mammalian development.

STORM super-resolution microscopy is able to identify ultrastructure of cell submembrane cytoskeleton in individual cells (Pan, Yan, Li, & Xu, 2018). Extending our understanding of the ultrastructure of the cytoskeleton to cells in a tissue and defining how this organization depends on tissue context will deepen our understanding of how cytoskeletal organization leads to cell and tissue scale mechanical changes during development. Quite possibly, the greatest challenge – both conceptually and computationally – will be to simultaneously analyze what is happening at several different length scales. This ability will be needed if we are to understand how forces feed-back to influence tissue shape, structure, and even cell fate. Thus, comprehensive, multiscale imaging will be an exciting future area of investigation in developmental biology.