Abstract
The N-terminal domain of the RNA binding protein TDP-43 (NTD) is essential to both physiology and proteinopathy; however, elucidation of its folding/unfolding still remains a major quest. In this study, we have investigated the biophysical behavior of intermediate ensembles employing all-atom molecular dynamics simulations in 8 M urea accelerated with high temperatures to achieve unfolded states in a confined computation time. The cumulative results of the 2.75 μs simulations show that unfolding of the NTD at 350 K evolves through different stable and meta-stable intermediate states. The free-energy landscape reveals two meta-stable intermediates (IN and IU) stabilized by non-native interactions, which are largely hydrophilic and highly energetically frustrated. A single buried tryptophan residue, W80, undergoes solvent exposure to different extents during unfolding; this suggests a structurally heterogeneous population of intermediate ensembles. Furthermore, the structure properties of the IN state show a resemblance to the molten globule (MG) state with most of the secondary structures intact. The unfolding of the NTD is initiated by the loss of β-strands, and the unfolded (U) states exhibit a population of non-native α-helices. These non-native unfolded intermediate ensembles may mediate protein oligomerization, leading to the formation of pathological, irreversible aggregates, characteristics of disease pathogenesis.
The N-terminal domain of the RNA binding protein TDP-43 (NTD) is essential to both physiology and proteinopathy; however, elucidation of its folding/unfolding still remains a major quest.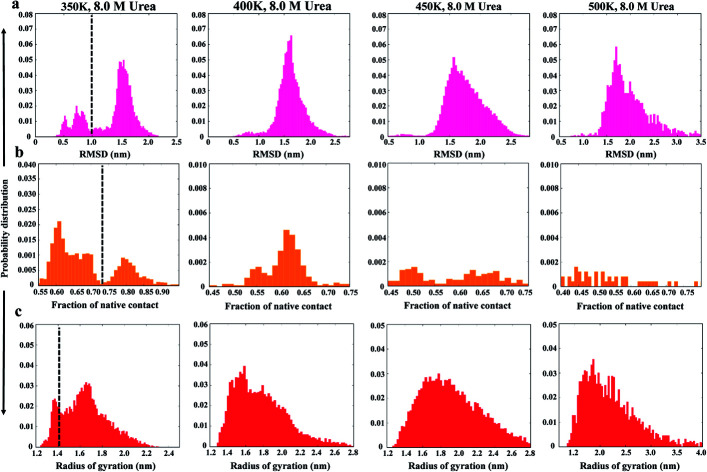
Introduction
Amyotrophic lateral sclerosis (ALS) and frontotemporal dementia (FTD) are two closely related debilitating adult-onset neurodegenerative diseases.1–3 The mislocalization and cytoplasmic ubiquitinated inclusions of TAR DNA binding protein-43 (TDP-43) are linked to majority of ALS and FTD.4 Several studies indicate that the possible mechanism of TDP-43-induced neurotoxicity includes a complex interplay between the loss of cellular functions and gain of toxic functions of TDP-43.5–7 TDP-43 belongs to a highly conserved heterogeneous nuclear ribonucleoprotein (hnRNP) that binds TG/UG repeat nucleic acids and plays an important role in RNA metabolism.8,9 TDP-43 comprises four functional domains: an N-terminal domain (NTD), two RNA recognition motifs (RRM1 and RRM2), and a glycine-rich, disordered C-terminal domain (CTD). The CTD is a low complexity, prion-like domain that harbors most of the ALS-linked mutations.10 This domain mediates protein–protein interactions and also self-interacts and undergoes phase separation and aggregation.11–13
After being ignored for almost six years since the discovery of TDP-43, the NTD has drawn significant attention recently; in the past few years, many studies have revealed that the NTD plays a role in the physiological functions of TDP-43 (ref. 14–18) as well as in its pathological aggregation and neurotoxicity.17,19–21 The solution and crystal structures of the NTD have been elucidated by NMR and X-ray crystallography. In 2014,14 Qin et al. reported that the NTD (residues 1–102) remains in both well-folded and unfolded structures in equilibrium, and the folded structure adopts an ubiquitin-like fold that binds single-stranded DNA. The first solution-structure of the stably folded NTD (residue 1–77) was solved by Mompean et al. in 2016.22 The structure of the NTD is a canonical β-barrel structure consisting of six β-strands and a short α-helix with a topology of β1β2 αβ3β6β4β5 (PDB ID: 2N4P). The same research group later published the solution structure of a longer NTD (residues 1–102; PDB ID: 5MRG) and described the atomistic model structure for a dimeric NTD observed in vitro.23 Very recently, Afroz et al. solved the crystal structure of the NTD for the first time and reported that NTD-mediated TDP-43 oligomerization results in the physiological oligomers of TDP-43.24
The NTD domain is highly conserved among eukaryotes25 and is stable and well-folded at pH 2.0 to 8.6 and temperatures of 5 °C to 40 °C, including physiological conditions.22,23,26 Many recent structural and functional studies of the NTD were performed on His-tagged constructs.14,18,22–24 These studies clearly showed that the NTD is stably folded and functional. Recently, Tsoi et al.26 also showed that NTD1–80 without His-tags adopts a similar fold to Mompean's His-tagged NTD1–77.22
Mompean et al.22 reported that the conformational stability of the NTD is highest at acidic pH and decreases with increasing pH. However, the protein becomes unfolded only at pH > 10.0 because of mutual repulsion of anionic residues (∼12 in number). Recently, Tsoi et al.26 showed that at low pH, the NTD becomes destabilized, which leads to its monomeric form. They reported the presence of multiple native thermodynamic states (i.e. N1 and N2) at physiological conditions and suggested that these two native states correspond to pH-dependent protonation–deprotonation of the single His 62. Several studies have reported an interesting dichotomy in TDP-43, where the NTD regulates normal TDP-43 structure and function16,24,27 while also participating in driving TDP-43 aggregation in TDP-43 proteinopathies.15–17,19 TDP-43 forms physiological and reversible oligomers mediated by the NTD, and these physiological oligomers may serve as precursors for pathological and irreversible protein inclusions. Thus, the physiological oligomers of TDP-43 form when the NTD is stable and well folded. However, unfolding of the NTD results in the formation of pathological inclusions.14,28 In this regard, biophysical behavior studies of folding dynamics and structural stability analysis of the NTD will be beneficial to understand the biological roles played by TDP-43 under physiological and pathological conditions.
High-temperature unfolding simulations are a useful system to study protein unfolding on computationally accessible time-scales.29 By starting from a relevant conformational state, these high-temperature MD simulations allow easier access to relevant intermediate states and can demonstrate that both native and non-native interactions contribute to stability. A large number of high-temperature MD experiments have demonstrated that the pathways of protein folding and unfolding significantly obey the principle of microscopic reversibility.30–32 Also, the unfolding pathways for the same protein do not depend on the force-fields utilized in MD studies.33 Indeed, the unfolding pathway has been demonstrated to be temperature-independent.30,34 Therefore, high-temperature MD simulations have been employed to investigate the unfolding pathways or stabilities of several proteins.35–39
To increase the rate of the unfolding process, both experimental and computational methods utilize high temperature, high pressure, low pH, or chemical denaturants (guanidinium chloride or urea). In the present work, we have employed all-atom MD simulations to obtain detailed insights into the unfolding and thermostability of the NTD in 8 M urea at 300 K, 350 K, 400 K, 450 K and 500 K. The results of the cumulative microsecond simulations indicate (i) the presence of stable intermediates (IN and IU) and the transition state (TS) along the unfolding pathway; (ii) the formation of a molten globule (MG) during an early unfolding intermediate, IN; (iii) conformationally heterogeneous IU stabilized by non-native contacts and hydrogen bonds; (iv) initiation of unfolding through disruption of β3; and (v) the presence of residual structures in the unfolded state. This study may provide further insights into the unfolding of the N-terminal domain of TDP-43, which contributes to protein aggregation and is thus implicated in pathological roles in neurodegenerative diseases.
Materials and methods
MD simulations
All-atom MD simulations were performed using Gromacs v5.1.4 with the CHARMM27 force field and SPC216 as a water model. The initial co-ordinates of the NTD of TDP-43 (PDB ID: 2N4P) were obtained from the Protein Data Bank.22 As a control simulation, the protein was solvated in pure water in a cubic box with a volume of 6 nm3. To conduct simulations in aqueous urea, the protein was placed centrally in a pre-equilibrated box (volume 6 nm3) of 8 M urea (865 molecules of urea and 4521 molecules of water). The parameters and topology files to prepare the aqueous mixture of urea molecules were taken from Camilloni et al.35 This parameter has been extensively used by our group as well as others to study protein unfolding.40–44 To neutralize the system, seven molecules of Na+ ions were added to the bulk (solvent). The prepared systems were minimized using the steepest descent method followed by the conjugant gradient method, with 10 000 steps for both. The system was equilibrated in two steps, NVT and NPT; each step was performed for 500 ps. Periodic boundary conditions (PBC) were exerted in all three x, y and z directions. Berendsen thermostat and Parrinello–Rahman pressure coupling were used to maintain the temperature and pressure, respectively. The bond lengths and hydrogen atoms were constrained using the LINC algorithm45 and particle mesh Ewald method;46 a grid space of 1.0 nm was used to evaluate the electrostatic interactions, and the van der Waals interactions were evaluated using the LJ potential with cutoff 1.2 nm. Finally, the NPT ensemble was used for the production run for 500 ns in pure water and 8 M urea at 300 K, with an integration time step of 2 fs; the coordinates and trajectory for velocity and energy were recorded for every 10 ps, respectively. To accelerate the unfolding kinetics, four independent runs were also carried out at 350 K, 400 K, 450 K and 500 K in 8 M urea. The analyses on the obtained trajectories were performed using Gromacs utilities and MDTraj-based Python scripts.47 The tools provided by the GROMACS program package were utilized to analyze different MD trajectories. The PyMOL (DeLano Scientific) and XMGrace programs were used to analyze and prepare publication-quality figures.
Fraction of native contacts
A protein in its folded native state is stabilized energetically and is driven by various contacts that are partially or fully but collectively involved in interactions to maintain the appropriate fold. We measured the fraction of native contacts as previously described.48 The native pairs were defined as all the pairs of heavy atoms i and j belonging to residues θi and θj that are in contact, provided that |θi − θj| > 3 and the distance between i and j is less than 4.5. Also, the fraction of native contacts is defined as:
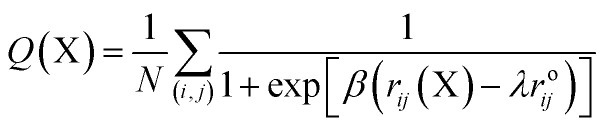 |
1 |
where N is the pairs of native contacts (i,j), rij (X) is the distance between i and j in configuration X, roij is the distance between i and j in the native state, β is the smoothing parameter with a value of 5 Å, and the factor λ accounts for fluctuations when contact is formed; it is taken as 1.8.
Free energy contour maps of the NTD
The free energy contour maps were established by calculating the normalized probability distribution based on a set of order parameters. We defined the free energy based on probability distribution (P) using the relation F = −RT ln P.
Here, we described the free energy map as a function of two order parameters, that is, the root mean square deviation (RMSD) and fraction of native contacts (Nc). We also constructed an additional free energy contour map as a function of the radius of gyration (Rg) and Nc to validate the analysis.
Residual frustration analysis
The Woylness group developed an algorithm to determine local frustration in a protein residue which indicates whether a contact between residues is energetically optimized in the folded state.49 This algorithm is now implemented in a web server, “Frustratometer”;50,51 it examines pairwise interactions between residues and evaluates the total energy changes. In this work, we used the “configurational frustration index”, in which the decoy set involves randomizing the identities as well as the distance and the density of interacting amino acids i and j. This scheme effectively determines the native pair with respect to a set of structural decoys that may be observed during the folding events. Accordingly, energetically favorable contacts between native residue pairs are considered to be minimally frustrated, whereas energetically unfavorable contacts in the native state are considered to be highly frustrated.
We analyzed the frustration in NTD during unfolding, and the minimally and highly frustrated contacts are depicted on the lowest-energy structure from the Boltzmann-reweighted structures from the MD simulations.
Results and discussion
Multiple unconstrained MD simulations of NTD solvated in aqueous 8 M urea solution at different temperatures (300 K, 350 K, 400 K, 450 K, and 500 K) were performed and analyzed by the simultaneous use of several parameters to enable a detailed characterization of the unfolding process of NTD. The simulations were carried out for 500 ns in water (at 300 K) and 8 M urea (at 300 K to 450 K) and for 250 ns (at 500 K); thus, the total simulation time was 2.75 μs.
Control MD simulations were carried out in water and 8 M urea at 300 K for 500 ns, respectively (Fig. S1†). The results clearly showed that the NTD in both water and 8 M urea at room temperature was stable and close to its native structure without any unfolding propensity. In water, the Cα root mean-square-deviation (RMSD) did not deviate greatly and stabilized around a value of <1.0 nm; meanwhile, the radius of gyration (Rg), fraction of native contacts (Nc) and solvent accessible surface area (SASA) of the NTD also remained stable during the simulations. However, in 8 M urea, slight increases in RMSD, Rg and SASA were observed along with a slight decrease in Nc. Thus, to accelerate the unfolding kinetics, the simulations in the presence of 8 M urea were augmented with higher temperatures;30,39,52 the details of the conformational changes are summarized in ESI Table 1.†
Temperature dependence of conformational dynamics
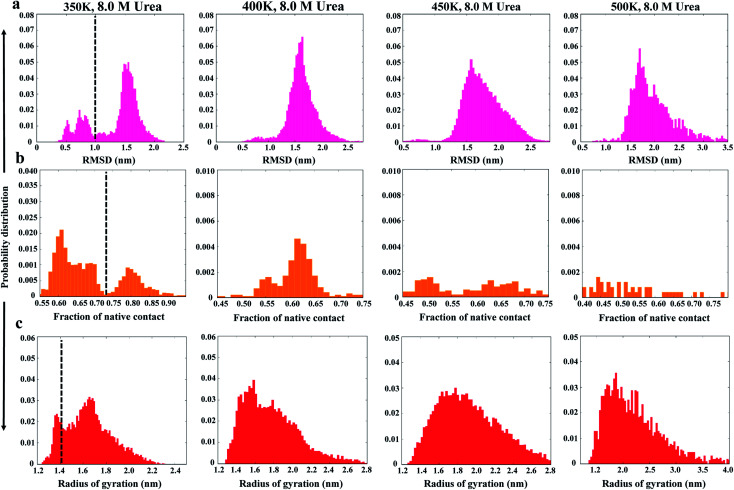
As a first step in characterizing the unfolding dynamics of the NTD, we studied the temperature dependence of several structural parameters obtained from MD trajectories in the range of 300 to 500 K. Fig. 1 summarizes the temperature dependence of the Cα RMSD (Fig. 1a), Nc (Fig. 1b), and Rg (Fig. 1c). We also show the convergence of these parameters in the ESI, Fig. S2.†
Fig. 1. Probability distributions of structural parameters: (a) Cα-RMSD, (b) number of native contacts (Nc), and (c) radius of gyration (Rg) in 8 M urea at 350 K (left panel) to 500 K (right panel). The dashed line defines the two different conformational states as native and non-native states.
As can be seen from the results, the NTD structure deviates greatly with increasing temperature, indicating progressive unfolding of the NTD. The shift in the probability distribution of RMSD toward higher values (Fig. 1a) and the shift toward lower values in Nc (Fig. 1b) clearly indicate loss of the native structure. At 350 K, the RMSD and Nc distributions reveal a distinct bimodal nature; this indicates the presence of two major states, native and non-native. The distribution at higher temperatures gradually shifts to a non-native state. Interestingly, the distributions also demonstrate the appearance of an intermediate state around an RMSD of ∼0.8 to 1.0 nm and an Nc of ∼50, which is largely populated at 350 K; this suggests that the transition occurs at this temperature. Thus, at 350 K, Nc displays higher fluctuations during the simulation, indicating the presence of several intermediate states between the folded and unfolded states (ESI, Fig. S2b†).
Alternatively, Rg remains relatively unchanged or slightly decreases with increasing temperature (Fig. 1c and S2c†), indicating that the protein assumes a compact molten globule structure upon the initial melting of the native structure. The transition from a compact molten globule-like state to a fully unfolded state (with a large Rg) occurs at much higher temperatures (450 to 500 K).
Unfolding of NTD monitored by solvent accessibility of Trp80
The MD trajectories in 8 M urea with different temperatures were then used to determine the solvent accessibility of an unfolding probe, Trp80 residue (Trp68 in Uniprot id: Q13148). The residue Trp80 (W80) is buried within the hydrophobic core of the protein as determined by NMR spectroscopy.22 The simulations at 350 K were used to investigate the urea-induced unfolding of the NTD in detail, with emphasis on characterization of the molten globule-like intermediate state. The results from the MD run at 350 K are shown in Fig. 2. The results at all other temperatures (300, 400, 450, and 500 K) in 8 M urea are shown in the ESI, Fig. S3–S6.†
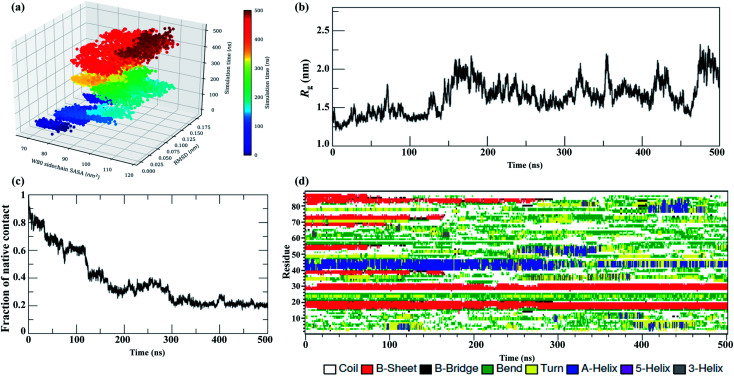
Fig. 2. Unfolding pathways of the NTD in 8 M urea at 350 K. (a) Evolution of the solvent-exposed surface area, SASA, of the W80 side chain and Cα-RMSD during unfolding. Each point on this plot is colored according to its time of occurrence according to the color scale shown. Time evolution of (b) Rg, (c) Nc, and (d) secondary structures.
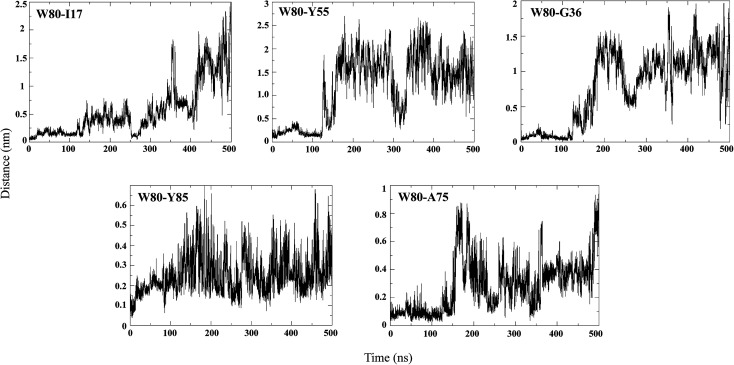
Fig. 2a shows the evolution of the side chain SASA of W80 along with the Cα RMSD during a 500 ns trajectory at 350 K. In the native state, W80 is solvent-exposed, with a side chain SASA of ∼70 nm2. At 350 K, W80 undergoes different extents of solvent exposure at different stages of unfolding, consistent with an experimentally observed decrease in fluorescence.22,26 The first transition of solvent exposure (SASA ∼ 80 to 95 nm2) is evident for a short time scale of 50 ns (from ∼80 to 130 ns) in a native-like ensemble with RMSD < 0.12 nm. This ensemble is referred to as IN hereafter. The side chain SASA of W80 increases as IN unfolds further on a longer time scale of 100 ns (∼200 to 300 ns). This partially unfolded intermediate ensemble (referred to as IU) is populated with an RMSD of 0.15 nm. The IU ensemble further unfolds to the unfolded state, U, with RMSD > 0.17 nm. This unfolded state displays the transition of W80 between partially buried and solvent-exposed states. The fluctuation of SASA in this state is larger than both IN and IU, suggesting that the environment around W80 is more malleable in the U state. Previous fluorescence experiments22 showed that solvent exposure of W80 is accompanied by a relatively small red shift in the λmax of W80 (from 328 to 350 nm); however, the reason for this shift is not clear. Here, we show that W80 in the U ensemble is fully solvent exposed in only a fraction of U molecules explored during the last ∼100 ns of the simulation (400 to 500 ns).
IU is a more structurally loose ensemble than IN and displays a loss of most of the Nc and secondary structures. Moreover, IU is much longer-lived than IN (in all temperature simulations), suggesting that most of the decrease in fluorescence intensity observed throughout the experiment is contributed by the IU ensemble. Further, W80 was also found to be transiently and infrequently buried in the IU and U ensembles, suggesting that the conformational ensembles are structurally heterogeneous and are populated at different stages of unfolding.
In addition to W80, a tyrosine residue (Y55) also shows transient fluctuations between partially buried and fully solvent-exposed states (ESI, Fig. S7†), suggesting structural heterogeneity within the IU ensemble.
The evolution of Rg (Fig. 2b) further suggests that the IN ensemble in which W80 is exposed is highly compact in nature, with Rg ∼ 1.30 nm, and remains native-like; this is also suggested by the RMSD (<1.0 nm). In contrast, the IU ensemble shifts slightly towards the unfolded side, with Rg > 1.70 nm and RMSD > 1.50 nm. We observed transient drops in the Rg and RMSD values, which suggests non-specific collapse of the structure. The evolution of Nc (Fig. 2c) further confirms that IN has a native-like structure (Nc ∼ 0.6), whereas the IU ensemble is more unfolded (Nc ∼ 0.35).
Interestingly, a comparison of the evolutions of the W80 side chain SASA and RMSD in higher temperature simulations (ESI, Fig. S3–S6†) displays a similar manner of unfolding, i.e. a compact molten globule native-like IN structure early in the unfolding process followed by a long-lived partially unfolded IU conformation and, eventually, the fully unfolded U conformation.
The results of the simulations presented in Fig. 2 and S3–S6† show that solvent exposure of W80 can occur on different time scales and is dependent on the temperature, suggesting that the reaction is non-cooperative and is not all-or-none. However, it remains to be determined whether this non-cooperativity is due to the presence of urea or increased temperature.
The evolution of the secondary structure was calculated using the DSSP program to obtain a detailed understanding of the structural changes during the unfolding process. Fig. 2d shows that the secondary structure of the NTD at 350 K remains fairly stable up to ∼100 ns, although the number of native contacts decreases to 60%. The unfolding process initiates with the disruption of β3 and β4 along with the loss of turns and bridges between these two strands. As unfolding continues, β6 is lost completely, followed by massive loss of the α-helix at the midpoint of the simulation. However, the N-terminal strands β1 and β2 remain mostly intact during the simulation.
The early unfolding steps at higher temperatures (450 K to 500 K) involve the sequential loss of β strands at the C-terminal, followed by loss of N-terminal strands and the α-helix (Fig. S3–S6†). Formation of the non-native helix was also evident during the simulation. Thus, the β-sheets were lost more quickly than the α-helix in urea at higher temperatures. These results are in good agreement with previously reported data.35,44
Tertiary contact map
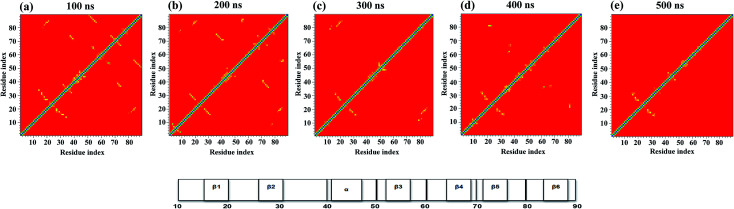
Fig. 3 shows the pairwise contact maps for the N → IN → IU → U unfolding process observed at 350 K. This enables us to obtain insights into the details of initial unfolding events and highlights the differences in the contacts formed during different stages of unfolding. A contact map of Cα atoms (≤6.0 Å) was used to characterize the unfolding of the NTD by showing the formation and loss of contacts between the residues.
Fig. 3. Tertiary contact map of the NTD unfolding pathway in 8 M urea at 350 K as seen at different time points. (a) 50 ns represents the N state, (b) 100 ns represents the IN state, (c) 200 ns represents the IU state, (d) 400 ns represents the transition state, and (e) 500 ns represents the U state. The horizontal bar on the right denotes the secondary structures present in the original NMR structure.
The contact map analysis implies that the loss of tertiary contacts during the unfolding pathway is gradual; however, the unfolding is initiated with weakening of the long-range contacts between β3–β6 and short range contacts between β4–β5 at 100 ns in the simulation (Fig. 3a). The contacts between β3 (52–56) and β-bridge residues (64–65) are also lost. Weakening of loop contacts (32–38) is observed in the IN ensemble and becomes more prominent in IU. Moreover, gains of some non-native contacts between the α-helix and β-hairpin residues (i.e. 40–70; 41–71) between the loop and β5 (i.e. 38–72) and the β-bridge and β4 (i.e. 64–68) are observed in the IN ensemble. However, long-range contacts between β1–β6 and between the α-helix and β5, as well as short-range contacts involving the N-terminal strand β1, β2 and the β-hairpin, remain intact (Fig. 3b); this indicates the preservation of this N-terminal core in the IN state.
During the next stage of unfolding, complete loss of long-range contacts between strands β3–β6 and short-range contacts between β4–β5 is clearly observed in IU. Furthermore, the contacts involving the α-helix and β5 are also disrupted completely. The contacts at both termini of the α-helix are weakened. Loss of many non-native contacts present in the IN ensemble is observed in IU, along with the formation of some new non-native contacts between the turn and β3 residues (i.e. 48–52 and 48–54). However, the long-range contacts between β1–β6, short-range contacts between β1–β2, and α-helical contacts remain intact (Fig. 3c), indicating that these N-terminal contacts are preserved in both the IN and IU ensembles.
The disruption of long range contacts between β1–β6 along with the appearance of new non-native contacts is observed in the transition state (∼300 to 400 ns) between the IU and U states. Interestingly, many short-range non-native contacts appeared between residues of β3 (52), β4 (67–68), bridge (37–38), loop (32–34), turn (47–50), and β5 (72), indicating the formation of a non-native unfolded transition state ensemble (Fig. 3d).
The IU ensemble further unfolds with predominant loss of the α-helix. However, the contacts involving β1, β2 and the β-hairpin remain intact, indicating the presence of a residual structure even in the unfolded conformation with Nc < 20% (Fig. 3e). The existence of a residual tertiary structure in the unfolded state may be due to the change in the environment of the aromatic residues (Trp, Tyr, and Phe) as the protein unfolding commences (see Fig. 2a and S7†). Also, a transient drop in Rg for the U ensemble is consistently observed, suggesting the presence of a collapsed structure in the U ensemble (Fig. 2b). The presence of residual structure in denatured states has been previously reported for many proteins.52–55
Furthermore, snapshots of the unfolding events at 350 K are shown in Fig. 4. The structural snapshot at 50 ns corresponds to a native (N) structure, where all the native tertiary contacts and secondary structures remain intact. Moving from the N state to IN at 100 ns, we can clearly observe disruption of the β3 and β4 strands; however, the N-terminal strands β1 and β2 and the α-helix remain intact. The conformation representing the IU ensemble (200 to 300 ns) is largely unfolded, with melting of the α-helix along with loss of β5 and β6. The structural snapshot of the transition structure (400 ns) shows further loss in the single α helix, along with the presence of non-native helical structures. The unfolded ensemble at 500 ns is characterized by the presence of largely unfolded and disordered structures. The unfolded state still contains the residual structure with intact β1 and β2, and the α helix is almost completely melted. Snapshots depicting the complete unfolding pathway of the NTD at a higher temperature (400 K) are shown in the ESI, Fig. S8.†
Fig. 4. Snapshots corresponding to the N, IN, IU, TS and U conformational states observed during the unfolding pathway of the NTD at 350 K.
Free-energy contour map of the NTD reveals stable intermediates
To map the unfolding pathway in 8 M urea at temperatures from 350 to 500 K, a two-dimensional free energy landscape (FEL) contour map was constructed from the joint probability distribution (P) of Nc with RMSD and Rg using the equation F = −RT ln P. The FEL plot shows that the transition from the native folded state to the unfolded state follows a minimum energy pathway evolving through different intermediates (Fig. 5). At 350 K, the highly rugged FEL shows the presence of three distinct global minima in addition to two well-resolved local minima, indicating the presence of several intermediates between the folded and unfolded conformations (Fig. 5a). These different energy minima are well separated by a relatively small energy barrier of ∼7.0 kJ mol−1. The plot shows that the protein quickly moves out from the native basin and explores a broad basin with an RMSD of ∼0.75 nm and Nc of ∼0.6 during 130 ns of the simulation; this corresponds to the IN ensemble. The IN ensemble is native-like, with similar Rg and Nc values (Fig. 5b).
Fig. 5. Free energy contour maps constructed from (a) Cα-RMSD versus native contact (left panel) and (b) Rgversus native contact (right panel) in 8 M urea at 350 K. The color is scaled according to kcal mol−1. Key minima (basins) in the maps are marked.
The protein then visits a much broader energy basin via a transition state; within this broader phase region, the protein explores two distinguishable minima separated by a very small energy barrier of <4.0 kJ mol−1. The first minimum (referred to as IU) is achieved from 200 to 300 ns of the simulation, with an RMSD of ∼1.50 nm and Nc of ∼0.35. IU is slightly swollen compared to the N state, with Rg ∼ 1.7. The second minimum (referred to as U) displays a largely populated phase space with an RMSD of ∼1.50 to 1.75 nm and the presence of ∼20% of native contacts.
Thus, the IN ensemble is a short-lived intermediate ensemble that is observed for 50 ns (80 to 130 ns) and is structurally compact (Rg ∼ 1.3 nm) and native-like (Nc ∼ 0.6) with most of the secondary structures intact but with a significant loss of tertiary contacts. These structural features are characteristic of the molten globule state. However, the IU ensemble is a looser structure (Nc ∼ 0.35; Rg ∼ 1.8 nm), with significant loss of secondary and tertiary structures. FEL at higher temperatures (400 K to 500 K) exhibited broad prominent minima with RMSD > 1.5 nm and Nc ∼ 0.1, representing the unfolded (U) state of the protein (Fig. S9†). For simplicity, we have shown two FEL contour maps in each row. The first column depicts the FEL calculated as a function of the Nc and RMSD pair, whereas the second column shows the FEL against Nc and Rg. The overlap between these two plots clearly suggests excellent agreement for the reported configurations.
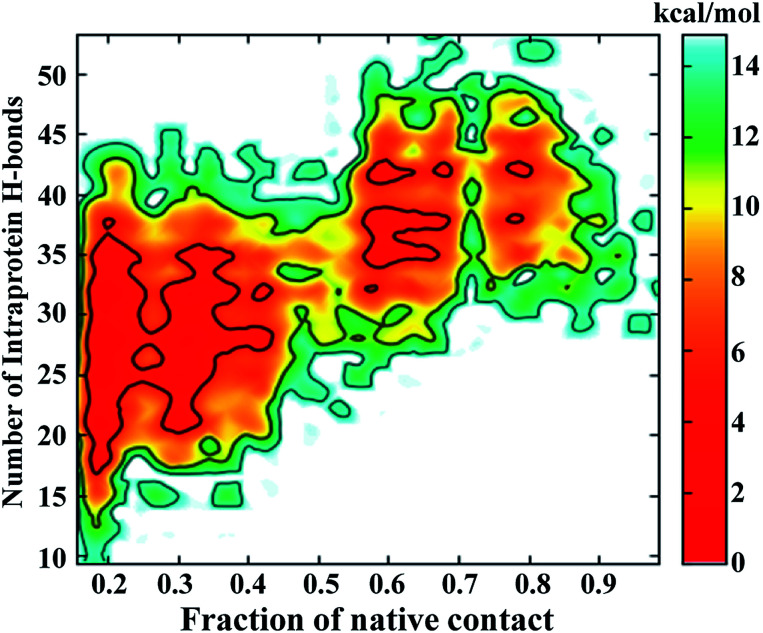
The FEL involving the number of intraprotein hydrogen bonds and the number of native contacts at 350 K is shown in Fig. 6. Remarkably, the number of intraprotein hydrogen bonds decreases from ∼40 to ∼20 along the unfolding pathway as the number of native contacts decreases from ∼70% to ∼20%. Thus, the significant decrease in non-native hydrogen bonds suggests the absence of misfolded states during the unfolding of NTD. However, at higher temperatures (400 K to 500 K), intraprotein hydrogen bonds are retained as the protein becomes completely unfolded, indicating the persistence of non-native hydrogen bonds (Figure S10†).
Fig. 6. FEL of the number of intraprotein hydrogen bonds versus the number of native contacts at 350 K.
Disruption of the hydrophobic core leads to solvent exposure of W80 during unfolding
An NMR study of the NTD (PDB ID: 2N4P)22 showed that W80 lies in the centre of the hydrophobic core of the protein and is involved in contacts with Ile17, Gly36, Tyr55, Ala75 and Tyr85. Hence, the pairwise distance distributions between these contacts were monitored during different stages of unfolding (Fig. 7). In the N state (0 to 50 ns), all the reported W80 contacts are within a distance of 0.5 nm, indicating the stability of the structure. In the IN ensemble (50–130 ns), these contacts were found to be stable up to ∼110 ns, after which the inter-atomic distances between them increased slightly; the maximum change in pair-distance was observed between W80–Y55. These results thus signify that the IN ensemble is native-like. The unfolding of IN to IU (200 to 300 ns) is accompanied by disruption of many of these contacts, with the maximum loss observed for W80–Y55. The contacts between W80–I17, W80–Y85 and W80–A75 are maintained. As unfolding progresses, the long-range contacts between W80–I17, W80–Y55 and W80–G36 are greatly disrupted. The short-range contacts between W80–Y85 and W80–A75 remain somewhat stable. As mentioned above, W80 explores both partially buried and solvent-exposed states in the IN and U ensembles, which is evident from the pairwise distance distribution among W80 contacts.
Fig. 7. Pairwise distance distribution of representative hydrophobic contacts during the simulation at 350 K.
Structural basis of the higher stability of the NTD
The intermediate state, IU, is moderately stabilized by the preservation of the intraprotein hydrogen bonds (due to the presence of intact β1 and β2 during unfolding) and the intramolecular contacts as well as the presence of partially buried non-polar residues W80 and Y55 in the side chain. To analyze the physico-chemical nature of the interacting residues, the COCOMAPS server56 was used. The inter-atomic contact maps of the NTD unfolding ensembles are shown in the ESI, Fig. S11,† where the residues are said to be in contact when at least two heavy atoms are separated by ≤5 Å.
As can be seen from the results, the contact map of N is essentially hydrophobic in nature, whereas the contacts in IU are predominantly hydrophilic in nature. The number of hydrophilic contacts in the IU ensemble is significantly higher than in the N and IN states, and the hydrophobic interactions are larger compared to the IN ensemble. In contrast, the contacts in IN exhibit equal numbers of hydrophilic and hydrophobic interactions. This result suggests that IU is stabilized by the presence of greater non-native hydrophilic–hydrophilic and hydrophobic–hydrophobic interactions. We therefore suggest that the stability of the intermediates causes NTD to be highly stable both thermodynamically and kinetically.
Distribution of frustration in the protein
The concept of frustration was originally introduced by Wolynes et al. to describe the protein folding landscape.49 According to the principle of minimal frustration, the protein folding process is considered to adopt a smooth-funneled energy landscape, avoiding energetic conflicts that exhibit frustration.57–60 However, local frustration is present in the protein to perform essential functions.61–66 In this work, we explored the relationship between non-native interactions, the presence of stable intermediates, and the residual frustration observed in the NTD.
We employed the ‘Frustratometer’ web server to compute local frustration in the native structure and the intermediates. According to the principle of minimal frustration, contacts in the native state should be minimally frustrated, i.e. energetically favorable. It has been previously shown that most of the native contacts in globular proteins are minimally frustrated (∼40%), while 10% contacts are highly frustrated in the native state.63,67 These highly frustrated contacts map to functional sites and are thought to be evolutionarily conserved.68
We calculated the configurational frustration index of the NTD, as shown in Fig. 8a. It can be seen that the NTD is less minimally frustrated compared to typical proteins. The results show that among all the native contacts, 26% are minimally frustrated (Fig. 8a, green line), compared with 37% in a typical protein, as shown by Ferreiro et al.63 However, the minimally frustrated contacts form a cluster around the protein core, as is observed in most proteins. The protein core consists of four β-sheets (β1 to β4) and an α-helix. Importantly, the highly frustrated contacts comprise 5% of the total contacts, which is less than what is expected in a globular protein (10%) (Fig. 8a, red line). A single large highly frustrated contact cluster is found in the β-hairpin region (residues 55–65) between β3 and β4. This region is unique in the NTD, and the nearby β5 strand is linked to the rest of the protein through H-bonds and hydrophobic interactions. Taken together, the NTD has fewer frustrated contacts and fewer minimally frustrated contacts, suggesting a different energy landscape compared to typical proteins.
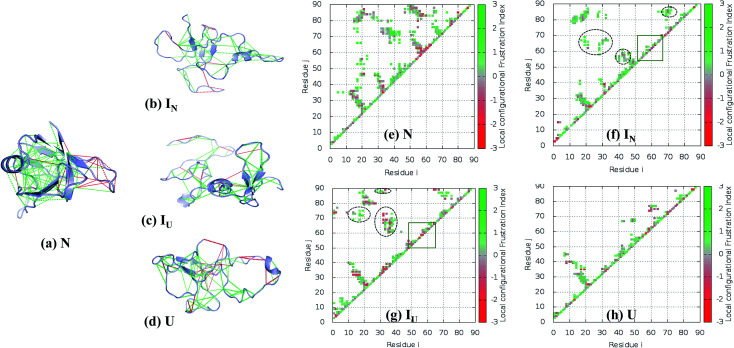
Fig. 8. Residual frustration analysis in the selected states of the NTD. (a) Local frustration is depicted on the native NTD structure (PDB : 2N4P). The large cluster of minimally frustrated interactions (green) defines the core of the protein, whereas some highly frustrated interactions (red) occur on the surface of the protein. Local frustration in the (b) IN, (c) IU, and (d) U states depicting the large changes in frustration profiles. (f–h) Contact maps of the corresponding transitions of the NTD compared with the native state, along with their frustration profiles. The distinct non-native clusters in the intermediate states are circled in black. Within the β-hairpin region (residues 55–62), many frustrated contacts remain unformed in the intermediate states (orange box). (e) Energetically favorable residue pair contacts of NTD.
The FEL of the NTD in 8 M urea at the transition temperature (350 K) indicates the presence of highly populated long-lived intermediates, IN and IU, during the 500 ns simulation run (Fig. 5a and b). The intermediate, IN, with Rg ∼ 1.3 nm is unusually compact, and the structure generally contains a three-stranded β-sheet core (β1, β2, and β6) (Fig. 8b). Meanwhile, the second intermediate ensemble, IU, contains a two-stranded β-sheet core (β1 and β2) (Fig. 8c). The IU ensemble displays a higher number of highly frustrated contacts (10%, red line) compared to IN (5%) and fewer minimally frustrated contacts (24%, green line) than IN (28%). The unfolded ensemble, U, displays more highly frustrated contacts (Fig. 8d).
To establish how the contact maps of the unfolding intermediates display residual frustration, we plotted the contact maps according to their frustration indices; these are shown in Fig. 8e–h. In the first intermediate structure, IN, residues of the α-helix (40–43) form many non-native contacts with β2 (28–29), β3 (55) and β-hairpin residues (57–59) (Fig. 8f, circled black dots) compared to the N structure (Fig. 8e). In addition, Val69 of β4 interacts non-natively with the residues of the loop region between β5 and β6 (80–84), Tyr 85 and Val 86 of β6. The residual local frustration reveals that these non-native contacts are minimally frustrated (Fig. 8b) and can stabilize the intermediate state through energetically favorable contacts that are not observed in the native state.
Similarly, the IU ensemble also displays the formation of non-native contacts between β1 (17–19) and Val69 (β4), Ile72 (β5) and Val87 (β6) (Fig. 8g, circled black dots). Also, β6 (87–88) interacts non-natively with the loop region (32–35) between β2 and the α-helix. These non-native contacts are minimally frustrated, imparting stability to the IU state. In addition to favorable interactions, IU also exhibits highly frustrated non-native contacts involving the loop region (32–39) and β-hairpin (55–65) (Fig. 8g).
Thus, whereas the core of the structure is stabilized by both native and non-native favorable interactions, the β-hairpin structure surrounding β3 and β4 does not show any particular native or non-native contacts in either IN or IU (Fig. 8f–g, orange box). Moreover, in this region, favorable interactions are absent and some highly frustrated interactions are found. We therefore expect that both the presence of local frustration and the rugged landscape of this β-hairpin region play important roles in the stabilization of the unfolding intermediates of the NTD. Indeed, this region behaves very similarly in the unfolding ensemble, as can be seen in Fig. 8h.
Conclusion
Structural integrity of the NTD is required for the proper function of TDP-43. The unfolded state of the NTD together with the disordered prion-like domain initiates irreversible aggregation of TDP-43, causing disease. A detailed account of the unfolding and thermodynamics behaviors of the NTD has been delineated using MD simulations. The cumulative data of ∼2.75 μs simulations enabled us to sample the complex conformational energy landscape of the NTD, which is characterized by the presence of multiple intermediates along the unfolded conformation at 350 K and the population of completely unfolded species at higher temperatures (400 K to 500 K). We found a rugged free energy basin surrounded by different metastable conformational states with comparable stabilities and a low energy barrier in 8 M urea at 350 K. At this temperature, we observed that during the early stage of unfolding, the initially solvent-buried W80 (and Y55) become solvent-exposed, giving rise to a native-like molten globule state, IN. IN eventually unfolds to IU, which is characterized by transitions between partial burial and exposure of W80 during unfolding, indicating conformational heterogeneity in IU. The structural plasticity of the environment around W80 in the IU ensemble results in the formation of non-native, tertiary interactions with exposure of the hydrophobic core. The secondary structure evolution also reveals the high stability of N-terminal β1 and β2 in IU and even the U ensemble. Moreover, local frustration and favorable non-native interactions stabilize the IU state. Thus, the simulation results suggest that non-native interactions along with persistence of the residual structure and hydrogen bonds during the unfolding of the NTD domain may mediate irreversible aggregation of the protein.
Conflicts of interest
The authors declare no conflict of interest.
Supplementary Material
Acknowledgments
A. P. and V. K. sincerely thank the Science and Engineering Research Board (SERB), Government of India for Young Scientist awards, YSS/2015/000228 and SB/YS/LS-161/2014, respectively. NKM is thankful to DBT, India for the fellowship (DBT/2016/JNU/695). All the authors sincerely thank SERB for the GPU computational facility (YSS/2015/000228).
Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra03368d
References
- Ling S. C. Polymenidou M. Cleveland D. W. Neuron. 2013;79:416–438. doi: 10.1016/j.neuron.2013.07.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar V. Islam A. Hassan M. I. Ahmad F. Eur. J. Med. Chem. 2016;121:903–917. doi: 10.1016/j.ejmech.2016.06.017. [DOI] [PubMed] [Google Scholar]
- Kumar V. Islam A. Hassan M. I. Ahmad F. Biochim. Biophys. Acta. 2016;1862:1742–1754. doi: 10.1016/j.bbadis.2016.06.011. [DOI] [PubMed] [Google Scholar]
- Neumann M. Sampathu D. M. Kwong L. K. Truax A. C. Micsenyi M. C. Chou T. T. Bruce J. Schuck T. Grossman M. Clark C. M. McCluskey L. F. Miller B. L. Masliah E. Mackenzie I. R. Feldman H. Feiden W. Kretzschmar H. A. Trojanowski J. Q. Lee V. M. Science. 2006;314:130–133. doi: 10.1126/science.1134108. [DOI] [PubMed] [Google Scholar]
- Lagier-Tourenne C. Cleveland D. W. Cell. 2009;136:1001–1004. doi: 10.1016/j.cell.2009.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee E. B. Lee V. M. Trojanowski J. Q. Nat. Rev. Neurosci. 2011;13:38–50. doi: 10.1038/nrn3121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cascella R. Capitini C. Fani G. Dobson C. M. Cecchi C. Chiti F. J. Biol. Chem. 2016;291:19437–19448. doi: 10.1074/jbc.M116.737726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buratti E. Baralle F. E. J. Biol. Chem. 2001;276:36337–36343. doi: 10.1074/jbc.M104236200. [DOI] [PubMed] [Google Scholar]
- Lukavsky P. J. Daujotyte D. Tollervey J. R. Ule J. Stuani C. Buratti E. Baralle F. E. Damberger F. F. Allain F. H. Nat. Struct. Mol. Biol. 2013;20:1443–1449. doi: 10.1038/nsmb.2698. [DOI] [PubMed] [Google Scholar]
- Buratti E. Adv. Genet. 2015;91:1–53. doi: 10.1016/bs.adgen.2015.07.001. [DOI] [PubMed] [Google Scholar]
- Buratti E. Brindisi A. Giombi M. Tisminetzky S. Ayala Y. M. Baralle F. E. J. Biol. Chem. 2005;280:37572–37584. doi: 10.1074/jbc.M505557200. [DOI] [PubMed] [Google Scholar]
- Kato M. Han T. W. Xie S. Shi K. Du X. Wu L. C. Mirzaei H. Goldsmith E. J. Longgood J. Pei J. Grishin N. V. Frantz D. E. Schneider J. W. Chen S. Li L. Sawaya M. R. Eisenberg D. Tycko R. McKnight S. L. Cell. 2012;149:753–767. doi: 10.1016/j.cell.2012.04.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molliex A. Temirov J. Lee J. Coughlin M. Kanagaraj A. P. Kim H. J. Mittag T. Taylor J. P. Cell. 2015;163:123–133. doi: 10.1016/j.cell.2015.09.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin H. Lim L. Z. Wei Y. Song J. Proc. Natl. Acad. Sci. U. S. A. 2014;111:18619–18624. doi: 10.1073/pnas.1413994112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C. K. Wu T. H. Wu C. Y. Chiang M. H. Toh E. K. Hsu Y. C. Lin K. F. Liao Y. H. Huang T. H. Huang J. J. Biochem. Biophys. Res. Commun. 2012;425:219–224. doi: 10.1016/j.bbrc.2012.07.071. [DOI] [PubMed] [Google Scholar]
- Zhang Y. J. Caulfield T. Xu Y. F. Gendron T. F. Hubbard J. Stetler C. Sasaguri H. Whitelaw E. C. Cai S. Lee W. C. Petrucelli L. Hum. Mol. Genet. 2013;22:3112–3122. doi: 10.1093/hmg/ddt166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romano V. Quadri Z. Baralle F. E. Buratti E. Prion. 2015;9:1–9. doi: 10.1080/19336896.2015.1011885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang L. L. Xue W. Hong J. Y. Zhang J. T. Li M. J. Yu S. N. He J. H. Hu H. Y. Sci. Rep. 2017;7:6196. doi: 10.1038/s41598-017-06263-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sasaguri H. Chew J. Xu Y. F. Gendron T. F. Garrett A. Lee C. W. Jansen-West K. Bauer P. O. Perkerson E. A. Tong J. Stetler C. Zhang Y. J. Brain Res. 2016;1647:57–64. doi: 10.1016/j.brainres.2016.04.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suzuki H. Shibagaki Y. Hattori S. Matsuoka M. Hum. Mol. Genet. 2015;24:1513–1527. doi: 10.1093/hmg/ddu563. [DOI] [PubMed] [Google Scholar]
- Budini M. Romano V. Quadri Z. Buratti E. Baralle F. E. Hum. Mol. Genet. 2015;24:9–20. doi: 10.1093/hmg/ddu415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mompean M. Romano V. Pantoja-Uceda D. Stuani C. Baralle F. E. Buratti E. Laurents D. V. FEBS J. 2016;283:1242–1260. doi: 10.1111/febs.13651. [DOI] [PubMed] [Google Scholar]
- Mompean M. Romano V. Pantoja-Uceda D. Stuani C. Baralle F. E. Buratti E. Laurents D. V. J. Biol. Chem. 2017;292:11992–12006. doi: 10.1074/jbc.M117.775965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Afroz T. Hock E. M. Ernst P. Foglieni C. Jambeau M. Gilhespy L. A. B. Laferriere F. Maniecka Z. Pluckthun A. Mittl P. Paganetti P. Allain F. H. T. Polymenidou M. Nat. Commun. 2017;8:45. doi: 10.1038/s41467-017-00062-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H. Y. Wang I. F. Bose J. Shen C. K. Genomics. 2004;83:130–139. doi: 10.1016/S0888-7543(03)00214-3. [DOI] [PubMed] [Google Scholar]
- Tsoi P. S. Choi K. J. Leonard P. G. Sizovs A. Moosa M. M. MacKenzie K. R. Ferreon J. C. Ferreon A. C. M. Angew. Chem., Int. Ed. Engl. 2017;56:12590–12593. doi: 10.1002/anie.201706769. [DOI] [PubMed] [Google Scholar]
- Wang A. Conicella A. E. Schmidt H. B. Martin E. W. Rhoads S. N. Reeb A. N. Nourse A. Ramirez Montero D. Ryan V. H. Rohatgi R. Shewmaker F. Naik M. T. Mittag T. Ayala Y. M. Fawzi N. L. EMBO J. 2018;37:e97452. doi: 10.15252/embj.201797452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C. K. Huang T. H. FEBS J. 2016;283:1239–1241. doi: 10.1111/febs.13676. [DOI] [PubMed] [Google Scholar]
- Daggett V. Levitt M. J. Mol. Biol. 1993;232:600–619. doi: 10.1006/jmbi.1993.1414. [DOI] [PubMed] [Google Scholar]
- Day R. Bennion B. J. Ham S. Daggett V. J. Mol. Biol. 2002;322:189–203. doi: 10.1016/S0022-2836(02)00672-1. [DOI] [PubMed] [Google Scholar]
- McCully M. E. Beck D. A. Daggett V. Biochemistry. 2008;47:7079–7089. doi: 10.1021/bi800118b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rizzuti B. Daggett V. Arch. Biochem. Biophys. 2013;531:128–135. doi: 10.1016/j.abb.2012.12.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazaridis T. Karplus M. Science. 1997;278:1928–1931. doi: 10.1126/science.278.5345.1928. [DOI] [PubMed] [Google Scholar]
- Daggett V. Fersht A. Nat. Rev. Mol. Cell Biol. 2003;4:497–502. doi: 10.1038/nrm1126. [DOI] [PubMed] [Google Scholar]
- Camilloni C. Rocco A. G. Eberini I. Gianazza E. Broglia R. A. Tiana G. Biophys. J. 2008;94:4654–4661. doi: 10.1529/biophysj.107.125799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding Y. Cai Y. Biopolymers. 2013;99:594–604. doi: 10.1002/bip.22220. [DOI] [PubMed] [Google Scholar]
- Dasmeh P. Kepp K. P. PLoS One. 2013;8:e80308. doi: 10.1371/journal.pone.0080308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J. Chen Y. Yang J. Hua Z. Biopolymers. 2015;103:247–259. doi: 10.1002/bip.22589. [DOI] [PubMed] [Google Scholar]
- Prakash A. Kumar V. Meena N. K. Hassan M. I. Lynn A. M. J. Biomol. Struct. Dyn. 2018:1–17. doi: 10.1080/07391102.2017.1422026. [DOI] [PubMed] [Google Scholar]
- Idrees D. Prakash A. Haque M. A. Islam A. Ahmad F. Hassan M. I. J. Biomol. Struct. Dyn. 2016;34:1987–1997. doi: 10.1080/07391102.2015.1100552. [DOI] [PubMed] [Google Scholar]
- Khan P. Prakash A. Haque M. A. Islam A. Hassan M. I. Ahmad F. Int. J. Biol. Macromol. 2016;91:1051–1061. doi: 10.1016/j.ijbiomac.2016.06.055. [DOI] [PubMed] [Google Scholar]
- Prakash A. Idrees D. Haque M. A. Islam A. Ahmad F. Hassan M. I. J. Biomol. Struct. Dyn. 2017;35:1295–1306. doi: 10.1080/07391102.2016.1179596. [DOI] [PubMed] [Google Scholar]
- Heyda J. Kozisek M. Bednarova L. Thompson G. Konvalinka J. Vondrasek J. Jungwirth P. J. Phys. Chem. B. 2011;115:8910–8924. doi: 10.1021/jp200790h. [DOI] [PubMed] [Google Scholar]
- Rocco A. G. Mollica L. Ricchiuto P. Baptista A. M. Gianazza E. Eberini I. Biophys. J. 2008;94:2241–2251. doi: 10.1529/biophysj.107.115535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hess B. Bekker H. Berendsen H. J. C. Fraaije J. G. E. M. J. Comput. Chem. 1997;18:1463–1472. doi: 10.1002/(SICI)1096-987X(199709)18:12<1463::AID-JCC4>3.0.CO;2-H. [DOI] [Google Scholar]
- Darden T. York D. Pedersen L. J. Chem. Phys. 1993;98:10089–10092. doi: 10.1063/1.464397. [DOI] [Google Scholar]
- McGibbon R. T. Beauchamp K. A. Harrigan M. P. Klein C. Swails J. M. Hernandez C. X. Schwantes C. R. Wang L. P. Lane T. J. Pande V. S. Biophys. J. 2015;109:1528–1532. doi: 10.1016/j.bpj.2015.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Best R. B. Hummer G. Eaton W. A. Proc. Natl. Acad. Sci. U. S. A. 2013;110:17874–17879. doi: 10.1073/pnas.1311599110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferreiro D. U. Hegler J. A. Komives E. A. Wolynes P. G. Proc. Natl. Acad. Sci. U. S. A. 2007;104:19819–19824. doi: 10.1073/pnas.0709915104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parra R. G. Schafer N. P. Radusky L. G. Tsai M. Y. Guzovsky A. B. Wolynes P. G. Ferreiro D. U. Nucleic Acids Res. 2016;44:W356–W360. doi: 10.1093/nar/gkw304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenik M. Parra R. G. Radusky L. G. Turjanski A. Wolynes P. G. Ferreiro D. U. Nucleic Acids Res. 2012;40:W348–W351. doi: 10.1093/nar/gks447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dasgupta A. Udgaonkar J. B. Das P. J. Phys. Chem. B. 2014;118:6380–6392. doi: 10.1021/jp410019f. [DOI] [PubMed] [Google Scholar]
- Neri D. Billeter M. Wider G. Wuthrich K. Science. 1992;257:1559–1563. doi: 10.1126/science.1523410. [DOI] [PubMed] [Google Scholar]
- Ackerman M. S. Shortle D. Biochemistry. 2002;41:13791–13797. doi: 10.1021/bi020511t. [DOI] [PubMed] [Google Scholar]
- Klein-Seetharaman J. Oikawa M. Grimshaw S. B. Wirmer J. Duchardt E. Ueda T. Imoto T. Smith L. J. Dobson C. M. Schwalbe H. Science. 2002;295:1719–1722. doi: 10.1126/science.1067680. [DOI] [PubMed] [Google Scholar]
- Vangone A. Oliva R. Cavallo L. BMC Bioinf. 2012;4(13 suppl.):S19. doi: 10.1186/1471-2105-13-S4-S19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frauenfelder H. Sligar S. G. Wolynes P. G. Science. 1991;254:1598–1603. doi: 10.1126/science.1749933. [DOI] [PubMed] [Google Scholar]
- Onuchic J. N. Luthey-Schulten Z. Wolynes P. G. Annu. Rev. Phys. Chem. 1997;48:545–600. doi: 10.1146/annurev.physchem.48.1.545. [DOI] [PubMed] [Google Scholar]
- Chavez L. L. Onuchic J. N. Clementi C. J. Am. Chem. Soc. 2004;126:8426–8432. doi: 10.1021/ja049510+. [DOI] [PubMed] [Google Scholar]
- Clementi C. Plotkin S. S. Protein Sci. 2004;13:1750–1766. doi: 10.1110/ps.03580104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferreiro D. U. Komives E. A. Wolynes P. G. Q. Rev. Biophys. 2014;47:285–363. doi: 10.1017/S0033583514000092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuglestad B. Gasper P. M. McCammon J. A. Markwick P. R. Komives E. A. J. Phys. Chem. B. 2013;117:12857–12863. doi: 10.1021/jp402107u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferreiro D. U. Hegler J. A. Komives E. A. Wolynes P. G. Proc. Natl. Acad. Sci. U. S. A. 2011;108:3499–3503. doi: 10.1073/pnas.1018980108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutto L. Latzer J. Hegler J. A. Ferreiro D. U. Wolynes P. G. Proc. Natl. Acad. Sci. U. S. A. 2007;104:19825–19830. doi: 10.1073/pnas.0709922104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gianni S. Camilloni C. Giri R. Toto A. Bonetti D. Morrone A. Sormanni P. Brunori M. Vendruscolo M. Proc. Natl. Acad. Sci. U. S. A. 2014;111:14141–14146. doi: 10.1073/pnas.1405233111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dixit A. Verkhivker G. M. PLoS One. 2011;6:e26071. doi: 10.1371/journal.pone.0026071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W. Wolynes P. G. Takada S. Proc. Natl. Acad. Sci. U. S. A. 2011;108:3504–3509. doi: 10.1073/pnas.1018983108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Husain S. Kumar V. Hassan M. I. J. Theor. Biol. 2018;449:14–22. doi: 10.1016/j.jtbi.2018.04.016. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.