A Two-Parameter Space to Tune Solid Electrolytes for Lithium Dendrite Constriction

Abstract

Li dendrite penetration, and associated microcrack propagation, at high current densities is one main challenge to the stable cycling of solid-state batteries. The interfacial decomposition reaction between Li dendrite and a solid electrolyte was recently used to suppress Li dendrite penetration through a novel effect of “dynamic stability”. Here we use a two-parameter space to classify electrolytes and propose that the effect may require the electrolyte to occupy a certain region in the space, with the principle of delicately balancing the two property metrics of a sufficient decomposition energy with the Li metal and a low critical mechanical modulus. Furthermore, in our computational prediction prepared using a combination of high-throughput computation and machine learning, we show that the positions of electrolytes in such a space can be controlled by the chemical composition of the electrolyte; the compositions can also be attained by experimental synthesis using core–shell microstructures. The designed electrolytes following this principle further demonstrate stable long cycling from 10 000 to 20 000 cycles at high current densities of 8.6–30 mA/cm² in solid-state batteries, while in contrast the control electrolyte with a nonideal position in the two-parameter space showed a capacity decay that was faster by at least an order of magnitude due to Li dendrite penetration.

Introduction

Solid-state batteries (SSBs) have emerged as paradigm-shifting technologies relative to conventional liquid electrolyte Li ion batteries.¹⁻⁴ One key difference between the two is that the pressure on most interfaces in Li ion batteries can be equilibrated through the liquid electrolyte, while SSBs without any liquid can develop a local stress field upon electrochemical decomposition. When a SSB is properly constricted mechanically, this local stress can make significant local modifications to the metastability and kinetic stability of future decompositions.^5,6 To quantify this effect, a constrained ensemble description was recently developed, where decompositions with positive reaction strains can in principle be suppressed through metastability if the local effective modulus, K_eff, is sufficiently large.⁷⁻⁹ In addition, the description also includes kinetic stability to prevent decomposition propagation through ionic passivation at the decomposition front if the local decomposition does not induce catastrophic crack propagation.^4,7K_eff (GPa) reflects the level of local mechanical constriction, with complicated contributions from the microstructure, the mechanical strength of the materials, the formation and stack pressures of battery devices, and the assembly procedures.^6,10,11 Therefore, K_eff is a local value that can only be estimated and can also vary in space throughout a SSB device. In our previous works, we swept K_eff in a reasonable range in computation to compare with experiment.

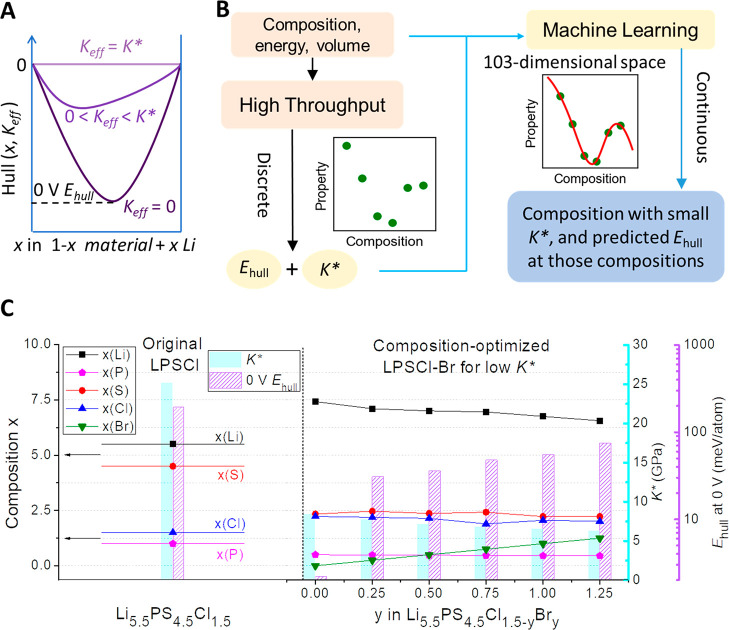
Since the Gibbs energy of the decomposition reaction, G_RXN, at the 0 V interface to the Li metal decreases in absolute value with the increasing local effective modulus K_eff, the G_RXN(x, K_eff) value will evolve from negative to zero at all possible x compositions in a pseudobinary calculation when K_eff evolves toward a critical threshold modulus, K*. We refer to E_hull as the largest magnitude of unconstrained G_RXN in this work, i.e., |G_RXN(x₀, 0 GPa)|, where x₀ gives the minimum value of G_RXN. That is to say, the decomposition can be completely suppressed through metastability, as illustrated by the zero-hull horizontal line at K_eff = K* in Figure 1A. This forms one foundation for quantitative discussion about the dynamic evolution of decomposition stabilities at the interface to the Li metal, where the dynamic stability is an experimental phenomenon found earlier.⁴

Figure 1.

The electrolyte dynamic stability design procedure and results. (A) Schematic illustration of the definition of (0 V) E_hull and K* in the reaction between a material and the Li metal. Note that E_hull will be discussed in terms of magnitude, i.e., referring to the absolute value. (B) Schematic flowchart of computational procedure. (C) Optimized compositions, decomposition energies E_hull, and critical moduli K* at various fixed Br compositions for LPSCl-Br with minimized K* (right panel). The left panel is for the values of the original LPSCl without doping or the minimization of K*. Through doping and minimization, a trend toward Li- and Cl- rich and S- and P-deficient compositions occurs.

Here, we first give a quantitative description of the varying dynamic stabilities of different electrolytes with Li dendrite, which has never before been articulated. In addition to the critical modulus K*, this dynamic stability further adds its interplay with the decomposition energy E_hull to the constrained ensemble description of mechanically constricted SSBs. On the contrary, within the constrained ensemble description, our recent model of the decomposition at 0 V interfaces for different sulfide electrolytes shows that the decomposition interphases are all electronically insulating, suggesting that electronic passivation may not be the main reason for the observed difference in the stabilities of these electrolytes at the interface to the Li metal.¹²

One important aspect of the dynamics resides in the evolution of K_eff with battery cycling at any given local spot in a SSB. Specifically, even if decomposition can happen at the surface of a local void or crack where the initial local effective modulus K_eff^min is nearly 0 GPa and thus smaller than K*, the decomposition can in principle be stopped when it fully fills the void space, because at that time further decomposition will have to experience an increased value of K_eff to overcome the local mechanical constriction from the boundary that defines the original void or crack space. Assuming that K_eff is the highest local mechanical modulus that can be increased by this process well before the generation of any new microcracks, then as long as the thermodynamic metastability condition of K_eff^max > K* can be satisfied at the time an existing void or microcrack is fully filled, the decomposition can be stopped at K_eff = K*, where K_eff < K* ≤ K_eff^max.

Since most sulfide electrolytes are unstable with Li metal at 0 V,^8,10,13 it is thus attractive to explore the possibility of using the dynamic process described above to inhibit the propagation of such interface decompositions instead of following the conventional wisdom to completely prevent the happening of the decomposition. Therefore, instead of simply looking for an electrolyte interface (electro)chemically stable to Li metal with very low or even zero interface decomposition energies, we actually welcome a certain level of decomposition. When a sufficient decomposition reaction promptly fills any local void or microcracks, either pre-existing or newly generated, to start to strongly interact with the boundary of the local space, our picture simultaneously requires that the local K_eff can be raised beyond K*, therefore immediately stopping the decomposition. This process is thus also entangled with the inhibition of crack generation and propagation, in a self-limiting way via mechanical constriction, as we will discuss in more details later. It is therefore important to design the right balance of sufficient decomposition energy and a low enough K* value so that the condition of K_eff^max ≥ K_eff > K* can be more easily satisfied during the decomposition-induced evolution of K_eff upon battery cycling, as the upper limit of local mechanical constriction K_eff is largely fixed in a particular battery design. For sulfide electrolyte SSBs, this value is around 20 GPa.^7,8,10,13

Designing electrolytes with an interface K* to Li metal well below 20 GPa thus forms one important aspect of the quantitative design of dynamic stability for Li dendrite constriction. Such a design can be realized by composition and microstructure control during electrolyte synthesis; as we will demonstrate later with detailed examples, this can be guided by high-throughput ab initio computations and machine learning approaches. It is worth noting that although the critical modulus K* here evolves from a related concept of K_crit, which we developed recently to describe the interface stability threshold at the cathode voltage,⁹ the two have some nontrivial differences, especially in connection with experimental procedures. In the case of calculating K_crit, a pseudobinary calculation was performed first to calculate the interphase formed due to chemical instability between an inorganic compound (such as a cathode) and the electrolyte to simulate the experimental step of mixing powder materials together to make electrode films. The interphase formation was thus calculated without applying an electrochemical potential or mechanical constriction. The value of K_crit in a running SSB was then determined simply by the energy cost of local pressurization that exactly canceled the decomposition reaction energy of the preformed interphase itself at a fixed x₀ composition of the preformed pseudobinary interphase. The calculation thus can be considered to be driven by an elevated voltage at K_eff = 0 GPa and did not further consider any other composition via the pseudobinary approach.

However, in this current case of calculating the critical modulus K* at the 0 V electrolyte interface to the Li metal, the approach must be modified due to our experimental design of mechanical constriction.^4,8 Since the graphite protection layer in the initial battery assembly prevents direct contact between the Li metal and the electrolyte layers, the initial chemical interphase calculation for K_crit no longer corresponds well to the experimental procedure. It is only during battery cycling that the Li metal growth related to dendrites or plating can form a contact with the electrolyte, which instead requires a pseudobinary electrochemical interface calculation between the two at 0 V. Here, to obtain the critical modulus K*, we thus require that the increased local mechanical constriction K_eff induced by decomposition can bring the Gibbs energy of the decomposition reaction to zero for all possible compositions in a pseudobinary interface calculation, as illustrated by the horizontal line at K_eff = K* in Figure 1A and described in the Experimental Section.

Although a smaller K* value can more easily satisfy the thermodynamic metastability condition in general, an additional complexity related to kinetics can still change the condition locally, which forms another important aspect in Li dendrite constriction. As mentioned earlier, both the maximum local effective modulus K_eff^max and the dynamic evolution of K_eff toward K_eff are localized and thus can vary in space in a SSB. This means that during a battery cycling the metastability condition may still be violated at certain special local spots due to inhomogeneity in the synthesis of materials, the engineering procedure, or the assembly condition of a SSB, even if a small value of K* has been designed at the electrolyte material level. At those special spots, the decomposition may not be stopped by mechanical constriction in a self-limiting way, thus potentially generating cracks. This will induce more decompositions associated with Li dendrite growth due to the fact that K_eff will drop to the minimum value immediately in any newly formed crack region. If this positive feedback loop of entangled decomposition and crack formation continues, then even a small percentage of such special initial spots will be able to generate continuous crack propagation and thus the associated Li dendrite penetration during battery cycling.

Therefore, in addition to designing a low K* value, another important aspect of the dynamic stability design is to enabling sufficient rate of interface decomposition to fill any newly formed microcracks faster than the speed of their propagation. This counterintuitive picture requires the decomposition to play the role of “concrete” or glue to promptly heal any microcracks so that crack propagation can be inhibited at the very early stage when the crack size is still very small and the propagation speed is still slow. This type of self-limiting local decomposition is especially important to inhibit those cracks generated by the stress field from the decomposition itself; otherwise, a positive feedback loop will propagate cracks to kill the battery during cycling, as observed in previous experiments triggered by Li dendrite growth.^4,14 The simplest thermodynamic quantity that can be used to indirectly estimate this kinetic effect is the absolute value of the unconstrained interface decomposition energy E_hull at K_eff = 0 GPa between the Li dendrite and the electrolyte. We expect a moderate decomposition energy, which is not too high or too low, to be designed at the interface so that sufficient decompositions are generated promptly to fill the crack while the decomposition and the value of K* are not too large to be stopped by mechanical constriction. We thus envision that an interface reaction with the combination of a low critical modulus K* and a sufficient decomposition energy E_hull will be an effective design to prevent dendrite growth and crack propagation through functional self-limiting decomposition. Therefore, the two property metrics of K* and E_hull may form a two-parameter space for the quantitative design of advanced electrolytes with an enhanced ability to constrict the Li dendrite in our dynamic picture.

In this work, we aim to provide the simplest but first quantification of the above dynamic stability picture to design such functional decomposition, using our unique high-throughput constrained pseudobinary interface computations to evaluate the K* and E_hull values of over 120 000 material interfaces to Li metal at K_eff ≥ 0 GPa on the basis of all the unconstrained ab initio energy and volume values of the over 120 000 material entries at K_eff = 0 GPa from the Materials Project. We further use machine learning to extract the information from the K* and E_hull values of all the 120 000 interphases in the broad range of K_eff ≥ 0 GPa to suggest solid electrolyte compositions that are likely to show small K* and sufficient E_hull values with Li metal (see the Experimental Section). Since the crack and decomposition related kinetics are complicated and also material-dependent, the ideal region for the E_hull value is not known a priori and is not universal. We thus take the approach of focusing on the optimization of K* and afterward examining the prediction of E_hull. Generally, sulfide electrolytes with Li-rich and S-deficient compositions that evolved from any input composition were preferred. Specifically, a composition modification of the sulfide electrolyte that can lead to K* < 20 GPa and 10 meV/atom < E_hull < 150 meV/atom will be good for the dynamic stabilities here, as estimated from the comparison of the predicted metrics in the two-parameter space with the tested performances of known electrolytes. The suggested change in composition was implemented in our experimental synthesis through the use of both doping to ensure the total composition control of the initial precursors and a core–shell strategy, where the shell composition was further modified from the core according to the predicted composition for a lower K* value.

This approach was demonstrated experimentally by doping the original electrolyte material of the Li argyrodite electrolyte Li_5.5PS_4.5Cl_1.5 (LPSCl) to form Li_5.5PS_4.5Cl_1.5–yX_y (LPSCl-X, where X = F, Br, or I and y = 0.4 or 0.15 for F or Br and I, respectively). Following our recent approach, both LPSCl and doped LPSCl-X were synthesized by solid-state reactions, and SSBs were assembled with a multilayer electrolyte configuration using graphite-protected Li metal as the anode and LiNi_0.83Mn_0.06Co_0.11O₂ (NMC811) single crystal particles as the cathode (see the Experimental Section).⁴ The control battery was made using only a single electrolyte layer of the undoped LPSCl; for comparison, the layer thickness was the same as the total electrolyte thickness of the multilayer configuration. The control battery shows a fast capacity decay in less than 1000 cycles at 8.6 mA/cm² to 80% the initial capacity. In contrast, when a central layer of LPSCl-X with the compositional modification guided by our computational design for moderate values of E_hull and low K* was inserted to form the multilayer configuration, the battery demonstrated stable cycling for over 25 000 cycles at 8.6 mA/cm² and stable cycling for 17 000 cycles at high current densities of 20 and 30 mA/cm², all of which occurred at the same cathode loading (2 mg/cm²) as the control battery. Furthermore, our designed battery can reach a cyclable current density of 43 mA/cm² or above. We thus demonstrated that the cycling stability of a SSB against lithium dendrite penetration can be improved by an order of magnitude compared with that of the control battery.

Our work thus shows that dynamic stability against lithium dendrite formation and penetration at the material level can be designed in the two-parameter space formed by the two property metrics at the interface to Li metal, namely the decomposition energy E_hull and the critical effective mechanical modulus K* , by targeting the region of moderate E_hull values and low K* values. The interplay between the two metrics in the two-parameter space thus plays an important role not only beyond the single-parameter description that focuses only on minimizing the critical modulus,⁹ but also in large contrast to the conventional strategy of minimizing the interface decomposition energy. Our two-parameter strategy here also upgrades the constrained ensemble toward a quantitative description of dynamic stability against Li metal.⁴ The goal can be reached through modifying the composition of the electrolyte as well as through modifying the composition of the electrolyte’s particle surface via chemical synthesis and sintering guided by computations. The battery cycling results suggest that our SSB, which was designed following the guidance from the two-parameter space, is not limited by the dendrite penetration-related critical current density up to at least 43 mA/cm².

Experimental Section

Density Functional Theory (DFT) Computation

The energies and volumes of LPSCl-core (Li_5.5PS_4.5Cl_1.5), LPSCl-X (Li_5.5PS_4.5Cl_1.25X_0.25, X = F, Br, I), and LGPS-core (Li₁₀GeP₂S₁₂) were calculated using DFT with the same setup as that for mp-985592 Li₆PS₅Cl in the Materials Project.

Pseudobinary Interface Computation at 0 V with DFT Data

The unconstrained (i.e., K_eff = 0 GPa) decomposition energies (E_hull) for a pseudo-phase A_xB_1–x are defined as the absolute value of hull energy, Hull(x, 0 GPa) or G_RXN (x, 0 GPa), which can be calculated by constructing phase diagram using the Python Materials Genomics library.¹⁵ At different x compositions, both the volume (V) of the pseudo phase and the reaction strain (ε) are different, and our unique constrained Hull(x, K_eff) can be calculated following the procedure from our previous works:^9,16

1

2

As a new definition in this work, we define K* as the critical K_eff when pseudo-phases at all x compositions show a zero decomposition energy at 0 V (in contrast to K_crit, which only requires the energy to be zero at x₀ of the preformed cathode interphase⁹).

3

If ε(x) ≤ 0, ε(x) will be defined to be 0 and K* will become infinite. For the situation where the material is intrinsically stable with Li, both E_hull and K* are zero by definition. The new method here, together with the machine learning model, expands the capability of the constrained ensemble prediction to the design of material (in)stabilities at 0 V to the lithium metal (dendrite) interface.

Machine Learning

Compositions, energies, and volumes of all 124 497 materials were queried from the Materials Project for our high-throughput calculations of decomposition energies (E_hull) and critical modulus (K*) values for the interfaces between the materials and the Li metal. Machine learning was applied to model the relation between macroscopic properties (composition, energy, and volume) and the target values (E_hull and K*). Machine learning models in this work are based on decision trees. A decision tree consists of hierarchical computation (decision) nodes. The data were input into the decision trees in the form (X, y) = ({x₁ ,x₂, ..., x_n }, y), where x_i are the features and y is a target value. Tree optimization includes choosing both the feature and the threshold for the criteria of each node that overall best split the set of items. Instead of measuring the error, better metrics such as the cross entropy and the Gini index are generally used to measure the goodness of the choice of criteria and the data split.¹⁷ Our input features consist of 103 dimensional composition vectors for the first 103 elements in the Periodic Table up to lawrencium (Lr). The composition vector is normalized with the sum equals to one. Specifically, for K* at 0 V, we also include values of x from 0 to 0.9 in our input for a better learning result. The target y was chosen as K* and the decomposition energy at different situations. For K* at 0 V, the target y is the K* at the corresponding x.

We split the data into 80:20 training and validation sets. For both K* and E_hull, our models achieved low training errors and comparable validation errors; more details are provided in the Supporting Information. The composition–target quantity relation was fit well, with little overfitting. Using the trained models with the target property y, we can predict the value of y at unknown compositions. Optimizations with fixed amounts of F, Br, or I, shown in Figures 1C and S2, include a 50% relative compositional change constraint on each element to avoid extinction of certain elements. Since most compounds are unstable with Li metal, the zero hull energy data are insufficient in the training set and thus the machine-learning-predicted zero hull energy reference has to be calibrated using DFT. LiCl shows a ∼0 eV decomposition energy with Li metal in DFT binary calculations (Figure S1), and the predicted decomposition energy for Li_0.49Cl_0.49S_0.01P_0.01 is 0.915 eV; thus, the decomposition energy is shifted down by 0.915 eV in Figures 1C, S2, and S7.

Synthesis of Materials

Li_5.5PS_4.5Cl_1.5, Li_5.5PS_4.5Cl_1.1F_0.4, Li_5.5PS_4.5Cl_1.35Br_0.15, and Li_5.5PS_4.5Cl_1.35I_0.15 were prepared by ball-milling and solid-state reactions. Stoichiometric amounts of Li₂S (99.9% purity, Alfa Aesar), P₂S₅ (99% purity, Sigma-Aldrich), LiF (>99% purity, Sigma-Aldrich), LiBr (>99% purity, Sigma-Aldrich), LiI(>99.9% purity, Sigma-Aldrich), and LiCl (>99% purity, Alfa Aesar) were weighted and milled for 16 h under argon protection. The precursor was transferred into a quartz tube and annealed at 550 °C for 1 h in an argon gas flow, with a heating rate of 5 °C/min and a cooling rate of 1 °C/min. LGPS (325 mesh) was purchased from MSE.

Scanning Electron Microscopy–Focused Ion Beam–Energy Dispersive Spectroscopy (SEM-FIB-EDS)

SEM-FIB-EDS was conducted on a FEI Helios 660 instrument. Solid-state electrolyte powder was dispersed onto carbon tape, which was then attached to a SEM stub. The sample was sealed in a plastic box in the glovebox with O₂ and H₂O < 0.1 ppm. The sample was quickly transferred to the SEM within ∼15 s to minimize the air exposure. The acceleration voltage was 10 kV, and the magnification was 10 000×. The solid electrolyte particle was etched by the focused ion beam, and the EDS line scan was conducted on the cross section of the particle after the etching.

X-ray Photoelectron Spectroscopy (XPS)

XPS samples were mounted onto the vacuum transfer module of a Thermo Scientific K-Alpha+ instrument to avoid any air exposure. XPS was performed with a beam size of 400 μm except for the cross section measurement shown in Figure 6, which was performed at 70 μm. Ar⁺ ion-milling was performed in the monoatomic mode with an ion energy of 1000 eV, which was estimated to mill Ta₂O₅ with a ∼140 GPa bulk modulus at 0.26 nm/s. Since LPSCl-based compounds have bulk moduli ∼20 GPa, which is 1/7 that of Ta₂O₅, the milling speed for LPSCl-X was estimated to be 7 × 0.26 nm/s = 1.82 nm/s, consistent with SEM-FIB-EDX results. The survey spectrum was used for quantification. All XPS results were fitted through peak differentiation and imitation via Avantage.

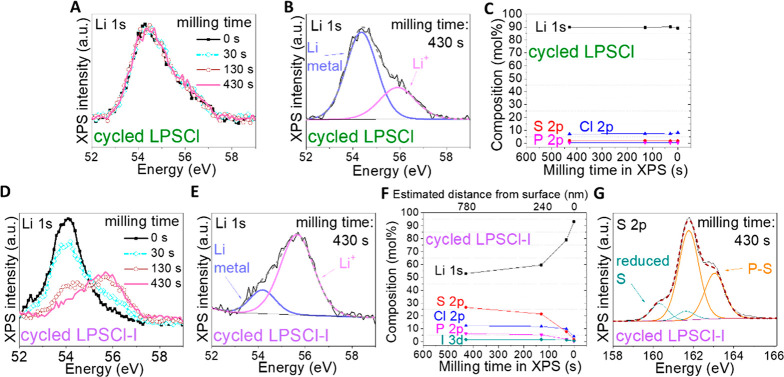
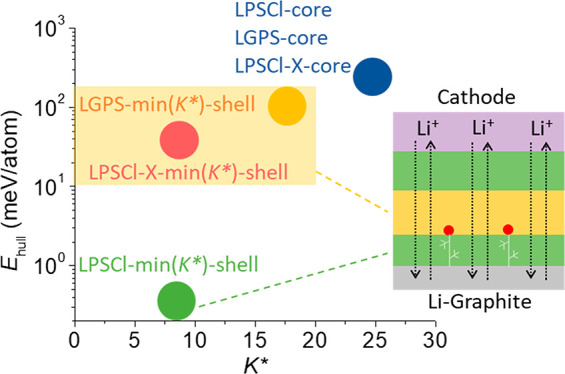
Figure 6.

XPS depth profile measurement of the cross sections of cycled battery pellets by in situ ion milling. For cycled LPSCl in the Li-G|LPSCl|811 battery ran at 8.6 mA/cm²: (A) Li 1s XPS at different milling times, (B) Li 1s XPS refinement of the sample milled for 430 s,; and (C) XPS quantification of elemental compositions at different ion-milling times. For cycled LPSCl-I in the Li-G|LPSCl|LPSCl-I|LGPS|811 battery run at 30 mA/cm²: (D) Li 1s XPS at different milling times, (E) Li 1s XPS refinement of the sample milled for 430 s, (F) XPS quantification of elemental compositions at different ion-milling times, and (G) S 2p XPS refinement of the sample milled for 430 s.

X-ray Diffraction (XRD)

XRD data were obtained using a Rigaku Miniflex 6G instrument. Powder samples were sealed with Kapton film in an argon-filled glovebox to prevent air contamination.

Electrochemistry

Solid-state batteries were made with the configuration of Li/graphite–LPSCl–central layer–(separating layer)–cathode matrix. The Li metal foil with a 0.63 cm diameter and a 25 um thickness (0.42 mg, 1.62 mAh, 5.2 mAh/cm²) was covered by a graphite thin film with a 0.95 cm diameter, which acted as the anode. The graphite layer was made by mixing 95 wt % graphite (BTR, China) with 5 wt % PTFE, and the capacity ratio of lithium to graphite was 2.5:1. For the electrolyte, 30 mg of LPSCl (120 μm thickness) and 100 mg of the central layer powder (400 μm thickness) were applied. A 60 mg separating layer (240 μm) of the same electrolyte powder in the cathode matrix was added when the central layer was different than that in the cathode matrix. Following a previous report, 1.9 wt % LiNbO₃ was coated on LiNi_0.83Mn_0.06Co_0.11O₂ (NMC811) (MSE Supplies).¹⁸ To serve as the cathode, 70 wt % bare 811 or LNO@811 was mixed with 30 wt % LPSCl or LGPS; an additional 3% PTFE was added to make a cathode film. The loading of the cathode was kept at 2 mg/cm² for all the battery tests. The battery was initially pressed at 460 MPa, and a stack pressure of 250 MPa was maintained by a pressurized cell. The batteries were cycled at 55 °C on an Arbin battery testing station in an environmental chamber with the humidity controlled at <10% inside a Memmert hpp110 system (Figures 4 and 5C–F), on a Solartron 1400 cell test system (Figure 5A and B), or on an LANHE battery test system (Figure 4B and D, green cycling curve). In this work, 1 C-rate = 150 mA/g. At the cathode active material level in Figure 5, the gravimetric energy density at 20 C-rate reaches 450 Wh/kg (3.53 V average discharge voltage) and that at 0.5 C-rate reaches 774 Wh/kg (3.80 V average discharge voltage).

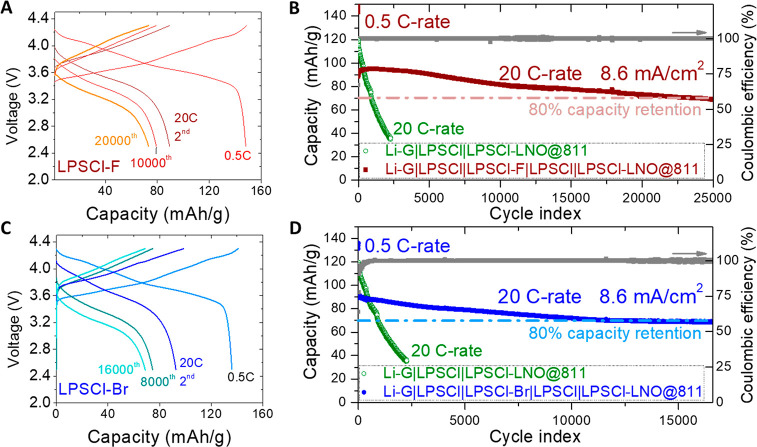
Figure 4.

Stable cycling of SSBs using composition-modified LPSCl-X with a reduced-shell critical modulusK*. The charge–discharge voltage curves and cycling performance, respectively, of SSBs designed using (A and B) LPSCl-F or (C and D) LPSCl-Br as the central electrolyte layer in the multilayer configuration. All batteries were cycled at 55 °C with LPSCl-X as the central layer sandwiched by LPSCl layers on both sides and using a LiNbO₃-coated NMC811 (LNO@811) cathode paired with a Li–graphite composite anode (Li-G). Battery configurations are shown in panels B and D. The cycling of the battery without the LPSCl-X central layer (green), whose electrolyte layer was the same thickness as that in the multilayer configuration for a fair comparison, is shown as a control.

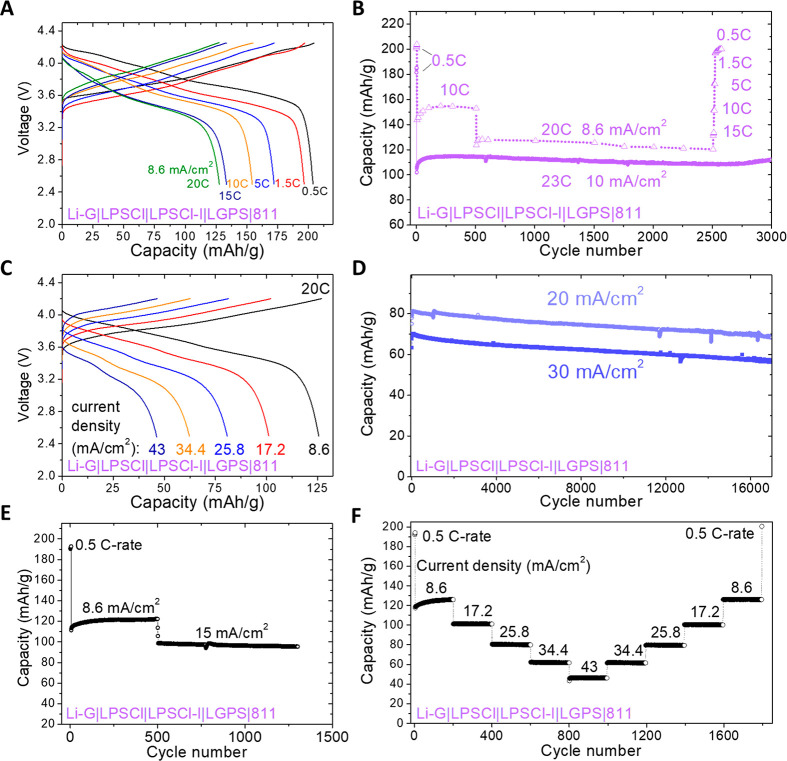
Figure 5.

High-capacity and high-rate capability of LPSCl-I|LGPS-based multilayer batteries. (A) Charge–discharge voltage curves measured at different rates for the LPSCl-I|LGPS|811 battery with the configuration described at the bottom of the panel. (B) Cycling performance at different C-rates from 0.5 to 20 C (8.6 mA/cm²) and that of a different battery for long-cycling at 10 mA/cm². (C) The charge–discharge voltage curves at extremely high current densities up to 43 mA/cm². (D) High-current-density long cycling performance at 20 and 30 mA/cm². (E) The battery cycling history before the 20 mA/cm² long cycling in panel D. (F) The battery cycling history before the long cycling at 30 mA/cm² in panel D.

Results and Discussion

The Electrolyte Dynamic Stability Design in K*-E_hull Space

As already mentioned in the introduction, Figure 1A illustrates the definitions of the decomposition energy E_hull and the critical modulus K* at 0 V that will be determined by our unique constrained pseudobinary interface simulations. The reaction energies G_RXN (the hull energy) at different mixing ratios (x) between a material and the Li metal were calculated at different local effective moduli K_eff (see the Experimental Section). The absolute value of the largest hull at a given value of K_eff is defined as 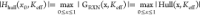. At K_eff = 0 GPa, we define E_hull = |H_hull (x₀, 0 GPa)|. For a reaction with positive reaction strain ε(x), increasing the value of K_eff can decrease the value of |Hull(x, K_eff)|; thus, there exists a critical value of K_eff at which all hull values become zero (the K_eff = K* line in Figure 1A). This defines the critical modulus K* as a function of the unconstrained hull energy Hull(x, 0 GPa), the reaction strain ε(x), and the reaction volume V(x) of the pseudobinary interphase, where 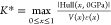. Two specific computational examples are provided in Figure S1. Therefore, although in general K* increases when E_hull increases, there is not a simple analytical relationship between K* and E_hull due to the fact that the x value that maximizes |Hull(x, 0 GPa)| may not simultaneously minimize V(x)ε(x). However, both parameters K* and E_hull are nevertheless deterministically calculated by our constrained pseudobinary approach, as described in the Experimental Section.

Figure 1B shows our computational design procedure for new compositions with lower values of K*. Using the material information on the composition, energy, and volume at unconstrained condition of K_eff = 0 GPa obtained from ab initio DFT simulations of the Materials Project, the decomposition energy E_hull at 0 V was calculated as a function of K_eff ≥ 0 GPa and the critical modulus K* was determined for 124 497 materials at the interface to the Li metal (see the Experimental Section for computational details). By applying machine learning to model the macroscopic properties of composition and energy and the target values of E_hull and K*,¹⁷ we were able to learn a relation from the discrete data points in the high-dimensional parameter space generated by high-throughput calculations. The relation can be further extrapolated to a continuous compositional space to perform composition optimizations toward smaller values of K* for any composition as the input.

Figure 1C shows the machine learning prediction of the composition change required to minimize the critical modulus K* for LPSCl-Br as an example. Compared with the original LPSCl composition, minimizing K* by changing the composition without doping any new elements (y = 0.00) can already reduce K* from 25.1 to 8.4 GPa, where the two main elements in the LPSCl composition are optimized to be S-deficient and Li-rich compared with the original one. Further doping Br by changing the composition (y) from 0 to several fixed values from 0.25 to 1.25 and minimizing K* increases the decomposition energy E_hull from 0 meV/atom to a moderate range of 30–75 meV/atom (still much lower than 237 meV/atom for the original LPSCl predicted by machine learning). This is associated with minor composition changes of other elements, while K* is still minimized to be around 10 GPa. Note that the 0 eV reference state for the decomposition energy with the Li metal in machine learning was aligned with the DFT result based on LiCl, which is stable at 0 V (see the Experimental Section and Figure S1). Similar compositional trends for reduced values of K* and moderate values of E_hull were also predicted for LPSCl-I and LPSCl-F (Figure S2).

Thus, in Figure 2 we summarize the distribution of several relevant electrolyte compositions in the phase space formed by K* and E_hull predicted by machine learning. The original LPSCl, Li₁₀GeP₂S₁₂ (LGPS), and LPSCl-X (X = F, Br, or I) compositions without K* minimization (the “core” ones in Figure 2) all show similar values of K* and E_hullthat occupy the region of high K* > 20 GPa and very high E_hull > 150 meV. This means if these electrolytes are synthesized into homogeneous particles based on the nominal composition in the chemical formula, they may not provide good dynamic stability. In contrast, the composition-modified LPSCl, LGPS, and LPSCl-X based on the machine learning minimization of K* (the min(K*)-shell ones in Figure 2) move toward the lower K* direction in the phase space, with a composition modification toward being Li-rich and S-deficient compared with the original (see the caption of Figure 2 for modified chemical formulas).

Figure 2.

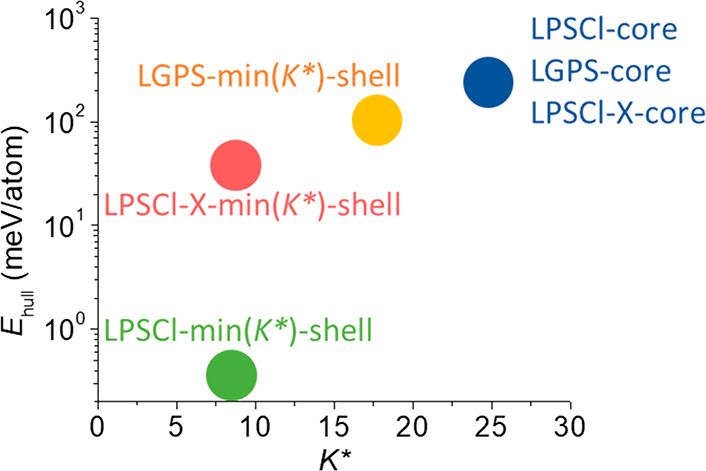
The distribution of a few representative electrolyte compositions in theK*–E_hull space. The central region in the space around LPSCl-X-min and LGPS-min should be targeted in the design and synthesis of the electrolyte. LPSCl-core and LGPS-core were predicted by machine learning from the nominal precursor compositions, i.e., the original composition of Li_5.5PS_4.5Cl_1.5 and Li₁₀GeP₂S₁₂, respectively, without minimizing K*. LPSCl-X-core includes the original compositions of Li_5.5PS_4.5Cl_1.1F_0.4, Li_5.5PS_4.5Cl_1.35Br_0.15, and Li_5.5PS_4.5Cl_1.35I_0.15. LPSCl-min(K*)-shell was predicted from the machine learning minimization of K*, with the LPSCl-core composition of Li_5.5PS_4.5Cl_1.5 as the initial input and the Li_7.4P_0.5S_2.3Cl_2.2 composition as the output. LGPS-min(K*)-shell was minimized from the LGPS-core original composition to give the modified composition of Li_14.2Ge_0.9P_1.8S₈. The region of LPSCl-X-min(K*) includes the minimizations from the LPSCl-X-core compositions (X = F, Br, and I), giving Li_7.9P_0.5S_3.1Cl_0.7F_0.25, Li_7.1P_0.5S_2.4Cl_2.2Br_0.375, and Li_7.2P_0.5S_2.3Cl_2.2I_0.375, respectively.

As we will show in the next section, the general trend of composition change suggested by these minimized compositions can be synthesized in the shell region of the particle, while the original nominal composition will form the main electrolyte phase in the core region of the particle. With a reasonable composition constraint in the range of 20–50% for the elements that is largely consistent with our X-ray photoelectron spectroscopy (XPS) and energy dispersive spectroscopy (EDS) experimental quantifications, the machine learning minimization brings the shell compositions of both LPSCl-X and LGPS to the central space region of K* < 20 GPa and E_hull = 10–150 meV. Since we know from previous experiments that LGPS can provide good dynamic stability against Li dendrite penetration as the central layer in the multilayer configuration,⁴ the LPSCl-X of interest here may also give a superior dynamic stability. The minimization of undoped LPSCl, however, gives a very low value of E_hull (Figure 2), which could lead to insufficient decomposition such that the crack propagation cannot be prevented promptly. Note that the X compositions chosen for LPSCl-X and fixed during minimization were estimated from the XPS elemental quantifications shown in Figures 3B and S3. Therefore, based on our dynamic stability picture, the K*-minimized LPSCl-X compositions with F, Br, and I doping are likely to show low K* and sufficient E_hull values for enhanced dynamic stability to suppress the Li dendrite penetration during battery cycling.

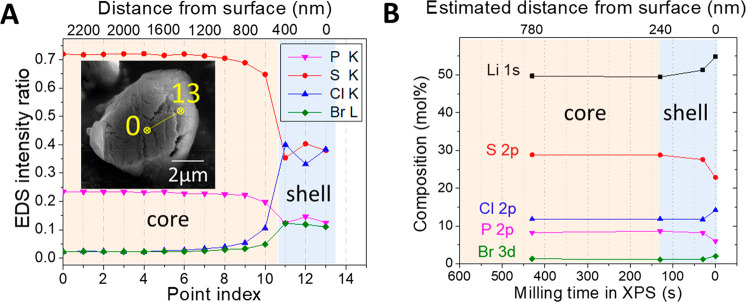
Figure 3.

Composition characterizations of the core–shell structure in LPSCl-Br particles. (A) SEM-EDS intensity ratio profile. The inset shows the line profile scanned from the cross section of a particle milled from FIB. (B) XPS depth profile quantification of elemental compositions at different times of the in situ ion-milling.

Composition Control and Core–Shell Microstructure

Starting from the composition suggested by our computational design for the chemical synthesis of LPSCl-X by solid-state reactions (see the Experimental Section), we find that the synthesized electrolytes have a core–shell microstructure. For example, the core–shell structure of LPSCl-Br was demonstrated by both EDS linescan from cross sections of particles milled by FIB in SEM and XPS depth profile from particles milled by in situ ion beams (Figure 3). The EDS line profile in Figure 3A shows that the LPSCl-Br shell is P- and S-deficient and Cl- and Br-rich. Figure 3B shows the XPS quantification of elemental compositions at different ion-milling depths, showing a consistent core–shell compositional trend similar to that of EDX. XPS also shows an additional information on the Li richness of the shell. The XPS depth profile shows the average shell thickness for all particles, which was estimated to be ∼240 nm (see the Experimental Section). This is largely consistent with the shell thickness determined from the SEM-EDS characterization. Similar trends were also found in LPSCl-F and LPSCl-I (Figure S3). The raw XPS data are shown in Table S1. Note that our XPS samples were transferred in an airtight sample holder from the glovebox to the XPS chamber to prevent air contamination.

The shell compositional changes are consistent with the predicted trend from minimizing the critical modulus K* (Figures 1C, and S2). This suggests that during high-temperature synthesis, the relatively low surface tension may also play the role of the surface effective modulus K_eff^s, which can minimize the surface critical modulus K*^,s through a composition gradient because having a stable surface during synthesis should satisfy K*^,s < K_eff. The X-ray diffraction (XRD) patterns, optical photos, and SEM images in Figures S4 and S5 show that LPSCl-X have the same F4̅3m space group as the parent LPSCl and have similar particle sizes. Note that although LPSCl-F and LPSCl-I have certain impurity phases, our electrolyte design to minimize K* (Figure 2) is based only on the machine learning of compositional information, regardless of the crystal phases.

Note that our EDS and XPS analyses of the original LPSCl without doping also show a core–shell structure, with a shell region that has a Li-rich and S-deficient composition (Figure S6). Due to the much lower E_hull value suggested by machine learning predictions at y = 0.00 for undoped LPSCl after K* minimization (Figures 1C, right panel, and 2), the shell composition of LPSCl is likely to be much more stable with Li metal than the core. This may explain previous experiments that showed the Li argyrodite electrolyte with a slightly lower Cl composition (i.e., Li₆PS₅Cl) than the LPSCl here (i.e., Li_5.5PS_4.5Cl_1.5) can also cycle in a direct contact with the Li metal,^2,12,19,20 which cannot be explained by the high E_hull value predicted based on the core composition (Figures 1C, left panel, and 2). This can also explain our previous findings^4,12 that LPSCl is more suitable than Li₆PS₅Cl to serve as the bottom layer in a direct contact with the Li–graphite composite layer in the multilayer configuration during battery cycling, most likely due to the lower E_hull value and thus the enhanced (electro)chemical stability of the LPSCl shell composition predicted here. Based on the picture of dynamic stability as elaborated in the introduction, however, the too low E_hull value of the LPSCl shell (Figure 2) may not be able to provide a sufficient rate of decomposition to promptly heal the microcracks, which is consistent with the cracks generated after battery cycling observed by SEM in our previous works.^4,12 LPSCl is thus not suitable to serve as the central electrolyte layer that requires dynamic stability to constrict the Li dendrite through localized self-limiting decomposition, while Li₆PS₅Cl is more suitable to do so due to the enhanced value of E_hull. The analysis here thus suggests that the borderline E_hull value of the Li₆PS₅Cl shell composition may be the reason that it can work as either the bottom or central layer electrolyte in the multilayer configuration¹² as well as the single layer electrolyte, although for the same reason its performance in either layer cannot be compared with the best multilayer configuration.

We note that LGPS also showed a Li-rich and S-deficient shell during our XPS analysis (Figure S7), consistent with the predicted compositional trend toward a lower K* value and a moderate E_hull value (Figures 2 and S7). This is also consistent with previous DFT and experimental findings that, despite being less stable with Li metal,^4,8,21 the LGPS used in our work can play a critical role in inhibiting Li dendrite growth as the central electrolyte layer through localized decompositions in a multilayer configuration of SSB.⁴ Furthermore, based on the compositions analyzed from their shells, LGPS and LPSCl-X were predicted by our machine learning platform to have K* and E_hull values in nearby regions in the two-parameter space in Figure 2, suggesting that, just like LGPS, LPSCl-X may also serve as a good central layer in the multilayer configuration to arrest Li dendrite growth through dynamic stability.

To test these different stabilities predicted above with the core–shell LPSCl as the control to the core–shell LGPS and the doping-induced core–shell LPSCl-X, we deposited Li metal to the electrolyte through discharge in an asymmetric battery assembly with the multilayer configuration of Li metal, followed by graphite (G), then LPSCl, then LGPS, then finally an electrolyte of interest here (LPSCl, LGPS, or LPSCl-X), i.e., Li-G|LPSCl|LGPS|electrolyte. The thin graphite layer was added between the Li metal and LPSCl to improve the interface chemical and mechanical stability during initial battery assembly.^5,8Figure S8 shows the XPS spectra and visual comparisons between the Li-deposited LPSCl, LPSCl-X, and LGPS. XPS analysis shows that the decomposition is the weakest for the Li-deposited LPSCl, while decomposition becomes stronger for LPSCl-X and LGPS, consistent with our E_hull and K* predictions in Figure 2.

Therefore, we successfully synthesized the suggested compositions for the shell of the core–shell LPSCl-X and LPSCl particles. The shell composition transforms LPSCl to be more stable with Li metal, but insufficient decomposition, likely due to the very low value of E_hull, makes it suitable only as the bottom layer near the anode in the multilayer configuration. In contrast, the moderate E_hull value of the shell composition makes the doping-induced core–shell LPSCl-X show sufficient decomposition despite being less stable with the Li metal, similar to LGPS.⁴ However, the decomposition of LPSCl-X at 0 V, like that of LGPS, could be stopped by mechanical constriction due to the lower critical modulus (K*) of the shell, making it a superior candidate as the central layer for stable battery cycling.

Superior Electrochemical Performance from Electrolyte Design

We first tested a control battery of Li-G|LPSCl|LNO@NMC811 with LiNbO₃ (LNO)-coated single-crystal particles of NMC811,¹⁸ or simply 811 embedded in LPSCl. It showed a high discharge capacity of 120 mAh/g at 20 C-rate; however, capacity decayed quickly within 1000 cycles to 80% of the initial high-rate capacity (Figure 4B and D). This is very possibly due to the decomposition and crack propagation induced by Li dendrite growth that was not self-limited .⁴ Moreover, many other Li-G|LPSCl|LNO@NMC811 batteries fail more often during the initial charging, with the signature phenomenon of a voltage sudden drop followed by a noisy voltage curve indicating shorting caused by Li dendrite penetration (Figure S9). To test the designed dynamic stability to LPSCl-X, we then inserted a layer of LPSCl-X to separate the single LPSCl layer into two layers, on each at the anode and cathode regions, and make the multilayer battery assembly Li-G|LPSCl|LPSCl-X|LPSCl|LNO@811, which hereafter is called the LPSCl-X battery. Note that for a fair comparison we made sure the total electrolyte thickness of the multilayer region of LPSCl|LPSCl-X|LPSCl was the same as that of the single LPSCl layer in the control battery. As shown in Figure 4, all LPSCl-X (X = F and Br) batteries were tested for five initial cycles at 0.5 C-rate, and subsequent cycles were at 20 C-rate (8.6 mA/cm²). The voltage and capacity decayed very slowly over 25 000 and 16 600 cycles for the LPSCl-F and LPSCl-Br batteries, respectively, with high Coulombic efficiencies (low Coulombic inefficiency mainly on the order of 10^–4–10^–3 as shown in Figure S10). Thus, we demonstrated that the cycling stability is improved by at least 10× when LPSCl-X was used as the central layer with moderate E_hull and low K* values in the shell compared to the LPSCl control with low E_hull and K* values in the shell. Note that the cycling stability of LPSCl-X here is on the same order as that of LGPS but was slightly higher, as the central layer ended at 10 000 cycles at the same rate.⁴ This is likely also due to battery assembly and cathode material differences in addition to the slight difference between the two electrolytes.

Here, we further introduce LGPS to the cathode layer, as we find that NMC811 paired with LGPS gives higher discharge capacities than NMC811 with LPSCl at a 2 mg/cm² cathode loading. However, the cathode interface stability is not the focus of the current work. Here, we simply combine this new cathode layer with an iodine-doping-induced core–shell LPSCl-I central layer in the multilayer configuration of Li-G|LPSCl|LPSCl-I|LGPS|811, called the LPSCl-I|LGPS|811 battery, to make a systematic demonstration of the stable cycling that can be reached by such a design at very high current densities. The battery degradation accelerated by long cycling periods and high current densities also help our following XPS analysis by magnifying signal changes by the cycling. Figure 5A shows the voltage curves at different rates, with a 128 mAh/g capacity at 20 C-rate. Figure 5B shows the cycling performance at different rates from low rates to high rates and then back to low rates. At 0.5 C-rate, the battery exhibited high discharge capacities near 200 mAh/g for five cycles before the rate was increased. Figure 5B also shows the cycling performance of another battery directly ramped up to 23 C-rate (10 mA/cm²). Figure S11 shows the low-rate cycling performance over 950 cycles.

We then used the highest capacity configuration of LPSCl-I|LGPS|811 to investigate the long cycling stability at extremely high rates. Figure 5C shows the initial cycle voltage profiles at different rates up to 43 mA/cm². Two batteries were cycled at 20 mA/cm² with an 81 mAh/g capacity and at 30 mA/cm² with a 70 mAh/g capacity, respectively, for 17 000 cycles (Figure 5D). The former battery was cycled at 8.6 mA/cm² for 500 cycles and at 15 mA/cm² for 800 cycles (Figure 5E) before the long cycling, while the latter was cycled at various current densities (Figure 5F) from 0.215 mA/cm² to a very high rate of 43 mA/cm² and back to 0.5 C, for 1800 cycles in total before the long cycling. It reached 101 mAh/g at 17.2 mA/cm², 81 mAh/g at 25.8 mA/cm², 62 mAh/g at 34.4 mA/cm², and 46 mAh/g at 43 mA/cm², and all capacities could be recovered back to low current densities. Figure S12 shows that the Coulombic inefficiencies of the two batteries are on the order of 10^–3.

Note that all these cycling tests were performed at a low cathode loading of 2 mg/cm². The goal was to demonstrate and assist the fundamental understanding that Li dendrite penetration can be inhibited at the material level by the dynamic stability design of the central electrolyte layer; if the wrong central electrolyte layer is used, such as the undoped LPSCl, the cycling performance is degraded by orders of magnitude even at the same low cathode loading. That said, we also think that a high cathode loading will complicate the discussion. For example, a high cathode loading will likely cause cracks to form in the electrolyte layers due to the high thickness and hence magnified geometric inhomogeneity of the plated lithium metal at the anode side during cycling rather than the microcracks caused by lithium dendrite penetration and the related electrochemical decomposition of interest here. The latter scenario from lithium dendrite formation and penetration is the focus in this work that can be controlled by the electrolyte chemistry as we demonstrated, while the former from thick lithium plating at a high cathode loading relies more on the design of battery device, especially at the anode side, which is an important direction to further explore in the future.

To more directly analyze and compare the self-limiting decompositions of LPSCl and LPSCl-X, SEM was used to observe the cross section of cycled cells, as shown in Figure S13. For LPSCl, large pores and an interconnected microcrack network were observed in the control battery of Li-G|LPSCl|LNO@811 cycled at 8.6 mA/cm² for around only 2500 cycles (Figures 4B and D and S13a2 and a4). On the contrary, the LPSCl-Br layer of the LPSCl-Br battery cycled at 8.6 mA/cm² for around 17 000 cycles (Figure 4CD, Figure S13b₂) and the LPSCl-I layer of the LPSCl-I|LGPS|811 battery cycled at 30 mA/cm² for around 17 000 cycles (Figure 5D, Figure S13c₂) were much more compact and had obviously lower amounts of large cracks. This is consistent with our picture described above about the dynamic stability design.

We further performed XPS for the central layer in the cross section of the battery pellet of the control battery Li-G|LPSCl|LNO@811 cycled at 8.6 mA/cm² after 2000 cycles (Figure 4BD) and for that of the Li-G|LPSCl|LPSCl-I|LGPS|811 battery cycled at 30 mA/cm² after 17 000 cycles (Figure 5D). For the control battery, the Li 1s peaks at different ion-milling durations are shown in Figure 6A, indicating there were very limited changes over the milling time. Figure 6B shows the refinement of the Li 1s peak at the 430 s milling time, which can be decomposed to a large peak at 54.4 eV and a peak at 55.9 eV. The 54.4 eV large peak can be assigned to Li metal,²² and the binding energy of 55.9 eV is the same as that of the Li 1s peak in the pristine LPSCl core (Table S1). The elemental compositions of the cycled LPSCl at different milling times are shown in Figure 6C, indicating negligible change over time with a high Li composition of around 90%. The large Li metal 1s peak and the abnormally high Li composition throughout milling indicate that a large amount of Li metal penetrated through the cracks distributed in the entire LPSCl layer and dominated the XPS signal at all milling depths. Meanwhile, this also means that the decomposition of the Li metal by LPSCl was insufficient. The XPS results here, together with the SEM crack morphology images (Figure S13a4), supports the prediction from our picture that the too low E_hull value of LPSCl (Figure 2) is not able to suppress Li dendrite penetration and entangled crack propagation through localized self-limiting decompositions.

In contrast, the XPS Li 1s peaks are shown in Figure 6D for the Li-G|LPSCl|LPSCl-I|LGPS|811 battery, where the intensity at around 54.4 eV decreases and the intensity at around 55.9 eV increases over the milling process. Similar to Figure 6B, the Li 1s peak of cycled LPSCl-I can also be decomposed to a Li metal peak and a Li⁺ peak with the same energy as the pristine LPSCl-I core (Figure 6E), suggesting that the Li metal composition within the total Li element decreases with milling. Figure 6F shows the elemental composition of cycled LPSCl-I, with a decreasing trend of Li and an increasing trend of all other elements toward a composition similar to that of the LPSCl-I core. The decreasing Li metal peak in the Li 1s spectrum and the decreasing Li composition over the milled depth profile indicate that Li dendrite formation and penetration was significantly suppressed and largely localized in the shell region of LPSCl-I. Furthermore, in contrast to the LPSCl S 2p XPS spectrum (Figure S14b), the S 2p XPS refinement spectrum of the sample of LPSCl-I milled for 430 s, shown in Figure 6G, indicates that the S element in cycled LPSCl-I was partially reduced, which should be caused by the decomposition of Li metal and LPSCl-I that happens when Li dendrite tries to penetrate but both decomposition and Li penetration are quickly suppressed and locally constricted by the shell region of LPSCl-I. This result supports our picture and prediction that LPSCl-X with moderate E_hull and low K* values can effectively arrest Li dendrite through self-limiting localized functional decompositions. The evolution of other elements related to Figure 6 can be found in Figure S14.

Conclusion

The work here further develops the constrained ensemble description of SSBs for a more quantitative design of electrolyte materials with dynamic stability against Li dendrite penetration by introducing for the first time the interplay between the critical modulus and the decomposition energy in the two-parameter space. The design combines high-throughput constrained pseudobinary interface computations, machine learning, and experimental synthesis to fine-tune the composition and microstructure of SBBs in the phase space formed by the critical modulus K* and the decomposition energy E_hull at the interface to the Li metal. We demonstrate that the combination of moderate E_hull and low K* values is the key design principle for electrolytes with the dynamic stability to serve as the central layer in the multilayer configuration.

The much more stable cycling of the composition-modified electrolyte at high current densities compared to that of the control electrolyte demonstrates that our picture of dynamic stability captures an important aspect at the level of new electrolyte material design for lithium-dendrite-proof SSBs. Although at the battery device level both the higher cathode loading and the lower stack pressure are equally important and should be addressed in the future, including them in the current work will complicate the discussion, as mentioned earlier. Note that although we noticed that certain specific halide doping procedures for the Li–argyrodite electrolyte were reported recently,^23,24 such a quantitative design through precise composition control within our two-parameter phase space and the experimental implementation through the core–shell strategy and related synthesis are proposed and demonstrated for the first time, representing a unique fundamental understanding with significant practical values. More importantly, our approach can be further applied to the design of broad types of electrolyte materials with similar dynamic stabilities to various interfaces, including sulfides,²⁵ halides,²⁶⁻²⁸ oxides,^29,30 ceramics, glasses,⁹ and polymers and their composites.

Glossary

ABBREVIATIONS

SSB

solid-state battery

LPSCl

Li_5.5PS_4.5Cl_1.5

LPSCl-X

Li_5.5PS_4.5Cl_1.5-yX_y, where X = F, Br, or I and y = 0.4 for F and 0.15, for Br and I

NMC811

LiNi_0.83Mn_0.06Co_0.11O₂

DFT

density functional theory

LGPS

Li₁₀GeP₂S₁₂

XPS

X-ray photoelectron spectroscopy

EDS

energy dispersive spectroscopy

SEM

scanning electron microscopy

XRD

X-ray diffraction

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacsau.2c00009.

• Additional computational results, additional XPS and SEM results, XRD results, and additional battery data (PDF)

Author Contributions

^† Y.W. and L.Y. contributed equally to this paper. X.L. conceived the physical picture and planned the research. Y.W. and X.C. performed DFT high-throughput calculations and machine learning. Y.W. and L.Y. performed the experiments. Y.W., L.Y., X.C., and X.L. analyzed data and wrote the manuscript. X. L. supervised all aspects of the research.

The authors declare no competing financial interest.