Stress tensor and constant pressure simulation for polarizable Gaussian multipole model

Abstract

Our previous article has established the theory of molecular dynamics (MD) simulations for systems modeled with the polarizable Gaussian multipole (pGM) electrostatics [Wei et al., J. Chem. Phys. 153(11), 114116 (2020)]. Specifically, we proposed the covalent basis vector framework to define the permanent multipoles and derived closed-form energy and force expressions to facilitate an efficient implementation of pGM electrostatics. In this study, we move forward to derive the pGM internal stress tensor for constant pressure MD simulations with the pGM electrostatics. Three different formulations are presented for the flexible, rigid, and short-range screened systems, respectively. The analytical formulations were implemented in the SANDER program in the Amber package and were first validated with the finite-difference method for two different boxes of pGM water molecules. This is followed by a constant temperature and constant pressure MD simulation for a box of 512 pGM water molecules. Our results show that the simulation system stabilized at a physically reasonable state and maintained the balance with the externally applied pressure. In addition, several fundamental differences were observed between the pGM and classic point charge models in terms of the simulation behaviors, indicating more extensive parameterization is necessary to utilize the pGM electrostatics.

I. INTRODUCTION

Atomistic simulations of biomolecules have been applied to various biological systems.² While additive nonpolarizable models continue to play dominant roles,^3–5 nonadditive polarizable models are emerging as a tool extending our capability of studying more complex biomolecular systems and processes. The nonpolarizable models typically use fixed atomic partial charges to model electrostatics. As a result, they incorporate only the polarization response to the environment (mostly in water) in a mean-field manner. Thus, the nonpolarizable models with excellent descriptions of the homogeneous bulk phase can be poor models treating gas-phase clusters or in cases where large scale conformational changes are accompanied by changes in dielectric environment.⁶ Another limitation of the nonpolarizable models is the use of partial atomic charges. This treatment often lacks the sufficient mathematical flexibility to accurately describe the electrostatic potential of nearby molecules. Williams showed that the optimal least-squares fitting of atom-centered partial charges resulted in relative root-mean-square errors of 3%–10% in reproducing the quantum electrostatic potentials at the grid points in a shell outside the surface of a series of small polar molecules.⁷ In summary, the importance of modeling polarization effects and the limitation of point charge models have been well documented.^6,8

To address the aforementioned issues, extensive efforts have been invested in the development of explicit polarizable models.^9–11 Several methods have been proposed, including explicit polarization in the molecular mechanics potentials, such as the Drude oscillator,^12,13 fluctuating charges,¹⁴ and induced dipoles.^6,15,16 Among these new models, the implementation of polarizable point dipoles was originally proposed by Applequist et al.¹⁷ It is a classical approach with a long history in molecular simulation.¹⁸ However, this model suffers from the so-called “polarization catastrophe,”¹⁹ which requires proper screenings for short range electrostatics.

Recently, Elking et al. proposed the polarizable multipole model with Gaussian charge densities.²⁰ A key benefit of the polarizable Gaussian Multipole model (pGM) is its screening of all the short-range electrostatic interactions in a physically consistent manner, as we discussed previously.²¹ We have presented an analytical formulation for the pGM model that is more suitable for molecular dynamics (MD) simulation due to the lack of explicit torque computation.¹ In addition, we further exploited a new local frame, the covalent basis vectors (CBVs), to preserve the physical symmetry and to better accommodate the fact that the permanent dipoles primarily resulted from the covalent bonds. Subsequent numerical tests show that, with enough accuracy involving both the pGM and the Particle Mesh Ewald (PME), the NVE simulation can be realized with a similar energy drift as in classic point charge models.¹

However, most of the real-world biological systems resemble constant pressure ensembles, which require our pGM model to be extended to NPT simulations. Andersen first proposed a new constant pressure method in which the volume was allowed to fluctuate, with its average value being determined by the balance between the internal stress in a system and the externally set pressure.²² Following his pioneering works, Nosé and Klein²³ and Darden²⁴ indicated how to extend the formulation to include the case of the long range charge–charge interactions. Toukmaji et al. introduced an efficient approach to include induced dipolar interactions,²⁵ and Sagui et al. extended the formulation to multipolar situations.²⁶ Recently, these virials for point induced dipoles and multipoles have been implemented for AMOEBA in Tinker-HP and Tinker9 [graphics processing unit (GPU)].²⁷ Additionally, there have been interesting discussions about pressure calculation related to the Ewald surface correction.^28,29 However, how to rigorously treat internal stress in a system with both permanent and induced dipoles is still unclear.

In this work, we present an analytical formulation of the stress tensor for both the flexible and rigid molecular systems modeled with the pGM model. We performed a finite difference test and confirmed that both are rigorously correct. Finally, we implemented the proposed pGM formalism in the context of PME into the SANDER program in Amber. Our NPT simulations of a 512-water system showed that the algorithm is stable as indicated by the time evolutions of pressure, temperature, density, and total system energy.

II. METHOD

A. Electrostatic potential of a pGM system

The total electrostatic energy of the system, as shown in our previous work,¹ is defined as

$$U_{pGM}=\sum _i^N\frac{1}{2}(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_i){\varphi }_i^0+\sum _i^N\frac{1}{2}({\stackrel{\rightharpoonup }{p}}_i\cdot {\nabla }_i){\varphi }_i^0.$$ (1)

Here, q_i, ${\stackrel{\rightharpoonup }{\mu }}_i$, and ${\stackrel{\rightharpoonup }{p}}_i$ are the charge, covalent dipole (i.e., permanent dipole), and induced dipole on atom i, respectively, and ${\varphi }_i^0$ is the electrostatic potential on atom i that is generated only by charges and covalent dipoles in the system. Later in this paper, we will denote ϕ_i as the electrostatic potential on atom i that is generated by charges, covalent dipoles, and induced dipoles in the system.

Due to the periodic boundary condition, ${\varphi }_i^0$ has to be obtained through a certain lattice summation technique, and here, the Ewald summation technique is used.

According to the Ewald summation,

$$\begin{array}{ll}\hfill {\varphi }_i^0& =\frac{1}{\pi V}{\sum }_{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\sum _j^N\left[\left(q_j+2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{\mu }}_j\right)\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\right]\right.\hfill \\ \hfill & \times \left.\exp \left(,-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}+\sum _{j\ne i}^{\infty }(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j)\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)-\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}}\hfill \\ \hfill & -\underset{{\stackrel{\rightharpoonup }{R}}_j\to {\stackrel{\rightharpoonup }{R}}_i}{\lim }(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_j)\frac{\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}}.\hfill \end{array}$$ (2)

Here, V is the volume of the box, $\stackrel{\rightharpoonup }{m}$ is the reciprocal lattice vector, and ${\stackrel{\rightharpoonup }{R}}_i$ and $R_{ij}=\left|{\stackrel{\rightharpoonup }{R}}_j-{\stackrel{\rightharpoonup }{R}}_i\right|$ are the coordinate of atom i and its distance to atom j, respectively. In addition, β₀ is the Ewald coefficient, whose value is usually between $\frac{1}{5}$–$\frac{1}{2}$ ${\stackrel{°}{\mathrm{A}}}^{-1}$ for typical biomolecular applications, and β_ij equals to $\frac{{\beta }_i{\beta }_j}{\sqrt{{{\beta }_i}^2+{{\beta }_j}^2}}$, where β_i and β_j are the Gaussian parameters for atoms i and j, respectively.

Below, we will use the following notation convention: all gradients paired with a dipole (covalent or induced) only apply to atom coordinates. For example, the gradient operator in ${\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_i$ only acts on the coordinates of atom i. On the other hand, all other gradient operators (not paired with a dipole) follow the standard convention.

B. Stress tensor

From its definition, stress tensor (virial) is the derivative of system Lagrangian with respect to the system size parameters, except for a constant pre-factor. In a typical biomolecular simulation, the simulating box can be described by the three column vectors that represent the edges of the box, ${\stackrel{\rightharpoonup }{u}}_1$, ${\stackrel{\rightharpoonup }{u}}_2$, and ${\stackrel{\rightharpoonup }{u}}_3$. Thus, a matrix h can be constructed from these three unit cell vectors, defined as the system shape parameters,

$$h=({\stackrel{\rightharpoonup }{u}}_1,{\stackrel{\rightharpoonup }{u}}_2,{\stackrel{\rightharpoonup }{u}}_3).$$ (3)

Thus, stress tensor $\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{V}}$ can be expressed as

$$\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{V}}\cdot {\left(h^{-1}\right)}^T=\frac{\partial L}{\partial h}=\frac{\partial T}{\partial h}-\frac{\partial U}{\partial h}.$$ (4)

Here, L represents the system Lagrangian, superscript “T” denotes transpose of the matrix, and T and U are kinetic and potential energies, respectively. The derivative with respect to matrix h is equivalent to differentiating L against each component of h, with the fractional coordinates of each atom held constant.

Because the kinetic energy expression is the same for a pGM system and a classic point charge system, the related virial terms are the same, so we omit their derivations here. There are many different components in the potential energy, but only the electrostatic part is different from other force fields in the current pGM model. Thus, we need to derive only the electrostatic components of the virial. This is to say, we are deriving the following quantity in this work:

$${\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{V}}}_{pGM}=-\frac{\partial U_{pGM}}{\partial h}\cdot {\left(h\right)}^T.$$ (5)

To do so, we first need to identify which quantities in Eq. (1) are dependent on matrix h.

C. Stress tensor in a pGM system

Quantities that obviously depend on h are as follows:

• 1.Atomic coordinates, ${\stackrel{\rightharpoonup }{R}}_i=s_{i1}{\stackrel{\rightharpoonup }{u}}_1+s_{i2}{\stackrel{\rightharpoonup }{u}}_2+s_{i3}{\stackrel{\rightharpoonup }{u}}_3$. Here, s’s are fractional coordinates and are constants when computing the derivatives with respect to h.
• 2.Atomic covalent dipoles, ${\stackrel{\rightharpoonup }{\mu }}_i=\sum _k^n{u}_{ik}\frac{{\stackrel{\rightharpoonup }{R}}_{ik}}{\left|{\stackrel{\rightharpoonup }{R}}_{ik}\right|}=\sum _k^n{u}_{ik}\frac{{\stackrel{\rightharpoonup }{R}}_k-{\stackrel{\rightharpoonup }{R}}_i}{\left|{\stackrel{\rightharpoonup }{R}}_{ik}\right|}$. Here, n refers to the number of atoms covalently connected to atom i (this notation will be used thoroughly in the paper), and u_ik is the dipole moment along the specific direction ${\stackrel{\rightharpoonup }{R}}_k-{\stackrel{\rightharpoonup }{R}}_i$, which is a constant. Noted that the definition of ${\stackrel{\rightharpoonup }{R}}_{ik}\equiv {\stackrel{\rightharpoonup }{R}}_k-{\stackrel{\rightharpoonup }{R}}_i$ is used throughout this manuscript.
• 3.System volume, V = det(h).
• 4.Reciprocal lattice vector, $\stackrel{\rightharpoonup }{m}=(k_1,k_2,k_3)\cdot h^{-1}$, where k₁, k₂, k₃ are integer constants.

The derivatives of these quantities with respect to h are given in Appendix A 1.

Moreover, the induced dipole, ${\stackrel{\rightharpoonup }{p}}_i$, is clearly dependent on h. However, there is no explicit expression of ${\stackrel{\rightharpoonup }{p}}_i$, as ${\stackrel{\rightharpoonup }{p}}_i$ is computed through a self-consistent iteration. In the following, we show how to obtain its derivatives.

As shown in our previous work,¹ the induced dipole can be expressed in the periodic system as

$$\begin{array}{c}{\stackrel{\rightharpoonup }{p}}_i={\alpha }_i\left({\stackrel{\rightharpoonup }{E}}_i^0+{\stackrel{\rightharpoonup }{E}}_i^{induced}\right)={\alpha }_i({\stackrel{\rightharpoonup }{E}}_i^0-\sum _j^N{\stackrel{\rightharpoonup }{T}}_{ij}\cdot {\stackrel{\rightharpoonup }{p}}_j),\\ {\stackrel{\rightharpoonup }{E}}_i^0=-{\nabla }_i{\varphi }_i^0,\end{array}$$ (6)

$$T_{ij}^{\alpha \beta }={\partial }_i^{\alpha }{\partial }_j^{\beta }\left\{\begin{array}{cc}\frac{1}{\pi V}{\sum }_{\stackrel{\rightharpoonup }{m}\ne 0}\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)+\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)-\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}}\hfill & \mathrm{if}i\ne j,\hfill \\ \frac{1}{\pi V}{\sum }_{\stackrel{\rightharpoonup }{m}\ne 0}\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)-\underset{{\stackrel{\rightharpoonup }{R}}_j\to {\stackrel{\rightharpoonup }{R}}_i}{\lim }\frac{\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}}\hfill & \mathrm{if}i=j.\hfill \end{array}\right.$$

Here α, β = 1, 2, 3 refer to x, y, z directions, respectively. The expression of $T_{ij}^{\alpha \beta }$ comes from the Ewald summation of ${\partial }_i^{\alpha }{\partial }_j^{\beta }\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}$. Thus, the summation for i ≠ j includes all the images in the periodic system. The introduction of

$$A_{ij}^{\alpha \beta }=\frac{1}{{\alpha }_i}({\delta }_{ij}^{\alpha \beta }+{\alpha }_i\cdot T_{ij}^{\alpha \beta })$$ (7)

leads to the following short-hand expression for the induced dipole:¹

$${\stackrel{\rightharpoonup }{p}}_i=\sum _j^N{\stackrel{\rightharpoonup }{A}}_{ij}^{-1}\cdot {\stackrel{\rightharpoonup }{E}}_j^0.$$ (8)

In Eq. (8), we have transferred the dependence of ${\stackrel{\rightharpoonup }{p}}_i$ on h to the dependence of ${\stackrel{\rightharpoonup }{A}}_{ij}^{-1}$ and ${\stackrel{\rightharpoonup }{E}}_j^0$ on h, and the dependence of ${\stackrel{\rightharpoonup }{E}}_j^0=-{\nabla }_j{\varphi }_j^0$ is already known. Thus, what is needed is to derive the dependence of ${\stackrel{\rightharpoonup }{A}}_{ij}^{-1}$ on h.

Given A · A⁻¹ = 1, we have

$$\begin{array}{ll}\hfill \frac{\partial {(A^{-1})}_{ij}^{\alpha \beta }}{\partial h}& =-{\left(A^{-1}\right)}_{i{i}^{\prime }}^{\alpha {\alpha }^{\prime }}\frac{\partial A_{i^{\prime }{j}^{\prime }}^{{\alpha }^{\prime }{\beta }^{\prime }}}{\partial h}{\left(A^{-1}\right)}_{j^{\prime }j}^{{\beta }^{\prime }\beta }\hfill \\ \hfill & =-{\left(A^{-1}\right)}_{i{i}^{\prime }}^{\alpha {\alpha }^{\prime }}\frac{\partial T_{i^{\prime }{j}^{\prime }}^{{\alpha }^{\prime }{\beta }^{\prime }}}{\partial h}{\left(A^{-1}\right)}_{j^{\prime }j}^{{\beta }^{\prime }\beta },\hfill \end{array}$$ (9)

where the Einstein’s index notation is employed for i′, j′, α′, and β′. We can now proceed to compute the derivatives for the energy term related to ${\stackrel{\rightharpoonup }{p}}_i$ in Eq. (1) as follows:

$$\begin{array}{ll}\hfill \frac{\partial -\sum _i^N\frac{1}{2}{\stackrel{\rightharpoonup }{p}}_i\cdot {\stackrel{\rightharpoonup }{E}}_i^0}{\partial h}& =\frac{1}{2}{E}_i^{0\alpha }{\left(A^{-1}\right)}_{i{i}^{\prime }}^{\alpha {\alpha }^{\prime }}\frac{\partial T_{i^{\prime }{j}^{\prime }}^{{\alpha }^{\prime }{\beta }^{\prime }}}{\partial h}{\left(A^{-1}\right)}_{j^{\prime }j}^{{\beta }^{\prime }\beta }{E}_j^{0\beta }-\sum _i^N{\stackrel{\rightharpoonup }{p}}_i\cdot \frac{\partial {\stackrel{\rightharpoonup }{E}}_i^0}{\partial h}\hfill \\ \hfill & =\frac{1}{2}{p}_{i^{\prime }}^{{\alpha }^{\prime }}\frac{\partial T_{i^{\prime }{j}^{\prime }}^{{\alpha }^{\prime }{\beta }^{\prime }}}{\partial h}{p}_{j^{\prime }}^{{\beta }^{\prime }}-\sum _i^N{\stackrel{\rightharpoonup }{p}}_i\cdot \frac{\partial {\stackrel{\rightharpoonup }{E}}_i^0}{\partial h}.\hfill \end{array}$$ (10)

Again, the Einstein’s index notation is employed here for i, j, α, β i′, j′, α′, are β′.

With the above preparations, we can calculate the electrostatic energy part of the virial from its definition,

$$\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{V}}\cdot {\left(h^{-1}\right)}^T=-\frac{\partial U}{\partial h_{\mu \nu }}=-\left(\frac{\partial U_{rec}}{\partial h_{\mu \nu }}+\frac{\partial U_{dir}}{\partial h_{\mu \nu }}+\frac{\partial U_{\mathrm{self}}}{\partial h_{\mu \nu }}\right),$$ (11)

$$\begin{array}{ll}\hfill \frac{\partial U_{rec}}{\partial h_{\mu \nu }}& =\frac{\partial \sum _i^N\frac{1}{2}\left(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_i\right)\frac{1}{\pi V}{\sum }_{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\sum _j^N\left[\left(q_j+2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{\mu }}_j\right)\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\right]\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}}{\partial h_{\mu \nu }}\hfill \\ \hfill & +\frac{1}{2}{p}_{i^{\prime }}^{{\alpha }^{\prime }}\frac{\partial {\partial }_{i^{\prime }}^{{\alpha }^{\prime }}{\partial }_{j^{\prime }}^{{\beta }^{\prime }}\frac{1}{\pi V}{\sum }_{\stackrel{\rightharpoonup }{m}\ne 0}\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_{j^{\prime }}\right)\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_{i^{\prime }}\right)}{\partial h_{\mu \nu }}{p}_{j^{\prime }}^{{\beta }^{\prime }}\hfill \\ \hfill & +\sum _i^N{\stackrel{\rightharpoonup }{p}}_i\cdot \frac{\partial {\nabla }_i\frac{1}{\pi V}{\sum }_{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\sum _j^N\left[\left(q_j+2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{\mu }}_j\right)\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\right]\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}}{\partial h_{\mu \nu }},\hfill \end{array}$$ (12)

$$\begin{array}{ll}\hfill \frac{\partial U_{dir}}{\partial h_{\mu \nu }}& =\frac{\partial \sum _i^N\frac{1}{2}(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_i)\sum _{j\ne i}^{\infty }(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j)\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)-\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}}}{\partial h_{\mu \nu }}+\frac{1}{2}{p}_{i^{\prime }}^{{\alpha }^{\prime }}\frac{\partial {\partial }_{i^{\prime }}^{{\alpha }^{\prime }}{\partial }_{j^{\prime }}^{{\beta }^{\prime }}\frac{\text{erf}\left({\beta }_{i^{\prime }{j}^{\prime }}{R}_{i^{\prime }{j}^{\prime }}\right)-\text{erf}\left({\beta }_0{R}_{i^{\prime }{j}^{\prime }}\right)}{R_{i^{\prime }{j}^{\prime }}}}{\partial h_{\mu \nu }}{p}_{j^{\prime }}^{{\beta }^{\prime }}\hfill \\ \hfill & +\sum _i^N{\stackrel{\rightharpoonup }{p}}_i\cdot \frac{\partial {\nabla }_i\sum _{j\ne i}^{\infty }(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j)\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)-\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}}}{\partial h_{\mu \nu }},\hfill \end{array}$$ (13)

$$\begin{array}{ll}\hfill \frac{\partial U_{\mathrm{self}}}{\partial h_{\mu \nu }}& =\frac{\partial \sum _i^N\frac{1}{2}\left(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_i\right)\left[-\underset{{\stackrel{\rightharpoonup }{R}}_j\to {\stackrel{\rightharpoonup }{R}}_i}{\lim }\left(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}}\right]}{\partial h_{\mu \nu }}+\frac{1}{2}{p}_{i^{\prime }}^{{\alpha }^{\prime }}\frac{\partial {\partial }_{i^{\prime }}^{{\alpha }^{\prime }}{\partial }_{j^{\prime }}^{{\beta }^{\prime }}\left[-\underset{{\stackrel{\rightharpoonup }{R}}_j\to {\stackrel{\rightharpoonup }{R}}_i}{\lim }\frac{\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}}\right]}{\partial h_{\mu \nu }}{p}_{j^{\prime }}^{{\beta }^{\prime }}+\sum _i^N{\stackrel{\rightharpoonup }{p}}_i\cdot \frac{\partial {\nabla }_i\left[-\underset{{\stackrel{\rightharpoonup }{R}}_j\to {\stackrel{\rightharpoonup }{R}}_i}{\lim }\left(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}}\right]}{\partial h_{\mu \nu }}.\hfill \end{array}$$ (14)

After careful derivation (see Appendix A 2 for details), the following results can be obtained:

$$\begin{array}{ll}\hfill \frac{\partial U_{rec}}{\partial h_{\mu \nu }}& =-\frac{1}{2\pi V}{\left(h^{-1}\right)}_{\mu \nu }^T{\sum }_{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\sum _j^N\left[q_j+2\pi i\stackrel{\rightharpoonup }{m}\cdot \left({\stackrel{\rightharpoonup }{\mu }}_j+{\stackrel{\rightharpoonup }{p}}_j\right)\right]\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\sum _i^N\left[q_i-2\pi i\stackrel{\rightharpoonup }{m}\cdot \left({\stackrel{\rightharpoonup }{\mu }}_i+{\stackrel{\rightharpoonup }{p}}_i\right)\right]\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}\hfill \\ \hfill & +\frac{1}{\pi V}{\sum }_{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\left(-\frac{1+\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}}{{\stackrel{\rightharpoonup }{m}}^2}\right)\left(-{\stackrel{\rightharpoonup }{m}}^{\mu }{h}_{\nu \gamma }^{-1}{\stackrel{\rightharpoonup }{m}}^{\gamma }\right)\sum _j^N\left[q_j+2\pi i\stackrel{\rightharpoonup }{m}\cdot \left({\stackrel{\rightharpoonup }{\mu }}_j+{\stackrel{\rightharpoonup }{p}}_j\right)\right]\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\sum _i^N\left[q_i-2\pi i\stackrel{\rightharpoonup }{m}\cdot \left({\stackrel{\rightharpoonup }{\mu }}_i+{\stackrel{\rightharpoonup }{p}}_i\right)\right]\right.\hfill \\ \hfill & \times \left.\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}+\frac{1}{\pi V}{\sum }_{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\sum _j^N\left[q_j+2\pi i\stackrel{\rightharpoonup }{m}\cdot \left({\stackrel{\rightharpoonup }{\mu }}_j+{\stackrel{\rightharpoonup }{p}}_j\right)\right]\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\sum _i^N\sum _k^n\left[\left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_{ik}{\mu }_{ik}\right)\left(-\frac{{\stackrel{\rightharpoonup }{R}}_{ik}^{\mu }{\stackrel{\rightharpoonup }{S}}_{ik}^{\nu }}{{\left|{\stackrel{\rightharpoonup }{R}}_{ik}\right|}^3}\right)\right]\right.\hfill \\ \hfill & \left.\times \exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}+\frac{1}{\pi V}{\sum }_{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\sum _j^N\left[q_j+2\pi i\stackrel{\rightharpoonup }{m}\cdot \left({\stackrel{\rightharpoonup }{\mu }}_j+{\stackrel{\rightharpoonup }{p}}_j\right)\right]\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\sum _i^N\left[\left(-2\pi i\right)\left(-{\stackrel{\rightharpoonup }{m}}^{\mu }{h}_{\nu \gamma }^{-1}{p}_i^{\gamma }\right)\right]\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}\hfill \\ \hfill & =-\frac{1}{2}{\left(h^{-1}\right)}_{\mu \nu }^T\cdot \sum _i^N\left[q_i{\left({\varphi }_{rec}\right)}_i-\left({\stackrel{\rightharpoonup }{\mu }}_i+{\stackrel{\rightharpoonup }{p}}_i\right)\cdot {\left({\stackrel{\rightharpoonup }{E}}_{rec}\right)}_i\right]+\frac{1}{\pi V}{\sum }_{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\left(-\frac{1+\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}}{{\stackrel{\rightharpoonup }{m}}^2}\right)\left(-{\stackrel{\rightharpoonup }{m}}^{\mu }{h}_{\nu \gamma }^{-1}{\stackrel{\rightharpoonup }{m}}^{\gamma }\right)S(\stackrel{\rightharpoonup }{m})S(-\stackrel{\rightharpoonup }{m})\right\}\hfill \\ \hfill & +\sum _i^N\sum _k^n\left[\left(-{({\stackrel{\rightharpoonup }{E}}_{rec})}_i\cdot {\stackrel{\rightharpoonup }{R}}_{ik}{\mu }_{ik}\right)\left(-\frac{{\stackrel{\rightharpoonup }{R}}_{ik}^{\mu }{\stackrel{\rightharpoonup }{S}}_{ik}^{\nu }}{{\left|{\stackrel{\rightharpoonup }{R}}_{ik}\right|}^3}\right)\right]+\sum _i^N{({\stackrel{\rightharpoonup }{E}}_{rec})}_i^{\mu }{h}_{\nu \gamma }^{-1}{p}_i^{\gamma },\hfill \end{array}$$ (15)

where $S(\stackrel{\rightharpoonup }{m})$ is the structure factor, defined as $\sum _j^N\left[q_j+2\pi i\stackrel{\rightharpoonup }{m}\cdot \left({\stackrel{\rightharpoonup }{\mu }}_j+{\stackrel{\rightharpoonup }{p}}_j\right)\right]\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)$, and

$$\begin{array}{ll}\hfill \frac{\partial U_{dir}}{\partial h_{\mu \nu }}& =-\sum _i^N\sum _k^n{u}_{ik}\left[\frac{{\left({\stackrel{\rightharpoonup }{E}}_{dir}\right)}_i^{\mu }{\stackrel{\rightharpoonup }{S}}_{ik}^{\nu }}{\left|{\stackrel{\rightharpoonup }{R}}_{ik}\right|}-{\left({\stackrel{\rightharpoonup }{E}}_{dir}\right)}_i\cdot {\stackrel{\rightharpoonup }{R}}_{ik}\frac{{\stackrel{\rightharpoonup }{R}}_{ik}^{\mu }{\stackrel{\rightharpoonup }{S}}_{ik}^{\nu }}{{\left|{\stackrel{\rightharpoonup }{R}}_{ik}\right|}^3}\right]\hfill \\ \hfill & -\frac{1}{2}\sum _i^N\sum _{j\ne i}^{\infty }\left\{q_i{\left({\stackrel{\rightharpoonup }{E}}_{dir}\right)}_{j\to i}^{\mu }({\stackrel{\rightharpoonup }{S}}_i^{\nu }-{\stackrel{\rightharpoonup }{S}}_j^{\nu })\right.\hfill \\ \hfill & +\left.{\left[\left({\stackrel{\rightharpoonup }{u}}_i+{\stackrel{\rightharpoonup }{p}}_i\right)\cdot {\left({\stackrel{\rightharpoonup }{E}}_{dir}\right)}_{j\to i}\right]}^{\mu }({\stackrel{\rightharpoonup }{S}}_i^{\nu }-{\stackrel{\rightharpoonup }{S}}_j^{\nu })\right\},\hfill \end{array}$$ (16)

$$\frac{\partial U_{\mathrm{self}}}{\partial h_{\mu \nu }}=-\sum _i^N\sum _k^n{u}_{ik}\left[\frac{{\left({\stackrel{\rightharpoonup }{E}}_{\mathrm{self}}\right)}_i^{\mu }{\stackrel{\rightharpoonup }{S}}_{ik}^{\nu }}{\left|{\stackrel{\rightharpoonup }{R}}_{ik}\right|}-{\left({\stackrel{\rightharpoonup }{E}}_{\mathrm{self}}\right)}_i\cdot {\stackrel{\rightharpoonup }{R}}_{ik}\frac{{\stackrel{\rightharpoonup }{R}}_{ik}^{\mu }{\stackrel{\rightharpoonup }{S}}_{ik}^{\nu }}{{\left|{\stackrel{\rightharpoonup }{R}}_{ik}\right|}^3}\right].$$ (17)

Here ${\stackrel{\rightharpoonup }{E}}_{rec},{\stackrel{\rightharpoonup }{E}}_{dir}$, and ${\stackrel{\rightharpoonup }{E}}_{\mathrm{self}}$ refer to the electrostatic fields resulting from the reciprocal part, direct part, or self-part of an Ewald summation, respectively. The notation for ϕ and $\stackrel{\rightharpoonup }{E}$ is similar. Furthermore, the following expressions for electric field and its derivatives are used:

$$\begin{array}{c}{\left({\stackrel{\rightharpoonup }{E}}_{dir}\right)}_{j\to i}=-(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j){\nabla }_i\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)-\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}},\\ {\left({\stackrel{\rightharpoonup }{E}}_{dir}\right)}_{j\to i}=-(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j){\nabla }_i{\nabla }_i\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)-\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}}.\end{array}$$ (18)

Adding up all the three terms above and removing the common factor $-{\left(h^{-1}\right)}^T$, the final expression of the electrostatic energy contribution to the virial is as follows:

$$\begin{array}{ll}\hfill V_{\mu \nu }& =\frac{1}{2}{\delta }_{\mu \nu }\cdot \sum _i^N\left[q_i{\left({\varphi }_{rec}\right)}_i-\left({\stackrel{\rightharpoonup }{\mu }}_i+{\stackrel{\rightharpoonup }{p}}_i\right)\cdot {\left({\stackrel{\rightharpoonup }{E}}_{rec}\right)}_i\right]-\frac{1}{\pi V}{\sum }_{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\frac{1+\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}}{{\stackrel{\rightharpoonup }{m}}^2}{\stackrel{\rightharpoonup }{m}}^{\mu }{\stackrel{\rightharpoonup }{m}}^{\nu }S\left(\stackrel{\rightharpoonup }{m}\right)S\left(-\stackrel{\rightharpoonup }{m}\right)\right\}\hfill \\ \hfill & -\sum _i^N{\left({\stackrel{\rightharpoonup }{E}}_{rec}\right)}_i^{\mu }{p}_i^{\nu }+\sum _i^N\sum _k^n{u}_{ik}\left[\frac{{\left({\stackrel{\rightharpoonup }{E}}_{dir}+{\stackrel{\rightharpoonup }{E}}_{\mathrm{self}}\right)}_i^{\mu }{\stackrel{\rightharpoonup }{R}}_{ik}^{\nu }}{\left|{\stackrel{\rightharpoonup }{R}}_{ik}\right|}-{\left({\stackrel{\rightharpoonup }{E}}_{rec}+{\stackrel{\rightharpoonup }{E}}_{dir}+{\stackrel{\rightharpoonup }{E}}_{\mathrm{self}}\right)}_i\cdot {\stackrel{\rightharpoonup }{R}}_{ik}\frac{{\stackrel{\rightharpoonup }{R}}_{ik}^{\mu }{\stackrel{\rightharpoonup }{R}}_{ik}^{\nu }}{{\left|{\stackrel{\rightharpoonup }{R}}_{ik}\right|}^3}\right]\hfill \\ \hfill & +\frac{1}{2}\sum _i^N\sum _{j\ne i}^{\infty }\left\{q_i{\left({\stackrel{\rightharpoonup }{E}}_{dir}\right)}_{j\to i}^{\mu }({\stackrel{\rightharpoonup }{R}}_i^{\nu }-{\stackrel{\rightharpoonup }{R}}_j^{\nu })+{\left[\left({\stackrel{\rightharpoonup }{u}}_i+{\stackrel{\rightharpoonup }{p}}_i\right)\cdot {\left({\stackrel{\rightharpoonup }{E}}_{dir}\right)}_{j\to i}\right]}^{\mu }({\stackrel{\rightharpoonup }{R}}_i^{\nu }-{\stackrel{\rightharpoonup }{R}}_j^{\nu })\right\}.\hfill \end{array}$$ (19)

D. Stress tensor of rigid molecules

Molecular dynamics simulations of bio-molecular systems are often conducted under certain constraints. The most common are distance constraints,

$${\left({\stackrel{\rightharpoonup }{R}}_i-{\stackrel{\rightharpoonup }{R}}_j\right)}^2-d_{ij}^2=0.$$ (20)

When molecules are under this kind of constraints, a molecule-based scaling in NPT simulations is often used to vary the box dimensions instead of atom-based scaling. In doing so, the atomic coordinate can be expressed as

$${\stackrel{\rightharpoonup }{R}}_i={\stackrel{\rightharpoonup }{R}}_{i0}+{\stackrel{\rightharpoonup }{d}}_i=s_{i0,1}{\stackrel{\rightharpoonup }{u}}_1+s_{i0,2}{\stackrel{\rightharpoonup }{u}}_2+s_{i0,3}{\stackrel{\rightharpoonup }{u}}_3+{\stackrel{\rightharpoonup }{d}}_i,$$ (21)

where ${\stackrel{\rightharpoonup }{R}}_{i0}$ is the molecular center to which atom i belongs (usually the mass center of the molecule), ${\stackrel{\rightharpoonup }{s}}_{i0}$’s are the fractional coordinates of the center, and ${\stackrel{\rightharpoonup }{d}}_i$ is the relative displacement of atom i from the center. Obviously, ${\stackrel{\rightharpoonup }{d}}_i$ is a constant vector during the box dimension scaling.

Thus, the virial tensor of a pGM system under this rigid body condition with distance constraints is

$$\begin{array}{ll}\hfill V_{\mu \nu }& =\frac{1}{2}{\delta }_{\mu \nu }\cdot \sum _i^N\left[q_i{\left({\varphi }_{rec}\right)}_i-\left({\stackrel{\rightharpoonup }{\mu }}_i+{\stackrel{\rightharpoonup }{p}}_i\right)\cdot {\left({\stackrel{\rightharpoonup }{E}}_{rec}\right)}_i\right]-\frac{1}{\pi V}{\sum }_{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\frac{1+\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}}{{\stackrel{\rightharpoonup }{m}}^2}{\stackrel{\rightharpoonup }{m}}^{\mu }{\stackrel{\rightharpoonup }{m}}^{\nu }S\left(\stackrel{\rightharpoonup }{m}\right)S\left(-\stackrel{\rightharpoonup }{m}\right)\right\}\hfill \\ \hfill & -\sum _i^N{\left({\stackrel{\rightharpoonup }{E}}_{rec}\right)}_i^{\mu }\left({\stackrel{\rightharpoonup }{\mu }}_i^{\nu }+{\stackrel{\rightharpoonup }{p}}_i^{\nu }+q_i{\stackrel{\rightharpoonup }{d}}_i^{\nu }\right)-\sum _i^N\left({\stackrel{\rightharpoonup }{\mu }}_i^{\gamma }+{\stackrel{\rightharpoonup }{p}}_i^{\gamma }\right){\left({\stackrel{\rightharpoonup }{E}}_{rec}\right)}_i^{\gamma \mu }{\stackrel{\rightharpoonup }{d}}_i^{\nu }+\frac{1}{2}\sum _i^N\sum _{j\ne i}^{\infty }\left\{q_i{\left({\stackrel{\rightharpoonup }{E}}_{dir}\right)}_{j\to i}^{\mu }({\stackrel{\rightharpoonup }{R}}_{i0}^{\nu }-{\stackrel{\rightharpoonup }{R}}_{j0}^{\nu })\right.\hfill \\ \hfill & +\left.{\left[\left({\stackrel{\rightharpoonup }{u}}_i+{\stackrel{\rightharpoonup }{p}}_i\right)\cdot {\left({\stackrel{\rightharpoonup }{E}}_{dir}\right)}_{j\to i}\right]}^{\mu }({\stackrel{\rightharpoonup }{R}}_{i0}^{\nu }-{\stackrel{\rightharpoonup }{R}}_{j0}^{\nu })\right\}.\hfill \end{array}$$ (22)

Here, index γ follows the Einstein’s summation notation. The derivation of the above expression is similar to what was described before for flexible molecules, so it is omitted here. The detail can be found in Appendix A 3.

E. Virial correction of screened system

In the current pGM setup, the electrostatic interactions are not screened, meaning all 1–2, 1–3, and 1–4 electrostatic interactions are considered at their full strength. This choice is based on the consideration of polarizability anisotropy.²¹ However, if electrostatic interactions between certain atoms are screened, the electrostatic virial correction can be defined as follows:

• (1)
  For flexible molecules,

  $$\begin{array}{ll}\hfill {\left(V_{\mu \nu }\right)}_{correction}& =\sum _i^N\sum _k^n{u}_{ik}\left[\frac{{\left(-{\stackrel{\rightharpoonup }{E}}_{screen}\right)}_i^{\mu }{\stackrel{\rightharpoonup }{R}}_{ik}^{\nu }}{\left|{\stackrel{\rightharpoonup }{R}}_{ik}\right|}-{\left(-{\stackrel{\rightharpoonup }{E}}_{screen}\right)}_i\cdot {\stackrel{\rightharpoonup }{R}}_{ik}\frac{{\stackrel{\rightharpoonup }{R}}_{ik}^{\mu }{\stackrel{\rightharpoonup }{R}}_{ik}^{\nu }}{{\left|{\stackrel{\rightharpoonup }{R}}_{ik}\right|}^3}\right]\hfill \\ \hfill & +\frac{1}{2}\sum _i^N\sum _{j\ne i}^{*\left(i\right)}\left\{q_i{\left(-{\stackrel{\rightharpoonup }{E}}_{screen}\right)}_{j\to i}^{\mu }({\stackrel{\rightharpoonup }{R}}_i^{\nu }-{\stackrel{\rightharpoonup }{R}}_j^{\nu })\right.\hfill \\ \hfill & +\left.{\left[\left({\stackrel{\rightharpoonup }{u}}_i+{\stackrel{\rightharpoonup }{p}}_i\right)\cdot {\left(-{\stackrel{\rightharpoonup }{E}}_{screen}\right)}_{j\to i}\right]}^{\mu }({\stackrel{\rightharpoonup }{R}}_i^{\nu }-{\stackrel{\rightharpoonup }{R}}_j^{\nu })\right\}.\hfill \end{array}$$ (23)
• (2)For rigid molecules,

$$\begin{array}{ll}\hfill {\left(V_{\mu \nu }\right)}_{correction}& =\frac{1}{2}\sum _i^N\sum _{j\ne i}^{*\left(i\right)}\left\{q_i{\left(-{\stackrel{\rightharpoonup }{E}}_{screen}\right)}_{j\to i}^{\mu }({\stackrel{\rightharpoonup }{R}}_{i0}^{\nu }-{\stackrel{\rightharpoonup }{R}}_{j0}^{\nu })\right.\hfill \\ \hfill & +\left.{\left[\left({\stackrel{\rightharpoonup }{u}}_i+{\stackrel{\rightharpoonup }{p}}_i\right)\cdot {\left(-{\stackrel{\rightharpoonup }{E}}_{screen}\right)}_{j\to i}\right]}^{\mu }({\stackrel{\rightharpoonup }{R}}_{i0}^{\nu }-{\stackrel{\rightharpoonup }{R}}_{j0}^{\nu })\right\}.\hfill \end{array}$$ (24)

Here, ${\stackrel{\rightharpoonup }{E}}_{screen}$ and ${\stackrel{\rightharpoonup }{E}}_{screen}$ are the electric field and its derivative generated by the screened interactions, and $*\left(i\right)$ represents the screened atom pairs of atom i.

Derivation of the above equations is given in Appendix A 4, which is similar to what was presented in our previous development.¹ However, it is important to point out that the screening has to be consistent throughout the model. In other words, we must screen the same interactions when computing both induced dipoles and forces. This is to ensure that the energy and corresponding forces are consistent under the same screening scheme.

III. RESULTS AND DISCUSSION

A. Finite difference validation

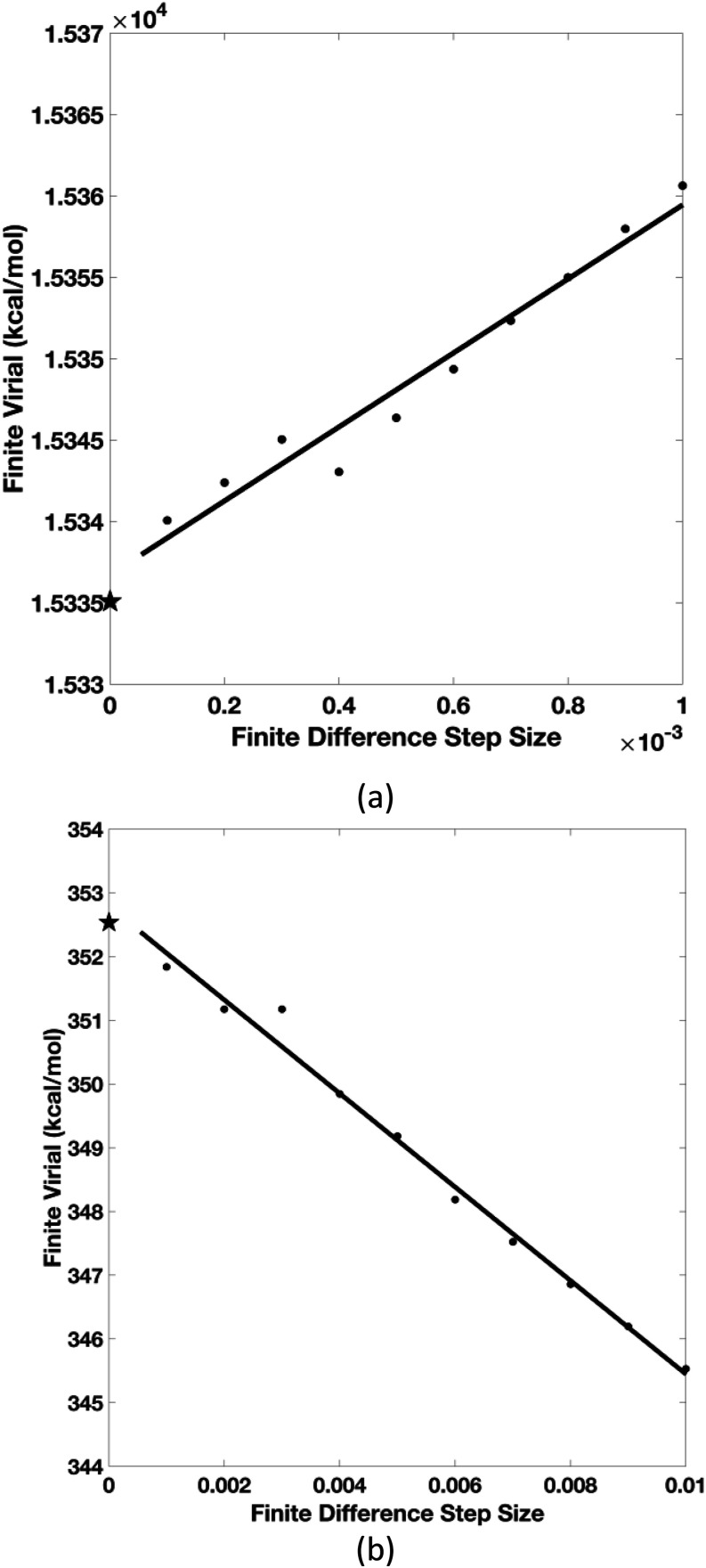
As we presented above, Eqs. (19) and (22) are the electrostatic virial expressions of flexible and rigid pGM molecular systems, respectively. To confirm the theoretical derivation, we performed a finite difference test, starting from the virial definition of Eq. (4), to assess whether the derivation is correct. Here, a cubic box with 512 water molecules, as in our previous study, was used,^1,21 and the dimension of the box is 33 $\stackrel{°}{\mathrm{A}}$. To guarantee high-precision energy calculation, the PME setup uses the following parameters: coefficient β₀ = 0.3 ${\stackrel{°}{\mathrm{A}}}^{-1}$, B-spline interpolation order = 9, FFT grid spacing = 0.33 $\stackrel{°}{\mathrm{A}}$, and direct space cutoff = 14.4 $\stackrel{°}{\mathrm{A}}$. The induced dipole convergence was also set to a very tight criterion of 10⁻¹². The setup leads to an energy accuracy level of ∼10⁻¹², so that the finite difference test can be carried successfully.

It is clear from Fig. 1 that both finite-difference virial values approach their respective analytical values in roughly linear fashions as the finite difference step sizes decrease, demonstrating that the numerical values converge to the analytical values. This finding confirms that the analytical virial expressions Eqs. (19) and (22) are correct when used to compute virials of the tested molecular system. Note also that the finite-difference steps in the rigid body system [Fig. 1(b)] are 10-time larger than the ones used in the flexible system [Fig. 1(a)]. This is because the virials of the rigid body system are much smaller (∼1/50) than those of the flexible system due to large intramolecular contributions that are sensitive to the distance variations in the finite difference calculations. Hence, rather small finite difference step sizes were needed. Such large intramolecular contributions were absent in the rigid-body system and a somewhat larger step sizes were used for numerical accuracy. The linear convergence trends illustrated in both the flexible and rigid body systems confirm the correctness of Eq. (22).

FIG. 1.

The finite-difference validation of the analytical virial expressions in the xx direction. (a) is for the flexible case and (b) is for the rigid body case. x axis refers to the proportional changes of simulation box dimension in the x direction. The star on the y axis is the analytical virial value given by Eqs. (19) and (22), respectively. The finite-difference values were obtained using Eq. (4). Testing along the yy and zz directions are available in the supplementary material. An additional set of testing was also conducted for a 4096-water box, available in the supplementary material.

B. NPT simulation of water box

To illustrate that the analytical formulation can achieve stable NPT simulations, we performed a test run for 1 ns of the water box containing 512 pGM water molecules.^1,21 The rigid-body formula, Eq. (22), was used in this test, and the water models were simply created from the standard TIP3P geometry by adding permanent and induced dipole moments and by setting the van der Waals parameters to be 9% of those in the standard TIP3P waters, to give a relatively reasonable density. We note that this pGM water model is yet to be optimized to reproduce any physical water properties. Here, a setup of lower energy accuracy was used for reasonable simulation throughput, with the Ewald coefficient β₀ = 0.4 ${\stackrel{°}{\mathrm{A}}}^{-1}$, B-spline interpolation order = 8, FFT grid spacing = 0.5 $\stackrel{°}{\mathrm{A}}$, and direct space cutoff = 9 $\stackrel{°}{\mathrm{A}}$. The induced dipole convergence criterion was also raised to 10⁻⁶. The simulation time step was chosen to be 1 fs. The temperature was set to 300 K and the pressure 1.0 bar. The Berendsen thermostat and barostat were used and all other dynamics simulation parameters were set as default from the Amber SANDER program. The job was run on a single core of an INTEL Xeon E5-4620 central processing unit (CPU) with a wall-clock time of 6.9 days.

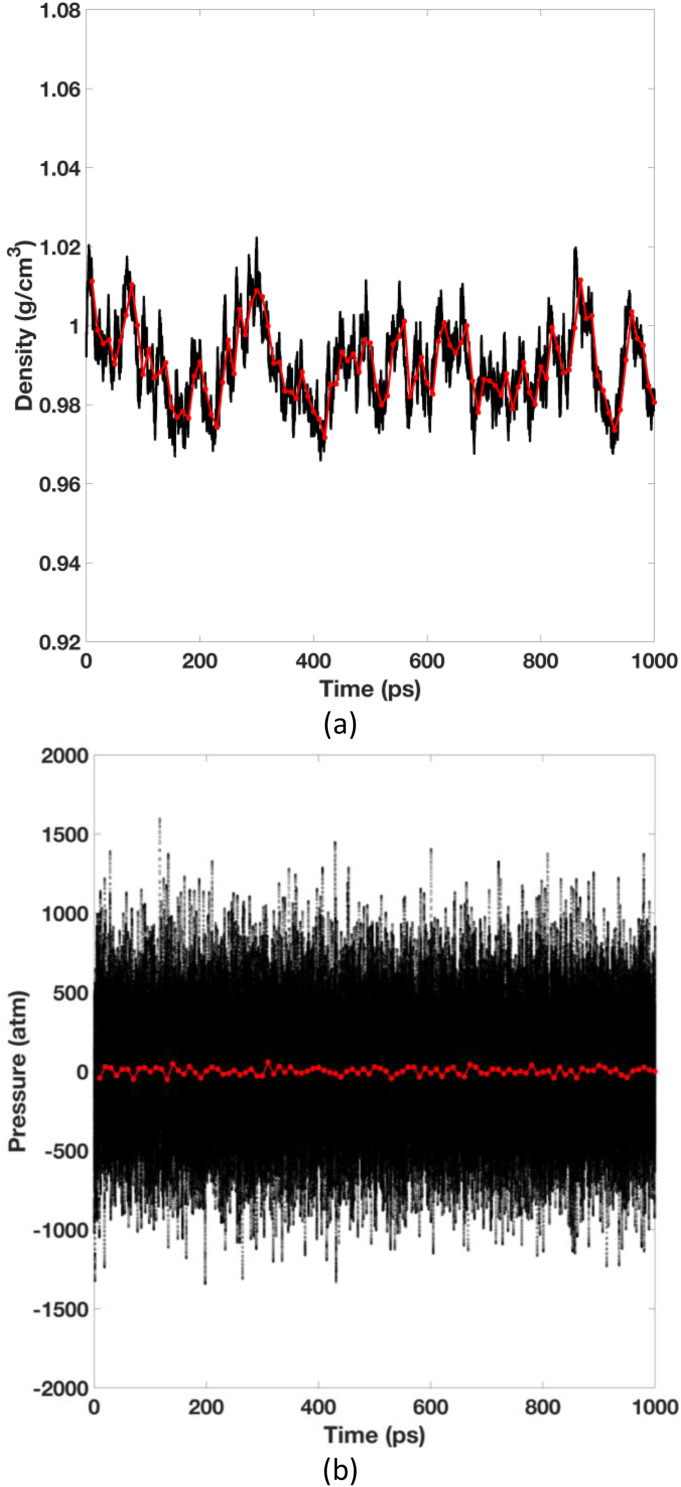
Figure 2 shows that the pGM/PME runs well under the NPT condition. Both density and pressure fluctuate around the equilibrium values, and the fluctuation ranges were similar to those observed for the classical point-charge models. The simulation was stable, no “polarization catastrophe” event was observed even if all interactions, including 1–2 and 1–3 interactions, were included.

FIG. 2.

Time evolutions of density and pressure of the NPT simulation for the 512-water box. The red lines are the running averages of every 10 ps. The time evolutions of total energy and temperature are available in the supplementary material. The time evolutions of density, total energy, and temperature of the Monte Carlo pressure-regulated simulation are also available in the supplementary material.

It is interesting to point out that the electrostatic component of the pGM water model is much smaller (∼1/10) than the TIP3P water model, even though the atomic charges are usually higher in polarizable models. This in part explains why we need to reduce the van der Waals parameters to 9% of the original TIP3P values, to match the much smaller electrostatic virial component so that the system would eventually equilibrate to a reasonable state. Indeed, the average density and pressure values are 0.99 g/cm³ and 1.0 bar during the 1 ns run, respectively. As a supporting evidence for the correct NPT implementation for the pGM model, we also implemented a Monte Carlo pressure regulation scheme for the pGM model, as no virial (pressure) calculation is needed in this regulation scheme.³⁰ The simulation followed the exact same setup and was found to stabilize at the same state, with the averaged density values of 0.99 g/cm³. The related plot of time evolutions of density, total energy, and temperature of Monte Carlo pressure regulation are available in the supplementary material.

The much-reduced electrostatic virial component is worth noting but a reasonable behavior. The induced dipoles in the pGM model are actively playing the role of electrostatic screening. As a result, the electrostatic interactions between water molecules are largely reduced, leading to much lower electrostatic virial component. This phenomenon shows that the polarizable pGM model is fundamentally different from classical point-charge models. Thus, its parameterization shall require extensive development and validation. Nevertheless, we reiterate that the goal of this development is not to develop a pGM water model, but to establish a constant pressure simulation protocol for polarizable methods, such as the pGM model.

Another interesting observation upon inspecting Fig. 2 is that the pGM water model exhibits a longer correlation time in density than the TIP3P water model, with pGM water’s density correlation time as long as 200–300 ps, rather than tens of picoseconds as is usually observed for point-charge water models. This effect could either result from the imperfect calibration of the pGM water tested here, the use of a barostat coupling constant that is too weak for the pGM model, or the inclusion of the explicit polarization in the pGM model, which requires longer time to equilibrate. Obviously, the point charge models also have certain level of polarization effect from reorientation of the molecules, but they certainly do not acquire any electronic polarization that is explicitly modeled with the induced dipoles. All these phenomena strongly suggest that the parameterization of pGM models requires extra care and extensive validations.

IV. CONCLUSION

In this work, we presented the derivation and implementation of an analytical method for achieving constant pressure simulation for the pGM model. Specifically, we derived the stress tensor expression for both the flexible and rigid body molecular system in the pGM electrostatic model, the trace of which gives the expression for internal stress. In addition, we showed how to correct the stress tensor if a short-range screening strategy is used in the force field development. Once the internal stress is obtained, by balancing it with the externally applied pressure through a certain type of barostat, a constant pressure simulation is readily realized.

Since the formulation of the stress tensor in pGM model is rather complex, we first performed a finite difference test to validate its correctness. We showed that for both the flexible and rigid-body systems, the finite-difference virial approaches the analytical values when decreasing the differentiation step size, confirming the accuracy of the derived expressions.

The tensor expression was implemented into the Amber/SANDER program and tested with a small box of 512 pGM water molecules. In the calculations, the revised TIP3P water geometry was applied, and the TIP3P van der Waals parameters were scaled down to 9% of the original values after imposing the pGM electrostatic interactions. After equilibration, the system was found to reach a reasonable density of 0.99 g/cm³ and pressure of 1.0 bar under the room temperature during the production run of 1 ns. A constant pressure simulation of the system with Monte Carlo pressure regulation scheme stabilized at the same state. This shows that the analytical stress tensor formula and its implementation are successful.

Several interesting differences were observed between the pGM water model and the TIP3P water model from which the pGM model was currently derived. Notably, the electrostatic virial was much smaller, requiring much smaller van der Waals parameters to reach reasonable water density. The density correlation time was also much longer. The observation strongly suggests that the pGM model, as a polarizable model, is fundamentally different compared to classic point charge models. Thus, the parameterization of the pGM model requires extra care and extensive validation, which is a major focus of the next step of our research.

SUPPLEMENTARY MATERIAL

The supplementary material includes finite-difference tests along the yy and zz directions of the 512-water box (Fig. S1), finite-difference tests along the xx directions of a 4096-water box (Fig. S2), time evolutions of total energy and temperature of the NPT simulation for the 512-water box (Fig. S3), time evolutions of density, total energy, and temperature of the Monte Carlo pressure-regulated NPT simulation (Fig. S4).

APPENDIX: MATHEMATICAL DETAILS

1. Several useful derivatives against h

$$\frac{\partial {\stackrel{\rightharpoonup }{R}}^{\alpha }}{\partial h_{\mu \nu }}={\delta }_{\alpha \mu }{\stackrel{\rightharpoonup }{S}}^{\nu },$$

$$\frac{\partial V}{\partial h_{\mu \nu }}=V{\left(h^{-1}\right)}_{\mu \nu }^T,$$

$$\frac{\partial {\left(h^{-1}\right)}_{\alpha \beta }}{\partial h_{\mu \nu }}=-{\left(h^{-1}\right)}_{\alpha \mu }{\left(h^{-1}\right)}_{\nu \beta },$$

$$\frac{\partial {\stackrel{\rightharpoonup }{m}}^{\alpha }}{\partial h_{\mu \nu }}=-{\stackrel{\rightharpoonup }{m}}^{\mu }{\left(h^{-1}\right)}_{\nu \alpha }.$$

2. Virial derivation

From previous discussions in the main text,

$$\frac{\partial U}{\partial h_{\mu \nu }}=\frac{\partial U_{rec}}{\partial h_{\mu \nu }}+\frac{\partial U_{dir}}{\partial h_{\mu \nu }}+\frac{\partial U_{\mathrm{self}}}{\partial h_{\mu \nu }}.$$

Since for the direct part and the self-part the only variable that depends on h is the atom coordinates $\stackrel{\rightharpoonup }{R}$, we have the following:

$$\begin{array}{ll}\hfill \frac{\partial U_{dir}}{\partial h_{\mu \nu }}& =\sum _i^N\frac{\partial {\stackrel{\rightharpoonup }{\mu }}_i}{\partial h_{\mu \nu }}\cdot {\nabla }_i\sum _{j\ne i}^{\infty }\left(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)-\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}}+\sum _i^N{\stackrel{\rightharpoonup }{p}}_i\cdot {\nabla }_i\sum _{j\ne i}^{\infty }\frac{\partial {\stackrel{\rightharpoonup }{\mu }}_j}{\partial h_{\mu \nu }}\cdot {\nabla }_j\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)-\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}}\hfill \\ \hfill & +\frac{1}{2}\sum _i^N\left(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_i\right)\sum _{j\ne i}^{\infty }\left(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j\right)\frac{\partial \frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)-\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}}}{\partial h_{\mu \nu }}+\frac{1}{2}\sum _i^N{\stackrel{\rightharpoonup }{p}}_i\cdot {\nabla }_i\sum _{j\ne i}^{\infty }{\stackrel{\rightharpoonup }{p}}_j\cdot {\nabla }_j\frac{\partial \frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)-\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}}}{\partial h_{\mu \nu }}\hfill \\ \hfill & +\sum _i^N{\stackrel{\rightharpoonup }{p}}_i\cdot {\nabla }_i\sum _{j\ne i}^{\infty }\left(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j\right)\frac{\partial \frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)-\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}}}{\partial h_{\mu \nu }}=\sum _i^N\frac{\partial {\stackrel{\rightharpoonup }{\mu }}_i}{\partial h_{\mu \nu }}\cdot {\nabla }_i\sum _{j\ne i}^{\infty }\left[q_j+\left({\stackrel{\rightharpoonup }{\mu }}_j+{\stackrel{\rightharpoonup }{p}}_j\right)\cdot {\nabla }_j\right]\hfill \\ \hfill & \times \frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)-\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}}+\frac{1}{2}\sum _i^N\left[q_i+\left({\stackrel{\rightharpoonup }{\mu }}_i+{\stackrel{\rightharpoonup }{p}}_i\right)\cdot {\nabla }_i\right]\sum _{j\ne i}^{\infty }\left[q_j+\left({\stackrel{\rightharpoonup }{\mu }}_j+{\stackrel{\rightharpoonup }{p}}_j\right)\cdot {\nabla }_j\right]\frac{\partial \frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)-\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}}}{\partial h_{\mu \nu }}\hfill \\ \hfill & =-\sum _i^N\frac{\partial {\stackrel{\rightharpoonup }{\mu }}_i}{\partial h_{\mu \nu }}\cdot {\stackrel{\rightharpoonup }{E}}_{dir}+\frac{1}{2}\sum _i^N\left[q_i+\left({\stackrel{\rightharpoonup }{\mu }}_i+{\stackrel{\rightharpoonup }{p}}_i\right)\cdot {\nabla }_i\right]\sum _{j\ne i}^{\infty }\left[q_j+\left({\stackrel{\rightharpoonup }{\mu }}_j+{\stackrel{\rightharpoonup }{p}}_j\right)\cdot {\nabla }_j\right]\frac{\partial \frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)-\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}}}{\partial {\stackrel{\rightharpoonup }{R}}_i}\cdot \left(\frac{\partial {\stackrel{\rightharpoonup }{R}}_i}{\partial h_{\mu \nu }}-\frac{\partial {\stackrel{\rightharpoonup }{R}}_j}{\partial h_{\mu \nu }}\right)\hfill \\ \hfill & =-\sum _i^N\sum _k^n{u}_{ik}\left[\frac{{\left({\stackrel{\rightharpoonup }{E}}_{dir}\right)}_i^{\mu }{\stackrel{\rightharpoonup }{S}}_{ik}^{\nu }}{\left|{\stackrel{\rightharpoonup }{R}}_{ik}\right|}-{\left({\stackrel{\rightharpoonup }{E}}_{dir}\right)}_i\cdot {\stackrel{\rightharpoonup }{R}}_{ik}\frac{{\stackrel{\rightharpoonup }{R}}_{ik}^{\mu }{\stackrel{\rightharpoonup }{S}}_{ik}^{\nu }}{{\left|{\stackrel{\rightharpoonup }{R}}_{ik}\right|}^3}\right]\hfill \\ \hfill & -\frac{1}{2}\sum _i^N\sum _{j\ne i}^{\infty }\left\{q_i{\left({\stackrel{\rightharpoonup }{E}}_{dir}\right)}_{j\to i}^{\mu }({\stackrel{\rightharpoonup }{S}}_i^{\nu }-{\stackrel{\rightharpoonup }{S}}_j^{\nu })+{\left[\left({\stackrel{\rightharpoonup }{u}}_i+{\stackrel{\rightharpoonup }{p}}_i\right)\cdot {\left({\stackrel{\rightharpoonup }{E}}_{dir}\right)}_{j\to i}\right]}^{\mu }({\stackrel{\rightharpoonup }{S}}_i^{\nu }-{\stackrel{\rightharpoonup }{S}}_j^{\nu })\right\}.\hfill \end{array}$$

Similarly, for the self-part,

$$\begin{array}{ll}\hfill \frac{\partial U_{\mathrm{self}}}{\partial h_{\mu \nu }}& =-\sum _i^N\sum _k^n{u}_{ik}\left[\frac{{\left({\stackrel{\rightharpoonup }{E}}_{\mathrm{self}}\right)}_i^{\mu }{\stackrel{\rightharpoonup }{S}}_{ik}^{\nu }}{\left|{\stackrel{\rightharpoonup }{R}}_{ik}\right|}-{\left({\stackrel{\rightharpoonup }{E}}_{\mathrm{self}}\right)}_i\cdot {\stackrel{\rightharpoonup }{R}}_{ik}\frac{{\stackrel{\rightharpoonup }{R}}_{ik}^{\mu }{\stackrel{\rightharpoonup }{S}}_{ik}^{\nu }}{{\left|{\stackrel{\rightharpoonup }{R}}_{ik}\right|}^3}\right]-\underset{{\stackrel{\rightharpoonup }{R}}_j\to {\stackrel{\rightharpoonup }{R}}_i}{\lim }\frac{1}{2}\sum _i^N\sum _{j\ne i}^{\infty }\left\{q_i{\left({\stackrel{\rightharpoonup }{E}}_{\mathrm{self}}\right)}_{j\to i}^{\mu }\left({\stackrel{\rightharpoonup }{S}}_i^{\nu }-{\stackrel{\rightharpoonup }{S}}_j^{\nu }\right)\right.+\left.{\left[\left({\stackrel{\rightharpoonup }{u}}_i+{\stackrel{\rightharpoonup }{p}}_i\right)\cdot {\left({\stackrel{\rightharpoonup }{E}}_{\mathrm{self}}\right)}_{j\to i}\right]}^{\mu }\left({\stackrel{\rightharpoonup }{S}}_i^{\nu }-{\stackrel{\rightharpoonup }{S}}_j^{\nu }\right)\right\}\hfill \\ \hfill & =-\sum _i^N\sum _k^n{u}_{ik}\left[\frac{{\left({\stackrel{\rightharpoonup }{E}}_{\mathrm{self}}\right)}_i^{\mu }{\stackrel{\rightharpoonup }{S}}_{ik}^{\nu }}{\left|{\stackrel{\rightharpoonup }{R}}_{ik}\right|}-{\left({\stackrel{\rightharpoonup }{E}}_{\mathrm{self}}\right)}_i\cdot {\stackrel{\rightharpoonup }{R}}_{ik}\frac{{\stackrel{\rightharpoonup }{R}}_{ik}^{\mu }{\stackrel{\rightharpoonup }{S}}_{ik}^{\nu }}{{\left|{\stackrel{\rightharpoonup }{R}}_{ik}\right|}^3}\right].\hfill \end{array}$$

However, the above approach cannot be applied for the reciprocal part of the virial. Thus, we must resort to a brute force calculation,

$$\frac{\partial U_{rec}}{\partial h_{\mu \nu }}=\left(1\right)+\left(2\right)+(3),$$

$$\left(1\right)=\frac{\partial \sum _i^N\frac{1}{2}\left(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_i\right)\frac{1}{\pi V}{\sum }_{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\sum _j^N\left[\left(q_j+2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{\mu }}_j\right)\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\right]\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}}{\partial h_{\mu \nu }},$$

$$\left(2\right)=\frac{1}{2}{p}_{i^{\prime }}^{{\alpha }^{\prime }}\frac{\partial {\partial }_{i^{\prime }}^{{\alpha }^{\prime }}{\partial }_{j^{\prime }}^{{\beta }^{\prime }}\frac{1}{\pi V}{\sum }_{\stackrel{\rightharpoonup }{m}\ne 0}\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_{j^{\prime }}\right)\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_{i^{\prime }}\right)}{\partial h_{\mu \nu }}{p}_{j^{\prime }}^{{\beta }^{\prime }},$$

$$\left(3\right)=\sum _i^N{\stackrel{\rightharpoonup }{p}}_i\cdot \frac{\partial {\nabla }_i\frac{1}{\pi V}{\sum }_{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\sum _j^N\left[\left(q_j+2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{\mu }}_j\right)\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\right]\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}}{\partial h_{\mu \nu }}.$$

For each part, we derive the following expressions:

$$\begin{array}{ll}\hfill \left(1\right)& =-\frac{1}{2\pi V}{\left(h^{-1}\right)}_{\mu \nu }^T\sum _{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\sum _j^N\left(q_j+2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{\mu }}_j\right)\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\sum _i^N\left(q_i-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{\mu }}_i\right)\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}\hfill \\ \hfill & +\frac{1}{\pi V}\sum _{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\left(-\frac{1+\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}}{{\stackrel{\rightharpoonup }{m}}^2}\right)\left(-{\stackrel{\rightharpoonup }{m}}^{\mu }{h}_{\nu \gamma }^{-1}{\stackrel{\rightharpoonup }{m}}^{\gamma }\right)\sum _j^N\left(q_j+2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{\mu }}_j\right)\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\right.\hfill \\ \hfill & \times \left.\sum _i^N\left(q_i-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{\mu }}_i\right)\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}+\frac{1}{\pi V}\sum _{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\sum _j^N(q_j+2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{\mu }}_j)\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\right.\hfill \\ \hfill & \times \left.\sum _i^N\sum _k^n\left[\left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_{ik}{\mu }_{ik}\right)\left(-\frac{{\stackrel{\rightharpoonup }{R}}_{ik}^{\mu }{\stackrel{\rightharpoonup }{S}}_{ik}^{\nu }}{{\left|{\stackrel{\rightharpoonup }{R}}_{ik}\right|}^3}\right)\right]\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\},\hfill \end{array}$$

$$\begin{array}{ll}\hfill \left(2\right)& =-\frac{1}{2\pi V}{\left(h^{-1}\right)}_{\mu \nu }^T\sum _{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\sum _j^N\left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{p}}_j\right)\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\sum _i^N\left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{p}}_i\right)\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}\hfill \\ \hfill & +\frac{1}{\pi V}\sum _{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\left(-\frac{1+\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}}{{\stackrel{\rightharpoonup }{m}}^2}\right)\left(-{\stackrel{\rightharpoonup }{m}}^{\mu }{h}_{\nu \gamma }^{-1}{\stackrel{\rightharpoonup }{m}}^{\gamma }\right)\sum _j^N\left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{p}}_j\right)\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\sum _i^N\left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{p}}_i\right)\right.\hfill \\ \hfill & \times \left.\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}+\frac{1}{\pi V}\sum _{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\sum _j^N(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{p}}_j)\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\right.\hfill \\ \hfill & \times \left.\sum _i^N\left[\left(-2\pi i\right)\left(-{\stackrel{\rightharpoonup }{m}}^{\mu }{h}_{\nu \gamma }^{-1}{p}_i^{\gamma }\right)\right]\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\},\hfill \end{array}$$

$$\begin{array}{ll}\hfill \left(3\right)& =-\frac{1}{\pi V}{\left(h^{-1}\right)}_{\mu \nu }^T\sum _{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\sum _j^N\left(q_j+2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{\mu }}_j\right)\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\sum _i^N\left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{p}}_i\right)\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}\hfill \\ \hfill & +\frac{2}{\pi V}\sum _{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\left(-\frac{1+\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}}{{\stackrel{\rightharpoonup }{m}}^2}\right)\left(-{\stackrel{\rightharpoonup }{m}}^{\mu }{h}_{\nu \gamma }^{-1}{\stackrel{\rightharpoonup }{m}}^{\gamma }\right)\sum _j^N\left(q_j+2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{\mu }}_j\right)\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\sum _i^N\left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{p}}_i\right)\right.\hfill \\ \hfill & \times \left.\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}+\frac{1}{\pi V}\sum _{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\sum _j^N\left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{p}}_j\right)\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\right.\hfill \\ \hfill & \times \left.\sum _i^N\sum _k^n\left[\left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_{ik}{\mu }_{ik}\right)\left(-\frac{{\stackrel{\rightharpoonup }{R}}_{ik}^{\mu }{\stackrel{\rightharpoonup }{S}}_{ik}^{\nu }}{{\left|{\stackrel{\rightharpoonup }{R}}_{ik}\right|}^3}\right)\right]\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}\hfill \\ \hfill & +\frac{1}{\pi V}\sum _{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\sum _j^N(q_j+2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{\mu }}_j)\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\sum _i^N\left[\left(-2\pi i\right)\left(-{\stackrel{\rightharpoonup }{m}}^{\mu }{h}_{\nu \gamma }^{-1}{p}_i^{\gamma }\right)\right]\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}.\hfill \end{array}$$

By adding together expressions for (1), (2), and (3), we arrive at the final result for $\frac{\partial U_{rec}}{\partial h_{\mu \nu }}$, which is shown in Sec. II.

3. Virial of rigid body systems

As in the derivation presented in Appendix A 2, for the direct part and the self-part, the only variable that depends on h is the atom coordinate $\stackrel{\rightharpoonup }{R}$. However, a major difference is that, for the rigid molecules, the covalent dipole $\stackrel{\rightharpoonup }{u}$ is a constant vector now. Thus, the derivation complexity is greatly reduced,

$$\begin{array}{ll}\hfill \frac{\partial U_{dir}}{\partial h_{\mu \nu }}& =-\frac{1}{2}\sum _i^N\sum _{j\ne i}^{\infty }\left\{q_i{\left({\stackrel{\rightharpoonup }{E}}_{dir}\right)}_{j\to i}^{\mu }({\stackrel{\rightharpoonup }{S}}_{i0}^{\nu }-{\stackrel{\rightharpoonup }{S}}_{j0}^{\nu })\right.\hfill \\ \hfill & +\left.{\left[\left({\stackrel{\rightharpoonup }{u}}_i+{\stackrel{\rightharpoonup }{p}}_i\right)\cdot {\left({\stackrel{\rightharpoonup }{E}}_{dir}\right)}_{j\to i}\right]}^{\mu }({\stackrel{\rightharpoonup }{S}}_{i0}^{\nu }-{\stackrel{\rightharpoonup }{S}}_{j0}^{\nu })\right\},\hfill \end{array}$$

$$\frac{\partial U_{\mathrm{self}}}{\partial h_{\mu \nu }}=0.$$

As for the reciprocal part, we follow the procedure presented in Appendix A 2,

$$\begin{array}{ll}\hfill \left(1\right)& =-\frac{1}{2\pi V}{\left(h^{-1}\right)}_{\mu \nu }^T\sum _{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\sum _j^N\left(q_j+2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{\mu }}_j\right)\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\sum _i^N\left(q_i-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{\mu }}_i\right)\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}\hfill \\ \hfill & +\frac{1}{\pi V}\sum _{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\left(-\frac{1+\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}}{{\stackrel{\rightharpoonup }{m}}^2}\right)\left(-{\stackrel{\rightharpoonup }{m}}^{\mu }{h}_{\nu \gamma }^{-1}{\stackrel{\rightharpoonup }{m}}^{\gamma }\right)\sum _j^N\left(q_j+2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{\mu }}_j\right)\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\sum _i^N\left(q_i-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{\mu }}_i\right)\right.\hfill \\ \hfill & \times \left.\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}+\frac{1}{\pi V}\sum _{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\sum _j^N\left[-2\pi i{\stackrel{\rightharpoonup }{m}}^{\mu }{h}_{\nu \gamma }^{-1}{\stackrel{\rightharpoonup }{\mu }}_j^{\gamma }\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\right.\right.\hfill \\ \hfill & \left.-\left.\left(q_j+2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{\mu }}_j\right)2\pi i{\stackrel{\rightharpoonup }{m}}^{\mu }{h}_{\nu \gamma }^{-1}{\stackrel{\rightharpoonup }{d}}_j^{\gamma }\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\right]\sum _i^N(q_i-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{\mu }}_i)\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\},\hfill \end{array}$$

$$\begin{array}{ll}\hfill \left(2\right)& =-\frac{1}{2\pi V}{\left(h^{-1}\right)}_{\mu \nu }^T\sum _{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\sum _j^N\left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{p}}_j\right)\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\sum _i^N\left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{p}}_i\right)\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}\hfill \\ \hfill & +\frac{1}{\pi V}\sum _{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\left(-\frac{1+\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}}{{\stackrel{\rightharpoonup }{m}}^2}\right)\left(-{\stackrel{\rightharpoonup }{m}}^{\mu }{h}_{\nu \gamma }^{-1}{\stackrel{\rightharpoonup }{m}}^{\gamma }\right)\sum _j^N\left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{p}}_j\right)\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\sum _i^N\left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{p}}_i\right)\right.\hfill \\ \hfill & \times \left.\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}+\frac{1}{\pi V}\sum _{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\sum _j^N\left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{p}}_j\right)\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\right.\hfill \\ \hfill & \times \left.\sum _i^N\left[\left(-2\pi i\right)\left(-{\stackrel{\rightharpoonup }{m}}^{\mu }{h}_{\nu \gamma }^{-1}{p}_i^{\gamma }\right)\right]\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}+\frac{1}{\pi V}\sum _{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\sum _j^N\left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{p}}_j\right)(-2\pi i{\stackrel{\rightharpoonup }{m}}^{\mu }{h}_{\nu \gamma }^{-1}{\stackrel{\rightharpoonup }{d}}_j^{\gamma })\right.\hfill \\ \hfill & \times \left.\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\sum _i^N\left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{p}}_i\right)\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\},\hfill \end{array}$$

$$\begin{array}{ll}\hfill \left(3\right)& =-\frac{1}{\pi V}{\left(h^{-1}\right)}_{\mu \nu }^T\sum _{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\sum _j^N\left(q_j+2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{\mu }}_j\right)\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\sum _i^N\left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{p}}_i\right)\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}\hfill \\ \hfill & +\frac{2}{\pi V}\sum _{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\left(-\frac{1+\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}}{{\stackrel{\rightharpoonup }{m}}^2}\right)\left(-{\stackrel{\rightharpoonup }{m}}^{\mu }{h}_{\nu \gamma }^{-1}{\stackrel{\rightharpoonup }{m}}^{\gamma }\right)\sum _j^N\left(q_j+2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{\mu }}_j\right)\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\sum _i^N\left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{p}}_i\right)\right.\hfill \\ \hfill & \times \left.\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}+\frac{1}{\pi V}\sum _{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\sum _j^N\left[-2\pi i{\stackrel{\rightharpoonup }{m}}^{\mu }{h}_{\nu \gamma }^{-1}{\stackrel{\rightharpoonup }{\mu }}_j^{\gamma }\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)-\left(q_j+2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{\mu }}_j\right)\right.\right.\hfill \\ \hfill & \times \left.\left.2\pi i{\stackrel{\rightharpoonup }{m}}^{\mu }{h}_{\nu \gamma }^{-1}{\stackrel{\rightharpoonup }{d}}_j^{\gamma }\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\right]\sum _i^N\left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{p}}_i\right)\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}\hfill \\ \hfill & +\frac{1}{\pi V}\sum _{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\sum _j^N(q_j+2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{\mu }}_j)\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\sum _i^N\left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{p}}_i\right)(2\pi i{\stackrel{\rightharpoonup }{m}}^{\mu }{h}_{\nu \gamma }^{-1}{\stackrel{\rightharpoonup }{d}}_i^{\gamma })\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}.\hfill \end{array}$$

By adding final expressions for (1), (2), and (3), we arrive at the result for $\frac{\partial U_{rec}}{\partial h_{\mu \nu }}$,

$$\begin{array}{ll}\hfill \frac{\partial U_{rec}}{\partial h_{\mu \nu }}& =-\frac{1}{2}{\left(h^{-1}\right)}_{\mu \nu }^T\cdot \sum _i^N\left[q_i{\left({\varphi }_{rec}\right)}_i-\left({\stackrel{\rightharpoonup }{\mu }}_i+{\stackrel{\rightharpoonup }{p}}_i\right)\cdot {\left({\stackrel{\rightharpoonup }{E}}_{rec}\right)}_i\right]+\frac{1}{\pi V}\sum _{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\left(-\frac{1+\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}}{{\stackrel{\rightharpoonup }{m}}^2}\right)\right.\hfill \\ \hfill & \times \left.\left(-{\stackrel{\rightharpoonup }{m}}^{\mu }{h}_{\nu \gamma }^{-1}{\stackrel{\rightharpoonup }{m}}^{\gamma }\right)S\left(\stackrel{\rightharpoonup }{m}\right)S\left(-\stackrel{\rightharpoonup }{m}\right)\right\}+\sum _i^N{\left({\stackrel{\rightharpoonup }{E}}_{rec}\right)}_i^{\mu }{h}_{\nu \gamma }^{-1}\left({\stackrel{\rightharpoonup }{\mu }}_i^{\gamma }+{\stackrel{\rightharpoonup }{p}}_i^{\gamma }+q_i{\stackrel{\rightharpoonup }{d}}_i^{\gamma }\right)+\sum _i^N\left({\stackrel{\rightharpoonup }{\mu }}_i^{\gamma }+{\stackrel{\rightharpoonup }{p}}_i^{\gamma }\right){\left({\stackrel{\rightharpoonup }{E}}_{rec}\right)}_i^{\gamma \mu }{h}_{\nu \xi }^{-1}{\stackrel{\rightharpoonup }{d}}_i^{\xi }.\hfill \end{array}$$

Finally, adding up all the above terms and removing the common factor $-{\left(h^{-1}\right)}^T$, the final expression is the one shown in Sec. II.

4. Screening correction

If certain short-range electrostatic interactions are screened, the pGM system energy can be expressed as

$$U=\sum _i^N\frac{1}{2}(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_i){\varphi }_i^{0*}+\sum _i^N\frac{1}{2}({\stackrel{\rightharpoonup }{p}}_i^{*}\cdot {\nabla }_i){\varphi }_i^{0*}.$$

Here, ${\varphi }_i^{0*}$ represents the electrostatic potential on atom i that is created by only charges and covalent dipoles that are not screened in the system, and ${\stackrel{\rightharpoonup }{p}}_i^{*}$ means the induced dipole on atom i that is created under the screening condition. Specifically,

$$\begin{array}{ll}\hfill {\varphi }_i^{0*}& =\frac{1}{\pi V}\sum _{\stackrel{\rightharpoonup }{m}\ne 0}\left\{\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\sum _j^N\left[\left(q_j+2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{\mu }}_j\right)\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\right]\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)\right\}+\sum _{\begin{array}{c}\hfill j\notin *\left(i\right)\hfill \\ \hfill j\ne i\hfill \end{array}}^{\infty }\left(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j\right)\hfill \\ \hfill & \times \frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)-\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}}-\underset{{\stackrel{\rightharpoonup }{R}}_j\to {\stackrel{\rightharpoonup }{R}}_i}{\lim }\left(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}}-\sum _{j\in *\left(i\right)}(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j)\frac{\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}},\hfill \end{array}$$

$$\begin{array}{c}{\stackrel{\rightharpoonup }{p}}_i^{*}={\alpha }_i({\stackrel{\rightharpoonup }{E}}_i^{0*}-\sum _j^N{\stackrel{\rightharpoonup }{T}}_{ij}^{*}\cdot {\stackrel{\rightharpoonup }{p}}_j^{*}),\\ {\stackrel{\rightharpoonup }{E}}_i^{0*}=-{\nabla }_i{\varphi }_i^{0*},\end{array}$$

$$T_{ij}^{*\alpha \beta }={\partial }_i^{\alpha }{\partial }_j^{\beta }\left\{\begin{array}{cc}\frac{1}{\pi V}\sum _{\stackrel{\rightharpoonup }{m}\ne 0}\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)+\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)-\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}}\hfill & \mathrm{if}i\ne j,j\notin *\left(i\right),\hfill \\ \frac{1}{\pi V}\sum _{\stackrel{\rightharpoonup }{m}\ne 0}\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)-\underset{{\stackrel{\rightharpoonup }{R}}_j\to {\stackrel{\rightharpoonup }{R}}_i}{\lim }\frac{\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}}\hfill & \mathrm{if}i=j,\hfill \\ \frac{1}{\pi V}\sum _{\stackrel{\rightharpoonup }{m}\ne 0}\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{\beta }_0^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right)\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)-\frac{\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}}\hfill & \mathrm{if}j\in *\left(i\right).\hfill \end{array}\right.$$

Here, $*\left(i\right)$ represent the screened atom pairs of atom i.

Before we calculate the correction term under screening conditions for virial, we want to first show the electrostatic force expression under screening. Following our previous paper, it can be easily shown that

$$\begin{array}{ll}\hfill {\stackrel{\rightharpoonup }{F}}_i^{covalent-covalent*}& =\sum _j^n{\nabla }_i\left({\stackrel{\rightharpoonup }{u}}_j\right)\cdot {\stackrel{\rightharpoonup }{E}}_j^{covalent*}+q_i{\stackrel{\rightharpoonup }{E}}_i^{covalent*}+{\stackrel{\rightharpoonup }{u}}_i\cdot {\stackrel{\rightharpoonup }{E}}_i^{covalent*}.\hfill \end{array}$$

The asterisk here means that the quantities are calculated under the screening condition.

The induced part, however, requires some extra attention:

$${\stackrel{\rightharpoonup }{F}}_i^{induced}={\stackrel{\rightharpoonup }{p}}_i^{*}\cdot {\stackrel{\rightharpoonup }{E}}_i^{induced*}+\sum _j^N{\nabla }_i({\stackrel{\rightharpoonup }{E}}_j^{covalent*})\cdot {\stackrel{\rightharpoonup }{p}}_j^{*}.$$

Here,

$$\begin{array}{ll}\hfill \sum _j^N{\nabla }_i\left({\stackrel{\rightharpoonup }{E}}_j^{covalent*}\right)\cdot {\stackrel{\rightharpoonup }{p}}_j^{*}& =\sum _{j\ne i}^N\sum _{\begin{array}{c}\hfill k\ne j\hfill \\ \hfill k\notin *\left(j\right)\hfill \end{array}}^n\left(-{\nabla }_i\left({\stackrel{\rightharpoonup }{u}}_k\right)\right)\cdot {\nabla }_k\left({\stackrel{\rightharpoonup }{p}}_j^{*}\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_{jk}{R}_{jk}\right)}{{\beta }_{jk}{R}_{jk}}-\sum _{\begin{array}{c}\hfill j\ne i\hfill \\ \hfill j\notin *\left(i\right)\hfill \end{array}}^N\left(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_i\right){\nabla }_i\left({\stackrel{\rightharpoonup }{p}}_j^{*}\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{{\beta }_{ij}{R}_{ij}}\hfill \\ \hfill & -\sum _{\begin{array}{c}\hfill k\ne i\hfill \\ \hfill k\notin *\left(i\right)\hfill \end{array}}^n{\nabla }_i\left({\stackrel{\rightharpoonup }{u}}_k\right)\cdot {\nabla }_k\left({\stackrel{\rightharpoonup }{p}}_i^{*}\cdot {\nabla }_i\right)\frac{\text{erf}\left({\beta }_{ik}{R}_{ik}\right)}{{\beta }_{ik}{R}_{ik}}-\sum _{\begin{array}{c}\hfill k\ne i\hfill \\ \hfill k\notin *\left(i\right)\hfill \end{array}}^N\left(q_k+{\stackrel{\rightharpoonup }{\mu }}_k\cdot {\nabla }_k\right){\nabla }_i\left({\stackrel{\rightharpoonup }{p}}_i^{*}\cdot {\nabla }_i\right)\frac{\text{erf}\left({\beta }_{ik}{R}_{ik}\right)}{{\beta }_{ik}{R}_{ik}}\hfill \\ \hfill & =\sum _j^N\sum _{\begin{array}{c}\hfill k\ne j\hfill \\ \hfill k\notin *\left(j\right)\hfill \end{array}}^n\left(-{\nabla }_i\left({\stackrel{\rightharpoonup }{u}}_k\right)\right)\cdot {\nabla }_k\left({\stackrel{\rightharpoonup }{p}}_j^{*}\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_{jk}{R}_{jk}\right)}{{\beta }_{jk}{R}_{jk}}-\sum _{\begin{array}{c}\hfill j\ne i\hfill \\ \hfill j\notin *\left(i\right)\hfill \end{array}}^N\left(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_i\right){\nabla }_i\left({\stackrel{\rightharpoonup }{p}}_j^{*}\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{{\beta }_{ij}{R}_{ij}}\hfill \\ \hfill & -\sum _{\begin{array}{c}\hfill k\ne i\hfill \\ \hfill k\notin *\left(i\right)\hfill \end{array}}^N\left(q_k+{\stackrel{\rightharpoonup }{\mu }}_k\cdot {\nabla }_k\right){\nabla }_i\left({\stackrel{\rightharpoonup }{p}}_i^{*}\cdot {\nabla }_i\right)\frac{\text{erf}\left({\beta }_{ik}{R}_{ik}\right)}{{\beta }_{ik}{R}_{ik}}\hfill \\ \hfill & =\sum _k^n\sum _{\begin{array}{c}\hfill j\ne k\hfill \\ \hfill j\notin *\left(k\right)\hfill \end{array}}^N\left(-{\nabla }_i\left({\stackrel{\rightharpoonup }{u}}_k\right)\right)\cdot {\nabla }_k\left({\stackrel{\rightharpoonup }{p}}_j^{*}\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_{jk}{R}_{jk}\right)}{{\beta }_{jk}{R}_{jk}}+q_i{\stackrel{\rightharpoonup }{E}}_i^{induced*}+{\stackrel{\rightharpoonup }{u}}_i\cdot {\stackrel{\rightharpoonup }{\mathrm{E}}}_i^{induced*}+{\stackrel{\rightharpoonup }{p}}_i^{*}\cdot {\stackrel{\rightharpoonup }{\mathrm{E}}}_i^{covalent*}\hfill \\ \hfill & =\sum _k^n{\nabla }_i\left({\stackrel{\rightharpoonup }{u}}_k\right)\cdot {\stackrel{\rightharpoonup }{E}}_k^{induced*}+q_i{\stackrel{\rightharpoonup }{E}}_i^{induced*}+{\stackrel{\rightharpoonup }{u}}_i\cdot {\stackrel{\rightharpoonup }{\mathrm{E}}}_i^{induced*}+{\stackrel{\rightharpoonup }{p}}_i^{*}\cdot {\stackrel{\rightharpoonup }{\mathrm{E}}}_i^{covalent*}.\hfill \end{array}$$

In the derivation here, we have used the fact that if $j\in *\left(i\right)$ then $i\in *\left(j\right)$ for any i and j.

So, the result for the force under the screening condition is

$${\stackrel{\rightharpoonup }{F}}_i^{*}=\sum _j^n{\nabla }_i\left({\stackrel{\rightharpoonup }{u}}_j\right)\cdot {\stackrel{\rightharpoonup }{E}}_j^{*}+q_i{\stackrel{\rightharpoonup }{E}}_i^{*}+({\stackrel{\rightharpoonup }{u}}_i+{\stackrel{\rightharpoonup }{p}}_i^{*})\cdot {\stackrel{\rightharpoonup }{E}}_i^{*}.$$

The asterisk here means that the quantities are calculated under the screening condition.

To derive the correction of screening for virial, we notice that the only variable in the correction term that depends on h is the atom coordinate $\stackrel{\rightharpoonup }{R}$, so, the virial correction is

$$\begin{array}{ll}\hfill \frac{\partial U_{correction}}{\partial h_{\mu \nu }}& =\frac{\partial \sum _i^N\frac{1}{2}(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_i)\sum _{j\ne i}^{\infty }(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j)\frac{-\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}}{\partial h_{\mu \nu }}\hfill \\ \hfill & +\frac{1}{2}{p}_{i^{\prime }}^{*{\alpha }^{\prime }}\frac{\partial {\partial }_{i^{\prime }}^{{\alpha }^{\prime }}{\partial }_{j^{\prime }}^{{\beta }^{\prime }}\frac{-\text{erf}\left({\beta }_{i^{\prime }{j}^{\prime }}{R}_{i^{\prime }{j}^{\prime }}\right)}{R_{i^{\prime }{j}^{\prime }}}}{\partial h_{\mu \nu }}{p}_{j^{\prime }}^{*{\beta }^{\prime }}\hfill \\ \hfill & +\sum _i^N{\stackrel{\rightharpoonup }{p}}_i^{*}\cdot \frac{\partial {\nabla }_i\sum _{j\ne i}^{\infty }(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j)\frac{-\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}}{\partial h_{\mu \nu }}.\hfill \end{array}$$

Following a similar derivation as in Appendix A 2, we can easily obtain the correction term for the virial expression under screening, as shown in Sec. II.

AUTHOR DECLARATIONS

Conflict of Interest

We declare there is no conflict of interest.

DATA AVAILABILITY

The algorithms developed in this study and the validation data are deposited in the Amber repository and will be made publicly available in the next Amber/AmberTools release at http://ambermd.org/.