Meta-Hybrid Density Functional Theory Prediction of the Reactivity, Stability, and IGM of Azepane, Oxepane, Thiepane, and Halogenated Cycloheptane

Abstract

The application of plain cycloalkanes and heterocyclic derivatives in the synthesis of valuable natural products and pharmacologically active intermediates has increased tremendously in recent times with much attention being paid to the lower cycloalkane members. The structural and molecular properties of higher seven-membered and nonaromatic heterocyclic derivatives are less known despite their stable nature and vast application; thus, an insight into their structural and electronic properties is still needed. Appropriate quantum chemical calculations utilizing the ab initio (MP2) method, meta-hybrid (M06-2X) functional, and long-range-separated functionals (ωB97XD) have been utilized in this work to investigate the structural reactivity, stability, and behavior of substituents on cycloheptane (CHP) and its derivatives: azepane, oxepane, thiepane, fluorocycloheptane (FCHP), bromocycloheptane (BrCHP), and chlorocycloheptane (ClCHP). Molecular global reactivity descriptors such as Fukui function, frontier molecular orbitals (FMOs), and molecular electrostatic potential were computed and compared with lower members. The results of two population methods CHELPG and Atomic Dipole Corrected Hirshfeld Charges (ADCH) were equally compared to scrutinize the charge distribution in the molecules. The susceptibility of intramolecular interactions between the substituents and cycloalkane ring is revealed by natural bond orbital analysis and intramolecular weak interactions by the independent gradient model (IGM). Other properties such as atomic density of states, intrinsic bond strength index (IBSI), and dipole moments are considered. It is acclaimed that the strain effect is a major determinant effect in the energy balance of cyclic molecules; thus, the ring strain energies and validation of spectroscopic specificities with reference to the X-ray crystallographic data are also considered.

1. Introduction

Heterocyclic or carbocyclic compounds, also known as heterocycles, constitute a class of organic ring-membered compounds characterized by the presence of at least two distinct elements, of which at least one is a heteroatom. Heterocyclic compounds are similar to cyclic organic compounds, but the presence of heteroatoms endows heterocyclic compounds with physical and chemical properties that are quite distinct from those of their carbon-ring analogues. When a carbon atom of a seven-membered carbocycle is replaced by a heteroatom, a corresponding seven-membered heterocyclic system is obtained depending on the hybridization state (sp² or sp³) and nature of the heterocycle. By virtue of substitution with a heteroatom in the resulting system, the electron density (ED) within the ring system is redistributed, thus causing a significant change in the molecular behavior and properties of the system, which enables further modification of several other molecular properties like reactivity, optoelectronic properties, etc. Hence, in the case of cycloheptane, in which all carbon atoms are equivalent, the replacement of one carbon atom produces a fully saturated heterocyclic system. Heterocyclic compounds are readily applicable in the synthesis of naturally occurring pigments, vitamins, and antibiotics, and some act as hallucinogens.^1,2

The most common heterocyclic compounds are the five- or six-membered rings containing heteroatoms of nitrogen (N), oxygen (O), and sulfur (S). Over the years, much attention has been paid to the fully saturated and unsaturated three- and four-membered rings because of their small sizes and well-known reactive nature and uses as intermediates, but the saturated and unsaturated seven-membered rings and higher members are stable but less investigated. Recently, much attention has been directed toward the unsaturated seven-membered ring systems due to their application in biochemistry, solar cells and photovoltaics, organic light-emitting diodes (OLEDs), and thin-film transistors. Heterocyclic compounds, in general, have become an important pharmacophore due to promising applications in medicine and nonlinear optics (NLO) fields.^1,2 Thus, we have substituted one carbon atom of cycloheptane with N, O, and S to obtain the corresponding heterocycles, viz, azepane, oxepane, and thiepane, to computationally elucidate their electronic properties, particularly reactivity and stability, and compare these properties to the parent cycloheptane and halo-substituted cycloheptane as well as other lower-member cyclic hydrocarbons using appropriate density functional theory (DFT) methods.

Some of the reasons why the study of halo-substituted compounds may be considered significant are the abundance of halogenated compounds in natural products and pharmacologically active compounds, which are increasingly being exploited. Several classes of halogenated compounds have been successfully applied in the synthesis of paints, dyes, adhesives, flame retardants, and solvents and the development of new materials. Despite the halogenation process being accompanied by the use of toxic chemicals, the application of halogens in the development of new products and molecules is still being utilized. It has been reported that the incorporation of halogens (carbon–halogen bond) increases the oxidative and thermal stability, which results in a lowering of the sensitivity of P450 toward oxidation.^3,4 It has also been reported that the carbon–halogen bond increases the biological membrane permeability of most compounds. Halogenated compounds are essentially significant in agricultural applications, and halogenation has been demonstrated to be an important tool for the development of efficient agricultural products.⁵

Electronic structure methods are accurate in investigating the basic electronic properties of molecules, and these methods have been utilized over the years to predict molecular behavior. The theoretical conformational analysis of seven-membered rings, thiepane and 1,4-oxathiepane, has long been reported.⁶ Also, numerous force fields were proposed to study the pseudorotational equilibria of cycloheptane.⁷ And most of the studies conducted revealed that cycloheptane and its derivatives, such as 1,4-dioxepane, 1,3-dioxepane, 6,7-dihydro-SH-1, etc., mostly prefer the chair, twist-chair, or twist-boat conformations depending on the position and presence of a heteroatom or double bonds in the molecular structure.^7,8 In another study conducted by Dillen,⁹ a holistic conformational analysis of azepane, oxepane, silepane, phosphepane, thiepane, and the azepanium cation was carried out by high-level electronic structure calculations, and the results compared appropriately with those of the well-known cycloheptane. The twist-chair conformation was the most stable conformation reported for the studied systems, and the chair conformation was mostly associated with the transition state. This study also reported that the presence of second-row heteroatoms lowers the relative energy of the boat conformations in comparison to the chair conformations. The structural and conformational stability of 1-chloromethyl-1-fluorosilacyclohexane has been reported, and Raman and infrared vibrational spectroscopy were conducted using the DFT/B3LYP/aug-cc-pVDZ and the MP2/aug-cc-pVDZ level of theory. It was observed that 1-chloromethyl-1-fluorosilacyclohexane may exist in 12 different conformations, of which the chair axial trans conformer was found to be the most stable conformer.¹⁰ It is worth noting that the aim of this study is not to investigate the conformational behavior of the chosen systems. However, the above citations have guided the understanding of the conformational behavior of the chosen systems and facilitated their geometry optimization to obtain the molecules to the correct energetic minima and conformation.

Other relevant citations to this study may include the study of 10 molecules chosen to represent the symmetrically disubstituted formaldehyde and thioformaldehyde investigated by ref (11) to elucidate their quantum chemical properties. Five-membered heterocyclic substituents containing a single group of 16 heteroatoms were taken into consideration to investigate the influence of heteroatom rings on quantum molecular properties such as dipole moment, frontier molecular orbital (MO), polarizabilities, and energetic stability for these studied systems. More so, insight from refs (12−15) has contributed significantly to this work.

To the best of our knowledge, the structural features and vibrational analysis of seven-membered nonaromatic heterocyclic compounds are less developed; although these compounds are usually stable and some have found practical application in pharmaceutical applications, insight into the structural and electronic properties is still needed. Also, the electronic, reactivity, and structural investigations of halogenated seven-membered cycloalkane (cycloheptane) derivatives have not been reported, and over the years, much attention has been paid to the lower-member heterocyclic ring compounds and lower-member cycloalkanes due to the paucity of the literature reported for these compounds. Thus, considering the vast application of plain cycloalkanes and the scarcity of research for these compounds, the theoretical reactivity and structural investigation of cycloheptane and its derivatives [oxepane, azepane, thiepane, fluorocycloheptane (FCHP), bromocycloheptane (BrCHP), and chlorocycloheptane (ClCHP)] was conducted using the meta-hybrid functional (M06-2X), long-range-separated functional (DFT/ωB97XD), and ab initio (MP2) methods to explore the structural characteristics, which might be helpful toward the advancement of research and application of these compounds in various fields. The optimized molecular structures of the compounds are presented in Figure 1. Understanding the intramolecular interactions in molecules is essential for theoretical research and practical purposes; thus, in this research, we attempted to explain the relationship between the resonance stabilization energy exhibited in the form of donor–acceptor interactions between the halogens and heteroatoms with the ring (the influence of substitution on cycloheptane rings) through the evaluation of electrostatic potential (ESP) distribution, natural bond orbital analysis (NBO), and electron density distribution by noncovalent interactions [independent gradient model (IGM)-based noncovalent interaction]. DFT calculations have been utilized in this work to explore global reactivity descriptors, Fukui function, intrinsic bond strength index (IBSI), atomic charges, validation of spectroscopic properties, and elucidation of vibrational specificities again with the intention of revealing how energy gap could influence the electronic properties of the chosen compounds.

Figure 1.

Optimized molecular structures of the studied compounds (a) azepane, (b) oxepane, (c) thiepane, (d) FCHP, (e) BrCHP (f) ClCHP, and (g) CHP.

2. Computational Details

The full geometry optimization of the respective systems was performed using the ab initio (MP2) method and the M06-2X method with the split-valence 6-311++G(d,p) and aug-cc-pVTZ basis sets using Gaussian 16.^16,17 Initial equilibrium structural minimization of the studied systems was conducted with the help of molecular mechanics force field geometry optimization computational module embedded in HyperChem 8.0 software.¹⁸ It is evident from the literature that higher-member cycloalkanes exist in diverse conformations. Therefore, to ensure that the correct and most stable conformation is selected for studies and in the exact energetic minima, a conformational search was conducted using the search module of HyperChem to obtain the different conformations for the modeled systems. The chair conformation was observed to be the most stable conformer from energetic observations and thus was selected for proper geometry optimization. This observation is in line with several reports on the conformations of cycloheptane and higher members, as cited in paragraph three of the Introduction section. The same computational approach was used to ascertain that the optimized structures correspond to local minima on the potential energy surface by conducting vibrational frequency calculations on the optimized structures; no arbitrary frequencies were observed, as shown in Tables S1–S7 of the Supporting Information (SI). For benchmarking and method selection, geometry optimization was performed using the DFT/ωB97XD, DFT/B3LYP, M06-2X, and MP2 methods using the 6-311++G(d,p) aug-cc-pVDZ, and aug-ccpVTZ basis sets.^19,20 Following the approach by refs (21−23), the ring strain energies of the respective molecules with reference to their acyclic counterparts were calculated. In all cases, the corrected ZPVE was utilized in the ring strain calculation. The energies of all acyclic counterparts were obtained by conducting ground-state equilibrium geometry optimizations using the MP2 method and the M06-2X functional with the aug-cc-pVTZ and 6-311++G(d,p) basis sets. Other surface and topological analyses were conducted with Multiwfn 3.7 dev.²⁴ The independent gradient model (IGM) weak interaction fingerprint plot and molecular electrostatic potential (ESP) isosurfaces were rendered via the GNU plot and visual molecular dynamics (VMD) software, respectively,²⁵ in conjunction with the exported files from Multiwfn. Investigation of the stabilization energy and charge transfer was conducted with the help of the NBO analysis program, and the results were analyzed using the UCA-Fukui program.^26,27 Structural analysis such as bond length, angle, and vibrational assignment as obtained from geometry optimization was achieved with the help of Vibrational Energy Distribution Analysis software (VEDA 4.1).²⁸

3. Results and Discussion

3.1. Energies and Dipole Moment

To validate the computational responsiveness of the studied systems to theoretical methods, the energies of the studied systems were computed and compared using the exchange–correlation functional (M06-2X) and range-separated functional (ωB97XD) as well as ab initio (MP2) calculation, as presented in Table 1. The energies and dipole moment obtained are very much comparable even though quantitative incongruity is non-negligible. The values of the calculated dipole moment were observed to fluctuate as the level of theory was increased and revealed that thiepane possesses the highest dipole moment compared to azepane and oxepane and that BrCHP was more polar. Dipole moment (μ) is very crucial when considering molecular stability in different electronic environments. The order of the dipole moment is thiepane > oxepane > azepane among the heterocycles, while for the halo-substituted derivatives, the order is BrCHP > ClCHP > FCHP. The comparable nature of these results is an indication of the accuracy and efficiency of the chosen computational approach for this study.

Table 1. Total Energies (in Hartree) and Dipole Moment of the Studied Compounds.

compounds	DFT/B3LYP SCF energy (Hartree)	dipole moment (Debye)	DFT/ωB97XD SCF energy (Hartree)	dipole moment (Debye)	M06-2X SCF energy (Hartree)	dipole moment (Debye)	MP2 SCF energy (Hartree)	dipole moment (Debye)
azepane	–291.242427	1.15	–291.204586	1.24	–291.146194	1.25	–290.588428	1.25
oxepane	–311.110443	1.44	–311.067495	1.55	–311.014223	1.58	–310.44712	1.59
thiepane	–634.099848	1.93	–634.057711	1.99	–633.992997	1.95	–633.05895	1.99
FCHP	–374.464569	2.33	–374.421952	2.37	–374.358411	2.35	–373.70489	2.42
ClCHP	–734.832824	2.74	–734.788052	2.69	–734.717848	2.68	–733.690514	2.73
BrCHP	–2848.769627	2.87	–2848.753278	2.72	–2848.690151	2.82	–2846.67841	2.86
CHP	–275.208609	0.012	–275.175393	0.0049	–275.111237	0.0055	–274.561808	0.0054

3.2. Structural Properties

The molecular geometries of the studied compounds have been determined experimentally via the gas-phase electron diffraction method reported elsewhere.^29,30 The crystallographic data for the heterocyclic derivatives studied in this work were obtained from the Cambridge Crystallographic Data Centre (CCDC) as reported by refs (29, 30) (CCDC Numbers: 1116875 and 707207). The crystallographic data for the halo-substituted derivatives and thiepane have not been reported; however, their synthesis can be achieved via suitable cyclization reactions of 1,6-disubstituted hexanes with diverse leaving groups and suitable catalysts. Thiepane has been successfully synthesized by the radical cyclization of 5-hexenethiol under photolytic conditions. Several other synthetic approaches could be deployed to afford the studied systems.^1,31 The crystal structure of azepane and oxepane shows two nonequivalent units bonded by intermolecular hydrogen bonds via the NH and O atoms, respectively. Having obtained the stable geometry from DFT calculations, it would be interesting to compare the modeled geometry to the available experimentally determined geometry; thus, we compared our calculated geometrical data with the experimental data by means of root mean square deviation (RMSD). The calculated geometrical parameters of the gas phase for the heterocyclic derivatives are presented in Table 2 along with the X-ray diffraction (XRD) data obtained from structural refinement. As observed, the average bond lengths for the C–N (1.459 Ǻ), C–O (1.434 Ǻ), C–S (1.842 Ǻ), and C–C (1.527 Ǻ) bonds from experimental data are quite similar to the calculated data, and the RMSD shows excellent conformity with the experimental values. The results for the computed bond angles show an increasing angle deviation in the range of 114.8–116.9° for C–C–C bond angles, while C–C–H angles maintained the 109.5° in most cases with a slight decrease from 109.49 to 107.9° as a result of ring strain, which might result in the deviation from the regular tetrahedral bond angle. The planarity of a molecule can be assessed through its dihedral angles. In general, 0, 180, or 360° dihedral angle indicates the presence of planarity in molecules. For the studied molecules, the observed dihedral angles of −163 (C4–C1–C2–H14), −175.90 (C1–C2–C3–H15), −156 (C2–C1–C4–H16), and −176 (C1–C2–C3–H15) indicate significant out-of-plane distortions from planarity.

Table 2. Experimental and Calculated Geometric Parameters for the Heterocyclic Derivatives Calculated at the M06-2X/6-311++G(d,p) and the MP2/aug-cc-pVTZ Level of Theory.

atoms	azepane (X-ray)	M06-2X/6-311++G(d,p)	MP2/aug-ccPVTZ	oxepane (X-ray)	M06-2X/6-311++G(d,p)	MP2/aug-ccPVTZ	thiepane (X-ray)	M06-2X/6-311++G(d,p)	MP2/aug-ccPVTZ
C1–C2	1.527	1.5335	1.5297	1.546	1.5283	1.5239	1.5391	1.5341	1.5303
C1–C4	1.527	1.5328	1.5289	1.510	1.5331	1.5285	1.5418	1.5368	1.5332
C2–C3	1.528	1.5297	1.5255	1.511	1.5389	1.5285	1.5348	1.5288	1.5253
C3–C5	1.526	1.5343	1.5294	1.511	1.5348	1.5312	1.5336	1.5293	1.5261
C4–C6	1.528	1.5395	1.5351	1.434	1.529	1.5248	1.532	1.5277	1.5241
C5–X	1.456	1.459	1.4602	1.434	1.4159	1.4225	1.8423	1.8226	1.8157
C6–X	1.459	1.4587	1.4593	1.363	1.4102	1.4164	1.852	1.8291	1.8204
N19–H20	1.02	1.0124	1.0122
RMSD		0.007	0.004		0.044	0.043		0.012	0.017
Bond Angle (Ǻ)
C2–C1–C4	111.167	112.9414	112.6682	109.158	113.6749	113.4912		113.695	113.2515
C3–C5–C–N19	112.168	114.4365	114.1215	114.519	115.6218	115.463		116.2287	115.7837
C4–C6–N19	109.062	117.1339	117.089	111.080	112.5323	112.4612		114.0879	113.5635
C–C–H	109.556	109.7392	109.3667	109.510	109.5672	109.5859		109.5322	109.3938
RMSD		4.286	4.199		2.436	2.323
Dihedral Angles
C1C4C6N19	–41.612	–39.3082	–39.8087	–73.612	52.1585	–72.2138		–72.3498	–72.2894
C2–C1–C4–H16	–74.232	–153.0755	–152.5683	–177.707	–157.5784	–156.3957		–142.2856	–141.4007
C1C4C6H12	168.626	–162.7305	–163.133	164.936	–163.8118	–163.7655		–46.7798	–45.7234

3.3. Strain Energy

The strain energy is an important parameter in assessing electronic properties and molecular stability, especially in cyclic systems. Several approaches have been developed to explain the strain energies of cyclic molecules. Most theoretical methods often require the computation of the total energies of the molecule of interest relative to an acyclic strain-free counterpart. The strain energies of the studied systems have been computed at the MP2/aug-cc-pVTZ and the M06-2X/6-311++G(d,p) level of theory in line with refs (21, 32). This approach involves the computation of the ring strain energy relative to the strain energy of the six-membered counterparts, which several studies had reported to be less strained among the cycloalkane family. The detailed procedure for computations can be found in the Supporting Information. The energies of all acyclic counterparts were obtained by ground-state geometry optimization at the same level of theory as the cyclic molecules. The resulting strain energies are presented in Table 3. The experimental strain energy for cycloheptane was reported to be 6.3 kcal/mol. Khoury et al. calculated the strain energy to be 8.0 kcal/mol using the s-homodesmotic approach.³³ In this study, the calculated strain energy was observed to be 6.38 kcal/mol from MP2 calculations and 5.69 kcal/mol with the M06-2X functional. Several reports have pointed out that the strain energies of cyclic molecules are influenced by heteroatom substitution or functionalization.³²⁻³⁵ Thus, our results are comparable to these reports. The influence of substitution with the halogen atoms is quite minimal when compared to the heteroatom effect on the CHP ring. Substitution with the F atom only causes a slight increase in the ring strain of about 0.28 kcal/mol, while substitution with the Cl and Br atoms increases the strain energy by 1.08 kcal/mol, thus accounting for the increased kinetic stability of the FCHP derivative as observed by other quantum chemical descriptors in this work. The replacement of the carbon atom with N, O, and S atoms was observed to cause an appreciable decrease in the ring strain of about 1.29, 0.61, and 0.56 kcal/mol, respectively. This minimal influence could result from the absence of electronic delocalization and the nonaromatic nature of the ring. However, note that a more significant influence is expected in the case of the unsaturated derivatives. The contribution of bond lengths, angles, and bond dissociation energies to ring strain has been reported to have a substantial effect.³² The calculated C–N–C, C–O–C, and C–S–C bond angles were found to be 116.2, 114.46, and 103.116°, respectively, at the MP2 level, while the XRD bond angles for these bonds were around 112.16 to 114.52°, thus indicating a significant deviation from the ideal geometry due to torsional and angle strain. The calculated C–C–C– bond angles around the halo-substituted derivatives were within 113.43–113.73°, which is significantly higher than the ideal 109.5° expected for an sp³-hybridized carbon atom. To fully appraise the contribution of bond angle deviation to the observed ring strain energy, it would be interesting to compare the observed changes in bond angles around the C–N–C, C–O–C, and C–S–C bonds and the point of halogen substitution in the studied compounds with other lower members. Thus, cyclohexane, which is considered strain-free from several experimental observations, was observed to possess an angle deviation of about 1.09° in the heterocyclic derivatives and 2.65° in the halo-substituted six-membered counterparts, while the five-membered counterparts exhibited an angle deviation of about 5.2° when substituted with N and O atoms and 15.9° in the case of the divalent sulfur atom. All of these factors contribute to the differences in the behavior of the heteroatoms within the ring. Thus, the reactivity or stability of the studied systems is very much dependent on the heteroatom and halogen substituent, respectively, and also specific to the ring size.

Table 3. Calculated Strain Energies (kcal/mol) for the Studied Compounds Estimated at the MP2 and the M06-2X Level of Theory.

CHP	azepane	oxepane	thiepane	FCHP	ClCHP	BrCHP
MP2 Level
6.38 kcal/mol	5.09 kcal/mol	5.77 kcal/mol	5.82 kcal/mol	6.55 kcal/mol	7.14 kcal/mol	7.04 kcal/mol
M06-2X Level
5.69 kcal/mol	5.33 kcal/mol	5.12 kcal/mol	6.17 kcal/mol	5.97 kcal/mol	6.77 kcal/mol	6.77 kcal/mol

3.4. Vibrational Analysis

Molecular vibrations are often considered distinctive physical properties, which are specific to any given molecule. The molecular vibrational properties of the studied compounds are presented in this study, and the experimental Fourier transform infrared (FT-IR) spectra for the studied compounds were obtained from the NIST database as determined by gas-phase transmittance spectroscopy. The spectra and normal modes of vibrations for the studied compounds are presented in Figures S1 and S2 of the Supporting Information. In the interim, 57 modes of vibrations were observed for cycloheptane and its associated halo-substituted derivatives, while 51 vibrational modes were obtained for oxepane and thiepane. Similarly, 54 modes of vibrations were obtained for azepane. Using the (3N-6) rule, 20 stretching, 19 bending, and 18 torsional modes of vibrations were obtained for CHP and halo-substituted derivatives, while 18 stretching, 17 bending, and 16 torsional modes were obtained for oxepane and thiepane and 19 stretching, 18 bending, and 17 torsional vibrational modes were recorded for azepane. The vibrational frequencies were calculated at the M06-2X/6-311++G(d,p) level of theory and compared with the experimentally reported data. Some selected frequencies and IR intensity along with their assignment and potential energy distribution (PED) are presented in Tables S1–S7, and the plots are equally presented in Section S1 of the SI.

3.4.1. CH Vibrations

The infrared spectra of cycloalkanes are similar to those of alkanes, except in situations where an alkyl substituent is absent. Moderately strong CH₂ scissoring frequencies observed between 1440 and 1470 cm^–1 were situated depending on the ring size. The C–H stretch frequency for alkanes and cycloalkanes show clearly absorption at 2850–3000 cm^–1; the calculated CH stretching absorptions for the studied compounds were observed at 2991, 3031 cm^–1 (CHP), 3001, 3027, 3049 cm^–1 (FCHP), 3001, 3024, 3049 cm^–1 (BrCHP), 3001, 3023, 3067 cm^–1 (ClCHP), 2942, 2968, 3068 cm^–1 (oxepane), 2992, 3025, 3043 cm^–1 (azepane), and 3001, 3005, 3085 cm^–1 (thiepane). These values are in close agreement with the experimentally reported data for these compounds.^29,30 The absorptions above 3000 cm^–1 can be attributed to the effect of the substituent, especially the difference in the electronegativities of the halogen atoms. Methyl groups and methylene groups of cycloalkanes normally have characteristic CH bending deformations at 1400–1470 cm^–1. However, the calculated CH bending deformations were observed at 1544–1403 cm^–1 (CHP), 1545–1430 cm^–1 (FCHP), 1543–1413 cm^–1 (BrCHP), 1544–1409 cm^–1 (ClCHP), 1542–1402 cm^–1 (oxepane), 1537–1421 cm^–1 (azepane,) and 1421–1533 cm^–1 (thiepane) for both symmetric and asymmetric deformations.

3.4.2. C–C Vibrations

The C–C stretching vibrations have variable frequencies and are usually weak. This generally occurs between 11,000 and 1000 cm^–1. The calculated C–C stretching vibrations for the studied molecules were observed at 1145 and 1129 cm^–1 (CHP), 1137 and 1161 cm^–1 (FCHP), 1147 and 1134 cm^–1 (BrCHP), 1136 and 1080 cm^–1 (ClCHP), 1139 and 1164 cm^–1 (oxepane), 1120 and 1045 cm^–1 (azepane), and 1125 and 1088 cm^–1 (thiepane), while the experimental data were obtained as weak absorptions between 1000 and 1500 cm^–1 for the halo-substituted derivatives and 1200–1300 cm^–1 for the heterocyclic derivatives.

3.4.3. C–X Vibrations Where X = (F, Br, and Cl)

The presence of heavy atoms and decrease in molecular symmetry results in the absolute mixing of vibrations; thus, the bond vibrations between the ring and halogen atom give appreciable information. C–Br bands are generally assigned in the frequency range of 680–450 cm^–1, while C–Cl bonds are assigned in the range of 850–550 cm^–1 depending on the configuration of the molecule. The absorption at 683 and 412 cm^–1 is assigned to C–Br stretching vibrations, while the absorptions at 724, 432, and 477 cm^–1 correspond to the C–Cl bond. The reported C–F vibrations were 1235 and 1232 cm^–1 for experimental and DFT calculations, respectively. However, in this study, the C–F stretching vibrations were assigned at 1021, 891, and 994 cm^–1. In-plane deformations for CH–Br and CH–Cl bonds were also observed, with the peaks at 1229 and 1176 and 1202 and 1236 cm^–1 corresponding to this vibration. Similarly, out-of-plane vibrations were observed at 237 and 226 (CCBr), 267 and 279 (CCCl), and 380 cm^–1 (FCC).

3.4.4. C–Y Vibrations Where Y = (N, O, S) and N–H Vibrations

The N–H band was observed as a singlet peak at 3529 cm^–1, which is near the experimental value observed at 3400 cm^–1. The NH rocking deformation was observed at 1500 and 1087 cm^–1 from theoretical calculations, while the corresponding transmission spectrum recorded in the gas phase shows this absorption as a broad band around 1499–1505 cm^–1. The band at 1176 cm^–1 is assigned to the C–N vibrations in azepane due to deformations. The characteristic C–O absorption was calculated at 1147 cm^–1 and experimentally observed at 1134 cm^–1. The vibrations of the C–S bond were assigned at 672–614 cm^–1 for the stretching modes. All vibrational modes of the respective groups conform with the experimental spectra.

3.5. Global Descriptors

Quantum chemical descriptors such as hardness (η), electronegativity (χ), chemical potential (μ), and softness, which provide substantial insight into the stability and reactivity of chemical systems, were estimated through Koopmans’ approximation and conceptual density functional theory (CDFT) including the ground-state ionization potential (IP), second vertical ionization potential, and electron affinity value of chemical systems.^36,37

The electronic properties such as ionization potential (IP), EA, and X as evaluated by Koopmans’ approximation are presented in Table 4. Quantities such as these give insight into the reactivity of the substituted cycloheptane molecules and other systems.³⁹ It can be inferred from Table 2 that the ionization potential values decrease in the order FCHP > CHP > ClCHP > BrCHP > oxepane > azepane > thiepane, with FCHP having the highest IP value. The electronegativity was observed to be highest in the FCHP and lowest in thiepane. This result clearly shows that the electronegativity value of the substituted group affects the entire system; this trend is seen in the halo-substituted derivatives as well as the hetero-substituted derivatives. The hardness is seen to increase for the FCHP and CHP molecule and decreases for azepane and thiepane. The hardness of a species, atom, ion, or molecule is a qualitative indication of how polarizable it is, that is, how much its electron cloud is distorted in an electric field. Chemical hardness is perceived as the capacity to resist electron density transfer with surrounding species.⁴⁰⁻⁴² Thus, CHP and FCHP are termed species with less propensity to exchange electron density with the immediate electronic environment by their high global hardness and low global softness values; this also shows that these species will likely be more reactive toward hard bases and generally more reactive. Thiepane has the highest softness and lowest hardness value and as such is the least reactive of the studied compounds toward soft bases based on Pearson’s hard–soft acid–base theory. CHP was observed to have the highest cubic electrophilicity index, while azepane and thiepane were observed to have the lowest values, indicating that they are the best nucleophiles while ClCHP is the strongest electrophile of all of the studied compounds.

Table 4. Highest Occupied Molecular Orbital–Lowest Unoccupied Molecular Orbital (HOMO–LUMO) Energy Variation and Quantum Chemical Descriptors.

chemical structure	CHP	FCHP	BrCHP	ClCHP	oxepane	azepane	thiepane
EHOMO (eV)	–9.713	–10.093	–8.862	–9.441	–8.684	–7.462	–7.319
ELUMO (eV)	–0.0098	–0.093	–0.188	–0.147	–0.045	–0.056	–0.086
energy gap (eV) (M06-2X)	9.71	10.0	8.67	9.29	8.64	7.41	7.23
energy gap (MP2)	12.600	12.938	12.086	12.082	11.839	10.420	9.708
ionization potential	9.713	10.093	8.862	9.441	8.684	7.462	7.319
electron affinity	0.0098	0.093	0.188	0.147	0.045	0.056	0.086
electronegativity	4.8613	5.093	4.5251	4.7938	4.3644	3.7591	3.7025
hardness	4.8515	5.0002	4.3374	4.6469	4.3194	3.7033	3.6166
softness	0.103	0.099	0.115	0.108	0.116	0.135	0.138
electrophilicity	2.435	2.594	2.361	2.473	2.205	1.908	1.895
chemical potential	–0.0098	–0.093	–0.188	–0.147	–0.045	–0.056	–0.086

Quantum chemical descriptors such as E_HOMO, E_LUMO, and ΔE (HOMO–LUMO) energy gap offer reasonable information concerning the reactivity and stability of molecules. The calculated quantum chemical parameters for the studied compounds are presented in Table 4. The ability of a molecule to donate or accept electrons is related to the HOMO and LUMO energy values. The higher the HOMO values, the greater the ability of a molecule to donate electrons, while lower values of LUMO energy correspond to a strong accepting ability.^40,43 The result for the energy gap shows a decreasing trend in the halo-substituted molecules in the order FCHP > ClCHP > BrCHP >, indicating that BrCHP is the softest of the halo-substituted CHP since it has been asserted that a molecule with small or no HOMO–LUMO gap is chemically reactive. This result is in line with the global hardness observation, which follows a similar trend. However, note that the difference in the energy gap observed is not highly significant. Therefore, the reactivity of the halo-substituted derivatives is comparable; however, this also shows that the energy gap is not the principal factor interplaying in the molecular reactivity, especially the halo-substituted derivatives. Some contributions from the electronegativity concept tend to dominate in some regards, and hence the increase in the band gap upon substitution with the fluorine atom was observed to be less reactive than other counterparts. The results indicate that the FCHP derivative is the most kinetically stable derivative with the highest band gaps of 8.16, 10.0, 11.7, and 12.9 eV, corresponding to B3LYP, M06-2X, ωB97XD, and MP2 calculations, respectively. All of the different functionals used to affirm this derivative to be more kinetically stable, which is in line with the chemistry of the substituted atom from the electronegativity concept since there is no pi-backdonation due to electron delocalization; therefore, the polarization in the C–F bond and electronic exchange is less in these derivatives. The BrCHP derivative was equally confirmed to be the least kinetically stable derivative, which means it is more reactive than other halo-substituted counterparts from band gap considerations. A similar trend was observed in the case of the heterocyclic derivatives, which indicates that oxepane is a more kinetically stable species with high band gaps of 11.8 and 10.2 eV obtained from MP2 calculations and ωB97XD functional, respectively. Low kinetic stability is associated with minimal band gap values due to the ease in energy for electrons to occupy a high-positioned HOMO or for electrons to be abstracted from a low-lying LUMO at the transition state of reactions.³⁸ In line with these, the kinetic stability of the halo-substituted compounds also follows the above trend, with the FCHP compound being the most kinetically stable derivative. The trend for the nonaromatic heterocycles also shows a decreasing reactivity and stability in the order oxepane > azepane > thiepane with the energy values of azepane and thiepane being closely similar, thus indicating their close kinetic stability. However, the energy gap computed with the MP2/au-ccPVTZ level of theory clearly indicates that thiepane is more kinetically stable with a difference of −0.7 eV. The result prompts that the reactivity and stability decrease in the order FCHP > CHP > ClCHP > BrCHP > oxepane > azepane > thiepane. As observed from the result, CHP and FCHP molecules possess the highest HOMO values as well as an energy gap, thus inferring that substitution with heteroatoms increases the reactivity of CHP, while substitution with highly electronegative fluorine decreases the kinetic stability of the ring.

3.6. Fukui Function (Reactivity Descriptor)

The conceptual density functional theory (CDFT), originally developed by Robert Parr, is a theoretical framework aiming for unraveling the reactivity of chemical systems. CDFT encompasses several notions and quantities, some of which can be utilized to predict favorable reactive sites and reactive character, and some can effectively compare the reactivity of several chemical species.^44,45 The Fukui function is a prominent concept in conceptual density functional theory; it has been extensively utilized in the prediction of reactive sites. The Fukui function is a real space function, which is commonly studied by utilizing the visualization of isosurfaces to facilitate quantitative comparison between different sites and atomic charge distribution.

In this study, single-point energy calculations were obtained for the molecular geometry optimized at the M06-2X/6-311++G(d,p) level of theory, and the Hirshfeld charges, condensed Fukui functions, and condensed dual descriptors (CDDs) were evaluated at the same level of theory. Table S9 in the SI shows some selected values of f⁺, f^–, and f₀ and Δf (condensed dual descriptor, CDD) obtained for CHP, FCHP, BrCHP, ClCHP, oxepane, azepane, and thiepane molecules. Analysis of the f⁺ values of the abovementioned compounds reveals that the most susceptible sites for nucleophilic reactions are mostly the electronegative atoms, and possibly these sites might likely be less prone to electrophilic attacks considering the negligible difference in f⁺ values. Similarly, the dual descriptor suggests the same sites as positive sites and thus unfavorable for an electrophilic attack. Electrophilicity and nucleophilicity are the intrinsic properties of molecules purported by the deficiency or abundance of electrons on specific atoms. This result correlates with the calculated CHELPG charges on these reactive sites; carbon atoms with positive charges as observed are unsuitable sites for electrophilic reactions, while negatively charged atoms are suitable sites of attack, which seems to correlate with the conventional knowledge of nucleophilic and electrophilic substitution reactions.

3.7. Population and Atomic Charge Analysis

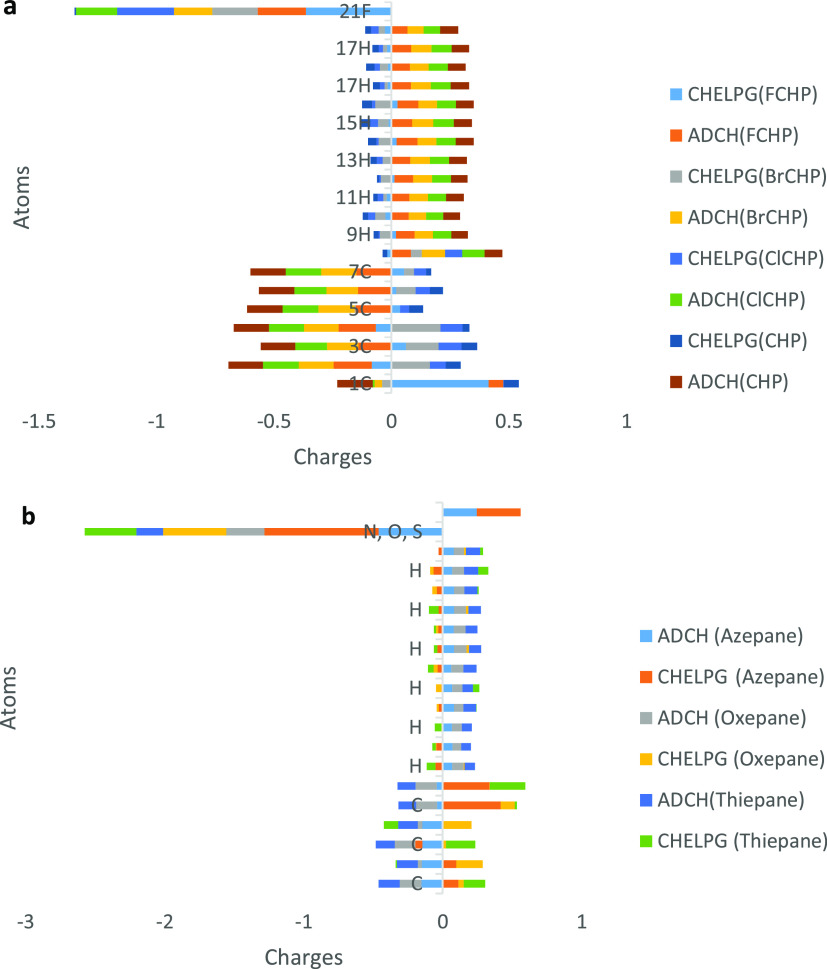
The significance of atomic charges in understanding the fundamental properties of molecules such as the direction for a reaction, atomic states in molecular systems, and sites of reaction cannot be overemphasized. The atomic charge is quite often the easiest way to predict the distribution of charge densities in molecules. Atomic charges find significant application in calculating electrostatic interactions by molecular force fields and computing condensed Fukui functions. The CHELPG (charges from electrostatic potentials using a Grid-based method) atomic charge scheme proposed by Breneman and Wiberg,⁴⁶ in which the molecular electrostatic potential at a given point around a molecule is reproduced, was employed in this study together with the Atomic Dipole Corrected Hirshfeld Charge (ADCH) method proposed by Tian Lu,⁴⁷ which is a sum of Hirshfeld charges and correction charge, was used to compute and reveal the most reactive sites in the compound and its overall reactivity. The CHELPG and ADCH charges of the studied compounds were evaluated using the Multiwfn program.²⁴ The results are presented in Tables S13–S20 of the SI and Figure 2 in the manuscript. It can be inferred from the results that the CHELPG charges on C1 bearing the halogen atom in FCH deviate from the value observed in the CHP molecule; this is due to the high electronegativity of the fluorine atom at this position. This charge on C1 is also seen to be positive when compared to other carbon atoms in the molecule, which is a clear indication of the weak electrostatic potential around the carbon atom due to the dipole moment of the bond. This effect was also observed in the ADCH charge of C1, which clearly shows a significant contribution to the dipole moment of the fluorine atom. The substitution of a fluorine atom at C1 was found to also influence the charges on the adjacent carbon and hydrogen atoms, causing the charges in this position to be positive when compared to others in the same molecule and the molecule without substitution. This interplay of the fluorine atom might result in the observed increase in the band gap of the FCHP derivative, thus causing a decrease in the reactivity of the overall FCHP derivative. For BCHP, both CHELPG and ADCH charges on the carbon atom bearing the halogen atom were slightly negative, which shows that the electrostatic potential around this atom is quite significant, and despite the dipole moment in the bond, the charge value, however, decreased in this position relative to other positions in the molecule and the halogen substituent was also seen to affect the charges on adjacent carbon atoms. The decrease in charge values was observed to be highly prominent in ClCHP at the carbon bearing the chlorine atom and the charge was positive for this position, indicating a weak electrostatic potential at this position. The CHELPG and ADCH charges on the hydrogen directly attached to the heteroatom in azepane were positive, while those on an adjacent atom were negative and closely similar and higher than the charge on other carbon atoms due to the effect of the heteroatom in the ring. The ADCH charges on C4 and C2 adjacent to the oxygen atom in oxepane were significantly less compared to other carbon atoms in the molecule due to the dipole moment in these bonds, which points toward the oxygen atom. The CHELP charge was higher in these positions compared to other positions; this affirms that there is a significant contribution from these carbon atoms to the atomic dipole moment of oxygen in the molecule. For thiepane molecule, the C5 and C6 atoms adjacent to the sulfur atom exhibited a similar ADCH charge, which was lower than that for other carbon atoms, while the CHELPG charge for C6 was quite higher than that for every other carbon atom in the molecule, which is a clear reflection of the high electrostatic potential at this position. The CHELPG charge of all carbon atoms in the CHP molecule was similar due to the symmetry and uniformity of the electrostatic potential around the molecule. The result obtained shows a perfect correlation between ADCH and CHELPG charges in predicting the electrostatic potential distribution and dipole moment contribution of atoms in the studied molecules. It also affirms the differences in the electron density distribution orchestrated by substitution.

Figure 2.

Comparison of ADCH and CHELPG Population Analysis for the studied compounds at the M06-2X/6-311++G(d,p) level of theory. (a) Halo-substituent derivatives and (b) heterocyclic derivates.

3.8. Density of States (DOS)

Density of states (DOS) is an essential phenomenon in solid physics. The exact number of states corresponding to a unit energy interval is designated by DOS. However, the energy levels of isolated systems are discrete, and thus the notion of DOS often becomes questionable. However, the augmentation of distinct quantum levels to curves generates an indispensable tool (DOS graph) for depicting and visualizing the contribution of molecular orbitals to various quantum states.⁴⁸ The distribution of molecular orbital levels of molecules can be brilliantly exhibited by the density of states (DOS), and the curves in the plot replicate the number of molecular orbitals at different quantum states in unit energy intervals. The total DOS (TDOS) map, partial DOS (PDOS) map, and overlap partial DOS (OPDOS) map of CHP, oxepane, azepane, thiepane, FCHP, BrCHP, and ClCHP with contributions from different sets of molecular orbitals were plotted by invoking Multiwfn, as explicated in Figure 3. The left-side axis corresponds to TDOS and PDOS, while the right side corresponds to OPDOS. The orbital properties are vividly revealed in different energy ranges in the graph. It is noticeable from the graphs of azepane, oxepane, and thiepane that the heteroatom defined as fragment 1 contributed minimally to the molecular orbitals (MOs) in the range of −13.6 to −5.4 eV (highest energy) and −10.9 to −5.4 eV (lowest energy) and therefore suggest the availability of minimal occupation states based on condensed matter physics theory,⁴⁹ while FCHP, BrCHP, and ClCHP also contributed negligibly in the range of −10.9 to −5.4 eV (lowest energy) and −13.6 to −8.2 eV (highest energy) with minimal occupancy quantum states. The major valence molecular orbitals are seen to be contributed by p-orbitals of carbon (fragment 2) and hydrogen (fragment 3), with a similar percentage contribution to the molecular orbitals (MOs). The positive values in the green curve, which is the OPDOS, indicate that the MOs in the corresponding energy range exhibit the bonding character between the defined fragments; likewise, the negative values suggest antibonding orbital behavior. However, it is observed that the OPDOS of all of the studied molecules overlaps in the negative range of the graph, thus indicating the presence of antibonding MOs in the molecules by virtue of the antagonistic orbital overlap, as explicated in Figure 3. Simulating the DOS for small-molecule systems aids in understanding the electronic distribution in specific energy levels and associated changes in properties and energy quantization within the systems.

Figure 3.

TDOS (black), PDOS, and OPDOS density of states map of the studied compounds. The dashed line indicates the position of the HOMO. The left axis is for total and partial density of states, the right axis is for overlap density of states. The isovalue of MO isosurfaces is 0.05. The insets correspond to the HOMO and LUMO plots for the studied system, respectively. a, b, c, d, e, f, and g correspond to azepane, oxepane, thiepane, FCHP, BrCHP, ClCHP, and CHP molecules.

3.9. Bond Order

3.9.1. Laplacian Bond Order (LBO)

Bond order is a quantitative description of chemical bonds and has been widely used by chemists to understand the nature of molecular electronic structure and predict molecular reactivity, aromaticity, and stability. It is an important concept in understanding the nature of the chemical bond. The Laplacian bond order (LBO) is defined as a scaled integral of negative parts of Laplacian of electron density in a fuzzy overlap space. The Laplacian bond order is obtained by integrating a negative part of Laplacian of electron density in the bonding region, and it has been demonstrated to strongly characterize actual bonding strength. It has also been reported in the literature to have a direct correlation with bond polarity, bond dissociation energy, and bond vibrational frequency⁵⁰ and is therefore utilized in this work. The calculated values for the LBO of oxepane, azepane, thiepane, FCHP, BrCHP, ClCHP, and CHP are presented in Table S11 of the SI.

The LBO of the C–C bond in the CHP was observed to be alternating, i.e., not uniformly distributed in the entire molecule. The LBO predicts the covalency in the carbon–halogen bond in the substituted CHP derivative to be in the order C–Cl (0.298) > C–Br (0.179) > C–F (0.049), thus showing the ionic nature of the C–Cl bond. The decrease in the value of the LBO for the C–F bond can be attributed to the strong repulsive interactions between the carbon atom and lone pairs of electrons on the fluorine atom or the highly polar nature of the bond. However, it can be observed from the result that the fluorine substituent has a significant effect on the bond order of adjacent carbon atoms, with the LBO of C1–C2, C1–C4 bonds adjacent to the fluorine atom exhibiting a higher order than other carbon atoms. This is likely due to the strong electron-withdrawing effect of the fluorine atom and the interaction between the C1 and the lone pairs on fluorine, which pushes the electron density toward C1–C4 and C1–C2 bonds. This same effect was also observed in the C1–C2 bond of oxepane, which has a higher order than other carbon atoms in the molecule. Nevertheless, the C2–O19 and C4–O19 bond order was lower compared to others. Comparing the LBO of the C-heteroatoms in oxepane, azepane, and thiepane, we observed the bond order to be C–N19 (0.711) > C-S19 (0.633) > C–O19 (0.299). This trend can be attributed to the increase in the atomic size between the two bonding atoms, which causes the region of space in which electrons are shared to become proportionately smaller as one of the bonding atoms becomes larger. Generally, this analysis is conducted to compare the similarities or differences in the bond order trend in substituting the CHP ring with any of the substituted groups, and the insight from these results is that the bond order does not decrease or increase linearly with the type of group substituted, but the covalency in or the ionic nature of bonds could play a more significant role.

3.9.2. Bond Polarity Index (BPI)

The result of the bond polarity index (BPI) of the studied compounds obtained by eq 1 is presented in Table 5. The bond polarity index between two atoms (A and B) is the ionic character between the two bonding species when excluding the pure covalent and homonuclear compositions.^51,52

1

where EI_A and EI_B are the energy indices of the two interacting species, EI_A^ref and EI_B^ref are the energy indices derived from computing the homonuclear reference molecules (ethane, urea, fluoromethane), x = N, S, O, Br, Cl, F, and y = carbon.

Table 5. Bond Polarity Index of the Studied Compounds.

compound	interacting atoms (x and y)	EI of atom x	EI of atom y	EI of reference atom x	EI of reference atom y	BPIxy
azepane	N19		–0.499667
	N19–C5	–0.511440		–0.659349	–0.718132	–0.0705
	N19–C6	–0.520813				–0.0710
oxepane	O19		–0.557084	–0.659349	–0.905877
	O19–C2	–0.535949				–0.2254
	O19–C4	–0.542034				–0.2315
thiepane	S19		–0.399802
	S19–C5	–0.493716		–0.659349	–0.617040	–0.0516
	S19–C6	–0.500086				–0.0579
BrCHP	Br21		–1.721563
	Br21–C1	–0.468814		–0.659349	–2.171155	–0.2590
	Br21–C2	–0.539780				–0.3300
	Br21–C4	–0.543390				–0.3336
ClCHP	Cl21		–0.462302
	Cl21–C1	–0.487663		–0.659349	–0.697793	–0.0638
	Cl21–C2	–0.533395				–0.1095
	Cl21–C4	–0.535960				–0.1121
FCHP	F21		–0.631278
	F21–C1	–0.476416		–0.659349	–0.992515	–0.18
	F21–C2	–0.517025				–0.2189
	F21–C4	–0.514987				–0.2168

The EI value in C–X interactions was derived from the calculation of substituted cycloheptane species, and EI^ref is the reference value, which is obtained by manipulating the homonuclear atoms. A greater proportion of the BPI between A and B signifies the presence of higher polarity.⁵²

The result shows that the polarity of the C–X bonds in the halogen-substituted compounds decreases in the order −0.26 (C–Br) > −0.18 (C–F) > −0.064 (C–Cl). In contrast to the C–F and C–Cl bonds, the value for the C–Br bond indicates that the bond is only slightly polarized with the polarization in the direction of the carbon atom. The charge distribution of the bond is expected to be in the direction of the halogen atom, which is more electronegative. However, a partial negative charge of −0.039 was observed in the carbon atom bearing the halogen atom. This shows that the average number of bonding electrons is minimally distributed, which accounts for the slight negative charge as opposed to the expected positive charge. This result also shows that there is no direct correlation between the bond polarities and the partial charges on bonding atoms and also that the position or distribution of bonded electrons contributes positively to the bond polarity. The bond polarity index of C–O, C–N, and C–S bonds in oxepane, azepane, and thiepane decreases in the order −0.2315 > −0.0579 > −0.0710 with the last value corresponding to the C–N bond

3.9.3. Intrinsic Bond Strength Index (IBSI)

The intrinsic bond strength index (IBSI) has been proposed to quantify the strength of chemical bonds based on the independent gradient model (IGM) framework. The IGM based on the Hirshfeld partition of molecular electron density (IGMH) is employed in this study. The IGMH-IBSI scheme offers substantial information via the local electron density contragradient distribution between two bonded pairs with the contribution of electron density from the two species.⁵³⁻⁵⁶ It can also be used to compare the strength of weak interactions between two atoms or groups. This molecular descriptor has been proven to correlate with the strength of covalent bonds and interactions. Thus, this descriptor is highly essential in understanding and appraising the strength of interactions between substituents and the ring atoms and hence utilized in this study.

The intrinsic bond strength index (IBSI) calculated using the IGM based on the Hirshfeld partition of molecular electron density (IGMH) using Multiwfn is presented in Table S10. It can be inferred from the plot of the halogen-substituted cycloheptane that the IBSI of the carbon–halogen bond is 0.6216 (C–F) > 0.22527 (C–Cl) > 0.17554 (C–Br). This shows that the IBSI for the carbon–halogen bond decreases as we go down the group. The decrease in the IBSI of the C–Br bond can be attributed to the long bond length of the C–Br bond since it has been reported in the literature that bond strength decreases with increasing bond length.^54,56 The IBSI of the carbon–heteroatom bond in oxepane, azepane, and thiepane shows that the IBSI decreases as the size of the heteroatom increases, and the order is C–N (0.4828) > C–O (0.41080) > C–S (0.25922). This trend seems to be in line with that reported by Klein et al.,⁵⁶ who observed that the IBSI increases from the left to right across the second period of the element in the periodic table. Comparing this result with the intrinsic bond strength scale, it can be confirmed that the IBSI is in the covalent range, thus affirming the presence of significant interactions in the selected bonds.

To further study the intramolecular interaction and quantify the interaction arising from the partitioning of electron densities between atoms in the studied compounds, the IGMH-dg^inter and IGMH-dg^intra isosurface and dg-signature of the studied molecules were plotted and visualized with the VMD program. The result is presented as inset in the noncovalent interaction plot in Figure 4. It clearly shows that the electron density of the C–Cl bond is slightly higher than that of C–F and C–Br for halogen-substituted cycloheptane, thus confirming a strong covalent interaction between the halogens and the ring as indicated by the color code in the RDG plot. However, the sign of the second eigenvalue of the electron density (ED) Hessian matrix, which clearly distinguishes repulsive (λ₂ > 0) interaction from attractive (λ₂ < 0) interactions shows that the sign(λ₂)ρ for the molecules is >0, indicating the presence of slight repulsive interactions and strong covalent interactions⁵⁴⁻⁵⁹ in the molecules as indicated by the intrinsic bond strength index scale. In the case of oxepane, azepane, and thiepane, the result shows that the C–N bond has a higher ED than C–O and C–S bonds, suggesting stronger covalent interactions. This strong interaction also results in a significant decrease in strain energy for these derivatives, subsequently causing a stabilizing effect. The value (dg-pair) of the compounds is in the order C–N (0.47) > C–S(0.44) > C–O(0.41) and the NCI plot shows a strong attractive interaction between the heteroatoms and carbon atoms with a strong possibility of hydrogen bond formation in azepane.

Figure 4.

Noncovalent interaction plots depicting the intermolecular interactions between the heteroatoms and halogens with the ring. (a) FCHP, (b) BrCHP, (c) ClCHP, (d) oxepane, (e) azepane, and (f) thiepane. The insets show the dg-pair inter- and intramolecular interaction signature of the studied compounds.

3.10. Natural Orbital Analysis (NBO)

The natural bond orbital analysis of compounds is one useful tool for probing the inter- and intramolecular interactions resulting from chemical bonds in molecules. It likewise functions as a resourceful tool for investigating charge transfer and conjugative interactions existing in molecules.^60,61 The NBO analysis also provides information vis-à-vis both filled and vacant orbitals, thus aiding the exploration of intra- and intermolecular interactions. The NBO simulation based on Weinhold’s approach reveals that when molecular orbitals are appropriately oriented, hyperconjugation can confer a stabilizing effect, which results from the delocalization of electron density from bonding or lone pair (filled Lewis type) to adjacent vacant or deficient orbitals (non-Lewis NBOs like antibonding or Rydberg). The stabilization energy for each donor (i) and acceptor (j) NBO can be defined in terms of the second-order perturbation energy (stabilization energy E(2)); generally, the higher the stabilization energy E(2), the greater the interaction existing between the donor (filled) and acceptor (vacant) orbitals^39,51

The NBO analysis was simulated at the M06-2X/6-311++G(d,p) level of theory using the NBO program to study the charge transfer, intramolecular rehybridization, and delocalization of electron density within the molecules, as presented in Table 6. The prominent intramolecular hyperconjugative interactions resulted in the highest stabilization of 4.10, 3.36, and 3.12 kcal/mol energy corresponding to σ(C3–CH16) → σ*(C1–C2), σ(C2–H9) → σ*(C1–H8), and σ(C3–H16) → σ*(C3–H10), respectively, for CHP, while those for FCHP were 3.95 kcal/mol corresponding to LP(2)F21 → σ*(C1–C4), 3.95 kcal/mol for σ(C2–H14) → σ*(C3–C5), 3.64 kcal/mol for σ(C4–H16) → σ*(C6–C7), and 3.41 kcal/mol for σ(C2–H9) → σ*(C1–H8). The highest stabilization energy of BrCHP as observed from the NBO analysis was 4.34 kcal/mol for the donor–acceptor interaction from σ(C3–H14) → σ*(C1–C2), 4.0 kcal/mol for σ(C2–H14) → σ*(C5–N), and 4.00 kcal/mol for σ(C6–H13) → σ*(C1–C4), while the highest E2 values for ClCHP were 4.03, 3.53, and 2.56 kcal/mol, which correspond to the interaction between σ(C2–H14) → σ*(C3–C5), σ(C2–H14) → σ*(C1–C4), and LP(2) Cl21 → σ*(C1–H8). For oxepane molecules, the highest stabilization energies (E2) resulting from donor–acceptor interactions were observed to be 6.98, 6.13, 5.78, and 4.50 kcal/mol arising from the interaction of LP(2) O19 → σ*(C4–C6), LP(2) O19 → σ*(C2–H8), σ(C1–H12) → σ*(C2–O19), and σ(C6–H17) → σ*(C4–O19), respectively; for azepane, it was observed from LP(1) N19 → σ*(C3–C5) with an E2 of 7.11 kcal/mol, σ(C1–H8) → σ*(C5–N19) with an E2 of 4.13 kcal/mol, and σ(C4–H16) → σ*(C6–N19), LP(1) N19 → σ*(C4–C6), and LP(1) N19 → σ*(C6–H12) with stabilization energies of 4.82, 8.91, and 4.08 kcal/mol, respectively. The thiepane molecule has its most significant interaction resulting in the stability of the system from LP(2) S19 → σ*(C3–C5), LP(2) S19 → σ*(C6–H12), and σ(C1–H3) → σ*(C2–C3) with stabilization energies of 5.67, 4.75, and 4.01 kcal/mol, respectively. This result suggests that the stability of the halogen-substituted cycloheptane is in the order BrCHP > ClCHP > FCHP based on the stabilization energy values since it has been asserted that the higher the stabilization energy, the greater the interaction and the higher the overall stability of the system. The increased stabilization interaction as observed for the FCHP derivative could result from a pi-backdonation from the fluorine lone pair, thus accounting for the increased kinetic stability as explicated by the band gap and other quantum chemical descriptors. However, in the case of the heterocycles, the oxepane molecule was seen to afford the highest perturbation energy resulting from the nonbonding interaction between the oxygen lone pair and the ring, thus accounting for the increased molecular stability as pointed by other stability descriptors. Thiepane exhibited the least E2 energy among the studied heterocyclic derivatives. These stabilization interactions between the lone pair orbitals and the antibonding orbitals increase the stability of these compounds. The detailed NBO data can be found in Table S12 of the SI.

Table 6. Second-Order Perturbation Theory Analysis of the Most Interacting NBOs of the Studied Compounds at the M06-2X/6-311++G(d,p) Level of Theory.

donor (i)	occupancy	acceptor (j)	occupancy	E(2)a [kcal/mol]	E(j)–E(i)b [au]	F(i, j)c [au]	hybrid	AO (%)
CHP
σC3–H16	1.97829	σ*C1–C2	0.01685	4.10	0.88	0.054	sp33.51	s(22.16%)p(77.80%)d(0.04%)
σC7–H21	1.98058	σ*C5–H11	0.01699	3.09	0.89	0.047	sp2.59	s(27.84%)p(71.97%)d(0.20%)
FCH
LP3(F21)	1.97535	σ*C1–C4	0.02694	3.95	0.78	0.049	sp99.99	s(0.10%)p(99.85%)d(0.05%)
σC3–H10	1.97814	σC5–H11	0.01667	3.31	0.89	0.048	sp3.53	s(22.11%)p(77.84%)d(0.04%)
σC2–H14	1.97572	σ*C1–C4	0.02694	3.35	0.88	0.049	sp3.42	s(22.61%)p(77.34%)d(0.05%)
BrCHP
σC3–H15	1.97560	σ*C1–C2	0.02326	4.34	0.87	0.055	sp3.52	s(22.11%)p(77.85%)d(0.04%)
σC4–C6	1.97371	σ*C1–Br21	0.04348	3.28	0.64	0.041	sp2.62	s(27.58%)p(72.23%)d(0.19%)
σC6–H13	1.97756	σ*C1–C4	0.02395	4.00	0.86	0.053	sp3.53	s(22.06%)p(77.90%)d(0.05%)
ClCHP
σC2–H14	1.97672	σ*C3–C5	0.01659	4.03	0.88	0.053	sp3.42	s(22.59%)p(77.36%)d(0.05%)
σC2–H9	1.97755	σ*C1–H8	0.02578	3.61	0.88	.050	sp3.47	s(22.38%)p(77.57%)d(0.05%)
Oxepane
σC6–H17	1.97481	σ*C4–O19	0.02542	4.50	0.79	0.053	sp3.48	s(22.32%)p(77.64%)d(0.04%)
σC4–H15	1.98146	σ*C2–O19	0.02544	3.12	0.81	0.045	sp3.14	s(24.12%)p(75.82%)d(0.06%)
Azepane
σC4–H16	1.97645	σC6–N19	0.01912	4.82	0.85	0.057	sp3.47	s(22.38%)p(77.57%)d(0.04%)
LP(1)N19	1.91097	σC3–C5	0.02909	7.11	0.66	0.062	sp7.15	s(12.26%)p(87.63%)d(0.10%)
Thiepane
σC1–H13	1.97863	*σC2–C3	0.01734	4.01	0.88	0.053	sp3.53	s(22.04%)p(77.91%)d(0.05%)
LP(2)S19	1.94015	σ*C3–C5	0.02631	4.75	0.61	0.049	sp99.99	s(0.47%)p(99.50%)d(0.02%)

^aE2 represents the energy of hyperconjugative interactions (stabilization energy).

^bEnergy difference between the donor and acceptor E(i) and E(j) NBO orbitals.

^cF(i, j) is the Fock matrix element between I and j NBO, and LP (n)a is a valence lone pair orbital (n) on atom (A).

3.11. Electrostatic Potential Distribution (ESP)

The molecular electrostatic potential is an essential tool in molecular modeling for the visualization of electron density distribution, understanding biointeraction and hydrogen bonding interaction, and visualization of reactive sites, and the charge distribution determines how molecules interact with one another. High regions of electrostatic potential are indications of the relative absence of electrons and likewise low regions of electrostatic potential are indicative of high electron density.⁶²⁻⁶⁴ Electrostatic potential ESP offers a visible molecular display of polarity and aids in the understanding of electronic structures of compounds modified by substitution (e.g., heteroatoms and halogen substituents); it shows the most vulnerable sites for nucleophilic and electrophilic substitution, charge delocalization, and intermolecular hydrogen bonding. The molecular electrostatic potential of CHP and its substituted derivatives in comparison to their corresponding cyclohexane counterparts is presented in Figure 5 mapped over 0.02 isosurfaces of electron density. The ESP isosurface is populated with a positive charge density (green) around the hydrogen atoms of the respective molecules, while a negative charge density is observed around the heteroatoms and halogen substituents. The ESP minimum isosurface values on the isosurface of the halogen-substituted derivatives range between −17.31 and −18.60 kcal/mol, while the minimum values on the heteroatom derivatives range between −24.50 and −33.49 kcal/mol. It is clear from the isosurface in Figure S10 that both the heteroatom and halo groups might be susceptible to electrophilic substitution, while the hydrogens are mostly susceptible to nucleophilic attacks. The entire CHP molecule is populated with a positive charge density over the hydrogen atoms, indicating sensitivity toward nucleophilic attack. These results clearly distinguish the reactive sites of electrophilic and nucleophilic attack, with the negative ESP corresponding to suitable sites for the electrophilic attack and positive sites for the nucleophilic attack, respectively. However, it will be interesting to examine the electron density distribution among other lower members, especially cyclohexane derivatives; thus, the ESP isosurfaces of the studied compound are plotted with reference to their six-membered counterparts as presented in Figure 5. A similar charge density distribution was observed; however, other molecular properties are significantly different with much dependence on ring size. Thus, there are specific electronic behaviors distinctive to the seven-membered derivatives from other lower members.

Figure 5.

Electrostatic potential distribution of the studied compounds with comparison to cyclohexane counterparts. (a, c, e, g, i, k) ESP isosurface plots of oxepane, azepane, thiepane, FCHP, BrCHP, ClCHP, and CHP; (b, d, f, h, j, l) ESP isosurface plots of cyclohexane and substituted derivatives.

4. Conclusions

The theoretical reactivity, stability, and structural investigation of azepane, oxepane, thiepane, FCHP, BrCHP, ClCHP, and CHP molecules have been explored and reported in detail using appropriate quantum chemical techniques with a brief comparison to the available experimental data reported for the studied systems. Quantum chemical calculations have been utilized in this work to explore global reactivity descriptors, Fukui function, density of states (DOS), intrinsic bond strength index (IBSI), atomic charges, and the second-order perturbation energy analysis using the natural bond orbital (NBO) program as well as noncovalent interactions. Molecular stability and substitution effect have also been estimated via the ring strain energy calculations at the MP2/aug-cc-pVTZ level of theory. The result for the reactivity of the halogen-substituted molecules as revealed by the energy gap shows a decreasing trend in the halogen-substituted molecules in the order FCHP > ClCHP > BrCHP. Conversely, the trend for the heterocyclic molecules also shows a decreasing reactivity and stability in the order oxepane > thiepane > azepane, with the energy values of azepane and thiepane being closely similar, indicating their close kinetic stability as well. Specific reactive sites for possible electrophilic and nucleophilic substitution have been identified by the dual descriptor. The electronic distribution within the cycloheptane and cyclohexane as well as lower-member counterparts as revealed by ESP is quite similar; however, the heteroatom behavior within each ring in the cycloheptane counterparts is quite distinct from cyclohexane and cyclobutane counterparts. The contribution of atomic orbitals to molecular orbitals has been revealed by the density of states (DOS) analysis. The NBO results suggest that the stability of the halogen-substituted cycloheptane is in the order BrCHP > ClCHP > FCHP based on the stabilization energy value, while in the case of the heterocyclic systems, the oxepane molecule is seen to exhibit the highest perturbation energy resulting from nonbonding interactions between the nitrogen lone pair and the ring; thus, it is the most stable derivative of the studied cycloheptane compounds. The results for the molecular stability and reactivity for the studied compounds correlate perfectly as all of the different descriptors indicate that similar derivatives either possess the highest stability or reactivity. The distribution of the electrostatic potential and electron density depends on the type of substituent atom attached to the ring, electronegativity difference, and also the charge distribution on the atoms. Significant noncovalent intramolecular interactions are observed between the heteroatoms and the rings and they contribute significantly to molecular stabilization. The type of substituent attached to the ring is seen to influence the charge distribution on adjacent atoms. The intrinsic bond strength index of the C–halogen bond decreases as the bond length increases, and it is observed to be decreasing down the group for the halogen-substituted compounds, while it decreases as the size of the heteroatom increases in the case of the heterocyclic derivatives. Most of these observations are quite distinct from the seven-membered derivatives, and substantial differences exist in other lower-member counterparts.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c07361.

• Gas phase calculated infrared spectra for the studied compounds (Figure S1); the corresponding experimental gas-phase transmittance infrared spectra (Figure S2); computed (M06-2X/6-311++G(d,p)) frequencies and respective assignment by PED (Tables S1–S7); geometric properties (bond length, bond angle, and dihedral angles) for the studied compounds (Table S8a,b); computed CDFT parameters for the studied compounds (Table S9) and the corresponding intrinsic bond strength index (Table S10); selected studied molecules and their corresponding straight chain isomers utilized in the computations of strain energies (Figure S3); the Laplacian bond order (LBO) for the studied compounds (Table S11); second-order perturbation energies of the most interacting NBOs for the studied compounds (Table S12); the atomic charges computed at the M06-2X/6-311++G(d,p) level (Tables S13–S20); wavelength of absorption, transition energies, and % contributions to excitation and oscillator strengths (Table S21); and UV transition data for the studied compounds (Figure S4) (PDF)

Author Contributions

^⊥ T.O.U. and H.L. authors should be regarded as joint first authors.

Author Contributions

H.L.: conceptualization, design, resources, analysis, supervision, review, and editing; T.O.U.: analysis, writing, review, editing, and manuscript final draft; E.C.A.: analysis; A.S.A.: resources, review, and editing; and E.A.E.: review and editing.

The authors declare no competing financial interest.

Notes

All data used to support the findings of this article are included within the article and in the Supporting Information.