Mechanisms of photoexcitation and photoionization in small water clusters

Abstract

The mechanisms of photoexcitation and photoionization in small water clusters in gas phase, (H₂O)_n; n = 2–3, are studied using the complete active-space second-order perturbation theory (CASPT2) with the aug-cc-pVDZ basis set. The present study characterizes for the first time the structures and energetics of common transition and intermediate complexes in the photoexcitation and photoionization mechanisms in the lowest singlet-excited state. The ab initio results showed that the photoexcitation of the water monomer by a single photon can directly generate [OH]˙ and [H]˙ in their respective electronic-ground states, and a single photon with approximately the same energy can similarly lead to the photoexcitation and also to the photoionization in the water clusters. The S₀ → S₁ excitation leads to strong polarization of the O–H⋯O H-bond and to the formation of the water dimer radical cation transition state complex [(H₂O)₂]⁺˙, from which [OH]˙, [H]˙, and [H₃O]⁺˙ can be generated. These products are obtained from [(H₂O)₂]⁺˙ by the direct dissociation of the O–H bond upon photoexcitation and by proton transfer and the formation of a metastable charge-separated Rydberg-like H-bond complex ([H₃O]⁺˙⋯[OH]˙) upon photoionization. The proposed mechanisms suggest that in the gas phase, the photoexcitation and photoionization processes are most likely bimolecular reactions, in which all the transition and intermediate charged species are more stabilized than in a unimolecular reaction. The theoretical results provide insights into the photoexcitation and photoionization mechanisms of molecular clusters and can be used as guidelines for further theoretical and experimental studies.

The S₀ → S₁ excitation leads to strong polarization and formation of [(H₂O)₂]⁺˙ from which both photoexcited and photoionized products are generated.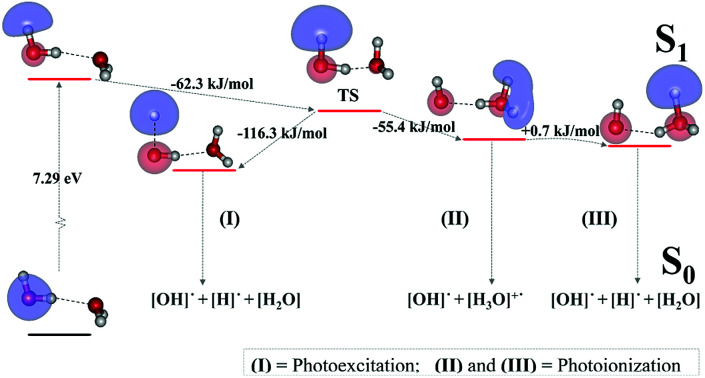

Introduction

The photochemistry of molecules in the Earth's atmosphere has been extensively studied in the past decades. The most important topic is the photolysis of small molecules, which leads to serious environmental problems. The photodissociation of water molecules is considered a prototypical reaction for theoretical and experimental studies of the O–H bond cleavage in excited electronic states.¹ Two different mechanisms for the photolysis of water molecules in gas phase were proposed, in which photoexcitation and photoionization represent the initial steps.² In the photoexcitation mechanism, the homolytic cleavage of the O–H bond is the primary process, which forms [H]˙ and [OH]˙ (eqn (1)). The [H]˙ radical further reacts with another [H₂O] molecule and generates [H₃O]⁺ and a hydrated electron ([e⁻]^hyd) as the end products (eqn (2)):

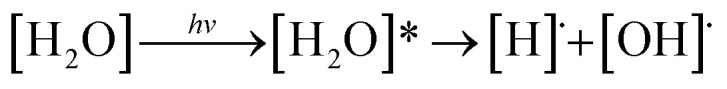1

[H]˙ + [H₂O] → [H₃O]⁺ + [e⁻]^hyd 2

In the photoionization mechanism, the ionic products [H₂O]⁺ and [e⁻]^hyd are primarily generated (eqn (3)), followed by a bimolecular reaction between [H₂O]⁺ and [H₂O] to produce [H₃O]⁺ and [OH]˙ (eqn (4)):

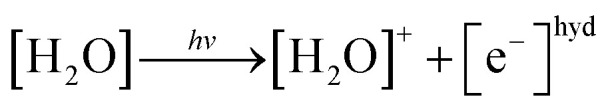3

[H₂O]⁺ + [H₂O] → [H₃O]⁺ + [OH]˙ 4

Although the total reactions are the same, starting from a single water molecule and ending with [H₃O]⁺, [OH]˙, and [e⁻]^hyd, the photochemistry of photoexcitation and photoionization are completely different. Ab initio calculations have showed that photoexcitation (eqn (1)) dominates in gas phase and corresponds to the HOMO–LUMO excitation (7.5 eV),³ whereas the photoionization of an isolated water molecule (eqn (3)) requires considerably higher energy (12.6 eV).⁴ The former is in accordance with UV spectroscopic experiments on single water molecules in gas phase, which indicated that the valence character of the lowest energy band of the electronic spectrum is broad, ranging from 6.8 to 8.2 eV (182–165 nm).⁵ Moreover, the maximum at 7.4 eV (168 nm)⁶ is associated with the direct photodissociation of the O–H bond into [OH]˙ and [H]˙ in the electronic ground state.⁷

The photoexcitation and photoionization of small water clusters, (H₂O)_n; n = 2–3, were studied using various quantum chemical methods and ab initio molecular dynamics (AIMD) simulations.² The AIMD results based on the complete active-space self-consistent field (CASSCF) method showed that the photoexcitation and photoionization processes are complementary in the singlet-excited state, and the photoionization process, which involves structural changes and a proton transfer in hydrogen bond (H-bond), is slower owing to the lack of [H]˙ radicals. At the beginning of the AIMD simulations, the transferring proton possesses a high kinetic energy, and the Eigen and Zundel complexes compete; after 500 fs, proton transfer takes place, leading to the formation of [H₃O]⁺ and [OH]˙.

Water molecules in the singlet- and triplet-excited states were theoretically studied using the extended multistate complete active-space with second-order perturbation theory (MS-CASPT2).⁷ The analysis of the valence and Rydberg characters of the lowest-lying (1¹B₁) state of different geometries showed that the 3s-Rydberg character dominates the ground-state equilibrium structure, which is transformed into a valence state upon 1b₁ → 4a₁ excitation via an extension of both the O–H bonds (C_2v symmetry). Low-lying excited states of H₂O, CH₃OH, and dimethyl ether (C₂H₆O) were studied using the Hartree–Fock method and improved virtual orbital (IVO) calculations.⁸ The results indicated that the low-lying excited states of these molecules are represented by the excitation of an oxygen lone-pair to a 3s or 3p Rydberg-like orbital located on the oxygen atom; moreover, due to the interaction between the electron-deficient hydrogen atoms, the Rydberg orbitals in water are more stable (i.e., have a lower excitation energy) than in CH₃OH and C₂H₆O.

The spectral signature of the hydrated electron in aqueous solutions was studied using ab initio calculations and density functional theory (DFT), in which the electronic ground state and the lowest singlet-excited state of the water dimer and the microsolvation of a hydronium radical (with up to two hydration shells) were primarily investigated.⁹ Because the potential energy curve as a function of the O–H coordinate obtained from CASPT2 calculations is barrierless, the S₀ → S₁ excitation of the water dimer leads to a concerted electron-hydrogen transfer in the H-bond and a separation of [H₃O]⁺ and [OH]˙. The hydrated hydronium ion is represented by a charge-separated complex, which is characterized by a H₃O⁺ ion and a localized-electron cloud.

The barrierless potential energy curve obtained contrasts with previous CASSCF results, in which the S₁ potential energy curve obtained based on a freeze-scan method exhibited a low energy barrier associated with proton transfer in the water dimer and the formation of the H₃O⁺ cation.¹⁰ This discrepancy was attributed to the lack of diffuse basis functions, which are essential for the calculation of σ* Rydberg orbitals, and the use of the freeze-scan method, in which the O–H potential energy curve is constructed by constraining all the structural parameters to their equilibrium values.⁹

In this work, the mechanisms of photodissociation of the water molecule and small water clusters in gas phase, (H₂O)_n; n = 2–3, were studied using CASPT2 with the aug-cc-pVDZ basis set. In contrast to the previous theoretical studies, which considered the photoexcitation and photoionization mechanisms separately,^2,9–11 the present study focused on common intermediate and transition state complexes in both processes in the lowest-singlet excited (S₁) state. The structures and energetics of the elementary steps as well as the relaxations of the structures of the excited molecules in the photodissociation processes were studied using the S₁ potential energy curves as a function of the degrees of freedom. The effects of the cluster size were studied and discussed in comparison with available theoretical and experimental data.

Computational methods

Our theoretical studies on protonated H-bonded systems showed that the dynamics and mechanisms of proton transfer could be reasonably studied based on the concept of presolvation.^12–14 In this approach, the smallest, most active intermediate complex in a systematically selected presolvation model is used as a representative system and studied in detail.^15–18 For example, for protonated water systems,^16,17 the rate-determining step of proton transfer in the electronic ground state is characterized by the interconversion between the close-contact (O–H⁺⋯O) and shared-proton (O⋯H⁺⋯O) structures in H₅O₂⁺. Moreover, the smallest, most active intermediate complex for photoacid dissociation in microhydrated hydroxylamine clusters in the S₁ state is the charge-separated Rydberg-like H-bond complex [NH₂O]˙⋯[H₃O]⁺˙.¹⁹ Therefore, to study the photoexcitation and photoionization processes in gas phase (eqn (1)–(4)), the water molecule and small water clusters, (H₂O)_n; n = 2–3, were used as model systems.²

To simplify the discussion, the water molecule and small water clusters were labeled with a three-character code, Gn-[m] and En-[m]; where G is the structure of the water cluster in the S₀ state; E is the structure of the water cluster in the S₁ state; n is the number of water molecules. The structures with the same number of water molecules are differentiated by m. For example, G2-[1] and E2-[1] are water dimers with similar structures in the S₀ and S₁ state, respectively, whereas E2-[1] and E2-[2] are different structures in the S₁ state.

Quantum chemical calculations

Ab initio calculations in the S₁ state were performed using the CASPT2 method, which has been successfully used in the past decades and widely accepted as a standard method for excited-state calculations.²⁰ Because photochemical reactions in water clusters involve covalent bond breaking and/or forming, at least two configurations representing close-shell and open-shell configurations must be included in the calculations;² the analysis of the valence and Rydberg character of the lowest-lying state showed that the 3s-Rydberg character dominates the ground-state equilibrium structure, which is transformed into a valence state upon S₀ → S₁ excitation via an extension of the O–H bond.⁷

The (H₂O)_n; n = 2–3 model clusters are considered too large for the CASPT2 geometry optimizations and calculations of the S₁ relax-scan potential energy curves, in which the energy gradients with respect to degrees of freedom are extensively computed. Therefore, to optimize the computational resources, the aug-cc-pVDZ basis set was used. Moreover, due to the fast convergence of the excitation energy, augmented basis sets with diffusion functions are recommended for singlet-state calculations.²¹ In addition, as the Hartree–Fock method⁸ and preliminary CASPT2 calculations showed that a single photon only excites one oxygen atom in the water molecule, the accuracy and CPU time were further compromised by assigning only four lone-pair electrons of one oxygen atom in the active orbitals while the remaining electrons were included in doubly occupied orbitals. For the water monomer, the four lone-pair electrons (n = 4) were assigned in four active orbitals (m = 4), whereas the remaining six electrons occupied three closed-shell orbitals (close = 3), abbreviated CASPT2(4,4). For the water dimer, the same number of electrons (n = 4) were assigned in six active orbitals (m = 6), whereas the remaining sixteen electrons occupied eight closed-shell orbitals (close = 8), abbreviated CASPT2(4,6). Based on the same approach, CASPT2(4,8) was used in the water trimer calculations.

To ensure that CASPT2 calculations with restricted number of active electrons (n = 4) and active orbitals did not lead in serious errors in the structural and energetic results, CASPT2 calculations with larger active spaces (close = 2) were performed on the water monomer and dimer, CASPT2(6,5) and (16,12), respectively. For the water trimer, due to excessive number of configuration state functions (CSF) and the limitation of our computer resources, CASPT2 calculations with close = 2 were not possible. Therefore, only twelve lone-pair electrons of the three oxygen atoms were assigned in twelve active orbitals, CASPT2(12,12) with close = 9. The information on the CASPT2 methods used in this work are summarized in Table 1. To characterize the S₀ → S₁ excited species, the spatial distributions of the HOMO and LUMO of the water clusters were computed and illustrated with the same value of the isosurface. All of the CASPT2 calculations were performed using a state-specific method included in the MOLPRO software package.^22,23 The Werner–Meyer–Knowles non-linear optimization method^24–26 was used in the orbital/state optimizations.

The CASPT2 methods, the number of CSF considered (N e-internal) and those generated by the CASPT2 method (N − 1 and N −2 e-internal) used in the calculations of (H₂O)_n; n = 1–3. n = number of active electrons; m = number of active orbitals; E^Ex = vertical excitation energies in eV.

Structure		CASPT2(n,m)	Number of CSFs			E Ex (eV)
			N e-internal	N − 1 e-internal	N − 2 e-internal
G1-[1]		(4,4)	20	20	16	7.20
		(6,5)	50	75	95	7.15
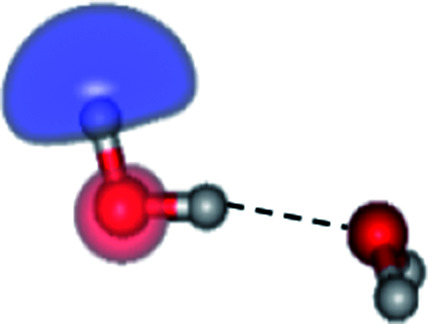
G2-[1]		(4,6)	105	70	36	7.29
		(16,12)	70 785	188 760	453 024	7.36
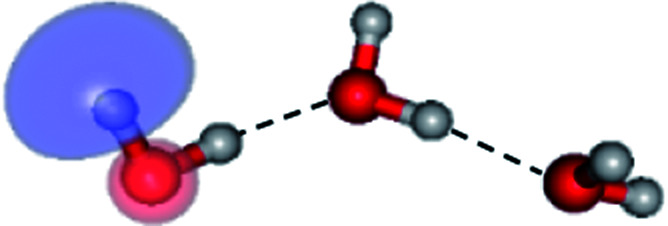
G3-[1]		(4,8)	336	168	64	7.17
		(12,12)	226 512	339 768	453 024	7.21
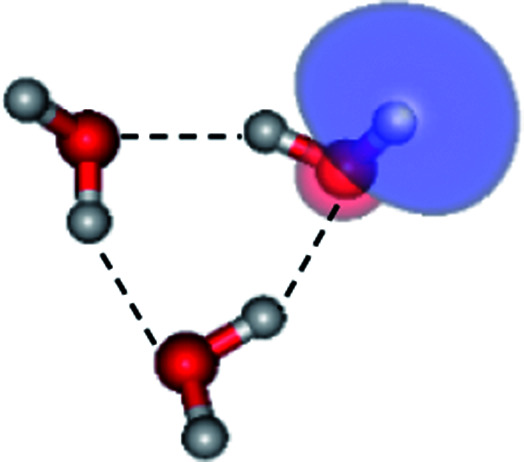
G3-[2]		(4,8)	336	168	64	7.62
		(12,12)	226 512	339 768	453 024	7.56

Equilibrium structures and potential energy curves

The water monomer and clusters in the S₀ state were fully optimized in the C₁ symmetry. To obtain fundamental information on the mechanisms of photoexcitation and photoionization in the S₁ state, the equilibrium and transition structures of the water monomer and dimer were calculated using the quadratic steepest decent (QSD) method included in the MOLPRO software package; the QSD method for transition state calculations is based on the image Hessian method of Sun and Ruedenberg.²⁷ To study the structural changes along the photodissociation paths, the S₁ potential energy curves as a function of the O–H coordinates were constructed using a relax-scan method and the S₀ potential energy curves were calculated at the same geometries.⁹

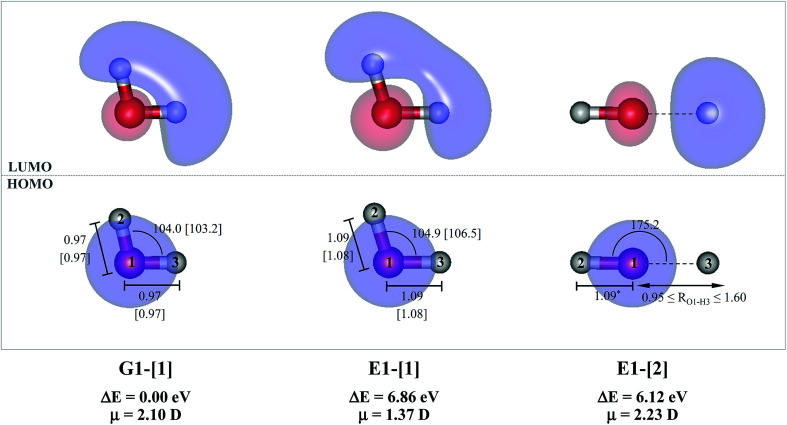
For the water monomer in the S₁ state, due to the predominance of the homolytic cleavage of an O–H bond into [OH]˙ and [H]˙, the S₁ relax-scan potential energy curve was constructed by constraining the O–H bond (R_O–H = 1.09 Å) while varying the other bond distance over the range of 0.95 to 1.60 Å (structure E1-[2] in Fig. 1). It should be noted that although the S₁ relax-scan potential energy curve with a constrained O–H bond is not realistic, we would like to obtain complete information to confirm that the S₁ potential energy curves obtained from CASPT2 calculations with restricted (CASPT2(4,4)) and extended complete active spaces (CASPT2(6,5)) lead to the same results for the water monomer.

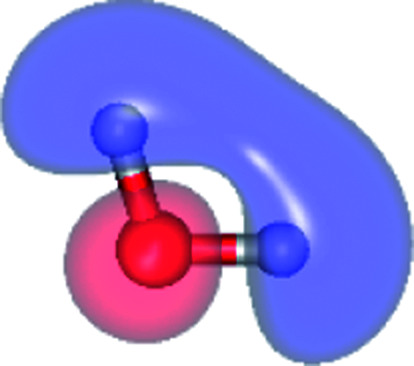
Fig. 1. G1-[1] and E1-[1] = equilibrium structures of the water monomer in C_2v symmetry obtained from CASPT2(4,4) calculations in the S₀ and S₁ states, respectively; E1-[2] = partially-constrained water monomer (R_O–H = 1.09 Å) used in the calculations of the S₁ relax-scan potential energy curve for the O–H dissociation. Distances and angles are in Å and degree, respectively. The values in square brackets were obtained from CASPT2(6,5) geometry optimizations. The value of the HOMO and LUMO isosurfaces is 0.065. ΔE = relative energies with respect to the total energy of G1-[1]; μ = dipole moment.

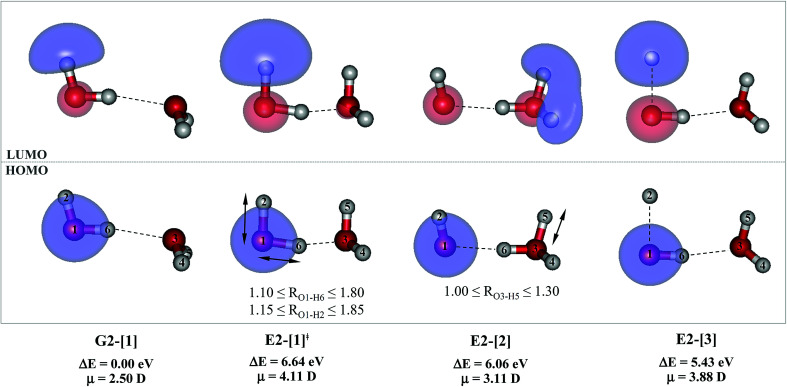
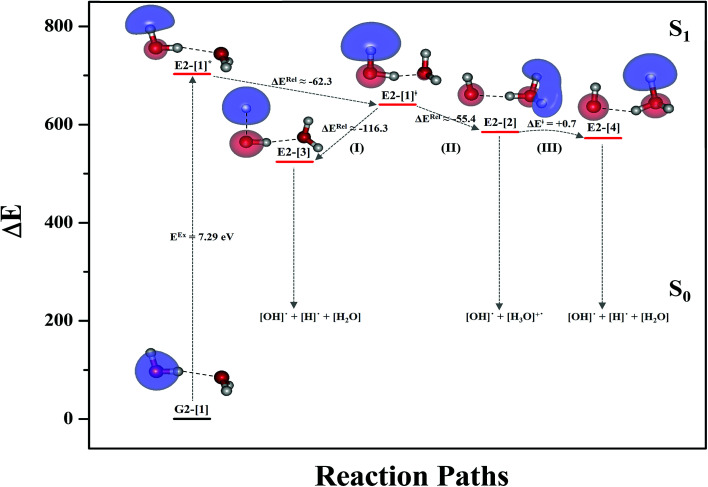
For the water dimer, based on literature survey and preliminary CASPT2 calculations in the S₀ and S₁ states, at least four structures (Fig. 2) were hypothesized to be involved in the photoexcitation and photoionization mechanisms; G2-[1] is the equilibrium structure in the S₀ state; E2-[1]^‡ and E2-[2] are the transition and equilibrium structures in the S₁ state, respectively; and E2-[3] is the direct O–H dissociation structure in the S₁ state. To calculate the S₁ relax-scan potential energy curve for the direct O–H dissociation (E2-[3]), the O₁–H₂ coordinate of the transition structure (E2-[1]^‡) was varied over the range of 1.15–1.85 Å. In the calculation of the S₁ relax-scan potential energy curve for the hydrogen/proton transfer in the H-bond, the O₁–H₆ coordinate of structure E2-[1]^‡ was varied over the range of 1.10–1.80 Å. Similarly, to construct the S₁ relax-scan potential energy curve for the hydrogen/proton transfer from the H₃O moiety of E2-[2], the O₃–H₅ coordinate was varied over the range of 1.00–1.30 Å. All the S₁ relax-scan potential energy curves were computed with a step of ΔR_O–H = 0.05 Å, and the coordinates on the S₁ relax-scan potential energy curves were used in the calculations of the S₀ potential energy curves.

Fig. 2. Structures of the water dimer obtained from CASPT2(4,6) calculations in the S₀ and S₁ states; G2-[1] = equilibrium structure in the S₀ state; E2-[1]^‡ = transition structure in the S₁ state; E2-[2] = equilibrium structure in the S₁ state; E2-[3] = O–H dissociated structure in the S₁ state. Distances are in Å and the value of the HOMO and LUMO isosurfaces is 0.065. ΔE = Relative energies with respect to the total energy of structure G2-[1]; μ = dipole moment.

Based on the same approach, the equilibrium and transition structures as well as the S₁ relax-scan potential energy curves for the photodissociation of the water trimer were computed using CASPT2 calculations. These calculations were performed to study the effect of the cluster size, especially the extension of the O–H⋯O chain, on the structure and energetics of the transition and intermediate complexes.

Results and discussion

The structure parameters and energies obtained from CASPT2 calculations with restricted complete active spaces are listed in Table S1.† The discussion will be focused primarily on the equilibrium and transition structures as well as on the relax-scan potential energy curves of the S₀ and S₁ states of the water monomer and dimer. Because the structures, energetics and S₁ relax-scan potential energy curves obtained from CASPT2 calculations with restricted and extended complete active spaces were not significantly different, the discussion will be made based on the CASPT2 results with restricted complete active spaces. The photoexcitation and photoionization mechanisms proposed based on the results of the water monomer and dimer were confirmed using the results of the water trimer. The multireference characters of the wave functions of the water monomer, dimer and trimer in the S₀ and S₁ states are discussed based on the main electronic configurations and the corresponding configuration interaction (CI) coefficients in Tables 2–4, respectively.

Structures of the water monomer, main electronic configurations and corresponding CI coefficients (cut-off = 0.05) obtained from CASPT2(4,4) and (6,5) calculations^a.

Structure		CASPT2(n,m)	S1		S0
			Conf.	CI coeff.	Conf.	CI coeff.
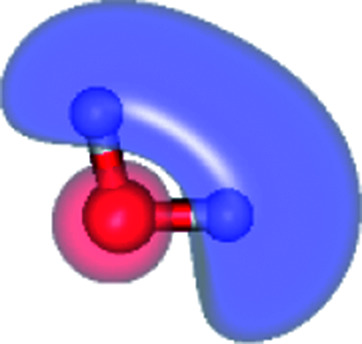
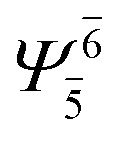
G1-[1]		(4,4)		0.9911	Ψ 0	0.9907
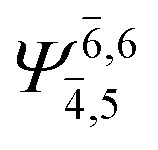
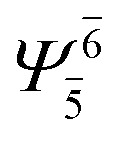
				0.0610		0.0500
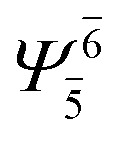
		(6,5)		0.9882	Ψ 0	0.9881
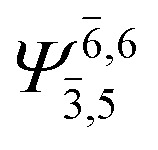
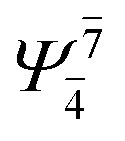
				0.0790		0.0777
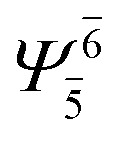
E1-[1]		(4,4)		0.9868	Ψ 0	0.9852
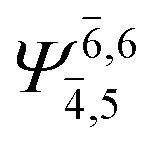
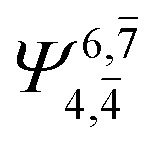
				0.0859		0.0756
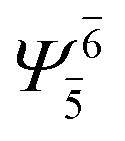
		(6,5)		0.9787	Ψ 0	0.9790
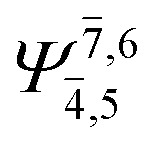
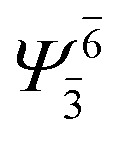
				0.1197		0.0951
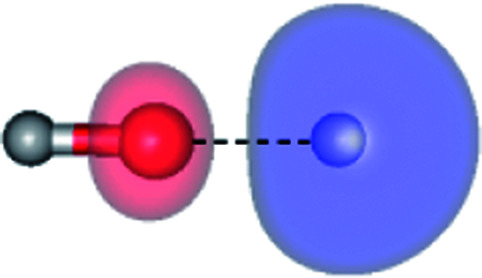
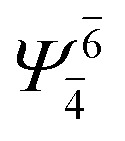
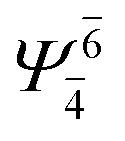
E1-[2]		(4,4)		0.9020		0.9020
			Ψ 0	0.3622	Ψ 0	0.3622
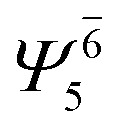
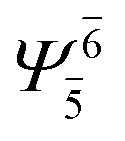
		(6,5)		0.9808		0.9808
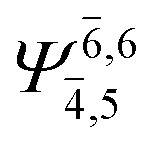
				0.1184		0.1183

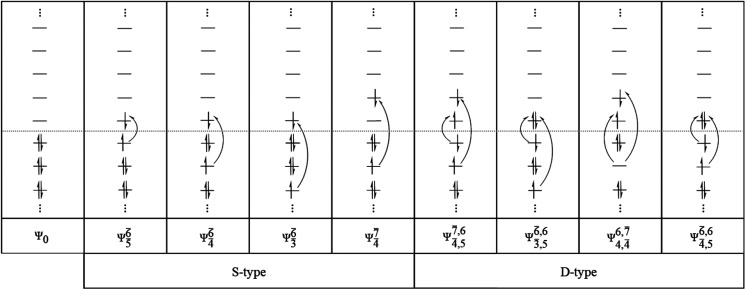
^a Ψ ^r and C^r_a = a → r singly excited determinant (S-type) and CI coefficient and; Ψ^r,s_a,b and C^r,s_a,b = a → r and b → s doubly excited determinant (D-type) and CI coefficient; the indices a and b, and r and s label occupied and virtual or unoccupied spin orbitals, respectively; a bar or lack of a bar is to denote beta (β) and alpha (α) spin orbitals, respectively.

Structures of the water dimer, main electronic configurations and corresponding CI coefficients (cut-off = 0.05) obtained from CASPT2(4,6) and (16,12) calculations^a.

Structure		CASPT2(n,m)	S1		S0
			Conf.	CI coeff.	Conf.	CI coeff.
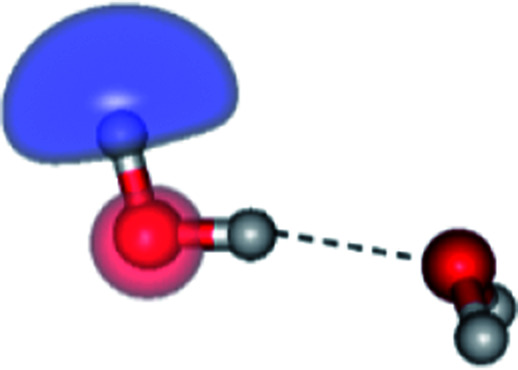
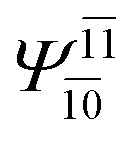
G2-[1]		(4,6)		0.9863	Ψ 0	0.9845
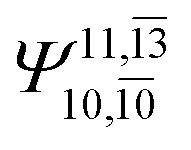
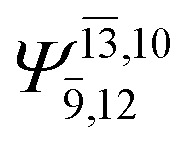
				0.1039		0.0546
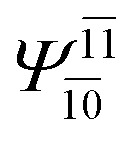
		(16,12)		0.9781	Ψ 0	0.9782
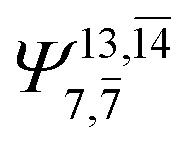
			—	—		0.0586
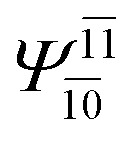
E2-[1]‡		(4,6)		0.9779	Ψ 0	0.9749
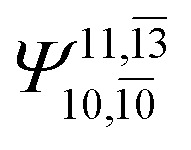
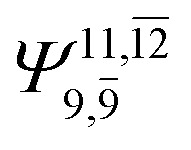
				0.0859		0.0787
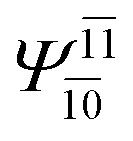
		(16,12)		0.9656	Ψ 0	0.9644
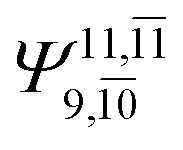
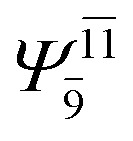
				0.1810		0.1459
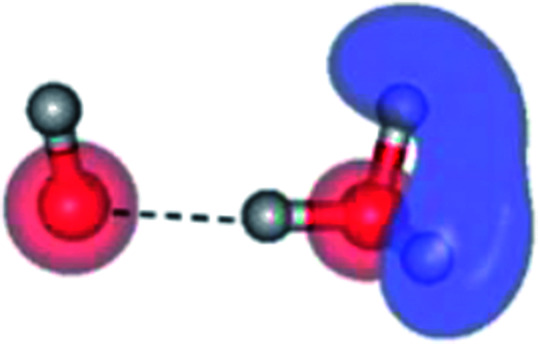
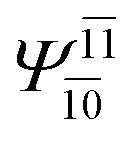
E2-[2]		(4,6)		0.9739	Ψ 0	0.9642
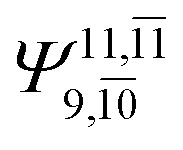
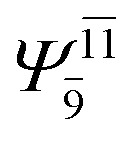
				0.1231		0.1046
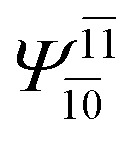
		(16,12)		0.9548	Ψ 0	0.9484
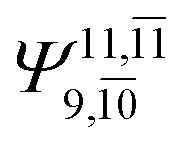
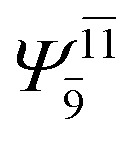
				0.1947		0.1680
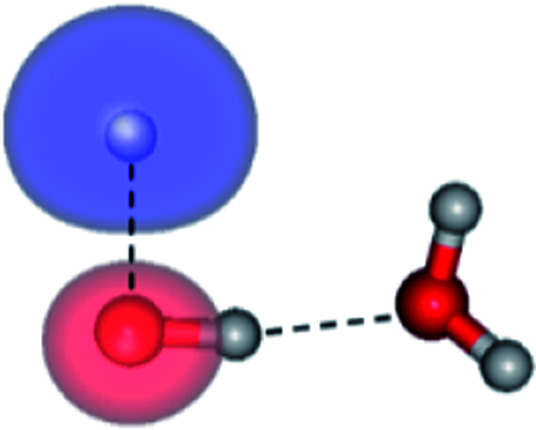
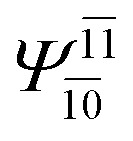
E2-[3]		(4,6)		0.9409	Ψ 0	0.8477
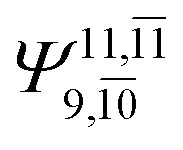
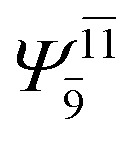
				0.3193		0.4003
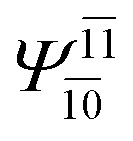
		(16,12)		0.9290	Ψ 0	0.8081
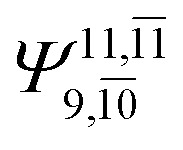
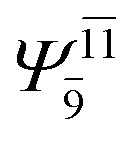
				0.3222		0.4479

^a Ψ ^r and C^r_a = a → r singly excited determinant (S-type) and CI coefficient and; Ψ^r,s_a,b and C^r,s_a,b = a → r and b → s doubly excited determinant (D-type) and CI coefficient; the indices a and b, and r and s label occupied and virtual or unoccupied spin orbitals, respectively; a bar or lack of a bar is to denote beta (β) and alpha (α) spin orbitals, respectively.

Structures of the water trimer, main electronic configurations and corresponding CI coefficients (cut-off = 0.05) obtained from CASPT2(4,8) and (12,12) calculations^a.

Structure		CASPT2(n,m)	S1		S0
			Conf.	CI coeff.	Conf.	CI coeff.
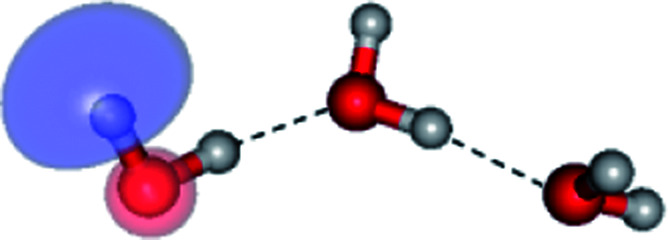
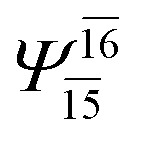
G3-[1]		(4,8)		0.9872	Ψ 0	0.9865
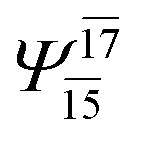
			—	—		0.1025
		(12,12)		0.9743	Ψ 0	0.9745
			—	—	—	—
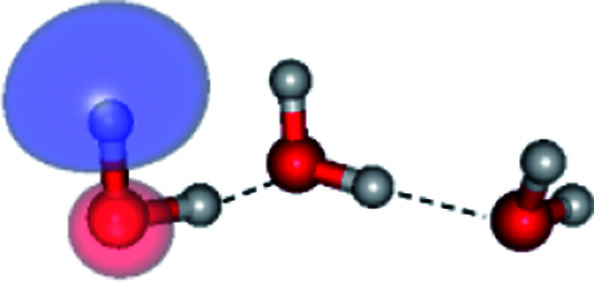
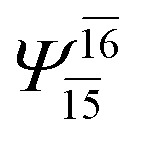
E3-[1]‡		(4,8)		0.9855	Ψ 0	0.9820
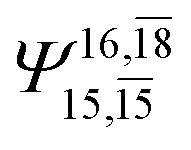
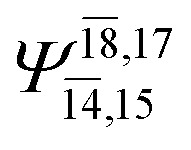
				0.0986		0.0597
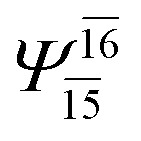
		(12,12)		0.9641	Ψ 0	0.9618
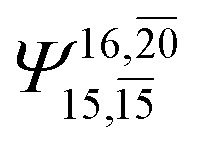
				0.0660	—	—
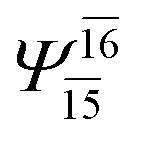
E3-[2]		(4,8)		0.9782	Ψ 0	0.9722
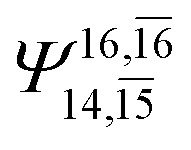
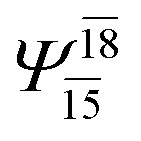
				0.0938		0.0970
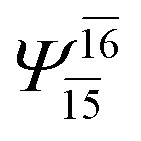
		(12,12)		0.9639	Ψ 0	0.9596
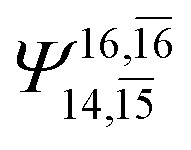
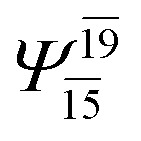
				0.0888		0.0812
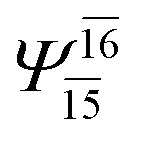
E3-[4]		(4,8)		0.9641	Ψ 0	0.9515
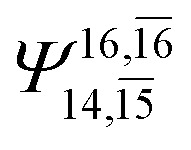
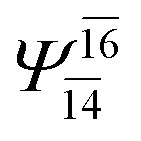
				0.2171		0.1899
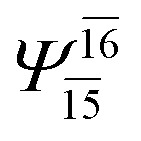
		(12,12)		0.9463	Ψ 0	0.9279
			—	—	—	—

^a Ψ ^r and C^r_a = a → r singly excited determinant (S-type) and CI coefficient and; Ψ^r,s_a,b and C^r,s_a,b = a → r and b → s doubly excited determinant (D-type) and CI coefficient; the indices a and b, and r and s label occupied and virtual or unoccupied spin orbitals, respectively; a bar or lack of a bar is to denote beta (β) and alpha (α) spin orbitals, respectively.

Equilibrium structures of the water monomer and dimer

The equilibrium structures of a single water molecule in the S₀ and S₁ state are shown with the spatial distributions of the HOMO and LUMO in Fig. 1. Following the CASPT2(4,4) geometry optimizations, the equilibrium structure of the water monomer in the S₀ state (G1-[1]) is characterized by R_O–H = 0.97 Å and ∠HOH = 104.0° with a S₀ → S₁ vertical excitation energy of E^Ex = 7.20 eV, which is in excellent agreement with the sharp UV absorption peak observed in the range of 6.9 to 7.5 eV.^5,6 Similar results were obtained from the CASPT2(6,5) geometry optimizations: R_O–H = 0.97 Å, ∠HOH = 103.2°, E^Ex = 7.15 eV. In the S₁ state, the CASPT2(4,4) geometry optimizations with C₁ symmetry led to the direct dissociation of an O–H bond (structure E1-[2] in Fig. 1), whereas the equilibrium structure with the symmetry constrained in the C_2v point group exhibited R_O–H = 1.09 Å and ∠HOH = 104.9° (E1-[1]). The latter values are comparable with the results obtained from the CASPT2(6,5) geometry optimizations: R_O–H = 1.08 Å and ∠HOH = 106.5°. The spatial distributions of the LUMO in Fig. 1 suggest a predominance of the charge-separated Rydberg-like complex in the S₁ state (structures G1-[1] and E1-[1] with C_2v symmetry) and a homolytic cleavage of the O–H bond to yield [H]˙ and [OH]˙ (structure E1-[2], with the HOMO–LUMO excitation energy of 10.38 eV).

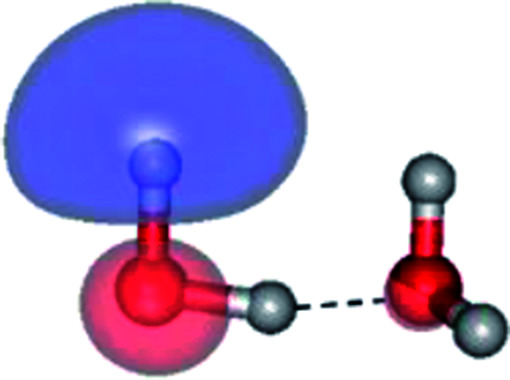
The characteristic structures of the water dimer in the S₀ and S₁ states obtained from CASPT2(4,6) calculations are included in Fig. 2. The equilibrium structure of the water dimer in the electronic ground state is characterized by R_O1–O3 = 2.94 and R_O1–H6 = 0.97 Å (G2-[1]), which are in excellent agreement with reported theoretical and experimental values, e.g., R_O–O = 2.93 and R_O–H = 0.97 Å.²⁸ Moreover, the calculations yield an S₀ → S₁ vertical excitation energy of E^Ex = 7.29 eV for G2-[1], which is comparable to that of the water monomer, E^Ex = 7.20 eV (G1-[1]). In the S₁ state, the CASPT2(4,6) geometry optimizations of the water dimer in the C₁ symmetry yielded a transition structure and a global minimum-energy geometry (structures E2-[1]^‡ and E2-[2] in Fig. 2, respectively). E2-[1]^‡ is characterized by an extraordinarily short H-bond (R_O1–O3 = 2.47 Å) and long O–H bonds in the water molecule acting as proton donor (H-bond: R_O1–H6 = 1.08 Å; non-H-bond: R_O1–H2 = 1.14 Å). The short R_O1–O3 distance indicates that structure E2-[1]^‡ is characterized by the [(H₂O)₂]⁺˙ radical cation or the water dimer cation (R_O1–O3 = 2.5 Å),²⁹ and the long R_O1–H6 distance reflects a strong dipole–dipole interaction in the O–H⋯O H-bond (μ = 4.11 D), which suggest the possibility of proton transfer. The long non-H-bond R_O1–H2 points to the homolytic cleavage of the O₁–H₂ bond and the formation of [H]˙, [OH]˙, and [H₂O] (E2-[3]). Structure E2-[1]^‡ could therefore be hypothesized to be the “primary transition structure” for both the photoexcitation and photoionization of the water dimer in the S₁ state. The existence of structure E2-[1]^‡ as the primary transition structure is in accordance with photoelectron-photoion coincident experiments,³⁰ in which [(H₂O)₂]⁺˙ was detected as a minor species with an upper limit of the lifetime of the transient [H₂O]⁺˙ radical cation of approximately 40 fs.³¹

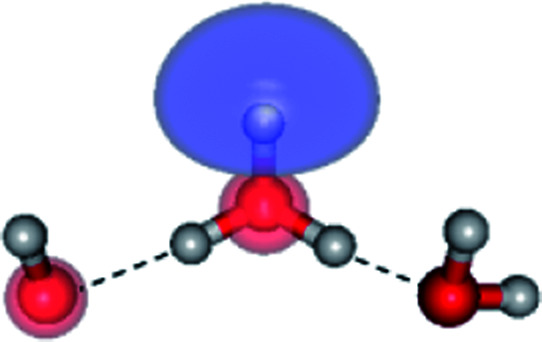
The global minimum-energy geometry of the water dimer in the S₁ state (structure E2-[2] in Fig. 2) confirms that the outstanding feature of the S₀ → S₁ excitation is the proton transfer in H-bond. In addition, based on the spatial distribution of the LUMO,¹⁹ structure E2-[2] with R_O1–O3 = 2.82 Å ([H₃O]⁺˙⋯[OH]˙) can be considered a charge-separated Rydberg-like H-bond complex, with the HOMO–LUMO excitation energy of 8.65 eV. A similar charge-separated Rydberg-like H-bond complex ([NH₂O]˙⋯[H₃O]⁺˙) was confirmed in a previous study to be the smallest, most active intermediate complex for proton transfer in the NH₂OH⋯H₂O system in the S₁ state.¹⁹ These intermediate complexes result from the redistribution of the electron density in the H-bond upon S₀ → S₁ excitation and are represented by electron clouds localized on the two hydrogen atoms of the non-H-bond O–H in the [H₃O]⁺˙.^9,32,33 It should be noted that because the CASPT2(4,6) geometry optimizations were performed without symmetry restrictions (i.e., with C₁ symmetry), one of the non-H-bond O–H distances in the [H₃O]⁺˙ moiety in structure E2-[2] (R_O3–H5 = 1.04 Å) is slightly longer than the other (R_O3–H4 = 1.02 Å). Therefore, the O₃–H₅ bond is anticipated to be susceptible to subsequence hydrogen/proton transfer.

Potential energy curves for the water monomer and dimer

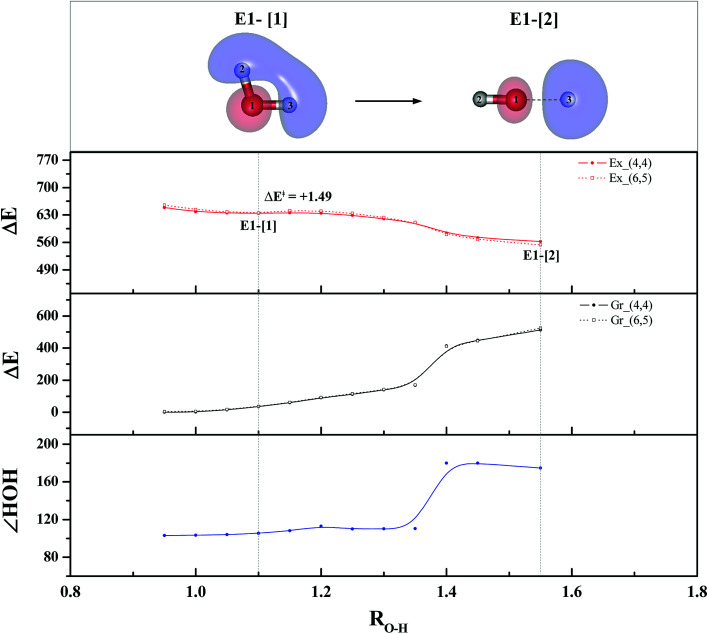
To study the energetics of the photoexcitation and photoionization processes (eqn (1)–(4)), the S₁ relax-scan potential energy curves as a function of the O–H coordinates of the water monomer and dimer were initially constructed using CASPT2(4,4) and (4,6) calculations and are shown in Fig. 3 and 4, respectively. For the water monomer with the R_O1–H2 distance constrained to 1.09 Å, the S₁ relax-scan potential energy curve as a function of R_O1–H3 exhibits a shallow minimum at R_O1–H3 = 1.09 Å (Fig. 3). The homolytic cleavage of the O₁–H₃ bond is accompanied by an increase in the ∠H₂O₁H₃ from 103 to 180°, with a low energy barrier of ΔE^‡ = 1.49 kJ mol⁻¹ at R_O1–H3 = 1.15 Å.

Fig. 3. The S₁ relax-scan potential energy curve (Ex_(4,4)) with respect to one of the O–H coordinates of the water monomer (structure E1-[2] in Fig. 1) obtained from CASPT2(4,4) calculations. The energies on the S₀ potential energy curve (Gr_(4,4)) were calculated at the same geometries. The relative energies (ΔE) are with respect to the total energy of structure G1-[1]. The dash-line curves are the S₀ and S₁ energies obtained from CASPT2(6,5) calculations, Gr_(6,5) and Ex_(6,5), respectively. The value of the LUMO isosurfaces is 0.065. Energies, distances and angles are in kJ mol⁻¹, Å and degree, respectively. ΔE^‡ = Energy barrier in kJ mol⁻¹.

Fig. 4. The S₁ relax-scan potential energy curves (Ex_(4,6)) as a function of the O–H coordinates of the water dimer obtained from CASPT2(4,6) calculations. The S₀ potential energy curves (Gr_(4,6)) were calculated at the same geometries. The dash-line curves are the S₀ and S₁ energies obtained from CASPT2(16,12) calculations, Gr_(16,12) and Ex_(16,12), respectively. The relative energies (ΔE) are with respect to structure G2-[1]. The value of the LUMO isosurfaces is 0.065. Energies and distances are in kJ mol⁻¹ and Å, respectively. The energy release (ΔE^Rel) and energy barrier (ΔE^‡) are in kJ mol⁻¹; ‡ = transition structure; (I) = photoexcitation; (II) and (III) = photoionization.

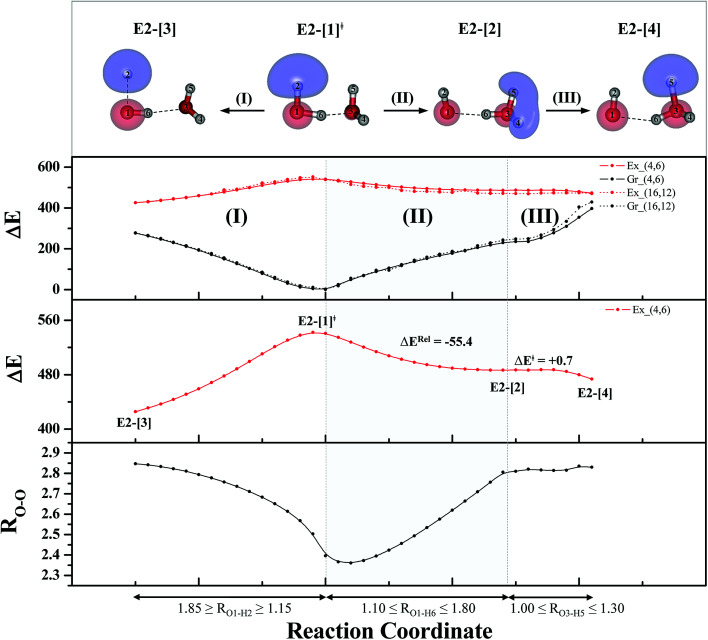
Based on the information obtained on the transition and equilibrium structures in Fig. 2, the S₁ relax-scan potential energy curves for the photoexcitation and photoionization processes of the water dimer were constructed using CASPT2(4,6) calculations. Starting from the [(H₂O)₂]⁺˙ radical cation (E2-[1]^‡), the S₁ relax-scan potential energy curves as a function of the non-H-bond and H-bond O–H coordinates were constructed and are shown in Fig. 4. The S₁ relax-scan potential energy curve for the photoexcitation in panel (I) is similar to that of the water monomer, which is characterized by a purely repulsive potential energy curve. The outstanding feature of the S₁ relax-scan potential energy curve for the proton transfer in panel (II) is a shallow potential energy well, corresponding to structure E2-[2] with R_O–O = 2.80 and R_O–H = 1.01 Å, and an energy release of ΔE^Rel ≈ −55.4 kJ mol⁻¹ due to the relaxation of E2-[1]^‡. The existence of a shallow minimum suggests that the photoionization process is non-concerted, which is supported by the Born–Oppenheimer molecular dynamics (BOMD) results based on the unrestricted Møller–Plesset second-order perturbation theory (UMP2),² in which the ionization process in the ionized water dimer ([(H₂O)₂]⁺) was considerably slower than the photoexcitation process. This finding is different from the results in ref. 9, in which the S₁ relax-scan potential energy curve obtained from CASPT2 calculations in the C_s symmetry with a larger step length (ΔR_O–H = 0.20 Å) is purely repulsive.

Because one of the non-H-bond O–H distances in the [H₃O]⁺˙ moiety of structure E2-[2] is longer than the other, the possibility of the hydrogen/proton transfer from [H₃O]⁺˙ was investigated. The S₁ relax-scan potential energy curve for the O₃–H₅ dissociation was tentatively constructed and is included in Fig. 4, panel (III). The potential energy curve indicates that the extension of the O₃–H₅ bond leads to structure E2-[4], with a small energy barrier of ΔE^‡ = 0.7 kJ mol⁻¹ for the O₃–H₅ dissociation. Because the S₁ relax-scan potential energy curve starts to decline at R_O3–H5 = 1.30 Å and E^Ex = 0.79 eV, the intersection of the S₀ and S₁ states, which generates [H]˙, [OH]˙, and [H₂O] in their respective electronic ground states, is anticipated to occur beyond this point.

Based on the equilibrium and transition structures as well as on the S₁ relax-scan potential energy curves obtained from CASPT2(4,6) calculations, the photoexcitation and photoionization mechanisms in the water dimer can be hypothesized to occur through the primary transition structure (E2-[1]^‡), as shown in Fig. 5. Starting from the ground-state geometry (G2-[1]), the S₀ → S₁ vertical excitation (E^Ex = 7.29 eV) leads to structure E2-[1]*, which is relaxed to the [(H₂O)₂]⁺˙ radical cation (E2-[1]^‡). Structure E2-[1]^‡ generates [H]˙, [OH]˙, and [H₂O] in their respective electronic-ground states either directly through photoexcitation (I) or indirectly through the metastable [H₃O]⁺˙⋯[OH]˙ Rydberg-like H-bond complex (structure E2-[2]) via O₃–H₅ dissociation from [H₃O]⁺˙, as seen in panel (II) and panel (III), respectively. The hypothesized mechanisms imply that the photoexcitation process in water clusters is not necessarily unimolecular as proposed in eqn (1) and (2), and the [(H₂O)₂]⁺˙ radical cation can be considered the smallest intermediate complex in the photoionization process (eqn (3) and (4)). The proposed water dimer as a precursor for the photodissociation processes is supported by a submillimeter-wave absorption spectrum of the Earth's atmosphere and experiments,^34,35 which suggested that the absorption results from the water dimer existing at low altitude in the troposphere and lower stratosphere.

Fig. 5. Mechanisms of the photoexcitation ((I)) and photoionization processes ((II) and (III)) of the water dimer in the S₁ state obtained from CASPT2(4,6) calculations. The relative energies (ΔE) in kJ mol⁻¹ are with respect to structure G2-[1]. The S₀ → S₁ vertical excitation energy (E^Ex) is in eV. ΔE^Rel and ΔE^‡ = energy release and barrier in kJ mol⁻¹, respectively; * = vertically excited structure; ‡ = transition state complex. The value of the LUMO isosurfaces is 0.065.

Equilibrium structures and potential energy curves for the water trimer

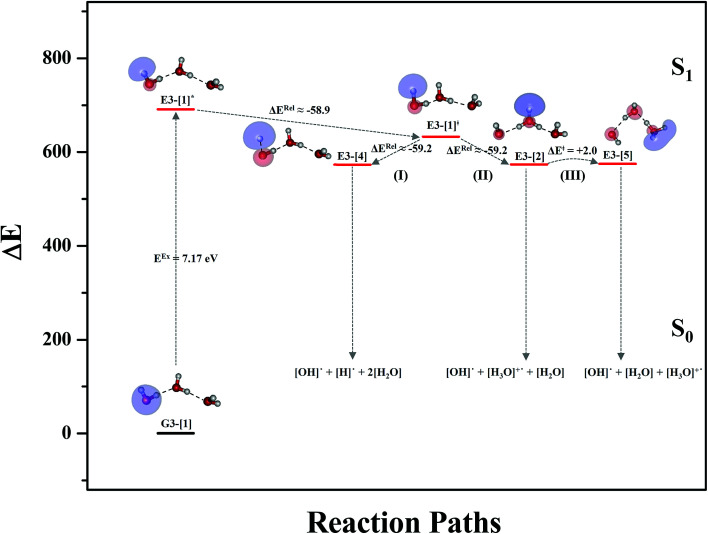
To confirm the mechanisms proposed in Fig. 5, CASPT2(4,8) calculations were performed on the water trimer, and the characteristic structures are shown with the spatial distributions of the HOMO and LUMO in Fig. 6. In the electronic-ground state, the global minimum-energy geometry of the water trimer is represented by a cyclic H-bonded structure (G3-[2]) with three equivalent O–H⋯O H-bonds (R_O–O = 2.81 Å) and a S₀ → S₁ vertical excitation energy of E^Ex = 7.62 eV (163 nm), whereas the local minimum-energy geometry is a linear H-bonded structure (G3-[1]) with R_O–O = 2.87 and 2.92 Å, R_O–H = 0.96–0.98 Å, and E^Ex = 7.17 eV (173 nm). Because the S₀ → S₁ vertical excitation energy is almost the same as that of the water monomer and dimer (7.20 and 7.29 eV, respectively), the energy of a single photon will excite only one oxygen atom in the water clusters; for the water dimer and trimer, the spatial distributions of the HOMO and LUMO in Fig. 2 and 6 suggest that a single photon vertically excites the oxygen lone-pair of the water molecule acting as proton donor, e.g., structures G2-[1] and G3-[1], and the lone-pairs and Rydberg orbitals of all of the oxygen atoms in the small water clusters are most likely not degenerate due to the H-bond formation.

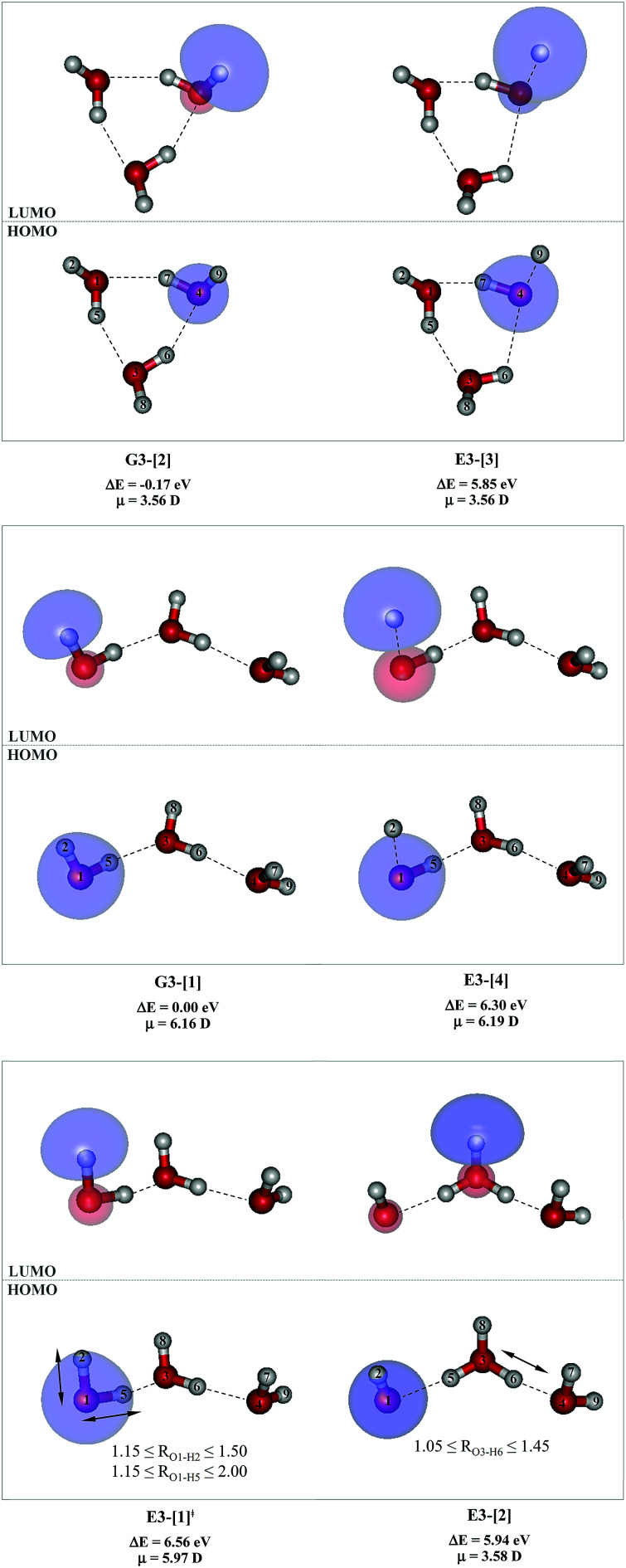
Fig. 6. Structures of the water trimer obtained from CASPT2(4,8) calculations in the S₀ and S₁ states; G3-[2] and G3-[1] = global and local minimum energy geometries in the S₀ state, respectively; E3-[1]^‡ = transition structure in the S₁ state; E3-[2] = equilibrium structure in the S₁ state; E3-[3] and E3-[4] = O–H dissociated structures in the S₁ state. ΔE = Relative energies with respect to the total energy of structure G3-[1]; μ= dipole moment. The value of the HOMO and LUMO isosurfaces is 0.065.

Because the linear H-bonded trimer (E3-[1]*) is energetically more stable (approximately 29 kJ mol⁻¹) than the cyclic H-bonded trimer (E3-[2]*), only the linear H-bond trimer was used as a representative system in the study of the effects of the cluster size. Starting from the transition structure E2-[1]^‡ with an additional water molecule, CASPT2 geometry optimizations yield structure E3-[1]^‡, in which the [(H₂O)₂]⁺˙ radical cation moiety is approximately the same as in structure E2-[1]^‡ (E3-[1]^‡; R_O1–O3 = 2.47, R_O1–H2 = 1.13, R_O1–H5 = 1.10 Å, μ = 5.97 D). Similarly, starting from the intermediate structure E2-[2] with one water molecule H-bonded to [H₃O]⁺˙, structure E3-[2] is obtained as the global minimum-energy geometry with a subunit resembling the [H₃O]⁺˙⋯[OH]˙ charge-separated Rydberg-like dimer (E3-[2]; R_O1–O3 = 2.78 and R_O3–O4 = 2.59 Å). These findings confirm that structures E2-[1]^‡ and E2-[2] are the smallest, most active transition and intermediate complexes for the photoionization process, and that proton transfer from the intermediate structure E2-[2] is possible owing to the H-bond chain extension.

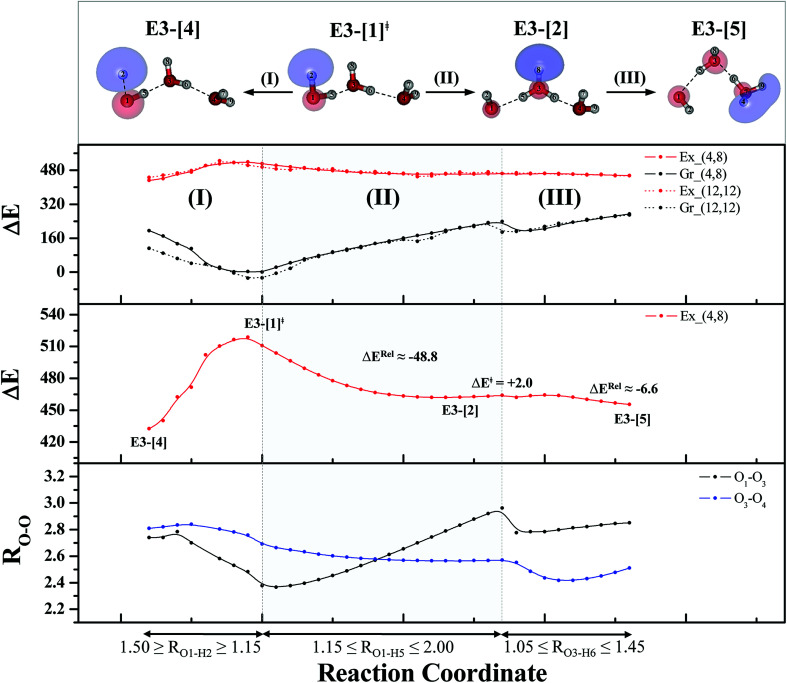
Comparison of the shapes of the S₁ relax-scan potential energy curves and the spatial distributions of the LUMO as a function of the O–H coordinates in Fig. 4 and 7 shows no significant differences between the photoexcitation and photoionization processes in the water dimer and trimer. Owing to the H-bond chain extension, the [H₃O]⁺˙⋯[OH]˙ charge-separated Rydberg-like moiety is stabilized, which is reflected in the high energy barrier for proton transfer in panel (III) (ΔE^‡ = 2.0 kJ mol⁻¹) compared to that of structure E2-[2] (ΔE^‡ = 0.70 kJ mol⁻¹). Based on the information obtained for the water trimer, the relative energies for the photoexcitation and photoionization mechanisms, in which the [(H₂O)₂]⁺˙ radical cation moiety being the primary transition structure, are illustrated in Fig. 8. These structural and energetic results for the water trimer confirm that the extension of the H-bond chain from n = 2 to 3 does not lead to significant changes in the transition and intermediate complexes, and the water dimer is the smallest transition structure in the photoionization process of water clusters in gas phase.

Fig. 7. The S₁ relax-scan potential energy curves (Ex_(4,8)) as a function of the O–H coordinates of the water trimer obtained from CASPT2(4,8) calculations. The S₀ potential energy curves (Gr_(4,8)) were calculated at the same geometries. The dash-line curves are the S₀ and S₁ energies obtained from CASPT2(12,12) calculations, Gr_(12,12) and Ex_(12,12), respectively. The relative energies (ΔE) are with respect to structure G3-[1]. The value of the LUMO isosurfaces is 0.065. Energies and distances are in kJ mol⁻¹ and Å, respectively. The energy release (ΔE^Rel) and energy barrier (ΔE^‡) are in kJ mol⁻¹; ‡ = transition structure; (I) = photoexcitation; (II) and (III) = photoionization.

Fig. 8. Mechanisms of the photoexcitation ((I)) and photoionization processes ((II) and (III)) of the water trimer in the S₁ state obtained from CASPT2(4,8) calculations. The relative energies (ΔE) are with respect to structure G3-[1] and in kJ mol⁻¹. The S₀ → S₁ vertical excitation energy (E^Ex) is in eV. ΔE^Rel and ΔE^‡ = energy release and barrier in kJ mol⁻¹, respectively; * = vertically excited structure; ‡ = transition state complex. The value of the LUMO isosurfaces is 0.065.

Analyses of electronic configurations and the CI coefficients

To obtain information on the electronic configurations and multireference characters in the photodissociation processes, the main electronic configurations and CI coefficients (cut-off = 0.05) of the water monomer, dimer and trimer in the S₀ and S₁ states, obtained from CASPT2 calculations with restricted and extended complete active spaces, are included in Tables 2–4, respectively; Ψ₀ and C₀ = ground state determinant and CI coefficient; Ψ^r_a and C^r_a = a → r singly excited determinant (S-type) and CI coefficient and; Ψ^r,s_a,b and C^r,s_a,b = a → r and b → s doubly excited determinant (D-type) and CI coefficient; the indices a and b, and r and s label occupied and virtual or unoccupied spin orbitals, respectively; a bar or lack of a bar is to denote beta (β) and alpha (α) spin orbitals, respectively.

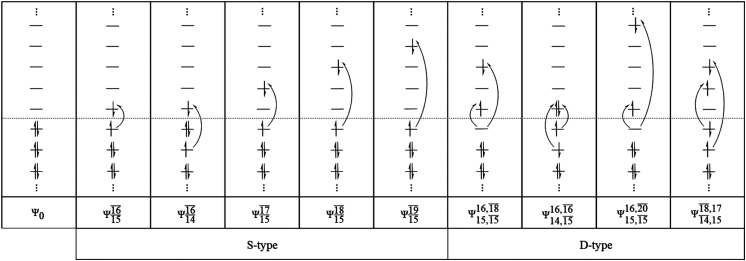
In the S₁ state, the analyses of the electronic configurations and CI coefficients obtained from CASPT2 calculations with restricted and extended complete active spaces show a common trend for the small water clusters. For example, for the water dimer, CASPT2(4,6) calculations in Table 3 suggest that singly excited determinants 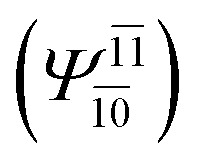dominate doubly excited determinants for the equilibrium (E2-[2]; 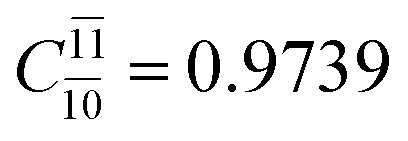; 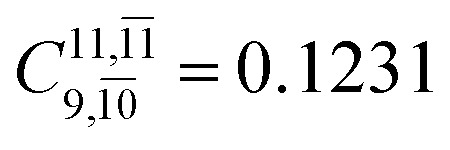) and transition structures (E2-[1]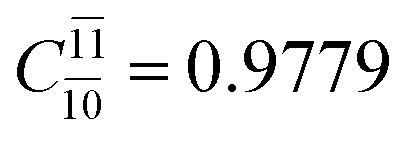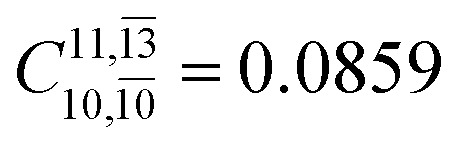^‡; ; ), whereas for the O–H dissociated structure, the contribution of the singly excited determinant 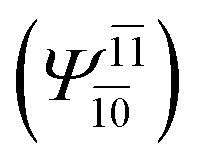decreases and that of the doubly excited determinant 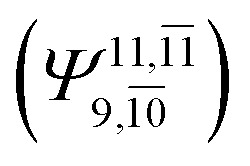increases (E2-[3]; 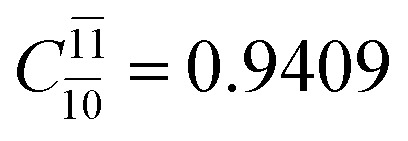and ).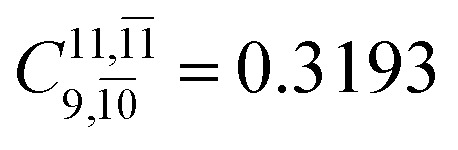

CASPT2 calculations with restricted and extended complete active spaces also show the dependence of the CI coefficients for the O–H dissociated structure in the S₀ state. For example, for the water dimer, CASPT2(4,6) calculations illustrate that the ground state configuration (Ψ₀) is outstanding for the equilibrium structure (G2-[1]; C₀= 0.9845), and upon the O–H dissociation, the contribution of Ψ₀ decreases, whereas that of the singly excited determinant 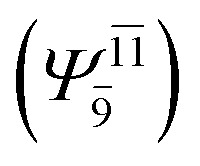increases (C₀ = 0.8477; 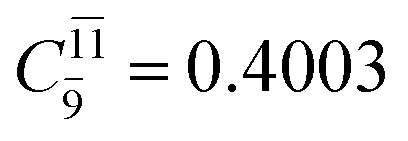). The discussion in this subsection leads to the conclusion that the multireference characters of the wave functions are important in both S₀ and S₁ states, especially for the O–H dissociated structures, and are not significantly changed with the number of water molecules.

Conclusion

Herein, the mechanisms of photoexcitation and photoionization of small water clusters in gas phase, (H₂O)_n; n = 2–3, were studied. In contrast to the previous theoretical studies, which considered the photoexcitation and photoionization processes separately, this study characterized the structures and energetics of common transition and intermediate complexes in the lowest singlet-excited (S₁) state and the effects of the cluster size. These objectives were achieved by performing CASPT2 geometry optimizations and transition state calculations without symmetry constraints (C₁ symmetry) and by allowing all the degrees of freedom to freely relax during the construction of the S₁ potential energy curves.

The S₁ relax-scan potential energy curves as a function of the O–H coordinates revealed that the photoexcitation of the water monomer by a single photon can directly generate [OH]˙ and [H]˙ in their respective electronic-ground states, and a single photon with approximately the same energy can similarly lead to the photoexcitation and also to the photoionization in the water clusters. The S₀ → S₁ excitation of the water clusters results in strong polarization in the O–H⋯O H-bond and thus in the formation of the primary transition structure for both photoexcitation and photoionization, which implies that the photoionization process can be activated by photon with the energy lower than the ionization threshold of water molecule (12.6 eV). This primary transition structure is characterized by the water dimer radical cation ([(H₂O)₂]⁺˙) with C₁ symmetry, from which [OH]˙, [H]˙, and [H₃O]⁺˙ can be generated through the homolytic cleavage of an O–H bond and through proton transfer to form the metastable charge-separated Rydberg-like H-bond complex ([H₃O]⁺˙⋯[OH]˙) upon photoexcitation and photoionization, respectively. These results are different from those of previously reported ab initio calculations in the C_s point group, in which the photoionization in the S₁ state was concluded to take place on a purely repulsive potential energy curve.

The results on the water trimer confirmed these findings and further concluded that the [(H₂O)₂]⁺˙ and [H₃O]⁺˙⋯[OH]˙ H-bonded complexes are the smallest transition and intermediate complexes in the photoionization process in the S₁ state; the ab initio results showed that increasing the size of the water clusters does not lead to significant changes in the structures and energetics of these charged species. The mechanisms proposed in this work further suggest that the photoexcitation and photoionization processes in gas phase are most likely bimolecular reactions, in which the transition and intermediate charged species are more stabilized than in a unimolecular reaction. These theoretical results provide insights into the photoexcitation and photoionization mechanisms of molecular clusters and can be used as guidelines for further theoretical and experimental studies.

Conflicts of interest

There are no conflicts to declare.