Skip to main content
PMC home page
RSC Advances logoLink to RSC Advances
. 2018 Nov 26;8(69):39414–39420. doi: 10.1039/c8ra07112h

Application of DFT-based machine learning for developing molecular electrode materials in Li-ion batteries†

Omar Allam 1,2,‡, Byung Woo Cho 1,2,‡, Ki Chul Kim 1,3,✉, Seung Soon Jang 1,4,5,6,✉
PMCID: PMC9090775  PMID: 35558035

Abstract

In this study, we utilize a density functional theory-machine learning framework to develop a high-throughput screening method for designing new molecular electrode materials. For this purpose, a density functional theory modeling approach is employed to predict basic quantum mechanical quantities such as redox potentials, and electronic properties such as electron affinity, highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO), for a selected set of organic materials. Both the electronic properties and structural information, such as the numbers of oxygen atoms, lithium atoms, boron atoms, carbon atoms, hydrogen atoms, and aromatic rings, are considered as input variables for the machine learning-based prediction of redox potentials. The large-set of input variables are further downsized using a linear correlation analysis to have six core input variables, namely electron affinity, HOMO, LUMO, HOMO–LUMO gap, the number of oxygen atoms and the number of lithium atoms. The artificial neural network trained using the quasi-Newton method demonstrates a capability for accurately estimating the redox potentials. From the contribution analysis, in which the influence of each input on the target are accessed, we highlight that the electron affinity has the highest contribution to redox potential, followed by the number of oxygen atoms, HOMO–LUMO gap, the number of lithium atoms, LUMO, and HOMO, in order.

In this study, we utilize a density functional theory-machine learning framework to develop a high-throughput screening method for designing new molecular electrode materials.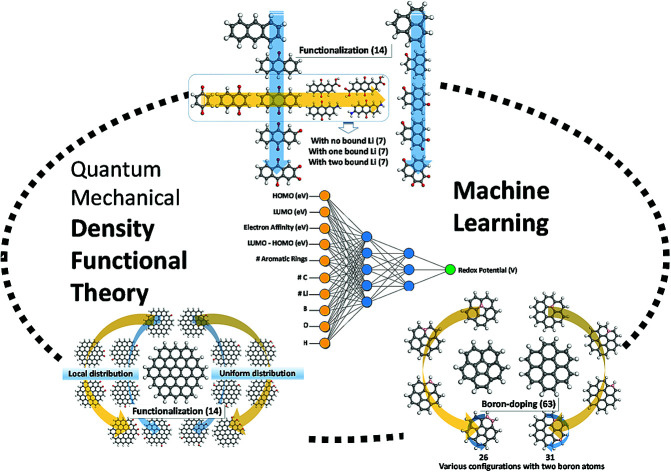graphic file with name c8ra07112h-ga.jpg

1. Introduction

Although a variety of alternative energy technologies such as wind energy, wave energy, and solar energy have been developed to overcome concerns regarding the energy crisis and environmental pollution,1–4 the intermittent characteristics of these sustainable energy technologies require advanced energy storage devices to stably offer electricity for stationary power plant applications.1–7 Furthermore, increasing demands on high performance electrochemical energy storage technologies have attracted lots of attention, especially focusing on high energy, charge, and power capacities.1–14 Among a number of available candidates, lithium-ion batteries have been recognized as one of the most promising secondary batteries due to their high energy and charge capacities in addition to their cyclic stability.2–9

However, it should be noted that the current lithium ion batteries suffer from several issues such as difficulty in the diffusion of lithium ions through the bulk phase of conventional transition metal oxides of positive electrodes; which results in poor power capacities.3,6 In order to resolve this problem, it is crucial to design novel cathode materials with enhanced ionic diffusivities without compromising the charge and energy densities.3–6 Therefore, it is very desirable to accomplish the following requirements in new cathode materials: (1) high cell voltages, (2) enhanced power capacities, (3) excellent charge and energy capacities.

In this context, the efforts to identify promising positive electrode materials with high performance have not been limited to only conventional transition metal oxides, but have also been extended to metal-free organic materials such as redox-active quinone molecules.15 Organic electrode materials are attractive because the cost of storing electrochemical energy can be potentially lowered by utilizing abundant available carbon-based materials. In addition, the light weight and robust mechanical properties possessed by carbon-based materials open a door towards new flexible battery for flexible electronic devices. Thus, graphene derivatives with high conductivity and vast accessible inner spaces8,9,16,17 and quinone derivatives with electrochemically active oxygens9–11,18–26 have been studied intensively as promising organic electrode materials.

It should be noted that quantitative molecular structure–electrochemical property relationships have not been thoroughly established yet; which means that there is no practical molecular structure design guideline to obtain desired specific levels of certain properties and commensurate performances. To avoid the time consuming “trial and error” approach, a more systematic procedure is desired to tune and design materials for target properties and performances.

In this study, we attempted to establish a machine learning based high-throughput screening method that can take a role as a predictive design guideline of molecular structures. It has two components: one is quantum mechanical density functional theory (DFT) modeling and another is the machine learning method. We have used DFT modeling method for carbon-based molecular electrode materials for battery8–13 and confirmed its accurate predictability for redox potentials with small uncertainty (<0.3 V). Specifically, in this contribution we aim to train a learning model for various carbon based electrode materials.8–13

Although DFT can produce high-fidelity predictions of redox potential, it is impractical to establish a predictive high-throughput screening method only based on DFT modeling. The main reasons are that (1) the effects of various molecular architectures are not linearly proportional to the target properties and (2) multistep quantum mechanical computations for predicting accurate redox potentials are computationally very expensive. Thus, we planned to use relatively light DFT computations to obtain basic quantum mechanical characteristics such as electron affinity (EA), highest occupied molecular orbital (HOMO), lowest unoccupied molecular orbital (LUMO), and so on, which can be used as input parameters for our learning model.

Machine learning (ML), a precursor to artificial intelligence, offers an algorithm that can achieve its predictive capability by learning from an input dataset.27 Through recent reports, it has been demonstrated that ML can be used in materials science in order to predict complex behaviours of materials and thereby to help explore vast chemical space for new materials discovery.27–29 For instance, once a machine learning algorithm is trained, it can provide an immediate estimate of complex electronic and electrochemical properties of materials, which otherwise would have taken a significantly longer time to obtain experimentally or computationally through DFT. Although the application of ML in materials science is still in an early stage, it should be of great interest to validate its capability as a high-throughput screening method.

Therefore, in this study we combine DFT and ML to build a high-throughput screening method for predicting redox potential (in V). We expect ML can be expanded to utilize experimental input parameters in principle; thus this study will be a small step forward in developing more complicated ML models as high-throughput screening methods for alternative battery electrode materials.

2. Computational methods

2.1. Redox potential and electronic properties

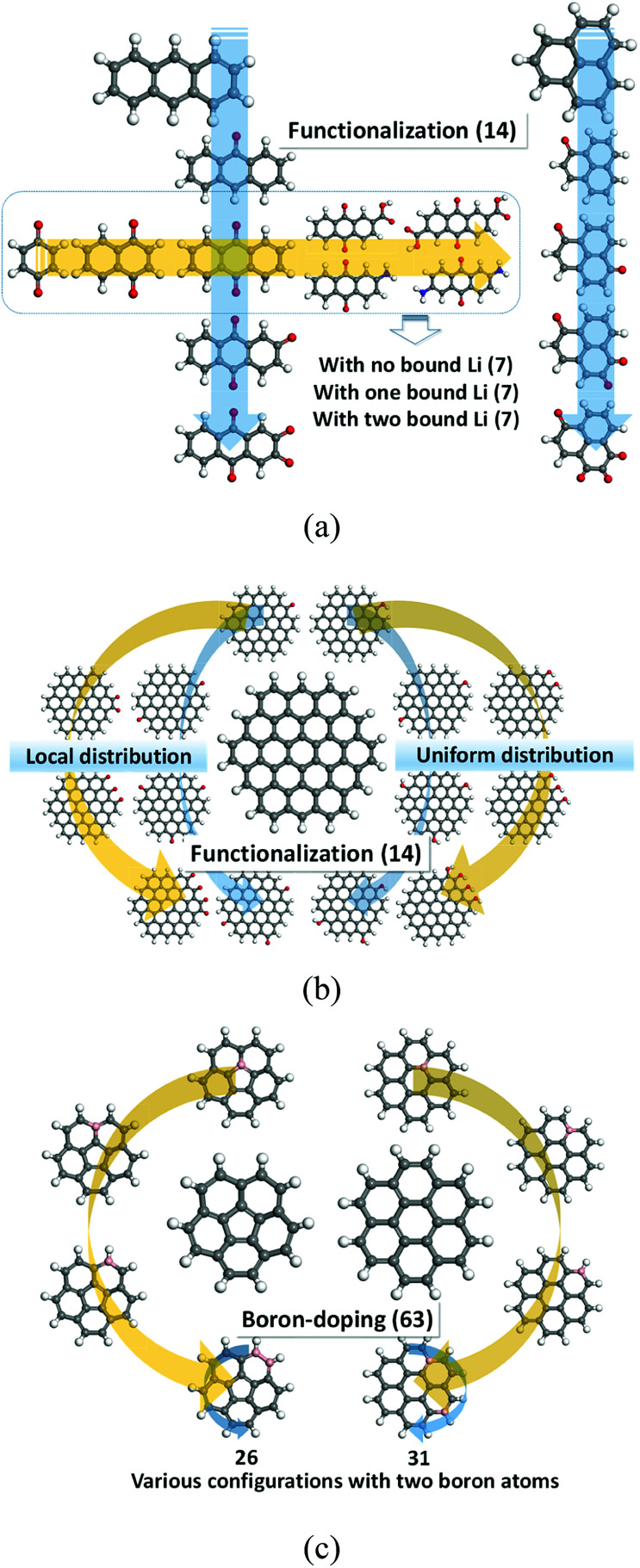
In this investigation, the role of DFT modelling is to characterize basic electronic properties of certain organic molecules (Fig. 1), such as electron affinity, HOMO, and LUMO as well as redox properties, which would be used as input data to train the ML. A full list of model compounds explored in this study is described in Tables S1–S6 in ESI.† Computational details on the DFT modelling approach employed to predict the redox potential are addressed in our previous studies.8–13,16,17 Thus, we briefly describe the computational methods. All the calculations were performed using Jaguar software30 with PBE0 to calculate the exchange correlation interactions31 and 6-31+G(d,p) basis set.32 All the organic materials of our interests were geometrically optimized in both neutral and anionic phases followed by vibrational frequency calculations to evaluate the reduction free energies at 298 K in the gas phase. Then, the solvation free energies were calculated using Poisson–Boltzmann implicit solvation model to approximate the solvation contributions to the free energies. The dielectric constant of 16.14 was used for the mixture of ethylene carbonate and dimethyl carbonate (the molar ratio of 3 : 7).

Fig. 1. Molecules used to train an artificial neural network: (a) quinone derivatives; (b) functionalized graphene fragments; (c) boron-doped graphene fragments.

Fig. 1

Open in a new tab

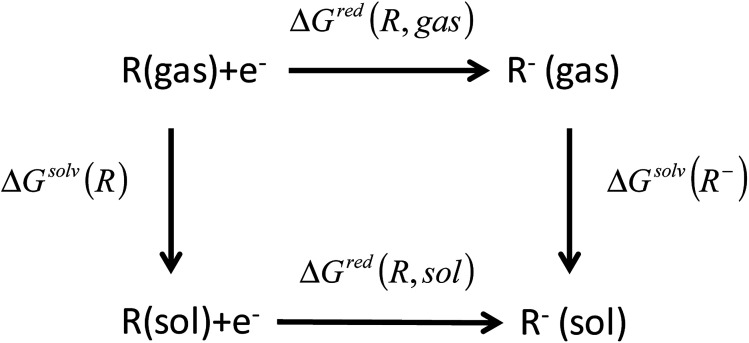
The reduction free energy in solution phase (ΔGred(R, sol)) can be computed through the thermodynamic cycle, as suggested by Truhlar et al. (Fig. 2).33,34 The redox potentials in solution phase were calculated from the reduction free energy in solution phase (ΔGred(R, sol)) which can be written as

ΔGred(R, sol) = ΔGred(R, gas) + ΔGsolv(R−) − ΔGsolv(R) 1

where ΔGred(R, gas), ΔGsolv(R−), and ΔGsolv(R) are the free energy change of a molecule for reduction in gas phase with vibrational contributions at 298.15 K, the solvation free energy of the molecule in anionic state, and the solvation free energy of the molecule in neutral state, respectively. Please note that our previous studies have verified that this computational approach provides accurate predictions for redox potentials in a great agreement with experimental values within an uncertainty of <0.3 V vs. Li/Li+.8–11

Fig. 2. Thermodynamic cycle used to calculate the equilibrium redox potential in the condensed phase.33,34.

Fig. 2

Open in a new tab

Then, the redox potential in solution phase with respect to Li/Li+ was calculated based on the free energy change for reduction in solution phase using the following equation:

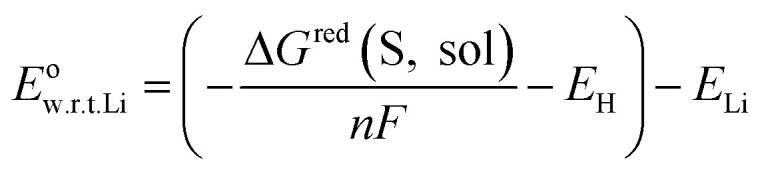2.1. 2

where n represents the number of electrons transferred, F represents the Faraday constant (96 485 C mol−1), EH and ELi represent the absolute potential of the hydrogen electrode (4.44 V),35 and the potential of Li electrode with respect to the standard hydrogen electrode (−3.05 V),36 respectively. The adiabatic electron affinity was employed to calculate the electron affinity of each molecule.

2.2. Machine learning approach

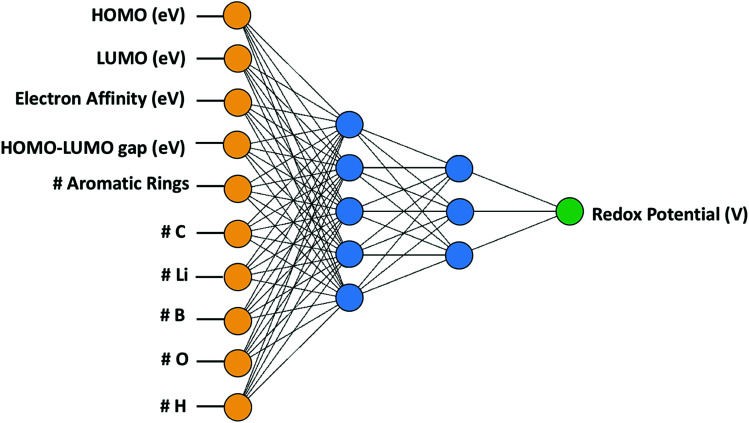
In this study, we employed artificial neural network (ANN) out of various ML algorithms. ANN was deemed suitable for our study as it possessed the ability of implicitly classifying complex nonlinear relationships among a relatively large number of variables.37 We trained the ANN using the quasi-Newton method37 which is arguably one of the most popular numerical optimization methods in a wide range of numerical applications. Compared to the Newton's method that requires the calculation of the Hessian matrix consisting of the second partial derivative of the loss function, the quasi-Newton method estimates the inverse Hessian matrix at each iteration using only the first partial derivative of the loss function without calculating the exact value of Hessian, which makes this method less expensive.37 For this purpose, the normalized squared error function was used in Neural Designer38 with a maximum iteration of 5000. As presented in Fig. 3, two hidden layers were used with five and three nodes in the first and second layer, respectively. It was determined that more hidden layers were unnecessary given the relatively small number of cases (114 cases) that were fed to our neural network, and additionally, a very satisfactory stage was reached, demonstrating an average error of 3.54% in predicting redox potential outside the original training set. Additional hidden layers and nodes were not used in this model to avoid the risk of the network causing the data overfitting.

Fig. 3. Artificial neural network with 10 input variables and two hidden layers.

Fig. 3

Open in a new tab

Even though one of the main disadvantages of ANN is that it can be computationally burdensome, this was not a major issue in this study due to the relatively small size of the data set. Please note that ANN was primarily used in this study for its regressive or interpolative capability to investigate the characteristics that influence the redox potential.

3. Results and discussions

3.1. Training artificial neural network

In order to determine the relationship between redox potential, the target property in this study, with various material properties, an artificial neural network (ANN) was trained using the quasi-Newton method training algorithm and the errors in predicting redox potentials by ANN were analysed using the normalized squared error method. In order to train the ANN, 108 data points were used out of the 114 data points, and six cases were obtained by other publications11,39 for assessing how accurately the ANN can predict redox potentials for the cases which were not used for training.

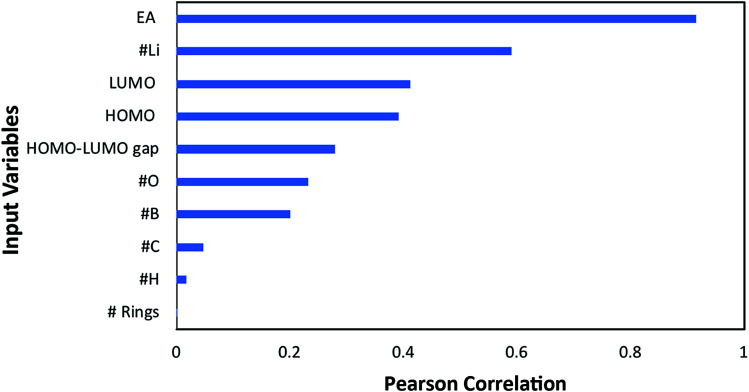
A preliminary analysis was performed to downsize the original 10 input variables (for those with the highest linear correlation with the target): electron affinity (EA), highest occupied molecular orbital (HOMO), lowest unoccupied molecular orbital (LUMO), the HOMO–LUMO gap, the number of aromatic rings, and the number of oxygen, carbon, boron, hydrogen, and lithium atoms. A linear correlation analysis was performed by calculating the Pearson correlation coefficients (PCC) whose absolute values are presented in Fig. 4. In this case, a PCC of 1 corresponds to complete linear correlation, whereas 0 corresponds to no linear correlation. The electron affinity, with an absolute PCC of 0.92, has the most strong linear correlation with the redox potential while the number of aromatic rings has nearly no correlation. Such high correlation between EA and RP is anticipated since EA is a measure of material's capability to attain an electron, which is a core process for electrochemical reduction. However. Please note that the EA cannot be used solely in predicting RP, which is why we need other input parameters.

Fig. 4. Pearson linear correlation factor of each input variable to the redox potential (target property).

Fig. 4

Open in a new tab

3.2. Optimizing artificial neural network

Based on the correlation analysis in Fig. 4, we selected six out of initially considered 10 input variables. This is performed since it is very likely that some input variables might have a negative effect on achieving accurate machine learning predictions. Thus, four input variables, namely the numbers of hydrogen atoms, boron atoms, carbon atoms, and aromatic rings, were deselected due to their insignificant or unclear correlation with redox potential. A neural network architecture composed of six inputs was deemed to be improved. The six input variables chosen were electron affinity, HOMO, LUMO, the HOMO–LUMO gap and the numbers of oxygen and lithium atoms.

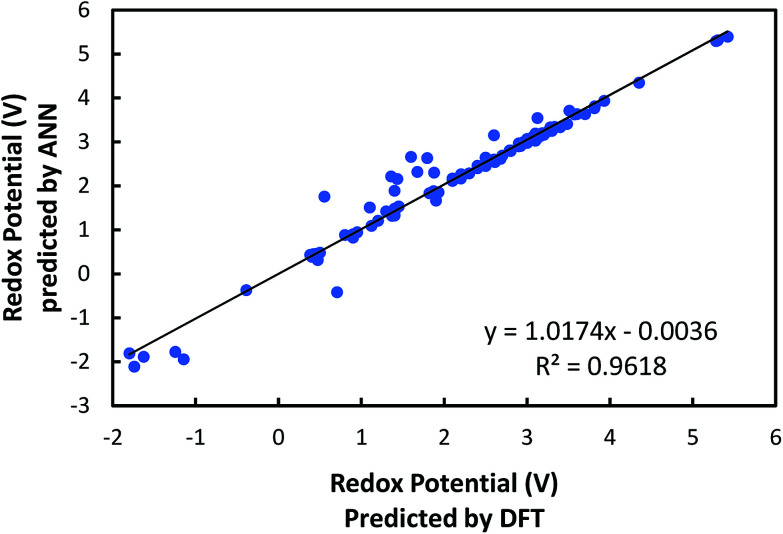
After training the ANN, a linear regression analysis was performed in order to evaluate the accuracy of our learning model in predicting redox potentials of organic molecular electrode materials. It is demonstrated from the linear regression shown in Fig. 5 that the correlation, slope, and, intercept are very close to 1, 1, and 0, respectively, indicating that the machine learning model with six input variables has a good predictability. Nevertheless, it is observed that ANN predictions show relatively significant errors for 11 cases at low normalized redox potential (<0.6 V). To resolve these discrepancies, we are investigating how to improve the accuracy of our current ANN further, specifically by searching for other responsible input variables.

Fig. 5. Comparison of the redox potentials predicted from machine learning with those predicted from DFT.

Fig. 5

Open in a new tab

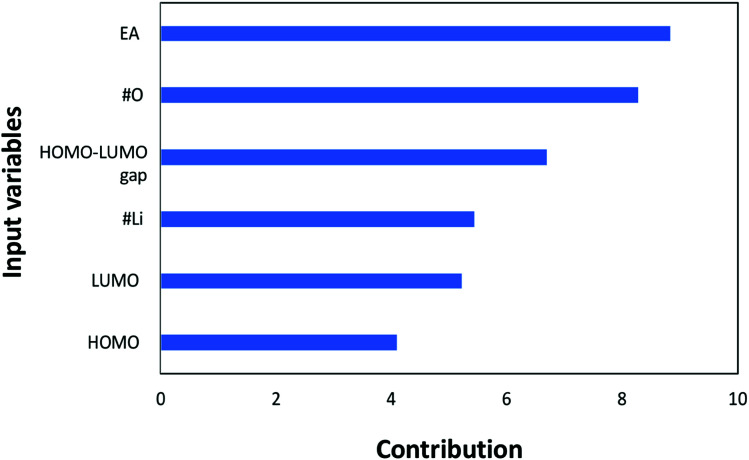
Next, the individual contributions of the input variables are also analyzed to evaluate their importance in affecting the redox potential. Please note that the contribution analysis in Fig. 6 is performed by investigating the error of the neural network when the corresponding input variable is removed in predicting the redox potential. If the contribution factor of an input variable is less than 1, the error of the neural network is decreased by removing the corresponding input variable, and vice versa. In other words, if an input has a contribution greater than 1, the ANN will be less accurate without the corresponding input variable. Fig. 6 shows that all the inputs are larger than 1, indicating that all the input variables are significantly important in determining the redox potential. The most noteworthy point in Fig. 6 is that the electron affinity has the highest contribution in the estimating the redox potential; this is followed by the number of oxygen atoms, the HOMO–LUMO gap, the number of lithium atoms, LUMO, and HOMO, respectively. It should be pointed out that although LUMO, HOMO, and HOMO–LUMO gap are not independent, a removal of any of these three variables led to an increase in the error of the neural network. Keeping these three variables reduces the error without incurring significant computational cost. Furthermore, despite not being completely independent, the contribution of HOMO–LUMO gap is greater than HOMO and LUMO alone. This is interesting since it would have been presumed that the contribution of the HOMO–LUMO gap would lie between the contributions of HOMO and LUMO given its dependency with both variables. Nevertheless, it is definitely worth further investigating to determine how to better optimize the model with only two out of the three aforementioned variables for more efficient and accurate prediction.

Fig. 6. Contributions of each input variable to the redox potential (target property) in the machine learning.

Fig. 6

Open in a new tab

3.3. Analyzing/validating artificial neural network

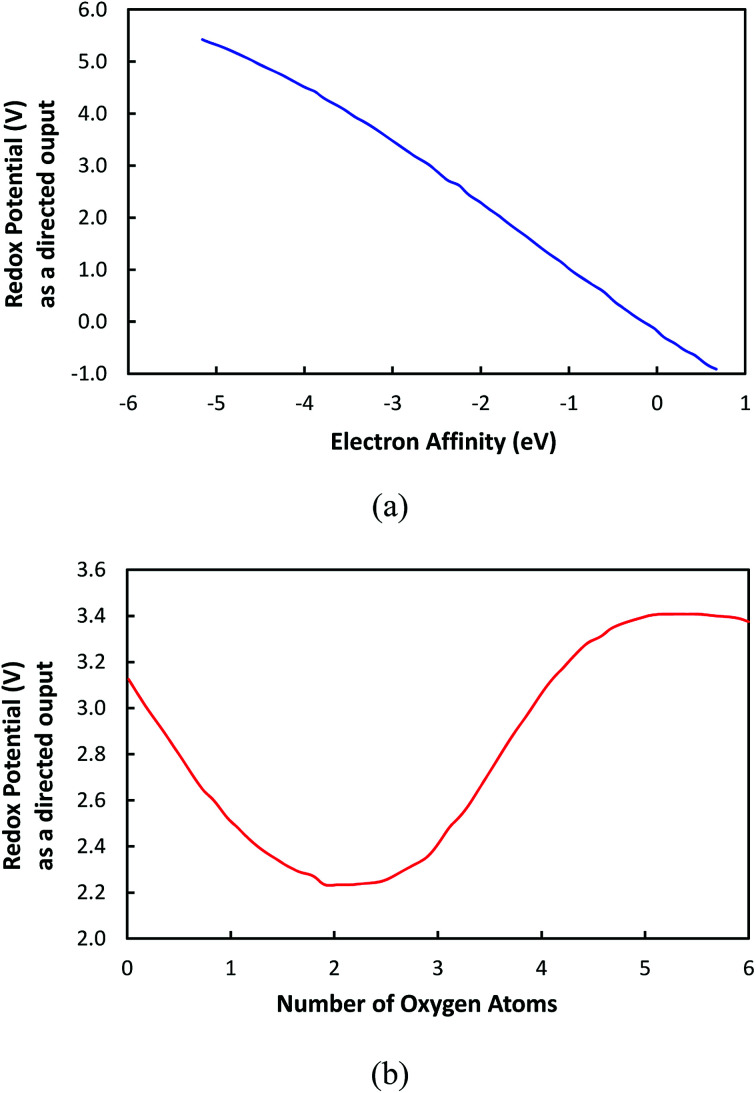
Furthermore, the effects that individual inputs had on the redox potential were examined. Fig. 7a and b show the change of redox potential as a function the electron affinity and the number of oxygen atoms, respectively. In this approach, the redox potential is considered as a directional output that is obtained by fluctuating one input variable while keeping all other input variables fixed. For this analysis, we used the a set of input variables summarized in Table 1, which were obtained by averaging the values of each input over all the cases in the data set. The directional output analysis aids with illustrating how a certain input variable affects the output redox potential while all other input variables are kept constant.

Fig. 7. The correlation of input variables to redox potential while other input variables are kept constant: (a) the electron affinity; (b) the number of oxygen atoms.

Fig. 7

Open in a new tab

The values of input variables used to investigate the directional outputs. These values were obtained by computing the average value for each input over the entire data set.

Variable Average values
HOMO (eV) −5.458
LUMO (eV) −2.944
EA (eV) −2.250
#O 0.8796
HOMO–LUMO gap (eV) 2.514
#Li 0.2129
Open in a new tab

Fig. 7a shows that the redox potential is monotonously decreased as a function of the EA, which indicates that the electron affinity is a governing variable in control redox potential. Therefore, it is shown that EA is a property that can be utilized to tune the redox potential of molecular electrode materials. On the other hand, in Fig. 7b, it is demonstrated that the redox potential is fluctuated as the number of oxygen atoms is increased. This is an unexpected result since it has been thought that the redox potential would be proportional to the number of oxygen atoms because the oxygen atom is known to have electron-withdrawing effects due to its high electronegativity, which would increase the electron affinity, as published previously.39 However, our model indicates that solely increasing the number of oxygen atoms (or any electronegative atoms) does not necessarily result in the increase of redox potential. Nevertheless, various aspects such as the distribution of oxygen atoms and the type of bond connectivity of oxygen atoms should be considered to obtain the complete understanding about the behavior of redox potential in Fig. 7b.

Lastly, the trained ANN was validated by comparing the redox potentials estimated by the learning model with those from DFT computations for the cases which were not included in the training data sets; namely the 6 cases obtained from other publications.11,39Table 2 shows the error in predicting the redox potential. The averaged error is approximately 3.54%. In this study, given the relatively limited size of the data set for training the ANN, the predictive capability of the trained ANN model is demonstrated from this relatively small error.

Comparison of redox potentials predicted from ANN with those cited from literatures.

Redox potential (V) from literatures11,39 Redox potential (V) predicted by ANN Error (%)
2.30 2.28 0.670
2.10 2.11 0.491
−1.80 −1.81 0.722
3.48 3.50 0.419
3.12 3.54 13.3
3.51 3.71 5.68
Average error 3.54
Open in a new tab

4. Summary

Although it has been well confirmed that DFT-based modeling can predict the electrochemical properties of molecular electrode materials very accurately,8–13,16,17,39 DFT modeling alone might not be practical for high-throughput screening because it is computationally time intensive. Therefore in this study, we attempted to establish a DFT-machine learning framework to develop a high-throughput screening method for facilitating the design of carbon-based molecular electrode materials. DFT computations were used to obtain basic quantum mechanical electronic properties which include electron affinity, HOMO, and LUMO, as input variables, in addition to the redox potentials as the target reference output. The numbers of oxygen atoms, lithium atoms, boron atoms, carbon atoms, hydrogen atoms, and aromatic rings were also initially considered as input invariables; and were selected or eliminated, depending on their influence on the redox potential.

Out of the various machine learning methods available, we employed artificial neural network (ANN) since it has been known to capture complicated nonlinear relationships among variables. First, a correlation analysis was performed as a preliminary screening method to downselect irrelevant input variables with low correlation; such as the numbers of hydrogen atoms, boron atoms, carbon atoms, and aromatic rings. Then, ANN was trained using quasi-Newton method, and its accuracy was validated by comparing the redox potentials predicted from ANN and those calculated from DFT modeling.

Next, the contribution analysis for each input variable to the redox potential was performed through investigating the error caused by the corresponding input variable when it was removed. From this analysis, it was found that the electron affinity has the highest contribution to redox potential, followed by the number of oxygen atoms, the HOMO–LUMO gap, the number of lithium atoms, LUMO, and HOMO in order respectively.

The ANN was further validated by estimating the redox potentials for 6 cases which were not included in the training dataset. The redox potentials predicted by ANN were in good agreement with those calculated from DFT modeling, whose averaged error was 3.54%.

Conflicts of interest

There are no conflicts to declare.

Supplementary Material

RA-008-C8RA07112H-s001

Acknowledgments

We acknowledge that Omar Allam and Byung Woo Cho were supported by President Undergraduate Research Award (PURA) of Georgia Institute of Technology. Ki Chul Kim appreciate the support from “Human Resources Program in Energy Technology” of the Korea Institute of Energy Technology Evaluation and Planning (KETEP), granted financial resource from the Ministry of Trade, Industry & Energy, Republic of Korea (No. 20174010201540).

†

Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra07112h

References

  1. Chen H. S. Cong T. N. Yang W. Tan C. Q. Li Y. L. Ding Y. L. Prog. Nat. Sci. 2009;19:291–312. doi: 10.1016/j.pnsc.2008.07.014. [DOI] [Google Scholar]
  2. Dunn B. Kamath H. Tarascon J. M. Science. 2011;334:928–935. doi: 10.1126/science.1212741. [DOI] [PubMed] [Google Scholar]
  3. Jeong G. Kim Y. U. Kim H. Kim Y. J. Sohn H. J. Energy Environ. Sci. 2011;4:1986–2002. doi: 10.1039/C0EE00831A. [DOI] [Google Scholar]
  4. Nitta N. Wu F. X. Lee J. T. Yushin G. Mater. Today. 2015;18:252–264. doi: 10.1016/j.mattod.2014.10.040. [DOI] [Google Scholar]
  5. Bruce P. G. Scrosati B. Tarascon J. M. Angew. Chem., Int. Ed. 2008;47:2930–2946. doi: 10.1002/anie.200702505. [DOI] [PubMed] [Google Scholar]
  6. Hassoun J. Panero S. Reale P. Scrosati B. Adv. Mater. 2009;21:4807–4810. doi: 10.1002/adma.200900470. [DOI] [PubMed] [Google Scholar]
  7. Bhatt M. D. O'Dwyer C. Phys. Chem. Chem. Phys. 2015;17:4799–4844. doi: 10.1039/C4CP05552G. [DOI] [PubMed] [Google Scholar]
  8. Liu T. Y. Kim K. C. Kavian R. Jang S. S. Lee S. W. Chem. Mater. 2015;27:3291–3298. doi: 10.1021/acs.chemmater.5b00314. [DOI] [Google Scholar]
  9. Kim S. Kim K. C. Lee S. W. Jang S. S. Phys. Chem. Chem. Phys. 2016;18:20600–20606. doi: 10.1039/C6CP02692C. [DOI] [PubMed] [Google Scholar]
  10. Liu T. Kim K. C. Lee B. Chen Z. M. Noda S. Jang S. S. Lee S. W. Energy Environ. Sci. 2017;10:205–215. doi: 10.1039/C6EE02641A. [DOI] [Google Scholar]
  11. Park J. H. Liu T. Y. Kim K. C. Lee S. W. Jang S. S. Chemsuschem. 2017;10:1584–1591. doi: 10.1002/cssc.201601730. [DOI] [PubMed] [Google Scholar]
  12. Sood P. Kim K. C. Jang S. S. ChemPhysChem. 2018;19:753–758. doi: 10.1002/cphc.201701171. [DOI] [PubMed] [Google Scholar]
  13. Sood P. Kim K. C. Jang S. S. J. Energy Chem. 2018;27:528–534. doi: 10.1016/j.jechem.2017.11.009. [DOI] [Google Scholar]
  14. Poizot P. Dolhem F. Energy Environ. Sci. 2011;4:2003–2019. doi: 10.1039/C0EE00731E. [DOI] [Google Scholar]
  15. Vadehra G. S. Maloney R. P. Garcia-Garibay M. A. Dunn B. Chem. Mater. 2014;26:7151–7157. doi: 10.1021/cm503800r. [DOI] [Google Scholar]
  16. Kang J. Kim K. C. Jang S. S. J. Phys. Chem. C. 2018;122:10675–10681. doi: 10.1021/acs.jpcc.8b00827. [DOI] [Google Scholar]
  17. Zhu Y. T. Kim K. C. Jang S. S. J. Mater. Chem. A. 2018;6:10111–10120. doi: 10.1039/C8TA01671B. [DOI] [Google Scholar]
  18. Yao M. Senoh H. Sakai T. Kiyobayashi T. Int. J. Electrochem. Sci. 2011;6:2905–2911. [Google Scholar]
  19. Song Z. P. Zhan H. Zhou Y. H. Chem. Commun. 2009:448–450. doi: 10.1039/B814515F. [DOI] [PubMed] [Google Scholar]
  20. Huskinson B. Marshak M. P. Suh C. Er S. Gerhardt M. R. Galvin C. J. Chen X. Aspuru-Guzik A. Gordon R. G. Aziz M. J. Nature. 2014;505:195–198. doi: 10.1038/nature12909. [DOI] [PubMed] [Google Scholar]
  21. Mitome H. Ishizuka T. Shiota Y. Yoshizawa K. Kojima T. Dalton Trans. 2015;44:3151–3158. doi: 10.1039/C4DT03358B. [DOI] [PubMed] [Google Scholar]
  22. Newman D. K. Kolter R. Nature. 2000;405:94–97. doi: 10.1038/35011098. [DOI] [PubMed] [Google Scholar]
  23. Song Z. P. Zhou H. S. Energy Environ. Sci. 2013;6:2280–2301. doi: 10.1039/C3EE40709H. [DOI] [Google Scholar]
  24. Liang Y. L. Tao Z. L. Chen J. Adv. Energy Mater. 2012;2:742–769. doi: 10.1002/aenm.201100795. [DOI] [Google Scholar]
  25. Chen H. Armand M. Demailly G. Dolhem F. Poizot P. Tarascon J. M. Chemsuschem. 2008;1:348–355. doi: 10.1002/cssc.200700161. [DOI] [PubMed] [Google Scholar]
  26. Chen H. Y. Poizot P. Dolhem F. Basir N. I. Mentre O. Tarascon J. M. Electrochem. Solid-State Lett. 2009;12:A102–A106. doi: 10.1149/1.3082038. [DOI] [Google Scholar]
  27. Mueller T., Kusne A. G. and Ramprasad R., in Reviews in Computational Chemistry, ed. A. L. Parrill and K. B. Lipkowitz, Wiley-Blackwell, Malden, 2016, vol. 29, pp. 186–273 [Google Scholar]
  28. Kim C. Pilania G. Ramprasad R. J. Phys. Chem. C. 2016;120:14575–14580. doi: 10.1021/acs.jpcc.6b05068. [DOI] [Google Scholar]
  29. Allam O. Holmes C. Greenberg Z. Kim K. C. Jang S. S. ChemPhysChem. 2018;19:2559–2565. doi: 10.1002/cphc.201800382. [DOI] [PubMed] [Google Scholar]
  30. Bochevarov A. D. Harder E. Hughes T. F. Greenwood J. R. Braden D. A. Philipp D. M. Rinaldo D. Halls M. D. Zhang J. Friesner R. A. Int. J. Quantum Chem. 2013;113:2110–2142. doi: 10.1002/qua.24481. [DOI] [Google Scholar]
  31. Adamo C. Scuseria G. E. Barone V. J. Chem. Phys. 1999;111:2889–2899. doi: 10.1063/1.479571. [DOI] [Google Scholar]
  32. Ditchfield R. Hehre W. J. Pople J. A. J. Chem. Phys. 1971;54:724–728. doi: 10.1063/1.1674902. [DOI] [Google Scholar]
  33. Winget P. Cramer C. J. Truhlar D. G. Theor. Chem. Acc. 2004;112:217–227. [Google Scholar]
  34. Lewis A. Bumpus J. A. Truhlar D. G. Cramer C. J. J. Chem. Educ. 2004;81:596–604. doi: 10.1021/ed081p1265.1. [DOI] [Google Scholar]
  35. Donald W. A. Leib R. D. O'Brien J. T. Bush M. F. Williams E. R. J. Am. Chem. Soc. 2008;130:3371–3381. doi: 10.1021/ja073946i. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Ong S. P. Chevrier V. L. Hautier G. Jain A. Moore C. Kim S. Ma X. H. Ceder G. Energy Environ. Sci. 2011;4:3680–3688. doi: 10.1039/C1EE01782A. [DOI] [Google Scholar]
  37. Hennig P. Kiefel M. J. Mach. Learn. Res. 2013;14:843–865. [Google Scholar]
  38. Neural Designer, v. 2.90, Artelnics, 2018 [Google Scholar]
  39. Kim K. C. Liu T. Y. Lee S. W. Jang S. S. J. Am. Chem. Soc. 2016;138:2374–2382. doi: 10.1021/jacs.5b13279. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

RA-008-C8RA07112H-s001
RA-008-C8RA07112H-s001.pdf (1.1MB, pdf)

Articles from RSC Advances are provided here courtesy of Royal Society of Chemistry

RESOURCES