A cubic room temperature polymorph of thermoelectric TAGS-85

Abstract

The alloy (GeTe)₈₅(AgSbTe₂)₁₅, commonly known as TAGS-85, is one of the best performing p-type thermoelectric materials in the temperature range 200–500 °C. In all reports thus far, TAGS-85 adopts a rhombohedral crystal structure at room temperature and undergoes a reversible transition to a cubic phase in the middle of the operating temperature range. Here, we report on a novel, metrically cubic polymorph of TAGS-85 that can be obtained at room temperature using a particular cooling protocol during initial synthesis. This polymorph transforms irreversibly on initial heating to a 21-layer trigonal structure containing ordered cation vacancy layers, driven by the spontaneous precipitation of argyrodite-type Ag₈GeTe₆. We show that the precipitation of Ag₈GeTe₆ is detrimental to the thermoelectric performance of TAGS-85 due to an increase in the vacancy concentration, which makes the samples more metallic in character and significantly reduces the Seebeck coefficient. The precipitation of Ag₈GeTe₆ can be suppressed by careful control of the synthesis conditions.

A new cubic polymorph of thermoelectric TAGS-85 irreversibly transforms to a trigonal layered phase on heating, with precipitation of Ag₈GeTe₆.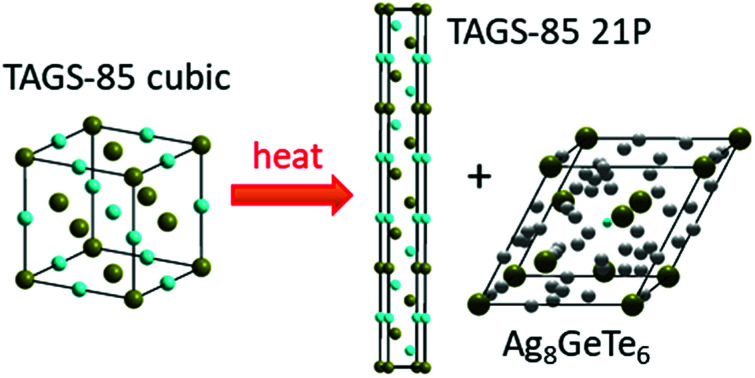

Introduction

Thermoelectric materials are being developed with the aim of efficiently converting thermal energy to electrical power.^1–4 The thermoelectric conversion efficiency of such materials is directly proportional to the so-called figure of merit ZT = S²σT/κ_total where S is the Seebeck coefficient, σ is the electrical conductivity and κ_total is the total thermal conductivity.

Thermoelectric materials derived from GeTe have attracted much attention in recent years due to their good performance and device reliability in the 200–500 °C range.^5,6 GeTe is a narrow band p-type semiconductor with a high concentration of vacancies on the cation sub-structure. These vacancies not only affect the electronic properties by the generation of two holes per vacancy, but can also scatter phonons, reducing the lattice thermal conductivity.⁷ GeTe-based thermoelectric materials exhibit a distinctive herringbone-like domain structure, which is also thought to provide a phonon scattering barrier mechanism and lower the lattice thermal conductivity further.⁸

Here we focus on the well-known solid solution (GeTe)_x(AgSbTe₂)_100−x, which is commonly referred to as TAGS-x. The TAGS-85 composition has reported ZT values in the range 1.2–1.4 at 500 °C, which is ∼30% lower than TAGS-80 at the same temperature.⁹ However, TAGS-85 is mechanically more stable¹⁰ and is thus generally preferred for applications. TAGS-x exhibit inherently complex nanostructures involving compositional and structural modulations, the spontaneous formation of nano-precipitates, twin and anti-phase domain boundaries, which all contribute to a low lattice thermal conductivity.^11–13

In the literature, TAGS-85 ceramics have been prepared and processed by different methods. In some cases ingots are obtained by direct quenching from the melt^14,15 or held first at an intermediate temperature,^11,12 and in other reports additional processing steps are carried out on as-prepared ingots such as subsequent annealing¹⁰ or grinding and hot-pressing.^9,16,17 Both from our own work¹⁸ and from other previous reports,^9,13–15 there are suggestions that TAGS-85 samples are often inhomogeneous or multi-phase in nature as evidenced by irregular or asymmetric peak shapes in X-ray diffraction measurements. This has motivated us to look more closely at whether the crystal structure and homogeneity can be influenced by careful control of the chemical synthesis conditions. We recently reported on the relationship between the structural and thermoelectric properties of TAGS-85 samples stabilized as a single-phase rhombohedral R3m structure at room temperature.¹⁸ Contrary to earlier reports of a direct phase transition to a face-centered cubic (Fm3̄m) phase above 380 °C, we showed that the transformation proceeds via an intermediate trigonal phase containing layers of ordered cation vacancies. In terms of electronic structure, it is thought that the high-temperature cubic phase of TAGS-85 and other GeTe-related materials exhibits a greater degree of valence band valley degeneracy than the rhombohedral phase, which might significantly enhance the Seebeck coefficient.^19,20 Therefore, it is of interest to study whether the transition to the cubic phase of TAGS-85 can be lowered in temperature. Here we report that a metastable cubic phase can indeed be stabilized at room temperature by careful adjustment of the synthesis conditions, but that it transforms irreversibly to a novel trigonal structure on initial heating. We study how the structural and thermoelectric properties of these phases evolve with repeated thermal cycling over the relevant operating temperature range.

Experimental

TAGS-85 samples were synthesized by reaction in evacuated sealed tubes. The elements Ge, Te, Ag and Sb (purity 99.99%) were weighed in stoichiometric amounts, mixed using a mortar and pestle and placed in a quartz ampule, which was evacuated to 10⁻² to 10⁻³ torr (1.33–0.133 Pa) using a rotary vane pump and then sealed using a flame; immediately before sealing the end of the ampule containing the reactants was cooled in liquid nitrogen. The ampule was heated in a tubular furnace at 850 °C for 1 hour to melt the reaction mixture, and the ampule was rotated every 10 minutes in order to ensure good homogeneity. Samples were then cooled to 500 °C over a period of 4 h, at which temperature they were held for different lengths of time before quenching to room temperature in water. The samples were obtained in the form of shiny ingots with irregular, approximately rectangular shapes. For physical property measurements, the ingots were sliced to appropriate dimensions using a diamond wire saw and then polished to obtain flat surfaces and uniform thickness.

X-ray powder diffraction (XRD) patterns were recorded on crushed ingots using a Bruker D8 diffractometer operating in Bragg–Brentano geometry with Cu Kα₁ radiation and combined with an Anton Paar TTK-450 hot stage. The sample chamber was evacuated to ∼10⁻³ mbar (∼0.1 Pa) prior to the heating stage being switched on. Temperature was varied using a TCU-100 control unit, which has a precision of within ±1 °C. Heating and cooling rates of 0.5 °C s⁻¹ between set-point temperatures were used; before beginning a measurement the sample was held for 300 s in order to ensure thermal equilibrium. A Huber G670 diffractometer operating in Guinier geometry with Cu Kα₁ radiation and combined with a closed-cycle refrigerator was used to obtain XRD data below room temperature. All data were analyzed using the GSAS software.²¹

Differential scanning calorimetry (DSC) and thermogravimetric analysis (TGA) measurements were performed using a TA-instruments STD 2960. A Pt crucible was used to measure ground up pieces of ingot over a temperature range of 30 °C to 600 °C at a rate of 1 K min⁻¹ under a flow of argon.

Seebeck coefficients and electrical conductivity were measured simultaneously using a Linseis LSR-3 apparatus, which utilizes a dc four-probe method. Thermal diffusivity (D_t) was measured by the laser flash method using a Linseis LFA1000 apparatus equipped with an InSb detector; samples were measured in a He atmosphere. Up to five data points of D_t were merged after evaluating the quality of the fitted model²² and excluding outliers at each temperature step of 50 °C, starting from 50 °C up to 450 °C. Thermal conductivity was calculated using the formula κ = D_t × d × C_p. Here the density d was calculated from the mass and volume of the sample determined by the Archimedes principle. The specific heat capacity C_p was obtained using the Dulong–Petit approximation, which has previously been shown to be valid for GeTe-based materials given the large experimental uncertainties involved in measurements of C_p.^9,19,23,24 We estimate that the ZT values obtained by combining the above measurements exhibit an uncertainty of ∼20%.

For TEM measurements, samples were sliced and glued inside brass tubes of 3 mm diameter and cut into disks. The disks were then ground, dimpled, and ion milled using a Gatan PIPS II at 6° with an accelerating voltage that was ramped from 4 kV to 0.2 kV to achieve electron transparency. TEM images and electron diffraction patterns were obtained using JEM 2010 and JEM 2010F microscopes operated at 200 kV. EDS measurements were performed in the TEM, using a Si(Li) detector. Cliff–Lorimer fitting without absorbance was performed using the NSS 2.3 software (Thermo Scientific) to obtain accurate composition information. In some cases, samples were prepared by a FIB (focused ion beam) technique. TEM images and electron diffraction patterns were then obtained with a Tecnai G2 F30 S-Twin at an accelerating voltage of 300 kV.

Results and discussion

We have previously reported that the procedure used to cool samples of TAGS-85 from the melt has a strong influence on the homogeneity of the phase that is obtained at room temperature.¹⁸ Single-phase samples can only be obtained by holding at an intermediate temperature; >3 h at 600 °C gives a pure rhombohedral phase whereas shorter holding times give multi-phase mixtures of rhombohedral phases with slightly different lattice parameters, implying varying chemical compositions. Here we show that a novel cubic polymorph of TAGS-85 can be obtained when the intermediate holding temperature during the initial cooling procedure is lowered to 500 °C.

This cubic room temperature phase, which we refer to as the C_RT phase, can be consistently obtained by holding the molten precursor at 850 °C for 1 h, cooling to 500 °C over 4 h, holding at this temperature for 3 h and then quenching in water. The cubic symmetry is evidenced by the single 220 XRD reflection shown in Fig. 1b. Longer holding times at 500 °C led to stabilization of a single rhombohedral phase at room temperature, evidenced by the splitting of the 220 peak into a doublet indexed as 211 and 101̄ in the rhombohedral setting (ESI, Fig. S1†), which suggests that the C_RT phase is metastable. Direct quenching from the melt yielded a doublet of broad peaks (Fig. S1†), indicating an inhomogeneous rhombohedral sample. The chemical composition of the as-synthesized C_RT sample was determined by EDX analysis performed at ten locations on the sample surface. The averaged chemical composition is listed in Table S1 of the ESI† and does not deviate significantly from the nominal stoichiometry of TAGS-85.

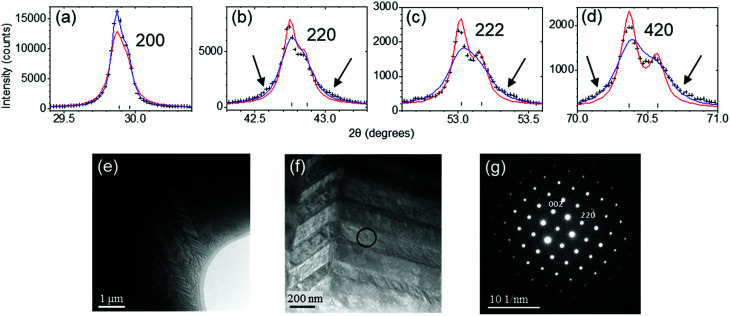
Fig. 1. Structural properties of C_RT phase of TAGS-85. (a)–(d) Selected XRD peaks of as-synthesized C_RT phase fitted without (red curve) and with (blue curve) the anisotropic microstrain broadening model. The arrows indicate broadening at the bases of peaks. All peaks appear as doublets due to Kα₁ and Kα₂ components of the X-ray beam. (e) and (f) Bright field TEM images for as-synthesized C_RT phase. (g) [11̄0] zone axis SAED pattern obtained from the single-domain area marked by the black circle in (f).

At room temperature all XRD peaks of the C_RT phase were indexed in the cubic Fm3̄m space group. The pattern could be fitted using a rock salt-type structure model in which Ge, Ag and Sb occupy the 4a Wyckoff position with coordinates (0, 0, 0) and Te occupies the 4b position with coordinates (0.5, 0.5, 0.5). In order to check whether a transition to the R-phase takes place below room temperature, we performed short XRD scans down to 20 K. The 220 peak did not split, indicating that the unit cell stays metrically cubic. In fitting the room temperature data the peak shapes were modeled using a pseudo-Voigt function; however, close inspection revealed a considerable degree of anisotropic broadening, particularly at the bases of some reflections such as 220, 222 and 420 as shown in Fig. 1b–d. The sharpest peaks are 200 (Fig. 1a) and 400 (not shown). The Stephens anisotropic microstrain broadening model²⁵ improved the fitting significantly but was unable to perfectly model those peaks exhibiting broadened bases. The refined crystallographic data for the C_RT phase at room temperature are summarized in Table 1 and the fitted XRD profile is shown in the ESI, Fig. S2.†

Crystallographic data for Rietveld refinement of C_RT phase of TAGS-85 at 295 K.

Space group (no.)	Fm3̄m (225)
Formula weight (g mol−1)	844.774
Lattice parameter (Å)	a = 5.9791(2)
Cell volume (Å3)	213.75(2)
Z (formula units per cell)	4
X-ray density (g cm−3)	6.563
Stephens anisotropic peak broadening parameters	S 400 = 0.16(2)
	S 220 = 0.95(4)
wRp	0.107
χ 2	3.263

The relatively sharp 200 and 400 XRD peaks suggest longer structural coherence along {100} than along other crystal directions. This is consistent with the bright-field TEM images in Fig. 1e and f, which reveal a herringbone domain structure. Similar domains have been observed in GeTe, where the stripes tend to be oriented along {100}.⁸ However, because such domains are only expected for the rhombohedral, polar phase of GeTe-related materials, it is likely that the C_RT phase is only metrically cubic and that the true symmetry is lower on local length-scales, which diffraction techniques would be unable to probe directly. Fig. 1g shows a [11̄0] zone axis SAED pattern obtained from the single domain marked by the black circle in Fig. 1f. The measured angle between the cubic (002) and (220) planes is 90.8°, consistent with a slight rhombohedral distortion. Further SAED patterns of the C_RT phase are presented and discussed in the ESI, Fig. S3,† but the results are inconclusive regarding symmetry. We note that similar metrically cubic phases have previously been observed for Ge_1−xSb_xTe, where small rhombohedral domains are strained and unable to establish their rhombohedral metrics.^20,26

High temperature structural properties

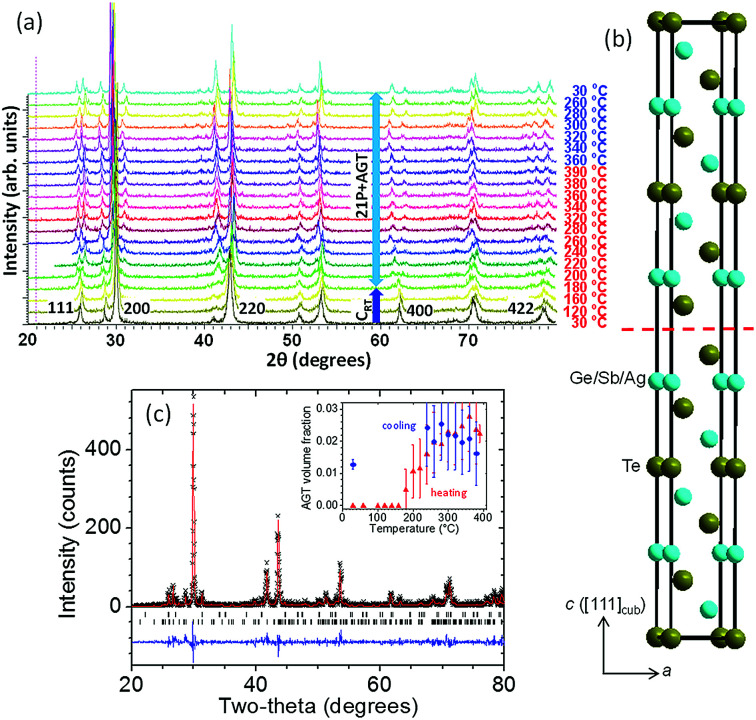
XRD data taken when the cubic C_RT phase was heated (Fig. 2a) show the appearance of new peaks at 180 °C followed by disappearance of the C_RT phase at 240 °C. The new set of peaks could be indexed using a trigonal unit cell with a = 4.215(3) Å, c = 38.27(7) Å at 240 °C. The c-axis of the trigonal structure corresponds to 21 alternating Te and Ge/Ag/Sb layers; we will refer to this structure hereafter as 21P following the Ramsdell notation,²⁷ where P indicates a primitive unit cell. Weak XRD peaks corresponding to Ag₈GeTe₆ appear as a second phase above 180 °C and coexist with the 21P phase up to the highest temperature measured (390 °C). The 21P phase does not transform back to C_RT on subsequent cooling to room temperature, thus the C_RT to 21P transition is irreversible. Following previous studies of TAGS and GeTe, we expect that another transition to a high-temperature cubic (C) phase might occur at temperatures above those accessed in our XRD measurements. Therefore, a DSC/TGA measurement was performed on heating from 30–600 °C under Ar atmosphere. The resulting curves are shown in the ESI, Fig. S4,† where a minimum in the DSC trace at 408 °C (endothermic) followed by a maximum centered at 449 °C (exothermic) is observed. We tentatively assign the endothermic peak to a 21P → C transition. The origin of the strong exothermic peak remains unclear. Increasing the temperature beyond ∼500 °C results in decomposition of the sample as shown by the onset of weight loss. A schematic diagram of the phase relations in these samples is shown in Fig. 3. The structure of the 21P phase was determined from data collected at 20 °C after one heating and cooling cycle. An initial structural model was built in which there are 11 cation layers and 11 anion layers, using space group P3̄m1. While fitting the XRD pattern, the layers were initially spaced equally and a set of soft constraints was added to keep the (Ge/Ag/Sb)–Te distances close to 3.00 Å, the average value in the rhombohedral phase. Refinement of the z-coordinates of all atoms was then carried out. The precipitation of Ag₈GeTe₆ (refined phase fraction ∼2% by volume) suggests that the 21P phase might be more cation deficient than as-synthesized TAGS-85. Therefore, the possibility of a “vacant” cation layer at the 1b (0, 0, 1/2) position was investigated and the fit significantly improved. The fitted XRD pattern measured at 20 °C is shown in Fig. 2c and a representation of the 21P structure is shown in Fig. 2b. The refined crystallographic data for 21P are listed in Table 2.

Fig. 2. High temperature structural properties of C_RT phase of TAGS-85. (a) XRD patterns collected on initial heating of as-synthesized C_RT phase from 30 °C to 390 °C (bottom to top), followed by cooling back to 30 °C. (b) Schematic representation of one unit cell of 21P structure. The red dashed line indicates a layer of Ge/Sb/Ag vacancies. (c) Observed (black data points), calculated (red line) and difference (blue line) XRD profiles of 21P phase (lower tick marks) with Ag₈GeTe₆ impurity (upper tick marks) at 20 °C after one heating + cooling cycle. The inset shows the evolution of the volume fraction of Ag₈GeTe₆ on initial heating (red) and subsequent cooling (blue).

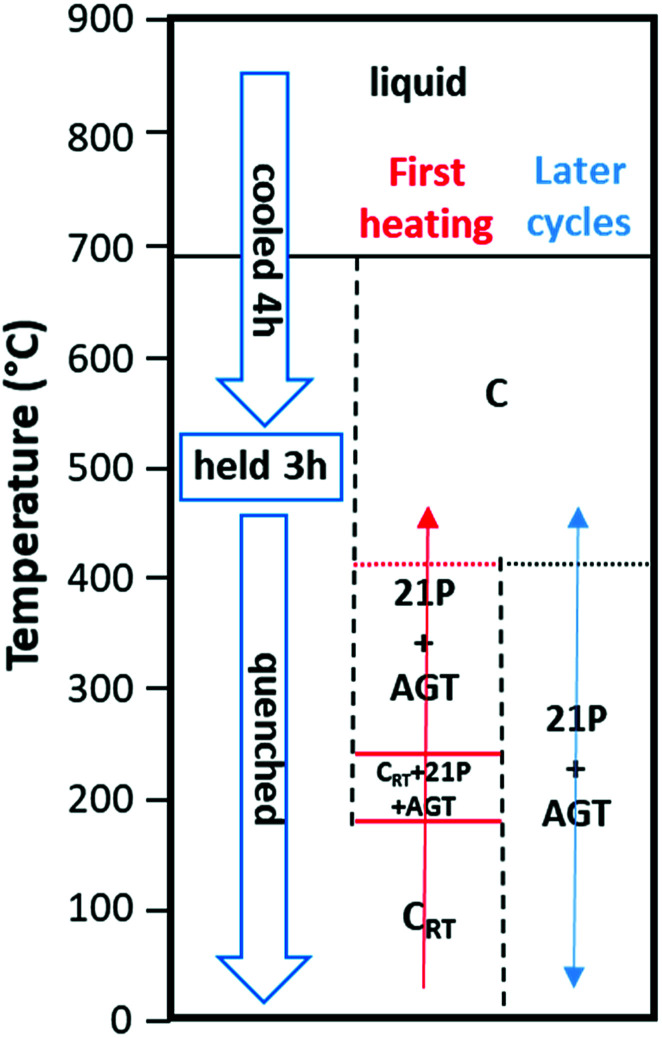
Fig. 3. Diagram showing phase transitions of C_RT phase that occur on heating and subsequent thermal cycling. The labels 21P and AGT denote the 21-layer TAGS-85 polymorph (see main text for details) and an Ag₈GeTe₆ impurity phase, respectively. Solid horizontal lines indicate phase transition temperatures determined within an uncertainty of ±10 °C and dotted horizontal lines indicate phase transition temperatures with a larger uncertainty than ±10 °C due to lack of data. These horizontal lines are color-coded: red = transition on initial heating only; black = transition on subsequent heating and cooling cycles.

Refined structural parameters of 21P phase at 20 °C: space group P3̄m1, a = 4.1914(4) Å, c = 38.288(7) Å; wR_p = 0.3407, χ² = 1.357.

Atom	Site	X	Y	z	Site occupancy	Uiso (Å2)
Te1	1a	0	0	0	1	0.043(5)
Ge2/Ag2/Sb2	2d	1/3	2/3	0.0449(13)	0.7391/0.1304/0.1304	0.069(5)
Te3	2d	2/3	1/3	0.0910(7)	1	0.043(5)
Ge4/Ag4/Sb4	2c	0	0	0.1393(8)	0.7391/0.1304/0.1304	0.069(5)
Te5	2d	1/3	2/3	0.1824(8)	1	0.043(5)
Ge6/Ag6/Sb6	2d	2/3	1/3	0.2314(9)	0.7391/0.1304/0.1304	0.069(5)
Te7	2c	0	0	0.2778(5)	1	0.043(5)
Ge8/Ag8/Sb8	2d	1/3	2/3	0.3245(9)	0.7391/0.1304/0.1304	0.069(5)
Te9	2d	2/3	1/3	0.3709(8)	1	0.043(5)
Ge10/Ag10/Sb10	2c	0	0	0.4219(8)	0.7391/0.1304/0.1304	0.069(5)
Te11	2d	1/3	2/3	0.4607(9)	1	0.043(5)

Note that a metastable pseudo-cubic phase possibly similar to C_RT has previously been reported for TAGS materials synthesized with intentionally large cation vacancy concentrations by varying the Ag/Sb ratio.²³ A similar irreversible phase transition was observed on initial heating, but to a 15-layer trigonal phase with considerable vacancy layer disorder; a further reversible transition to a cubic structure took place above 400 °C. The as-synthesized pseudo-cubic phase was characterized by (111) vacancy layers that only extend over a few nm in the lattice and are not ordered in periodic fashion; they form “parquet like” multidomain nanostructures when observed by HRTEM. Heating this disordered cubic phase induces a vacancy diffusion process and transformation to a more thermodynamically stable trigonal phase in which the vacancies become ordered in layers in long-range periodic fashion, forming van der Waals gaps. Similar phases and transitions have been observed in other materials related to TAGS, for example (GeTe)_nSb₂Te₃ (commonly known as GST).²⁸ For example, Ge₂Sb₂Te₅, Ge₁Sb₄Te₇, Ge₁Sb₂Te₄ and Ge₃Sb₂Te₆ adopt trigonal structures consisting of 9, 12, 21, and 33 alternating anion and cation layers, respectively.^28–30 Analogous phase transitions have also been reported for GST materials doped with In, Co and Sn.^31–33 Our TAGS-85 samples are nominally stoichiometric and charge-balanced. However, it is possible that TAGS samples contain intrinsically high defect concentrations that have a tendency toward ordering with heat treatment. We note that there are also several reports of localized structural distortions in rocksalt-type binary IV–VI semiconductors such as GeTe, SnTe, PbTe and PbS that appear cubic to diffraction techniques.^34–39 Rather than involving short-range ordering of cation vacancies, the lowering of local symmetry in the “cubic” phases of these systems is thought to be associated with the relative displacement of the cation substructure with respect to the anion substructure along the cubic [111] direction (rhombohedral distortion). However, the concentration of cation vacancies might have a significant influence on the ordering length and magnitude of these ferroelectric-type displacements.³⁹ It has also been reported in the case of GeTe that the cubic polymorph contains more cation vacancies than the rhombohedral polymorph.⁴⁰ Anharmonic thermal vibrations further complicate the picture^41,42 and might falsely appear as atomic displacements to local structural probes such as pair distribution function analysis of diffraction data.⁴³ Further work is thus required to better understand the relationship between cation vacancy ordering and the ordering of atomic displacements in IV–VI materials.

Thermoelectric properties

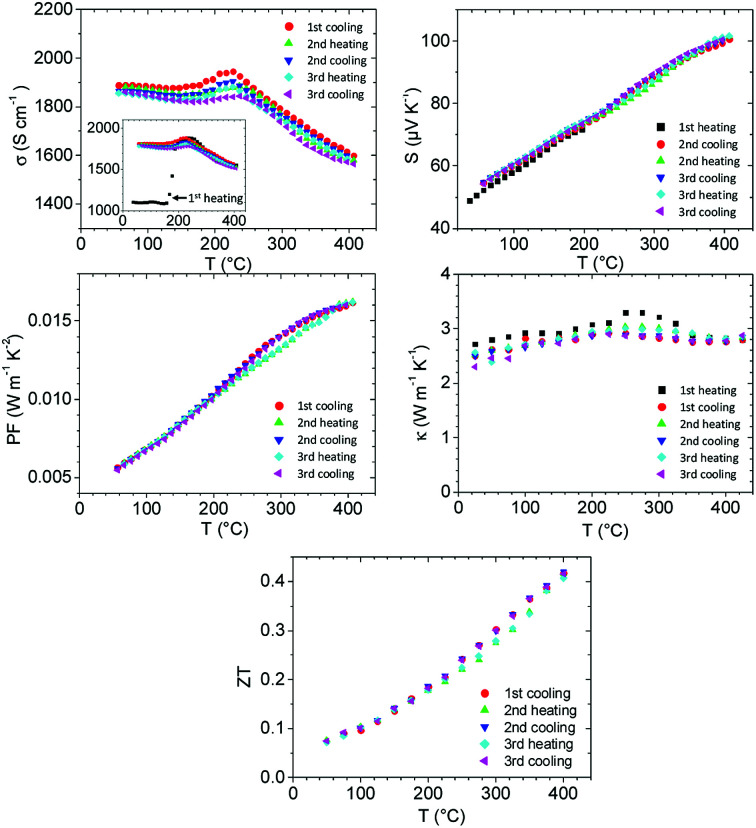
The thermoelectric properties of the C_RT phase were measured over three thermal cycles between room temperature and 400 °C on slices from the same ingot with 90–93% of the density determined from XRD data, as shown in Fig. 4. Measurements on two different samples were averaged to obtain σ, S and PF. Thermal conductivity was measured on two further samples and the data were also averaged. Averaging was performed because the measured properties on different samples were reproducible to within ∼5% (σ and S) and ∼10% (κ) after the first heating cycle.

Fig. 4. Thermoelectric properties of C_RT/21P phase of TAGS-85 over three thermal cycles. The electrical conductivity σ, Seebeck coefficient S and power factor PF are averaged from measurements on two samples, neglecting the initial heating cycle. The inset to the σ plot shows data for the initial heating cycle of one sample. The thermal conductivity κ was measured on two further samples and averaged. The figure of merit ZT was obtained by combining the averaged data presented here.

For the initial heating cycle only, the electrical conductivity varied greatly between the two samples. For one sample the electrical conductivity was initially only ∼1100 S cm⁻¹ in the as-synthesized C_RT phase. A sudden increase to ∼1800 S cm⁻¹ was observed at ∼180 °C where the irreversible transformation to the 21P phase occurs (inset to the plot of σ in Fig. 4). In contrast, the initial electrical conductivity of the second sample was no different to that on subsequent thermal cycles. Therefore, averaging of the data was performed only from the first cooling cycle onwards. The main feature of the electrical conductivity plot is a broad maximum at ∼230 °C with no hysteresis. There is no evidence from XRD for any phase transition at this temperature after the initial heating cycle. However, the maximum temperature attainable of 390 °C in our XRD measurements was insufficient to reach the expected transformation to the high-temperature cubic structure observed by DSC measurement. It is possible that this phase was reached during the electrical conductivity/Seebeck measurement (highest temperature 406 °C), in which case the reverse C → 21P transition might be significantly lowered on subsequent cooling.

The electrical conductivity is ∼40% higher than in our previously reported rhombohedral TAGS-85 samples¹⁸ but the Seebeck coefficient is much lower, only reaching 100 μV K⁻¹ at 400 °C and giving a lower power factor of 0.0016 W m⁻¹ K⁻². The high electrical conductivity is reflected in a high thermal conductivity, which rises slightly from ∼2.5 W m⁻¹ K⁻¹ at 50 °C to ∼2.9 W m⁻¹ K⁻¹ at 400 °C. Consequently, the maximum ZT is just over 0.4 at 400 °C. The significantly worse thermoelectric properties of the C_RT/21P phase might be partially due to the higher volume fraction of the Ag₈GeTe₆ precipitate, which is ∼2% compared to ∼1% for our previous rhombohedral samples.¹⁸ This issue might also be linked to the different density of cation vacancy layers in the 21P structure of the current study and the 39-layer (39P) structure previously obtained on heating rhombohedral samples. The 21P structure has roughly double the density of vacancy layers, which might lead to a self-doping effect and a hole concentration that is higher than optimal with respect to thermoelectric performance. In an earlier study of (GeTe)₈₀(Ag_ySb_2−yTe_3−y)₂₀ (TAGS-80) it was proposed that the poorer performance of silver-rich compositions could partly be attributed to a higher concentration of Ag₈GeTe₆ impurity.¹³ From our previous and current investigations it appears that the precipitation of Ag₈GeTe₆ in TAGS materials is spontaneous and therefore unavoidable. However, the concentration of the precipitate can be controlled by the initial synthesis conditions, which in turn appears to determine the density of cation vacancies. A larger concentration of vacancies leads to more metallic character and poorer thermoelectric performance.

Conclusions

We have obtained a novel metrically cubic (C_RT) polymorph of TAGS-85 at room temperature by careful adjustment of the synthesis conditions. Peak width analysis of our XRD data and the observation of a complex domain structure by TEM suggest that the symmetry of the C_RT phase might be lower on local length scales. This polymorph transforms irreversibly on heating to a new trigonal (21P) structure that contains ordered layers of cation vacancies. This occurs together with the spontaneous precipitation of ∼2% Ag₈GeTe₆ by volume. The C_RT polymorph and its associated trigonal phase exhibit higher electrical conductivity than the better studied rhombohedral polymorph but a much lower Seebeck coefficient and power factor, which is thus detrimental to the thermoelectric performance. The precipitation of cation-rich Ag₈GeTe₆ appears to occur more readily for the cubic polymorph, leaving additional cation vacancies. TAGS-85 thus becomes more metallic in character with inferior thermoelectric properties. Our study suggests that the best thermoelectric properties of TAGS-85 are obtained when the spontaneous precipitation of Ag₈GeTe₆ is minimized, which can be achieved by careful control of the synthesis conditions.

Conflicts of interest

There are no conflicts to declare.