Δ-Quantum machine-learning for medicinal chemistry

Abstract

Many molecular design tasks benefit from fast and accurate calculations of quantum-mechanical (QM) properties. However, the computational cost of QM methods applied to drug-like molecules currently renders large-scale applications of quantum chemistry challenging. Aiming to mitigate this problem, we developed DelFTa, an open-source toolbox for the prediction of electronic properties of drug-like molecules at the density functional (DFT) level of theory, using Δ-machine-learning. Δ-Learning corrects the prediction error (Δ) of a fast but inaccurate property calculation. DelFTa employs state-of-the-art three-dimensional message-passing neural networks trained on a large dataset of QM properties. It provides access to a wide array of quantum observables on the molecular, atomic and bond levels by predicting approximations to DFT values from a low-cost semiempirical baseline. Δ-Learning outperformed its direct-learning counterpart for most of the considered QM endpoints. The results suggest that predictions for non-covalent intra- and intermolecular interactions can be extrapolated to larger biomolecular systems. The software is fully open-sourced and features documented command-line and Python APIs.

Many molecular design tasks benefit from fast and accurate calculations of quantum-mechanical (QM) properties. 3D message-passing neural networks for Δ-quantum machine-learning enable fast access to DFT-level QM properties for drug-like molecules.

Introduction

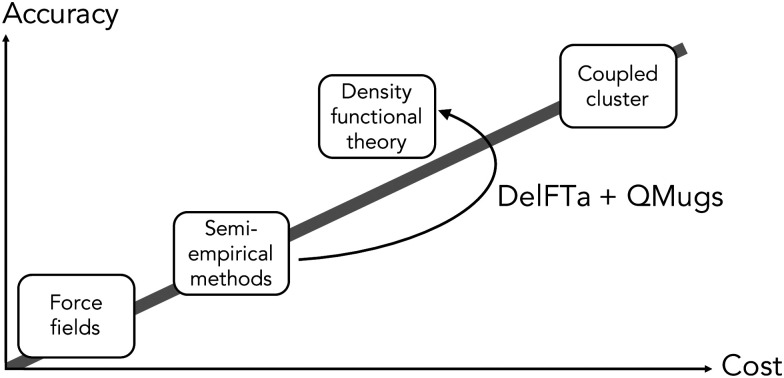
The electronic structure of drug-like molecules is responsible for various drug-relevant properties, such as molecular recognition in protein–ligand complexes,^1–3 drug-induced photo-toxicity,^4,5 reactivity for covalent ligand–protein interaction,^6–8 cell membrane permeability,⁹ or three-dimensional (3D) conformation energies.¹⁰ However, despite advances in density functional theory (DFT) approaches,^11,12 which are widely regarded as a compromise between accuracy and computational cost,^13,14 calculating quantum-mechanical (QM) properties at this level of theory for many or for sizable molecules remains a computationally expensive task. Cheaper alternatives such as force fields¹⁵ and semiempirical methods^16,17 have become popular alternatives, albeit with reduced accuracy. To overcome some of these issues, there has been a recent surge of interest in quantum machine-learning (QML), a set of techniques which aim to approximate quantum observables through statistical modeling approaches.^18–22 Geometric deep learning in particular, a discipline focused on the investigation of neural network architectures that incorporate symmetry information into their design,^23–25 has become an active topic of research. Recent advances in geometric deep learning, such as the development of E(3)-equivariant neural networks, have led to improved prediction accuracy of energies,^26–28 forces for molecular dynamics simulations,^29–31 and wave functions in the form of local bases of atomic orbitals.^32,33

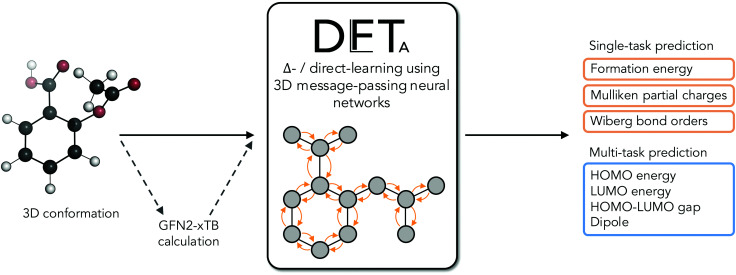
In parallel to these developments, Δ-QML (delta-QML) approaches, which aim to learn corrections between computationally inexpensive QM methods and more accurate, albeit more expensive ones, have been shown to deliver promising results.³⁵ Machine-learned corrections of this kind have been reported for both coupled cluster theory^36,37via DFT, and for DFT via the semiempirical family of methods GFN-xTB,^38,39 as well as for other combinations.⁴⁰ However, despite their encouraging performance, to the best of our knowledge there are currently no open-source implementations of Δ-QML or readily available trained models, which limits their widespread adoption. Addressing this need, we present DelFTa, an open-source deep-learning toolbox that enables both fast and accurate approximations of molecular electronic properties on the DFT^41,42 level of theory. Models were trained on the QMugs⁴³ dataset, which consists of ∼2 M molecular conformers with of a comprehensive array of QM observables both at semiempirical and DFT levels of theory for each structure. Specifically, QM observables were learned at the ωB97X-D/def2-SVP level of theory, either directly or via Δ-learning through corrections to the semiempirical GFN2-xTB method^17,44–46 (Fig. 1). To this end, E(3)-invariant three-dimensional (3D) message-passing neural networks (MPNNs) were employed, which are able to learn properties at either the global molecular, atom, and bond levels²⁵ (Fig. 2) and whose predictions are invariant to translations or rotations of the input molecule. The potential utility of the presented DelFTa approach is threefold:

Fig. 1. Overall idea behind the DelFTa software package. Δ-learning models were trained to predict the correction (Δ) between observables computed with a lower-cost semiempirical baseline method (GFN2-xTB) and the corresponding DFT-level reference method (ωB97X-D/def2-SVP). Visualization inspired by ref. 34.

Fig. 2. Schematic of the Δ-learning concept and application. A three-dimensional (3D) molecular conformation is used as an input to either a single- or multi-task trained message-passing neural network (MPNN). When a Δ-learning endpoint is requested, an additional GFN2-xTB calculation is carried out, and the network is tasked with predicting the correction (Δ) between this baseline value and its ωB97X-D/def2-SVP analogue. If a direct-learning prediction is requested, the network outputs an approximation to the ωB97X-D/def2-SVP value, without using the GFN2-xTB baseline.

(1) The models provided expand the Δ-QML prediction landscape for drug-like molecules by providing access to commonly-used properties such as formation energies, as well as previously-unreported ones, such as energies of the highest occupied and lowest unoccupied molecular orbitals (HOMO and LUMO, respectively), HOMO/LUMO gaps, dipole moments, Mulliken partial charges, and Wiberg bond orders for covalent and non-covalent bonds.

(2) We investigate several key concepts of QML for applications in drug-relevant chemical space; namely, (i) the advantages and limitations of Δ – compared to direct-learning, (ii) the utility of multi- over single-task learning paradigms for molecular properties, (iii) the dependence of prediction errors on training set size, and (iv) the extrapolation capabilities of the trained machine-learning models to non-covalent intra- and intermolecular interactions in biomolecules.

(3) We provide a fully open-sourced and user-friendly software package via command-line and Python APIs that includes all trained models, as well as extensive documentation and tutorials. Interested researchers will be able to use the provided models, train new ones, or build upon them.

The DelFTa approach enables access to a variety of QM properties at DFT accuracy in a fast and user-friendly manner can be routinely used in numerous relevant applications in molecular modeling and design.

Methods

Reference dataset and dataset splits

DelFTa was built upon the QMugs⁴³ data collection, which comprises ∼2 M conformers of over 665 k molecules extracted from the ChEMBL database (release 27),⁴⁷ to obtain training, validation, and test sets. It includes QM properties at two levels of theory, namely the semiempirical method GFN2-xTB^17,44–46 and DFT (ωB97X-D/def2-SVP^41,42).

Each molecule in the QMugs dataset, associated with a unique ChEMBL identifier, was assigned to either training, validation or test sets, with all conformers of one molecule becoming part of the same set. A validation set composed of ∼29 k molecules was used for hyperparameter optimization and early stopping. All optimized models were tested on three test sets of ∼29 k molecules each (∼88 k individual conformers). As in the QMugs dataset, some molecules with distinct ChEMBL identifiers are represented with the same SMILES⁴⁸ notation (i.e., the same 2D molecular graph), all molecules with the same SMILES were assigned to the same test set to avoid information leakage (see ref. 43 for details).

While the production models available in the DelFTa application were trained on the entire QMugs dataset, model performance was also benchmarked for different training set sizes featuring both single molecular conformations per molecule (100, 1 k, 10 k, 100 k and ∼547 k training samples) as well as multiple ones (∼1.6 M individual conformers of ∼547 k distinct molecules). For the formation energy models, all conformers of the same molecule were grouped within the same train-validation-test splits, correspondingly yielding training set sizes of approximately 300, 3 k, 30 k, 300 k and 1.6 M samples. Fig. S1 (ESI†) shows a schematic of the data splitting approach.

Neural network architecture and training details

The 3D-MPNNs used in this work are based on the E(3)-Equivariant Graph Neural Network (EGNN) architecture.^27,49 Δ-learning models for all endpoints y_i, at either global, node, or edge levels, associated with the i-th molecular conformation, were trained to predict the difference y^Δ_i between DFT-computed properties (y^DFT_i ∈ ^k) and GFN2-xTB equivalents (y^GFN2-xTB_i ∈ ^k), specifically:

y^Δ_i = y^DFT_i − y^GFN2-xTB_i. 1

Direct-learning models were trained on y^DFT_i values only. Molecular conformations were represented as fully-connected 3D graphs 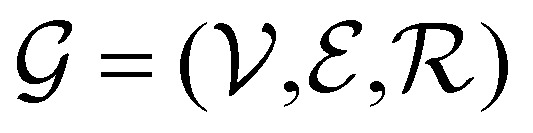, where 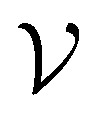corresponds to its set of nodes (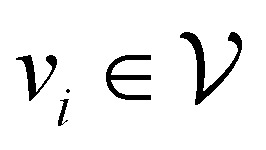), 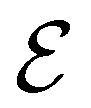to its set of adjacent edges (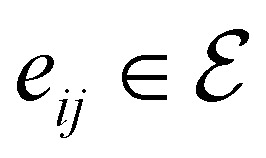) and 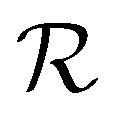to associated Cartesian coordinates in 3D space (r_i ∈ ³). Initial node features v⁰_i were obtained via a linear embedding of the respective atom types. Edge features r_ij were obtained via a sinusoidal and cosinusoidal encoding of the pairwise diatomic distances ‖r_i − r_j‖²₂ (i.e., a Fourier-like encoding scheme).

An Equivariant Graph-Convolutional Layer (EGCL) was applied over all edges e_ij of the graph. It uses the node embeddings of v^l_i at layer l as well as their respective atomic positions r_i to produce updated node representations v^l+1_i:

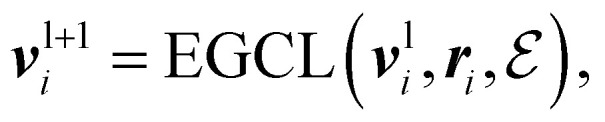2

using the following message-passing mechanism:

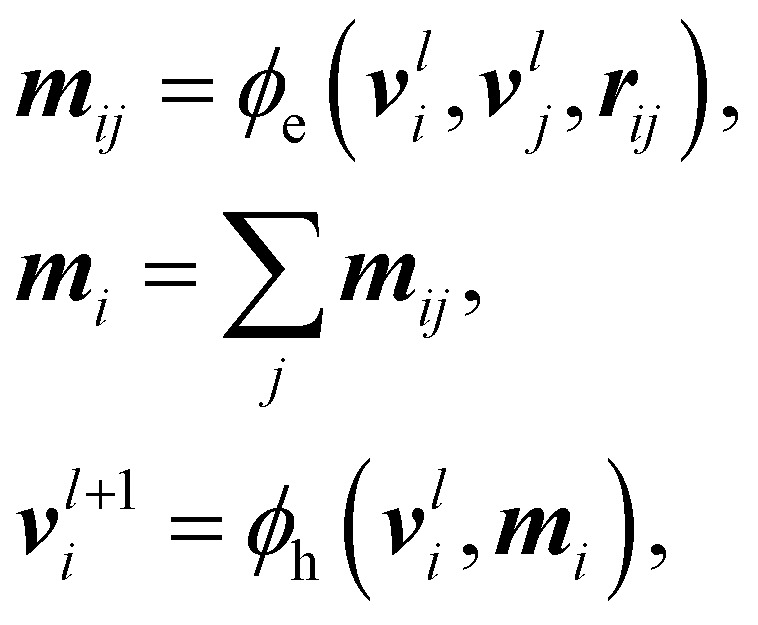3

where ϕ_h, ϕ_e are node and edge non-linear transformations, respectively, modeled with multilayer Perceptrons non-linearized with the SiLU activation function,⁵⁰m_ij the computed edge message features, and m_i the aggregated message features per node.

After five message-passing steps, node features v_i were sum-pooled for extensive properties (i.e., formation energy), and mean-pooled for intensive ones⁵¹ (i.e., dipole, orbital energies, HOMO–LUMO gap) and then mapped to their corresponding target shapes via an additional multi-layer Perceptron. In the specific cases of the node- or edge-based endpoints (i.e., Mulliken partial charges and Wiberg bond orders), the learned node-level v_i and message-level features m_ij were used directly for prediction.

While we employed MSE losses for the intensive properties and Mulliken partial charge models, the ones used for the formation energy and Wiberg bond order endpoints were composed of two terms. Similar to previous work,^38,39,52 in the case of formation energy (eqn (4)) a first loss term minimized the error on the absolute formation energy y_abs, while a second term minimized the relative energy differences between the different geometries of the same molecule y_rel:

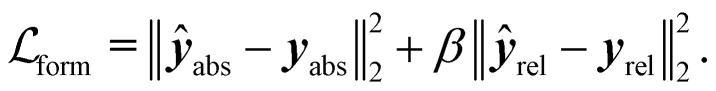4

Specifically training the model to differentiate between conformer energies was motivated by the relevance of this task in identifying the most stable conformers within an ensemble or assessing reaction barriers.⁵³ In the case of Wiberg bond orders (eqn (5)), the first term minimized the error on covalent bonds y_cov, and the second term that on non-covalent interactions y_non:

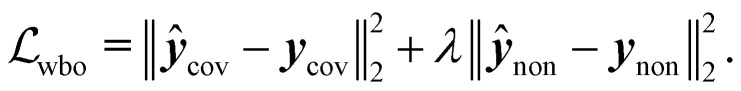5

Both β and λ values were optimized on the validation set and set to β = 1, and λ = 5 × 10⁻² (see ESI† Section 1 for further details). The following network hyperparameters were used in all models considered in this study: (i) node dimension v_i = 128, (ii) message passing dimension m_ij = 32 for molecular and atomic models and 64 for the Wiberg bond order models, (iii) number of sinusoidal and cosinusoidal distance encoding features: 32, (iv) number of EGCLs: 5, and (v) number of global multi-layer Perceptrons: 3, each containing 256 hidden units. Because most of the considered endpoints feature different numerical ranges, which could cause optimization instability issues during the training of the multi-task models, a min–max standardization strategy was applied using the 1st and 99th percentiles of each endpoint, thereby also avoiding outlier scaling problems.

Networks for all endpoints, and for both Δ- and direct-learning models, were trained using the Adam stochastic gradient descent optimizer⁵⁴ with a starting learning rate of 10⁻³ and 10⁻⁴ for all single-task and multi-task models, respectively. An early-stopping strategy that monitored the monotonic decrease of the chosen loss function on the chosen validation set was adopted (see ESI† Section 1 for further details).

Processing of biomolecules

The structures were retrieved from the Protein Data Bank (PDB)⁵⁵ and preprocessed with the MOE software⁵⁶ (version 2019.0102). Since bond orders are intrinsically local properties, and in order to make DFT calculations feasible, atoms which were farther away than one additional residue from the non-covalent interactions of interest were removed and the resulting radicals were padded with hydrogens (see ESI† Section 4 for further details). QM reference values were obtained via Psi4⁵⁷ (version 1.3.2) using the ωB97X-D functional and the def2-SVP basis set.

Results

Predictive performance

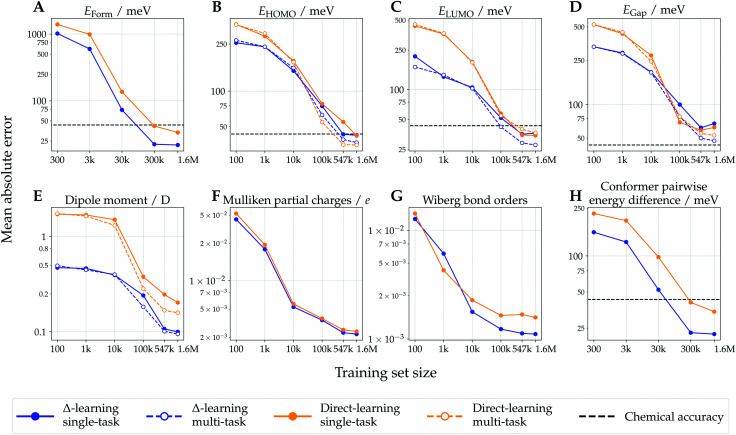
Test-set learning curves of models trained with varying training-set sizes are shown in Fig. 3. Mean absolute errors (MAEs) w.r.t. DFT reference values decreased with increasing training set size, generally resulting in linear correlation recorded on log–log plots due to their inverse power law relationship.^58,59 For most of the considered endpoints, the Δ-learning models consistently achieved a better predictive performance (lower MAEs) than their direct-learning counterparts. This performance gap was observed for most training set sizes, highlighting the usefulness of Δ-learning in low-data regimes. For the prediction of formation energy and relative conformer energy differences, the Δ-learning models achieved performance surpassing chemical accuracy (1 kcal mol⁻¹ ≈ 43.4 meV) for all training set sizes larger than 300 k conformers, while direct-learning models required 1.6 M training points. For all computationally intensive molecular endpoints (i.e. those not depending on the system size, such as orbital energies or dipoles), the performance of multi-task models was superior to that of their single-task counterparts, with the exception of direct-learning on LUMO energies for which both single- and multi-task models achieved similar performance.

Fig. 3. Learning curves of Δ- and direct-learning model for extensive (panels A and H) and intensive (panels B–E) molecular properties, and for atom- and bond-centered properties (panels F and G). These show the mean absolute error (MAE) as a function of training set size (axes in logarithmic scale) computed on the three test sets comprised of ∼29 k molecules (∼88 k conformers). For the energy models (panels A and H), all conformers of the same molecule are grouped within the same train-validation-test splits (see Methods). For intensive molecular properties (panels B–E), learning curves are shown for both single-task and multi-task learning paradigms. Chemical accuracy thresholds are indicated for energy and orbital energy models (1 kcal mol⁻¹ ≈ 43.4 meV).³⁹.

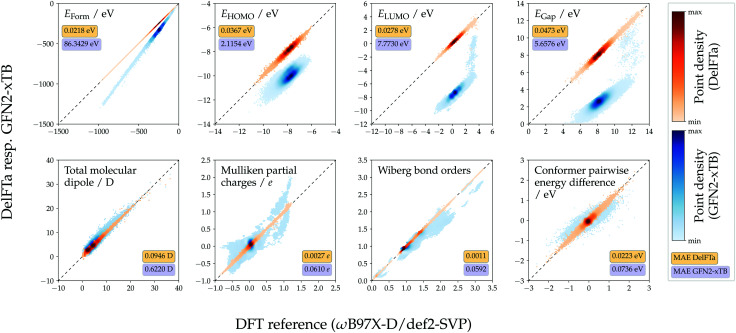
The predictive performance of the models trained on 1.6 M training conformers was analyzed in more detail. Table 1 shows MAEs w.r.t. the ωB97X-D/def2-SVP reference values obtained for the test sets, and compares them to those of the semiempirical baseline method GFN2-xTB. For all considered endpoints and models, the DFT reference values were more closely approximated with the proposed machine-learning models than with GFN2-xTB. For most of the considered endpoints, the Δ-learning approach yielded lower MAEs than its direct-learning counterpart. However, the direct-learning approach achieved a slightly lower MAE (35.0 meV vs. 36.7 meV for Δ-learning) for the prediction of HOMO energies, which can be attributed to the fact that HOMO energies calculated with the DFT and GFN2-xTB methods, respectively, correlated to a lesser degree than other considered endpoints. Scatter plots showing Δ-predicted properties versus their DFT reference values are provided in Fig. 4. Direct-learning approaches also yielded higher accuracies than the semiempirical baseline GFN2-xTB for all considered endpoints (see Fig. S2, ESI†).

MAEs (±1 standard deviation) for the baseline (GFN2-xTB) as well as the Δ- and direct-learning models w.r.t. the DFT reference values (ωB97X-D/def2-SVP). Results computed for ∼88 k molecules (∼263 k conformers) from the three test sets. Wiberg bond order results only for bonds where GFN2-xTB values were available. The lowest MAE w.r.t. reference values are highlighted.

Property	Unit	GFN2-xTB	DelFTa
			Δ-learning	Direct-learning
Formation energy	meV	86343 (± 39)	21.78 (± 0.10)	33.50 (± 0.05)
HOMO energy	meV	2115.4 ± (0.5)	36.7 (± 0.1)	35.0 (± 0.1)
LUMO energy	meV	7773.0 (± 0.7)	27.8 (± 0.2)	36.8 (± 0.2)
HOMO–LUMO gap	meV	5658 (± 1)	47.3 (± 0.2)	52.9 (± 0.1)
Total molecular dipole	D	0.622 (± 0.002)	0.0946 (± 0.0006)	0.1588 (± 0.0006)
Mulliken partial charges	e	0.0610 (± 0.0000)	0.0027 (± 0.0000)	0.0029 (± 0.0000)
Wiberg bond orders	—	0.0592 (± 0.0001)	0.0011 (± 0.0000)	0.0017 (± 0.0000)
Conformer pairwise energy difference	meV	73.6 (± 0.4)	22.29 (± 0.06)	34.27 (± 0.08)

Fig. 4. Calculated versus DFT reference values (ωB97X-D/def2-SVP). Mean absolute errors (MAEs) computed for Δ-learning models and for the GFN2-xTB baseline in ∼88 k test-set molecules (∼263 k conformers). Δ-learning predictions obtained using the models trained on the 1.6 M conformer training set, and in the multi-task setting for all intensive endpoints. Wiberg bond order results only for bonds where GFN2-xTB values were available. Colorbars scaled individually for each property.

Utility of Δ-learning

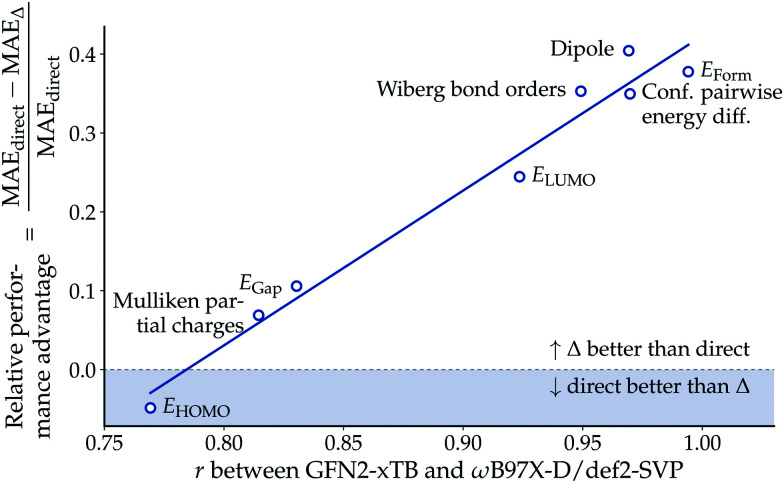
While Δ-learning models generally outperformed their direct-learning analogues in our experiments, the observed performance difference was not uniformly distributed across the endpoints. To investigate under which conditions the Δ-learning paradigm is advantageous over direct-learning, we analyzed the relative performance difference between the two approaches as a function of the Pearson correlation coefficient r between baseline (GFN2-xTB) and reference (ωB97X-D/def2-SVP) values. Fig. 5 indicates that the relative performance advantage of Δ-learning is positively correlated to the correlation r between baseline and reference values. This result confirms the intuitive understanding that Δ-learning provides a larger performance advantage over direct-learning the more information the baseline method provides.

Fig. 5. Relative performance advantage of Δ– over direct-learning. The figure shows the model performance against the Pearson correlation coefficient r between semiempirical (GFN2-xTB) and DFT (ωB97X-D/def2-SVP) methods. The solid line shows a least-squares linear fit.

Non-covalent interactions in biomolecules

Many tasks in medicinal and bioorganic chemistry encompass the study of non-covalent intra- (e.g. secondary-structure-stabilizing) and intermolecular (e.g. protein–ligand) interactions.^60,61 Modelling of non-covalent interactions with semiempirical methods has previously been shown to be challenging.⁶² Given the biological relevance of these molecular interactions, it is desirable to develop QML models which can accurately extrapolate from small molecules (e.g., bioactive ligands) to larger biomolecules (e.g., peptides), foregoing the need for the expensive DFT calculations associated with structures of such size.

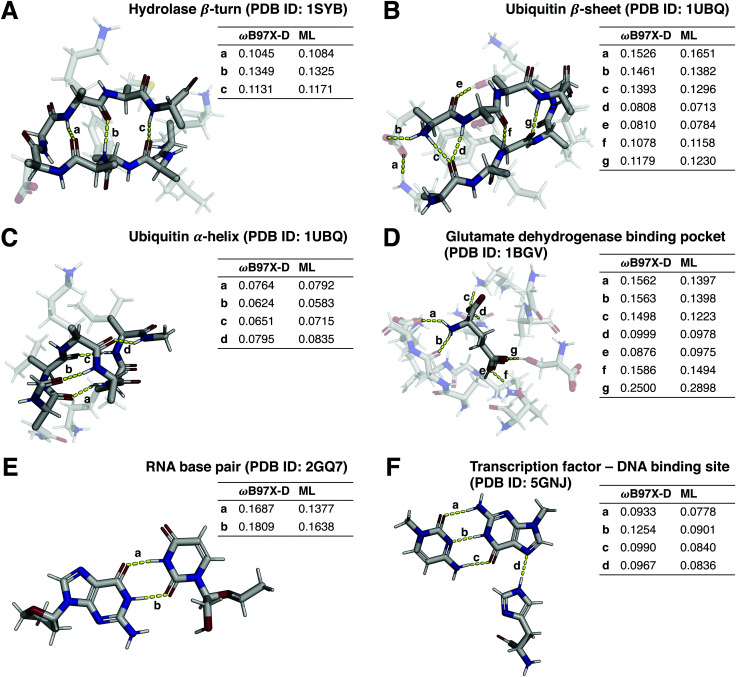
Towards that end, we preliminarily investigated the generalization capabilities of direct-learning QML models for selected biomolecular systems with crucial non-covalent interactions by comparing predicted Wiberg bond orders to DFT reference values. Δ-learning models were not considered in these analyses, as bond order values for many non-covalent interactions of interest are not provided by the GFN2-xTB semiempirical method. The investigated structures (Fig. 6) include a hydrolase β-turn,⁶³ a β-sheet and an α-helix of ubiquitin,⁶⁴ glutamate in a glutamate dehydrogenase binding pocket,⁶⁵ an uracil-adenine base pair in an RNA structure,⁶⁶ and a transcription factor binding to a cytosine–guanine base pair of a DNA structure.⁶⁷

Fig. 6. Non-covalent interactions in selected biomacromolecules. For panels (A–D), non-backbone residues resp. protein pockets shown semi-transparently for visual clarity. Interactions with DFT-calculated Wiberg bond orders between 0.05 and 0.8 shown, and both calculated (ωB97X-D/def2-SVP) and predicted (ML, using models trained on 1.6 M datapoints) values tabulated. Interactions with solvent atoms and between atoms spaced less than six covalent bonds apart not shown. White: hydrogen, gray: carbon, red: oxygen, blue: nitrogen.

By training only on monomers of drug-like molecules and their intramolecular interactions, as included in the QMugs dataset, the models successfully extrapolated to non-covalent intra- and intermolecular interactions in biomacromolecules including monomers and dimers. For instance, weak hydrogen bonds (Wiberg bond order <0.1), such as the ones found in α-helices (Fig. 6(C)), as well as strong hydrogen bonds (Wiberg bond order <0.1), such as the ones found in the RNA base pairs (Fig. 6(E)), β-turns/sheets (Fig. 6(A) and (B)), and in the glutamate binding pocket (Fig. 6(D)), were accurately predicted. However, we observed reduced predictive capabilities for some interactions such as hydrogen bonds with phosphate groups (Fig. S4, ESI†).

Benchmarking

We compared the implementation of the DelFTa deep-learning architecture used in this work to the one originally reported in ref. 27, for the QM9 dataset,⁶⁸ a benchmark used in previous QML studies, which features quantum observables for ∼134 k small molecules. The same DelFTa model architecture used for the direct-learning of formation energies was retrained on the QM9 training set (∼100 k molecules), validated and tested on its respective validation and test sets (∼15 k molecules each). The trained models achieved an MAE of 11.9 ± 0.7 meV in three independent model runs, which is comparable to the originally-reported performance (12 meV).²⁷ The lower overall error of the models trained on QM9 compared to those trained on QMugs (11.9 meV and 33.5 meV, respectively) can be attributed to two key differences between the datasets, namely atom type diversity (10 different atom types in QMugs, 5 in QM9), and molecular size (up to 100 heavy atoms in QMugs, and up to 9 heavy atoms in QM9, respectively).

Since DelFTA models were trained on uncharged molecules but had shown predictive capabilities for charged biomolecules, we quantitatively investigated the models’ performance on 176 randomly-sampled charged conformers corresponding to 59 molecules extracted from the test sets (see Table S2 for details, ESI†). Compared to uncharged molecules, the predictive performance decreased moderately for Mulliken partial charges and Wiberg bond orders, and substantially decreased for other endpoints (see Table S3, ESI†). Based on these results, we discourage the use of the DelFTa models provided in the accompanying software for out-of-distribution molecules.

Listing 1 A small snippet highlighting the main predictive capabilities of the DelFTa Python package and its integration with Pybel. Molecules, with or without associated 3D geometry, can be supplied via a wide array of file types.

Finally, we explored the model performance (trained on ωB97X-D/def2-SVP DFT data) on a set of molecules whose DFT reference values were computed with a more comprehensive basis set (ωB97X-D/def2-QZVP). Calculations for 2,874 conformations corresponding to 958 distinct molecules with this larger basis set did not indicate superior performance of Δ-over direct learning (see Fig. S3 for details, ESI†). Furthermore, Mulliken partial charges on the ωB97X-D/def2-QZVP level of theory were better approximated using GFN2-xTB than with either of the provided machine-learning models. This was expected as GFN2-xTB better approximates charges computed with the larger basis set than the chosen DFT reference used throughout this study (ωB97X-D/def2-SVP).

Software

DelFTa is fully implemented in the Python programming language⁶⁹ and uses the PyTorch⁷⁰ (version 1.8.0) and PyTorch Geometric packages⁷¹ (version 1.7.2) to enable model training and inference. A minimalist code example for the usage of the package is provided in Listing 1. Semiempirical calculations at the GFN2-xTB^17,44–46 level of theory are computed via open-source xtb binaries. All molecular manipulation routines (including optional generation of initial 3D coordinates and GFN2-xTB geometry optimization) are integrated into DelFTa and handled via the Pybel package⁷² and OpenBabel⁷³ Python bindings. The software is fully open-sourced, available on GitHub (https://github.com/josejimenezluna/delfta) under a permissive AGPLv3 license, and distributed through the conda package manager.⁷⁴ A Docker⁷⁵ container is also provided for easier accessibility and to ensure long-term functionality. Furthermore, DelFTa provides extensive documentation for its code and APIs. Tutorials in the form of several didactic Jupyter notebooks⁷⁶ are also available.

On a computer with a consumer-grade graphics processing unit, DelFTA predicts all considered endpoints at a speed of approximately 50 and 5 molecules per second for the direct and Δ-learning models respectively, with the latter approach mostly bottlenecked by the additionally-required baseline GFN2-xTB calculations.

Discussion

QML models were trained for a wide variety of endpoints on a large dataset of quantum observables. Models were validated for both Δ- and direct-learning, as well as single- and multi-task paradigms. The results suggest that both Δ- and direct-learning models have improved accuracy over the GFN2-xTB baseline in approximating ωB97X-D/def2-SVP reference values. For the majority of the considered endpoints, Δ-learning models displayed lower MAEs than their direct-learning analogues at roughly the same computational cost as GFN2-xTB. Additionally, the Wiberg bond order models were able to approximate non-covalent interactions in larger biomolecular systems.

We foresee many applications for the hereby provided models in both supervised and generative molecular pipelines. For instance, featurization with quantum-derived properties, such as partial charges and nuclear magnetic resonance shifts, was shown to increase the performance of reactivity prediction with graph neural networks in low-data regimes.⁷⁷ Similar effects may also be anticipated in medicinal chemistry as the electronic structure of drug-like molecules governs many related properties. Potential examples include the influence of (i) HOMO/LUMO energies on phototoxicity,^4,5 (ii) dipole moments on aqueous solubility^78,79 and membrane permeability,^9,80 and (iii) formation energies on 3D-conformer ensembles⁹ or site-of-metabolism prediction.⁸¹

Future prospective applications will reveal the practical applicability and usefulness of these models in drug discovery-related tasks. The current limitations are twofold, concerning the modelling performance and the models’ applicability domain. With regard to modelling performance, we noted that while the Δ-learning approach affords substantial improvements over its direct-learning analogue w.r.t. target DFT reference values, this does not necessarily hold in the case of HOMO energies, probably owing to the limited correlation of the baseline and reference methods. Furthermore, some of the observations regarding the performance advantages do not necessarily hold for reference values computed with a more comprehensive basis set. Limitations with regard to the applicability domain mostly stem from the underlying QMugs dataset, which was conceived with medicinal chemistry applications in mind. For example, it does not feature organometallic complexes, polymers, crystalline structures, or molecular systems including dimers, radicals, excited electronic states, higher-order spin states, off-equilibrium structures or charged molecules. Specifically for charged molecules we observed substantially decreased predictive performance in this study. Adequate models for these types of molecular structures will require training data that specifically covers the respective chemical space, and therefore remain a subject of future work.

Conflicts of interest

G. S. is a cofounder of inSili.com LLC, Zurich, and a consultant to the pharmaceutical industry.