Multi‐Site Concordance of Diffusion‐Weighted Imaging Quantification for Assessing Prostate Cancer Aggressiveness

Abstract

Background

Diffusion‐weighted imaging (DWI) is commonly used to detect prostate cancer, and a major clinical challenge is differentiating aggressive from indolent disease.

Purpose

To compare 14 site‐specific parametric fitting implementations applied to the same dataset of whole‐mount pathologically validated DWI to test the hypothesis that cancer differentiation varies with different fitting algorithms.

Study Type

Prospective.

Population

Thirty‐three patients prospectively imaged prior to prostatectomy.

Field Strength/Sequence

3 T, field‐of‐view optimized and constrained undistorted single‐shot DWI sequence.

Assessment

Datasets, including a noise‐free digital reference object (DRO), were distributed to the 14 teams, where locally implemented DWI parameter maps were calculated, including mono‐exponential apparent diffusion coefficient (MEADC), kurtosis (K), diffusion kurtosis (DK), bi‐exponential diffusion (BID), pseudo‐diffusion (BID*), and perfusion fraction (F). The resulting parametric maps were centrally analyzed, where differentiation of benign from cancerous tissue was compared between DWI parameters and the fitting algorithms with a receiver operating characteristic area under the curve (ROC AUC).

Statistical Test

Levene's test, P < 0.05 corrected for multiple comparisons was considered statistically significant.

Results

The DRO results indicated minimal discordance between sites. Comparison across sites indicated that K, DK, and MEADC had significantly higher prostate cancer detection capability (AUC range = 0.72–0.76, 0.76–0.81, and 0.76–0.80 respectively) as compared to bi‐exponential parameters (BID, BID*, F) which had lower AUC and greater between site variation (AUC range = 0.53–0.80, 0.51–0.81, and 0.52–0.80 respectively). Post‐processing parameters also affected the resulting AUC, moving from, for example, 0.75 to 0.87 for MEADC varying cluster size.

Data Conclusion

We found that conventional diffusion models had consistent performance at differentiating prostate cancer from benign tissue. Our results also indicated that post‐processing decisions on DWI data can affect sensitivity and specificity when applied to radiological–pathological studies in prostate cancer.

Level of Evidence

1

Technical Efficacy

Stage 3

Prostate cancer accounts for one in five new cancer diagnoses in men, with an estimated 193,000 new cases in 2020, ¹ although not all cases are high risk. Ongoing imaging evaluations are aimed at better differentiating aggressive from indolent disease to avoid over‐treatment of non‐aggressive prostate cancer and to accurately detect tumors that have high metastatic potential. ² Advancements in multi‐parametric magnetic resonance imaging (MP‐MRI) such as T₂‐weighted and diffusion‐weighted imaging (DWI) have yielded substantial improvement for prostate cancer detection and MP‐MRI is increasingly used for justifying and guiding biopsy. ³

DWI is commonly used for diagnosing prostate cancer and is weighted heavily as a deciding factor in the Prostate Imaging Reporting and Data System (PIRADSv2.1) grading scale for radiographic diagnosis. ² , ⁴ , ⁵ Tissue micro‐structure strongly influences diffusion properties and abnormalities such as dense cellularity or atrophic glands can result in distinct imaging signatures. ⁶ However, the calculation of quantitative diffusion values varies by fitting algorithms and recent collaborative studies have looked to quantify differences between sites. ⁷

There are three common fitting schemes for deriving quantitative maps from DWI. The apparent diffusion coefficient (ADC) is calculated from a mono‐exponential fit of the different b‐values from the DWI data and is the most common metric used for evaluation of prostate cancer. ² , ⁴ , ⁵ More complex diffusion models have been developed to separate tissue diffusivity from capillary microperfusion. ⁸ , ⁹ By assuming a bi‐exponential relationship between both diffusion and perfusion effects, the intra‐voxel incoherent motion (IVIM) computes both pseudo‐diffusion (BID*) and perfusion fraction (F). ⁸ , ⁹ Kurtosis (K) and diffusion kurtosis (DK) models measure deviations of diffusion from a Gaussian distribution ¹⁰ due to cellular restriction.

The aim of this study, by a collaborative group ¹¹ , ¹² , ¹³ , ¹⁴ organized by the National Cancer Institute (NCI), was to undertake a multi‐institutional study to quantify whether prostate cancer detection varies due to differences in DWI fitting algorithms. In addition, we also measure changes in perceived cancer differentiation due to varying post‐processing parameters were investigated as were changed due to varying the pathologist performing the ground truth annotations.

Methods

This study was proposed and organized through an NCI working group. Investigators from the central organizing institution and 14 other institutions participated. Data were collected at the central site and distributed to each satellite institution for processing. Fourteen implementations were included in this project from investigators at MCW (Team 2), University of Washington, Johns Hopkins University, University of Michigan, University of Texas at Austin, University of Texas Southwestern Medical Center, Oregon Health and Science University, Memorial Sloan Kettering Cancer Center, Mount Sinai, Brigham and Women's Hospital, and Barrows Neurological Institute, in no particular order. Resulting maps were then sent back to the central site for analysis. A diagram showing the design in this study can be seen in Fig. 1.

FIGURE 1.

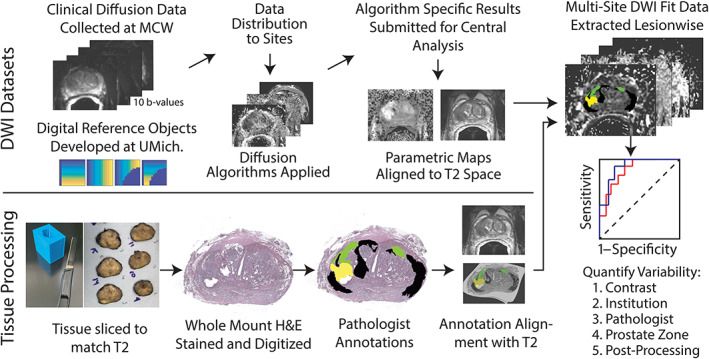
Schematic representation of the experimental design. Top: Raw diffusion data distributed to partner institutions in DICOM format, partner institutions return fits to MCW where they were manually aligned to the T2‐weighted image. Bottom: Post‐surgery, tissue was sliced to match the T2‐weighted image using patient‐specific slicing jigs. Whole‐mount samples were stained and annotated by a pathologist. Annotations were then aligned to the T2‐weighted image. ¹⁵ , ¹⁶ , ¹⁷ , ¹⁸ Right: Pathologist annotations and fits from multiple institutions were combined for analysis to determine variability in prostate cancer sensitivity and specificity.

Patient Population and Data Acquisition

This study was IRB‐approved at the central site. All patients provided written informed consent. Inclusion criteria required patients to undergo MRI prior to prostatectomy and have high‐quality images. Thirty‐nine consecutive patients met the first inclusion criterion, scanned between December 2014 and August 2016. Six patients were subsequently excluded due to excessive motion on their MRI. Imaging from the remaining 33 patients (demographics and cancer stage indicated in Table 1) was acquired on a 3‐T MRI scanner (General Electric, Waukesha, WI) using an endorectal coil and phased‐array torso coil. The MP‐MRI sequences comprised of field‐of‐view optimized and constrained undistorted single shot (FOCUS) DWI ¹⁹ with 10 b‐values (b = 0, 10, 25, 50, 80, 100, 200, 500, 1000, and 2000 seconds/mm²), NEX: 1, 2, 1, 1, 1, 2, 2, 4, 8, 12 respectively, repetition time/echo time (TR/TE) = 4/69–99 msec; interpolated resolution = 0.625 mm × 0.625 mm × 4 mm voxels, acquisition matrix 80 × 80, FOV 160 mm × 160 mm, echo train length 1 (80 echos). Additionally, an anatomical T₂‐weighted multi‐slice dataset was acquired (acquisition matrix 384 × 256, TR = 5000 msec, TE = 0.125 s, FA = 111 echo train length 24, interpolated 0.234 mm × 0.234 mm × 3 mm, FOV 120 mm × 120 mm). Robotic prostatectomy was performed approximately 2 weeks later and the extracted prostate was sectioned using patient‐specific custom three‐dimensional‐printed slicing jigs to match orientation and 3 mm slice thickness of the T₂‐weighted image. ⁶ , ¹⁵ , ²⁰

TABLE 1.

Patient Demographics and Clinical Data (N = 33, Age 59.7 ± 5.7)

Patient No.	Age (Years)	PSA (ng/mL)	Gleason Score	Gleason Grade				T Stage	EPE	Number of PIRADS Lesions	PIRADS Score
				G3	G4‐FG	G4‐Cr	G5
1	61	13.1	3 + 4 (=7)	1	1	0	0	T3a	1	1	PR4
2	68	4.5	3 + 4 (=7)	1	1	0	0	T2c	0	2	PR5, PR5
3	59	6.6	3 + 4 (=7)	1	0	0	0	T2c	0	2	PR3, PR4
4	56	4.4	5 + 4 (=9)	1	1	1	1	T3a	1	1	PR5
5	64	6.3	4 + 3 (=7)	1	1	1	0	T3a	1	1	PR5
6	55	4.9	3 + 4 (=7)	1	1	0	0	T3b	0	1	PR4
7	58	21.9	3 + 4 (=7)	1	1	1	0	T2c	0	1	PR5
8	60	3.0	3 + 4 (=7)	1	1	1	0	T2c	0	2	PR4, PR2
9	71	6.6	3 + 4 (=7)	1	1	1	0	T2c	0	2	PR5, PR3
10	59	5.5	3 + 4 (=7)	1	1	1	0	T3a	1	1	PR5
11	57	5.0	3 + 4 (=7)	1	1	1	0	T3a	1	3	PR4, PR4, PR2
12	49	4.9	3 + 3 (=6)	1	0	0	0	T2c	0	2	PR4, PR4
13	58	6.5	3 + 3 (=6)	1	0	0	0	T2c	0	3	PR4, PR4, PR4
14	60	4.5	3 + 3 (=6)	1	0	1	0	T2a	0	1	PR3
15	66	11.0	3 + 4 (=7)	1	1	1	1	T3a	1	1	PR4
16	52	4.9	3 + 4 (=7)	1	1	0	0	T2c	0	1	PR4
17	63	5.2	3 + 4 (=7)	1	1	1	0	T3a	1	2	PR4, PR4
18	62	6.9	3 + 4 (=7)	1	1	1	1	T2c	0	0	0
19	56	6.4	3 + 3 (=6)	1	0	0	0	T2a	0	1	PR2
20	55	3.4	3 + 3 (=6)	1	0	0	0	T2c	0	1	PR3
21	61	10.3	4 + 5 (=9)	1	1	1	0	T3b	0	1	PR4
22	45	7.2	3 + 3 (=6)	1	0	0	0	T2a	0	1	PR4
23	53	18.5	3 + 4 (=7)	1	1	0	0	T2c	0	1	PR3
24	59	7.3	4 + 3 (=7)	1	1	1	1	T2c	0	1	PR5
25	61	5.0	3 + 4 (=7)	1	0	0	0	T2a	0	3	PR4, PR4, PR2
26	54	17.2	3 + 4 (=7)	1	1	1	0	T2c	0	3	PR4, PR5, PR4
27	68	18.7	3 + 4 (=7)	1	1	1	0	T3b	0	2	PR5, PR4
28	63	4.9	3 + 4 (=7)	1	1	1	0	T2c	0	3	PR4, PR4, PR4
29	59	4.0	3 + 4 (=7)	1	1	1	0	T2c	0	1	PR4
30	59	2.8	3 + 3 (=6)	1	1	0	0	T2c	0	2	PR5, PR4
31	66	5.9	3 + 4 (=7)	1	1	1	1	T3a	1	1	PR4
32	66	5.2	3 + 4 (=7)	1	1	1	0	T2c	0	0	0
33	67	8.2	4 + 5 (=9)	1	1	0	0	T2c	0	1	PR4

EPE = extraprostatic extension from pathology report; PSA = prostate specific antigen.

Histo‐Pathological Analysis

Prostate samples were cut at 4 μm thickness, and whole‐mount sections were hematoxylin and eosin (H&E) stained, digitized, and annotated by a urological fellowship‐trained pathologist (K.I., 23 years of experience) (Fig. 1). A total of 169 slides were included. Each slice was manually aligned to the T₂‐weighted image using control points and a non‐linear transform. Regions with tears and histology artifacts were excluded with manually placed ROIs applied after the spatial transform. Annotations of different Gleason patterns were brought into MRI space using the same non‐linear transform. ⁶ , ¹⁹ Pathologist‐annotated (K.I.) regions that consisted of at least 200 contiguous voxels axially (11 mm² in plane, 33 mm³) were included, which resulted in 231 cancer (CA) regions of interest (ROIs), and 564 ROIs not associated with cancer (benign atrophy, BA). These ROIs were used to extract the quantitative parametric diffusion values. A subset of slides was annotated by five pathologists from four universities with 23 (K.I.), 15 (W.H.), 13 (G.P.), 11 (T.A.), and 1 (W.P.) year of experience. This subset included 33 slides from 28 patients. ¹⁵

Diffusion Signal Fitting

DICOM datasets obtained with FOCUS DWI were de‐identified to meet HIPPA compliance and distributed to the collaborating sites for analysis. Each site was asked to calculate diffusion parameter maps using publicly available or locally developed software, implemented to fit DWI signals. The individual methods used for each site implementation are detailed in the supplement, and in Table 2. ⁷ , ⁸ , ⁹ , ¹⁶ , ¹⁷ , ¹⁸ , ²¹ , ²² , ²³ , ²⁴ , ²⁵ , ²⁶ , ²⁷ , ²⁸ , ²⁹ , ³⁰ , ³¹ These methods included a mono‐exponential fit (parameter: MEADC), diffusion kurtosis (parameters: kurtosis [K] and diffusion [DK]), ¹⁰ and a bi‐exponential fit (parameters: diffusion (BID), BID*, and F). ⁸ Each site submitted the calculated maps back to the central site for comparative analysis. Sites were not required to fit each model in order to maximize participation in this collaborative research project. The site‐specific parametric maps were aligned and resampled to the T2‐weighted image at the coordinating site to ensure the same resampling code was used.

TABLE 2.

Site Implementation Methods and Submitted Image Format

	Site‐Specific Processing											Central Analysis Processing
	MEADC	IVIM	K	MEADC b‐Values	IVIM b‐Values	K b‐Values	Constraints	Submission Image Format	Code/Tool	Link	Citation	Reorient	Scaling
SI1	X	X	X	<2000	≤200	0, 100, 200, 500, 1000, 2000		NIFTI	In House Matlab		8, 9, 23	X	X
SI2	X	X	X	All	All	All		NRRD	DWModeling SlicerProstate extension	DWIModeling (https://github.com/SlicerProstate/SlicerProstate/tree/master/DWModeling)	26		X
SI3	X	X		All	All			DICOM	IB Diffusion, Osirix Plug‐in		8	X	X
SI4	X		X	All		<2000		DICOM	In House Matlab		23		X
SI5	X	X	X	All	≥200	All	X	NIFTI	In House Matlab/QUAMPER		8, 9, 23	X	X
SI6		X			All			NIFTI	In House Matlab		9, 21	X	X
SI7	X	X	X	≥200	All	≥200	X	MHD	In House Matlab		21, 23, 27	X	X
SI8		X	X		All	All	X	NIFTI	In House Matlab		9, 23	X	X
SI9	X	X	X	All	≥200 (BID), ≤50 (F BID*)	≥200	X	DICOM	In House Matlab		8, 9, 23		X
SI10	X	X		All	≥200		X	NIFTI	ADCmap Osirix Plugin	ADCmap (https://github.com/mribri999/ADCmap)	8	X	X
SI11	X		X	All		All		DICOM	In House imFIAT		10	X	X
SI12	X	X		All	All			DICOM	ImageJ and Custom C++ Code		8	X	X
SI13	X	X	X	All	All	All		NIFTI	Osirix UMM Diffusion Plugin		8, 10, 32		X
SI14		X			All		X	NIFTI	ADCmap Osirix Plugin	ADCmap (https://github.com/mribri999/ADCmap)	8	X	X

MEADC = mono‐exponential apparent diffusion coefficient; IVIM = intra‐voxel incoherent motion; K = kurtosis.

Digital Reference Object Design

Two separate digital reference objects (DROs) were created for the IVIM and Kurtosis models. ³² Methods for the DRO analysis are detailed in the supplement.

Correlation Analysis

To determine concordance of the quantitative parametric maps submitted, median values were calculated from pathologist‐defined region, and a percent difference calculation and a Pearson correlation coefficient were calculated. This was done in both cancerous regions (G3+) and benign atrophy.

In Vivo Data Extraction and Cancer Differentiation

For each parametric map submitted by the sites, median values were calculated from each pathologist‐defined region. An empirical receiver operating characteristic (ROC) curve was calculated for each fit to determine the ability of each contrast to differentiate regions of cancer. Two classification tasks were considered: cancer (G3+) vs. benign atrophy, and low‐grade (LG = G3) vs. high‐grade (HG = G4+). The area under the curve (AUC) served as the metric of interest to assess concordance between site implementations.

Clustergram Analysis

To visually measure group concordance and similarity, clustergrams were created comparing the value within each lesion across all sites who submitted a given fit. Median values were extracted from all lesions greater than 200 voxels in‐plane. For each lesion, a SD was calculated quantifying variability across implementations for a given fit. SDs were then sorted and displayed using Matlab (Mathworks Inc, Natick, MA).

Zonal Anatomy

ROIs defining prostate peripheral zone (PZ) and transition zone (TZ) were manually drawn on the T₂‐weighted image and verified by a radiologist. Zone masks were used to determine the location of each pathologist annotation. In cases where a lesion crossed the zone boundary, the mode was used to determine the predominant zone. The ROC analysis was repeated within each contrast, plotting cancer vs. benign atrophy stratified by zone.

Index Lesion

The ROC analysis was repeated including only the index lesion to mirror the experimental setup of biopsy‐confirmed radiology studies. The index lesion was defined as the largest in‐plane pathologically confirmed cancerous region. A matching number of benign atrophy regions were included in the analysis.

Annotation Extraction Metric

The metric for extracting values from the region of interest was varied and the receiver operating characteristic analysis was repeated. Mean, median, and 10th percentile values were tested (90th percentile for kurtosis fits). A cluster limit of 200 was used for this analysis.

Cluster Limit

The ROC analysis was repeated varying the minimum lesion size required to be included in the analysis. Cluster limits of 100, 200, 300, 400, and 500 voxels were tested. With T ₂ ‐weighted voxels being 0.234 mm × 0.234 mm × 3 mm, this corresponded to within slice areas of 5.5, 11.00, 16.5, 22, and 27.5 mm² (16.5, 33, 49.5, 66, and 82.5 mm³). In DWI image space, this was approximately 10, 20, 30, 40, and 50 voxels. Both conditions, cancer vs. benign, and low‐grade vs. high‐grade were evaluated.

Multi‐Pathologist Analysis

The ROC analysis was repeated varying the pathologist annotating the ground truth. This analysis was performed on a subset of 33 slides annotated by five pathologists. A cluster limit of 200 was used and median values were taken from the ROIs. Cancer vs. regions left unlabeled by all five pathologists (unlabeled consensus) ¹⁵ was tested in addition to HG vs. LG.

Statistical Comparisons

Basic descriptive statistics of mean and SD values of ROC AUC analysis for each contrast, site implementation, and condition were calculated. To measure differences between implementations, we used a Levene's test applied to the SD. To quantify differences in the ROC AUC between contrasts and implantations, we used a linear model with contrast as a covariate, with MEADC as the baseline category, with the sandwich standard error estimates being used to account for lack of homoscedasticity between groups. ³³ Pairwise comparisons were performed (consistency and contrast comparisons), with the Tukey's honestly significant difference procedure used to correct P‐values for multiple comparisons. P < 0.05 was considered significant (R‐software, v3.6.3; www.r-project.org).

Results

Sample images from each site and software implementation applied to the same slide can be seen in Fig. 2. Sites were not required to fit each model to maximize participation. Submitted maps varied in noise levels and visual interpretability, which was most evident in BID* and F. Universally, regions of cancer showed a decrease in ADC, BID, and DK compared to benign atrophy, and an increase in K.

FIGURE 2.

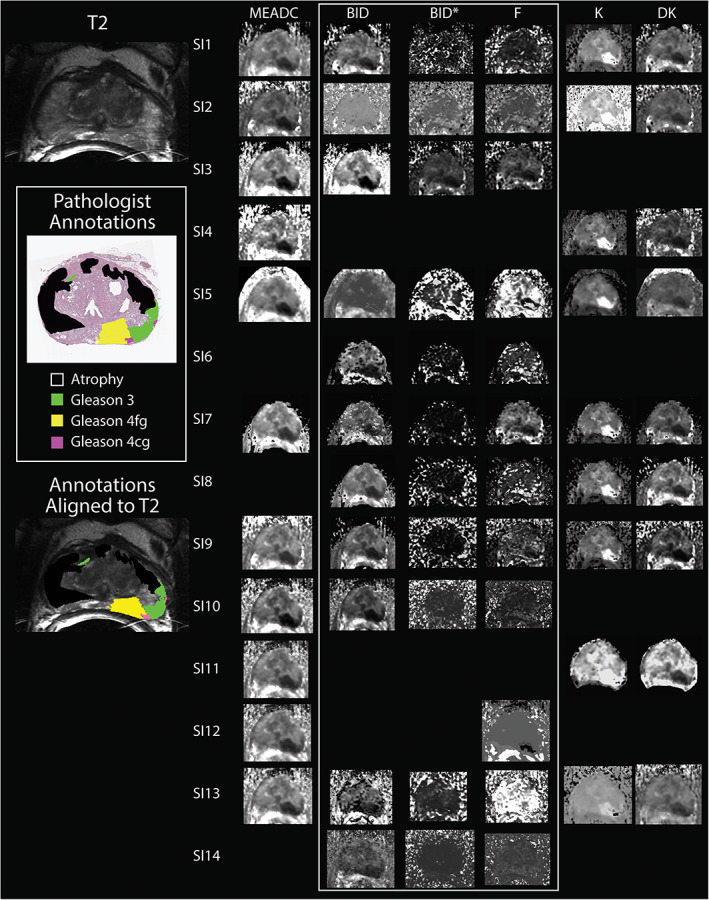
A summary of submitted site diffusion‐weighted imaging (DWI) fit parameter maps aligned to a pathologist‐annotated whole‐mount histology slide. Left: The corresponding T2‐weighted slice, pathologist annotations in histology space containing a dominant G4 fused gland (G4FG) tumor (yellow) with a secondary G3 region (green) and two small G4 cribriform gland (G4CG) tumors (Pink). ⁶ Left bottom shows the pathologist annotations aligned in MRI space and overlaid on the T2. Right: Site implementations included mono‐exponential apparent diffusion coefficient (MEADC), bi‐exponential diffusion (BID), pseudo‐diffusion (BID* [×10⁻³ mm²/second]), and perfusion fraction (BID [×10⁻³ mm²/second], BID* [×10⁻³ mm²/second], and F), and kurtosis and kurtosis diffusion (K and DK). Some sites submitted multiple sets of fits, each implementation is separated and treated separately. Relative contrast differences between sites are notable in the MEADC images, but independent of implementation the tumor has decreased diffusion compared to surrounding tissue. Bi‐exponential fits showed notable contrast differences between site implementation while kurtosis fits were notably similar.

Correlation Analysis

The correlation analysis revealed similar patterns in percent difference and correlation coefficient in both normal and cancerous ROIs. Mono‐exponential ADC, K, and DK were more similar between sites than the IVIM fits (Fig. 3). Value ranges are shown in Tables S1 and S2 in the Supplemental Material. Larger variability of bi‐exponential model parameters was also consistent with observations for noise‐free DRO (Fig. S1 in the Supplemental Material), although with smaller absolute percent‐deviations.

FIGURE 3.

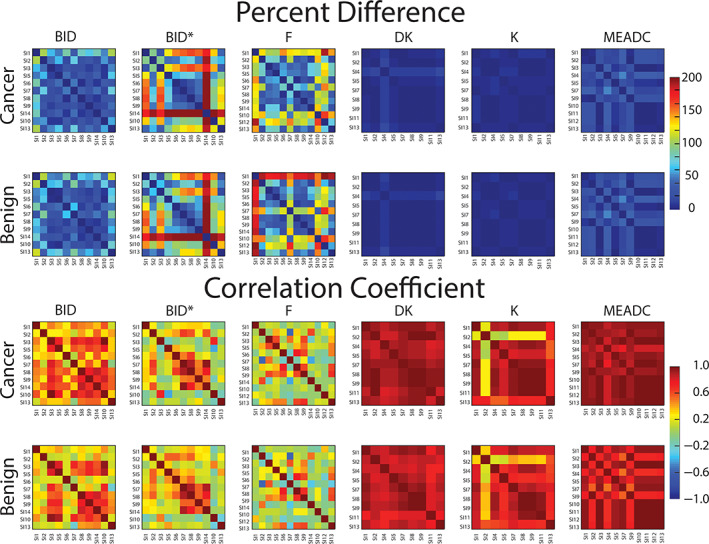
Percent difference matrix comparing DWI parameters between site implementation (SI) and between classes of cancer and normal (Top). Pearson correlation coefficient matrices comparing DWI parameters between SI and classes of cancer and non‐cancer (Bottom). MEADC, K, and DK show the least percent difference across sites and the highest correlation. Data are shown in Tables S2 and S3 in the Supplemental Material. DWI = diffusion‐weighted imaging; MEADC = mono‐exponential apparent diffusion coefficient; K = kurtosis; DK = diffusion kurtosis.

Variation in Cancer Differentiation

The ROC analysis calculated using a cluster limit of 200 and a median value from each ROI is shown in Fig. 4. Comparing cancer to benign atrophy, MEADC had a median AUC of 0.78, range 0.76–0.80, while BID, BID*, and F had median values of 0.71, 0.56, 0.61 respectively, and ranges of 0.53–0.80, 0.51–0.81, and 0.52–0.80 respectively. Kurtosis models resulted in median AUC of 0.78 and 0.75 for DK and K respectively with ranges of 0.76–0.81 and 0.72–0.76 respectively. Comparing G3 to G4+, MEADC had a median AUC of 0.67, range 0.66–0.68, while BID, BID*, and F had median values of 0.60, 0.54, 0.59 respectively, and ranges of 0.52–0.68, 0.50–0.69, and 0.51–0.69 respectively. Kurtosis models resulted in median AUC of 0.67 and 0.64 for DK and K respectively with ranges of 0.65–0.70 and 0.63–0.65 respectively. Values are summarized in Table S3 in the Supplemental Material. Across all contrasts cancer vs. benign atrophy resulted in a higher AUC than low‐grade vs. high‐grade.

FIGURE 4.

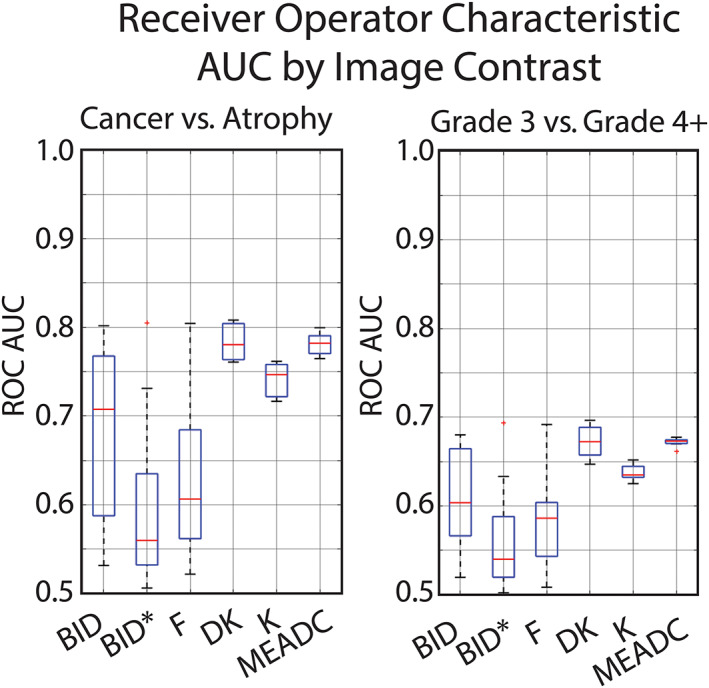
Boxplot showing area under the curve receiver operating characteristic (ROC AUC) variability by site implemented fits. Left: Cancer (G3+) vs. benign atrophy. Right: Gleason 3 vs. Gleason 4+. ROC AUC was calculated lesion‐wise using the median value in each pathologist annotated region larger than 200 voxels. A tighter boxplot indicates less cancer differentiation variability between site implementations.

Statistical Comparisons

Comparing the ROC AUCs between contrasts and conditions (BA vs. CA, and HG vs. LG), MEADC significantly outperformed all other contrasts with the exception of DK and K. DK outperformed all bi‐exponential parameters across conditions. Statistical results are detailed in Table 3. Comparing contrast‐specific ROC AUC variance between conditions, we found that MEADC and K had significantly less variance between site‐specific ROC AUC compared to BID, for both conditions, and trended towards significance for the other bi‐exponential parameters, consistent with what can visually be seen in Fig. 4 (Levene's test P < 0.05 corrected for multiple comparisons). Statistical results from each comparison are detailed in Table 4.

TABLE 3.

Statistical Results Comparing Site Implementation ROC AUC Values Between Contrasts and Conditions Cancer vs. Benign Atrophy (CAvBA), and Low‐Grade vs. High‐Grade Cancer (LGvHG)

CAvBA	BID	BIDS	BIPF	DK	K	MEADC
BID		0.988	0.982	0.054	0.040*	0.011*
BIDS			1.000	0.203	0.162	0.060
BIPF				0.204	0.162	0.058
DK					1.000	0.998
K						1.000
MEADC

LGvHG	BID	BIDS	BIPF	DK	K	MEADC
BID		0.999	0.898	0.094	0.017	0.005*
BIDS			0.983	0.196	0.044*	0.014*
BIPF				0.512	0.169	0.069
DK					0.988	0.942
K						1.000
MEADC

ROC AUC = receiver operating characteristic area under the curve; BID = bi‐exponential diffusion; DK = diffusion kurtosis; K = kurtosis; MEADC = mono‐exponential apparent diffusion coefficient.

*P < 0.05.

TABLE 4.

Statistical Results Comparing the Contrast‐Specific Variances Between ROC AUC Across Conditions CvBA and LGvHG

CvBA	BID	BIDS	BIPF	DK	K	MEADC
BID		0.177	0.538	0.029	0.505	0.032*
BIDS			0.955	<0.001*	<0.001*	<0.001*
BIPF				<0.001*	<0.001*	<0.001*
DK					<0.001*	0.998
K						<0.001*
MEADC

LGvHG	BID	BIDS	BIPF	DK	K	MEADC
BID		0.260	0.696	0.015*	0.710	0.012*
BIDS			0.939	<0.001*	<0.001*	<0.001*
BIPF				<0.001*	0.006*	<0.001*
DK					<0.001*	1.000
K						<0.001*
MEADC

ROC AUC = receiver operating characteristic area under the curve; BID = bi‐exponential diffusion; DK = diffusion kurtosis; K = kurtosis; MEADC = mono‐exponential apparent diffusion coefficient.

Zonal Anatomy

The results from the zone analysis are shown in Fig. S3, with data shown in Table S4 in the Supplemental Material. The median AUCs for PZ were 0.81, 0.77, 0.77, 0.73, 0.58, and 0.63 for MEADC, DK, K, BID, BID*, and F respectively. For TZ, median AUCs were 0.84, 0.74, 0.86, 0.72, 0.60, and 0.62 respectively. Summary values with ranges are shown in Table S4 in the Supplemental Material, where in general, the IVIM parameters showed greater variability in range and overall lower performance compared to the kurtosis and mono‐exponential parameter maps. Across site implementations, kurtosis performed better in the TZ than the PZ; however, all other parameter maps were roughly equivalent independent of zone.

Index Lesion

The results of the index lesion analysis are shown in Table S5 and Fig. S4 in the Supplemental Material. The median AUCs were 0.82, 0.75, 0.58, 0.62, 0.79, and 0.77 for MEADC, DK, K, BID, BID*, and F respectively. While MEADC remains similar to the other experiments, the BID and BID* parameter maps become less variable under this condition, while the DK and K maps become more variable between site implementations.

Clustergram Analysis

The results of the clustergram analysis are shown in Fig. S2 in the Supplemental Material for each of the contrasts. The heat maps shown indicate SD from the mean for each value. More consistency and grouping were seen in the MEADC, K, DK, and BID, with less consistency seen in BID* and F. For MEADC, K, and DK, results indicated that four site implementations were virtually identical in values.

Cluster Limit

The results of the cluster limit analysis are detailed in Fig. 5, with values shown in Table S4 in the Supplemental Material. Across both conditions (high‐grade vs. low‐grade and cancer vs. benign atrophy) parameter maps AUC increased as minimum cluster to be included was increased from 100 to 500 T₂‐resolution voxels in 100 increments. Increases in median AUC went from 0.74 to 0.87, 0.69 to 0.80, 0.71 to 0.85, 0.68 to 0.77, 0.51 to 0.60, and 0.59 to 0.65 for MEADC, DK, K, BID, BID*, and F respectively. Independent of cluster limit, mono‐exponential ADC and the kurtosis fit parameters showed smaller ranges of variability between sites. Additionally, the variability between sites in the IVIM parameter maps tended to increase as cluster limit was increased (Fig. 5). Figure S5 in the Supplemental Material shows the number of lesions included in the analysis at each step, indicating that the number of lesions across all conditions decreased by more than half as the cluster limit increased from 100 to 500.

FIGURE 5.

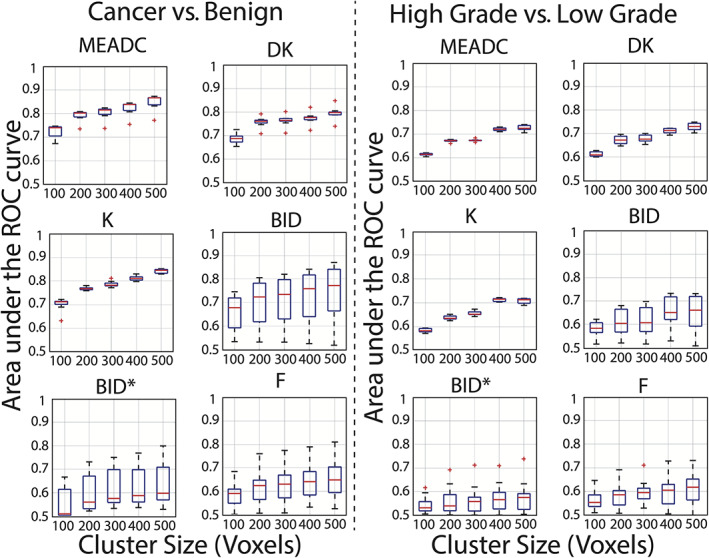
Receiver operator characteristic area under the curve (ROC AUC) for all institutions grouped by fit and repeated varying the minimum lesion size included in the analysis. Lesion size limit was varied from 100 voxels to 500 voxels stratifying G3+ vs. benign atrophy (Left) and stratifying G3 from high‐grade tumors (Right). There is a trend towards increasing AUC as the cluster limit for inclusion becomes more selective in both cancer vs. benign and low‐grade vs. high‐grade. Fits that are highly variable between sites remain highly variable independent of cluster limit.

Extraction Metric

The results of varying the extraction metric (median, mean, or 10th percentile) are shown in Table S7 and Fig. S6 in the Supplemental Material. While the median value across all sites is relatively consistent independent of which metric is chosen, the variability between sites is highly dependent on the metric used to extract a value from an ROI.

Multi Pathologist

The results of the multi pathologist experiment are shown in Fig. 6. Varying the ground truth had a substantial effect on both the median AUC as well as the extent of the inter‐site‐variability. MEADC, DK, and K values calculated from observer 5's annotations had the greatest AUC and tightest range of AUC between sites at differentiating cancer from regions left unlabeled by all pathologists (unlabeled consensus). Numeric results are shown in Table S8 in the Supplemental Material. The AUCs from BID varied by observer showed consistency between site implementation with the exception of a few outliers, while BID* and F both showed large ranges of AUC regardless of the observer defining ground truth.

FIGURE 6.

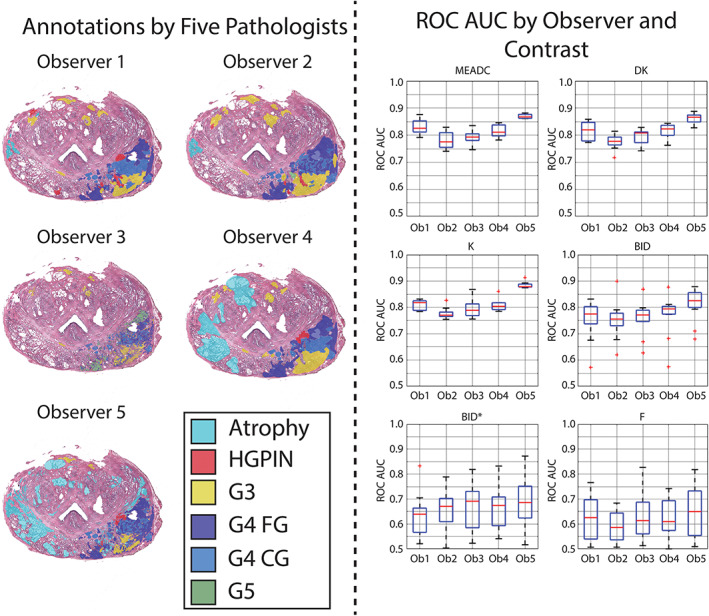
Area under the curve receiver operator characteristic (ROC AUC) for cancer vs. regions left unlabeled by all pathologists (unlabeled consensus) annotations varying the pathologist annotating the slides. Left: Sample annotations from all five observers on a representative whole‐mount prostate slide. Right: Boxplots showing AUCs varying the image contrast and observer annotating the slides. Median values were extracted from regions of interest (ROIs) greater than 200 voxels in plane.

Discussion

This study tested inter‐site concordance of diffusion‐derived parametric maps on the same pathologically validated prostate cancer dataset under a variety of post‐processing conditions. In addition to measuring the consistency of values between sites, inter‐site variability in performing a diagnostic task was measured. We found that mono‐exponential and kurtosis diffusion models were reliably calculated independent of implementation (high correlation between site implementations) and performed well at differentiating prostate cancer (consistently high ROC AUC between implementations). Values calculated from IVIM algorithms varied more between sites (low correlation between site implementations, large range of ROC AUC between sites), although those that applied physical constraints performed better at differentiating prostate cancer (high ROC AUC). In addition, we found that post‐processing decisions made at the central analysis site such as ROI sizes and varying the observer defining ground truth, affected the diagnostic potential of all DWI parametric maps, as measured by ROC AUC.

The correlation analysis demonstrated the stability of each fit across sites. The mono‐exponential and kurtosis fits had a low percent difference and high correlation coefficient independent of which pair of sites was analyzed. Of the diffusion fits included in this study, six MEADC fit implementations resulted in almost identical maps and values. Kurtosis was likewise consistent across institutions and provided as good or better contrast than ADC with respect to identifying high‐grade tumors. The IVIM contrasts were much less similar between implementations, both in normal and cancerous regions.

A number of post‐processing parameters were tested. Varying the minimum lesion size included in the analysis caused approximately 0.1 increase in AUC independent of contrast and site implementation. With the exception of this analysis explicitly testing size, an ROI cluster limit of 200 voxels (11 mm²) was selected to capture all clinically significant tumors as outlined in PI‐RADSV2. For DWI acquisition, typical cluster sizes are only 2–15 acquired voxels, highly susceptible to partial volume at lesion boundaries. ⁶ However, anatomical boundaries are more clearly seen in T₂ imaging, and thus aligning the annotations with the T₂ images results in a more accurate alignment. This limitation partially explains cluster‐size sensitivity of the corresponding lesion AUC analysis for DWI‐derived parameters.

Prior work measuring inter‐pathologist variability annotating Gleason patterns has been done on tissue microarrays, ³⁴ , ³⁵ and in whole‐mount prostate samples. ¹⁵ Interestingly, varying the pathologist performing the gold‐standard annotations changed the resulting ROC AUC in the contrasts that varied minimally between site implementations (MEADC, K, and DK). While in most cases observers marked similar areas overall, the size and boundaries of the lesions varied between observers as expected. Partial volume and lesion size limitations resulted in different numbers of ROIs included from each pathologist, which may partially explain the differences in ROC AUC.

The b‐values used to calculate the IVIM fits varied between implementations. Additionally, some sites chose to apply post‐calculation filters such as upper and lower bounds, non‐negativity constraints, or other error reduction techniques on their parameter maps to ensure physical values. Those that included physical constraints and other post‐fitting filters had the highest ROC AUC (sites 2, 3, 5, 7, and 10). The b‐values used in the DWI fitting also varied in the implementations of K, DK, and MEADC at different sites. This variability in implementation may explain why some sites MEADC values were consistently higher than others, though the ability to differentiate cancer was not adversely affected with MEADC.

The top performing site implementations for MEADC varied only slightly, so no general recommendations can be made by our conclusions. For the IVIM submissions, in general, the sites that chose to implement constraints on the values calculated performed better due to having less outlier values. The choice of b‐values included in the fitting did not appear to affect the top performing implementations, as there was a mix of submissions that used all provided b‐values, and those that limited the b‐values included in fitting. Regarding kurtosis, the top performing implementations used all b‐values provided, but generally all performed similarly so no consensus recommendations can be offered beyond constraining values.

Limitations

One major limitation to this study is the relatively small cohort of 33 patients. We felt there was a balance between including a larger cohort and increasing the analysis burden on the external sites. Future studies should increase the N and reduce the scope to less fitting models. Regarding the patient cohort, there were wide ranges in the PIRADS scores, Gleason scores, and PSA levels, and there may be potential bias as all the subjects included had a prostatectomy. While this was essential for the pathological validation, our conclusions may not generalize to patients that, for example, undergo radiation treatment rather than surgery. Future studies should determine whether DWI performance between sites varies dependent on PIRADS score, Gleason score at diagnosis, and National Comprehensive Cancer Network risk stratification, as these analyses were beyond the scope of this study. Unfortunately, with our small cohort, we were statistically under powered to split it into smaller subgroups. Additional future studies should determine whether cancer detection varies between repeated pre‐surgical quantitative DWI, both in the same scanner, and between vendors.

Anatomical landmarks are more readily apparent on the higher resolution T₂‐weighted images and thus using T₂ space for an analysis using aligned pathology is the best practice for creating a reliable ground truth. However, efforts to convert, align, scale, and resample the diffusion maps to the T₂ resolution for comparison to the ground truth pathologist annotations may have introduced minor alignment differences between submissions. These potential sources of error should be mitigated in the future with a consensus on data format and orientation standards for large multicenter research studies.

Conclusion

This study tested inter‐site concordance of diffusion‐derived parametric maps on the same pathologically validated prostate cancer dataset under a variety of post‐processing conditions. We found that conventional diffusion models (mono‐exponential and kurtosis fits) had less variability between algorithms in differentiating prostate cancer and performed significantly better overall. More complex IVIM models, in some implementations, also performed well at differentiating prostate cancer, although were more inconsistent between algorithms due to varying constraints and resulted in non‐diagnostic AUCs of less than 0.70. We also found that post‐processing decisions made at the central analysis site affected the diagnostic potential of all DWI parametric maps, as measured by ROC AUC. These results indicate that a careful selection, explanation of methods, understanding of their effects on the ROC AUC, and code sharing will ease the adoption of advanced quantitative imaging into the clinical setting.

Conflict of Interest

Author KMS has ownership interest in IQ‐AI and financial interest in Imaging Biometrics LLC.

Supporting information

Appendix S1. Supporting Information