Abstract
Multispectral photoacoustic (PA) imaging faces two major challenges: the spectral coloring effect, which has been studied extensively as an optical inversion problem, and the spectral crosstalk, which is basically a result of non-ideal acoustic inversion. So far, there is no systematic work to analyze the spectral crosstalk because acoustic inversion and spectroscopic measurement are always treated as decoupled. In this work, we theorize and demonstrate through a series of simulations and experiments how imperfect acoustic inversion induces inaccurate PA spectrum measurement. We provide detailed analysis to elucidate how different factors, including limited bandwidth, limited view, light attenuation, out-of-plane signal, and image reconstruction schemes, conspire to render the measured PA spectrum inaccurate. We found that the model-based reconstruction outperforms universal back-projection in suppressing the spectral crosstalk in some cases.
Keywords: Multispectral photoacoustic imaging, Quantitative photoacoustic imaging, Photoacoustic image reconstruction, Photoacoustic computed tomography, Optoacoustic computed tomography, Spectral crosstalk
1. Introduction
PA imaging (PAI; alternatively, optoacoustic imaging) combines the penetration depths of ultrasound with light absorption contrasts [1], [2]. In principle, by scanning the wavelength of the excitation light in PAI, the absorption spectra of intrinsic biological substances and extrinsically administered contrast agents can be measured, and then the material composition can be imaged by spectral unmixing [3], [4], [5]. One representative application is the imaging of blood oxygen saturation (sO2) [6], [7], [8].
Unlike traditional spectroscopic imaging, where the spectrum of the excitation light is known a priori, in PAI the excitation spectrum inside deep tissue is affected by the wavelength-dependent tissue absorption and scattering, thus becoming unknown [9]. Termed the “spectral coloring effect”, the above problem has been tackled using model-based iterative method [10], [11], [12], deep learning [13], [14], [15], [16], [17], eigenspectra decomposition [15], [18], [19], and other methods [20], [21], [22], [23], [24], [25]. All methods implementing spectral unmixing have to assume that the PA spectra at all image pixels or voxels are accurately measured in the first place. In PA imaging, image artifacts are produced by non-ideal PA signal detection, including limited angular acceptance, limited view, limited bandwidth, insufficient spatial sampling, etc. Here, we use “limited angular acceptance” to refer to the limited detection view perpendicular to the imaging plane. The effective thickness of the imaging plane (i.e., elevational resolution) is determined by the geometric focus of the transducer elements, such as in linear and ring arrays. In such imaging systems, an in-plane signal acceptance less than 360° is referred to as “limited view”. Since these artifacts are generated acoustically, they seem to be independent of the optical wavelength. As a result, people may assume that spectral unmixing techniques can still be applied, in the presence of the above-mentioned acoustic artifacts.
Upon scrutiny, however, the problem is more intricate and the assumption that the deficiencies in acoustic detection are decoupled with the wavelength of the excitation light is wrong. Our study has shown that the various types of image artifacts commonly encountered in PA imaging do induce spectral crosstalk (defined below) between even remotely separated points. In communication, “crosstalk” refers to the phenomenon by which a signal transmitted on one channel creates an undesired effect in another channel. Here, we use the term “spectral crosstalk” to refer to the phenomenon by which the spectrum of one pixel or voxel is affected by the spectra of other pixels or voxels in PA imaging. In the following text, we used “PA spectrum” to refer to the initial pressure spectrum and “reconstructed PA spectrum” to refer to the spectrum of the reconstructed PA images. The consequence is that the measurement of the PA spectrum is intrinsically inaccurate (the reconstructed PA spectrum is different from the PA spectrum), even in the absence of noise. The mechanism of the spectral crosstalk is complicated and system-dependent. Up to now, acoustic inversion methods for PA image reconstruction have been extensively studied [26], [27], [28], [29], [30], [31], [32], [33], [34], [35], [36], [37], [38], [39], [40], [41], [42], [43], [44], [45], [46]. Some of them touched on the connection between non-ideal acoustic reconstruction and PA spectrum distortion: Kazakeviciute et al. proposed a strategy to reduce the influence of random noise and artifacts on the PA spectrum, in which the artifacts were unified into statistical “noise” and removed by a statistical signal processing method [34]; Prakash et al. proposed a model-based reconstruction method with nonnegative constraint and showed its effect on the reconstructed PA spectrum [39]; Li et al. analyzed and proposed a method to suppress the spectral error caused by sparse sampling [43]. But as far as we know, there is no systematic research to analyze the influence of the imperfect acoustic inversion on multispectral PA imaging. In this work, we will build a mathematical model for the spectral crosstalk phenomenon, and employ numerical simulations to exemplify and quantitatively analyze the contribution of various factors. Our conclusions were validated using phantom experiments. We also compared the performance of a model-based (MB) algorithm [47] and the BP algorithm in terms of spectral reconstruction accuracy. When the model is reasonably accurate, the MB method can effectively reduce the spectral crosstalk caused by limited angular acceptance, but for the crosstalk caused by other factors, it has no obvious advantage. In addition, different constraints were employed in the MB method to test their performance in suppressing the spectral crosstalk.
2. Methods
2.1. Mathematical model
In the framework of BP, delay and sum (DAS) [48] or MB reconstruction (in which the iteration step is fixed, without constraint), the excitation, propagation, acquisition, and reconstruction of the PA signal are a series of linear processes, which can be represented using the following equations:
| (1) |
| (2) |
where is the initial pressure distribution (here the initial pressure distribution in 3D space is reshaped into a column vector) and is the corresponding reconstructed image at the n-th wavelength. is the total number of wavelengths. is the reconstruction process. E is the receiving process with the acousto-electric impulse response (EIR) of receiving transducer included, and H is the PA wave propagation process, in which the spatial impulse response (SIR) of the receiving transducer is considered. The reconstruction process and results in this work are acoustic reconstructions, optical inversion is not considered in this work. For the BP or DAS reconstruction, can be discretized into a matrix; for the MB reconstruction when the gradient descent method is used: ,where is the raw PA data, is the result of the j-th iteration and is the step size. If the initial value is set to 0, , then can be expressed as matrix where J is the number of iterations and . Both and are independent of the excitation wavelengths. The case of multispectral imaging can then be compactly written as:
| (3) |
The PA spectrum at a fixed position corresponds to one row in the I matrix, denote that position using index m:
| (4) |
Then, the reconstructed PA spectrum at the same position can be expressed as:
| (5) |
In the above equation, both and k are position indices, K is the total number of positions in a PA image. is jointly determined by the absorption spectrum and the illumination spectrum at the same position, is determined by PA signal propagation, detection, and reconstruction. At the same time, is the (m, k) element of matrix A. We define as the crosstalk coefficient quantifying the severity of spectral contamination at position m due to the spectrum at position k, and as the m-th position’s crosstalk component contributed by all other positions. For an ideal reconstruction, the reconstructed PA spectrum is consistent with the initial pressure spectrum. Mathematically, for all pixel index m.
To illustrate how data acquisition and image reconstruction affect the value of crosstalk coefficient , we numerically calculated matrix under non-ideal detection conditions, including limited angular acceptance, limited bandwidth, limited view, and sparse spatial sampling. To construct matrix , matrix H was generated by the CDMMI method [47], the convolution process of EIR and the PA signal was represented by matrix E. For the BP reconstruction, the reconstruction process was written in matrix form. For the MB reconstruction, we took as 1000 and s as 0.1. The initial pressure distribution was discretized into a matrix, with a pixel size of 0.1 mm. The speed of sound was set to 1500 m/s, the PA signal was sampled at 40 MHz with 1200 sampling points. Several identical point transducers were evenly arranged on the circle with a diameter of 50 mm. For a 128-channel array, H is a matrix with 153,600 () rows and 40,401 () columns, E is a matrix with 153,600 () rows and 153,600 () columns, and R is a matrix with 40,401 () rows and 153,600 () columns. According to (1), (2), matrix A represents the linear mapping from the initial pressure distribution ( vector) to the reconstructed PA distribution ( vector). The m-th row of A represents the crosstalk coefficients of pixel m due to the contamination by all image pixels; the m-th column of A represents the crosstalk coefficients of all pixels due to the contamination by pixel m.
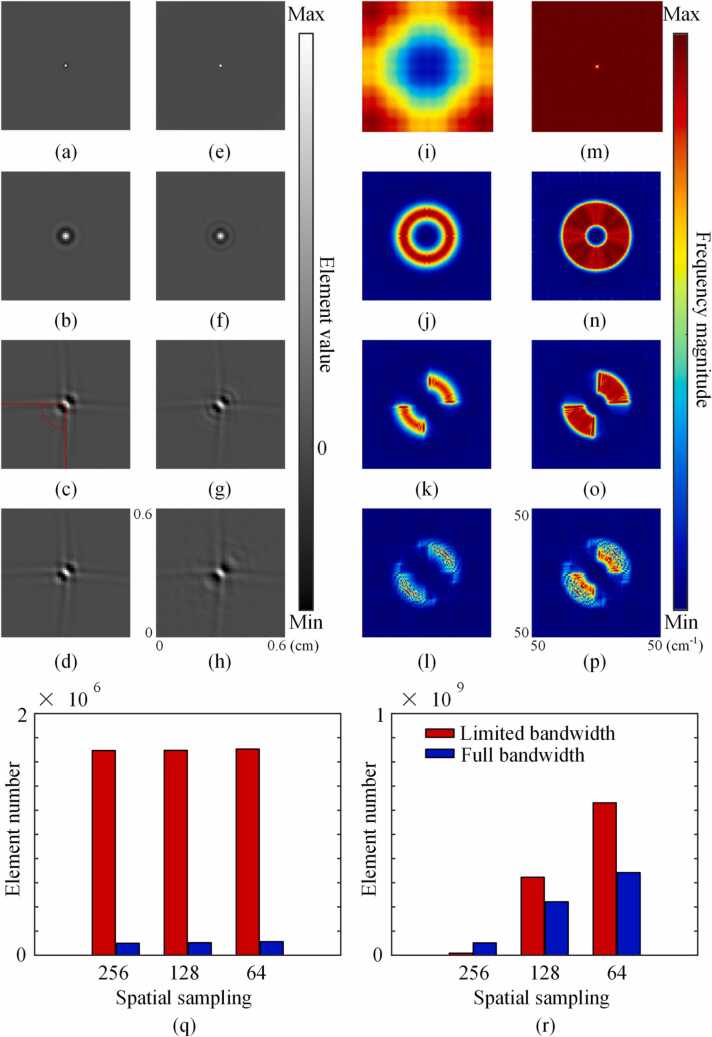
We numerically calculated matrix A corresponding to 360° view 64-, 128- and 256-channel arrays, both with a finite bandwidth (2.5 MHz center frequency, 75% bandwidth) and without any bandwidth limit; We also calculated matrix A corresponding to 90° view, 32- and 64-channel arrays, with a finite bandwidth (2.5 MHz center frequency, 75% bandwidth). Because matrix A is too large (), we just studied its 20,201st column which is a vector representing the crosstalk coefficients at all image pixel due to the 20,201st pixel. is proportional to the linearly-reshaped PSF of the 20,201st pixel. To convert back into a matrix that directly represents a 2D image, we normalized by , and reshaped into a matrix L, in which the largest element was L(101,101), as shown in Fig. 1(a).
Fig. 1.
Numerical simulation of the matrix A. (a) to (h) are maps of based on back projection (BP) reconstruction or model-based (MB) reconstruction with different conditions: (a-d) Maps of based on BP reconstruction, (e-h) Maps of based on MB reconstruction. (a, e) 256 transducers, 360° view, no bandwidth limit; (b, f) 256 transducers, 360° view, with bandwidth limit; (c, g) 64 transducers, 90° view, with bandwidth limit, dashed lines in (c) mark the angular range of detection; (d, h) 32 transducers, 90° view, with bandwidth limit. (i) to (p) are the magnitude parts of the Fourier transform of (a) to (h). (q) Amount of element whose value is greater than 0.1 in matrix A under different spatial sampling conditions based on BP reconstruction. 64/128/256 transducers, 360° view, with/without a bandwidth limit. (r) Amount of element whose value is greater than 0.01 and less than 0.1 in matrix A under different spatial sampling conditions based on BP reconstruction. 64/128/256 transducers, 360° view, with/without a bandwidth limit.
The value of L based on BP reconstruction is shown in Fig. 1(a-d), whose corresponding Fourier transform is shown in Fig. 1(i-l). In the ideal situation, only L(101,101)is non-zero, meaning that an artifact-free image is reconstructed (only a bright pixel in the center). However, due to the limited angular acceptance in the direction perpendicular to the imaging plane, the crosstalk coefficients between pixel (101,101) and the surrounding pixels became prominent. As shown in Fig. 1(a), some negative values appeared surrounding pixel(101,101). In the frequency domain, it is shown as a high pass filter (Fig. 1(i)). If a limited bandwidth is further imposed, the distribution of the crosstalk coefficients becomes wider and their amplitudes become larger (Fig. 1(b)). So far, the amplitude and distribution of the crosstalk coefficient are characterized by high value, short-range, and are insensitive to the spatial sampling frequency. Then, a quarter-ring was applied for signal detection (with the sensor density unchanged). Fig. 1(c) shows the crosstalk coefficient map under this limited-view scenario (dashed lines mark the angular range of detection). In this case, a “cross” pattern appeared whose shape was defined by the angular span of the array with respect to the field point. Finally, we further reduced the number of detectors by half, this produced stronger streak artifacts as shown in Fig. 1(d). The crosstalk created in the last two cases was relatively weak, long-range, and was sensitive to the spatial sampling frequency. In order to better illustrate the characteristics of the above different types of crosstalk, we analyzed the off-diagonal elements in matrix A (the crosstalk coefficients). We classified the off-diagonal elements whose absolute value was greater than 0.1 (the m-th column in matrix A was normalized by the element A(m, m)) into one category, and those whose absolute value was between 0.01 and 0.1 into another. As shown in Fig. 1(q-r), the number of the first category was relatively small which was very sensitive to the frequency bandwidth but hardly affected by the spatial sampling frequency. It corresponds to the non-zero crosstalk coefficients generated by limited angular acceptance and limited bandwidth in Fig. 1(a-b). The second category had a large number which was closely related to the spatial sampling frequency, corresponding to the crosstalk coefficients generated by sparse spatial sampling. As for the MB reconstruction, it can satisfactorily reduce the crosstalk coefficients due to limited angular acceptance, as shown in Fig. 1(e, m). The non-zero crosstalk coefficients imposed by limited bandwidth were also reduced due to the addition of EIR in the model matrix . For the non-zero crosstalk coefficients generated by limited view and sparse sampling, MB did not perform obviously better than BP (although the distributions in Fig. 1(o-p) are broader that those in Fig. 1(k-l), there are little differences in their angular range). The information loss in the angular direction is the main cause of the error due to limited view and sparse sampling, and MB does not outperform BP in supplementing the lost angular information.
The existence of the off-diagonal element in matrix A is the physical basis of spectral crosstalk, and is determined by the PA detection and reconstruction methods. However, in actual imaging, the degree of spectral crosstalk at a certain position does not depend entirely on , but is closely related to the distribution of initial pressure () in the field of view. To facilitate the analysis of spectral crosstalk, we define the ratio between the lengths of the normal and parallel components with respect to as to measure the degree of spectral crosstalk at position m:
| (6) |
| (7) |
According to the definition, in the extreme case when the spectral information of a position is lost, is close to infinity. When is close to 0, the reconstructed spectrum has a strong correlation with the initial spectrum. As discussed above, is determined by the imaging system and the reconstruction algorithm, which will influence . However, is further affected by the object being imaged. For a simple example, a disk and a point target were placed in the ring array imaging system. The center of the disk and the point target were rotationally symmetric with respect to the center of the field of view (FOV). The two targets had the same initial pressure. After reconstruction, the brightness of the center point of the disk target was weaker than that of the point target, despite due to symmetry, of the two positions were the same. The reason for the above discrepancy was that the center of the disk was affected by the crosstalk components from adjacent points (i.e., corresponding crosstalk coefficients due to the limited angular acceptance or limited bandwidth, as shown in Fig. 1(a-b)). With the formula (5), (6), (7), spectral crosstalk becomes evident when two conditions are met:
Condition 1: Deficient acoustic detection to cause coupling between different locations, according to (5).
Condition 2: In the reconstructed image, the signal strengths of the pixels with different PA spectra are dramatically different. Here, signal strength refers to the “apparent brightness” of a feature in a reconstruction image. The weak features always have small or , so strong features contaminate weak features more easily according to (6), (7).
2.2. Simulation platform
2.2.1. Transducer arrays
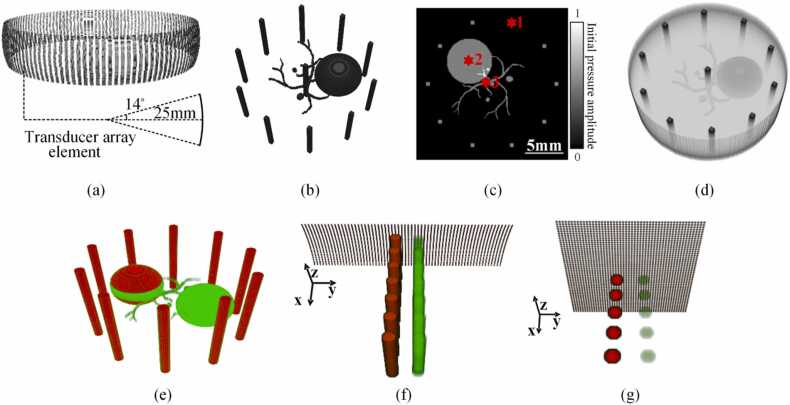
To better elucidate how various factors generate spectral crosstalk, we performed numerical simulations based on ring array, linear array, and planar PACT system. The ring array system consists of 256 transducers which are evenly distributed on a circle (diameter: 50 mm) and focused in the elevational direction (see Fig. 2(a)). The focal length of the transducer is 25 mm and its elevational numerical aperture is 0.25, leading to an elevational resolution of 1.6 mm at the center frequency of 2.5 MHz. For the linear array, we used the same transducer elements as in the ring-array simulation. 128 transducers were evenly arranged in a straight line with an inter-element spacing of 300 µm. For the planar array, 50 × 50 point transducers were evenly distributed in a plane, with an inter-element spacing of 200 µm.
Fig. 2.
Schematic diagrams of the transducer arrays and the digital phantoms. (a) Ring transducer array. (b) 3D illustration of Phantom 1. (c) Central section of Phantom1. (d) 3D illustration of Phantom2. (e) 3D illustration of Phantom 3. (f) 3D schematic of the linear array (only shows the sensing elements) and Phantom 5. (g) 3D schematic diagram of the planar array and Phantom 6. The red stars in (c) represent the positions of the analysis in Section 3.1.4 (for details see text).
2.2.2. Digital phantoms
Six digital phantoms were designed to study the relationship between the non-ideal signal detection or reconstruction methods and spectral crosstalk.
Phantom 1: The object consisted of eleven cylindrical targets lying perpendicular to the imaging plane. The diameter of the cylinders was 0.6 mm. Ten of them were evenly arranged on a circle with a diameter of 8.5 mm, and one was located in the center of the FOV. A vessel-like PA target was located in the imaging plane. A big sphere with a diameter of 6 mm and three small spheres with diameters of 0.3 mm, 0.5 mm, 0.8 mm were placed next to the vessel target, with their mid-planes aligned with the imaging plane. The initial pressures on all targets were shown in Fig. 2(b). Fig. 2(c) depicts the distribution of the targets in the imaging plane.
Phantom 2: The effect of light fluence attenuation was taken into account in this phantom experiment. In this case, the absorptive targets shown in the previous example (Fig. 2(b)) were embedded in a cylinder background with a diameter of 20 mm, as shown in Fig. 2(d). The cylinder had uniform scattering and absorption properties, defined by a reduced scattering coefficient of 11 cm−1 and an absorption coefficient of 0.3 cm−1 [49], [50]. The absorption coefficient of the targets was 1.3 cm−1 [49], [50] which is similar to that of the mouse liver. 564 isotropic point light sources are evenly distributed on the outer rim of the cylinder at three different heights (0, 2, and 4 mm from the imaging plane). The three-dimensional fluence distribution was obtained by Monte Carlo simulation [51]. In this phantom, only the absorptive targets shown in Fig. 2(b) generated PA pressure which was the product of their absorption coefficient and the local light fluence. The absorber of the cylinder background was used to attenuate the light fluence.
Phantom 3: To better quantify the spectral crosstalk caused by in-plane and out-of-plane artifacts, another phantom for multispectral imaging was designed. We modified Numerical Phantom 1 in Fig. 2(b) such that two 6 mm-diameter spheres, instead of one, were put in the FOV. In Fig. 2(e), green represents deoxyhemoglobin, and red is oxyhemoglobin; the concentrations of oxyhemoglobin and deoxyhemoglobin were equal. In particular, one of the spheres exhibits a sandwich structure, where the thickness of the deoxyhemoglobin slice in the middle is 1.6 mm-thick (which is the same as the elevational resolution of the system at the center frequency of 2.5 MHz). While Phantom 1 and 2 were used for the single-wavelength test, Phantom 3 was designed for the multispectral test ranging from 700 nm to 900 nm.
Phantom 4: Phantom 4 is modified from Phantom 3, which only retained the middle 1.6 mm-thick slice of Phantom 3, which includes the middle 1.6 mm-thick slice of the two spherical targets, the whole vessel-like target, and the middle 1.6 mm-thick slice of the cylindrical targets.
Phantom 5: For linear array simulation, two columns of identical cylindrical targets (each column contains 8 targets) were positioned at different depths, all of them were perpendicular to the imaging plane, as shown in Fig. 2(f). Red and green represent oxyhemoglobin and deoxyhemoglobin, respectively; the concentration of oxyhemoglobin was four times that of deoxyhemoglobin.
Phantom 6: For planar array simulation, the PA targets were identical spheres with a diameter of 1 mm placed at different depths, as shown in Fig. 2(g). Red and green represent oxyhemoglobin and deoxyhemoglobin, respectively; the concentration of oxyhemoglobin was four times that of deoxyhemoglobin. Phantom 5 and Phantom 6 were used for the multispectral test, similar to Phantom 3. For Phantom 3–6, light attenuation inside the phantoms was not considered – the initial PA pressure was evenly distributed within each target with its value defined by the hemoglobin concentration.
2.2.3. Simulation of the forward process
All PA forward data was generated by k-Wave [52], which is a MATLAB toolbox in which the properties of the transducers and the digital phantoms can be easily defined. In this study, the grid was set to 0.1 mm and the sampling rate was 40 MHz. The medium was assumed to be homogeneous with a speed of sound of 1500 m/s, which is close to that of water at room temperature. For the curved transducer mentioned in Section 2.2.1, we divided each of its element into point transducers. The signal received by each point detector was obtained with k-Wave, then for each curved element, we summed over all point detectors to obtain the overall signal of that element.
When the light fluence attenuation was taken into account, the three-dimensional fluence distribution was generated by MCXLAB [51], which is a MATLAB toolbox for light fluence calculation. In the toolbox, the absorption and scattering distributions as well as the surface light intensity distribution can be set arbitrarily.
2.3. Phantom experiment
A phantom experiment was performed to demonstrate the existence of the spectral crosstalk and verify our analysis. As shown in Fig. 3, three weakly absorbing disks were positioned near the center of the field of view (FOV), the diameter of the disks varied from 1 mm to 3 mm. Ten strongly absorbing disks with diameters of 1 mm were evenly distributed on a circle with a radius of 8.5 mm. To avoid the difficulty of controlling the blood oxygenation precisely, we selected black ink as the chromophore of the central disks, and the surrounding small disks were stained with blue ink. At 700 nm, the absorption coefficient of the blue ink was 6 times that of the black ink. So, the blue ink will be the main source of spectral crosstalk. We made the agar phantom into two pieces such that the outer “contaminators” could be removed or included, as shown in Fig. 3(a) and (b), which allowed the spectral crosstalk to be switched on and off easily. We refer to “spectral crosstalk” in this experiment as the crosstalk components from the surrounding “contaminators”, excluding the crosstalk components from the central disks themselves since their influences are much weaker. A 256-channel focused ring array was used for PA signal detection. The system employed an OPO laser (SOLAR LP604) with a 10 ns pulse width and 10 Hz repetition rate for PA excitation. The laser beam was coupled into a customized fiber bundle to provide uniform illumination around the imaged object. A full-ring ultrasound array (Imasonic Inc., 256 elements, 5.5 MHz central frequency, 60% bandwidth) was used for PA signal detection. The radius of the ring array was 50 mm, the focal width (elevational resolution) inside the imaging FOV was roughly 1 mm, and the thickness of all the targets was 1 mm. Two customized preamplifiers with 20 dB gain were directly connected to the ring array, the output of the preamplifiers was further amplified by 40 dB and sampled at 40 MHz using two data acquisition units (Analogic Corp., SonixDAQ).
Fig. 3.
Photos of the experimental phantom. (a) The complete phantom. (b) The same phantom without the surrounding contaminators.
We first took PA images without the surrounding contaminators, at eleven wavelengths evenly distributed from 700 nm to 800 nm. This image acquisition process was repeated after the second piece of agar containing the contaminators was added. Wiener filter was used to remove the influence of EIR in the original PA signal.
Next, we compared the degree of spectral crosstalk of the center disks under BP and MB reconstructions. Denoting as the reconstructed PA spectrum with the surrounding “contaminators” (spectral crosstalk “on”), and as the reconstructed PA spectrum without the “contaminators” (spectral crosstalk “off”), a mask was added to ensure that remained positive at all wavelengths.
2.4. Reconstruction methods
As we have discussed in Section 2.1, the spectral crosstalk encountered in PA tomography is fundamentally due to the non-ideal signal detection which renders the acoustic inversion problem ill-posed. In different imaging scenarios (i.e., different detection geometry, sensor property, and object property, etc.), the performance of different reconstruction algorithms varies, thus the severity of spectral crosstalk must rely on the reconstruction method being used. Here we provide examples to illustrate how the spectral crosstalk can be suppressed by properly choosing or modifying the image reconstruction algorithm. Nevertheless, an analysis which comprehensively considers all available algorithms and all possible combinations of detection schemes and object properties can be too lengthy and beyond the scope of this work, so we confine ourselves to discussing only BP and one type of MB method with simple numerical phantoms.
In order to reduce the influence of spectral crosstalk, we propose two strategies: (1) Identify the positions with large and suppress the corresponding . This method can be easily implemented in the BP algorithm but will artificially alter A to potentially degrade image fidelity. (2) Optimize A to approach an identity matrix, which will ultimately eliminate any inter-pixel crosstalk. The iterative MB approach is inherently suitable for this task. At the same time, in the MB reconstruction, one can easily add regularization terms. After adding the regularization terms, the reconstruction process can no longer be expressed in a matrix format, so we used a numerical phantom to verify the role of these regularization terms in suppressing the spectral crosstalk.
2.4.1. Back-projection reconstruction
Cai et al. proposed a method similar to the strategy (1) to remove the streak artifact by suppressing the projection curves generated by strong light absorbers [53]. The method is effective, but its limitations are also obvious: First, true image features can be incorrectly identified as artifacts and get suppressed; second, the choice of the suppression ratio is subjective; third, this method is only applicable to crosstalk generated by sparse sampling, and may result in image quality degradation. Therefore, we didn't implement the corresponding method of strategy (1), but directly used the standard back-projection algorithm.
2.4.2. Model-based reconstruction
Many studies have proven that MB image reconstruction provides higher accuracy and image quality [26], [28], [29], however their immunity to spectral crosstalk has not been quantitatively studied before. Here, we compare the performance of the BP and the MB reconstruction (with and without regularization) in terms of spectral recovery accuracy. We used a model matrix built with the CDMMI method [47] in the MB method. The optimization problem in the MB reconstruction can be expressed as:
| (8) |
| (9) |
where is the raw PA data, is the initial pressure vector to be solved, is the estimation of , and are regularization parameters. is the matrix element of (PA image). Here, we considered TV regularization and Tikhonov regularization . Considering the non-negative characteristics of the initial pressure values, non-negative constraints can be added:
| (10) |
In this case, the iterative method is no longer a simple gradient descent, but a projected gradient method. When x migrates to the boundary position, it will advance according to the projection of the negative gradient along the boundary.
2.5. Relative spectral error
In Section 2.1, we defined and to illustrate the relationship between the degree of spectral crosstalk and PA detection, reconstruction and imaging targets. But is complex to calculate. We define an almost equivalent and more concise quantitative value "relative spectral error" to measure the difference between the reconstructed PA spectrum and the ground truth spectrum. The definition of the "relative spectral error" is as follows:
| (11) |
where and represent the reconstructed and the ground truth PA spectra, respectively, both evaluated at position . The relative spectral error defined above was used in all simulation and phantom experiments.
3. Results
3.1. Influence of non-ideal signal detection
In Section 2.1, we introduced the mechanisms of spectral crosstalk, now we analyze a variety of contributing factors and use three representative PACT systems to further exemplify the problem. We employ rigorous simulations to reach conclusions quantitatively. In this section, the BP reconstruction was adopted.
3.1.1. Limited angular acceptance and limited bandwidth
The first factor considered here is the limited angular acceptance. The receiving angle of a real PA imaging system is always limited, as shown in Fig. 2(a), which results in differential reception of signals from different parts of an object. For example, the PA wave emitted by a cylindrical target is mainly in the direction perpendicular to the target. If acoustic detection is focused in one plane, a cylindrical target (e.g., blood vessel) may appear brighter perpendicular to the image plane, than lying in the plane. As a result, limited angular acceptance not only contributes to Condition 1, but it may also give rise to Condition 2. Limited detection bandwidth also contributes to spectral crosstalk. To see this, consider the simplest case of a spherical target, the central frequency of its PA signal is [30].
| (12) |
where d is the diameter and is the speed of sound. Accordingly, a center frequency of 5 MHz corresponds to spherical absorbers with a diameter of 0.2 mm. Thus, a non-uniform frequency response suppresses image features that are significantly smaller or larger than 0.2 mm. As such, similar to limited-view detection, a limited detection bandwidth subjects the system to both Conditions 1 and 2.
3.1.2. Out-of-plane crosstalk
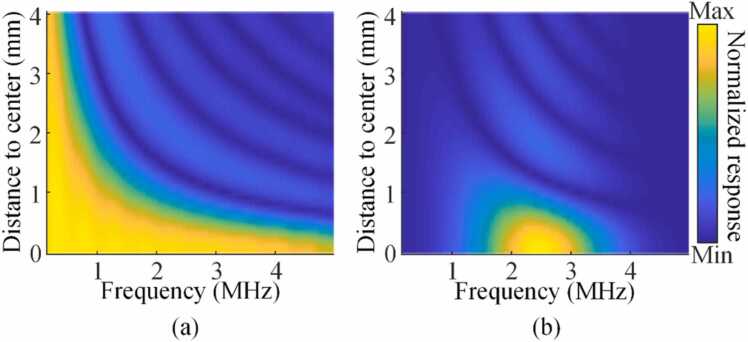
For focused transducers, the focusing capability is directly related to the frequency. The relationship between the −6 dB focal width and the acoustic wavelength is as follows [30]:
| (13) |
where is the focal length and is the aperture size of the transducer. While in PA imaging, people often try to increase the detection bandwidth for better image fidelity (this helps reduce spectral crosstalk by increasing , thus simultaneously alleviates Condition 1 and 2), yet as more low-frequency components are received, the sectioning capability of the system drops such that one always measures a blended spectrum by integrating along the elevational direction. Fig. 4 shows the frequency response of the transducer (a single transducer element in Fig. 2(a)) with a spherical target placed at different elevational heights, the two cases of infinite and finite (center frequency: 2.5 MHz, −3 dB bandwidth: 75%) receiving bandwidth were considered. The k-Wave toolbox and a ball target whose diameter was 100 µm were used to simulate the response. Even for an ideal transducer with infinite bandwidth, at low frequencies, the sectioning capability was almost lost which was bound to induce serious out-of-plane spectral crosstalk.
Fig. 4.
The relationship between spatial response and frequency bandwidth of the transducer. (a) Spatial response of transducer with infinite receiving bandwidth. (b) Spatial response of transducer with limited receiving bandwidth (center frequency: 2.5 MHz, −3 dB bandwidth: 75%).
3.1.3. Light attenuation
Biological tissues exhibit strong scattering and absorption, resulting in the rapid decrease of light intensity along the depth direction. For example, shallow blood vessels are often much brighter than deeper ones after reconstruction (without digital fluence compensation), thus generating spectral crosstalk due to Condition 2. Compared with bright field illumination, dark field illumination can make the cross-sectional fluence distribution more uniform, at the cost of potentially greater spectral coloring and out-of-plane artifacts.
3.1.4. Spectral crosstalk in different detection geometries
3.1.4.1. Ring array
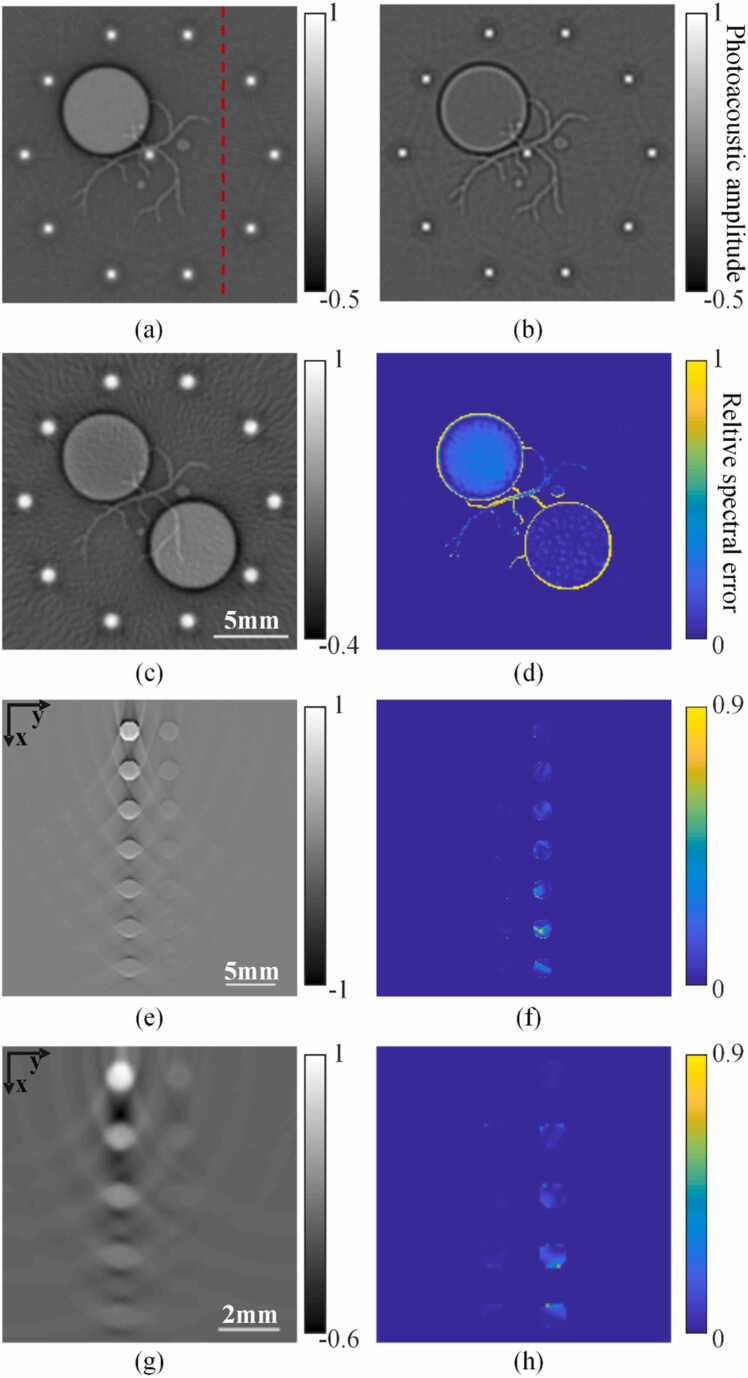
The ring array is shown in Fig. 2(a). At first, we neglect light fluence attenuation and Phantom 1 in Fig. 2(b) was used. Fig. 5(a) and (b) show the reconstructed images under full and limited bandwidth (center frequency: 2.5 MHz, 3 dB bandwidth: 75%). Quantitative analysis was carried out at three positions (Fig. 2(c)). As shown in Table 1, in the case of full bandwidth, the perpendicular vessels were 30 times brighter than the in-plane vessel; more strikingly, in the case of limited bandwidth, the perpendicular vessels were 70 times brighter than the inner region of the big sphere. Next, we considered the effect of light fluence attenuation and Phantom 2 was used. Table 2 shows the initial pressure at the three test locations (Fig. 2(c)), from which the influence of light attenuation and illumination scheme can be clearly seen. The above simulations show that even with the same absorption coefficient, the brightness of different objects may appear dramatically different due to a variety of reasons. To make things worse, the absorption of biological tissue is spatially inhomogeneous, which tends to exacerbate spectral crosstalk due to Condition 2. Spatial sampling plays an important role in causing spectral crosstalk. To show this, we used Phantom 1 and set the sensor number to 32, 64, 128 and 256. We estimated the severity of signal crosstalk by calculating the standard deviation of the pixel value along the dashed line in Fig. 5(a), the results are shown in Table 3. Under various conditions shown in the tables, the listed values at Positions 1, 2, 3 and dashed line are relative, and we set Position 1 as the reference for normalization.
Fig. 5.
PA spectral crosstalk in three types of arrays. (a) Reconstructed image of Phantom 1 without transducer bandwidth limit. (b) Reconstructed image of Phantom 1 with transducer bandwidth limit. (c-d) Reconstructed image and relative spectral error of Phantom 3. (e-f) Reconstructed image and relative spectral error of Phantom 5 with the linear array system. (g-h) Reconstructed image and relative spectral error of Phantom 6 with the planar array system. The red dashed line in (a) represents the positions of the analysis in Section 3.1.4 (for details see text).
Table 1.
Influence of detection angle and bandwidth on feature brightness.
| Position | Absorption coefficient | Reconstruction |
|
|---|---|---|---|
| Full BW | Limited BW | ||
| 1 | 1 | 1 | 1 |
| 2 | 1 | 0.215 | 0.013 |
| 3 | 1 | 0.034 | 0.213 |
Table 2.
Influence of light attenuation on feature brightness.
| Position | Illumination height |
||
|---|---|---|---|
| 0 mm | 2 mm | 4 mm | |
| 1 | 1 | 1 | 1 |
| 2 | 0.0714 | 0.197 | 0.404 |
| 3 | 0.0526 | 0.155 | 0.380 |
Table 3.
Influence of spatial sampling density on crosstalk strength.
| Number of elements | 32 | 64 | 128 | 256 | |
|---|---|---|---|---|---|
| Full BW | 0.0787 | 0.0466 | 0.0207 | 0.0082 | |
| Limited BW | 0.0865 | 0.0621 | 0.0313 | 0.0096 |
Based on Table 1, Table 3, even in the case of sufficient sampling (256 channel), the amplitude of the crosstalk is comparable to that of some important features, no matter whether the influence of EIR is removed. According to Table 3, the crosstalk signal will increase sharply when the number of the spatial sample decreases. If light fluence attenuation is also taken into account, the situation will be even worse.
In order to better quantify the spectral crosstalk caused by in-plane and out-of-plane artifacts, Phantom 3 was adopted in the following test. In this simulation, full bandwidth signal reception was assumed. We adopted back projection for image reconstruction. Fig. 5(c) is the reconstruction result at 760 nm. Fig. 5(d) shows the distribution of the relative spectral error. According to Fig. 5(d), the spectral error of the sphere with the sandwich structure is still large. Apparently, the remaining error is due to the spectral leakage from the upper and lower parts of the sphere. At the same time, the spectral error of the in-plane blood vessel is also large, due to small value of with the limited angular acceptance of the ring array.
3.1.4.2. Linear and planar arrays
Linear arrays are commonly employed for clinical use. The transducer elements of the linear arrays are similar to those in the ring array (focused in one direction), so the problem of limited angular acceptance in the elevational direction also exists. In addition, the crosstalk caused by the limited-view detection in the lateral direction becomes a major factor to generate spectral crosstalk. The problem of fluence attenuation will be more serious due to the one-sided illumination. Another problem is that the numerical aperture in the lateral direction decreases with depth, consequently the brightness of the same target will decrease rapidly with depth after reconstruction (under uniform light illumination). The overall effect is that the signal strength decays very fast with depth in the image, thus deeper regions are prone to spectral crosstalk (both Condition 1 and 2). The situation for planar array is similar to linear array. PA initial pressure images (900 nm) were reconstructed using BP and the results are shown in Fig. 5(e) and (g). The relative spectral error due to the crosstalk can be seen in Fig. 5(f) and (h). The error appears to be highly inhomogeneous and increases with depth, as expected.
3.2. Influence of reconstruction methods
3.2.1. Numerical simulation results
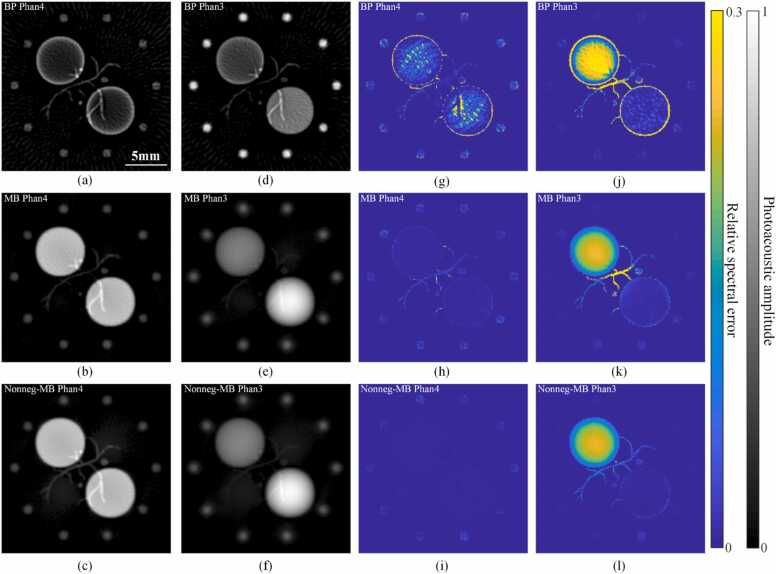
Phantom 3 and 4 were used to analysis the influence of reconstruction methods. The results of BP, MB (no regularization) and non-negative MB (no regularization) are shown in Fig. 6. For Fig. 6, the first and third column (a-c, g-i) show the results of Phantom 4, and the second and fourth column (d-f, j-l) show the results of Phantom 3. As shown in Fig. 6(a), for the BP reconstruction, the signals of the two large circular targets were very weak, in other words, was very small. At the same time, the vascular feature was subject to negative crosstalk at the edge of the circular targets, which was affected by the limited angular acceptance (Section 2.1/3.1.1). As shown in Fig. 6(d), when the imaging target was replaced with a complete three-dimensional phantom (Phantom 3), the intensity of the circular targets increased obviously, which was caused by the addition of the out-of-plane signals. According to Fig. 6(b), for the MB reconstruction, we can see that the crosstalk to the circular targets caused by the limited angular acceptance was reduced. At the same time, the artifacts in the image were reduced, indicating that the MB method can effectively reduce the off-diagonal elements in the A matrix. However, the central vascular feature was still affected by the negative value of the circular target (the thickness of the vascular target in the z direction was about half that of the circular target in Phantom 4). After adding non-negative constraints, the strength of the middle vascular feature effectively recovered, as shown in Fig. 6(c). For the complete three-dimensional phantom (Phantom 3), the large circular targets’ signal also showed obvious enhancement, which was due to the out-of-plane signal (Fig. 6(e-f)). At the same time, the central vascular feature after adding non-negative constraints in Fig. 6(f) was significantly clearer than that in Fig. 6(e).
Fig. 6.
Reduction of spectral crosstalk by MB reconstruction and non-negative constraints. (a) Image reconstructed of Phantom 4 with BP. (b) Image reconstructed of Phantom 4 with MB. (c) Image reconstructed of Phantom 4 with non-negative MB. (d) Image reconstructed of Phantom 3 with BP. (e) Image reconstructed of Phantom 3 with MB. (f) Image reconstructed of Phantom 3 with non-negative MB. (a-f) are displayed with negative values set to 0. (g-l) Relative spectral error maps corresponding to (a-f).
Analyzing the relative spectral error, the MB reconstruction with nonnegative constraints greatly eliminated the in-plane spectral crosstalk (which was considered to be caused by limited angle acceptance and sparse sampling here) which was shown in Fig. 6(g-i). However, the MB reconstruction had limited effect on the out-of-plane spectral crosstalk. Compare Fig. 6(j) and (k), the relative spectral error of the circular target in the upper left corner decreased, which should be the result of the increase of at the in-plane position. Due to the addition of out-of-plane signal, the negative crosstalk of the vascular target was more serious, which can be alleviated after adding nonnegative constraints, as shown in Fig. 6(l).
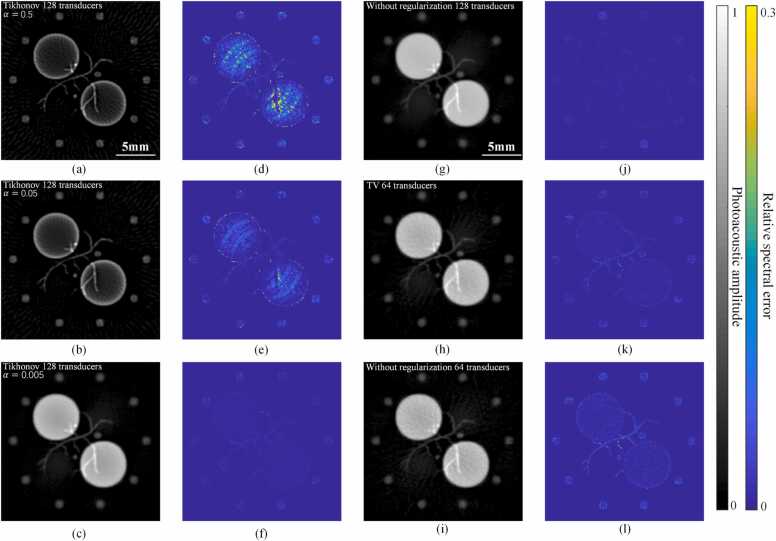
Next, Tikhonov and TV regularization were added, while Phantom 4 was used here. The signals collected by the actual system often contain various levels of noise, thus Tikhonov regularization is always employed to ensure the stability of the iteration. We evaluated the effectiveness of Tikhonov regularization on the MB method’s ability to overcome spectral crosstalk. Fig. 7(a-c) show the reconstruction image at a single wavelength under = 0.5, 0.05 and 0.005 (arbitrary unit), and Fig. 7(d-f) show the corresponding relative spectral error. It can be seen that a large Tikhonov regularization term inhibited the effect of MB method on suppressing the spectral crosstalk. This similar effect was also mentioned in literature [26]. TV regularization is a common technique in medical imaging. In PA imaging, it is considered to be an effective method to suppress the sparse sampling artifacts. Here we tested its performance on spectral crosstalk caused by sparse sampling. Fig. 7(g) and (j) show the reconstruction results of the MB method and their corresponding relative spectral error, using a 128-channel ring array. Fig. 7(i) and (l) show the results after the sampling density was reduced by half. It can be seen that the degree of spectral crosstalk was increased. Fig. 7(h) and (k) are the result of adding the TV regularization term. The spectral crosstalk was improved to some extent, but is still larger than the crosstalk in Fig. 7(j).
Fig. 7.
Effect of Tikhonov and TV regularization on spectral crosstalk. (a-c) Images reconstructed with different Tikhonov regularization parameter, (a) = 0.5, (b) = 0.05, (c)= 0.005. (d-f) are the relative spectral error of (a-c). (g) Image reconstructed by the MB method without regularization, the number of transducers is 128. (h) Image reconstructed by the MB method with TV regularization, the number of transducers is 64. (i) Image reconstructed by the MB method without regularization, the number of transducers is 64. (j-l) are the relative spectral error corresponding to (g-i).
3.2.2. Phantom experiment results
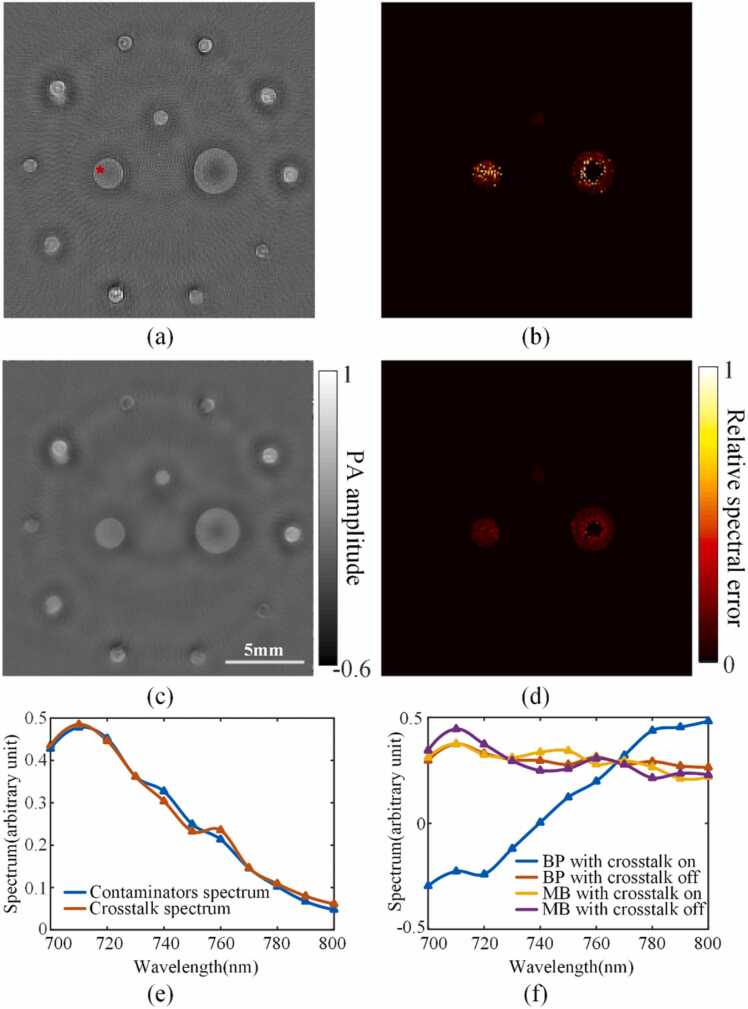
The images at 740 nm illumination and their corresponding relative spectral error distributions are shown in Fig. 8(a, b) (BP) and Fig. 8(c, d) (MB). The Tikhonov and TV regularization were added in MB reconstructions. Obviously, the artifacts in the images reconstructed with the MB algorithms were significantly less. The dark area in the disk target was significantly reduced. And the TV regularization also suppressed the streak artifacts. As shown in Fig. 8(b, d), the degree of spectral crosstalk was significantly reduced with the MB algorithms.
Fig. 8.
Phantom experiment results. (a) PA image acquired at 740 nm of the phantom shown in Fig. 3(a), reconstructed with BP. (b) Relative spectral error of (a). (c) PA image acquired at 740 nm of the phantom shown in Fig. 3(a), reconstructed with MB. (d) Relative spectral error of (c). (e) The PA spectra of the contaminators (blue ink) and the crosstalk spectrum at the red star position in (a). (f) PA spectra with BP and MB reconstructions at the red star position in (a).
To verify the spectral crosstalk in the experiment, a series of “differential images” at all the wavelengths were calculated. At each wavelength, the image with and without the surrounding contaminators were reconstructed. We subsequently subtracted the image with the contaminators from the those without the contaminators to obtain a “differential image”. The absolute value of the spectrum of each pixel in the differential image is termed the “crosstalk spectrum”. We further measured the PA spectrum of blue ink, termed here as the “contaminator spectrum”. As shown in Fig. 8(e), there is a high correlation between the crosstalk spectrum and the contaminator spectrum at the position labeled by the red star in Fig. 8(a). The PA spectra at the red star positions with BP and MB reconstructions were shown in Fig. 8(f), the spectra of the MB reconstruction were similar with and without the contaminators. For the BP reconstruction, there was a huge difference between the spectra with and without the contaminators. Here, the “crosstalk spectrum” in Fig. 8(e) was subtracted from the contaminator-free PA spectrum (subtraction means the artifacts were negative), leading to serious spectral crosstalk.
It should be noted that the relative spectral error at the center of the largest disk was zero, which was due to the application of the mask (see Section 2.3). Even without the surrounding contaminators, the center of the largest disk had a negative value for both the BP and MB reconstructions. This was caused by: 1. The frequency of the PA signal corresponding to the largest disk was outside the response range of the transducer and its interfacing electronics, so even if the EIR was corrected, the signals could not be recovered completely; 2. Light intensity attenuated significantly towards the center of the disk.
4. Discussion and conclusion
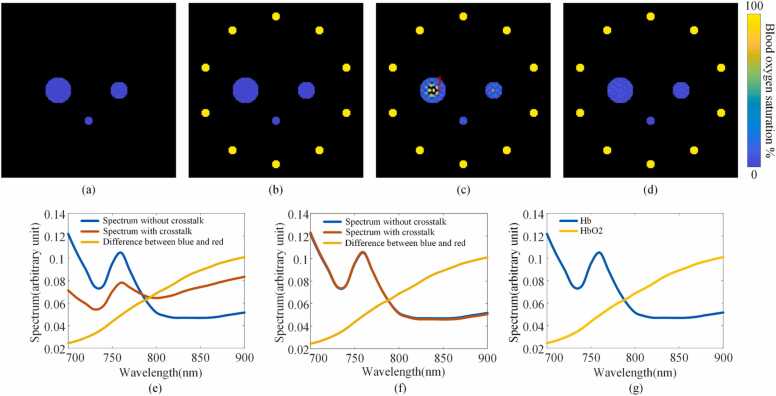
In this paper, we introduced the concept of spectral crosstalk caused by imperfect acoustic inversion in multispectral PA imaging. The spectral crosstalk phenomenon is independent of the spectral coloring effect in multispectral PA imaging, and is added upon spectral coloring to make spectroscopic analysis more challenging. The following simulation was designed to highlight how spectral crosstalk can affect real applications such as the estimation of saturation of oxygen (sO2). Similar to the phantom experiment, ten surrounding small disks were designed as the sources of spectral crosstalk, and the chromophore in these disks was oxyhemoglobin. In the middle region, there were three disks whose chromophore was deoxyhemoglobin. Fig. 9(a) shows the situation when the outer “contaminators” were removed (spectral crosstalk “off”) and Fig. 9(b) shows the situation when the outer “contaminators” were included (spectra crosstalk “on”). The simulation was carried out in 3D with the same parameters in Section 2.2.3. The thickness of all the disks was 1 mm.We then used BP and MB to reconstruct multispectral PA images. Here, the light fluence was independent of the wavelength and position (the spectral coloring effect was not considered). The reconstructed multispectral PA data were linearly unmixed to solve the sO2 values. To show the sO2 map, the positions with negative values or with no target were set to black. Fig. 9(c, d) show the estimated sO2 by BP and MB, respectively. Fig. 9(c) clearly shows that the sO2 values calculated based on the BP reconstruction were significantly higher at certain positions inside the middle disks (theoretically sO2 was zero because they were set to be purely deoxyhemoglobin, as shown in Fig. 9(b)). For MB, the calculated sO2 values were closer to the ground truth. The reconstructed PA spectra at the red star position (position 1) in Fig. 9(c) were analyzed to prove that the inaccurate estimation was caused by the crosstalk components of the outer “contaminators”. As shown in Fig. 9(e, f), the blue and red lines represent the reconstructed PA spectra when the crosstalk was turned “off” and “on” respectively, and the yellow lines are the difference between them. All spectra were normalized. The “difference spectrum” is reminiscent of the spectrum of oxyhemoglobin (Fig. 9(g)). This experiment showed that spectral crosstalk can render sO2 estimation inaccurate even in the absence of spectral coloring. In our study, we established a mathematical model to analyze the mechanism of spectral crosstalk caused by various factors. Through simulation and phantom experiments, the spectral crosstalk in real PA imaging systems were demonstrated. Here, we assumed that the medium is acoustically uniform and lossless. Although not discussed, it is expected that spectral crosstalk can be induced by non-uniform sound speed and frequency-dependent acoustic attenuation. How these factors come into play is similar to the discussed aspects in terms of generating non-vanishing off-diagonal elements in the A matrix. The concept of relative spectral error was proposed as a new quantitative value to measure the quality of multispectral PA image reconstruction. This evaluation index can test the spectral crosstalk in reconstructed image for the linear algorithm. For nonlinear reconstruction methods or image enhancement methods (such as multiply DAS [54], [55] or neural network post-processing methods [56]), the influence of nonlinear algorithms on the spectra can be tested at the same time. For the BP algorithm, there are some modified methods that can reduce the impact of one type of spectral crosstalk (caused by streak artifacts), but these methods have unavoidable tradeoff and should be used with care. For focused ring- and linear array systems, the high pass effect as a result of their limited angular acceptance can play a role: even if the probe has excellent low-frequency response, a large portion of the low-frequency features in the image will still be lost. At the same time, the contradiction between frequency response and spatial response makes it difficult to obtain the in-plane low-frequency signal alone. Therefore, the low frequency characteristics in the plane are often subject to serious spectral crosstalk.
Fig. 9.
Numerical simulation of spectral crosstalk in oxygen saturation imaging. (a) Digital phantom without surrounding contaminators. (b) Digital phantom with surrounding contaminators. (c) sO2 map calculated based on BP reconstruction. (d) sO2 map calculated based on MB reconstruction. (e) PA spectra at position 1 in (c) reconstructed by BP. (f) PA spectra at the same position reconstructed by MB. (g) Absorption spectra of oxyhemoglobin and deoxyhemoglobin.
To reduce the spectral crosstalk, the MB methods are in principle superior since they aim at optimizing matrix A towards an identity matrix. At the same time, some constraints can be easily added to reduce the morbidity of reconstruction. In this paper, we verified that these constraints can reduce the spectral crosstalk, and we also verified that adding nonlinear regularization terms can facilitate spectral recovery. However, model mismatch often exists to jeopardize their performance. Other reconstruction algorithms are not discussed and should be analyzed case by case since the performance of a certain reconstruction algorithm is determined by the entire imaging process (imaged objects and the detection scheme, etc.).
In conclusion, we have analyzed in detail the cause of spectral crosstalk due to imperfect acoustic detection and inversion. The notion that the artifacts in the initial pressure images are independent of the spectroscopic measurement, and thus multispectral PA images are spectrally accurate despite being spatially distorted is wrong. Bad acoustic inversion tends to cause coupling between close-by or remotely located pixels such that the spectra of bright image features will contaminate those of the dim ones. We have listed a number of factors that can cause dramatic difference in the signal strengths of reconstructed features. When performing quantitative analysis such as sO2 estimation, pixels with weak signals are more prone to spectral crosstalk. An algorithm is in need to quantitatively evaluate the pixel-wise credibility of the experimentally measured PA spectrum in the future.
Funding
The work was financially supported by the National Natural Science Foundation of China (61971265, 61735016), the Innovation Fund of Tsinghua-Fuzhou Institute for Data Technology, grants from Institute of Precision Healthcare, Tsinghua University and Tsinghua-Foshan Institute of Advanced Manufacturing.
Declaration of Competing Interest
C.M. has a financial interest in TsingPAI Technology Co., Ltd., which did not support this work.
Biographies

Hongzhi Zuo graduated from the School of Optics and Photonics, Beijing Institute of Technology, Beijing, China in 2019. He is now studying for a doctorate degree in the Department of Electronic Engineering, Tsinghua University, Beijing, China. His research focuses on multispectral photoacoustic imaging and its biomedical applications.

Manxiu Cui received his Bachelor degree from the Department of Electronic Engineering, Tsinghua University, Beijing, China in 2020. He is currently a graduate student in Caltech Optical Imaging Laboratory at California Institute of Technology, Pasadena, CA, USA. His research interest is photoacoustic imaging and wavefront shaping.

Xuanhao Wang is a Ph.D. candidate in the Department of Electronic Engineering, Tsinghua University, Beijing, China. His Ph.D. research, started in 2017, mainly focuses on the development of photoacoustic computed tomography systems for small animal whole-body imaging.

Cheng Ma received his B.S. degree in Electronic Engineering from Tsinghua University, Beijing, China in 2004. He obtained his Ph. D. degree in Electrical Engineering from Virginia Tech, Blacksburg, VA, USA in 2012. From 2012 to 2016, he was a postdoctoral research associate in the Department of Biomedical Engineering at Washington University in St Louis, St. Louis, MO, USA. From May 2016 to present, he is an assistant professor in the Department of Electronic Engineering at Tsinghua University. His research interests include biophotonic imaging and sensing, in particular photoacoustic imaging and wavefront shaping.
References
- 1.Wang L.V. Multiscale photoacoustic microscopy and computed tomography. Nat. Photonics. 2009;3(9):503–509. doi: 10.1038/nphoton.2009.157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wang L.V., Hu S. Photoacoustic tomography: in vivo imaging from organelles to organs. Science. 2012;335:1458–1462. doi: 10.1126/science.1216210. 00:00:00, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Taruttis A., Ntziachristos V. Advances in real-time multispectral optoacoustic imaging and its applications. Nat. Photonics. 2015;9(4):219–227. 2015/04/01. [Google Scholar]
- 4.Razansky D., Distel M., Vinegoni C., Ma R., Perrimon N., Köster R.W., Ntziachristos V. Multispectral opto-acoustic tomography of deep-seated fluorescent proteins in vivo. Nat. Photonics. 2009;3(7):412–417. [Google Scholar]
- 5.Razansky D., Buehler A., Ntziachristos V. Volumetric real-time multispectral optoacoustic tomography of biomarkers. Nat. Protoc. 2011;6(8):1121–1129. doi: 10.1038/nprot.2011.351. [DOI] [PubMed] [Google Scholar]
- 6.Li L., Zhu L., Ma C., Lin L., Yao J., Wang L., Maslov K., Zhang R., Chen W., Shi J., Wang L.V. Single-impulse panoramic photoacoustic computed tomography of small-animal whole-body dynamics at high spatiotemporal resolution. Nat. Biomed. Eng. 2017;1(5) doi: 10.1038/s41551-017-0071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zalev J., Richards L.M., Clingman B.A., Harris J., Cantu E., Menezes G.L.G., Avila C., Bertrand A., Saenz X., Miller S., Oraevsky A.A., Kolios M.C. Opto-acoustic imaging of relative blood oxygen saturation and total hemoglobin for breast cancer diagnosis. J. Biomed. Opt. 2019;24(12):1–16. doi: 10.1117/1.JBO.24.12.121915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Li M., Tang Y., Yao J. Photoacoustic tomography of blood oxygenation: a mini review. Photoacoustics. 2018;10:65–73. doi: 10.1016/j.pacs.2018.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cox B., Laufer J.G., Arridge S.R., Beard P.C. Quantitative spectroscopic photoacoustic imaging: a review. J. Biomed. Opt. 2012;17(6) doi: 10.1117/1.JBO.17.6.061202. [DOI] [PubMed] [Google Scholar]
- 10.Buchmann J., Kaplan B., Powell S., Prohaska S., Laufer J. Three-dimensional quantitative photoacoustic tomography using an adjoint radiance Monte Carlo model and gradient descent. J. Biomed. Opt. 2019;24(6):1–13. doi: 10.1117/1.JBO.24.6.066001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Two-dimensional quantitative photoacoustic image reconstruction of absorption distributions in scattering media by use of a simple iterative method, Appl. Opt., 45(8), 2006, pp. 1866–1875. [DOI] [PubMed]
- 12.Quantitative photoacoustic tomography based on the radiative transfer equation, Opt. Lett., 34(12), 2009, pp. 1765–1767. [DOI] [PubMed]
- 13.Kirchner T., Grohl J., Maier-Hein L. Context encoding enables machine learning-based quantitative photoacoustics. J. Biomed. Opt. 2018;23(5):1–9. doi: 10.1117/1.JBO.23.5.056008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gröhl J., Kirchner T., Adler T., Maier-Hein L. Confidence estimation for machine learning-based quantitative photoacoustics. J. Imaging. 2018;4(12) [Google Scholar]
- 15.Olefir I., Tzoumas S., Restivo C., Mohajerani P., Xing L., Ntziachristos V. Deep learning-based spectral unmixing for optoacoustic imaging of tissue oxygen saturation. IEEE Trans. Med. Imaging. 2020;39(11):3643–3654. doi: 10.1109/TMI.2020.3001750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bench C., Hauptmann A., Cox B. Toward accurate quantitative photoacoustic imaging: learning vascular blood oxygen saturation in three dimensions. J. Biomed. Opt. 2020;25(8) doi: 10.1117/1.JBO.25.8.085003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Cai C., Deng K., Ma C., Luo J. End-to-end deep neural network for optical inversion in quantitative photoacoustic imaging. Opt. Lett. 2018;43(12):2752–2755. doi: 10.1364/OL.43.002752. [DOI] [PubMed] [Google Scholar]
- 18.Tzoumas S., Nunes A., Olefir I., Stangl S., Symvoulidis P., Glasl S., Bayer C., Multhoff G., Ntziachristos V. Eigenspectra optoacoustic tomography achieves quantitative blood oxygenation imaging deep in tissues. Nat. Commun. 2016;7:12121. doi: 10.1038/ncomms12121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Olefir I., Tzoumas S., Yang H., Ntziachristos V. A Bayesian approach to eigenspectra optoacoustic tomography. IEEE Trans. Med. Imaging. 2018;37(9):2070–2079. doi: 10.1109/TMI.2018.2815760. [DOI] [PubMed] [Google Scholar]
- 20.Cui M., Zuo H., Wang B., Wang X., Ma C. A convex cone method for accurate blood oxygenation photoacoustic imaging. Proc. SPIE. 2020 [Google Scholar]
- 21.Leino A.A., Lunttila T., Mozumder M., Pulkkinen A., Tarvainen T. Perturbation Monte Carlo method for quantitative photoacoustic tomography. IEEE Trans. Med. Imaging. 2020;39(10):2985–2995. doi: 10.1109/TMI.2020.2983129. [DOI] [PubMed] [Google Scholar]
- 22.Mitcham T., Taghavi H., Long J., Wood C., Fuentes D., Stefan W., Ward J., Bouchard R. Photoacoustic-based sO2 estimation through excised bovine prostate tissue with interstitial light delivery. Photoacoustics. 2017;7:47–56. doi: 10.1016/j.pacs.2017.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hussain A., Hondebrink E., Staley J., Steenbergen W. Photoacoustic and acousto-optic tomography for quantitative and functional imaging. Optica. 2018;5(12) [Google Scholar]
- 24.Jeng G.S., Li M.L., Kim M., Yoon S.J., Pitre J.J., Jr., Li D.S., Pelivanov I., O’Donnell M. Real-time interleaved spectroscopic photoacoustic and ultrasound (PAUS) scanning with simultaneous fluence compensation and motion correction. Nat. Commun. 2021;12(1):716. doi: 10.1038/s41467-021-20947-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Li L., Shemetov A.A., Baloban M., Hu P., Zhu L., Shcherbakova D.M., Zhang R., Shi J., Yao J., Wang L.V., Verkhusha V.V. Small near-infrared photochromic protein for photoacoustic multi-contrast imaging and detection of protein interactions in vivo. Nat. Commun. 2018;9(1):2734. doi: 10.1038/s41467-018-05231-3. 2018/07/16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Dean-Ben X.L., Buehler A., Ntziachristos V., Razansky D. Accurate model-based reconstruction algorithm for three-dimensional optoacoustic tomography. IEEE Trans. Med. Imaging. 2012;31(10):1922–1928. doi: 10.1109/TMI.2012.2208471. [DOI] [PubMed] [Google Scholar]
- 27.Hu P., Li L., Lin L., Wang L.V. Spatiotemporal antialiasing in photoacoustic computed tomography. IEEE Trans. Med. Imaging. 2020;39(11):3535–3547. doi: 10.1109/TMI.2020.2998509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Huang C., Wang K., Nie L., Wang L.V., Anastasio M.A. Full-wave iterative image reconstruction in photoacoustic tomography with acoustically inhomogeneous media. IEEE Trans. Med. Imaging. 2013;32(6):1097–1110. doi: 10.1109/TMI.2013.2254496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Rosenthal A., Razansky D., Ntziachristos V. Fast semi-analytical model-based acoustic inversion for quantitative optoacoustic tomography. IEEE Trans. Med. Imaging. 2010;29(6):1275–1285. doi: 10.1109/TMI.2010.2044584. [DOI] [PubMed] [Google Scholar]
- 30.Tian C., Pei M., Shen K., Liu S., Hu Z., Feng T. Impact of system factors on the performance of photoacoustic tomography scanners. Phys. Rev. Appl. 2020;13(1) [Google Scholar]
- 31.Xu M., Wang L.V. Analytic explanation of spatial resolution related to bandwidth and detector aperture size in thermoacoustic or photoacoustic reconstruction. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2003;67(5 Pt 2) doi: 10.1103/PhysRevE.67.056605. [DOI] [PubMed] [Google Scholar]
- 32.Queiros D., Dean-Ben X.L., Buehler A., Razansky D., Rosenthal A., Ntziachristos V. Modeling the shape of cylindrically focused transducers in three-dimensional optoacoustic tomography. J. Biomed. Opt. 2013;18(7) doi: 10.1117/1.JBO.18.7.076014. [DOI] [PubMed] [Google Scholar]
- 33.Ding L., Luis Dean-Ben X., Lutzweiler C., Razansky D., Ntziachristos V. Efficient non-negative constrained model-based inversion in optoacoustic tomography. Phys. Med. Biol. 2015;60(17):6733–6750. doi: 10.1088/0031-9155/60/17/6733. [DOI] [PubMed] [Google Scholar]
- 34.Kazakeviciute A., Ho C.J., Olivo M. Multispectral photoacoustic imaging artifact removal and denoising using time series model-based spectral noise estimation. IEEE Trans. Med. Imaging. 2016;35(9):2151–2163. doi: 10.1109/TMI.2016.2550624. [DOI] [PubMed] [Google Scholar]
- 35.Matthews T.P., Poudel J., Li L., Wang L.V., Anastasio M.A. Parameterized joint reconstruction of the initial pressure and sound speed distributions for photoacoustic computed tomography. SIAM J. Imaging Sci. 2018;11(2):1560–1588. doi: 10.1137/17M1153649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Cai C., Wang X., Si K., Qian J., Luo J., Ma C. Feature coupling photoacoustic computed tomography for joint reconstruction of initial pressure and sound speed in vivo. Biomed. Opt. Express. 2019;10(7):3447–3462. doi: 10.1364/BOE.10.003447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Jin H., Zhang R., Liu S., Zheng Y. Fast and high-resolution three-dimensional hybrid-domain photoacoustic imaging incorporating analytical-focused transducer beam amplitude. IEEE Trans. Med. Imaging. 2019;38(12):2926–2936. doi: 10.1109/TMI.2019.2917688. [DOI] [PubMed] [Google Scholar]
- 38.Biton S., Arbel N., Drozdov G., Gilboa G., Rosenthal A. Optoacoustic model-based inversion using anisotropic adaptive total-variation regularization. Photoacoustics. 2019;16 doi: 10.1016/j.pacs.2019.100142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Prakash J., Mandal S., Razansky D., Ntziachristos V. Maximum entropy based non-negative optoacoustic tomographic image reconstruction. IEEE Trans. Biomed. Eng. 2019;66(9):2604–2616. doi: 10.1109/TBME.2019.2892842. [DOI] [PubMed] [Google Scholar]
- 40.Chowdhury K.B., Prakash J., Karlas A., Justel D., Ntziachristos V. A synthetic total impulse response characterization method for correction of hand-held optoacoustic images. IEEE Trans. Med. Imaging. 2020;39(10):3218–3230. doi: 10.1109/TMI.2020.2989236. [DOI] [PubMed] [Google Scholar]
- 41.Cui M., Zuo H., Wang X., Deng K., Luo J., Ma C. Adaptive photoacoustic computed tomography. Photoacoustics. 2021;21 doi: 10.1016/j.pacs.2020.100223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kim M., Jeng G.S., Pelivanov I., O’Donnell M. Deep-learning image reconstruction for real-time photoacoustic system. IEEE Trans. Med. Imaging. 2020;39(11):3379–3390. doi: 10.1109/TMI.2020.2993835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Li X., Zhang S., Wu J., Huang S., Feng Q., Qi L., Chen W. Multispectral interlaced sparse sampling photoacoustic tomography. IEEE Trans. Med. Imaging. 2020;v39(11):3463–3474. doi: 10.1109/TMI.2020.2996240. [DOI] [PubMed] [Google Scholar]
- 44.Treeby B.E., Varslot T.K., Zhang E.Z., Laufer J.G., Beard P.C. Automatic sound speed selection in photoacoustic image reconstruction using an autofocus approach. J. Biomed. Opt. 2011;16(9) doi: 10.1117/1.3619139. [DOI] [PubMed] [Google Scholar]
- 45.Feng J., Deng J., Li Z., Sun Z., Dou H., Jia K. End-to-end Res-Unet based reconstruction algorithm for photoacoustic imaging. Biomed. Opt. Express. 2020;11(9):5321–5340. doi: 10.1364/BOE.396598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Xu M., Wang L.V. Universal back-projection algorithm for photoacoustic computed tomography. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2005;71(1 Pt. 2) doi: 10.1103/PhysRevE.71.016706. [DOI] [PubMed] [Google Scholar]
- 47.Liu H., Wang K., Peng D., Li H., Zhu Y., Zhang S., Liu M., Tian J. Curve-driven-based acoustic inversion for photoacoustic tomography. IEEE Trans. Med. Imaging. 2016;35(12):2546–2557. doi: 10.1109/TMI.2016.2584120. [DOI] [PubMed] [Google Scholar]
- 48.Sandeep Kumar K., Manojit P. Experimental validation of tangential resolution improvement in photoacoustic tomography using modified delay-and-sum reconstruction algorithm. J. Biomed. Opt. 2016;21(8):1–8. doi: 10.1117/1.JBO.21.8.086011. [DOI] [PubMed] [Google Scholar]
- 49.Alexandrakis G., Rannou F.R., Chatziioannou A.F. Tomographic bioluminescence imaging by use of a combined optical-PET (OPET) system: a computer simulation feasibility study. Phys. Med. Biol. 2005;50(17):4225–4241. doi: 10.1088/0031-9155/50/17/021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Jacques S.L. Corrigendum: optical properties of biological tissues: a review. Phys. Med. Biol. 2013;58(14):5007–5008. doi: 10.1088/0031-9155/58/11/R37. [DOI] [PubMed] [Google Scholar]
- 51.Yu L., Nina-Paravecino F., Kaeli D., Fang Q. Scalable and massively parallel Monte Carlo photon transport simulations for heterogeneous computing platforms. J. Biomed. Opt. 2018;23(1):1–4. doi: 10.1117/1.JBO.23.1.010504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Treeby B.E., Cox B.T. k-Wave: MATLAB toolbox for the simulation and reconstruction of photoacoustic wave fields. J. Biomed. Opt. 2010;15(2) doi: 10.1117/1.3360308. [DOI] [PubMed] [Google Scholar]
- 53.Cai C., Wang X., Si K., Qian J., Luo J., Ma C. Streak artifact suppression in photoacoustic computed tomography using adaptive back projection. Biomed. Opt. Express. 2019;10(9):4803–4814. doi: 10.1364/BOE.10.004803. 2019/09/01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ma X., Peng C., Yuan J., Cheng Q., Xu G., Wang X., Carson P.L. Multiple delay and sum with enveloping beamforming algorithm for photoacoustic imaging. IEEE Trans. Med. Imaging. 2020;39(6):1812–1821. doi: 10.1109/TMI.2019.2958838. [DOI] [PubMed] [Google Scholar]
- 55.Mozaffarzadeh M., Mahloojifar A., Orooji M., Adabi S., Nasiriavanaki M. Double-stage delay multiply and sum beamforming algorithm: application to linear-array photoacoustic imaging. IEEE Trans. Biomed. Eng. 2018;65(1):31–42. doi: 10.1109/TBME.2017.2690959. [DOI] [PubMed] [Google Scholar]
- 56.Hsu K.-T., Guan S., Chitnis P.V. Comparing deep learning frameworks for photoacoustic tomography image reconstruction. Photoacoustics. 2021;23 doi: 10.1016/j.pacs.2021.100271. [DOI] [PMC free article] [PubMed] [Google Scholar]