Foundational Number Sense Training Gains Are Predicted by Hippocampal–Parietal Circuits

Abstract

The development of mathematical skills in early childhood relies on number sense, the foundational ability to discriminate among quantities. Number sense in early childhood is predictive of academic and professional success, and deficits in number sense are thought to underlie lifelong impairments in mathematical abilities. Despite its importance, the brain circuit mechanisms that support number sense learning remain poorly understood. Here, we designed a theoretically motivated training program to determine brain circuit mechanisms underlying foundational number sense learning in female and male elementary school-age children (7–10 years). Our 4 week integrative number sense training program gradually strengthened the understanding of the relations between symbolic (Arabic numerals) and nonsymbolic (sets of items) representations of quantity. We found that our number sense training program improved symbolic quantity discrimination ability in children across a wide range of math abilities including children with learning difficulties. Crucially, the strength of pretraining functional connectivity between the hippocampus and intraparietal sulcus, brain regions implicated in associative learning and quantity discrimination, respectively, predicted individual differences in number sense learning across typically developing children and children with learning difficulties. Reverse meta-analysis of interregional coactivations across 14,371 fMRI studies and 89 cognitive functions confirmed a reliable role for hippocampal–intraparietal sulcus circuits in learning. Our study identifies a canonical hippocampal–parietal circuit for learning that plays a foundational role in children's cognitive skill acquisition. Findings provide important insights into neurobiological circuit markers of individual differences in children's learning and delineate a robust target for effective cognitive interventions.

SIGNIFICANCE STATEMENT Mathematical skill development relies on number sense, the ability to discriminate among quantities. Here, we develop a theoretically motivated training program and investigate brain circuits that predict number sense learning in children during a period important for acquisition of foundational cognitive skills. Our integrated number sense training program was effective in children across a wide a range of math abilities, including children with learning difficulties. We identify hippocampal–parietal circuits that predict individual differences in learning gains. Our study identifies a brain circuit critical for the acquisition of foundational cognitive skills, which will be useful for developing effective interventions to remediate learning disabilities.

Introduction

Number sense, the ability to discriminate quantities, is predictive of academic achievement and professional success (National Mathematics Advisory Panel, 2008; Jordan et al., 2009). In particular, weaknesses in mapping symbolic numbers (e.g., the symbol 2) to their magnitude representations (e.g., two objects) in early childhood are associated with difficulties in subsequent mathematical skill acquisition (Rousselle and Noël, 2007; De Smedt and Gilmore, 2011). Knowledge about the neural mechanisms that support number sense acquisition in children can provide important insights into neurobiological markers of individual differences in learning and inform more effective interventions. Here, we develop a theoretically motivated training protocol to address a critical gap in our understanding of the acquisition of foundational skills and the brain circuits that predict learning in early elementary school children.

Recent studies have begun to uncover a crucial role for the hippocampal memory system in mathematical skill acquisition (Menon and Chang, 2021; Supekar et al., 2021). Most previous studies of mathematical cognition have focused on cortical regions, most notably the posterior parietal cortex; consequently, the role of medial temporal lobe regions in mathematical cognition and learning has received less attention because of this corticocentric focus. Notably, in a study on arithmetic fact learning (e.g., 3 + 5 = 8), hippocampal functional connectivity with multiple cortical regions predicted individual differences in performance gains in children (Supekar et al., 2013). Furthermore, the strength of this association with learning was stronger than the connectivity of the intraparietal sulcus (IPS), a brain region consistently implicated in representation of numerical quantities across symbolic and nonsymbolic formats (Butterworth and Walsh, 2011; Piazza and Eger, 2016). These findings provide support for theoretical models that suggest that hippocampal circuitry is critical during early stages of math skill acquisition (Menon, 2016; Menon and Chang, 2021). Here, we test the hypothesis that brain circuits linking the hippocampus, a brain region crucial for binding new information (Eichenbaum, 2004; Olsen et al., 2012; Zeithamova and Bowman, 2020), with parietal cortical areas important for representation of numerial quantity supports foundational number sense learning.

We developed a number sense training protocol that emphasized strengthening children's understanding of the relations between symbolic and nonsymbolic representations of quantity (Fig. 1A,B). To probe learning during an important period for building foundational cognitive skills, we recruited 96 children, 7–10 years old, with a broad range of math abilities. Functional, diffusion, and structural MRI scans acquired before training and training-related changes in performance on symbolic quantity discrimination were used to determine integrity of brain circuits associated with learning in response to number sense training (Fig. 1C–E). Our first goal was to determine whether number sense training is effective in children, including typically developing (TD) children and those with mathematical learning difficulties (MLD). Our second goal was to identify functional brain circuits that predict children's gains in number sense following training. We used task-independent, resting-state functional MRI to measure intrinsic functional connectivity, which is thought to reflect integrity of functional circuitry (Greicius et al., 2003) and is considered to be a relatively stable measure compared with task-dependent fMRI. Our third goal was to determine, as an adjunct to intrinsic functional connectivity measures, whether number sense training gains are predicted by white matter pathways linking the hippocampus with the parietal cortex. We used an advanced high angular resolution diffusion imaging (HARDI) protocol, which examines complex fiber tracts (Tuch et al., 2002) to enable high-quality reconstructions of white matter pathways. The final goal of our study was to expand on findings from our training study to investigate the broader role of hippocampal–parietal circuits in learning across a large set of fMRI studies using reverse meta-analysis (see below, Materials and Methods). We examined coactivations of hippocampus and parietal cortex across 14,371 published fMRI studies in relation to 89 cognitive functions to determine whether hippocampal–parietal functional circuits identified in the present study constitute a canonical circuit for learning.

Figure 1.

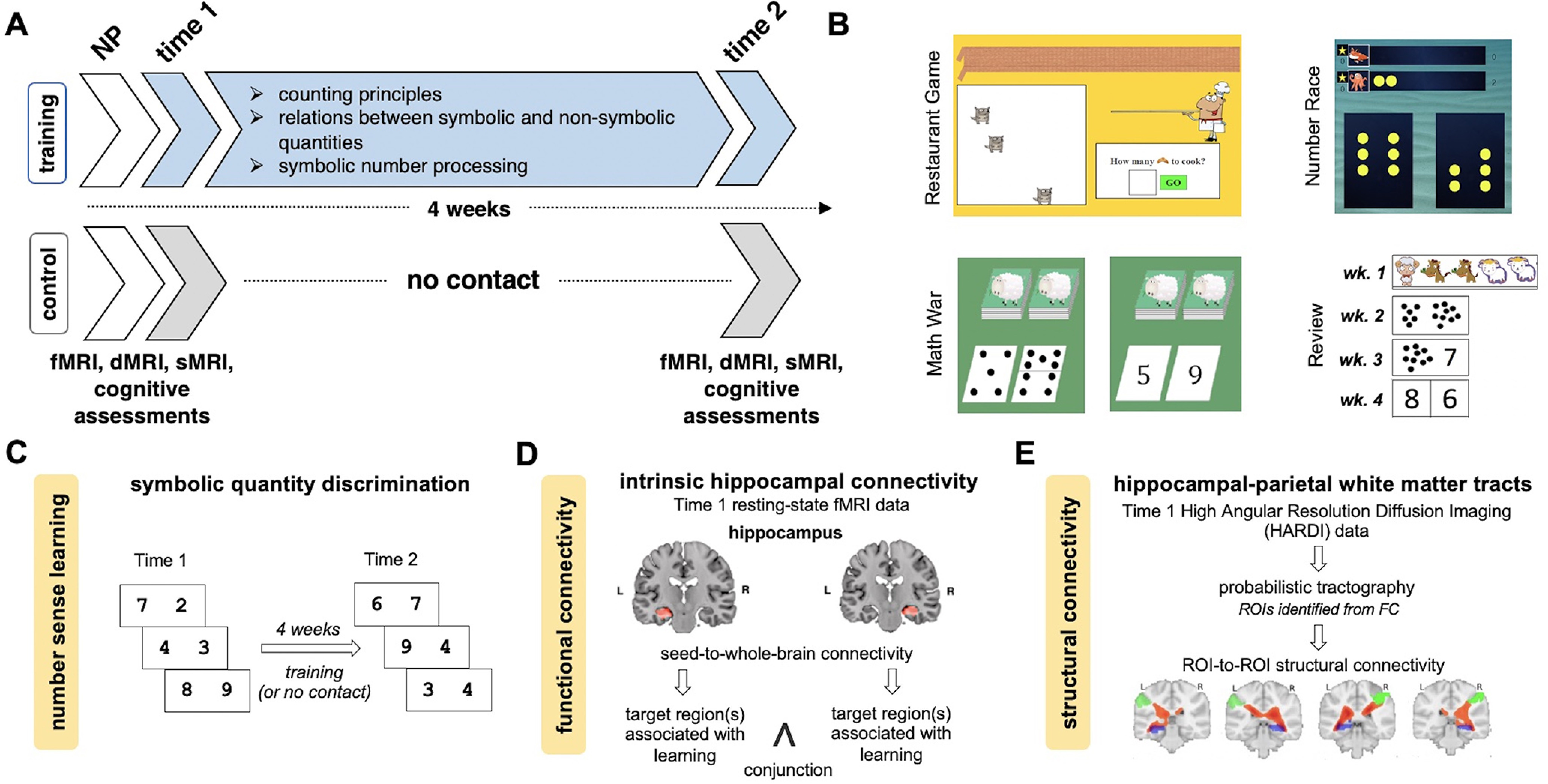
Overview of study design, sample training materials, and schematic illustration of analysis approach. A, The study involved the following sessions: pretraining demographic and neuropsychological (NP) assessments; pretraining (time 1) cognitive assessments and brain imaging, including task-related and resting-state fMRI, diffusion MRI (dMRI) using a high angular resolution diffusion imaging sequence, and high-resolution structural MRI (sMRI); number sense training (in the training group; see below, Materials and Methods) or no contact (in the control group); and post-training (time 2) brain imaging and cognitive assessments identical to pretraining. Children in the training group engaged in progressive learning activities across 4 weeks to strengthen their understanding of the relations between symbolic and nonsymbolic representations of quantity. B, Across 4 weeks of one-on-one tutoring sessions, children in the training group completed a variety of activities with a tutor (see below, Materials and Methods). C, Children's number sense learning was measured by changes in efficiency in symbolic quantity discrimination task from time 1 to time 2 in response to 4 weeks of number sense training (or no contact). D, Using Time 1 resting-state fMRI data, hippocampal seed-to-whole-brain connectivity analysis was performed to assess intrinsic functional connectivity of the hippocampus predictive of number sense learning. A conjunction analysis was performed between left and right hippocampal functional connectivity patterns to identify overlapping target regions associated with learning. ROI-based analysis was used to examine the association between functional connectivity and learning in training and control groups. E, Using high angular resolution diffusion imaging data, probabilistic tractography was performed using ROIs identified from functional connectivity (FC) analysis. Structural connectivity strengths between the ROIs were estimated for each subject to test the associations with number sense learning. ROI-based analysis was performed to examine the relation between structural connectivity and learning in training and control groups.

Materials and Methods

Participants

A total of 96 children in second and third grades (age, mean = 8.19, SD = 0.63, 54 females) recruited with flyers sent to schools and posted at libraries and community centers in the San Francisco Bay Area participated in the study. All participants were right-handed and did not report any current neurologic or psychiatric illness. Among them, 66 children (age, mean = 8.15, SD = 0.65, 35 females) participated in the training program and 30 children (age, mean = 8.27, SD = 0.61, 19 females) served as no-contact controls. MLD in children was identified using normed-based cutoff criteria applied to math fluency, similar to those in previously published studies (Iuculano et al., 2015; Rosenberg-Lee et al., 2015; Jolles et al., 2016). Children who scored at or below 90 (25th percentile or below) on the Math Fluency subtest of the Woodcock–Johnson Third Edition (WJ-III; Woodcock et al., 2001) were included in the MLD group (mean = 85.61, SD = 3.97), and children who scored above 90 were included in the TD group (mean = 103.65, SD = 9.09). No participant was excluded because of MLD or TD status.

All study protocols were approved by the Stanford University School of Medicine Institutional Review Board, and informed consent was obtained from the parents of the children. Children received $50 for completing each MRI scanning session, $50 for completing a neuropsychological assessment battery, and $50 for participating in the training program. Twenty-seven children were excluded from resting-state fMRI analysis because of no structural MRI data acquired (n = 3), poor structural MRI image quality (n = 6), missing behavioral data from fMRI task (n = 2), or inadequate whole-brain coverage or excessive head movement (n = 16; see below, fMRI preprocessing) in the scanner. For diffusion MRI analysis, 13 children were additionally excluded because of incomplete diffusion MRI data acquisition (n = 1), poor diffusion MRI data quality (n = 10), or identification as extreme outliers in structural connectivity measures (n = 2). The final resting-state fMRI analysis sample included 52 children (18 children with MLD, 34 TD children) and 17 children in the training and control group, respectively; the diffusion MRI analysis sample included 43 children (15 children with MLD, 28 TD children) and 13 children in the training and control group, respectively.

Experimental design and statistical analyses

The current study examined the brain circuit mechanisms that predict the acquisition of foundational cognitive skills, following integrative number sense training. The overall study design is summarized in Figure 1A. Children completed MRI scanning session and cognitive assessments before and after training (in the training group) or no contact (in the control group). The no-contact control group participated in all aspects of the study except for training to control for normal business-as-usual schooling (Fuchs et al., 2009) and determine the specificity of brain circuits that predict gains in intervention.

Children in the training group completed a 4 week number sense training program (3 d/week, for ∼60 min/d), which focused on strengthening of children's understanding of the relations between symbolic and nonsymbolic representations of quantities ranging from 1 to 9. The first week of training began with a review of counting principles, followed by practice in enumeration and comparisons between nonsymbolic quantities (sets of items or dot arrays) in the second week; comparisons between nonsymbolic and symbolic (Arabic numbers) quantities in the third week; and finally, comparisons between symbolic quantities in the fourth week. Training with nonsymbolic numbers included in weeks 2 and 3 was used to scaffold children's learning of symbolic numbers through mapping nonsymbolic quantities to verbal (number words) or visual (Arabic numerals) symbolic numbers. This was followed by training with symbolic numbers, without the use of nonsymbolic numbers, in the final week. Response to training was examined using a symbolic quantity discrimination task acquired before and after training.

For statistical analyses of behavioral data, two-sample t tests, χ² tests, and multivariate (M)ANOVA were performed for comparisons between groups of age, gender, or neuropsychological assessments. A repeated-measures ANOVA with time as a within-subject factor and group as a between-subject factor was conducted to assess the effects of training on symbolic quantity discrimination task performance. Follow-up paired t tests examined changes in task performance (learning gains) in each group. In addition, two sample t tests assessed differences in learning gains and pretraining and post-training differences in task performance between groups. Spearman correlations were used for analysis on relations between behavioral measures and brain–behavior relations to minimize influence of potential outliers. In addition to frequentist statistics (e.g., p values), Bayes factor (BF) was used to assess presence or absence of evidence for H₁ or H_o (Keysers et al., 2020). BF values >3 provide evidence for H₁. BF values between 0.33 and 3 provide absence of evidence. BF values below 0.33 provide evidence of absence (evidence for H_o).

Details on statistical analyses of brain imaging data are described below in Intrinsic functional connectivity analysis, Structural connectivity analysis, and Cross-validation analysis. For the procedures for identifying cognitive functions associated with interregional coactivations reported in fMRI studies, see below, Reverse meta-analysis.

Training sessions

Across 4 weeks, children in the training group completed a variety of activities with a tutor (Fig. 1B; Table 1). Generally, in each training session, children received a lesson on counting or comparisons, played computerized and interactive games, and completed review worksheets (counting or comparisons). Quantities from 1 to 9 were used in all activities. On successful completion of each activity, children added to a sticker sheet.

Table 1.

Training activities in each session (three sessions/week)

	Lessons	Games	Review
Week 1	• Counting • Video of a sock puppet counting	• Restaurant Game (Blair, 2013a,b)	• Counting
Week 2	• Comparison • Math Circles	• Number Race (Wilson et al., 2006) • Math War (Iuculano et al., 2015) • Comparing Speed	• Comparison between nonsymbolic quantities
Week 3	• Comparison • Math Circles	• Number Race (Wilson et al., 2006) • Math War (Iuculano et al., 2015) • Comparing Speed	• Comparison between nonsymbolic and symbolic quantities
Week 4	• Comparison • Beat Your Score (Chang et al., 2019)	• Number Race (Wilson et al., 2006) • Math War (Iuculano et al., 2015) • Comparing Speed	•Comparison between symbolic quantities

Lessons

In tutoring sessions in week 1, the tutor provided a lesson on counting by reviewing counting principles with examples of correct and incorrect counting of erasers; after the lesson, children viewed a video of a sock puppet counting and were asked to determine whether the sock puppet counted correctly. In tutoring sessions from weeks 2–4, children were asked to count out loud from 1 to 9 and were reminded that each number they counted going up was bigger than the number before it. Then, in weeks 2 and 3 children completed the Math Circles exercise, where they enumerated the number of erasers in each of two Math Circles on the table and determined which number was bigger than the other. In week 2, lesson on nonsymbolic quantities, the tutor put two sets of erasers of different quantities in the two Math Circles (one quantity in each Math Circle). In week 3, lesson on nonsymbolic and symbolic quantities, the tutor put a card showing a number (Arabic numeral) and a set of erasers of quantities different from the number on the card in the two Math Circles. In week 4, lesson on symbolic quantities, the tutor administered a number-ordering version of the exercise Beat Your Score (Chang et al., 2019), where the child was asked to order four decks of cards with quantities in nonsymbolic (array of dots), mixed (symbolic and nonsymbolic), or symbolic (Arabic numeral) format more quickly each time they ordered the cards. For each deck of cards, children completed the ordering of cards three times after the tutor shuffled the cards, with the goal of beating their previous time taken to order the cards on the third time for at least three decks of cards.

Games

In week 1, children played the computerized Restaurant Game (Blair, 2013a,b), in which they enumerated the number of dishes to cook for the presented number of animals. From weeks 2 to 4, children played an adapted version of the computerized game Number Race (Wilson et al., 2006), which was structured to align with the progression of training activities (comparison between nonsymbolic quantities in week 2, symbolic and nonsymbolic quantities in week 3, and symbolic quantities in week 4) and did not include arithmetic training. Children also played Math War (Iuculano et al., 2015), an interactive game with the tutor in which they determined the larger quantity between two sets of dot arrays (week 2), between one set of dot arrays and a number (week 3), and between two numbers (week 4). In each Math War game, the child and the tutor each had a deck of cards from which they drew one card at a time. The child first wrote down the number on their card and the number on the tutor's card and then marked the larger number. The game continued until the child and tutor drew all their cards. Finally, children played Comparing Speed with the tutor, where the child and the tutor identified cards with quantities one value above or below the quantities on the cards on the table. The cards had quantities in nonsymbolic (week 2), symbolic and nonsymbolic (week 3), or symbolic (week 4) format. In each Comparing Speed game, the tutor first put four cards on the table with quantities of 4, 5, 6, and 7. Then the child and tutor each took five cards from two decks of cards, one for the child, another for the tutor. The child and the tutor placed their cards on top of any of four cards on the table when their cards had quantities one value above or below the quantities on the cards on the table. The child and the tutor drew more cards from their decks, keeping up to five cards in their hands. The game continued until the child finished placing their deck of cards and won the game.

Review worksheets

The review worksheets consisted of counting the number of animals (week 1) or identifying the larger quantity between two nonsymbolic (week 2), symbolic and nonsymbolic (week 3), or symbolic (week 4) quantities. Children circled, matched, or wrote the number of animals (week 1) or circled the larger quantity (weeks 2–4) on the worksheet. Accuracy was emphasized in the worksheets from weeks 1 to 3; the worksheet included 42 trials in week 1, 24 trials in week 2, and 48 trials in week 3. In week 4, children were given 1 min to complete 24 symbolic number comparison trials on the worksheet.

Symbolic quantity discrimination task

Before and after training (or no contact), children performed one run of the symbolic quantity discrimination task in the MRI scanner in which they had to determine which of two symbolic numbers presented on the screen was larger (Fig. 2A). A total of 64 trials including comparison of pairs of quantities 1 through 9 (excluding 5) were presented in each run. Participants were instructed to press a left button if the left side had a larger quantity and the right button otherwise. Half of the trials had a near distance (1 unit) between the two quantities (e.g., 7:6), and the remaining trials had a far distance (5 units) between the two quantities (e.g., 3:8). Numerical magnitude was matched between the two distance conditions with an equal distribution of big (sum of pair of quantities >10) and little (sum of pair of quantities <10) conditions. Our main outcome measure, number sense learning, was assessed by gains in performance efficiency in the symbolic quantity discrimination task. This was measured by the difference in symbolic quantity discrimination task efficiency (Townsend and Ashby, 1978), obtained by accuracy divided by reaction time, from pretraining to post-training, with higher scores representing greater efficiency gains.

Figure 2.

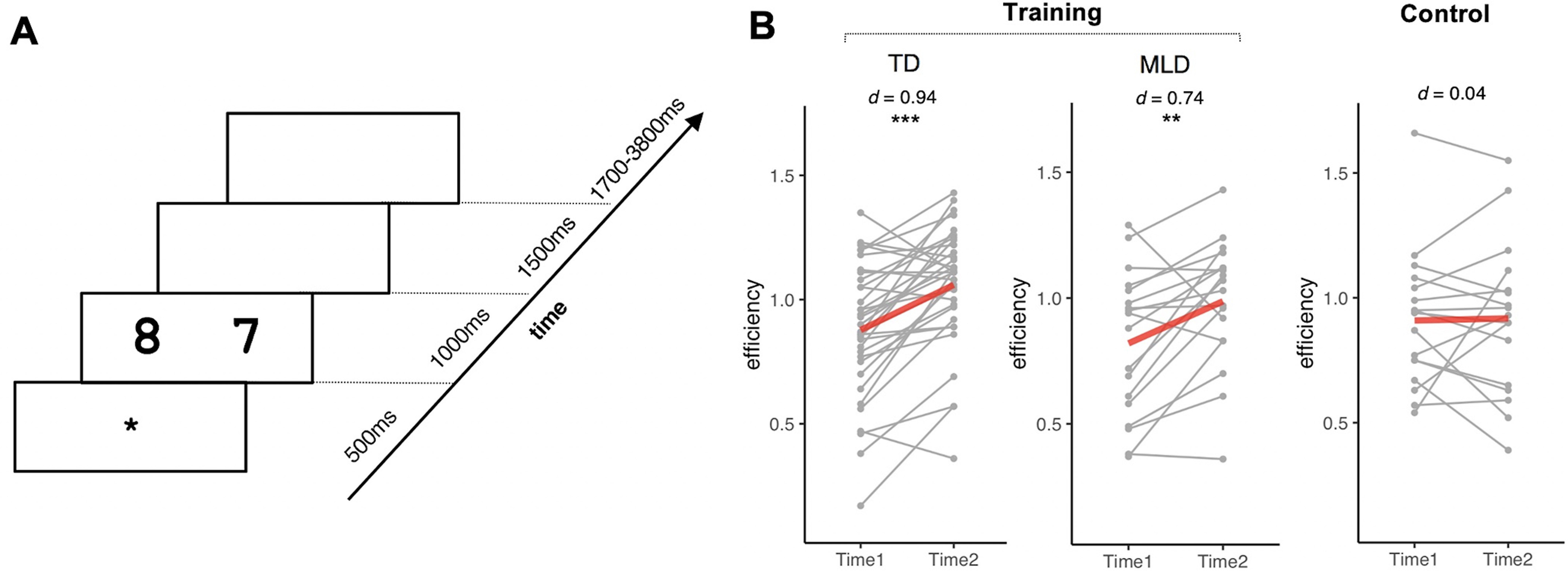
Symbolic quantity discrimination task design and behavioral results. A, Before and after training (or no contact), children completed one run of symbolic quantity discrimination task in the fMRI scanner. Participants first saw a fixation cross, followed by horizontal presentation of two quantities in Arabic numbers. Participants were instructed to press the left button if the left side had a larger quantity and the right button if the right side had a larger quantity. After the button press, a blank screen was presented to fill up the response phase, followed by a jittered intertrial interval. The duration of each phase is shown in milliseconds. B, Four weeks of training improved performance on symbolic quantity discrimination task in both training groups of TD children and children with MLD but not in the no-contact control group. **p < 0.01, ***p < 0.001.

MRI data acquisition

Images were acquired on a 3T Signa scanner (General Electric) using a custom-built head coil at the Stanford University Richard M. Lucas Center for Imaging. Head movement was minimized during the scan by cushions placed around the participant's head. A total of 31 axial slices (4.0 mm thickness, 0.5 mm skip) parallel to the anterior commissure–posterior commissure line and covering the whole brain were imaged using a T2* weighted gradient echo spiral in-out pulse sequence (Glover and Lai, 1998) with the following parameters: TR = 2 s, TE = 30 ms, flip angle = 80°, 1 interleave. The field of view was 22 cm, and the matrix size was 64 × 64, providing an in-plane spatial resolution of 3.4375 mm. The total length of the run was 6 min and 10 s. To reduce blurring and signal loss from field inhomogeneity, an automated high-order shimming method based on spiral acquisitions was used before acquiring functional MRI scans (Kim et al., 2002). High-resolution T1-weighted 3D MRI sequences were acquired to facilitate anatomic coregistration of fMRI maps, with the following parameters: spin quantum number = 400 ms, TR = 5.9 ms; TE = minimum; flip angle = 11°; field of view = 240 mm; matrix size = 256 × 192; 170 axial slices (1.0 mm thickness).

A state-of-the-art diffusion-weighted single-shot spin-echo, echo planar imaging HARDI pulse sequence was used for more precise examination of white matter fibers, including crossing fibers (Tuch et al., 2002), with the following parameters: TR = 5.3 s; TE = minimum; flip angle = 90°; field of view = 260 mm; matrix size = 128 × 128; and 50 axial slices (2.9 mm thickness, no spacing). The high b value (2500 s/mm²) was obtained by applying gradients along 150 different diffusion directions.

fMRI preprocessing

Resting-state functional MRI data were analyzed using SPM12 (http://www.fil.ion.ucl.ac.uk/spm/). The first five volumes were not analyzed to allow for T1 equilibration. A linear shim correction was applied separately for each slice during reconstruction (Glover and Lai, 1998). Images were realigned to the first scan to correct for motion and slice acquisition timing, coregistered to each individual's structural T1 images, spatially transformed to standard stereotaxic space based on the Montreal Neurologic Institute (MNI) coordinate system, resampled every 2 mm using sinc interpolation, and smoothed with a 6 mm full-width half-maximum Gaussian kernel to decrease spatial noise before statistical analysis. A bandpass filter (0.00–0.1 Hz) was applied to the smoothed data to remove high-frequency artifacts. Translational movement in millimeters (x, y, z) and rotational motion in degrees (pitch, roll, yaw) were calculated based on the SPM12 parameters for motion correction of the functional images of each subject. We excluded participants with movement larger than 10 mm in any of the x, y, z directions. Mean scan-to-scan displacement of movement did not exceed 0.5 mm for all participants.

Intrinsic functional connectivity analysis

Intrinsic functional connectivity analysis was conducted using resting-state fMRI to investigate specific functional circuits that relate to change in symbolic quantity discrimination task performance with training. Regions of interest (ROIs) for functional connectivity were selected from Brainnetome (Fan et al., 2016) parcellations of the left and right hippocampus (rostral and caudal subdivisions combined). Seed-to-whole-brain functional connectivity for each ROI was estimated by extracting eigenvalues of time series of all voxels within the ROI, regressing out the global mean signal, white matter signal, cerebrospinal fluid signal, and six motion parameters. A bandpass filter (0.008–0.1 Hz) was applied to reduce high-frequency noise. Functional connectivity maps were then submitted to a second-level analysis to examine whether the connectivity of these regions at the voxel-by-voxel level is predictive of learning (pretraining to post-training efficiency in symbolic quantity discrimination task).

Pretraining performance on symbolic quantity discrimination was regressed out to control for regression to the mean, a known phenomenon in intervention studies (Barnett et al., 2004), and to obtain more precise estimates of intervention effects (Pocock et al., 2002; Thompson et al., 2015). This analysis approach allowed us to minimize the potential influence of pretraining performance on learning. In the current study, the association between change in performance and pretraining performance on symbolic quantity discrimination was significant in the training (ρ = −0.50, p < 0.001) but not in the control (ρ = −0.18, p = 0.49) group, which indicates that the degree to which pretraining performance influences changes in performance varied between groups.

Significant clusters were identified using a height threshold of p < 0.005 with multiple comparisons correction at p < 0.05 after gray matter masking. This statistical threshold was chosen to balance between type I and type II errors in the current study, considering that larger sample sizes are typically needed to detect effects with a more stringent threshold (Carter et al., 2016). The cluster threshold was determined based on Monte Carlo simulations (Forman et al., 1995; https://afni.nimh.nih.gov/pub/dist/doc/manual/AlphaSim.pdf; Nichols and Hayasaka, 2003) implemented in custom MATLAB scripts, similar to previous studies (Cho et al., 2011; Rosenberg-Lee et al., 2011; Cho et al., 2012; Iuculano et al., 2014; Qin et al., 2014; Iuculano et al., 2015; Rosenberg-Lee et al., 2018). Ten thousand iterations of random 3D images, with the same resolution and dimensions as the fMRI data, were generated. The resulting images were masked for gray matter and then smoothed with the same 6 mm FWHM Gaussian kernel used to smooth the fMRI data. The maximum cluster size was then computed for each iteration, and the probability distribution was estimated across the 10,000 iterations. Based on this procedure, 67 voxels corresponding to p < 0.05 were used for the cluster threshold. Anatomical locations of brain regions were identified by Automated Anatomical Labeling (Tzourio-Mazoyer et al., 2002), Harvard-Oxford (Desikan et al., 2006), and Juelich histologic (Eickhoff et al., 2005) atlases.

Follow-up ROI-based analyses were performed to visualize the results, ensure that the results were not driven by outliers, and confirm differences in correlation between brain and behavioral measures across groups. ROIs were defined as 6 mm spheres centered at the peak of the left IPS identified from hippocampal connectivity patterns in the training group and its contralateral region for the right IPS. Similar to the whole-brain analysis (see above), pretraining symbolic quantity discrimination task efficiency was regressed out from symbolic quantity discrimination task efficiency gains and connectivity estimates in each group.

Structural connectivity analysis

Diffusion images were preprocessed to correct artifact issues from movement and eddy currents using Functional MRI of the Brain Software Library (FSL) 5.0.11 (Andersson and Sotiropoulos, 2016). Then, probabilistic tractography to estimate structural connectivity between the left and right hippocampus and the left and right IPS ROIs was performed in native volume space using the FSL probtrackX (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/; Behrens et al., 2007). The hippocampus ROIs were from Brainnetome (Fan et al., 2016) parcellations (rostral and caudal subdivisions combined), and the IPS ROIs were from Brainnetome (Fan et al., 2016) parcellations that overlapped with target ROIs identified from intrinsic functional connectivity analysis [superior parietal lobule (lateral area 5) and inferior parietal lobule (rostrodorsal area 40) subdivisions combined; left IPS] and the contralateral regions (right IPS). These ROIs were warped to each subject's diffusion space, which was achieved by registering the B0 image of each subject's diffusion MRI image to MNI space using Advanced Normalization Tools (Avants et al., 2006). ROIs were then dilated 3 mm into the white matter to avoid biases generated by superficial white matter tracts (Thomas et al., 2014). Structural connectivity between two ROIs, A and B, was computed by the probability that diffusion images provide evidence that a white matter connection exists between these ROIs. This was calculated by the ratio between the number of tracts with origin in A or B reaching the other region and the total number of tracts seeded on A or B. Tracts were only considered if they stayed within the white matter and had a minimum length of 5 mm between the ROIs. Finally, these measures were corrected for distance bias using the approach proposed by Donahue et al. (2016). To estimate structural connectivity between the ROIs, 5000 tracts were seeded at each ROI for each individual, based on a preliminary analysis that determined the number of seeds needed to stabilize the connectivity measure. We computed structural connectivity strength between each pair of ROIs per subject. ROI-based analyses were then performed to assess the relation between hippocampal–parietal structural connectivity and learning, using similar procedures described in intrinsic functional connectivity analysis.

Cross-validation analysis

A machine-learning approach with balanced fourfold cross-validation combined with linear regression (https://github.com/poldrack/regressioncv; Cohen et al., 2010; Supekar et al., 2013) was conducted to investigate the robustness of brain-based predictors of individual differences in number sense learning gains. Learning gain as a dependent variable and the brain-based predictor (connectivity) as an independent variable were treated as inputs to a linear regression algorithm; r(predicted, observed), a measure of how well the independent variable predicts the dependent variable, was first estimated using a balanced fourfold cross-validation procedure. Participants were assigned to one of four folds. A linear regression model was built using three folds, leaving out the fourth, and this model was then used to predict the data in the left-out fold. This procedure was repeated four times to compute a final r(predicted, observed) representing the correlation between the data predicted by the regression model and the observed data. Finally, the statistical significance of the model was assessed using a nonparametric testing approach. The empirical null distribution of r(predicted, observed) was estimated by generating 1000 surrogate datasets under the null hypothesis that there is no association between changes in numerical skills and brain-based predictor.

Reverse meta-analysis

To examine the role of the hippocampal–parietal functional circuits, we conducted a novel reverse meta-analysis of inter-regional coactivation of the hippocampus and the parietal cortex, using regions identified in the present study, reported across 14,371 published fMRI studies up until July 2018 from the Neurosynth (Yarkoni et al., 2011) database and 89 cognitive atlas terms (CogAt; Poldrack et al., 2011; see Fig. 7A). The hippocampal ROIs were from Brainnetome (Fan et al., 2016) parcellations (rostral and caudal subdivisions combined), and the parietal ROIs were from Brainnetome (Fan et al., 2016) parcellations that overlapped with target ROIs identified from intrinsic functional connectivity analysis [superior parietal lobule (lateral area 5) and inferior parietal lobule (rostrodorsal area 40) subdivisions combined; left IPS] and the contralateral regions (right IPS).

Figure 7.

Reverse meta-analysis of 14,371 fMRI studies and cognitive functions reveals a significant association between hippocampal–parietal functional circuits and learning. A, A reverse meta-analysis was performed to map hippocampal–parietal functional circuits identified in the current study to cognitive functions (see above, Materials and Methods). B, The top 5% cognitive functions that are mentioned in published articles where coactivations of the left or right hippocampus (HIPP) and the left or right IPS are reported. L, Left; R, right.

Our reverse meta-analysis estimated the probability that a term related to a cognitive function was mentioned in an fMRI study, provided that activations in both the hippocampus and parietal cortex were also reported. For instance, we estimated the probability as follows for any given study: P (term “learning” is mentioned | activations are reported in the left hippocampus and in the left parietal cortex).

This probability was estimated across different domains and contexts in the neuroimaging literature. We performed this analysis on ipsilateral and contralateral hippocampal–parietal circuits on both hemispheres (i.e., left hippocampus–left IPS, right hippocampus–left IPS, left hippocampus–right IPS, right hippocampus–right IPS). To estimate these probabilities, we programmed this hypothesis in the probabilistic logic language Neurolang (https://neurolang.github.io; Iovene and Wassermann, 2020) using the full Neurosynth (Yarkoni et al., 2011) open access database, version 0.7.

To estimate reverse meta-analysis probabilities, we followed the following steps. First, we encoded the probability of a term being present in a study by thresholding the term frequency (TF)–inverse document frequency (IDF) value of the term being present at 10⁻³, in agreement with Neurosynth implementation (Yarkoni et al., 2011). Second, we considered the probability of a region being reported in a given study as directly proportional to the number of activations within the regions being present in the study for which we resampled the activation foci to 4 mm³ voxels in MNI152 space. Third, terms were filtered using the CogAt (Poldrack et al., 2011) ontology to ensure that only those relating to cognitive processes (see Fig. 7B, 89 terms) were taken into account. To assess the stability of our estimations, we computed the confidence interval of our reverse meta-analysis probability estimations, and we split the 14,371 studies in 20 equal folds, maximizing the measurements for estimation. Finally, the top 5% probable terms were considered to be sufficient evidence for associations with analyzed circuits.

Our analysis resulted in the selection of 25 of 356 associations (four circuits, 89 terms), which was above the 95th percentile of probable term mentions for studies where hippocampal–parietal circuits were reported. For these top 5% terms, the maximum probability was estimated, across all splits, at 0.34 ± 0.011 for the term memory being mentioned in studies where left hippocampus and right IPS activations are simultaneously reported, and the minimum was estimated at 0.10 ± 0.005 for mentioning the term recognition in studies where left hippocampus and left IPS activations are simultaneously reported. Hence, the SD for all top 5% probabilities, is an order of magnitude smaller than the estimated probability, pointing out to a high confidence in our estimation.

Results

Comparison of neuropsychological measures between groups

A total of 96 children in second and third grades (age, mean = 8.19, SD = 0.63, 54 females) participated in number sense training or served as no-contact controls (Fig. 1). Sixty-nine of these children had high-quality behavioral and fMRI data (see above, Materials and Methods). We used two-sample t tests, χ² tests, and MANOVA to compare age, gender, or neuropsychological assessments between the training and control groups.

Children in the training and control groups did not significantly differ in age (t₍₆₇₎ = 0.66, p = 0.51, Cohen's d = 0.18, BF = 0.33) and gender (${\chi }^2$₁ = 0.41, p = 0.52, $\phi$ = 0.08, BF = 0.38; Table 2). A MANOVA between training and control groups on multiple neuropsychological assessments, including the Wechsler Abbreviated Scale of Intelligence (WASI; Wechsler, 1999; Full-Scale, Verbal, and Performance IQ) and WJ-III (Math Fluency, Calculation, Applied Problems, Letter-Word Identification, and Word Attack) subtests (F_(8,60) = 0.56, p = 0.807) showed no significant difference between groups. Two-sample t tests confirmed that children in the training and control groups did not significantly differ in WASI (|t|values < 0.55, p values > 0.58, |Cohen's d| < 0.16, BF values < 0.33) and WJ-III subtests (t values < 1.31, p values > 0.19, Cohen's d < 0.37, BF values < 0.57; Table 2).

Table 2.

Resting-state fMRI data analysis sample

	Training	Control	${\chi }^2$ Test or two-sample t test
	Mean (SD)	Mean (SD)	${\chi }^2$1 or t(67)	p	φ or Cohen's d	BF
Female to male ratio	27:25	11:6	0.41	0.523	0.08	0.38
Age	8.21 (0.61)	8.32 (0.56)	0.66	0.513	0.18	0.33
WASI
Verbal IQ	109.25 (12.81)	107.35 (11.59)	−0.54	0.590	−0.15	0.32
Performance IQ	105.44 (14.73)	105.53 (11.41)	0.02	0.982	0.01	0.28
Full-scale IQ	108.04 (12.78)	107.29 (10.02)	−0.22	0.828	−0.06	0.29
WJ-III
Math fluency	97.40 (11.56)	101.41 (9.08)	1.30	0.198	0.36	0.56
Calculation	104.90 (14.44)	106.88 (11.87)	0.51	0.611	0.14	0.31
Applied problems	104.42 (13.15)	106.59 (10.88)	0.61	0.542	0.17	0.33
Letter-word identification	109.35 (9.40)	112.00 (8.84)	1.02	0.309	0.29	0.43
Word Attack	106.73 (9.42)	107.41 (6.98)	0.27	0.785	0.08	0.29

Time 1 demographics and neuropsychological measures of 4 week number sense training (training) and no-contact control (control) groups.

TD children and children with MLD in the training group were well matched in age (t₍₅₀₎ = 1.47, p = 0.15, Cohen's d = 0.43, BF = 0.69) and gender (${\chi }^2$₁ = 0.01, p = 0.93, $\phi$ = 0.01, BF = 0.34; Table 3). A MANOVA revealed a significant difference between TD and MLD groups on combined neuropsychological assessments (F_(8,43) = 8.09, p < 0.001). TD children and children with MLD in the training group were well matched on IQ measures (|t|values < 1.22, p values > 0.23, |Cohen's d| < 0.36, BF values < 0.53; Table 3). As expected, children with MLD performed significantly worse than TD children on all WJ-III math subtests (|t|values > 3.17, p values < 0.003, |Cohen's d| > 0.92, BF values > 14.57). Children with MLD also performed poorly on WJ-III reading subtests, compared with TD children (|t|values > 2.01, p values < 0.05, |Cohen's d| > 0.58), although there was insufficient evidence for group difference (0.33 < BF values < 3).

Table 3.

Resting state fMRI data analysis sample

	TD_Training	MLD_Training	${\chi }^2$ Test or two-sample t test
	Mean (SD)	Mean (SD)	${\chi }^2$1 or t(50)	p	φ or Cohen's d	BF
Female to male ratio	17:17	10:8	0.01	0.929	0.01	0.34
Age	8.12 (0.57)	8.38 (0.68)	1.47	0.148	0.43	0.69
WASI
Verbal IQ	109.85 (12.23)	108.11 (14.14)	−0.46	0.646	−0.13	0.32
Performance IQ	107.24 (13.62)	102.06 (16.50)	−1.21	0.231	−0.35	0.52
Full-scale IQ	109.44 (11.70)	105.39 (14.59)	−1.09	0.281	−0.32	0.47
WJ-III
Math fluency	103.65 (9.09)	85.61 (3.97)	−8.00	<0.001	−2.33	>100
Calculation	109.18 (14.46)	96.83 (10.70)	−3.18	0.002	−0.93	14.58
Applied problems	109.06 (10.08)	95.67 (14.04)	−3.97	<0.001	−1.16	105.31
Letter-word identification	111.21 (9.00)	105.83 (9.38)	−2.02	0.049	−0.59	1.47
Word Attack	108.88 (9.62)	102.67 (7.73)	−2.36	0.022	−0.69	2.65

Time 1 demographics neuropsychological measures of TD children and children with MLD in the training group (TD_training and MLD_training).

In summary, children included in training and control groups were well matched in terms of age, gender, and IQ, as well as other standardized measures of math and reading abilities. TD children and children with MLD in the training group were matched in age, gender, and IQ. Compared with TD children, children with MLD performed poorly on both math and reading assessments, consistent with observations that comorbidity is one of the characteristics of MLD (Kaufmann and von Aster, 2012; Landerl et al., 2013). Nonetheless, strong evidence (BF values > 10) for group differences in math ability and insufficient evidence (0.33 < BF values < 3) for group differences in reading ability indicate specific impairments in math skills in children with MLD. As shown in Tables 4 and 5, these results are similar for the sample included in diffusion MRI data analysis (a subset of resting-state fMRI data analysis sample). In subsequent behavioral data analyses, we use the sample from resting-state fMRI data analysis.

Table 4.

Diffusion MRI data analysis sample

	Training	Control	${\chi }^2$ Test or two-sample t test
	Mean (SD)	Mean (SD)	${\chi }^2$1 or t(54)	p	φ or Cohen's d	BF
Female to male ratio	22:21	7:6	<0.01	>0.999	<0.01	0.28
Age	8.21 (0.64)	8.39 (0.56)	0.92	0.360	0.29	0.43
WASI
Verbal IQ	109.35 (12.85)	109.15 (12.12)	−0.05	0.962	−0.02	0.31
Performance IQ	103.95 (14.05)	106.23 (11.48)	0.53	0.597	0.17	0.35
Full-scale IQ	107.30 (12.82)	108.54 (10.37)	0.32	0.752	0.10	0.32
WJ-III
Math fluency	97.67 (11.66)	101.77 (8.76)	1.17	0.248	0.37	0.53
Calculation	105.26 (13.41)	107.77 (12.09)	0.61	0.548	0.19	0.36
Applied problems	103.88 (12.08)	109.85 (10.16)	1.61	0.113	0.51	0.86
Letter-word identification	108.93 (9.13)	111.00 (8.42)	0.73	0.469	0.23	0.38
Word attack	106.58 (9.65)	106.38 (6.32)	−0.07	0.945	−0.02	0.31

Time 1 demographics and neuropsychological measures of 4 week number sense training (training) and no-contact control (control) groups.

Table 5.

Diffusion MRI data analysis sample

	TD_Training	MLD_Training	${\chi }^2$ Test or two-sample t test
	Mean (SD)	Mean (SD)	${\chi }^2$1 or t(41)	p	φ or Cohen's d	BF
Female to male ratio	15:13	7:8	0.01	0.911	0.02	0.38
Age	8.15 (0.61)	8.33 (0.70)	0.91	0.370	0.29	0.43
WASI
Verbal IQ	109.00 (12.11)	110.00 (14.55)	0.24	0.811	0.08	0.32
Performance IQ	105.86 (13.69)	100.40 (14.51)	−1.22	0.229	−0.39	0.56
Full-scale IQ	108.25 (11.98)	105.53 (14.54)	−0.66	0.514	−0.21	0.37
WJ-III
Math fluency	103.86 (9.56)	86.13 (3.50)	−6.90	<0.001	−2.21	>100
Calculation	108.71 (14.11)	98.80 (9.30)	−2.44	0.019	−0.78	3.05
Applied problems	108.46 (10.05)	95.33 (11.09)	−3.94	<0.001	−1.26	81.81
Letter-word identification	110.82 (8.82)	105.40 (8.93)	−1.91	0.063	−0.61	1.29
Word attack	108.86 (10.38)	102.33 (6.47)	−2.21	0.033	−0.71	2.03

Time 1 demographics and neuropsychological measures of TD children and children with MLD in the training group (TD_training and MLD_training).

Changes in performance on symbolic quantity discrimination in response to 4 weeks of number sense training

To assess children's behavioral performance on the symbolic quantity discrimination task (Fig. 2A), we measured efficiency (Townsend and Ashby, 1978), derived from dividing accuracy by reaction time, to control for variations in speed accuracy trade-off and to reduce the number of statistical tests required. Higher efficiency scores indicated better performance. A repeated-measures ANOVA on efficiency with time (pre/post) as a within-subject factor and group (training/control) as a between-subject factor was conducted to assess the effects of training on symbolic quantity discrimination task performance. Follow-up paired t tests examined changes in task performance (learning gains) in each group and two sample t tests assessed differences in learning gains and pretraining and post-training differences in task performance between groups.

A repeated-measures ANOVA on symbolic quantity discrimination task efficiency revealed a main effect of time (F_(1,67) = 29.37, p < 0.001, ${\eta }_p{}^2$ = 0.30) and an interaction between time and group (F_(1,67) = 8.31, p = 0.005, ${\eta }_p{}^2$ = 0.11). There was no significant main effect of group (F_(1,67) = 0.21, p = 0.65, ${\eta }_p{}^2$ < 0.01). Training significantly improved symbolic quantity discrimination task efficiency in the training group (t₍₅₁₎ = 6.28, p < 0.001, Cohen's d = 0.87, BF > 100), but not in the control group (t₍₁₆₎ = 0.17, p = 0.86, Cohen's d = 0.04, BF = 0.25, Fig. 2B). Both TD children (t₍₃₃₎ = 5.47, p < 0.001, Cohen's d = 0.94, BF > 100) and children with MLD (t₍₁₇₎ = 3.16, p = 0.006, Cohen's d = 0.74, BF = 8.43) improved with large individual differences in both groups (coefficient of variation: TD children, 1.06; children with MLD, 1.34). In addition, learning gains—changes (pretraining to post-training) in symbolic quantity discrimination task efficiency—were not significantly different between the two training groups (two-sample t test, t₍₅₀₎ = −0.26, p = 0.80, Cohen's d = −0.08, BF = 0.30). These results demonstrate that 4 weeks of number sense training improved symbolic quantity discrimination ability in both TD children and children with MLD.

Surprisingly, our sample of children with MLD did not perform poorly on symbolic quantity discrimination compared with TD children either before (t₍₅₀₎ = −0.71, p = 0.48, Cohen's d = −0.21, BF = 0.36) or after (t₍₅₀₎ = −1.01, p = 0.32, Cohen's d = −0.30, BF = 0.44) training, with comparable variability between groups across time (coefficient of variation range: TD children, 0.23–0.31; children with MLD, 0.26–0.35; test of variance: F values < 1.14, p values > 0.73). Post hoc analysis revealed that children's performance on all measures of WJ-III math subtests were not significantly correlated with symbolic quantity discrimination before training in either group ($\text{ρ}$ values < 0.21, p values > 0.42, BF values < 0.65). These results suggest that there is a large variability in these children's ability to perform on basic numerical tasks and that mathematical difficulties may be present even in the absence of number sense deficits.

Association between intrinsic functional connectivity of the hippocampus and training-induced number sense learning

To test our central hypothesis that hippocampal functional circuits underpin number sense learning, we performed seed-to-whole-brain functional connectivity analyses using the left and right hippocampal ROIs derived from the Brainnetome (Fan et al., 2016). We first examined hippocampal connectivity patterns associated with number sense learning in the training group as a whole, and then followed up with analysis on TD children and children with MLD. Our analyses of associations between hippocampal connectivity and number sense learning controlled for pretraining symbolic quantity discrimination ability (see above, Materials and Methods).

Training group

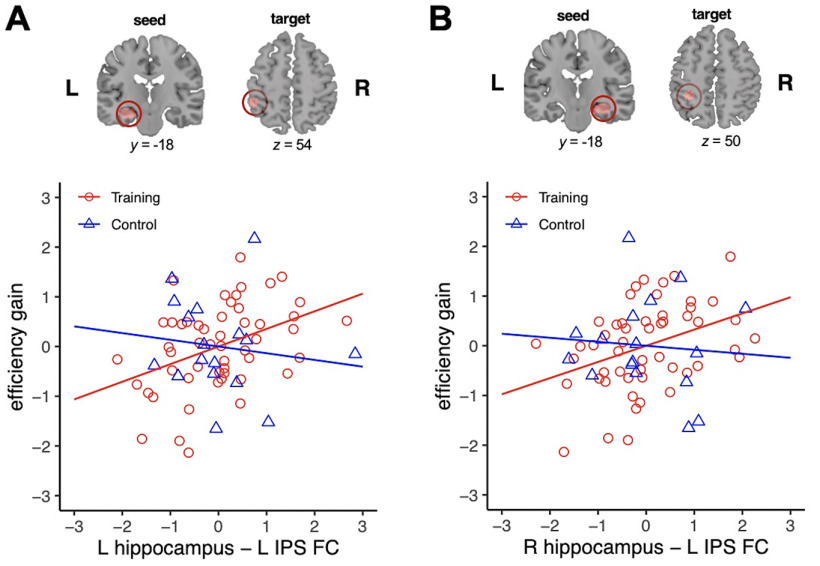
Functional connectivity of the left and right hippocampal ROIs with the left IPS before training was positively correlated with number sense learning in the training group (height threshold, p < 0.005; cluster extent threshold, p < 0.05; Fig. 3A,B; Tables 6, 7). Similar results were observed at a more stringent height threshold (p < 0.001, uncorrected). A conjunction analysis of connectivity patterns across the left and right hippocampal ROIs confirmed a single overlapping target region in the left IPS, as identified by the Juelich Histologic Atlas, positively associated with number sense learning (Fig. 3C). The left cuneus was identified as an overlapping target region negatively associated with number sense learning. Follow-up ROI-based correlation analyses were conducted in the training and control groups, using the functional connectivity between both the left and right hippocampal regions and the left IPS region identified in the training group. Similar to results from whole-brain regression analysis, hippocampal functional connectivity with the left IPS predicted number sense learning in the training group (left hippocampus: ρ = 0.42, p = 0.002, BF = 18.10; right hippocampus: ρ = 0.41, p = 0.003, BF = 9.93; Fig. 4A,B; Table 8). This association was not significant in the control group (left hippocampus: ρ = −0.20, p = 0.45, BF = 0.56; right hippocampus: ρ = −0.14, p = 0.59, BF = 0.53). A balanced fourfold cross-validation combined with linear regression (see above, Materials and Methods) further validated the robustness of findings in the training group. Functional connectivity of the left hippocampus (r(pred,actual) = 0.33, p = 0.002) and the right hippocampus (r(pred,actual) = 0.32, p = 0.002) with the left IPS was predictive of gains in symbolic quantity discrimination task efficiency following training. This relationship was not significant in the control group for both the left and right hippocampal ROIs (p values > 0.50).

Figure 3.

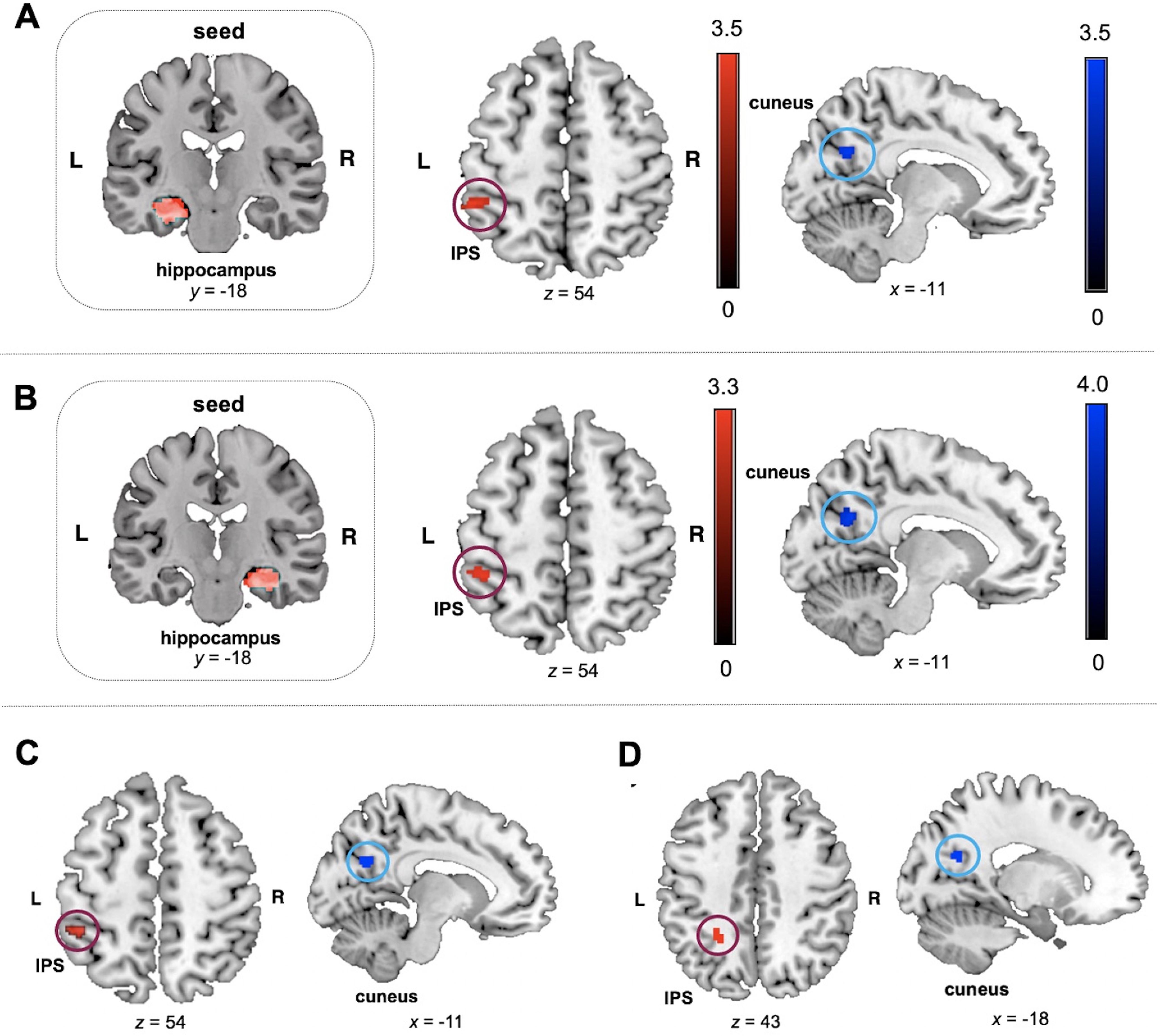
Hippocampal functional connectivity predicts number sense training gains. A, B, Functional connectivity before training of the left and right hippocampal ROIs, selected from Brainnetome (Fan et al., 2016) parcellations, with the left IPS positively (red) predicted learning (efficiency gains in symbolic quantity discrimination) in the training group. Hippocampal connectivity with the left cuneus was negatively (blue) correlated with learning. C, Conjunction analysis of functional connectivity patterns revealed the left IPS and the left cuneus to be an overlapping target region across the left and right hippocampal seed-to-whole-brain connectivity positively (red) and negatively (blue) associated with learning, respectively, in the training group. D, In TD children in the training group, hippocampal functional connectivity with the left IPS was positively associated with learning (red) and that with the left cuneus was negatively associated with learning (blue). In children with MLD in the training group, conjunction analysis did not yield any overlapping target region across the left and right hippocampal seed-to-whole-brain functional connectivity associated with learning. L, Left; R, right.

Table 6.

Brain regions showing positive and negative relations between functional connectivity with the left hippocampus and symbolic quantity discrimination efficiency gain in response to 4 week number sense training

Region	Number of voxels	Peak intensity	MNI coordinates x, y, z (mm)
Positive relation
Training
L, IPS/SMG/SPL	83	3.49	−48, −42, 54
Training, TD children
L, IPS/SPL/SMG	69	4.59	−24, −48, 42
L, MFG/PCG/SFG	68	4.18	−22, 12, 50
Training, children with MLD (none)
Negative relation
Training
L, CUN/PCUN	112	3.48	−10, −64, 26
Training, TD children
L SOG/CUN/PCUN	243	4.46	−22, −62, 24
Training, children with MLD (none)

CUN, Cuneus; MFG, middle frontal gyrus; PCG, precentral gyrus; PCUN, precuneus; SFG, superior frontal gyrus; SMG, supramarginal gyrus; SOG, superior occipital gyrus; SPL, superior parietal lobule; L, left; R, right.

Table 7.

Brain regions showing positive and negative relations between functional connectivity with the right hippocampus and symbolic quantity discrimination efficiency gain in response to 4 week number sense training

Region	Number of voxels	Peak intensity	MNI coordinates x, y, z (mm)
Positive relation
Training
L, IPS/SPL/SMG	156	3.33	−34, −40, 50
Training, TD children
L IPS/SPL/SMG	75	4.20	−24, −48, 44
Training, children with MLD (none)
Negative relation
Training
L, CUN/PCUN	140	3.92	−12, −62, 28
Training, TD children
L, PCUN/PCC	86	4.69	−4, −50, 10
L, SOG/CUN/PCUN	138	3.95	−22, −62, 24
R, SMG/AG/IPS	219	3.71	38, −52, 28
L, AG/LOC	147	3.44	−40, −76, 44
Training, children with MLD
R, CUN/LOC/OP	314	7.56	14, −90, 30

AG, Angular gyrus; CUN, cuneus; LOC, lateral occipital cortex; OP, occipital pole; PCUN, precuneus; SMG, supramarginal gyrus; SOG, superior occipital gyrus; SPL, superior parietal lobule; L, left; R, right.

Figure 4.

Hippocampal–parietal functional circuits predict number sense training gains. A, B, Scatter plots of the relationship between functional connectivity (FC) of the left (A) and right (B) hippocampus with the left IPS and changes in efficiency in symbolic quantity discrimination (efficiency gain) in children who received training (Training) and no-contact control group (Control). Greater FC with the left IPS predicts efficiency gain in the Training group (all ρ values > 0.40, all p values < 0.004), but not in the Control group (all |ρ| values < 0.21, all p values > 0.44). Target (IPS) regions of interest were identified using a 6 mm sphere centered on the peak voxel to estimate FC. L, Left, R, right.

Table 8.

Correlations between functional and structural connectivity and symbolic quantity discrimination efficiency gain in 4 week number sense training (training) and no-contact control (control) groups

	Training (N = 52†; 43‡)			Control (N = 17†, 13‡)
	ρ	p	BF	ρ	p	BF
Functional connectivity
L HIPP–L IPS	0.42**	0.002	18.10	−0.20	0.445	0.57
R HIPP–L IPS	0.41**	0.003	9.93	−0.14	0.589	0.53
L HIPP–R IPS	−0.10	0.500	0.33	−0.14	0.586	0.54
R HIPP–R IPS	0.15	0.289	0.34	−0.10	0.708	0.55
Structural connectivity
L HIPP–L IPS	−0.04	0.821	0.39	0.16	0.603	0.57
R HIPP–L IPS	−0.20	0.190	0.61	−0.08	0.803	0.75
L HIPP–R IPS	−0.12	0.448	0.54	0.08	0.803	0.59
R HIPP–R IPS	−0.03	0.865	0.38	−0.25	0.415	1.10

^†Number of participants included in functional connectivity analysis.

^‡Number of participants included in structural connectivity analysis.

**p < 0.01.

Boldface BF values (>3) provide evidence for H₁. BF values between 0.33 and 3 provide absence of evidence (i.e., insufficient evidence for either H₁ or H_o; Keysers et al., 2020). HIPP, Hippocampus; L, left; R, right.

Direct comparisons of correlation coefficients between training and control groups revealed a significant difference in the relationship between functional connectivity with the left IPS and learning for the left (Z = 2.15, p = 0.02) and the right (Z = 1.90, p = 0.03) hippocampus. Additional correlational analyses were conducted to examine the specificity of left-lateralized IPS functional connectivity patterns associated with learning. Here, the functional connectivity of the left and the right hippocampus with the right IPS (a contralateral region of the left IPS identified in the whole training group) did not significantly relate to number sense learning in the training or control group (ρ values < 0.16, p values > 0.28, BF values < 0.56; Table 8).

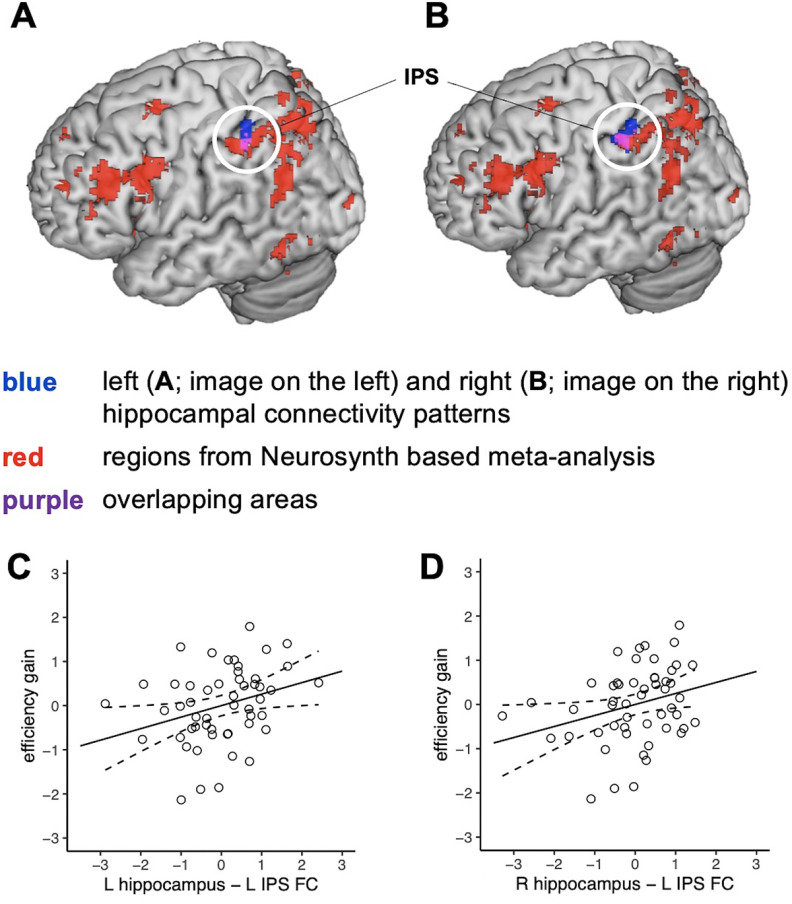
Additional analysis confirmed that IPS regions identified from the current study overlap with the left IPS region identified from Neurosynth-based meta-analysis, using the term “arithmetic” as defined in a previous study (Supekar et al., 2021; Fig. 5A,B), which indicates that the IPS region identified from our whole-brain analysis converges with the region previously shown to be involved in math cognition. Finally, when using the IPS region identified from Neurosynth-based meta-analysis, the association between hippocampal–left IPS circuits and learning in response to number sense training remained significant (left hippocampus–left IPS: ρ = 0.35, p = 0.011; right hippocampus–left IPS: ρ = 0.30, p = 0.03; Fig. 5C,D).

Figure 5.

Hippocampal connectivity with a left IPS region, identified using Neurosynth-based meta-analysis, predicts number sense training gains. A, B, Left IPS regions (white circle) overlap across (A) left and (B) right hippocampal connectivity patterns identified in the current study and the IPS region identified from Neurosynth-based meta-analysis. C, D, Scatter plots of the relationship between functional connectivity (FC) of the (A) left and (B) right hippocampal with the left IPS region identified from Neurosynth-based meta-analysis. FC between the hippocampus and left IPS correlates with changes in efficiency in symbolic quantity discrimination (efficiency gain) following number sense training (all ρ values > 0.29, all p values < 0.04). The IPS region of interest was identified using a 6 mm sphere centered on the peak voxel to estimate FC. L, Left, R, right.

Together, these results demonstrate that bilateral hippocampal functional connectivity with a common target in the left IPS is predictive of learning in response to a 4 week number sense training.

TD and MLD groups

We next examined whether hippocampal functional circuits predict number sense learning similarly or differently between children with and without MLD. We first separately conducted seed-to-whole-brain connectivity analyses for the left and right hippocampus in TD children and children with MLD. In TD children, functional connectivity of the left and right hippocampal ROIs with the left IPS predicted number sense learning (Tables 6, 7), similar to the results in the whole training group. In a conjunction analysis of the connectivity patterns across the left and right hippocampal ROIs, TD children showed the left IPS as an overlapping region positively associated with learning and the left cuneus as an overlapping region negatively associated with learning (Fig. 3D), again replicating the results of the whole training group. In contrast to the distinctive pattern observed with the TD group, whose functional connectivity between hippocampal regions and the left IPS was positively associated with learning, children with MLD showed no brain regions as targets from hippocampus to whole-brain connectivity positively associated with number sense learning, for either left or right hippocampal ROIs (Tables 6, 7). For the right hippocampus, its connectivity with the right cuneus was negatively associated with learning in children with MLD, a similar pattern observed in TD children, although in the contralateral side of the cuneus. Considering the possibility that hippocampal–left IPS circuits were not detected at the whole-brain level because of a more heterogeneous sample in the MLD group, we next performed ROI-based correlation analyses for both groups.

Using the left IPS region identified in the whole training group as the target ROI, we found that hippocampal functional connectivity with the left IPS is positively associated with number sense learning in the TD group (left hippocampus: ρ = 0.43, p = 0.01, BF = 3.98; right hippocampus: ρ = 0.38, p = 0.03, BF = 4.58; Table 9) as well as in children with MLD (left hippocampus: ρ = 0.52, p = 0.03, BF = 2.20; right hippocampus: ρ = 0.52, p = 0.03, BF = 0.93). In a cross-validation analysis (see above, Materials and Methods), functional connectivity of the left (r(pred,actual) = 0.26, p = 0.02) and right hippocampus (r(pred,actual) = 0.37, p = 0.006) with the left IPS was predictive of learning in TD children. In children with MLD, the relationship between functional connectivity and learning did not reach statistical significance at p < 0.05 in the left (r(pred,actual) = 22, p = 0.06) and right (r(pred,actual) = 0.10, p = 0.15) hippocampus.

Table 9.

Correlations between functional and structural connectivity and symbolic quantity discrimination efficiency gain in TD children and children with MLD in the training group (TD_Training and MLD_Training)

	TD_Training (N = 34†, 28‡)			MLD_Training (N = 18†, 15‡)
	ρ	p	BF	ρ	p	BF
Functional connectivity
L HIPP–L IPS	0.43*	0.012	3.98	0.52*	0.026	2.20
R HIPP–L IPS	0.38*	0.025	4.58	0.52*	0.027	0.93
L HIPP–R IPS	−0.16	0.358	0.44	<0.01	0.997	0.50
R HIPP–R IPS	0.03	0.855	0.39	0.32	0.197	0.54
Structural connectivity
L HIPP–L IPS	−0.07	0.734	0.42	−0.11	0.694	0.59
R HIPP–L IPS	−0.23	0.238	1.33	−0.25	0.362	0.54
L HIPP–R IPS	−0.05	0.806	0.43	−0.38	0.164	0.91
R HIPP–R IPS	0.03	0.897	0.41	−0.24	0.398	0.57

^†Number of participants included in functional connectivity analysis.

^‡Number of participants included in structural connectivity analysis.

*p <0.05.

Boldface BF values (>3) provide evidence for H₁. BF values between 0.33 and 3 provide absence of evidence (i.e., insufficient evidence for either H₁ or H_o; Keysers et al., 2020). HIPP, Hippocampus; L, left; R, right.

Direct comparisons of correlation coefficients between TD and MLD groups revealed no significant difference in the relationship between hippocampal functional connectivity with the left IPS and learning gains (left hippocampus: Z = 0.37, p = 0.36; right hippocampus: Z = 0.56, p = 0.29). Finally, similar to the results from the whole training group, functional connectivity of the left and right hippocampus with the right IPS did not significantly relate to learning in TD children or children with MLD (ρ values < 0.33, p values > 0.19, BF values < 0.55; Table 9).

To further address whether the relation between hippocampal–parietal functional connectivity and number sense learning varies as a function of individual differences in math ability, we additionally used a dimensional approach. In a multiple regression model, number sense learning (gains in symbolic quantity discrimination task efficiency) was entered as a dependent variable, hippocampal–parietal connectivity (left hippocampus to left IPS or right hippocampus to left IPS link), math ability (WJ-III Math Fluency), and interaction between hippocampal–parietal connectivity and math ability were entered as independent variables, and the pretraining symbolic number comparison efficiency was entered as a covariate. We found a significant main effect of hippocampal–parietal connectivity (left hippocampus to left IPS: b = 0.36, SE = 0.12, t = 3.13, p = 0.003; right hippocampus to left IPS: b = 0.32, SE = 0.12, t = 2.57, p = 0.01) but no significant main effect of math ability or interaction between hippocampal–parietal connectivity and math ability (t values < 0.81, p values > 0.42) on number sense learning.

In summary, in TD children, both left and right hippocampal functional connectivity with the left IPS predicted training-induced number sense learning, similar to that in the whole training group. Although hippocampal–left IPS circuits were not detected at the whole-brain level, children with MLD showed hippocampal–left IPS functional connectivity associated with number sense learning in ROI-based analysis, which was relatively weaker but not significantly different from that in TD children. Finally, additional analysis using math ability as a continuous variable confirmed that the relation between hippocampal–parietal connectivity and learning did not significantly vary between individuals with different levels of math ability.

Association between hippocampal–parietal white matter pathways and training-induced number sense learning

To determine whether structural integrity plays a similar role in learning as functional circuitry, we examined the relation between pretraining hippocampal–parietal white matter connectivity and number sense learning. Using probabilistic tractography of HARDI data, we identified long-range anatomic connections between the hippocampus and IPS, identified from functional connectivity analysis, averaged across all children (Fig. 6; see above, Materials and Methods) and assessed the relation between hippocampal–parietal structural connectivity and number sense learning. In contrast to the functional connectivity results, however, we did not observe evidence for structural connectivity of the hippocampus with IPS associated with training-related gains in symbolic quantity discrimination task (|ρ| values < 0.21, p values > 0.18, BF values < 0.62; Table 8). Further, there were no significant associations between structural connectivity between hippocampus and IPS and number sense learning in TD children and children with MLD (|ρ| values < 0.39, p values > 0.16, BF values < 1.34; Table 9).

Figure 6.

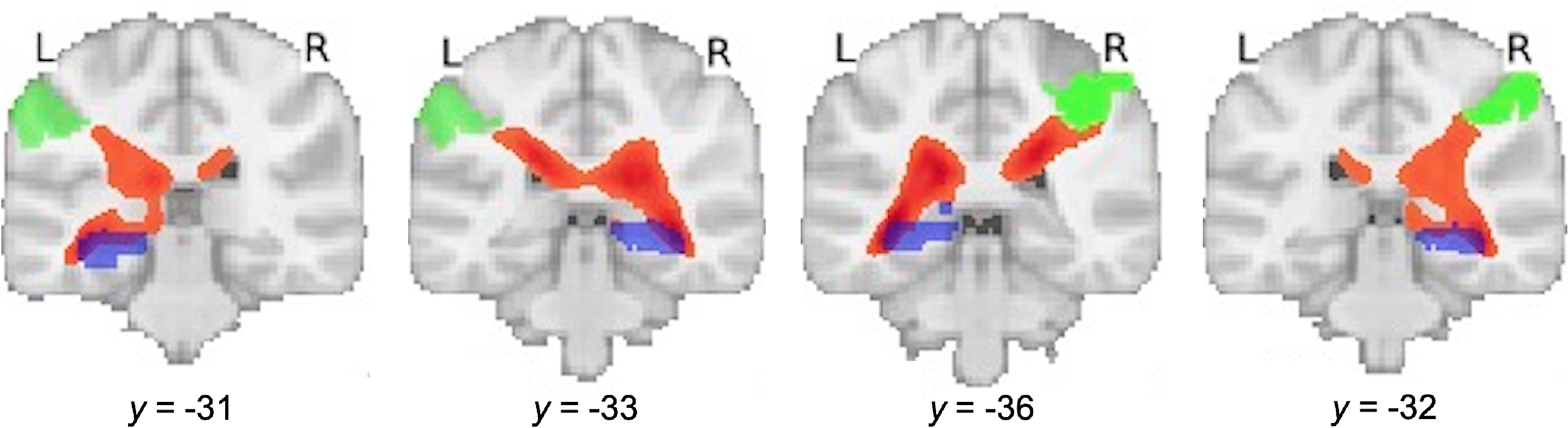
Hippocampal–parietal white matter tracts in children. White matter tracts (depicted in orange) are identified between the hippocampus (purple) and IPS (light green), averaged across all children using probabilistic tractography of high angular resolution diffusion imaging data. IPS ROIs were selected from Brainnetome (Fan et al., 2016) parcellations that overlapped with target ROIs identified in functional connectivity analysis (left IPS) and contralateral regions (right IPS) to estimate hippocampal–parietal structural connectivity. L, Left; R, right.

To further address the potential contribution of structural connectivity measures to learning, we conducted multiple regression analysis to determine whether functional and structural connectivity measures together predicted number sense learning better than each measure alone. Specifically, we examined whether the full model (Model 4) including all hippocampal–IPS functional and structural connectivity measures as predictors, compared with including functional or structural connectivity measures alone (Models 2 and 3, respectively), better predict number sense learning (Table 10). Here, we found that the full model (Model 4) explained most variance in number sense learning (adjusted R² = 0.54, F_(9,33) = 6.55, p < 0.001), significantly better than the model including structural connectivity measures alone (Model 3; $\Delta$R² = 0.33, p < 0.001, BF > 100). Critically, there was insufficient evidence (0.33 < BF < 3) that the full model including both functional and structural connectivity measures (Model 4) explain additional variance in learning, compared with the model including functional connectivity measures alone (Model 2; $\Delta$R² = 0.14, p = 0.026, BF = 2.26). Thus, we did not observe evidence that structural connectivity measures jointly predict number sense learning over and above functional connectivity measures.

Table 10.

Model comparison between multiple regression analysis including functional and/or structural connectivity measures as predictors of symbolic quantity discrimination efficiency gain in the training group (N = 43)

Model fit	Adjusted R2	F	df		p
Model 1: Baseline (1 + Control)	0.25	14.73***	1, 41		<0.001
Model 2: (Baseline + FC)	0.44	7.50***	5, 37		<0.001
Model 3: (Baseline + SC)	0.22	3.33*	5, 37		0.014
Model 4: (Baseline + FC + SC)	0.54	6.55***	9, 33		<0.001
Model comparison	$\Delta$ R2	F	df	p	BF
Model 2 (Model 1 + FC) vs Model 1 (Baseline)	0.24	4.45**	4	0.005	7.33
Model 3 (Model 1 + SC) vs Model 1	0.05	0.62	4	0.65	0.05
Model 4 (Model 2 + SC) vs Model 2	0.14	3.17*	4	0.026	2.26
Model 4 (Model 3 + FC) vs Model 3	0.33	7.61***	4	<0.001	>100

Control, Time 1 symbolic quantity discrimination task efficiency; functional connectivity, estimates of ipsilateral and contralateral functional connectivity between left and right hippocampus and left and right intraparietal sulcus; structural connectivity, estimates of ipsilateral and contralateral structural connectivity between hippocampus and intraparietal sulcus. FC, functional connectivity; SC, structural connectivity.

*p < 0.05,

**p < 0.01,

***p < 0.001. Boldface BF (>3) provides evidence for H₁. BF values between 0.33 and 3 provide absence of evidence (i.e., insufficient evidence for either H₁ or H_o). BF values below 0.33 provide evidence of absence (evidence for H_o; Keysers et al., 2020).

Together, these results suggest that the integrity of white matter pathways between the hippocampus and IPS in early childhood is not predictive of number sense learning in the current study. In addition, we observed evidence for joint associations between hippocampal–IPS functional circuits and number sense learning, independent of the underlying structural connectivity.

Reverse meta-analysis of associations between hippocampal–parietal circuits and cognitive functions

To further determine the functional role of hippocampal–IPS circuits identified in the current study, we conducted a reverse meta-analysis across 14,371 published fMRI studies up until July 2018 from the Neurosynth (Yarkoni et al., 2011) database in relation to 89 CogAt terms (Poldrack et al., 2011). To perform reverse meta-analysis relating a cognitive function with a specific circuit, we computed the probability that a term associated with a cognitive function is mentioned in a study, given that the study jointly reports activations in the left or right hippocampus and left or right IPS. We considered sufficient evidence for an association if its probability is among the 5% most probable term associations for all analyzed circuits (see above, Materials and Methods). This meta-analysis tool allowed us to synthesize a wealth of findings from previous research and generalize the findings of hippocampal–parietal circuits across various tasks and analysis approaches (Müller et al., 2018).

Our results from reverse meta-analysis show that coactivations of both the left and right hippocampus and IPS are significantly associated with the term learning as well as related terms, encoding, memory, and retrieval (Fig. 7). The term recognition was associated with coactivations of the left hippocampus and left IPS and those of bilateral hippocampus and right IPS. Two terms, attention and working memory, were associated with coactivations of the right hippocampus and bilateral IPS. The term emotion was associated with coactivations of the right hippocampus and right IPS. Finally, the term perception was associated with coactivations of the left hippocampus and left IPS. Notably, no other cognitive atlas terms were significantly associated with hippocampal–parietal functional circuits. These meta-analytic findings from a large set of fMRI studies expand on findings from our training study and provide converging evidence for a strong association between hippocampal–parietal functional circuitry and learning and related functions.

Discussion

The current study examined brain circuit mechanisms of learning in response to an integrative number sense training during an important developmental period for foundational cognitive skill acquisition. Our results reveal that number sense training significantly improves symbolic quantity discrimination ability in both TD children and children with MLD, and that hippocampal–left IPS functional circuits predict number sense training gains. Our findings provide important insights into brain-based biomarkers for early identification of individual differences in acquisition of number sense and inform interventions targeting individual needs (Hale et al., 2010).

We found that our integrative number sense training was effective across children with a wide range of abilities. Our results build on previous training studies that enhance understanding of numerical magnitudes in children (Wilson et al., 2006; Kucian et al., 2011; Dyson et al., 2013). Our study maximized effectiveness of training by uniquely combining computerized games with tutoring activities using physical manipulatives and provides new insights into the development of effective hybrid interventions across children with different backgrounds. More generally, individualized training programs designed to enhance integration of symbolic and nonsymbolic representations of quantity may have the potential to build strong foundations for mathematical learning across all children.

It is noteworthy that before training, we did not observe poor number sense in our sample of children with MLD who performed significantly worse than TD children on assessments of arithmetic problem solving and mathematical reasoning, similar to the previous observation that difficulties in math problem solving may be present even in the absence of number sense deficits (Peters et al., 2020). As MLD is considered a heterogeneous disorder with multiple cognitive deficits (Fias et al., 2013; Kaufmann et al., 2013), further studies that employ assessments in various cognitive domains may help determine multidimensional neurocognitive deficits in MLD. In addition, development of classification of subtypes of MLD will be an important avenue for future research.

Our next goal was to investigate whether the integrity of hippocampal–parietal circuits predicts individual differences in number sense training gains in children. We identified an intrinsic functional circuit that links the hippocampus, a hub for learning and memory, with a parietal region consistently implicated in numerical quantity representation, which predicts number sense learning. Our finding converges on previous studies demonstrating the key functional role of the hippocampus in the development of arithmetic skills in children (Menon, 2016; Menon and Chang, 2021) and learning and memory more broadly (Zeithamova and Bowman, 2020). Notably, this contribution occurred even though our number sense training did not require rote memorization of facts and is consistent with emerging evidence for a role of the hippocampus in binding cognitive representations (Degonda et al., 2005; Olsen et al., 2012).

Our finding is also consistent with previous evidence indicating the role of IPS in representation of quantities (Cohen Kadosh et al., 2007; Piazza and Eger, 2016). Remarkably, functional connectivity of the left and right hippocampus identified a single region in the left IPS that predicted learning. Previous studies have found that compared with its right hemisphere homolog, the left IPS is particularly important for symbolic number processing (Ansari, 2007; Piazza et al., 2007; Bugden et al., 2012; Sokolowski et al., 2017) and that with age and increased proficiency in numerical skills, there is an increase in left IPS activity (Rivera et al., 2005; Ansari, 2008; Emerson and Cantlon, 2015; Bugden et al., 2016). In this context, it is possible that our finding of left-lateralized IPS response may be reflective of increased proficiency for symbolic numbers.

In addition to the left IPS as a converging target region for the left and right hippocampal functional circuits positively associated with number sense learning, the left cuneus, implicated in low-level visual processing (Vanni et al., 2001), was identified as a target region negatively associated with number sense training gains. This finding suggests that children's number sense learning likely relies on enhanced semantic representation of quantity, rather than visual perception of numbers. In fact, greater hippocampal functional connectivity with a visual region (cuneus) predicted poor learning. No other brain regions were identified as overlapping target regions across the left and right hippocampal functional connectivity associated with learning. Together, our findings demonstrate a key role for hippocampal–parietal circuits in children's number sense learning.

Our whole-brain analysis of subgroups of children revealed that TD children recapitulate the hippocampal–left IPS functional circuit-related learning as seen in the combined group. Although no significant target regions were detected in hippocampal connectivity positively associated with learning in children with MLD, possibly because of modest sample size in this group, additional analysis confirmed that the association between hippocampal–left IPS circuits and learning was similar in the TD and MLD groups, consistent with our observation of comparable training gains in the two groups. Thus, our findings identify hippocampal–left IPS functional circuit as a novel locus of learning that supports acquisition of fundamental building blocks of numerical proficiency across all children, including those with learning disabilities. Future studies with a larger sample of children with MLD may further clarify heterogeneous profiles of learning-related hippocampal circuits.

Probabilistic tractography of HARDI data revealed the presence of long-range anatomic connections between the hippocampus and the parietal cortex in 7- to 10-year-old children, replicating observations in younger children (Ngo et al., 2017). In contrast to findings from functional circuit analysis, however, structural connectivity between the hippocampus and IPS did not relate to individual differences in learning. In addition, although hippocampal–parietal functional connectivity measures jointly predicted learning over and above measures of structural integrity, we did not find evidence that structural connectivity measures jointly predict learning over and above functional connectivity measures. Thus, although hippocampal–parietal white matter tracts appear to be formed by early childhood, precisely how they contribute to number sense learning remains unresolved. Crucially, our study provides evidence for emergent functional properties of hippocampal–parietal circuits as significant and independent neural predictors of number sense learning, which may inform early identification of individual differences in response to intervention. Future studies using larger datasets with an active control group may help identify generalizable predictive features of learning and further determine specific mechanisms underlying acquisition of foundational cognitive skills.

Finally, our findings converge on results from a reverse meta-analysis in which we examined the role of hippocampal–parietal functional links identified in the present study. Across 14,371 fMRI studies and 89 cognitive atlas terms, our analysis revealed a significant association between bilateral hippocampal–IPS functional circuits and the term learning, along with related terms memory, encoding, and retrieval. Interactions between the hippocampus and neocortex are known to be crucial for memory formation (McClelland et al., 1995; Tse et al., 2007), and hippocampal connectivity with parietal and frontal cortical regions have been shown to be associated with longitudinal gains in memory retrieval fluency in children (Qin et al., 2014). Together, our findings identify specific hippocampal–neocortical functional circuitries that may contribute to learning and memory consolidation.

Although involvement of the hippocampus in learning and memory is well known, the specific role of hippocampal–IPS functional circuits has been less clear as research on the role of parietal cortex in memory has emphasized its angular gyrus subdivision in episodic memory (Sestieri et al., 2017). The angular gyrus, as part of the default mode network, is crucial for generating integrated representation of information retrieved from episodic memory (Binder and Desai, 2011). In contrast, the IPS, as part of the dorsal attention network, is crucial for representing and manipulating visuospatial perceptual information (Uddin et al., 2010). Consistent with this view, we found that IPS-relevant terms, specifically perception, attention, and working memory, are associated with hippocampus–IPS circuits. In the context of number sense learning, we propose that these functions, together with learning and memory, support the formation of semantic associations between quantities presented in nonsymbolic and symbolic formats. Thus, findings from a reverse meta-analysis of a large corpus of fMRI studies and our training study suggest that hippocampal–IPS circuits constitute a distinct canonical circuit for integrating and manipulating mnemonic and visuospatial information that plays a foundational role in children's cognitive skill acquisition. More broadly, interventions designed to engage these brain circuits, such as integrative number sense training in the current study, may effectively promote learning across various cognitive domains.

In summary, the current study demonstrates that core learning and memory functional circuits anchored in the hippocampus play an important role in learning number sense, a fundamental building block of mathematical skill acquisition. Notably, the left IPS, implicated in numerical proficiency, was a convergence zone for the left and right hippocampal functional circuits that predict individual differences in number sense learning. Our study provides foundational knowledge about brain circuit mechanisms that propel learning in all children and delineates a robust target for effective interventions and monitoring response to cognitive training.