Real-time dynamic simulation for highly accurate spatiotemporal brain deformation from impact

Abstract

Real-time dynamic simulation remains a significant challenge for spatiotemporal data of high dimension and resolution. In this study, we establish a transformer neural network (TNN) originally developed for natural language processing and a separate convolutional neural network (CNN) to estimate five-dimensional (5D) spatiotemporal brain–skull relative displacement resulting from impact (isotropic spatial resolution of 4 mm with temporal resolution of 1 ms). Sequential training is applied to train (N = 5184 samples) the two neural networks for estimating the complete 5D displacement across a temporal duration of 60 ms. We find that TNN slightly but consistently outperforms CNN in accuracy for both displacement and the resulting voxel-wise four-dimensional (4D) maximum principal strain (e.g., root mean squared error (RMSE) of ~1.0% vs. ~1.6%, with coefficient of determination, R² >0.99 vs. >0.98, respectively, and normalized RMSE (NRMSE) at peak displacement of 2%–3%, based on an independent testing dataset; N = 314). Their accuracies are similar for a range of real-world impacts drawn from various published sources (dummy, helmet, football, soccer, and car crash; average RMSE/NRMSE of ~0.3 mm/~4%–5% and average R² of ~0.98 at peak displacement). Sequential training is effective for allowing instantaneous estimation of 5D displacement with high accuracy, although TNN poses a heavier computational burden in training. This work enables efficient characterization of the intrinsically dynamic brain strain in impact critical for downstream multiscale axonal injury model simulation. This is also the first application of TNN in biomechanics, which offers important insight into how real-time dynamic simulations can be achieved across diverse engineering fields.

1. Introduction

Dynamic simulation is ubiquitous across diverse engineering fields [1]. This type of simulation models time-varying behavior of a system described by differential equations solved by the simulation to obtain state variables over time. Unlike a static simulation in which output only relies on the current input, the entire response history including prior inputs, internal variables and outputs is also critical for the current output in a dynamic simulation. Therefore, achieving real-time dynamic simulation remains a significant challenge, especially for high-dimensional data [2,3].

In computational biomechanics, artificial neural networks are often used to substantially improve dynamic simulation efficiency. For example, a fully connected neural network was used to speed up the Total Lagrangian Explicit Dynamics algorithm in soft tissue dynamic simulation [4], achieving real-time performance in flexible multibody dynamics [5]. More sophisticated long short-term memory (LSTM) [6] and sparse autoencoder [7] neural networks are also employed to approximate time-series data and to generate thermodynamics-aware reduced-order models, respectively. More recently, a three-dimensional (3D) convolutional neural network (CNN) was developed to process dynamic axial crushing typically used in vehicle crashworthiness applications [8]. The success of these studies inspires further explorations of how modern neural networks can be employed to facilitate diverse dynamic simulations.

In the field of biomechanical mechanism of traumatic brain injury (TBI), head injury models are also widely used to simulate dynamic head impact [9]. The model discretizes the brain’s spatial domain to assemble a large system of equations according to nonlinear and viscoelastic material properties of the brain and tissue boundary conditions. For a given head impact, explicit time integration is often used to model the nonlinear transient event, in which a time increment is solved relatively efficiently but the time increment must be small enough (i.e., typically on the order of 10⁻⁷ s for the brain due to its material properties and millimeter spatial resolution) to ensure accuracy [10]. As a result, it requires hours [11–13] or days [14,15] to simulate a typical head impact of ~100 ms, even on a high-performance computing platform. The poor impact simulation efficiency precludes the use of head injury models for large-scale TBI studies or adoption for injury prediction on the sports field.

1.1. Previous studies in TBI

To substantially reduce impact simulation runtime, reduced order models oversimplify the whole brain as a single unit to approximate peak maximum principal strain (MPS), regardless of the anatomical location or time of occurrence [16,17]. In contrast, a pre-computation technique idealizes arbitrary impact rotational kinematic profiles into triangular shapes, which allows for efficient interpolation or extrapolation of element-wise MPS based on a large pre-computed database [18]. The latter approach was extended to a CNN to instantly estimate regional [19] and whole-brain [20] MPS with high accuracy for impacts in contact sports, and, importantly, without any simplification to impact profile. Recently, the technique was further extended to automotive head impacts [21], where impact kinematic profiles are generally more complex with much longer durations than those in contact sports (e.g., <100 ms vs. 300–500 ms). The CNN technique conceptualizes a time-varying head impact kinematic profile as a 2D image, which allows for synchronous capture of the temporal variation of impact kinematics along the three anatomical axes known to be important to brain strain [22,23]. It is notably more advantageous and robust than previous efforts, as no simplification to either the head injury model or kinematic input is necessary.

Nevertheless, a limitation with prior studies is that they focus on static peak MPS but ignore its intrinsically dynamic characteristics, where minimum principal strain or compression [24] as well as strain rate [25] are also important to neuronal injury. Dynamic tissue strain is also critical for microscale injury models as it serves as input to drive the deformation of individual axons [26]. Although such history information is available from model simulation, this requires substantial simulation runtime and, thus, is infeasible to handle a large number of impacts such as those in contact sports.

Therefore, the goal of this study is to further extend our previous work to rapidly estimate the entire spatiotemporal brain strains, beyond the spatially detailed but “static” peak strains of the whole brain [20]. This would allow utilizing the complete brain strain dynamics for future TBI investigations, such as to enable multiscale axonal injury model simulations [26], to produce strain and strain rate features for machine learning in injury prediction [27], and to develop cumulative injury risks based on tissue strain and strain-rate from many head impacts [28]. The techniques developed here may also offer insight into how they can be extended to real-time dynamic simulation in diverse problems and broad engineering fields [29,30].

1.2. Deep learning models for spatiotemporal data

To date, neural network architectures for modeling spatiotemporal data are mostly based on either recurrent neural network (RNN; e.g., video-based force estimation in robot-assisted surgery [31]) or CNN (e.g., to process both spatial and temporal information in surgical video analysis [32]). A Deep learning architecture combining both CNN and RNN via LSTM was also used for video-based gesture recognition [33]. Applications of deep learning models for high-dimensional spatiotemporal data have also emerged. For example, CNN models with four-dimensional (4D) filters were developed for CT image reconstruction [34] and segmentation [35]. Sparse convolution was proposed for 3D video-based segmentation [36]. Based on the RGB video images, temporal CNN was used for surgical force prediction [37].

A potential limitation with RNN and CNN is that they may not be well suited to handle long-range dependencies. For RNNs, they suffer from vanishing gradient when using gradient-based approaches and backpropagation for training [38]. For CNNs, they suffer from limited receptive fields of convolutional filters, which are defined as the region of input space that generates output features [39]. This may put them at a disadvantage when modeling transient dynamic head impact as brain spatiotemporal responses depend on the entire history of impact loading. In addition, RNNs are also not well suited for parallel training as they need to process the sequence data recursively, which decreases efficiency [40].

1.3. Transformer neural network (TNN)

A breakthrough in modeling sequential data is the transformer neural network (TNN) originally developed for natural language processing (NLP) [41]. It employs a self-attention mechanism to learn the feature at each element by calculating a weighted sum of features using pair-wise affinities across all elements within a single sequence [42]. TNN is found to be more effective than RNN and CNN in modeling long-range data with higher efficiency due to the ability for parallelization [40]. Recently, TNNs have been successfully applied to computer vision (e.g., object detection [43,44] and image recognition [45,46]) and medical imaging (e.g., brain tumor and spleen segmentation [39] and multi-modal brain image classifications [47]).

To the best of our knowledge, nevertheless, TNN has not been employed in biomechanical engineering, including impact biomechanics such as traumatic head impact simulation. Given that impact-induced brain strain depends on the complete history of head kinematics serving as simulation input [22,23], we hypothesize that a TNN is also effective in learning and predicting the spatiotemporal evolution of brain deformation. In addition, to compare TNN with the more commonly employed CNN for estimating high-dimensional spatiotemporal data, we also extend our previous CNN model [20] to rapidly estimate spatiotemporal brain deformation, as a comparison.

1.4. Five-dimensional (5D) spatiotemporal displacement

FE model simulation generates node-wise displacement from which element-wise strain is derived, the latter of which is typically the response of interest. A displacement in a 3D space is a 1 × 3 vector while a strain tensor is a 3 × 3 symmetric matrix with six unique components. Therefore, we choose displacement for training and prediction as it approximately halves the amount of data to handle. Only relative brain–skull displacement (simulated displacement subtracting the rigid-body skull motion) is relevant to brain strain. When the relative brain–skull displacement field is generated at voxel corner nodes of an image volume, voxel-wise strain can be easily determined with high efficiency (details described later and in [48]).

Even with this arrangement, a 5D displacement field (a 3D voxelized image volume with two additional dimensions for displacement components and time, respectively) is necessary. This poses a significant challenge for neural network training due to the high spatial and temporal resolution (on the order of mm and ms, respectively) and the number of training samples (thousands). Therefore, we further adopt a sequential training strategy [49] and a multi-task neural network architecture to reduce computational burden. Our main contributions are:

1. Develop a TNN and a separate CNN to estimate 5D spatiotemporal relative brain–skull displacement field, from which we derive a 4D strain field. This significantly improves over the previous work limited to a static 3D distribution of peak MPS [20] that ignores the dynamic nature of brain strain. To the best of our knowledge, this is the first application of TNN in biomechanical engineering, including in injury biomechanics and traumatic brain injury.

2. Adopt a sequential training strategy and multi-task TNN/CNN to separate the dynamic event into multiple intervals, which reduce the high demand of computing resources for training the entire data at once. After training, a single neural network is available to estimate the complete 5D spatiotemporal displacement on any computer including lower-end laptops.

3. Finally, we choose to train and estimate relative brain–skull displacement resampled on a voxelized isotropic grid instead of element-wise strain tensor directly. This not only reduces the amount of data to handle but also provides voxelized displacement and strain in a standard image format to greatly facilitate multimodal analysis and data sharing in the future [48].

2. Methods

2.1. Anisotropic Worcester head injury model

All head impacts were previously simulated using the anisotropic Worcester Head Injury Model (WHIM) Version1.0 (Fig. 1; [50]). The model was created with high mesh quality and geometrical accuracy based on high-resolution T1-weighted magnetic resonance image (MRI) of a concussed athlete [51]. In total, the model contains 56.6k nodes and 55.1k hexahedral elements for the brain with an average element size of 3.3 ± 0.79 mm. It adopts a hyper-viscoelastic material model of the brain and further incorporates anisotropy of the white matter based on whole-brain tractography [52]. Specifically, an Ogden material model is used to prescribe the hyperelasticity of the entire brain, including gray and white matter [51]. The viscoelasticity is described by a two-term Prony series [50], with the dimensionless relaxation modulus and time constants drawn from an in vivo shearing dynamic test at a large range of frequency [53]. The white matter anisotropy is implemented via the Holzapfel–Gasser–Ogden (HGO) constitutive model, which allows incorporating fiber orientation and dispersion parameters based on tractography fractional anisotropy directly into the strain energy function.

Fig. 1.

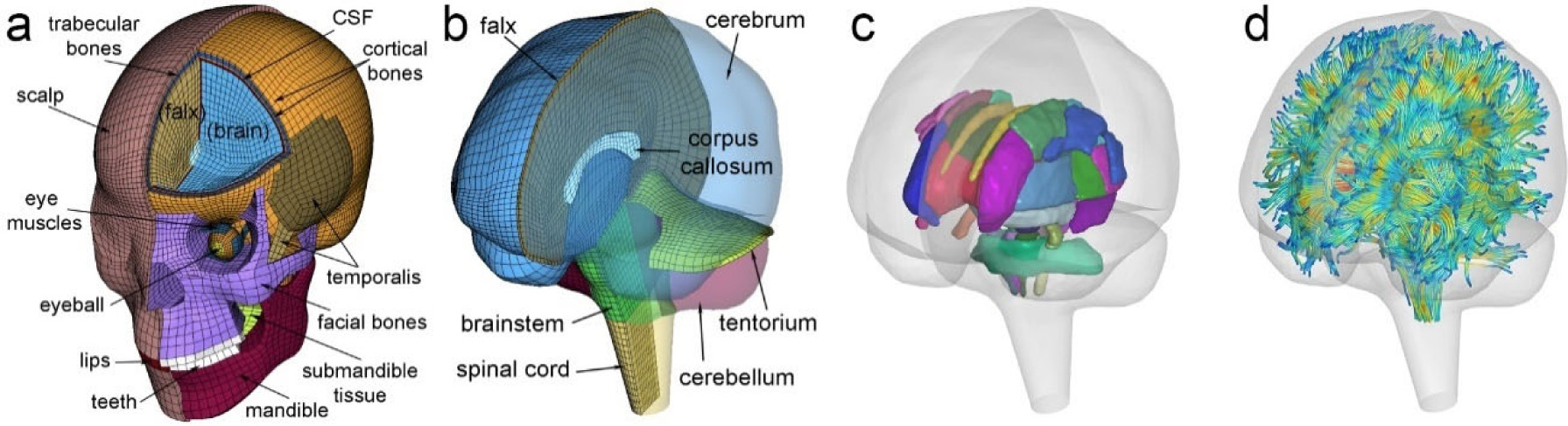
The exterior features (a) and intracranial components (b) of the anisotropic Worcester Head Injury Model (WHIM, V1.0) showing 50 deep white matter regions of interest (c) and a subset of white matter tractography fibers color-coded by their fractional anisotropy values (d).. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Details of the material parameters and their values have been reported in previous publications for the brain [50] and other components such as the falx, tentorium, dura, cerebrospinal fluid, etc. [51]. For the brain, the initial (and equivalently, the long-term) shear stiffness value has been calibrated to yield a comparable elementwise peak strain magnitude relative to the previous isotropic WHIM V1.0 [50]. Both the isotropic [51] and anisotropic [50] WHIMs have been extensively validated in terms of relative brain–skull displacement in cadaveric impacts and in strain across a wide-range of blunt impact conditions (high- and mid-rate cadaveric impacts and in vivo head rotations). They both achieve an average peak strain magnitude ratio (simulation vs. experiment) of 0.94 ± 0.30 based on marker-based strains in 12 cadaveric impacts [54]. A ratio of 1.00 ± 0.00 would indicate an identical peak response relative to experiment (albeit errors in experimental data, themselves, should not be ignored). The head coordinate system was chosen such that the posterior-to-anterior, right-to-left, and inferior-to-superior directions corresponded to the x, y, and z directions, respectively.

2.2. Data preprocessing

A total of N = 5184 impacts previously simulated were used in this study for training [20]. For impacts potential of causing mild TBI without significant skull deformation such as those in contact sports, it is common to simplify the skull as a rigid body [55]. Consequently, impact location and directionality become irrelevant to brain deformation simulation because the head kinematic motion is fully described by the skull linear acceleration and rotational acceleration (or equivalently, velocity), which are often prescribed at the head center of gravity. Given that linear acceleration generates little strain due to the brain’s near incompressibility property as confirmed in multiple head injury models [23,56], only head rotational kinematics are necessary for head impact simulation.

In this study, impact rotational kinematics were generated through data augmentation based on impacts measured in American college football, boxing, and mixed martial arts (N = 110; 6 batches) [57] and those reconstructed in the laboratory (N = 53; 8 batches) [58]. For the former, video confirmation was used to verify that each recording indeed corresponded to a true positive head impact rather than a spurious event. This ensured that the augmented training data were realistic. Data augmentation involved permuting head rotational velocity (v_rot) components about the three anatomical directions (3! = 6; each batch generates six times of data) with further random perturbation of the rotational axis and random scaling of v_rot peak magnitudes, as detailed previously [19]. The augmented data were targeted to uniformly sample rotational peak velocity magnitude in the range of 2–40 rad/s, relevant to the vast majority of real-world impacts in contact sports [59].

All impacts had a head rotational azimuth angle, θ (determined at the time when the resultant v_rot was at peak [60]) constrained to one half of the sampling range ([−90°, 90°] vs. [−180°, 180°]) due to WHIM symmetry about the mid-sagittal plane [19]. This maximized the use of head impact profiles for generating unique brain responses (i.e., essentially, halved the amount of data required). All impact profiles had a duration of 100 ms. For each impact, head v_rot and acceleration (a_rot) profiles were concatenated (with the latter scaled to 1% to ensure a comparable data range) as neural network input. Combining the two channels of signals was found to improve accuracy in estimating strain spatial distribution [20]. The simulated relative brain–skull displacements (3 components along the x, y, and z anatomical directions) were resampled onto a voxelized isotropic grid of 4 mm × 4 mm × 4 mm resolution, with a temporal resolution of 1 ms. The output for each simulated impact of 100 ms was a 5D matrix of size of 46 × 35×36 × 3×101. A 3D brain mask was finally applied to exclude non-brain areas, which reduced the output from 173.9k (46 × 35×36 × 3) to 71.1k at each time frame.

Fig. 2 reports the peak magnitudes of relative brain–skull displacement (after subtracting rigid-body skull motion) and MPS of the whole brain averaged from the entire dataset at each time frame. To focus on larger strain magnitudes most relevant to injury and to reduce computational burden, we empirically limited the training and prediction to the range of 31st to 90th time frames, for a total of 60 ms duration at a temporal resolution of 1 ms. This was sufficient for performance verification using an independent dataset (N = 314; details below).

Fig. 2.

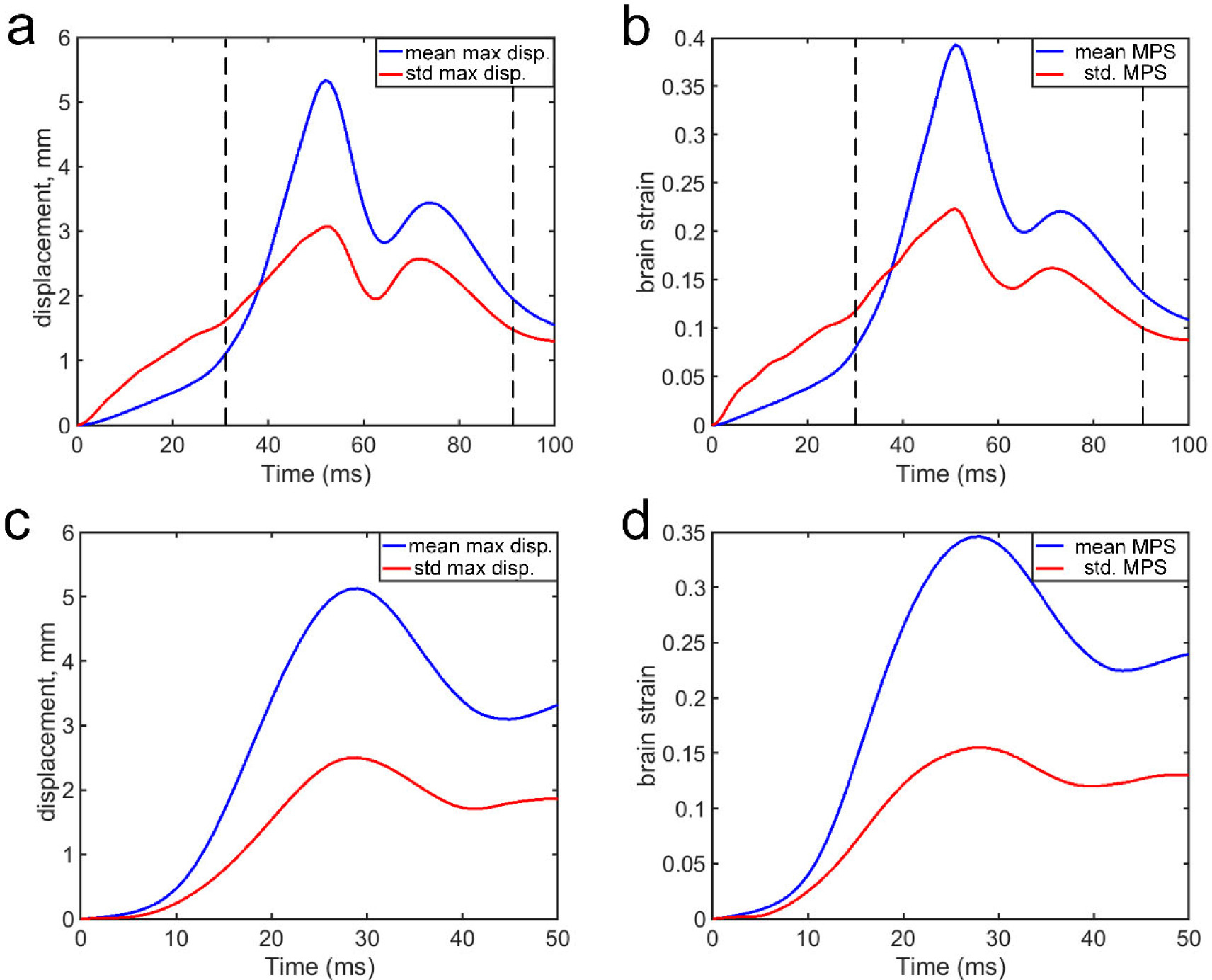
Peak relative brain–skull displacement magnitude (a; in mm) and MPS (b) averaged from the entire training dataset (N = 5184) at a temporal resolution of 1 ms (for a duration of 100 ms). Empirically, only data within 31–90 ms were utilized for training and estimation. The corresponding relative brain–skull displacement magnitude (c; in mm) and MPS (b) for independent testing dataset (N = 314).

2.3. Baseline training for multiple independent models

It was infeasible to use the entire dataset to train a single TNN or CNN to predict the complete 60 time frames (from 31st to 90th; Fig. 2) on our computing platform (Linux 256 GB for CPU, 36 GB for Nvidia V100 GPU). Therefore, the impact duration was empirically divided into 6 intervals of 10 consecutive time frames. For each interval, a baseline TNN or CNN model was independently trained to predict displacement within each time interval. An empirical batch size of 40 and 500 epochs were used to train baseline TNN models. For CNN models, a batch size of 256 and 400 epochs were used, following the previous study [20]. The following loss function was used:

$$l_k=\frac{1}{3}\sum _{i=1}^3(\frac{1}{N}\sum _{j=1}^N{(x_{ij}-y_{ij})}^2),$$ (1)

$$los{s}_{task}=\frac{1}{M}\sum _{k=1}^M{w}_k*l_k,$$ (2)

where x_ij and y_ij are the estimated and directly simulated displacements for the ith component (i = 1, 2, and 3, for a total of 3 displacement components) and the jth training sample (total of N), respectively; l_k and w_k are the loss and the corresponding weighting factor in kth time frame; M is the number of consecutive time frames (10 for each baseline model); and finally, task is the given assigned “task” representation from 1 to 6, where task1 indicated the time interval from 81st to 90th, task 2 indicated 71st to 80th, until task 6 for interval from 31st to 40th. The task representation followed a reverse order of the time interval sequence to facilitate sequential training (below). For simplicity, all the weighting factors were set to 1.0 (i.e., equal weighting). A 5-fold cross-validation was used to test the performance based on predicted displacement components. Specifically, the dataset was randomly divided into five approximately equal folds. Four folds were combined for training while the remaining fold was used for testing. The process was repeated five times so that each fold was tested exactly once, and their average performances were reported.

2.4. Sequential training for a single model

To train a single TNN or CNN model without substantial memory requirement, a sequential training strategy [49] was used, along with a corresponding multi-task network architecture. The basic idea was to mix training samples from the previous training tasks or time intervals into the current one while limiting the total training sample size (Fig. 3).

Fig. 3.

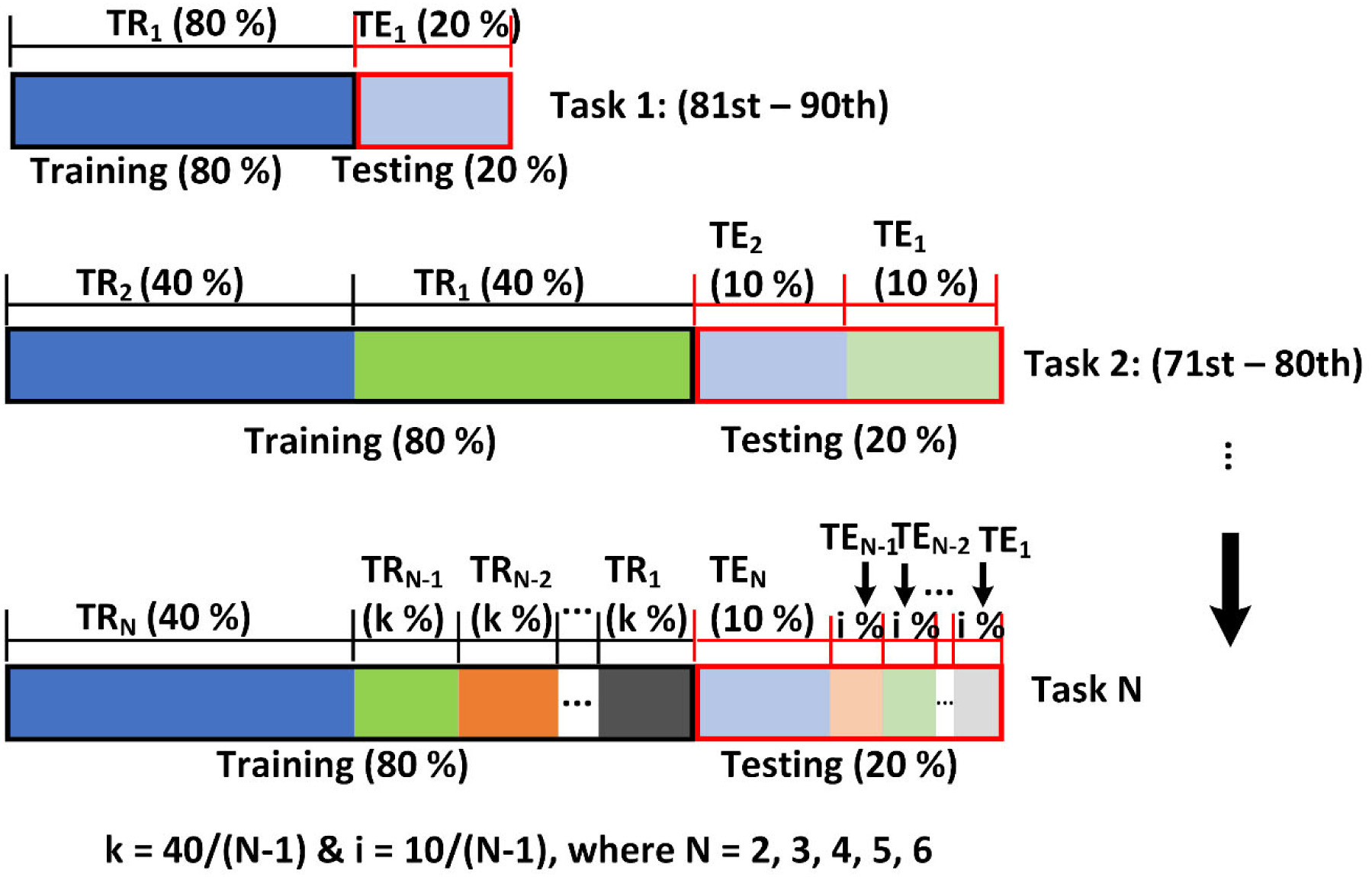
Illustration of the sequential training strategy with a 5-fold cross validation (training (TR) and testing (TE) split by 80% and 20%, respectively). In all tasks, only selected temporal intervals from the entire impact cases (N = 5184) are used for training and testing.

Intuitively, the longer the input time history is, it is likely more challenging to train and maintain a high accuracy. However, displacement and strain from later time frames are typically of larger values than the initial ones (Fig. 2), and are, thus, more relevant to brain injury. Therefore, we chose a reverse order of time intervals for sequential training to ensure that later stage predictions were sufficiently accurate. Specifically, the baseline model corresponding to the last time interval (i.e., task 1 of 81st to 90th ms) served as the starting point, because it had the longest time input history or input size than the first time interval (i.e., task 6 of 31st to 40th) of the shortest history. For the second training task of the preceding time interval, samples from both time intervals were mixed and divided into training and testing samples. The sample size for the second task was effectively doubled compared to the baseline. For subsequent tasks of the preceding time intervals, however, the total sample size was maintained a constant, with the current interval always having half of the samples (split to training and testing) while the percentages from previous tasks following the formulars shown in the figure (Fig. 3). This strategy ensured that more “recent” tasks will have more training/testing samples while more “distant” tasks will have less, as they have participated in training/testing less or more often, respectively.

2.5. Multi-task TNN and CNN architectures

To enable sequential training, it was necessary to provide the specific task as input. A multi-head encoder TNN designed for NLP [41] was adapted. Since the TNN requires the input to be a 1D vector, the 3 channels of v_rot and the corresponding 3 channels of a_rot were first reformatted into a matrix format of 6 × 101 (0 to 100 ms) before being reshaped into a vector. Using a similar approach previously developed for CNN [49], a 1 × 6 vector was used to represent the 6 training tasks. With trial and error, the optimized TNN architecture (Fig. 4) starts with an input layer of size of 612 (a 1D vector for concatenated input of 6 × 101, and 1 × 6 for task representation), followed by a standard 1D positional encoding (with 64 embedded dimensions) and two identical layers of Transformer encoder. They are followed by one fully connected layer for linear projection [41] with encoder output (612 × 64) as input and a linearly projected 1D vector as output (612 × 1 units). This is followed by another fully connected layer with 618 units for input (612 units from the previous layer and another fresh 1 × 6 task identifiers to ensure unambiguous representation, as output from the Transformer encoder may have altered the values of the previous task representation). Finally, 71.1k units are used for displacement output using a linear activation function. Using a subset of data, the number of TNN encoder layers was also determined to best balance performance and computational resources, and to avoid any potential underfitting. In contrast, overfitting was mitigated by using dropout and early stopping [21,61].

Fig. 4.

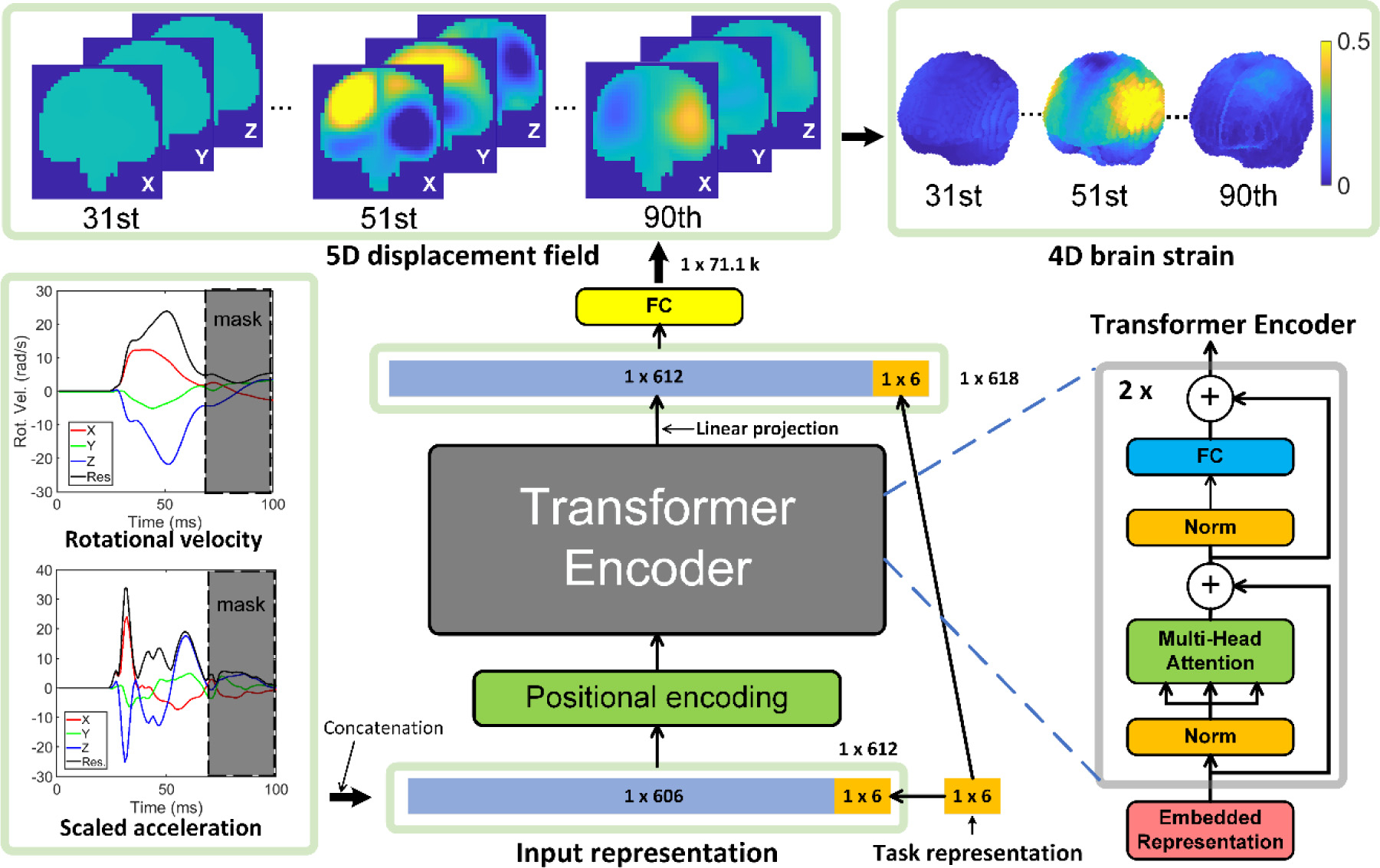
The overall framework of the multi-task TNN architecture to predict time-dependent relative brain–skull displacement, from which brain strain and strain rate are calculated subsequently. A binary mask is applied to the kinematic input to avoid influence from “future” information. FC: fully connected layer.

Given that the current output depends on the past and current input but not on future input, we explicitly applied a binary mask in input to avoid influence from “future” information [62] (i.e., setting v_rot and a_rot to zero for (i + 1)st ms and beyond when predicting displacement at the ith ms).

For multi-task CNN, the previous architecture [20] was modified so that the number of units in the last fully connected layer matched with the number of displacement component outputs. Similar to the TNN, each baseline CNN model was targeted to train 10 consecutive time frames with the same loss functions (Eqs. (1) and (2)) and with a binary mask applied to input [62]. A one-hot task (1 × 6) representing a learned bias [49] was added to each CNN filter output of the first convolution layer through linear projection. Then, the same task vector was concatenated into the input of the first fully connected layer (Fig. 5).

Fig. 5.

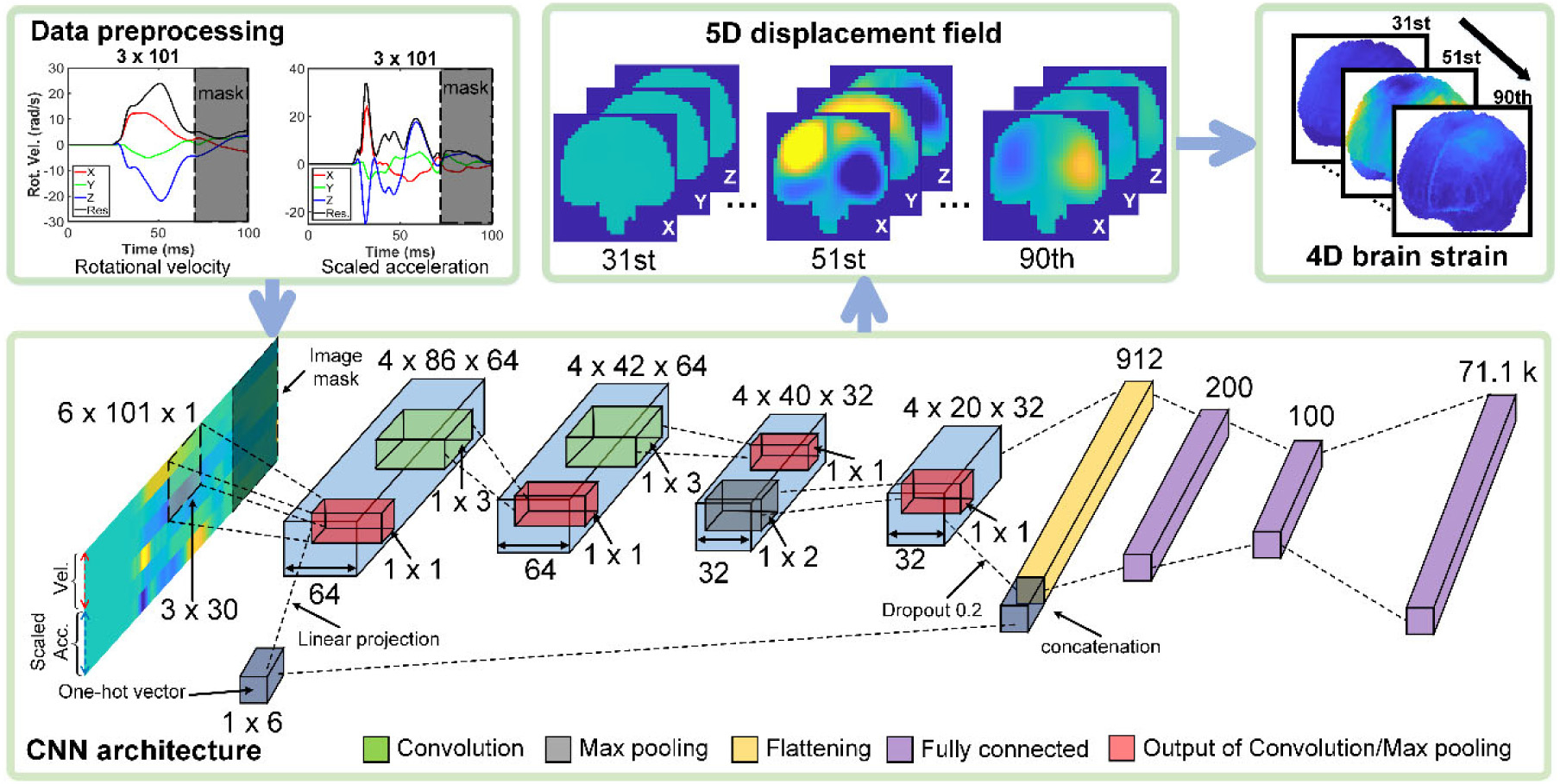
CNN architecture adapted for multi-task training to predict time-dependent relative brain–skull displacement. At a given time frame, future information in input is masked.

2.6. Voxel-wise brain strain from voxelized relative brain–skull displacement field

When a nodal displacement field is resampled onto a regular grid lattice of size of p × q × r (e.g., via scattered interpolation), a voxel-wise strain field at the lattice centroids of size of (p − 1) × (q − 1) × (r − 1) can be obtained. A voxel is a special 8-noded hexahedral element whose displacement can be represented by the weighted average of nodal displacements, u_i, according to shape functions, N_i (ξ, η, ζ):

$$\mathbf{u}=\sum _{i=1}^8{N}_i(\xi ,\eta ,\zeta ){\mathit{u}}_i.$$ (3)

To derive voxel-wise strain, the deformation gradient, F, is calculated as:

$$\mathbf{F}=\mathbf{I}+\nabla \mathbf{u}=\mathbf{I}+\frac{\partial \mathbf{u}}{\partial \mathbf{X}}=\mathbf{I}+\frac{\partial \mathbf{u}}{\partial \mathbf{\Xi }}\frac{\partial \mathbf{\Xi }}{\partial \mathbf{X}}=\mathbf{I}+\frac{\partial \mathbf{u}}{\partial \mathbf{\Xi }}{\mathbf{J}}^{-1},$$ (4)

where X_i are the voxel corner nodal coordinates, Ξ = Ξ(ξ, η, ζ) are their corresponding nodal coordinates in the natural coordinate system, I is an identity matrix, and $\mathbf{J}=\frac{\partial \mathbf{X}}{\partial \mathbf{\Xi }}$ is the Jacobian matrix. In this study, we calculated engineering strain following the finite strain theory. The following holds:

$$\mathbf{V}=\sqrt{\mathbf{F}\times {\mathbf{F}}^{\prime }},$$ (5)

$$\mathbf{\epsilon }=\mathbf{V}-\mathbf{I}.$$ (6)

where V is the left stretch tensor in the current configuration, and ε is the strain tensor of interest [10]. For an isotropic voxel whose nodes are regularly positioned, J degenerates into an identity matrix, I (with a proper linear scaling). This greatly simplifies the strain tensor calculation. The MPS is the maximum eigenvalue of the strain tensor [63]. The customized strain calculation was verified against Abaqus [10] to yield identical results. More details of the displacement voxelization scheme and extensive accuracy assessment are reported recently [48]. In this study, brain–skull displacements from FE model simulation were resampled into an isotropic 4 mm × 4 mm × 4 mm voxelized image volume at every time frame (of temporal resolution of 1 ms).

2.7. Performance evaluations

2.7.1. Cross-validation

A 5-fold cross-validation was used to evaluate performance for estimated displacement magnitude and the corresponding MPS with the directly simulated counterparts in terms of root mean squared error (RMSE) and coefficient of determination (R²) averaged from all testing samples at every time frame. We chose to report RMSE instead of a normalized version for objective accuracy evaluation due to the small magnitudes of displacements at the early phase of impact (Fig. 2). Performances were compared between TNN and CNN and between their baseline and sequential training strategies.

2.7.2. Independent testing

The TNN and CNN were then re-trained using the entire training dataset to further conduct an independent testing (N = 314), using both the baseline and sequential training. This impact dataset was measured in high-school football using mouthguard with video confirmation of true positive impact [64]. Each impact has a duration of 50 ms. To satisfy the TNN/CNN input requirement, shifting and replicated padding [19] were used so that the impact profile occurred in the range of 31st–80th ms.

The TNN/CNN models developed here instantly produce the spatiotemporal brain strains, which can be used to derive peak, “static” MPS. Therefore, we further compared performance against our previous work for either scalar, peak MPS [19] or MPS distribution [20] of the whole brain. The estimated 5D displacement was used to generate 4D voxel-wise strain (Eqs. (3)–(6)), which was further used to produce a scalar, zero-dimensional (0D) 95th-percentile peak MPS of the whole brain or 3D voxel-wise peak MPS. To ensure fair comparison, the previous CNN models [19,20] were re-trained using the same impact cases as adopted in this study. The same independent dataset (N = 314) was used for evaluation.

An extra step may be necessary when evaluating the independent dataset because the head rotational azimuth angle, θ, was not constrained (vs. constrained to ∥θ∥ < 90° for the training dataset). For impacts with θ outside of the sampling range (i.e., ∥θ∥ > 90°), displacement x, y, and z components were mirrored about the mid-sagittal plane. The y component was further negated (i.e., multiplied by −1) to produce a symmetrical displacement field about the mid-sagittal plane (Fig. 6) before comparing with the TNN/CNN estimated counterparts.

Fig. 6.

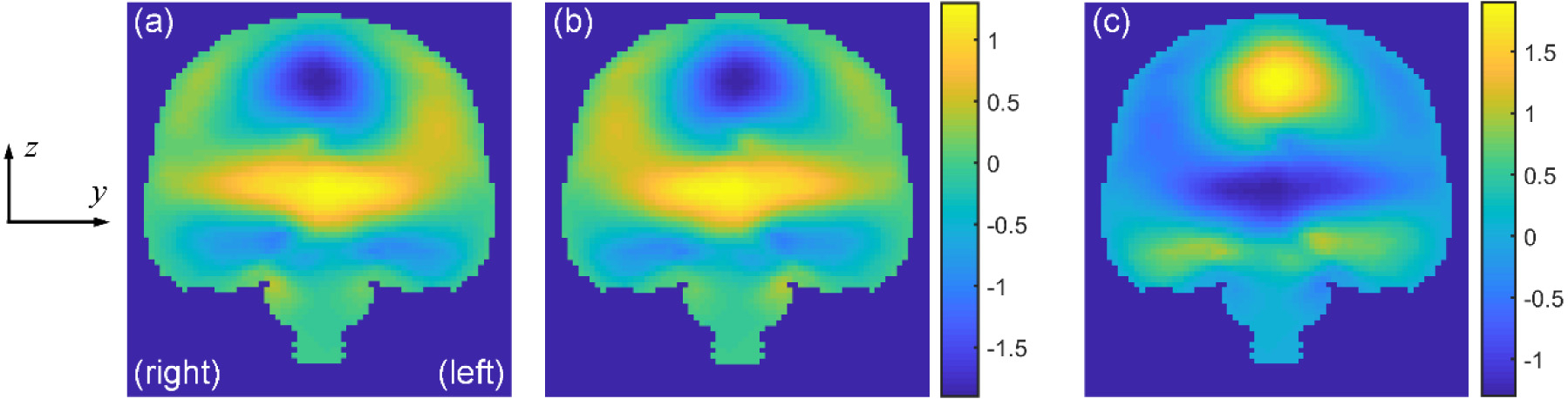
For impacts with rotational azimuth angle outside of the sampling range (i.e., ∥θ∥ > 90°, determined at the time when the resultant v_rot reached the peak), displacement x, y, and z components are mirrored about the mid-sagittal plane (a and b). The y component is further negated (i.e., multiplied by −1; c). This will produce a symmetrical relative brain–skull displacement field about the mid-sagittal plane.

2.7.3. Independent testing using a variety of representative impacts

We further evaluated 11 representative impacts from a variety of published sources, including impacts in football [51,65], soccer [66], dummy [27,60,67,68] and helmet [55] tests, as well as those reconstructed in car crashes [69]. The estimation accuracy was limited to the first 60 ms with significant non-zero v_rot.

2.8. Attention weights

Attention weights from the TNN self-attention layer have shown to offer some model interpretability, such as in pattern analysis in NLP [70] and computer vision [45]. We used an idealized head impact for exploration. A triangulated head a_rot profile (peak magnitude of 4500 rad/s² and impulse duration of 10 ms [18]) was used as input to generate spatiotemporal relative brain–skull displacement. The acceleration and corresponding velocity profiles were shifted so that they started from 31st ms, and replicated padding was used to extend to 100 ms as TNN required. The resulting heatmaps of normalized attention weights [70] were compared (for simplicity, only weights in the second layer are shown, as those in the first layer were rather noisy).

2.9. Data analysis

Cross-validation and independent testing were used to evaluate TNN/CNN accuracies, using either baseline or sequential training and based on either relative brain–skull displacement or MPS. For the independent testing, we also reported normalized RMSE (NRMSE) at the time of maximum relative displacement (as normalized by the maximum displacement) for a more comprehensive evaluation. The resulting 4D MPS for the independent dataset was further used to generate a scalar, 0D peak MPS or 3D “static” peak MPS for comparison with the two previous CNN models [19,20]. In addition, we showcased how a 4D field of MPS strain-rate can be conveniently generated. For further accuracy assessment, 11 representative impact cases from diverse published sources were also employed. Finally, we explored how TNN attention weights were used for brain deformation prediction.

All neural networks were implemented in Pytorch [71] and trained with adaptive moment estimation (adam) optimizer with a learning rate of 0.0001. It took a full day for each baseline TNN training and a full week for sequential training (training time for the second task was doubled; Intel Xeon E5–2698 with 256 GB and V100 GPU with 36 GB). In contrast, each CNN baseline training required ~5 h and ~35 h for sequential training. For both TNN and CNN, predicting a full 5D displacement field required <0.1 sec on any computer including lower-end laptops without GPU. At each time point, producing the corresponding 3D voxelwise strain took 2 s with parallelization. A forward difference method was used for strain rate calculation, which took <0.1 s for the entire 4D image volume. All data analyses were conducted in MATLAB (R2020a; Mathworks, Natick, MA).

3. Results

3.0.1. 5-Fold cross-validation

Fig. 7 compares the testing performances of TNN and CNN in terms of RMSE and R² aggregated from the five folds. For both displacement and MPS, TNN outperformed CNN with generally smaller RMSE and consistently higher R². For TNN, sequential training led to a larger RMSE in early time frames (e.g., <50 ms) but smaller RMSE in later time frames (e.g., >60 ms), with little difference in R². For CNN, however, sequential training generally degraded performance compared to the baseline (higher RMSE and lower R²). For both TNN and CN, R² was relatively poor for the first 10 ms (<0.9) with small RMSE as many impact cases had not yet started to deform the brain in the early time frames (e.g., Fig. 8 for response at 31st ms). However, for the majority of time frames, TNN sequential training consistently had a testing RMSE <1% in MPS with R² consistently >0.90.

Fig. 7.

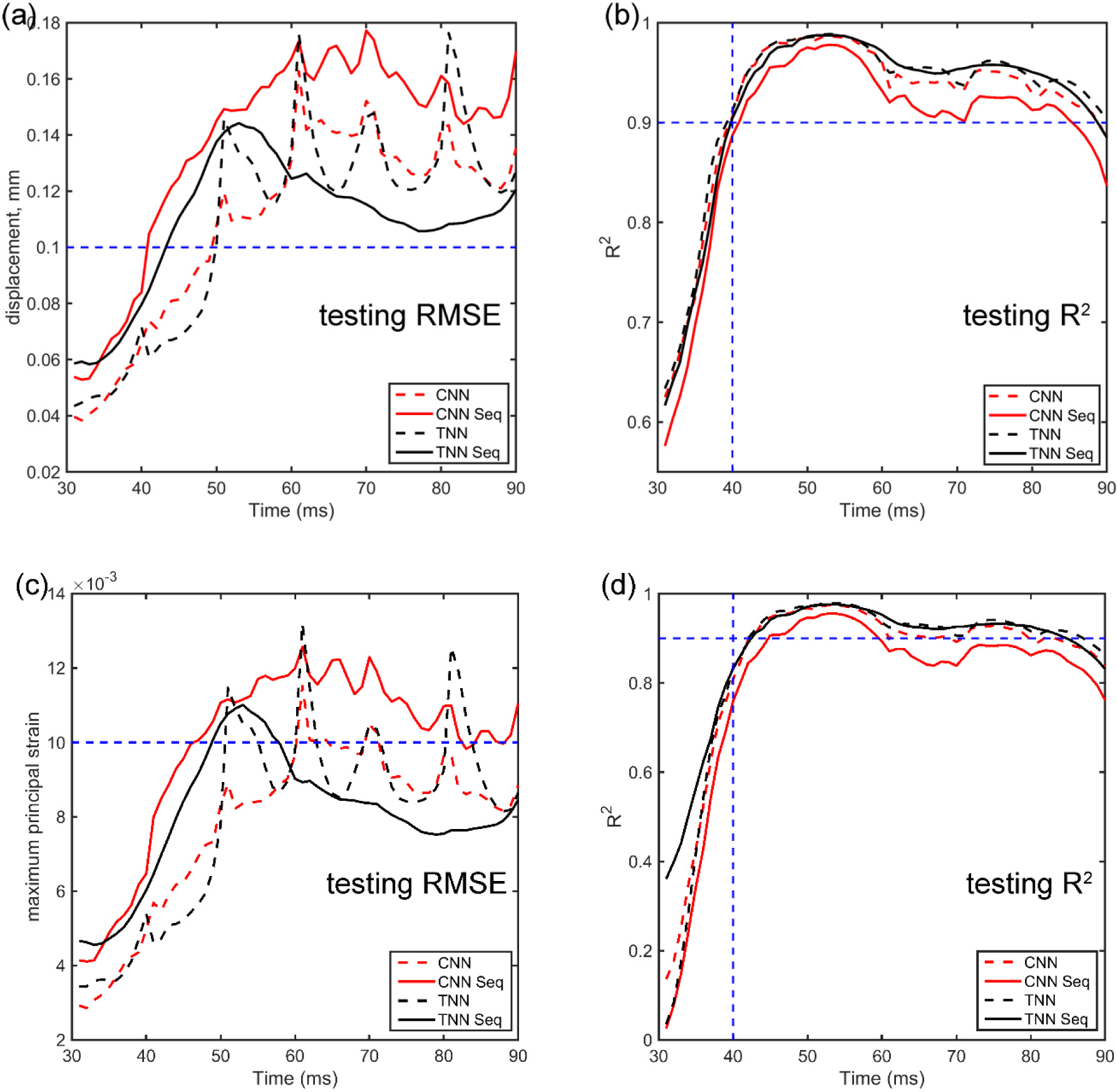
Summary of average RMSE and R² combined from the 5-fold cross-validation testing datasets using TNN and CNN, with either the baseline or sequential training strategy, for displacement magnitude (a and b) and MPS (c and d). The relatively poorer R² in the first 10 ms was mainly because the displacement magnitudes were low in the early stage of impact with small RMSE as well.

Fig. 8.

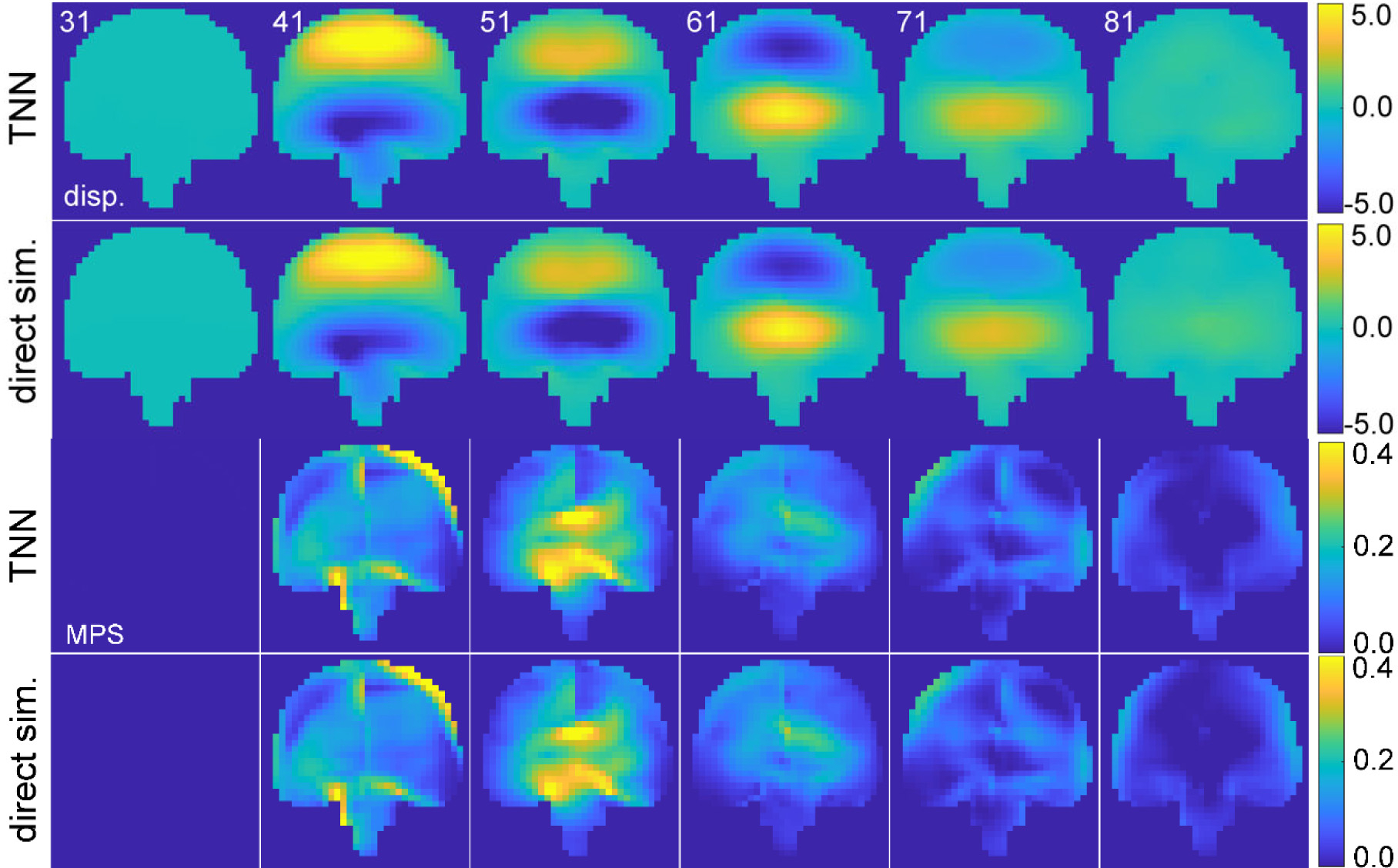
TNN-estimated and directly simulated displacement (y-component showing in-plane motion) in the coronal plane (top two rows; in mm) and the corresponding MPS at 6 discrete time points (bottom rows). Discontinuity in MPS near the mid-sagittal plane due to the falx is evident for this predominantly coronal impact, which also leads to high strains in the corpus callosum (at time of 51 ms). The corresponding head impact v_rot and a_rot profiles are provided in the Supplementary material (Fig. S1).

Fig. 8 compares the TNN-estimated displacement and MPS (with sequential training) with those from direct model simulation for a representative impact. Both TNN and CNN, with either sequential or baseline training, produced visually indistinguishable results. At the beginning of the sequence, the brain had not started deforming. The peak MPS value occurred in the middle of the prediction time window, which significantly subsided near the end of the time window.

3.0.2. Independent testing

Fig. 9 reports RMSE and R² for displacement magnitude and MPS using the independent testing dataset from 31st ms to 80th ms (for a total duration of 50 ms). The TNN achieved a maximum RMSE of ~1% with R² > 0.99 for MPS, whereas the CNN had a maximum RMSE of ~1.6% with R² > 0.98 for MPS. The maximum R² for displacement was close to 1.0 for both TNN and CNN. At the time of peak displacement, the TNN had an NRMSE of 2.1–2.7% (baseline vs. sequential), while the CNN had an NRMSE of 3.4–3.5% (baseline vs. sequential). Fig. 10 compares TNN-estimated displacement and MPS (with sequential training) with those from direct simulation at 5 distinct time points.

Fig. 9.

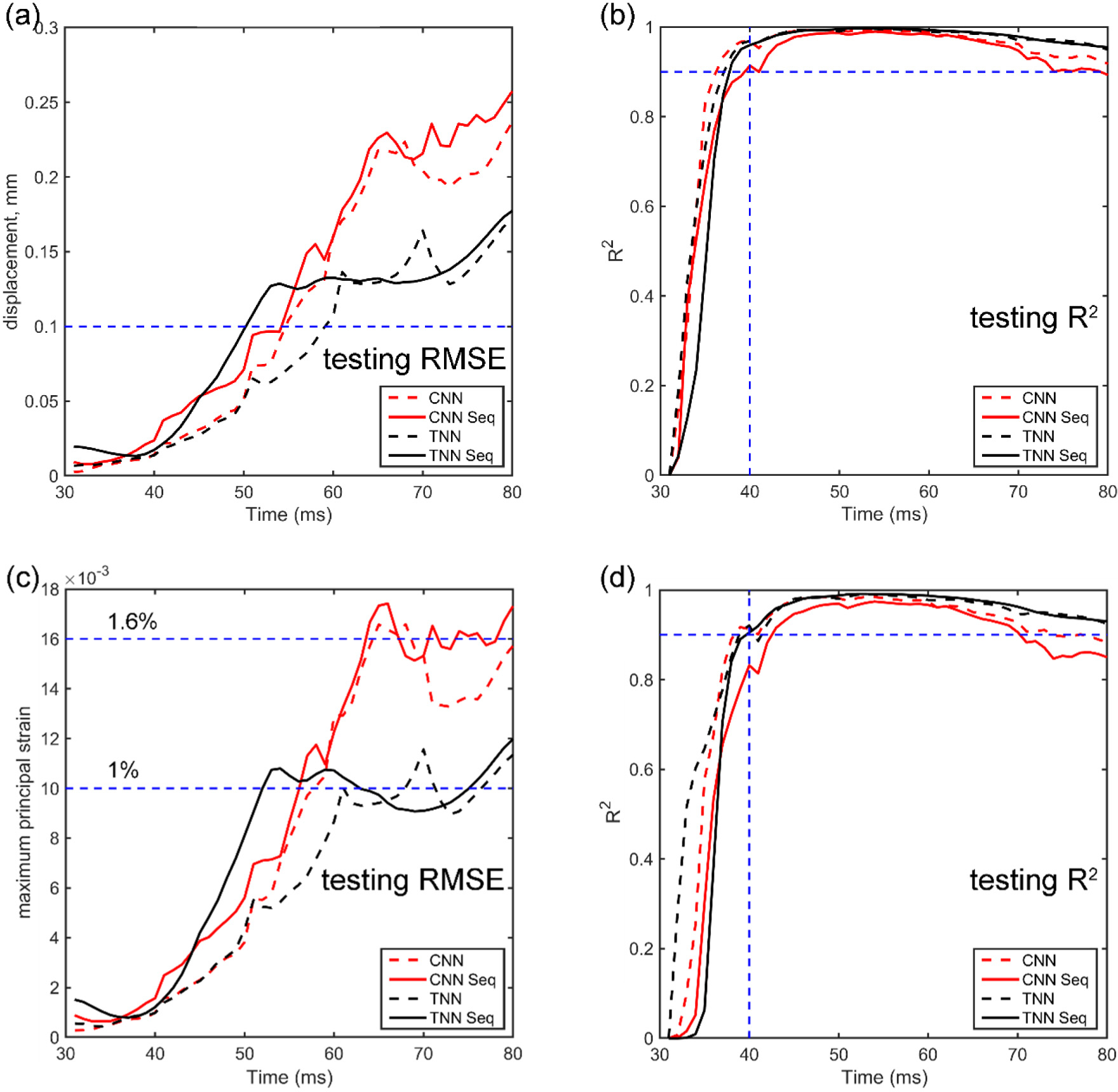
Summary of average RMSE and R² from independent testing using TNN and CNN for displacement magnitude (a and b), with either the baseline or sequential training strategy. The resulting MPS (c and d) are directly calculated from the voxelized displacement field.

Fig. 10.

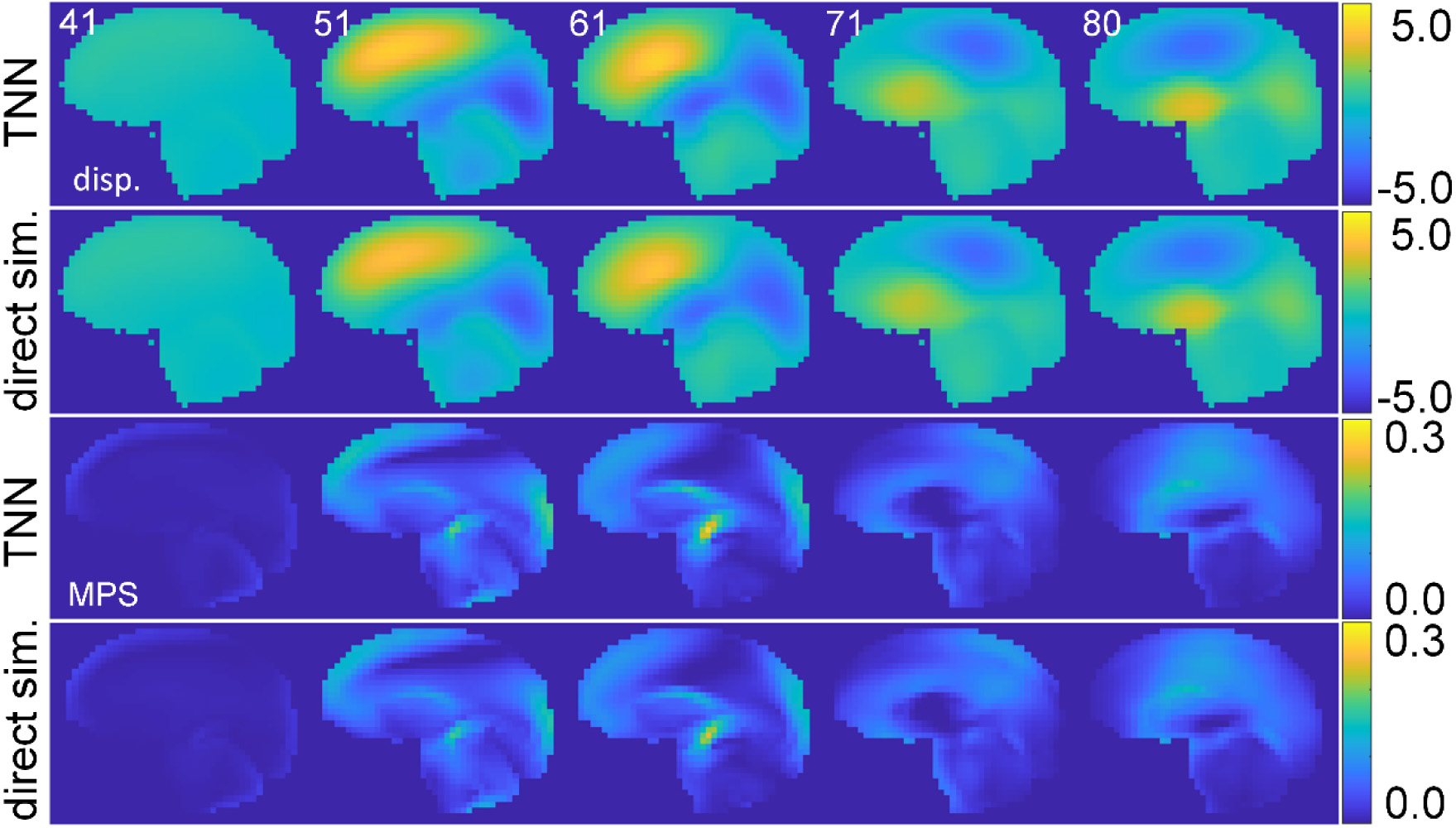
TNN-estimated (virtually the same with those from CNN, and thus, the latter are not shown) and directly simulated out-of-plane y-displacement in the sagittal plane (top two rows; in mm) and the corresponding MPS at 5 discrete time points (bottom rows). The impact was a largely oblique head rotation in the independent testing dataset unseen by the training process. The corresponding head impact v_rot and a_rot profiles are provided in the Supplementary material (Fig. S2).

Finally, the MPS strain rate is also compared for this case using TNN sequential training for illustration (Fig. 11), due to the relevance to injury [25]. The average RMSE, NMRSE, and R² across all time points were 1.650 rad/s², 12.4%, and 0.824, respectively. The best performances at a selected time point were 1.572 rad/s², 7.8%, and 0.906, respectively.

Fig. 11.

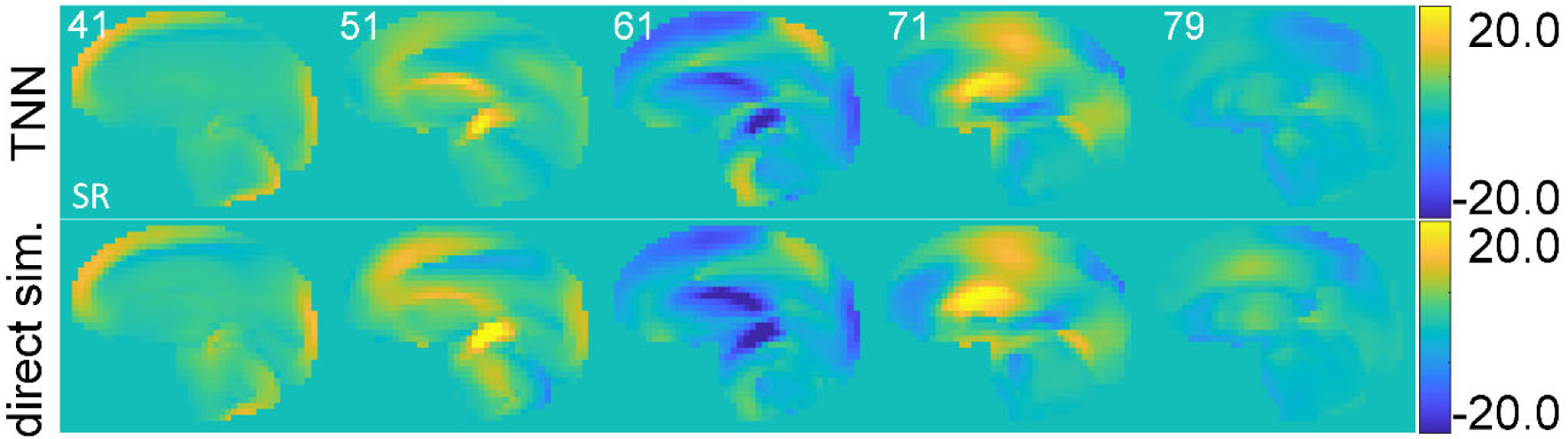
Comparisons of MPS strain rate (SR; in s⁻¹) between TNN estimation (sequential training) and those derived from direct WHIM simulation for the same selected impact case as in Fig. 10. The strain rate was obtained by forward difference along the temporal direction; thus, the last time frame for SR was at 79th ms.

Tables 1 and 2 compare the performances when estimating 0D or 3D peak MPS with the same independent dataset (N = 314). Baseline TNNs consistently performed the best, although improvement was slight for most cases, except relative to 3D peak MPS (R² of 0.977 vs. 0.897).

Table 1.

Performance comparisons for a scalar, 0D peak MPS of the whole brain using an independent testing dataset (N = 314) relative to a previous CNN model. Bold indicates best performances.

0D peak MPS	TNN (Sequential)	TNN (Baseline)	CNN (Sequential)	CNN (Baseline)	CNN [19]
RMSE	0.024	0.013	0.025	0.024	0.015
R 2	0.973	0.991	0.965	0.971	0.962

Table 2.

Performance comparisons for voxel-wise 3D peak MPS relative to another previous CNN model. Bold indicates best performances.

3D peak MPS	TNN (Sequential)	TNN (Baseline)	CNN (Sequential)	CNN (Baseline)	CNN [20]
RMSE	0.015	0.011	0.016	0.014	0.015
R 2	0.971	0.977	0.956	0.965	0.897

3.0.3. Performance for 11 representative impact cases from various sources

Table 3 reports performances for 11 impacts from various published sources. Only performances when displacements reached peak are reported for simplicity. The ranges of RMSE and R² for TNN were 0.103–0.560 and 0.919–0.998, respectively. For CNN, they were 0.077–0.788 and 0.926–0.994, respectively. Except for case 10 (car crash), all R² values were >0.95, with the highest of 0.998. Detailed performances at every time frame and for baseline models are in the Supplementary material (Figs. S3–S5). For some cases, the CNN could have a poor performance at some time points in terms of R². However, the TNN appeared more robust, especially with the sequential training.

Table 3.

Performance comparisons in terms of RMSE (mm), NRMSE (in percentage; at peak displacement), and R² for TNN/CNN sequential training when the estimated maximum displacement is at peak for 11 impacts selected from various published sources. Impact type and peak resultant υ_rot (rad/s) and a_rot (krad/s²) are also shown. More detailed performance comparisons at each time frame and for baseline TNN and CNN models are reported in the Supplementary material. HS, high school; CL: college; Bold indicates minimum or maximum for range.

Case # (Ref)	Impact type	υrot	arot	RMSE/NRMSE/R2 (TNN Seq.)	RMSE/NRMSE/R2 (CNN Seq.)
1 [51]	HS football	35.2	5.19	0.239/2.5%/0.996	0.409/4.3% 0.984
2 [51]	HS football	55.64	6.23	0.446/3.2%/0.992	0.788/5.6%/0.974
3 [60]	Dummy	30.80	7.70	0.507/4.8%/0.962	0.46¼.3%/ 0.961
4 [55]	Helmet	24.63	5.23	0.201/3.3%/0.998	0.133/2.2%/0.994
5 [27]	Dummy	34.20	6.40	0.248/2.8%/0.994	0.151/1.7%/0.994
6 [65]	CL football	12.55	1.69	0.107/2.7%/0.989	0.244/6.2%/0.984
7 [67]	Dummy	24.55	3.15	0.163/3.4%/0.987	0.287/6.1%/0.968
8 [68]	Dummya	41.98	3.06	0.339/4.7%/0.953	0.119/1.7%/0.994
9 [66]	Soccer	7.56 b	0.39	0.103/7.2%/0.975	0.077/5.4%/0.981
10 [69]	Car crash	20.22b	3.82	0.568/8.3%/0.919	0.592/8.7%/0.926
11 [69]	Car crash	77.63	6.05	0.339/3.1%/0.990	0.438/4.0%/0.984
Mean (std.)		33.18 (19.91)	4.45 (2.22)	0.296 (0.158)/4.2% (1.9%)/0.978 (0.024)	0.336 (0.224)/4.6% (2.2%)/0.977 (0.020)

^aOnly resultant profile available, which was applied to simulate a sagittal rotation.

^bPeak υ_rot values within the first 60 ms.

3.1. Attention weights

Fig. 12 illustrates TNN attention weights for an idealized axial rotation over time. Earlier (41st–61st), peak v_rot (peaked at 41st ms) always had relatively higher weights, indicating its importance in determining brain deformation.

Fig. 12.

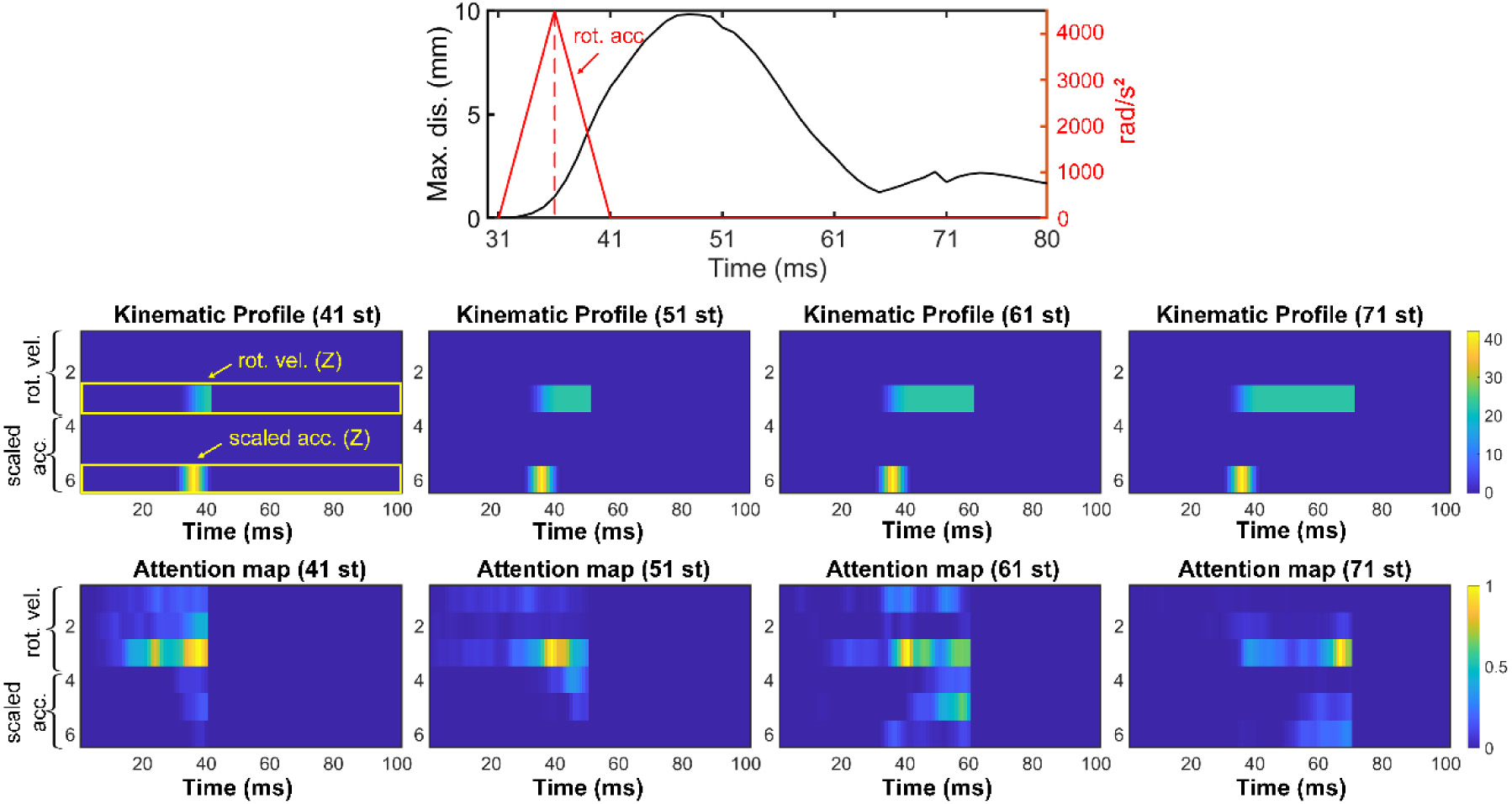
Heatmaps of normalized attention weights at 4 time points. Top: head axial a_rot impulse and the corresponding maximum brain–skull relative displacement over time. Middle: masked kinematic profiles in a 6 × 101 image format. Bottom: corresponding normalized attention weights. A higher attention is around peak velocity in earlier time frames, which shift towards the current velocity magnitude at later times. This suggests the importance of the time lag between brain deformation and the rotational impulse resulting from viscoelasticity.

This agreed with the previous biomechanical investigation [18], where it was shown that the peak v_rot, not a_rot, was important for brain strain in a single-axis rotation. Later, (61st and 71st time frames), the v_rot magnitude at the current time (vs. that at the peak) also showed high weights. Displacement at these time frames already subsided (Fig. 12, top), suggesting the time lag between peak v_rot and current time was important for brain deformation. This was not surprising due to brain’s unique viscoelasticity properties. Nevertheless, some noise was also evident, as non-zero weights also occurred in channels corresponding to the x- and y-axes not relevant to the simulated brain deformation.

4. Discussion

In this study, we developed a transformer (TNN) and a convolutional neural network (CNN) to estimate spatiotemporal deformation of the brain in impact in (near) real-time and with high accuracy, achieving an R² of up to 1.0 for displacement (Fig. 9b). In terms of MPS, they achieved an RMSE of ~1.0% and ~1.6% with R² > 0.99 and > 0.98, respectively, when displacement had sufficient magnitude using impacts in the independent testing dataset (Fig. 9). The TNN was slightly but consistently more accurate than CNN, especially at later time frames (e.g., see RMSE after 50th ms in cross-validation (Fig. 7) and after 60th ms in independent testing (Fig. 9)).

Similarly, the TNN slightly outperformed CNN when comparing 0D and 3D peak MPS as well (Tables 1 and 2). The previous CNN for 3D peak MPS [20] was notably less accurate (R² of 0.897 vs. 0.977 here; Table 2). This may be the result of lacking temporal correlation among brain voxels as they reached their respective peak MPS at different times, which precluded using a binary mask to avoid influence from “future” information. This contrasted with the scalar, 0D peak strain (Table 2), as no temporal correlation was necessary for a single brain voxel. By explicitly modeling the temporal correlation among voxels, both TNN and CNN developed here achieved a high estimation accuracy. The binary mask (Figs. 4 and 5) indeed improved accuracy. For example, when using the CNN to estimate displacement field at the 41st ms, applying a mask improved R² from 0.93 to 0.95, and RMSE decreased from 0.08 to 0.06.

The TNN and CNN also retained similar accuracies across a range of real-world impacts from a variety of published sources (dummy, helmet, football, soccer, and car crash). Both peak v_rot and a_rot in these additional independent test cases had a rather large range (e.g., from 7.56 rad/s in soccer to 77.63 rad/s in car crash, and from 0.39 krad/s² to 7.70 krad/s² in dummy test; Table 3). With sequential training, both TNN and CNN achieved an average RMSE and NRMSE of ~0.3 mm and ~4%, respectively, with an average R² of ~0.98, when the relative brain–skull displacements achieved peak values. These high accuracies suggest the potential broad applications of the two neural networks developed here for future real-world applications.

Nevertheless, the soccer impact and a car crash impact (cases #9 and #10) seemed to have relatively poorer performances for both TNN and CNN, likely due to their larger differences in impact kinematics relative to those in the training dataset derived from contact sports. While the soccer impact was also from contacts sports, their peak rotational velocity and acceleration were lower than most other sports (Table 3). Car crash impacts are also found to have different features in kinematics than those in contact sports (e.g., generally more complex head motion with longer duration [21]). The accuracy differences among the cases were more pronounced when evaluating the complete temporal evolution of predicted displacements (Figs. S3–S5). While TNN mostly maintained a comparable performance throughout the time frames, the CNN, especially with sequential training at later time frames, had some poor R² at some time points for certain cases. This was consistent with its relatively poorer performance in cross-validation (Fig. 7) and independent testing (Fig. 9), which may have been the result of limited receptive fields for the CNN architecture [39].

Regardless, the TNN accuracy improvement was marginal relative to CNN overall. This was somewhat in conflict with the notion that TNN is notably superior in mimicking long-range relationships [41,43]. A possible contributor to the high CNN accuracy here may be related to the brain’s viscoelasticity, which limits the brain mechanical responses to depend strongly only on “recent” loading history. As illustrated in Fig. 12 (top), there was a ~14 ms delay in brain deformation relative to the a_rot impulse for this particular impact, and the peak deformation subsided after ~15 ms due to energy loss. Therefore, there is a finite length of impact loading history important for brain deformation at the current time frame, for which the CNN achieved sufficient accuracy. This observation may have important implications when extending the current work to automotive head impacts [21] typically of a much longer impact duration (300–500 ms vs. 100 ms here). The CNN may achieve sufficient estimation accuracy without a heavy computational burden in training as found with TNN (35 h vs. a full week via sequential training for a 60 ms time interval). Therefore, the CNN developed in this study may be a more suitable neural network architecture for automotive head impacts.

4.1. Sequential training

Reproducing spatiotemporal data of high dimension and resolution while at the same time, in real-time, is inherently challenging due to the large data size but limited computational resources. In this study, we chose a relatively coarser spatial resolution (of 4 mm) while retaining a high temporal resolution (of 1 ms) to preserve fidelity for strain rate calculation. This was illustrated in Fig. 11 using TNN with sequential training. The NRMSE increased from 2.7% for MPS to 7.8% for SR, which was expected due to the additional temporal differentiation from MPS that would amplify error. It is possible to further improve SR prediction accuracy by using MPS or SR directly as the training dataset, with the caveat of losing information on the detailed strain or strain rate tensor. Alternatively, components of strain or strain rate tensors can also be used directly as training dataset, which may be feasible for a smaller subregion.

Due to constraint of limited computational resources, it was not feasible to train a single TNN/CNN model on our computing hardware. Therefore, sequential training [49] was adopted to limit the training sample size by essentially reusing samples from the previous training tasks. In both cross-validation (Fig. 7) and independent testing (Fig. 9), there was virtually no difference in performance in terms of R² for TNN, but it slightly degraded for CNN compared to the baseline models. However, the relative performance comparison was inconclusive in terms of RMSE (e.g., higher RMSE early and lower or comparable RMSE later for TNN with sequential training, while higher or comparable RMSE for CNN with sequential training). In addition, we chose to start the sequential training from the last time interval of the longest loading history, where its NRMSE was found to be higher than that in the first interval with the shortest history. This retrospectively justified the use of the reverse order in sequential training.

We also made the choice of training and predicting an impact duration of 60 ms so that to focus on larger brain deformation of higher strains that are more relevant to brain injury. Other ad hoc choices regarding the number of time intervals and the length of each interval were mostly to maximize the GPU memory usage in each training task while minimizing the number of training sessions for the multi-task models. This was especially important for the TNN. Nevertheless, when adopting the techniques for other dynamic simulations, these hyperparameters should be adjusted accordingly to maximize efficiency.

4.2. Comparison with other related work

TNN models for NLP and computer vision usually have a much larger training dataset to allow inclusion of many encoder layers (e.g., 300 million images with 12–32 layers for the Vision Transformer [45]). In contrast, our TNN model only has 2 encoder layers due to the relatively small training dataset so that to avoid overfitting. However, our dataset from FE simulation was noise-free and the output brain displacements among neighboring voxels were also highly correlated, both spatially and temporally. These characteristics helped reduce the complexity of our neural networks. In contrast, data for NLP or computer vision applications often involve large variations in text structure and semantics [72] or in image resolution and object size [73], respectively.

When comparing with other CNN models for spatiotemporal data estimation, previous models often require high dimensional filters to process high-dimensional input. For example, 4D CNN filters were incorporated to process 4D spatiotemporal CT [34] and 4D OCT data [74]. In contrast, our problem only utilizes a 2D “static image” of a relatively low dimension to represent head impact kinematics, which does not require high-dimensional filters.

4.3. 5D Relative displacement field

Predicting a 5D displacement field not only significantly reduces data size, but also enables convenient reconstruction of a voxel-wise strain tensor field. This is important to establish dynamic strains along white matter fiber tracts necessary to drive microscale axonal injury models [26]. The voxelized displacement field and resulting voxel-wise strain/strain tensor in a medical image format may be especially useful in promoting multimodal biomechanical analysis [50,75], where mesh-image mismatch is common that would prevent direct information exchange. By resampling the displacement according to a co-registered medical image volume at the voxel corner nodes, voxel-wise strain at voxel centroids can be easily obtained to eliminate mesh-voxel mismatch. Given that a voxel is a special type of hexahedral element, a high efficiency is achieved because the Jacobian matrix (Eq. (2)) degenerates into an identity matrix in strain tensor calculation [48]. Nevertheless, it was important to use the relative brain–skull displacement in this study, rather than that directly from impact simulation in the global coordinate system. The latter contained rigid-body skull motion typically of a larger magnitude, which would dominate the neural network response to yield a poor estimation accuracy of brain strain (verified but not shown).

4.4. Implications

This work has important implications across diverse engineering fields. First, the real-time efficiency and highly accurate estimation of brain strains from the TNN/CNN developed here improve our own previous work (Tables 1 and 2) [19,20]. They could enable a head injury model to serve as an active monitoring tool for head impacts in diverse contact sports. As impact sensors are now widely deployed, they provide the necessary input for instantaneous feedback of detailed brain strains. This could improve concussion risk mitigation strategies and to reduce the incidence and severity of concussion.

Second, this study also opens a new avenue to efficiently study the intrinsic dynamics of brain strain in TBI. Until recently, this information has not been utilized in conventional injury studies, but it is important to characterize local neuronal tissue loading environment critical to drive multiscale axonal injury models [26]. This may allow uncovering the underlying pathological changes causal of brain injury [76]. The comprehensive characterization of strain and the resulting strain rate would also allow conveniently generating “dynamic” features of brain responses that could improve injury prediction performance than peak, “static” features. The image representation of brain strain/strain rate may also greatly facilitates correlation with neuroimaging [77,78], without complications from mesh-image mismatch [50].

Finally, the TNN and CNN models developed here may have broad implications for tissue dynamic simulations in diverse biomechanical fields, including the spectrum of injury biomechanics such as the head/brain, neck, extremities, and the whole body [63], various surgical simulations for computer-aided surgery [79,80], complex dynamic musculoskeletal architectures [81], and other broad engineering field [29,30]. Time series data are commonly used as input to these problems, similarly to the head kinematics employed here. A data-driven, real-time dynamic simulation may ultimately enable a model for routine clinical use that cannot be otherwise achieved.

4.5. Limitations

A limitation of the study was that the resampled displacement/strain at a relatively coarse spatial resolution (4 mm voxel vs. 3.3 mm average brain element size) due to computing hardware constraint. This limitation may be addressed by training a TNN/CNN for a targeted brain region at a finer spatial resolution, such as in the corpus callosum. In this case, transfer learning may be utilized to facilitate training and to reduce computational burden. Since all impact simulations assumed a rigid body skull and entirely relied on head rotational velocity and acceleration, the TNN/CNN predictions may not be extended to situations of significant skull deformation such as in severe head injury with skull fracture. Nevertheless, for mild car crash impacts where rigid body skull assumption remains valid, more such cases in training are necessary to improve their prediction accuracy (Table 3; [21]).

Explainable deep learning models are useful to provide insights into the decision-making process (e.g., acute intracranial hemorrhage detection [82] and Alzheimer’s disease classification [83]). Nevertheless, we only investigated the TNN normalized attention weights with an idealized impact (Fig. 12), which largely agreed with expected brain biomechanical interpretation. However, there was still unexpected/unexplainable noise. In addition, our current CNN architecture does not generate a channel-wise attention map, which precluded the investigation into its decision-making process. Explaining how the TNN/CNN makes the prediction for an arbitrary head impact is outside the scope of the current work and will be explored in the future.