Integrative clustering methods for multi-omics data

Abstract

Integrative analysis of multi-omics data has drawn much attention from the scientific community due to the technological advancements which have generated various omics data. Leveraging these multi-omics data potentially provides a more comprehensive view of the disease mechanism or biological processes. Integrative multi-omics clustering is an unsupervised integrative method specifically used to find coherent groups of samples or features by utilizing information across multi-omics data. It aims to better stratify diseases and to suggest biological mechanisms and potential targeted therapies for the diseases. However, applying integrative multi-omics clustering is both statistically and computationally challenging due to various reasons such as high dimensionality and heterogeneity. In this review, we summarized integrative multi-omics clustering methods into three general categories: concatenated clustering, clustering of clusters, and interactive clustering based on when and how the multi-omics data are processed for clustering. We further classified the methods into different approaches under each category based on the main statistical strategy used during clustering. In addition, we have provided recommended practices tailored to four real-life scenarios to help researchers to strategize their selection in integrative multi-omics clustering methods for their future studies.

1 |. INTRODUCTION

Integrative analysis of multi-omics data has drawn the scientific community’s attention. Recent technological advances have generated various omics data with the hope of gaining greater insight into the underlying mechanism of diseases. For example, single-cell RNA sequencing has provided new biological mechanisms in some rare cell populations (B. Hwang et al., 2018; Stark et al., 2019); also, the newly developed Illumina EPIC array has revealed methylation differences associated with complex phenotypes (Mansell et al., 2019); and mass spectrometry-based proteomics has played an essential part in studying proteins that could have a significant impact on biology and medicine (Aebersold & Mann, 2003). Leveraging these multi-omics data potentially provides a more comprehensive view of the disease mechanism or of the biological processes. Based on the research question(s), different integrative methods may respond to different demands. On the other hand, dimensions of different types of omics data vary tremendously and each of them has its own biological properties. For example, each sample may have around 20,000 gene expression profiles, over 480,000 methylation sites, and millions of single-nucleotide polymorphism (SNP). Thus, the data types and the biological questions of interest should be both taken into consideration for multi-omics data analysis. For instance, when integrating SNP data and “other” types of omics data (e.g., transcriptomic, epigenomic, proteomic, and metabolomics), the idea that SNPs affect other omic markers may lead to genome-wide QTL analysis naturally (Sun & Hu, 2016). However, with various interaction networks between those “other” omics data types, the modeling strategy could be different from the one proposed for the integration of SNP data and a single type of “other” omics data (Dimitrakopoulos et al., 2018). Hasin et al. (2017) grouped multi-omics approaches into three categories, “genome first,” “phenotype first,” and “environment first,” depending on the focus of the investigation. This reflects the importance of determining the biological question before conducting the multi-omics analysis.

Disease subtyping is one of the major biological questions of interest which can be addressed by clustering methods. Integrative multi-omics clustering is an unsupervised integrative method specifically used to find coherent groups of samples or features by utilizing information across multi-omics data. It has wide applications, especially in cancer studies. For example, Curtis et al. (2012) integrated copy number and gene expression data and revealed novel subgroups of breast tumors with distinct clinical outcomes. The Cancer Genome Atlas Networks (TCGA) group further demonstrated the existence of four subtypes of breast cancer by combining data from different platforms, including genomic DNA copy number arrays, DNA methylation, exome sequencing, messenger RNA arrays, and microRNA sequencing (Cancer Genome Atlas Network, 2012). Mo et al. (2013) showed distinct tumor subtypes of colorectal cancer through the integrative clustering approach. These multi-omics clustering results provided a novel molecular stratification of cancers, suggesting both the biological mechanisms and potential targeted therapies for the diseases.

However, applying integrative multi-omics clustering is both statistically and computationally challenging due to various reasons, for example, high dimensionality and heterogeneity. Many proposed integrative multi-omics clustering methods have intended to address these challenges. Several recent reviews have discussed those methods (Chauvel et al., 2019; Pierre-Jean et al., 2019; Rappoport & Shamir, 2018; Tini et al., 2019; D. Wang & Gu, 2016). Chauvel et al. evaluated and grouped six methods into two categories based on the mathematical techniques implemented in the integrative clustering. Tini et al. compared five methods and discussed their performance under different conditions of noise and signal strength across data types. Pierre-Jean et al. extended the scope of their survey and included 13 methods. However, it lacked a systematic way to group methods, and its inclusion criteria mainly depended on the availability of R packages. Rappoport et al. gave a more comprehensive review, including multi-omics clustering methods developed either by the bioinformatic or machine learning community with a benchmark. But it lacked mathematical detail for each method. Wang et al. restricted their review to the application of cancer classifications. In general, these reviews did not provide a practical guideline for real-life applications. In this review, we summarized integrative multi-omics clustering methods based on not only the integrating strategy of the multi-omics data but also the statistical approach used during clustering. Specifically, we classified these methods into three categories: concatenated clustering, clustering of clusters, and interactive clustering. We further grouped the methods into different approaches under each category. In addition, we have provided recommended practices under different scenarios for real-life applications for future studies.

We organized the remainder of this review as follows: we first present the methods including their mathematical basis under three categories in Section 2. We then provide recommendations for researchers under four scenarios in Section 3. Finally, we conclude this review in Section 4 with the future challenges of integrative multi-omics clustering methods.

2 |. METHODS

Throughout this review, we denote A as a matrix, a as a vector, a as a scalar, and A^T as the transpose of the matrix A. This notation is consistent when using other letters. X^k denotes the n × p_k data matrix from the kth type of omics data, where n is the number of samples, p_k is the number of features in the kth type of omics data, and ${\sum }_{K=1}^K{p}_k=p$ (i.e., the total number of features is p). Therefore, $X_{ij}^k$ is the value of the jth feature for the ith sample in the k th data type.

We classified integrative multi-omics clustering methods into three major categories based on when and how the multiple omics data are processed for clustering (Figure 1). (1) Concatenated clustering: first construct one data matrix based on all omics data and then perform the clustering analysis. (2) Clustering of clusters: either perform clustering on each omics dataset, followed by integrating the primary clustering results; or transform each omics dataset into a particular form to summarize the samples’ relationship, followed by combining the processed data thus yielding the final clustering results. (3) Interactive clustering: simultaneously integrate data and perform clustering through assigning parameters or component allocation variables to connect multi-omics data. Under each category, we further classified each method into different groups based on its implementation strategy. We summarized all the methods mentioned in this review with their corresponding category and approach in Table 1.

FIGURE 1.

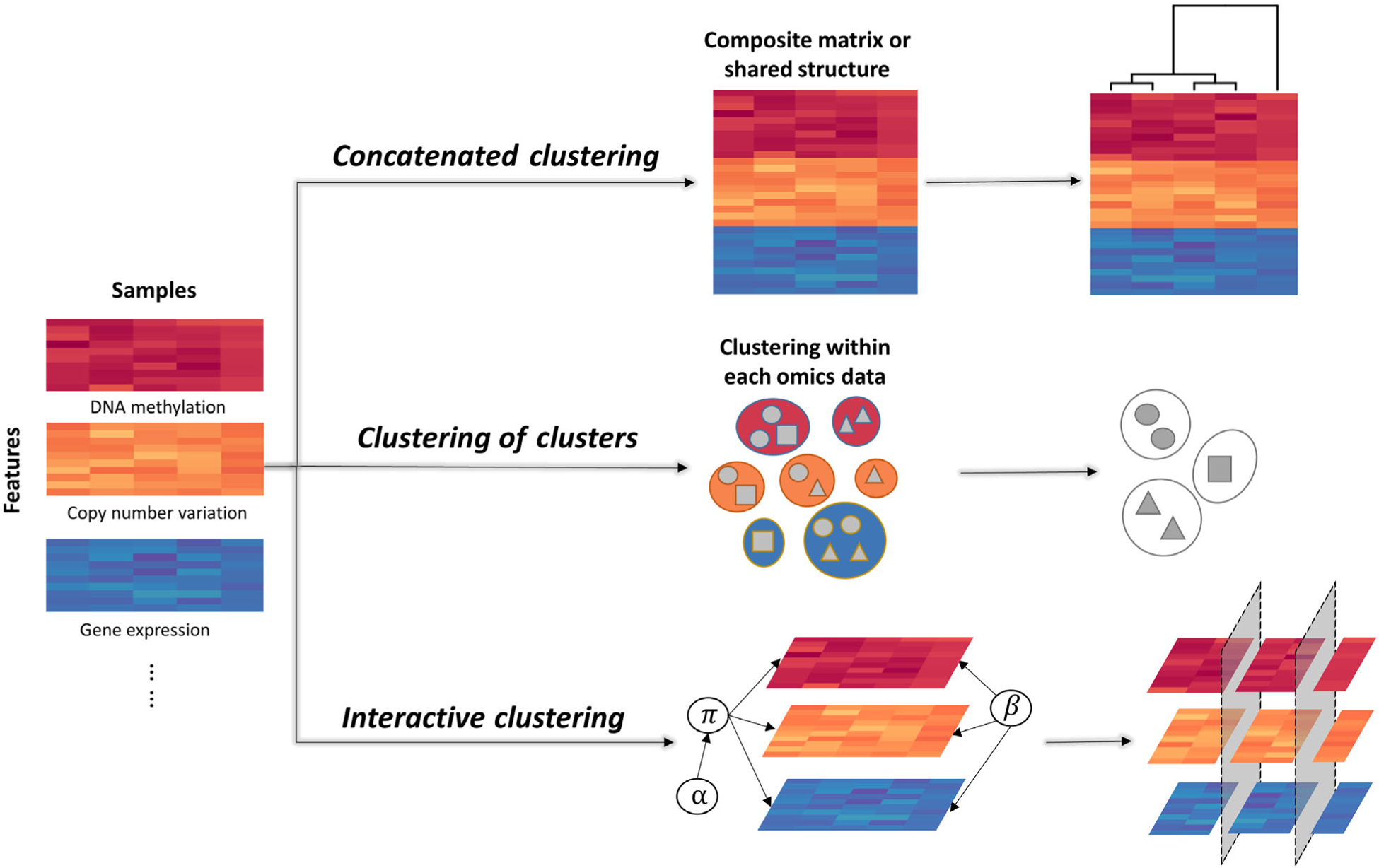
Three categories of integrative multi-omics clustering methods. Multi-omics data (e.g., DNA methylation, copy number variation, gene expression) are collected for each sample. Integrative multi-omics clustering methods can be used to analyze such data and produce sample clusters. We summarized those methods into three categories. Concatenated clustering: combine the multi-omics data into one matrix or search for the shared structure, followed by the final clustering; clustering of clusters: Obtain the clustering information from each omics dataset first and follow by the final clustering; interactive clustering: simultaneously integrate multi-omics data and perform clustering

TABLE 1.

Summary of integrative multi-omics clustering methods under three categories and different approaches

Category	Approach	Method	Description	Strength	Weakness	Implementation
Concatenated clustering	Joint latent model	iCluster (iClusterPlus, iClusterBayes)	Assume all omics data originate from a low dimensional latent matrix which can be used for the final clustering with probabilistic model	Feature selection	Computationally intensive	R
		moCluster	Use the sparse consensus principal component to define a set of latent variables to get the final clustering	Efficient with convergence to a deterministic solution	Delicate normalization procedure required	R
	Low-rank approximation	LRAcluster	Assume different omics data are independent conditional on the stacked parameter matrix with low-rank constraints	Convex objective function leading to a global solution	No feature selection	R
		JIVE	Decompose each data into three parts: low-rank approximation for joint variation, low-rank individual variation, and residual noise	Account for individual data variation; feature selection	Only applicable to continuous data; not robust to outliers	Matlab, R
	Non-negative matrix factorization	jNMF (iNMF, intNMF)	Approximate each omics data by a product of two non-negative matrices and minimize the approximation error	Feature selection	Local optimal solution only	Matlab, Python, R
	K-means related	IS-K means	Extend sparse K-means for multi-omics data through normalization and incorporate prior knowledge to select biologically meaningful features	Can incorporate prior knowledge	Only applicable to continuous data; delicate normalization procedure required	R
	Graph-based	PARADIGM	Develop a probabilistic graphical model and construct an integrated pathway activity matrix for features which can be used for clustering	Can incorporate prior knowledge	Pathway knowledge required; need submit data into the designated website to run the analysis	Web/API
Clustering of clusters	Perturbation-aided	COCA	Implement consensus clustering approach (generate perturbed datasets through resampling)	Direct apply on different omics data without the need of normalization	No feature selection	NA
		PINS (PINSPlus)	Generate perturbed datasets by adding Gaussian noise to the original data and choose the optimal number of clusters through perturbation	Robust to data with noise	No feature selection	R
	Similarity-based	Spectrum	Construct sample-wise similarity matrix for each omics data using its proposed kernel first and then combine them to construct a Laplacian matrix followed by spectral clustering to get the final clustering	Robust to data with noise; computational efficient	No feature selection	R
		SNF (ab-SNF, NEMO)	Construct sample-wise similarity matrix for each omics data first and then fuse them together followed by the final clustering	Computational efficient; can deal with mixed type of data	No feature selection	R, Matlab
		CIMLR	Multiple kernel learning method that learns the similarity matrix that best fits the data through an optimization procedure constructed by a set of Gaussian kernels	Feature selection	Gaussian kernels only	R, Matlab
		rMKL-LPP	Multiple kernel learning method that simultaneously optimizes kernel weight and projects data into a lower dimensional space	Flexibility of incorporating multiple different kernels	No feature selection	Upon request
Interactive clustering	Dirichlet mixture model-based	MDI	Use Dirichlet-multinomial mixture model with data dependence captured by parameters at the allocation level	Can deal with mixed type of data; no requirement for a consistent clustering structure	Computational intense with many parameters to specify	Matlab
		BCC	Use Dirichlet mixture model to simultaneously identify the dependence and heterogeneity across multi-omics data	Allow heterogeneity of multi-omics data when identify the overall clustering	No feature selection; a consistent clustering structure required	R
		PSDF	Use two-level hierarchy of Dirichlet process mixture model to separate concordant samples with feature selection	Feature selection; No requirement for a consistent clustering structure	Only integrate two omics data; Discretization of input data required	Matlab

Notes: Methods in the parenthesis are extended methods based on the original method in front of the parentheses. NA, not available.

2.1 |. Concatenated clustering

One intuitive strategy for integrative multi-omics clustering is to combine different omics data first and then apply a direct clustering method. When combining omics data, one can either put all the omics data into a big composed matrix or one can search for the shared structure among the omics data. Some normalized procedures may be applied to combine omics data to make them comparable. Performing dimension reduction by searching for the shared structure in the combined omics data can assist the following clustering. In the clustering analysis for multi-omics data, finding shared information from different omics is an inevitable part. The methods in this category find shared information first, and then perform clustering, which is different from the methods in another two categories discuss later. We further summarized methods into the following five groups based on their primary statistical approach.

2.1.1 |. Joint latent model

This group of methods assumes that all omics data share a set of low dimensional latent variables, which generate the observed high-dimensional data. Mathematically, we can write the general model for the kth omics data X^k, as:

$$X^{k^T}=W^{k}Z+E^k,$$

$$Z~N_q(0,I),$$

where Z, a q × n matrix, is the joint latent structure shared by all K types of omics data, W^k is the omics-specific loading matrix, and E^k is the uncorrelated error matrix with zero mean and diagonal covariance matrix ${\psi }^k=\text{diag}\left({\sigma }_1^{k^2},\dots ,{\sigma }_{p_k}^{k^2}\right)$. The core of this approach is to find the joint latent variables, followed by any type of standard clustering algorithm, such as K-means, hierarchical clustering, on the joint latent variables to obtain the final clustering results. In general, this type of approach is easy to implement; however, it has two major challenges: the difficulty in the biological interpretations of latent variables as well as the data heterogeneity among different omics data. Due to different scales, it often requires proper data normalization prior to the analysis. Below, we have illustrated a few representative methods.

iCluster (Shen et al., 2009) assumes a Gaussian joint latent model for which a low dimensional cluster membership matrix is shared by all omics data on the same samples. We can derive the joint likelihood on the assumption of conditional independence of observed omics data given the shared latent variable Z which collectively captures the correlative structure between omics data. iCluster incorporates a lasso type (L₁-norm) penalty on the loading matrix W to identify essential features and uses the Expectation-Maximization (EM) algorithm to get the mean of the cluster membership matrix on which a final cluster assignment can be achieved through a standard K-means. iCluster is only applicable to continuous data. iClusterPlus (Mo et al., 2013), the extended iCluster, accommodates continuous, binary, count, and multicategory data through generalized linear models. However, both iCluster and iClusterPlus suffer from an intense computational burden due to evaluating an excessive number of tuning parameters and different numbers of clusters for the analysis. iClusterBayes (Mo et al., 2018) was thus developed to solve this issue. Instead of using regularization in the likelihood to select features, iClusterBayes introduced an additional indicator variable with value 0 or 1 for Bayesian variable selection. With a prior distribution setting for parameters, the Metropolis-Hasting algorithm can be applied to jointly sample the latent and indicator variables from their posterior distribution for statistical inference. As there is no longer a need to fine-tune parameters like in iCluster or iClusterPlus, iClusterBayes is more computationally efficient.

Instead of using the EM algorithm as suggested, above, for the iCluster series, moCluster (Meng et al., 2016) utilizes the sparse consensus principal component analysis and the nonlinear iterative partial least squares algorithm to estimate the latent variables. This method was reported to be 100× to 1000× faster than iCluster/iClusterPlus since it can converge to a deterministic solution. However, it requires a delicate normalization procedure. In addition to the centering and scaling features in each dataset, the authors also weight each data matrix by the inverse of its first eigenvalue to allow different matrices to contribute comparable variance to the first few joint latent variables.

2.1.2 |. Low-rank approximation

This type of approach aims to find the low-dimensional subspace of high-dimensional data and cluster on the reduced subspace. It shares a similar intuition with the joint latent model approach, that is, it assumes a low-dimensional matrix, which well represents the clustering structure of samples across different omics data. The main difference is that the low-rank approximation approach enforces certain constraints on data to introduce low-rank or low-dimensional space instead of assuming joint latent variables although there could be overlapping between these two approaches for some methods.

Low-rank-approximation-based multi-omics data clustering (LRAcluster) (Wu et al., 2015) develops its low-rank approximation based on an integrative probabilistic model. It assumes different datasets are independent conditioning on the parameter matrix. It sets low-rank constraints on the stacked parameter matrix Θ leading to a penalty of model complexity in the joint likelihood of data. The objective function becomes $\underset{\Theta }{\text{min}}{\sum }_{K=1}^{K}L\left({\Theta }^k;X^k\right)+\mu |\Theta {|}^{*}$, where L(.) is the negative log likelihood function of data based on the probabilistic model (continuous data using Gaussian distribution, binary data using a Bernoulli distribution, and count data using a Poisson distribution), μ is a tuning parameter and |.|* denotes the nuclear norm of the matrix. Singular value thresholding-like method is used to optimize the objective function, and K-means is applied to find the final clustering assignment on the low-dimensional subspace. One appealing part of this method is that its objective function is convex, which leads to a global solution.

Joint and individual variation explained (JIVE) (Lock et al., 2013; O’Connell & Lock, 2016) decomposes each omics dataset into three parts: a low-rank approximation for joint variation, a low-rank individual variation, and residual noise. It can be expressed as $X^{k^T}=J^k+A^k+E^k,J={\left(J^{1^T},\dots ,J^{K^T}\right)}^T$, where J^k is the submatrix of joint structure J associated with X^k, A^k is the individual structure of X^k, and E^k is the error matrix with zero expectation. Meanwhile, the joint and individual variations are assumed to be uncorrelated. Low-rank constraints are set for both joint variation and individual variation (i.e., rank(J) = q, rank(A^k) = q^k). By minimizing the sum of squared error, the joint and individual structure can be estimated iteratively. A cluster analysis on either the joint structure or the individual structure can help cluster samples either based on all the omics data or concerning each omics dataset. Besides, JIVE can be viewed as an extension of the joint latent model by adding an omics-specific term: $X^{k^T}=W^{k}Z+U^k{S}^k+E^k$, where the q × n matrix Z is the common score, summarizing the sample variability across K omics data, and W^k is the p_k × q loading matrix for the first q components. U^kS^k is the additional omics-specific term where U^k is the loading matrix, and S^k is the score matrix for the kth omics data. Thus, the joint and individual structures, J and A^k, can be estimated through singular value decomposition-type methods. However, this method is not robust to outliers and only applicable to continuous data.

2.1.3 |. Non-negative matrix factorization

The basic idea of the non-negative matrix factorization (NMF) approach is to approximately decompose the kth omics data matrix X^k into a product of two non-negative matrices, that is, one common basis matrix Z and one omics-specific coefficient matrix W^k. The n × q matrix Z can be used to identify the sample clustering membership and the q × p_k matrix W^k can be used to identify features that contribute to clusters. The objective function can be formulated as:

$$\underset{Z,W^1,\dots ,W^K}{\text{min}}\sum _{k=1}^K\Vert X^k-Z{W}^k{\Vert }_F,s.t.Z\ge 0and{W}^k\ge 0,$$

where ‖.‖_F denotes the Frobenius norm. It can be solved through a multiplicative algorithm (Lee & Seung, 1999). This approach is closely related to the joint latent model approach when assuming Z is the common latent structure even though a non-negativity constraint is used here. However, the objective function of NMF is not convex, potentially leading to a local solution only.

Joint NMF (jNMF) (S. Zhang et al., 2012) applies the NMF framework to identify correlative modules (i.e., groups of correlated features for all or a subset of samples), also called multi-dimensional modules (md-modules), in multi-dimensional omics data, which can be further used to cluster samples. jNMF searches for the shared basis matrix Z across multi-omics datasets through minimizing the squared Euclidean error function: $\underset{Z,W^1,\dots ,W^K}{\text{min}}\sum _{k=1}^K\Vert X^k-Z{W}^k\Vert {}_F^2$.. The coefficient matrices W^k can be used to identify md-modules based on the user-defined criteria such as the largest entity of each column of W^k. Samples can be further grouped into either md-module-specific or not md-module-specific groups based on the columns of shared basis matrix Z for each md-module. jNMF uses the generalized multiplicative update rules to arrive at the shared basis matrix and the coefficient matrices iteratively. Because it is a local optimization procedure, multiple attempts using different initial values are required to reach the final solution. Two proposed integrative NMF methods (iNMF and intNMF) were developed based on the aforementioned jNMF method. iNMF (Yang & Michailidis, 2016) extends jNMF to accommodate the heterogeneous effects from different omics data via an additional term V^kW^k. Its objective function then becomes $\underset{Z,W^1,\dots ,W^K,V^1,\dots ,V^K}{\text{min}}{\sum }_{K=1}^K\Vert X^k-\left(Z+V^k\right)W^k\Vert {}_F^2+\lambda {\sum }_{K=1}^K\Vert V^k{W}^k\Vert {}_F^2,V^k\ge 0$. In other words, iNMF puts a penalty on the Frobenius norm of the heterogeneous term to retain identifiability. It is more robust to heterogeneous noise across different omics data. Moreover, iNMF can additionally incorporate an L1-norm penalty on the elements of the coefficient matrix W^k to induce sparsity in feature selection. intNMF (Chalise & Fridley, 2017), in contrast, focuses on clustering samples using different omics data. It does not assume any distribution of data and uses weights θ^k to combine different data with objective function as $\underset{Z,W^1,\dots ,W^K}{\text{min}}{\sum }_{K=1}^K{\theta }^k\Vert X^k-Z{W}^k\Vert {}_2$. Defined by the users, the weights θ^k for example, can be the maximum of the mean sums of squares among all omics data divided by the mean sum of squares of each omics data $(i.e.,{\theta }^k=\frac{\text{max}\left(\text{mean}\left(\Vert X^k{\Vert }_2\right),k=1,\dots ,K\right)}{\text{mean}\left\{\Vert X^k\Vert {}_2\right\}})$. Instead of a multiplicative update algorithm, intNMF uses alternating least square algorithms to arrive at the estimation since the objective function becomes convex in Z given W^k and vice versa. Only basis matrix Z has to be initialized. The final sample clustering membership is determined by the largest entry in each row of basis matrix Z.

2.1.4 |. K-Means related

The K-means method originally discussed partitioning observations into k sets through minimizing the within-cluster sum of squares (WCSS) (MacQueen, 1967). Assuming the total number of clusters is D, we denote G = (G₁, …, G_D) the clustering results, with G_d be the collection of samples in cluster d. We can write the objective function of the K-means as:

$$\underset{G}{\text{min}}\sum _{d=1}^D\frac{1}{n_d}\text{WCSS}\left(G_d\right)=\underset{G}{\text{min}}\sum _{\text{d}=1}^D\frac{1}{n_d}\sum _{i,i\text{'}\in G_d}\sum _j{\left(X_{i,j}-X_{i\text{'},j}\right)}^2,$$

where n_d is the number of samples in cluster d, j stands for the jth feature. Minimizing the WCSS is equivalent to maximizing the between-cluster sum of squares (BCSS) since the total sum of squares (TSS) is a constant (i.e., TSS = WCSS + BCSS). Some extensions of K-means methods were proposed to handle omics data (Friedman & Meulman, 2004; Witten & Tibshirani, 2010). Sparse K-means, for example, can effectively select features and perform sample clustering simultaneously (Witten & Tibshirani, 2010). It targets at maximizing the weighted BCSS, subject to constraints on the weights to enforce a sparse solution. To apply a K-means-related approach to multi-omics data, a specific normalization procedure is required to make features from different omics data comparable. This method requires a preselected number of clusters, and it can only apply to continuous data.

Integrative sparse K-means (IS-K means) (Huo & Tseng, 2017) extends sparse K-means to deal with multi-omics data through normalizing the BCSS by the TSS, $R_j(G)=\frac{{\text{BCSS}}_j(G)}{{\text{TSS}}_j(G)}$. Also, it incorporates overlapping group structure of features through adding a group lasso penalty term in the objective function to select biologically meaningful features in the clustering procedure. The feature group information can come from prior knowledge like biological databases.

2.1.5 |. Graph-based

A graph-based approach considers the network structures between features such as pathways among genes, proteins, and so on when integrating multiple omics data. The probabilistic graphical model (PGM) is often used to represent the regulatory structure with parameter inferences, and prior knowledge on the pathways is usually required for this type of approach.

PAthway Recognition Algorithm using Data Integration on Genomic Models (PARADIGM) (Vaske et al., 2010) develops a PGM based on factor graphs that can integrate different genomic and functional genomic datasets to infer the molecular pathways altered in a patient sample. Each node in the factor graph represents different measurement levels of genes, proteins, and so on and can be either activated, nominal, or deactivated relative to a control level. It generates an integrated pathway activity (IPA) matrix whose rows represent different entities (e.g., a protein-coding gene, a small molecule, a complex, a gene family, or an abstract process) and columns represent samples based on multi-omics data. Entities belonging to the same pathway will be grouped in rows. Each element of the IPA matrix is an IPA score, a signed analog of the log-likelihood ratio, representing how likely the entity is activated/null/deactivated in the corresponding sample, for each pathway separately. The IPA matrix can then be used to cluster samples via hierarchical clustering. This method requires prior knowledge of pathways and requires users to upload the data to the designated website to run the analysis.

2.2 |. Clustering of clusters

As the name of this category suggests, clustering of clusters shares the idea of obtaining clustering information from each omics first and then constructing an overall grouping that represents the relationship between samples followed by a final clustering. The primary clustering information can come from many places such as: directly clustering on each omics dataset, clustering on perturbed data, or constructing a sample-wise similarity matrix on each omics dataset. These approaches extract the shared information from different omics’ data after performing clustering for each omics. The methods in this category exhibit a different logic compared to the concatenated clustering, and avoid the possible information loss from the dimension reduction step. We summarized methods under this category into two groups, a perturbation-aided approach and a similarity-based approach, according to their main strategy.

2.2.1 |. Perturbation-aided

The main goal of the perturbation-aided approach is to reach a more reliable clustering assignment with perturbed datasets by either using a resampling technique or adding noise to the original data. A standard clustering algorithm can then be applied to each of the perturbed omics datasets and the agreement of clustering results can be assessed among multiple runs. Assuming that we have H perturbed datasets, an n × n connectivity matrix M^(h) represents samples relationship for the hth perturbed data, where n is the number of samples:

$$M_{ij}^{(h)}=\{\begin{array}{c}1,\text{ if sample }i\text{ and }j\text{ belong to the same cluster }\\ 0,\text{ otherwise }\end{array},h=1,\dots ,H.$$

Then an overall n × n consensus matrix C can be calculated based on all connectivity matrices (i.e., M^(h), h = 1, …, H) to help determine the final clustering. The construction of the consensus matric C varies among methods. In general, methods within this approach are robust to noisy data because of the perturbation procedure. More details about each method are described below.

Cluster-of-cluster assignments (COCA) (Hoadley et al., 2014) implemented the consensus clustering approach in the problem of integrative multi-omics clustering. Consensus clustering originates from the idea that the clustering results should be robust to the sampling variability (Monti et al., 2003). It uses a resampling technique to generate perturbed datasets followed by multiple runs of a standard clustering algorithm to create connectivity matrices. Then the consensus matrix C can be calculated as a normalized sum of connectivity matrices of all the perturbed datasets: $C_{ij}=\frac{{\sum }_h{M}_{ij}^{(h)}}{{\sum }_h{I}_{ij}^{(h)}}$, where the indicator function $I_{ij}^{(h)}=1$ if both samples i and j are present in the hth perturbed dataset and 0 otherwise. Thus, each entry of C represents the proportion of multiple runs that two samples are clustered together. Hierarchical clustering can then be applied to the distance matrix, 1 − C, to determine the final clustering memberships. COCA implemented the consensus clustering method to integrate multi-omics data, where connectivity matrices were built based on each omics dataset and then put them together to construct the consensus matrix C to represent samples’ relationship. The method was applied on six platforms of omics data including DNA copy number, DNA methylation, mRNA expression, microRNA expression, protein expression, and somatic point mutation, from 12 types of cancer and clustered samples into 11 major subtypes which have shown clinical importance from the Kaplan-Meier survival analysis.

Perturbation clustering for data INtegration and disease Subtyping (PINS) (T. Nguyen et al., 2017) generates perturbed datasets by adding noise and aims to choose the optimal number of clusters through perturbation before conducting the final clustering. PINS first applies K-means on the original data and builds (D − 1) connectivity matrices M², …, M^D for all possible numbers of clusters, where D is the largest number of clusters considered. It then generates H perturbed datasets by adding Gaussian noise to the original data and repeating the same process to build connectivity matrices on each perturbed dataset. Then by averaging those connectivity matrices for each possible number of clusters, we can get perturbed connective matrices M′², …, M′^D. The difference matrix ${\tilde{M}}^d$, with ${\tilde{M}}_{ij}^d=\left|M_{ij}^d-M{\text{'}}_{ij}^d\right|$, between the original and the perturbed connectivity matrix reflects the stability of clustering. The smaller ${\tilde{M}}_{ij}^d$, the more robust the connectivity between sample i and j, which can be used to determine the optimal number of clusters based on the most robust clustering results against perturbation. For K types of omics data, the optimal number of clusters is chosen based on each omics data as above and K connectivity matrices then can be built using the optimal number of clusters as M¹, …, M^K. Then the average pair-wise connectivity matrix (i.e., the consensus matrix) C can be calculated as $C_{ij}=\frac{{\sum }_{K=1}^K{M}^k}{K}$. A similarity-based clustering algorithm such as hierarchical clustering can be applied on the distance matrix 1 − C to determine the final clustering memberships. PINS is robust against noise by building the resilience of sample connectivity under perturbations. However, its running time is relatively long and there is no weight adjustment for different omics data.

PINSPlus (H. Nguyen et al., 2019) extended PINS by utilizing ensemble strategy (i.e., applying more than one type of clustering algorithm) on the consensus matrix to identify the clustering that agrees the most among multi-omics data. Thus, it can ensure the identified clusters are consistent and robust against the choice of clustering algorithms. Also, an early stopping criterion is implemented for the process of building perturbed connectivity matrices. Together with parallel computing, the computational efficiency of PINSPlus is largely improved compared to PINS.

2.2.2 |. Similarity-based

In general, this type of approach constructs a sample similarity matrix for each omics dataset first and then integrates similarity matrices across all omics data into one followed by the final clustering. Assuming each omics dataset, we have sample data (x₁, …, x_n) where x_i, i = 1, …, n, is a vector for sample i with all features in that omics dataset. The key component of the similarity-based approach is to construct an n × n sample similarity matrix W based on different kernels defined by each method to represent the samples’ relationship. This approach becomes more popular these days since it can address the common challenges in the integrative multi-omics clustering methods. By constructing a sample-wise similarity matrix, it overcomes not only the data heterogeneity problem, but also the problem of small n large p. However, this approach generally cannot perform feature selection. Related methods are further described below.

Spectrum (John et al., 2020) extended the spectral clustering to be able to handle multi-omics data. Spectral clustering was originally designed for single-view data as a similarity- and graph-based method. It mainly uses eigenvectors of the Laplacian matrix derived from the data to perform further clustering (Ng et al., 2001). Given a dataset with n samples and a similarity matrix W, it first constructs the similarity graph to model the local neighborhood relationships between samples and then computes the Laplacian matrix $\mathcal{L}$. It uses first d eigenvectors of $\mathcal{L}$ to represent data and follows with the standard K-means (von Luxburg, 2007). Equivalently, the objective function is $\underset{U}{\text{maxtrace}}\left(U^T\mathcal{L}U\right),\text{ s.t. }{U}^{T}U=I$,s:t:U^TU = I , where U is an n × d matrix. Apply the K-means algorithm on U to obtain the cluster memberships (Ng et al., 2001). Kumar et al. (2011) proposed a spectral clustering method under multi-view setting through a co-regularization framework with an objective function of $\underset{U^1,\dots ,U^K}{\text{max}}{\sum }_{k=1}^K\mathit{\text{trace}}\left(U^{k^T}{\mathcal{L}}^k{U}^k\right)+\lambda {\sum }_{1\le k,l\le K,k\ne l}\mathit{\text{trace}}\left(U^k{U}^{k^T}{U}^l{U}^{l^T}\right),\text{ s.t. }{U}^{k^T}{U}^k=I$. However, it was not designed for omics data. Spectrum, on the other hand, was developed for multi-omics data. The authors of Spectrum proposed a self-tuning density-aware kernel as $W_{ij}=\text{exp}\left(\frac{-{\rho }^2\left(x_i,x_j\right)}{{ϵ}_i{ϵ}_j\left(\text{CNN}\left(x_i,x_j\right)+1\right)}\right)$, where, ρ(x_i, x_j) denotes the Euclidean distance between sample i and j, ϵ_i is local scaling parameter for sample i, CNN(x_i, x_j) is the number of samples in the inter-section between the two sets of nearest neighbors of sample i and j, based on Zelnik-Manor self-tuning kernel (Zelnik-Manor & Perona, 2005) and Zhang density-aware kernel (X. Zhang et al., 2011). Spectrum uses a tensor product graph integration and diffusion technique to combine similarity matrices across multi-omics data and reduce noise (Shu & Latecki, 2016). Finally, Laplacian matrix $\mathcal{L}$ is constructed based on the combined similarity matrix and Gaussian mixture model clustering is used to get the final clustering memberships on the eigenvector matrix of $\mathcal{L}$.

Similarity network fusion (SNF) (B. Wang et al., 2014) is a well-represented method belonging to the similarity-based approach of integrative multi-omics clustering. SNF uses a scaled exponential similarity kernel to construct the sample similarity matrix W with $W_{ij}=\text{exp}\left(-\frac{{\rho }^2\left(x_i,x_j\right)}{\mu {ϵ}_{i,j}}\right)$, where, ρ(x_i, x_j) denotes the Euclidean distance for continuous variables between sample i and j, μ is a hyperparameter that can be empirically set and ${ϵ}_{i,j}=\frac{\text{mean}\left(\rho \left(x_i,N_i\right)\right)+\text{mean}\left(\rho \left(x_j,N_j\right)\right)+\rho \left(x_i,x_j\right)}{3}$ which is used to eliminate the scaling problem, mean(ρ(x_i, N_i)) is the average value of the distances between sample i and each of its neighbors. The authors proposed to use chi-squared distance for discrete variables and agreement-based measure for binary variables. After similarity matrices being constructed for samples from available datasets, they will be fused into one similarity matrix to represent the full spectrum of underlying data. An n × n normalized similarity matrix P and an n × n affinity matrix S are defined as below for the integration or fusion process for multiple similarity matrices based on different omics data:

$$P_{ij}=\{\begin{array}{c}\frac{W_{ij}}{2\sum _{l\ne i}{W}_{il}},j\ne i\\ \frac{1}{2},j=i\end{array}and{S}_{ij}=\{\begin{array}{l}\frac{W_{ij}}{\sum _{l\in N_i}{W}_{il}},j\in N_i\hfill \\ 0,\text{ otherwise }\hfill \end{array},$$

where N_i is the set of neighbors for sample i. Then the similarity fusion process is conducted iteratively by:

$$P_{(t+1)}^k=S^k\times \left(\frac{\sum _{m\ne k}{P}_{\left(t\right)}^m}{K-1}\right)\times {\left(S^k\right)}^T,k=1,\dots ,K,$$

for the tth iterations and the kth omics data. The fused normalized similarity matrix is $P_{\mathit{\text{fused }}}=\frac{{\sum }_{K=1}^K{P}_{(t+1)}^k}{K}$ after t iterations. Spectral clustering (Ng et al., 2001) then can be applied on the P_fused to generate the final clustering.

Association-signal-annotation boosted SNF (ab-SNF) (Ruan et al., 2019) extended SNF by adding weights to features when constructing sample similarity matrix. The weights can be determined by the feature-level association strengths with the outcome, such as association p-value, as well as annotation signals, such as relationship indicators between a gene and a disease. More specifically, assuming we have a continuous feature m, we can calculate the p-value of feature m (i.e., p_m), from the model comparing disease samples with normal samples at feature m. Then the feature-level weight can be defined as $\mathcal{W}{t}_m=\frac{-{\text{log}}_{10}\left(p_m\right)}{{\sum }_{m=1}^M\left(-{\text{log}}_{10}\left(p_m\right)\right)}$, where M is the total number of features of that data type. The weighted distance $\rho \left(x_i,x_j\right)=\sqrt{{\sum }_{m=1}^{M}w{t}_m{\left(X_{im}-X_{jm}\right)}^2}$. For a binary feature m, the weight can be an indicator function to represent whether a feature is important based on prior knowledge, such as if we know a gene m is a mutation gene for a certain disease, we can set wt_m = 1 and wt_m = 0 otherwise. Then the weighted distance becomes $\rho \left(x_i,x_j\right)={\sum }_{m=1}^{M}w{t}_m\left|X_{im}-X_{jm}\right|$. By incorporating the weights, ab-SNF was reported to outperform the original SNF in disease subtyping. However, SNF and ab-SNF both need a separate procedure to handle missing values if not all omics data available for each sample. This could be an issue in real-world practice. NEighborhood based Multi-Omics clustering (NEMO) (Rappoport & Shamir, 2019) was, therefore, developed to address this issue by allowing some samples to have only partial omics data available. It uses a similarity measure based on the radial basis function kernel (Buhmann, 2009) to construct a similarity matrix for the kth omics dataset, $W_{ij}^k=\frac{1}{\sqrt{2\pi }{ϵ}_{ij}^k}\text{exp}\left(-\frac{\Vert x_i^k-x_j^k\Vert }{2{ϵ}_{ij}^k{}^2}\right)$ where is a normalizing factor which controls for the density of samples by averaging the squared distance of the ith and jth samples to their nearest neighbors and the squared distance between these two samples. Then NEMO defines the relative similarity matrix RS for each omics dataset to measure the similarity between two samples relative to their κ nearest neighbors, $R{S}_{ij}^k=\frac{W_{ij}^k}{{\sum }_{r\in r_i^k}{W}_{ir}^k}\times I\left(j\in {\eta }_i^k\right)+\frac{W_{ij}^k}{{\sum }_{r\in {\eta }_j^k}{W}_{jr}^k}\times I\left(i\in {\eta }_j^k\right)$, where I(.) is the indicator function. We can obtain the average relative similarity matrix ARS by averaging the relative similarity matrix across omics data with observed values, $AR{S}_{ij}=\frac{1}{\left|J{M}_{ij}\right|}{\sum }_{k\in J{M}_{ij}}R{S}_{ij}^k$, where JM_ij denotes the omic types available for both samples. Again, spectral clustering can be applied to the ARS to get the final clustering.

Cancer Integration via Multi-kernel Learning (CIMLR) (Ramazzotti et al., 2018) aims to integrate multi-omics data to reveal molecular subtypes of cancer. It is an extension of Single-cell Interpretation via Multi-kernel LeaRning (SIMLR) (B. Wang et al., 2017). Unlike SNF that uses one kernel to construct a sample similarity matrix, SIMLR is a multikernel learning method that learns the similarity matrix that best fits the data by combing multiple kernels. SIMLR defines each kernel as: $Kernel\left(x_i,x_j\right)=\frac{1}{{ϵ}_{ij}\sqrt{2\pi }}\text{exp}\left(-\frac{\Vert x_i-x_j\Vert {}_2^2}{2{ϵ}_{ij}^2}\right)$, where ϵ_ij can be calculated with different scales: ${ϵ}_{ij}=\frac{\sigma \left({\mu }_i+{\mu }_j\right)}{2},{\mu }_i=\frac{{\sum }_{l\in \text{KNN}\left(x_i\right)}\Vert x_i-x_j\Vert {}_2}{\kappa }$, where KNN(x_i) represents samples that are top κ neighbors of sample i. Thus, each kernel is decided by a pair of parameters (σ, κ). CIMLR extended SIMLR by constructing the same number of Gaussian kernels for K omics. All constructed kernels will be used to find the n × n sample similarity matrix W through the following optimization procedure:

$$\begin{gathered} \underset{W,L,v}{\text{min}}-{\sum }_{i,j,m}{v}_m{\mathit{\text{Kernel}}}_m\left(x_i,x_j\right)W_{ij}+\beta \Vert W{\Vert }_F^2+\gamma \text{tr}\left(L^T\left(I_n-W\right)L\right)+\rho {\sum }_m{v}_m\text{log}{v}_m \\ \text{ s.t. }{L}^{T}L=I_D,{\sum }_m{v}_m=1,v_m\ge 0,{\sum }_j{W}_{ij}=1,\text{ and }{W}_{ij}\ge 0, \end{gathered}$$

where D is the number of clusters, m is the kernel index over all kernels across K omics data, ν_m is the weight for the mth kernel, β and γ are non-negative tuning parameters, ‖. ‖_F denotes the Frobenius norm, and L is an auxiliary low-dimensional matrix enforcing the low rank constraint on W. It then applies K-means based on the similarity matrix W for the final clustering. Additionally, CIMLR can also perform feature selection through a hypergeometric test.

Regularized multiple kernels learning with locality preserving projections (rMKL-LPP) (Speicher & Pfeifer, 2015) is also a multikernel learning method that can integrate multi-omics data and perform cancer subtype identification. It adopts the multiple kernels learning for dimensionality reduction (MKL-DR) framework (Lin et al., 2011) which integrates multiple kernel learning (i.e., optimizes the weights that linearly combines a set of kernel matrices to generate a unified kernel matrix) into the graph embedding (S. Yan et al., 2007) for dimensionality reduction. MKL-DR defines different types of kernels based on the data type, the mth dissimilarity-based kernel matrice ${\mathit{\text{Kernel}}}_m\left(x_i,x_j\right)=\text{exp}\left(\frac{-d_m^2\left(x_i,x_j\right)}{{ϵ}_m^2}\right)$, where ϵ_m is a positive constant. rMKL-LPP extended MKL-DR by adding a regularization term to avoid overfitting and it applied locality preserving projections algorithm (LPP) (He & Niyogi, 2003) for dimensionality reduction with the optimization problem as:

$$\begin{gathered} \underset{A,\beta }{\text{min}}{\sum }_{i,j=1}^n\Vert A^T{\mathcal{K}}^i\beta -A^{\top }{\mathcal{K}}^j\beta {\Vert }^2{W}_{ij}\text{ s.t. }{\sum }_{i,j=1}^n\Vert A^T{\mathcal{K}}^i\beta {\Vert }^2{R}_{ij}=\text{const}.,\Vert \beta {\Vert }_1=1, \\ {\beta }_m\ge 0,m=1,2,\dots ,M\cdot {\mathcal{K}}^i=\left(\begin{array}{ccc}{\text{ Kernel }}_1\left(x_1,x_i\right)& \cdots & {\text{ Kernel }}_M\left(x_1,x_i\right)\\ ⋮& \ddots & ⋮\\ {\text{ Kernel }}_1\left(x_n,x_i\right)& \cdots & {\text{ Kernel }}_M\left(x_n,x_i\right)\end{array}\right), \end{gathered}$$

where A is an n × q projection matrix and q is user-defined (q is usually smaller than the number of features p to achieve dimension reduction), β is an M × 1 coefficient vector, ${\mathcal{K}}^i$ is an n × M kernel matrix for sample i which can be constructed by different kernel functions, M is the total number of kernels and each omics dataset may have multiple kernels. The (i, j)-entry of the similarity matrix W is equal to 1 if i ∈ N_κ(j) or j ∈ N_κ(i) and 0 otherwise, N_l(i) is the set of the κ nearest neighbors for sample i, and $R_{ij}={\sum }_{l=1}^n{W}_{il}$, if i = j and 0 otherwise. A and β are iteratively optimized until convergence and K-means can be performed on the projected samples $A^T{\mathcal{K}}^i\beta ,i=(1,\dots ,n)$ to obtain the final clustering. This method has the flexibility of incorporating multiple kernels per data type. This not only improves the performance but also removes the need of preselecting the optimal kernel. The authors applied this method on five cancer datasets and identified biologically meaningful subgroups for cancers with significantly different survival.

2.3 |. Interactive clustering

Instead of performing two-step procedures like those above-mentioned, methods covered in this category conduct the integration and clustering simultaneously. These methods assign parameters or allocation variables to link the dependence across different omics data. Under such settings, a consistent clustering structure across multi-omics data is not necessary, which provides a more flexible setup. Methods in this category usually incorporate ideas of the Dirichlet mixture model and Bayesian statistics.

2.3.1 |. Dirichlet mixture model-based

This type of approach usually assumes that data originate from a Dirichlet mixture model with a general form: $p(x)={\sum }_{m=1}^M{\pi }_{m}f\left(x\mid {\theta }_m\right),m=1,\dots ,M$, where p(x) denotes the probability density for data with M components, π_m’s are mixture proportions, f is a parametric density with associated parameters θ_m and different types of data can be modeled using different densities. Let (u₁, …, u_n) be the component allocation variables for n samples where u_i ∈ {1, …, M}, i = 1, …, n and π_m = P(u_i = m). Under a Bayesian framework, Dirichlet priors are usually put on Π = (π₁, …, π_M). Gibbs sampling can be used to approximate the posterior distributions of parameters of interest and the posterior of component allocation variables are directly related to the final clustering of samples. When M → ∞, the model becomes a Dirichlet process (DP). On one hand, this approach provides flexible probabilistic models for different omics data. On the other hand, it naturally captures the clustering structure through decomposing data into M components. However, this approach usually requires one to specify many parameters in advance.

Multiple dataset integration (MDI) (Kirk et al., 2012) can integrate multiple omics data of different types (e.g., continuous, categorical, time series). It was originally designed for clustering genes but it can be easily applied for clustering samples. For n samples/genes from K omics data, MDI models each omics data using a Dirichlet-multinomial allocation (DMA) mixture model (Green & Richardson, 2001) with component allocation variables u_ik ∈{1, …M}, i = 1, …, n; k = 1, …, K; M is set by users and was set as n/2 here. MDI then links all DMA models at the level of the component allocation variables via the conditional prior $p\left(u_{i1},\dots ,u_{iK}\mid \varphi \right)\propto {\prod }_{k=1}^K{\pi }_{u_{ik}k}{\prod }_{k=1}^{K-1}{\prod }_{l=k+1}^K(1+{\varphi }_{kl}I\left(u_{ik}=u_{il}\right))$, where ϕ is a collection of K(K − 1)/2 parameters that controls the strength of association between pair of omics data, ${\pi }_{u_{ik}k}$ is the mixture proportion associated with component u_ik in the kth DMA model. Gibbs sampling is used to approximate the parameters’ posterior probabilities. MDI first identifies the samples/genes that tend to be allocated to the same component across a subset of or all omics data followed by the final clustering using the sampled component allocations. One main advantage of MDI is that it does not require the common clustering structure across all omics data. As there are many parameters to specify, the scalability of MDI needs improvement.

Bayesian consensus clustering (BCC) (Lock & Dunson, 2013) aims to simultaneously identify the dependence (i.e., overall clustering) and the heterogeneity (i.e., omics-specific clustering) across multi-omics data. Similar to MDI, BCC models each omics dataset with a Dirichlet mixture model. But BCC assumes there is an overall clustering across multi-omics data and a separate omics-specific clustering adhere to the overall clustering. Let $\text{Let }{l}_i^k\in (1,\dots ,M)$ represent the kth omics-specific component allocation variable and u_i ∈ (1, …, M) represent the overall component allocation variable for sample i. The dependence between omics-specific clustering $l^k=\left(l_1^k,\dots ,l_n^k\right)$ and the overall clustering u = (u₁, …, u_n) is modeled through the following:

$$P\left(l_i^k=m\mid u_i\right)=v\left(l_i^k=m,u_i,{\alpha }^k\right)=\{\begin{array}{c}{\alpha }^k,\text{ if }{u}_i=m\\ \frac{1-{\alpha }^k}{M-1},\text{ otherwise }\end{array},$$

where ${\alpha }^k\in \left[\frac{1}{M},1\right]$ controls the adherence of the kth omics data to the overall clustering. M is selected to maximize the mean of omics-specific adherence to the overall clustering. Then the probability for a sample belongs to an omics-specific cluster is $P\left(l_i^k=m\mid \Pi \right)={\pi }_m{\alpha }^k+\left(1-{\pi }_m\right)\frac{1-{\alpha }^k}{M-1}$. And based on Bayes’ rule, the conditional distribution of u_i can be written as $P\left(u_i=m\mid \Pi ,{\left\{L^k,{\alpha }^k\right\}}_{k=1}^K\right)\propto {\pi }_m{\prod }_{k=1}^{K}v\left(l_i^k,u_i=m,{\alpha }^k\right)$. Again, through the Gibbs sampling procedure, posterior distributions of omics-specific and overall allocation variables can be estimated to determine the final clustering.

Patient-specific data fusion (PSDF) (Yuan et al., 2011) is based on Bayesian nonparametric modeling. Unlike MDI and BCC, it utilizes a two-level hierarchy of the DP mixture model (Antoniak, 1974; Ferguson, 1973) and mainly integrates two omics datasets (e.g., copy number and gene expression data). DP mixture model may be derived from the above general form of Dirichlet mixture model when M → ∞ (Rasmussen, 2000). The sample i is indicated as fused (r_i = 1), if the clustering structure for this sample between two omics data is concordant, or as unfused (r_i = 0) if it is contradictory. The prior probability of fusion is defined by P(r_i = 1) = w, where w can be set by users, w = 0.5 in the PSDF paper. The hyperparameters of the hierarchical DP consist of the baseline probability measure H, and the concentration parameters γ and α₀. This method allows the possibility of taking the product of likelihoods over the two omics data, so if sample i is fused, θ_i = (θ_1i θ_2i)~F₃; if unfused, θ_1i~F₁ and θ_2i~F₂, where θ represents the likelihood parameters under each case. And then we have $F_1~DP\left({\alpha }_0,F_0^{(1)}\right)$, $F_2~DP\left({\alpha }_0,F_0^{(2)}\right)$, F₃~DP(α₀, F₀), and F₀(θ₁, θ₂)~DP(γ, H), where $F_0^{(k)}$ represents the marginal distribution of θ_k under F₀, k = 1, 2. Additional indicator parameters for features are introduced for the feature selection purpose. Gibbs sampling is used to estimate the posterior probability of parameters of interest. By incorporating the sample fusion information in the DP mixture model, it no longer requires the assumption of a consistent clustering structure between two omics datasets, which shares the intention with MDI. In principle, this method can be extended to integrate more than two omics datasets. However, the authors reported that it would become unwieldy if they did so. Another limitation of PSDF is that it can only handle discretized input data, so data preprocessing is required before modeling.

3 |. IMPLEMENT RECOMMENDATION

We have surveyed a number of integrative multi-omics clustering methods based on their theoretical properties. When it comes to real-life applications, it is necessary to pinpoint the appropriate methods for the various circumstances. Here we list four different situations that researchers commonly face with recommended methods in Table 2. We also point out the difference between methods under the same scenario. Overall, we hope our recommendations can help researchers to strategize their analyses using integrative multi-omics clustering for their future research.

TABLE 2.

Four scenarios with recommended methods

Scenarios	Required characteristics for method	Recommended methods
I. (Feature selection): The need to identify clinically relevant disease subtypes and driving molecular signatures which can be targeted for treatment	Performing both sample clustering and feature selection	iCluster; iClusterPlus; iClusterBayes; intNMF; IS-K means; CIMLR; PSDF
II. (Mixed-type data): Large scale genomic data of mixed-type in large consortia	Integrating mixed type of data	iClusterPlus; iClusterBayes; moCluster; LRAcluster; MDI; SNF; CIMLR; rMKL-LPP; PINS; PINSPlus
III. (Computational efficiency): Concern on the computational resources and consumption of time	Computationally efficient	Spectrum; SNF; ab-SNF; NEMO; CIMLR; rMKL-LPP
IV. (Knowledge integration): Leveraging the prior knowledge	Incorporating prior information	IS-K means; PARADIGM

Scenario I (feature selection):

Many large-scale cancer genomics studies have demonstrated the benefit of using proper integrative multi-omics clustering methods to generate biologically meaningful cancer subtypes and to identify potential therapeutic targets, for example, studies related to breast cancer, lung cancer, and stomach cancer (Cancer Genome Atlas Network, 2012; Cancer Genome Atlas Research Network, 2012, 2014). Therefore, the capabilities of clustering samples and feature selection are both desired, especially in translational research for precision medicine. The following methods would meet the needs: iCluster and its extensions (iClusterPlus and iClusterBayes), intNMF, IS-K means, CIMLR, and PSDF. iClusterPlus extended iCluster by allowing the integration of multi-type omics data through generalized linear models. iClusterBayes is more computationally efficient than iCluster and iClusterPlus based on a Bayesian model with no tuning parameters. intNMF is an NMF approach without assumption of model distribution. IS-K means can additionally incorporate prior knowledge to identify biologically meaningful driving features. CIMLR’s feature selection procedure cannot be achieved simultaneously with clustering. PSDF utilizes a more flexible nonparametric Bayesian method to cluster samples and select informative features but becomes unwieldy when applying to more than two omics datasets.

Scenario II (mixed-type data):

An unprecedented amount of mixed-type genomic data, binary (somatic mutation), categorical (copy number gain, normal, loss), and continuous (gene expression), for various cancers have been provided by large consortia or in public depositories such as TCGA http://cancergenome.nih/gov, Gene Expression Omnibus http://www.ncbi.nlm.nih/gov/geo/, and Sequence Read Archive http://www.ncbi.nlm.nih.gov/sra. The integrative clustering methods that can deal with mixed-type data are demanded for this scenario. Therefore, we recommended the following methods: iClusterPlus, iClusterBayes, moCluster, LRAcluster, MDI, SNF, CIMLR, rMKL-LPP, PINS, and PINSPlus. A generalized linear model is usually applied to incorporate mixed-type of data for likelihood-based methods such as iClusterPlus, iClusterBayes, and LRAclusters. iClusterBayes, moCluster, and LRAclusters have less computational cost than iClusterPlus. moCluster requires different normalization steps for different types of data. LRAcluster can result in a stable global solution as its objective function is convex. MDI does not require a consistent clustering structure across multi-omics data. SNF, CIMLR, and rMKL-LPP all belong to the similarity-based approach which is generally more computationally efficient. SNF cannot select features. CIMLR can prioritize features through a hypergeometric test. rMKL-LPP uses multiple kernels learning method and adds a regularization term to avoid overfitting during the optimization procedure. PINS and PINPlus both are robust to noisy data, but can be computationally intensive.

Scenario III (computational efficiency):

Although computational capacity has exponentially increased over time, not every researcher has access to a cost-efficient computing infrastructure. Even with enough computational resources, the scalability and consumption of time could be a concern when analyzing multi-omics data. Computationally efficient methods become much more appealing under this setting. Therefore, methods belonging to similarity-based approach are recommended since they are quite efficient by integrating omics data in the space of samples, including SNF and its extensions ab-SNF and NEMO, CIMLR, and rMKL-LPP. In general, the similarity-based approach cannot perform feature selection. Spectrum uses its own proposed kernel to construct sample-wise similarity matrix. SNF uses Euclidean distance between samples and exponential similarity kernel to construct the similarity matrix. ab-SNF is a weighted version of SNF which incorporates phenotype information. NEMO extended SNF to include partially available data for samples. CIMLR and rMKL-LPP are both multiple kernel learning methods with optimization procedure. CIMLR only considers Gaussian kernels, but it can select features. rMKL-LPP has the flexibility of incorporating different kernels per omics dataset.

Scenario IV (knowledge integration):

There is growing biological knowledge, for example, interactions between genes, the potential cis-acting regulatory mechanism between copy number variation, and methylation and gene expression. Researchers may want to utilize this accumulated knowledge to guide the clustering procedure for more biologically meaningful results. Also, there are many publicly available databases providing the related information, such as pathway databases KEGG (Ogata et al., 1999), Reactome (Joshi-Tope et al., 2005), Gene Ontology (Ashburner et al., 2000), and so on. However, only limited integrative multi-omics clustering methods can borrow prior biological information, including IS-K means and PARADIGM. IS-K means groups features based on prior knowledge (e.g., pathway information) and incorporates them in the objective function through a group lasso penalty. Thus, it can select critical groups (e.g., pathways) during the clustering procedure although it can only deal with continuous data. PARADIGM can incorporate pathway information, but it requires users to upload data to the designated website to perform the analysis.

4 |. CONCLUSION

We have summarized integrative multi-omics clustering methods into three general categories, concatenated clustering, clustering of clusters, and interactive clustering based on when and how multi-omics data are processed for clustering. Depending on the main strategy used during clustering, we further classified methods into different approaches under each category. We discussed the mathematical basis for each method and its strengths and weaknesses. One uniqueness of this work is that we also outlined four general scenarios with preferred methods for researchers to strategize their selection of integrative multi-omics clustering methods for their future studies.

Concatenated clustering is a straightforward strategy for integrative multi-omics clustering, following a natural logic that finds shared information first and performs clustering base on the shared information later. This is an obvious difference comparing to another two categories of methods. Joint latent model, low-rank approximation, and NMF intuit that a low-dimensional matrix can represent the sample clustering membership across multi-omics data. Notably, some methods can be grouped into more than one of these three approaches based on how the data matrix is decomposed. For example, JIVE can be viewed as a low-rank approximation approach if the data matrix is composed of the summation of low-rank constrained joint structure and individual structure, and an error matrix. JIVE also can be viewed as a joint latent model approach if the joint structure is further constructed by a product of a joint latent matrix and data-specific loading matrix. In addition, if all elements in the joint latent matrix and data specific loading matrix are restricted to be non-negative, JIVE even can be viewed as an NMF approach. Noisy data is commonly seen in the integrative analysis of multi-omics data, and concatenated clustering methods are generally sensitive to data with noise. Methods from clustering of clusters, on the contrary, perform well for noisy data. The perturbation-aided approach itself is based on perturbation generated by either resampling or adding noise to the original data. Therefore, methods from the perturbation-aided approach generally can provide a more reliable clustering result. Similarity-based approach such as Spectrum and SNF were also reported robust to noise (John et al., 2020; Tini et al., 2019). One major concern for clustering of clusters is whether the primary clustering information across different omics data is consistent before performing further integrative clustering. If not, the final clustering results may not be meaningful. Thus, it is worth applying some measures to evaluate the consistency of primary clustering results, such as the Rand index (Rand, 1971), adjusted Rand index (Hubert & Arabie, 1985), Jaccard similarity (Levandowsky & Winter, 1971), variation of information (Meilă, 2003), and so on.

As mentioned in the very beginning, determining the biological question before conducting the multi-omics analysis is very important. We focus on the disease subtyping using multi-omics data which can be addressed by the integrative multi-omics clustering methods included in this review. In addition, people may also be interested in identifying potential therapeutic targets for diseases which is related to clustering methods that can select features, as discussed in the above Scenario I of implement recommendation. Feature selection can be achieved by incorporating a penalty term in the objective function or by adding Bayesian indicator variables/parameters in many methods from concatenated clustering and interactive clustering. However, most methods from clustering of clusters cannot perform feature selection because either the perturbation procedure or the similarity construction procedure relies on information from all features, except for CIMLR which includes a second step to select features through a hypergeometric test. Feature selection also has been studied in the model-based clustering methods which incorporate variable selection procedure although not under multi-omics settings (Fop & Murphy, 2018; Guo et al., 2010; Zhou et al., 2009). Besides, some of our included methods can address some specific questions other than disease subtyping. For example, jNMF can identify correlated profiles across different type of measures (e.g., gene expression, DNA methylation, microRNA expression); PARADIGM can infer sample-specific pathway activities from multi-omics data.

Some limitations of this review must be acknowledged. First, we focus more on integrative multi-omics clustering methods that can lead to direct sample assignments. Some other integrative clustering methods were not included here, for example, correlation and covariance-based methods and their extensions (Hotelling, 1936; D. Hwang et al., 2004; Witten & Tibshirani, 2009; Wold et al., 2001). They can also be interesting if researchers want to disentangle the correlations between omics data. Second, because we assume that the same group of features contributes to the clusters instead of different groups of features contributing to different clusters, only one-dimensional clustering methods were discussed here. For the two-dimensional clustering methods, for example, bi-clustering, people may consult with a recent systematic review by Padilha and Campello (2017). Third, we only listed four common scenarios with recommendations in this work for a general guidance or as a starting point. In real applications, situations can be much more complicated and require more effort to choose the appropriate method.

Even though many integrative multi-omics clustering methods have been developed as described above, many potential areas still require further investigation. For example, most methods require a common clustering structure shared by all omics data. This may not be the case in real-world data, especially when the omics data are generated from very different aspects of the same samples. How to properly assess this inconsistent clustering structure among multi-omics data is difficult. Even though we have methods like MDI and PSDF which can address part of this issue, they have limitations such as too many parameters to specify and computational cost. Therefore, there is still much work to do in this area. Current clustering methods generally assume that samples can all be grouped into some clusters. However, some samples may just be outliers due to many reasons, for example, mistakenly measured. Therefore, these samples should not be considered for any clusters. Currently, there is a paucity of methods that can deal with this situation. This could be especially important in biological studies. As the quick increase of our domain knowledge, methods that can incorporate prior information is worthy of further study in the near future. Currently there are several methods available for performing clustering while taking into account for prior knowledge (Dotan-Cohen et al., 2007; Huang & Pan, 2006; Tari et al., 2009; Verbanck et al., 2013), as well as methods for integrative analysis for multi-omics data assisted by prior knowledge (de Tayrac et al., 2009; Tong et al., 2020; J. Yan et al., 2018). It is an interesting and important research topic to develop methods for clustering of multi-omics data that take advantage of prior information.