LHSPred: A web based application for predicting lung health severity

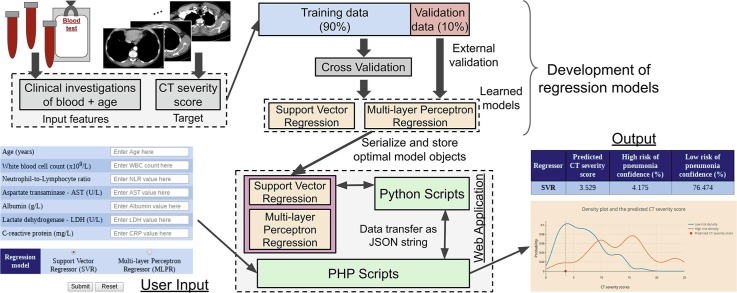
Graphical abstract

Abstract

Background and objectives

The computed tomography (CT) scan facilities are crucial for diagnosis of pulmonary diseases and are overburdened during the current pandemic of novel coronavirus disease 2019 (COVID-19). LHSPred (Lung Health Severity Prediction) is a web based tool that enables users to determine a score that evaluates CT scans, without radiologist intervention, and predict risk of pneumonia with features of blood examination and age of patient. It can help in early assessment of lung health severity of patients without CT-scan results and also enable monitoring of post-COVID lung health for recovered patients.

Methods

This tool uses Support Vector Regression (SVR) and Multi-Layer Perceptron Regression (MLPR), trained on COVID-19 patient data reported in the literature. It allows to compute a score (CT severity score) that evaluates the involvement of lesions in lung lobes and to predict risk of pneumonia. A web application was implemented that uses the trained regression models.

Results

The application has proven to be effective and user friendly in a clinical setting for pulmonary disease treatment. The SVR model achieved Pearson correlation coefficient (PCC) of 0.77 and mean absolute error (MAE) of 2.239 while determining the computed tomography (CT) severity score. The MLPR model achieved PCC of 0.77 and MAE of 2.309. Thus, it can be applied as a useful tool in predicting pneumonia in the post COVID-19 era.

Conclusion

LHSPred can be used as a decision support system by the clinicians and as a tool for self-assessment by the patients with only six blood test input features.

1. Introduction

The primary organ affected by novel coronavirus (nCoV-2019) is the lung and causes pneumonia and lung fibrosis that leads to severity or death. Due to the novel coronavirus disease 2019 (COVID-19) pandemic, enough high resolution computed tomography (HRCT) scan facilities are also lacking, even for COVID recovered patients. In recent months, many countries (e.g. United Kingdom, South Africa, Brazil and India) are affected by a second wave of the pandemic from novel variants of the virus [1]. The high rate of reproduction of these variants results in a higher rate of infections [2]. The manufacturing and logistics constraints have also slowed down the vaccination process. This increases the risk of rapid degradation of lung health [3]. The rising number of daily cases of infection have imposed a heavy burden on the healthcare and COVID-testing facilities. Hence, early prediction of lung health severity of the vulnerable population without radiological inputs is an absolute necessity.

Radiological imagery such as computed tomography (CT) and chest X-ray (CXR) were proven to be diagnostically more efficient compared to the gold standard of reverse-transcription polymerase chain reaction (RT-PCR) tests for early diagnosis of coronavirus infection [4], [5]. Recognition of CT features like ground glass opacities (GGO), consolidation and number of lung lobes affected by lesions are important to detect coronavirus pneumonia manifestation [6]. Currently, the use of machine learning (ML) tools is evolving for computer aided analysis of chest CT scan images for COVID-19 classification and detection of lung lesions [7], [8]. A major challenge for ML-based diagnosis of COVID-19 detection of CT images is the need for a large number of images to train the prediction models. Gaur et al. (2022) countered this challenge by using a transfer learning strategy to train deep learning models for COVID-19 detection with small number of CT images and achieved good performance to mitigate the problem of high false negatives in RT-PCR [9]. Combination of signal processing, deep learning and transfer learning techniques to analyze CXR images for COVID-19 diagnosis achieved an excellent accuracy of 100% on a dataset consisting of over 1400 CXR images [10]. Thus, the use of radiological features to develop ML models for COVID-19 diagnosis have certainly showed high efficiency. But, our objective is to use ML for the prediction of lung-health status and disease progression in patients who are already infected with COVID-19, since these patients show a wide spectrum of lung severity – mild, moderate, severe and critical [11]. These prognostic prediction tasks require repetitive investigations to assess the state of the patient regularly. So, there is a need to use clinical features (instead of radiological inputs) to train ML models for prognosis because repetitive radiological investigations are costly, and undesirable due to the shortage of radiological facilities during this pandemic situation. Several clinical features were shown to be effective markers for prediction of pneumonia severity and mortality. Wu et al. (2020) achieved good accuracy in pneumonia severity prediction using seven features including age, lymphocytes, C-reactive protein (CRP) and lactic dehydrogenase (LDH) [12]. Assaf et al. (2021) reported that the white blood cells (WBC), lymphocytes count and oxygen saturation as the most contributory factors for critical COVID-19 [13]. Liu et al. (2021) predicted risk of critical COVID-19 with only four clinical features [14]. CRP, LDH and age of patient were also proven to be significant in COVID-19 mortality [15].

Feng et al. (2020) proposed a CT (computed tomography) severity score (CTSS) that evaluates the extent of lesions from CT scans [16]. CTSS was defined as a unit-less integer metric in the range 0–25 that is obtained by aggregating individual scores from the five lung lobes, where each lobe is scored by a radiologist in the range 0–5 as per involvement of lesions. Scores of 0, 1, 2, 3, 4 and 5 for each lobe implies no involvement of lesions, <=5% involvement, 6–25% involvement, 26–50% involvement, 51–75% involvement and > 75% involvement respectively. They proved that clinical features and the CTSS are statistically significant in prediction of risk of progression of coronavirus pneumonia. They also showed that clinical features from blood samples and age of patients were strongly correlated with the CTSS. So, we leverage the already-proven correlation between CTSS and clinical features to automate the calculation of CTSS from those features using regression models. Such an automation should reduce the burden of radiologists to manually annotate and quantify lung lesions. Regression based optimization is also used in other fields, such as Brain-Computer Interface (BCI), for automatic detection of motor imagery tasks from electro-encephalogram data [17]. In general, regression models are used to automate the prediction of scores having continuous values, such as the CTSS.

Here, we present LHSPred (Lung Health Severity Prediction) - a web based tool to assess lung health severity by determining the CTSS from blood sample examination features and age using regression-based methods and further classify patients with low and high risk of pneumonia. Due to few input features, this tool can also be used by COVID recovered and pneumonia risk patients for regular lung health assessment.

2. Methodology

2.1. Datasets

The data of 247 COVID-19 patients was obtained from the publicly available dataset [16]. The original dataset consisted of 32 features including demographic, clinical and CT characteristics. There were 7 features among them that were either reported as risk factors for progression of pneumonia or strongly correlated with CTSS – namely age, WBC count, neutrophil–lymphocyte ratio (NLR), aspartate aminotransferase (AST), albumin, LDH and CRP. The characteristics of the features are given in Table 1 . The CTSS of patients with high risk of pneumonia (n = 25, min = 2, max = 25, inter-quartile range (IQR) = 7, median = 14) was significantly greater (F-value = 65.693, p-value < 0.05 using ANOVA) than those with low risk (n = 222, min = 1, max = 18, IQR = 5, median = 6). The data was split randomly into two sets: Set-A (90%, n = 222) and Set-B (10%, n = 25).

Table 1.

Characteristics of the features used by regression models to determine CT severity score.

Features	Range	Inter-quartile Range (IQR)	Median	F-value a	p-value a	Reported by Feng et al. (2020) b	p-value < 0.05
Age	19–82	21.75	44.5	45.155	1.54 × 10-10	Yes	Yes
Platelet count	35–458	85.75	178	1.29	0.257	No	No
WBC	1.01–14.42	1.912	4.555	1.125	0.290	Yes	No
NLR	0.611–9	1.806	2.69	58.042	7.54 × 10-13	Yes	Yes
Total bilirubin	4.05–39.2	7.517	11.615	0.195	0.659	No	No
ALT	1.19–98	15.157	20.07	13.811	2.6 × 10-4	No	Yes
AST	10–80	11.395	24.39	35.893	8.42 × 10-9	Yes	Yes
Albumin	23.8–65.9	5.223	37.5	74.592	1.19 × 10-15	Yes	Yes
Creatinine	−3.2–288.7	22.973	51.02	1.21	0.272	No	No
CK	17–798.3	74.658	76.1	7.304	0.007	No	Yes
LDH	7.1–565	81.6	177.65	114.276	9.43 × 10-22	Yes	Yes
CRP	0.01–120	30.48	21.31	109.838	4.16 × 10-21	Yes	Yes

^a F-values and p-values were calculated with univariate linear regression.

^b Feng et al. (2020) reported these features as risk factors of pneumonia progression and correlated to CT severity score. Abbreviations WBC - White Blood Cell count; NLR - Neutrophil-to-Lymphocyte Ratio; ALT - Alanine aminotransferase; AST - Aspartate aminotransferase; CK - Creatinine Kinase; LDH - Lactic dehydrogenase; CRP - C-Reactive Protein.

2.2. Regression models

We used Support Vector Regression (SVR) and Multi-Layer Perceptron Regression (MLPR) to determine the CTSS [18], [19]. The data in Set-A were used to train the regression models with cross validation and the samples in Set-B were used as blind data for the purpose of external validation. Standardization of features was performed using equation (1) -.

$$z=\frac{\left(x-\mu \right)}{\sigma }$$ (1)

where, x is the value of a feature, µ is the mean value and σ is the standard deviation of the feature in the training samples. K-fold cross validation was performed with k = 3, 5, 10. The regression models were trained with 3 feature combinations – (i) All 12 clinical features in the dataset, (ii) 8 clinical features with p-value < 0.05, and (iii) 7 clinical features reported by Feng et al. (2020) as risk factors for pneumonia progression and correlated to CTSS [16].

2.2.1. Hyperparameter optimization

The models were trained with different hyperparameters using grid-search technique. There were three hyperparameters of MLPR algorithms that were tuned – hidden layer size, activation function and learning rate. The number of nodes in the input and output layers of the MLPR architecture are constant (not tuneable), and equal to the number of input features and target variables respectively. In our study, there was only one node in the output layer as there is a single target variable – CTSS. There were 12, 8 and 7 nodes in the input layer for different models trained with the respective feature combinations (all features in the dataset, features with p-value < 0.05, and features reported by Feng et al. [16]). For SVR models, the tuneable hyperparameters varies with the choice of kernel. The parameter grids used in grid-search algorithm for different models are given in Table 2 . Grid search algorithm performed an exhaustive search on the parameter grid, that is, models were trained with every hyperparameter combination and a comparison of their performances was done.

Table 2.

Parameter grids used by grid-search algorithm for hyperparameter optimization.

Model	Parameter grid	No. of combinations
MLPR	hidden layer size × activation function × learning rate where, hidden layer size = {(50), (1 0 0), (1 5 0), (2 0 0), (2 5 0), (3 0 0), (50,10), (100,20), (150, 30), (200,40)}, activation function = {ReLU, logistic}, learning rate = {0.01, 0.001, 0.0001, 0.00001}	80
SVR (kernel = RBF)	C × gamma × epsilon where, C = {5, 10, 15, 20} gamma = {0.1, 0.01, 0.001, 0.0001} epsilon = {0.001, 0.01, 0.1, 0.5, 0.8}	80
SVR (kernel = polynomial)	C × gamma × epsilon × degree × coefficient where, C = {1, 5, 10, 15} gamma = {0.1, 0.01, 0.001} epsilon = {0.01, 0.1, 0.5, 0.8} degree = {2, 3} coefficient = {1, 2, 3, 4}	384
SVR (kernel = linear)	C × epsilon where, C = {1, 5, 10, 15} epsilon = {0.01, 0.1, 0.5, 0.7}	16

Abbreviations: MLPR = Multi-Layer Perceptron Regression; RBF = Radial Basis Function; ReLU = Rectified Linear Unit; SVR = Support Vector Regression.

2.2.2. Performance metrics

The different performance metrics used to evaluate the regression models are as follows.

Mean Squared Error (MSE) – It is the mean of the square of errors between the actual and predicted values of the target variable. It is computed using equation (2).

$$\mathit{MSE}=\frac{1}{n}\sum _{i=1}^n{({\mathit{actual}}_i-{\mathit{predicted}}_i)}^2$$ (2)

where, n denotes the number of samples.

Mean Absolute Error (MAE) – It is the mean of the absolute errors between the actual and predicted values of the target variable. It is computed using equation (3).

$$\mathit{MAE}=\frac{1}{n}\sum _{i=1}^n({\mathit{actual}}_i-{\mathit{predicted}}_i)$$ (3)

where, n denotes the number of samples.

Pearson Correlation Coefficient (PCC) – It is the ratio of covariance of the actual and predicted values of a target variable and the product of standard deviations. It is computed using equation (4). The PCC values range from −1 to + 1, such that + 1, 0 and −1 denote perfect correlation, no correlation and inverse correlation respectively.

$$\mathit{PCC}=\frac{\mathit{covariance}(actual,predicted)}{{\sigma }_{\mathit{actual}}{\sigma }_{\mathit{predicted}}}$$ (4)

where, σ denotes standard deviation.

The MSE was selected as the benchmark metric for choosing the optimal model.

The development of regression models and evaluation of their performance was performed using the Python library- scikit-learn. The model objects were serialized as files using Joblib and were stored in a web server.

2.3. Prediction of risk of pneumonia

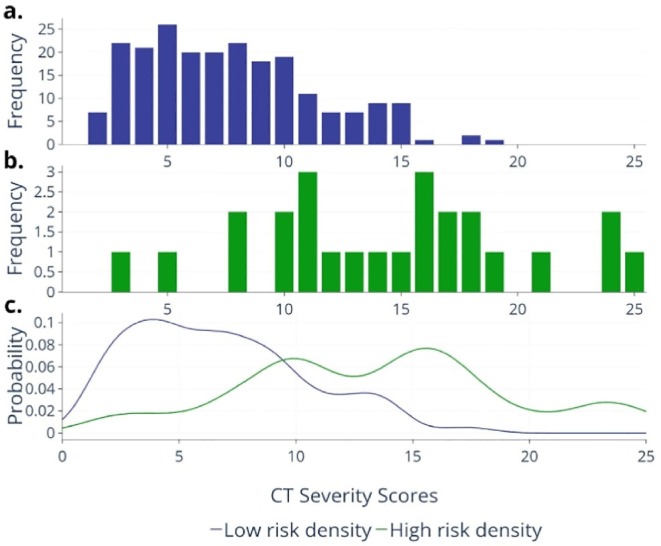
The CTSS values of patients with low and high risk of pneumonia in the input dataset were split to obtain two distributions of CTSS values. These distributions are plotted in Fig. 1 a and Fig. 1b. Taking the CTSS as a random variable, the probability density functions were computed for high risk (f_high) and low risk (f_low) patients. The values f_high(x) and f_low(x) denote the probabilities of the CTSS value being “x” for high-risk and low-risk patients respectively. Kernel Density Estimation (KDE) was used with Gaussian kernel for estimation of f_high and f_low in a non-parametric manner [20] The probability densities are plotted in Fig. 1c.

Fig. 1.

Histograms showing distribution of CT Severity Score (CTSS) values in patients with (a) high risk and (b) low risk of pneumonia. (c) Probability density functions, f_low (blue curve) and f_high (green curve), estimated using Kernel Density Estimation method.

The confidence of low risk (C_low) and high risk (C_high) of pneumonia was computed using equations (5), (6) respectively.

$$C_{\mathit{low}}\left(s\right)={\int }_s^{25}{f}_{\mathit{low}}\left(x\right)dx$$ (5)

$$C_{\mathit{high}}\left(s\right)={\int }_0^s{f}_{\mathit{high}}\left(x\right)dx$$ (6)

where, s is the CTSS predicted by the regression models. Here, 0 and 25 are the minimum and maximum values of CTSS respectively because there are five lung lobes and each one is scored in the range 0–5. A patient was predicted as “High risk” if C_high > C_low; and as “Low Risk” otherwise. The visualization of the confidence values (C_low and C_high) is shown in Fig. SF1 of Supplementary data. It shows that C_low > C_high when the predicted CTSS is a low value in the range of 0–5 (Fig. SF1a), and the patient is stratified into “Low Risk” category. As the predicted CTSS increases to a value > 14 (as seen in Fig. SF1b), it can be observed that the C_high also increases while the C_low decreases, and the patient is labelled as “High Risk” when C_high > C_low.

2.4. Web application

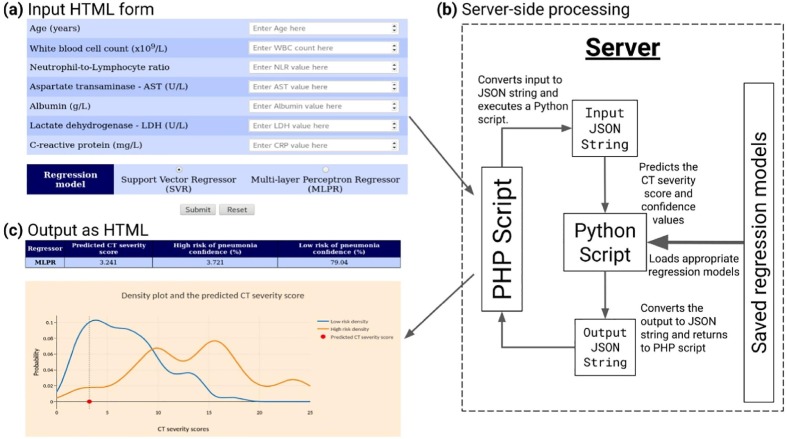
We developed an easy-to-use web application that serves as a graphical tool to invoke the underlying regression models. This set-up provides a fully automatic workflow that includes user input of the seven features, deployment of the regression models and display of output with decisions (CTSS and pneumonia-risk with confidences). To make the user input parameters minimum, the regression models trained with the 7 features reported by Feng et al. (2020) were used in the web server [16]. The user-input facility was provided through an HTML form and the server-side processing was developed using PHP language. The PHP script validates the input and converts it to a JSON (JavaScript Object Notation) string- a popular data-interchange format. It then executes a Python script with the JSON string as argument. The task of the Python script is to load the appropriate regression model saved in the server and perform the prediction of CTSS and confidence values. It also converts the output also as a JSON string and transfers it back to the PHP script. Then, the PHP script processes the output JSON and sends it to the user as HTML. The working of the system is depicted in Fig. 2 .

Fig. 2.

Flow of data in the web application; (a) the input HTML form, (b) the server, and (c) the output page.

The web application was deployed on an “Apache HTTP” server running Python 3.4. The packages used were Scikit-learn (version 0.20.0), NumPy (version 1.16.6), SciPy (version 1.2.3) and Joblib (version 0.14.1). All packages were installed in a Python virtual environment. The plot in the output is displayed using the Plotly JavaScript library. The web application was also tested to run with Python 2.7. The versions of packages used for Python 2.7 were the same as for Python 3.4, except for NumPy (version 1.11.3).

3. Results

SVR models were created with radial basis function (RBF), polynomial (poly) and linear kernels and other hyperparameters for tuning with the grid-search algorithm. The optimal SVR model used a RBF kernel with C = 10, gamma = 0.01 and epsilon = 0.001. Also, different architectures of MLPR models with one and two hidden layers were constructed and trained with both logistic and rectified linear unit (ReLU) activation functions with constant learning rates. The optimal MLPR model was constructed with a single hidden layer of 200 nodes using a ReLU activation function and constant learning rate = 0.0001. The architecture of the optimal MLPR model is shown in Fig. SF2 of Supplementary data. All the models were trained using k-fold cross validation with k = 3, 5, 10. Both SVR and MLPR models showed optimal performance for k = 5. The performance for regression of CTSS and pneumonia-risk prediction by the optimal models are given in Table 3 and Table 4 respectively. The detailed performance of the models with all hyperparameter and feature combinations, and cross validation folds are given in Supplementary data (Tables – ST1 – ST36). The CTSS regression and pneumonia-risk prediction performance of models that were trained with all features in the dataset and statistically significant features (p-value < 0.05; using univariate linear regression) are given in Supplementary data (Tables – ST37 – ST40).

Table 3.

Performance results for regression of CT severity score (CTSS).

Model	Regression performance on training dataset with 5-fold CV			Regression performance on validation dataset
	MAE	MSE	PCC	MAE	MSE	PCC
SVR	2.239	8.088	0.768	2.731	12.668	0.621
MLPR	2.309	8.300	0.765	2.838	13.611	0.577

Abbreviations: CV = Cross Validation; MAE = Mean Absolute Error; MLPR = Multi-Layer Perceptron Regression; MSE = Mean Squared Error; PCC = Pearson Correlation Coefficient; SVR = Support Vector Regression.

Table 4.

Performance results for prediction of risk of pneumonia.

Model	Prediction performance on training data			Prediction performance on validation data
	Accuracy	Sensitivity	Specificity	Accuracy	Sensitivity	Specificity
SVR	81.55%	0.75	0.82	80%	0.67	0.82
MLPR	81.54%	0.76	0.83	80%	0.67	0.82

Abbreviations: MLPR = Multi-Layer Perceptron Regression; SVR = Support Vector Regression.

Confidence values of > 50% for low risk and high risk of pneumonia were achieved for 0 ≤ CTSS < 6 and 14 < CTSS ≤ 25 respectively. The confidence values of risk of pneumonia for different ranges of predicted CTSS are given in Table 5 . The variation of confidence values with the predicted CTSS is plotted in Fig. SF3 of Supplementary data.

Table 5.

Confidence values of predicting low and high risk of pneumonia for different predicted CT severity scores.

Predicted CT severity score range	Confidence range of low risk of pneumonia (%)	Confidence range of high risk of pneumonia (%)	Absolute difference between high and low risk of pneumonia (%)
0–2	99.39–90.64	0–1.64	99.39–89
2–4	88.57–71.28	2.02–5.08	86.55–66.2
4–6	68.69–51.62	5.54–8.98	63.15–42.64
6–8	49.27–33.36	9.61–15.91	39.66–17.45
8–10	31.24–19	17.14–27.91	14.1–8.91
10–12	19–10.95	27.91–40.37	8.91–29.42
12–14	10.95–3.99	40.37–51.3	29.42–47.31
14–16	3.99–1.26	51.3–65.89	47.31–64.63
16–18	1.26–0.28	65.89–78.77	64.63–78.49
18–20	0.28–0	78.77–85.17	78.49–85.17
20–22	0–0	85.17–89.27	85.17–89.27
22–25	0–0	89.27–96.97	89.27–96.97

4. Using the web application

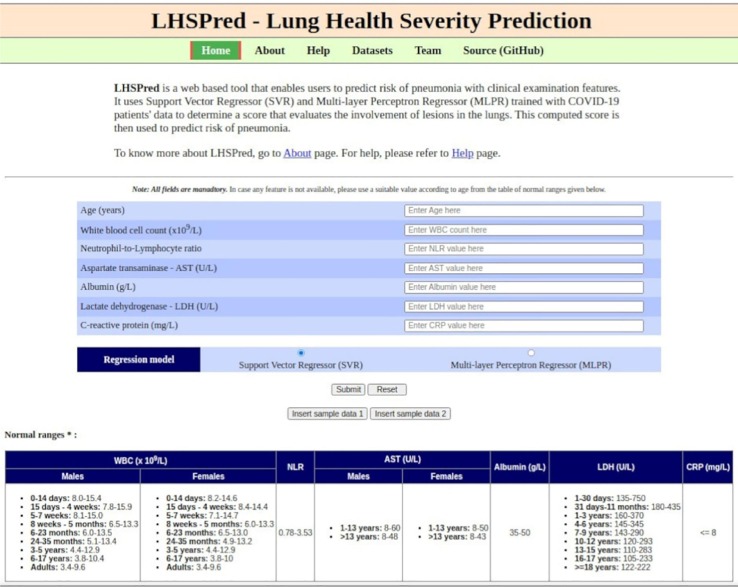
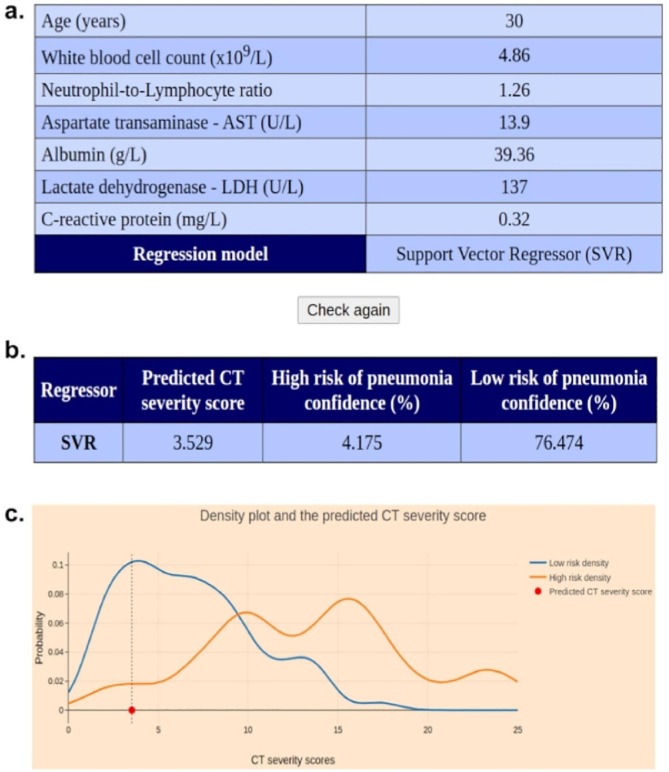
The homepage of LHSPred is shown in Fig. 3 . Users need to fill up all the mandatory input fields in the form - the six clinical features, age and the choice of regression model to be used for prediction. In case of unavailability of data for any feature, users can use the table of normal ranges, given at the bottom of the webpage, to add a suitable normal value. There are also buttons to insert two sets of sample data for quick demonstration. Users can clear all the inserted values with the “Reset” button. Finally, users can click the “Submit” button to get the output.

Fig. 3.

Screenshot of LHSPred homepage.

The output page is shown in Fig. 4 . First, there is a table showing the input values provided by the user (Fig. 4a). Next, a result table (Fig. 4b) is displayed that contains the regression algorithm used, the predicted CTSS and confidence values of high and low risk of pneumonia. Lastly, an interactive graph is displayed that plots the densities f_high and f_low, along with the predicted CTSS (Fig. 4c). There is a menu bar that appears on hovering the mouse pointer on the graph to zoom, pan and download it.

Fig. 4.

Different sections in the output page. (a) Table showing the inputs supplied, (b) Table showing the results - predicted CTSS, confidences of high and low risk of pneumonia, (c) Plot showing the densities f_high (orange curve) and f_low (blue curve), and the predicted CTSS (red point).

5. Discussion

The earlier work by Feng et al. (2020) proposed a technique for manually scoring CT scans to quantify the severity of lung lesions in pneumonia patients and used logistic regression with clinical and CT features (including the CT severity score) to classify the patients into high-risk and low-risk [16]. We, on the other hand, used age and the other significant clinical features of blood from the same dataset to build an estimator to computationally determine the CT severity score and predict the risk of pneumonia. They had used datasets from two different hospitals: one for training and other for validation purposes. We noticed that the range of CTSS values in that training dataset was 0–17. This meant that the estimators cannot summarize the samples with CTSS values > 17. So, we merged the two datasets and then randomly selected 10% samples for external validation and the rest for training. Another work of COVID-19 severity prediction based on CT severity scores performed a statistical analysis to find a threshold to discriminate severe patients [21]. Instead, our web application computes the confidences of both – low and high risk of pneumonia. Also, combination of CTSS and clinical parameters were used for prediction of mortality due to COVID-19 pneumonia [22]. This approach of using CTSS directly as a feature requires the users to provide the CTSS which can be computed only with the help of radiologists whereas the regression models in our web application allows for automatic calculation of the CTSS. The work by Wu et al. (2020) is very similar to our work in terms of the features used for COVID-19 severity prediction [12]. They also used age and six other features from blood tests (proportion of lymphocytes, CRP, LDH, urea, creatine kinase and calcium) of a much larger cohort of 725 patients (239 for training, 60 for validation and 426 for external validation) in a wider geographical area (China, Belgium and Italy). They developed logistic regression models to classify patients into low, medium and high risk classes directly from the clinical features, and found cut-off probabilities to differentiate these classes. In contrast, we compared two regression models (SVR and MLPR) for computing a consolidated score (CTSS) for every patient and, subsequently, used CTSS-based confidence values to perform the risk-stratification task and to find the cut-off values of the CTSS. They did not implement any cross-validation and reported similar performance with an accuracy of 80.1%, sensitivity of 84.6% and specificity of 73.7% for external validation. We, on the other hand, used k-fold cross validation with k = 3, 5, 10 to avoid overfitting.

We also trained regression models with other feature combinations – all 12 clinical features in the dataset and 8 features where p-value < 0.05. The CTSS regression performance with these feature sets was sub-optimal but a slight increase in risk-prediction accuracy was observed. The models trained with features reported by Feng et al. (2020) were chosen as optimal as similar performance was achieved using less number of features [16]. For predicted CTSS of <6, confidence of low risk of pneumonia is >50%. While, for predicted CTSS of >14, confidence of high risk of pneumonia is >50%. The sensitivity and specificity values of pneumonia-risk prediction denotes that the ability of accurate prediction of both high and low risk patients are similar and that the accuracy is not skewed towards any class. The density curve of CTSS of high risk can be seen in Fig. 1(c) as multimodal and flatter as compared to the low risk density curve. The data was highly imbalanced with a low number of high risk samples. More high risk samples would have allowed the scores of high risk patients to be more clustered and an improved performance of the prediction could have been achieved. In addition to the features used in this work, clinical parameters such as D-dimer, blood urea nitrogen (BUN) and respiratory rate were also known to be associated with pneumonia [23]. In future, availability of information for these parameters to train the prediction models could lead to an improved performance. Furthermore, with additional data points, we can improve the reliability of the probability densities that could lead to better risk stratification.

6. Conclusion

We developed a web based tool that uses regression models to score CT scan reports from only 7 input features and predict risk of pneumonia. The automated determination of CT severity score can reduce the workload of radiologists significantly during this pandemic. It can be used by doctors for early detection of patients with high risk in order to offer better therapeutics. It can also be used by pneumonia risk patients during the second wave of the pandemic and COVID-recovered patients to self-monitor their lung health regularly without radiological inputs.

7. Availability of data and materials

LHSPred is available at http://dibresources.jcbose.ac.in/ssaha4/lhspred. Source code and data are available at https://github.com/ttsudipto/lhspred.

Funding

This work is supported by Indian Council of Medical Research [Project ID 2019-0075].

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: