A truth-based primal-dual learning approach to reconstruct CT images utilizing the virtual imaging trial platform

Abstract

Inherent to Computed tomography (CT) is image reconstruction, constructing 3D voxel values from noisy projection data. Modeling this inverse operation is not straightforward. Given the ill-posed nature of inverse problem in CT reconstruction, data-driven methods need regularization to enhance the accuracy of the reconstructed images. Besides, generalization of the results hinges upon the availability of large training datasets with access to ground truth. This paper offers a new strategy to reconstruct CT images with the advantage of ground truth accessible through a virtual imaging trial (VIT) platform. A learned primal-dual deep neural network (LPD-DNN) employed the forward model and its adjoint as a surrogate of the imaging’s geometry and physics. VIT offered simulated CT projections paired with ground truth labels from anthropomorphic human models without image noise and resolution degradation. The models included a library of anthropomorphic, computational patient models (XCAT). The DukeSim simulator was utilized to form realistic projection data emulating the impact of the physics and geometry of a commercial-equivalent CT scanner. The resultant noisy sinogram data associated with each slice was thus generated for training. Corresponding linear attenuation coefficients of phantoms’ materials at the effective energy of the x-ray spectrum were used as the ground truth labels. The LPD-DNN was deployed to learn the complex operators and hyper-parameters in the proximal primal-dual optimization. The obtained validation results showed a 12% normalized root mean square error with respect to the ground truth labels, a peak signal-to-noise ratio of 32 dB, a signal-to-noise ratio of 1.5, and a structural similarity index of 96%. These results were highly favorable compared to standard filtered-back projection reconstruction (65%, 17 dB, 1.0, 26%).

1. INTRODUCTION

The recent advancements of data-driven methods and deep learning algorithms in image processing and transformation have led to utilize deep neural network (DNN)-based algorithms in medical imaging [1]. The variety of applications such as de-noising [2], [3], image harmonization [4–5], and CT image reconstructions [6] are some of the recent examples. In many cases, de-noising and harmonization can be regarded as image-to-image transformation problems. While, for CT reconstruction, the transformation is from sinogram domain to reconstructed image domain. The solution to this inverse problem can be improved utilizing DNNs. This approach, so-called learned optimization, has shown promising results to solve ill-posed inverse problems [7–9].

Besides the importance of architecture for data-driven algorithms, training a DNN itself is challenging, especially in medical imaging applications where there is limited access to training data and a high level of complex components such as patient body and imaging systems. Moreover, the concerns regarding patient privacy and the accuracy of ground truth have highlighted the importance of data acquisition for data-driven methods. To address the drawbacks, we developed a reconstruction algorithm that utilizes a learned primal-dual DNN, taking advantage of the state-ofthe-art virtual imaging trial (VIT) [10] framework for the training process. The generated training data and ground truth entail the patient body habitus complexity and imaging systems attributes that impact the projection data. The deployed DNN learns the primal and dual operators to map the noisy sinogram data to the attenuation map.

2. MATERIALS AND METHODS

In the subsequent sections, the VIT framework for generating the required training data and associated ground truth are elaborated. Afterwards, the network architecture, training procedure, and evaluation methods are presented.

2.1. Ground Truth and Training images

Three handers simulated sinogram data, and the corresponding attenuation maps were generated for training the network. Ten random axial slices of the computational patient models were simulated. The computational models’ body habitue were adopted from ten different 4D extended cardiac-torso (XCAT) phantoms [11–13]. The lung parenchyma’s texture and material in the XCATs were to match tissue-equivalent linear attenuation coefficients. The XCAT phantoms were virtually imaged using DukeSim, modeling a commercial-equivalent CT scanner at three dose levels as low, medium, and high dose values (50, 100, 150 mAs) at 120 kV energy threshold. The reference map was the known HU value of the attenuation map in the XCAT phantoms, and input images for training were the noisy sinograms corresponding with each of the axial slices with 736 detector columns and 1152 projections per rotation. The attenuation map was created with 512 × 512 pixels, covering a field of view of 50 cm.

2.2. Network Architecture

The employed architecture was adopted from the Learned primal-dual (LPD) network and the developed mathematical terminology in [8]. Mathematically speaking, the reconstruction of the attenuation map from the corresponding sinogram data can be formulated as an inverse problem such as:

$$y_o=\tau \left(x_t\right)+{\delta }_y,$$ (1)

where y_o ∈ Y, x_t ∈ X, δ_y, and τ(. ): X → Y stand for observation data (sinogram), signal (attenuation map), observation noise, and forward operator, respectively. To approximate x_t from y_o, the negative log-likelihood of the signal can be minimized. Since the reconstruction problem is an ill-posed, a regularization term is needed to stabilize the solution which leads to solving the following optimization problem:

$$\underset{x\in X}{min}\hspace{1em}L\left(\tau (x),y_o\right)+\lambda R(x),$$ (2)

where L is the loss function, R is the regularization term, and λ ≥ 0 is the regularization coefficient. Utilizing the primal-dual hybrid gradient (PDHG) method [14], Eq. (2) can be solved iteratively. In i^th iteration, the primal and dual variables are calculated as:

$$\begin{gathered} y_{i+1}=pro{x}_{{\left[L\left(.,y_o\right)\right]}^{*},\sigma }\left(y_i+\sigma \tau \left(x_i\right)\right) \\ {x}_{i+1}=pro{x}_{R,\zeta }\left(x_i-\zeta {\left[\partial {\tau }_{\mid x_i}\right]}^{*}\left(y_{i+1}\right)\right)\hspace{1em}i\ge 1,y_i\in Y,x_i\in X \\ {x}_{i+1}=x_i+\gamma \left(x_{i+1}-x_i\right), \end{gathered}$$ (3)

where in above, [L(. , y_o)]* stands for the Fenchel conjugate of L(. , y_o), ${\left[\partial {\tau }_{\mid x_i}\right]}^{*}$ adjoint of the derivative of the forward operator in point x_i, and σ, ζ, γ are positive hyper-parameters (0 ≤ γ ≤ 1), and prox_G,α (f) is the proximal operator mathematically defined as:

$$pro{x}_{G,\alpha }(f)={\mathit{\text{argmin}}}_{f^{\prime }\in F}\left[G\left(f^{\prime }\right)+\frac{1}{2\alpha }\Vert f^{\prime }-f{\Vert }^2\right].$$ (4)

It is a complex task to calculate proximal operators and conjugates– especially when employing a commonly used L₁ norm regularization, like total variation. Also, setting proper hyper-parameters is not a simple job and requires trial and error. To circumvent these challenges, we recast the above formulation as parameterized operators and trained the trainable parameters on a finite-horizon iteration. Moreover, instead of strictly enforcing the network’s over-relaxed updating policies, we let the network learn how these updates should be included. In this implementation, we employed Radon ray transform for the forward operator. Hence, ${\left[\partial {\tau }_{\mid x_i}\right]}^{*}={\tau }^{*}$. Therefore, similar to [8], for each iteration, we have:

$$\begin{gathered} y_{i+1}={\Delta }_{{\theta }_D^i}\left(y_i,\tau \left(x_i\right),y_o\right) \\ {x}_{i+1}={\Phi }_{{\theta }_P^i}\left(x_i,{\tau }^{*}\left(y_{i+1}\right)\right).i\in \left[1,\cdots ,i_{max}\right] \end{gathered}$$ (5)

For the initial guess, we used the filtered backprojection (FBP) approximation of the sinogram (x₁), and zero initialization of y₁. The adopted architecture (Fig. 1) was an iterative DNN with five iteration blocks. Each block consisted of three layers of convolutional neural networks (CNNs) with one skip connection. We employed the Parametric Rectified Linear Units (PReLU) function [15] as an activation function after internal CNNs layers and the Sigmoid function at the final layer. We used the Operator Discretization Library (ODL) [16] to carry out the forward and pseudoinverse projections as GPU-enabled layers to speed up the learning phase and guide the network in a physics-informed manner. These layers had no trainable parameters and only projected their inputs into the sensory and reconstruction domains.

Figure 1:

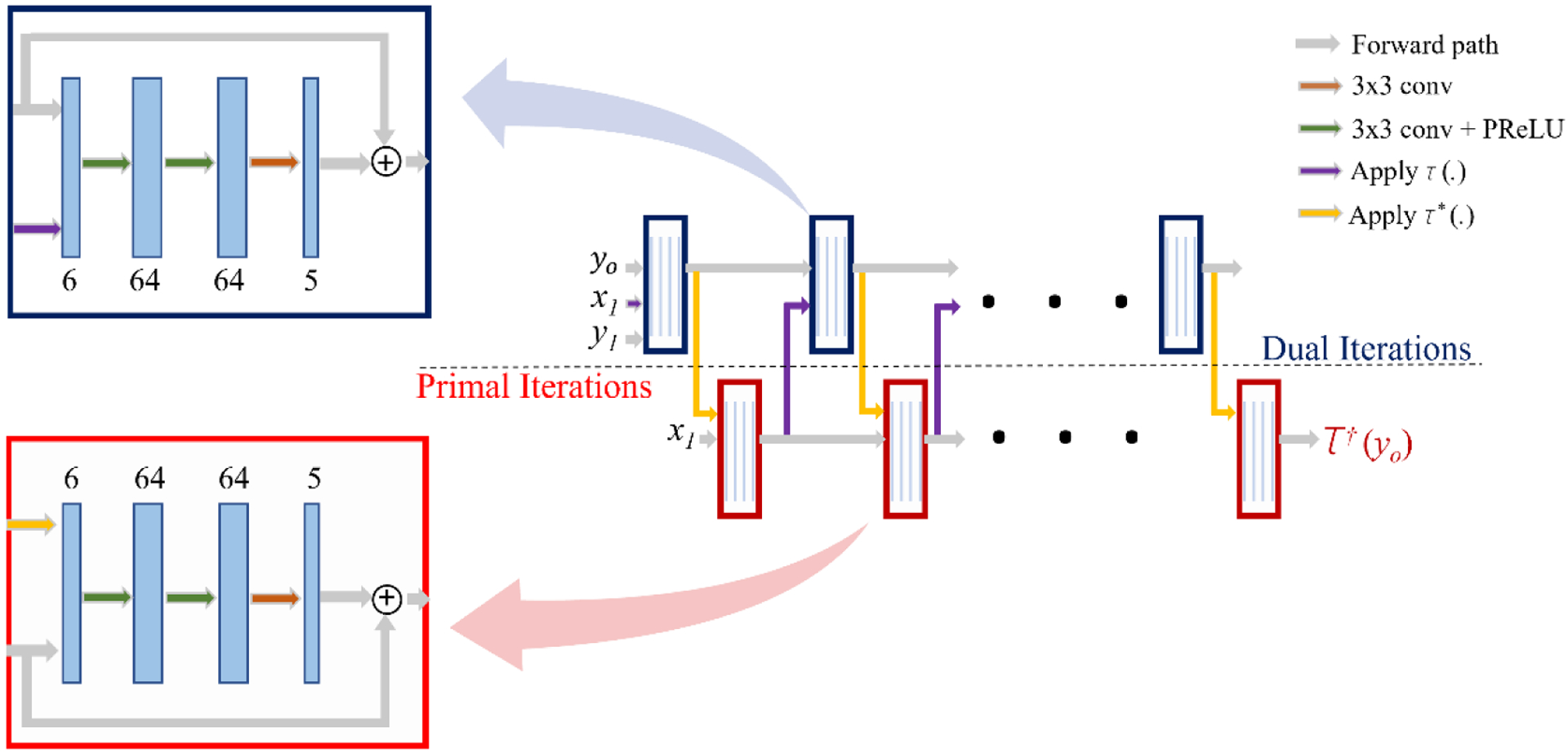
The architecture of the employed network [7]. The inputs are sinogram (y_o), initial primal guess (x₁=FBP(y_o)), and initial dual guess (y₁ = 0). The output is the reconstructed attenuation map (τ^†(y₀)). Each colored block is either dual iteration (navy blue blocks) or primal iteration (red blocks). Each block consists of four CNN layers (blue layers) first three followed by the PReLU (green arrows) and ReLU (orange arrows) activation functions. Moreover, in each block, one skip connection has been embedded, as depicted in the zoomed boxes.

2.3. Training and Evaluation

We separated all associated images with one XCAT as the validation set and used the rest of the images for training purposes. The sinogram data, ground truth attenuation maps, and FBP approximation of the attenuation maps were normalized into images with pixel values within [0,1] intervals. For training the network, we used the Adam optimizer. The initial learning rate was set to be 10⁻⁵. We used the cosine annealing method to schedule the learning rate. The running average gradient and its square coefficients were set to be (0.95,0.99). We used the mean square root (MSE) loss function to carry out the training and update the weights.

To evaluate the performance of the network, the normalized root mean squared error (NRMSE) of the reconstructed image with respect to the ground truth, structural similarity index (SSIM), signal-to-noise ratio (SNR), and peak signal-to-noise ratio (PSNR) on validation set were calculated. The obtained results were also compared to the performance of the conventional FBP method.

3. RESULTS

The quantitative results on the performance of the neural network and FBP-based reconstruction are reported in Table 1. Fig. 2 compares the visual performance of the network with respect to the FBP reconstruction algorithm for three different slices of the phantom in the validation set at three different dose levels. The obtained results indicated that the proposed algorithm provided reconstructed images with improved PSNR (> 32 dB vs. 18 dB), SNR (> 1.5 vs. 1.0), SSIM (> 96% vs. 26%), and NRMSE (< 12.1% vs. 65%), compared to the FBP images.

Table 1:

The quantitative evaluation of the results. Comparison of the DNN-based and FBP-based reconstruction algorithms performance.

Method	NRMSE (%)	SSIM (%)	PSNR (dB)	$\text{SNR}\left({}^{\mid {\mathit{\text{mean}}}_{HU}\mid }/S{D}_{HU}\right)$
LPD-DNN	12.1	96.8	32.4	1.56
FBP	65.5	25.9	17.7	1.02

Figure 2:

The network outputs are compared to the corresponding ground truth and the FBP-based reconstruction algorithm. The zoomed area in red, green, and yellow squares represent the DNN output, ground truth, and FBP-based output, respectively. From top to bottom, different reconstructed slices at high, medium, and low dose image acquisition settings.

Qualitatively, the LPD-DNN images had superior clarity compared to the FBP images (Fig. 2, high dose image). LPD-DNN provided a more accurate representation of the lung’s parenchyma (Fig. 2, medium dose image). Furthermore, the LPD-DDN successfully reduced the image noise from low dose images, resulting in images that indicate a distinct breakdown of the attenuation map (Fig. 2, third row zoomed images).

4. NEW OR BREAKTHROUGH WORK TO BE PRESENTED

The proposed framework delineates a great potential to design DNN-based reconstruction algorithms. The superiority of the developed framework relied on two main cornerstones: 1) Following the governing line of thought in the analytical approach to solve the inverse problem, and 2) training the LPD network architecture with a virtual image trial. The VIT platform offers access to a more accurate depiction of the ground truth as well as a wider range of training data with various parameters. These two features enable us to overcome data acquisition limitations and improve the generalizability of DNN-based reconstruction techniques.

5. CONCLUSION

We developed a deep neural network approach to reconstruct the attenuation map from the noisy sinogram data. We formed an iterative DNN based on a regulated primal-dual hybrid optimization method traditionally used to solve ill-posed problems such as image reconstruction. Preliminary findings showed that the developed reconstruction method, both qualitatively and quantitatively, outperforms a filtered back projection method.