High Magnetic Anisotropy of a Square-Planar Iron-Carbene Complex

Abstract

Among Earth-abundant catalyst systems, iron-carbene intermediates that perform C-C bond forming reactions such as cyclopropanation of olefins and C-H functionalization via carbene insertion are rare. Detailed descriptions of the possible electronic structures for iron-carbene bonds are imperative to obtain better mechanistic insights and enable rational catalyst design. Here, we report the first square-planar iron-carbene complex (^MesPDP^Ph)Fe(CPh₂), where [^MesPDP^Ph]^2- is the doubly-deprotonated form of [2,6-bis(5-(2,4,6-trimethylphenyl)-3-phenyl-1H-pyrrol-2-yl)pyridine]. The compound was prepared via reaction of the disubstituted diazoalkane N₂CPh₂ with (^MesPDP^Ph)Fe(thf) and represents a rare example of a structurally characterized, paramagnetic iron carbene complex. Temperature-dependent magnetic susceptibility measurements and applied-field Mössbauer spectroscopic studies revealed an orbitally near-degenerate S = 1 ground state with large unquenched orbital angular momentum resulting in high magnetic anisotropy. Spin-Hamiltonian analysis indicated that this S = 1 spin system has uniaxial magnetic properties arising from a ground M_S = ±1 non-Kramers doublet that is well-separated from the M_S = 0 sublevel due to very large axial zero-field splitting (D = −195 cm⁻¹, E/D = 0.02 estimated from magnetic susceptibility data). This remarkable electronic structure gives rise to a very large, positive magnetic hyperfine field of more than +60 T for the ⁵⁷Fe nucleus along the easy magnetization axis observed by Mössbauer spectroscopy. Computational analysis with complete active space self-consistent field (CASSCF) calculations provides a detailed electronic structure analysis and confirms that (^MesPDP^Ph)Fe(CPh₂) exhibits a multiconfigurational ground state. The majority contribution originates from a configuration best described as a singlet carbene coordinated to an intermediate-spin Fe^II center with a (d_xy)²{(d_xz),(d_z2)}³(d_yz)¹(d_x2_–y2)⁰ configuration featuring near-degenerate d_xz and d_z2 orbitals.

Graphical Abstract

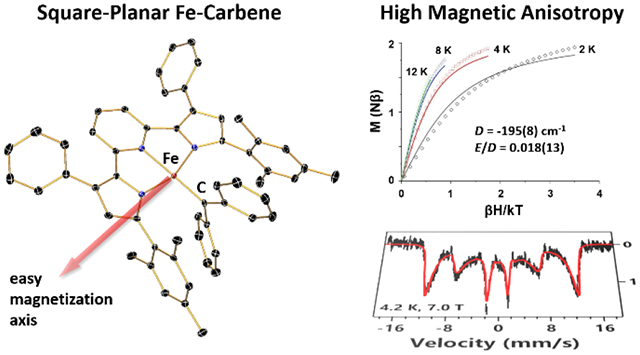
The square-planar compound (^MesPDP^Ph)Fe(CPh₂) is the first example of an iron carbene complex containing an intermediate-spin iron center. This unique electronic structure gives rise to a paramagnetic ground state with large unquenched orbital angular momentum. The resulting highly anisotropic magnetic properties are established by magnetic susceptibility measurements and applied-field Mössbauer spectroscopy. Computational analysis using the spectroscopy-oriented configuration interaction (SORCI) method provides further insight and reproduces the unusual magnetic behavior of the complex.

Introduction

Transition-metal carbene complexes are a hallmark of organometallic chemistry¹ and have long been studied due to a fundamental interest in their unique metal-carbon multiple bonds^2,3 and the resulting reactivity in organometallic transformations and catalysis.^4,5 Several important CR₂ group transfer reactions, such as cyclopropanation of olefins,⁶ C–H functionalization via carbene insertion,^7,8 and olefin metathesis,^9,10 rely on metal carbene species as key reactive intermediates that facilitate the construction of complex carbon frameworks in organic synthesis.^11,12 The broad range of observed reactivity stems from the diverse electronic structures of the metal-carbene complexes, depending on the carbene substituents and the metal center involved. Aside from N-heterocyclic carbenes, which show relatively sparse reactivity and are often used as strongly σ-donating spectator ligands in catalysis,¹³ more reactive carbene ligands are typically assigned to one of three distinct classes: a) Fischer-type carbenes, which are electrophilic at carbon and prefer low-valent, electron-rich metal centers;^14,15 b) Schrock-type carbenes or alkylidenes, which are nucleophilic at carbon and prefer high-valent, electron-poor metal centers;^16,17 and c) carbene radicals, which have been implicated in several catalytic C–H and C–C bond forming reactions and have attracted significant interest in recent years.^18–22

Among transition-metal carbene complexes, reactive iron-carbene species occupy a prominent role because they present an attractive Earth-abundant alternative to more well-established catalyst systems based on precious metals (Figure 1).^23–25 The first reported iron-catalyzed carbene-transfer reaction utilized the cationic complex [CpFe(CO)₂(THF)]BF₄ as the precatalyst.²⁶ Several isolable and structurally characterized iron-carbene complexes [CpFeL₂CR₂]⁺ (L = CO, phosphine) with a variety of cyclopentadienyl derivatives have been reported and exhibit the expected piano-stool geometry.^27–29 In addition to CpFe-based systems, iron-porphyrin complexes were among the first catalyst precursors for cyclopropanation and C–H insertion reactions.^30–32 While these reactions were inspired by isoelectronic oxygen-atom transfer reactivity in cytochrome P450 enzymes and utilized biomimetic metalloporphyrin models, recent research using bioengineered cytochrome P450s has allowed the development of biorthogonal CR₂ transfer reactivity with iron-carbenes as key intermediates.^33–35 Using macrocyclic porphyrin ligands as a blueprint for the generation of iron-carbene species, a number of square-pyramidal iron-carbene complexes with C₄-,³⁶ N₄-,^37–39 and O₄-macrocyclic^40,41 supporting ligands have been prepared and structurally characterized. More recently, iron-carbene complexes without cyclopentadienyl or tetradentate macrocyclic ligands were reported by the groups of Chirik²¹, Wolczanski,⁴² and Iluc.⁴³ The former work utilized the pincer-type bis(imino)pyridine (PDI) as the supporting ligand, which resulted in the formation of a four-coordinate iron-carbene unit with a structure intermediate between square-planar and tetrahedral geometry. The studies by Wolczanski and Iluc incorporated the carbene fragment into a chelating ligand framework and allowed the formation of iron-carbene complexes with octahedral or trigonal-bipyramidal coordination environments, respectively.

Figure 1.

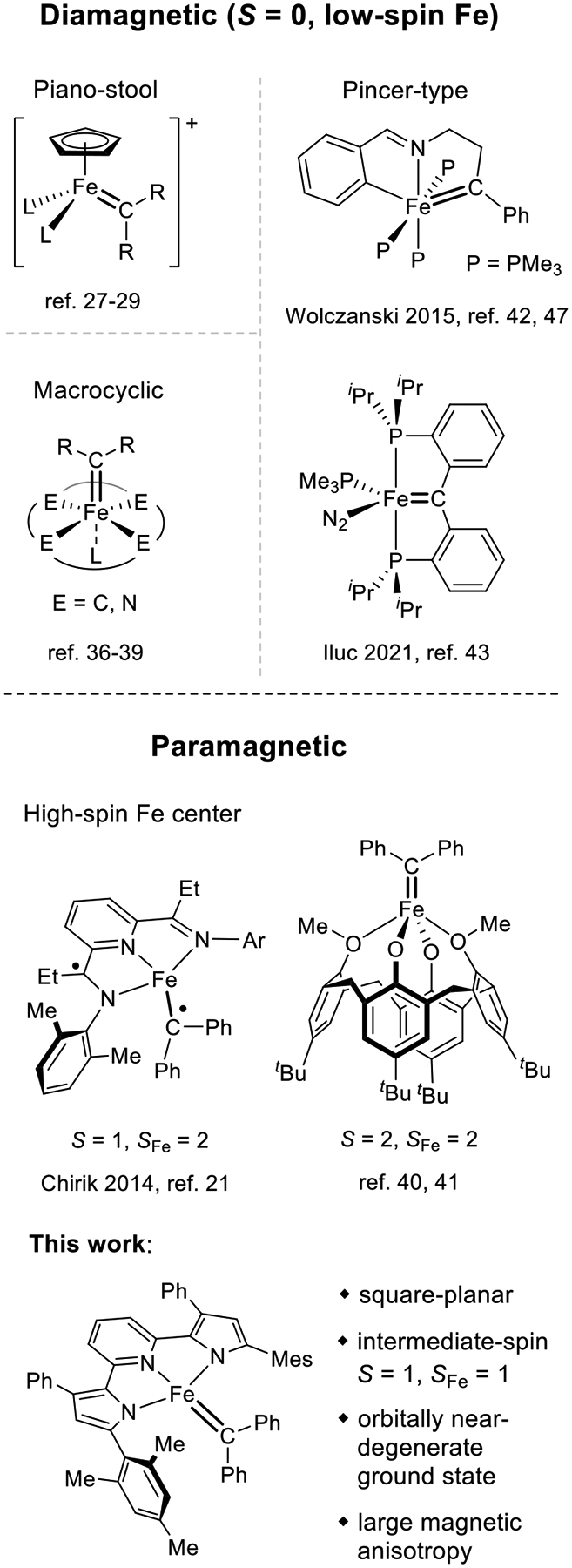
Types of structurally characterized iron-carbene complexes, highlighting the rarity of paramagnetic examples and the novelty of a strictly planar coordination environment for this class of compounds.

The accurate description of the electronic structure of iron-carbene bonds remains an ongoing challenge. Due to the availability of several readily accessible oxidation and spin states for iron, a clear assignment of the CR₂ unit as neutral carbene, monoanionic carbene radical, or dianionic alkylidene is not straightforward. This dilemma is most clearly reflected in the well-studied porphyrin-based iron-carbene complexes, which exhibit a diamagnetic ground state. These complexes can formally be described as low-spin Fe^II species containing a neutral singlet carbene fragment or as low-spin Fe^IV compounds (S_Fe = 0) with a dianionic alkylidene ligand. A third electronic structure encompassing a low-spin Fe^III center antiferromagnetically coupled to a carbene radical was proposed by Shaik and co-workers based on density functional theory (DFT) calculations.⁴⁴ While most recent spectroscopic and computational results favor an Fe^II carbene description,^39,45,46 the debate cannot be considered as fully settled. Similar ambiguities in electronic structure exist for other diamagnetic iron-carbene species including cyclopentadienyl-based complexes, Jenkins’ C₄-macrocyclic “all carbene iron alkylidene”,³⁶ and the compounds reported by Wolczanski,⁴² all of which have been described as Fe^IV alkylidene complexes. Notably, the assignment for Wolczanski’s compounds was revised to Fe^II carbene in a later publication.⁴⁷

Paramagnetic iron-carbene species are exceedingly rare. To date, the only well-characterized mononuclear examples are the calix[4]arene-based derivatives by Floriani and co-workers (S = 2)^40,41 and the PDI-based system by Chirik and co-workers (S = 1).²¹ While both systems are best described as high-spin Fe^II complexes (S_Fe = 2) based on computational studies, the former contains a neutral carbene ligand while the latter incorporates a monoanionic carbene radical and a one-electron reduced PDI^1- radical ligand, which are both antiferromagnetically coupled to the iron center resulting in a triplet ground state. Additionally, Holland et al. have reported a diiron complex with a bridging alkylidene moiety.^48,49 Weak antiferromagnetic coupling between the two high-spin Fe^II centers in this dinuclear complex is mediated through the alkylidene ligand, resulting in a paramagnetic material at room temperature.

In this paper, we report the first example of an iron-carbene complex with a distorted square-planar coordination environment. The results of a combined experimental and computational study indicate that the complex (^MesPDP^Ph)Fe(CPh₂), where [^MesPDP^Ph]^2- is the doubly deprotonated form of [2,6-bis(5-(2,4,6-trimethylphenyl)-3-phenyl-1H-pyrrol-2-yl)pyridine], exhibits a triplet ground state that is best described as containing an intermediate-spin iron center. This electronic structure is unprecedented in iron-carbene complexes and imparts highly anisotropic magnetic properties with large internal magnetic fields due to unquenched orbital angular momentum.

Results and Discussion

Synthesis and structural characterization of (^MesPDP^Ph)Fe(CPh₂).

Inspired by our previous report of successful nitrene group transfer to (PDP)Fe complexes using organic azides,⁵⁰ the reaction of (^MesPDP^Ph)Fe(thf) with diphenyldiazomethane, N₂CPh₂, was targeted as a straightforward strategy for the formation of a pyridine dipyrrolide iron-carbene complex (Scheme 1). Most isolable iron-carbene complexes reported to date contain diphenyl-substituted carbene moieties, highlighting the straightforward availability and handling of the N₂CPh₂ reagent and the increased stability of the FeCPh₂ unit compared to other iron-carbenes. Addition of one equivalent of N₂CPh₂ to a diethyl ether slurry of (^MesPDP^Ph)Fe(thf) at room temperature resulted in a gradual color change of the mixture from dark red to brown over 16 h accompanied by formation of a brown precipitate. IR spectroscopic measurements showed no indication of a diazomethane stretching mode (Figure S5), confirming complete consumption of N₂CPh₂ and suggesting the identity of the product was unlikely to be the diazoalkane adduct (^MesPDP^Ph)Fe(N₂CPh₂). Following workup, a dark green-brown solid identified as (^MesPDP^Ph)Fe(CPh₂) was isolated in 64% yield.

Scheme 1.

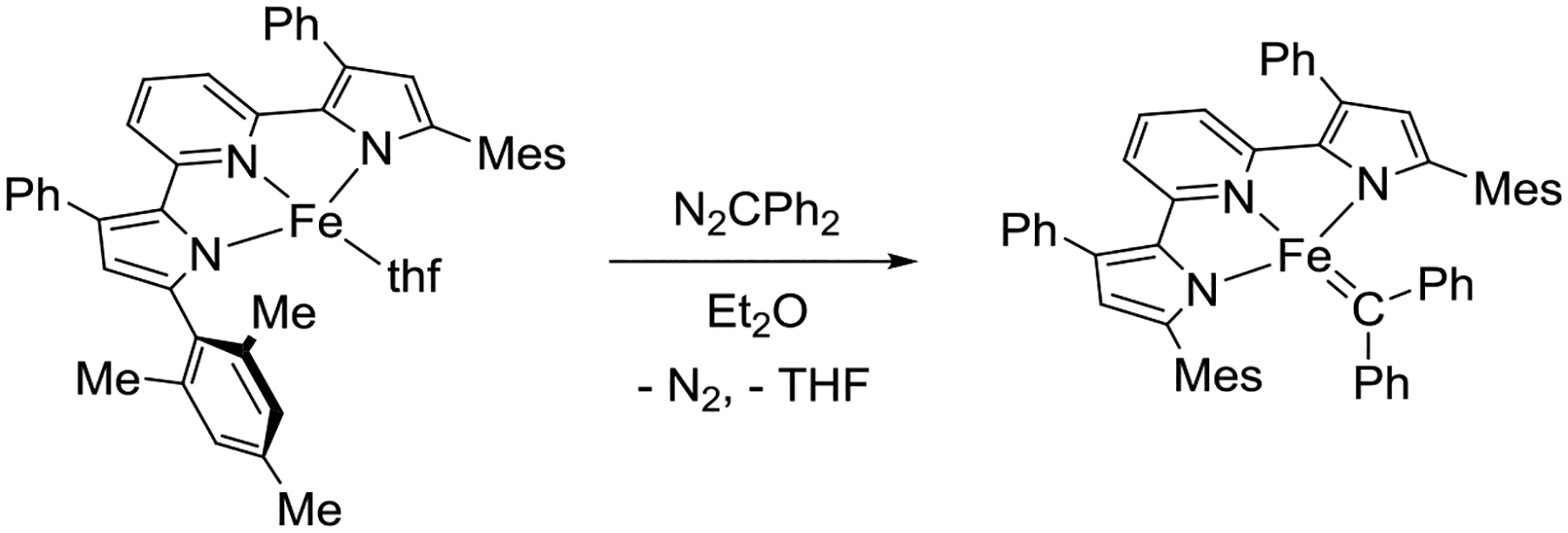
Synthesis of (^MesPDP^Ph)Fe(CPh₂). For better readability, selected 2,4,6-trimethylphenyl substituents are abbreviated as Mes.

Single crystals suitable for X-ray diffraction analysis were obtained by slow evaporation of a concentrated diethyl ether solution of (^MesPDP^Ph)Fe(CPh₂) at −35 °C, and the molecular structure of the complex is shown in Figure 2. The coordination environment around the iron center is best described as distorted square-planar. The geometric arrangement of the three nitrogen donors of the PDP ligand, the carbene carbon, and the iron center is close to perfectly planar with a sum of angles around iron of 360.19(17)° and a N(2)-Fe(1)-C(44) angle of 176.20(9)°. This is substantially different from the more distorted geometry of the only previously reported pincer-containing carbene complex, (PDI)Fe(CPh₂), by Chirik and coworkers.²¹ In these systems, a reduction in the N_py-Fe-C_carbene angle to approximately 150° is accompanied by a lift of the iron center by more than 0.7 Å above the plane defined by the three nitrogen atoms of the pincer. The largest deviation from ideal square-planar geometry in (^MesPDP^Ph)Fe(CPh₂) is imposed by the reduced bite angle of the PDP ligand resulting in a N(1)-Fe(1)-N(3) angle of 159.35(8)°. The Fe–N bond lengths in (^MesPDP^Ph)Fe(CPh₂) (Fe(1)-N(1), 1.958(2) Å; Fe(1)-N(2), 1.978(2) Å; Fe(1)-N(3), 1.946(2) Å) are significantly shorter than those in the high-spin starting material (^MesPDP^Ph)Fe^II(thf) (all Fe–N_PDP > 2 Å).⁵¹ These structural parameters are consistent with an unoccupied σ*-antibonding d_x2-y2 orbital and either intermediate- or low-spin Fe^II/Fe^III configurations or an Fe^IV oxidation state at iron. Further supporting this assignment, the Fe(1)-C(44) bond of 1.850(2) Å is significantly shorter than those reported for high-spin iron-carbene complexes with S = 2 ground states (Fe–C, 1.92–1.97 Å). At the same time, this bond distance is slightly longer than the Fe–C bonds reported for diamagnetic, low-spin iron-carbene complexes with square-pyramidal or piano-stool geometries (Fe–C, 1.76–1.81 Å) favoring an intermediate-spin state assignment for (^MesPDP^Ph)Fe(CPh₂). The torsion angles between the two phenyl substituents on the carbene and the π-system of iron-carbene bond are small at 13.59° and 29.52°, indicating conjugation with the carbene.

Figure 2.

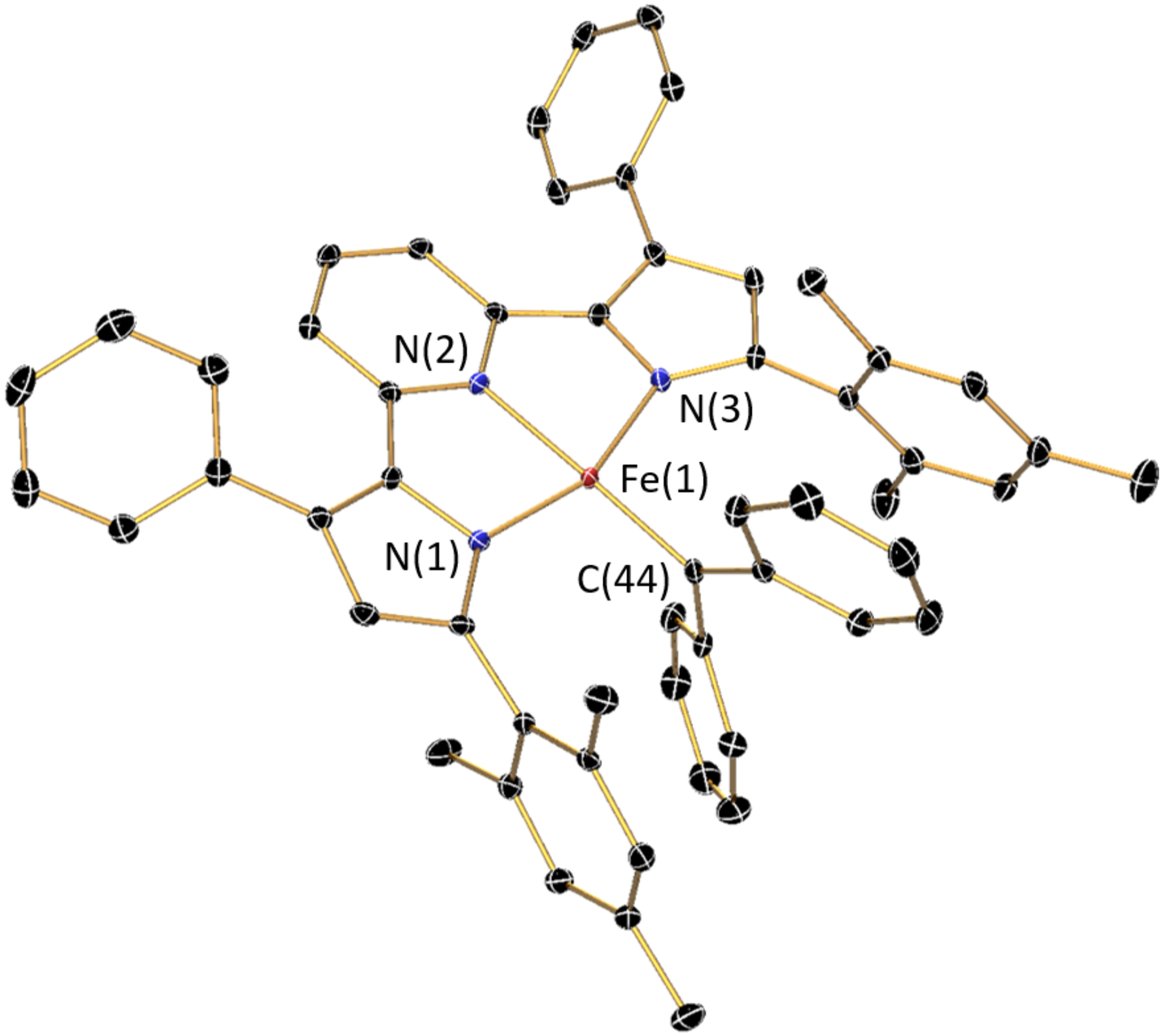
Representation of the solid-state molecular structure of (^MesPDP^Ph)Fe(CPh₂) at 30% probability ellipsoids. Hydrogen atoms are omitted for clarity.

In agreement with these considerations based on the solid-state structural analysis, ¹H NMR spectroscopy established a paramagnetic ground state for (^MesPDP^Ph)Fe(CPh₂) with chemical shifts observed between −55.2 and 91.4 ppm in benzene-d₆ solution at 25 °C (Figure S1). The 12 paramagnetically broadened resonances are consistent with a C_2v symmetric structure in solution. The signal for the 4-pyridine proton, which was readily assigned based on its unique integral value for a single proton, is located at −16.56 ppm. This significant upfield shift compared to the diamagnetic reference value of an aromatic proton is characteristic for 4-pyridine protons in paramagnetic (PDP)Fe compounds with planar four-coordinate ligand environments.⁵¹ Notably, two additional resonances can be observed below 10 ppm, which is unusual for (PDP)Fe systems. Considering that the remaining resonances show shifts similar to previously reported complexes, the features at −16.39 and −55.22 ppm were assigned to the ortho- and para-protons of the diphenylcarbene fragment, respectively. The large upfield shifts suggest significant β spin population for these protons, which was confirmed by computational studies (vide infra).

Solid-State Magnetic Properties.

Magnetic susceptibility data for (^MesPDP^Ph)Fe(CPh₂) obtained by SQUID magnetometry are shown in Figure 3. The χT value at 300 K is 2.45 cm³ K mol⁻¹ (μ_eff = 4.43 μ_B), much higher than the spin-only value predicted for an S = 1 species (1.00 cm³ K mol⁻¹; μ_eff = 2.83 μ_B), and lies between the values expected for S = 3/2 (1.87 cm³ K mol⁻¹; μ_eff = 3.87 μ_B) and S = 2 (3.00 cm³ K mol⁻¹; μ_eff = 4.90 μ_B) spin states. When the sample is cooled from 300 K to 20 K, the χT value gradually decreases to 2.00 cm³ K mol⁻¹ (μ_eff = 4.00 μ_B). Upon further cooling to 2 K, a much sharper decline to 0.79 cm³ K mol⁻¹ (μ_eff = 2.51 μ_B) is observed. Reduced magnetization data for (^MesPDP^Ph)Fe(CPh₂) are shown in Figure 3; notably, no saturation is achieved in these curves, and the large splitting of the isotherms indicates significant influence from zero-field splitting. Several different models for the magnetic susceptibility and reduced magnetization data were tested, including both S = 1 and S = 2 spin states as well as positive and negative values for the axial zero-field splitting parameter D. Ultimately, an S = 1 model with a large, negative zero-field splitting D and small rhombicity E/D provided the best model for the susceptibility and reduced magnetization data. Note that within this model the splitting and shape of the reduced magnetization isotherms are not very sensitive to D, which far exceeds the available thermal energy at experimental temperatures, but rather reflect the small rhombicity E/D. The fitted parameters are provided in Table 1.

Figure 3.

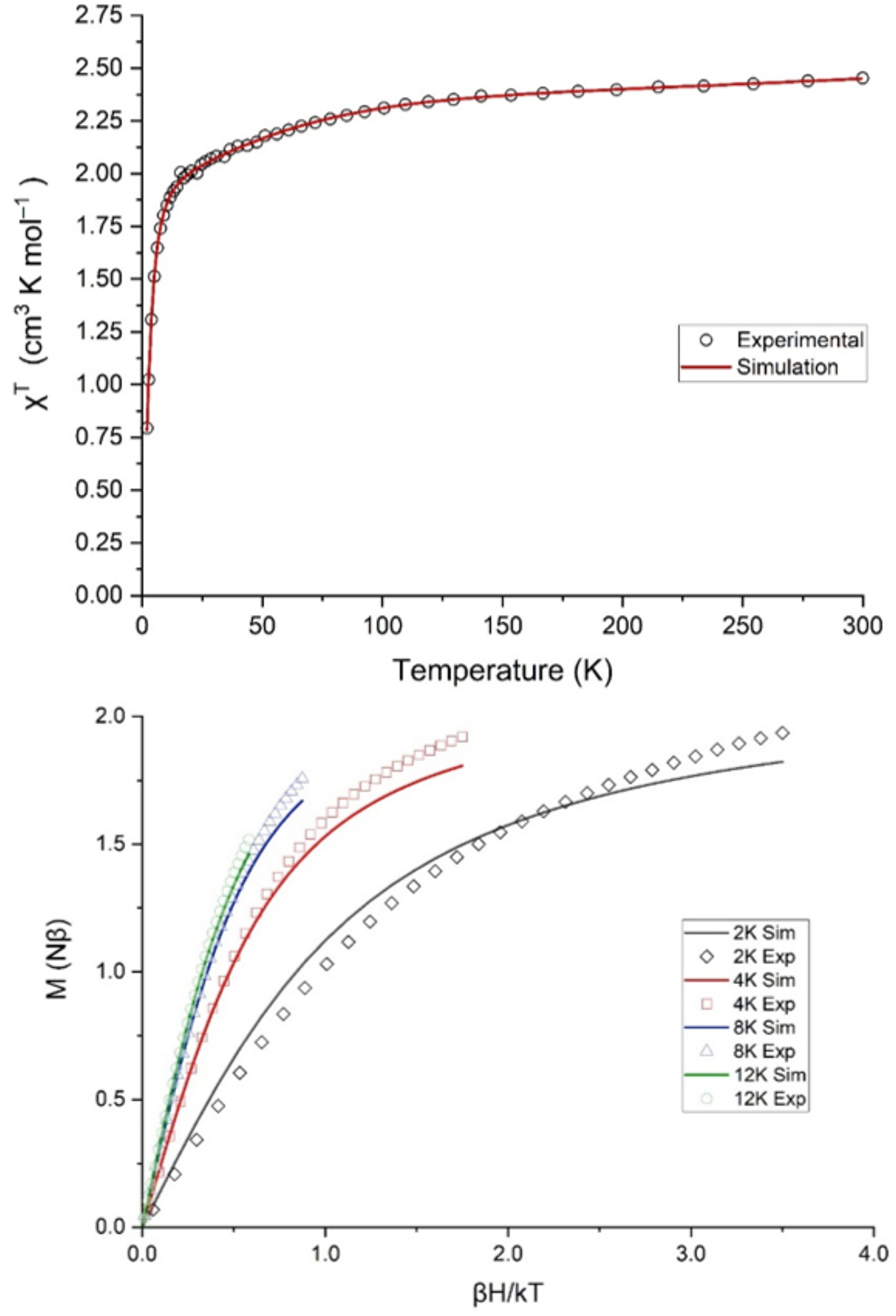
Variable temperature magnetic susceptibility data (top) and field-swept (0 – 7 T) reduced magnetization curves (bottom) for (^MesPDP^Ph)Fe(CPh₂). Solid lines indicate the best fit to the data using the model described in the text.

Table 1.

Comparison of Parameters Obtained from the Fits of SQUID Magnetometry Data, ⁵⁷Fe Mössbauer Spectroscopic Data, and Computational Analysis.

Parameter	SQUID Magnetometry	Mössbauer Spectroscopy	CASSCF/SORCI	CASSCF/NEVPT2
S	1	1	1	1
D a	−195(8) cm−1	-b	−126 cm−1	−95 cm−1
E/D	0.018(13)	0.04c	0.01	0.05
g	[2.00(4) 2.01(6) 3.95(4)]	[2.00d 2.00d 3.58]	[2.00 2.26 4.00]	[1.90 2.09 3.06]
TIP	882 · 10−6 cm3 mol−1	--	--	--
δ	--	0.20 mm s−1	--	--e
ΔE Q a	--	−2.81 mm s−1	--	−2.84 mm s−1
η a	--	0.45	--	0.45
A/(g n β n ) a	--	[−7.1 −10.0 72.3] T	--	--
Γ	--	0.30 mm s−1	--	--

^aThe orientation of the principal coordinate systems for g, D, and A tensors are set as collinear, while the coordinate system for the electric field gradient (EFG) tensor is rotated by an Euler angle β = 90° (ZYZ convention).

^bMössbauer data only reflect the properties of the quasi-degenerate M_S = ±1 doublet, therefore the magnitude of D is undetermined.

^cMössbauer data determines the rhombic zero-field splitting parameter E to be 4 cm⁻¹, by using D = −100 cm⁻¹ to simulate the data, E/D is effectively 0.04.

^dThe spectra are insensitive to g_x and g_y. g_z was estimated through both 4.2 K and 100 K data.

^eNo calibration data are available in the literature.

Key features of the fitted parameters are extremely large g anisotropy, with a g_max of 3.95 giving rise to the unusually high χT values for an S = 1 system. The axial zero-field splitting (ZFS) parameter D is also very large and negative, −195 cm⁻¹. Though it was possible to model a rhombic term E, the rhombicity, E/D, is near zero (E/D = 0.018, E = 3.5 cm⁻¹). The g_mid and g_min values exhibited an inverse correlation with one another while no direct relationship was observed with the g_max term, which remained consistently between 3.93 and 3.95. When the model was allowed to freely refine with no boundaries applied to the input parameters, the g values were found to be 0.00(4), 2.85(5), and 3.93(7), which substantially deviate from that of a free electron (2.0023). However, when either g_min or g_mid is bound to 2.00, a good fit is obtained with g values of 2.00(3), 2.06(9), 3.95(4) or 2.00(4), 2.01(6), 3.95(4), respectively. Subsequent inclusion of a temperature independent paramagnetic (TIP) component improved the fit further.

The large magnetic anisotropy indicated by the axial ZFS parameter D and the highly anisotropic g tensor suggests significant magnetic contributions due to unquenched orbital angular momentum resulting from an orbitally near-degenerate ground state for (^MesPDP^Ph)Fe(CPh₂). Similar near-degenerate electronic configurations are rare for iron complexes, but often impart remarkable magnetic properties. Most closely related to the results presented in this work, square-planar iron(II) octaethyltetraazaporphyrin investigated by Yee et al. shows unusually high effective magnetic moments for an intermediate-spin Fe^II complex (S = 1; μ_eff > 4.0 μ_B) and exhibits spontaneous magnetization below a Curie temperature of 5.6 K due to a canted ferromagnetic state in solid phase.^52–54 Three-coordinate high-spin Fe^II complexes (S = 2) reported by Holland, Münck et al. display comparable uniaxial magnetization properties and large axial ZFS parameters to those reported here for (^MesPDP^Ph)Fe(CPh₂).⁵⁵ Finally, a linear high-spin Fe^I complex (S = 3/2) with large axial anisotropy described by Long et al. exhibits a remarkably high barrier for spin reversal for a molecular transition metal compound resulting in single-molecule magnetic behavior below 4.5 K.⁵⁶ The same group more recently reported similar magnetic properties for a series of linear high-spin Fe^II (S = 2) complexes.⁵⁷

Mössbauer Spectroscopy.

Further insight into the electronic structure of the iron center in (^MesPDP^Ph)Fe(CPh₂) and the resulting magnetic properties was obtained by ⁵⁷Fe Mössbauer spectroscopy. The 4.2 K zero-field spectrum of a sample containing a solid powder of (^MesPDP^Ph)Fe(CPh₂) suspended in mineral oil exhibited a quadrupole doublet with an isomer shift, δ, of 0.20 mm s⁻¹, a quadrupole splitting, |ΔE_Q|, of 2.81 mm s⁻¹, and a linewidth, Γ, of 0.40 mm s⁻¹ (Figure 4, left). The observation of a quadrupole doublet at 4.2 K indicates that (^MesPDP^Ph)Fe(CPh₂) has an integer spin ground state (S = 0, 1, 2, …). The Mössbauer measurements at elevated temperatures (80 K and 140 K) revealed that the quadrupole splitting is temperature dependent (|ΔE_Q| = 2.75 mm s⁻¹ at 80 K and 2.71 mm s⁻¹ at 140 K, Figures S2 and S4). This spectroscopic behavior strongly suggests the presence of a low-lying excited state having a different orbital state than that of the ground state. The relatively low isomer shift (δ = 0.20 mm s⁻¹ at 4.2 K and 0.17 mm s⁻¹ at 140 K) reflects the short metal-ligand bond lengths observed crystallographically and is inconsistent with a high-spin configuration at iron, which should exhibit a significantly higher value as exemplified by δ values above 0.40 mm s⁻¹ for (PDI)Fe(CPh)₂ complexes (S = 2),²¹ which have a similar ligand environment to that of (^MesPDP^Ph)Fe(CPh₂). In combination with the observation that diamagnetic iron-carbene complexes show isomer shifts below 0.10 mm s⁻¹,^39,42,45 the zero-field Mössbauer data support an S = 1 ground state for (^MesPDP^Ph)Fe(CPh₂). This description is further supported by the variable-temperature variable-field (VTVH) Mössbauer data discussed below.

Figure 4.

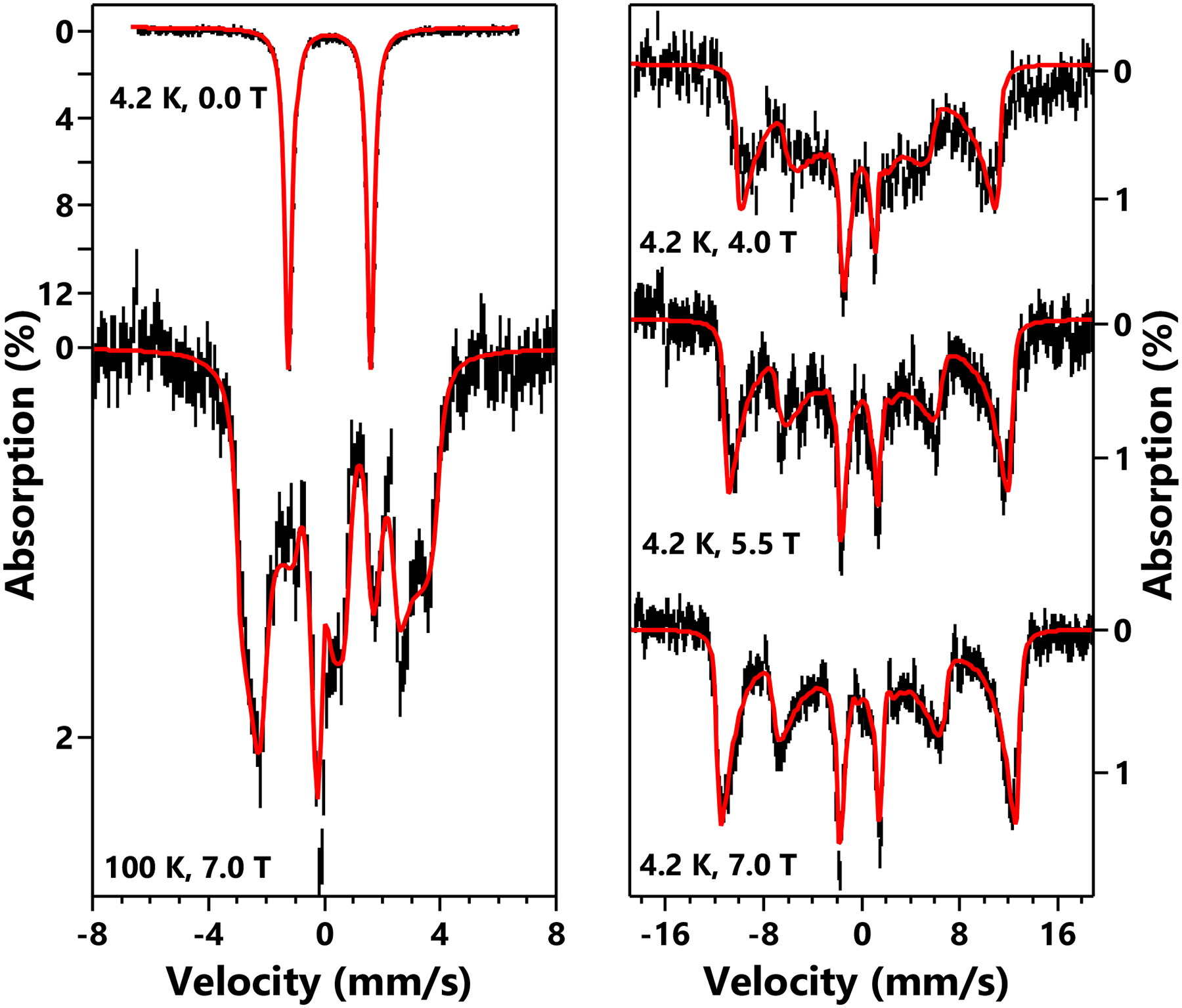
Variable Field Variable Temperature Mössbauer spectra (black vertical bars) of a sample containing (^MesPDP^Ph)Fe(CPh₂) as a fine solid powder suspended in mineral oil and corresponding simulations (red curves) using an S = 1 spin Hamiltonian. The simulation parameters are: D = −100 cm⁻¹, E = 4 cm⁻¹, g_z = 3.5, A_z/g_zβ_z = +73 T, δ = 0.2 mm s⁻¹, ΔE_Q = −2.81 mm s⁻¹, η = 0.45. Euler angle of the EFG tensor rotating from the principal axes of the ZFS tensor is [0, 90, 0] (in ZYZ convention). The values for g_x and g_y are fixed at 2, A_x/g_xβ_x and A_y/g_yβ_y are not determined. The measurement conditions are listed in the figure. The external magnetic field is parallel to the γ-radiation.

The VTVH Mössbauer data were measured on a finely powdered sample suspended in mineral oil. To rule out potential solid-state effects in the data measured on the solid powder sample, such as intermolecular magnetic interactions and/or textural effects, additional spectra were collected on a frozen toluene solution containing 51.4 mM (^MesPDP^Ph)Fe(CPh₂). No solid-state effect was detected (Figure S3). Due to the weaker signals generated from the frozen solution sample containing only natural abundance iron, we will focus our discussion solely on the data measured on the solid powder sample. The applied field (parallel to the observed γ-radiation) induces a strong internal field (B_int) reflected in the Mössbauer data recorded at 4.2 K for (^MesPDP^Ph)Fe(CPh₂) (Figure 4, right). B_int increases rapidly with increasing applied field, which is typical behavior for an integer spin system with negative axial ZFS (D). The magnetic hyperfine field is close to saturation at an applied field of 5.5 T and increases only slightly at an applied field of 7 T. Based on this behavior, we conclude that the internal field experienced by the iron center of (^MesPDP^Ph)Fe(CPh₂) is large and positive (the estimated B_int at 7 T applied field is ≈ +65 T). These results collectively indicate that significant orbital contributions dominate the magnetic hyperfine field, which suggests that the ground state of (^MesPDP^Ph)Fe(CPh₂) exhibits large unquenched orbital angular momentum. The large value for B_int is consistent with applied-field Mössbauer studies conducted for other iron complexes with highly anisotropic magnetic properties resulting from orbitally near-degenerate configurations as discussed above.^54–56

The Mössbauer data are best simulated in the framework of an S = 1 spin Hamiltonian described below:

$$\widehat{H}=D\left({\widehat{S}}_z^2-\frac{2}{3}\right)+E\left({\widehat{S}}_x^2-{\widehat{S}}_y^2\right)+\beta \widehat{\mathit{\text{S}}}\cdot \mathit{\text{g}}\cdot \widehat{\mathit{\text{B}}}+\widehat{\mathit{\text{S}}}\cdot \mathit{\text{A}}\cdot \widehat{\mathit{\text{I}}}-g_n{\beta }_n\widehat{\mathit{\text{B}}}\cdot \widehat{\mathit{\text{I}}}+{\widehat{H}}_Q$$

$${\widehat{H}}_Q=\frac{eQ{V}_{z^{\prime }{z}^{\prime }}}{12}\left[3{\widehat{I}}_{z^{\prime }}^2-I\left(I+1\right)+\eta \left({\widehat{I}}_{x^{\prime }}^2-{\widehat{I}}_{y^{\prime }}^2\right)\right]$$

All quantities have their conventional meanings.⁵⁸ The principal axes of the electric field gradient (EFG) tensor are expressed in (x’,y’,z’), which do not have the same orientation with the principal axes of the zero field splitting (ZFS) tensor for (^MesPDP^Ph)Fe(CPh₂) (see below). The simulations unambiguously require a large negative D value, but the exact value cannot be determined from the Mössbauer data. This observation indicates that the complex likely exhibits a quasi-degenerate orbital ground state. Although the spin Hamiltonian cannot describe the entire energy spectrum of the spin triplet for such an electronic system, it can still be used to analyze the Mössbauer features originating from the quasi-degenerate ground state doublet, |±1’>, of the S = 1 spin manifold (|±1’> are the linear combination of |+1> and |−1> M_S sublevels when E ≠ 0). With such a large and negative D value, the ground doublet is essentially isolated from the excited sublevel (|0>) of the S = 1 spin manifold at 4.2 K. The |±1’> doublet produces an easy magnetization axis along the z direction with the saturation spin expectation values of <S_z> = ±1. The spin expectation values of the other two principal components (<S_x> and <S_y>) are close to zero. Thus, this ground state doublet generates a uniaxial internal magnetic field (B_int,z >> B_int,x, B_int,y ≈ 0). We can further view such an isolated two-level system as a fictitious S = 1/2 species with g_x = g_y = 0 and an off-diagonal matrix element of Δ/2 (in the language of the S = 1 spin Hamiltonian, Δ/2 = E, and the Mössbauer data presented here are quite sensitive to E).

Based on the above descriptions, we simulated the Mössbauer data recorded at 4.2 K and obtained the following parameters (by fixing D = −100 cm⁻¹): E = 4 cm⁻¹, g_z ≈ 3.5, A_z/g_zβ_z = +73 T (g_x, g_y, A_x and A_y are not determined). The large deviation of g_z from the free electron g value of 2 is consistent with the large positive A_z, thus confirming that (^MesPDP^Ph)Fe(CPh₂) exhibits large unquenched orbital angular momentum in the ground state. For such a uniaxial system, the EFG tensor cannot be fully determined by the Mössbauer data at 4.2 K. Instead, the data are only sensitive to the EFG component that is aligned parallel to the easy magnetization direction, which is the z direction of the ZFS tensor. As a result, we obtained eQV/2 = +0.75 mm s⁻¹. In comparison, the magnitude of quadrupole splitting is determined to be 2.81 mm s⁻¹ by the zero-field spectrum recorded at 4.2 K (Figure 4, left). If we assume η = 0 (the asymmetry parameter of the EFG tensor), the largest component of the EFG tensor should be eQ|V_z’z’|/2 = 2.81 mm s⁻¹. Thus, the simulation result suggests that the largest component of the EFG tensor is not parallel to the easy magnetization axes of the system and is rotated from the principal axes of the ZFS tensor. We thus measured a Mössbauer spectrum at 100 K under 7 T applied field. The simulation of this spectrum (assuming the fast electronic relaxation limit) revealed that the largest component of the EFG tensor is negative. The principal axis of the EFG tensor is rotated by 90° with respect to that of the ZFS tensor with an Euler angle of β = 90° (by using a ZYZ convention), which means that the largest component of the EFG tensor is aligned along the y direction defined by the ZFS tensor (the relative orientation of the ZFS tensor with respect to the molecular frame will be defined in the calculation section). In addition, η is determined to be ~ 0.5. All simulation parameters are listed in the caption for Figure 4 and in Table 1.

Taken together, the Mössbauer spectra of (^MesPDP^Ph)Fe(CPh₂) reveal an electronic ground state having large unquenched orbital angular momentum, which leads to high magnetic anisotropy consistent with the magnetic susceptibility data obtained by SQUID magnetometry. The EFG tensor of the quadrupole interactions is rotated by 90° from the easy magnetization direction. This unusual electronic structure most likely originates from quasi-degenerate orbital states.

DFT Calculations.

To obtain a better understanding of the unusual electronic structure of (^MesPDP^Ph)Fe(CPh)₂ revealed by applied-field Mössbauer spectroscopy, broken-symmetry DFT calculations were performed. Note that for all discussions of computational results, a coordinate system defining the four-coordinate plane of the molecule as the xy-plane was used, in which the x-axis is aligned with the Fe–C bond (Figure 5). While this designation is inconsistent with the idealized C_2v symmetry of the complex, which would designate the principal axis as the z-axis (here the C₂ axis containing the Fe–C and Fe–N_pyridine vectors), it facilitates analysis by ligand field theory, as will become apparent in the discussion of molecular orbital manifolds.

Figure 5.

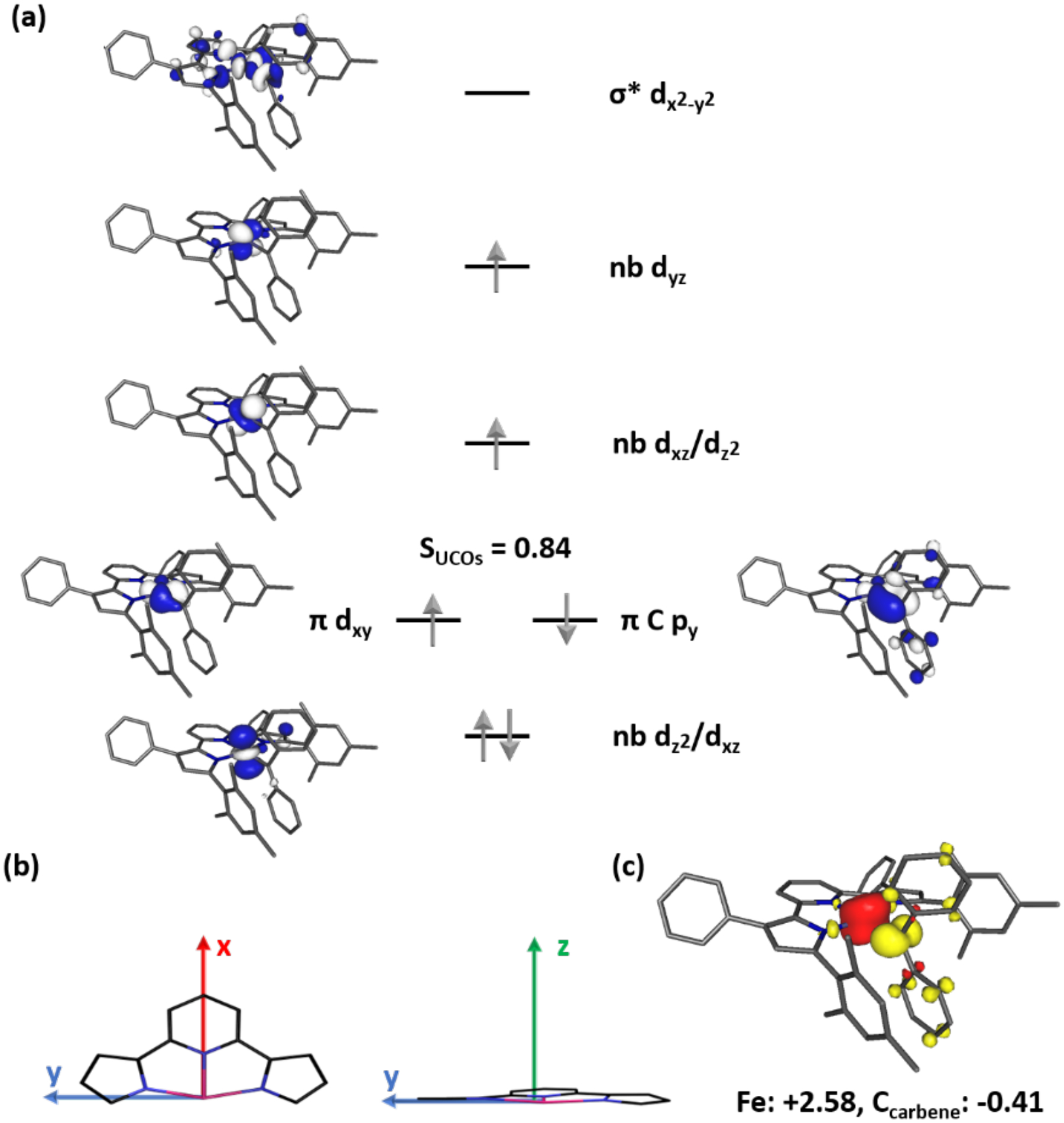
(a) Qualitative molecular orbital diagram for (^MesPDP^Ph)Fe(CPh)₂ from a B3LYP DFT calculation. (b) Coordinate system used in the discussion of computational results. (c) Spin density plot obtained from a Mulliken population analysis (red, positive spin density; yellow, negative spin density).

Using the crystal structure of the complete molecule without any truncations as a starting point for geometry optimizations, three different computational methods were tested by using the BP86 (GGA), B3LYP (hybrid), and TPSSh (hybrid meta-GGA) functionals. Assuming an S = 1 ground state, all three approaches provided qualitatively similar electronic structures and reliably reproduced the experimentally observed geometric features within the expected computational accuracy (Table S2).^59,60 Independent of the applied functional, a simple spin-unrestricted triplet model (UKS3) resulted in spontaneous symmetry breaking and provided an electronic structure identical to the one obtained using a broken-symmetry (BS(3,1)) approach (Table S3). Within the broken-symmetry model, this electronic structure solution is best described by an intermediate-spin Fe^III center (S_Fe = 3/2) with (d_z2/d_xz)²(d_xy)¹(d_xz/d_z2)¹(d_yz)¹(d_x2-y2)⁰ configuration antiferromagnetically coupled to a carbene radical (S_CPh2 = 1/2). Interestingly, mixing of the d_xz and d_z2 orbitals in a molecule with a C_2v symmetric coordination environment at iron provided a first indication for an orbitally near-degenerate electronic state as suggested experimentally. The level of d_xz/d_z2 mixing proved to be highly functional dependent with majority contributions from d_z2 for B3LYP (48.9% d_z2, 22.5% d_xz) and nearly equal contributions for BP86 (41.7% d_z2, 41.0% d_xz). The broken-symmetry character for (^MesPDP^Ph)Fe(CPh)₂ is clearly reflected in the Mulliken spin populations (shown for B3LYP in Figure 5, see Figure S6 for BP86 and TPSSh), which revealed significant spin on the carbene fragment. This is consistent with the unusual upfield shifts of the ortho- and para-protons on the carbene phenyl-substituents observed by ¹H NMR spectroscopy. According to the B3LYP calculations, these protons carry negative spin populations of 3.16·10⁻³ and 3.02·10⁻³, significantly exceeding the predicted spin density on any other protons in the molecule.

A closer analysis of the molecular orbital manifold (Figure 5) revealed that the magnetic coupling between the carbene radical and the metal center is mediated via two singly occupied orbitals (SOMOs) of predominantly C_carbene p_y and Fe d_xy character. These two magnetic orbitals exhibit very high spatial overlap in the 0.86–0.92 range, inversely dependent on the amount of Hartree-Fock exchange in the functional (BP86: 0%, TPSSh: 10%, and B3LYP: 20%). Based on the magnetic orbital overlap, a low diradical character of only 15–25% was calculated following the approach introduced by Neese and coworkers.⁶¹ The amount of diradical character follows the typically observed trend of reduced values for pure GGA functionals compared to hybrid versions. The high overlap values and the associated low diradical indices are indicative of significant covalency in the Fe=C_carbene interaction and may be more consistent with the traditional description as Fe^II–carbene, Fe^IV–alkylidene, or resonance between these two electronic states.

To test the validity of our electronic structure calculations in comparison to experimentally observed properties, several spectroscopic parameters were computed (Table 2). For many iron complexes, the calculation of ⁵⁷Fe Mössbauer parameters has been shown to provide reliable validation of the electronic structure assignments based on DFT.^62,63 Most notably, none of the DFT approaches used in this study provided satisfactory agreement with the experimentally determined parameters. While the BP86 calculations accurately reproduced the isomer shift (δ_BP86 = 0.27 mm s⁻¹), significant deviations outside of the acceptable range were observed for the quadrupole splitting (ΔE_Q^BP86 = −3.84 mm s⁻¹). In contrast, both hybrid functionals provided reasonable values for ΔE_Q (ΔE_Q^B3LYP = −2.56 mm s⁻¹, ΔE_Q^TPSSh = −2.95 mm s⁻¹) but failed to deliver acceptable values for δ (δ_B3LYP = −0.08 mm s⁻¹, δ_TPSSh = −0.01 mm s⁻¹). Additionally, the calculation of g values using DFT provided a g tensor with only moderate g anisotropy, in stark disagreement with the experimental values. The latter result is not surprising given the well-known inability of DFT methods to correctly describe the low-lying excited states that are required to reproduce the magnetic properties of systems with large unquenched orbital angular momentum due to strong SOC and orbitally near-degenerate configurations.

Table 2.

Comparison of Calculated and Experimental Spectroscopic Parameters of (^MesPDP^Ph)Fe(CPh₂).

Method	δ /mm s−1 a	ΔEq /mm s−1	η	[gmax gmid gmin]	D / cm−1	E/D
BP86	0.27	−3.84	0.30	2.11 2.06 2.02	13.7	0.03
TPSSh	−0.01	−2.95	0.37	2.08 2.06 2.01	27.6	0.14
B3LYP	−0.08	−2.56	0.31	2.17, 2.12, 2.01	−10.5	0.14
(SA-) CASSCF/NEVPT2	--b	−2.84c	0.45c	3.06, 2.09, 1.90	−97	0.05
SA-CASSCF/SORCI	--d	--d	--d	4.00, 2.26, 2.00	−126	0.01
Experiment	0.20	−2.81	0.45	3.95, 2.01, 2.00	−195	0.02

^aCalculated using δ = α(ρ − C) + β. (BP86: α = −0.425, β = 7.916, C = 11810; TPSSh: α = −0.376, β = 4.130, C = 11810; B3LYP: α = −0.366, β = 2.852, C = 11810) according to ref.⁶³.

^bNo calibration data are available in the literature.

^cFrom a CASSCF calculation using only the ground state without state averaging.

^dCalculation not attempted using this method.

The inability to accurately reproduce the spectroscopic properties of (^MesPDP^Ph)Fe(CPh)₂ in combination with the ambiguities in electronic structure assignment from DFT analysis highlight the complexity of Fe-carbene interactions and prompted further investigations by multi-configurational complete active space self-consistent field (CASSCF) calculations.

Ab-initio calculations.

To more accurately consider SOC between the ground state and low-lying excited states in (^MesPDP^Ph)Fe(CPh)₂, scalar-relativistic CASSCF calculations were performed. These calculations employed the complete molecular structure from X-ray diffraction analysis with optimized hydrogen atom positions. According to literature precedent,^64,65 a balanced active space for (^MesPDP^Ph)Fe(CPh)₂ should include the five Fe-centered 3d orbitals, the σ-bonding ligand-centered partner orbital for the d_x2-y2 orbital, and the p_y orbital of the carbene carbon giving rise to a minimum description as CASSCF(8,7). Contributions from the π-system of the PDP ligand, similar to those previously observed for redox-active ligands with extended π-systems such as porphyrins, were initially examined by including the complete set of 18 π-electrons in 16 π-orbitals in the active space of a CASSCF(26,23)-ICE⁶⁶ calculation (ICE = iterative configuration expansion). However, no indication of PDP ligand radical formation was observed (Table S4, Figure S11). A separate CASSCF(16,15)-ICE calculation exploring contributions from the phenyl substituents of the carbene was conducted but showed no qualitative changes to the electronic structure (Table S4, Figure S12). Accordingly, neither the orbitals of the PDP π-system nor those of the phenyl substituents on the carbene were included in the active space for any calculations presented below. To account for radial dynamic correlation, the iron 4d orbitals were included in the active space giving rise to a CASSCF(8,12) approach. Inclusion of these high-energy orbitals has been shown to be critical to obtaining an accurate electronic description for systems with M≡E (M = Mn or Fe; E = O or N) multiple bonds that are closely related to iron carbenes.^67,68

As displayed in Figure 6, the ground-state wavefunction of (^MesPDP^Ph)Fe(CPh)₂ obtained by a CASSCF(8,12) calculation features predominant contributions (76%) from the electron configuration (nb d_xz/d_z2)²(σ)²(π)²(nb d_yz)¹(nb d_z2/d_xz)¹(π*)⁰(σ*)⁰. Notably, the four natural orbitals representing the σ- and π-bonding and antibonding Fe–C interactions all exhibit significant contributions from iron and carbene orbitals, emphasizing again the highly covalent nature of the Fe=C bond. Nevertheless, the majority contributions of approximately 70% of the iron d_x2-y2 and d_xy orbitals to the empty σ* and doubly-occupied π orbital, respectively, are most consistent with a description as intermediate-spin Fe^II with a coordinated singlet carbene. The second largest contribution to the ground state wavefunction is represented by the configuration (nb d_xz/d_z2)²(σ)²(π)¹(nb d_yz)¹(nb d_z2/d_xz)¹(π*)¹(σ*)⁰, corresponding to an intermediate-spin Fe^III center antiferromagnetically coupled to a carbene radical consistent with the broken-symmetry DFT results, but shows a significantly reduced weight of only 7%. An additional configuration, (nb d_xz/d_z2)²(σ)²(π)⁰(nb d_yz)¹(nb d_z2/d_xz)¹(π*)²(σ*)⁰, best interpreted as an intermediate-spin Fe^IV alkylidene contributes with a weight of only 4%. Based on this CASSCF(8,12) ground state, a diradical index of 40% was established following a protocol reported by Neese and coworkers.^69,70 This multiconfigurational character of the CASSCF(8,12) wavefunction is also apparent from the spin population obtained via Mulliken population analysis (Figure S8), which resembles the one of the BS(3,1) DFT solutions. Reassuringly, the computed CASSCF(8,12) ground state accurately reproduces the electric field gradient at the iron center established by applied-field Mössbauer spectroscopy, providing values of ΔE_Q = −2.84 mm s⁻¹ and η = 0.45, which are in excellent agreement with experiment.

Figure 6.

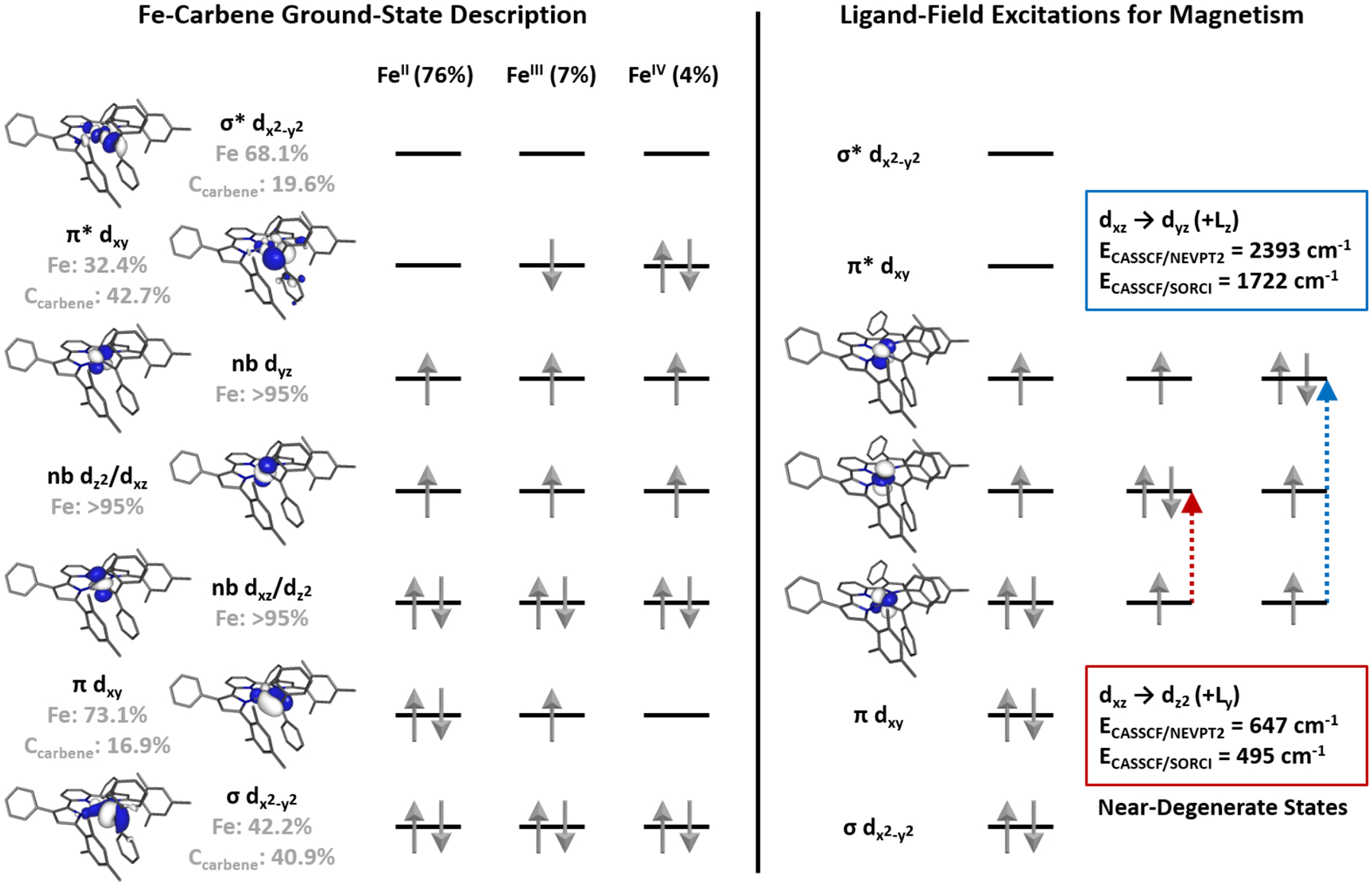
Left: Natural orbitals and electron configurations for the three most important configurations obtained from a ground-state CASSCF(8,12) calculation. The occupation numbers of the orbitals are shown below the orbital labels (nb = nonbonding) and atomic contributions to the molecular orbitals are shown in gray. The double d-shell is omitted for clarity. Right: Low energy ligand field excitations obtained from a SA-CASSCF(8,12) including the two lowest energy triplet excited states. The interaction between these states and the ground state are responsible for large orbital angular momentum contributions, giving rise to large magnetic anisotropy.

With a satisfactory description of the ground-state electronic structure in hand, state-averaged (SA-)CASSCF calculations were performed to probe the nature of the large magnetic anisotropy observed experimentally. Because the anisotropy of the g tensor originates from SOC between the ground state and low-lying excited states of the same spin multiplicity, only triplet states were included in the SA-CASSCF wavefunction. Corrections to the individual state energies due to dynamic electron correlation were accounted for using N-electron valence perturbation theory (NEVPT2). Inclusion of the first six triplet excited states during a SA-CASSCF(8,12)/NEVPT2 calculation followed by g tensor analysis using effective Hamiltonian theory resulted in pronounced g-anisotropy due to significant SOC (Table 2). The most important contributions were provided by the two lowest energy excited states that were found to be only 647 cm⁻¹ and 2,393 cm⁻¹ higher in energy than the ground state, consistent with an orbitally near-degenerate system. Additional mixing from higher energy triplet states, all of which lie >10,000 cm⁻¹ above the ground state, did not significantly impact the results of the calculations and were excluded in all reported calculations. This modification is consistent with the fact that the magnitude of the deviation of the observed g values from that of the free electron (g_e = 2.0023) caused by SOC is inversely proportional to the energy difference of the spin-orbit coupled states. The two dominant excited states correspond approximately to the ligand-field excitations d_xz → d_z2 and d_xz → d_yz and restore orbital angular momentum in the y and z direction of the chosen reference frame, respectively. The orientation of the principal components of the g tensor is shown in Figure 7 and demonstrates that the largest g value (g_max= 3.06), associated with the easy magnetization axis, lies in the molecular plane and is perpendicular to the Fe–C bond as expected based on the lowest energy excited state (d_xz → d_z2). Due to the higher energy of the d_xz → d_yz excitation, the g_mid value is significantly closer to g_e at 2.09 and is very similar to the g_min value at 1.90. This nearly axial symmetry of the calculated g tensor is consistent with the results from our magnetochemical and applied-field Mössbauer spectroscopic studies.

Figure 7.

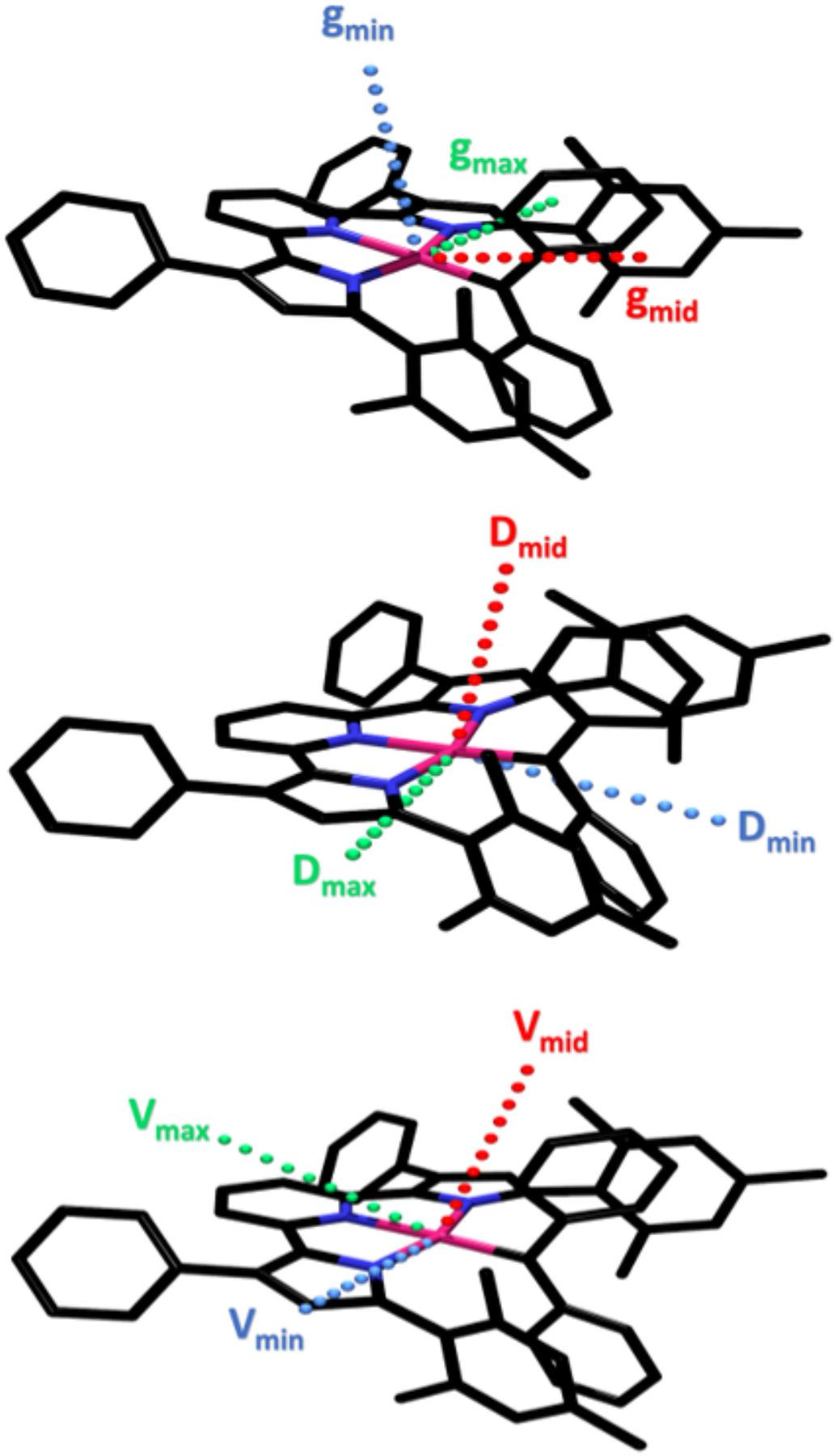
Orientation of the principal components for the g tensor (top), the D tensor (middle), and electric field gradient (bottom) in (^MesPDP^Ph)Fe(CPh)₂. Note that the change of direction between g_max and D_max results from the fact that D is negative for (^MesPDP^Ph)Fe(CPh)₂ while g is by definition positive.

Further computational analysis of the magnetic properties allowed the calculation of ZFS parameters using effective Hamiltonian theory (Table 2). While the magnitude of the calculated axial ZFS parameter (D = −97 cm⁻¹) was significantly smaller than the experimental value of −195 cm⁻¹ obtained from the fit of the temperature-dependent magnetic susceptibility data, the calculations correctly predicted the sign of D and qualitatively reproduced the remarkably large magnetic anisotropy observed for (^MesPDP^Ph)Fe(CPh)₂. Similar to the computational analysis of the g tensor, closer inspection of the D tensor revealed nearly perfectly axial symmetry with a computed E/D value of 0.05 in good agreement with experiment. As shown in Figure 7, the largest components, g_max and D_max, of the two tensors describing the magnetic properties of (^MesPDP^Ph)Fe(CPh)₂ are almost perfectly aligned with each other and in perpendicular orientation to the Fe–C bond. In contrast, the largest component of the EFG tensor, V_max, is oriented almost perfectly parallel to the Fe–C bond, highlighting that our computational approach is consistent with the spectroscopic data from applied field Mössbauer spectroscopy that required a 90° rotation of V_max with respect to the easy magnetization axis to obtain a satisfactory fit.

While the SA-CASSCF(8,12)/NEVPT2 approach was able to qualitatively reproduce the experimentally observed large g anisotropy significantly better than the simple DFT approach, the magnitude of the magnetic anisotropy was still considerably underestimated. To obtain an even higher-level computational description, we turned to the spectroscopy-oriented configuration interaction (SORCI) framework. Due to the high computational cost of these calculations, a truncated version of the carbene complex without substituents on the PDP ligand, (^HPDP^H)Fe(CPh₂), was used. A SA-CASSCF(8,12)/SORCI calculation followed by g tensor analysis employing the sum-over-states (SOS) approach provided even more anisotropic g values than the NEVPT2 calculation in closer agreement with experiment (Table 2). Careful analysis of the configuration interaction vectors revealed that the dominant SOC contributions are again due to d_xz → d_z2 and d_xz → d_yz excited states with even smaller energy gaps than obtained via SA-CASSCF/NEVPT2 of 495 cm⁻¹ and 1,722 cm⁻¹, respectively, reflecting the orbitally near-degenerate ground state. Consistent with improvements of the calculated magnetic properties, the ZFS parameters described by D = −126 cm⁻¹ and negligible rhombicity (E/D = 0.01) are improved through the SORCI approach when benchmarked against experiment.

As is apparent from the comparison of our CASSCF/NEVPT2 and CASSCF/SORCI results, small changes in the computed excitation energies result in substantial changes in the predicted ZFS parameters and g values. This subtle interplay between SOC matrix elements and excitation energies is typical in cases with near-degeneracy and makes obtaining quantitatively accurate results for such systems extremely difficult.⁶⁷ Considering that many aspects of the real system are not included in the calculations (e.g. intermolecular interactions for solid state measurements or solvation effects for solution experiments) and that truncations of the molecular geometry were necessary in the case of the SORCI approach to limit computational costs, our computational results provide an excellent description of (^MesPDP^Ph)Fe(CPh₂) within the limitations of the applied methodology.

Taken together, our computational studies suggest that the electronic ground state of (^MesPDP^Ph)Fe(CPh₂) exhibits multiconfigurational character with majority contributions from a configuration best described as an intermediate-spin Fe^II center coordinated to a neutral singlet carbene (CPh₂⁰). Smaller contributions from a configuration represented by an intermediate-spin Fe^III ion antiferromagnetically coupled to a carbene radical are important to obtain an accurate CASSCF wavefunction. In this respect, (^MesPDP^Ph)Fe(CPh₂) provides a good example for the necessity of higher-level computational approaches to capture the electronic ground state of complexes with Fe=E multiple bonds. The excited state energies obtained via SA-CASSCF/NEVPT2 or SORCI methods and the derived spectroscopic parameters are in excellent agreement with experiment and support an orbitally near-degenerate ground state for (^MesPDP^Ph)Fe(CPh₂). This specific electronic structure gives rise to the unusual magnetic properties of this iron-carbene complex.

Conclusions

In this study, we have reported the first example of an iron-carbene complex with a square-planar coordination environment. This unprecedented geometric structure for a molecule with an Fe=C multiple bond is supported by a pincer-type pyridine dipyrrolide ligand and results in a unique electronic structure best described as featuring an intermediate-spin Fe^II center coordinated to a singlet carbene fragment. As a rare example for a paramagnetic iron-carbene species, (^MesPDP^Ph)Fe(CPh₂) features an orbitally near-degenerate ground state that results in remarkably large magnetic anisotropy allowing internal fields of more than +60 T due to unquenched orbital angular momentum. These unusual magnetic properties for a molecular iron complex were established experimentally through a combination of SQUID magnetometry and applied-field ⁵⁷Fe Mössbauer spectroscopy.

Ab-initio calculations using CASSCF in combination with the spectroscopy-oriented configuration interaction method successfully reproduced the spectroscopic parameters and provided further insight into the multiconfigurational ground state of (^MesPDP^Ph)Fe(CPh₂). While the major contribution to the ground-state wavefunction is indeed provided by a configuration best described as intermediate-spin Fe^II with a neutral singlet carbene, there is significant influence from a microstate with an intermediate-spin Fe^III ion antiferromagnetically coupled to a carbene radical. Our detailed computational study contrasting DFT and ab-initio methodologies emphasizes the need for high level wavefunction–based approaches including configuration interaction methods to accurately describe the electronic structures of complexes with Fe=E (E = O, NR, CR₂) multiple bonds.

Experimental Details

General Considerations.

All air- and moisture-sensitive manipulations were carried out using standard Schlenk line and cannula techniques or in an MBraun inert atmosphere drybox containing an atmosphere of purified nitrogen. Solvents for air- and moisture-sensitive manipulations were dried and deoxygenated using a Glass Contour Solvent Purification System and stored over 4 Å molecular sieves. All solids were dried under high vacuum, all liquids were dried over CaH₂ and vacuum transferred into oven dried glassware in order to bring into the glovebox. Deuterated benzene (benzene-d₆) and dichloromethane (CD₂Cl₂) for NMR spectroscopy were purchased from Cambridge Isotope Laboratories and distilled from sodium metal and calcium hydride, respectively. (^MesPDP^Ph)Fe(thf)⁵¹ and diphenyldiazomethane⁷¹ were prepared following reported literature procedures.

Safety Considerations.

Diazomethane derivatives are known toxic and energetic materials that may decompose violently via explosion upon input of energy from external sources (heat, light, pressure). While we did not encounter any problems or dangerous situations during the course of this study, all experiments involving diphenyldiazomethane were performed on small scale with less than 200 mg of diazomethane reagent. All manipulations outside of the drybox were performed behind a blast shield. Diphenyldiazomethane was stored in the dark at −35 °C in the drybox.

Preparation of (^MesPDP^Ph)Fe(CPh)₂:

To a 20 mL scintillation vial equipped with a magnetic stir bar was added 500 mg (0.691 mmol) of (^MesPDP^Ph)Fe(thf) and 5 mL of diethyl ether. Vigorous stirring of the mixture afforded a maroon suspension. In a separate vial, 175 mg (1.3 eq, 0.902 mmol) of diphenyldiazomethane was dissolved in 5 mL of diethyl ether. The solution of diphenyldiazomethane was added dropwise to the vial containing the iron compound. After 16 hrs, a dark precipitate was evident. The precipitate was isolated on a medium porosity glass frit and dried in vacuo. The resulting dark solid was transferred to a separate vial and extracted into a minimum amount of benzene, resulting in an olive-green solution. The benzene extracts were then passed through a plug of Celite and collected in a round bottom flask. Additional benzene (10 mL) was utilized to completely wash the Celite plug until washings were completely colorless. Removal of volatiles and subsequent trituration with pentane afforded a dark brown solid identified as (^MesPDP^Ph)Fe(CPh₂). Yield: 362 mg (0.443 mmol, 64%). μ_eff = 3.8(2) μ_B (295 K, magnetic susceptibility balance). ¹H NMR (400 MHz, benzene-d₆; δ, ppm): (s, 2H), (s, 4H), (s, 4H), (s, 12H, ortho-mesityl-CH₃), (s, 4H), (s, 4H), (s, 2H), (s, 2H), (s, 6H, para-mesityl-CH₃), (s, 2H), (s, 1H, 4-pyridineH), (s, 4H). Anal. Calcd for (^MesPDP^Ph)Fe(CPh₂), C₅₆H₄₇FeN₃: C, 82.24; H, 5.79; N, 5.14. Found: C, 82.24; H, 5.90; N, 5.06. Slow evaporation of a diethyl ether solution at −35 °C provided dark single crystals of (^MesPDP^Ph)Fe(CPh₂) suitable for X-ray diffraction.

Physical Measurements.

¹H NMR spectra were acquired at 25 °C on a Varian INOVA^Unity 600 MHz spectrometer equipped with a 5 mm inverse broadband PFG probe, on an Agilent 400 MHz DD2 spectrometer equipped with a 5 mm One NMR probe, or a JEOL JNM-ECZ400S/L1 spectrometer equipped with a 5 mm ROYAL NMR probe. All chemical shifts are reported relative to SiMe₄ using ¹H (residual) chemical shifts of the solvent as a secondary standard. Elemental analyses were performed at Robertson Microlit Laboratories, Inc., in Ledgewood, NJ. Room temperature magnetic susceptibility measurements were conducted with a Johnson Matthey Mark 1 instrument that was calibrated with HgCo(SCN)₄. Magnetic susceptibility and reduced magnetization data were collected using a MPMS3 Quantum Design SQUID magnetometer. Underlying diamagnetism was corrected by using tabulated Pascal’s constants.⁷² Variable temperature data were collected on microcrystalline samples sealed tightly packed in gelatin capsules in the temperature range of 2 – 300 K. A small applied field of 0.1 Tesla was used to avoid orientation effects during the measurement. Four variable temperature/field reduced magnetization curves were collected at fixed temperatures of 2, 4, 8, and 12 K with the field swept from 0 – 7 T. Fitting of the magnetic data was performed using PHI. Zero-field ⁵⁷Fe Moössbauer spectra were collected on a SEE Co. Moössbauer spectrometer (MS4) with a ⁵⁷Co/Rh radiation source at 80 K in constant acceleration mode. The temperature in the sample chamber was controlled by a Janis Research Co. CCS-850 He/N2 cryostat within an accuracy of ±0.3 K. Applied-field Mössbauer spectra were recorded with two spectrometers, using Janis Research (Wilmington, MA) SuperVaritemp dewars that allow studies in applied magnetic fields of up to 8.0 T in the temperature range from 1.5 to 200 K. A LakeShore Model 331A temperature controller was used to control the temperature in experiments. Polyoxymethylene cups were used as sample holders for Mössbauer samples. The powder sample was prepared as a frozen suspension of polycrystalline solid in degassed Nujol. To protect the sample, the mineral oil was mixed quickly with the powder and the mixture was immediately frozen with a pre-cooled Al block in the glovebox. The solution sample was prepared in the glovebox using rigorously dried and deoxygenated toluene. The solution was subsequently frozen using a liquid nitrogen cooled cold-well. No sample degradation was detected in the zero-field Mössbauer spectrum for either sample preparation. Mössbauer spectral simulations were performed using the WMOSS software package (SEE Co, Edina. Minnesota) and SpinCount software developed by Prof. Michael Hendrich at Carnegie Mellon University. Isomer shifts are quoted relative to α-Fe metal at 298 K. SpinCount was used to generate all the Mössbauer related figures.

Computational Methods.

All calculations were performed using the ORCA quantum chemical program package v4.2.1.^73,74 Geometry optimizations and single-point property calculations were carried out with the BP86,^75,76 TPSSh,⁷⁷ and B3LYP⁷⁸ density functionals to gauge the effects of Hartree-Fock exchange. In all cases, scalar-relativistic effects were included via the Douglas-Kroll-Hess (DKH) formalism.⁷⁹ The calculations were accelerated by using RI^80,81 (resolution of identity, BP86) and RIJCOSX⁸² (resolution of identity for the Coulomb part and a chain of spheres algorithm for the Hartree−Fock exchange part, TPSSh and B3LYP) approximations when appropriate. All auxiliary basis sets were generated via the autoaux procedure.⁸³ In geometry optimizations, tight optimization thresholds were employed and noncovalent interactions were considered via atom-pairwise dispersion corrections with Becke−Johnson (D3BJ) damping.^84,85 The relativistically-adapted triple-ζ quality basis set, DKH-def2-TZVP, was used for Fe and the atoms in the first coordination sphere, while the remaining atoms were treated with the DKH-def2-SVP basis set.⁸⁶ DFT property calculations employed increased integration grids (Grid5 nofinalgrid Gridx7) and the specialized core-property basis set CP(PPP)⁶² on Fe with increased radial integration accuracy (specialgridintacc 7). The isomer shifts were extracted by comparing the calculated electron density (excluding relativistic effects) to previously reported calibration data.^63,87 The g-tensor and ZFS were calculated via a coupled-perturbed self-consistent field (CP-SCF) approach as implemented in ORCA.⁸⁸

All multi-configurational complete-active-space self-consistent field (CASSCF) calculations⁸⁹ were performed on the X-ray structure with optimized hydrogen positions. The relativistically-adapted def2-TZVPP basis set⁸⁶ was used on all atoms and scalar relativistic effects were again treated with the DKH formalism. State-averaged CASSCF (SA-CASSCF) calculations including dynamic electron correlation via N-electron valence perturbation theory in the domain-based local pair natural orbital framework (DLPNO-NEVPT2)⁹⁰ were employed to calculate the zero-field splitting and g-tensors using effective Hamiltonian theory.^91,92 The spectroscopy-oriented configuration interaction (SORCI) framework⁹² employing the sum-over-states (SOS) formulation⁹³ was also used to calculate the g-tensor. Due to the computational demand of the latter method, a truncated model was used in combination with the def2-TZVP(-f) basis set.⁸⁶ Spin-orbit coupling (SOC) was handled via the spin-orbit mean-field (SOMF) approximation as implemented in ORCA.^94,95 All orbital and spin-density plots were generated using the program Gabedit.⁹⁶ More computational details including input files can be found in the supporting information.