Frequency-Resolved Connectome Hubs and Their Test-Retest Reliability in the Resting Human Brain

Abstract

Functional hubs with disproportionately extensive connectivities play a crucial role in global information integration in human brain networks. However, most resting-state functional magnetic resonance imaging (R-fMRI) studies have identified functional hubs by examining spontaneous fluctuations of the blood oxygen level-dependent signal within a typical low-frequency band (e.g., 0.01–0.08 Hz or 0.01–0.1 Hz). Little is known about how the spatial distributions of functional hubs depend on frequency bands of interest. Here, we used repeatedly measured R-fMRI data from 53 healthy young adults and a degree centrality analysis to identify voxelwise frequency-resolved functional hubs and further examined their test-retest reliability across two sessions. We showed that a wide-range frequency band (0.01–0.24 Hz) accessible with a typical sampling rate (f_sample = 0.5 Hz) could be classified into three frequency bands with distinct patterns, namely, low-frequency (LF, 0.01–0.06 Hz), middle-frequency (MF, 0.06–0.16 Hz), and high-frequency (HF, 0.16–0.24 Hz) bands. The functional hubs were mainly located in the medial and lateral frontal and parietal cortices in the LF band, and in the medial prefrontal cortex, superior temporal gyrus, parahippocampal gyrus, amygdala, and several cerebellar regions in the MF and HF bands. These hub regions exhibited fair to good test-retest reliability, regardless of the frequency band. The presence of the three frequency bands was well replicated using an independent R-fMRI dataset from 45 healthy young adults. Our findings demonstrate reliable frequency-resolved functional connectivity hubs in three categories, thus providing insights into the frequency-specific connectome organization in healthy and disordered brains.

Supplementary Information

The online version contains supplementary material available at 10.1007/s12264-021-00812-7.

Introduction

Resting-state functional magnetic resonance imaging (R-fMRI) studies have revealed that the human brain is well organized into a large-scale functional network (the functional connectome) that consists of spatially distributed but interconnected regions [1–3]. With the assistance of the graph-theoretical approach, researchers have identified several hub regions in the functional connectome with extensive connections, which are primarily located in the medial and lateral frontal and parietal cortices, as well as the lateral temporal lobe [4–6]. These functional hubs play crucial roles in information transmission and integration across the whole brain [7, 8] and show relatively high rates of cerebral blood flow [6] and glucose metabolism [9]. Also, the functional hub configuration is correlated with individual cognitive performance (e.g., working memory) [10] and exhibits alterations in many neuropsychiatric disorders such as Alzheimer’s disease, coma, and bipolar disorder [11–14]. Thus, exploring functional hubs could offer rich insights into the mechanisms underlying cognition and brain disorders.

Until recently, most R-fMRI studies identified brain hubs of the functional connectome using spontaneous blood oxygen level-dependent (BOLD) signals within a low-frequency component (usually 0.01–0.08 Hz or 0.01–0.1 Hz) [2, 7] and ignored the potential influence of the frequency band selected. Accumulating evidence has revealed frequency-dependent features of both functional connectivity profiles [15, 16] and functional hubs [17–20]. Several functional hubs, such as the medial frontal cortex, and well-organized functional networks, such as the default-mode network, have been reported in high-frequency bands with frequencies >0.1 Hz [17, 21, 22]. However, previous studies primarily focused on functional hubs over several prior or uniform frequency bands, implicitly ignoring the inherent principles underlying the frequency-dependent patterns in brain networks. Little is known regarding whether there is an intrinsic mode governing the frequency specificity of functional brain hubs. Moreover, whether the frequency specificity of the functional hubs is reliable over time remains to be elucidated.

Here, we used an R-fMRI dataset of repeated scans from 53 healthy young adults and a voxelwise whole-brain functional network analysis to comprehensively investigate the frequency-dependence of the functional hubs in the resting-state human brain. Such a voxelwise approach provides a natural node definition (i.e., imaging voxels) with a high spatial resolution and prevents potential parcellation-dependent biases [23]. Specifically, we focused on the spatial patterns of degree centrality maps across a wide frequency range (0.01–0.24 Hz) accessible with a typical sampling rate (f_sample = 0.5 Hz). For each participant, degree centrality maps were separately generated for each of ten fine-grained frequency bands that were suggested in Wu et al. [16]. We aimed to determine (1) whether there are certain categories that govern the frequency-dependent shifts in the spatial pattern of functional hubs and (2) if there are, how the functional hubs change across different categories and whether they are reliable across sessions and are replicable in an independent dataset.

Materials and Methods

Participants

Repeatedly measured R-fMRI data were obtained from the Connectivity-based Brain Imaging Research Database (C-BIRD) at Beijing Normal University [24]. Fifty-seven healthy young adults (M/F: 30/27, age: 23.05 ± 2.29 years) underwent repeated MRI scans in two sessions with an interval of ~6 weeks (40.94 ± 4.51 days) between two sessions. Written informed consent was given by each participant, and the study was approved by the Institutional Review Board of the State Key Laboratory of Cognitive Neuroscience and Learning at Beijing Normal University. All participants were right-handed, native Chinese speakers and had no history of neurological or psychiatric disorders. This dataset has been used in previous test-retest reliability studies regarding graph metrics in voxelwise functional networks [11, 25]. Notably, R-fMRI data from four participants were discarded from the current analysis due to excessive head motion (n = 3) or missing slices (n = 1) in the fMRI data. R-fMRI data from the remaining 53 participants (M/F: 28/25; age: 23.09 ± 2.36 years) were used in the present study.

Data Acquisition

All MRI data were obtained using a Siemens Trio Tim 3.0T scanner (Siemens, Erlangen, Germany) with a 12-channel phased-array head coil in the Imaging Center for Brain Research, Beijing Normal University. All participants underwent repeated MRI scans in two sessions. The first session consisted of two R-fMRI runs in addition to T1, T2, and diffusion MRI scans. The two R-fMRI runs were performed separately at the beginning (S1) and the end of the session (~20 min apart). The second session included one R-fMRI scan (S2), a T1 MRI scan, and a diffusion MRI scan in order. R-fMRI data were acquired using a T2*-weighted echo-planar imaging (EPI) sequence with the following parameters: repetition time (TR)/echo time (TE) = 2,000 ms/30 ms, flip angle (FA) = 90°, field of view (FOV) = 200 × 200 mm², matrix = 64 × 64, interleaved axial slice number = 33, slice thickness/gap = 3.5/0.7 mm, and volume number = 200. During the scans, participants were instructed to rest and relax with their eyes closed and not fall asleep. High-resolution structural images were acquired by using a T1-weighted sagittal, 3D magnetization prepared rapid gradient echo (MP-RAGE) sequence with the following parameters: TR/TE = 2,530 ms/3.39 ms, inverse time = 1,100 ms, FA = 7°, FOV = 256 × 256 mm², matrix = 256 × 256, interleaved sagittal slice number = 144, slice thickness = 1.3 mm. Importantly, we used the repeatedly measured R-fMRI data (i.e., S1 and S2) scanned at the beginning of both sessions in the subsequent analysis to exclude the potential influence of the scanning order. The R-fMRI data in S1 were used for the main analysis, and the data in S2 were used to assess the reliability of the results over a long-term interval.

Data Preprocessing

R-fMRI data were preprocessed using Data Processing Assistant for Resting-State fMRI (DPARSF; http://www.restfmri.net/forum/DPARSF) [26] and SPM8 (http://www.fil.ion.ucl.ac.uk/spm). Briefly, the first five volumes were removed to allow magnetic field stabilization and to account for the participants’ adaptation to the scanning circumstance. Next, we performed slice timing and head motion correction and estimated mean framewise displacement (FD [27]) over time. During this step, three participants (ID: N0006, N0016, and N0027) were excluded due to excessive head motion (translation >2 mm or rotation >2°) during at least one of the two scans. The mean FD was <0.5 mm for all participants in both sessions (mean FD range: 0.10 ± 0.04 mm for S1 and 0.11 ± 0.04 mm for S2). The remaining functional images were spatially normalized to the Montreal Neurological Institute (MNI) space based on a unified segmentation algorithm [28] and resampled to 3-mm isotropic voxels. Specifically, the individual T1 image was first segmented into gray matter, white matter, and cerebrospinal fluid maps with prior tissue maps in SPM as reference. The individual functional images were co-registered with the T1 image and then spatially transformed to the MNI space by applying the transformation parameters obtained from the segmentation of the T1 image. Next, we performed linear de-trending, nuisance regression, and temporal bandpass filtering. During the nuisance regression, 24 head motion parameters [29] and global, cerebrospinal fluid, and white matter signals were removed through multivariate linear regression to reduce the influence of head motion and physiological noise. The preprocessed time courses were used for the subsequent functional network analysis. Of note, we did not perform spatial smoothing that could introduce artificial functional connectivities among spatially adjacent voxels [30].

Specifically, to investigate the frequency-specific features of functional hubs, ten fine-grained frequency bands, which were accessible with the current, commonly used sampling rate (f_sample = 0.5 Hz), were separately used during temporal bandpass filtering: 0.01–0.02 Hz, 0.02–0.04 Hz, 0.04–0.06 Hz, 0.06–0.08 Hz, 0.08–0.10 Hz, 0.10–0.12 Hz, 0.12–0.14 Hz, 0.14–0.16 Hz, 0.16–0.20 Hz, and 0.20–0.24 Hz as suggested by Wu et al. [16]. The 0.00–0.01 Hz band was not considered because BOLD signals in this frequency band are usually assumed to reflect non-neural signals caused by low-frequency drifts [31]. Considering the 1/f-like power spectra of BOLD signals [32, 33], we set a wide bandwidth for the relatively high-frequency bands (0.16–0.20 Hz and 0.20–0.24 Hz) to increase the total power within these bands. A power spectral analysis of the gray matter signal further confirmed the decreasing power over the ten fine-grained frequency bands (Fig. S1, for details, see the “Power Spectral Analysis” section in Supplementary Materials). To allow comparisons with functional hubs reported in traditional R-fMRI studies [4, 6, 7], we also included the typical frequency band 0.01–0.10 Hz as a reference.

Frequency-Resolved Nodal Degree Centrality Analysis

To identify frequency-dependent functional hubs, we performed a voxelwise degree centrality analysis for each frequency band. The investigation was constrained within a gray matter mask (n = 50,756 voxels), which included brain areas with a prior gray matter probability >0.2 provided from SPM8. For each participant, a voxelwise degree centrality map was constructed for each frequency band of interest. Specifically, the degree centrality of each voxel was characterized by its averaged functional connectivity strength with all the other voxels [4, 6, 34]. Given voxel i, its degree centrality was calculated as follows:

$$k_i=\frac{1}{N-1}\sum _{j\ne i}{z}_{\mathit{ij}},r_{\mathit{ij}}>r_{\mathit{th}}$$

where r_ij denotes the Pearson’s correlation between the time series of voxel i and voxel j, z_ij denotes Fisher’s r-to-z transformation of the correlation element r_ij, and r_th is a correlation threshold used to remove as many potentially spurious correlations as possible. Here, the correlation threshold r_th was set at 0.2 [11, 22]. We considered only positive correlations due to the ambiguous physiological interpretation of negative correlations [35–37]. For each participant, we obtained 11 frequency-specific voxelwise degree centrality maps — ten for the fine-grained frequency bands and one for the typical frequency band. The individual degree centrality maps were spatially smoothed with a Gaussian kernel (full width at half maximum = 6 mm) to reduce the influence of image noise and inter-subject anatomical variability and ensure the validity of the Gaussian random field (GRF) theory for statistical analysis [38]. The spatially smoothed degree maps were further transformed to Z-score values to improve comparability across participants and frequency bands. Briefly, the degree centrality of each voxel was transformed into a Z-score value by subtracting the mean degree value across the whole brain and then dividing by the SD. Finally, for each participant, we obtained a degree centrality map in terms of Z-score values for each frequency band of interest. We also generated a group-level degree centrality map for each band by averaging individual maps across participants.

Analysis of Spatial Similarity Among Frequency Bands

To explore the influence of frequency bands on the spatial locations of functional hubs, we compared the spatial patterns of the group-level degree centrality maps among different frequency bands. First, we compared the maps of the ten fine-grained frequency bands with that of the typical frequency band. Second, we estimated pairwise spatial similarity among the ten fine-grained frequency bands by calculating Pearson’s correlation coefficients across voxels and obtained a 10 × 10 frequency-to-frequency similarity matrix.

We applied a hierarchical clustering analysis to quantify the convergence and divergence of the degree centrality maps among different frequency bands. Briefly, a distance matrix was obtained by inverting the frequency-to-frequency similarity matrix (i.e., subtracting the values from 1). Then, the average linkage agglomerative algorithm was applied to the distance matrix. This algorithm treated each frequency band as a separate cluster in the initial state. Then it progressively merged pairs of clusters with the minimum distance (i.e., the maximum spatial similarity) into a new cluster until all clusters merged into a single cluster. At each merging step, the distance between any two clusters was redefined as the average distance between the degree centrality maps in the first and the second clusters. The hierarchical clustering procedure is displayed in a dendrogram that shows the iterative clustering process. Degree centrality maps in the same cluster were more similar in the spatial pattern than those in different clusters. We determined the optimal cluster number by optimizing the silhouette coefficient [39]. Here, we found a two-cluster division corresponding to the highest silhouette coefficient (coefficient = 0.79) (Fig. 1B, right). Considering the inappropriate sizes of two clusters (8 vs 2), we further divided the larger cluster into two sub-clusters according to the optimal silhouette coefficient estimated within this cluster (coefficient = 0.60).

Fig. 1.

Spatial distributions of frequency-resolved degree centrality maps and their spatial similarity. A Group-level degree centrality maps for ten fine-grained frequency bands and the typical frequency band (0.01–0.1 Hz). Only voxels with Z-score values >0 are displayed. The hemispheric maps were visualized using a toolbox BrainNet Viewer (http://www.nitrc.org/projects/bnv/, [40]). B Spatial similarities in degree centrality maps among ten fine-grained frequency bands and the corresponding dendrogram. Three characteristic frequency bands were obtained by using the agglomerative hierarchical clustering algorithm.

Analysis of Degree Centrality in Three Characteristic Frequency Bands

Using the hierarchical clustering analysis, we found that the ten fine-grained frequency bands were classified into three clusters (Fig. 1B, right), each of which comprised adjacent frequency bands, including the low frequency (LF) band at 0.01–0.06 Hz, the middle frequency (MF) band at 0.06–0.16 Hz, and the high frequency (HF) band at 0.16–0.24 Hz. These three frequency bands are hereafter referred to as characteristic frequency bands. Next, we focused on spatial patterns of the degree centrality maps in these bands. Briefly, we preprocessed the data again by separately using the LF, MF, and HF bands in the temporal bandpass filtering. Finally, for each characteristic frequency band, we generated individual degree centrality maps in terms of Z-score values and the corresponding group-level map according to the procedure described above (see the section titled “Frequency-resolved Nodal Degree Centrality Analysis”).

To quantify how frequency bands affected the degree centrality values, we applied a voxelwise one-way repeated-measures analysis of variance (ANOVA) to individual degree centrality maps. The resulting F-value maps were corrected for multiple comparisons using the GRF theory (i.e., voxel P-value < 0.001, cluster P-value < 0.05) [41]. Furthermore, post hoc paired t-tests were applied between every possible pair of characteristic frequency bands (MF vs LF, HF vs MF, and HF vs LF). Significance levels of the t-maps were also corrected for multiple comparisons using the GRF theory (i.e., voxel P-value < 0.001, cluster P-value < 0.05).

Identifying Consistent Functional Hubs in Each Frequency Band

A previous study pointed out that functional connectivity profiles of the human brain vary substantially across individuals [42]; this variance may introduce inter-subject variability into the spatial pattern of functional hubs. For each characteristic frequency band, we identified consistent functional hubs across participants. The functional hubs were first identified at the individual level and were defined as brain regions showing relatively high degree centrality (i.e., Z-score >1). To assess the across-subject consistency in the spatial distribution of functional hubs, we calculated the probability of occurrence as hubs across all participants for each voxel. The regions with occurrence probabilities >0.4 were referred to as consistent functional hubs across participants.

Reliability Analysis of Degree Centrality Maps

Since the participants underwent repeated R-fMRI scanning (S2) ~6 weeks later, we could ascertain the reliability of the main findings. First, we re-performed the same hierarchical clustering analysis on the degree centrality maps in the ten fine-grained frequency bands obtained from R-fMRI data in S2. The same three characteristic frequency bands, LF, MF, and HF, were obtained, indicating the reliability of the clustering. Then, we assessed whether the frequency-resolved degree centrality maps were reproducible at the individual level. For each characteristic frequency band, we calculated the inter-session (i.e., S1 and S2) similarity of individual degree centrality maps within the same participants or between different participants. Specifically, given a participant of interest, the intra-subject similarity was defined as the spatial similarity of degree maps of this participant between two sessions, which is independent of direction. The inter-subject similarity of this participant was estimated for each direction. The inter-subject similarity from S1 to S2 was defined as the mean spatial similarity of the degree centrality map of this participant in S1 with degree centrality maps of all the other participants in S2. The inter-subject similarity from S2 to S1 was defined similarly by reversing S1 and S2. We assessed significant differences between the intra-subject and inter-subject similarities using paired t-tests for each direction (i.e., S1 to S2 and S2 to S1). Finally, we evaluated the test-retest reliability of the voxelwise degree centrality between two sessions (i.e., S1 and S2) using an index of intra-class correlation coefficient (ICC). Given a voxel, an ICC value was estimated as follows [43]:

$$\text{ICC}=\frac{\text{bMS}-\text{wMS}}{\text{bMS}+\left(m-1\right)\text{wMS}}$$

where bMS and wMS denote between- and within-subject mean squares, respectively, and m denotes the number of repeated measurements (here, m = 2). The test-retest reliability of each voxel was assessed according to the following criteria [44]: low reliability with an ICC < 0.4, fair to good reliability with 0.4 ≤ ICC < 0.75, and excellent reliability with an ICC ≥ 0.75.

Validation Analysis

We investigated whether the classification of the three characteristic frequency bands depended on the data preprocessing and network analysis strategies.

Global Signal Regression

Global signal regression (GSR) is a controversial issue for the preprocessing of R-fMRI data [37]. In the main analysis, we included the global signal in the nuisance regression to better remove the effects of head motion [45, 46] and physiological noise [47]. To investigate the influence of the global signal, we undertook the nuisance regression again without GSR. We also evaluated the stability of the global signal effect by comparing results between S1 and S2.

Correlation Thresholds

During the degree centrality estimation, a correlation threshold was applied to remove potentially spurious functional connectivities. Besides the threshold of r_th = 0.2, we calculated individual degree maps with two other thresholds, r_th = 0 and r_th = 0.1, and performed the hierarchical clustering analysis again. These analyses were undertaken on the R-fMRI data in S1.

Reproducibility Analysis

We used an independent R-fMRI dataset to investigate the replicability of the three characteristic frequency bands and the corresponding degree centrality patterns. This dataset comprised R-fMRI data from 45 healthy young adults (M/F: 22/23, age: 21.57 ± 4.96 years) (https://fcon_1000.projects.nitrc.org/indi/CoRR/html/bnu_3.html) (for details, see Supplementary Materials). These R-fMRI scans were acquired with a typical sampling rate (TR = 2 s, f_sample = 0.5 Hz) in the eyes-closed condition. We undertook data preprocessing and network analysis following the same procedure as the main analysis.

Statistical Analysis

All data are shown as the mean ± SD. The influence of the frequency band on the voxelwise degree centrality values was assessed by comparisons between LF, MF, and HF bands using one-way repeated-measures ANOVA followed by post hoc paired t-tests. The intra- and inter-subject similarities of degree centrality maps were compared using paired t-tests. The statistical analysis was performed with the statistical toolbox in Matlab 2015b software (Mathworks, Natick, USA).

Results

Frequency-Dependent Degree Centrality Maps

The group-level degree centrality maps for the typical frequency band (0.01–0.1 Hz) and the ten fine-grained frequency bands are shown in Fig. 1A. Consistent with previous studies, the degree centrality map of the typical frequency band was spatially heterogeneous, with high values primarily located in the medial and lateral frontal and parietal cortices. The ten maps in the fine-grained frequency bands maintained a high spatial similarity to that of the typical frequency band (range of similarity r: 0.78–0.86, mean ± SD = 0.81 ± 0.03), while their spatial patterns gradually changed across frequency bands (Fig. 1A). Specifically, as the frequency increased, the centrality of the default-mode and medial visual regions became obscure, and the centrality of subcortical regions, the medial temporal lobe, and the cerebellum became more evident. The spatial similarity among these ten maps was also estimated (Fig. 1B, left). A high spatial similarity was found among all frequency bands except for the two highest bands, suggesting a potential separation between the LF and HF bands. Through hierarchical clustering analysis, we derived three characteristic frequency bands consisting of adjacent bands: LF (0.01–0.06 Hz), MF (0.06–0.16 Hz), and HF (0.16–0.24 Hz) (Fig. 1B, right).

Degree Centrality Maps in Three Characteristic Frequency Bands

Group-level degree centrality maps exhibited marked differences across the three characteristic frequency bands (Fig. 2A). In the LF band (0.01–0.06 Hz), regions with high degree centrality were mainly located in the medial and lateral frontal and parietal cortices, the middle temporal gyrus, and medial visual areas. In the MF band (0.06–0.16 Hz), high centrality values were mainly located in the medial prefrontal cortex, angular gyrus, supramarginal gyrus, precuneus, superior temporal gyrus, parahippocampal gyrus, amygdala, and several cerebellar regions. In the HF band (0.16–0.24 Hz), a high degree of centrality was primarily evident in the medial prefrontal cortex, superior temporal gyrus, superior parietal lobule, parahippocampal gyrus, amygdala, thalamus, and several cerebellar regions. Voxelwise one-way repeated-measures ANOVA revealed significant effects of the frequency band on the degree centrality in a wide range of brain regions (Fig. 2B, GRF correction, voxel P < 0.001, cluster P < 0.05). Compared with the LF band, several default-mode regions (e.g., the medial prefrontal cortex, precuneus, and angular gyrus), the middle frontal gyrus, and visual regions exhibited lower degree centrality in the MF and HF bands, while the superior temporal gyrus, parahippocampal gyrus, and several subcortical (e.g., amygdala and thalamus) and cerebellar regions exhibited higher degree centrality in the MF and HF bands. Notably, some regions showed significant differences between any pair of frequency bands (Fig. 2C), such as the precuneus, supramarginal gyrus, and parahippocampal gyrus.

Fig. 2.

Frequency-resolved degree centrality maps in three characteristic frequency bands and their differences. A Group-level degree centrality maps in three characteristic frequency bands. Only voxels with Z-score values >0 are displayed. B Frequency effects on the degree centrality maps revealed by one-way repeated-measures ANOVA. C Pairwise differences in degree centrality among the three frequency bands. Overlapping regions were defined as regions showing significant differences in all three comparisons (MF vs LF, HF vs MF, and MF vs LF). In B and C, significance levels of the statistical results were corrected for multiple comparisons across regions with the GRF theory (voxel P < 0.001, cluster P < 0.05). LF, low-frequency band; MF, middle-frequency band; HF, high-frequency band.

Consistent Functional Hubs in the Three Characteristic Frequency Bands

For each characteristic frequency band, functional hubs were identified at the individual level. We found that the spatial locations of the functional hubs substantially varied across individuals. In the LF band, consistent functional hubs across participants (occurrence probability >0.4) were mainly located in the precuneus, angular gyrus, and medial and lateral prefrontal cortex (Fig. 3, left). In the MF and HF bands, consistent functional hubs were primarily located in the medial prefrontal cortex, superior temporal gyrus, parahippocampal gyrus, amygdala, and some cerebellar regions, with additional hubs noted in the angular gyrus and precuneus in the MF band and the superior parietal lobule in the HF band (Fig. 3, middle and right).

Fig. 3.

Probability maps as functional hubs in the three characteristic frequency bands. The occurrence probability of each voxel as hubs was defined as the fraction of participants in which the voxel was identified as a functional hub. Here, we show consistent functional hubs with occurrence probabilities >0.4. LF, low-frequency band; MF, middle-frequency band; HF, high-frequency band.

Reliable Frequency-dependent Maps Across Sessions

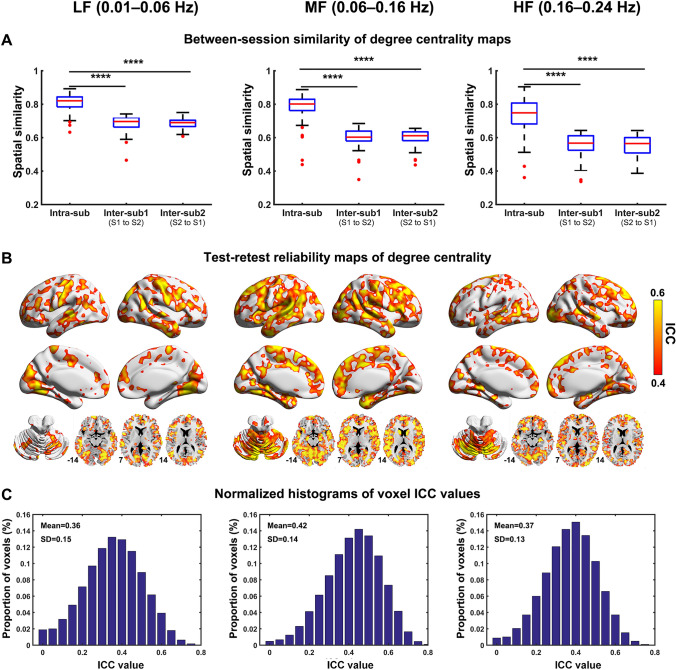
Using repeatedly measured R-fMRI data (i.e., S2) from the same participants, the same three characteristic frequency bands were obtained using the hierarchical clustering analysis (Fig. 4). We further assessed the reliability of the degree centrality maps between the two sessions. First, we found that individual degree centrality maps exhibited high spatial similarities between the two sessions in all frequency bands (Fig. 5A). The intra-subject similarity (mean ± SD: 0.81 ± 0.05 for the LF band; 0.78 ± 0.09 for the MF band; 0.73 ± 0.11 for the HF band) was significantly higher than the inter-subject similarity in either direction (Bonferroni-corrected P < 0.0001), regardless of the frequency band (Fig. 5A). For each frequency band, the voxelwise test-retest reliability was evaluated using an ICC value. The reliability maps were spatially inhomogeneous and frequency-dependent (Fig. 5B), with a mean value of 0.36 for the LF band, 0.42 for the MF band, and 0.37 for the HF band (Fig. 5C). In terms of reliability categories, ~39.6% of the voxels in the LF band exhibited fair to good reliability (ICC ≥0.4) and were mainly located in several default-mode regions (e.g., the medial prefrontal cortex, precuneus, and middle temporal gyrus), the lateral frontal cortex, and sensorimotor and visual regions. In the MF and HF bands, the proportion of voxels exhibiting fair to good reliability changed to 59.1% and 43.6%, respectively. For the MF band, the increased reliability was primarily found in the medial prefrontal cortex, medial temporal lobe, and several subcortical (e.g., the caudate nucleus, amygdala, and thalamus) and cerebellar regions.

Fig. 4.

Reproducibility of the three characteristic frequency bands (S2). A Group-level degree centrality maps for ten fine-grained frequency bands and the typical frequency band (0.01–0.1 Hz). Only voxels with Z-score values >0 are displayed. B Spatial similarities in degree centrality maps among ten fine-grained frequency bands and the corresponding dendrogram. Three characteristic frequency bands were obtained by using the agglomerative hierarchical clustering algorithm. All results were obtained from R-fMRI data of the same participants acquired in the second session (S2), which occurred approximately six weeks later.

Fig. 5.

Reliability of individual-level degree centrality maps between two sessions. A Spatial similarities of degree centrality maps between two sessions. Intra-sub denotes intra-subject similarity. Inter-sub denotes inter-subject similarity estimated in two directions separately (i.e., S1 to S2, and S2 to S1). ****P < 0.0001, Bonferroni-corrected. B Test-retest reliability maps of degree centrality. Only voxels with ICC values >0.4 are displayed. C Normalized histograms of voxel ICC values across the brain.

Validation Results

We assessed the influence of several data preprocessing and network analysis strategies on the identification of the three characteristic frequency bands.

Influence of GSR

Without GSR, we also detected three characteristic frequency bands for each session (Fig. S2). However, the ranges of these bands were slightly different from those obtained with GSR, particularly the LF and MF bands. Specifically, compared with the classification with GSR, the frequency band at 0.04–0.06 Hz shifted from the LF to the MF band for S1 (Fig. S2A), and the frequency band at 0.01–0.02 Hz moved from the LF to the MF band for S2 (Fig. S2B). These results indicate an unstable effect of the global signal on the hierarchical clustering analysis, particularly on the LF band.

Influence of Correlation Thresholds

We identified the same three characteristic frequency bands, regardless of the correlation thresholds (r_th = 0 and 0.1) used for the connectivity estimation (Fig. S3).

Reproducibility Results

Based on the independent dataset, we identified the same three characteristic frequency bands: LF (0.01–0.06 Hz), MF (0.06–0.16 Hz), and HF (0.16–0.24 Hz) (Fig. S4A). For each characteristic frequency band, the group-level degree centrality map showed a high spatial similarity with that in the main analysis (r = 0.98, for the LF band; r = 0.97 for the MF band; r = 0.95 for the HF band, all P < 0.001 with spatial autocorrelation corrected [48]) (Fig. S4B).

Discussion

Using repeatedly measured R-fMRI data and a voxelwise degree centrality analysis, we explored the spatial patterns of frequency-resolved functional hubs in the resting human brain and their inter-session reliability in the frequency domain. Our main findings are as follows. First, the wide range of frequencies (0.01–0.24 Hz) accessible with the typical sampling rate (f_sample = 0.5 Hz) was subdivided into three characteristic frequency bands (i.e., LF, 0.01–0.06 Hz; MF, 0.06–0.16 Hz; and HF, 0.16–0.24 Hz) showing distinct degree centrality patterns. Differences among these bands were primarily located in several default-mode areas, the medial temporal lobe, amygdala, thalamus, visual regions, and some cerebellar regions. Second, functional hubs were predominantly located in the medial and lateral frontal and parietal cortices in the LF band and the medial prefrontal cortex, superior temporal gyri, parahippocampal gyrus, amygdala, and some cerebellar regions in the MF and HF bands. Third, the frequency-specific degree centrality maps were reliable across scanning sessions at the individual level. Fourth, we replicated the three characteristic frequency bands and the frequency-specific degree centrality patterns in an independent dataset.

Frequency-Resolved Spatial Patterns of Functional Hubs

This study is a natural extension of the existing studies that had explored the frequency dependence of functional hubs [15, 17, 18, 20]. In line with these studies, we demonstrated significant effects of different frequency bands on degree centrality across a wide range of brain regions. Moreover, we used a hierarchical clustering approach to explore the intrinsic modes underlying the fine-grained frequency bands. The same three characteristic frequency bands (LF, MF, and HF) were identified by evaluating repeated R-fMRI data from two sessions (S1 and S2) (Figs 1 and 4) and an independent R-fMRI dataset (Fig. S4). These findings indicate the existence of a reliable structure that governs the frequency-specificity of functional hubs. In the LF band (0.01–0.06 Hz), prominent functional hubs were located in several default-mode regions, which agrees well with previous findings regarding the low-frequency component [4, 6, 22, 34]. Nevertheless, the functional hubs showed distinct spatial patterns in the MF and HF bands (0.06–0.24 Hz). These findings suggest that the amygdala and medial temporal lobe also work as functional hubs in brain networks, in addition to the default-mode regions, but in a higher frequency band. The frequency specificity of functional hubs may reflect the different roles of these hubs in information integration and communication.

A prior study suggests that long-range connectivities tend to be dominant in the LF band, while short-range connectivities may span a relatively wide frequency range [16]. Thus, we speculate that the frequency specificity of different hubs may be related to their distinct functional connectivity profiles. The default-mode network, usually found in the LF band, is involved in a wide range of cognitive functions (e.g., social, self-referential inference, and autobiographical memory) that require information integration and coordination across multiple sensory modalities [49, 50]. These regions show the greatest geodesic distance from primary sensory or motor areas [51] and act as long-range hubs of information integration [6, 22, 52]. In addition, several default-mode regions (e.g., the angular gyrus, precuneus, and medial prefrontal cortex) were also identified as functional hubs in the MF or HF band, indicating a functional subdivision of the default-mode network. The presence of the medial prefrontal cortex as hubs in the HF band may be related to its extensive short-range connections, as reported by Liao et al. [22]. The amygdala plays an essential role in integrating sensory and internal-state information for emotional processing [53]. It has abundant connections throughout the brain [54] and has been identified as a functional hub with extensive weak connectivities [55]. The presence of the amygdala in the MF and HF bands suggests that this region may be involved in extensive short-range connectivities. In addition to physical distance, recent studies have indicated that the strengths of within- and between-system (e.g., default-mode and subcortical) connectivities shift as a function of frequency [18], which may also affect the frequency features of functional hubs located in different functional systems.

Interestingly, several studies have demonstrated frequency-specific spatial distributions in the local properties of BOLD signals, such as signal power [56], the amplitude of low-frequency fluctuations [57], and regional homogeneity [58]. We found that the frequency-dependent degree centrality maps found in this study were similar to the frequency-dependent spatial distributions of BOLD signal power reported by Baria et al. [56]. This spatial similarity is consistent with a recent study demonstrating a positive spatial correlation between regional BOLD signal power and functional connectivity [59]. Together, these findings suggest that the region-dependent frequency specificities of degree centrality may be attributed to the spectral characteristics of BOLD oscillations. However, the mechanism linking regional spectral properties to the degree centrality of that region warrants further investigation.

Individual Variability in the Degree Centrality of Functional Hubs

Functional connectivity patterns in the human brain show substantial variation across individuals, underlying individual differences in cognition and behavior [42, 60–62]. Of note, most of the previous studies have explored individual variability in the functional organization within a typical low-frequency component (i.e., <0.1 Hz), which is thought to reflect the intrinsic coordination of neural activity in the brain [1, 2]. Here, we found that the spatial patterns of functional hubs varied across participants, regardless of the frequency band considered. Moreover, the intra-subject similarity was significantly greater than that between subjects. These findings indicate that the functional organization in the higher frequency bands (i.e., MF and HF) also positively contributes to individual differences. Hence, these higher-frequency signals cannot be simply treated as artifacts due to non-neural noise. Since the dominant locations of functional hubs shifted from the default-mode regions to the temporal, subcortical, and cerebellar regions, we speculate that characterizing individual variability in multiple characteristic frequency bands may provide complementary information. This approach may improve the sensitivity in detecting system-specific functional reconfigurations involved in cognitive tasks or brain disorders. Compatible with this speculation, a very recent study involving individuals with major depressive disorder demonstrated frequency-dependent decreases in degree centrality in functional networks, such as alterations in the visual areas in the LF band of 0.01–0.1 Hz and the anterior cingulate cortex in the HF band of 0.175–0.25 Hz [20].

Test-Retest Reliability of Frequency-Resolved Degree Centrality

Reliable network metrics are essential for inferring convincing conclusions from both basic and clinical studies [63, 64]. Previous studies have investigated the test-retest reliability of voxelwise degree centrality obtained from the low-frequency BOLD fluctuations [22, 25, 34]. However, the reliability of degree centrality in higher frequency bands (i.e., >0.1 Hz) is poorly understood. Using repeatedly measured R-fMRI data of the same participants, we were able to assess the long-term test-retest reliability of degree centrality in three characteristic frequency bands (LF, MF, and HF). The frequency-resolved hub regions (e.g., default mode regions, the medial temporal lobe, and the amygdala) usually showed fair to good reliability in the corresponding frequency band (Fig. 5). The reliability of functional hubs was in line with previous findings [22, 25, 65], which may be attributable to the lower sensitivity of the functional hubs to slight connectivity fluctuations between two sessions. Our findings indicate that categorizing frequencies into the three characteristic bands is a valid approach to detect the frequency specificity of functional hubs during rest.

Further Considerations

Several issues should be considered in the future. First, previous studies have demonstrated that resting-state functional networks obtained from slow fluctuations (<0.1 Hz) show system-dependent electrophysiological signatures [66]. It is important to explore the biophysical basis underlying the emergence of the three characteristic frequency bands by fusing R-fMRI data with other electrophysiological techniques, such as electroencephalography or magnetoencephalography. Second, the three characteristic frequency bands were obtained based on the spatial patterns of degree centrality maps. Whether these frequency bands are applicable to other topological properties of brain networks such as nodal betweenness or efficiency has not yet been explored. Third, we identified functional hubs across a wide frequency range (0.01–0.24 Hz) beyond the typical frequency component. Although a global signal regression strategy has been used to reduce the effects of physiological (i.e., respiratory and cardiac) signals [37, 45, 67], the potential influence of these confounding issues cannot be excluded. Future studies should monitor respiratory and cardiac signals and apply advanced preprocessing strategies to better reduce the influence of non-neural signals. Fourth, prior studies revealed that global signals are associated with head motion, physiological noise, and individual mental states [37]. Thus, the unstable effects of the global signal reported here could be attributable to inter-session fluctuations of these factors. Finally, we focused on the subdivision of a frequency band (0.01–0.24 Hz) from the commonly used sampling rate (i.e., TR = 2 s, f_sample = 0.5 Hz). Notably, newly developed imaging sequences with sub-second sampling rates (e.g., multiband EPI) have become increasingly popular [68, 69]. Introducing a higher sample rate will be valuable in reducing the potential bias of physiological noise and extending the range of the high-frequency band of interest. In the future, it will be promising to use sub-second multiband R-fMRI data to investigate the frequency-resolved functional hubs in a wide frequency band, particularly the frequency band beyond the traditional approach (e.g., >0. 3 Hz).

Supplementary Information

Below is the link to the electronic supplementary material.

Conflict of interest

The authors declare no competing financial interests.