Abstract
Airborne dispersion of the novel SARS-CoV-2 through the droplets produced during expiratory activities is one of the main transmission mechanisms of this virus from one person to another. Understanding how these droplets spread when infected humans with COVID-19 or other airborne infectious diseases breathe, cough or sneeze is essential for improving prevention strategies in academic facilities. This work aims to assess the transport and fate of droplets in indoor environments using Computational Fluid Dynamics (CFD). This study employs unsteady Reynolds-Averaged Navier-Stokes (URANS) simulations with the Euler-Lagrange approach to visualize the location of thousands of droplets released in a respiratory event and their size evolution. Furthermore, we assess the dispersion of coughing, sneezing, and breathing saliva droplets from an infected source in a classroom with air conditioning and multiple occupants. The results indicate that the suggested social distancing protocol is not enough to avoid the transmission of COVID-19 since small saliva droplets ( ≤ 12 μm) can travel in the streamwise direction up to 4 m when an infected person coughs and more than 7 m when sneezes. These droplets can reach those distances even when there is no airflow from the wind or ventilation systems. The number of airborne droplets in locations close to the respiratory system of a healthy person increases when the relative humidity of the indoor environment is low. This work sets an accurate, rapid, and validated numerical framework reproducible for various indoor environments integrating qualitative and quantitative data analysis of the droplet size evolution of respiratory events for a safer design of physical distancing standards and air cleaning technologies.
Keywords: COVID-19, CFD, Pandemics, Airborne transmission, Probability density function, Indoor environments
1. Introduction
The high rate of new infections for the novel SARS-CoV-2 (COVID-19) is mainly attributed to the transport of this pathogen through saliva droplets exhaled from infected humans [[1], [2], [3], [4], [5], [6], [7]]. Depending on the type of respiratory event, the number of saliva droplets can reach at least 3000 when an infected person talks for 5 min, 3000 each time the infected person coughs, and as many as 40000 when the infected person sneezes [[8], [9], [10]]. In general, a respiratory event can generate aerosol particle sizes ranging from 1 to 2000 μm. In the case of coughing, the sizes of the droplets range between 8 and 16 μm and between 4 and 8 μm for sneezing [11]. Understanding how these saliva droplets of infected individuals spread in environments such as schools, hospitals, restaurants, and offices, is essential for developing ventilation controls, updating sanitizing protocols, and redesigning seating layouts [12].
The airflow and saliva droplet transport of human coughs and sneezes in indoor environments have been extensively studied using analytical [4,[13], [14], [15]], experimental [4,[16], [17], [18]], and numerical methods [[19], [20], [21], [22], [23], [24]]. Among these methods, numerical simulation has emerged to be a popular tool for studying droplet transport problems due to the recent progress in the High-Performance Computing (HPC) field in terms of processing power, development of advanced algorithms, and the storage capacity of computers. It also offers versatility in approximating solutions compared to experimental methods, especially under restricted confinement and social distancing protocols that are essential to preserving the world economy and population's health.
[19,25] studied transport, dispersion, and evaporation of saliva droplets considering the effect of relative humidity in the environment. They found that the 6 ft (1.8288 m) social distance “rule” is sufficient to avoid transmission of COVID-19 when the wind speed is 0 km/h as the droplets evaporate and fall to the ground before reaching 6 ft (1.8288 m). However, it is no longer valid for wind speeds greater than 0 km/h, since under these conditions the droplets could travel further, particularly due to the small size of these droplets [20]. performed computational fluid dynamics (CFD) simulations of coughing and sneezing to predict evaporation and dispersion of droplets in a quiescent background. In this study they found that droplets evaporate to the non-volatile core faster at lower relative humidity (typically occur in cooler climates) [21]. developed numerical simulations and mathematical models to quantitatively predict the dispersion and settling time of the droplets produced when a human coughs [22]. modeled the evaporation and dispersion of cough droplets in quiescent air using CFD with an Euler-Lagrange approach. They found that the effect of inhomogeneous humidity field induced by vapor exhalation affects the dynamics of the droplets. Moreover, the evaporation and transport of droplets larger than 100 μm are not affected by the airflow pattern in the vapor plume since the velocity of the droplets is larger than the vapor plume expansion velocity [22]. Numerical simulations with more advanced methods such as large-eddy simulations (LES) and direct numerical simulations (DNS), which accurately capture the characteristics of turbulent jet flows, have become one of the most popular ways to assess the dispersion of coughing droplets in indoor environments [26,27]. studied the characteristics of a human cough jet development in a quiescent indoor environment using LES simulations. They found that LES simulations predict the temporal development of a human cough very well compared to unsteady Reynolds-Averaged Navier-Stokes (URANS) and experimental data [28]. performed DNS simulations to characterize the puff dynamics of a violent expiratory event such as a mild cough. They discovered that DNS simulations agree with analytical methods in predicting horizontal ranges, although the trajectory of the puff front and the entrainment rate vary substantially.
Although numerical simulations of coughing, sneezing, and breathing on the spread of infectious respiratory droplets in indoor environments is an active research field, many challenges are still to be addressed. First, most literature uses analytical models and experimental data of steady cough/sneeze jets to validate the results of the numerical simulations. Even though it is a valid assumption, previous experiments have shown that a human cough behaves as a puff rather than a steady jet [23,29,30]. Second, as introduced previously, LES and DNS are the most advanced methods for cough/sneeze flow simulations. These methods can improve the accuracy of turbulent cough/sneeze puff prediction in indoor environments [27,28,[31], [32], [33], [34]]. However, the significantly refined grid and time-dependent algorithm in turbulence resolution make it too expensive in terms of computational cost, especially for many practical applications such as complex scenarios with multiple infectious sources in a room and external conditions. Third, no previous studies have reported or shown the droplet size evolution of a cough/sneeze puff from CFD derivations to the best of our knowledge. Determining the droplet size distribution and evolution of a coughing, sneezing or a breathing puff could be critical to predicting important large-scale processes such as the probability of infection of a healthy individual given the viral load that a saliva droplet can retain.
Considering the challenges mentioned above, a salient question becomes. Is it possible to develop a basic numerical simulation framework that can provide accurate predictions, be suitable for application in various indoor scenarios, and be affordable in terms of computation time for facilities authorities, engineers, and designers? This work aims to answer this question by predicting the turbulent transport of infectious respiratory droplets and their size distribution evolution using URANS simulations with an Euler-Lagrange approach. The results of the simulations are analyzed quantitatively and qualitatively. The qualitative analysis aims to show the location of thousands of droplets released from the mouth of an infected individual at different times; meanwhile, the quantitative analysis is performed to evaluate the spatiotemporal traces of the droplet population using statistical methods. The novelty of our study lies in the use of an accurate, rapid, and validated numerical framework reproducible for various indoor environments, along with statistical analysis of the droplet size evolution of respiratory events for a safer design of physical distancing standards and air cleaning technologies, specifically in academic facilities. The framework's validation process shows no significant differences in predicting critical parameters related to modeling respiratory flows between proposed URANS and more sophisticated models such as LES. The proficiency of this numerical framework was exhibited in the design of a disinfection robot amid the COVID-19 pandemic [35]. The rapid and accurate solutions obtained from the URANS simulations helped optimize the robot's disinfection efficiency in risk zones of a classroom where commercial air cleaning technologies have difficulties reaching.
The remainder of this paper is organized as follows. Section 2 provides a framework to model and validate the continuous and discrete phase of expiratory activities in a quiescent indoor environment. The URANS model is validated against available experimental, analytical, and LES simulations data. In this section, we focus on the analysis of droplets exhaled for coughing because it is a common symptom of infected people with COVID-19 or other airborne infectious diseases such as tuberculosis [36,37] and sneezing since the speed and the number of droplets exhaled is large enough to increase the risk of infection [17,38]. Furthermore, we neglect the spreading of the droplets due to the thermal plume developed by a human with high temperature, e.g., an infected individual with fever. We adopt this assumption since the momentum of the expired puff, coughing or sneezing, is a more dominant mechanism than the buoyancy-driven thermal plume transporting the saliva droplets in the streamwise direction of the room [39,40]. Section 3 presents the results and discussion. The first part of section 3 discusses the results of the quiescent indoor environment. On the other hand, the second part discusses the implication of the dispersion of infectious droplets in a classroom with air conditioning during a lecture with several students and a teacher. For the classroom scenario, we consider the thermal plume effect developed by the heat generation of the students sitting and the teacher standing. Finally, section 4 provides concluding remarks and future work.
2. Methods
In this study, two computational domains are set up: the Eulerian CFD computational domain and the discrete particle-phase modeling domain using the Lagrangian description. Modeling of respiratory droplets requires heat, mass, and momentum balance between the discrete and continuous phases. A two-way coupling scheme is used to simultaneously solve the governing discrete and continuous phase equations until the solutions in both phases have converged.
2.1. Geometry and computational domain
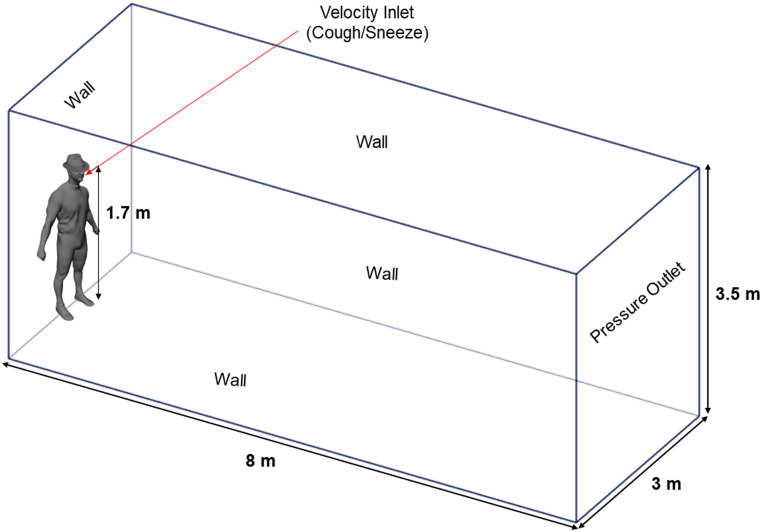
The computational domain consists of a closed room environment with an infected person at one end of the room. The room geometry is a rectangular domain of 3 m×8 m × 3.5 m (width x length x height), with a small cylinder of 21 mm diameter representing an average human mouth located at 1.70 m from the floor [23]. We use the human model shown in the computational domain of Fig. 1 for illustrating purposes, which means that it was not included in the numerical simulations of the quiescent room. We discretize and refine the computational domain with an unstructured tetrahedral mesh using ANSYS Fluent R1 2020 [41], as is shown in Fig. 2 . After performing a grid independence study detailed in AppendixA, we chose a mesh of 384,419 elements to perform the simulations.
Fig. 1.
3D Model Geometry and computational domain.
Fig. 2.
Quiescent room mesh.
2.2. Airflow turbulence modeling
For turbulent airflow modeling of the cough/sneeze puff in indoor environments, the URANS with the Renormalization Group (RNG) k-ϵ turbulence model was implemented in the simulations for its accuracy, computing efficiency, and robustness [42]. The incompressible RANS conservation equations for mass and momentum are given in the Cartesian tensor form as:
| (1) |
| (2) |
and the Reynolds stresses are modeled to close the equations with the Boussinesq hypothesis [43]:
| (3) |
the transport equations for the two-equation RNG k-ϵ turbulence model are given as:
| (4) |
and,
| (5) |
where α k and α ϵ are the inverse effective Prandtl numbers for k and ϵ, respectively [41]. G b is the generation of turbulence kinetic energy due to buoyancy, and G k represents the generation of turbulence kinetic energy due to the mean velocity gradient. Constants C 1 ϵ and C 2 ϵ are derived analytically by the RNG theory [44], which have values of 1.42 and 1.68, respectively. The turbulent viscosity μ t is given by:
| (6) |
with a constant value C μ = 0.0845, derived using RNG theory. The R ϵ term in the RNG k-ϵ model is the main difference from the standard k-ϵ model. This term significantly improves the accuracy for rapidly strained flows [41,45]. The R ϵ term is given by:
| (7) |
where,
| (8) |
the room is modeled with a background temperature of 21 °C, 50% relative humidity (RH), and a constant value of 0 Pa was imposed on the pressure outlet boundary condition. All walls were treated as adiabatic with the non-slip wall condition. The velocity-pressure coupling parameter was handled with the SIMPLE method [46]. The PRESTO! (PREssure STaggering Option) schemes were used for the pressure discretization [41,47], and for the space discretization a second order upwind scheme was used for the convective terms in the governing equation.
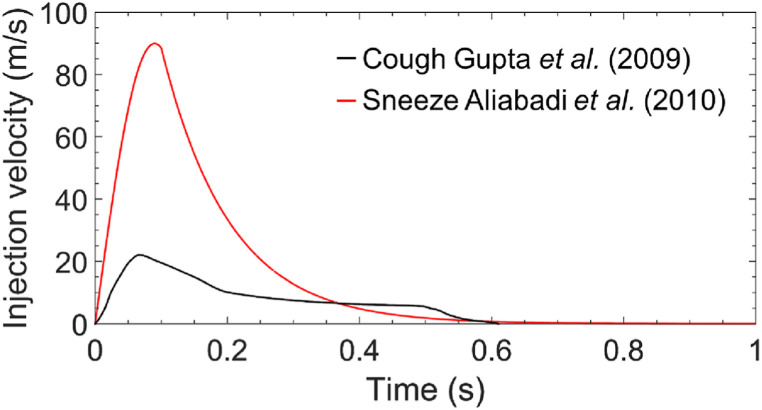
In this study, we used two realistic human cough and sneeze velocity profiles, as shown in Fig. 3 . These velocity profiles based on previous works [20,23] were used as the boundary condition for the saliva droplets ejected from the inlet in the streamwise direction x. The coughing puff lasts 0.61 s with a cough peak velocity around 22.06 m/s occurring at 0.066 s after the onset of the coughing, and the sneezing puff lasts 0.61 s with a sneeze peak velocity around 89.90 m/s occurring at 0.1 s after the onset of sneezing. The total time of analysis is 5 min of physical time for both cases. A non-uniform time step for both discrete and continuous phases of 0.001 s up to 1 s, 0.01 s up to 60 s, and 0.1 s up to 5 min were used. We chose these time step sizes at different instants of the simulations with an adaptive time step strategy based on the stability requirements of time-integration schemes using the Courant–Friedrichs–Lewy (CFL) condition [41,48]. We adjusted the time step size by increasing or decreasing it in order to guarantee that the Courant number remains equal or below 1 [49].
Fig. 3.
Bulk injection velocity profile as function of time for coughing and sneezing.
2.3. Discrete phase modeling (DPM)
The transport of respiratory droplets can be estimated by the governing equation of the discrete phase in the Cartesian coordinates. This equation is an integration of the force balance on the particle in the Lagrangian reference frame and can be written as:
| (9) |
with,
| (10) |
where, μ is the molecular viscosity, ρ is the density of the fluid, ρ p is the density of the particle, D p the diameter of the particle, and C D is the drag coefficient of the particle. Further information about the calculation of C D can be found in Ref. [41]. The first and second terms on the right-hand side of the equation correspond to the drag and buoyancy/gravity forces.
To study the evaporation process of droplets, FLUENT uses different correlations called laws, which vary according to the nature of the particle and physical models based on the energy balance of the particle [41]. For droplet mass and temperature change, heat and mass transfer mechanisms are convection and evaporation, and the radiation is neglected. Therefore, the energy balance equation for the droplet is defined as:
| (11) |
where, m p is the droplet mass, C p is the droplet heat capacity, T p is the droplet temperature, h is the convective heat transfer coefficient, T ∞ is the temperature of continuous phase, dm p/dt is the rate of evaporation, A p is the droplet surface, and h f g is the latent heat.
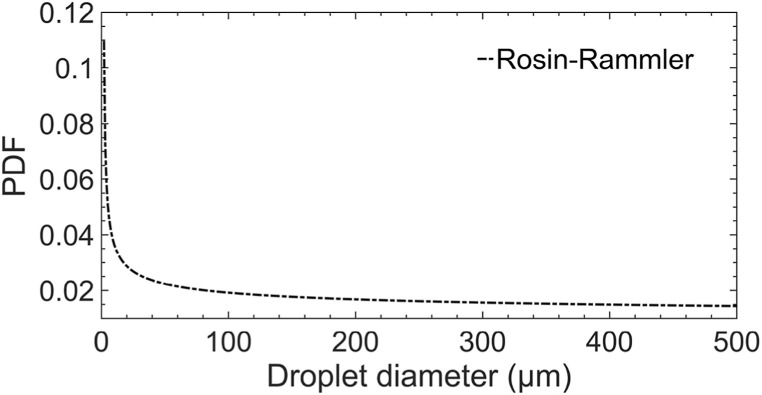
For the discrete phase, the Lagrangian method was used to track saliva droplets with hybrid implicit and trapezoidal schemes. To emulate a real human cough and sneeze, saliva droplets are ejected from the mouth with a size distribution ranges from 1 to 500 μm as is shown in Fig. 4 . This droplet size spectrum was fitted with a Rosin-Rammler distribution according to the experimental data found in Ref. [11]. The fitting parameters are given by the following equation:
| (12) |
where, n is the spread parameter,d is the diameter of the saliva droplet, and is the size constant.
Fig. 4.
Initial droplet distribution.
A total number of 5000 droplets were injected from the inlet for the coughing and sneezing events, respectively. The evaporation of the droplets was also considered by assuming that 94% of injected droplet mass fraction represents evaporating water and the remaining 6% non-volatile matter represents the electrolytes, mucus, and enzymes of the saliva [20]. The saliva droplets temperature was assumed as 35° C, and the turbulent flow effects in the droplets were considered in this study using a Discrete Random Walk (DRW) approach [41,50,51].
2.4. Model validation
To validate the airflow or continuous phase modeling, we compare the maximum streamwise penetration distance (X p), which is the variation of the longest flow distance along the streamwise direction, as a function of time for the cough and sneeze flow obtained in the unsteady RANS (URANS) simulations with experiments developed by Wei and Li [30] and Large Eddy Simulations (LES) performed by Bi et al. [26,27]. Wei and Li [30] estimated the maximum streamwise penetration distance of a real cough in two stages. A starting-jet stage and an interrupted-jet stage. The starting-jet stage is when the cough starts and the fluid is released with an inlet time-dependent velocity profile U(t), while the interrupted-jet stage is when the fluid supply is finished. In the experiment, the characteristic velocity of the real-human cough flow (U c) is defined as:
| (13) |
where t i is the time that a cough flow last. The characteristic Reynolds number is given by:
| (14) |
where ν is the kinematic viscosity of the fluid, and D is the diameter of the nozzle used for the experiments. In this comparison, we select two experimental cases, described as case 9 and case 10 in Ref. [30]. The Reynolds number used in the experiments [30], the LES modeling [26], and the cough and sneeze URANS modeling performed in this study are summarized in Table 1 .
Table 1.
Reynolds number for the experiments, LES and URANS modelling.
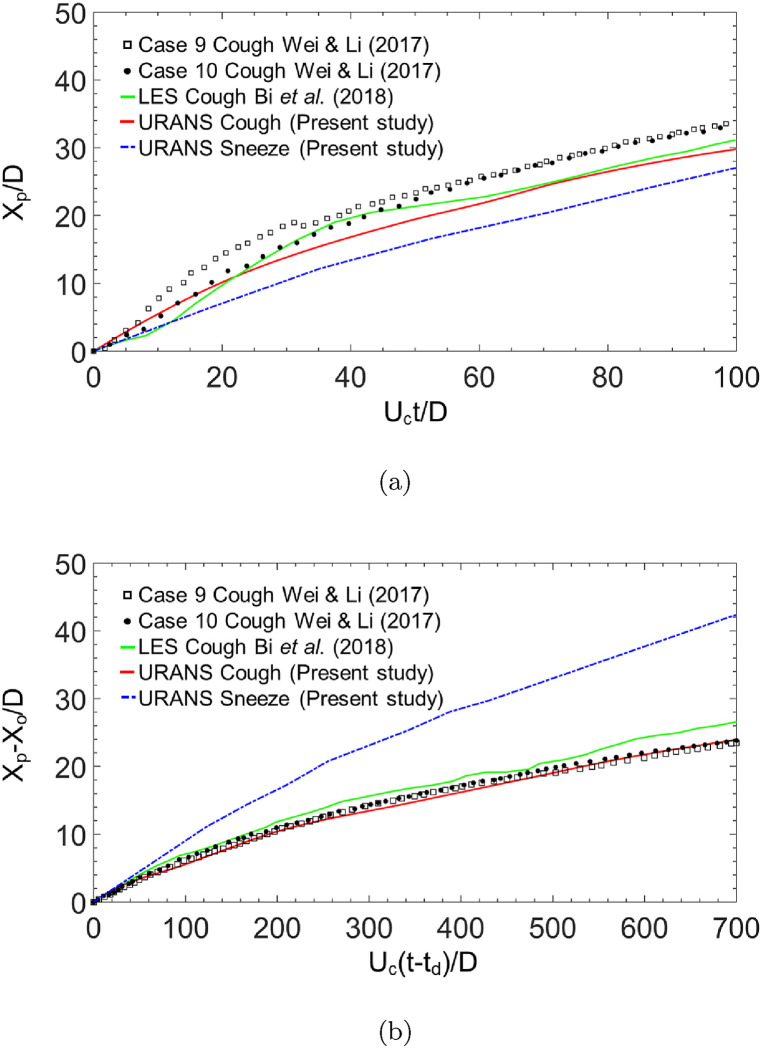
Fig. 5(a) shows the comparison of streamwise penetration distance of the cough and sneeze as a function of time in a dimensionless form in the starting jet stage between the present URANS, two sets of experimental data [30], and LES [26] results. Compared with the experimental values, the maximum mean relative error predicted from URANS and LES are 19.61% and 15.62%, respectively. On the other hand, Fig. 5(b) illustrates the comparison of streamwise penetration distance of the cough and sneeze against time in a dimensionless form in the interrupted jet stage. In Fig. 5(b) two constants, the virtual origin in the interrupted jet stage (Xo) and (td) the extrapolated temporal origin in the interrupted jet stage, are introduced to maintain the comparison initializing from (0, 0). Compared with the experimental values, the maximum mean relative error predicted from URANS and LES are 8.31% and 9.92%, respectively. For both stages, the URANS cough results are in good agreement with the experiments, and no significant difference was found in accuracy between the URANS and the LES simulation performed by Bi et al. [26, 27] predicting the streamwise penetration of a coughing jet flow in a quiescent indoor environment. For the URANS sneeze, the results show a higher streamwise penetration difference in comparison with cough experiments and numerical results. This higher streamwise penetration reached in the sneeze results is expected because in sneezing events there is a further increase in the Reynolds number in comparison with breathing, speaking or coughing [30].
Fig. 5.
Comparison of the maximum streamwise penetration distance as a function of time at (a) starting-jet stage (b) interrupted-jet stage.
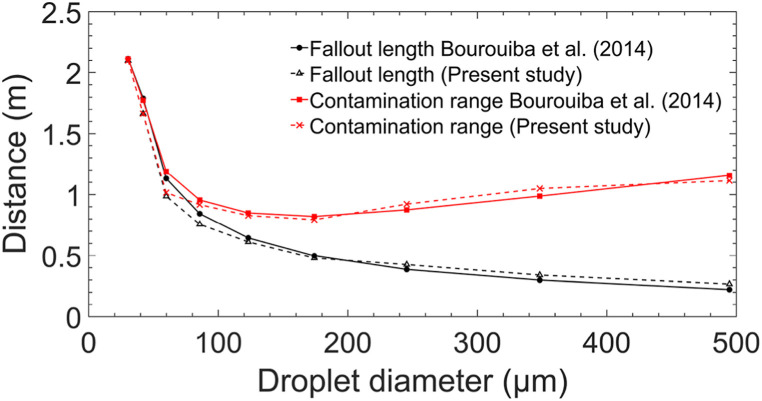
To validate the discrete phase, in Fig. 6 , we compare the numerical results of the fallout length and contamination range of the saliva droplets exhaled when a person infected coughs with the predictions obtained analytically by Ref. [4]. The fallout length is the streamwise distance from which the droplets start to separate from the turbulent cough puff. The contamination range is the maximum streamwise distance of deposition of the droplets. Fig. 6 shows that droplets with a diameter ≤ 50 μm separate from the cloud and reach their deposition at larger distances than droplets ranging from 60 μm to 500 μm. We can observe this trend in both the theoretical prediction proposed in Ref. [4] and the numerical simulations results of the present study. Compared with the analytical values, the mean relative error predicted from URANS for the contamination range and the fallout length are 5.22% and 9.34%, respectively. This suggest that for the prediction of the fate of the droplets released in a cough event, our results are in good agreement with analytical studies.
Fig. 6.
Comparison of the fallout length and contamination range for different droplet sizes.
3. Results and discussion
3.1. Airflow field visualization in a quiescent environment
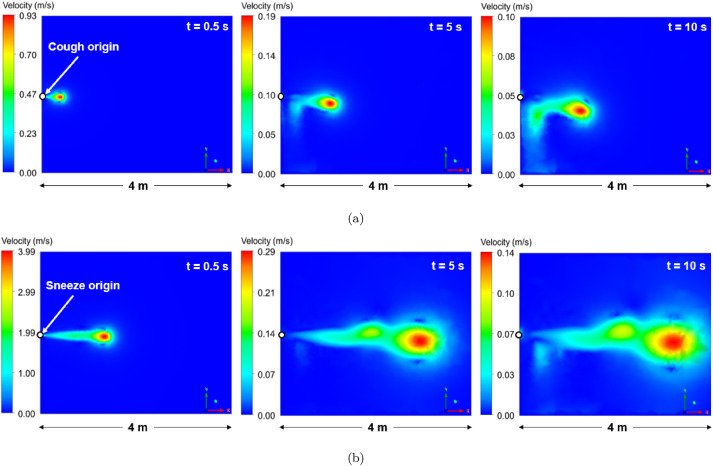
Fig. 7 shows instantaneous velocity contours of the continuous phase in the X − Y plane at three different times (0.5 s, 5 s, 10 s) when an infected person of 1.70 m in height coughs or sneezes. The cough and sneeze exhaled from the mouth generates a puff, set up with the time-dependent velocity profiles described in section 2.1 using a UDF (User-Defined Function) in ANSYS Fluent R1 2020. The cough and sneeze disperses into the quiescent room initially with an axisymmetric velocity distribution, which is larger in the region close to the centerline (Potential Core) than those far away from the centerline (Shear Layer) [52]. From Fig. 7, it is evident that 10 s after leaving the mouth, this turbulent puff penetrates the domain and modifies the quiescent ambient over considerably longer distances than the recommended social distancing of 1.8288 m to prevent COVID 19 transmission. Even though the cough puff reduces its momentum after leaving the mouth, a lower velocity magnitude of this puff can carry both small saliva droplets (aerosols) and the saliva droplets that have evaporated into a nuclei diameter (D p, c) ≤ 12 μm [22,25].
Fig. 7.
Instantaneous velocity contours at 0.5 s, 5 s, and 10 s after a person (a) coughs and (b) sneezes.
Although the URANS model failed to predict the different scales of the separated flow as is shown in other studies [26,28,53], the airflow patterns developed by the coughing and sneezing puffs over time approximate to the images captured in a high-speed camera in Refs. [16,17]. Moreover, owing to the lower computational cost of the URANS model, it was possible to run the simulations up to 5 min after the puff left the mouth, evidencing that this puff can travel in the streamwise direction up to 4 m when an infected person coughs and up to 8 m when sneezes. These findings are in good qualitative agreement to distances reached in other analytical and experimental investigations [4,14,16,30].
3.2. Effect of the puff velocity on the droplet dynamics in a quiescent environment
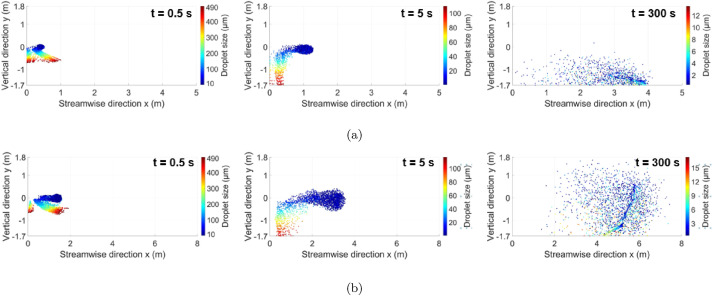
We analyze the trajectory of the droplets exhaled by coughing and sneezing using instantaneous contours of droplet diameters. Fig. 8 shows the evolution of the droplets in three different instants; Fig. 8(a) corresponds to coughing and Fig. 8(b) for sneezing. These contours show the dispersion of a total of 5000 droplets injected from the origin (y = 0 and x = 0) and penetration in the vertical and horizontal directions. The 5000 droplets were injected into the room from the origin using the time-dependent cough and sneeze velocity profiles described in section 2.2. For coughing and sneezing, we assumed a constant relative humidity of 50% and a total temperature of the room of 21° C.
Fig. 8.
Instantaneous droplet sizes contours at at 0.5 s, 5 s, and 300 s after a person (a) coughs and (b) sneezes.
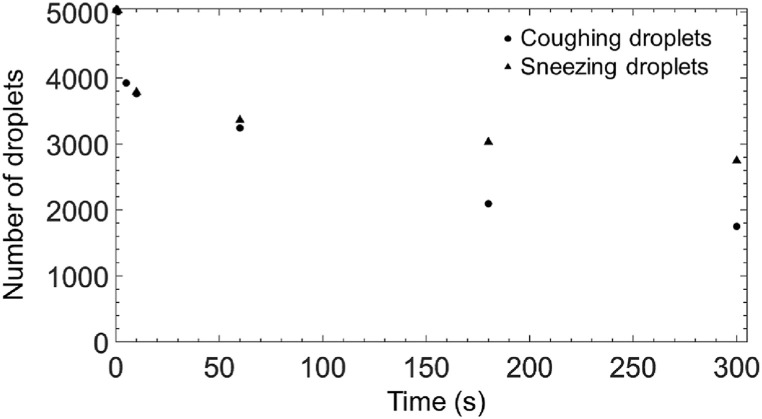
Overall, for both coughing and sneezing cases, the transport of smaller droplets ( ≤ 12 μm) is highly dominated by the airflow of the turbulent puff. Therefore, these droplets remain in the air longer than larger droplets ( ≥ 50 μm), which reach the ground in less than 10 s after the exhale because of gravitational force. Regarding the effect of the puff velocity, when the velocity is initially high, as in the case of sneezing, the turbulent puff penetrates greater streamwise distances within the domain. This allows smaller droplets that are more prone to the effects of the drag force to remain and travel in the air in regions close to the respiratory system of a healthy human. In fact, if both coughing and sneezing contours are observed at 300 s, it can be noted that droplets smaller droplets ( ≤ 12 μm) remain in the air for both cases. However, in the case of sneezing, they reach longer in both vertical and streamwise direction. Fig. 9 shows the lifetime of the 5000 droplets released initially from the mouth for coughing and sneezing cases. Before 60 s, the number of droplets in the air is identical for both coughing and sneezing cases. However, after 60 s, the number of droplets decreases at a lower rate for sneezing than in the case of coughing, which suggests that a high-velocity respiratory event could increase the risk of infection of a healthy person also because a more significant number of droplets will remain in the air.
Fig. 9.
Sneezing and coughing droplets lifetime.
3.3. Effect of the relative humidity in a quiescent environment
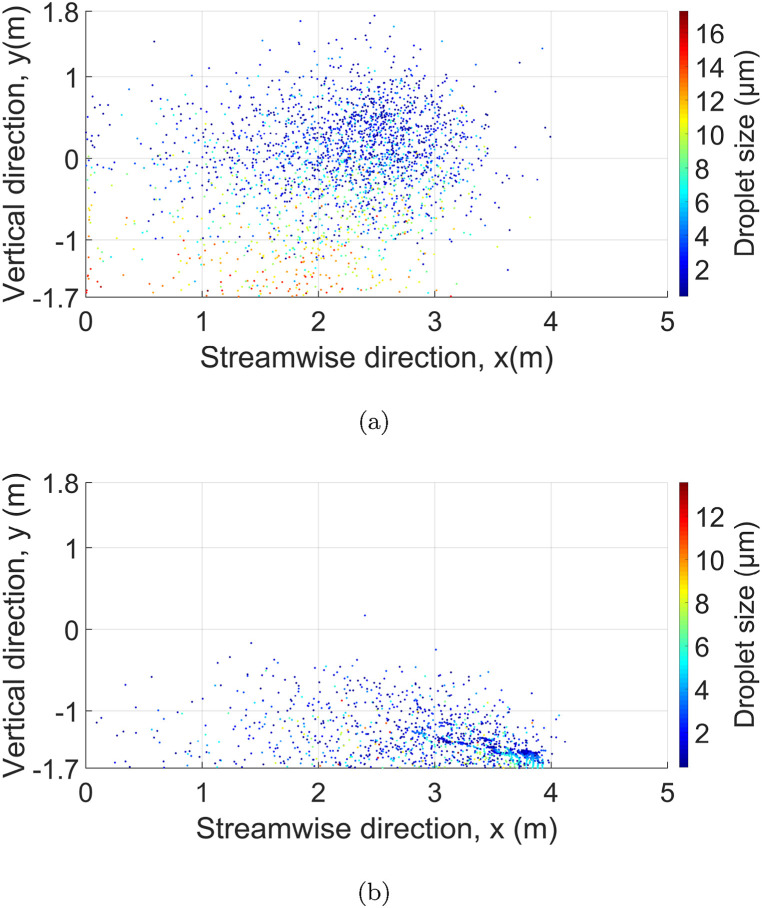
Relative humidity (RH) in indoor environments play an important role in the airborne transmission of infectious diseases by respiratory droplets [25,54,55]. RH inside a room can vary according to the season of the site or Heating, ventilation, and air conditioning (HVAC) working conditions. Fig. 10 shows the distribution of droplets 5 min after a person cough under two different RH conditions, 0%, and 50%, inside the room at a constant temperature of 21° C. Fig. 10(a) shows the distribution of coughing droplets at 0% RH. It is evident that after 5 min, droplets with a diameter size of ≤ 17 μm remain in air with high dispersion in all locations of the room, increasing the probability of the droplets being inhaled by a healthy person. Even though viral load in small droplets is lower than that of large droplets [56], higher concentrations of the load traveling for more extended periods of time in closed environments could increase infection probability [57]. One of the reasons why these smaller droplets remain in air for more extended periods and in higher concentrations than the larger ones is due to the fast evaporation process of the droplets and aerosols to the droplet nuclei [54]. Due to this, the droplets do not sink immediately to the ground. Instead, the droplets will travel longer distances inside and close to the turbulent puff produced when the infected person coughs. On the other hand, Fig. 10(b) shows the spreading of droplets when the RH is 50%; In this case, the spreading of droplets in the vertical location of the room is lower than in 0% RH conditions, which means that in humid indoor environments, the risk of inhalation of droplets by the respiratory system of a healthy person is lower than dry indoor environments [[58], [59], [60], [61]]. The low spreading of droplets in the vertical location of the room when the environment is humid (RH = 50%) is because, in moist air conditions, droplet evaporation is slower than in dry conditions, and the dehydration of them more minor, making the droplets settle into the ground faster [54].
Fig. 10.
Instantaneous droplet sizes contours at (a) 50% RH and (b) 0% RH at 5 min after coughing.
Since the vapor pressure, and therefore the relative humidity, is dependent on temperature, different values of temperature will affects the droplet distribution. For instance, previous studies on the effect of temperature on airborne diseases have shown a decrease in viability of the pathogens when temperature increases (summer season), which coincides with an increment in the relative humidity in regions with seasonality [54,62]. On the other hand, previous studies have shown that in winter the low outdoor temperatures indirectly leads to low relative humidity (dry air) indoor environments [54]. Heating facilities in winter dries the cold air coming in from the outside, causing the relative humidity to drop at levels of 10–40%. In this study, we maintain the temperature constant to understand the effect of controlling relative humidity in an indoor environment regardless external temperature conditions. We only considered relative humidity over temperature to have a control over using several variables in the simulation, which could make it costly in terms of computation time. This is a limitation of our study and can be considered as a future work.
3.4. Evolution of initial droplet size distribution in a quiescent environment
Unlike the analysis done in the previous sections, where we visualize the location of thousands of coughing and sneezing droplets over time, now we focus on the lifetime of their initial distribution since the infection and transmission capability of a cough or sneeze puff relies fundamentally upon the droplet size distribution and viral load carried on dry droplet nuclei [63].
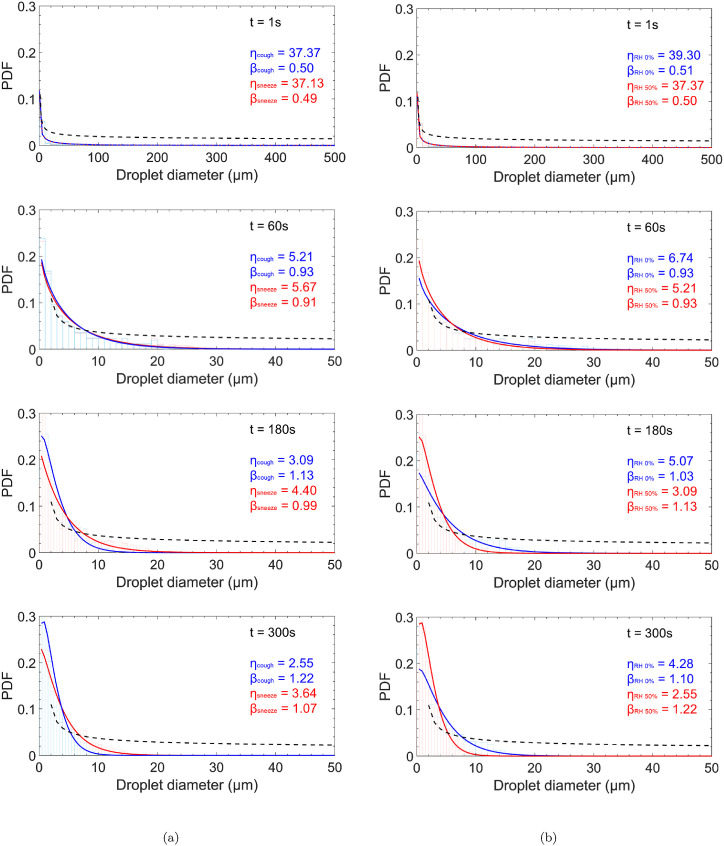
Fig. 11 shows the evolution of the initial droplet size distribution (dashed black lines) escaping from the mouth as probability density functions (PDFs). Fig. 11(a) for coughing and sneezing, and Fig. 11(b) for coughing under two different RH conditions, 0% and 50%, inside the room at a constant temperature of 21° C. We obtain these functions using the discrete phase data from the CFD simulations and fitting this in a two-parameter Weibull distribution, which functions admirably for populations of water and water-like droplets [64]. This version of the Weibull distribution has two parameters, shape (β) and scale (η). The shape (β) or slope parameter describes how the data, in this case, the droplet sizes, are distributed. For example, low shape values result in a right-skewed curve, while higher values give left-skewed curves. On the other hand, The scale parameter (η) represents the variability present in the distribution. Large values of the scale parameter in the Weibull distribution mean that it will be more spread out. On the contrary, it will be more concentrated if the scale parameter has small values [65].
Fig. 11.
(a) Probability density functions for coughing and sneezing at 1 s, 60 s, 180 s and 300 s after an infected person coughs or sneezes. (b) Probability density functions for 50% and 0% RH at 1 s, 60 s, 180 s and 300 s after an infected person coughs.
Overall, based on the PDFs shown in Fig. 11, it is evident that large droplets ( ≥ 50 μm) survive less than 10 s and the smaller ones ( ≤ 17 μm) survive up to 5 min, with most of them traveling inside the turbulent puff. Fig. 11(a) shows the comparison between coughing and sneezing at three different times at 50% RH and a temperature of 21° C. For both cases, 1 s after the droplets are released from the mouth, their distribution in the room has a behavior similar to the initial distribution which is unimodal and positively skewed.
At 1 s, the scale parameter (η) is 37.3, and the shape parameter (β) is 0.50 for the case of coughing, and η = 37.13 and β = 0.49 for sneezing. The difference between parameters for the two cases is negligible (0.45%), which means that during the 1 s, the exhaled airflow velocity does not affect the droplet distribution. One minute after the respiratory event occurred, the range of sizes of the droplets that remains in the room is less than the initial one due to gravity's effects that affect large droplets. The distribution in both cases is unimodal and positively skewed with η = 5.21, β = 0.93 for coughing, and η = 5.67, β = 0.91 for sneezing. Finally, 300 s later, the distribution remains unimodal and positively skewed for both cases. However, the parameters behave differently, for coughing η = 2.55, β = 1.28 and η = 3.64, β = 1.07 for sneezing. This difference is more evident in Fig. 11(a), where the population of droplets ranging 0.39–4 μm is higher for coughing than sneezing. Conversely, from 4 μm to 15 μm, the population of droplets is higher for sneezing than coughing.
Fig. 11(b) shows the PDFs for 50% and 0% RH at three different times after an infected person coughs. In general, for both cases, the distribution of droplets at 1 s is similar to the initial. At 1 s, η is 39.3 and β is 0.51 for 0% RH and η = 37.3, β = 0.0 for 50%RH. After 1 min, the distribution in both cases is unimodal and positively skewed with η = 6.74, β = 0.93 for 0% RH, and η = 5.21, β = 0.93 for 50% RH. At 300 s, the distribution remains unimodal and positively skewed for both cases. With parameters η = 4.28, β = 1.10 for 0% RH and η = 2.55, β = 1.28 for 50% RH. After 300 s, it is evident that at lower RH (dry), the population of droplets ranging from 4 to 15 μm is higher than the environment with higher RH (humid). It coincides with the visualization of droplets in Fig. 10, where a higher quantity of droplets with large size remains in the air at 300s for 0% RH than 50% RH.
3.5. Implications of droplet dispersion in a classroom
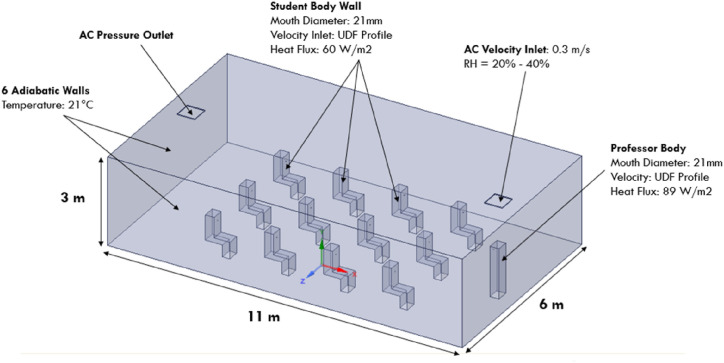
Thanks to the development and release of vaccines against the COVID-19, the reopening phase of academic facilities is a reality. However, there is still a global concern that cases of COVID-19 may increase as a consequence of new variants of the virus and resistance to vaccinating. In order to help authorities to identify the highest risk zones of infection in a classroom, we develop a model that considers the interaction of an infected source that breathes, sneezes, or coughs in a group of twelve students and a teacher, as is shown in Fig. 12 . In this model, we use the insights from the framework developed in the quiescent room model to discretize the computational domain and set up the simulations. We discretize the classroom with 1254063 tetrahedron elements after developing a mesh independence study similar to the implemented for the quiescent indoor environment. As is shown in Fig. 12, the droplet dispersion of breathing, coughing, and sneezing in the classroom was investigated assuming a constant velocity of 0.3 m/s in the inlet of the air conditioning, adiabatic walls with a constant temperature of 21°C, and the heat flux produced from the body of the sitting students and the standing professor 60 W/m2 and 89 W/m2 respectively. Cough and sneeze saliva droplets are ejected from the mouth of an infected student seated in the third row with a size distribution ranges from 1 to 500 μm and the unsteady velocity profiles described in section 2. On the other hand, we impose a sinusoidal function with a peak exhalation velocity of 16.43 L/min and a frequency of 0.274 Hz [[66], [67], [68], [69]], to eject 1000 breathing saliva droplets every 10 s from the mouth of an infected student.
Fig. 12.
Classroom model and boundary conditions.
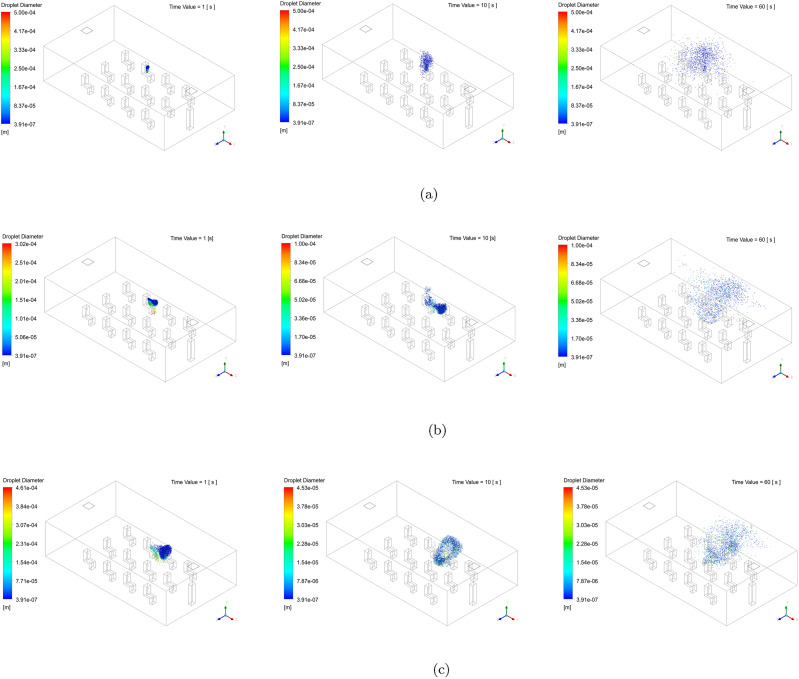
Fig. 13 shows the droplet dynamics of an infected student in the third row that breathes, coughs and sneezes, at 1s, 10s, and 60 s. In Fig. 13(a), when the infected student breaths for 60 s, it is evident that saliva droplets travel above the student's head. It is expected since the thermal plume of the body will transport the droplets that lie close to the body by natural convection in the vertical direction. Therefore, the impact of breathing droplets will not affect a student located in the front, back, and lateral seats of the infected student after breathing continuously for 10 s. However, after 60 s of continuous breathing a lower population of small droplets can reach the seat of a student seated in the back. Fig. 13(b) illustrates the location of thousands of droplets released when an infected student in the third row coughs. It is evident from Fig. 13(b) that a small population of droplets will travel above the head during the first second, while a significant population of those will travel in the streamwise direction, directly impacting a student in the front seat. As is expected, the high velocity of the coughing event shows that the momentum-driven flow is more dominant than the buoyancy-driven flow in the final fate of the droplets. Fig. 13(c) depicts the transport and fate of sneezing droplets. Likewise the coughing case, during sneezing, the droplets impact a student located in the front and lateral seat of the infected source in a short period of time. However, sneezing droplets do not have a high impact on the risk of infection of a healthy student in the back seat. This could be attributed to the fact that an insignificant number of droplets remain close to the body of the infected student, which could travel in the back direction for the combined effect of the thermal plume and the air conditioning flow.
Fig. 13.
Instantaneous droplet sizes contours at at 1 s, 10 s, and 60 s after an infected student seated in the third row of a classroom (a) breaths (b) coughs and (c) sneezes.
The aforementioned results suggest that the transport and fate of droplets produced by an infected student in a classroom with air conditioning vary according to the nature of the respiratory event. A coughing event of an infected student in the classroom affects students located in lateral, back, and front seats. A breathing event affects students in the back seats, and a sneezing event impacts healthy students in the front and lateral seats. In the case of sneezing, the impact on the infection of a person behind the infected person is not evident in 60 s. Therefore, it is crucial to reproduce these simulations in more extended periods since the flow produced by the air conditioning could influence the stochastic transport of droplets throughout the classroom, especially the smaller droplets that remain floating in the air [[70], [71], [72], [73]].
Several experimental and numerical studies have demonstrated that using different air changes per hour rates (ACH) in indoor environments affects the risk of airborne transmission of SARS-CoV-2 and other respiratory infectious diseases [12,74,75]. Increasing ACH and installing multiple HVAC units with adequate air filtration reduce the aerosol transmission in the far-field (distances larger than the 6 foot-rule) because it enhances the rate at which the circulating contaminated air gets filtered. However, for close contact and the current physical distancing, this increase in the air exchange rates would not be enough, especially if the respiratory event has higher velocity values [74]. On the other hand, more HVAC units could accelerate the temperature and RH control inside a building. Considering that temperature and RH affect pathogen's viability, having more HVAC units would be an essential parameter in designing and improving the air quality of indoor environments. Nevertheless, installing multiple HVAC units and increasing air exchange rates requires more energy and more investment in new equipment.
The analysis of multiple HVAC units and air exchange rates is a limitation of this study. Instead, we used one HVAC unit in the ceiling operating with a typical air velocity of a classroom [76] to identify the highest risk zones of infection once a student or a professor cough, sneeze, or breathe. Specifically, if we consider that installing multiple HVAC units and increasing air exchange rates generate a financial constraint for most schools worldwide.
4. Conclusions
The results of the simulations suggest that droplets of an infected person with COVID-19 can spread more than the social distancing recommendation (1.8288 m), in closed and calm environments. Small droplets ( ≤ 12 μm) can travel up to 4 m in the streamwise direction 5 min after an infected person cough and two-fold that distance in the case of sneezing. The spread of droplets in the vertical direction shows that a person's height matters regarding his/her infection risk. Children and adults of short heights are more exposed to larger droplets, which contain a high viral load.
The performed CFD simulations with the URANS model are in very good agreement with previous experiments and theoretical models. No significant difference was found in accuracy between the URANS and the LES model predicting the streamwise penetration of a coughing jet flow in an indoor environment. Even though URANS model cannot capture the different scales of the turbulent flow like other advanced numerical models [[26], [27], [28],53], the low computational cost of the URANS model made this captivating for designing technologies to prevent the spread of airborne diseases and preserve the world economy. The practical application of the URANS model was demonstrated in the design of a disinfection robot amid the COVID-19 and future pandemics [35]. The use of results from URANS simulations helped optimize the robot's disinfection efficiency in infection risk zones of a classroom where commercial air cleaning technologies face difficulties reaching.
When an infected person sneezes in a closed environment, the risk of infection in healthy people increases since the lifetime of droplets in the air is higher than in the case of coughing. Moreover, in an indoor environment at low relative humidity, droplets evaporate to droplet nuclei faster than in high humidity conditions. Therefore, instead of instantaneously reaching the ground, smaller droplets remain airborne, traveling inside the puff and increasing the virus' residence time in the air at locations where it is easier to be inhaled by a healthy individual's respiratory system.
We characterized the population of droplets residing in a calm indoor environment with probability density functions fitted with Weibull distribution. These distributions show many saliva droplets with an average diameter ranging 2–5 μm, residing longer time in the air compared to the case of large droplets, since the droplet size decreases to ∼50% of their original diameter in a short time [77].
The numerical approach used in this study offers a significant quantity of data regarding the complex dynamics of the droplets exhaled in different respiratory activities. The integration with a statistical analysis of the population of droplets reveals a more profound outlook of the lifetime of the droplets to optimize the efficiency of disinfection and detection technologies [35,78,79]. Further work will use the output of these high-fidelity simulations for developing quasi-real-time CFD simulations and machine learning surrogate models of the coughing and sneezing droplets under different local ambient conditions precisely, at more prolonged periods.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The authors would like to acknowledge that the project was funded by Intel Corporation within the Pandemic Response Technology Initiative (PRTI) Intel Corporation Grant No. 4720008238, the Kenninger family endowment, and the Fulbright-Icetex scholarship. The views within this study are of the authors and do not represent the funding agency.
A. Mesh independence test
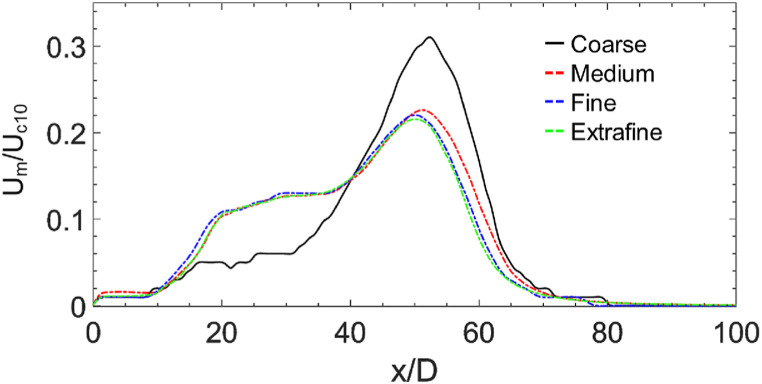
To guarantee that numerical results were independent of the mesh size, we use three different mesh sizes of 182,675 elements, 384,419 elements, 989,236 elements, and 1,898,322 named as coarse, medium, fine, and extrafine, respectively. The parameter selected to evaluate the mesh independent test is the dimensionless centerline velocity decay of the turbulent puff across the streamwise direction at t = 5s. We normalize the centerline velocity (U m), taking as a reference the 10% of the characteristic velocity (U c) of the real-cough velocity profile. From Figure14, it can be observed that medium, fine, and extrafine meshes have very similar centerline velocity decay profiles in contrast to the coarse mesh, which differs in its behavior in several zones of the centerline. Moreover, comparing the medium mesh results against the fine and extrafine mesh, we found a maximum difference of the centerline velocity decay of 3.5% and 4.2%, respectively. Finally, to perform the simulations of the other cases we chose the medium mesh since the results show a good balance between numerical accuracy and computational time.
Fig. 14.
Effect of mesh size on dimensionless cough puff centerline velocity.
References
- 1.Morawska L., Milton D.K. It is time to address airborne transmission of coronavirus disease 2019 (covid-19) Clin. Infect. Dis. 2020;71(9):2311–2313. doi: 10.1093/cid/ciaa939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lewis D. Is the coronavirus airborne? experts can't agree. Nature. 2020;580(7802):175. doi: 10.1038/d41586-020-00974-w. [DOI] [PubMed] [Google Scholar]
- 3.Morawska L., Cao J. Airborne transmission of sars-cov-2: the world should face the reality. Environ. Int. 2020;139 doi: 10.1016/j.envint.2020.105730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bourouiba L., Dehandschoewercker E., Bush J.W. Violent expiratory events: on coughing and sneezing. J. Fluid Mech. 2014;745:537–563. [Google Scholar]
- 5.Morawska L., Johnson G., Ristovski Z., Hargreaves M., Mengersen K., Corbett S., Chao C.Y.H., Li Y., Katoshevski D. Size distribution and sites of origin of droplets expelled from the human respiratory tract during expiratory activities. J. Aerosol Sci. 2009;40(3):256–269. doi: 10.1016/j.jaerosci.2008.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Seminara G., Carli B., Forni G., Fuzzi S., Mazzino A., Rinaldo A. Rendiconti Lincei. Scienze fisiche e naturali; 2020. Biological Fluid Dynamics of Airborne Covid-19 Infection; pp. 1–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wei J., Li Y. Airborne spread of infectious agents in the indoor environment. Am. J. Infect. Control. 2016;44(9):S102–S108. doi: 10.1016/j.ajic.2016.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cole E.C., Cook C.E. Characterization of infectious aerosols in health care facilities: an aid to effective engineering controls and preventive strategies. Am. J. Infect. Control. 1998;26(4):453–464. doi: 10.1016/S0196-6553(98)70046-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sterling T.R., Haas D.W. Transmission of mycobacterium tuberculosis from health care workers. N. Engl. J. Med. 2006;355(2):118–121. doi: 10.1056/NEJMp068015. [DOI] [PubMed] [Google Scholar]
- 10.Tang J., Li Y., Eames I., Chan P., Ridgway G. Factors involved in the aerosol transmission of infection and control of ventilation in healthcare premises. J. Hosp. Infect. 2006;64(2):100–114. doi: 10.1016/j.jhin.2006.05.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Duguid J. The size and the duration of air-carriage of respiratory droplets and droplet-nuclei. Epidemiol. Infect. 1946;44(6):471–479. doi: 10.1017/s0022172400019288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bazant M.Z., Bush J.W. A guideline to limit indoor airborne transmission of covid-19. Proc. Natl. Acad. Sci. Unit. States Am. 2021;118(17) doi: 10.1073/pnas.2018995118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.de Oliveira P.M., Mesquita L.C., Gkantonas S., Giusti A., Mastorakos E. Evolution of spray and aerosol from respiratory releases: theoretical estimates for insight on viral transmission. Proc. Royal Soc. A. 2021;477(2245) doi: 10.1098/rspa.2020.0584. 20200584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wei J., Li Y. Enhanced spread of expiratory droplets by turbulence in a cough jet. Build. Environ. 2015;93:86–96. [Google Scholar]
- 15.Chaudhuri S., Basu S., Saha A. Analyzing the dominant sars-cov-2 transmission routes toward an ab initio disease spread model. Phys. Fluids. 2020;32(12):123306. doi: 10.1063/5.0034032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bourouiba L. Turbulent gas clouds and respiratory pathogen emissions: potential implications for reducing transmission of covid-19. JAMA. 2020;323(18):1837–1838. doi: 10.1001/jama.2020.4756. [DOI] [PubMed] [Google Scholar]
- 17.Bourouiba L. A sneeze. N. Engl. J. Med. 2016;375(8):e15. doi: 10.1056/NEJMicm1501197. [DOI] [PubMed] [Google Scholar]
- 18.Johnson G.R., Morawska L. The mechanism of breath aerosol formation. J. Aerosol Med. Pulm. Drug Deliv. 2009;22(3):229–237. doi: 10.1089/jamp.2008.0720. [DOI] [PubMed] [Google Scholar]
- 19.Dbouk T., Drikakis D. On coughing and airborne droplet transmission to humans. Phys. Fluids. 2020;32(5) doi: 10.1063/5.0011960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Aliabadi A.A., Rogak S.N., Green S.I., Bartlett K.H. Vol. 44441. 2010. Cfd simulation of human coughs and sneezes: a study in droplet dispersion, heat, and mass transfer; pp. 1051–1060. (ASME International Mechanical Engineering Congress and Exposition). [Google Scholar]
- 21.Zohdi T. Modeling and simulation of the infection zone from a cough. Comput. Mech. 2020;66(4):1025–1034. doi: 10.1007/s00466-020-01875-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Li X., Shang Y., Yan Y., Yang L., Tu J. Modelling of evaporation of cough droplets in inhomogeneous humidity fields using the multi-component eulerian-Lagrangian approach. Build. Environ. 2018;128:68–76. doi: 10.1016/j.buildenv.2017.11.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gupta J.K., Lin C.-H., Chen Q. Flow dynamics and characterization of a cough. Indoor Air. 2009;19(6):517–525. doi: 10.1111/j.1600-0668.2009.00619.x. [DOI] [PubMed] [Google Scholar]
- 24.Bale R., Li C.-G., Yamakawa M., Iida A., Kurose R., Tsubokura M. Proceedings of the Platform for Advanced Scientific Computing Conference. 2021. Simulation of droplet dispersion in covid-19 type pandemics on fugaku; pp. 1–11. [Google Scholar]
- 25.Feng Y., Marchal T., Sperry T., Yi H. Influence of wind and relative humidity on the social distancing effectiveness to prevent covid-19 airborne transmission: a numerical study. J. Aerosol Sci. 2020;147:105585. doi: 10.1016/j.jaerosci.2020.105585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Bi R. Vol. 5314. University of Western Ontario; Electronic Thesis and Dissertation Repository: 2018. A Numerical Investigation of Human Cough Jet Development and Droplet Dispersion.https://ir.lib.uwo.ca/etd/5314 [Google Scholar]
- 27.Bi R., Ali S., Savory E., Zhang C. A numerical modelling investigation of the development of a human cough jet. Eng. Comput. 2021 [Google Scholar]
- 28.Fabregat A., Gisbert F., Vernet A., Dutta S., Mittal K., Pallarès J. Direct numerical simulation of the turbulent flow generated during a violent expiratory event. Phys. Fluids. 2021;33(3) doi: 10.1063/5.0042086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.VanSciver M., Miller S., Hertzberg J. Particle image velocimetry of human cough. Aerosol. Sci. Technol. 2011;45(3):415–422. [Google Scholar]
- 30.Wei J., Li Y. Human cough as a two-stage jet and its role in particle transport. PLoS One. 2017;12(1) doi: 10.1371/journal.pone.0169235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gimenez J.M., Idelsohn S.R., Oñate E., Löhner R. A multiscale approach for the numerical simulation of turbulent flows with droplets. Arch. Comput. Methods Eng. 2021;28(6):4185–4204. doi: 10.1007/s11831-021-09614-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ng C.S., Chong K.L., Yang R., Li M., Verzicco R., Lohse D. Growth of respiratory droplets in cold and humid air. Physical Review Fluids. 2021;6(5) [Google Scholar]
- 33.Katre P., Banerjee S., Balusamy S., Sahu K.C. Fluid dynamics of respiratory droplets in the context of covid-19: airborne and surfaceborne transmissions. Phys. Fluids. 2021;33(8) doi: 10.1063/5.0063475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Trivedi S., Gkantonas S., Mesquita L.C., Iavarone S., Oliveira P.M.d., Mastorakos E. Estimates of the stochasticity of droplet dispersion by a cough. Phys. Fluids. 2021;33(11) doi: 10.1063/5.0070528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Yang H., Balakuntala M.V., Quiñones J.J., et al. Robotics and Autonomous Systems; 2021. Occupant-centric Robotic Air Filtration and Planning for Classrooms for Safer School Reopening amid Respiratory Pandemics. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Country W. WHO; Geneva, Switzerland: 2020. Technical Guidance-Coronavirus Disease (Covid-19) [Google Scholar]
- 37.Aliabadi A.A., Rogak S.N., Bartlett K.H., Green S.I. Preventing airborne disease transmission: review of methods for ventilation design in health care facilities. Adv. Preventive Med. 2011;2011 doi: 10.4061/2011/124064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Jennison M.W. The dynamics of sneezing–studies by high-speed photography. Sci. Mon. 1941;52(1):24–33. [Google Scholar]
- 39.Fontes D., Reyes J., Ahmed K., Kinzel M. A study of fluid dynamics and human physiology factors driving droplet dispersion from a human sneeze. Phys. Fluids. 2020;32(11) doi: 10.1063/5.0032006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Liu S., Novoselac A. Transport of airborne particles from an unobstructed cough jet. Aerosol. Sci. Technol. 2014;48(11):1183–1194. [Google Scholar]
- 41.Fluent A. Vol. 33. ANSYS; Canonsburg, PA: 2013. (Ansys Fluent Theory Guide 15.0). [Google Scholar]
- 42.Hang J., Li Y., Jin R. The influence of human walking on the flow and airborne transmission in a six-bed isolation room: tracer gas simulation. Build. Environ. 2014;77:119–134. doi: 10.1016/j.buildenv.2014.03.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Versteeg H.K., Malalasekera W. Pearson Education; 2007. An Introduction to Computational Fluid Dynamics: the Finite Volume Method. [Google Scholar]
- 44.Orszag S.A. Renormalisation group modelling and turbulence simulations. Near-Wall Turbulent Flows. 1993 [Google Scholar]
- 45.Escue A., Cui J. Comparison of turbulence models in simulating swirling pipe flows. Appl. Math. Model. 2010;34(10):2840–2849. [Google Scholar]
- 46.Montazeri H., Blocken B., Hensen J.L. Cfd analysis of the impact of physical parameters on evaporative cooling by a mist spray system. Appl. Therm. Eng. 2015;75:608–622. [Google Scholar]
- 47.Patankar S. Taylor & Francis; 2018. Numerical Heat Transfer and Fluid Flow. [Google Scholar]
- 48.Courant R., Friedrichs K., Lewy H. On the partial difference equations of mathematical physics. IBM J. Res. Dev. 1967;11(2):215–234. [Google Scholar]
- 49.Chen C., Liu W., Lin C.-H., Chen Q. Comparing the Markov chain model with the eulerian and Lagrangian models for indoor transient particle transport simulations. Aerosol. Sci. Technol. 2015;49(10):857–871. [Google Scholar]
- 50.Dehbi A. Prediction of extrathoracic aerosol deposition using rans-random walk and les approaches. Aerosol. Sci. Technol. 2011;45(5):555–569. [Google Scholar]
- 51.Mofakham A.A., Ahmadi G. On random walk models for simulation of particle-laden turbulent flows. Int. J. Multiphas. Flow. 2020;122 [Google Scholar]
- 52.Abdel-Rahman A. A review of effects of initial and boundary conditions on turbulent jets. WSEAS Trans. Fluid Mech. 2010;4(5):257–275. [Google Scholar]
- 53.Chong K.L., Ng C.S., Hori N., Yang R., Verzicco R., Lohse D. Extended lifetime of respiratory droplets in a turbulent vapor puff and its implications on airborne disease transmission. Phys. Rev. Lett. 2021;126(3) doi: 10.1103/PhysRevLett.126.034502. [DOI] [PubMed] [Google Scholar]
- 54.Božič A., Kanduč M. Relative humidity in droplet and airborne transmission of disease. J. Biol. Phys. 2021:1–29. doi: 10.1007/s10867-020-09562-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Li H., Leong F.Y., Xu G., Ge Z., Kang C.W., Lim K.H. Dispersion of evaporating cough droplets in tropical outdoor environment. Phys. Fluids. 2020;32(11) doi: 10.1063/5.0026360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Riediker M., Tsai D.-H. Estimation of viral aerosol emissions from simulated individuals with asymptomatic to moderate coronavirus disease 2019. JAMA Netw. Open. 2020;3(7) doi: 10.1001/jamanetworkopen.2020.13807. e2 013 807–e2 013 807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Lippmann M., Yeates D., Albert R. Deposition, retention, and clearance of inhaled particles. Occup. Environ. Med. 1980;37(4):337–362. doi: 10.1136/oem.37.4.337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Tamerius J., Nelson M.I., Zhou S.Z., Viboud C., Miller M.A., Alonso W.J. Global influenza seasonality: reconciling patterns across temperate and tropical regions. Environ. Health Perspect. 2011;119(4):439–445. doi: 10.1289/ehp.1002383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Moriyama M., Hugentobler W.J., Iwasaki A. Seasonality of respiratory viral infections. Annual Rev. Virol. 2020;7:83–101. doi: 10.1146/annurev-virology-012420-022445. [DOI] [PubMed] [Google Scholar]
- 60.Visseaux B., Burdet C., Voiriot G., Lescure F.-X., Chougar T., Brugière O., Crestani B., Casalino E., Charpentier C., Descamps D., et al. Prevalence of respiratory viruses among adults, by season, age, respiratory tract region and type of medical unit in paris, France, from 2011 to 2016. PLoS One. 2017;12(7) doi: 10.1371/journal.pone.0180888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Pica N., Bouvier N.M. Environmental factors affecting the transmission of respiratory viruses. Curr. Opin. virol. 2012;2(1):90–95. doi: 10.1016/j.coviro.2011.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Hurst C.J. 1991. Modeling the Environmental Fate of Microorganisms. Plus 0.5em Minus 0.4emAmerican Society for Microbiology. [Google Scholar]
- 63.Rosti M., Olivieri S., Cavaiola M., Seminara A., Mazzino A. Fluid dynamics of covid-19 airborne infection suggests urgent data for a scientific design of social distancing. Sci. Rep. 2020;10(1):1–9. doi: 10.1038/s41598-020-80078-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Liu Y., Laiguang Y., Weinong Y., Feng L. On the size distribution of cloud droplets. Atmos. Res. 1995;35(2–4):201–216. [Google Scholar]
- 65.Forbes C., Evans M., Hastings N., Peacock B. Statistical Distributions. 4th. John Wiley & Sons; 2011. [Google Scholar]
- 66.Xu C., Nielsen P., Gong G., Liu L., Jensen R. Measuring the exhaled breath of a manikin and human subjects. Indoor Air. 2015;25(2):188–197. doi: 10.1111/ina.12129. [DOI] [PubMed] [Google Scholar]
- 67.Georgescu M.R., Meslem A., Nastase I. Accumulation and spatial distribution of co2 in the astronaut's crew quarters on the international space station. Build. Environ. 2020;185:107278. [Google Scholar]
- 68.Mahjoub Mohammed Merghani K., Sagot B., Gehin E., Da G., Motzkus C. A review on the applied techniques of exhaled airflow and droplets characterization. Indoor Air. 2021;31(1):7–25. doi: 10.1111/ina.12770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Berlanga F., Olmedo I., Ruiz de Adana M. Experimental analysis of the air velocity and contaminant dispersion of human exhalation flows. Indoor Air. 2017;27(4):803–815. doi: 10.1111/ina.12357. [DOI] [PubMed] [Google Scholar]
- 70.Chirico F., Sacco A., Bragazzi N.L., Magnavita N. Can air-conditioning systems contribute to the spread of sars/mers/covid-19 infection? insights from a rapid review of the literature. Int. J. Environ. Res. Publ. Health. 2020;17(17):6052. doi: 10.3390/ijerph17176052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Correia G., Rodrigues L., Da Silva M.G., Gonçalves T. Airborne route and bad use of ventilation systems as non-negligible factors in sars-cov-2 transmission. Med. Hypotheses. 2020;141 doi: 10.1016/j.mehy.2020.109781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Rahmani A.R., Leili M., Azarian G., Poormohammadi A. Sampling and detection of corona viruses in air: a mini review. Sci. Total Environ. 2020;740 doi: 10.1016/j.scitotenv.2020.140207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Mirzaie M., Lakzian E., Khan A., Warkiani M.E., Mahian O., Ahmadi G. Covid-19 spread in a classroom equipped with partition–a cfd approach. J. Hazard Mater. 2021;420:126587. doi: 10.1016/j.jhazmat.2021.126587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Cotman Z.J., Bowden M.J., Richter B.P., Phelps J.H., Dibble C.J. Factors affecting aerosol sars-cov-2 transmission via hvac systems; a modeling study. PLoS Comput. Biol. 2021;17(10) doi: 10.1371/journal.pcbi.1009474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Allen J.G., Ibrahim A.M. Indoor air changes and potential implications for sars-cov-2 transmission. JAMA. 2021;325(20):2112–2113. doi: 10.1001/jama.2021.5053. [DOI] [PubMed] [Google Scholar]
- 76.Zhao W., Lestinen S., Mustakallio P., Kilpeläinen S., Jokisalo J., Kosonen R. Experimental study on thermal environment in a simulated classroom with different air distribution methods. J. Build. Eng. 2021;43 [Google Scholar]
- 77.Xie X., Li Y., Chwang A., Ho P., Seto W. How far droplets can move in indoor environments–revisiting the wells evaporation–falling curve. Indoor Air. 2007;17(3):211–225. doi: 10.1111/j.1600-0668.2007.00469.x. [DOI] [PubMed] [Google Scholar]
- 78.Yang H., Balakuntala M.V., Moser A.E., Quiñones J.J., Doosttalab A., Esquivel-Puentes A., Purwar T., Castillo L., Mahmoudian N., Voyles R.M. 2021 IEEE International Conference on Robotics and Automation (ICRA) 2021. Enhancing safety of students with mobile air filtration during school reopening from covid-19. 10 757–10 763. [Google Scholar]
- 79.Quinones J., Doosttalab A., Castano V., Castillo L. Bulletin of the American Physical Society; 2020. Numerical Study of the Particles Dispersion Expelled during Breathing, Coughing, and Sneezing in Public Indoor Environments. [Google Scholar]