Motivating Sample Sizes in Adaptive Phase I Trials via Bayesian Posterior Credible Intervals

Summary.

In contrast with typical Phase III clinical trials, there is little existing methodology for determining the appropriate numbers of patients to enroll in adaptive Phase I trials. And, as stated by Dennis Lindley in a more general context, “[t]he simple practical question of ‘What size of sample should I take’ is often posed to a statistician, and it is a question that is embarrassingly difficult to answer.” Historically, simulation has been the primary option for determining sample sizes for adaptive Phase I trials, and although useful, can be problematic and time-consuming when a sample size is needed relatively quickly. We propose a computationally fast and simple approach that uses Beta distributions to approximate the posterior distributions of DLT rates of each dose and determines an appropriate sample size through posterior coverage rates. We provide sample sizes produced by our methods for a vast number of realistic Phase I trial settings and demonstrate that our sample sizes are generally larger than those produced by a competing approach that is based upon the nonparametric optimal design.

1. Introduction

Phase I oncology trials of chemotherapeutic agents have had a conceptually simple goal: to determine which doses of an agent can be given to patients before an unacceptable fraction, 0 < θ < 1, of patients begins to experience dose-limiting toxicities (DLTs). Statistically speaking, we have an unknown dose-response curve, and we assign doses to patients and use their data to identify the desired quantile θ on the curve while attempting to minimize the number subjects exposed to highly toxic doses (Rosenberger and Haines, 2002).

There are numerous approaches for designing Phase I trials; see Table 1 of Braun (2014) for examples. Our work focuses upon a specific design known as the Continual Reassessment Method (CRM) (O’Quigley et al., 1990), which adopts a parametric model f (d; β), that is monotonic in d to describe how the probability of DLT is related to dose d. The logistic model f (d; β) = exp[3 + exp(β)d]/(1 + exp[3 + exp(β)d]) and the socalled “power” model f (d; β) = d^exp(β) are models commonly used in the CRM. The parameter β is given a prior distribution with mean μ (usually μ = 0) and variance σ² and support on the real line. We sequentially update the posterior distribution of β as each enrolled subject or cohort of subjects is observed for the occurrence of DLT. We use the resulting posterior distribution for the probability of DLT for each dose to determine the dose assignment for the next cohort; this assignment is usually the dose whose posterior probability of DLT is closest to θ. Final mean posterior DLT probabilities for each dose are computed once all patients have been observed; the MTD is often defined as the dose whose posterior mean probability is closest to θ, although the MTD can be defined in other ways (Babb et al., 1998).

A competitor to the CRM is the 3 + 3 design (Storer, 1989), which is an algorithm that determines acceptability of doses from the outcomes seen in three-patient cohorts. One of the appealing features of the 3 + 3 design is its pre-determined maximum sample size of six patients per dose. However, this sample size is simply an artifact of the design and has no statistical motivation. In fact, the sample size used in 3 + 3 designs is often woefully insufficient to provide evidence that the MTD has been correctly identified, motivating the recent practice of enrolling additional patients at the proposed MTD in a so-called “expansion cohort” (Boonstra et al., 2015; Iasonos and O’Quigley, 2016).

Certainly, there are sample size formulae for a myriad of Phase III trial designs; even Phase II trials using a Simon two-stage design (Simon, 1989) are provided with a sample size. However, the crux of these methods lies in traditional hypothesis testing, in which explicit null and alternative hypotheses are stated. In adaptive Phase I trials, although we certainly have a model parameter, our primary goal is not based in inference for that parameter. Instead, the model and parameter are simply used to facilitate a way to compare the probabilities of toxicity of each dose in order to identify the MTD. Historically, simulation has been the only real avenue for determining appropriate sample sizes for Phase I trials (Tighiouart and Rogatko, 2012), although Cheung (2013b) recently developed the first systematic approach to sample size determination specific to the CRM, the details of which will be presented in Section 2.

Our work presents an alternative to the approach of Cheung (2013b), which is based upon an asymptotic frequentist approximation. Instead, our approach is founded in Bayesian sample size estimation, for which numerous prior research exists (Pham-Gia and Turkkan, 1992; Joseph et al., 1995; Pham-Gia, 1997; M’Lan et al., 2008). We will describe our approach in Section 2 and demonstrate the results of our methods via simulation in Section 3, as well as compare those results to those of Cheung (2013b). We will conclude with a summary and discussion in Section 4.

2. Methods

2.1. Notation

We have a set of J clinical doses, D₁ < D₂ < . . . < D_J, and wish to determine which of the doses has a DLT rate closest to the targeted DLT rate θ. We let p_j denote the DLT rate for dose j = 1,2, . . . J and assume that the p_j can be modeled with a one-parameter function of dose, f (E_j; β), in which β is the unknown parameter and E_j is a modified value of D_j to encourage better model fit of f (·). The values E₁, E₂, . . . , E_J are based upon a vector of a priori values known as the skeleton. Although there are a variety of ways of selecting a skeleton and methods for averaging results over multiple skeletons (Yin and Yuan, 2009b), we will use the methods of Lee & Cheung (Lee and Cheung, 2009) to define our skeleton, which are implemented in the function getprior in the dfcrm library (Cheung, 2013a) created for the statistical package R (R, 2016). In both the power model and the logistic model, the parameter β is allowed to take any value on the real line. Thus, it is standard to assume that the prior distribution for β, which we denote g (β), is Gaussian with mean zero and variance σ², with the value of σ² treated as a design parameter whose value is fixed at a specific value. Methods for determining appropriate values of σ² have been proposed (Lee and Cheung, 2011; Zhang et al., 2006).

Although the CRM was first proposed to assign the first patient at the a priori MTD defined by the skeleton, it is now more accepted that the first subject be assigned to the lowest dose to avoid concerns of overdosing early in the trial. The dose assigned to each new subject i = 2, 3, . . . N is determined from the data collected on all previously enrolled subjects. We let E_[k] , k = 1, 2 . . . , i − 1 denote the dose assignment for enrolled subject k, which is among the values E₁, E₂, . . . , E_J, and let Y_k = 1 and Y_k = 0 indicate respectively that subject k has or has not had a DLT. Before subject i is enrolled, we have a likelihood $L_{i-1}(\beta \mid \mathit{Y},\mathit{E})={\prod }_{k=1}^{i-1}f{\left(E_{[k]};\beta \right)}^{Y_k}{\left[1-f\left(E_{[k]};\beta \right)\right]}^{1-Y_k}$, from which we can compute the posterior distribution

$$h_{i-1}(\beta \mid \mathit{Y},\mathit{E})=\frac{L_{i-1}(\beta \mid \mathit{Y},\mathit{E})g(\beta )}{{\int }_{-\infty }^{\infty }{L}_{i-1}(\beta \mid \mathit{Y},\mathit{E})g(\beta )d\beta },$$

in which Y = {Y₁, Y₂, . . . , Y_i−1} and E = {E_[1], E_[2], . . . , E_[i−1]}. We then use h (β | Y, E) to compute ${\tilde{\mu }}_{i-1}$, the posterior mean of β, from which we obtain ${\tilde{p}}_{ij}=f\left(E_j;{\tilde{\mu }}_{i-1}\right)$, the posterior estimate of the probability of DLT for dose j. Patient i is then assigned to the dose with ${\tilde{p}}_{ij}$ closest to the target DLT rate θ, subject to possible dose assignment restrictions. We now describe methods for determining how large N should be before terminating the trial.

2.2. Sample Size via Cheung (2013b)

For Phase I trials using the CRM, Cheung (2013b) determined a lower bound for the sample size based on theoretic properties of what is known as the nonparametric optimal design (NOD) (O’Quigley et al., 2002). The NOD is a simulation-based approach in which potential DLT outcomes are generated for every patient for every dose, which contrasts with an actual trial in which a single DLT outcome is observed for each patient at a specific dose. For a given sample size N, the NOD estimates p_j for each dose j from the observed proportion of DLTs in the N simulated outcomes. Given that the NOD determines DLT rates using JN observations, as well as the unbiased and minimum variance properties of sample proportions, the performance of the NOD is viewed as a benchmark for the performance of any CRM design that determines DLT rates from N observations. Thus, any sample size determined from the nonparametric optimal design is seen as a lower bound for the needed sample size of any CRM design.

As a result, using the asymptotic properties of the estimators used in the NOD, Cheung (2013b) developed his sample size lower bound as follows. For a given number of doses J and a targeted DLT rate θ, we first specify J vectors of hypothetical DLT rates P₁, P₂ , . . . P_J, in which P_k = {p_1k, p_2k, . . . , p_Jk} and p_jk is the probability of DLT for dose j = 1, 2, . . . , J in vector k = 1, 2, . . . J. Each P_k is defined such that

$$\begin{gathered} p_{jk}=\theta \text{if}j=k \\ \frac{p_{j+1,k}}{1-p_{j+1,k}}=R\frac{p_{jk}}{1-p_{jk}}\text{if}j>k \\ \frac{p_{jk}}{1-p_{jk}}=R\frac{p_{j-1,k}}{1-p_{j-1,k}}\text{if}j<k \end{gathered}$$

for a given odds ratio R ≥ 1. In other words, we have J settings, dose k is the true MTD in setting k, and neighboring doses in each setting have DLT rates that differ from each other through an odds ratio R. For each setting k, defined by P_k, we could run simulations to compute ${\widehat{PCS}}_k$, an estimate for the probability of correct selection (PCS) of the MTD when dose k is the MTD. We denote the metric $A_N(\theta ,J,R)={\sum }_{k=1}^J{\widehat{PCS}}_k/K$, which is the average PCS over all the settings examined. Typically, we select N over a grid search of possible values until A_N (θ, J, R) reaches a desired threshold.

To avoid the need for simulation, Cheung (2013b) demonstrated that

$$A_N(\theta ,J,R)\approx \frac{1}{J}+\left(1-\frac{1}{J}\right)\left[2\text{Φ}\left\{w_1(\theta ,R,N)+w_2(\theta ,R,N)\right\}-1\right],$$

in which Φ {·} is the CDF of a standard normal distribution and

$$\begin{gathered} w_1(\theta ,R,N)=\frac{\sqrt{N}}{2}\frac{\theta -{\alpha }_1+0.5N^{-1}}{\sqrt{\theta (1-\theta )+{\alpha }_1\left(1-{\alpha }_1\right)+2{\alpha }_1(1-\theta )}} \\ {w}_2(\theta ,R,N)=\frac{\sqrt{N}}{2}\frac{{\alpha }_2-\theta -0.5N^{-1}}{\sqrt{\theta (1-\theta )+{\alpha }_2\left(1-{\alpha }_2\right)+2\theta \left(1-{\alpha }_2\right)}} \\ {\alpha }_1=\frac{\theta }{\theta +R-R\theta } \\ {\alpha }_2=\frac{R\theta }{1-\theta +R\theta } \end{gathered}$$

Thus, for a given desired probability of correct selection, A_N (θ, J, R), number of doses, J, and variation in DLT rates, R, the corresponding sample size can be determined. As expected, the necessary sample size will increase with increases in A_N (θ, J, R) and J, and will decrease with increases in R. Such a calculation is provided by the function getn in the dfcrm library (Cheung, 2013a) created for the statistical package R (R , 2016). We emphasize that this function is for a design in which the DLT rates are modeled via the power model, with a prior variance of 1.34 for the model parameter, and assumes that the first subject is assigned to the median dose value. We will use the sample sizes produced by this function in Section 3 as a comparator for the sample sizes produced by our method, which we describe next.

2.3. Bayesian Sample Size Determination

Recall that the CRM uses a one-parameter model p_j = f (E_j; β) for the DLT rate of each dose j and a prior distribution is placed on β. This prior distribution leads to a prior distribution for each p_j that often lacks a closed-form expression. We denote this prior distribution as $\mathcal{F}\left(m_j,v_j\right)$ with prior mean m_j and prior variance v_j. Because each p_j is a binomial parameter, an obvious simplification is to approximate $\mathcal{F}\left(m_j,v_j\right)$ with a Beta distribution with parameters

$$a_j=m_j\left[\frac{m\left(1-m_j\right)}{v_j}-1\right]$$ (1)

$$b_j=\left(1-m_j\right)\left[\frac{m\left(1-m_j\right)}{v_j}-1\right].$$ (2)

The values of m_j and v_j can be approximated either through sampling directly from the prior of β and computing the resulting means and variances of each p_j or by using a Taylor series expansion. With N subjects receiving dose j, in whom we see Y DLTs, we know that p_j has a posterior Beta distribution with parameters a_j + Y and b_j + (N − Y); we denote this posterior distribution as f_j (p | Y, N). See Morita et al. (2010) & Morita et al. (2012) for use of this approximation in other settings.

For a vector of true DLT rates π = {π₁, π₂, . . . π_J} and the targeted DLT rate θ, we define j_θ as the index of the dose whose DLT rate is closest to θ, that is, dose j_θ is the true MTD among the doses being studied. Note that in the methods of Cheung (2013b), π is determined directly from the odds ratio R and one of the doses is specified to have DLT exactly equal to θ. Our methods are applicable to any general vector of DLT rates, although certainly an approximate odds ratio could be determined from a given vector of DLT rates in order to apply the methods of Cheung (2013b).

We will use the location and spread of f_jθ (p | Y, N) to help determine when N is “large enough,” somewhat related to the stopping rule proposed by Ishizuka and Ohashi (2001). Intuitively, as N grows larger, the posterior mean of p_jθ will get closer to π_jθ and the posterior variance of p_jθ will continually shrink. Likewise, the posterior distributions of the DLT rates of all other doses will become more peaked around their respective true DLT rates. Thus, as the sample size N increases, the posterior distributions will have less and less overlap with each other, allowing for the determination of the MTD, which is dose j_θ, with more and more precision.

Our desired level of precision will be defined by two parameters ϕ and γ_ℓ. We define an interval ${\mathcal{I}}^{*}=\theta \pm \varphi$ of acceptable DLT rates around the target θ. Intuitively, as ϕ gets larger (smaller), the necessary sample size should decrease (increase). We propose that the value for ϕ should be the average distance between the true DLT rates of adjacent doses, that is, if all the DLT rates differ from the doses directly adjacent to them by an average of 10 points, then ϕ = 0.10. This metric is obviously related to the odds ratio R used by Cheung (2013b), although we focus on the absolute differences between the true DLT rates rather than the absolute difference of the log-odds of the true DLT rates.

The sample size formula of Cheung (2013b) varies with the number of doses J; our approach also will reflect the number of doses implicitly through the definition of ϕ. For example, suppose, we are studying five doses, and we assume the doses have true DLT rates of π = {0.05, 0.12, 0.20, 0.30, 0.45}; currently ϕ would be equal to 0.10. If the study were expanded to include a sixth dose, the value of ϕ will possibly change to reflect the location of the DLT rate of this sixth dose relative to the original five doses. If the sixth dose had a DLT rate of 0.55, then ϕ would remain at 0.10, which makes sense because this dose is even further from the MTD than the fourth and fifth doses, so that few, if any patients would be assigned to this dose and little additional information would be gleaned from including this dose. In contrast, if the sixth dose had a true DLT of 0.35, we now have ϕ = 0.06, which would lead to a much larger sample size because correctly identifying the MTD would require more information than that required by the original five doses. We can consider our parameter ϕ analogous to the parameter α, which is the false positive, or Type I error, rate considered in traditional sample size calculations.

Given the interval ${\mathcal{I}}^{*}$, we can compute $\gamma (N,Y)={\int }_{{\mathcal{I}}^{*}}{f}_{j_{\theta }}(p\mid Y,N)dp$, which is a posterior interval probability (PIP) for dose j_θ, specifically the amount of posterior mass for p_jθ in the interval ${\mathcal{I}}^{*}$. Since this PIP is conditional upon the observed number of DLTs Y out of N subjects, we compute $\overline{\gamma }(N)={\sum }_{y=0}^{y=N}\gamma (N,y)Bin\left(N,p_{j_{\theta }}\right)$, which is a weighted average of PIP values over the density of Y, which has a binomial distribution with parameters N and $p_{j_{\theta }}$. Our second parameter, γ_ℓ defines the minimum amount of PIP we desire at the true MTD, and is analogous to power, or the true positive rate, used in traditional sample sizes.

Thus, our sample size algorithm is as follows:

1. Select J, the number of doses to be studied, θ, the targeted DLT rate, the dose-toxicity model f (E_j; β) with corresponding skeleton values E₁, E₂, . . . E_J, and σ², the prior variance for β;

2. Determine the parameters of each beta distribution defined in equations (1) and (2);

3. Select a vector of true DLT rates π = (π₁, π₂, . . . , π_J) which then determines $\varphi ={\sum }_{j=1}^{J-1}\left({\pi }_{j+1}-{\pi }_J\right)/(J-1)$;

4. Select a value for γ_ℓ , the minimum desired amount of mass in ${\mathcal{I}}^{*}=(\theta -\varphi ,\theta +\varphi )$ for the posterior distribution of DLT rates for the MTD;

5. Select a vector of possible sample sizes $\mathcal{N}$, and for each value $N\in \mathcal{N}$, compute the resulting value of $\overline{\gamma }(N)$;

6. Find the smallest value of N such that $\overline{\gamma }(N)\ge {\gamma }_{\ell }$.

As a practical example, suppose we have five doses under study and our targeted DLT rate is θ = 0.30. We will use the power model with the model parameter β having a prior variance of σ² = 1.34. We have a vector of skeleton DLT rates {0.06, 0.16, 0.30, 0.45, 0.59} so that the middle dose is the a priori MTD. The prior distribution for β places a prior mean and variance on the DLT rates for each dose; we find the parameters of a beta distribution that correspond to each mean and variance. For example, the prior mean and variance for the DLT rate of the first dose are 0.17 and 0.05, respectively, which correspond to beta distribution parameters a₁ = 0.33 and b₁ = 1.58 from equations (1) and (2). Similar computations are made for the remaining four doses.

The sample size is now a function of the actual DLT rates of the five doses and the desired value of γ_ℓ, the posterior coverage level. Suppose the vector of true DLT rates for the five doses is {0.05, 0.16, 0.28, 0.39, 0.50}, so that the average difference between adjacent DLT rates is ϕ = 0.11. This defines an interval of ${\mathcal{I}}^{*}=(\theta -\varphi ,\theta +\varphi )=(0.19,0.41)$. Suppose, we now wish to find a sample size that supports a PIP of γ_ℓ = 0.70 in the interval (0.19, 0.41). We simply iteratively examine a range of sample sizes until we find the smallest sample size that achieves the desired PIP level. In this example, we obtain a sample size of N = 37. R code for this calculation can be found in the Web Supplement.

If we were to change the true DLT rates to {0.10, 0.20, 0.30, 0.40, 0.50}, we now have a value ϕ = 0.10, which results in a larger sample size of N = 45 because the value of ϕ is now smaller than before. We could also return to our original setting and instead reduce the prior variance of β in half to be σ² = 0.67, which leads to smaller sample size of N = 35. Alternatively, we could leave the prior variance unchanged at σ² = 1.34, and instead change the skeleton to be {0.00, 0.01, 0.06, 0.16, 0.30}, leading to a sample size of N = 37. These two sample size values are practically identical to the original sample size of N = 37 and demonstrate that the choices of prior variance and skeleton have much less impact on the sample size than does the vector of true DLT rates.

3. Numerical Studies

We now compare and contrast the sample sizes produced by our method and by the method of Cheung (2013b). We have J ∈ {4, 5, 6} doses under study and the targeted DLT rate equal to θ ∈ {0.20, 0.25, 0.30}. We use the empiric model with a prior variance of 1.34 for the model parameter, which is the default value in the R function crmsim. Skeleton values were determined via the R function getprior (Lee and Cheung, 2011) using a half-width of θ/4, as recommended in Cheung (2013b). The skeleton was computed assuming the third dose was the MTD. True DLT rates are equally spaced from a value p_min ∈ {0.05, 0.10, 0.15, 0.20} to a value p_max ∈ {0.3, 0.4, 0.5, 0.6, 0.7}, which combined with the selected values of J and θ, determine the location of the MTD. Each of the settings defined by a combination of J, θ, p_min, and p_max results in a value of ϕ for our proposed methods, as well as an approximate odds ratio R necessary for the methods of Cheung (2013b). The value of R was approximated as exp{logit(θ + ϕ) − logit(θ)}, where logit(x) = log(x) − log(1 − x).

For each setting, we computed the necessary sample size using our methods for values of the desired minimum posterior coverage γ_ℓ ∈ {0.6, 0.7, 0.8, 0.9}. We then ran 1000 simulations of Phase I trials designed with the CRM using each of the resulting sample sizes in order to compute both the posterior distribution of the model parameter β as well as the dose identified as the MTD at the end of the study. From these 1000 simulations, we computed the average posterior mass of the interval θ ± ϕ and $\widehat{PCS}$, the proportion of simulations in which the MTD was correctly identified. We computed these values separately for studies assigning the median dose to the first subject, which was used in the methods of Cheung (2013b), and for studies assigning the lowest dose to the first subject, which is more commonly used in practice. We then used the value of $\widehat{PCS}$ from each approach in the R function getn in order to compute the suggested sample size from the methods of Cheung (2013b). Code for generating the simulation results is available in the Web Supplement, although an R library is being generated and will be made publicly available at the Comprehensive R Archive Network (CRAN) when completed.

Due to space limitations, results for a subset of all the settings are presented in four tables that can be found in the Web Supplement. There is one table for each for the four possible values of γ_ℓ, and each table contains results for 24 settings. The same 24 settings are summarized in each of the four tables so that corresponding rows in each table can be directly compared to each other to observe how the sample size increases with γ_ℓ.

Figure 1 provides a visual summary of the results when γ_ℓ = 0.60 (left panels) and γ_ℓ = 0.70 (right panels). Each of the six panels provides a range of a sample sizes produced using our proposed method, as well as a corresponding range of sample sizes computed using the method of Cheung (2013b) that have the same probability of correct selection $(\widehat{PCS})$ as our method. Each panel also provides the actual average coverage rate produced by the sample size from our method. For example, the upper left-hand plot in Figure 1 demonstrates that with four doses, our method produces sample sizes ranging from 13 to 18 subjects, with an actual coverage rate of 0.70 and $\widehat{PCS}=0.44$. The corresponding sample sizes from Cheung’s method range from 5–6 subjects.

Figure 1.

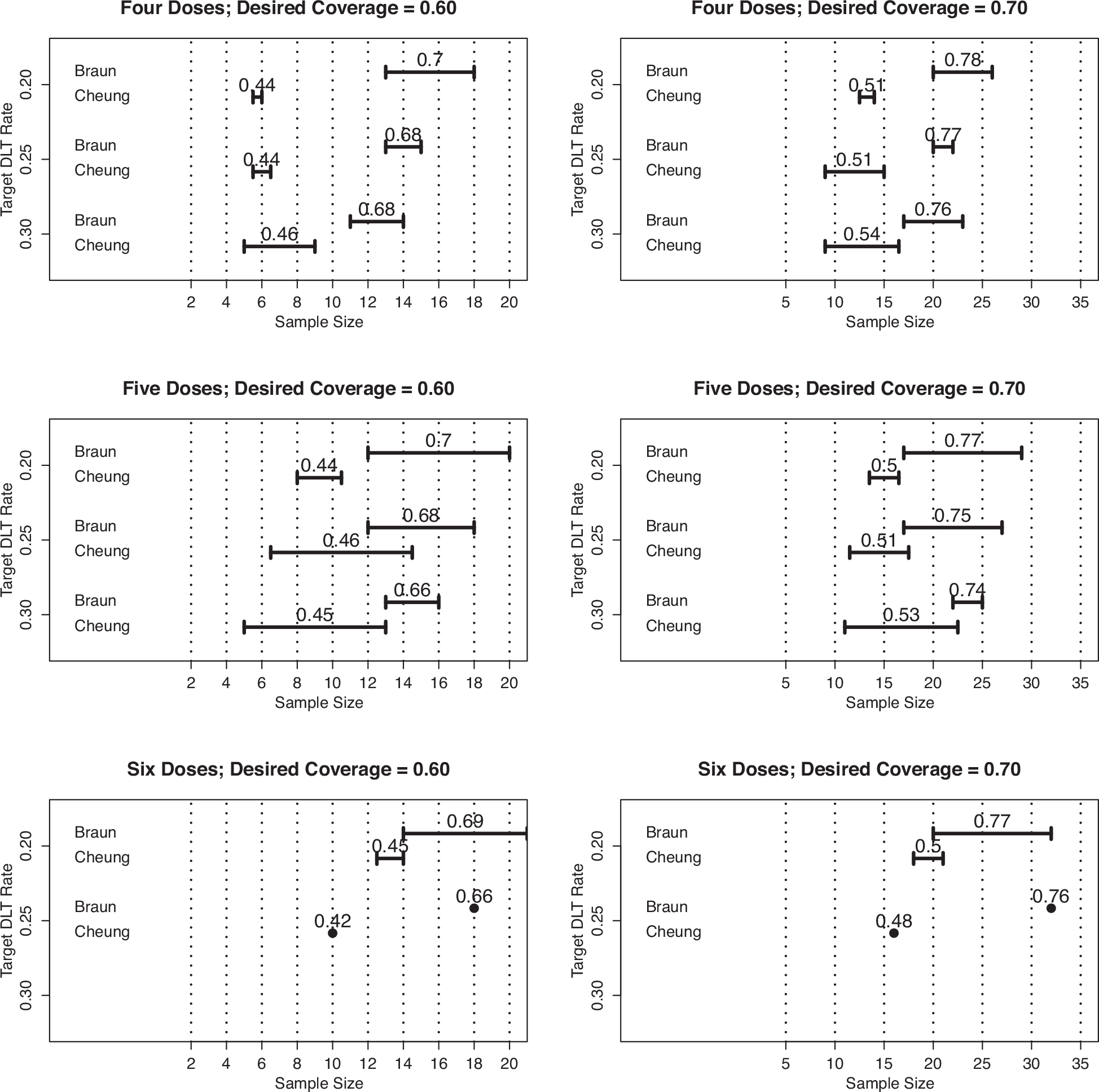
Ranges of sample sizes produced by proposed method (Braun) and that of Cheung (2013b), for studies of four doses (row 1), five doses (row 2), and six doses (row 3), with desired coverage rates of γ_ℓ = 0.60 (column 1) and γ_ℓ = 0.70 column 2). The value above the ranges for Braun’s method is the actual coverage rate, while the value above the ranges for Cheung’s method is the actual probability of correct selection (PCS).

In all six panels of Figure 1, we can draw some general conclusions. First, we see that for a given probability of correct selection, our method suggests that the sample sizes of Cheung (2013b) are too small, which we expect. Second, the actual coverage rates are a bit higher than the desired value, but are generally close enough to suggest the beta distributions provide a good approximation. Third, the sample size from our method is (a) relatively invariant to the targeted DLT rate θ, (b) increases when the desired coverage rate increases, and (c) increases slightly as the number of doses increases. Last, there are suggestions that a desired coverage rate of γ_ℓ corresponds to a probability of correct selection that is about 20 points lower, that is, γ_ℓ = 0.60 corresponds roughly to $\widehat{PCS}=0.40$.

Figure 2 provides a visual summary of the results when γ_ℓ = 0.80 (left panels) and γ_ℓ = 90 (right panels) and supports the conclusions reached from Figure 1. We do see in Figure 2 that there is a smaller difference between the sample sizes produced by our method and by Cheung (2013b) than seen in Figure 1, although the sample sizes of Cheung (2013b) remain lower than what is needed for the given value of $\widehat{PCS}$. From the sample size values in Figure 2, we also see that a desired coverage rate of 0.80 or higher requires a sample size larger than what is actually used in most trials.

Figure 2.

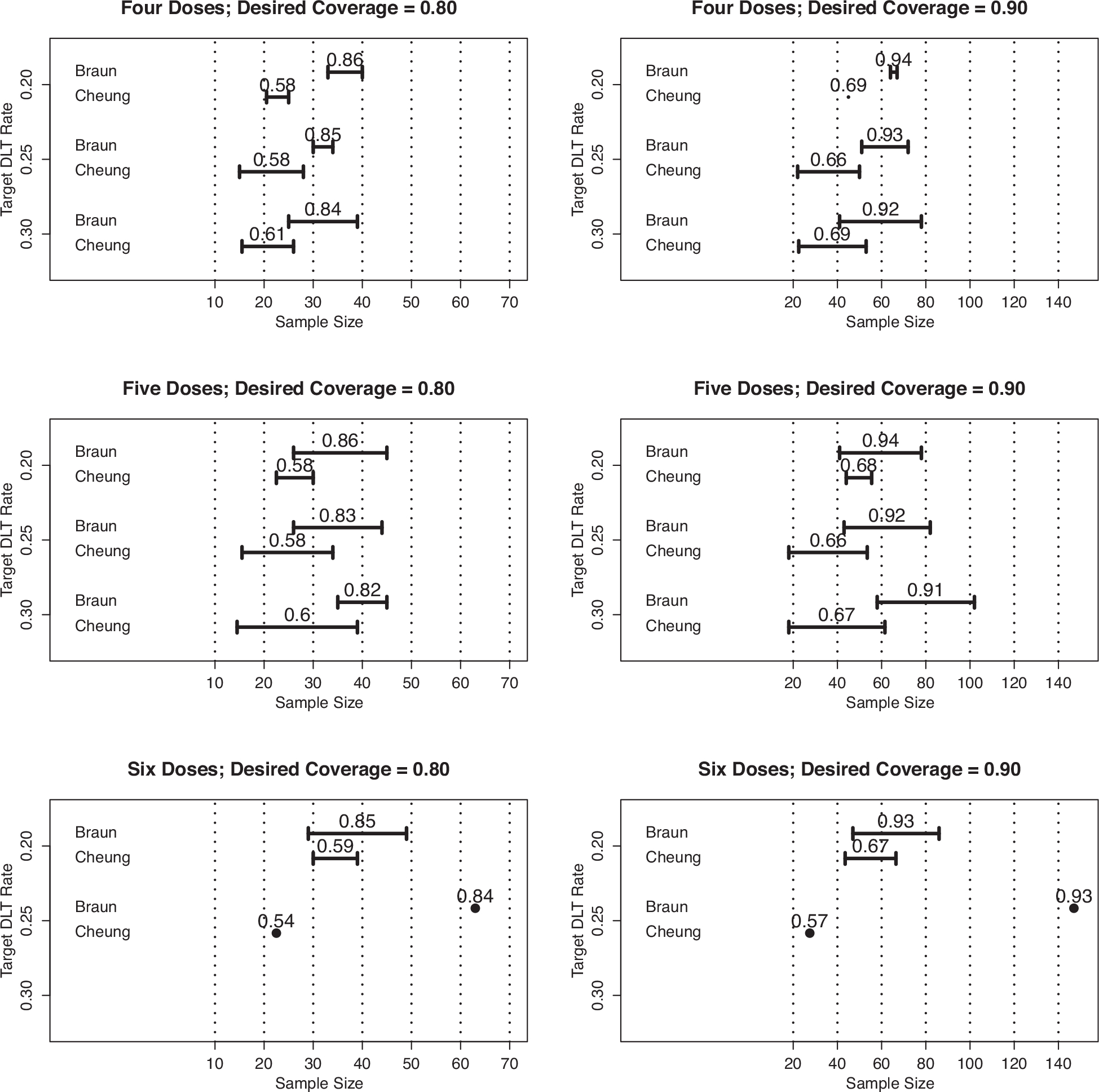
Ranges of sample sizes produced by proposed method (Braun) and that of Cheung (2013b), for studies of four doses (row 1), five doses (row 2), and six doses (row 3), with desired coverage rates of γ_ℓ = 0.80 (column 1) and γ_ℓ = 0.90(column 2). The value above the ranges for Braun’s method is the actual coverage rate, while the value above the ranges for Cheung’s method is the actual probability of correct selection (PCS).

4. Discussion

Our work supports the growing body of research demonstrating the superiority of adaptive designs to algorithmic ones (Iasonos et al., 2008; Jaki et al., 2013) and suggests that the sample sizes used in actual Phase I trials are likely insufficient for finding a chemotherapy dose that will be used in future Phase II trials. We note that, for a resulting sample size N, our methods have implicitly assumed that all N subjects have been treated at the true MTD, with no patients treated at the other doses. This contrasts to the actual design of an adaptive trial, in which roughly 50% of patients would be treated at the MTD, with fewer patients treated at doses directly above and below the MTD and even fewer patients treated at all other doses. The two designs, however, have very similar levels of efficiency for identifying the MTD.

Although our methods have not assumed a “greedy” dose-assignment algorithm, in which each patient or cohort of patients is assigned to the dose currently believed to be the MTD, our methods do require that the CRM will be consistent (Cheung and Chappell, 2002; Shen and O’Quigley, 1996). In other words, dose assignments cannot get “stuck” at a non-MTD dose ad infinitum, so that correctly identifying the MTD does not improve with sample size (Azriel et al., 2011; Oron and Hoff, 2013). We did examine our methods with settings in which the CRM has been shown to not be consistent, and found that the resulting sample sizes, which were unusually large (in the range of 300 to 500 subjects), led to a much smaller coverage rate than that desired. Thus, when our method suggests that hundreds of subjects will be necessary, there is a warning that non-consistency of the CRM could be an issue, which can be determined easily with the methods of Cheung and Chappell (2002).

We would like to expand our methods to other designs, such as combination trials of two agents (Yin and Yuan, 2009a; Braun and Jia, 2013; Mander and Sweeting, 2015) and partial follow-up of toxicity outcomes (Cheung and Chappell, 2000; Yuan and Yin, 2011). We hope that our methods provide a springboard from which appropriate sample sizes can be determined for these more complex and contemporary adaptive Phase I trial designs.