Can Machine Learning Accurately Predict Postoperative Compensation for the Uninstrumented Thoracic Spine and Pelvis After Fusion From the Lower Thoracic Spine to the Sacrum?

Abstract

Study Design:

Consecutively collected cases.

Objective:

To determine if a machine-learning (ML) program can accurately predict the postoperative thoracic kyphosis through the uninstrumented thoracic spine and pelvic compensation in patients who undergo fusion from the lower thoracic spine (T10 or T11) to the sacrum.

Methods:

From 2015 to 2019, a consecutive series of adult (≥18 years old) patients with adult spinal deformity underwent corrective spinal fusion from the lower thoracic spine (T10 or T11) to the sacrum. Deidentified data was processed by a ML system-based platform to predict the postoperative thoracic kyphosis (TK) and pelvic tilt (PT) for each patient. To validate the ML model, the postoperative TK (T4-T12, instrumented thoracic, and uninstrumented thoracic) and the pelvic tilt were compared against the predicted values.

Results:

A total of 20 adult patients with a minimum 6-month follow-up (mean: 22.4 ± 11.3 months) were included in this study. No significant differences were observed for TK (predicted 37.6° vs postoperative 38.3°, P = .847), uninstrumented TK (predicted 33.9° vs postoperative 29.8°, P = .188), and PT (predicted 23.4° vs postoperative 22.7°, P = .754). The predicted PT and the TK of the uninstrumented thoracic spine correlated well with postoperative values (uninstrumented TK: R² = 0.764, P < .001; PT: R² = 0.868, P < .001). The mean error with which kyphosis through the uninstrumented thoracic spine can be measured was 4.8° ± 4.0°. The mean error for predicting PT was 2.5° ± 1.7°.

Conclusion:

ML algorithms can accurately predict the spinopelvic compensation after spinal fusion from the lower thoracic spine to the sacrum. These findings suggest that surgeons may be able to leverage this technology to reduce the risk of proximal junctional kyphosis in this population.

Introduction

In adult spinal deformity (ASD), surgery often involves a lengthy segmental fusion where the upper instrumented vertebra (UIV) enters the thoracolumbar junction. This can result in compensatory changes in the uninstrumented cervical and thoracic spine, the pelvis, as well as the lower extremities. ¹ Excessive kyphosis through the uninstrumented thoracic spine can increase anterior compressive forces at the UIV and the adjacent vertebra above the UIV (UIV + 1), which is a contributor to the development of proximal junctional kyphosis/failure (PJK/PJF) and often leads to high revision rates.^2-6 A plethora of literature exists on the clinical and radiographic risk factors for PJK.^3,7-18 However, prevention of PJK remains unsolved and is still a relatively common postoperative complication.

One possible solution to predicting the postoperative compensation after deformity correction is through machine learning (ML), which has the potential to assist in solving complex medical questions. Through extensive clinical data mining, deep learning algorithms, and predictive analytics, ML can potentially provide personalized outcome predictions for individual patients.^19-21 ML algorithms can provide spinal surgeons with patient-specific preoperative plans, while simultaneously improving on the algorithm over time as it receives postoperative feedback as part of an iterative learning process and thus, allowing surgeons to improve patient outcomes and mitigate complications.

In this study, we sought to determine if a proprietary industry-created ML algorithm can accurately predict postoperative compensation of ASD patients in the uninstrumented thoracic spine and pelvis after a long fusion with a UIV in the lower thoracic spine (T10 or T11) to the sacrum. To our knowledge, this is the first study to examine the accuracy of ML technology to predict compensatory mechanisms in patients with ASD.

Methods

Patient and Radiographic Data

Following institutional review board approval, we reviewed a consecutive series of adult spinal deformity (≥18 years old) patients treated with a corrective posterior spinal instrumentation and fusion with a UIV in the lower thoracic spine (T10 or T11) and lower instrumented vertebra (LIV) at the sacrum between 2015 and 2019. All surgeries were performed by a single surgeon and the radiographic films were performed at a single center with a minimum follow-up of 6 months. For both preoperative and postoperative full-length radiographs, patients were positioned standing with their elbows flexed, at approximately 45°, with their fingertips touching their clavicles. As patient data needs to be deidentified for third-party analytics, only radiographic factors were included in the ML model; thus, patient factors such as age, gender, and body mass index were not included.

A comprehensive list of sagittal spinopelvic measurements was recorded preoperatively and postoperatively. Regional radiographic measurements included C2 slope, cervical lordosis (CL) (C2-C7 Cobb angle), T1 slope, T1 – CL (T1 minus CL), thoracic kyphosis (TK, T4-T12 Cobb angle), thoracolumbar kyphosis (TL, T10-L1 Cobb angle), and lumbar lordosis (LL, L1-S1 Cobb angle). Pelvic parameters included pelvic incidence (PI), pelvic tilt (PT), sacral slope (SS), and lumbo-pelvic mismatch (PI minus LL). Kyphosis was measured across the fused (instrumented TK) and unfused (uninstrumented TK) thoracic spine. Global radiographic parameters included sagittal vertical axis (SVA), cervical SVA (cSVA), T1 spinopelvic inclination (T1-SPI), T9 spinopelvic inclination (T9-SPI), C2 pelvic angle (CPA), cervicothoracic pelvic angle (CTPA), and T1 pelvic angle (TPA).

Thoracic compensation in the uninstrumented spine was defined as the difference between the postoperative (or predicted) and the preoperative baseline TK values and pelvic compensation was defined as the difference between post- and preoperative PT values. Independent t tests and analysis of variance (ANOVA) was used for continuous variables and statistical significance was defined as a P value <.05. SAS Studio Version 3.4 (SAS Institute Inc) was used for all statistical analyses.

Model Generation

In a data-driven capacity, deidentified data was processed by an ML system-based platform (Medicrea) to predict the postoperative TK and PT for each patient. More specifically, Medicrea used the Python programming language and the Scikit-Learn, which is a free software machine learning library for Python, for data processing and the development of regression-based algorithms. The proprietary model was used to analyze preoperative images and set the actual postoperative lumbar lordosis (LL) as the “target LL” (Figure 1). In Figure 1, the “red” line is the preoperative alignment and the “thin blue” line is the predicted alignment based on a target LL. The “thick blue” line is the planned surgery from T10 to pelvis. The ML algorithm has more than 4000 patients in its database and thus performs predictive analytics to anticipate postoperative global and regional alignment parameters (Figure 2). The target alignment is also used to generate custom precontoured rods to be used intraoperatively for these patients. A difference of up to 6° between the predicted and actual postoperative TK was considered acceptable and a difference of up to 4° between the predicted and actual postoperative PT was accepted. Outliers were defined as those with a difference greater than acceptable. The outliers were included in the comparative analyses and linear regressions. To validate the predictive models, the postoperative TK (T4-T12, instrumented thoracic, and uninstrumented thoracic) and the PT were compared against the predicted values. The model’s ability to identify successful (PT ≤ 25°, uninstrumented ΔTK ≤ 15°) and unsuccessful (PT > 25°, uninstrumented ΔTK > 15°) outcomes was also evaluated. Higher PT is known to correlate with worse patient outcomes and this threshold has been used in prior literature. ²² The ΔTK refers to the difference between postoperative (or predicted) minus the preoperative uninstrumented TK. The ΔTK threshold was used to define reciprocal kyphosis which has also been used in prior literature. ²³

Figure 1.

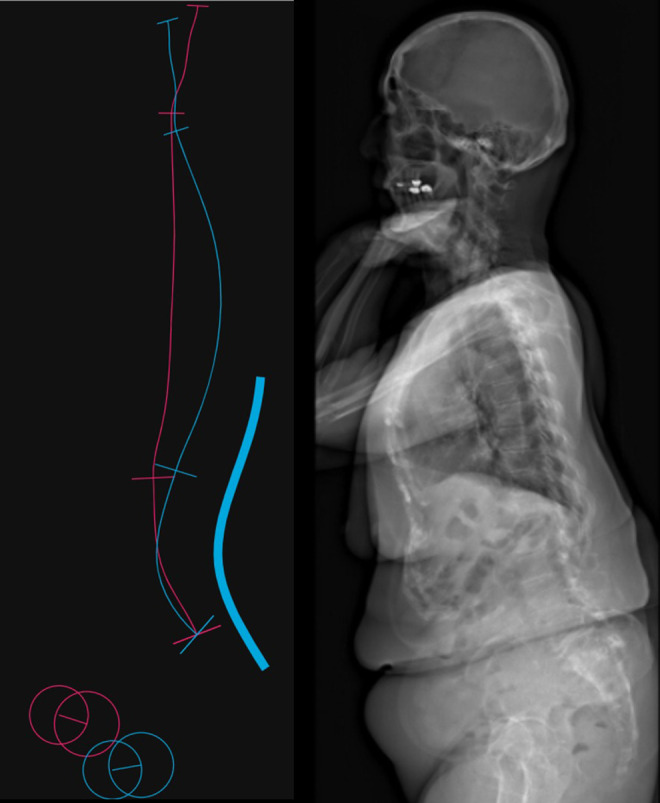
A proprietary model was used to analyze preoperative images and set the actual postoperative lumbar lordosis (LL) as the “target LL.” The “red” line is the preoperative alignment and the “thin blue” line is the predicted alignment based on a target LL. The “thick blue” line is the planned surgery from T10 to pelvis.

Figure 2.

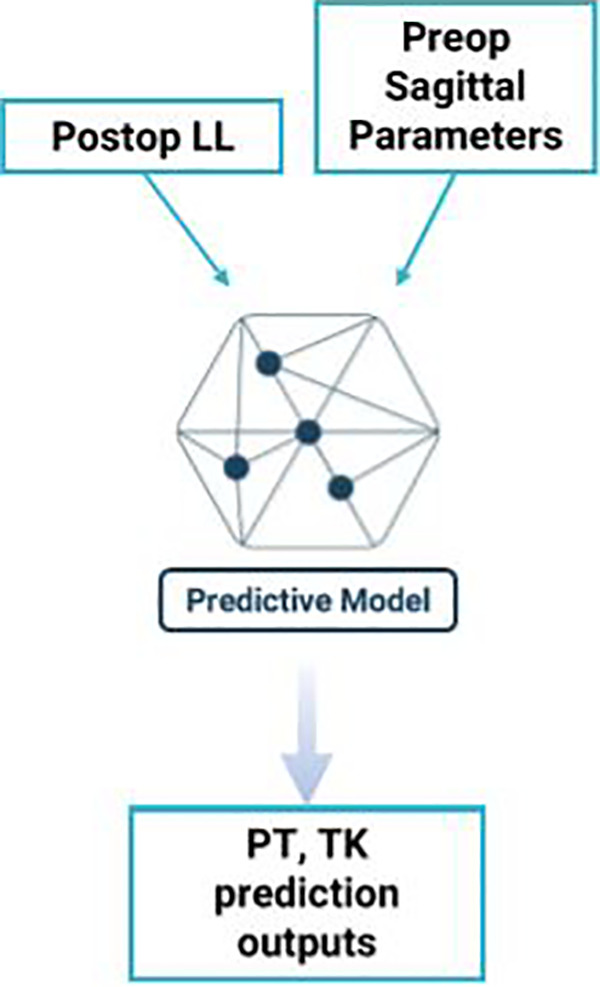
A schematic for the machine learning algorithm.

Results

A total of 20 adult patients with a minimum 6-month follow-up were included in this study. The most recent postoperative full-length standing films were taken at a mean ± standard deviation of 22.4 ± 11.3 months after surgery. Three patients had postoperative films taken prior to their 1-year postoperative follow-up. All patients had a primary diagnosis of ASD. The mean age was 62.0 ± 10.5 years, and 55.0% were female. About 45.0% of patients had a prior spine surgery.

Significant improvement in several sagittal parameters were observed between the postoperative and preoperative values, including L1-L4 (postoperative −10.4° vs preoperative −0.05°, P = .01), LL (postoperative −42.1° vs preoperative −26.5°, P = .003), PI-LL (postoperative 9.3 vs preoperative 25.1, P = .002), T5-T12 (postoperative 34.5° vs preoperative 20.3°, P < .001), T9 SPI (postoperative −12.1 vs preoperative −8.2, P = .019), and TK (postoperative 38.3° vs preoperative 24.7°, P < .001). The TK for instrumented levels did not significantly change between preoperative versus postoperative (P = .057). Most of the change in TK was driven by the uninstrumented levels of the thoracic spine (postoperative 29.8° vs preoperative 20.9°, P = .014) (Table 1).

Table 1.

The Pre- and Postoperative Cervical, Thoracic, and Lumbopelvic Radiographic Parameters.

Parameter	Preoperative	Postoperative	P
C2 slope	16.9 (15.3)	16.6 (11.5)	.942
CL	−9.8 (16.5)	−12.2 (14.8)	.643
CPA	26.7 (14.5)	22.3 (9.6)	.290
CTPA	1.7 (1.6)	2.2 (1.4)	.385
L1-L4	−0.05 (14.4)	−10.4 (9.7)	.011*
L4-S1	−26.4 (15.2)	−31.8 (10.7)	.205
LL	−26.5 (19.1)	−42.1 (11.4)	.003*
PI	51.6 (12.2)	51.5 (12.2)	.981
PI-LL	25.1	9.3 (10.2)	.002*
SS	26.5 (9.3)	28.9 (9.2)	.429
SVA	67.5 (73.5)	38.2 (37.6)	.122
T1 SPI	0.26 (7.1)	−2.4 (3.9)	.147
T1 slope	29.7 (16.4)	29.9 (12.5)	.956
T1-CL	19.7 (14.7)	17.9 (11.4)	.682
T2-T5	14.4 (9.5)	13.6 (9.4)	.783
T5-T12	20.3 (13.1)	34.5 (8.2)	<.001*
T9 SPI	−8.2 (6.1)	−12.1 (3.8)	.019
TL	5.8 (16.0)	8.7 (13.1)	.526
TPA	25.3 (13.5)	20.2 (8.7)	.166
cSVA	17.0 (13.7)	20.4 (12.5)	.446
TK (T4-T12)	24.7 (13.8)	38.3 (9.5)	<.001*
Instrumented TK	3.8 (8.1)	8.4 (7.1)	.057
Uninstrumented TK	20.9 (11.9)	29.8 (9.6)	.014*
Pelvic tilt	25.1 (9.6)	22.7 (8.3)	.403

Abbreviations: CL, cervical lordosis; CPA, C2 pelvic angle; CTPA, cervicothoracic pelvic angle; LL, lumbar lordosis; PI, pelvic incidence; SS, sacral slope; SVA, sagittal vertical axis; SPI, spinopelvic inclination; TL, thoracolumbar kyphosis; TPA, T1 pelvic angle; cSVA, cervical sagittal vertical axis; TK, thoracic kyphosis.

* Statistically significant (P < .05).

When comparing the predicted against the postoperative values, there were no significant differences for TK (predicted 37.6° vs postoperative 38.3°, P = .847), uninstrumented TK (predicted 33.9° vs postoperative 29.8°, P = .188), and PT (predicted 23.4° vs postoperative 22.7°, P = .754). (Table 2). In the linear regression analysis, the predicted PT and the TK of the un-instrumented thoracic spine correlated well with postoperative values (uninstrumented TK R² = 0.764, P < .001; PT R² = 0.868, P < .001) (Figures 3 and 4). The mean error with which kyphosis through the uninstrumented thoracic spine can be measured was 4.8° ± 4.0°. The mean error for predicting PT was 2.5° ± 1.7°. No statistically significant differences between the predicted and postoperative values were seen for the amount of compensation in the uninstrumented TK (predicted 12.9° vs postoperative 8.8°, P = .080) and PT (predicted −2.4° vs postoperative −2.4°, P = .988). The positive predictive value (PPV) and negative predictive value (NPV) for excessive PT was 77.8% and 81.8%, respectively. The PPV and NPV for reciprocal uninstrumented TK was 50% and 100%, respectively.

Table 2.

A Comparison of the Predicted and Postoperative Thoracic Kyphosis (TK) and Pelvic Tilt.

	Postoperative	Predicted	P
TK (T4-T12), deg	38.3 (9.5)	37.6 (10.2)	.847
Uninstrumented TK, deg	29.8 (9.6)	33.9 (9.8)	.188
Pelvic tilt, deg	22.7 (8.7)	23.4 (7.1)	.754

Figure 3.

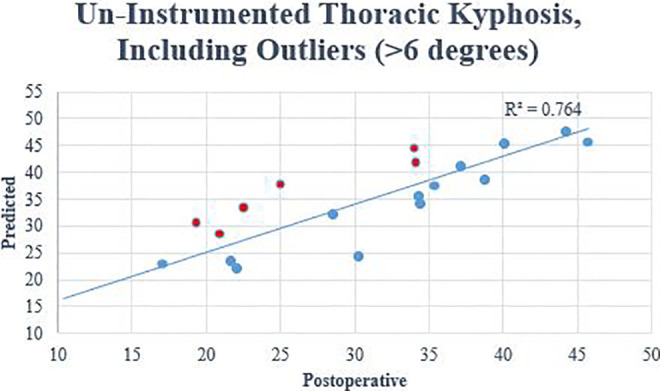
The predicted versus the postoperative values for the thoracic kyphosis in the uninstrumented spine after surgery. Outliers are included.

Figure 4.

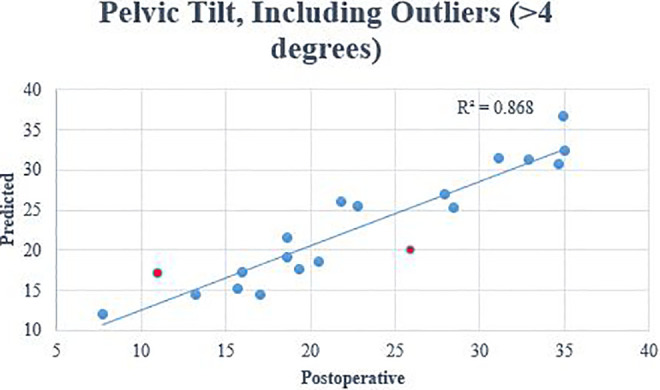
The predicted versus the postoperative values for the pelvic tilt after spine surgery. Outliers are included.

There were 6 patient outliers for predicting TK in the uninstrumented spine and 2 outliers for predicting the PT. One patient was an outlier for both TK and PT. All outliers for the uninstrumented TK were over-estimated compared to postoperative values (error range: 7.8-12.7), which suggests that the model over estimates the flexibility of the uninstrumented spine. This explains the excellent NPV and relatively worse PPV for reciprocal TK. Interestingly, these outliers had higher instrumented TK than preoperative values (postoperative 8.3 vs preoperative 2.9, P = .130), but these differences were not significant between outlier and no outlier groups (outlier 5.4 vs no outlier 4.4, P = .608).

An example of an outlier can be represented by patient XY (Figure 5). Patient XY was a 76-year-old man with adult spinal deformity and a positive sagittal imbalance. Surgical treatment included a posterior spinal instrumentation and fusion from T10 to the ilium. Preoperatively, his PT and TK were measured as 22° and 21°, respectively. The PT correction achieved was greater than predicted (postoperative 11°; predicted 17°). The TK compensation was underestimated (postoperative 40°; predicted 28°). The apparent knee flexion differences between preoperative (69°) and postoperative (22°) likely contributed to unaccounted compensatory mechanisms as the ML algorithm in its current state does not analyze reciprocal changes in the lower extremities.

Figure 5.

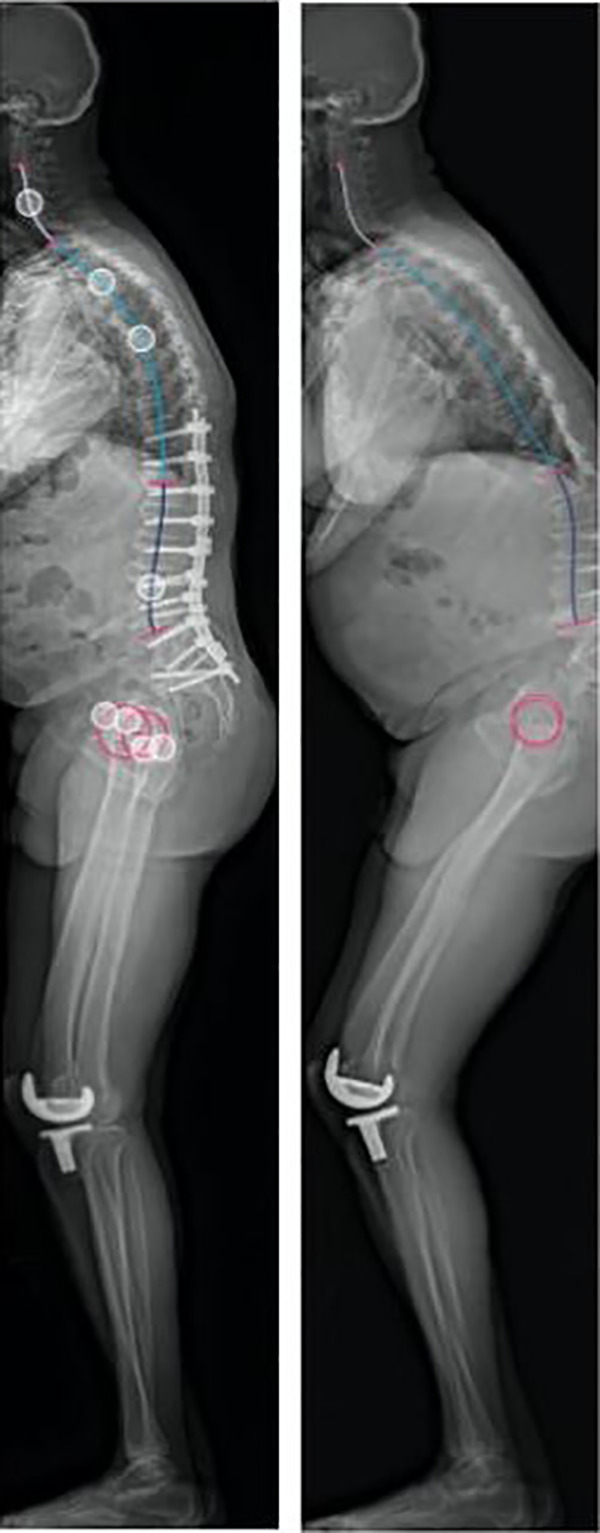
Patient XY is an example of an outlier for thoracic kyphosis in our study. He underwent fusion from T10 to pelvis. Preoperative lateral film is on the left and the postoperative film is on the right.

One patient in our study had radiographic PJK at 1-year postoperatively but was not considered an outlier for uninstrumented TK (5.9°). She was asymptomatic and did not require a revision surgery. Briefly, this was a 61-year-old woman with long-standing low back pain and lower extremity radiculopathy. She had prior spine surgery (posterior spine decompression and fusion L2-4) nearly 10 years ago. Given persistent symptoms and disability likely related to the pseudoarthrosis at L2-3 and overall sagittal imbalance, she underwent revision surgery from T10 to ilium, posterior column osteotomy, and transforaminal lumbar interbody fusion L3-4 and L4-5. Preoperatively, her T4-12 TK was 14.5° and her PT was 26.1°. The predicted PT was similar (postoperative 27.9° vs predicted 27°); however, the postoperative T4-12 TK was substantially higher than predicted (postoperative 37.4° vs predicted 29.6°). This difference was most likely due to the excessive TK in the instrumented spine (postoperative 20.3° vs predicted 6.6°) and less related to the uninstrumented TK (postoperative 17.1° vs predicted 23°).

Discussion

Spurred by advances in technology and an ever-increasing accumulation of data, ML has become a focus in health care over the past 10 years. Major reasons for the growing attraction toward ML include the potential for models to quickly learn from new data and process complex, nonlinear relationships that conventional regression models might fail to comprehend. Spine studies are already showing promise in the ability of ML methods to provide improved diagnostics, risk stratification, and even leverage imaging data for better clinical prognostication.^19,21,24-27 A high-risk spine population that will likely benefit from continued ML research are patients with ASD.^28,29

In ASD surgery, it is well-established that restoring sagittal balance is correlated with improved health-related quality of life and clinical outcomes.^30-33 However, when surgery is performed, the correction of a deformity can induce spontaneous compensatory mechanisms in unfused segments.^1,34,35 These changes can be progressive leading to worse pain, disability, and complications, such as pseudarthrosis or PJK, that require a revision surgery as well as undesirable costs.^36-38 Although it is recognized that maximizing preoperative planning is essential to avoid suboptimal postoperative alignment and anticipate potential compensatory changes, predicting these changes in alignment remains a significant challenge for spine surgeons. ³⁹

A number of prior studies have proposed mathematical formulas to improve a surgeon’s ability to predict postoperative alignment. In a retrospective series of 219 patients, Lafage et al ⁴⁰ were the first to construct and validate predictive models for PT and SVA in patients with ASD after undergoing a pedicle subtraction osteotomy. Using multilinear regressions, these authors determined that postoperative PT could be predicted by the following equation: PT = 1.14 + 0.71 × PI – 0.52 × (maximal lumbar lordosis) – 0.19 × (maximal thoracic kyphosis). Similarly, SVA could be calculated based on the following equation: SVA = −52.87 + 5.9 × PI – 5.13 (maximal lumbar lordosis) – 4.45 × PT – 2.09 × (maximal thoracic kyphosis) + 0.566 × age. These models demonstrated good performance with a mean error of 4.3° for PT and a mean error of 29 mm for SVA. A clear advantage of these 2 models is that they included either fixed (eg, PI, age) or surgically modifiable (eg, LL, TK) factors. In other words, a surgeon could intraoperatively correct the LL and use these equations to predict subsequent pelvic retroversion and global alignment. These same authors further validated their results through a multicentered study. ²² The median absolute error for predicting PT was 4.1° and the median absolute error for predicting SVA was 27 mm. Their models were successful in predicting unsuccessful outcomes (NPV = 0.98), but less reliable in predicting successful outcomes (PPV = 0.76). In another retrospective review, Smith et al ⁴¹ compared 5 mathematical models to predict optimal postoperative SVA (<5 cm) in ASD surgery patients. The reported formulas by Lafage et al ⁴⁰ demonstrated the greatest accuracy. Although these models provide tremendous insight, it is important to note that the coefficients of these current models are static in nature. In other words, these models are not capable of adapting to new data. Therefore, significant model performance variability might occur for different spine surgical practices. Furthermore, these models did not account for changes that might occur in the unfused spine. It is known that the unfused spinal segments often move independently into positions that are opposite to the direction of the fused spinal segments.^1,42 A predictive model that can predict these changes preoperatively would be invaluable for reducing future PJK risk.

Currently, there is a paucity of literature with regard to predicting thoracic compensation after ASD surgery. Ohba et al ⁴³ studied 66 ASD patients who underwent spinal fusion from the lower thoracic spine (T8-10) to the pelvis with a minimum 1-year follow-up. In their study, they found a significant positive correlation between increased LL and increased TK (r = 0.51, P < .001). Furthermore, they found that those with a decreased postoperative lordosis distribution index had a higher postoperative TK, which likely contributed to the PJK risk. ⁴³ In another study, Protopsaltis et al ²³ performed a multicenter retrospective review to study thoracic compensation and its association with postoperative reciprocal thoracic kyphosis and PJK in patients with ASD who underwent a fusion to the sacrum with an upper instrumented vertebra in the lower thoracic spine. In contrast to our study, these authors calculated the expected thoracic kyphosis (eTK) from the following equation eTK = PI – 20. This equation was derived from the validated formula from Schwab et al ⁴⁴ (LL = ½ (PI + TK) + 10 with the assumption that LL = PI. The eTK was not statistically different from the postoperative TK for those who either maintained TK or had reciprocal change in TK (≥15° in the unfused thoracic spine). Interestingly, patients exhibiting reciprocal change in TK were more likely to develop PJK and have worse health-related quality of life scores. The findings of this study demonstrate that mathematical equations can approximate thoracic kyphosis for those with and without compensation; however, it is unclear how accurate these predictions are for the unfused spine against actual postoperative values. Furthermore, the success of this model hinges on the assumption that LL = PI, which may be inconsistent to apply to all patients with ASD.

In comparison to prior studies, this is the first study to examine the degree to which ML can predict compensation for ASD patients. In our study, strong correlations were observed between postoperative and predictive values for both pelvic tilt and TK (uninstrumented TK R² = 0.764, P < .001; PT R² = 0.868, P < .001). The mean error for the predicted estimates for TK in the uninstrumented spine was <5°. These findings demonstrate that a ML model can accurately predict the postoperative compensation in the pelvis and the unfused portions of the thoracic spine. With this level of precision, thoracic kyphosis and pelvic compensation can be anticipated and accounted for during preoperative planning.

A number of limitations should be considered for this study. First, this study had a relatively small sample size, which may limit the identification of possible differences in other radiographic parameters in this study. Normally, a small sample size limits the generalizability of a study’s findings as well; however, the purpose of this study was to demonstrate the capability of ML. By its very nature, ML is meant to be personalized and adapt for each user based on the perpetual flow of new data. Next, the minimum follow-up was 6 months postoperative. It is likely that TK and pelvic compensation changes with time which may affect model reliability. It is important to note, however, that the mean follow-up was closer to 2 years (mean 21.9 months) with only 3 patients with follow up prior to 1-year. Finally, the ML model did not include a comprehensive set of patient factors such as medical comorbidities, bone density, or surgical techniques which can influence PJK risk. Although, even without this data, the ML model still performed significantly well.

Conclusion

ML algorithms can accurately predict compensation in the un-instrumented thoracic spine and pelvis after spinal fusion from the lower thoracic spine to the sacrum. These findings suggest that surgeons may be able to leverage this technology in the preoperative setting to reduce the risk of complications, such as PJK. It is important to note that even a perfectly calibrated model will not eliminate all uncertainty nor will it directly translate into better care for patients. As ML technology continues to be integrated in spine care, the task for the surgeon should be to combine machine learning with experienced clinician judgement to allow for improved delivery of care.