Abstract
The brain generates complex sequences of movements that can be flexibly configured based on behavioral context or real-time sensory feedback1, but how this occurs is not fully understood. We developed a novel ‘sequence licking’ task in which mice directed their tongue to a target that moved through a series of locations. Mice could rapidly branch the sequence online based on tactile feedback. Closed-loop optogenetics and electrophysiology revealed that tongue/jaw regions of primary somatosensory (S1TJ) and motor (M1TJ) cortices2 encoded and controlled tongue kinematics at the level of individual licks. In contrast, tongue ‘premotor’ (anterolateral motor, ALM) cortex3–10 encoded latent variables including intended lick angle, sequence identity, and progress toward the reward that marked successful sequence execution. Movement-nonspecific sequence branching signals occurred in ALM and M1TJ. Our results reveal a set of key cortical areas for flexible and context-informed sequence generation.
The world presents itself to us as a series of sensations arising from our own actions, which in turn elicit further actions in an intricate sensorimotor loop. Orofacial sensorimotor control is essential for exploration, communication, and survival, and is exquisitely orchestrated11–14. To investigate the cortical control of complex orofacial movements, we trained head-fixed mice to use sequences of directed licks to advance a motorized port through 7 consecutive positions, either from left to right or right to left, after an auditory cue (15 kHz, 0.1 s) that signaled the start of a trial (Fig. 1a; Supplementary Video 1). Each transition from one position to the next was driven in a closed-loop by a single lick touching the port. Thus, if a lick missed the port, it would remain at the same position until the tongue eventually made contact. The port was no longer movable after the mouse finished the 7 positions and a water droplet was delivered as a reward after a short delay (0.25 s, or 0.5 s in two mice). The next trial then started with a sequence in the opposite direction after a random inter-trial interval (ITI; mean duration: 6 s).
Fig. 1. Sequence licking task.
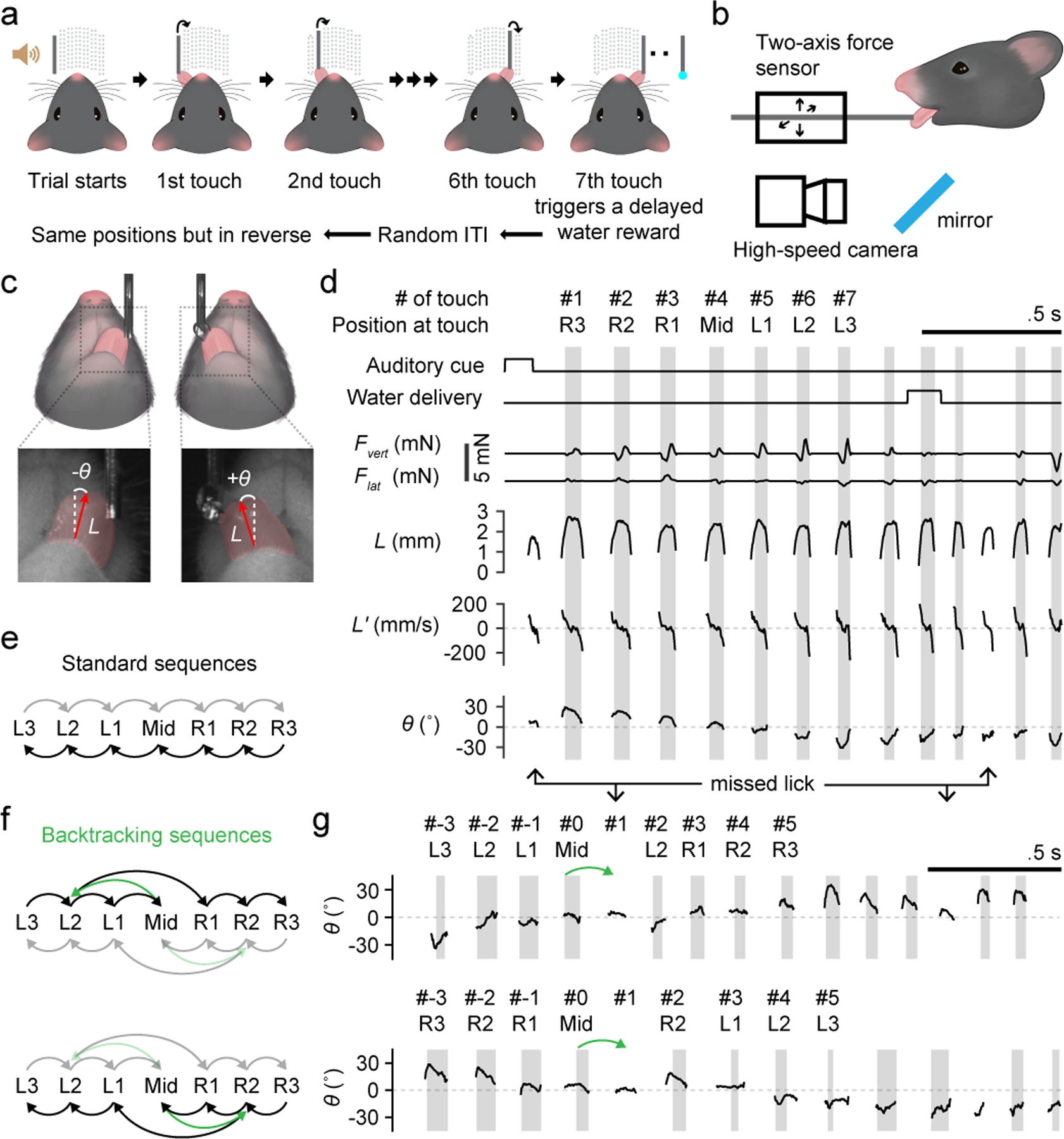
a, Schematic of the (standard) sequence licking task.
b, Schematic of contact force measurement and high-speed (400 Hz) videography in relation to a head-fixed mouse.
c, Top, schematics of the bottom view of a mouse licking at the water port. Bottom, zoomed-in view (5 × 5 mm) of example high-speed video frames. Vectors overlaid in red are outputs from the regression deep neural network (DNN) and point from the base to the tip of the tongue. Tongue length (L) is defined by the vector length. Tongue angle (θ) is the rotation of the vector from midline. Red shading depicts tongue shape.
d, Time series of task events and behavioral variables during an example trial. Variables recorded from the force sensors include the vertical lick force (Fvert, positive acts to lift the port up) and the lateral lick force (Flat, positive acts to push the port to the right). Kinematic variables including L, its rate of change (L’) and θ were derived from high-speed video. Periods of tongue-port contact are shaded in gray and are numbered (#) sequentially. R3, R2, R1, Mid, L1, L2 and L3 indicate the 7 port positions from the rightmost to the leftmost.
e, Transition diagram depicting the two standard sequences. Darker arrows from right to left correspond to the example trial in (d).
f, Transition diagrams depicting sequences with backtracking (green). Darker arrows in each diagram correspond to the example trials on the right in (g).
g, Example trials of a left-to-right sequence (top) and a right-to-left sequence (bottom) where the port backtracked (green arrows) when a mouse touched Mid. Licks including both touches and misses are indexed with respect to the lick at Mid.
We measured instantaneous tongue angle (θ), tongue length (L), vertical and lateral components of contact force (Fvert and Flat), and contact duration during sequences (Methods; Fig. 1b–d; Extended Data Fig. 1a–d). In addition to the continuous θ measurement, we will use scalar angle value θshoot to denote the angle of the tongue shooting out in each lick (Methods), and use capital Θ to represent unified tongue angles after the sign in right-to-left sequences is flipped to pool data from both sequence directions.
Mice modulated each lick to reach different target locations (Extended Data Fig. 1e,f). In addition to stereotypic licking kinematics, expert mice showed remarkable sequence execution speed, with the 7 positions completed in about a second (Extended Data Fig. 1h). Mice performed the task in darkness with no visual cues to guide the licks. Control experiments (Methods) showed that mice did not rely on auditory (Extended Data Fig. 1i) or olfactory (Extended Data Fig. 1j) cues, but did require tactile feedback from the tongue (Extended Data Fig. 1k). Mice reached proficiency in standard sequences (Fig. 1e) after ~1500 trials of training (Methods; Extended Data Fig. 1l–n).
To determine whether sequence generation was “ballistic”, or capable of flexible reconfiguration based on sensory feedback, we varied the task by introducing unexpected port transitions after mice learned standard sequences (Fig. 1f; Supplementary Video 2). On a randomly interleaved subset (1/3 or 1/4) of trials, when a mouse licked at the middle position, the port would backtrack two steps rather than continue to the anticipated position. Mice previously trained only with standard sequences learned (Methods; Extended Data Fig. 2a,b) to detect the change of port transition, branch out to the new position and finish the sequence (Fig. 1g, Extended Data Fig. 2c,d). On average, it took 1 to 2 missed licks before mice quickly relocated the port (Extended Data Fig. 2e). Head-fixed mice can thus learn to perform complex and flexible licking sequences guided by sensory feedback.
Optogenetic inhibition screen
To determine which brain regions contribute to performance of our sequence licking task, and at which points during execution, we performed systematic optogenetic silencing6. In different sessions, bilateral inhibition was centered at each of five regions (Fig. 2a; Extended Data Fig. 3a): ALM15 cortex (also including part of M1TJ), M1B cortex16,17, S1TJ cortex2,18, the barrel field of primary somatosensory cortex (S1BF), and the trunk subregion of primary somatosensory cortex (S1Tr, including part of posterior parietal cortex, PPC). For each region, inhibition was triggered with equal probability (10%) at sequence initiation, mid-sequence, or the start of water consumption (Extended Data Fig. 3b). Stimulation at mid-sequence and at consumption was triggered in closed-loop by the middle touch and by the first touch after water delivery, respectively.
Fig. 2. Optogenetic inhibition and single-unit activity survey across cortical regions during sequence execution.
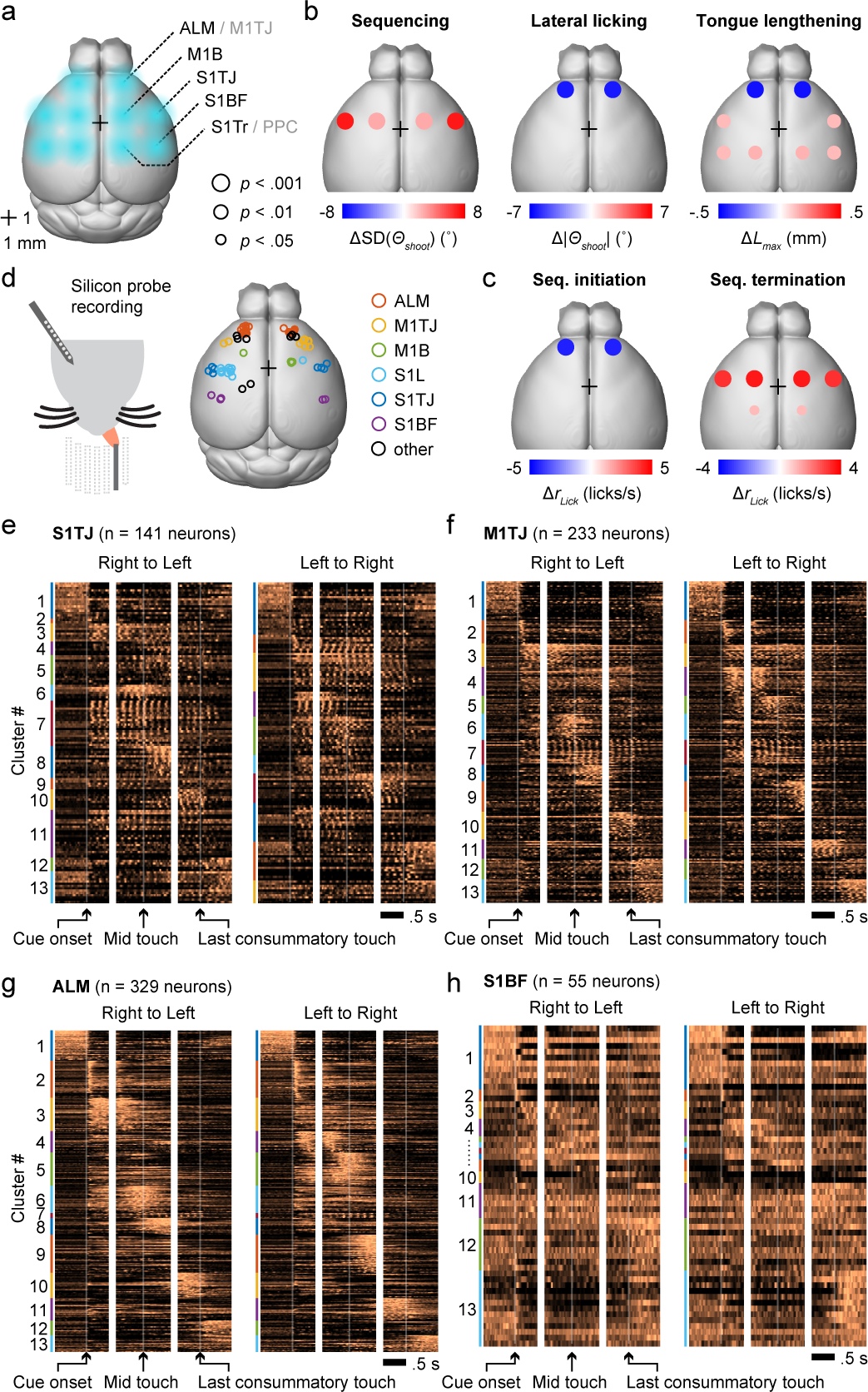
a, Schematic showing the dorsal view of a mouse brain (Allen Mouse Brain Atlas, Brain Explorer 2). Overlaid spots in blue shading depict the five bilateral pairs of sites for illumination of the target cortical regions. Bregma is marked by a 1 mm × 1 mm crosshair.
b, Summary of changes in licking kinematics resulting from bilateral photoinhibition of each area, quantified across all three inhibition periods (Methods). Plots summarize the quantifications shown in Extended Data Fig. 3j. Dot color depicts the amount of increase (red) or decrease (blue) in the indicated behavioral variable for trials with photoinhibition compared with those without. Dot size represents the level of statistical significance. Changes with p > 0.05 are not plotted. Two-tailed hierarchical bootstrap test with Bonferroni correction for 15 comparisons. n = 7 mice.
c, Summary of changes in lick rate resulting from bilateral photoinhibition of each area during either sequence initiation (left) or sequence termination (right). Plots summarize the quantifications shown in Extended Data Fig. 3k (top and bottom rows). Conventions and statistical tests as in (b), but with Bonferroni correction for 30 comparisons.
d, Left, silicon probe recording during the sequence licking task. Right, histologically verified locations of silicon probe recordings.
e, Normalized PETHs of all S1TJ neurons plotted as heatmaps, aligned to three periods in each sequence direction. Neurons are grouped by functional clusters (Results) and labeled by color bands.
f, Same as (e) but for all M1TJ neurons.
g, Same as (e) but for all ALM neurons.
h, Same as (e) but for all S1BF neurons.
TJ, tongue and jaw; B, body; BF, barrel field (whiskers); Tr, trunk; L, limbs.
Somatosensory inputs both provide information about external objects and enable proprioceptive sensing of the body’s position19 for motor control20,21. Missing sensory feedback can make effortless manipulations surprisingly difficult despite unchanged motor capability22. Normally executed sequences were stereotyped across trials. Therefore, in a given time bin during the sequence, across-trial variability in lick angle (quantified by SD(Θshoot)) was relatively low. When S1TJ was inhibited, however, sequences became disorganized and no longer stereotyped (examples in Extended Data Fig. 3g and Supplementary Video 3). As a result, SD(Θshoot) increased significantly compared with no inhibition (Fig. 2b, left). Despite disorganized targeting, the ability to direct licks to the sides (i.e. |Θshoot|) was uncompromised (Fig. 2b, middle). Inhibiting S1TJ also did not shorten the length of licks (Fig. 2b, right), though slight but statistically significant increases were observed. Full quantifications of data summarized in Fig. 2b appear in Extended Data Fig. 3j. Together, these data suggest that S1TJ inhibition left intact the core motor capabilities required for tongue protrusions and licking, but corrupted their proper targeting, possibly due to missing sensory feedback.
In contrast, when inhibiting ALM/M1TJ, mice had reduced ability to direct licks to the sides (Fig. 2b, middle; example in Extended Data Fig. 3h), and showed decreased length of lick (Fig. 2b, right). Inhibiting M1B caused only minor increases in lick angle variability with no decrease in angle deviation or lick length. Inhibiting S1BF or S1Tr changed no aspects of lick control.
ALM has been shown to be important in motor preparation of directed single licks to obtain water reward10,15,23. Here, we found that inhibiting ALM/M1TJ at sequence initiation strongly suppressed production of licking sequences (Fig. 2c, left; Supplementary Video 4). In 4 of 7 mice, licks were largely absent (Extended Data Fig. 3k, top panel under ALM/M1TJ). Inhibiting S1TJ caused more moderate suppression, with no obvious change from inhibiting other regions. When applied at mid-sequence, ALM/M1TJ inhibition also suppressed the production of licks, although less strongly. Inhibiting other regions at mid-sequence showed little or no effect. Full quantifications appear in Extended Data Fig. 3k, top and middle rows.
When a sensorimotor sequence reaches its normal stopping point, one might intuitively expect movement to cease in a passive rather than active manner. To our surprise, when inhibiting S1TJ or M1B at water consumption, mice were impaired at stopping ongoing sequences (Fig. 2c, right; Extended Data Fig. 3k, bottom row; example in Supplementary Video 5). This prolonged licking was not due to additional attempts to reach the port for water, as mice continuously made successful contacts, nor did we inhibit the water-responsive gustatory cortex24,25.
To test the possibility that inhibition of S1TJ or M1B caused persistent lick bouts due simply to spread of inhibition to other regions, we repeated the above experiments with half the illumination power (2 mW) (Extended Data Fig. 3l,m). Effects of ALM/M1TJ inhibition on sequence initiation, tongue length and angle control, and of S1TJ inhibition on angle control, remained largely consistent with, though weaker than, our previous results using higher power (4 mW). At consumption, inhibiting S1TJ or M1B resulted in similarly strong deficits in terminating ongoing sequences (Extended Data Fig. 3m, bottom row). Therefore, the observed deficit in sequence termination was not due to spread of inhibition. Rather, our results indicate that sequence termination is an active process26 mediated collectively by S1TJ and M1B.
Sequence tiling of single-unit responses
We used silicon probes to record from multiple brain regions from both hemispheres (Fig. 2d) during the task, obtaining 1537 single-units and 303 multi-units (Methods; Extended Data Fig. 4a–e) from 57 recording sessions. Perievent time histograms (PETHs) of single-unit spiking (Fig. 2e–h, example neurons in Extended Data Fig. 4f–h) exhibited a wide variety of patterns prior to, during, and after sequence execution. Spiking that gave rise to the PETHs was consistent across trials (Methods; Extended Data Fig. 4i). To present these PETHs in a way that reflects the main themes observed in the population activity, we pooled neurons from all brain regions and clustered their PETHs using non-negative matrix factorization (NNMF; Methods).
We observed that single-neuron responses tile the sequence progression (Fig. 2e–h, Extended Data Fig. 4k), with more ALM neurons tuned to sequence initiation (Extended Data Fig. 4l). S1TJ and M1TJ contained more neurons (e.g. cluster #7; Extended Data Fig. 4k,m) that show greater modulation by individual licks (Extended Data Fig. 4n,o). Patterns of activity arising from these single-unit responses might encode behavioral variables important for sequence control.
Hierarchical population coding
Our sequence licking task requires the brain to encode instantaneous tongue length (L) and angle (θ), presumably both for motor output and sensory feedback. Encoding of velocity (L’) could also be used to indirectly control tongue position. Sequence identity (I) and relative sequence time (τ) can be used to represent the sequence-level organization of individual licks beyond instantaneous control. The variable τ can also serve as a proxy for sequence progress or “distance to goal”. The five behavioral variables, L, L’, θ, I and τ, were measured (or derived) at 2.5 ms resolution (Fig. 3a). Conveniently, any pair of these variables is uncorrelated (Extended Data Fig. 5b). Therefore, being able to encode one is of little or no help with encoding any other.
Fig. 3. Populations code with increasing levels of abstraction across cortical areas.
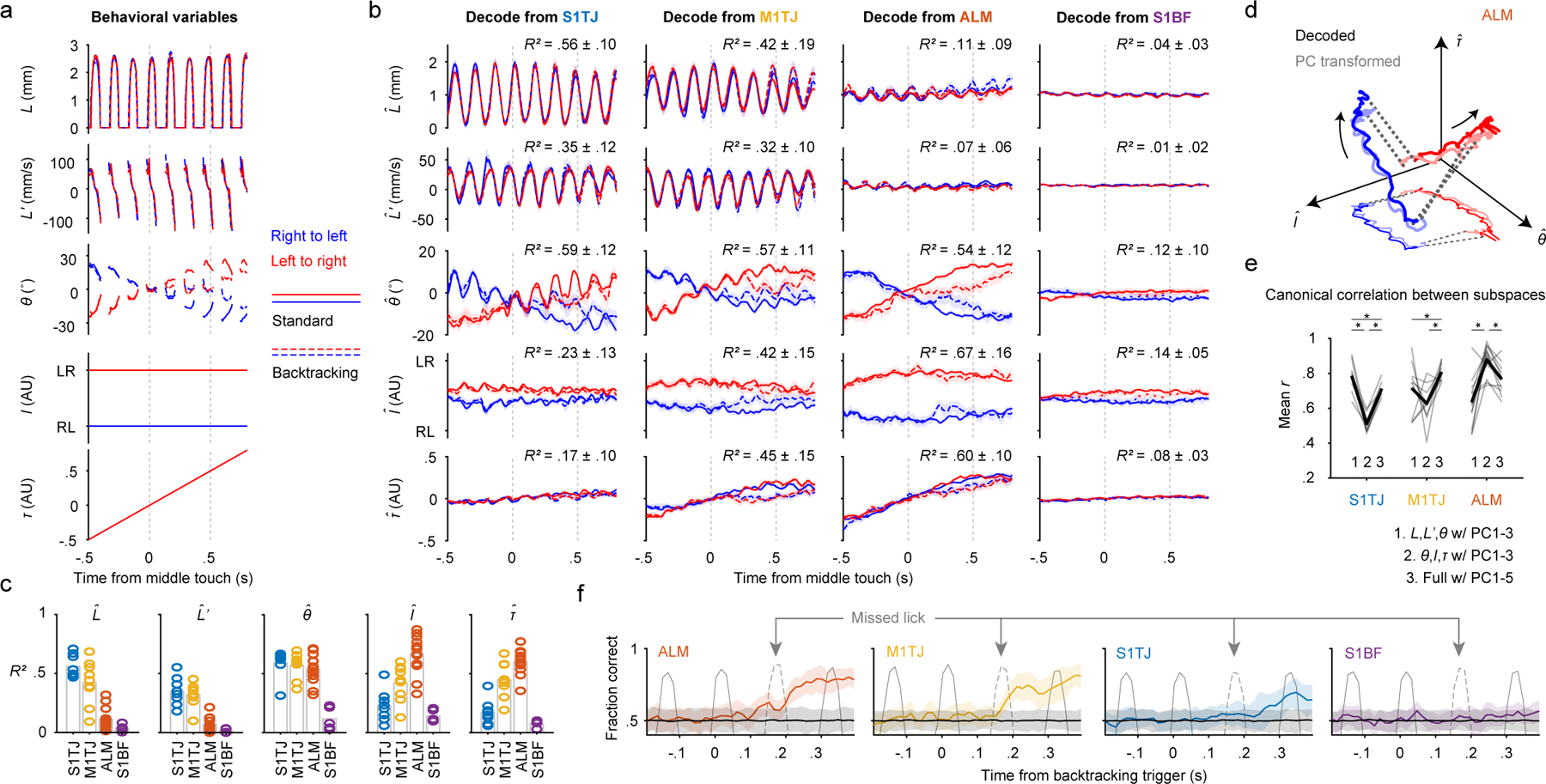
a, Time series of the behavioral variables (mean ± 99% bootstrap confidence interval; n = 2684 trials) for different sequence types. Time points where >80% of trials had no observations are not plotted.
b, Decoding of the five behavioral variables (rows) from populations recorded in S1TJ, M1TJ, ALM, and S1BF (columns). Crossvalidated R2 for each region and variable is given (mean ± SD). S1TJ, n = 8 sessions; M1TJ, n = 9 sessions; ALM, n = 13 sessions; S1BF, n = 5 sessions for all Fig. 3 panels unless otherwise noted. Same plotting conventions as in (a).
c, Bars show means of R2 values from (b). Circles show R2 for individual sessions.
d, Neural trajectories from ALM (mean) during standard sequences (linked by dashed lines). Arrows indicate direction of time. Decoded trajectories (darker thick curves) are overlaid with trajectories (lighter thick curves) in the space of the top 3 PCs, after a linear transformation. A projection into the I-θ plane is depicted with thinner and lighter curves.
e, Mean canonical correlation coefficients (r) for each neural population (gray traces) across three conditions. Average mean r values for each condition are shown in black. ∗ p < 0.001, not significant p > 0.05 otherwise, paired two-tailed permutation test.
f, Classification of standard vs backtracking sequences from population activity. Accuracy is the fraction of trials correctly classified (mean ± 95% hierarchical bootstrap confidence interval; ALM, n = 6 sessions). Colored traces and error shadings are from original data, black traces and shadings from data with randomly shuffled trial labels. Average time series of tongue length are overlaid (gray traces) to show the concurrent behavior. The dashed gray traces indicate licks that unexpectedly missed the port as a result of the port backtracking.
For each recording session, we performed separate linear regressions (Methods) to obtain unit weights (and a constant) for each of the five behavioral variables, such that a weighted sum of instantaneous spike rates from simultaneously recorded units (32 ± 13 units; mean ± SD) plus the constant best predicted the value of a behavioral variable. We used crossvalidated R2 values to quantify how well the recorded population of neurons encoded each behavioral variable27.
The five behavioral variables were decoded from population activity on a single-trial basis (examples in Extended Data Fig. 5c,d). Overall, S1TJ and M1TJ had stronger coding of L and L’ compared with ALM and the control region S1BF (Fig. 3b,c). S1TJ, M1TJ, and ALM, but not S1BF, all showed comparable encoding of θ (Fig. 3b,c). However, the traces of decoded θ in S1TJ and M1TJ contained rhythmic fluctuations that were absent in ALM, despite similar overall levels of encoding of θ (R2 values). These fluctuations indicate that M1TJ and S1TJ encoded θ in a more instantaneous manner, whereas ALM encoded θ in a continuously modulated manner that may provide a control signal for the intended lick angle or represent the position of the target port.
Higher-level cortical regions are in part defined by the presence of more abstract (or latent) representations of sensory, motor and cognitive variables28. Compared with L, L’ and θ, which describe the kinematics of individual licks, sequence identity (I) and relative sequence time (τ) describe more abstract motor variables. In ALM we found the strongest encoding of both I and τ (Fig. 3b,c). Encoding of I and τ became progressively weaker in M1TJ, S1TJ, and S1BF, respectively. Overall, these results reveal a neural coding scheme with increasing levels of abstraction across S1TJ, M1TJ and ALM during the execution of flexible sensorimotor sequences.
Good decoding may come from a small fraction of informative units or from dominant activity patterns across a population. Distinguishing these requires comparing the similarity between activity patterns captured by the coding axes (defined by the vector direction of regression weights), as shown above, and the dominant patterns in population activity identified in an unsupervised manner. In each recording session, we obtained neural trajectories in the coding subspaces (the subspaces spanned by coding axes) and trajectories in principal component (PC) subspaces (the subspaces spanned by the first few PCs) via PCA. Trajectories in PC subspaces depict dominant patterns in population activity but the PCs per se need not have any behavioral relevance. To see if neural trajectories in coding and PC subspaces were the same except for a change (rotation and/or scaling) in reference frame, we used canonical correlation analysis (Methods) to find the linear transformation of the two trajectories such that they were maximally correlated29.
After transformation, trajectories of the ALM population in the subspace of the top three PCs aligned (Fig. 3d) and correlated (Fig. 3e; group 2 in ALM) well with the trajectories in the subspace encoding θ, I, and τ. This indicates that the dominant neural activity patterns in the ALM population encoded θ, I and τ. Since ALM minimally encoded L and L’, including these in the coding subspaces decreased the correlation with PC trajectories (Fig. 3e; group 1 and 3 in ALM). The decoded trajectories and PC trajectories in M1TJ and S1TJ also showed a strong correlation but only when the coding subspaces included L and L’.
Across regions, the sum of variance explained (VE) by the five coding axes reached about half that of the top five PCs (Methods; Extended Data Fig. 5e). The five coding axes were largely orthogonal with each other (Extended Data Fig. 5f), indicating that they not only captured dominant neural dynamics but did so efficiently with little redundancy.
Sequence branching signals in ALM, M1TJ
In backtracking sequences, mice licked back to a previous angle to relocate the port and then progressed through the rest of the sequence. The opposing deflections in the decoded θ from backtracking trials matched this behavior (Fig. 3a,b, dashed curves for θ). This is not surprising since M1TJ and ALM are expected to encode the changed motor program, and S1TJ to signal the resulting proprioceptive or reafferent feedback. However, the motor cortical mechanisms that allow sensory feedback to integrate with unfolding motor programs30–35 could involve a movement-nonspecific signal to indicate sequence branching.
We used linear SVM to classify trials into either backtracking or standard sequences based on population activity at each time bin (Methods). Within each class, about equal numbers of left-to-right and right-to-left sequences were pooled so classifiers could not rely on the coding of specific licking movements. ALM and M1TJ activity started to predict the presence or absence of backtracking during the initial missed lick (Fig. 3f). We randomly shuffled class labels to determine chance-level classification accuracy. Interestingly, S1TJ populations showed only a statistically insignificant trend toward being able to distinguish backtracking from standard sequences (Fig. 3f), at much later time points (Extended Data Fig. 5g). As expected, S1BF populations showed no prediction.
Context-dependent coding of subsequences
Complex sequences can be composed of different combinations of subsequences. The same subsequence can be used in multiple complex sequences, and it is crucial for the brain to keep track of the context in which a subsequence is executed36–39. To search for such sequence context signals, we trained mice on two new sequences where the port steps in a “zigzag” fashion from one side to the other, then steps back, and then again steps to the other side (Fig. 4a,b, Supplementary Video 6). The two sequences have symmetrical movements. By fixing one and shifting the other forward or backward in time, it is possible to find subsequences that have the same licking movements but different sequence contexts (Fig. 4c). There are in total four ways to shift and match subsequences, and we focused on the three licks in the middle (Fig. 4d) for analysis.
Fig. 4. Context-dependent coding of subsequences in ALM.
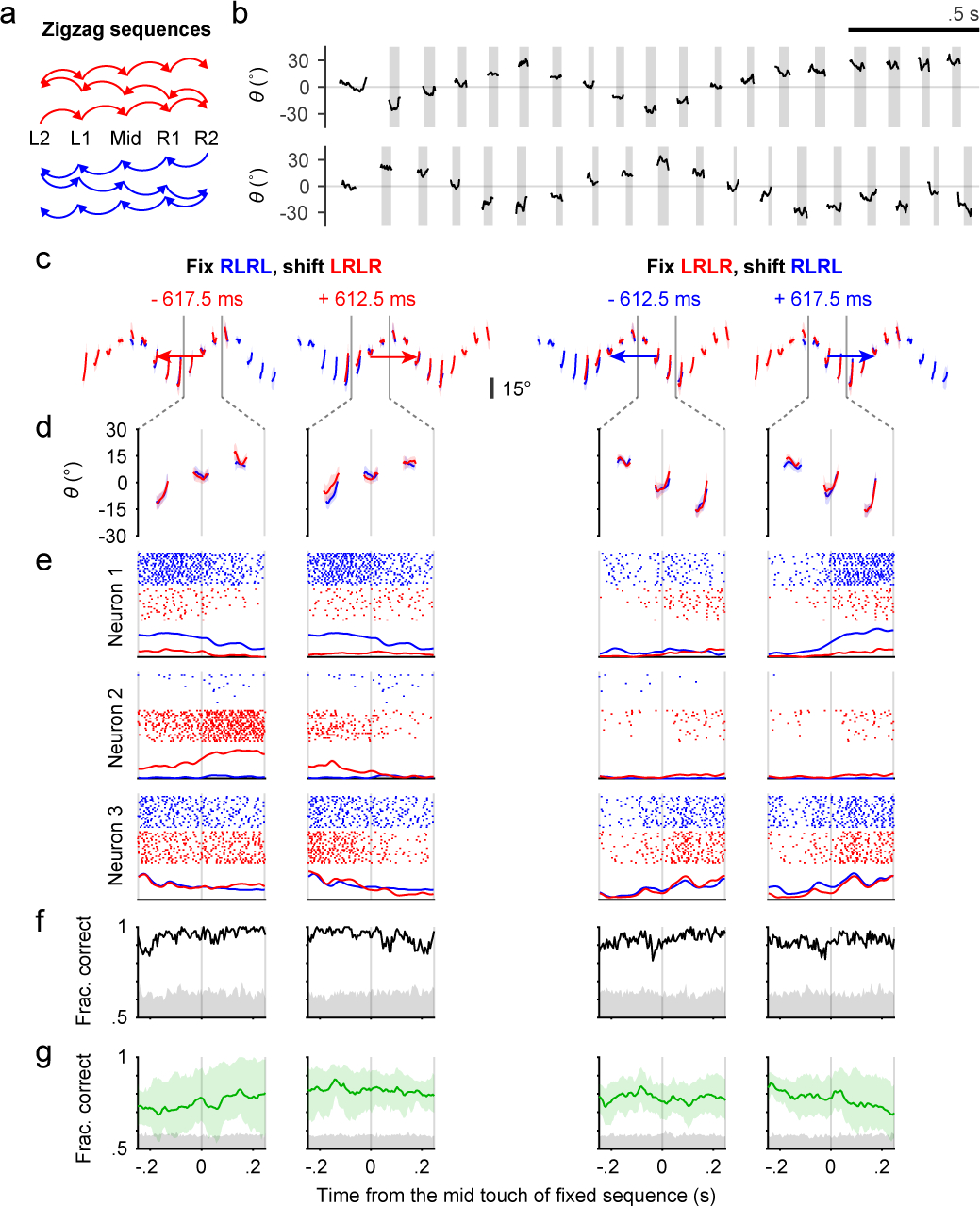
a, Transition diagrams depicting the two “zigzag” sequences, which contain symmetrical transitions.
b, Example trials showing patterns of tongue angle in the two “zigzag” sequences.
c, The four ways to shift and match subsequences. Colored traces show tongue angles from an example session (mean ± SD). Arrow colors indicate the sequence to be shifted. Arrow lengths and the number in milliseconds shows how much the chosen sequence must be shifted in order to match the other. Two gray vertical bars indicate the time window for analysis.
d, Zoomed-in plots of (c) showing the three licks in the middle of matched subsequences.
e, Example rasters and PETHs for three simultaneously recorded neurons. PETHs are normalized to each neuron’s maximum spike rate across the four shifts.
f, Classification accuracy (black trace) for sequence identity based on population activity for the session in (c-e). Chance accuracy (gray shading) was determined by randomly shuffling sequence labels.
g, Similar to (f) but showing mean ± 95% hierarchical bootstrap confidence interval across sessions (n = 6) and mice (n = 3).
Three simultaneously recorded ALM neurons illustrate three types of response (Fig. 4e). The first neuron preferentially fired during blue-colored sequences, and the second during red-colored sequences, whereas the third responded faithfully to the physical movements with no clear sequence preference (Fig. 4e, neurons 1–3, respectively). Using population activity as a predictor, linear SVM classifiers (Methods) were able to predict the sequence identity, or context, in the example session (Fig. 4f) and across sessions and mice (Fig. 4g). Chance-level classification accuracy was determined by shuffling the sequence labels.
Our results provide strong evidence that mouse ALM neurons encode complex sequences with combined information about both physical movements and the latent sequence context.
Reward modulation in ALM
In the decoding analysis for standard sequences, the τ coding axis was identified by fitting models to link neural activity and relative sequence time. We performed the same decoding analysis with “zigzag” sequences and found a similar ramping pattern of τ (Extended Data Fig. 5h). The monotonic coding of τ therefore does not require a constant sequence direction. However, if τ faithfully represents time, the downward deflection of traces from backtracking sequences (Fig. 3b) should not appear, as time advances regardless of what the animals do. This suggests representation of a “distance to goal”40, which might correspond to arrival at the last port position, water delivery, finishing water consumption, etc.
ALM contained single neurons (Extended Data Fig. 6a) that fired actively during sequence execution but abruptly decreased firing upon tongue contact with water, even though mice continued with ~5 consummatory licks (Extended Data Fig. 6b) of similar or more strongly modulated kinematics and force (Extended Data Fig. 6c). The τ decoded from ALM populations showed similar time courses (Extended Data Fig. 6d, top left).
ALM activity was thus modulated by reward41 so as to signal reward expectation in a manner that smoothly increased as mice approached water delivery regardless of sequence direction or lick angle, that was suppressed by the delay of progress upon backtracking, and that terminated at water delivery despite continued licking. Coding of I and θ followed more complex time courses compared to τ (Extended Data Fig. 6d,e).
ALM encodes upcoming sequences
In our task, sequences alternated direction across trials (Extended Data Fig. 7a). Before each trial there was no cue to indicate the starting side. Expert mice nevertheless usually initiated sequences from the correct side without exploring the other (Extended Data Fig. 7b), suggesting internal maintenance of information about target position (TP) during ITIs. Brain regions maintaining such information may contribute to organizing higher-level sequences across trials.
In ALM, we found simultaneously recorded units that fired persistently to specific TP values during the ITI (Extended Data Fig. 7c). A linear model fitted using data from the second prior to cue onset showed smooth population decoding of TP across the span of many trials (Extended Data Fig. 7d). On average, ALM populations showed stronger encoding of TP (Extended Data Fig. 7e,f) compared to other regions. When using this model to decode during sequence execution, the resulting traces from two sequence directions crossed at mid-sequence (Extended Data Fig. 7g), showing similar structure as θ. None of the regions, including ALM, encoded time or a distance to trial start (Extended Data Fig. 7h), perhaps because our ITI contained an exponential portion (Methods) that made the time to trial start unpredictable7.
Together, our results from behavior, population electrophysiology and optogenetics define key sensory and motor cortices in mice that govern hierarchical execution of flexible, feedback-driven sensorimotor sequences.
Methods
Mice
All procedures were in accordance with protocols approved by the Johns Hopkins University Animal Care and Use Committee (protocols: MO18M187, MO21M195). Mice were housed in a room on a reverse light-dark cycle, with each phase lasting 12 hours, and maintained at 20–25°C and 30–70% humidity. Prior to surgery, mice were housed in groups of up to 5, but afterwards housed individually. Fifteen mice (12 male, 3 female) were obtained by crossing VGAT-IRES-Cre (Jackson Labs: 028862; B6J.129S6(FVB)-Slc32a1tm2(cre)Lowl/MwarJ)42 with Ai32 (Jackson Labs: 012569; B6;129S-Gt(ROSA)26Sortm32(CAG-COP4*H134R/EYFP)Hze/J)43 lines. Two (1 male, 1 female) were heterozygous VGAT-ChR2-EYFP (Jackson Labs: 014548; B6.Cg-Tg(Slc32a1-COP4*H134R/EYFP)8Gfng/J)44 mice. Twelve (9 male, 3 female) were wild-type mice, including nine C57BL/6J (Jackson Labs: 000664) mice, one wild-type littermate for each of VGAT-ChR2-EYFP, TH-Cre (Jackson Labs: 008601; B6.Cg-7630403G23RikTg(Th-cre)1Tmd/J)45, and Etv1-Cre−/− (Jackson Labs: 013048)46. Two were male TH-Cre mice. Two (1 male, 1 female) were Advillin-Cre (Jackson Labs: 032536; B6.129P2-Aviltm2(cre)Fawa/J)47 mice. Mice ranged in age from ~2–9 months at the start of training. A set of behavioural testing sessions typically lasted ~1 month (Supplementary Table 1).
Surgery
Prior to behavioural testing, mice underwent the implantation of a metal headpost. For surgical procedures, mice were anesthetized with isoflurane (1–2%) and kept on a heating blanket (Harvard Apparatus). Lidocaine or Bupivacaine was used as a local analgesic and injected under the scalp at the start of surgery. Ketoprofen was injected intraperitoneally to reduce inflammation. All skin and periosteum above the dorsal surface of the skull was removed. The temporal muscle was detached from the lateral edges of the skull on either side and the bone ridge at the temporal-parietal junction was thinned using a dental drill to create a wider accessible region. Metabond (C & B Metabond) was used to cover the entirety of the skull surface in a thin layer, seal the skin at the edges, and cement the headpost onto the skull over the lambda suture.
To make the skull transparent, a layer of cyanoacrylate adhesive was then dropped over the entirety of the Metabond-coated skull and left to dry. A silicone elastomer (Kwik-Cast) was then applied over the surface to prevent deterioration of skull transparency prior to photostimulation. Buprenorphine was used as a post-operative analgesic and the mice were allowed to recover over 5–7 days following surgery with free access to water.
For silicon probe recording, a small craniotomy of about 600 μm in diameter was made for implantation of a ground screw. The skull was thinned using a dental bur until the remaining bone could be carefully removed with a tungsten needle and forceps. Following this, one or more craniotomies of about 1 mm in diameter were made over the sites of interest for silicon probe recording. Craniotomies were protected with a layer of silicone elastomer (Kwik-Cast) on top. Additional craniotomies were usually made in new locations after finishing recordings in previous ones.
Task control
Task control was implemented with an Arduino-based system (Teensy 3.2 and Teensyduino), including the generation of audio (Teensy Audio Shield). Custom MATLAB-based software with a graphical user interface was developed to log task events and change task parameters. Touches between the tongue and the port were registered by a conductive lick detector (Svoboda lab, HHMI Janelia Research Campus), where the mouse acted as a mechanical switch that opened (no touch) or closed (with touch) the circuit. Any mechanical switch has electrical bouncing issues when a contact is weak and unstable. To handle bouncing during loose touches, we merged any contact signals with intervals less than 60 ms.
The auditory cue that signaled the beginning of each trial was a 0.1 s long, 65 dB SPL, 15 kHz pure tone. Touches that occurred during the auditory cue were not used to trigger port movement as they were likely due to impulsive licking rather than a reaction to the cue.
The lick port was motorized in the horizontal plane by two perpendicular linear stages (LSM050B-T4 and LSM025B-T4, Zaber Technologies), one for anterior and posterior movement and the other for left and right. A manual linear stage (MT1/M, Thorlabs) installed in the vertical direction controlled the height of the lick port. The motors were driven by a controller (X-MCB2, Zaber Technologies) which was in turn commanded by the Teensy board via serial interface communication. Although the linear stages were set up in cartesian coordinates, we specified the movement of the port using a polar coordinate system. For a chosen origin of the polar coordinates, the seven port positions were arranged in an arc symmetrical to the midline with equal spacing (in arc length) between adjacent positions (Fig. 1a).
A movement of the lick port was triggered by the onset of a touch during sequence performance. A second port movement could not be triggered within a refractory period of 80 ms, which prevented mice from driving a sequence by constantly holding the tongue on the port (although we never observed such behavior). When a movement was triggered, the port first accelerated (477 or 715 mm/s2) until the maximal speed (39.3 mm/s) was reached, then maintained the maximal velocity, and decelerated until it stopped at the end position. The acceleration and deceleration phases were always symmetrical, such that the maximal velocity might not be reached if the distance of travel was short.
The movement was typically in a straight line. For 4 of the 9 mice, when the two positions were not adjacent (e.g. at backtracking and the following transition), the port would move in an outward half circle whose diameter was the linear distance separating the two positions. This arc motion minimized the chance of mice occasionally catching the port prematurely before the port stopped. Nevertheless, catching the port prematurely did not trigger the next transition in a sequence because, in this case, the port movement could only be triggered again after 200 ms from the start of backtracking (and 300 ms after the following touch). As a result, mice always needed to touch the port at the fully backtracked position in order to continue progress in a sequence.
The control of port movement was similar for zigzag sequences except that five port positions were used instead of seven, the refractory period before the next trigger was 100 ms, the acceleration was 2000 mm/s2, the maximal speed was 75 mm/s, and every port movement traveled along an outward half circle.
Mice performed the task in darkness with no visual cues about the position of the port. To prevent mice from using sounds emitted by the motor to guide their behavior, we played two types of noise throughout a session. The first was a constant white noise (cutoff at 40 kHz; 80 dB SPL) and the second was a random playback (with 150–300 ms interval) of previously recorded motor sounds during 12 different transitions.
Two-axis optical force sensors
A stainless steel lick tube was fixed on one end to form a cantilever. Mice licked the other free end, producing a small displacement (< ~0.1 mm at the tip for 5 mN) of the tube. Two photointerrupters (GP1S094HCZ0F, Sharp) placed along the tube (Extended Data Fig. 1c,d) were used to convert the vertical and horizontal components of displacement into voltage signals. Specifically, the cantilever normally blocked about half of the light passing through, outputting a voltage value in the middle of the measurement range. Pushing the tip down caused the cantilever to block more light at the vertical sensor and thereby decreased the output voltage; conversely, less force applied at the tip resulted in increased voltage. For the horizontal sensor, pushing the tube to the left or right decreased or increased the voltage output, respectively. Output was amplified by an op-amp then recorded via an RHD2000 Recording System (Intan Technologies).
By design (the circuit diagram and the displacement-response curve are available in the GP1S094HCZ0F datasheet), the force applied at the tip of the lick tube and the sensor’s output voltage follow a near linear relationship within a range of forces. To find this range, we measured the voltages (relative to baseline) with different weights added to the tip. Excellent linearity (R2 = 0.9999) was achieved up to >20 mN (Extended Data Fig. 1d). In contrast, the maximal force of a lick was on average about 4 mN (Extended Data Fig. 1f).
The motorization of the lick tube introduced mechanical noise to the force signals. The spectral components of these noises were mainly at 300 Hz and its higher harmonics, presumably due to the resonance frequency of the tube, whereas the force signal induced by licking occupied much lower frequencies. Therefore, we low-pass (at 100 Hz) filtered the original signal (sampled at 30 kHz) to remove the motor noise. Additional interference came from the 850 nm illumination light used for high-speed video, which leaked into the optical sensors (mainly in early experiments with 2 mice) and caused slow fluctuations in the baseline over seconds. To mitigate this slow drift, we used a baseline estimated separately for each individual lick as follows. We first masked out the parts of the signal when the tongue was touching the port, then linearly interpolated to fill in these masked out lick portions using the neighboring (i.e. no touch) values. These interpolated time series served as the baseline for each lick. Since the lick force was only a function of voltage change compared to baseline, the above procedure would at most negligibly affect the force estimation. Due to the dependency of this procedure on complete touch detection, we excluded 8 sessions from behavioral quantifications in Fig. 1, Extended Data Figs. 1 and 2 where only touch onsets were correctly registered.
High-speed videography and tongue tracking
High-speed video (400 Hz, 0.6 ms exposure time, 32 μm/pixel, 800 pixels × 320 pixels) providing side- and bottom-views of the mouth region was acquired using a 0.25X telecentric lens (55–349, Edmund Optics), a PhotonFocus DR1-D1312-200-G2-8 camera, and Streampix 7 software (Norpix). Illumination was via an 850 nm LED (LED850-66-60, Roithner Laser) passed through a condenser lens (Thorlabs).
Three deep convolutional neural networks were constructed (MATLAB 2017b, Neural Network Toolbox v11.0) to extract tongue kinematics and shape from these videos. The first network classified each frame as “tongue-out” if a tongue was present, or “tongue-in” otherwise. This network was based on ResNet-50 48 (pretrained for ImageNet), but the final layers were redefined to classify the two categories using a softmax layer and a classification layer that computes cross-entropy loss. A total of 37658 frames were manually labeled in which 1611 frames were set aside as testing data. Image augmentation was performed to expand the training dataset. A standard training scheme was used with a mini-batch size of 32 and a learning rate of 1×10−4 to 1×10−5. The fully trained network achieved a high accuracy in classifying the validation data (Extended Data Fig. 1a).
The second network assigned a vector from the base to the tip of the tongue in each frame classified as “tongue-out”. L and θ were derived from this vector (Fig. 1c). A total of 12095 frames were manually labeled in which 643 frames were used only for testing. The architecture and training parameters of this network are similar to those of the classification network except that the final layers were redefined to output the x and y image coordinates of the base, tip and two bottom corners (not used in analysis) of the tongue with mean absolute error loss. The regression error of the fully trained network in testing data was 3.1 ± 5.4° for θ and 0.00 ± 0.13 mm for L (mean ± SD). This performance was comparable to human level (Extended Data Fig. 1b). Specifically, a subset of frames (separate from testing data) was labeled by each of five human labelers. The variability in human judgement was quantified by the differences between L and θ from individual humans and the human mean for each frame. We also computed the differences between L and θ from the network and the human mean for each frame. The two distributions showed a comparable variability, although the network showed small biases (L: humans 0 ± 0.11 mm, network −0.05 ± 0.10 mm; θ: humans 0 ± 5.7° SD, network 3.3 ± 5.5° SD; mean ± SD).
In a subset of trials and in frames classified as “tongue-out”, the third network, a VGG13-based SegNet49, extracted the shape of the tongue by semantic image segmentation, i.e. classifying each pixel as belonging to a tongue or not. Human labelers used a 10-vertex polygon to encompass the area of the tongue in a total of 3856 frames. The training parameters were similar to the other networks except for a mini-batch size of 8 and a learning rate of 1×10−3.
Behavioural training
Behavioural sessions occurred once per day during the dark phase and lasted for approximately an hour or until the mouse stopped performing, whichever came earlier. Mice would receive all of their water from these sessions, unless it was necessary to supply additional water to maintain a stable body weight. The amount of water consumed during behaviour was measured by subtracting the pre-session volume of water in the dispenser from the post-session volume. On days where their behaviour was not tested they received 1 ml of water. Mice were water restricted (1 ml/day) for at least 7 days prior to beginning training. Whiskers and hairs around the mouth were trimmed frequently to avoid contact with the port.
The precise position of the implanted headpost varied across mice, so each mouse required an initial setup of the lick port’s positions. The lick port moved in an arc with respect to a chosen origin (see “Task control”). The origin was initially set at the midline of the animal and 2 mm posterior from the posterior face of the upper incisors. If there was any yaw of the head, the whole arc was rotationally shifted accordingly. The lick port’s z-axis was manually adjusted until the lick port was approximately 1 mm below the interface between upper and lower lips when the mouth was closed.
In initial training sessions, the distance between the leftmost (L3) and the rightmost (R3) lick port position was reduced, the radius of the arc was shortened, and the water reward was larger. As mice learned the task, both the L3 to R3 distance and the radius of the arc were gradually increased over a few days of training (Extended Data Fig. 1m). The difficulty of the task was increased whenever the mouse showed improvements in performing the task at the current port distance, radius, and reward size. The difficulty remained constant in two conditions: either when the maximum set of parameters had been met (a radius of 5 mm for males and 4.5 mm for females) or if the mouse appeared demotivated (typically indicated by a significant decrease in the number of trials and licks). During the initial training sessions, water was occasionally supplemented at other points during the sequence to encourage licking behaviour. The amount of water reward per trial was eventually lowered to ~3 μL. For 3 of the 33 mice included in this study, we first trained them to lick in response to the auditory cue with the lick port staying at fixed positions. After mice responded consistently to the go cue, we shifted to the complete task with gradually increased difficulty. Although the 3 mice performed similarly to others when well trained, this procedure proved to be less efficient than beginning with the complete task.
Once a mouse had become adept at standard sequences, they were trained on the backtracking sequences. The first 9 fully trained mice were used in backtracking related analyses; later mice used for other purposes were not always fully trained in backtracking. For 5 of the 9 mice, we first trained them with backtracking trials in only one direction and added the other direction once they mastered the first. For 3 of the 9 mice, backtracking trials and standard trials were organized into separate blocks of 30 trials each. In developing this novel task, we tested subtle variations in the detailed organization of trial types, such as varying the percentage of backtracking trials in a block, or different forms of jumps in the port position. Details appear in Supplementary Table 1. Two of these 3 mice continued to perform the block-based backtracking trials during recording sessions. All 9 mice eventually learned backtracking sequences but showed mixed learning curves (Extended Data Fig. 2a,b). About 3 mice were more biased toward previously learned standard sequences and tended to miss the port many times before relocating the lick port through exploration. The other 6 mice more readily made changes.
The shaping processes for zigzag sequences in a total of 4 mice all differed. Empirically, however, training on standard sequences first until proficiency and then on zigzag sequences could produce desirable performance.
Hearing loss
Hearing loss experiments were performed to exclude the possibility that mice used sounds produced by the motors to localize the motion of the lick port during sequence performance. To induce temporary hearing loss (~27.5 dB attenuation)50, we inserted two earplugs made of malleable putty (BlueStik Adhesive Putty, DAP Products Inc.) into the ear canal openings bilaterally under microscopic guidance. Earplugs were shaped like balls and then formed appropriately to cover the unique curvature of each ear canal. When necessary, the positioning of the earplugs was readjusted, or larger balls were inserted. Five well trained mice performed one “earplug” session and one control session. Mice did not have experience with earplugs prior to the earplug session. In earplug sessions, mice were first anesthetized under isoflurane to implant earplugs (taking 11–12.5 mins), then were put back in the homecage to recover from anesthesia (taking 10–11.5 mins), and performed the task after recovery. In control sessions, mice were anesthetized for the same duration and allowed to recover for the same duration before performing the task.
Odor masking
Odor masking experiments were performed to exclude the possibility that mice used potential odors emanating from the lick port to localize its position during sequence performance. A fresh air outlet (1.59 mm in diameter) was placed in front of the mouse and aimed at the nose from ~2 cm away with ~45° downward angle. We checked the coverage of air flow (2 LPM) by testing whether a water droplet (~3 μL) would vigorously wobble in the flow at various locations, and confirmed that both the nose and all the seven port positions were covered. Prior to the test session, head-fixed mice were habituated to occasional air flows when they were not performing sequences. In the test session, the air flow was turned off first and turned on continuously after the 100th trial (in four mice) until the end of the session, or turned on first and turned off after the 100th trial (in two mice). The air-off period served as the control condition for the air-on period.
Tongue numbing
Tongue numbing experiments were performed to directly test whether proper sequence execution depended on tactile feedback from the tongue. The sodium channel blocker lidocaine is used clinically to block signals from somatosensory afferents in the periphery. Before a behavioural session, mice were anesthetized under isoflurane, and a cotton ball soaked with 2% lidocaine (for numbing) or saline (as control) was inserted into the oral cavity, covering the tongue. After 10 min, the cotton ball was removed, the anesthesia was terminated, and the mice woke up in a behavioral setup to perform standard sequences. Since lidocaine has a relatively short half-life, we limited the analysis to trials performed within ~30 min after removing the cotton ball. One of the six mice was excluded from analysis as it was unable to perform the task within ~30 min after its tongue was numbed.
Electrophysiology
Two types of silicon probe were used to record extracellular potentials. One (H3, Cambridge Neurotech) had a single shank with 64 electrodes evenly spaced at 20 μm intervals. The other (H2, Cambridge Neurotech) had two shanks separated by 250 μm, where each shank had 32 electrodes evenly spaced with 25 μm intervals. Before each insertion, the tips of the silicon probe were dipped in either DiI (saturated), CM-DiI (1 mg/mL) or DiD (5–10 mg/mL) ethanol solution and allowed to dry. Probe insertions were either vertical or at 40° from the vertical line depending on the anatomy of the recorded region and surgical accessibility. Once fully inserted, the brain was covered with a layer of 1.5% agarose and ACSF, and was left to settle for ~10 minutes prior to recording. Based on the depth of the probe tip, the angle of penetration, and the position of these sites, the location of units could be determined. Units recorded outside the target structure were excluded from analysis.
Extracellular voltages were amplified and digitized at 30 kHz via an RHD2164 amplifier board and acquired by an RHD2000 system (Intan Technologies). No filtering was performed at the data acquisition stage. Kilosort51 was used for initial spike clustering. We configured Kilosort to highpass filter the input voltage time series at 300 Hz. The automatic clustering results were manually curated in Phy for putative single-unit isolation. We noticed a previously reported issue of Phy double counting a small fraction of spikes (with exact same timestamps) after manually merging certain clusters, thus duplicated spike times in a cluster were post-hoc fixed to keep only one.
Cluster quality was quantified using two metrics (Extended Data Fig. 4a–c,e). The first was the percentage of inter-spike intervals (ISI) violating the refractory period (RPV). We set 2.5 ms as the duration of the refractory period and used 1% as the RPV threshold above which clusters were regarded as multi-units. It has been argued that RPV does not represent an estimate of false alarm rate of contaminated spikes52,53 since units with low spike rates tend to have lower RPV while high spike rate units tend to show higher RPV even if they are contaminated with the same percentage of false positive spikes. Therefore, we estimated the contamination rate based on a reported method52. A modification was that we computed a cluster’s mean spike rate from periods where the spike rate was at least 0.5 spikes/s rather than from an entire recording session. As a result, the mean spike rate reflected more about neuronal excitability than task involvement. Any clusters with more than 15% contamination rate were regarded as multi-units. Combining these two criteria in fact classified fewer single-units than using a single, though more stringent, RPV of 0.5%. A low RPV can fail potentially well isolated fast spiking interneurons whose ISIs can frequently be shorter than the set threshold.
Photostimulation
We used the “clear-skull” preparation13, a method that greatly improves the optical transparency of intact skull (see the Surgery section of the Methods), to non-invasively photoactivate channelrhodopsin-expressing GABA-ergic neurons and thus indirectly inhibit nearby excitatory neurons (Extended Data Fig. 3a).
Bilateral stimulation of the brain was achieved using a pair of optic fibers (0.39 NA, 400 μm core diameter) that were manually positioned above the clear skull prior to the beginning of each behavioural session. These optic fibers were coupled to 470 nm LEDs (M470F3, Thorlabs). The illumination power was externally controlled via WaveSurfer (http://wavesurfer.janelia.org). Each stimulation had a 2 s long 40 Hz sinusoidal waveform with a 0.1 s linearly modulated ramp-down at the end. The peak powers in the main experiments were 16 mW and 8 mW. We used the previously reported 50% transmission efficiency of the clear-skull preparation54 and report the estimated average power in the Results. There was a 10% chance of light delivery triggered at each of the following points in a sequence: cue onset, the middle touch, or the first touch after water delivery. To ensure that the light from photostimulation did not affect the mouse’s performance through vision, we set up a masking light with two blue LEDs directed at each of the mouse’s eyes. Each flash of the masking light was 2 s long separated by random intervals of 5–10 s. This masking light was introduced several training sessions in advance of photostimulation to ensure the light no longer affected the behaviour of the mouse. In addition, the optic fibers were positioned to shine light from ~5–10 mm above the animal’s head on these days leading up to photostimulation.
In a subset of silicon probe recording sessions (related to Extended Data Fig. 3c–f), we used an optic fiber (0.3 NA, 400 um core diameter) to simultaneously photoinhibit the same (within 1 mm) or a different cortical region (~1.5 or ~3 mm away) via a craniotomy. The tip of the fiber was kept ~1 mm away from the brain surface. For testing the efficiency of photoinhibition, the same 2 s photostimulation was applied but only at the mid-sequence, with 7.5% probability for each of the four powers (1, 2, 4 and 8 mW). For each isolated unit, the photo-evoked spike rate was normalized to that obtained during the equivalent 2 s time window without photostimulation. To avoid a floor effect, we also excluded units that on average fired less than one spike during the no stimulation windows. We classified units as putative pyramidal neurons if the width of the average spike waveform (defined as time from trough to peak) was greater than 0.5 ms, and as putative fast spiking (FS) interneurons if shorter than 0.4 ms or if units had more than twice the firing rate during 8 mW photostimulations than during periods of no stimulation.
With the light powers we used in the main experiments (4 mW each hemisphere), light within 1 mm distance reduced mean spike rate of putative pyramidal cells (Extended Data Fig. 3c–e) by 91%, light at ~1.5 mm away by 61%, and ~3 mm away by 19% in behaving animals (Extended Data Fig. 3f). Interestingly, the mean spike rate of putative fast spiking (FS) neurons at ~3 mm away was also reduced by 19%, rather than showing an increase due to photoactivation, suggesting that the decreased activity of both pyramidal and FS neurons was likely due to a reduction of cortical input. In contrast, light shined within 1 mm increased the mean spike rate of FS neurons by 739% and at ~1.5mm by 140%.
Histology
Mice were perfused transcardially with PBS followed by 4% PFA in 0.1 M PB. The tissue was fixed in 4% PFA at least overnight. The brain was then suspended in 3% agarose in PBS. A vibratome (HM 650V, Thermo Scientific) cut coronal sections of 100 μm that were mounted and subsequently imaged on a fluorescence microscope (BX41, Olympus). Images showing DiI and DiD fluorescence were collected in order to recover the location of silicon probe recordings. The plotted coordinates of recording sites (Fig. 2d) were randomly jittered by ± 0.05 mm to avoid visual overlap.
General data analysis
All analyses were performed in MATLAB (MathWorks) version 2019b unless noted otherwise.
The first trial and the last trial were always removed due to incomplete data acquisition. Trials in which mice did not finish the sequence before video recording stopped were excluded from the analyses that involved kinematic variables of tongue motion.
We assigned mice of appropriate genotypes to experimental groups arbitrarily, without randomization or blinding. We did not use statistical methods to predetermine sample sizes. Sample sizes are similar to those reported in the field.
Behavioral quantifications
The duration of individual licks was variable. In order to average quantities within single licks (Fig. 1 and Extended Data Figs. 1,2,6), we first linearly interpolated each quantity using the same 30 time points spanning the lick duration (from the first to the last video frame of a tracked lick). L’ was computed before interpolation. When the tongue was short, the regression network showed greater variability in determining θ and sometimes produced outliers. Thus, we detected and replaced outliers using the MATLAB “filloutliers” function (with “nearest” and “quartiles” options), and only included θ when L was longer than 1 mm. In addition, any “lick” with a duration shorter than 10 ms was excluded.
For licks occurring at the most lateral positions, the tongue would typically “shoot” out and quickly, but only briefly, reach a maximal deviation from midline (|θ|max) (Extended Data Fig. 1g). As a result, the onset of touch mostly occurred around |θ|max. When analyzing licks which may or may not have contact, we use θshoot, defined as the θ when L reaches 0.84 maximal L (Lmax), to succinctly depict the lick angle (Extended Data Fig. 1g).
The instantaneous lick rate was computed as the reciprocal of the inter-lick interval. The instantaneous sequence speed was defined as the reciprocal of the duration from the touch onset of a previous port position to the touch onset of the next.
Values in the learning curves (Extended Data Figs. 1l,m and 2a,b) were averaged in bins of 100 trials, with 50% overlap of consecutive bins.
The behavioral effects of photoinhibition (Extended Data Fig. 3j–m) were quantified in two steps. First, we used 0.2 s time bins to compute Θshoot, Lmax, the rate of licks, and the rate of touches as functions of time for each trial. The time series of SD(Θshoot) was computed from binned Θshoot across trials in each experiment condition and each session. Second, bins within a time window during photoinhibition (or equivalent time for trials without inhibition) were averaged to yield a single number. The time window was typically 1 s following the start of photoinhibition. The shorter window helped to minimize the effects “bleeding over” from mid-sequence to initiation, and from consumption to mid-sequence. However, this was not an issue for the consumption period, and we instead used the 2 s window during which light was delivered (Fig. 2c, right; “Cons” in Extended Data Fig. 3k,m). Fig. 2b,c present the same results quantified in Extended Data Fig. 3j–m but directly plotting changes in means between conditions on schematic brain images.
Standardization of inter-lick intervals within lick bouts
Due to individual variability, different mice tended to lick at slightly different rates within lick bouts. The same mouse might also perform a bit faster in one sequence direction than the other. Even in a given direction, a mouse might start faster and then slow down a little, or go slower first and faster later. When aligning trials from heterogeneous sources, a 10% difference in lick rate, for instance, will result in a complete mismatch (reversed phase) of lick cycle after only 5 licks. Therefore, prior to the analyses that are sensitive to inconsistent lick rates (Figs. 2e–h, 3, 4, and Extended Data Figs. 4, 5, 6, 7, except for Extended Data Fig. 4f,g,h), we linearly stretched or shrunk inter-lick intervals (ILIs) within each lick bout to a constant value of 0.154 s (i.e. 6.5 licks/s), which is around the overall mean. The lick timestamps used to compute ILIs were the mid time of the duration of each lick. A lick bout was operationally defined as a series of consecutive licks in which every ILI must be shorter than 1.5 × the median of all ILIs in the entire behavioral session. ILIs outside lick bouts were unchanged. For ease of programming, we compensatorily scaled the time between the last lick of a trial and the start of the next trial to maintain an unchanged global trial time. Original time series, including spike rates and L’, were obtained prior to standardizing ILIs. After standardization, the behavioral and neural time series were resampled uniformly at 400 samples/s.
Trial selection for standard and backtracking sequences
After standardizing lick bout ILIs, we used a custom algorithm to select a group of trials with the most similar sequence performance. First, all trials of the same sequence type in a behavioral session were collected and a time window of interest was determined. In Fig. 2e–h and Extended Data Fig. 4, we used 0 to 0.5 s from cue onset, −1 to 1 s from middle touch, and −0.5 to 0.7 s from last consummatory touch for the respective periods. In Fig. 3, we used −1 to 1 s from middle touch. In Extended Data Fig. 6, we used −0.5 to 1 s from the first lick touching water. Next, for each trial, we created three time histograms (with 10 ms bin size), one for all licks, one for all touches, and one for touches that triggered port movements. The three time histograms were then smoothed by a Gaussian filter (100 ms kernel width, 20 ms SD). Concatenating them along time gave a single feature vector that depicts the licking pattern and performance for the trial. Finally, pairwise euclidean distances were computed among feature vectors of all candidate trials and we chose a subset of N trials with the lowest average pairwise distance, i.e. those that have the most similar lick and touch patterns. The number N was set to 1/3 of available candidate trials with a minimal limit of N = 10 trials. We used this relatively low fraction mainly to handle the greater behavioral variability in sequences with backtracking. To handle trial-to-trial variability in sequence initiation time (defined as the interval from the cue onset to first touch onset), which was not captured in our feature vectors, prior to clustering we limited trials to those with sequence initiation time less than 1 second.
Trial selection and subsequence matching for zigzag sequences
After standardizing lick bout ILIs, we limited candidate trials to those with perfect sequence execution, i.e. no missed licks or breaks. To find the time shift that gave the best match between two subsequences, as illustrated in Fig. 4c, we first computed the median time series of tongue angles (θ) for each of the two sequence types. Next, we identified the best time shifts as those corresponding to the peaks of a cross-correlogram between the two time series.
Analysis of zigzag sequences was intended to reveal if neurons encoded sequence context (i.e. identity) during periods with the same subsequence movements. To aid this purpose, we further selected trials whose θ were closest to the median θ computed from trials of either sequence type pooled together, unless the resulting number of trials was less than 1/3 of all candidate trials.
Hierarchical bootstrap
Directly averaging trials pooled across animals assumes that data from different animals, acquired in different sessions, come from the same distribution. Potentially meaningful animal-to-animal and session-to-session variability is thereby underestimated. To account for this variability, where noted we performed a hierarchical bootstrap procedure55 when computing confidence intervals and performing statistical tests. In each iteration of this procedure, we first randomly sampled animals with replacement, then, from each of these resampled animals, sampled sessions with replacement, and then trials from each of the resampled sessions. The statistic of interest was then computed from each of these bootstrap replicates.
PETH and NNMF clustering
Spike rates were computed by temporal binning (bin size: 2.5 ms) of spike times followed by smoothing (15 ms SD Gaussian kernel). The smooth PETHs were computed by averaging spike rates across trials. Each unit has 6 PETHs: 3 time windows (for sequence initiation, mid-sequence and sequence termination) each in 2 standard sequences (left to right and right to left). We excluded inactive units whose maximal spike rate across the 6 PETHs was less than 10 spikes/s. For the rest, we normalized PETHs of each unit to this maximal spike rate.
To evaluate the consistency of neuronal spiking across trials, we quantified the uncertainty in PETHs using a variant of bootstrap crossvalidation. Specifically, for each neuron and in a given run, we randomly split the trials into two halves and computed PETHs with each half. We then computed the root mean squared error (RMSE) between the two sets of PETHs, producing a single RMSE value. This procedure was performed for every neuron and was repeated 200 times. The mean RMSE value for each neuron across the 200 runs is shown in Extended Data Fig. 4i.
To construct inputs to NNMF, the 6 PETHs of each unit were downsampled from 2.5 ms per sample to 25 ms per sample and were concatenated along time to form a single feature vector.
NNMF is a close relative of principal component analysis (PCA) and has gained increasing popularity for processing neural data56. The algorithm finds a small number of activity patterns (non-negative left factor, analogous to principal components in PCA) along with a set of weights for each neuron (non-negative right factor), so that the original PETHs can be best reconstructed by weighted sums of those activity patterns. As a result, a small number of activity patterns (or dimensions) is usually able to capture the main structure of the original PETHs, and a neuron’s weights quantify the degree to which its activity reflects each pattern. In the context of clustering, each pattern describes representative activity of a cluster, and the pattern with the greatest weight for a neuron determines its cluster membership.
NNMF was performed using the MATLAB function “nnmf” with default options. In order to find the best number of clusters, we tested a range of numbers with bootstrap crossvalidation to see what cluster number produced the most consistent cluster membership. In each bootstrap iteration, NNMF with a given cluster number was applied using 50% of randomly sampled neurons. The extracted activity patterns were used to compute cluster memberships for the other 50% of neurons that were held-out. This process was repeated 1000 times. The final cluster membership of a neuron was the one that had the highest likelihood of containing that neuron. We ran this method with the number of clusters set to each value from 6 to 20, and found that 13 clusters achieved the best consistency (Extended Data Fig. 4j), quantified as the mean likelihood that a neuron was grouped in the same cluster across all bootstrap iterations.
Quantification of rhythmic licking modulation in spike PETHs
Neuronal responses modulated by rhythmic licking should show a modulation frequency that matches the rate of licks (~6.5 licks/s during sequence execution), with a phase shift that may vary from neuron to neuron. Therefore, we first quantified the rhythmicity by fitting a sinusoidal function, f(t) = A · sin(2πωlickt + Φ) + C, to each PETH (Extended Data Fig. 4n), where the free parameter Φ shifts the function in phase, A and C scale and offset the function vertically to match the neuronal firing rate, and ωlick is a constant of 6.5. Next, a Pearson’s correlation coefficient (r) was computed between a mid-sequence PETH and its best fitted sinusoids. Every neuron had two r values, one for each sequence direction. The final rhythmicity was represented by the average of the two (ravg).
Principal component analysis (PCA)
The input to PCA was the normalized spike rates of simultaneously recorded single- and multi-units (Extended Data Fig. 4d). The original spike rates were first computed by temporal binning (2.5 ms bin size, i.e. 400 samples/s) of spike times followed by smoothing (15 ms SD Gaussian kernel). To obtain normalized spike rates, we divided the original spike rates by the maximum spike rate or 5 Hz, whichever was greater. We adopted this “soft” normalization technique29 to prevent weakly firing units from contributing as much variance as actively firing units. The percent variance explained (VE) by principal components was simply derived from the singular values.
Linear regression and decoding
A linear model can be expressed as
where t is the time in a recording session, n is the number of simultaneously recorded units, yt is the behavioral variable at t, is the normalized spike rate of the i-th unit at t, wi is the regression coefficient for the i-th unit, c is the intercept, ϵt is the error term, and is the matrix notation form of the summed multiplications.
The normalized population spike rates were computed in the same way as those for PCA. Note that though the normalization was only necessary for PCA, it did not affect the goodness of fit, R2, of linear models. The behavioral variable was either tongue length (L), tongue velocity (L’), tongue angle (θ), sequence identity (I), target position (TP), or relative sequence time (τ) (Fig. 3a, Extended Data Figs. 5,7). L, L’ and θ were directly available at 400 samples/s. However, these variables had values only when the tongue was outside of the mouth. Therefore, samples without observed values were either set to zero (for L) or excluded from regression (for L’ and θ). I was defined as 1 if the sequence was from right to left and 2 if left to right. τ simply took sample timestamps as its values. TP was the same as I but defined based on the upcoming sequence.
Predicting single responses with dozens of predictors is prone to overfitting. Therefore, we chose the elastic-net57 variant of linear regression (using MATLAB function “lasso” with ‘Alpha’ set to 0.1), which penalizes big coefficients for redundant or uninformative predictors. A parameter λ controls the strength of this penalty. To find the best λ, we configured the “lasso” function to compute a 10-fold crossvalidated mean squared error (cvMSE) of the fit for a series of λ values. The smallest cvMSE indicates the best generalization, i.e. the least overfit. We conservatively chose the largest λ value such that the cvMSE was within one standard error of the minimum cvMSE. For each model, we derived the R2 from this cvMSE and reported it in Fig. 3 and Extended Data Figs. 5,7.
Linear decoding can be expressed as
where is the decoded behavioral variable at t, w and c are the coefficients obtained from regression, and rt is the vector of normalized population spike rates at t. We did not perform additional crossvalidation in decoding because (1) 30% of the decoding for standard sequences (0.5 to 0.8 s in Fig. 3 and −1.3 to −1 s in Extended Data Fig. 7) was from new data; (2) all decoding in backtracking sequences and during consumption periods was from new data; and (3) the model has been proven the best generalization via crossvalidation when selecting λ.
The matrix notation form of the equation, rTw, shows that the linear decoding can be geometrically interpreted as projecting the vector of population spike rates r onto the axis in the direction of vector w, and reading out the length of the projection (scaled by ||w||, plus the intercept c). We therefore referred to this axis as the coding axis. To compute VE for each coding axis, we first obtained its unit vector and projected population spike rates onto it. The variance of the projected values is Var(explained). The total variance, Var(total), of the population activity is the sum of variance of all units. Finally, VE equals Var(explained) / Var(total) × 100%.
Support-vector machine (SVM) classification
First, to prepare a denoised version of the predictors for more robust classification, we performed PCA with normalized population spike rates, and projected the spike rates onto the first 12 principal components. The projected activity was then downsampled from 400 to 66.7 samples/s (Fig. 3f) or 200 samples/s (Fig. 4f,g) to reduce subsequent computation time. Class labels were the sequence identity values, including standard vs backtracking types (Fig. 3f), or the two types of zigzag sequence (Fig. 4).
Classification was performed independently for each time bin with the MATLAB “fitcsvm” function. Linear kernels were used for all classifications. Trials were weighted so that the chance classification accuracy was 0.5 even if the two classes did not have equal numbers of trials. The results were computed with 10-fold crossvalidation. All other function parameters were kept as the defaults. The null classification results were obtained using the same procedure but with randomly shuffled class labels.
Canonical correlation analysis
The canonical correlation analysis seeks linear transformations of two vectors of random variables such that the Pearson’s correlation coefficients between the transformed vectors are maximized:
where X and Y are vectors of random variables, and are transformation vectors for the i-th iteration, N is the number of dimensions in X or Y, whichever is smaller. Matrices A and B will be used to represent the concatenated transformation vectors across all iterations.
In the present analysis, X and Y were matrices of sampled data for each session. X contained time series of the decoded behavioral variables (L, L’, θ, I, τ; zero centered). Y contained the projection of neural activity onto the top principal components obtained from PCA. We focused our analysis on standard sequences, with a time window of −0.5 to 0.8 s relative to the middle touch. The linearly decoded or PC-projected data were averaged across trials with the same sequence direction. Averaged data from the two sequence directions were concatenated along time.
Canonical correlations were computed using the MATLAB “canoncorr” function between matrices with a selected subset of dimensions. In Fig. 3d, Y was transformed using AT−1BTY so that the pattern could be best aligned with the patterns of X. In Fig. 3e, N correlation coefficients (r) quantified the correlation between each pair of Ui and Vi. The average r across the N values reflected the overall alignment between the two transformed matrices.
Data availability
Data are available from the corresponding author upon request.
Code availability
MATLAB code used to analyze the data is available at GitHub and from the corresponding author upon request.
Extended Data
Extended Data Fig. 1. Behavioral measurements, performance, and control experiments.
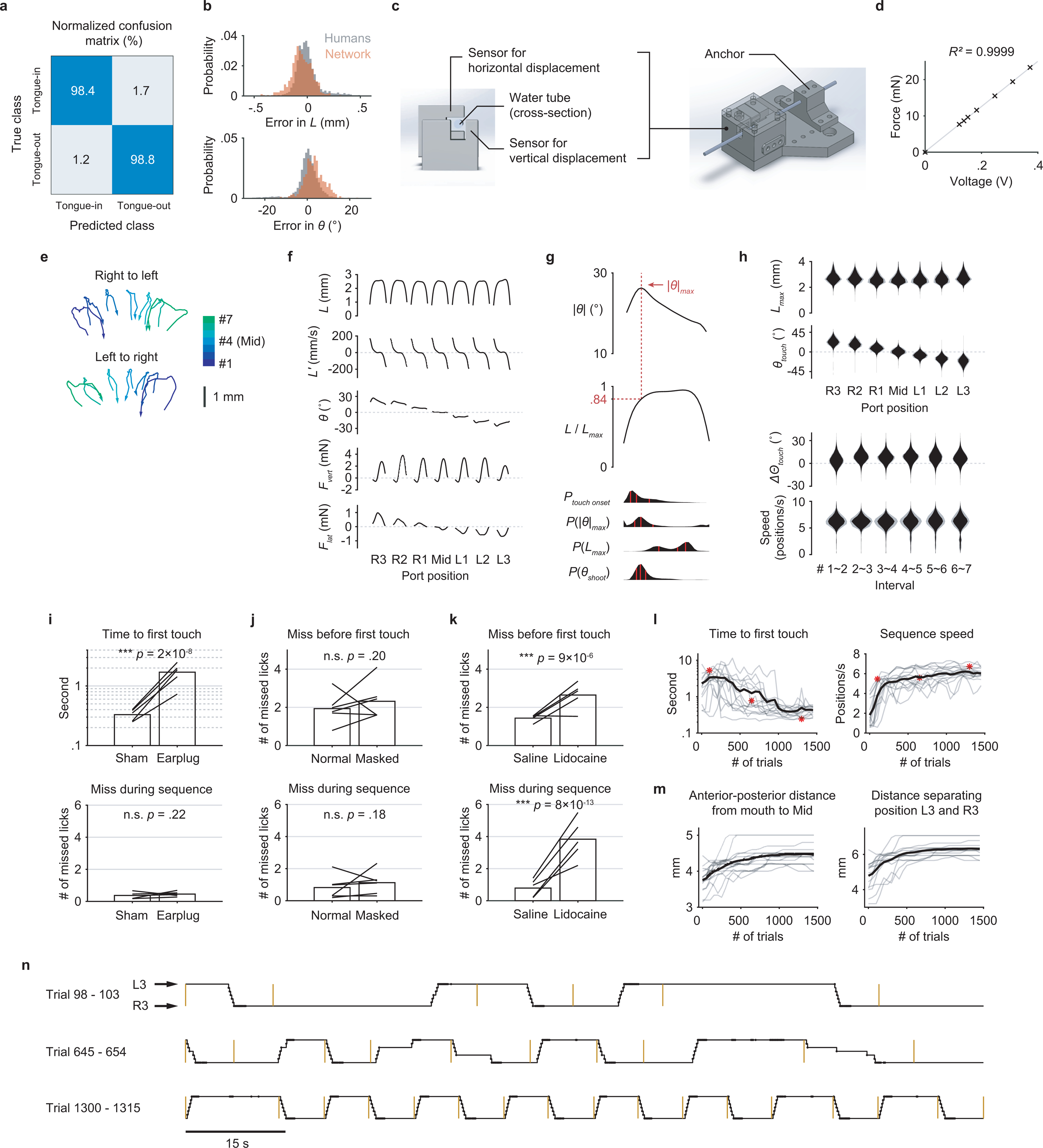
a, Confusion matrix showing the performance of the classification network. The numbers represent percentages within each (true) class (n = 1696 frames).
b, Performance of the regression network. Top, the gray probability distribution shows how L from five human individuals varied from the mean L across the five. The red distribution shows how predicted L varied from the human mean. Bottom, similar quantification as the top but for θ. n = 573 frames.
c, CAD images of the sensor core (left) and the assembly (right) with a lick tube.
d, Linear relationship between the applied force and the sensor output voltage.
e, Two example trials showing the trajectories of the tongue tip when a mouse sequentially reached the 7 port positions, for both sequence directions. Arrows indicate the direction of time within each trajectory.
f, Patterns of kinematics and forces of single licks at each port position (n = 25683 trials from 17 mice; mean ± 95% bootstrap confidence interval). The duration of individual licks was normalized.
g, Top, the pattern of angle deviation from midline (|θ|) of single licks pooled from R3 and L3. The vertical line indicates maximum |θ| (|θ|max). Middle, tongue length (L) expressed as a fraction of its maximum (Lmax). The horizontal line indicates, on average, the fraction where |θ|max occurred. Bottom, time aligned probability distributions showing when touch onset, |θ|max, Lmax, or θshoot occurred. Red lines mark quartiles. n = 25683 trials from 17 mice. Lick patterns show mean ± 95% bootstrap confidence interval.
h, Top, probability distributions of Lmax and θtouch for licks at each port position. Bottom, probability distributions of the change in Θtouch (ΔΘtouch) and instantaneous sequence speed (Methods) for each interval separating port positions. Distributions show mean ± SD across n = 17 mice.
i, Median time to first touch (top) and the average number of missed licks during sequence performance (bottom) in control (Sham) versus hearing loss (Earplug) conditions. Bars show group means and lines show data from individual mice. ∗∗∗ p < 0.001, n.s. p > 0.05, paired one-tailed bootstrap test, n = 5 mice.
j, Average number of missed licks before first touch (top) and during sequence performance (bottom) in control (Normal) versus odor masking (Masked) conditions. Same statistical tests as in (i), n = 6 mice.
k, Similar to (j) but comparing control (Saline) versus tongue numbing (Lidocaine) conditions. n = 5 mice.
l, Learning curves for 15 individual mice (gray) and the mean (black) showing a reduction in sequence initiation time (left) in response to the auditory cue and an increase in sequence speed (right). The three red asterisks correspond to the three examples of sequence performance shown in (n).
m, Gradual increase in task difficulty (Methods) accompanying the improved performance shown in (l).
n, Depiction of example sequences performed by a mouse in alternating directions across consecutive trials at different stages of learning. Trial onsets are marked by yellow bars. Port positions shown in the black trace are overlaid with touch onsets (dots).
Extended Data Fig. 2. Performance in backtracking sequences.
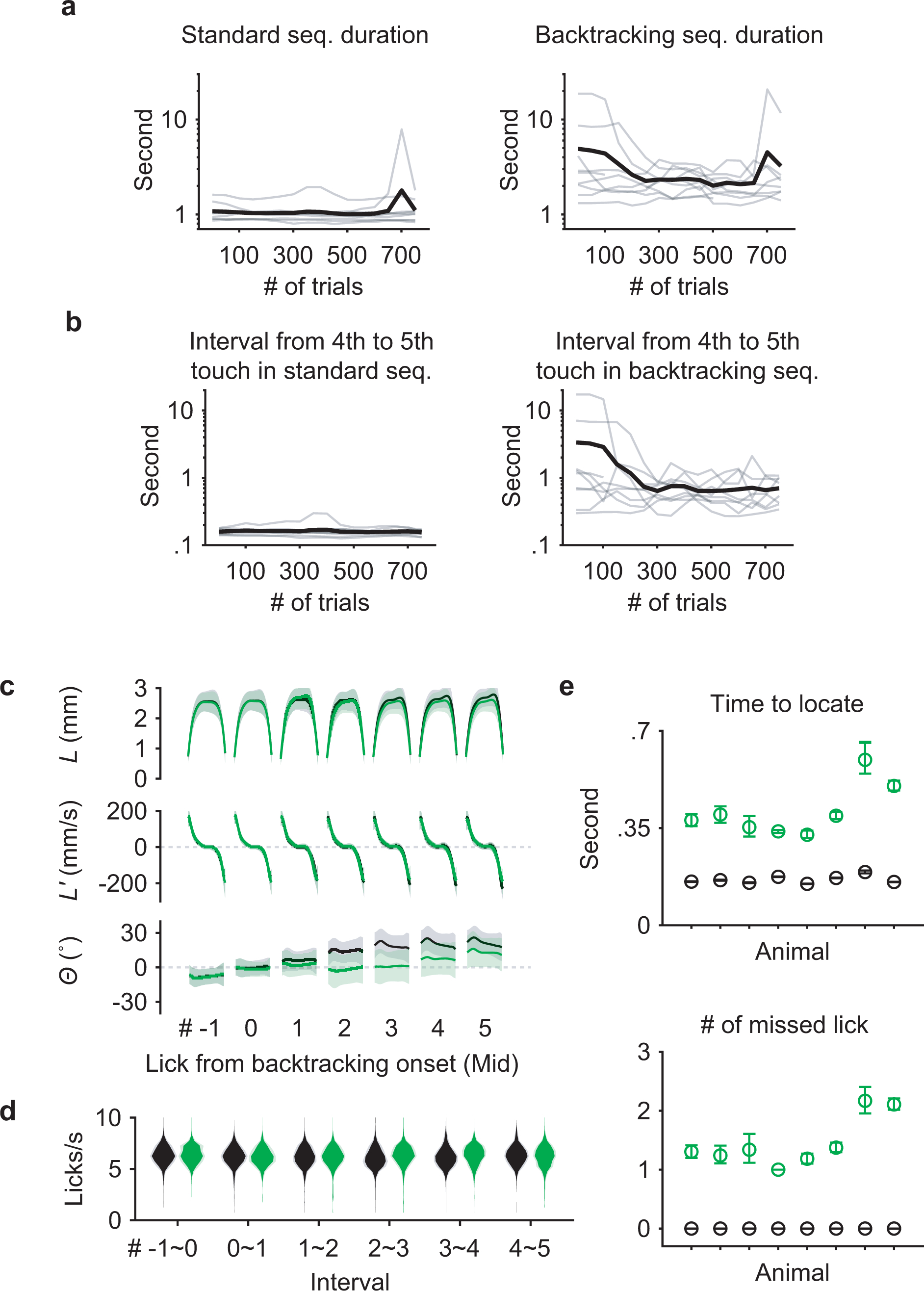
a, Learning curves for 9 individual mice (gray) and the mean (black) showing the duration of time spent to perform standard (left) and backtracking (right) sequences.
b, Similar to (a) but limited to the interval following the middle lick in standard (left) or backtracking (right) sequences.
c, L, L’ and Θ patterns for seven consecutive licks aligned at the Mid touch (#0). Licks in standard sequences (n = 7458 trials) are shown in black, those in backtracking sequences (n = 2695 trials) are in green. Mean ± SD.
d, Probability distributions of instantaneous lick rate for each interval separating consecutive pairs of the seven licks during standard (black) or backtracking (green) sequences (n = 8 mice; mean ± SD).
e, Top, time to locate the port at its next position during the 4th interval, for standard sequences (black) or for sequences when the port backtracked (green). Bottom, the number of missed licks during the 4th interval. Mean ± 95% bootstrap confidence interval. n = 7458 standard and 2695 backtracking sequences from 47 total sessions.
Extended Data Fig. 3. Closed-loop optogenetic inhibition defines cortical areas involved in sequence control.
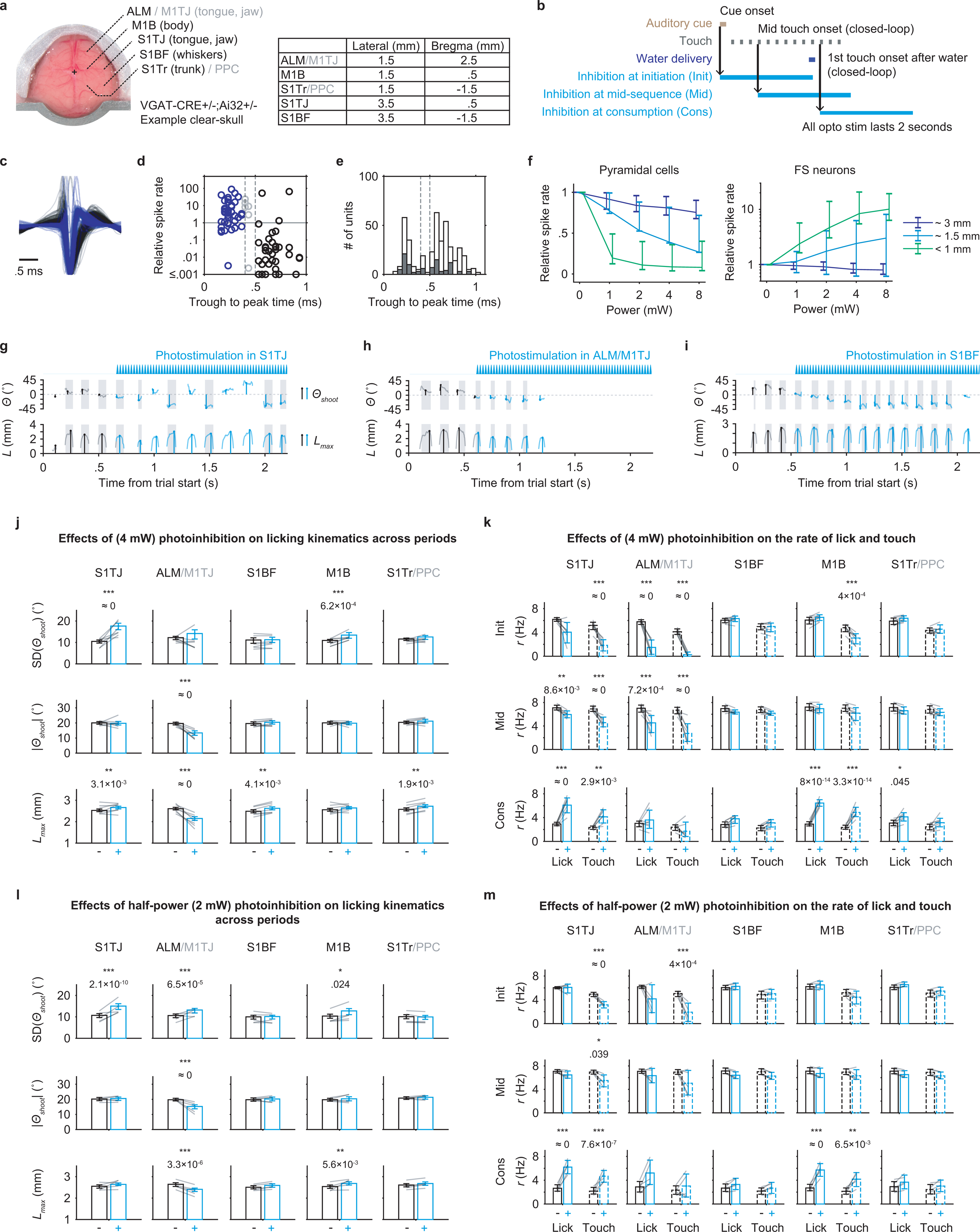
a, Left, dorsal view of an example “clear-skull” preparation. Right, table shows the center coordinates used for illumination for each target region.
b, Triggering scheme for photoinhibition at sequence initiation, mid-sequence and water consumption.
c, Average spike waveform of putative pyramidal cells (black; n = 224) and putative FS neurons (blue; n = 117), normalized to the amplitude of negative peaks.
d, Relationship between spike widths (defined as the trough to peak time of average waveform) and changes in mean spike rate under opto illumination (4mW, within 1 mm) relative to baseline. Pyramidal cells (black; n = 42) and FS neurons (blue; n = 41) were classified by the two thresholds (dashed lines at 0.4 and 0.5 ms) with ambiguous units (gray; n = 6) in the middle.
e, Distributions of spike widths from neurons in (d) (filled bars; n = 89) and from all neurons (empty bars; n = 414) including those where illuminations were not at recording sites. Classification thresholds are shown in dashed lines.
f, Left, inhibition efficiency of putative pyramidal cells as a function of light power and distance away from the center of illumination (n = 224 units total). Right, similar to left but showing the excitation efficiency of putative FS neurons (n = 117 units total). Mean ± 95% hierarchical bootstrap confidence interval.
g, Example trial with S1TJ inhibition triggered at mid-sequence. Instantaneous tongue angle (Θ) and length (L) are shown in lighter traces. Shooting angles (Θshoot) and maximum length (Lmax) of each lick are marked using stems on top of the instantaneous traces. The blue waveform indicates photostimulation. Traces and markers during photostimulation are colored blue.
h, Similar to (g) but inhibiting ALM/M1TJ.
i, Similar to (g) but inhibiting S1BF.
j, Changes in licking kinematics (rows) when inhibiting each of the five brain regions (columns), quantified across all three inhibition periods (Methods). Bar plots show mean ± 99% hierarchical bootstrap confidence interval. Gray lines show the data of individual mice. Two-tailed hierarchical bootstrap test, ∗∗∗ p < 0.001, ∗∗ p < 0.01, ∗ p < 0.05, n.s. p ≥ 0.05, after Bonferroni correction for 15 comparisons.
k, Changes in the rate of lick (solid bars) and touch (dashed bars) at each of the inhibition periods (rows) when inhibiting each of the five brain regions (columns). Plot style and statistical tests are the same as in (j) but using Bonferroni correction for 30 comparisons.
l, Same convention as in (j) but showing results with half-power (2 mW) inhibition.
m, Same convention as in (k) but showing results with half-power (2 mW) inhibition.
Extended Data Fig. 4. Characterization of single-unit responses.
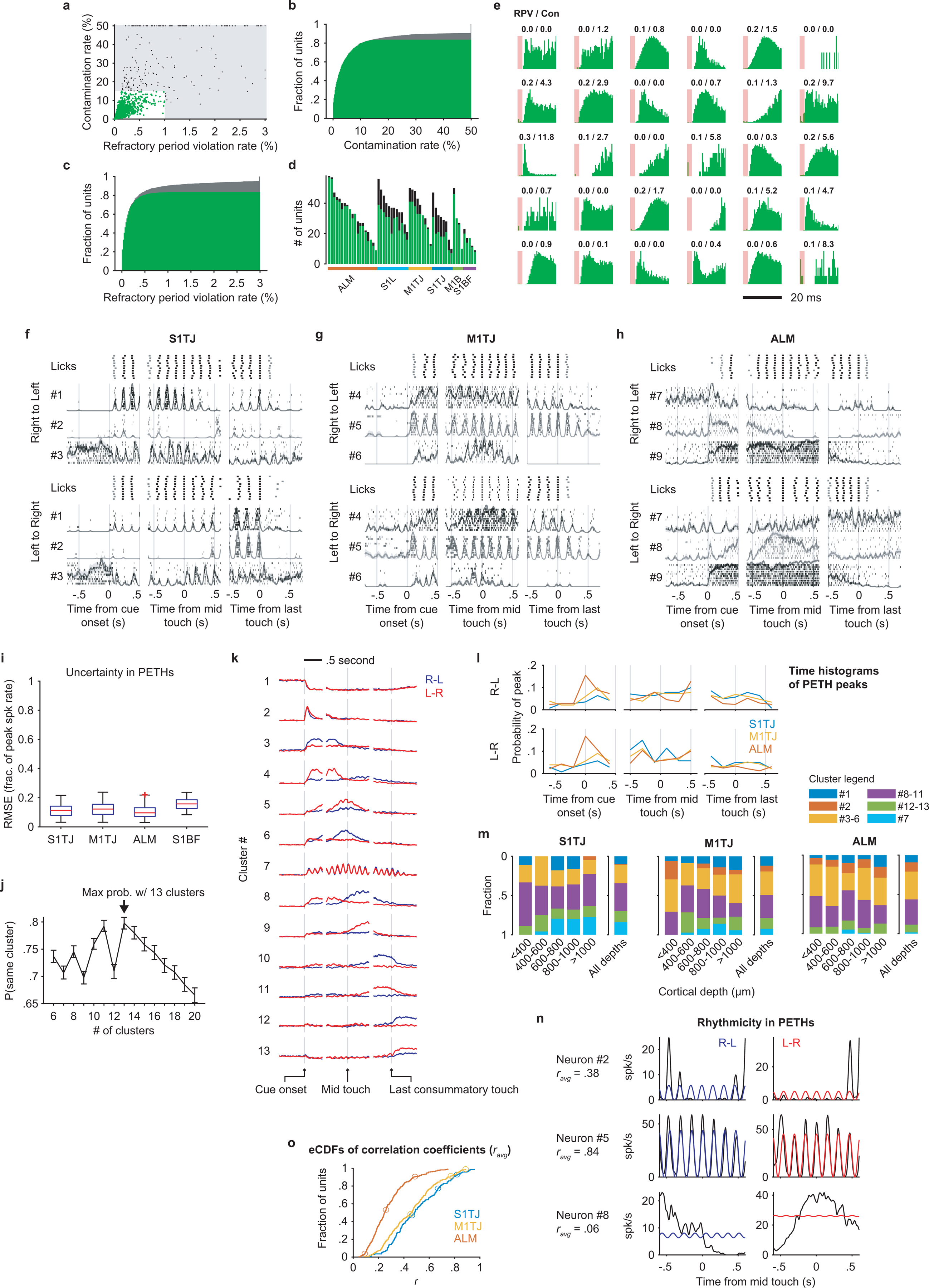
a, Contamination rates and refractory period violation rates of all recorded single- (green) and multi-units (black). The shaded region shows the thresholds for assignment as multi- vs single-unit.
b, CDF of contamination rate including single- (green) and multi-units (gray).
c, Same as (b) but for refractory period violation rate.
d, The number of single- (green) and multi-units (black) recorded in each session, grouped by brain area.
e, ISI histograms of randomly selected single-units. Refractory period violation rates (RPV) and contamination rates (Con) are labeled on the top (in percent).
f, Responses of three simultaneously recorded S1TJ neurons during right-to-left (top half) or left-to-right (bottom half) licking sequences, aligned at cue onset (left column), middle touch (middle column), and the last consummatory touch (right column). For each sequence direction, the first row shows rasters of lick times (touches in black and misses in gray) from 10 selected trials (Methods). Stacked below are spike rasters and the corresponding PETHs (mean ± SE) from the same 10 trials for each example neuron.
g, Same as (f) but for three example neurons from M1TJ.
h, Same as (f) but for three example neurons from ALM.
i, Uncertainty in mean spike rate (normalized to peak) estimated by bootstrap crossvalidation (Methods). Each data point is the bootstrap average value of the root mean squared error (RMSE) for a single neuron. Data (n = 804 neurons) are grouped by brain region and presented in whisker-box plots (centre mark: median, bounds of box: 25th and 75th percentiles, max whisker length: 1.5 times IQR, no max or min limit).
j, The probability (mean ± 95% bootstrap confidence interval) of a PETH being consistently grouped into the same cluster across bootstrap iterations for different total numbers of clusters. Maximal consistency was achieved when using thirteen clusters for NNMF (arrow).
k, NNMF components that represent each of the thirteen PETH clusters. Right-to-left (blue) and left-to-right (red) activities (mean ± 95% bootstrap confidence interval) are overlaid together. The vertical lines are located at time zero in each period. The height of the lines represents the scale of normalized neuronal activity from 0 to 1.
l, Histograms of PETH peak times. Plot organization and time alignment are the same as in (f).
m, Proportions of neurons from different clusters at different cortical depths. Some clusters with similar types of response were grouped together for better readability. ALM (n = 324), M1TJ (n = 233) and S1TJ (n = 119).
n, Quantification of rhythmicity in PETHs. Black traces are mid-sequence PETHs of three example neurons in (f), (g), and (h). Colored traces show the best fit licking rhythms (6.5 Hz sinusoids). Average Pearson’s correlation coefficients (ravg) of the left-to-right and right-to-left fits are shown beneath neuron IDs.
o, Empirical CDFs of ravg for neurons in S1TJ, M1TJ, and ALM. Circles mark the values of the 9 example neurons in (f), (g), and (h).
Extended Data Fig. 5. Additional analyses for population coding.
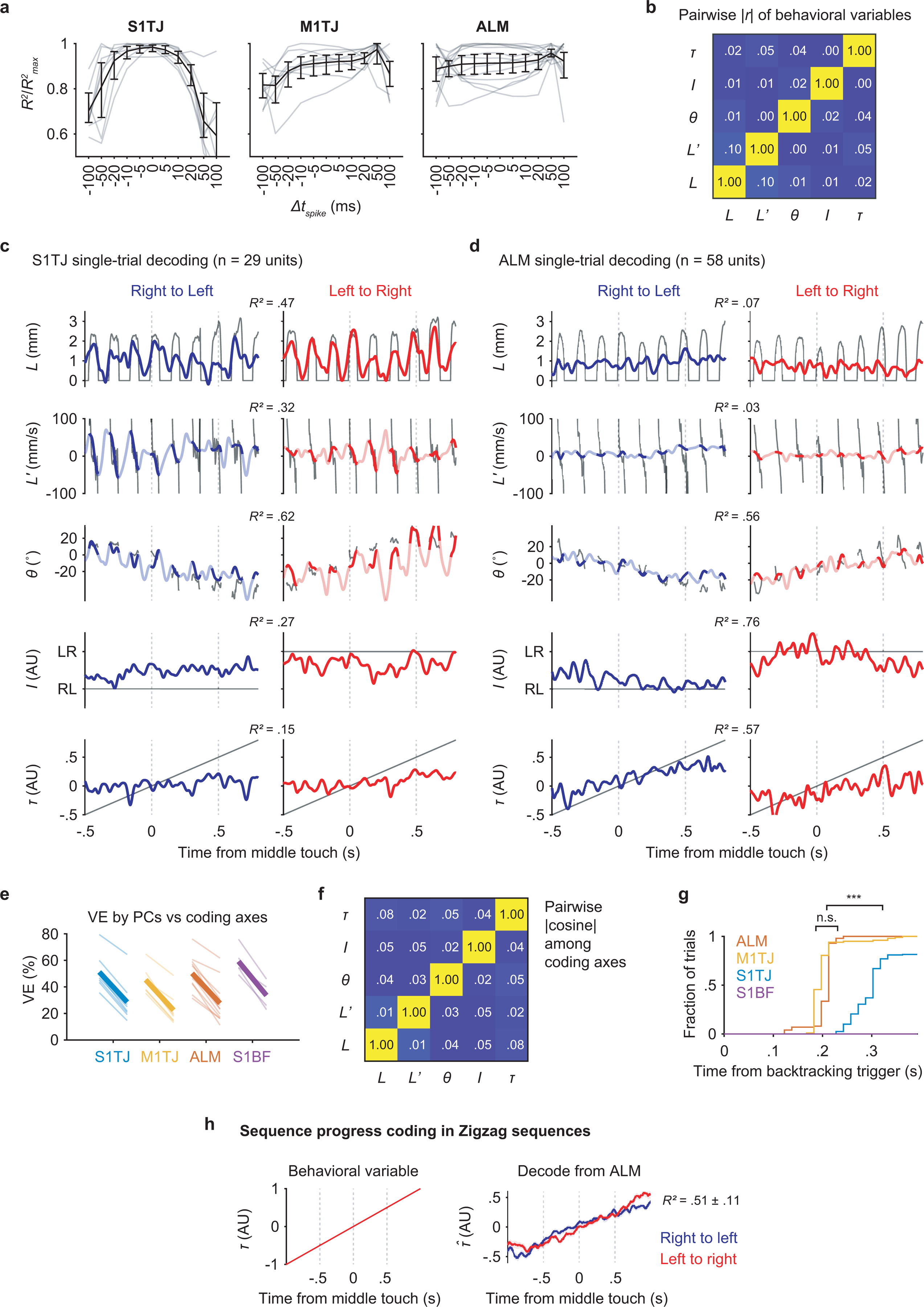
a, Relative goodness of fit of tongue angle regressions with a range of shifts in spike times. Black traces and error bars show mean ± 95% bootstrap confidence interval. Lighter traces show individual recordings. (S1TJ, n = 8 sessions; M1TJ, n = 9 sessions; ALM, n = 13 sessions)
b, Absolute pairwise Pearson’s correlation coefficients among the five behavioral variables (mean; n = 35 sessions).
c, Single-trial decoding of the five behavioral variables (rows; black traces) from 29 simultaneously recorded S1TJ units in a right-to-left (left) and a left-to-right (right) sequence.
d, Same as (c) but decoding from 58 simultaneously recorded units in ALM.
e, Total percent variance explained (VE) by the first five principal components (left in each region) versus that by the five coding axes (right in each region) during sequence execution. Lighter lines show individual recording sessions and thicker lines show the means.
f, Absolute pairwise cosine values among coding axes (mean; n = 35 sessions).
g, Cumulative time histograms showing the fraction of trials that could be correctly classified as a standard vs backtracking sequence as time progresses. Two-tailed bootstrap test, ∗∗∗ p ≈ 0, n.s. p = 0.91.
h, Same as sequence progress in Fig. 3a,b, but for “zigzag” sequences.
Extended Data Fig. 6. Reward modulation of activity in ALM.
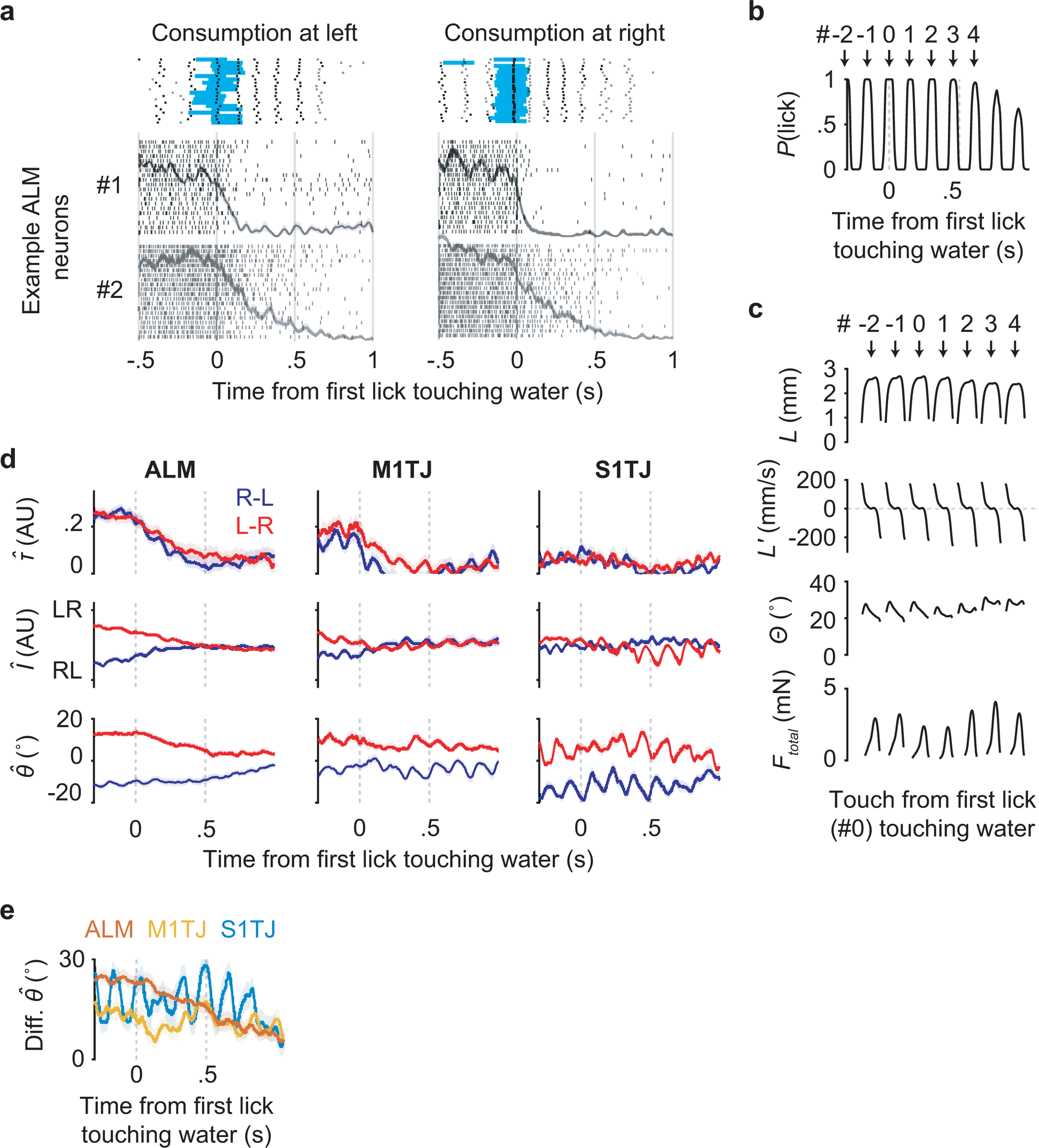
a, Responses of two simultaneously recorded ALM neurons (#1 and #2) aligned at the first lick (specifically the middle of a tongue-out period) that touched water reward. For each sequence direction, shown at top are rasters of lick times (touches in black and misses in gray) and the duration of water delivery (blue) from 20 selected trials (Methods). Stacked below are spike rasters and the corresponding PETHs from the same 20 trials for each example neuron.
b, The probability of licking (i.e. tongue-out) as a function of time. Licks are sequentially indexed with respect to the first lick (#0) touching the water.
c, Patterns of kinematics and force for single licks around the first lick (#0) touching water (n = 25289 trials; mean ± 95% bootstrap confidence interval). The duration of individual licks was normalized. The total force (Ftotal) is the vector sum of vertical and lateral forces.
d, Decoding of τ, I and θ (mean ± 99% bootstrap confidence interval) from neuronal populations recorded in ALM (n = 13 sessions), M1TJ (n = 9 sessions), and S1TJ (n = 8 sessions) in right-to-left (blue) or left-to-right (red) trials around the consumption period.
e, The difference between the decoded θ traces in right-to-left versus left-to-right trials. Same data source, mean and error presentation as in (d).
Extended Data Fig. 7. Coding of upcoming sequences in ALM.
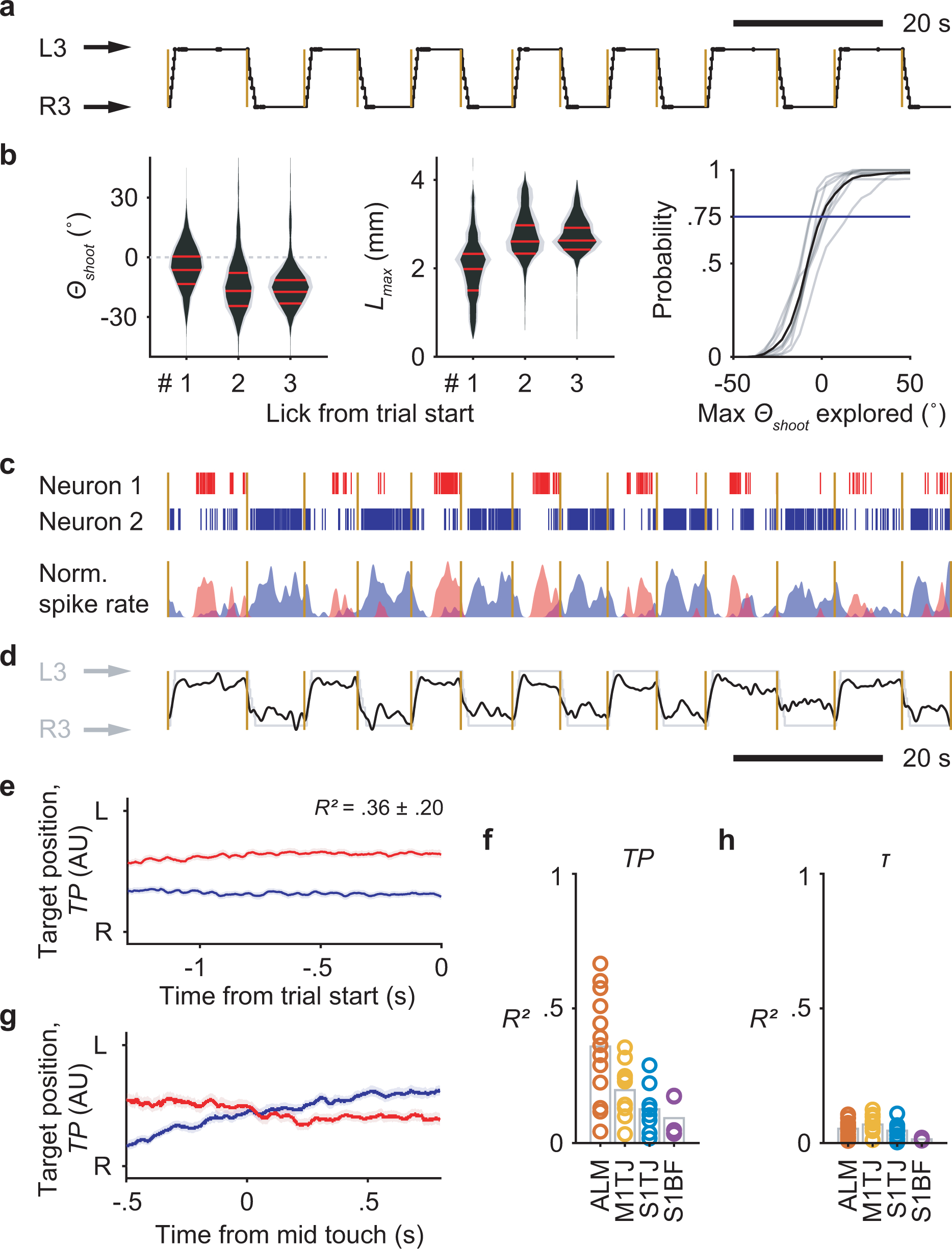
a, Depiction of sequences performed by a mouse in alternating directions across 14 consecutive trials. Trial onsets are marked by yellow lines. Port positions shown in the black trace are overlaid with touch onsets (dots).
b, Probability distributions of Θshoot (left) and Lmax (middle) for the first 3 licks at the start of a sequence (n = 8 mice; mean ± SD). The negative y-axis of Θshoot points to the side at which the port is located. The CDF (right; 8 individual mice in gray and the mean in black) of the maximal Θshoot explored before touching the port (at the side of negative Θshoot). The blue line shows the probability of successfully locating the port without exploring beyond the midline.
c, Top, rasters of two example neurons which had persistent and target position (TP) selective firing during the 14 consecutive trials in (a). Bottom, normalized and smoothed (0.25 s SD Gaussian kernel) spike rates of the two neurons.
d, Decoded instantaneous TP (dark trace) from 58 simultaneously recorded units in ALM, overlaid with normalized port position (light trace).
e, Decoding of TP from ALM (mean ± 99% bootstrap confidence interval) before upcoming right-to-left trials (blue) or left-to-right trials (red). Crossvalidated R2 is shown (mean ± SD; n = 13 sessions).
f, Goodness of fit for linear models that predict TP during ITIs, quantified by crossvalidated R2.
g, Using the same linear models in (e) to decode TP during execution of standard right-to-left (blue) or left-to-right (red) sequences (mean ± 99% bootstrap confidence interval).
h, Same as (f) but for τ.
Supplementary Material
Acknowledgements
We thank William Olson, Rajan Dasgupta, Yi-Ting Chang, Varun Chokshi, Jeremiah Cohen, Michael Economo, and Karel Svoboda for comments on the manuscript; Ali Aly, Yun Hwang, Hokin Deng for assistance with experiments and data curation; Varun Chokshi and William Olson for sharing animals; Bilal Bari and Jeremiah Cohen for VGAT-Cre;Ai32 mice; Travis Babola for suggestions on the hearing loss experiment. This work was supported by NIH grants R01NS089652 and 1R01NS104834-01 to D.H.O., and center grant P30NS050274.
Footnotes
Competing interests
The authors declare no competing interests.
References
- 1.Rosenbaum DA Human motor control. (Elsevier Inc, 2010). [Google Scholar]
- 2.Mayrhofer JM et al. Distinct Contributions of Whisker Sensory Cortex and Tongue-Jaw Motor Cortex in a Goal-Directed Sensorimotor Transformation. Neuron S0896627319306348 (2019) doi: 10.1016/j.neuron.2019.07.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chen T-W, Li N, Daie K & Svoboda K A Map of Anticipatory Activity in Mouse Motor Cortex. Neuron 94, 866–879.e4 (2017). [DOI] [PubMed] [Google Scholar]
- 4.Economo MN et al. Distinct descending motor cortex pathways and their roles in movement. Nature 563, 79–84 (2018). [DOI] [PubMed] [Google Scholar]
- 5.Gao Z et al. A cortico-cerebellar loop for motor planning. Nature 563, 113–116 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Guo ZV et al. Flow of Cortical Activity Underlying a Tactile Decision in Mice. Neuron 81, 179–194 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Inagaki HK, Fontolan L, Romani S & Svoboda K Discrete attractor dynamics underlies persistent activity in the frontal cortex. Nature 566, 212–217 (2019). [DOI] [PubMed] [Google Scholar]
- 8.Li N, Chen T-W, Guo ZV, Gerfen CR & Svoboda K A motor cortex circuit for motor planning and movement. Nature 519, 51–56 (2015). [DOI] [PubMed] [Google Scholar]
- 9.Li N, Daie K, Svoboda K & Druckmann S Robust neuronal dynamics in premotor cortex during motor planning. Nature 532, 459–464 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Komiyama T et al. Learning-related fine-scale specificity imaged in motor cortex circuits of behaving mice. Nature 464, 1182–1186 (2010). [DOI] [PubMed] [Google Scholar]
- 11.Kurnikova A, Moore JD, Liao S-M, Deschênes M & Kleinfeld D Coordination of Orofacial Motor Actions into Exploratory Behavior by Rat. Curr. Biol. CB 27, 688–696 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.McElvain LE et al. Circuits in the rodent brainstem that control whisking in concert with other orofacial motor actions. Neuroscience 368, 152–170 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Welker WI Analysis of Sniffing of the Albino Rat 1). Behaviour 22, 223–244 (1964). [Google Scholar]
- 14.Chartier J, Anumanchipalli GK, Johnson K & Chang EF Encoding of Articulatory Kinematic Trajectories in Human Speech Sensorimotor Cortex. Neuron 98, 1042–1054.e4 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Svoboda K & Li N Neural mechanisms of movement planning: motor cortex and beyond. Curr. Opin. Neurobiol. 49, 33–41 (2018). [DOI] [PubMed] [Google Scholar]
- 16.Ayling OGS, Harrison TC, Boyd JD, Goroshkov A & Murphy TH Automated light-based mapping of motor cortex by photoactivation of channelrhodopsin-2 transgenic mice. Nat. Methods 6, 219–224 (2009). [DOI] [PubMed] [Google Scholar]
- 17.Guo J-Z et al. Cortex commands the performance of skilled movement. eLife 4, e10774 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Clemens AM, Fernandez Delgado Y, Mehlman ML, Mishra P & Brecht M Multisensory and Motor Representations in Rat Oral Somatosensory Cortex. Sci. Rep. 8, 13556 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Proske U & Gandevia SC The proprioceptive senses: their roles in signaling body shape, body position and movement, and muscle force. Physiol. Rev. 92, 1651–1697 (2012). [DOI] [PubMed] [Google Scholar]
- 20.Franklin DW & Wolpert DM Computational mechanisms of sensorimotor control. Neuron 72, 425–442 (2011). [DOI] [PubMed] [Google Scholar]
- 21.Shadmehr R, Smith MA & Krakauer JW Error correction, sensory prediction, and adaptation in motor control. Annu. Rev. Neurosci. 33, 89–108 (2010). [DOI] [PubMed] [Google Scholar]
- 22.Chesler AT et al. The Role of PIEZO2 in Human Mechanosensation. N. Engl. J. Med. 375, 1355–1364 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Inagaki HK, Inagaki M, Romani S & Svoboda K Low-Dimensional and Monotonic Preparatory Activity in Mouse Anterior Lateral Motor Cortex. J. Neurosci. Off. J. Soc. Neurosci. 38, 4163–4185 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Stapleton JR Rapid Taste Responses in the Gustatory Cortex during Licking. J. Neurosci. 26, 4126–4138 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Accolla R, Bathellier B, Petersen CCH & Carleton A Differential Spatial Representation of Taste Modalities in the Rat Gustatory Cortex. J. Neurosci. 27, 1396–1404 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jin X & Costa RM Start/stop signals emerge in nigrostriatal circuits during sequence learning. Nature 466, 457–462 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kriegeskorte N & Douglas PK Interpreting encoding and decoding models. Curr. Opin. Neurobiol. 55, 167–179 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Russo AA et al. Neural Trajectories in the Supplementary Motor Area and Motor Cortex Exhibit Distinct Geometries, Compatible with Different Classes of Computation. Neuron 107, 745–758.e6 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Russo AA et al. Motor Cortex Embeds Muscle-like Commands in an Untangled Population Response. Neuron 97, 953–966.e8 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Evarts EV & Tanji J Reflex and intended responses in motor cortex pyramidal tract neurons of monkey. J. Neurophysiol. 39, 1069–1080 (1976). [DOI] [PubMed] [Google Scholar]
- 31.Heindorf M, Arber S & Keller GB Mouse Motor Cortex Coordinates the Behavioral Response to Unpredicted Sensory Feedback. Neuron 99, 1040–1054.e5 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Pruszynski JA et al. Primary motor cortex underlies multi-joint integration for fast feedback control. Nature 478, 387–390 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Scott SH, Cluff T, Lowrey CR & Takei T Feedback control during voluntary motor actions. Curr. Opin. Neurobiol. 33, 85–94 (2015). [DOI] [PubMed] [Google Scholar]
- 34.Stavisky SD, Kao JC, Ryu SI & Shenoy KV Motor Cortical Visuomotor Feedback Activity Is Initially Isolated from Downstream Targets in Output-Null Neural State Space Dimensions. Neuron 95, 195–208.e9 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bollu T et al. Cortex-dependent corrections as the tongue reaches for and misses targets. Nature 1–6 (2021) doi: 10.1038/s41586-021-03561-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Tanji J Sequential Organization of Multiple Movements: Involvement of Cortical Motor Areas. Annu. Rev. Neurosci. 24, 631–651 (2001). [DOI] [PubMed] [Google Scholar]
- 37.Desrochers TM, Burk DC, Badre D & Sheinberg DL The Monitoring and Control of Task Sequences in Human and Non-Human Primates. Front. Syst. Neurosci. 9, (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Shima K & Tanji J Neuronal activity in the supplementary and presupplementary motor areas for temporal organization of multiple movements. J. Neurophysiol. 84, 2148–2160 (2000). [DOI] [PubMed] [Google Scholar]
- 39.Tanji J & Shima K Role for supplementary motor area cells in planning several movements ahead. Nature 371, 413–416 (1994). [DOI] [PubMed] [Google Scholar]
- 40.Sohn J-W & Lee D Order-Dependent Modulation of Directional Signals in the Supplementary and Presupplementary Motor Areas. J. Neurosci. 27, 13655–13666 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Chabrol FP, Blot A & Mrsic-Flogel TD Cerebellar Contribution to Preparatory Activity in Motor Neocortex. Neuron 103, 506–519.e4 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Vong L et al. Leptin action on GABAergic neurons prevents obesity and reduces inhibitory tone to POMC neurons. Neuron 71, 142–154 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Madisen L et al. A toolbox of Cre-dependent optogenetic transgenic mice for light-induced activation and silencing. Nat. Neurosci. 15, 793–802 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Zhao S et al. Cell type–specific channelrhodopsin-2 transgenic mice for optogenetic dissection of neural circuitry function. Nat. Methods 8, 745–752 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Savitt JM Bcl-x Is Required for Proper Development of the Mouse Substantia Nigra. J. Neurosci. 25, 6721–6728 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Taniguchi H et al. A resource of Cre driver lines for genetic targeting of GABAergic neurons in cerebral cortex. Neuron 71, 995–1013 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Zhou X et al. Deletion of PIK3C3/Vps34 in sensory neurons causes rapid neurodegeneration by disrupting the endosomal but not the autophagic pathway. Proc. Natl. Acad. Sci. 107, 9424–9429 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.He K, Zhang X, Ren S & Sun J Deep Residual Learning for Image Recognition. ArXiv151203385 Cs (2015). [Google Scholar]
- 49.Badrinarayanan V, Kendall A & Cipolla R SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. ArXiv151100561 Cs (2015). [DOI] [PubMed] [Google Scholar]
- 50.Mowery TM, Kotak VC & Sanes DH Transient Hearing Loss Within a Critical Period Causes Persistent Changes to Cellular Properties in Adult Auditory Cortex. Cereb. Cortex 25, 2083–2094 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Pachitariu M, Steinmetz NA, Kadir SN, Carandini M & Harris KD Fast and accurate spike sorting of high-channel count probes with KiloSort. 9. [Google Scholar]
- 52.Hill DN, Mehta SB & Kleinfeld D Quality Metrics to Accompany Spike Sorting of Extracellular Signals. J. Neurosci. 31, 8699–8705 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Navratilova Z, Godfrey KB & McNaughton BL Grids from bands, or bands from grids? An examination of the effects of single unit contamination on grid cell firing fields. J. Neurophysiol. 115, 992–1002 (2016). [DOI] [PubMed] [Google Scholar]
- 54.Guo ZV et al. Flow of Cortical Activity Underlying a Tactile Decision in Mice. Neuron 81, 179–194 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Saravanan V, Berman GJ & Sober SJ Application of the hierarchical bootstrap to multi-level data in neuroscience. ArXiv200707797 Q-Bio (2020). [PMC free article] [PubMed] [Google Scholar]
- 56.Williams AH & Linderman SW Statistical Neuroscience in the Single Trial Limit. ArXiv210305075 Q-Bio Stat (2021). [DOI] [PubMed] [Google Scholar]
- 57.Zou H & Hastie T Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Stat. Methodol. 67, 301–320 (2005). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data are available from the corresponding author upon request.


