Abstract
Uncertainty quantification is a formal paradigm of statistical estimation that aims to account for all uncertainties inherent in the modelling process of real-world complex systems. The methods are directly applicable to stochastic models in epidemiology, however they have thus far not been widely used in this context. In this paper, we provide a tutorial on uncertainty quantification of stochastic epidemic models, aiming to facilitate the use of the uncertainty quantification paradigm for practitioners with other complex stochastic simulators of applied systems. We provide a formal workflow including the important decisions and considerations that need to be taken, and illustrate the methods over a simple stochastic epidemic model of UK SARS-CoV-2 transmission and patient outcome. We also present new approaches to visualisation of outputs from sensitivity analyses and uncertainty quantification more generally in high input and/or output dimensions.
Keywords: Uncertainty quantification, History matching, Stochastic epidemic model, SEIR, Calibration
0. Introduction
Uncertainty Quantification (UQ) is a statistical framework for conducting formal analysis of sensitivities and deficiencies in computer models, often referred to as simulators, and their subsequent calibration to known measured quantities, allowing for a greater understanding of influential parameters and variables in an efficient manner. Due to the fact that these simulators can be highly computationally intensive to run for a single set of parameters, running likelihood-based methods for calibration and inference can be challenging or prohibitive, despite parameter estimation and model fitting being a vital part of the modelling process. The process of UQ allows modellers to calibrate these types of models to real data (that is find (ranges of) parameter values that give model outputs close to the equivalent observed reality); understand aspects of the model that are otherwise hidden to them; and inform possible directions for model improvement. The process involves the construction of a computationally more simplistic statistical model called an emulator, carefully trained on a set of test runs of the simulator, that is able to take the place of the much more computationally demanding simulator in calibrating the parameters to observed data. The emulator is then used to interpolate regions of parameter space that the underlying simulator was not run for.
Predictive mathematical models for epidemics are fundamental for understanding the spread of the epidemic and also plan effective control strategies (Giordano et al., 2020), the success of which is essential given the dangers to public health and the economy. One type of predictive mathematical model is an SIR model, which categorises the whole population into susceptible (S), infectious (I) and recovered/died (R) individuals. Variations on the SIR model have been studied to more accurately model more complex infection mechanisms, by way of adding further classes (Chauhan et al., 2014). Many variants and extensions of these models can be implemented, such as SEIR model (where E stands for exposed), which acts as an intermediate between the susceptible and the infected populations. These models have many uses, including simulating trajectories of epidemics under different scenarios or be used to determine the basic reproduction number (or ), which informed on the average number of cases generated by a single infectious individual in a fully susceptible population. It can also help explain the change in the number of people needing medical attention throughout the pandemic (Beckley et al., 2013).
Elsewhere in this special issue, Swallow et al. (2022) discuss major challenges in UQ for epidemic models, whilst here we specifically explain how to conduct UQ for an exemplar stochastic model of SARS-CoV-2 transmission, based on the current recommended methodologies for stochastic computer models. In this paper we will outline a framework for conducting formal sensitivity analysis and uncertainty quantification on a stochastic forward simulation epidemic model applied to the SARS-COV2 pandemic in Scotland. This tutorial will highlight the main aspects of the uncertainty quantification paradigm and the decisions that need to be considered, using the case study as an exemplar for other models. We also propose novel visualisation approaches for easily inferring important quantities from high-dimensional uncertainty outputs. The paper is outlined according to the steps taken in a full UQ framework, that is sensitivity analysis, emulation, validation, calibration and finally visualisation. We then work through each of these steps for the stochastic epidemic model under consideration.
We note here that there many choices that need to be made as part of the process and the choices made will vary dependent on the exact simulator of interest. The implications of these choices should be tested and justified for the specific simulator of interest.
1. Application: the epidemic model
1.1. Epidemic modelling framework
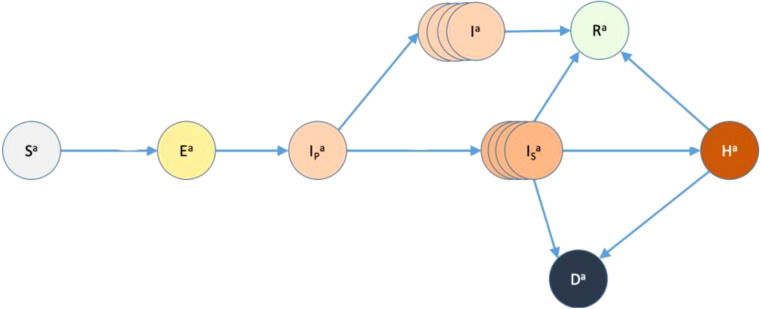
In this paper, we used a simple stochastic modelling framework designed to predict the level of infection of COVID-19 at community level during the first epidemic wave occurring in Scotland (Porphyre et al., 2020). The simulator was designed to answer 2 main questions: (1) how long COVID was circulating before lockdown was implemented? (2) what is the impact of lockdown during the first wave, and would it be sufficient to control outbreak? In addition, the model aimed to clarify the role of asymptomatic people in the population. The aim is to outline the general process of UQ in a simplified tutorial fashion, with the aim of enabling other modellers to implement similar approaches to their own simulators. The epidemiological model is structured as an SEIR with hospitalisation and death model, where there are three levels of infection, a class H for hospitalised people and class D for those that have died. R relates to a compartment for those recovered from the disease. The three levels of infection in this model are pre-clinically infectious (), infectious and asymptomatic () and infectious and symptomatic (), with the way that they connect with other classes shown in Fig. 1.
Fig. 1.
Diagram showing the flow of the population between the different classes. number of susceptibles, number of exposed, = number of pre-clinically infectious, number of infectious and asymptomatic, number of infectious and symptomatic, = number of recovered, number of hospitalised, number of fatalities. The arrows show how people can move from one class to another (Porphyre et al., 2020).
1.2. Inputs
This model has a total of 16 inputs shown in Table 1. Of these inputs, 14 are treated as unknown parameters and will be formally included in the sensitivity analysis and calibration. The remaining two are choices that are simulation-specific quantities, such as hospital bed capacity. These inputs are required to run the simulator but are not considered as part of the model calibration procedure. For each parameter, a suitable sample range is given, obtained from elicitation with a domain expert, and a description can also be found in Table 1.
Table 1.
The name, description and recommended range of each input parameter into the model (Porphyre et al., 2020).
| Parameter name | Description | Range |
|---|---|---|
| Probability of Infection | ||
| Probability of Infection for Health Care Workers |
||
| Mean number of Health Care Worker to patient contacts per day |
||
| Proportion of population observing social distancing |
||
| Proportion of normal contact made by people self-isolating |
||
| Age-dependent probability of developing symptoms |
||
| Risk of death if not hospitalised |
Fixed at 1 | |
| Rate of primary infection prior to lockdown |
||
| Mean latent period (days) | ||
| Probability of juvenile developing symptoms |
||
| Mean asymptomatic period (days) |
||
| Mean time to recovery if symptomatic (days) |
||
| Mean symptomatic period prior to hospitalisation (days) |
||
| Mean hospitalisation stay (days) |
||
| Hospital bed capacity | Fixed at 10000 | |
| Reduction factor of infectiousness for asymp. infectious people |
1.3. Outputs
The output of the model for a single run is a time series consisting of 200 days where the number of cases, hospital deaths and total deaths taking place is listed on each day. In this paper, we are only emulating over the total deaths over the 200 day period. As this model is stochastic, running the model with the same input values will yield a different answer each time. To gain an understanding of the distribution of the outputs, the mean and variance of 1000 model runs for each set of input runs is taken and used to build the emulator. The mean will act as a design point in the sense that the mean of the emulator will pass through that point, however the uncertainty will not reduce to 0 at that point as it normally would for a Gaussian Process emulator; instead the uncertainty at that point will be proportional to the variance of those 1000 runs. Therefore two emulators are being built, one for the mean of the 140 sets of 1000 model runs and one for the variance of 140 sets of 1000 model runs. Although here we emulate the mean and variance of the model output, other quantities such as quantiles and could also be emulated if these are of interest. This could be the case if, for example, extreme values are of particular concern to practitioners.
We now work through the UQ approach on the specific stochastic epidemic model outlined in Section 3.
2. Sensitivity analysis
When considering a deterministic model (note that a stochastic model can be made deterministic by making a random seed an input O’Hagan, 2006), sensitivity analysis (SA) is the process of understanding how changes in the input parameters influence . Generally, the SA can be divided into two groups: local and global. While, in the former, we study the impact of input variation on the output uncertainty at a specific point in the input space, the whole variation range of the input parameters is considered in the latter. The advantage of a local SA, such as a Morris design (Morris, 1991), is that it does not require a prior distribution for the inputs. However, a local SA is of limited value when understanding the consequences of uncertainty about (Oakley and O’Hagan, 2004). In the global SA, each input is considered as a random variable and the associated uncertainty is described in terms of probability distributions. This makes the model output a random variable, even if is deterministic, because the input uncertainty induces the response uncertainty. As per convention that random variables are represented by capital letters, we show the model output as where consists of independent random variables. From now on, any reference to SA refers to global SA.
In this work we focus on “variance-based” SA as proposed by Sobol (Sobol’, 2001). This method breaks down the output variance and attributes portions of that uncertainty to the uncertainty in each of the input variables (Saltelli et al., 1999, Sobol’, 2001). This is key to understanding how much influence each input has on the changes in the output and can assist in informing what inputs should form part of the emulation. If we can conclude that one or more inputs have negligible effect on the output, that input no longer necessarily needs to be included in the calibration and can instead be modelled as a random variable. This is cheaper computationally as modelling one less input means fewer design points required to build an accurate emulator.
The Sobol method is based on the following functional ANOVA decomposition (Sobol’, 2001)
in which is a constant and the remaining elementary functions are mean zero and mutually independent with each other. Taking the variance of the terms in the above equation, we have:
where represents the response uncertainty caused by the uncertainty of , reflects the output uncertainty due to the second order effect (interaction) of , and so on. More precisely, and are defined as
| (1) |
| (2) |
where () stands for all input factors except ( and ). Dividing the terms by gives the first order/main effect of : that shows the relative importance of . The same rule applies in computing the higher order effects, e.g. . The total order effect of (denoted by ) measures the main effect of together with its interactions with all the other inputs. The total order effect is useful to determine noninfluential inputs; is said to be insignificant if is close to zero. The interaction of with the other factors is simply the difference between its main and total order effects: .
The sensitivity indices (first and total order effects) can be estimated using Monte Carlo and in section 3.3 we show the results of that calculation. In addition to Monte Carlo (which can often be seen as expensive computationally (Aderibigbe, 2014)), we can use parts of the Gaussian Process emulator to remove the Monte Carlo aspect from the calculations (Oakley and O’Hagan, 2004). This is laid out in https://mogp-emulator.readthedocs.io/en/latest/methods/proc/ProcVarSAGP.html.
Given that our model is stochastic, we first emulate the simulator and then apply the variance-based sensitivity analysis to the predictive mean of the emulator. This approach is a valid way to estimate the first order indices (Iooss and Ribatet, 2009, Marrel et al., 2012) and still can be used to have an approximation to the total order effect of parameters. The results of the analysis can be found in Fig. 2. The total effect of all 14 input variables are shown segregated into main effects and interaction terms, clearly showing the extreme importance of (age-dependent probability of developing symptoms) compared to the other variables with (probability of infection) the second most significant. There are 3 more inputs that seem to have more than a negligible effect on the output, namely , and .
Fig. 2.
The main effect (blue) and interaction (red) of all 14 inputs to the output, as calculated by Monte Carlo. The height of the bar represents the total order effect. All variables are in the same order as in Table 1. Notable ones are . (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
What is also notable is the level of interaction taking place between the variables, whether second-order, third-order, fourth-order etc is not possible to tell. However, it seems probable that a large amount of interaction is taking place between and given the size of the interaction effect on Fig. 2 compared with the size of interaction from . The majority of the effect from is from interaction showing that they are not significant enough to affect the output on their own.
The importance of this analysis is determining which of the input parameters are important in terms of variation in the output. This may be of interest directly in helping inform policy. Clearly from this model, the probability of developing systems is one of the most important parameters. This could suggest community testing to identify asymptomatic cases may be an appropriate intervention to reduce the severity of the epidemic. Sensitivity analysis can also be important in informing the next step of the UQ framework, that is building the statistical emulator and choosing which inputs to build into it, but care should be taken in using it to completely define the emulator structure.
3. Emulation
A simulator can be regarded as a mathematical function that produces an output , here denoted as a vector but could equally be a scalar or matrix, from an input vector , i.e. (O’Hagan, 2006). Throughout this paper, however, we are only considering one output from the simulator at a time, i.e. , to simplify the process for those new to these techniques. These simulators can take anywhere between a fraction of a second to minutes, hours, days or even weeks to complete one input run. This is a major problem because processes such as variance-based sensitivity analysis, one type of sensitivity analysis, could require millions of model runs (O’Hagan, 2006, Lee et al., 2011) to get reasonable measures of uncertainty. Running the simulator for each of these input combinations in this case would take far too long.
Emulation is the process by which the simulator is replaced by a statistical surrogate model, which can be run more efficiently than the simulator can (Lee et al., 2011). The emulator hence acts as a statistical approximation of the simulator (O’Hagan, 2006) and its behaviour as a function of its inputs. There are many choices for what that statistical approximation should be, from simple linear regression up to complex multivariate predictive models, but frequently a stochastic process is used, where the mean is denoted as with a distribution around that mean describing how likely those points are to be part of (O’Hagan, 2006). A common feature of the simulator is that it is a smooth function as this allows information about values of to inform our judgements about for close to (Oakley and O’Hagan, 2002). To train the emulator, we evaluate the simulator at a number of locations in the input space , these points are called design points. Also, should represent a plausible interpolation and extrapolation, and the distribution around should express uncertainty on how the simulator might interpolate and extrapolate (O’Hagan, 2006). The specific type of emulator that is being used in this paper is a Gaussian Process (GP) emulator. GPs have many attractive properties that make them desirable for emulation, including their analytical tractability and the variety of covariance kernels that can be used to represent the dependence structures and associated uncertainties. However, we note here that this is a specific choice for which there are many alternatives. The process for building a GP emulator is described in the following
Building Gaussian process emulators
Gaussian Process emulators have several features:
-
1.
design points: for a deterministic model the mean of the distribution - - passes through each design point , and the variance around at each design point is 0, given that we know the function is certain to pass through the point . These design points need to be evaluated by the simulator (consequently taking up the majority of computation time to build the emulator) to construct the Gaussian Process emulator.
-
2.prior mean function: as there are only a finite amount of design points to use in the building of the emulator, this implies that we only have certainty on the outputs of the simulator in a finite region of space. Therefore an initial estimation is needed to emulate away from the design points and in space where we are uncertain. The prior mean function takes the form of
where contains regression functions which we are required to specify and is calculated using the form of the regression functions, design points and covariance functions. For now, we only need to specify , i.e. the form of the prior. For example for a linear prior or for a constant prior. -
3.covariance function: whilst we have the requirement that the emulator passes through the design points and the space away from the design points is represented by the prior; we still need to have the ability to interpolate between the design points but then gradually regress to the prior when we are far away from any design points. This is where the covariance function comes in. It is of the form
where is the correlation function that decreases as increases and satisfies (Oakley and O’Hagan, 2002). This acts as the prior covariance function. In this work, is the squared exponential/Gaussian function which is of the following form
with hyperparameter defining the characteristic length-scale for each input variable . This covariance function is infinitely differentiable meaning the subsequent GP will be very smooth (Rasmussen and Williams, 2008) and is useful under the assumption that the output varies smoothly across the input space. It can frequently be the case that a smooth covariance function is not appropriate for modelling the relationship between input and output, and alternatives such as Matèrn covariance functions are often more appropriate. The exact choice should be governed by the model output, with the smoother option specified here chosen as the optimum in minimising RMSE. The values of these length-scales are determined using a process called ‘model-selection’ which requires us to maximise this log-likelihood function (derived in section 2.3 of Rasmussen and Williams, 2008):(3)
where ; with being the Gram matrix which in itself depends on the model length scales (defined below), a vector of nugget terms on each design point and the number of design points. The parameters are estimated from data by finding the parameter combination that maximises the likelihood in Eq. (4).(4)
Using these assumptions we can construct the emulator as follows:
| (5) |
| (6) |
where:
Looking at Eqs. (5), (6), note that is the posterior mean function (where is the prior mean function) and is the posterior covariance function (where is the prior covariance function) (Oakley and O’Hagan, 2002, Oakley and O’Hagan, 2004), where posterior means after the Gaussian Process emulator has been built, whereas prior means before it was built.
To construct an approximate 95% uncertainty bound, one only has to plot two lines
| (7) |
where the uncertainty bound lies between them.
3.1. Building the emulator
The emulator was built using the Gaussian process methodology described in previous sections. Prior ranges for the parameters are given in Table 1, which determined the limits of the Latin Hypercube design. Probabilities and proportions were assumed to be between zero and one.
4. Validation
The fitted Gaussian process emulator is used to make inferences about the simulator, and equally take its place in calibration to the real world. As such, it is therefore very important that confidence in those inferences using the emulator can be ensured. To do this we can use validation to verify the ability of the emulator to mimic the behaviour of the underlying model (Challenor, 2013). Validation often means comparing the output of the emulator with that of the simulator to minimise their differences (O’Hagan, 2006). We can use the posterior covariance function to construct an approximate frequentist confidence interval around the posterior mean function (seen in (Eq. (7))). Although we are conducting Bayesian updating of the mean and variance functions, the Gaussian marginal distributions will mean that a central limit theorem approximation to the uncertainty will be relatively accurate. If, for example, 95% of the validation points are in the 95% confidence interval then that represents a good fit. If not then the emulator may be overfitting/underfitting: overfitting being the emulator is so reliant on the training data that anything outside it is less likely to be well represented; and underfitting being the emulator is not using the training data to its full extent to accurately represent the simulator (see Bastos and O’Hagan, 2009 for more details).
To test how well the GP emulator represents the simulator, 20 further points were sampled (called validation points) across the same input space as the design points and using Latin Hypercube Sampling. These points are listed in appendix 2. Looking at Fig. 3, 19 points out 20 (95%) lie in the 95% confidence interval, implying that the emulator is a good fit and coverage probability.
Fig. 3.
The GP Prediction (black points) of the mean response (red points) at 20 test points. Dashed lines is 95% confidence interval. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
5. Calibration
Calibration is the mechanism of using data to constrain the model parameters such that the model output matches some aspect of the observed reality. There are many ways of calibrating models, whether through minimising a loss function, maximising a statistical likelihood or conducting a full Bayesian inference procedure (see Swallow et al., 2022 for discussion of these approaches in epidemic modelling). In the case of the epidemiological model under consideration here, direct calibration using approaches such as particle MCMC (pMCMC) (Andrieu et al., 2010) may be feasible, and calibration using Approximate Bayesian Computation (Beaumont, 2003) is also possible. In fact, the latter is an option in the model code directly. In more complex models, however, this will not be feasible due to computational costs and calibration using emulation will be the most realistic or only approach.
In the UQ framework, the method of history matching is commonly used to conduct model calibration Vernon et al. (2014). History matching is the process of sequentially ruling out regions of parameter space that are inconsistent with the observed data, where inconsistency will be discussed further below. Parameter combinations are generated, in what are called parameter ‘waves’, and used to build a new emulator. Those regions of parameter space that are sufficiently inconsistent with the observed data to lie outside of an acceptable region of error are deemed ‘ruled out’ and the remaining space, the ‘not ruled out yet (NROY)’ space then forms the basis of the next parameter wave. The process terminates according to a specified stopping rule, which can be based on a specified tolerance threshold of remaining parameter space or when subsequent waves fail to reduce the space any further.
In terms of notation, the goal of calibration is using observations to learn about the parameter inputs (Salter et al., 2019). These observations represent measurements of the real (but unknown) system y, a process represented via the formula
| (8) |
where is the observation error (Bower et al., 2010). This represents the discrepancy between the recorded observation and reality. There also exists another type of discrepancy between the appropriate choice and true system value (Bower et al., 2010). This can be expressed by the formula
| (9) |
where is the model discrepancy. Combining Eqs. (8), (9) gives the expression
| (10) |
The aim is to find all possible values such that (10) is satisfied where the collection of these points are defined in Vernon et al. (2014) as . This is done by ruling out points in that feasibly cannot give an evaluation sufficiently close to . The portions of input space that are left after this procedure are called space.
This means we need to be able to evaluate all of the input space to test the implausibility of these points in relation to the observations . For most complex models however, this is not possible therefore we need to represent the uncertainty for points we haven not yet evaluated (Vernon et al., 2014). We build an emulator with the form from Section 3 to resolve this issue. For any in the space we can examine how plausible the difference in value between and the evaluation is for any using an implausibility measure (Williamson and Vernon, 2013). This takes the form of
| (11) |
where is the Gaussian Process emulator. Therefore the desired points are defined by the set
| (12) |
where is chosen to maintain an upper-bound for that distance between observation and model evaluation whilst taking into account the uncertainty in the emulator at for any . The threshold is usually chosen to have the value of 3 (see Pukelsheim, 1994 for justification).
Algorithm for History Matching
We define an algorithm to conduct History Matching (HM) for a single output . Steps 1-3 denote the first wave of HM, with steps 4–5 denoting the second. Repeat steps 4–5 to perform more waves if required.
-
1.
Create a large (maximin) Latin Hypercube of points (in this paper points) in dimensions, using the same upper and lower bounds for those dimensions as used when creating the Latin Hypercube Sample (LHS) for the emulator. This allows us to judge what percentage of input space has been ruled out as it will correspond with what proportion of those points are not in NROY space as calculated by the implausibility function in Eq. (11).
-
2.
Build a GP emulator using design points (recommended from Loeppky et al., 2009) where the length scales of that emulator are chosen according to Maximum Likelihood Estimation from Eq. (4). The emulator is constructed using the package ‘DiceKriging’ in the statistical environment .
-
3.
Input all of the points into Eq. (11) where is the GP emulator from step 2. As explained above, the inputs that give an implausibility greater than 3 will be ruled out (see below for more detail), the inputs that give an implausibility less than or equal to 3 are defined as a.k.a. NROY space. This completes the first wave of History Matching.
-
4.
Build a GP emulator with another set of design points uniformly sampled from .
-
5.
Input all NROY points into (11) where is the GP emulator from step 4. The inputs that give an implausibility greater than 3 will be ruled out, the inputs that give an implausibility less than or equal to 3 are defined as a.k.a. NROY space.
Here, we aimed to remove individual points in space that have very little to no chance to give the desired output. Although a value of is chosen as per Pukelsheim (1994), one could adjust to make NROY space more restrictive (by lowering ) or less restrictive (by increasing ). By reducing input space, the range of the individual input parameters can be shortened which has the benefit of giving a smaller posterior uncertainty on the output. This may be driven by implications of uncertainty or by the requirements of policy makers.
Vernon et al. (2018) presented a similar algorithm but has some differences to one presented here; mainly that after wave 1, the samples from that are chosen to build the next emulator are sampled from the proportion of points that still remain in NROY, however Vernon et al. (2018) used a ‘well chosen’ set of runs potentially using Latin Hypercube which we only use for the first wave in this paper. A second difference is that we are only emulating one output whereas Vernon et al. (2018) not only emulate more than one but also the amount of emulated outputs can change in each wave.
Calibration of the epidemiological model
Firstly we must choose the value(s) we wish to use to calibrate the model. One aspect of the pandemic that has been challenging for many statisticians and modellers is the variety of data streams available and their associated definitions of the population they are measuring. We therefore choose to calibrate the model to two different measures of mortality in Scotland. Firstly we calibrate the model to cumulative deaths reported on death certificates, and then we conduct a second independent calibration to the model using deaths reported within 28 days of a positive test.
The algorithm for this process is shown in Section 5, where in this application , the upper and lower bounds for the input dimensions are defined in Table 1, represents the first death figure, represents the second and when building the emulator at each wave, a Gaussian kernel is used (see Eq. (3)). These length scales are chosen using maximum likelihood via maximising Eq. (4) using the R package ‘DiceKriging’. for from Eq. (4) corresponds to the variance at each evaluation (because the model is stochastic we run it 1000 times for each set of inputs).
The two death statistics are:
-
1.
Those who died within 28 days of a positive test in Scotland in the first 200 days of the pandemic. This date being 17th September 2020. This figure is .
-
2.
Those who had COVID-19 on their death certificate in Scotland over the same time period. This figure is .
This data has been obtained from https://coronavirus.data.gov.uk/.
The variance for the observation error Var and the variance for the model discrepancy Var which represents the model predicting the output within of the observation 95% of the time. Andrianakis et al. (2015) also use an additional error term which accounts for the stochasticity of the model which is denoted as Ensemble Variability. Whilst they add an extra term in the implausibility measure Eq. (11) to account for this, in this paper we account for the stochasticity by building two emulators; one for the mean of the outputs, and one for the variance of the outputs.
In this subsection, we are looking:
-
1.
to see if it is possible to reduce the ranges of the input parameters from those seen in Table 1 by calibrating towards the two death figures. This can be visualised by analysing an Optical Density Plot (ODP) which displays (amongst other things) what portion of an inputs’ range is contained in NROY space.
-
2.
at how changing the prior of the emulators built in each HM wave influences the amount of space ruled out.
-
3.
at how modelling different variables as noise influences the amount of space ruled out. It is likely to change the uncertainty levels in the emulator given that the uncertainty attributed to the variables modelled as noise would be reduced.
-
4.
to see if all uncertainty was removed from the emulator at each wave, what the NROY space would be. This would show how much influence the model discrepancy and observation error have on the overall input space and show the effectiveness of the History Matching process.
-
5.
at how the length scales of each variable impact on the uncertainty on each variable and thus the amount of ruled out space on that wave.
Mortality within 28 days of a positive test
In this subsection, we perform 4 waves of history matching, calibrating towards . We use a constant prior and no variables are treated as noise. It serves as an introduction towards the second death figure where a more in-depth analysis takes place.
We found that very quickly, the rate of change of NROY decreases rapidly the more waves are completed, particularly by wave 3. What we also found is when we remove all uncertainty from the emulator (i.e. we have a perfect emulator in that it matches the simulator for all inputs) the amount of NROY space is much smaller. Thus showing how little effect the observation error and model discrepancy have on the overall uncertainty compared to the emulator uncertainty. Both of these facts are demonstrated using Table 2 and are trends found across all the waves of History Matching that are conducted in this section.
Table 2.
Column 2 shows the percentage of space satisfying eq. (12) after the corresponding wave of history matching. Column 3 shows the percentage of space that could have been ruled out had there been no uncertainty in both the emulator for the mean and the emulator for the variance built for the corresponding wave.
| Wave no | NROY | Max NROY |
|---|---|---|
| 1 | 33.29% | 0.8% |
| 2 | 21.59% | 1.98% |
| 3 | 20.74% | 2.18% |
| 4 | 20.58% | 2.15% |
Looking at Fig. 4 and in particular down the diagonal; despite ruling out nearly 70% of input space on the first wave, it is only on two variables that we are able to visualise the space being ruled out: and . Looking at Fig. 2 the reason behind this finding becomes clear. As the two variables with the most total effect, the fact that they are restricted to a smaller range shows their influence on the output. If those variables were set to a higher value (closer to 1) then the number of deaths would see an increase, however changing one of the other variables ( for example), would make little to no change given its lack of influence on the output seen from Fig. 2.
Fig. 4.
An optical density plot for wave 1 of calibration of model towards . On the diagonal shows a density plot displaying how the NROY space is concentrated for each variable. For the upper and lower triangles, they are made up of windows showing the interactions between two variables. Each window has been divided up into a 50 × 50 grid of cells where in each cell there is a colour. In the upper triangle, the colour shows what proportion of points in that cell are in NROY; this range is between 0 and 1 and shown on the top scale. In the lower triangle, the colour shows what the smallest implausibility is out of the points in that cell; this range is between 0 and 3 (any implausibility greater than 3 is set to 3) and shown on the bottom scale.
What we also see from Fig. 4 is the level of interaction between and , particularly in the upper triangle, we see a higher proportion of points that are in NROY space if at least one of those variables is close to 0. In addition, looking at that same window we see that having both of these variables set to 0 is also in NROY space, but having these variables set to 0 would result in no infections and no symptoms resulting in no outbreak. This was also true in wave 3’s ODP, meaning the death figures we are calibrating towards are actually quite low in respect to how large the output could be. As a final point, looking again at the upper triangle you again see the importance of these two variables; this time the interactions that those variables have with the rest. Those interactions consist only of restricting one of the important variables whilst the other has free choice.
COVID-19 mentioned on the death certificate
In this subsection, we perform several experiments with varying combinations of numbers of waves, forms of priors and noise settings. We are calibrating towards .
As we have seen in the previous subsection and from Fig. 2, there are a 5 variables which encapsulate the vast majority of the uncertainty, namely , , , and with the first 2 being the most prominent. The form of the prior on the emulator should be chosen to incorporate any beliefs we have about the form of the simulator (Oakley and O’Hagan, 2002) hence if the vast majority of the uncertainty is within these 5 variables then representing them in the prior may help to obtain a more accurate emulator which in turn would rule out more space.
For this reason in the first experiment, we calibrated towards using a constant prior, a linear prior over the 2 most influential variables and a linear prior over the 5 most influential variables. As the remaining 9 variables have very little total effect we treated a varying number of them as noise in an attempt to reduce the uncertainty on the output. We combined the two options for emulation (priors and noise) in our first experiment and conducted 3 waves of History Matching with different combinations of priors and noise. The list of priors were: constant (i.e. ), , and . These priors were chosen to gradually incorporate a higher proportion of influence on the output within the prior and therefore to measure to what extent including more variables in the prior has on reducing space. The list of noise settings were: ‘none treated as noise’, ‘all but and treated as noise’ and ‘all but and treated as noise’.1 The cut off of three waves has been chosen given that the model acts as a simpler version of the more complicated epidemiological model (which has closer to 30 input variables). We could have performed (and have in some cases did perform) more waves of History Matching with certain combinations of prior and noise, however as HM with the more complex model is more expensive computationally (due to it having more variables), we want to rule out as much space as possible with the fewest number of waves.
Looking at Fig. 5, in the majority of cases, by wave 3 the NROY space had reduced to approximately 20%. However, given that we want to remove input space in as few waves as possible, then analysis will not just be reserved for after 3 waves. When we treat all but the most effective 5 variables as noise then by wave 1, a higher proportion of space has been ruled out when compared to the other 2 noise settings. The likely reason behind this can be attributed to less uncertainty arising from those variables that are being treated as noise, meaning less points will satisfy the condition from (12) given that the variance would have decreased. What is also prevalent is that after three waves, all the calibrations where all but and are treated as noise performed the worst than the other two noise settings. Perhaps too much of the uncertainty in the model was being attributed to noise which causes the uncertainty bounds to increase and therefore less regions of space are ruled out.
Fig. 5.
4 plots showing how NROY space reduces over 3 waves of History Matching whilst using different combinations of priors and noise. ‘No noise’: none of the variables are treated as noise. ‘All but 2 Noise’: and are treated as variables, the rest as noise. ‘All but 5 noise’: , , , and are treated as variables, the rest as noise.
Despite the three wave cutoff, we want to see how much space can be removed by doing more waves and whether this tailoring-off effect continues. From Table 2 we see the maximum amount of space that can be ruled out is far greater than the results we have seen thus far. Table 3 shows a very gradual decrease in NROY space and not getting close to the maximum that can be achieved. However looking at the percentage change of NROY between waves 3 and 4, it was much smaller compared to the change between waves 4 and 5 or 5 and 6. Interestingly, by running wave 4 but using a different random seed (meaning selecting a new random set of design points from ) - named 4.2 - that wave ruled out an order of magnitude more space. We consider the length scales in the emulators to explore why this occurs.
Table 3.
This table shows the percentage of space that remains after doing waves of History Matching. At wave 4, two different seeds were used (denoted by 4 and 4.2) where waves 5 and 6 follow from wave 4 and waves 5.2, 6.2, 7.2 and 8.2 follow from wave 4.2.
| Wave no | NROY (%) | Wave No | NROY (%) |
|---|---|---|---|
| 1 | 34.98 | ||
| 2 | 24.60 | ||
| 3 | 21.22 | ||
| 4 | 21.19 | 4.2 | 20.90 |
| 5 | 20.41 | 5.2 | 20.26 |
| 6 | 19.87 | 6.2 | 20.04 |
| 7.2 | 19.76 | ||
| 8.2 | 19.06 |
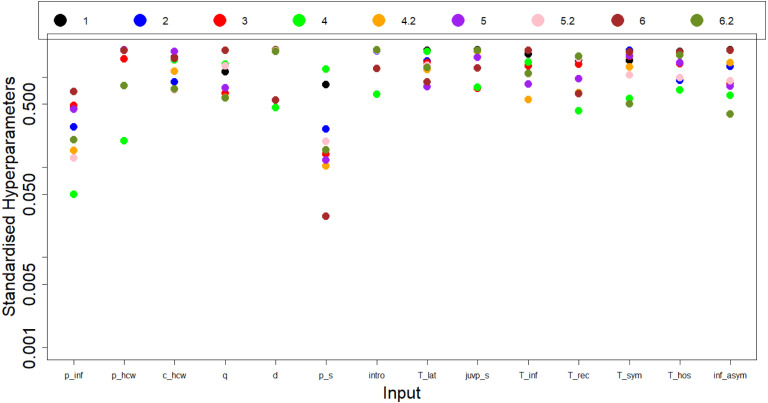
As discussed in the ‘Emulation’ section, Maximum Likelihood Estimation (MLE) is used to determine the length scales for the GP emulator. Looking at Fig. 6, we see the length scales for each input variable over many waves of history matching. Looking at the two most influential variables ( and ), the length scales for wave 4 appear to be outliers with respect to the length scales of other waves which may have been caused by a poor optimisation of MLE from Eq. (4) due to a local maxima. Compare this to wave 4.2 where the length scales are close to those of other waves. This could explain why so little space was ruled out for that wave. Given how a lot of other length scales for wave 4 also appear to be outliers this can give evidence that is was a so-called ‘rogue wave’ given how the length scales for wave 4.2 were not outliers in respect to the other waves.
Fig. 6.
This shows a plot of the length scales for each of the variables after extending the number of waves from 3 to 6. Wave 4 has 2 different versions: 4 and 4.2, with the following waves named 5 and 6, and 5.2 and 6.2 respectively. Standardised hyperparameters are the length scales ( from (3)) divided by the respective ranges of each parameter in Table 1.
Extension to multiple outputs
Due to the time series nature of the outputs, aggregation to a single output ignores the correlation inherent in the temporal data. This temporal structure may further assist in ruling out regions of parameter space. We therefore also conduct an additional calibration of the model to multiple outputs as follows. This has multiple benefits:
-
1.
One problem that arose when calibrating on a single output was ‘rogue waves’. This occurred due to the length scales being improperly determined by way of the maximum likelihood estimation (Eq. (4)) optimising to a poor result, leading to large variances and resulting in not ruling much space out for that wave. Calibrating to multiple outputs reduces the impact caused by rogue waves as emulators are built for each output. This means we can avoid ‘rogue waves’ as if one emulator does not optimise well then there are other emulators to rely on for ruling out space.
-
2.
The biggest computational cost in uncertainty quantification is running the model; so being able to make more use of data obtained from the model runs will (relatively speaking) not take a significant amount of extra computational resources.
In this section we choose 5 outputs to emulate, this being the total number of deaths up to days 60, 65, 70, 75 and 200. Epidemic curves are often highly sensitive to early time points, however the simulator used had already been carefully calibrated to these early time points, hence they were not deemed informative through sensitivity analysis. We aim to capture the trajectory of the epidemic by including these days as well as capturing the overall picture over the 200 days. The total deaths on these days are 1620, 1839, 2018, 2184 and 2560 respectively (number of people who died from COVID-19 within 28 days of a positive test in Scotland).2 We use our algorithm for history matching to calibrate separately towards each of these outputs and calculate the implausibility for a given input to each observation and take the maximum of those implausibilities. This ensures any parameter must be plausible at all timepoints in order for it to not be ruled out. In more formal terms, we define NROY space as the following.
with being a vector of implausibilities for a given input vector towards each observation. We choose our observation error to be 1% of the observation with the model discrepancy remaining the same calculation () as with one output.
We see in Table 4 that after 4 waves with 5 outputs we rule out more space than was ruled out in 8 waves with one output (see Table 3). Through using multiple outputs we have halved the computation time as half the amount of ensembles were evaluated by the model as when calibrating towards a single output. We do note, however, that further waves were not particularly successful at ruling out further space as tolerance below this level dropped within the emulator error and model stochasticity.
Table 4.
This table shows the proportion of space that has been ruled out using 5 outputs (cumulative number of deaths for days 60, 65, 70, 75 and 200.
| 5 Outputs | NROY (%) |
|---|---|
| Wave 1 | 32.4 |
| Wave 2 | 27.7 |
| Wave 3 | 24.6 |
| Wave 4 | 16.2 |
6. Ensemble visualisation
In supporting the above processes involving the exploration of high dimensional parameter spaces and the comparative analysis of model runs and model calibration attempts, data visualisation literature offers several techniques and approaches, which could broadly be classified under the broad area of ensemble visualisation (Wang et al., 2018). (Phadke et al., 2012) define “ensemble” as “a collection of datasets representing independent runs of the simulation, each with slightly different initial parameters or execution conditions” and stated visualisation to be a “promising approach to analysing an ensemble”. While the literature on visualisation and visual analysis of ensemble data is substantial as outlined by the survey by Wang et al. (2018), we discuss here two important relevant areas for an UQ framework, namely multidimensional visualisation and parameter space analysis. Examples of these visualisation approaches will then be applied to the emulated model below.
6.1. Multidimensional visualisation
Multivariate data, those which contain three or more variables, make finding patterns and trends in large data tables challenging. Effective data analysis can be provided, however, by the use of multivariate data visualisation techniques. The Survey of Surveys (SoS) on information visualisation by McNabb and Laramee (2017) provided 13 surveys on multivariate and hierarchy topics, some of which approach multivariate analysis more broadly as a multi-faceted analysis (Kehrer and Hauser, 2012).
Multivariate visualisations use different design strategies in data exploration on a two-dimensional plane. Keim and Kriegel (1996) classify visual data exploring methods for multivariate data into six categories: geometric, icon-based, pixel-oriented, hierarchical, graph-based, and hybrid. Some of the multivariate visualisations are presented and explained further.
Scatter plots show the relationship of and variables, while the addition of colour and glyphs can represent two more variables. However, a scatter plot matrix includes multiple scatter plots presented in a matrix format that displays a combination of attributes. Another multivariate visualisation technique, Parallel coordinate plot, introduced by Inselberg (2008), transforms multivariate relations into 2D patterns. Each data variable is represented by uniformly located vertical axes. Data records are indicated by edges that intersect with each scaled axis at a point corresponding to the value. The view shows distributions of data attributes and reveals relationships between adjacent data variables.
Glyphs are identified by Ward (2002) as graphical entities that convey one or more data value(s) via attributes such as shape, size, colour, and position. They are commonly used to represent complex, multivariate data sets in data visualisation. A survey by Borgo et al. (2013) describes glyphs as “a small visual object that can be used independently and constructively to depict attributes of a data record or the composition of a set of data records”. Various visual elements, such as shape, colour, size or orientation can be used in the creation of glyphs, allowing the display of multi-dimensional data properties.
Interaction is a fundamental aspect of data visualisation that is key for the exploration, analysis, and presentation of data (Dimara and Perin, 2019). The survey by Kosara et al. (2003) focuses on interaction methods that are used in information visualisation such as focus+context and multiple views. Focus+Context (F+C) visualisation is a popular approach that enables the user to zoom in on specific areas of the data or filter the data when the data are too large to search directly.
A radar chart is a visual representation of multiple data points and their variations. Data variables are represented by axes, which are evenly spaced and arranged radially around a central point. The size and shape of the polygons can be used to compare variables and see overall differences (Liu et al., 2008). Another technique is pixel-based visualisation, in which the visualisation is filled with an array of sub-windows portraying dense coloured pixel displays mapping multivariate data dimensions (Keim, 2000). Each attribute value is represented by the colour of a single pixel. The pixels are typically sorted based on another variable, presenting similar values to be clustered that enables easy comparisons and trend recognition. A stacked display divides the data space into two-dimensional sub-spaces that are stacked on top of each other, depicting one coordinate system within another. The outer coordinates of a two-dimensional layout can be used to display the first two attributes, dividing the area into smaller areas (Claessen, 2011).
When the multi-objective data is a continuous process it can help to represent the data using a visual encoding that represents changes on the continuous scale. For example, heatmaps (colour or otherwise) or function plots can be used. Furthermore, slicing is a visualisation method that retains this continuous nature in the data. Examples include HyperSlice (van Wijk and van Liere, 1993) (a 2D heatmap plot for every pair of input parameters where the change in colour represents the function value around a particular ‘focus point’) and Sliceplorer (Torsney-Weir et al., 2017) (which uses function plots to show multiple focus points at a time).
Uncertainty visualidation.
While uncertainty is involved in most data processing, reasoning with uncertainty is difficult for both novices and experts (Padilla et al., 2020). Besides the difficulty in the empirical evaluation of uncertainty (Hullman et al., 2018), it is also a challenge for visualisation designers due to practical problems in creating visualisations associated with decision making process (Kamal et al., 2021). Ensemble data sets contain a collection of estimates for each simulation variable, allowing for a better understanding of potential results and the associated uncertainty while ensemble visualisations sample the space of projections that can be generated by a model with uncertainty (Potter et al., 2009, Liu et al., 2016).
Dimensionality reduction (DR).
has been widely applied in information visualisation over the past 20 years (Espadoto et al., 2019). DR techniques aim to build a lower-dimensional space in which compressed features are extracted to represent their corresponding high-dimensional multivariate data (Engel et al., 2012). Assume denotes a data observation , a mapping function is used to project the data observation into a compact representation . In this manner, the transformed low-dimensional data can be easily plotted for visual analytics. Popular DR techniques include traditional linear mapping functions, e.g., PCA and ICA (Fang et al., 2013), and non-linear mapping functions, e.g., tsne (Van der Maaten and Hinton, 2008) and umap (McInnes et al., 2018) which are useful for exploring uninformativeness or redundancy in data to reduce the feature dimensionality These DR methods can be further integrated with above-mentioned visualisation tools for a range of multivariate analysis tasks (Sacha et al., 2016) such as exploring the relations between variables (Turkay et al., 2012).
6.2. Parameter space analysis
The role played by the input parameters is a key aspect that sets ensemble data visualisation aside from traditional data visualisation challenges. Investigation of the parameter space is part of the journey towards understanding the ensemble as a whole and how ranges of outputs relate to ranges of input parameters. Visual parameter space analysis techniques support interactive sampling of the parameter space to select candidate input parameter sets while also relating these combinations to the collection of outputs (Sedlmair et al., 2014). Interaction techniques aim to flexibly and iteratively define parameter sets and ranges (Konyha et al., 2006), and comparative visualisations methods aim to concurrently assess many collections of outputs (Gleicher et al., 2011). Both of these approaches stand out as some fundamental strengths of visualisation to support parameter space analysis.
Parameter selection.
such as in Sedlmair et al. (2014), classifies visual parameter space exploration techniques into local-to-global and global-to-local. Local-to-global strategies start from inspection of a specific sampled simulation run and provide ways to navigate through other runs. Global-to-local strategies start with an overview over all runs and then allow for detailed exploration of specific runs. No matter the strategy which may be adopted analysis of the parameter space includes several tasks including, but not limited to: optimisation, partitioning, uncertainty, and sensitivity analysis. Pajer et al. (2017) introduce several visualisation techniques employed to address these challenges including clustering (Bergner et al., 2013), slicing (van Wijk and van Liere, 1993), scatter plots (Chan et al., 2010). For optimisation in the context of Pareto-optimal solutions, several approaches exist in visualisation. Approaches include matrices of bi-objective slices (Lotov et al., 2004, Torsney-Weir et al., 2018), parallel coordinates (Bagajewicz and Cabrera, 2003, Heinrich and Weiskopf, 2013), and self-organising maps (Schreck et al., 2013).
Model visualisation.
To explore aspects of the simulation model itself, visualisations often employ coordinated multiple views (Roberts, 2007) of the input and output parameter spaces. These use interactive selection to explore the relationship between different combinations of input and output parameters. Visual representations include heat maps (Spence and Tweedie, 1998), parallel coordinates (Berger et al., 2011), or contour lines (Piringer et al., 2010). In some cases these visualisations use an emulator model internally such as Torsney-Weir et al. (2011), which used a Gaussian process model, or Mühlbacher and Piringer (2013), which used linear regression models.
Discussion
In this paper we have outlined a principled approach to conducting Gaussian process emulation of a stochastic epidemic model, which allows the ability of the modeller to determine important sensitivities, uncertainties and potential biases in the modelling framework. We have shown that building an emulator for both the mean and variance for the model is possible using design points and shown to be accurate using validation (section 3.2) given that 95% of validation points lie in the 95% confidence interval (as seen in Fig. 3), showing that neither overfitting nor underfitting is occurring. This is despite the simulator being stochastic which could have made emulating it quite difficult, but using the mean and the variance of the 1000 runs meant being able to capture the randomness of the outputs and still manage to incorporate that into the emulator.
Furthermore, it has been shown via Fig. 2 that only inputs out of the have more than a negligible impact on the output with the probability of developing symptoms and being infected being the first and second most influential inputs respectively. Levels of interaction between the variables was also important in some cases, with most of the effect from the third, fourth and fifth most influential variables coming from interactions with other variables. Accounting and assessing these higher order interactions is therefore highly important.
Uncertainty Quantification remains a highly under-used tool in epidemic modelling and we provide here the main steps in the UQ process. The challenge in encouraging the more general use of these approaches both in the building of models but also in the estimation process is one that should not be underestimated, and the provision of general software and tutorials facilitating users to apply these methods for their own models is highly overdue. Some of the decisions in the process may seem arbitrary, however in reality it is vital that these are made carefully with input from knowledgeable domain experts and modellers. Our aim in this manuscript is to begin that process of demystification.
There still remain significant challenges in modelling complex stochastic models, and Swallow et al. (2022) in this issue outlines these in detail. In particular this paper highlights challenges remaining in UQ of stochastic models of a hypothetical future pandemic. Some of the challenges in visualisation of uncertainty have also been touched on here, more details of which can be found in Chen et al. (2020).
CRediT authorship contribution statement
Michael Dunne: Contributed to the conceptual development of methods, Wrote most of the code and ran the analyses under the supervision of PC, IV and BS, Writing – review & editing, Signed the final manuscript. Hossein Mohammadi: Contributed to the conceptual development of methods, Wrote most of the code and ran the analyses under the supervision of PC, IV and BS, Signed the final manuscript. Peter Challenor: Contributed to the conceptual development of methods, Signed the final manuscript. Rita Borgo: Contributed to the conceptual development of methods, Visualisation, Writing – review & editing, Signed the final manuscript. Thibaud Porphyre: Contributed to the conceptual development of methods, Designed, Developed, Wrote the code of the simulator, Provided domain expertise throughout, Signed the final manuscript. Ian Vernon: Contributed to the conceptual development of methods, Signed the final manuscript. Elif E. Firat: Contributed to the conceptual development of methods, Visualisation, Writing – review & editing, Signed the final manuscript. Cagatay Turkay: Contributed to the conceptual development of methods, Visualisation, Signed the final manuscript. Thomas Torsney-Weir: Contributed to the conceptual development of methods, Visualisation, Signed the final manuscript. Michael Goldstein: Contributed to the conceptual development of methods, Signed the final manuscript. Richard Reeve: Facilitated the initial set up of the working group, with BS chairing weekly meetings and steering the group direction, Contributed to the conceptual development of methods, Signed the final manuscript. Hui Fang: Contributed to the conceptual development of methods, Signed the final manuscript. Ben Swallow: Contributed to the conceptual development of methods, Writing – review & editing, Signed the final manuscript.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The authors would like to thank the Isaac Newton Institute for Mathematical Sciences, Cambridge, United Kingdom, for support during the Infectious Dynamics of Pandemics programme where work on this paper was undertaken. This work was supported by EPSRC, United Kingdom grant no. EP/R014604/1. RR was funded by STFC, United Kingdom grant no ST/V006126/1.
The original working group was set up as part of the Scottish Covid-19 Response Consortium. This work was undertaken in part as a contribution to the Rapid Assistance in Modelling the Pandemic (RAMP) initiative, coordinated by the Royal Society.
I.V. gratefully acknowledges Wellcome funding (218261/Z/19/Z) and EPSRC funding (EP W011956).
T.P gratefully acknowledges funding from the Scottish Government Rural and Environment Science and Analytical Services Division, United Kingdom, as part of the Centre of Expertise on Animal Disease Outbreaks (EPIC). T.P. would also like to thank the French National Research Agency and Boehringer Ingelheim Animal Health France for support through the IDEXLYON project (ANR-16-IDEX-0005) and the Industrial Chair in Veterinary Public Health , as part of the VPH Hub in Lyon. We also thank Qiru Wang and Robert Laramee for their visualisation tool development.
Footnotes
We used the function from the package in to build all the emulators seen throughout this paper; by treating variables as noise we exclude them from the command within (note that the command within is different to the sampling design specified before in this paper) meaning that the excluded variables are then accounted for in the variance of the emulator.
The model in its calculations already calibrates towards days hence we are choosing the days following that.
References
- Aderibigbe A. first ed. University of Ibadan; 2014. A Term Paper on Monte Carlo Analysis/simulation. URL: https://www.researchgate.net/publication/326803384_MONTE_CARLO_SIMULATION. [Google Scholar]
- Andrianakis I., Vernon I.R., McCreesh N., McKinley T.J., Oakley J.E., Nsubuga R.N., Goldstein M., White R.G. Bayesian history matching of complex infectious disease models using emulation: A tutorial and a case study on HIV in Uganda. PLoS Comput. Biol. 2015;11(1) doi: 10.1371/journal.pcbi.1003968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrieu C., Doucet A., Holenstein R. Particle Markov chain Monte Carlo methods. J. R. Stat. Soc. Ser. B Stat. Methodol. 2010;72(3):269–342. [Google Scholar]
- Bagajewicz M., Cabrera E. Pareto optimal solutions visualization techniques for multiobjective design and upgrade of instrumentation networks. Ind. Eng. Chem. Res. 2003;42(21):5195–5203. [Google Scholar]
- Bastos L.S., O’Hagan A. Diagnostics for gaussian process emulators. Technometrics. 2009;51(4):425–438. doi: 10.1198/TECH.2009.08019. [DOI] [Google Scholar]
- Beaumont M.A. Estimation of population growth or decline in genetically monitored populations. Genetics. 2003;164(3):1139–1160. doi: 10.1093/genetics/164.3.1139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckley R., Weatherspoon C., Alexander M., Chandler M., Johnson A., Bhatt G.S. first ed. Tennessee State University; 2013. Modeling epidemics with differential equations. URL: https://www.tnstate.edu/mathematics/mathreu/filesreu/GroupProjectSIR.pdf. [Google Scholar]
- Berger W., Piringer H., Filzmoser P., Gröller E. Uncertainty-aware exploration of continuous parameter spaces using multivariate prediction. Comput. Graph. Forum. 2011;30(3):911–920. [Google Scholar]
- Bergner S., Sedlmair M., Moller T., Abdolyousefi S.N., Saad A. Paraglide: Interactive parameter space partitioning for computer simulations. IEEE Trans. Vis. Comput. Graphics. 2013;19(9):1499–1512. doi: 10.1109/TVCG.2013.61. [DOI] [PubMed] [Google Scholar]
- Borgo R., Kehrer J., Chung D.H., Maguire E., Laramee R.S., Hauser H., Ward M., Chen M. Eurographics (State of the Art Reports) 2013. Glyph-based visualization: Foundations, design guidelines, techniques and applications; pp. 39–63. [Google Scholar]
- Bower R.G., Goldstein M., Vernon I. Galaxy formation: a Bayesian uncertainty analysis. Bayesian Anal. 2010;5(4):619–669. URL: https://projecteuclid.org/journals/bayesian-analysis/volume-5/issue-4/Galaxy-formation-a-Bayesian-uncertainty-analysis/10.1214/10-BA524.full? [Google Scholar]
- Challenor P. Experimental design for the validation of kriging metamodels in computer experiments. J. Simul. 2013;7(4):290–296. [Google Scholar]
- Chan, Y.-H., Correa, C.D., Ma, K.-L., 2010. Flow-based scatterplots for sensitivity analysis. In: 2010 IEEE Symposium on Visual Analytics Science and Technology. pp. 43–50.
- Chauhan S., Misra O.P., Dhar J. Stability analysis of sir model with vaccination. Am. J. Comput. Appl. Math. 2014;4(1):17–23. [Google Scholar]
- Chen M., Abdul-Rahman A., Archambault D., Dykes J., Slingsby A., Ritsos P.D., Torsney-Weir T., Turkay C., Bach B., Brett A., Fang H., Jianu R., Khan S., Laramee R.S., Nguyen P.H., Reeve R., Roberts J.C., Vidal F., Wang Q., Wood J., Xu K. 2020. RAMPVIS: TOwards a new methodology for developing visualisation capabilities for large-scale emergency responses. ArXiv:2012.04757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Claessen J. Eindhoven University of Technology; Eindhoven: 2011. Visualization of multivariate data. (Ph.D. thesis) [Google Scholar]
- Dimara E., Perin C. What is interaction for data visualization? IEEE Trans. Vis. Comput. Graphics. 2019;26(1):119–129. doi: 10.1109/TVCG.2019.2934283. [DOI] [PubMed] [Google Scholar]
- Engel D., Hüttenberger L., Hamann B. Visualization of Large and Unstructured Data Sets: Applications in Geospatial Planning, Modeling and Engineering-Proceedings of IRTG 1131 Workshop 2011. Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik; 2012. A survey of dimension reduction methods for high-dimensional data analysis and visualization. [Google Scholar]
- Espadoto M., Martins R.M., Kerren A., Hirata N.S., Telea A.C. Toward a quantitative survey of dimension reduction techniques. IEEE Trans. Vis. Comput. Graphics. 2019;27(3):2153–2173. doi: 10.1109/TVCG.2019.2944182. [DOI] [PubMed] [Google Scholar]
- Fang H., Tam G.K.-L., Borgo R., Aubrey A.J., Grant P.W., Rosin P.L., Wallraven C., Cunningham D., Marshall D., Chen M. Visualizing natural image statistics. IEEE Trans. Vis. Comput. Graphics. 2013;19(7):1228–1241. doi: 10.1109/TVCG.2012.312. [DOI] [PubMed] [Google Scholar]
- Giordano G., Blanchini F., Bruno R., Colaneri P., Filippo A.D., Matteo A.D., Colaneri M. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nature Med. 2020;26(6):855–860. doi: 10.1038/s41591-020-0883-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gleicher M., Albers D., Walker R., Jusufi I., Hansen C.D., Roberts J.C. Visual comparison for information visualization. Inf. Vis. 2011;10(4):289–309. [Google Scholar]
- Heinrich J., Weiskopf D. In: Eurographics 2013 - State of the Art Reports. Sbert M., Szirmay-Kalos L., editors. The Eurographics Association; 2013. State of the art of parallel coordinates. [Google Scholar]
- Hullman J., Qiao X., Correll M., Kale A., Kay M. In pursuit of error: A survey of uncertainty visualization evaluation. IEEE Trans. Vis. Comput. Graphics. 2018;25(1):903–913. doi: 10.1109/TVCG.2018.2864889. [DOI] [PubMed] [Google Scholar]
- Inselberg A. Handbook of Data Visualization. Springer; 2008. Parallel coordinates: visualization, exploration and classification of high-dimensional data; pp. 643–680. [Google Scholar]
- Iooss B., Ribatet M. Global sensitivity analysis of computer models with functional inputs. Reliab. Eng. Syst. Saf. 2009;94(7):1194–1204. Special Issue on Sensitivity Analysis. [Google Scholar]
- Kamal A., Dhakal P., Javaid A.Y., Devabhaktuni V.K., Kaur D., Zaientz J., Marinier R. Recent advances and challenges in uncertainty visualization: a survey. J. Vis. 2021:1–30. [Google Scholar]
- Kehrer J., Hauser H. Visualization and visual analysis of multifaceted scientific data: A survey. IEEE Trans. Vis. Comput. Graphics. 2012;19(3):495–513. doi: 10.1109/TVCG.2012.110. [DOI] [PubMed] [Google Scholar]
- Keim D.A. Designing pixel-oriented visualization techniques: Theory and applications. IEEE Trans. Vis. Comput. Graphics. 2000;6(1):59–78. [Google Scholar]
- Keim D.A., Kriegel H.-P. Visualization techniques for mining large databases: A comparison. IEEE Trans. Knowl. Data Eng. 1996;8(6):923–938. [Google Scholar]
- Konyha Z., Matkovic K., Gracanin D., Jelovic M., Hauser H. Interactive visual analysis of families of function graphs. IEEE Trans. Vis. Comput. Graphics. 2006;12(6):1373–1385. doi: 10.1109/TVCG.2006.99. [DOI] [PubMed] [Google Scholar]
- Kosara R., Hauser H., Gresh D.L. Eurographics (State of the Art Reports) 2003. An interaction view on information visualization. [Google Scholar]
- Lee L.A., Carslaw K.S., Pringle K.J., Mann G.W., Spracklen D.V. Emulation of a complex global aerosol model to quantify sensitivity to uncertain parameters. Atmos. Chem. Phys. 2011;11(23):12253–12273. [Google Scholar]
- Liu L., Boone A.P., Ruginski I.T., Padilla L., Hegarty M., Creem-Regehr S.H., Thompson W.B., Yuksel C., House D.H. Uncertainty visualization by representative sampling from prediction ensembles. IEEE Trans. Vis. Comput. Graphics. 2016;23(9):2165–2178. doi: 10.1109/TVCG.2016.2607204. [DOI] [PubMed] [Google Scholar]
- Liu W.-Y., Wang B.-W., Yu J.-X., Li F., Wang S.-X., Hong W.-X. 2008 International Conference on Machine Learning and Cybernetics, vol. 2. IEEE; 2008. Visualization classification method of multi-dimensional data based on radar chart mapping; pp. 857–862. [Google Scholar]
- Loeppky J.L., Sacks J., Welch W.J. Choosing the sample size of a computer experiment: A practical guide. Technometrics. 2009;51(4):366–376. [Google Scholar]
- Lotov A., Bushenkov V., Kamenev G. Springer US; 2004. Interactive Decision Maps: Approximation and Visualization of Pareto Frontier, vol. 89. [Google Scholar]
- Van der Maaten L., Hinton G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008;9(11) [Google Scholar]
- Marrel A., Iooss B., Da Veiga S., Ribatet M. Global sensitivity analysis of stochastic computer models with joint metamodels. Stat. Comput. 2012;22:833–847. [Google Scholar]
- McInnes L., Healy J., Melville J. 2018. Umap: Uniform manifold approximation and projection for dimension reduction. arXiv preprint arXiv:1802.03426. [Google Scholar]
- McNabb L., Laramee R.S. Computer Graphics Forum, vol. 36. Wiley Online Library; 2017. Survey of surveys (SoS)-mapping the landscape of survey papers in information visualization; pp. 589–617. [Google Scholar]
- Morris M.D. Factorial sampling plans for preliminary computational experiments. Technometrics. 1991;33(2):161–174. [Google Scholar]
- Mühlbacher T., Piringer H. A partition-based framework for building and validating regression models. IEEE Trans. Vis. Comput. Graphics. 2013;19(12):1962–1971. doi: 10.1109/TVCG.2013.125. [DOI] [PubMed] [Google Scholar]
- Oakley J.E., O’Hagan A. BayesIan inference for the uncertainty distribution of computer model outputs. Oxf. Univ. Press Behalf Biom. Trust. 2002;89(4):769–784. [Google Scholar]
- Oakley J.E., O’Hagan A. Probabilistic sensitivity analysis of complex models: A Bayesian approach. J. R. Stat. Soc. Ser. B Stat. Methodol. 2004;66(3):751–769. [Google Scholar]
- O’Hagan A. Bayesian analysis of computer code outputs: A tutorial. Reliab. Eng. Syst. Saf. 2006;91(10–11):1290–1300. [Google Scholar]
- Padilla L., Kay M., Hullman J. 2020. Uncertainty visualization. [Google Scholar]
- Pajer S., Streit M., Torsney-Weir T., Spechtenhauser F., Möller T., Piringer H. Weightlifter: Visual weight space exploration for multi-criteria decision making. IEEE Trans. Vis. Comput. Graphics. 2017;23(1):611–620. doi: 10.1109/TVCG.2016.2598589. [DOI] [PubMed] [Google Scholar]
- Phadke M.N., Pinto L., Alabi O., Harter J., Taylor II R.M., Wu X., Petersen H., Bass S.A., Healey C.G. Visualization and Data Analysis 2012, vol. 8294. International Society for Optics and Photonics; 2012. Exploring ensemble visualization; p. 82940B. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piringer H., Berger W., Krasser J. HyperMoVal: interactive visual validation of regression models for real-time simulation. Comput. Graph. Forum. 2010;29(3):983–992. [Google Scholar]
- Porphyre T., Bronsvoort M., Fox P., Zarebski K., Xia Q., Gadgil S. 2020. Scottish COVID response consortium (SCRC): EERA model overview. [Google Scholar]
- Potter K., Wilson A., Bremer P.-T., Williams D., Doutriaux C., Pascucci V., Johhson C. Vol. 180. IOP Publishing; 2009. Visualization of uncertainty and ensemble data: Exploration of climate modeling and weather forecast data with integrated visUS-CDAT systems. (Journal of Physics: Conference Series). [Google Scholar]
- Pukelsheim K. The three sigma rule. Amer. Statist. 1994;48(2):88–91. [Google Scholar]
- Rasmussen C.E., Williams C.K.I. MIT Press; 2008. Gaussian Processes for Machine Learning. [Google Scholar]
- Roberts, J., 2007. State of the Art: Coordinated and Multiple Views in Exploratory Visualization. In: 5th International Conference on Coordinated and Multiple Views in Exploratory Visualization. pp. 61–71.
- Sacha D., Zhang L., Sedlmair M., Lee J.A., Peltonen J., Weiskopf D., North S.C., Keim D.A. Visual interaction with dimensionality reduction: A structured literature analysis. IEEE Trans. Vis. Comput. Graphics. 2016;23(1):241–250. doi: 10.1109/TVCG.2016.2598495. [DOI] [PubMed] [Google Scholar]
- Saltelli A., Tarantola S., Chan K.P.-S. A quantitative model-independent method for global sensitivity analysis of model output. Technometrics. 1999;41(1):39–56. [Google Scholar]
- Salter J.M., Williamson D.B., Scinocca J., Kharin V. Uncertainty quantification for computer models with spatial output using calibration-optimal bases. J. Amer. Statist. Assoc. 2019;114(528):1800–1814. [Google Scholar]
- Schreck T., Chen S., Amid D., Shir O., Limonad L., Boaz D., Anaby-Tavor A. 2013 IEEE Pacific Visualization Symposium (PacificVis) Institute of Electrical and Electronics Engineers; United States: 2013. Self-organizing maps for multi-objective Pareto frontiers; pp. 153–160. [Google Scholar]
- Sedlmair M., Heinzl C., Bruckner S., Piringer H., Möller T. Visual parameter space analysis: A conceptual framework. IEEE Trans. Vis. Comput. Graphics. 2014;20(12):2161–2170. doi: 10.1109/TVCG.2014.2346321. [DOI] [PubMed] [Google Scholar]
- Sobol’ I. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simulation. 2001;55(1):271–280. The Second IMACS Seminar on Monte Carlo Methods. [Google Scholar]
- Spence R., Tweedie L. The attribute explorer: Information synthesis via exploration. interacting with. Computers. 1998;11:137–146. [Google Scholar]
- Swallow B., Birrell P., Blake J., Burgman M., Challenor P., Coffeng L.E., Dawid P., De Angelis D., Goldstein M., Hemming V., Marion G., McKinley T.J., Overton C., Panovska-Griffiths J., Pellis L., Probert W., Shea K., Villela D., Vernon I. Challenges in estimation, uncertainty quantification and elicitation for pandemic modelling. Epidemics. 2022;in press doi: 10.1016/j.epidem.2022.100547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torsney-Weir T., Möller T., Sedlmair M., Kirby R.M. Hypersliceplorer: interactive visualization of shapes in multiple dimensions. Comput. Graph. Forum. 2018;37(3):229–240. [Google Scholar]
- Torsney-Weir T., Saad A., Möller T., Weber B., Hege H.-C., Verbavatz J.-M., Bergner S. Tuner: principled parameter finding for image segmentation algorithms using visual response surface exploration. IEEE Trans. Vis. Comput. Graphics. 2011;17(12):1892–1901. doi: 10.1109/TVCG.2011.248. [DOI] [PubMed] [Google Scholar]
- Torsney-Weir T., Sedlmair M., Möller T. Sliceplorer: 1D slices for multi-dimensional continuous functions. Comput. Graph. Forum. 2017;36(3):167–177. [Google Scholar]
- Turkay C., Lundervold A., Lundervold A.J., Hauser H. Representative factor generation for the interactive visual analysis of high-dimensional data. IEEE Trans. Vis. Comput. Graphics. 2012;18(12):2621–2630. doi: 10.1109/TVCG.2012.256. [DOI] [PubMed] [Google Scholar]
- Vernon I., Goldstein M., Bower R. Galaxy formation: Bayesian history matching for the observable universe. Statist. Sci. 2014;29(1):81–90. [Google Scholar]
- Vernon I., Liu J., Goldstein M., Rowe J., Topping J., Lindsey K. Bayesian uncertainty analysis for complex systems biology models: Emulation, global parameter searches and evaluation of gene functions. BMC Syst. Biol. 2018;12(1):1–29. doi: 10.1186/s12918-017-0484-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J., Hazarika S., Li C., Shen H.-W. Visualization and visual analysis of ensemble data: A survey. IEEE Trans. Vis. Comput. Graphics. 2018;25(9):2853–2872. doi: 10.1109/TVCG.2018.2853721. [DOI] [PubMed] [Google Scholar]
- Ward M.O. A taxonomy of glyph placement strategies for multidimensional data visualization. Inf. Vis. 2002;1(3–4):194–210. [Google Scholar]
- van Wijk J.J., van Liere R. 1993. Hyperslice - visualization of scalar functions of many variables. [Google Scholar]
- Williamson D., Vernon I. 2013. Efficient uniform designs for multi-wave computer experiments; pp. 1–31. arXiv:1309.3520, URL: http://arxiv.org/abs/1309.3520. [Google Scholar]