Tradeoffs between ventilation, air mixing, and passenger density for the airborne transmission risk in airport transportation vehicles

Abstract

Airport transportation vehicles, such as buses, aerotrains, and shuttles, provide important passenger transfer services in airports. This study quantitatively investigated COVID-19 aerosol infection risk and identified acceptable operational conditions, such as passenger occupancy rates and duration of rides, given the performance of vehicle ventilation. The greatest risk to the largest number of passengers is from an index case whose exhaled breath would take the longest time to exit the vehicle. The study identified such a case based on ventilation patterns, and it tracked the spread of viral aerosols (5 μm) by using the Wells-Riley equation to predict aerosol infection risk distribution. These distributions allowed a definition of an imperfect mixing degree (δ) as the ratio of actual risk and the calculated risk under a perfect mixing condition, and further derived regression equations to predict δ in the far-field (FF) and near-field (NF) of each passenger. These results revealed an order of magnitude higher aerosol infection risk in NF than in FF. For example, with a ventilation rate of 58 ACH (air changes per hour) and a 45% occupancy rate, unmasked passengers should stay up to 15 min in the bus and 35 min in the shuttle to limit infection risk in NF within 10%. These also indicate that masking is an important and effective risk reduction measure in transportation vehicles, especially important in NF. Overall, the analysis of imperfect air mixing allows direct comparison of risks in different transportation vehicles and a structured approach to development of policy recommendations.

1. Introduction

Coronavirus Disease 2019 (COVID-19), which is caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), was first reported in December 2019, and then it developed into a pandemic in March. It is transmitted quite effectively and can be transmitted by people who are mildly ill or even asymptomatic [1]. Particularly, this pandemic has trigged an unprecedented level of public fear of travel [2]. As a result, the global passenger traffic fell by 80% between April and May 2020 compared to January and February 2020 [3]. To regain public confidence for air travel, effective and thorough infection controls during the curb-to-curb journey must be put into place. This journey, termed airport ground transportation, mainly comprises of airside, terminal, and car park transfers for airline passengers and airport employers. There have been several outbreak events of COVID-19 related to buses, which are a representative type of airport transportation vehicles. For example, Shen et al. did a cohort study on an on-bus outbreak of COVID-19 occurred in Zhejiang, China, on January 19, 2020 [4]. During a 100-min round trip on a full occupied bus, 24 out of 67 susceptible individuals (excluding the driver) were infected, showing an attack rate of 34.3% (95% CI: 24.1%∼46.3%). Specifically, attack rate was 41.4% in the high-risk zone which included seats in the same row and within 2 or 3 rows of the index case, and 28.9% in the low-risk zone included the seats in other rows. Because no significant increased risk was found in the part of the bus closer to the index case (source), airborne transmission was likely to be a partial transmission route. Moreover, Luo et al. reported an outbreak caused by an index case (source) on two bus trips in Hunan, China, on January 22, 2020 [5]. 7 out of 48 passengers (including the driver) got infected during the first 2.5-h trip by a full occupied tour coach, and 2 out of 12 passengers (including the driver) got infected during the second 1-h trip by a minibus. The attack rate during a 2.5-h ride on a bus was estimated to be 15% (95% CI: 6%∼24%). Importantly, some cases could not be explained by the transmission routes via droplets or fomites, showing the potential for airborne transmission as well.

Currently, airborne transmission via fine aerosols with an aerodynamic diameter ≤5 μm is now established as a transmission route for SARS-CoV-2 [[6], [7], [8], [9], [10]], and recognized by the World Health Organization (WHO) [11] and Center for Disease Control (CDC) [12]. These viral aerosols are shed from respiratory secretions through the normal activities of exhaling, talking, coughing, and sneezing. Because SARS CoV-2 travels in droplets, the virus can be transported in the air current and kept viable for up to 3 h [13]. Infectious aerosols pose a risk for people whether they are near an index case or elsewhere in a confined space. Physical distancing offers time for mixing to reduce airborne concentrations while crowding in congregate settings such as transport and queuing increases the risk of near-field (NF) transmissions of infectious aerosols dispersed in a passenger exhaled breath. Because SARS CoV-2 is transmitted by aerosols, air change rates, mixing and ventilation systems play an important role in mitigating risk.

We have investigated ventilation impacts on the airborne transmission of influenza for a university operated shuttle bus, with three mixing ventilation designs generally applied in the buses [14,15]. A validated Computational Fluid Dynamics (CFD) method was used to solve the fluid mechanics that underlies the spread of viral aerosols in the bus; in addition, the Wells-Riley equation [16] was integrated into CFD to estimate infection risk. In the simulations, the bus was assumed to be fully occupied with 26 seated and four standing individuals, including the driver. The locations of passengers in proximity to the infectious case and air return/exhaust opening, and the configuration of the ventilation system differentiated airborne transmission on a bus. The farther a passenger is from the bus air return/exhaust opening, the longer the passenger's exhaled gas will stay in the bus. Moreover, a 10-min exposure to the viruses from a source with a quantum generation rate (GRq) of 67 quanta/h, can result in an infection risk up to 10.1% for another seated passenger, and up to 27.2% for a standing passenger.

The ground transportation vehicles, such as buses, can have high occupant densities (ODs) compared to other non-transport indoor settings that are 20–40 times higher than in office buildings [17]. In the present post-lockdown phase, with the increase in public transport ridership, it became difficult for the travelers to strictly abide by physical distancing policy [18]. For example, a study on Washington DC metro system showed that if implementing 1.5-m distancing, 23% of the total number of passengers will remain unsatisfied during the peak hour [19]. Meanwhile, occupancy in public transport can create situations where ventilation efficiency is impeded. Preventing virus spread poses unprecedented challenges to public transport. Ventilation efficiency with respect to aerosol infection risk needs to be considered for the ground transportation vehicles, helping to manage infection risk.

Risk mitigation strategies for air travel must include all aspects of the passenger experience, including the use of shuttle buses external to the terminal and buses and trains internal to the airport complex. Accordingly, this study assesses the NF and far-field (FF) airborne infection risks in the vehicles with focus on the impacts of OD and ventilation design. We first used a ventilation efficiency index, e.g., residual lifetime of air (RLTa) to choose the index case, whose exhaled gas stay longer than the other passengers indoors [20]. Then, we integrated the drift-flux model [21] into CFD to account for the gravity of particles and simulate the spread of viral aerosols containing SARS-CoV-2, from the index case's exhalation. The Wells-Riley equation [16] was applied to estimate the aerosol infection risk of COVID-19 based on the calculated quanta concentrations. In addition, we introduce a new index to evaluate the degree for imperfect mixing (δ), and derived the regression equations to demonstrate OD's impact on δ.

2. Methodology

This study developed CFD models for three typical airport transportation vehicles with different ventilation designs and occupancy levels, including airport bus (Cobus 3000), airport shuttle (Ford E450), and aerotrain (Mitsubishi Heavy Industrial, Crystal Mover), to account for the possible transmission settings in the transfer of passengers between terminal and aircrafts parked off-gate, between the terminal and car parking location, and between the terminals in the airport, respectively. The details about the modeling of vehicle space, air distribution and exhaust, turbulent flow, and viral spread, as well as the assessment for air mixing and airborne infection risk are given below.

2.1. Vehicle models

Fig. 1(a) shows the vehicles' inner spatial configuration, created according to the manufactural manuals publicly on-line or from airport operators. For each vehicle, the CFD models were developed with the specified occupancies, including capacity, occupancy rate (OR), and OD, as listed in Table 1, and people were uniformly distributed in the cabin in each model as shown in Fig. 1(b). The bus has only six two-seat rows located in the middle and rear parts. One passenger was simulated in each row, at the window side in the bus models. Specifically, the bus model with 15%OR presents an occupancy following the 6-ft (1.86 m) physical distancing rule in the bus. The shuttle's capacity matches the number of seats plus a wheel securement area; therefore, all passengers shall be seated. Moreover, only for the shuttle the driver is considered as an occupant because the driver zone is part of the cabin. The aerotrain models have eight seated passengers.

Fig. 1.

CAD models for empty vehicles and CFD models for the vehicles with a 25% OR.

Table 1.

Simulation cases.

Vehicle type	Empty Volume (m3)	Floor area (m2)	Occupancy conditions
			Capacity	OR	# of people	OD (#/m2)
Bus	69.7	29.0	110	15%	17	0.59
				25%	27	0.93
				35%	38	1.31
				45%	50	1.72
Shuttle	27.5	13.5	11	25%	3	0.22
				35%	4	0.30
				45%	5	0.37
Aerotrain	54.4	23.3	105	25%	26	1.12
				35%	36	1.55
				45%	47	2.02

The bus's air distribution composes of linear and round type inlets. We simplified the linear inlets of the bus as rectangular openings with one at each side close to the ceiling. These two inlets have the same length and area as the original design. In the front and middle part of the bus, there are additional six round openings, indicating higher air supply in these areas than in the rear part. The bus's outlet (air return/exhaust) includes two rectangular openings located in the middle of the ceiling. The shuttle has an air-conditioner attached on the celling in the rear part, which has an inlet and an outlet. In addition, there are four inlets set on the frontal panel under the windshield. The aerotrain has only linear inlets uniformly distributed on both sides of the ceiling. Its two outlets are set in the front and rear part of the vehicle, respectively. Using data collected in a previous study evaluating a typical shuttle bus [14,15], the vehicles were designed to be ventilated at a ventilation rate of 58 ACH with air supply temperature to be 20.2 °C. Air was assumed to be 100% clean air to examine the best performance to identify possible upper limits of passenger loads. This ACH is high but within the capability of the vehicles' air-conditioning and ventilation systems.

The total number of spatial cells varies between 5.23 M and 7.61 M for the bus models, between 2.52 M and 2.64 M for the shuttle models, and between 4.43 M and 6.06 M for the aerotrain models. According to our previous bus study, these models have fine grids [14,15]. As a result, all of the CFD models were created with the EquiAngle skewness smaller than 0.8 and aspect ratio smaller than 6 to ensure the good grid quality.

2.2. CFD methods to calculate flow field

In our previous study, we have validated and applied the CFD methods to simulate the spread of viral bioaerosols with influenza viruses in a bus environment [14,15]. In this study, we used the same CFD methods, but with the realizable k-ε model [22], because this model offers certain advantages over the previously used standard κ-ε turbulent mode [23], suitable for approximating turbulence due to buoyancy flows [24]. The simulations adopted the SIMPLE algorithm, with the Boussinesq assumption to account for the buoyancy force on convective flows around the warm/cold surfaces. The complete formulation is given in Ref. [22]. For the spatial discretization, PRESTO! was used for pressure, with first order upwind for scalar, and second-order upwind for other terms. The convergence criteria were 5 × 10⁻⁴ for continuity, velocities and turbulent terms, 1 × 10⁻⁶ for energy, and 1 × 10⁻¹⁵ for scalar.

The boundary conditions are summarized in Table 2 . The seated and standing human bodies were simplified and made up of 13 rectangular parts: face, head, trunk (including neck), left and right arms, hands, thighs, legs and feet. These human body models, as well as the boundary conditions for the human body sections, exhaled gas at mouth, vehicle inner surfaces such as windows, windshield, floor and lights, and air supply temperature were from our previous bus study [14,15]. Specifically, the window and floor surfaces in the aerotrain were assumed to be adiabatic, as aerotrains usually run in an enclosed environment with little influences of ambient environment. The air was supplied at the normal directions of the inlets, with the velocities calculated based on the ventilation rate, which was 58 ACH [15].

Table 2.

Boundary conditions.

Boundary	Bus	Shuttle	Aerotrain
Inlet	Area: 0.548 m2; Vel: 2.055 m/s; T: 20.2 °C	Area: 0.149 m2; Vel: 2.981 m/s; T: 20.2 °C	Area: 1.153 m2; Vel: 0.76 m/s; T: 20.2 °C
Outlet	Free slip
Light	No slip; T: 25 °C
Window	No slip; 16.8 °C		No slip; adiabatic
Windshield	N/A	No slip; 31.8 °C	No slip; adiabatic
Seated human body	No slip; 23 °C for legs, 24 °C for trunk, 28 °C for head, 30 °C for feet & thighs, 34 °C for face & hands
Standing human body	No slip; 24 °C for legs, thighs & trunk, 28 °C for head, 30 °C for feet, 33.5 °C for face, 34 °C for hands
Mouth of source	Area: 0.0003 m2; Vel: 1.07 m/s for passenger and 1.87 m/s for driver; T: 34 °C
Other walls	No slip; adiabatic

2.3. Residual lifetime of air (RLTa)

RLTa shows the mean time for a parcel of air at any given indoor location (including an exhaled breath) takes to reach the outlet (air return/exhaust) [20]. For an infectious person, a larger RLTa value would mean that his/her exhaled viruses could have a longer indoor resident time than others. Kato et al. [25] proposed the CFD-based procedure to calculate RLTa by solving the passive scalar transport equation with reversed flow field that was calculated in advance. With this procedure, a tracer gas is uniformly and continuously generated throughout the indoor space, and the air mass from the outlet (considered as inlet) is gradually contaminated as it is regarded as proportional to the time elapsed from the time the air leaves the outlet until it reaches the location.

2.4. Calculation of the spread of viral aerosols

We used the Wells-Riley equation [16] as follows to estimate the probability of airborne transmission of SARS-CoV-2 virus.

$$P=1-e^{-p{C}_{p}t}$$ (1)

where P is the probability of infection, C _p is the quanta concentration in the inhalation (quanta/m3), p is the breathing rate (m³/s), and t is the total exposure time. The idea of quantum was conceived by Wells [26] to represent the infectious aerosols attached with viruses, with the exposure to one quantum of infectious aerosols giving an average probability of 63% of getting infected. In CFD, we used an active scalar to simulate the spread of quanta based on the drift-flux particle model [21] with the following governing equation:

$$\nabla \bullet \left((\overrightarrow{V}+\overrightarrow{V_s})C\right)=\nabla \bullet ((\lambda +{\lambda }_t)\nabla C)+S$$ (2)

where C is quanta concentration (quanta/m3), $\overrightarrow{V}$ is the velocity vector of air (m/s), $\overrightarrow{V_s}$ is the setting velocity vector of quanta (m/s), λ and λ _t are laminar and turbulent diffusivity (m²/s), and S is the source term (quanta/m³·s). $\overrightarrow{V_s}$ can be calculated using the aerosols' density and size with Stokes' law; therefore, it accounts for the gravitational force on the infectious aerosols. Here, we assumed that the aerosols had an aerodynamic diameter of 5 μm, and we ignored the influence of indoor humidity and temperature on aerosol size and the deposition of aerosols on the solid surface.

Using a fitting approach with the reproductive numbers observed in the COVID-19 outbreaks, Dai and Zhao estimated that the SARS-CoV-2's GRq varied in 14–48 quanta/h [27]. Moreover, Buonanno et al. estimated that GRq could be over 100 quanta/h when an asymptomatic index case was doing light activities, based on the viral load measured in the sputum [28]. Accordingly, we used three GRq values in this study, 18 quanta/h, 48 quanta/h, and 100 quanta/h.

2.5. Regression modeling for assessing OD's impact on infection risk

The regression models are given as following:

$$r=\delta r_{pm}$$ (3)

$$\delta =a{e}^{b\bullet \rho }$$ (4)

where r _pm is the probability of infection under perfect mixing condition, ρ is the occupant density in #/m², calculated as the number of people per unit floor area, and a, b are the coefficients of regression models.

We first calculated δ by Eq. (3); then, we derived the regression models for δ in the format as given in Eq. (4) by the Matlab Curve Fitting Toolbox [29]. In Eq. (4), r can be calculated by Eq. (1) based on the volume-weighted average quanta concentration in the breathing zone, and rpm can be calculated with Eq. (1) using the quanta concentration under perfect mixing conditions. When using Eq. (1), the breathing rate was set to be 0.008 m³/min, representing a relatively quiet state with a metabolic rate of 1.0 met [30].

The regression models for δ were derived for NF and FF, respectively. Here, we defined the breathing zone as the region between the heights of 1.1 m and 1.8 m above the floor, took FF as the breathing zone throughout the whole indoor space, and assumed NF as the breathing zone within the distance of 0.9 m (3 ft) to the index case.

3. Results

The RLTs results will be introduced first to determine the index case for each model. Then, we will introduce the results on the spread of viral aerosols, and the infection risk. Finally, we will present the results for the regression models for δ.

3.1. Distribution of RLTa

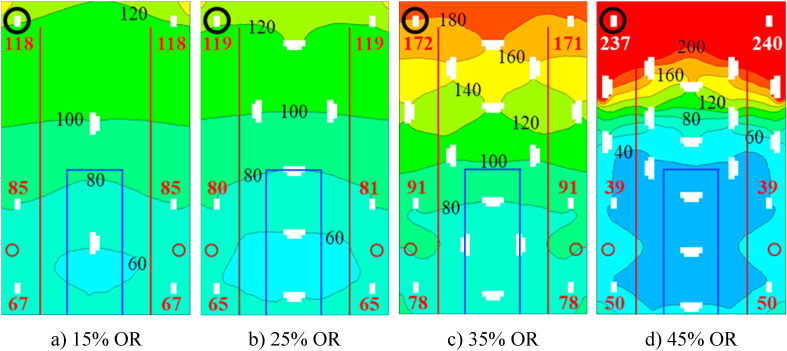
Before calculating the spread of viral particles in the vehicles, we calculated RLTa to evaluate the OD's impact on how fast exhaled viruses can be exhausted and to determine the location for index case. Fig. 2 illustrates the RLTa spatial distributions (in seconds) for a horizontal cross section at 1.24 m height (mouth level of seated passengers) in the bus with different OR. The highest RLTa values are always observed for the seated passengers in the rear of the bus. The pattern of RLTa is altered substantially at higher OR, with greater RLTa values where distant to the outlet, and smaller RLTa values where underneath the outlet. The results are similar at the height of standing passengers; however, the longest RLTa is always found at the mouth of the passengers seated in the rear corner, regardless of OR. The seated passenger, who is circled in black in Fig. 2(a), is taken as a hypothetical source of viral aerosol, i.e., the index case. Note that we also choose the passenger seated at the left corner in the 45%OR case to have the index case same in all bus cases, given that the RLTa for the passenger is only 3s less than the maximum RLTa.

Fig. 2.

RLTa distribution of (in seconds) at the height of the seated passengers' mouth in the bus. The top of the figure represents the rear of the bus. The bold red/white numbers are area-weighted averages of the RLTa at the seated passenger's mouth opening. All white shapes represent the horizontal cross-sections of passengers. The larger shapes show torso and arm cross sections of standing passengers while the small shapes represent head cross sections of seated passengers. The infectious source is designated by the black circle. The outlet is outlined by blue lines, and the inlets are designated by red lines and circles. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)

In the shuttle and aerotrain, as illustrated in Fig. 3 , we also observed that the RLTa is primarily determined by the distance to the outlet. Moreover, in the aerotrain, for the seated passengers that have the similar distances to the outlet, the distribution of standing passengers between them and the outlet will determine who has a higher RLTa for exhaled air. As a result, the driver was chosen as the index case for the shuttle, and a passenger seated in the middle was chosen as the index case for the aerotrain.

Fig. 3.

RLTa distribution of (in seconds) at the height of the seated passengers' mouth in the shuttle and aerotrain with 25% OR and 45% OR, respectively. The top of the figure represents the rear of the vehicles. All white shapes represent the horizontal cross-sections of passengers. The larger shapes show torso and arm cross sections of standing passengers while the small shapes represent head cross sections of seated passengers. Gray shapes in a) and b) are the structures to fix a wheelchair. The infectious source is designated by the black circle, and the bold red number is the RLTa value at the mouth. The outlets are designated by light green lines, and the outlets are designated by red lines (no inlets can be shown in the section for shuttle). (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)

3.2. Spread of viral aerosols

Fig. 4 demonstrates the spread of viral aerosols exhaled from the index case with a GRq of 100 quanta/h (22) in the bus for different occupancies. The location of outlet clearly determines the extension of the spread of viral aerosols with the concentrations of >0.1 quanta/m³ mostly in the region between the index case and rear outlet, regardless of the increase in OR. In this region, it is clear that the iso-surfaces with a concentration ≥0.3 quanta/m³ gradually extend with the increase in OR, and they cover most of the region when OR reaches 45%. This trend of the spread of viral aerosols with the OR increase is also very clear in the aerotrain although the concentration distribution is different.

Fig. 4.

Spread of viral aerosols in the bus with different ORs, assuming an infectious passenger shedding at 100 quanta/h. Outlet is designated by red lines. The infectious source is designated by the black circle. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)

3.3. Impact of occupancy and duration on infection risk

We compared infectious risks under different occupancy scenarios where mixing efficiency is altered. Fig. 5 (a) and (b) display the risk for another passenger in the FF and NF, respectively, using the viral concentrations averaged with cell volumes as weights. The dashed line refers to the risk with assumed perfect mixing. Note that most of the curves in Fig. 5 are in the linear rising phase of the power function, i.e., Eq. (1), due to the small concentration values. The shuttle with the smallest internal volume has the highest infection risk under perfect mixing condition. When the vehicle is occupied, the FF infection risk and its increase are highest in the bus and lowest in the aerotrain under each occupancy condition. However, the FF infection risk is lower than 5.5% after a 60-min exposure regardless of OR and vehicle type. In contrast, NF infection risk is much higher than the FF infection risk at the same OR in each of the vehicles modelled. In the bus, it approaches 34.4% after a 60-min exposure when the vehicle is near half full (45%OR). For both FF and NF, the infection risk is highest for the bus and lowest for the aerotrain under each occupancy condition.

Fig. 5.

Influence of occupancy on the a) FF infection risk, and b) NF infection risk, in bus (top), shuttle (middle), and aerotrain (bottom), with a source to be 100 quanta/h.

3.4. Impact of occupancy on δ

δ represents the departure from idealized perfect mixing of air within the vehicle. The departure from perfection conditions is due mainly to people and other obstructions, and it leads to less dispersion of aerosols and a higher concentration of viruses. Viral concentrations will be higher in the immediate vicinity of the infectious person and in throughout the interior space. δ allows direct comparison of ventilation efficiency in removal of viruses from the passenger breathing zone for the vehicle under different conditions. The regression equations for δ were derived for both FF and NF in the transportation vehicles to explore the relationship between occupancy and transmission risk. Table 3 summarizes the δ values calculated based on the CFD results and the regression equations for the vehicles. δ is always highest for the bus, no matter NF or FF and regardless of OR. In each vehicle, with a fixed OR, the δ values are irrelated to source strength. In addition, δ indicates an exponential relationship with OD, which varies with vehicle type. Fig. 6 compares the fitted curves for the FF and NF for different vehicles. Log₁₀(δ) always increases with OD or OR. All the curves show the similar slopes for the increase in log₁₀(δ) with OR. For each vehicle, the increase of log₁₀(δ) with OD also has the similar slopes for the NF and FF. In addition, the occupancy has much more impact on δ for the NF than for the FF, especially in the bus. Comparing the results for the shuttle and aerotrain, under each occupancy condition, δ is smaller for the FF but larger for the NF in the shuttle. The higher δ values for the NF in the shuttle should be caused by the local spatial configuration around the driver, where the driver was surrounded by the solid surfaces at five directions.

Table 3.

δ calculated based on CFD results of quanta distribution in the breathing zone and the resulting regression equations. (P-value < 0.0000).

Vehicle type		δ for each OR				Regression models ($\delta =a{e}^{b\bullet OD}$)
		15%	25%	35%	45%	a	b	RMSE	R2	Adjust R2
FF	Bus	2.7	2.9	3.4	4.7	1.8028	0.543	0.00324	0.992	0.991
	Shuttle		1.1	1.2	1.5	0.69652	2.0387	0.00203	0.996	0.996
	Aerotrain		1.4	1.7	1.8	1.1198	0.22842	0.000962	0.998	0.998
NF	Bus	17.5	19.5	29.7	35.7	11.527	0.66604	0.0261	0.991	0.990
	Shuttle		3.9	4.8	6.0	1.9973	2.9754	0.000222	1	1
	Aerotrain		2.7	4.4	5.1	1.4627	0.63907	0.00806	0.980	0.977

Fig. 6.

Variations of δ with OD (left) and OR (right).

4. Discussion

Source location, i.e., the distance to the air exhaust, is a decisive factor in the RLTa and aerosol infection risk in vehicles. Regression models were used to estimate the greatest infection risk caused by the source that has the longest RLTa and results in potentially highest exposure to aerosolized viruses. As a result, aerosol infection risk is calculated to be less than 5.5% for a 60-min exposure in the vehicles for FF transmission and up to 34.4% for NF transmission in the bus. According to the simulation results for the bus and shuttle, with a ventilation rate of 58 ACH and ORs up to 45%, unmasked passengers should stay no more than 15 min in the bus and 35 min in the airport shuttle to limit an aerosol infection risk in NF within 10% of baseline risk. Note that we used the GRq values up to 100 quanta/h corresponds to the higher end of the SARS-CoV-2 values computed by Buonanno et al. [28]. While such value was estimated from transmission events with a relatively high attack rate, the enhanced transmissibility from the Delta variant [31] should make our assumptions still relevant. However, this study is not specified for the superspreading events, which will produce a GRq far beyond 100 quanta/h.

According to a recent study specified for SARS-CoV-2, wearing a cotton mask, a medical mask, and a N95 mask can reduce the uptake of the virus droplets/aerosols, by approximately 20–40%, 50% and 80–90%, respectively, for the index case, and by approximately 60–80%, 60–80%, and 100%, respectively, for the recipient, at a distance of 0.5 m between two people [32]. As demonstrated in Fig. 5, even by wearing a cotton mask, the NF risk in a bus with 45% OR can be reduced to 1.3%–3.3% for an exposure time of 15 min, which is lower than the FF aerosol infection risk when not wearing a mask. Wearing a mask is a very effective measure for individual protection again the spread of COVID-19, which can be widely spread by asymptomatic patients. Particularly, better masks, such as KN95 and N95 are recommended for preventing the spread of Omicron variant [33], which may be 2 to 3 times more transmissible than Delta [34].

This study confirms that the airborne infection risk is particularly high for the passengers standing between the index case and outlet, and this risk is increased with the occupancy. Meanwhile, if an infectious passenger is near an outlet, then increased occupancy rates have little effect on the spread of viral aerosols because the infected exhaled gas is quickly removed by the air vent intake. In the COVID-19 outbreaks on the two vehicles in Hunan, China (5), there were no secondary cases approximate to the outlet. But due to the low ceilings in the bus and shuttle (around 2.1 m), a passenger may get infected if this person stands close to the outlet.

The configuration of the ventilation system is critical for airborne infection control. With the same OR, aerotrain has a higher OD, but lower infection risks than bus, because its uniform distribution of air supply and exhaust results in the reduction of airborne transmission, thus partly offsetting the adverse effect of increased occupancy. Our previous study [15] about influenza transmission on a shuttle bus reached similar conclusions.

The shuttle with low occupant loads but high densities had infection risk higher than what was found for the aerotrain. The log10(δ)-OD curves have the highest slopes in the shuttle implying that an increase in occupancy will cause greater deterioration in air mixing leading to higher transmission risk. In our shuttle simulation, air was exhausted from the rear. Therefore, it is important that the driver wears a protective face mask and preferably is fully vaccinated. To further protect shuttle riders, occupancy and trip duration should be limited.

In this study, the ventilation rate is fixed at a high value of 58 ACH to examine the impact of occupancy on transmission. Actual ventilations rates, passenger loadings, and trip duration will certainly vary. These simulations serve as a guide to airports, airlines, and bus fleet managers on how to mitigate airborne transmission risk. Furthermore, the results provide insights on relative risk tradeoffs among ventilations, passenger loads (separations), and trip duration. Fortunately, transit times for airport buses and aerotrains are short (minutes), but shuttle buses are often used to transfer flight crews, airport staff and passengers to locations off airport property (hours). Depending on where remote parking or public transit is located, the distance to hotels and car rentals as well as traffic can force considerably longer-than-normal transit times for airport gate and terminal transfers.

This study did not perform a specified validation for the applied CFD modeling method, because we have already conducted the validation for the CFD modeling of a bus in our previous study [14]. The boundary conditions were referenced from the previous study as well [15]. The difference between the current and previous CFD modeling methods is in the turbulence model. This study applied the realizable k-ε model instead of the standard k-ε model, because this model is considered to be more suitable for approximating the buoyancy flows. In a CFD study specified for indoor airflow and contaminant particle transportation [35], it is found that the realizable k-ε model successfully captures the flow trend and reasonably predicts the airflow velocity. Although the realizable k-ε model also underpredicts the air velocity, but with much less prediction error than the standard k-ε model (11% vs. 17%). Moreover, this study also finds that for the small particles with diameters ≤10 μm, the particle concentration indicates insensitive to the particle diameter. This finding is consistent with the conclusion by Chen & Zhao [36], that the droplet nuclei size plays an important role only for the droplets with initial diameter greater than 10 μm. Therefore, it is feasible to use drift-flux model [21] to simulate the spread of the viral aerosols with a diameter ≤5 μm with an active scalar.

5. Conclusions

This study investigated aerosol infection risk in airport ground transportation vehicles, including bus, shuttle, and aerotrain, with focus on the impacts of occupancy and ventilation design. This investigation assumed an unmasked infectious person was present. A more realistic transmission risk would consider community infection rates, compliance with face masks requirements, if applicable, and ability to keep adequate physical separation. Overall, simulations reveal the factors pertinent to the risk of transmission in airport vehicles: (1) air distribution markedly impacts the transmission risk in vehicles; (2) the risk caused by an index case depends on his/her location in the vehicle, relative to air return/exhaust; (3) an increase in occupant density in specific transportation vehicles increases risk by reducing individual ventilation rate and air mixing effectiveness in the passenger breathing zone; (4) local viral concentration and associated risk depend on proximity to an infectious individual; and (5) the imperfect mixing in densely populated vehicles has an important influence on the near-field dispersion of viruses and results in much higher risk than the risk calculated with the perfect-mixing assumption.

CRediT authorship contribution statement

Shengwei Zhu: Writing – original draft, Visualization, Validation, Software, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Tong Lin: Data curation. Jose Guillermo Cedeno Laurent: Writing – review & editing, Investigation. John D. Spengler: Conceptualization, Funding acquisition, Resources, Supervision, Writing – review & editing. Jelena Srebric: Writing – review & editing, Supervision, Resources, Project administration, Methodology, Investigation, Funding acquisition, Conceptualization.

Declaration of competing interest

The authors declare the following financial interests/personal relationships which may be considered as potential competing interests:

Jelena Srebric reports financial support was provided by The Airlines for America. Jelena Srebric reports financial support was provided by National Science Foundation.