Abstract
SARS‐CoV‐2 continues to evolve and the vaccine efficacy against variants is challenging to estimate. It is now common in phase III vaccine trials to provide vaccine to those randomized to placebo once efficacy has been demonstrated, precluding a direct assessment of placebo controlled vaccine efficacy after placebo vaccination. In this work, we extend methods developed for estimating vaccine efficacy post placebo vaccination to allow variant specific time varying vaccine efficacy, where time is measured since vaccination. The key idea is to infer counterfactual strain specific placebo case counts by using surveillance data that provide the proportions of the different strains. This blending of clinical trial and observational data allows estimation of strain‐specific time varying vaccine efficacy, or sieve effects, including for strains that emerge after placebo vaccination. The key requirements are that the surveillance strain distribution accurately reflects the strain distribution for a placebo group throughout follow‐up after placebo group vaccination, and that at least one strain is present before and after placebo vaccination. For illustration, we develop a Poisson approach for an idealized design under a rare disease assumption and then use a proportional hazards model to address staggered entry, staggered crossover, and smoothly varying strain specific vaccine efficacy. We evaluate these methods by theoretical work and simulations, and demonstrate that useful estimation of the efficacy profile is possible for strains that emerge after vaccination of the placebo group. An important principle is to incorporate sensitivity analyses to guard against misspecification of the strain distribution.
Keywords: clinical trial, Cox regression, SARS‐CoV‐2, sieve analysis, vaccine
1. INTRODUCTION
Multiple COVID‐19 vaccine trials have demonstrated substantial short term efficacy, though the durability of vaccination is, at this time, unknown. Recent work has developed methods to assess waning vaccine efficacy for vaccine trials where the placebo group is vaccinated. 1 , 2 , 3 , 4 By assuming the effect of vaccination is the same over calendar time, the placebo‐controlled vaccine efficacy profile is recoverable long after all placebo volunteers received vaccine. This work assumed that the vaccine efficacy, at any given time since vaccination, was similar for all circulating strains. However, multiple new strains or variants have emerged with improved transmissibility, and the vaccine efficacy for new strains may be less than for the original strains. 5 , 6
In this article, we develop approaches for settings where new virus strains emerge over time and the vaccine may have efficacy that varies by strain and time since vaccination. Differential vaccine efficacy by strain is known as sieve analysis. 7 , 8 The simplest and most robust approach to sieve analysis is to apply the methods given above separately to each strain. However, this approach fails for strains that emerge after the placebo group is vaccinated and with little overlap of strains pre and post placebo vaccination, sieve effects may be poorly estimated. For such strains, new approaches are needed. In this work, we develop a new method that leverages strain surveillance data. 9 It requires that the distribution of strains in the placebo trial participants (whether actual or counterfactual) matches the proportions observed in the community and that at least one strain is present before and after placebo vaccination. This allows imputation of strain specific case counts for a counterfactual placebo group that recovers placebo controlled vaccine efficacy, in a fashion similar to Reference 1.
We extend this strain‐specific analysis to a mark‐based approach, 10 , 11 where the vaccine efficacy of a virus is assumed to vary smoothly with a quantitative phenotype of the virus, for example, from a neutralization assay which measures the in vitro efficacy of a vaccine against specific strains. These approaches allow for time‐varying placebo controlled strain‐specific vaccine efficacy profile to be recovered for strains that emerge after the placebo group is vaccinated.
We develop a basic Poisson approach for an idealized setting under a rare disease assumption and carefully delineate how bias is introduced if the surveillance strain distribution differs from the placebo group. Simulations are performed to illuminate key features. We then develop a Cox regression approach which seamlessly accommodates the complexities of phase III vaccine trials. The method is computationally intensive and can require up to near copies of the dataset where is the number of cases, though standard software can be used to fit the model. We evaluate the Cox approaches via simulation and analyze example datasets meant to approximate the Moderna and Pfizer Phase III efficacy trials over the period September 2020 to September 2021.
2. SURVEILLANCE ANCHORED SIEVE ANALYSIS
2.1. Preliminaries
We begin by reviewing the idealized development of Reference 1. Suppose we have a large placebo controlled vaccine trial with simultaneous entry and follow‐up over a fixed period of time . For simplicity, we assume equal randomization to the two arms; this assumption is relaxed in the supplementary materials. The trial is a deferred vaccination design and all placebo volunteers are vaccinated halfway through the trial. Thus period 1 allows a contrast of vaccine vs placebo while period 2 allows a contrast of immediate vs deferred vaccination. Let denote randomization to the placebo and vaccine, respectively, and define as the total number of cases in arm in period . We assume is approximately Poisson with mean which follows from a rare disease assumption. We define as the expected placebo case count in period whether actual or counterfactual . Note that in period 1, but in period 2, the placebo group is vaccinated so . We define vaccine efficacy in period K as
thus VE is the early effect of vaccine immediately after vaccination and VE the late effect of vaccine after one period has elapsed. We can directly estimate the early vaccine efficacy as , but in period 2, we have no placebo group and is not directly estimable.
Nonetheless, we can recover the placebo controlled late vaccine efficacy by assuming portability of the immediate effect of vaccination, as shown in Reference 1. Under this assumption . Thus which is estimated by . We can estimate the late placebo controlled vaccine efficacy over period 2 as
For a more elegant development involving Cox regression with smoothly varying VE that allows for staggered entry trials, dropout, covariate adjustment, etc. see References 2, 3, 4. These approaches work fine if a single strain circulates in periods. But if a new strain emerges in period 2, and the efficacy profile differs for this new strain, this approach will not work. The problem is that the newly vaccinated in period 2, who face the new strain, will have different vaccine efficacy than the newly vaccinated did in period 1, who faced the old strain. Thus new methods are needed.
2.2. New strains after placebo vaccination
Suppose that in period 1, only a ancestral strain circulates, while in period 2 a new variant strain, , emerges. To accommodate two strains , we define , and VE to be the strain‐specific counts, means, and vaccine efficacies of the previous section. We want to recover the early and late strain specific placebo controlled vaccine efficacies VE, VE, respectively, but have no placebo arm for . Suppose that community surveillance of the circulating strains is done. Let be the proportion of strain in period in the community. Under the assumption that the distribution of infecting strains in the community, that is, , matches that of the placebo group in the trial, whether actual or counterfactual, we can recover time‐varying placebo controlled vaccine efficacy. Note that since the ratio determines so only the ratio need to be correctly specified.
To illustrate key concepts, we provide a schematic in Figure 1. The key idea is to infer strain specific case counts for a period 2 counterfactual placebo group. We do this in two stages. The early vaccine efficacy over period 1 for or ancestral virus is estimated as . In period 2, this estimated is applied to the newly vaccinated placebo arm, that is, deferred vaccination arm, thus inferring 5 ancestral cases under the assumption of portability of vaccine efficacy for the newly vaccinated. The community surveillance ratio of 2:1 for :, is then applied to the inferred 5 ancestral cases, thus inferring 10 variant cases. This follows from assuming the surveillance strain distribution matches the exposure distribution for the trial. With these counterfactual placebo cases for ancestral and variant strains, placebo controlled variant vaccine efficacy for the newly vaccinated can be estimated as . For those vaccinated one period earlier, the variant and ancestral VEs are estimated as and , respectively.
FIGURE 1.
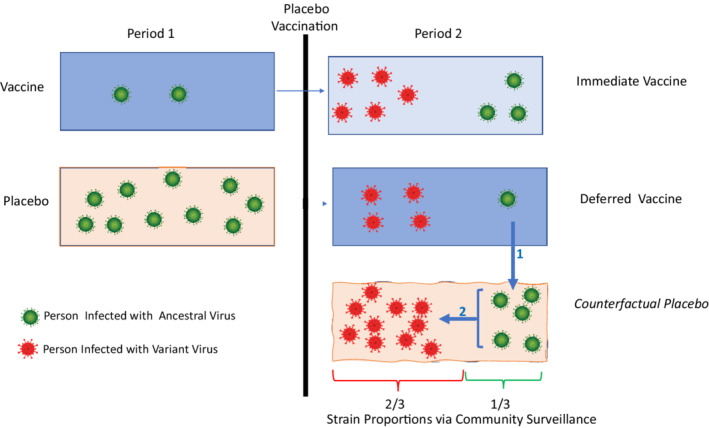
Imputation of strain specific cases for a counterfactual placebo group in period 2. Imputation #1 of 5 ancestral (green) cases follows from portability of ancestral VE of 0.80 for the newly vaccinated which is estimated in period 1. Imputation # 2 of 10 variant (red) cases follows from the 2:1 variant:ancestral case split seen in the surveillance cohort. With ancestral and variant placebo case counts, early and late vaccine efficacy for ancestral and variant strains is easy to calculate. For example, early vaccine efficacy for the variant strain (VE) is estimated as . Using the notation of Table 1, we have period 1 counts of , and period 2 counts of
Table 1 provides the parameterization for the Poisson counts whose mean , depends on the surveillance based probabilities , and the overall expected placebo cases counts in period , , and VE. Here and . We call this approach surveillance anchored sieve analysis (SASA) as the surveillance proportions “anchor” the mean of the Poisson model with serving as offsets to the mean. We assume they are based on a large sample relative to the trial and treat them as constants. With these as fixed constants, we can estimate the six parameters (,VE,VE,VE,VE) using the six counts (). For details, see the supplementary materials “GLM analysis for the Poisson model” which additionally allows Poisson error for the surveillance data.
TABLE 1.
The relationship between mean case counts , period 2 surveillance strain proportions , overall placebo mean cases , and time varying strain specific vaccine efficacy VE for a two period deferred vaccination design
| Group | Period 1 | Period 2 | Strain | ||
|---|---|---|---|---|---|
| Immediate vaccination |
|
|
Ancestral | ||
| Immediate vaccination | ‐ |
|
Variant | ||
| Deferred vaccination |
|
|
Ancestral | ||
| Deferred vaccination | ‐ |
|
Variant |
Note: Only ancestral strain is observed in period 1 but a new variant strain emerges in period 2.
2.3. Bias evaluation
The key assumption of SASA is that the surveillance distribution of strains matches what we would see in an unvaccinated placebo group, whether actual or counterfactual. The matching can be directly examined during the placebo controlled era of the trial. In the post placebo vaccination era, it is an unexaminable assumption. We next explore the potential bias in VE from a surveillance system that is somewhat different from a counterfactual placebo group.
The expected ratio of cases for to in period 2 for the recently vaccinated placebo group is
| (1) |
which can be solved for VE, the VE for the variant strain in the newly vaccinated:
| (2) |
To estimate VE we can plug in from the surveillance distribution, VE estimated from period 1, and estimated from period 2 data into (2). Suppose that the surveillance proportions are incorrectly specified as and . Then the RHS of (2) is not VE but VE
| (3) |
where the second line follows by replacing with the RHS of (1). An analogous result obtains for VE, the late vaccine efficacy for the new strain following 1 period of vaccination, with VE replacing VE in Equation (3).
We can evaluate (3) to explore the extent of the bias. For example if the truth is VE and but we use (0.40) then VE = 0.93 (0.85) both of which are within 6% of the true value. On the other hand, if VE then the VEs are 0.67 (0.25) which are substantially biased. The potential bias increases with decreasing VE. Another feature is that bias can be substantial for rare variants. Suppose VE with true but we use Then VE. Thus in applying these methods one should be cautious about rare variants.
For the ancestral strain, there is no bias for VE with misspecification of the s as the proportion cancels out of the ratio
and we obtain VE by plugging in VE and
Effectively, the early and late VEs of the ancestral strain are estimated by restricting to ancestral data in periods 1 and 2, thus durability of vaccine efficacy, that is, VE = VE does not depend on the s.
2.4. Simulation
To evaluate the statistical performance of the SASA estimates of vaccine efficacy, we conducted a small simulation meant to loosely track a simplified version of the Pfizer or Moderna Phase III Trials of mRNA vaccines. To generate the data, we set the placebo mean number of cases or with an early vaccine efficacy of 90% for ancestral virus. During period 2, a new variant emerges and accounts for half of the infections as determined by surveillance sampling. This is meant to approximate the emergence of a new variant in the US with an expectation it will dominate in the summer (see the supplementary materials). We set the period 2 counterfactual placebo group mean case count as . We consider five scenarios, the last two where the strain distribution is misspecified.
Vaccine efficacy is 90% throughout follow‐up for ancestral and variant strains with .
Vaccine efficacy wanes from 90% to 80% for ancestral and from 80% to 60% for variant with .
Vaccine efficacy is 90% throughout follow‐up for ancestral and variant strains with .
Vaccine efficacy is 90% throughout follow‐up for ancestral and variant strains with , but incorrect offsets of 0.60,0.40 are used.
Vaccine efficacy is 90% throughout follow‐up for ancestral and variant strains with , but incorrect offsets of 0.40,0.60 are used.
For each trial, we simulate Poisson counts () and estimate and the VE parameters using Poisson regression with parameterization given by Table 1 and correct (cases 1‐3) or biased (cases 4 and 5) offsets. We also test for waning efficacy , and for sieve effects, .
Each row in Table 1 is based on 10 000 simulated trials. Code is provided in the supplementary materials and results are provided in Table 2 which demonstrates that we can accurately recover ancestral strain VEs for period 1 and period 2 for all scenarios. We accurately recover the variant VE under cases 1 to 3 and with moderate bias for cases 4 and 5.
TABLE 2.
Simulated performance of surveillance anchored sieve analysis for an idealized two period deferred vaccination design
| Ancestral strain | Variant strain | Test | Test | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Scenario | VE | VE | VE | VE |
|
|
Period 1 | Period 2 | ||
| 1. Reference | 0.8998 | 0.8955 | 0.8955 | 0.8958 | 0.0499 | 0.0451 | 0.0475 | 0.0460 | ||
| (0.0105) | (0.0336) | (0.0337) | (0.0337) | |||||||
| 2. Waning VE | 0.9000 | 0.7909 | 0.7902 | 0.5814 | 0.8235 | 0.9856 | 0.8055 | 0.9709 | ||
| (0.0105) | (0.0598) | (0.0609) | (0.1143) | |||||||
| 3. | 0.8999 | 0.8868 | 0.8868 | 0.8870 | 0.0415 | 0.0496 | 0.0373 | 0.0438 | ||
| (0.0105) | (0.0626) | (0.0540) | (0.0546) | |||||||
| 4. a | 0.8998 | 0.8954 | 0.8429 | 0.8425 | 0.0469 | 0.0477 | 0.2856 | 0.2840 | ||
| (0.0104) | (0.0332) | (0.0519) | (0.0513) | |||||||
| 5. a | 0.9000 | 0.8952 | 0.9298 | 0.9298 | 0.0454 | 0.0470 | 0.2793 | 0.2804 | ||
| (0.0105) | (0.0336) | (0.0230) | (0.0228) | |||||||
Note: During period 1 (period 2) the expected actual (counterfactual) placebo case count is 1000 (500). The true VE except for scenario 2 with VE, VE, VE = 0.80, 0.80,0.60. The VE columns report the Monte Carlo means and (standard deviations). The right columns report the rejection rates for and , respectively, based on a Wald test. 10 000 trials are simulated per row.
True ratio is as given but offsets incorrectly use ratio of 1.00.
Under case 1, the ratio of variances for estimates that are indirectly estimated (VE, VE,VE) compared to the directly estimated VE is about . This is partly due to having about 4 times more expected placebo cases in period 1 compared to period 2, and partly due to VE being directly estimated. Nonetheless, a confidence interval for an indirectly estimated VE is still fairly tight at about (0.84, 0.96) for a “typical” trial where . The probability of rejecting at no waning efficacy (ie, no change in early vs. late efficacy), , or rejecting no sieve effect, for , are appropriately about 0.05 under their respective nulls.
Under case 2 with waning VE, the estimates are again unbiased, and with greater standard deviations, due to the VEs being farther from 1.00. The power to detect waning efficacy is high for ancestral strain (a contrast of 4 random variables) and very high for variant (a contrast of 2 random variables). Power to a sieve effect matches the powers for waning efficacy under case 2 because the expected Wald statistics for strain‐specific waning efficacy equals the expected Wald statistics for period specific sieve effects.
Under scenario 3 with the variant dominant in period 2, the estimates again appear unbiased but with an increase in the standard deviation by about 50% compared to reference case 1 for the indirectly estimated parameters. The standard deviation for VE is unchanged.
Under scenarios 4 and 5 with misspecification of the proportions in period 2, the ancestral estimates are unbiased and there is no inflation of the type I error rate for testing of waning efficacy for the ancestral or variant strains. There is substantial inflation of the type I error rate for a test of sieve effect, but moderate bias of about 6% (Scenario 4) and +3% (Scenario 5), for the VEs of the variant strain. The inflation of the type I error rate for a test of sieving is noticeable.
The Poisson approach is useful for conceptual understanding and high‐level evaluation of an idealized situation with a rare disease. However, this approach does not easily accommodate nonconstant strain specific vaccine efficacy that can vary smoothly across the pre and post crossover eras. Cox modeling handles this easily and is discussed next.
3. COX MODELS
The Cox model can seamlessly accommodate staggered entry and crossover, dropout, covariate adjustment, placebo event rate varying with calendar time, stratification by site, strains coming and going, and strain specific VE varying smoothly with time. The Cox model can recover the per‐exposure vaccine efficacy provided (1) the exposures to each infecting strain are the same in the placebo and vaccine arm, which should be achieved in a blinded trial which is a small portion of the population and (2) the per‐exposure disease probabilities are correctly specified (eg, as a function of time or covariates). 7 , 12 , 13 Furthermore, the bias evaluation of Section 2.3 applies approximately to the Cox model given the connection between the two, see Reference 14. The main disadvantage of the Cox approach is computational complexity.
Following the parameterization of Reference 4, let be the time since study initiation, be the enrollment and vaccination times for person , and be the indicator of whether person is vaccinated at time . To clarify the time index, if the first person is enrolled on September 1, 2020, then this is ; is September 3, 2020, and a person who enrolls on September 4, 2020 has . As an example parameterization that allows for a smoothly declining vaccine efficacy, suppose that the cause‐specific hazard for the risk of first infection by strain is given by
| (4) |
where is the placebo baseline hazard (whether actual or counterfactual) for infection by strain , and is the indicator function. This formulation (4) reduces to the Prentice approach to competing risks. 15 However, vaccine efficacy for strains that emerge after the placebo group is vaccinated cannot be estimated with this approach as for everyone after placebo vaccination. To see this, note that the partial likelihood contribution for a strain case at calendar time is
| (5) |
where is the set of volunteers who are still at risk at time . Because emerges after placebo vaccination, cancels out for all partial likelihood contributions, so and are not estimable. However, and thus whether VE is constant, can be assessed. We call this the strain specific sieve approach (SSSA).
For Cox regression, the key idea of Figure 1 is rendered as an assumption that the cause‐specific hazards have a relationship anchored by the strain distribution of the surveillance data. Let be the true proportion of strain viruses at time in the surveillance cohort, and let be the hazard of infection by any strain at calendar time . We write
| (6) |
where we have substituted from (4) with , a nuisance parameter times a known function.
To illustrate how the estimation works, consider the partial likelihood contribution for a person who is infected with strain at calendar time after all have been vaccinated. The likelihood contribution is
| (7) |
where is the set of circulating strains observed over follow‐up. Note that remains in the likelihood throughout follow‐up. So even if strain emerges after all have been vaccinated, we recover the immediate post vaccination vaccine efficacy for as . This recovery is analogous to what we saw in Figure 1 which demonstrated recovery of period 1 VE for a strain that emerged in period 2.
We can also apply SASA to the setting where we have a phenotypic mark for strain , and vaccine efficacy depends on . This builds on work by Juraska and Gilbert, 10 , 11 and is illustrated for HIV by Corey et al. 16 To fix ideas, suppose that is the readout from a neutralization assay using pseudo‐virus with pooled sera collected shortly after vaccination. An example mark‐based parameterization with time constant vaccine efficacy is given by
| (8) |
| (9) |
With this model, we have the vaccine efficacy vary smoothly with the mark but constant in time as
| (10) |
Due to the potential for bias due to misspecification of , it is appealing to apply the mark‐based approach with unspecified. For strains that are present in the pre‐crossover era, ) can be left unspecified. Indeed each infecting virus can be viewed as a different strain so that there are as many strains as cases. Effectively, each strain defines a stratum in the Cox model. However for strains that emerge post‐crossover, there is a subtlety. Post crossover data provides no information about or . To see this note that in the post‐crossover era the partial likelihood contribution reduces to a constant
| (11) |
As a consequence of this subtly, suppose there are two strains with different marks V(0),V(1) in the pre‐crossover era, and a new strain with yet another V(2) mark in the post‐crossover era. One can estimate (9) with unspecified, using a data set with all the pre and post crossover data, but the post‐crossover data is not used and it is a bald extrapolation to plug in V(2) into (10) to estimate VE for the emergent strain.
We note that one can view (8) as a kind of smoothly parameterized Method B Lunn‐McNeil approach to competing risks 17 where for .
4. ESTIMATION
Estimation of the SASA Cox model is nonstandard due to the presence because of the surveillance data, multiple variants, and multiple sites. To allow for multiple sites let be the true surveillance proportion for strain at time at site . In this section, we use a piecewise constant approximation which averages over discrete intervals, for example , for 2‐week intervals.
4.1. Specification of
We estimate using the GISAID database (https://www.gisaid.org), which contains the genetic sequences of infecting SARS‐CoV‐2 strains from around the globe starting in January 2020. 18 The sequences used for this article are from the corpus of whole‐genome sequences made available be GISAID, and they were downloaded on 08 July 2021. All sequences in the GISAID database from the United States ( = 539 812) and from Mexico ( = 13 557) were used. The GISAID accession numbers, which uniquely identify each sequence, are available in the supplementary materials. We determine their lineages and WHO variant status using the Phylogenetic Assignment of Named Global Outbreak LINeages (PANGOLIN) (https://github.com/cov‐lineages/pangolin) software. Additionally, each sequence has information about its country of origin and the date of submission, and for the United States, the state of the submitting lab is also included.
Specification of depends on the granularity needed for analysis, the abundance of the different strains, the similarity of the strain distribution over location, and assumptions or data about which variants/lineages have similar vaccine efficacy over time. A coarse analysis might be to group lineages/variants into two or three strains, say Delta, Alpha, and otherwise. Or a set of 4 or 5 variants might be initially examined and then pooled into a smaller number of strains with similar vaccine efficacy. The location could be regional and would apply to all clinical trial sites in the region. If is close to 0 and a strain case occurs in week at location , it will have substantial influence. We thus recommend examining the influence of cases for which is small, say <0.05. This can be accomplished by comparing parameter estimates with and without such cases. Figure 2 shows the weekly distribution of WHO lineages over time for 10 regions of the contiguous United States from January 2020 through June 2021.
FIGURE 2.
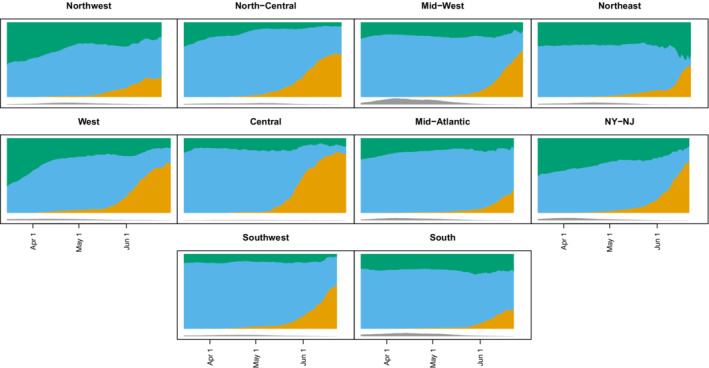
The plots of the moving averages (7 days) of proportions of different variants out of those not missing variant information. The Delta variant (including Delta+K417N) is orange, the Alpha variant is blue, and all other nonmissing variants are green. Values are plotted from March 15, 2021 to June 30, 2021, but some regions do not have data all the way until June 30 (eg, Northwest). Underneath the main figure are gray regions which are proportional to the sample size of the averages, with the bottom of the color plot at the value . For example, the largest sample size is 16 469 for the Mid‐West region on April 8, 2021, but most have much smaller sample sizes especially in late June. Regions defined at https://fortune.com/2021/07/07/the‐delta‐variant‐is‐now‐dominant‐in‐the‐u‐s‐see‐the‐states‐where‐its‐most‐prevalent
A mark‐based analysis is more complex as in principle each infecting virus might yield a unique mark . If each infecting virus were classified as a different strain then is zero except the one when a case of type occurs and becomes 1. Such a strain distribution implies that post‐crossover data provide no information about time‐constant sieve effects. Thus to glean information post‐crossover, we are led to defining as fairly coarse as described above.
4.2. Estimation of Cox model parameters
The partial likelihood is the product of contributions like that of (7). For each two‐week period, we create a dataset of all volunteers who have not had an event before that period. For each event within the 2‐week period, we determine each individual's vaccination status and time since vaccination at the time of that event. For a dataset of strains, we make copies of the information for each person for period but with an offset which equals for strain and an indicator of an event. Once an individual has an event within period she is removed from the risk set for that period and subsequent periods. So for a study with 100 periods and 4 strains, we make 400 copies, each of which includes approximately individuals, where is the number randomized.
Stratification by site is especially important when using SASA. To see this, suppose only one site is accruing cases in June and has a 50:50 split of ancestral strain to variant while all other sites have a 90:10 split ancestral strain to variant. Consider a model with time‐constant VEs and a variant case that occurs after the placebo group has been entirely vaccinated. The site stratified partial likelihood is proportional to while the unstratified partial likelihood is approximately proportional to . The latter likelihood is tantamount to substantially misspecifying the offsets which, as has been shown, leads to bias. Details with a simple example dataset and SAS code are provided in the supplementary materials.
5. SIMULATION
In this section, we apply the Cox model approach to a scenario that loosely approximates the Moderna and Pfizer vaccine trials. A simulated trial enrolls 30 000 subjects uniformly in September 2020 and randomizes equally to vaccine or placebo. The placebo event rate is constant from September 1, 2020 through March 31, 2021, with a mean number of placebo cases of about 1000. All placebo volunteers receive vaccine on April 1, 2021 and from April to September 1, 2021, the mean counterfactual placebo case count is about 750. There are three strains with strains 1 and 2 emerging in February and June, respectively, and strain 0 disappearing in July (see the supplementary materials). We define a period as one month and specify a mark for . We generate data under two scenarios using a mark model with hazard function for person given by
where is the time since September 1, 2020, the time of enrollment for volunteer , is 0 before vaccination and 1 after vaccination. There is only one site and is constant within each calendar month. The baseline is a constant. Vaccine efficacy varies smoothly with , but does not depend on time since vaccination.
Under scenario 1 so VE,VE,VE = (0.90,0.90,0.90) while under scenario 2 so VE,VE,VE = (0.92, 0.78, 0.39).
We estimate three different models with time‐constant VE which are reported in the left half of Table 3.
- Constant VE SSSA
- Constant VE SASA
- Constant VE Mark‐based SASA
TABLE 3.
Monte Carlo estimates and (standard deviations) of vaccine efficacy for 100 simulated deferred vaccination trials
| Constant VE | Time‐varying VE | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| VE | VE | VE |
|
|
|
||||
| No sieve effects | |||||||||
| TRUTH | 0.90 | 0.90 | 0.90 | 0.00 | 0.00 | 0.00 | |||
| SSSA | 0.901 | 0.899 | ‐ | 0.007 | 0.001 | 0.004 | |||
| (0.0099) | (0.0245) | ‐ | (0.0431) | (0.0268) | (0.0533) | ||||
| SASA | 0.901 | 0.900 | 0.900 | 0.006 | 0.001 | 0.002 | |||
| (0.0093) | (0.0176) | (0.0250) | (0.0403) | (0.0274) | (0.0516) | ||||
| SASA Mark | 0.901 | 0.901 | 0.899 | ||||||
| (0.0091) | (0.0138) | (0.0250) | |||||||
| SASA* | 0.904 | 0.879 | 0.877 | 0.011 | 0.008 | 0.016 | |||
| (0.0091) | (0.0228) | (0.0287) | (0.0405) | (0.0272) | (0.0518) | ||||
| SASA Mark* | 0.902 | 0.891 | 0.876 | ||||||
| (0.0089) | (0.0147) | (0.0288) | |||||||
| SASA** | 0.904 | 0.882 | 0.920 | 0.004 | 0.010 | 0.011 | |||
| (0.0094) | (0.0171) | (0.0167) | (0.0374) | (0.0287) | (0.0516) | ||||
| SASA Mark** | 0.899 | 0.908 | 0.915 | ||||||
| (0.0093) | (0.0112) | (0.0174) | |||||||
| Sieve effects | |||||||||
| TRUTH | 0.92 | 0.78 | 0.39 | 0.00 | 0.00 | 0.00 | |||
| SSSA | 0.918 | 0.776 | ‐ | 0.000 | 0.001 | 0.007 | |||
| (0.0098) | (0.0436) | ‐ | (0.0504) | (0.0194) | (0.0194) | ||||
| SASA | 0.917 | 0.778 | 0.390 | 0.003 | 0.000 | 0.002 | |||
| (0.0090) | (0.0296) | (0.1039) | (0.0468) | (0.0193) | (0.0181) | ||||
| SASA Mark | 0.917 | 0.776 | 0.387 | ||||||
| (0.0079) | (0.0234) | (0.1034) | |||||||
| SASA* | 0.919 | 0.738 | 0.271 | 0.0127 | 0.0146 | 0.010 | |||
| (0.0088) | (0.0376) | (0.1256) | (0.0482) | (0.0190) | (0.0183) | ||||
| SASA Mark* | 0.916 | 0.758 | 0.300 | ||||||
| (0.0080) | (0.0260) | (0.1211) | |||||||
| SASA** | 0.922 | 0.774 | 0.596 | 0.015 | 0.014 | 0.008 | |||
| (0.0088) | (0.0249) | (0.0584) | (0.0412) | (0.0196) | (0.0183) | ||||
| SASA Mark** | 0.914 | 0.821 | 0.626 | ||||||
| (0.0082) | (0.0183) | (0.0583) | |||||||
Note: Estimates are provided both for strain specific and mark parameterized vaccine efficacy models. The left half fits models with a time constant VE, while the right half fits models with a log‐linear decline in VE. The rows without asterisk denote correct specification of while * (**) denote misspecifications.
To examine durability of vaccine efficacy, we additionally fit two non‐mark models. These are reported in the right half of Table 3.
- Time‐varying VE SSSA
- Time‐varying VE SASA
To illustrate sensitivity analyses, we fit models where the most common strain in any given month is specified as instead of , while the other strains are proportionally reduced so that the remaining sums to one. We analogously reduce the most common strain by (). Note that for with two strains perturbs to or , respectively, as was done in the Poisson simulations. We denote these perturbations by * and **, respectively. In practice, misspecified offsets are likely to be too high sometimes and too low sometimes, which should tend to cancel out and reduce bias. So these consistent perturbations may be more consequential than would be expected in practice.
The fitted estimates for vaccine efficacy from the constant VE models are given in the left half of Table 3 while the right half provides the slope estimates from the time‐varying VE models. The top half corresponds to scenario 1 with constant 90% VE for all strains. The first three pairs of rows are for correctly specified models. All approaches are unbiased for all VE estimates and all methods have similar standard deviations for VE. For VE SASA‐Mark is more efficient than SASA which is more efficient than SSSA with substantial efficiency gains (ratio of squared standard deviations) of for SASA Mark compared to SSSA. VE is not estimable using SSSA and has the same estimated standard deviation for SASA and SASA Mark. Both SSSA and SASA provide unbiased estimates of .
Looking at the next four pairs of rows, we see that the SASA results are fairly robust to misspecification of the strain distribution with mean VE estimates ranging from 0.88 to 0.92 for SASA and SASA‐Mark. The estimates of the slope are robust to misspecification of and their standard deviations are very similar to when is correctly specified.
The bottom panel reports results for scenario 2 with a strong sieve effect. Under correct specification (first three pairs of rows) all methods appear unbiased for VE though with larger standard deviations for and compared to VE,VE = (0.90, 0.90). The efficiency gain for VE under SASA Mark is compared to SSSA which is similar to the setting with VE. Under misspecification, we see modest bias for VE ranging from (0.74 to 0.82) for the various approaches, and more substantial bias for VE ranging from 0.27 to 0.63 for the various approaches. As before, all approaches appear unbiased for so vaccine durability is accurately assessed.
In summary, the SSSA approach, which treats each strain completely separately and is free of concerns about misspecification, is the most robust approach for estimating VE and also provides reliable inference about strain specific waning or . For strains that are unreliably estimated with SSSA, or emerge post crossover, SASA can add useful information. For high VE, SASA is fairly robust while for low VE it is less so. Nonetheless, even for strains with lower VE, the analysis is informative. In scenario 2, we could conclude that strain 2 has lower efficacy than strain 0 and nonzero efficacy. Such conclusions are not possible without employing SASA. Use of the mark parameterized approach can result in greater efficiency in some scenarios with just three strains. With a large number of strains, a mark‐based approach should be even more efficient.
In the supplementary materials, we provide additional simulations with a much lower event rate with an expected number of placebo cases in the pre‐crossover and post‐crossover eras of 130 and 100, respectively. This lower event rate is meant to roughly approximate the Novavax phase III clinical trial. The behavior of the different methods is relatively similar, though the standard deviations are larger.
In practice, we recommend reporting the confidence intervals for different perturbations of the s, along with the unperturbed s to fully convey uncertainty. The specific perturbation would depend on the trial being analyzed. A summary could report the minimum lower bound and maximum upper bound of all confidence intervals. Because of the potential for rare variants to have substantial impact, for example, an explicable variant case when is near zero, sensitivity analyses such as rerunning the model after removing individual cases can assess influence. In our development, we used a linear function of time to describe waning vaccine efficacy. In practice splines or polynomials may provide a better fit and should be evaluated.
6. EXAMPLE
To illustrate the use of these approaches, in this section, we analyze a simulated dataset from the bottom scenario of Table 3 with VE,VE,VE = (0.92,0.78,0.39). Cases counts for the simulated data set are given in Table 4 along with the average placebo community proportion:
where is the set of indices of subjects with events in period of type strain . The statistic averages the s at the times of events. This average should match that of a placebo group if the VEs are the same across strains and constant over time. We see that the observed placebo counts in the pre‐crossover period of 871 and 118 align with the averages of 0.86 and 0.14.
TABLE 4.
Case counts by arm, strain, and period for a simulated COVID‐19 trial along with the average
| Pre‐crossover | Post‐crossover | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strain |
|
|
|
|
|
|
||||||
| 0 | 0.86 | 871 | 93 | 0.06 | 7 | 8 | ||||||
| 1 | 0.14 | 118 | 34 | 0.60 | 137 | 130 | ||||||
| 2 | 0.00 | 0 | 0 | 0.34 | 132 | 142 | ||||||
Table 5 presents estimates from the SSSA and SASA models. Both approaches are close to the true generating values and both estimate slope terms close to zero. The standard errors for the slopes are similar between SSSA and SASA as is the standard error for . The ratio of variances for , , is about 20% less for SASA . Of course SSSA cannot estimate the VE for strain 2 which emerges post‐crossover and SASA estimates a VE of 0.50 with a 95% confidence interval of (0.33,0.67) which includes the true value of 0.39. The sensitivity analyses have little impact on the slope estimates, and little impact on the estimates of VE and VE,but the VE estimate ranges from 0.39 to 0.65, which aligns with the evaluation of Table 2.
TABLE 5.
Estimates and standard errors of vaccine efficacy and for a simulated COVID‐19 trial
| Constant VE | Time‐varying VE | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Method | VE | VE | VE |
|
|
|
|||
| SSSA | 0.90 | 0.73 | ‐ | 0.019 | 0.020 | 0.001 | |||
| (0.011) | (0.053) | ‐ | (0.049) | (0.019) | (0.019) | ||||
| SASA | 0.90 | 0.75 | 0.50 | 0.011 | 0.026 | 0.004 | |||
| (0.011) | (0.047) | (0.087) | (0.048) | (0.018) | (0.018) | ||||
| SASA* | 0.90 | 0.70 | 0.39 | 0.027 | 0.041 | 0.019 | |||
| (0.011) | (0.047) | (0.108) | (0.048) | (0.018) | (0.017) | ||||
| SSSA** | 0.91 | 0.74 | 0.65 | 0.028 | 0.041 | 0.017 | |||
| (0.010) | (0.036) | (0.055) | (0.045) | (0.019) | (0.018) | ||||
Note: Models with unspecified (SSSA) or based on surveillance data (SASA) are estimated. The left panels are for models with constant VE while the right panels estimate a time‐varying VE. Two sensitivity analyses are run where the dominant strain is over‐reported* and under‐reported**.
We provide the estimated VE curves from the SASA model with time‐varying VE in Figure 3, along with pointwise 95% confidence intervals. The estimated vaccine efficacies are fairly flat with the largest confidence intervals for strain , which has a relatively low VE and no placebo group, both of which increase confidence interval width.
FIGURE 3.
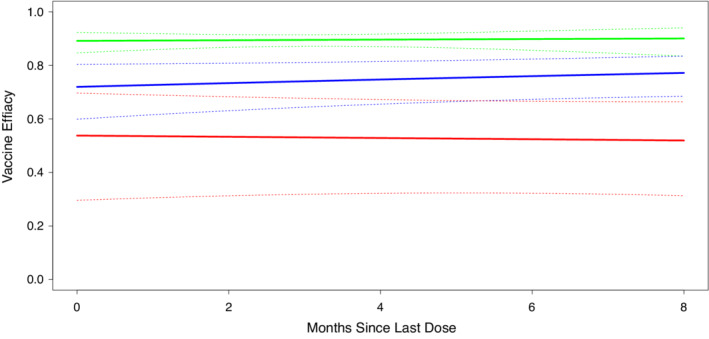
SASA estimates of time‐varying strain specific vaccine efficacy using a log‐linear function of time since vaccination. Strains 0 and 1 are colored green and blue, respectively, and circulate before and after crossover. Strain 2 is colored red and circulates after crossover. Pointwise 95% confidence intervals are given by dashed lines
7. DISCUSSION
Naively applying existing methods for estimating vaccine durability after placebo group vaccination results in an uninterpretable estimate of vaccine effect as the impact of waning efficacy is hopelessly confounded with differential vaccine effect on different strains. This confounding was recognized as an important limitation with the existing methods. 1 , 2 , 3 , 4 This provides methods that permit estimation of time‐varying strain specific vaccine efficacy. The simplest and most robust is to apply the deferred vaccination methods separately to each strain. However this approach is only viable for strains that occur while there is still a placebo group. The major contribution of this article is to demonstrate how to use vaccine trial data coupled with strain surveillance data to estimate strain‐specific placebo controlled vaccine efficacy profiles for variants that emerge after all are vaccinated. The key requirement is that the distribution of strains for a counterfactual placebo group matches that within the community. This assumption might be violated for several reasons, for example, the trigger for including individuals in the surveillance dataset is different from the case definition of disease in the trial and this changes the distribution of variants, or the surveillance data might draw from a different sublocation than the trial participants and the distribution of variants differs. This assumption can be examined during placebo controlled periods of a trial, but post crossover it cannot be directly examined. In practice, we advocate sensitivity analyses where the estimated placebo strain distribution is realistically varied to provide a range of VE estimates.
Supporting information
Data S1 Supplementary material
Data S2 Supplementary material
ACKNOWLEDGEMENTS
We would like to thank Peter Gilbert for helpful comments. We would also like to thank the GISAID database for their compilation and curation of the full‐genome SARS‐CoV‐2 sequences that were used in this study, and all of the submitting and originating laboratories for submitting their sequenced genomes for public use. A list of all submitting and originating laboratories for all of the sequences used in this study are available in the supplementary materials.
Follmann D, Fay M, Magaret C. Estimation of vaccine efficacy for variants that emerge after the placebo group is vaccinated. Statistics in Medicine. 2022;41(16):3076–3089. doi: 10.1002/sim.9405
DATA AVAILABILITY STATEMENT
Data sharing is not applicable to this article as no new data were created or analyzed in this study.
REFERENCES
- 1. Follmann D, Fintzi J, Fay MP, et al. A deferred‐vaccination design to assess durability of COVID‐19 vaccine effect after the placebo group is vaccinated. Ann Intern Med. 2021;174(8):1118‐1125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Lin DY, Zeng D, Gilbert PB. Evaluating the long‐term efficacy of coronavirus disease 2019 (COVID‐19) vaccines. Clin Infect Dis. 2021;73(10):1927‐1939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Tsiatis AA, Davidian M. Estimating vaccine efficacy over time after a randomized study is unblinded. Biometrics. 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Fintzi J, Follmann D. Assessing vaccine durability in randomized trials following placebo crossover. Stat Med. 2021;40(27):5983‐6007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Kupferschmidt K, Wadman M. Delta variant triggers new phase in the pandemic; 2021.
- 6. Reardon S. How the delta variant achieves its ultrafast spread. Nature. 2021;21(3). [DOI] [PubMed] [Google Scholar]
- 7. Gilbert PB. Comparison of competing risks failure time methods and time‐independent methods for assessing strain variations in vaccine protection. Stat Med. 2000;19(22):3065‐3086. [DOI] [PubMed] [Google Scholar]
- 8. Gilbert PB, Self S, Rao M, Naficy A, Clemens J. Sieve analysis: methods for assessing how vaccine efficacy depends on genotypic and phenotypic pathogen variation from vaccine trial data. J Clin Epidemiol. 2001;54:68‐85. [DOI] [PubMed] [Google Scholar]
- 9. Krause PR, Fleming TR, Longini IM, et al. SARS‐CoV‐2 variants and vaccines. N Engl J Med. 2021;385(2):179‐186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Juraska M, Gilbert PB. Mark‐specific hazard ratio model with multivariate continuous marks: an application to vaccine efficacy. Biometrics. 2013;69(2):328‐337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Juraska M, Gilbert PB. Mark‐specific hazard ratio model with missing multivariate marks. Lifetime Data Anal. 2016;22(4):606‐625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Rhodes PH, Halloran ME, Longini IM Jr. Counting process models for infectious disease data: distinguishing exposure to infection from susceptibility. J R Stat Soc Ser B. 1996;58:751‐762. [Google Scholar]
- 13. Follmann D, Huang CY. Incorporating founder virus information in vaccine field trials. Biometrics. 2015;71(2):386‐396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Laird N, Olivier D. Covariance analysis of censored survival data using log‐linear analysis techniques. J Am Stat Assoc. 1981;76(374):231‐240. [Google Scholar]
- 15. Prentice RL, Kalbfleisch JD, Peterson AV Jr, Flournoy N, Farewell V, Breslow N. The analysis of failure times in the presence of competing risks. Biometrics. 1978;4:541‐554. [PubMed] [Google Scholar]
- 16. Corey L, Gilbert PB, Juraska M, et al. Two randomized trials of neutralizing antibodies to prevent HIV‐1 acquisition. N Engl J Med. 2021;384(11):1003‐1014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Lunn M, McNeil D. Applying Cox regression to competing risks. Biometrics. 1995;51(2):524‐532. [PubMed] [Google Scholar]
- 18. Elbe S, Buckland‐Merrett G. Data, disease and diplomacy: GISAID's innovative contribution to global health. Global Chall. 2017;1(1):33‐46. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data S1 Supplementary material
Data S2 Supplementary material
Data Availability Statement
Data sharing is not applicable to this article as no new data were created or analyzed in this study.


