Maize brace root mechanics vary by whorl, genotype and reproductive stage

Abstract

Background and Aims

Root lodging is responsible for significant crop losses worldwide. During root lodging, roots fail by breaking, buckling or pulling out of the ground. In maize, above-ground roots, called brace roots, have been shown to reduce susceptibility to root lodging. However, the underlying structural–functional properties of brace roots that prevent root lodging are poorly defined. In this study, we quantified structural mechanical properties, geometry and bending moduli for brace roots from different whorls, genotypes and reproductive stages.

Methods

Using 3-point bend tests, we show that brace root mechanics are variable by whorl, genotype and reproductive stage.

Key Results

Generally, we find that within each genotype and reproductive stage, the brace roots from the first whorl (closest to the ground) had higher structural mechanical properties and a lower bending modulus than brace roots from the second whorl. There was additional variation between genotypes and reproductive stages. Specifically, genotypes with higher structural mechanical properties also had a higher bending modulus, and senesced brace roots had lower structural mechanical properties than hydrated brace roots.

Conclusions

Collectively these results highlight the importance of considering whorl-of-origin, genotype and reproductive stage for the quantification of brace root mechanics, which is important for mitigating crop loss due to root mechanical failure.

INTRODUCTION

Roots are critical for plant health and productivity, including their pivotal role in anchoring plants in the ground. In agriculture, a failure of plant anchorage causes significant crop loss and is referred to as root lodging (Carter and Hudelson, 1988; Berry et al., 2004; Rajkumara, 2008; Fedenko et al., 2015; Hostetler et al., 2021). During root lodging, roots fail by breaking, buckling and/or pulling out of the ground (Easson et al., 1992; Ennos et al., 1993; Crook and Ennos, 1993, 1994; Erndwein et al., 2020). With root breaking (Fig. 1A) and buckling specifically, roots fail when the mechanical load exceeds root structural tolerance. Despite the apparent role of root mechanics in limiting root lodging, a detailed survey of root structural mechanical variation has not been performed (Stubbs et al., 2019).

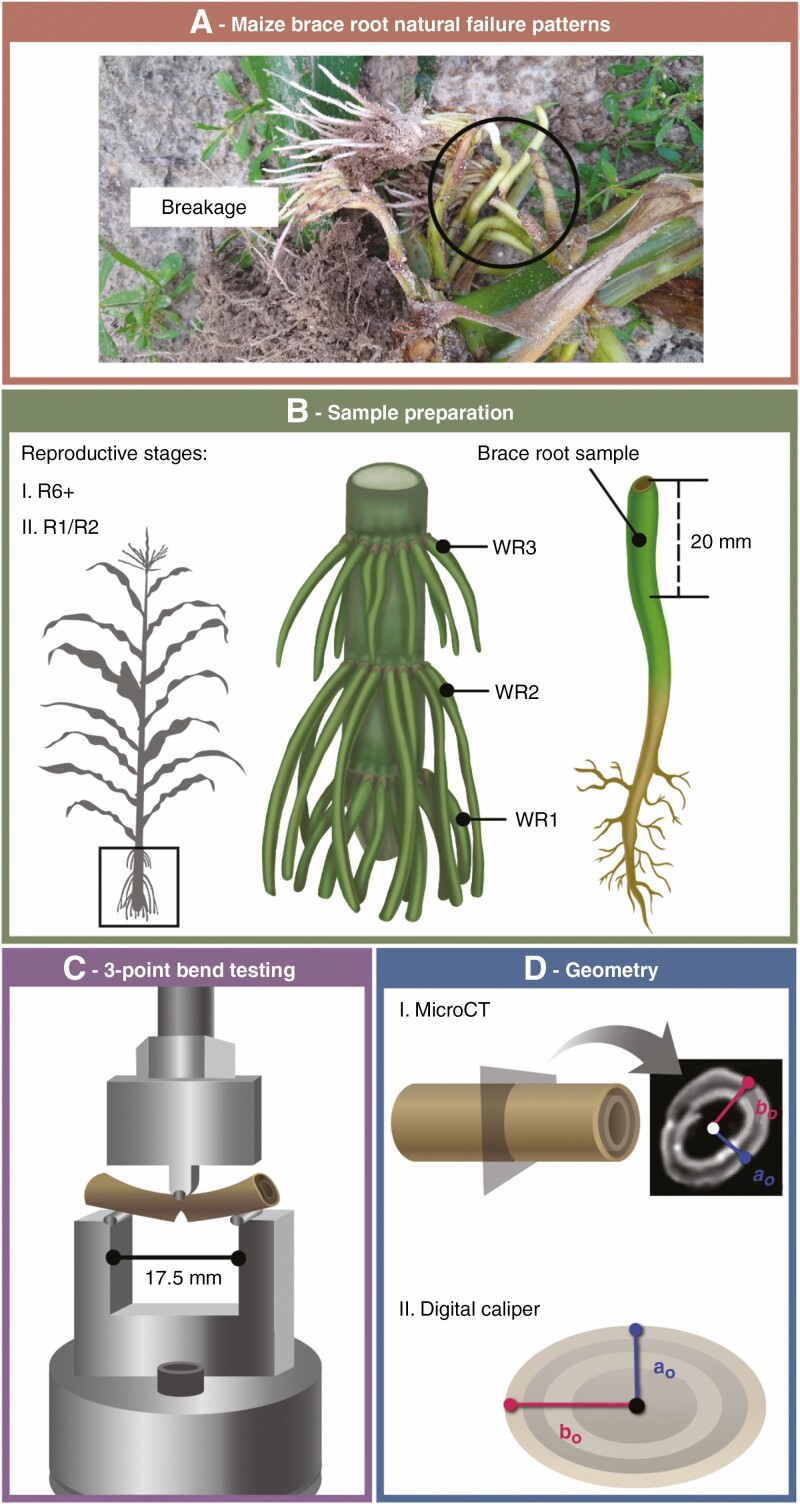
Fig. 1.

Overview of methods for sample preparation, 3-point bend testing and quantification of brace root geometry. (A) Maize brace roots break when the mechanical load exceeds tolerance. This failure is one mechanism of root lodging in maize. (B) Maize brace roots were studied at the R6+ (senesced) and R1/R2 (hydrated) reproductive stages. Brace roots were collected from the whorl closest to the ground (WR1) and the second whorl (WR2). The first 20 mm of each brace root (closest to the stalk) was used for testing. (C) The 3-point bend fixture was 17 mm with the load cell anvil applied to the centre of the brace root sample at a constant rate of displacement until failure. Root failure is illustrated with the notch in the bottom of the brace root. (D) Brace root geometry was quantified by either microCT scanning (R6+ samples) or digital callipers (R1/R2 samples).

In maize (Zea mays), root lodging causes between 7 and 25 % yield losses in the USA, with the detrimental impact on yield increasing as plants reach reproductive maturity (Carter and Hudelson, 1988; Tirado et al., 2021). The mature maize root system is composed of root whorls that develop from stem nodes both below (crown roots) and above (brace roots) the ground, which are collectively called nodal roots (Blizard and Sparks, 2020). Previous studies have analysed the structural mechanics of maize nodal roots via 3-point bending and shown that root mechanics are whorl-specific (Ennos et al., 1993; Goodman and Ennos, 2001). These studies demonstrated that brace roots have higher structural mechanical properties and a lower bending modulus compared to crown roots (Ennos et al., 1993; Goodman and Ennos, 2001).

In this study, we expand upon previous studies and analyse the impact of whorl, genotype and reproductive stage on maize brace root structural mechanics. We, and others, have shown that brace roots are critical for anchorage and resistance to root lodging (Liu et al., 2012; Sharma and Carena, 2016; Shi et al., 2019; Reneau et al., 2020; Hostetler et al., 2022). We have further shown that there is variation in the contribution of brace roots to anchorage between whorls, with the whorl closest to the ground contributing the most (Reneau et al., 2020). Here, we address the hypothesis that brace root structural mechanics vary by whorl, genotype and reproductive stage. To test this, we selected three temperate inbred lines (Zea mays L. cv. B73, Oh43 and A632) based on their agronomic importance (Liu et al., 2003) and variation in the contribution of brace roots to anchorage (Hostetler et al., 2022). We subjected two whorls of brace roots to 3-point bend tests from these three inbred lines at two reproductive stages (hydrated and senesced brace roots), and we show that the structural mechanical properties and bending moduli vary by genotype and reproductive stage. Together, these results highlight the importance of understanding brace root structural mechanics in the context of whorl-of-origin, genotype and growth stage for future crop improvement.

MATERIALS AND METHODS

Plant material

Seeds from three inbred maize genotypes (Zea mays L. cv. B73, cv. Oh43 and cv. A632) were grown in the summers of 2019 and 2020. Seeds were planted on 22 May, 2019 and 1 June, 2020 in two replicate plots in Newark, DE, USA (39°40′N, 75°45′W). Weather data for the Newark field site can be found by selecting the Newark, DE-Ag Farm station on the Delaware Environmental Observing System (http://www.deos.udel.edu). In both years, fields were treated with a pre-emergence (Lexar at 8.18 L ha⁻¹ and Simazine at 2.81 L ha⁻¹) and post-emergence (Accent at 0.05 L ha⁻¹) herbicide. At the time of planting, ammonium sulphate (21-0-0 at 100.88 kg ha⁻¹, fertilizer) and COUNTER 20G insecticide (at 6.16 kg ha⁻¹) were applied. Approximately 1 month after planting, when plants were at knee high, additional fertilizer was supplied (30 % urea ammonium nitrate at 374.16 L ha⁻¹).

In 2019, brace roots were collected at reproductive maturity/senescence (R6+, ~123 d after planting) from whorls that entered the ground, and designated as whorl 1 (bottom-most whorl, whorl closest to the ground), whorl 2 (subsequent whorl, whorl originating from the second node above the ground) and whorl 3 (whorl originating from the third node above the ground, Fig. 1B). Brace roots were not collected if they showed signs of disease or splintered during collection. Brace roots were stored in coin envelopes until 3-point bend testing and micro-computed tomography (microCT) scanning. In 2020, brace roots were removed from whorls 1 and 2 at the silking/blistering reproductive stage (R1/R2, ~67 d after planting). Brace roots collected at the R1/R2 stage were placed on a damp paper towel to maintain moisture and subjected to 3-point bend tests immediately following collection.

Quantification of the brace root contribution to anchorage

The brace root contribution to anchorage (BRC) was determined in situ by comparing the slope of the force–deflection curve of maize plants with brace roots removed (None) to the slope of the force–deflection curve of maize plants with brace roots intact (All), as previously described (BRC = None/All; Reneau et al., 2020; Hostetler et al., 2022). Plants were tested before removal of brace roots and again after removal of each subsequent whorl (starting with removal of the top-most whorl). These data enabled us to determine the overall contribution of brace roots to anchorage as well as the contribution of each individual whorl. A brace root contribution to anchorage ratio close to 1 indicates that anchorage was not impacted by the removal of brace roots, whereas a ratio close to 0 indicates that anchorage was predominantly dependent on brace roots entering the ground.

Quantification of structural mechanical properties using 3-point bending

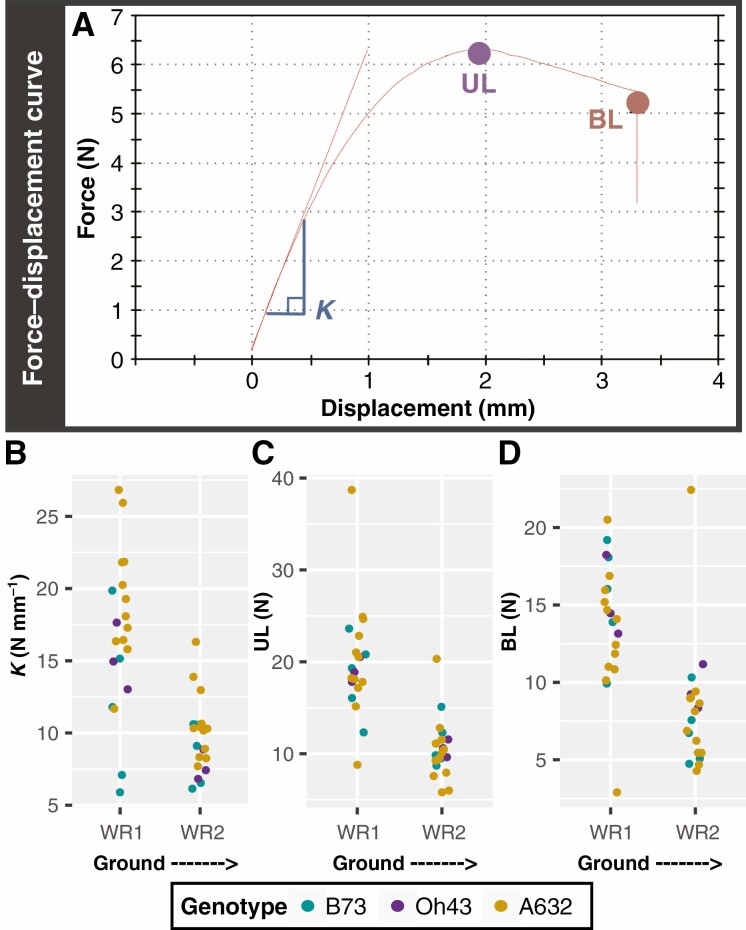
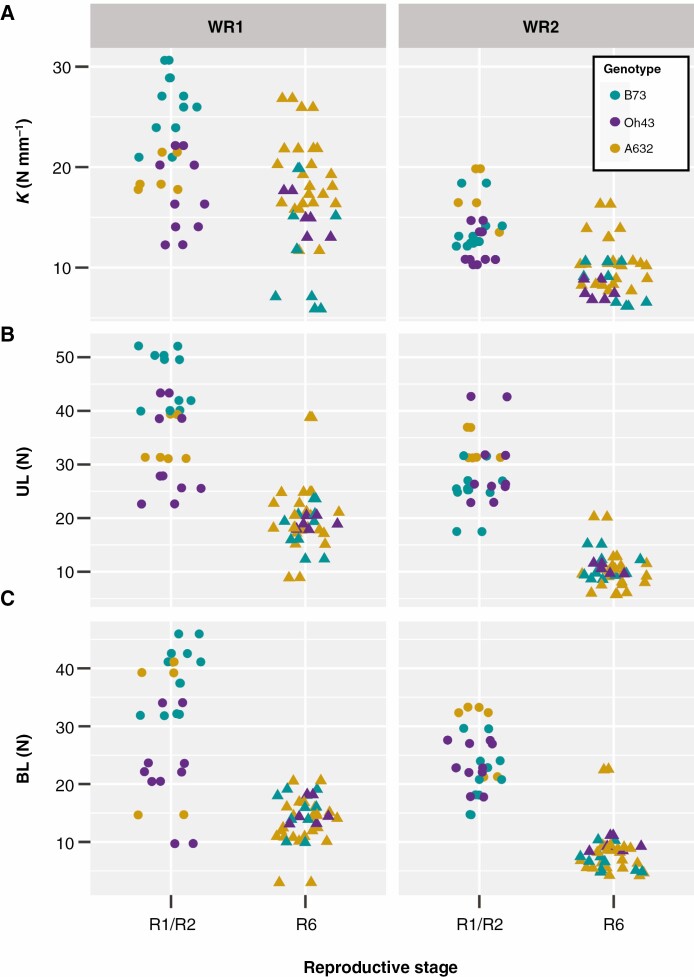
A custom 3-point bend fixture was machined with a 17.5-mm span length (Fig. 1C; Supplementary Data Figure S1), which was the longest span of a straight brace root section that could be reliably isolated. For R6+ brace root samples, the span length to diameter ratio (a_o × 2, where a_o is the minor axis perpendicular to bending, Fig. 1D; Fig. S2) ranged from 11 : 1 to 3 : 1 with an average ratio of 5 : 1. For the R1/R2 brace root samples, the span length to diameter ratio (a_o × 2) ranged from 3 : 1 to 5 : 1 with an average ratio of 4 : 1. Brace roots were trimmed to include only the 20 mm of root closest to the stem (Fig. 1B). At least two brace roots per whorl were tested for at least three plants per genotype and reproductive stage. Brace root samples were tested using an Instron 5943 (Norwood, MA, USA) equipped with a 100-N load cell (Instron 2530 Series static load cell). Each brace root sample was placed on the fixture and adjusted for midpoint loading (Fig. S1). Prior to testing, each sample was preloaded to 0.2 N and 3-point bend tests were performed by constant rate displacement of the top fixture at 1 mm min^–1, until root failure. Force–displacement data were captured with Bluehill 3 software (Instron). Testing continued until failure, which was defined as the first steep decline in the force–displacement curve (Fig. 2A) and characterized as a crack forming in the brace root sample opposite the loading site. For complex biological tissues such as brace roots, the underlying cell layers probably have different structural mechanical properties that contribute to the overall tissue mechanics. For example, roots are often considered structured as two concentric hollow cylinders of lignified tissue (Ennos et al., 1993; Chimungu et al., 2015). However, the structural mechanical properties of individual brace root cell layers are unknown, and thus we consider only the properties of the entire root in this study (Niklas and Spatz, 2012). Structural mechanical properties were extracted from force–displacement curves (Fig. 2A) using Bluehill 3 software. Structural stiffness (K) was defined as the linear slope of the force–displacement curve; ultimate load (UL) was defined as the maximum force the sample withstood before failure; break load (BL) was defined as the force upon fracture, illustrated as the sharp drop in the force–displacement curve (Fig. 2A).

Fig. 2.

The structural mechanical properties of maize brace roots are greater for whorls closer to the ground at the R6+ reproductive stage. (A) Example of a force–displacement curve from an R6+ brace root subjected to 3-point bending. (B) The structural stiffness (K) was defined as the linear slope of the force–displacement curve, the ultimate load (UL) was defined as the highest force the sample withstood without failure and the break load (BL) was defined as the force upon fracture. (B–D) A two-way ANOVA showed that: (B) K was impacted by both whorl (P < 0.05) and genotype (P < 0.05), with whorls closer to the ground (WR1) having a higher K than whorls farther away (WR2), and A632 having higher K compared to B73. (C) UL was impacted by whorl (P < 0.05), with whorls closer to the ground (WR1) having a larger UL. (D) BL was impacted by whorl (P < 0.05), with whorls closer to the ground (WR1) having a larger BL. WR – whorl.

Quantification of brace root geometry

Sample geometry was measured in two ways based on sample constraints. For the senesced root samples (R6+), brace root geometry was quantified by microCT (Fig. 1D) analysis. For microCT analysis, brace root samples were inserted into a low-density upholstery foam fixture to provide a supportive bed that would not appear on the scan (Supplementary Data Fig. S2) and samples were scanned with a Bruker Skyscan 1276 (voxel size of 42.32 µm, 40 kV, 100 µA, 203 ms exposure time, angular step of 0.4°). Scans were reconstructed using Bruker Nrecon software, and Fiji software (Schindelin et al., 2012) was used to measure the brace root radii from the centre of microCT scans to the exterior of the sample (a_o – the minor axis perpendicular to bending and b_o – the major axis parallel to bending) (Fig. 1D; Fig. S2D). Brace root diameter was determined by doubling radii (a_o and b_o) quantifications.

In contrast, fresh tissue (R1/R2) geometry was measured immediately upon collection with a digital caliper (DC) (NEIKO 01407A, 0–6 inch), which minimized the time to testing and brace root dehydration. Brace root samples are frequently ovular; therefore, the largest diameter (majorDC) and smallest diameter (minorDC) (Fig. 1D) were measured at the midpoint of the brace root section, which is the loading site during 3-point bend testing (Fig. 1C; Fig. S1). The sample radii (a_o – the minor axis perpendicular to bending and b_o – the major axis parallel to bending) were calculated by taking half of the digital calliper measurements.

Quantification of the second moment of area (I)

Quantifying the area through which a stress operates is challenging for irregular biological structures such as brace roots (Niklas and Spatz, 2012). Therefore, previous studies assessing root mechanics have used a geometric simplification and considered the root as a solid cylinder (Ennos et al., 1993; Goodman and Ennos, 1996, 1997, 1998, 2001). In this study, we have a high-resolution geometric quantification of the brace roots from microCT scans (Supplementary Data Fig. S2), thus allowing us to evaluate this geometric simplification for calculating the second moment of area (I). The second moment of area of R6+ brace root samples was calculated using two different approaches: (1) true, where the second moment of area is calculated directly by CT Analyzer software (Bruker, Belgium); and (2) simplified, where brace root geometry is considered a solid cylinder as in previous studies (eqn 1):

$${\displaystyle \begin{array}{l}{\displaystyle I=\frac{\pi }{4}(a_o^3\times b_o)}\end{array}}$$ (1)

where π = 3.1415, a_o is the minor axis perpendicular to bending, and b_o is the major axis parallel to bending. The true second moment of area was calculated from the microCT scanned images. For each sample, images were resliced along the root axis (Data Viewer, Brunker, Belgium), and cross-sectional stacks were then thresholded to separate the brace roots from the background. The second moment of area was then calculated with the 2D analysis function for each thresholded sample at the mid-length, using CT Analyzer software. Three values of the true second moment of area were extracted from the CT Analyzer software: I_true major, I_true minor and I_true average.

I and I_true were compared with a Pearson correlation analysis in R v.4.0.2 (R Core Team, 2013). Comparison of the I_true (major, minor and average) with the simplified I assumption showed high positive correlations (r > 0.83) (Supplementary Data Fig. S3). Based on the high correlation between these data, we conclude that a simplified geometry to a solid cylinder, as used in previous studies (Ennos et al., 1993; Goodman and Ennos, 1996, 1997, 1998, 2001), is a reasonable approximation for brace root geometry. Thus, the second moment of area of the brace roots was calculated with simplified geometry (eqn 1), and I was used throughout the paper to enable comparison between this study and previous results.

Quantification of material properties

The structural bending modulus (E) was calculated using the equation for a centre-loaded beam supported at both ends by a lower fixture (eqn 2 adapted from Al-Zube et al., 2018).

$${\displaystyle \begin{array}{l}{\displaystyle E=K\times \frac{L^3}{48I}}\end{array}}$$ (2)

where K is the structural stiffness, L is the fixture span length (17.5 mm for samples tested here) and I is the second moment of area (calculated with simplified geometry, eqn 1).

Statistical analysis

All statistical analyses were performed in R v.4.0.2 (R Core Team, 2013). The data used in this paper are as follows: contribution to anchorage (overall contribution; whorl 1 ratio; whorl 2 ratio; whorl 3 ratio), structural mechanical properties (K; UL; BL), brace root geometry [major diameter; minor diameter, and the second moment of area (I)] and material properties [bending modulus (E)]. An analysis of variance (ANOVA) was used for all statistical tests. A Shapiro–Wilk test was used to determine if data were normally distributed, and when data were not normally distributed (P < 0.05), data were transformed with Tukey’s ladder of Powers from the rcompanion package v.2.3.26 (Mangiafico, 2021). Transformed values were then used in the ANOVA. If a significant difference was found (P < 0.05), a post-hoc Tukey honest significant difference (HSD) test was used to test all pairwise comparisons.

For contribution to anchorage data, a two-way ANOVA was run to test the effect of genotype (B73, Oh43, A632) and number of brace root whorls in the ground (one whorl, two whorls, three whorls) on the overall contribution to anchorage, and the effect of genotype and individual whorls (whorl 1, whorl 2, whorl 3) on the individual whorl ratio. For structural mechanical properties, brace root geometry and material properties, data from brace roots within the same whorl for each plant were averaged to provide a single value per whorl per plant. These data were then tested with a two-way ANOVA, where the effect of genotype (B73, Oh43, A632) and whorl (whorl 1, whorl 2) were considered within a reproductive stage (R1/R2 or R6+). Additionally, for structural mechanical properties and I, a three-way ANOVA was used to test the effect of genotype (B73, Oh43, A632), whorl (whorl 1, whorl 2) and reproductive stage (R1/R2, R6+). Pearson correlation analyses were run on structural mechanical properties and brace root geometry. All figures were generated in R with the ggplot2 package v.3.3.3 (Wickham, 2016).

Data availability

All raw data and R scripts used to process and analyse data are available at: https://github.com/EESparksLab/Hostetler_Erndwein_et_al_2021.

RESULTS

Brace root whorls closer to the ground have a greater contribution to anchorage

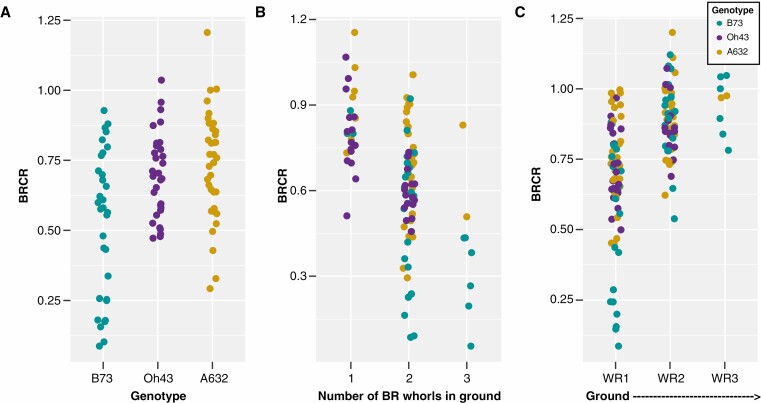
The inbred lines used in this study had a variable, but overlapping contribution of brace roots to anchorage (Fig. 3A; Supplementary Data Tables S1 and S2; Hostetler et al., 2022). The brace root contribution to anchorage is described by comparing the slope of the force–deflection curve with brace roots removed to the slope of the force–deflection curve with brace roots intact, with a ratio close to 1 indicating a low contribution of brace roots to anchorage and a ratio close to 0 indicating a high contribution of brace roots to anchorage (Reneau et al., 2020). For all genotypes, the brace root contribution to anchorage was greater when there are more whorls in the ground (P_{Number of Whorls} = 5.63e⁻⁴) (Fig. 3B; Tables S1 and S2). Additionally, brace root whorls closer to the ground contributed more than brace roots from higher whorls for all three genotypes (P_Whorl = 4.44e⁻¹⁴) (Fig. 3C; Tables S1 and S2). These data confirm and expand upon our previous results (Reneau et al., 2020) to demonstrate that brace roots contribute to anchorage and the whorl closest to the ground has the greatest contribution relative to the other whorls. Since a third whorl (numbered in order of developmental progression from the ground up; Fig. 1B) of brace roots is rarely observed in these genotypes (Fig. 3C; Table S2; Reneau et al., 2020), we quantified the mechanics of brace roots from whorls 1 and 2 only (Fig. 1B).

Fig. 3.

Brace roots are important for anchorage and whorls closer to the ground contribute more at the R6+ reproductive stage. (A) The brace roots from three maize genotypes (B73, Oh43, A632) had variable contributions to anchorage. (B) The brace root contribution to anchorage was greater when there were more whorls of brace roots in the ground. (C) The brace root whorl closest to the ground (WR1) contributed the most to anchorage. BR – brace root; WR – whorl; BRCR – brace root contribution ratio. A BRCR close to 1 indicates anchorage is not impacted by the removal of brace roots, whereas a BRCR close to 0 indicates anchorage is dependent on the number of brace root whorls entering the ground.

Brace roots from whorls closer to the ground are more stiff

Brace roots were collected from the same plants that were measured for their brace root contribution to anchorage, and the structural mechanical properties of brace roots from whorl 1 and whorl 2 were measured using 3-point bend testing (R6+, Fig. 1B, C; Supplementary Data Fig. S1). For complex biological tissues such as brace roots, we consider the structural properties of the entire root (called structural mechanical properties throughout; Niklas and Spatz, 2012). Consistent with a higher contribution to anchorage, structural mechanical properties were significantly higher for brace roots from whorl 1 compared to brace roots from whorl 2 regardless of genotype (P_Whorl = 8.99e⁻⁷, P_Whorl = 1.11e⁻⁷, P_Whorl = 6.38e⁻⁵ for K, UL and BL respectively) (Fig. 2B–D, Table 1; Tables S3 and S4). In addition to the differences between whorls within a genotype, there were also differences between genotypes for structural stiffness (K) (P_Genotype = 1.49e⁻³). Specifically, the K for A632 was higher than the K for B73 within each whorl, although genotypes did not differ for UL (P_Genotype = 0.96) or BL (P_Genotype = 0.64) (Tables S3 and S4). These findings are consistent with the genotypic differences observed for the brace root contribution to anchorage (Tables S1 and S2). Collectively, these results demonstrate that brace roots from whorls closer to the ground are stronger than brace roots from whorls further from the ground (higher on the stalk).

Table 1.

The impact of whorl, genotype and reproductive stage on brace root structural mechanical properties, geometry and bending moduli.

		R6			R1/R2
		B73	Oh43	A632	B73	Oh43	A632
K (N mm–1)	WR1	11.95 ± 5.77	15.21 ± 2.32	19.30 ± 4.34	26.25 ± 3.46	17.00 ± 4.13	19.19 ± 2.01
	WR2	8.60 ± 2.15	7.70 ± 1.05	10.68 ± 2.55	13.80 ± 2.36	12.03 ± 1.96	16.61 ± 3.16
UL (N)	WR1	18.43 ± 4.35	19.10 ± 1.34	20.66 ± 7.19	45.66 ± 5.60	31.59 ± 8.91	33.93 ± 4.66
	WR2	11.06 ± 2.68	10.64 ± 0.96	10.20 ± 3.83	25.28 ± 4.55	29.90 ± 7.78	33.20 ± 3.24
BL (N)	WR1	15.39 ± 3.61	15.24 ± 2.61	13.04 ± 4.36	38.49 ± 5.75	22.01 ± 8.68	31.68 ± 14.76
	WR2	6.88 ± 2.23	9.58 ± 1.40	8.30 ± 4.82	21.70 ± 5.12	23.46 ± 3.99	28.97 ± 6.68
MajorD (mm)	WR1	5.717 ± 0.590	5.459 ± 0.760	5.738 ± 0.618	5.715 ± 0.370	5.590 ± 0.790	4.923 ± 0.194
	WR2	4.742 ± 0.400	4.836 ± 0.057	4.122 ± 0.721	5.014 ± 0.290	5.528 ± 0.393	5.115 ± 0.303
MinorD (mm)	WR1	4.832 ± 0.622	3.817 ± 0.497	4.274 1.132	5.308 ± 0.315	5.178 ± 0.912	4.478 ± 0.161
	WR2	3.577 ± 0.366	2.929 ± 0.307	2.631 0.695	4.695 ± 0.258	5.159 ± 0.493	4.707 ± 0.357
I (mm4)	WR1	33.80 ± 15.06	15.95 ± 8.70	27.38 ± 19.44	34.17 ± 17.49	43.11 ± 26.17	21.77 ± 2.71
	WR2	11.06 ± 4.02	6.08 ± 1.72	4.91 ± 5.15	21.52 ± 10.09	38.67 ± 13.55	26.70 ± 7.51
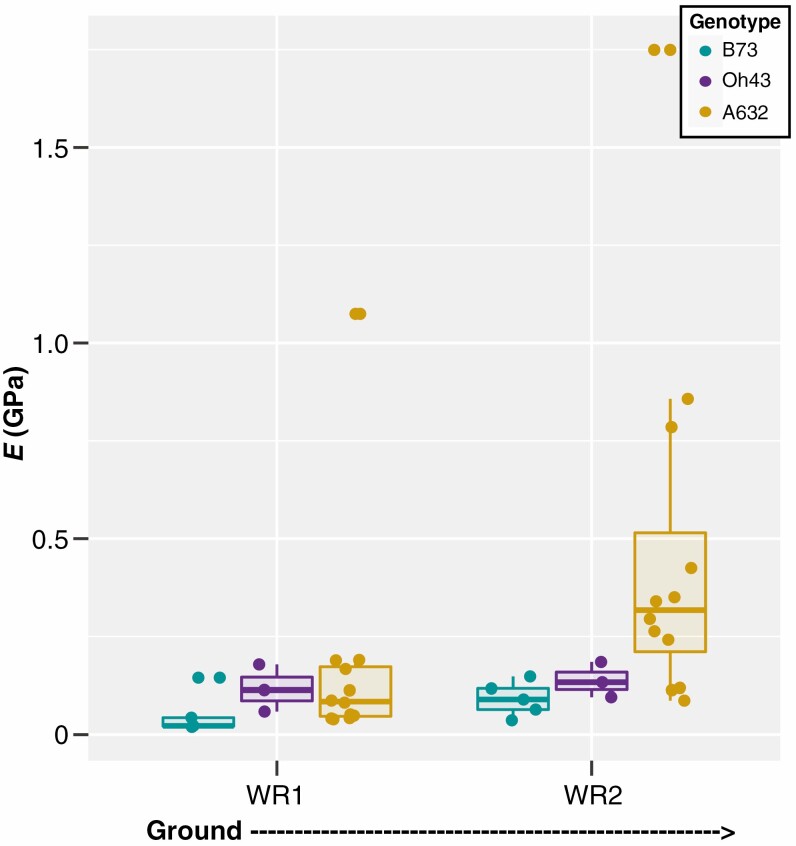
E (GPa)	WR1	0.05 ± 0.05	0.12 ± 0.06	0.18 ± 0.29	0.10 ± 0.06	0.06 ± 0.04	0.09 ± 0.01
	WR2	0.09 ± 0.04	0.14 ± 0.04	0.47 ± 0.47	0.09 ± 0.07	0.03 ± 0.01	0.07 ± 0.02

Data are group means ± s.d. for the structural stiffness (K), ultimate load (UL), break load (BL), the major diameter (MajorD), minor diameter (MinorD), second moment of area (I) and bending modulus (E) for three maize genotypes (B73, Oh43 and A632) at two reproductive stages (R6+ and R1/R2). The structural mechanical properties (K, UL and BL) were extracted from force–displacement curves from a custom 3-point bend fixture that spanned 17.5 mm in length. A minimum of two roots per plant and three plants per genotype/reproductive stage were used to calculate group means. WR – whorl.

Brace roots from whorls closer to the ground are larger

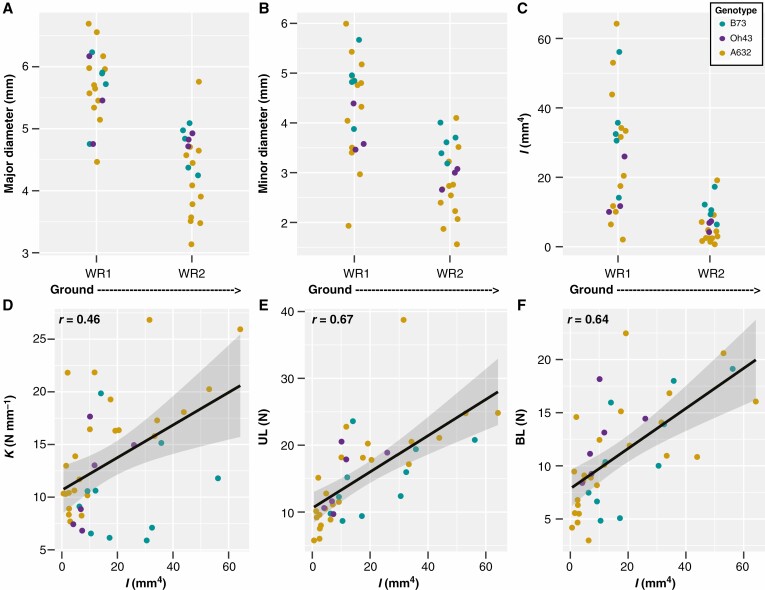
The differences in brace root structural mechanics between whorls may be related to the distribution of forces across different cross-sectional areas, with larger cross-sectional areas able to withstand greater forces. Previous studies have shown that nodal root diameters increase sequentially as root development progresses towards the shoot (Hoppe et al., 1986; Ennos et al., 1993), although these studies have primarily measured underground crown roots. Indeed, we found the opposite trend when considering just brace roots; both the major and minor diameters of brace roots were reduced as root development progressed from whorl 1 to whorl 2 (P_Whorl = 1.23e⁻⁷ and P_Whorl = 2.75e⁻⁶ for the major and minor diameters respectively) (Fig. 4A, B; Supplementary Data Tables S3 and S4).

Fig. 4.

Brace root geometry partially explains structural mechanical properties with whorls closer to the ground being larger at the R6+ reproductive stage. (A–C) A two-way ANOVA showed that: (A) the major diameter of brace roots was impacted by whorl (P < 0.05), with whorls closer to the ground (WR1) having a larger diameter; (B) the minor diameter of brace roots was impacted by both whorl (P < 0.05) and genotype (P < 0.05), with whorls closer to the ground (WR1) having a larger minor diameter, and B73 had a larger diameter than Oh43 and A632; and (C) the second moment of area (I) was impacted by both whorl (P < 0.05) and genotype (P < 0.05), with whorls closer to the ground (WR1) having a larger I, and B73 having a larger I than A632. (D–F) Pearson correlation analyses showed that structural mechanical properties were positively correlated with the second moment of area (I). (D) K was positively correlated with I (r = 0.46). (E) UL was positively correlated with I (r = 0.67). (F) BL was positively correlated with I (r = 0.64). WR – whorl.

Additionally, the distribution of forces during bending can be described by the distribution of material away from the axis of the root – the second moment of area (I), which considers both the major and minor radii relative to the plane of bending. Like brace root diameter, I was larger for whorl 1 than for whorl 2 (P_Whorl = 1.38e⁻⁶) (Fig. 4C, Table 1; Supplementary Data Tables S3 and S4), and correlations between structural mechanical properties and I were positive and varied (r = 0.46–0.67) (Fig. 4D-F). These results are consistent with larger roots having greater bending strength (Figs 2 and 4; Tables S3 and S4). These results also highlight the importance of considering underground nodal roots (crown roots) (Hoppe et al., 1986; Ennos et al., 1993) separately from above-ground nodal roots (brace roots).

The bending modulus of brace roots varies by whorl and genotype

Our results support a relationship between brace root geometry and structural mechanical properties; however, it is possible that there are also differences in the material properties of the brace roots (e.g. cell wall composition or structure). To assess material properties, the bending modulus (E) was calculated, which enables a universal comparison of the brace root’s ability to resist bending, with a higher value for E indicating a higher resistance to bending. Interestingly, brace roots from whorl 1 had lower E than brace roots from whorl 2 (P_Whorl = 5.39e⁻⁴) (Fig. 5, Table 1; Supplementary Data Tables S3 and S4), which is opposite of what was observed for structural mechanical properties (Fig. 3). In other words, whorl 2 has a higher resistance to bending (Fig. 5), but an overall lower strength (Fig. 3) compared to whorl 1 regardless of genotype. In addition, there was a genotype effect on E (P_Genotype = 1.25e⁻³), with A632 having an overall higher E compared to B73, but neither genotype was different from Oh43 (Tables S3 and S4). These genotypic relationships were the same relative to the relationships identified for K and I (Figs 3 and 4; Tables S3 and S4). The difference in E between whorls and genotypes suggests an underlying difference in material properties between brace root whorls and genotypes. However, E was calculated from the geometric simplification of I as a solid cylinder. To ensure that this geometric simplification did not result in the differences observed between whorls, we measured the true second moment of area (I_true) from microCT scans of each root, and calculated E from the I_true. Calculation of E from I_true retained the differences between whorls and genotypes (Tables S5 and S6), indicating that the differences in E are due to underlying material properties, and not the geometric simplification.

Fig. 5.

Brace root bending modulus varies by whorl and genotype at the R6+ reproductive stage. A two-way ANOVA showed that the bending modulus (E) of maize brace roots varied by both whorl (P < 0.05) and genotype (P < 0.05). The E values of brace roots from whorls closer to the ground were lower than those from whorls higher on the stalk, and A632 had a higher bending modulus than B73. WR – whorl.

Brace root structural mechanical properties and geometry are genotype-dependent at early reproductive stages

Brace root mechanics were originally assessed at the R6+ reproductive stage to mirror the timing of the assessment of the brace root contribution to anchorage. However, in 2020, a tropical storm caused root lodging at our Newark field site (65 d after planting; R1/R2 reproductive stage) and provided a unique opportunity to assess brace root mechanics at a growth stage when a natural lodging event occurred. To determine if results from senesced brace roots (R6+ stage) are consistent with hydrated brace roots (R1/R2 stage), we subjected R1/R2 reproductive stage brace roots from whorl 1 and whorl 2 to 3-point bend tests (Fig. 1C; Supplementary Data Figure S1) and quantified brace root geometry.

Analysis of the structural mechanical properties at the R1/R2 reproductive stage showed that the effect of whorl was genotype-dependent (P_{Whorl*Genotype} = 0.05, P_{Whorl*Genotype} = 2.85e⁻³, P_{Whorl*Genotype} = 0.02 for K, UL and BL respectively) (Supplementary Data Fig. S4, Tables S3 and 4). Specifically, B73 was the only genotype where hydrated brace roots mirror the results of senesced brace roots, with whorl 1 being stronger than whorl 2 for K, UL and BL. Like B73, Oh43 had a higher K for whorl 1 than for whorl 2, but there were no differences between whorls for UL or BL. In contrast, A632 showed no differences between whorls for any of the structural mechanical properties. Unlike the senesced samples, the differences in structural mechanical properties were not explained by brace root geometry, with the geometries showing no significant difference by whorl [P_Whorl = 0.11, P_Whorl = 0.25, P_Whorl = 0.43, for the major diameter, minor diameter and I respectively, all three non-significant (n.s.)] and low correlations between structural mechanical properties and geometry (Fig. S5, Tables S3 and S4). These results contrast with previous studies showing that nodal root geometry increases with subsequent whorls (Hoppe et al., 1986; Ennos et al., 1993), and demonstrates that hydrated brace roots have similar geometry between whorls. Lastly, we found that E did not differ between whorls (P_Whorl = 0.14), although B73 and A632 brace roots had a higher E than Oh43 (P_Genotype = 3.07e⁻³) (Fig. S6, Tables S3 and S4). There was no apparent relationship between brace root mechanics and lodging susceptibility. Collectively, these results suggest that brace root mechanics must be interpreted in the context of reproductive stage and genotype to understand how brace root mechanics contribute to root function.

Structural mechanical properties are variable by growth stage within a genotype

Maize plants are monocarpic and thus the start of reproductive development (R1) marks the end of growth and the start of senescence. Senescence is characterized by the breakdown of cells and remobilization of nutrients, which results in dehydration (Nooden, 2012). The loss of turgor pressure accompanied by dehydration has a variable impact on tissue mechanics and depends on whether the cells are thin-walled (e.g. parenchyma) or thick-walled (e.g. sclerenchyma) (Niklas and Spatz, 2012). Given the thick-walled structure of maize brace roots (Hoppe et al., 1986; Chimungu et al., 2015), we hypothesized that dehydration would have a minimal impact on structural mechanical properties. However, when comparing the structural mechanical properties of brace roots between whorls, genotypes and reproductive stages, we found that the structural mechanical properties of senesced plants are lower than those of hydrated plants (Fig. 6). There was a significant three-way interaction of whorl by genotype by reproductive stage for K and UL (P_{Whorl*Genotype*Reproductive Stage} = 0.01 and P_{Whorl*Genotype*Reproductive Stage} = 0.03 for K and UL respectively), but the differences were most dramatic for UL (Supplementary Data Tables S7 and S8). For UL, whorl 2 was significantly different by stage for all three genotypes, whereas whorl 1 was significantly different by stage for B73 only. As expected, the changes in structural mechanics were not associated with a change in I (P_{Whorl*Genotype*Reproductive Stage} = 0.41, n.s.) (Supplementary Data Tables S7 and S8). In other words, the root geometry does not change during senescence, and thus any changes in structural mechanics are due to the process of senescence itself (e.g. loss of turgor pressure). Collectively, these data suggest that senescence had a significant impact on structural mechanics, and the magnitude of this impact varied by genotype and whorl.

Fig. 6.

Structural mechanical properties are lower from senesced roots (R6+) compared to hydrated roots (R1/R2). A three-way ANOVA showed that: (A) the structural stiffness (K) was impacted by whorl, genotype and reproductive stage (P < 0.05). Brace roots from the bottom whorl (WR1) of B73 were significantly lower at the R6+ reproductive stage than the R1/R2 reproductive stage. (B) The ultimate load (UL) was impacted by whorl, genotype and reproductive stage (P < 0.05). The UL was significantly lower for the R6+ reproductive stage within the same whorl for B73 (WR1 and WR2), Oh43 (WR2) and A632 (WR2). (C) The break load (BL) was not impacted by whorl, genotype or reproductive stage (P ≥ 0.05). On average brace roots had a lower BL at the R6+ reproductive stage, but these differences were not statistically significant.

DISCUSSION

Previous research in maize root biomechanics has shown that nodal roots originating higher on the stalk have progressively higher structural mechanical properties and lower bending moduli (Ennos et al., 1993; Goodman and Ennos, 2001). However, these previous studies only measured five whorls of crown roots and one whorl of brace roots in one genotype and at one growth stage. Therefore, it was unclear if the same trends in root structural mechanical properties and bending moduli could be extended to additional brace root whorls, genotypes or growth stages. In this study, we demonstrate that whorl, genotype and reproductive stage each influence the brace root structural mechanical properties, geometry and bending moduli.

We have shown that brace roots from whorls closer to the ground contribute more to anchorage, with brace roots from whorl 1 contributing the most (Reneau et al., 2020; Fig. 3). Although roots from whorl 1 were generally stronger than roots from whorl 2, we found a minimal relationship between the brace root contribution ratio of individual whorls and brace root structural mechanical properties (data not shown). This result is consistent with our previous work, which showed that multiple brace root phenotypes are responsible for predicting the brace root contribution to anchorage (Hostetler et al., 2022). Interestingly, among brace root phenotypes, our previous work identified brace root width (i.e. diameter) as the top predictor for the brace root contribution to anchorage at R6+ (Hostetler et al., 2022). The importance of diameter in this predictive model may reflect the importance of brace root structural mechanics, which are partially driven by geometry, as expected, and shown in this study.

When considering differences between brace root whorls within each genotype and reproductive stage, we found that brace roots from higher on the stalk (whorl 2) had lower structural mechanical properties and higher bending moduli compared to brace roots from whorl 1. This contradicts previous results from crown roots, which showed that roots from higher nodes have greater strength and lower bending moduli (Ennos et al., 1993; Goodman and Ennos, 2001). As we have highlighted in this study, the conclusions from crown roots cannot always be extended to brace roots (e.g. increasing diameters). These differences between crown and brace roots are probably driven by the different environments that these roots emerge in – either the soil (crown roots) or air (brace roots). Regardless, these data suggest an inverse relationship between structural mechanical properties and bending moduli within brace root whorls (Figs 2 and 5). One explanation for this inverse relationship is that larger diameter roots have higher structural mechanics since they can distribute loads over a greater area but have relatively less structural tissues. In other words, maize roots have been considered as two concentric structural cylinders of lignified tissue, with non-structural intervening parenchyma tissues (Ennos et al., 1993; Chimungu et al., 2015). Under this assumption, larger diameter root have more parenchymal area, which leads to lower overall material mechanics. Our results support this assumption, and emphasize the importance for future studies to consider the whorl-origin of the nodal roots and whether this node is located above or below ground.

Our results further expand on previous studies in one genotype to demonstrate that there is variation in brace root structural mechanical properties and bending moduli between genotypes. Interestingly, genotypes with higher structural mechanical properties also have higher bending moduli at both reproductive stages. This suggests that the inverse relationship between structural mechanical properties and bending moduli observed between whorls is a within-genotype phenomenon. Overall, these results highlight the potential for future work aimed at determining the genetic and environmental regulation of brace root mechanics for crop improvement.

Lastly, we aimed to understand how senescence impacts brace root mechanics. We posited that there would be minimal changes in structural mechanical properties between reproductive stages, because brace roots are composed of thick-walled structural elements (Hoppe et al., 1986; Chimungu et al., 2015), which are less impacted by turgor pressure (Niklas and Spatz, 2012). However, our results show that the structural mechanical properties are lower after senescence, suggesting that the contribution of thin-walled parenchyma cells is impacting the overall mechanics. This suggests that the concentric rings of lignified tissues are not the only tissues contributing significantly to brace root mechanics. Future work aimed at dissecting the tissue-specific contribution of each cell layer to the overall structural mechanics will be important to refine targets for crop improvement.

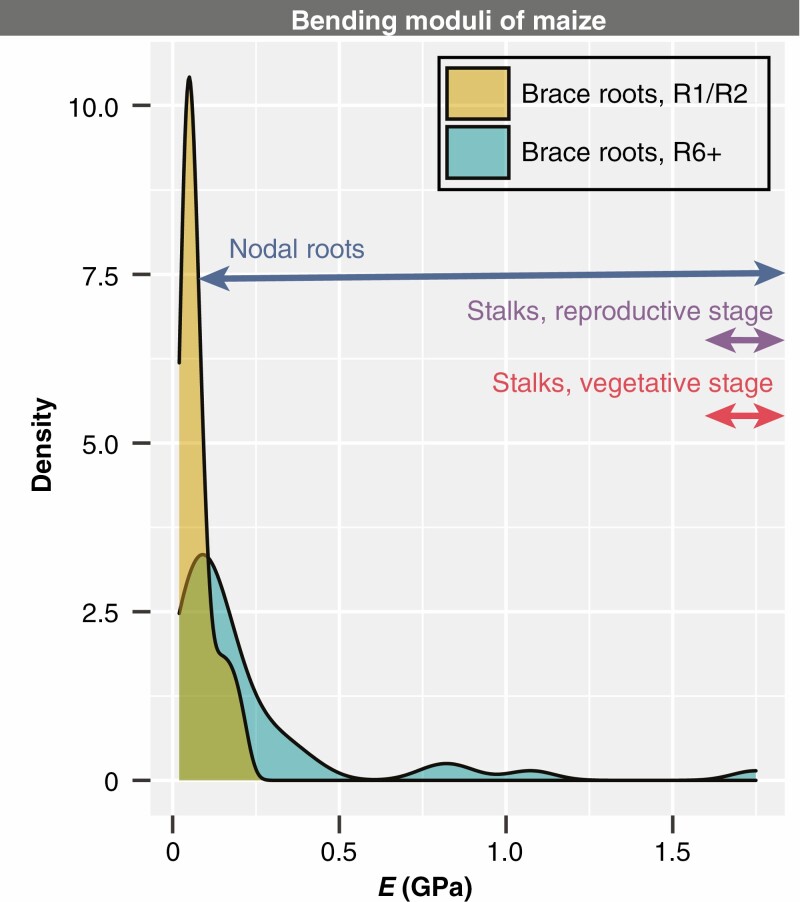
The data presented here expand our understanding of the factors that impact maize root mechanics and show variation in brace root mechanics is specific to whorl-origin, genotype and reproductive stage. Interestingly, despite the variation we observed in this study, the bending moduli are within the range of previous reports on root mechanics (Fig. 7). In contrast, the bending moduli of stalks are greater, suggesting that stalks can resist bending more than roots. One explanation for the different ranges of bending moduli is that roots must retain the ability to flex and absorb forces, which is probably a key strategy to maintain anchorage (Stubbs et al., 2019). Overall, this work sets the foundation to address additional open questions about the genetic and environmental basis of root mechanics, the functional consequences of mechanical variation, and the underlying tissue mechanics that lead to organ-level structural mechanics.

Fig. 7.

The bending moduli of maize brace roots at the R6+ and R1/R2 reproductive stage are like those of other studies. A comparison of the bending moduli of the brace roots from this study with the bending moduli of maize roots and stems from previous studies shows that brace root samples are comparable with other maize roots samples. Nodal root data are from Ennos et al. (1993) and Goodman and Ennos (2001); Stalks, reproductive stage data are from Goodman and Ennos (1997, 1998); Stalks, vegetative stage data are from Goodman and Ennos (1996); Stalks, R6+ data are from Al-Zube et al. (2018).

SUPPLEMENTARY DATA

Supplementary data are available online at https://academic.oup.com/aob and consist of the following. Figure S1. Overview of the setup for 3-point bend testing. Figure S2. Quantification of R6+ brace root geometry from microCT scans. Figure S3. The simplified assumption of the second moment of area is a reasonable approximation of the true I. Figure S4. The variation in structural mechanical properties of maize brace roots depends on genotype for the R1/R2 reproductive stage. Figure S5. Brace root geometry does not differ among whorls or genotypes at the R1/R2 reproductive stage. Figure S6. Brace root material properties vary by genotype but not whorl for the R1/R2 reproductive stage. Table S1. Two-way ANOVA results for the brace root contribution to anchorage ratio and the ratio of individual whorls. Table S2. Pairwise comparisons for the brace root contribution to anchorage ratio and the ratio of individual whorls. Table S3. Two-way ANOVA results for the structural mechanical properties, geometry and material properties of maize brace roots at the R6+ and R1/R2 reproductive stage. Table S4. Pairwise comparisons for the structural mechanical properties and material properties of maize brace roots at the R6+ and R1/R2 reproductive stage. Table S5. Two-way ANOVA results for the bending modulus calculated from I_solid, I_true major, I_true minor and I_true average. Table S6. Pairwise comparisons for the bending modulus calculated from I_true major, I_true minor and I_true average. Table S7. Three-way ANOVA results for the structural mechanical properties, geometry and the second moment of area of maize brace roots. Table S8. Pairwise comparisons for the structural mechanical properties and the second moment of area of maize brace roots.

FUNDING

This research was made possible by funding from the University of Delaware Research Foundation and the Thomas Jefferson Fund to E.E.S.