Fragility Fractures in Postmenopausal Women: Development of 5-Year Prediction Models Using the FRISBEE Study

Abstract

Context

Individualized fracture risk may help to select patients requiring a pharmacological treatment for osteoporosis. FRAX and the Garvan fracture risk calculators are the most used tools, although their external validation has shown significant differences in their risk prediction ability.

Objective and Methods

Using data from the Fracture Risk Brussels Epidemiological Enquiry study, a cohort of 3560 postmenopausal women aged 60 to 85 years, we aimed to construct original 5-year fracture risk prediction models using validated clinical risk factors (CRFs). Three models of competing risk analysis were developed to predict major osteoporotic fractures (MOFs), all fractures, and central fractures (femoral neck, shoulder, clinical spine, pelvis, ribs, scapula, clavicle, sternum).

Results

Age, a history of fracture, and hip or spine BMD were predictors common to the 3 models. Excessive alcohol intake and the presence of comorbidities were specific additional CRFs for MOFs, a history of fall for all fractures, and rheumatoid arthritis for central fractures. Our models predicted the fracture probability at 5 years with an acceptable accuracy (Brier scores ≤ 0.1) and had a good discrimination power (area under the receiver operating curve of 0.73 for MOFs and 0.72 for central fractures) when internally validated by bootstrap. Three simple nomograms, integrating significant CRFs and the mortality risk, were constructed for different fracture sites. In conclusion, we derived 3 models predicting fractures with an acceptable accuracy, particularly for MOFs and central fractures. The models are based on a limited number of CRFs, and we constructed nomograms for use in clinical practice.

Osteoporosis is a serious public health concern, with over 200 million people worldwide who have an increased risk of fragility fractures, resulting in premature death or a decreased quality of life because of acute pain, long-suffering, and disability. It also results in a heavy social financial burden (1). Pharmacological treatments reduce fracture incidence by 30% to 60% (1, 2) and postfracture mortality rate by 10% (3, 4). However, despite the efficacy of available drugs, only 20% to 30% of women at high risk of fracture are treated (5, 6).

A major risk factor for fractures is a low bone mineral density (BMD) (7). Therefore, osteoporosis is operationally defined in terms of BMD decrease as compared to that of young adults (8). However, BMD alone does not reliably predict fracture risk as >50% of women aged ≥50 years who sustained a fragility fracture were not osteoporotic at dual X-ray absorptiometry (DXA), and 60% of women aged ≥60 years with osteoporosis did not fracture within a 13-year follow-up period (8, 9). Other factors such as a prior fracture, advancing age, a family history of hip fracture, excessive bone loss, low body mass index (BMI), falls, smoking, and alcohol behavior are also independently associated with fracture risk (10).

On these grounds, several fracture risk assessment tools have been developed, among which FRAX, Garvan, and Qfracture (11) are the most largely used. Qfracture relies only on clinical risk factors (CRFs) without BMD and has not been validated outside the United Kingdom. FRAX and Garvan have been internationally validated, but their external calibration was not always found to be optimal, notably because the distribution of risk factors and of fracture types vary across different populations (12-15). In terms of predictive accuracy, these tools have been reported to have area under the receiver operating curve (AUROC) values ranging between 0.6 and 0.8, which is considered to be acceptable to good (14, 15). This suboptimal performance is inherent to the stochastic aspect of external factors causing fractures (eg, low trauma, physical strain) but could also result in part from the fact that some important risk factors were not included in the risk estimation, such as falls in the FRAX tool. Therefore we evaluated, in Belgium, the distribution of the internationally validated CRFs included in the FRAX or Garvan models in a prospective cohort study of volunteer postmenopausal women (60-85 years). We also tested in this cohort the predictive value of other validated CRFs, such as sleep disturbances (insomnia, use of sleeping pills), early nonsubstituted menopause, and sedentary lifestyle, evaluating whether adding the latter CRFs would improve fracture prediction (16). We developed 3 models for the absolute fracture prediction according to the future fracture sites: major osteoporotic fractures (MOFs; similar to FRAX), all fractures (similar to the Garvan fracture risk calculator), and central fractures prediction (femoral neck, shoulder, clinical spine, pelvis, ribs, scapula, clavicle, sternum).

Materials and Methods

The Fracture Risk Brussels Epidemiological Enquiry (FRISBEE) is an ongoing prospective epidemiological study in a population-based cohort of 3560 volunteer postmenopausal women aged 60 to 85 years at study inclusion, from the area of Brussels, Belgium, recruited between July 2007 and June 2013. Details of the cohort and study design were previously published (16). In our cohort, at baseline, 12.5% of subjects were on antiosteoporotic treatment and another 6% started the treatment during the follow-up period.

We assessed the CRFs that were included in FRAX or Garvan prediction models or other validated CRFs such as early nonsubstituted menopause (occurring before 45 years of age), a sedentary lifestyle, fall history (incidence of falls during the last year before fracture), sleep disturbances, education level, and the presence of various comorbidities, including untreated hyperthyroidism, inflammatory bowel diseases, diabetes, chronic malnutrition, chronic liver disease, adjuvant therapy with aromatase inhibitors, chronic obstructive pulmonary disease, prolonged immobilization, history of hyperparathyroidism, other endocrine causes of bone loss, and organ transplantation (16). A BMI < 20 and ≥ 30 kg/m² was used as CRF.

Participants were followed yearly by phone call and the follow-up is planned to last at least 10 years. Incident low-trauma (ie, falls from a standing height or less) or nontrauma fractures, classified as MOFs (clinical spine, hip, distal forearm, humerus), central fractures (femoral neck, shoulder, clinical spine, pelvis, ribs, scapula, clavicle, sternum), or any other fracture, including peripheral ones, were recorded during each annual follow-up. Fractures of fingers, toes, skull, and face were excluded for this analysis. All fractures were validated by radiographs or by a surgical report. We could thus exclude false-positive self-reported fractures and include adjudicated fractures not reported by the patients, unveiled by a thorough check of participants medical files (17, 18).

BMD of the lumbar spine (L₁ to L₄) and of the hip (femoral neck, trochanter, and total hip) was measured with a Hologic System 4500 W (Hologic, Inc., Marlborough, MA, USA).

The threshold considered for defining osteoporosis at both the lumbar spine and total hip was a BMD (assessed by DXA) of at least 2.5 SDs (ie, T score ≤−2.5) below the reference database obtained in Belgian population, which was similar with data obtained in young healthy US women 20 to 30 years old (19).

As both spinal BMD and femoral neck BMD were included, a multicollinearity test was conducted for each model to make sure there was no variable with variance inflation factor (VIF) > 4 or with a tolerance < 0.2 (20).

Informed consent was obtained from each woman by return mail. The protocol was accepted by the Ethics Committee of all participating sites (approval number B07720072493).

Statistical Analysis

For analysis of baseline characteristics, usual statistics such as mean and SDs were used to describe continuous variables. Categorical variables were described as frequencies and percentages.

For the competing risk analysis, time to event was defined as the delay between baseline interview and the first MOF fracture, the first central fracture, or any fracture according to the model developed. Fracture is our event of interest, and death is a competing event. When applied in this competing risk situation, traditional Cox proportional hazard model results in the fitting of a cause-specific hazards model (death is simply censored) and the estimated parameters of the model reflect the impact of a covariate on a cause-specific hazard but not necessarily on the cumulative incidence, which was the aim of this study.

For this purpose, the subdistribution regression method developed by Fine and Gray can produce a more accurate prediction for individual subjects (21). Cumulative incidence functions (CIF) of fractures were calculated at 5 years separately for the whole cohort and by age, prior fracture, history of fall, and all other subjects’ characteristics. Gray’s test was performed for comparing CIFs for each characteristic.

For the multivariable analysis, Fine and Gray proportional subdistribution hazard models were derived separately for each type of fracture (MOFs, central, and all fractures). Schoenfeld-type residuals and weighted Schoenfeld-type residuals were inspected to detect violations of the proportional subdistribution hazards assumption. No violations were detected for any of the variables included in the 3 models (20).

Age, BMI, and BMD were introduced as continuous variables. Subdistribution hazard ratios (sHR) associated with low bone mass are presented for a decrease of BMD of 0.1 g/cm² and those associated with age for 1 additional year. The variable selection relied on a score method (best subset selection) and a backward selection method. All the variables were introduced in the multivariable analysis, and the best subset of covariates containing at most 1 non-significant variable was selected for a further backward selection (20).

Best subsets selection compares all possible models using a specified set of predictors and displays the best-fitting models that contain 1 predictor, 2 predictors, and so on. At the end, the final models and their summary statistics needed to be compared and 1 final model to be selected. We used a backward selection for that matter (20).

The coefficients of the selected variables (sHR) were used to build the nomograms.

Calibration of the models was evaluated by calibration curves and by the Brier score (22). The calibration curve compares the predicted probability with the observed probability at a certain time point (5 years in our study). A perfect calibration curve lies on the identity line.

Finally, we performed an internal validation of Brier’s scores using the bootstrap approach by generating 2000 bootstrap samples for each model (22). The discrimination ability of the models was estimated by the AUROC curves.

For the CIF analysis, we used SAS 9.4 (proc life test with the CIF option). The SAS macro PSHREG was used for the creation of the long format data set and the derivation of the multivariable model (20). R software (3.6.1 version) was used (Rstudio) for the nomograms (“rms” package) (23). For the calibration and the discrimination analyses we used the package of survival (score function) and for the bootstrap analysis the “pec” package (22).

All other analyses were performed with SAS. All analysis results were interpreted using a 2-sided significance level of 5%.

We performed a concordance analysis to compare the estimated risk prediction between our MOFs model and classical models, FRAX (MOFs) and Garvan (all fractures). The intraclass correlation coefficient (ICC) estimates and their 95% CIs were calculated using SPSS statistical package version 26 (SPSS Inc, Chicago, IL, USA) based on a mean rating (k = 2), consistency agreement, and 2-way mixed-effects model (24). ICC values <0.5, between 0.5 and 0.75, between 0.75 and 0.9, and >0.90 are indicative of poor, moderate, good, and excellent reliability, respectively (24).

Results

The analysis was performed on the entire cohort (n = 3560 women) included between July 2007 and June 2013. Subjects were followed for 5 years after inclusion or until the occurrence of the first fracture, loss of follow-up, or death within the 5 years follow-up period. A total of 9.2% (309/3560) of subjects were lost to follow-up (249 could not be recontacted, 33 refused to participate after the baseline visit, 27 moved abroad). Those subjects were taken into account by statistical methods in the same way as those who did not present a fracture during the duration of the study. The reasons for which they were lost to follow-up were not associated with a fracture event.

During the 5 years follow-up period, we registered 121 deaths occurring without fracture and 410 fractures, of which 277 were central fractures and 304 were MOFs. Baseline characteristics of included participants are presented in Table 1. For the whole cohort, the average age (±SD) was 70.1 ± 6.4 years [median (25th-75th percentile): 69.2 (64.6-75.3)] and the average BMI (±SD) was 26.0 ± 4.8 kg/m². A total of 27.1% of the participants presented a history of fracture, and 19.8% presented a history of fall in the year preceding the fracture; 13.3% of the participants presented osteoporosis, and 53.2% presented osteopenia at DXA evaluation. The most common sites of fracture are listed in Table 2. As showed in the Supplementary Table (25), treated subjects had more CRFs and a higher fracture risk at baseline.

Table 1.

Baseline characteristics of all subjects, divided into 2 groups according to the occurrence of a fragility fracture during a 5-years follow-up period

Characteristics	All/total n (%)	Any fracture	No fracture	Coefficient	HR (95% CI)	P-value
Age, years	70.1 ± 6.4/3560	72.2 ± 6.65	69.8 ± 6.3	0.05	1.05 (1.04-1.06)	<0.0001
Age, 68-75 years	1233/3560 (34.6)	151 (36.83)	1082 (34.3)	0.29	1.33 (1.09-1.64)	0.01
Age, >75 years	923/3560 (25.9)	151 (36.83)	772 (24.5)	0.72	2.06 (1.67-2.55)	<0.0001
BMI (kg/m2)	25.9 ± 4.8/ 3560	25.6 ± 4.7	26 ± 4.8	-0.02	0.98 (0.97-0.99)	0.04
BMI (<20 kg/m2)	342/3560 (9.6)	47 (11.5)	295 (9.4)	0.20	1.22 (0.97-1.54)	0.10
History of fracture	958/3533 (27.1)	167 (40.9)	791 (25.3)	0.61	1.84 (1.59-2.14)	<0.0001
History of fall	702/3531 (19.9)	105 (25.8)	597 (19.1)	0.36	1.44 (1.21-1.70)	<0.0001
Corticosteroids use	273/3537 (7.7)	41 (10.1)	232 (7.4)	0.24	1.28 (0.99-1.64)	0.06
Parental hip fracture	462/3451(13.4)	56 (14.1)	406 (13.3)	0.12	1.12 (0.91-1.38)	0.28
Comorbiditiesa	424/3560 (11.9)	60 (14.6)	364 (11.6)	0.22	1.24 (1.01-1.53)	0.04
Sedentary lifestyle	198/3537 (5.6)	38 (9.3)	160 (5.1)	0.23	1.26 (0.95-1.68)	0.12
Sleep disturbances	1833/3500 (52.4)	216 (53.6)	1617 (52.1)	0.13	1.14 (0.97-1.32)	0.08
Rheumatoid arthritis	38/3560 (1.1)	8 (2)	30 (1)	0.45	1.57 (0.87-2.82)	0.14
Education level (<9 years)	1280/3537 (36.2)	154 (37.8)	1126 (35.9)	-0.03	0.98 (0.84-1.13)	0.74
Excessive alcohol intake (≥3 units)	274/3535 (7.8)	37 (9.1)	237 (7.6)	0.05	1.05 (0.80-1.38)	0.71
Smoking	400/3537 (11.3)	53 (13)	347 (11.1)	0.17	1.18 (0.95-1.47)	0.13
Early non-substituted menopause	201/3549 (5.7)	25 (6.1)	176 (5.6)	0.14	1.16 (0.86-1.55)	0.34
Osteoporosis	475/3498 (13.6)	95 (23.2)	380 (12.1)	1.10	2.99 (2.39-3.74)	<0.0001
Osteopenia	1895/3498 (54.2)	224 (54.6)	1671 (53.1)	0.53	1.69 (1.40-2.04)	<0.0001

Values are given as mean ± SD or n (%).

Abbreviations: BMI, body mass index; HR, hazard ratio.

^aComorbidities are described in the Methods section.

Table 2.

Fractures distribution (only the first fracture was considered)

Fracture site	All fractures (n = 410)	MOFs (n = 304)	Central fractures (n = 277)
Hip	37 (9.0)	41 (13.5)	41 (14.8)
Shoulder	52 (12.7)	52 (17.1)	52 (18.8)
Clinical spine	43 (10.5)	115 (37.8)	115 (41.5)
Distal forearm	90 (22.0)	96 (31.6)	—
Pelvis	24 (5.8)	—	24 (8.7)
Rib	31 (7.6)	—	32 (11.6)
Scapula	5 (1.2)	—	5 (1.8)
Clavicle	6 (1.5)	—	7 (2.5)
Sternum	1 (0.2)	—	1 (0.3)
Other sites	121 (29.5)	—	—

Fracture sites are given as n (%) within each category. n varies because only the first fracture site is considered within each category.

For each model, significant CRFs were determined by univariate analyses (CIF), and a multivariable analysis was performed by the Fine and Gray method to derive the 3 models described in the following discussion. As treatment did not interact significantly with fracture risk in multivariable analysis, treated subjects were not excluded from the final analysis.

Major Osteoporotic Fractures

Older subjects, those with a history of fracture, a history of fall, presence of comorbidities, or osteoporosis at DXA had a higher cumulative incidence of MOFs. Obesity and early nonsubstituted menopause were also associated with a higher cumulative incidence of MOFs (Table 3). Differences between both groups (with and without fracture) were not significant for the other evaluated CRFs (ie, low BMI, history of corticosteroid use, parental hip fracture, sedentary lifestyle, sleep disturbances, rheumatoid arthritis, lower education level, excessive alcohol intake, and smoking).

Table 3.

Cumulative incidence function analysis of major osteoporotic fractures for each clinical risk factor

	Fracture events: 304 MOF fractures/competing events: 122 deaths
MOF fractures CRF	Event, n (%)	5-year CIF, %	P-value	n total
Age group			<0.0001	3560
≤67 years	62 (20.4)	4.9
68-75 years	103 (33.9)	8.1
≥76 years	139 (45.7)	15.1
Obesity			0.01	3560
Yes	45 (14.8)	6.8
No	259 (85.2)	9
History of fracture			<0.0001	3533
Yes	137 (45.1)	14.1
No	167 (54.9)	6.6
History of falls			0.03	3531
Yes	83 (27.7)	12.1
No	217 (72.3)	7.7
Comorbidities			0.001	3560
Yes	48 (15.8)	11.6
No	256 (84.2)	8.3
Early nonsubstituted menopause			0.01	3549
Yes	20 (6.6)	10.6
No	283 (93.4)	8.5
BMD status			<0.0001	3498
Osteoporosis	86 (29.4)	18.5
Osteopenia	165 (56.3)	8.8
Normal	42 (14.3)	3.8
T-score hip			<0.0001	3457
≤−2.5	29 (10)	28.6
>−2.5 TS	261 (90)	7.9
T-score femoral neck			<0.0001	3457
≤−2.5	47 (16.2)	22.17
>−2.5	243 (83.8)	7.6
T-score spine			<0.0001	3452
≤−2.5	51 (17.6)	16.2
>−2.5	239 (82.4)	7.7

Abbreviations: BMD, bone mineral density; CRF, clinical risk factor; MOF, major osteoporotic fractures.

For this model, the Fine and Gray multivariable analysis retained as independent factors for fracture prediction: age (sHR per year 1.05, 95% CI 1.04-1.06, P < 0.0001), total hip BMD (sHR 1.32, 95% CI 1.20-1.45, P < 0.0001), a history of fracture (sHR 1.56, 95% CI 1.30-1.85, P < 0.001), spine BMD (sHR 1.10, 95% CI 1.03-1.19, P = 0.01), excessive alcohol intake (sHR 1.39, 95% CI 1.01-1.90, P = 0.04), and presence of comorbidities (sHR 1.27, 95% CI 1.00-1.60, P = 0.04) (Table 4).

Table 4.

The Fine and Gray proportional subdistribution hazard model for major osteoporotic fractures

CRF	Coefficient	sHR (95% CI)	P value
History of fracture	0.45	1.56 (1.30-1.85)	<0.0001
Total hip BMD (by 0.1 g/cm2)	0.28	1.32 (1.20-1.45)	<0.0001
Age	0.05	1.05 (1.04-1.06)	<0.0001
Spine BMD (by 0.1 g/cm2)	0.10	1.10 (1.03-1.19)	0.01
Excessive alcohol intake (≥3 units/day)	0.32	1.39 (1.01-1.90)	0.04
Comorbidities	0.24	1.27 (1.00-1.60)	0.05

Abbreviations: BMD, bone mineral density; CRF, clinical risk factor; sHR, subdistribution hazard ratio.

The obtained ICC, when comparing our MOFs prediction model with FRAX for MOFs prediction and Garvan for all fractures prediction, was equal to 0.817 (95% CI 0.805-0.829) and 0.687 (95% CI 0.666-0.707), respectively.

All Fractures

The 5-year cumulative incidence for all fractures was significantly higher in subjects older than 85, in those presenting a history of fracture, a history of fall, comorbidities, or osteoporosis at DXA (Table 5). Differences between both groups (with and without fracture) were not significant for the other evaluated CRFs (ie, low BMI, obesity, corticosteroid use, history of parental hip fracture, sedentary lifestyle, sleep disturbances, rheumatoid arthritis, education level, excessive alcohol intake, smoking, early nonsubstituted menopause).

Table 5.

Cumulative incidence function analysis of all fractures for each clinical risk factor

	Fracture events: 410 all fractures/competing events: 121 deaths
All fractures CRF	Event, n (%)	5-year CIF, %	P-value	Total n
Age			<0.0001	3560
≤67 years	108 (26.3)	8.2
68-75 years	151 (36.8)	12.2
≥76 years	151 (36.8)	16.9
History of fracture			<0.0001	3533
Yes	172 (42.1)	17.7
No	237 (58)	9.3
History of falls			<0.0001	3531
Yes	105 (25.8)	15.2
No	302 (74.2)	10.8
Comorbidities			0.04	3560
Yes	60 (14.6)	14.5
No	350 (85.4)	11.3
BMD status			<0.0001	3498
Osteoporosis	95 (23.9)	20.4
Osteopenia	224 (56.4)	11.9
Normal	78 (19.7)	7
T-score total hip			<0.0001	3457
≤−2.5	29 (7.4)	28.5
>−2.5	363 (92.6)	10.9
T-score femoral neck			<0.0001	3457
≤−2.5	53 (13.5)	24.9
>−2.5	339 (86.5)	10.5
T-score spine			<0.0001	3452
≤−2.5	57 (14.6)	18.1
>−2.5	334 (85.4)	10.8		3560

Abbreviations: BMD, bone mineral density; CIF, cumulative incidence function; CRF, clinical risk factor.

Using the Fine and Gray competing risk regression model, we obtained subdistribution adjusted hazard ratios (sHR) that reflect the impact of each characteristic on the rate of fracture in subjects who are either fracture free or who have experienced a competing event (death or loss to follow-up) (21). In multivariable analysis, differences remained significant for age (sHR per year 1.03, 95% CI 1.02-1.04, P < 0.0001), total hip BMD (sHR 1.36, 95% CI 1.28-1.46, P < 0.0001), history of fracture (sHR 1.50, 95% CI 1.28-1.75, P < 0.0001) and history of fall (sHR 1.32, 95% CI 1.12-1.57, P = 0.001). Coefficients used to build the nomograms are presented in Table 6.

Table 6.

The Fine and Gray proportional sub-distribution hazard model for all fractures

CRF	Coefficient	sHR (95% CI)	P-value
History of fracture	0.40	1.50 (1.28-1.75)	<0.0001
Total hip BMD (by 0.1 g/cm2)	0.31	1.36 (1.28-1.46)	<0.0001
Age	0.03	1.03 (1.02-1.04)	<0.0001
History of fall	0.28	1.32 (1.12-1.57)	0.001

Abbreviations: BMD, bone mineral density; CRF, clinical risk factor; sHR, subdistribution hazard ratio.

Central Fractures

Similar to the all-fractures model, the 5-year cumulative incidence for central fractures was significantly higher in subjects older than 85, with a history of fractures, a history of fall, comorbidities, or osteoporosis on DXA. Additional significant CRFs were a low BMI, obesity, a history of corticosteroid use, presence of rheumatoid arthritis, sleep disturbances, lower educational level, and history of early nonsubstituted menopause (Table 7). Differences between both groups (with and without fracture) were not significant for the other evaluated CRFs (ie, parental hip fracture history, sedentary lifestyle, excessive alcohol intake, or smoking).

Table 7.

Cumulative incidence function analysis of central fractures for each clinical risk factor

	Fracture events: 277 central fractures/Competing events: 124 deaths
Central fractures CRF	Event, n (%)	5-year CIF, %	P-value	n total
Age			<0.0001	3560
≤67 years	56 (20.2)	4.5
68-75 years	98 (35.4)	7.6
≥76 years	123 (44.4)	13.4
Low BMI			0.01	3560
Yes	39 (14.1)	11.8
No	238 (85.9)	7.5
Obesity			0.02	3560
Yes	39 (14.1)	5.9
No	238 (85.9)	8.3
History of fracture			<0.0001	3533
Yes	122 (44.)	12.6
No	155 (56)	6.1
History of falls			0.01	3531
Yes	72 (26.3)	10.5
No	202 (73.7)	7.2
Corticosteroid use			0.02	3537
Yes	31 (11.2)	11.8
No	246 (88.8)	7.6
Comorbidities			<0.0001	3560
Yes	47 (17)	11.4
No	230 (83)	7.4
Sleep disturbances			0.05	3500
Yes	154 (56.4)	8.5
No	119 (43.6)	7.2
Rheumatoid arthritis			0.001	3560
Yes	9 (3.3)	23.7
No	268 (96.8)	7.7
Education level			0.01	3537
<9 years	122 (44)	9.7
≥9 years	155 (56)	6.9
Early nonsubstituted menopause			0.02	3549
Yes	18 (6.6)	9.6
No	258 (93.5)	7.8
BMD status			<0.0001	3498
Osteoporosis	82 (30.8)	17.6
Osteopenia	142 (53.4)	7.6
Normal	42 (15.8)	3.8
T-score hip			<0.001	3457
≤−2.5	27 (10.3)	26.6
>−2.5	236 (89.7)	7.1
T-score femoral neck			<0.0001	3457
≤−2.5	43 (16.4)	20.3
>−2.5	220 (83.7)	6.9
T-score spine			<0.0001	3452
≤−2.5	52 (19.8)	16.6
>−2.5	211 (80.2)	6.8

Abbreviations: BMD, bone mineral density; CIF, cumulative incidence function; CRF, clinical risk factor.

The following predictive factors for central fractures were significant in a multivariable analysis: age (sHR per year 1.06, 95% CI 1.04-1.07, P < 0.001), total hip BMD (sHR 1.39, 95% CI 1.25-1.53, P < 0.0001), history of fracture (sHR 1.47, 95% CI 1.22-1.77, P  < 0.001), spine BMD (sHR 1.08, 95% CI 1.004-1.66, P = 0.04), and presence of rheumatoid arthritis (sHR 2.42, 95% CI 1.33-4.39, P = 0.004) (Table 8).

Table 8.

The Fine and Gray proportional subdistribution hazard model for central fractures

CRF	Coefficient	sHR (95% CI)	P-value
History of fracture	0.38	1.47 (1.22-1.77)	<0.0001
Total hip BMD (by 0.1 g/cm2)	0.33	1.39 (1.25-1.53)	<0.0001
Age	0.06	1.06 (1.04-1.07)	<0.0001
Rheumatoid arthritis	0.88	2.42 (1.33-4.39)	0.004
Spine BMD (0.1 g/cm2)	0.08	1.08 (1.004-1.66)	0.04

Abbreviations: BMD, bone mineral density; CRF, clinical risk factor; sHR, subdistribution hazard ratio.

There were no multicollinearity problems in the analyses, as indicated by a maximum VIF (cutoff < 4) of 1.77 for predicting the MOFs, 1.09 for predicting all fractures, and 1.76 for predicting the central fractures and by a tolerance above the fixed cutoff > 0.2, at 0.6 for MOFs, 0.9 for all fractures, and at 0.6 for central fractures.

Construction and Validation of Competing Risk Nomograms

Using these data, we constructed nomograms to predict the 5-year cumulative probability of MOFs, all fractures and central fractures (Fig. 1).

Figure 1.

Competing risk nomogram predicting 5-year cumulative probabilities for major osteoporotic fractures (MOFs) (A), all fractures (B), and central fractures (C).

For a particular subject, each significant variable has a corresponding score according to the top scale, and by adding up all scores, we get a total score according to the bottom scale (total points axis). By drawing a vertical line down to the 5-years risk line, we can obtain the individual 5-years probability of fracture (Fig. 1).

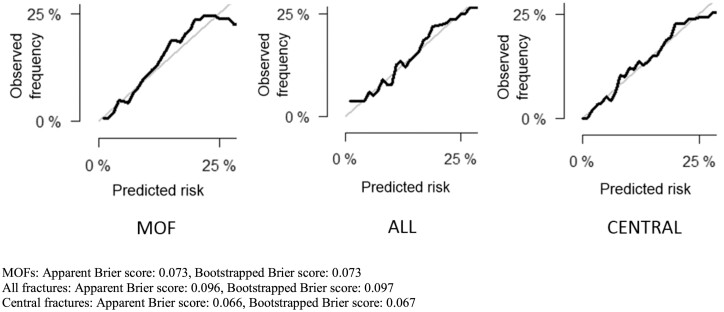
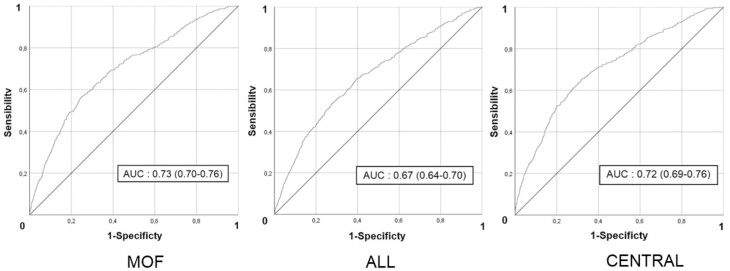
For MOFs, the apparent Brier score was 0.073, and the bootstrapped Brier score was 0.073 (Fig. 2). The AUROC of the nomogram for MOFs prediction was 0.73 (95% CI 0.70-0.76) (Fig. 3). For all fractures, the AUROC was 0.67 (95% CI 0.64-0.70) (Fig. 3). The apparent Brier score was 0.096, and the bootstrapped Brier score was 0.097 (Fig. 2). For central fractures, the apparent Brier score was 0.066, and the bootstrapped score was 0.067 (Fig. 2). The AUROC of the nomogram for central fractures prediction was 0.72 (95% CI 0.69-0.76) (Fig. 3).

Figure 2.

Calibration curves for 5-year prediction for major osteoporotic fractures (MOFs), all fractures, and central fractures. The diagonal light grey line indicates reference line on which ideal nomogram would lie (perfect prediction). Solid lines indicate current nomogram performances.

Figure 3.

Receiver operating characteristic curves for major osteoporotic fractures (MOFs), all fractures, and central fractures. MOFs: apparent Brier score: 0.073, bootstrapped Brier score: 0.073. All fractures: apparent Brier score: 0.096, bootstrapped Brier score: 0.097. Central fractures: apparent Brier score: 0.066, bootstrapped Brier score: 0.067.

As treated patients were included in their derivation, we tested the discrimination and calibration of our models for treated and untreated patients separately. We did not find any significant discrimination or calibration bias for the treated patients in the 3 models, although there was a trend for a slightly weaker prediction in treated subjects. Results are presented in Supplementary Figure 1 (26) (calibration curves of the 5-year prediction models for MOFs, all fractures, and central fractures and for treated participants) and Supplementary Figure 2 (27) (ROC curves for MOFs, all fractures, and central fractures for treated and untreated participants.)

Discussion

The calculation of an individualized absolute fracture risk to identify patients requiring a pharmacological treatment for osteoporosis is recommended in most guidelines (28). According to Kanis et al, the accuracy of risk prediction for hip fractures and MOFs is higher if CRFs are taken into account besides BMD (10). Models including validated CRFs have thus been developed for fracture risk prediction. However, the most adequately studied tools, FRAX and Garvan fracture risk calculator, showed significant differences in the predicted risk of fracture (12-14).

These differences result from the fact that these models use different profiles of risk factors while each specific factor has a different weight to calculate the risk gradient (15).

Despite the scientific basis of FRAX and its strengths, several limitations are recognized. Various procedures have been proposed to overcome different limitations (29), but the most widely used FRAX tool in clinical practice remains the conventional one without adjustments, which make its implementation in standard practice more complicated and time-consuming.

A major limitation of the Garvan fracture risk calculator is that the competing mortality risk is not taken into account, resulting in an overestimation of fracture risk for individuals whose life expectancy is less than 5 or 10 years. The FRAX model takes into account the competing risk of death (30), but the adjustment for the mortality risk in FRAX is based on mortality rates for the population, which may affect the accuracy of the estimates. Berry et al compared the results of traditional survival analysis (Kaplan-Meier or Cox proportional hazards regression) with a competing risk approach to estimate the risk of a second hip fracture and concluded indeed that in older populations (median age at first fracture was 81 years and ranged from 45 to 99 years) survival analysis overestimated the 5-year risk of second hip fracture by 37% and the 10-year risk by 75% when compared with competing risk estimates (31). Our previous studies of existing prediction models applied to patients included in the FRISBEE cohort (14, 32) showed important calibration problems in part linked, for MOFs, to the discordance between MOFs/hip incident ratios and those used for the Belgium FRAX construction (32).

In this work, we developed new models of fracture risk prediction using CRFs included in the FRAX or Garvan models and some additional validated risk factors. Our statistical approach was based on the subdistribution regression method developed by Fine and Gray, which takes into consideration the competing risk of mortality. Three models were developed to estimate the fracture risk according to fracture site: MOFs prediction (similar to FRAX), all fractures prediction (similar to Garvan fracture risk calculator), and central fractures prediction. A model for hip fractures could not be constructed because of the limited number of events.

Only 3 CRFs used in the FRAX were retained in multivariable Fine and Grey analysis for MOFs prediction: age, a history of fracture, and excessive alcohol intake. Unlike FRAX, total hip BMD and spine BMD, but not femoral neck BMD, were independent predictors of MOFs. Comorbidities also appeared as an independent predictor.

Our nomogram for all fractures prediction retained the same CRFs as Garvan fracture risk calculator (age, total hip BMD, history of fracture, history of fall). It is not surprising that falls are retained in the all-fractures models, since a large amount of these fractures affect peripheral bones, explaining also the absence of spine BMD as an independent predictor.

The third model is a nomogram for central fracture prediction. The relatively recent concept of central fractures (33, 34) is justified by a higher morbidity and mortality after a rib or pelvis fracture (included in central fractures), compared with wrist fracture, which is part of MOFs (35-38). The incidence of these particular central fractures (rib, pelvis fractures) in our cohort was high, being the fifth and sixth in order of frequency, respectively, after the 4 classical MOFs. We have shown previously that a central fracture was more predictive for a subsequent fracture than a MOF (39). Our nomogram for central fracture prediction was based on 5 CRFs (age, total hip BMD, history of fracture, spine BMD, rheumatoid arthritis ). These CRFs are the same than for MOFs except for the absence of alcohol and comorbidities and the inclusion of rheumatoid arthritis, which is known to be a strong independent risk factor for vertebral fractures.

Eventually, it is notable that the 3 CRFs common to the 3 models—namely, age, total hip BMD, and a history of fragility fracture—are also those which are the most powerful and universally recognized risk factors for osteoporotic fractures.

Our nomograms were internally validated by the bootstrap method, showing a good discrimination, with AUROC similar to existing models (FRAX and Garvan) of 0.73 for MOFs and 0.72 for central fractures, which is considered clinically acceptable (15). In terms of internal calibration, the calibration curves performed well with Brier scores ≤ 0.1 (40).

Based on the 95% CI of the ICC estimate, the concordance analysis between our MOFs prediction model and FRAX (for MOFs prediction) or Garvan (for all fracture prediction) was indicative of good reliability and moderate reliability, respectively.

A major strength of the present study is the reliability of our database, as the self-reported fractures were well documented in the participants medical files, allowing to exclude false-positive self-reports and to add fractures that were not self-reported (17, 18). Another strength is the simplicity of the nomograms, with a small number of CRFs easy to obtain from a patient in the clinical setting (41).

A weakness of the study, also present in the current FRAX model, is the lack of quantification of some risk factors (falls, corticosteroid doses, number of fractures, fracture recency) (39, 41). The models should also be validated in other populations.

Another weakness of this study could be the fact that treated patients were included. To be noted, 9.5% of patients from the Dubbo cohort used to construct the Garvan fracture risk calculator were also under antiosteoporotic treatment (42), and Leslie et al (43) showed that osteoporosis treatment did not significantly change the accuracy of the risk of MOF prediction by the FRAX model.

In our study, the calibration of our models for treated and untreated patients showed no significant calibration bias for the treated patients. Excluding treated patients would have reduced the power of the study. Fracture prediction tools are used to identify individuals who need a pharmacological treatment. By including in the statistical analysis treated participants, our models may help clinicians to further evaluate fracture risk in individuals who are already treated and guide treatment changes or withdrawal.

The use of both BMDs, spine and total hip, could also be interpreted as a limitation of present study, but as the VIF and tolerance tests showed, there was no multicollinearity problem.

In conclusion, using a competing risk approach, we propose 3 simple nomograms that integrate most important CRFs, specific for different fracture sites, with a reasonable prediction accuracy, particularly for MOFs and central fractures. Our model for central fractures prediction is the first one to be proposed. All 3 models should contribute to a better and individualized approach to predict fracture risk. These nomograms should still be externally validated. They could then be placed onto a website to benefit of a more user-friendly interface.

Financial Support

This research was partly supported by IRIS-Recherche and CHU Brugmann (Brussels, Belgium).

Author Contributions

The authors confirm that all of the authors participated in the preparation of the manuscript.

Disclosures

The authors declare no known conflicts of interest associated with this publication that could be perceived as prejudicing the impartiality of the research reported.

Data Availability

Some or all data sets generated during and/or analyzed during the current study are not publicly available but are available from the corresponding author on reasonable request.