Abstract
This review article attempts to evaluate the accuracy of intraocular lens power calculation formulae in short eyes. A thorough literature search of PubMed, Embase, Cochrane Library, Science Direct, Scopus, and Web of Science databases was conducted for articles published over the past 21 years, up to July 2021. The mean absolute error was compared by using weighted mean difference, whereas odds ratio was used for comparing the percentage of eyes with prediction error within ±0.50 diopter (D) and ±1.0 D of target refraction. Statistical heterogeneity among studies was analyzed by using Chi-square test and I2 test. Fifteen studies including 2,395 eyes and 11 formulae (Barrett Universal II, Full Monte method, Haigis, Hill-RBF, Hoffer Q, Holladay 1, Holladay 2, Olsen, Super formula, SRK/T, and T2) were included. Although the mean absolute error (MAE) of Barrett Universal II was found to be the lowest, there was no statistically significant difference in any of the comparisons. The median absolute error (MedAE) of Barrett Universal II was the lowest (0.260). Holladay 1 and Hill-RBF had the highest percentage of eyes within ±0.50 D and ±1.0 D of target refraction, respectively. Yet their comparison with the rest of the formulae did not yield statistically significant results. Thus, to conclude, in the present meta-analysis, although lowest MAE and MedAE were found for Barrett Universal II and the highest percentage of eyes within ±0.50 D and ±1.0 D of target refraction was found for Holladay 1 and Hill-RBF, respectively, none of the formulae was found to be statistically superior over the other in eyes with short axial length.
Keywords: Cataract, intraocular lens, mean absolute error, median absolute error, power calculation formulae, short eyes
Cataract surgery remains one of the most commonly performed ophthalmological procedures worldwide owing to the aging population and increasing life expectancy.[1,2] Even in a meticulously performed surgery, the actual visual outcome can match the expected visual outcome by accurate biometry.
The advent of optical biometry circumvented the operator-induced bias encountered in ultrasound biometry. Soon partial coherence interferometry (PCI) became the gold standard optical biometer owing to its precision in measurements along with ease of use in clinical settings.[3] Optical low coherence reflectometry (OLCR) and swept-source optical coherence tomography biometers were its successors, which although maintained the same precision of measurements, provided additive information on several parameters such as lens thickness, central corneal thickness, anterior chamber depth (ACD), horizontal white-to-white diameter, and corneal radii.[4] The incorporation of these parameters into the intraocular lens (IOL) power calculation formulae gave a better prediction of the effective lens position.
However, among the wide range of available formulae, none is completely accurate in all scenarios. Modern formulae show comparable refractive outcomes in eyes with normal axial length (AL).[5] But when we deal specifically with short eyes (AL <22 mm), they gave variable results. Hence, the deliberation for choosing the most accurate formula, so as to obtain an optimal postoperative visual outcome in the subgroup of short eyes continues. In 2018, a meta-analysis on short eyes had already been carried out by Wang et al.[6] With set down of protocols for conducting a study on IOL power accuracy, it was recommended to compare median absolute error (MedAE) rather than mean absolute error (MAE) and also includes the percentage of eyes with prediction error (PE) within ±0.25, ±0.50, and ±1.0 diopter (D) of target refraction.[7,8] Hence, the present meta-analysis was carried out taking into account these recommendations.
Methods
We carried out this meta-analysis according to the Preferred Reporting Items for Systematic Reviews and Meta-Analyses statement.[9] Ethics committee approval was not required as our review relied entirely on publicly available data that are already published. Nonetheless, the study methods adhered to the tenets of the Declaration of Helsinki.
Search methods
Two authors independently searched PubMed, Embase, Cochrane Library, Science Direct, Scopus, and Web of Science databases for research articles published over the past 21 years, up to July 2021. Search terms used for PubMed were short eyes* OR short axial length* AND Phacoemulsification AND Calculat* OR Formula* AND IOL. The title and abstract of the retrieved literature were then screened. The selected articles were further filtered by reading the full text and assessed for eligibility. Articles cited in the reference list of these eligible articles were also screened manually.
Inclusion and exclusion criteria
The studies included in the meta-analysis met the following inclusion criteria: (1) population: (a) patients older than 18 years of age, (b) eyes with AL less than 22 mm; (2) intervention: (a) biometry done by optical method, (b) eyes that underwent uneventful phacoemulsification surgery; (3) comparison: at least two of the following IOL power calculation formulae used – Barrett Universal II, Haigis, Hill-RBF, Hoffer Q, Holladay 1, Holladay 2, and SRK/T; (4) outcome: studies that reported at least one of the three outcome measures – MAE, MedAE, or percentage of eyes with PE within ±0.50 and ±1.0 D of target refraction; (5) study design: Prospective and retrospective.
The exclusion criteria were as follows: (1) history of corneal refractive surgery; (2) any ocular pathology affecting refraction; (3) toric, multifocal, piggyback IOL, or IOLs not implanted in the bag; (4) older generation formulae such as Binkhorst II, SRK I, or SRK II used; (5) review articles, studies under trial, editorials, conference abstracts, previous meta-analysis, discussion papers, full text not available in English, or animal studies.
Data extraction
Two authors extracted data regarding study design, methodology, participant demographics, and baseline characteristics from all included studies independently and matched their results. Any discrepancy found was resolved by discussion and confirmation with the third author. If standard deviation (SD) data could not be extracted from full-text articles or even after contacting the authors, we used the mean SD of the remaining studies.
Quality assessment
The study quality was assessed by using a modified checklist adapted from the Quality Assessment of Diagnostic Accuracy Studies–2 (QUADAS-2) tool.[10] The evaluation of bias was divided into four domains: patient selection, index test, reference standard, and last, flow and timing of patients. Applicability concerns were assessed using three domains: patient selection, index test, and reference standard. Each domain could have a high risk, low risk, or unclear risk of bias.
Statistical analysis
Data were analyzed for MAE, MedAE, and percentage of eyes with PE within ±0.50 and ±1.0 D of target refraction. We analyzed the relative effect size of continuous outcomes like MAE using weighted mean difference (WMD) with 95% confidence interval (CI). The relative effect size of the percentage of eyes with PE within ±0.50 and ±1.0 D of target refraction, which was a binary outcome, was calculated as odds ratio (OR) with a 95% CI. Statistical methods utilized were inverse variance for continuous data and Mantel–Haenszel for dichotomous data. A P value less than 0.05 was considered statistically significant in both. Statistical heterogeneity among studies was analyzed by using Chi-square test and I2 test. When the I2 value was more than 50% and P value was less than 0.1, random-effect model was used for analysis; otherwise a fixed-effect model was used. Sensitivity analysis was conducted to identify sources of significant heterogeneity. Te funnel plot was used to assess publication bias. Only descriptive analysis was performed for MedAE as it is not suitable for meta-analysis. Statistical analysis was carried out using Review Manager software (RevMan, Version 5.4).[11]
Results
Literature selection results
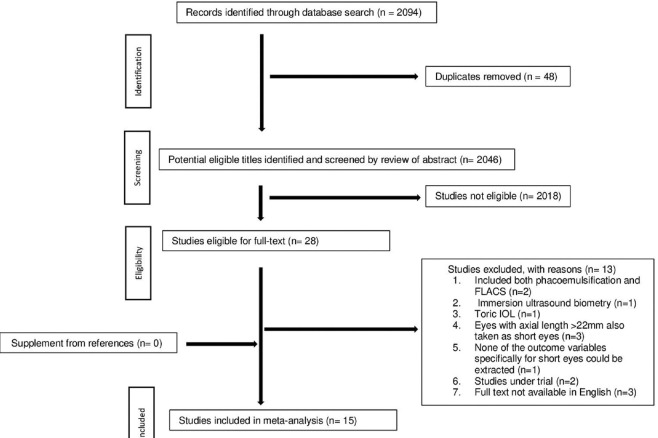
The detailed process of literature search and study selection is depicted in Fig. 1. Initially, 2,094 studies were identified through a database search. After the removal of 48 duplicate studies, 2,046 eligible titles were identified and screened by review of the abstract. Of these, 28 full-text articles were retrieved. After excluding 13 studies based on predefined inclusion criteria, 15 studies were included in this meta-analysis.
Figure 1.
Flow chart of article selection. Abbreviations: FLACS = Femtosecond laser-assisted cataract surgery; IOL=Intraocular lens
Study characteristics
The characteristics of eligible studies are summarized in Table 1. A total of 2,395 eyes with AL in the range of 18.77 to 21.99 mm were included in the analysis. The sample size ranged from 15 to 608 eyes. Formulae included were Barrett Universal II, Haigis, Hill-RBF, Hoffer Q, Holladay 1, Holladay 2, and SRK/T. A few studies also used newer generation formulae such as the Full Monte method, Kane, Ladas Super formula, Olsen, and T2.
Table 1.
Characteristics of study participants
| Study | Year | Country | Study design | Number of eyes | Age (years±SD) | Axial length, mm±SD (Range) | Method of calculating RPE | Lens Constant Used |
|---|---|---|---|---|---|---|---|---|
| Aristodemou et al.[15] | 2011 | United Kingdom | Retrospective | 608 | NA | 21.57 (20.00-21.99) | Postop SE-PR | Optimized constants |
| Cooke and Cooke[23] | 2016 | USA | Retrospective | 41 | NA | 21.69 (20.84-22.00) | Postop SE-PR | Optimized constants |
| Darcy et al.[25] | 2020 | UK | Retrospective | 766 | NA | ≤ 22 | Postop SE-PR | Optimized constants For Haigis a0- optimized, a1, a2- ULIB |
| Day et al.[17] | 2012 | UK | Retrospective | 163 | 57±10 | 21.2±0.60 (19.23-21.98) | Postop SE-PR | Optimized constants |
| Eom et al.[18] | 2014 | South Korea | Retrospective cross-sectional | 75 | 70.1±6.8 | 21.69±0.29 (20.32-21.99) | Postop SE-PR | Optimized constants |
| Gavin and Hammond[16] | 2008 | UK | Retrospectively Prospective | 41 | NA | 21.51 (20.29-21.96) | PR-Postop SE | Manufacturer’s constants |
| Gökce et al.[19] | 2017 | USA | Retrospective case series | 86 | 72±8 | 21.53±0.56 (18.80-22.00) | Postop SE-PR | Optimized constants |
| Kane et al.[5] | 2016 | Australia | Retrospective case series | 156 | NA | ≤22 | Postop SE-PR | Optimized constants |
| Kane et al.[26] | 2017 | Australia | Retrospective case series | 137 | NA | ≤22 | Postop SE-PR | Optimized constants |
| Khatib et al.[21] | 2021 | India | Retrospective observational | 66 | NA | Postop SE-PR | Optimized constants | |
| Shrivastava et al.[20] | 2018 | India | Retrospective observational | 50 | 58.54±10.36 | 21.61±0.27 (20.76-21.96) | Postop SE-PR | Optimized constants |
| Srivannaboon et al.[22] | 2013 | Thailand | Prospective comparative | 15 | NA | 21.44 (18.77-21.94) | Postop SE-PR | ULIB constants |
| Terzi et al.[27] | 2009 | Germany | Retrospective | 19 | 53±7 | 21.24±0.55 (20.13-21.97) | PR-Postop SE | Optimized constants |
| Wang et al.[6] | 2013 | China | Retrospective | 33 | NA | 21.52±0.47 | Postop SE-PR | Optimized constants |
| Zhao et al.[13] | 2018 | China | Retrospective | 139 | NA | <21 | PR-Postop SE | ULIB constants |
|
| ||||||||
| Study | Version of biometer | Method of K measurement | Follow-up | Refraction | IOL implanted | Formulae used | ||
|
| ||||||||
| Aristodemou et al.[15] | NA | IOLMaster | 1 month | Subjective | Sofport IOL and Akreos Fit IOL | Hoffer Q, Holladay 1, SRK/T | ||
| Cooke and Cooke[23] | Lenstar LS 900 (Version 3.02) and IOLMaster (Version 5.4) | Optical biometer (both OLCR and PCI) | 3 weeks to 3 months | Subjective | AcrysofSN60WF | Barrett Universal II, Haigis, Hoffer Q, Holladay 1, Holladay 2No Ref, Holladay 2Pre surg Ref, Olsenstandalone, OlsenOLCR SRK-T, Super Formula, T2 | ||
| Darcy et al. | IOLMaster (Carl Zeiss, Meditec, AG) | IOLMaster | NA | Subjective | SA60AT, Superflex Aspheric920 H, C-Flex Aspheric970C, AkreosAdaptAO | Barrett Universal II, Haigis, Hill-RBF, Hoffer Q, Holladay1, Holladay 2, Kane, Olsen, SRK/T | ||
| Day et al.[17] | IOLMaster (Carl Zeiss, Meditec, Inc, Dublin, CA, USA) | IOLMaster | 2-17.7 weeks | Autorefraction (Topcon KR8000 series autorefractor) Topcon, Rotterdam, The Netherlands | Akreos AO, Akreos Adapt, Corneal ACR6D, OculentisLentis L302-1 | Haigis, Hoffer Q, Holladay1, SRK/T | ||
| Eom et al.[18] | IOLMaster (Version 5.02) | IOLMaster | 3-10 weeks | Autorefractor/Keratometer (RK-F1; Canon, Tokyo, Japan) | Alcon Acrysof IQ | Haigis, Hoffer Q | ||
| Gavin and Hammond[16] | IOLMaster (Zeiss-Humphrey systems) | IOLMaster | 2-3 weeks | Autorefractometer (Canon AR-2, Canon, Tokyo) | AllerganMA60 | Hoffer Q, SRK/T | ||
| Gökce et al.[19] | Lenstar LS900 (Version V 4.1.1, Haag Streit AG) | Lenstar | >3 weeks | Subjective | Alcon Acrysof SN60WF, SN6AT, SA60AT, Tecnis, ZCBOO, ZCT | Barrett Universal II, Haigis, Hill-RBF, Hoffer Q, Holladay 1, Holladay 2, and Olsen | ||
| Kane et al.[5] | IOLMaster (Version 5.4, Carl Zeiss, Meditec, AG) | IOLMaster | 2 weeks | Subjective | AcrysofIQSN60WF | Barrett Universal II, Haigis, Hoffer Q, Holladay1, Holladay 2, SRK/T, T2 | ||
| Kane et al. | IOLMaster (Version 5.4, Carl Zeiss, Meditec, AG) | IOLMaster | 2 weeks | Subjective | Acrysof IQ SN60WF | Barrett Universal II, Full Monte method, Hill- RBF, Holladay 1, Ladas Super formula | ||
| Khatib et al.[21] | Lenstar LS 900 | Lenstar | 2 weeks | Subjective | Acrysof IQ SN60WF, Tecnis ZCB00 | Barrett Universal II, EVO, Hill-RBF | ||
| Shrivastava et al.[20] | IOLMaster 500 (Version 5.4, Carl Zeiss, Meditec, AG) | IOLMaster | 1 month | Autorefractometer (Accuref K-900/R-800, Rexxam Co. Ltd.) | Acrysof SN6CWS | Barrett Universal II, Haigis, Hill- RBF, Hoffer Q, Holladay 2, SRK/T | ||
| Srivannaboon et al.[22] | IOLMaster (Carl Zeiss, Meditec, Jena, Germany) | IOLMaster | 3 months | Subjective | Hoya PY60AD | Haigis, Hoffer Q, Holladay 2 with LT, Holladay 2 without LT | ||
| Terzi et al. | IOLMaster (Carl Zeiss, Meditec, AG) | AL by PCI, Keratometry not clear | 1 month | Subjective | Acrysof SA60AT, Sensar AR40e | Haigis, Hoffer Q, Holladay 2, SRK/T | ||
| Wang et al.[6] | IOLMaster (Carl Zeiss, Jena, Germany) | IOLMaster | 3 months | Autorefractometer (Topcon AR, Tokyo, Japan) | Acrysof SA60AT | Haigis, Hoffer Q, Holladay 1, SRK/T | ||
| Zhao et al.[13] | Zeiss IOLMaster (Version 4.02) | AL- IOLMaster, Manual keratometry | 1-3 months | Subjective | AA4203 | Haigis, Hoffer Q, Holladay 1, Holladay 2, SRK/T | ||
Postop SE=postoperative spherical equivalent; PR=predicted refraction; ULIB=User Group for Laser Interference Biometry; AL=axial length; OLCR=optical low-coherence reflectometry; PCI=partial coherence interferometry
Quality of included studies
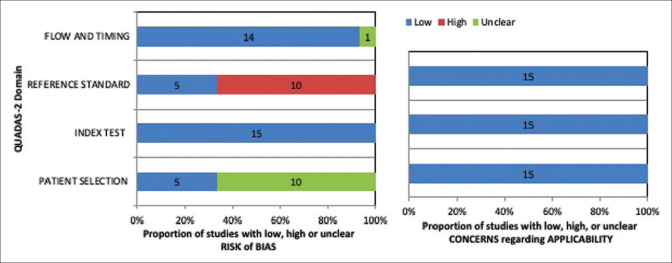
A modified checklist adapted from QUADAS-2 tool was employed to assess the study quality [Fig. 2]. Detailed assessment questionnaire and its results are provided [Additional File 1]. Ten of the 15 studies did not report whether the patient selection was consecutive or random and hence had an unclear risk of bias. On analyzing the reference standard used, 10 studies had a high risk of bias due to the use of subjective refraction for calculating postoperative spherical equivalent (SE). Most of the studies were of high quality as far as index tests, the inclusion of patients, the flow of patients, and applicability were concerned.
Figure 2.
Quality assessment of the included studies based on modified QUADAS-2 tool. Abbreviations: QUADAS-2 = Quality Assessment of Diagnostic Accuracy Studies-2
Outcomes
The outcome variables included in our analysis were MAE, MedAE, and the percentage of eyes with PE within ±0.50 and ±1.0 D of target refraction. This meta-analysis included 2,395 eyes, of which 1,302 eyes were analyzed for Barrett Universal II, 1,543 eyes for Haigis, 1,105 eyes for Hill-RBF, 2,192 eyes for Hoffer Q, 2,129 eyes for Holladay 1, 1,272 eyes for Holladay 2, and 2,016 eyes for SRK/T formulae.
Mean absolute error
The MAE and standard error of all the formulae included in the analysis showed the lowest value for Barrett Universal II [Fig. 3 (I)]. It performed equally well as Haigis, Hoffer Q, and SRK/T with WMD and 95% CI of −0.00 (−0.04, 0.03) for the three pairs [Fig. 3IIA, B, and C]. The WMD and 95% CI of Barrett Universal II with Hill-RBF, Holladay 1, and Holladay 2 were 0.02 (−0.01, 0.06); 0.02 (−0.01, 0.06), and 0.03 (−0.01, 0.06), respectively [Fig. 3II D, E, and F]. Although the MAE of Barrett Universal II was found to be the lowest, there was no statistically significant difference in any of the comparisons.
Figure 3.
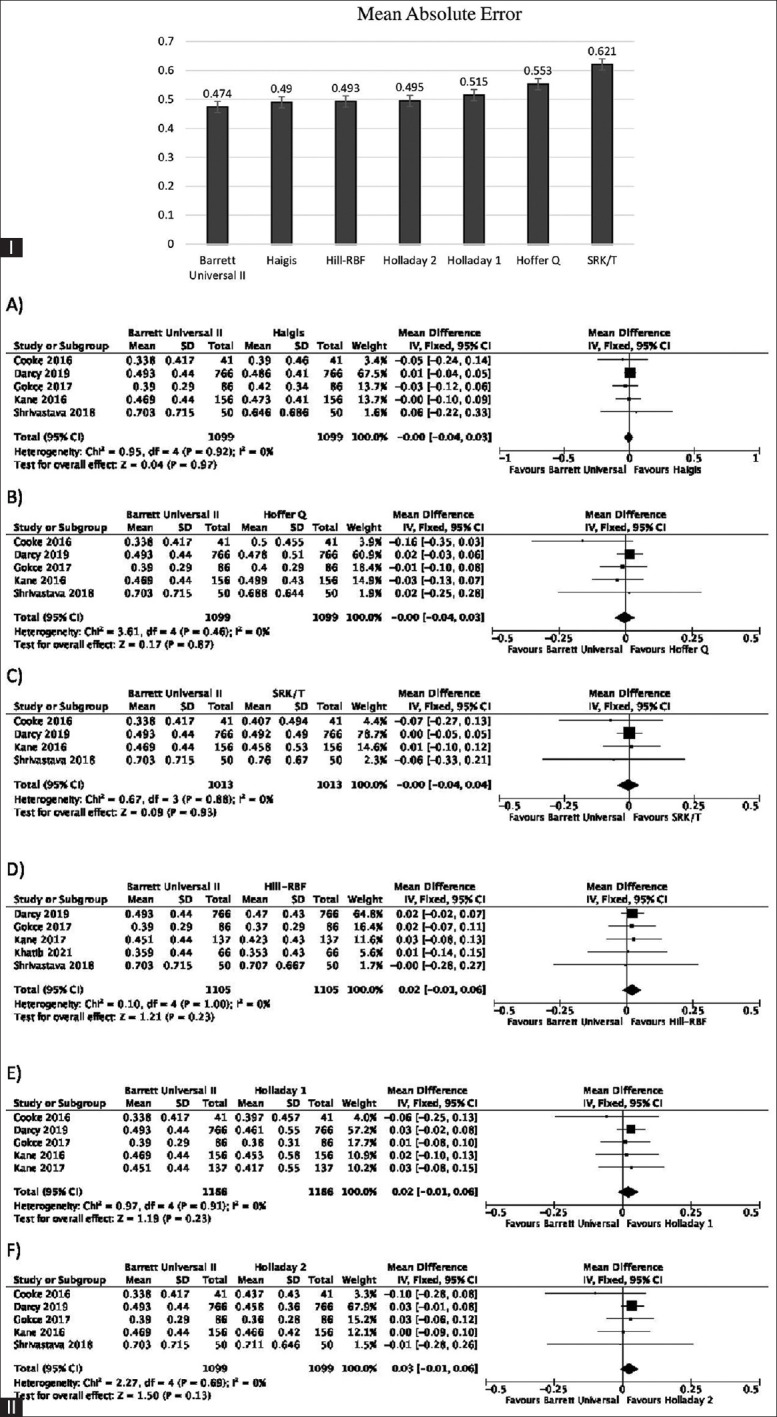
(I) The overall MAE and standard error of all formulae included in analysis. (II) Forest plots showing comparison of MAE between Barrett Universal II and Haigis (A), Hoffer Q (B), SRK/T (C), Hill-RBF (D), Holladay 1 (E), and Holladay 2 (F). Abbreviations: MAE = Mean absolute error; D = Diopter; PE = Prediction error
Median absolute error
Table 2 shows the descriptive analysis of MedAE of all the formulae included in the analysis. Nine of the 15 studies have reported this parameter. The MedAE of Barrett Universal II was the lowest (0.260) followed by Hill-RBF (0.300), Holladay 1 (0.302), Haigis (0.308), Holladay 2 (0.320), SRK/T (0.327), and Hoffer Q (0.340).
Table 2.
Descriptive analysis of median absolute error of all the formulae included in the analysis
| Formula | Number of studies | Range |
|---|---|---|
| Barrett Universal II | 7 | 0.260-0.540 |
| Full Monte | 1 | 0.462 |
| Haigis | 11 | 0.308-0.570 |
| Hill-RBF | 5 | 0.300-0.520 |
| Hoffer Q | 13 | 0.340-0.580 |
| Holladay 1 | 9 | 0.302-0.630 |
| Holladay 2 | 8 | 0.320-0.560 |
| Olsen | 3 | 0.325-0.350 |
| Super formula | 2 | 0.320-0.370 |
| SRK/T | 10 | 0.327-0.690 |
| T2 | 2 | 0.341-0.415 |
Percentage of eyes with prediction error within ±0.50 D of target refraction
Fig. 4(I) shows the percentage of eyes with PE within ±0.50 D of target refraction of all the formulae included in the analysis. Holladay 1 had the highest percentage of eyes. On analyzing the forest plots, OR and 95% CI of Holladay 1 as compared with Barrett Universal II, Haigis, Hill-RBF, Hoffer Q, Holladay 2, and SRK/T formulae were 0.91 (0.68,1.21), P value = 0.51, 0.95 (0.73, 1.25), P value = 0.73, 0.94 (0.63, 1.40), P value = 0.76, 0.85 (0.72, 1.02), P value = 0.08, 1.10 (0.77, 1.57), P value = 0.59, and 1.19 (0.99, 1.43), P value = 0.07, respectively, as shown in Fig. 4(II). None of the comparisons showed statistically significant results [Additional file 3 (4.4MB, tif) ].
Figure 4.
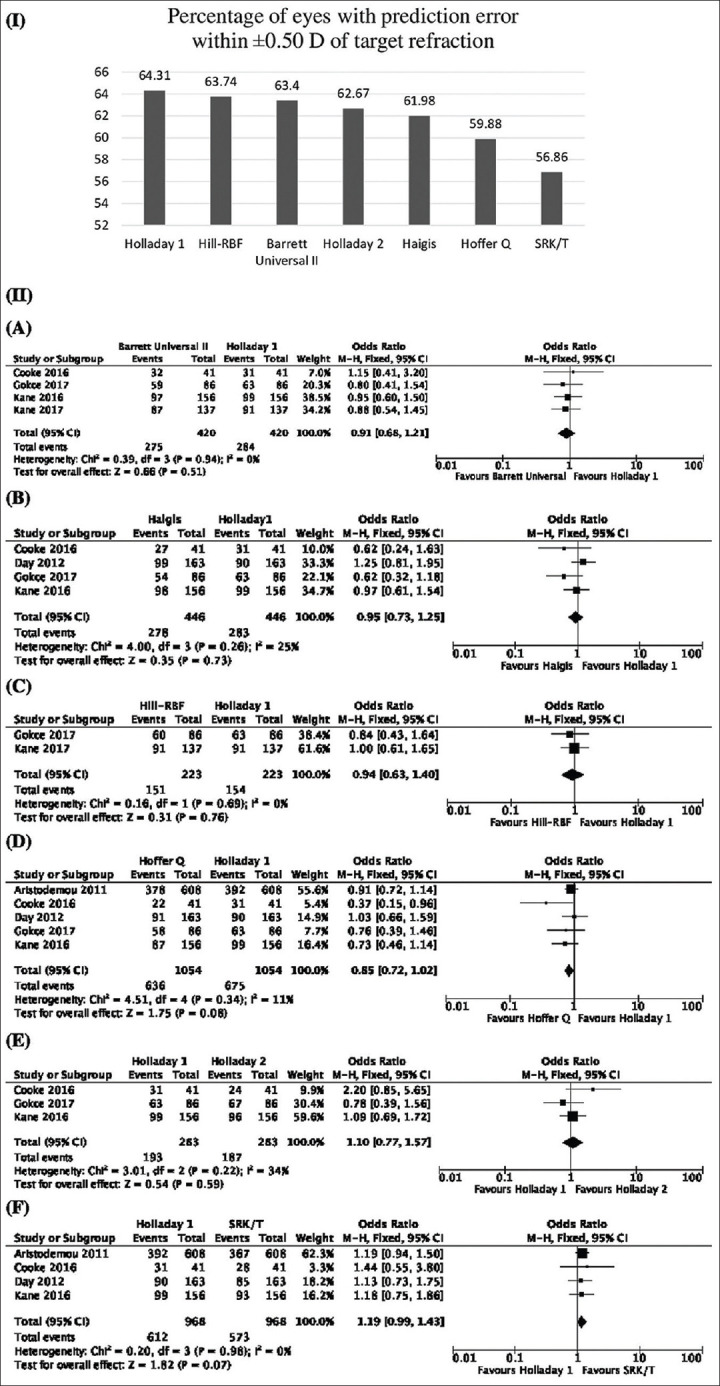
(I) Percentage of eyes with prediction error within ±0.50 D of target refraction of all the formulae included in the analysis. (II) Forest plots showing comparison between Holladay 1 and Barrett Universal II (A), Haigis (B), Hill-RBF (C), Hoffer Q (D), Holladay 2 (E), and SRK/T (F). Abbreviations: D = Diopter; PE = Prediction error
Percentage of eyes with prediction error within ±1.0 D of target refraction
Hill-RBF had the highest value when the percentage of eyes with PE within ±1.0 D of target refraction was considered [Additional file 4 (6.8MB, tif) (I)]. On analyzing the forest plots none of the comparisons yielded statistically significant results [Additional file 4 (6.8MB, tif) (II)].
There was only one study that reported the percentage of eyes with PE within ±0.50 and ±1.0 D for comparison between Hill-RBF and SRK/T formulae, and hence forest plots were not made according to the Cochrane Collaboration guidelines.[12]
Heterogeneity and I2
Additional file 2 (4.7MB, tif) (B, C, D, and E) shows both substantial as well as statistical heterogeneity on comparison of MAE of Haigis with Hoffer Q, Holladay 1, Holladay 2, and SRK/T. A random-effect model was chosen in these cases. On doing a sensitivity analysis [Additional file 5 (1.7MB, tif) ], it was observed that I2 reduced to 0% in all the four comparisons by omitting the study by Zhao et al.[13] The result was more in favor of Holladay 2, although not statistically significant when the above-mentioned study was excluded from the comparison between Haigis and Holladay 2. However, the results were not altered in the rest of the comparisons.
Publication bias
The funnel plot drawn for comparison between Haigis and Hoffer Q, which included 11 studies, showed that the study by Zhao et al.[13] was outside the funnel [Additional file 6 (399.5KB, tif) ].
Discussion
MAE had long been reported as a parameter for comparing formula accuracy. As suggested by Hoffer et al.,[7] absolute error does not follow normal Gaussian distribution; so reporting and comparing MedAE gives a better idea about formula accuracy. MedAE, by negating the effect of outliers, had an added advantage. The reporting percentage of eyes within ±0.50 and ±1.0 D of target refraction is also recommended as this parameter is most closely related to patient satisfaction after surgery. With this background present, meta-analysis was carried out by comparing all the recommended parameters, that is, MAE, MedAE, and percentage of eyes with PE within ±0.50 and ±1.0 D of target refraction, to find the best-performing formula in short AL eyes.
Studies conducted in various parts of the world have advocated different formulae for eyes with short AL. Hoffer Q, a preferred formula for short eyes, has been reported as the most accurate in the study done by Hoffer[14]; although the study included only 10 short eyes and used ultrasound biometry. Also a study by Aristodemou et al.[15] considered it to give the best refractive outcome in eyes shorter than 21.00 mm; while between 21.00 and 21.49 mm, it was found to be equally good as Holladay 1. It is worthwhile to mention here that MAE was the only parameter compared in this study. Gavin and Hammond[16] considered Hoffer Q as an accurate formula in short eyes, but the comparison was done only against SRK/T. In a study by Day et al.,[17] although Hoffer Q had the lowest MAE on using manufacturer’s constants; all formulae performed equally well after lens constant optimization.
Contrary to this, Haigis has been described as the most accurate formula in short eyes by some authors. Zhao et al.[13] found optimized Haigis formula more accurate than other formulae in eyes with AL less than 21 mm. A study done by Eom et al.[18] found it to be more accurate as compared with Hoffer Q when ACD was less than 2.4 mm. The meta-analysis carried out by Wang et al.[6] has also recommended Haigis as the formula of choice for short eyes. But a general consensus regarding the formula of choice in short eyes is still missing.
In the present analysis, although Barrett Universal II had the lowest MAE and MedAE, the results were not statistically significant when compared with the rest of the formulae. Holladay 1 and Hill-RBF had the highest percentage of eyes within ±0.50 and ±1.0 D of target refraction, respectively. Yet their comparison with the rest of the formulae also did not yield statistically significant results. Our results were in concordance with that of Kane et al.[5] who found no statistical difference between the formulae analyzed, thus making it difficult to choose any one IOL power calculation formula over the other, in eyes with short AL. The study results of Gökce et al.,[19] Shrivastava et al.,[20] and Khatib et al.[21] were in agreement with this.
Over a period of years, there have been continuous developments in the field of IOL power calculation. It is an established fact now that optimization of lens constant has to be mandatorily done for conducting any study on IOL calculation accuracy. In this analysis, Gavin and Hammond[16] used the manufacturer’s constant and found Hoffer Q better, whereas Srivannaboon et al.[22] and Zhao et al.[13] used User Group for Laser Interference Biometry constants. The results of Srivannaboon et al.[22] showed no statistically significant difference between the formulae, whereas Zhao et al.[13] found Haigis formula to be more appropriate. It is interesting to note that in studies using optimized constants, none of the formulae was found to be statistically superior over the other. Second, the method of calculating refractive prediction error (RPE) also influences the results. Although most studies have calculated RPE as postoperative SE minus predicted refraction (PR), there are also a few, which have taken PR minus postoperative SE as RPE. Hence, this fact has to be considered before statistical analysis and comparing formula accuracy. Third, the difference in version and make of the optical biometers also affects the study results. This fact has been clearly established in the study by Cooke and Cooke[23] who showed that, in the subgroup of short eyes, Barrett Universal II achieved the best results when PCI measurements were used, whereas Olsen outperformed other formulae on using OLCR values. The strength of the current meta-analysis is that we have contemplated on all the above-mentioned facts and hence put forth a complete picture by analyzing the recommended parameters of formula accuracy, that is, MAE, MedAE, and percentage of eyes with prediction errors within ±0.50 and ±1.0 D of target refraction rather than only MAE as done by Wang et al.[6]
As an effort to minimize heterogeneity and reduce bias, our meta-analysis excluded studies where optical biometry was not used. The random-effect model was used in cases with substantial as well as statistical heterogeneity. Sensitivity analysis showed that I2 reduced to 0% in all the four pairs of comparison (Haigis with Hoffer Q, Holladay 1, Holladay 2, and SRK/T) by omitting the study of Zhao et al.[13] On analyzing, we found that in a study by Zhao et al.,[13] although AL measurement was done by IOLMaster; keratometry was done manually. The subgroup analysis of the keratometry method showed that the difference is statistically significant (P = 0.03), which was accounted for the source of heterogeneity. It is also a well-known fact that racial differences can affect the accuracy of IOL calculations.[24] The studies included in this meta-analysis are from various regions of the world, thus making our results more generalized rather than pertaining to a particular subcontinent.
Conclusion
Thus, to conclude, in the present meta-analysis, although lowest MAE and MedAE were found for Barrett Universal II and highest percentage of eyes within ±0.50 D and ±1.0 D of target refraction was found for Holladay 1 and Hill-RBF, respectively, none of the formulae was found to be statistically superior over the other in eyes with short AL.
Availability of data and materials
All data analyzed in this study are included in the article and its additional files.
Financial support and sponsorship
Nil.
Conflicts of interest
There are no conflicts of interest.
Additional file 1
Modified check-list adapted from the QUADAS-2 tool
Assessment of risk of bias
Domain 1: Patient selection
Question 1: Was a consecutive or random sample of patients enrolled?
• ‘yes’ low risk of bias
• ‘unclear’ unclear risk of bias
• ‘no’ high risk of bias.
Question 2: Did the study avoid inappropriate exclusions?
• ‘no’ for < 10% of patients or ‘yes’ low risk of bias
• ‘unclear’ unclear risk of bias
• ‘no’ for 10% of patients high risk of bias.
Domain 2: Index test
Were the index test result read without knowing the result of the reference standard?
• ‘yes’ low risk of bias
• ‘unclear’ unclear risk of bias
• ’no’ high risk of bias
Domain 3: Reference standard
Could the calculation of refractive prediction error have introduced bias?
• Objective Refraction low risk of bias
• ‘unclear’ unclear risk of bias
• Subjective refraction high risk of bias
Domain 4: Flow and timing
Question 1: Did all patients receive the same reference standard?
• ‘no’ but for < 10% of patients or ‘yes’ low risk of bias
• ‘unclear’ unclear risk of bias
• ‘no’ for 10% of patients high risk of bias.
Question 2: Was there an appropriate interval between the index test and reference standard?
• post-operative refraction done two weeks or later after surgery low risk of bias
• ‘unclear’ unclear risk of bias
• post-operative refraction done within two weeks of surgery high risk of bias.
Assessment of applicability concerns
Domain 1: Patient selection
Is there concern that included patients do not match review question?
• ‘no’ low risk of bias
• ‘unclear’ unclear risk of bias
• ‘yes’ high risk of bias
Domain 2: Index test
Is there concern that index test, its conduct or interpretation differ from review question?
• ‘no’ low risk of bias
• ‘unclear’ unclear risk of bias
• ‘yes’ high risk of bias.
Domain 3: Reference standard
Is there concern that target condition as defined by the reference standard does not match the review question?
• ‘no’ low risk of bias
• ‘unclear’ unclear risk of bias
• ‘yes’ high risk of bias.
Quality assessment of the included studies based on modified QUADAS- 2 tool
Quality assessment of the included studies based on modified QUADAS- 2 tool
| Study | Risk of bias | Applicability concerns | |||||
|---|---|---|---|---|---|---|---|
|
|
|
||||||
| Patient selection | Index test | Reference standard | Flow and timing | Patient selection | Index test | Reference standard | |
| Aristodemou 2011 | ☺ | ☺ | ☹ | ☺ | ☺ | ☺ | ☺ |
| Cooke 2016 | ☺ | ☺ | ☹ | ☺ | ☺ | ☺ | ☺ |
| Darcy 2020 | ☺ | ☺ | ☹ | ? | ? | ☺ | ☺ |
| Day 2012 | ☺ | ☺ | ☺ | ☺ | ☺ | ☺ | ☺ |
| Eom 2014 | ? | ☺ | ☺ | ☺ | ☺ | ☺ | ☺ |
| Gokce2017 | ? | ☺ | ☹ | ☺ | ☺ | ☺ | ☺ |
| Gavin 2008 | ? | ☺ | ☺ | ☺ | ☺ | ☺ | ☺ |
| Kane 2016 | ? | ☺ | ☹ | ☺ | ☺ | ☺ | ☺ |
| Kane 2017 | ? | ☺ | ☹ | ☺ | ☺ | ☺ | ☺ |
| Khatib 2021 | ? | ☺ | ☹ | ☺ | ☺ | ☺ | ☺ |
| Shrivastava 2018 | ? | ☺ | ☺ | ☺ | ☺ | ☺ | ☺ |
| Srivannaboon 2013 | ☺ | ☺ | ☹ | ☺ | ☺ | ☺ | ☺ |
| Terzi 2009 | ? | ☺ | ☹ | ☺ | ☺ | ☺ | ☺ |
| Wang 2013 | ? | ☺ | ☺ | ☺ | ☺ | ☺ | ☺ |
| Zhao 2018 | ? | ☺ | ☹ | ☺ | ☺ | ☺ | ☺ |
☺ Low Risk, ☹ High Risk, ? Unclear Risk
References
- 1. Busbee BG, Brown MM, Brown GC, Sharma S. Incremental cost-effectiveness of initial cataract surgery. Ophthalmology. 2002;109:606–12. doi: 10.1016/s0161-6420(01)00971-x. [DOI] [PubMed] [Google Scholar]
- 2. Lundstrom M, Wendel E. Duration of self-assessed benefit of cataract extraction:A long term study. Br J Ophthalmol. 2005;89:1017–20. doi: 10.1136/bjo.2005.065961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Kaswin G, Rousseau A, Mgarrech M, Barreau E, Labetoulle M. Biometry and intraocular lens power calculation results with a new optical biometry device:Comparison with the gold standard. J Cataract Refract Surg. 2014;40:593–600. doi: 10.1016/j.jcrs.2013.09.015. [DOI] [PubMed] [Google Scholar]
- 4. Kunert KS, Peter M, Blum M, Haigis W, Sekundo W, Schutze J, et al. Repeatability and agreement in optical biometry of a new swept-source optical coherence tomography–based biometer versus partial coherence interferometry and optical low-coherence reflectometry. J Cataract Refract Surg. 2016;42:76–83. doi: 10.1016/j.jcrs.2015.07.039. [DOI] [PubMed] [Google Scholar]
- 5. Kane JX, Van Heerden A, Atik A, Petsoglou C. Intraocular lens power formula accuracy:Comparison of 7 formulas. J Cataract Refract Surg. 2016;42:1490–500. doi: 10.1016/j.jcrs.2016.07.021. [DOI] [PubMed] [Google Scholar]
- 6. Wang Q, Jiang W, Lin T, Wu X, Lin H, Chen W. Meta-analysis of accuracy of intraocular lens power calculation formulas in short eyes. Clin Exp Ophthalmol. 2018;46:356–63. doi: 10.1111/ceo.13058. [DOI] [PubMed] [Google Scholar]
- 7. Hoffer KJ, Aramberri J, Haigis W, Olsen T, Savini G, Shammas HJ, et al. Protocols for studies of intraocular lens formula accuracy. Am J Ophthalmol. 2015;160:403–5. doi: 10.1016/j.ajo.2015.05.029. e1. [DOI] [PubMed] [Google Scholar]
- 8. Wang L, Koch DD, Hill W, Abulafia A. Pursuing perfection in intraocular lens calculations:III. Criteria for analyzing outcomes. J Cataract Refract Surg. 2017;43:999–1002. doi: 10.1016/j.jcrs.2017.08.003. [DOI] [PubMed] [Google Scholar]
- 9. Liberati A, Altman DG, Tetzlaff J, Mulrow C, Gøtzsche PC, Ioannidis JPA, et al. The PRISMA statement for reporting systematic reviews and meta-analyses of studies that evaluate healthcare interventions:Explanation and elaboration. BMJ. 2009;339:b2700. doi: 10.1136/bmj.b2700. doi:https://doi.org/10.1136/bmj.b2700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Whiting PF, Rutjes AWS, Westwood ME, Mallett S, Deeks JJ, Reitsma JB, et al. QUADAS-2:A revised tool for the quality assessment of diagnostic accuracy studies. Ann Intern Med. 2011;155:529–36. doi: 10.7326/0003-4819-155-8-201110180-00009. [DOI] [PubMed] [Google Scholar]
- 11. Review Manager (RevMan) [Computer program] Version 5.4, The Cochrane Collaboration. 2020 [Google Scholar]
- 12. Schu?nemann HJ, Oxman AD, Higgins JPT, Vist GE, Glasziou P, Guyatt GH. Chapter 11:Presenting results and 'Summary of findings'tables. Higgins JPT, Green S, editors. Cochrane Handbook for Systematic Reviews of Interventions Version 5.1.0 [updated March 2011]. The Cochrane Collaboration. 2011 [Google Scholar]
- 13. Zhao Y, Wang Z, Zhao S, Wang K, Zhu S. Which IOL formula should be used to determine the lens power estimation?A data analysis based on 3258 eyes. Int J Clin Exp Med. 2018;11:8646–50. [Google Scholar]
- 14. Hoffer KJ. Clinical results using the Holladay 2 intraocular lens power formula. J Cataract Refract Surg. 2000;26:1233–7. doi: 10.1016/s0886-3350(00)00376-x. [DOI] [PubMed] [Google Scholar]
- 15. Aristodemou P, Knox Cartwright NE, Sparrow JM, Johnston RL. Formula choice:Hoffer Q, Holladay 1, or SRK/T and refractive outcomes in 8108 eyes after cataract surgery with biometry by partial coherence interferometry. J Cataract Refract Surg. 2011;37:63–71. doi: 10.1016/j.jcrs.2010.07.032. [DOI] [PubMed] [Google Scholar]
- 16. Gavin EA, Hammond CJ. Intraocular lens power calculation in short eyes. Eye. 2008;22:935–8. doi: 10.1038/sj.eye.6702774. [DOI] [PubMed] [Google Scholar]
- 17. Day AC, Foster PJ, Stevens JD. Accuracy of intraocular lens power calculations in eyes with axial length<22.00 mm. Clin Exp Ophthalmol. 2012;40:855–62. doi: 10.1111/j.1442-9071.2012.02810.x. [DOI] [PubMed] [Google Scholar]
- 18. Eom Y, Kang SY, Song JS, Kim YY, Kim HM. Comparison of Hoffer Q and Haigis formulae for intraocular lens power calculation according to the anterior chamber depth in short eyes. Am J Ophthalmol. 2014;157:818–24. doi: 10.1016/j.ajo.2013.12.017. [DOI] [PubMed] [Google Scholar]
- 19. Gökce SE, Zeiter JH, Weikert MP, Koch DD, Hill W, Wang L. Intraocular lens power calculations in short eyes using 7 formulas. J Cataract Refract Surg. 2017;43:892–7. doi: 10.1016/j.jcrs.2017.07.004. [DOI] [PubMed] [Google Scholar]
- 20. Shrivastava AK, Behera P, Kumar B, Nanda S. Precision of intraocular lens power prediction in eyes shorter than 22 mm:An analysis of 6 formulas. J Cataract Refract Surg. 2018;44:1317–20. doi: 10.1016/j.jcrs.2018.07.023. [DOI] [PubMed] [Google Scholar]
- 21. Khatib ZI, Haldipurkar SS, Shetty V, Dahake H, Nagvekar P, Kashelkar P. Comparison of three newer generation freely available intraocular lens power calculation formulae across all axial lengths. Indian J Ophthalmol. 2021;69:580–4. doi: 10.4103/ijo.IJO_943_20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Srivannaboon S, Chirapapaisan C, Chirapapaisan N, Lertsuwanroj B, Chongchareon M. Accuracy of Holladay 2 formula using IOLMaster parameters in the absence of lens thickness value. Graefes Arch Clin Exp Ophthalmol. 2013;251:2563–7. doi: 10.1007/s00417-013-2439-8. [DOI] [PubMed] [Google Scholar]
- 23. Cooke DL, Cooke TL. Comparison of 9 intraocular lens power calculation formulas. J Cataract Refract Surg. 2016;42:1157–64. doi: 10.1016/j.jcrs.2016.06.029. [DOI] [PubMed] [Google Scholar]
- 24. Savini G, Negishi K, Hoffer KJ, Lomoriello DS. Refractive outcomes of intraocular lens power calculation using different corneal power measurements with a new optical biometer. J Cataract Refract Surg. 2018;44:701–8. doi: 10.1016/j.jcrs.2018.03.027. [DOI] [PubMed] [Google Scholar]
- 25. Darcy K, Gunn D, Tavassoli S, Sparrow J, Kane JX. Assessment of the accuracy of new and updated intraocular lens power calculation formulas in 10?930 eyes from the UK National Health Service. J Cataract Refract Surg. 2020;46:2–7. doi: 10.1016/j.jcrs.2019.08.014. [DOI] [PubMed] [Google Scholar]
- 26. Kane JX, Van Heerden A, Atik A, Petsoglou C. Accuracy of 3 new methods for intraocular lens power selection. J Cataract Refract Surg. 2017;43:333–9. doi: 10.1016/j.jcrs.2016.12.021. [DOI] [PubMed] [Google Scholar]
- 27. Terzi E, Wang L, Kohnen T. Accuracy of modern intraocular lens power calculation formulas in refractive lens exchange for high myopia and high hyperopia. J Cataract Refract Surg. 2009;35:1181–9. doi: 10.1016/j.jcrs.2009.02.026. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data analyzed in this study are included in the article and its additional files.