Abstract
In this study, we aim to reveal hidden patterns and confounders associated with policy implementation and adherence by investigating the home‐dwelling stages from a data‐driven perspective via Bayesian inference with weakly informative priors and by examining how home‐dwelling stages in the USA varied geographically, using fine‐grained, spatial‐explicit home‐dwelling time records from a multi‐scale perspective. At the U.S. national level, two changepoints are identified, with the former corresponding to March 22, 2020 (9 days after the White House declared the National Emergency on March 13) and the latter corresponding to May 17, 2020. Inspections at U.S. state and county level reveal notable spatial disparity in home‐dwelling stage‐related variables. A pilot study in the Atlanta Metropolitan area at the Census Tract level reveals that the self‐quarantine duration and increase in home‐dwelling time are strongly correlated with the median household income, echoing existing efforts that document the economic inequity exposed by the U.S. stay‐at‐home orders. To our best knowledge, our work marks a pioneering effort to explore multi‐scale home‐dwelling patterns in the USA from a purely data‐driven perspective and in a statistically robust manner.
1. INTRODUCTION
The outbreak of coronavirus disease in 2019 (COVID‐19) caused by SARS‐CoV‐2 has led to an unprecedented global crisis, posing a wide range of health, economic, and social challenges. As of May 6, 2021, 32,313,016 cases and 575,491 deaths had been reported in the USA, according to the Centers for Disease Control and Prevention (CDC) (CDC, 2021). While sustained transmission has continued globally, some countries have entered their second or third wave of the epidemic (Nouvellet et al., 2021; WHO, 2021).
In response to the COVID‐19 pandemic, various non‐pharmacological interventions were implemented to restrain population movement, including social distancing, stay‐at‐home orders, the closing of workplaces and schools, and internal/external travel controls. These interventions aim to reduce the physical contact with virus sources and decelerate the transmission rate. Experiences from a wide range of countries have proved that the reduction in mobility and increase in stay‐at‐home duration resulting from these policy interventions are largely responsible for the reduced transmission of SARS‐CoV‐2 (Badr et al., 2020; Chang et al., 2021; Gatto et al., 2020; Kraemer et al., 2020; Shim, Tariq, Choi, Lee, & Chowell, 2020). Despite the wide adaptation of social distancing measures, ensuring people refrain from unnecessary outdoor activities in rich and/or poor regions, in urban and/or rural areas, and in authoritarian and/or open societies, is the ultimate human challenge (Van Rooij et al., 2020). As expected, the disparities in policy compliance started to be noted at different geographic scales (Cartenì, Di Francesco, & Martino, 2020; Gao, Rao, Kang, Liang, & Kruse, 2020; Huang, Li, Jiang, Li, & Porter, 2020; Huang, Li, Lu, et al., 2020; Li et al., 2020), and many pieces of evidence have proved that geographical differences in transmission and death rates are linked to how strictly social restriction policies are implemented (Engle, Stromme, & Zhou, 2020; Hoeben, Bernasco, Suonperä Liebst, Van Baak, & Rosenkrantz Lindegaard, 2021).
In the USA, mitigation measures to limit outdoor activities and large gatherings have been implemented by federal and local governments, with different temporal coverage, effectiveness, and stringency (Chernozhukov, Kasahara, & Schrimpf, 2021; Raifman et al., 2020). Furthermore, the voluntary nature of these mitigation measures (Yan et al., 2021) exaggerated the discrepancies in policy compliance, as people with various political affiliations, socioeconomic statuses, and demographic backgrounds tend to respond to restrictions differently (Czeisler et al., 2020; Painter & Qiu, 2020). After the declaration of the National Emergency by the White House on March 13, 2020, California was the first state to implement a statewide stay‐at‐home order on March 16, 2020 (Moreland et al., 2020). In the following 8 days, more than 50% of the U.S. population were under stay‐at‐home orders, and this number grew to 95% by April 4, 2020 (Baek, McCrory, Messer, & Mui, 2020). Despite the implementation of intensive policies by the state and county officials in March and April 2020, a number of studies have revealed considerably disparate policy adherence at various geographical scales (Chang et al., 2021; Hu et al., 2021; Huang et al., 2021; Iio, Guo, Rees, & Wang, 2020; Lee et al., 2020; Pan et al., 2020). The second and third waves of the COVID‐19 infection in the USA also indicated that piled restrictions issued in March and April 2020 were not as effective as expected. Thus, it is necessary to revisit the compliance of social distancing policies and stay‐at‐home orders during the first wave of the COVID‐19 pandemic in the USA to provide better policy implications for potential resurges.
Since the outbreak of COVID‐19, commercial companies (e.g., Google, Apple, Baidu, SafeGraph, Cuebiq, and Descartes Labs) have released aggregated, anonymized mobility reports to assist the acquisition of human mobility information regarding how people actively lowered their exposure to COVID‐19 by reducing traveled distances or by increasing home‐dwelling time. One notable mobility dataset is SafeGraph's Social Distancing Metrics (detailed in Section 2), which provides human movement and home‐dwelling time records collected from roughly 10% of mobile devices in the USA (SafeGraph, 2019). Because of its high penetration ratio, SafeGraph becomes the preferred data source used by many COVID‐19‐related studies that require accurate, fine‐scale, representative mobility records (e.g., Banerjee, Nayak, & Zhao, 2021; Chang et al., 2021; Charoenwong, Kwan, & Pursiainen, 2020; Huang et al., 2022; Sun, Pan, Zhou, Xiong, & Zhang, 2020). Some recent works modeled the increase in home‐dwelling time using selected socioeconomic variables in the 12 largest U.S. city clusters by comparing situations before and under stay‐at‐home orders (e.g., Huang et al., 2022). However, the definition of stages (i.e., “before the stay‐at‐home order” and “under the stay‐at‐home order”) is often purely policy driven (i.e., policy implementation), neglecting the hidden patterns associated with different policy adherence levels. To our best knowledge, few efforts have been made to identify social distancing stages in the USA revealed from home‐dwelling time records from varying spatial scales and in a data‐driven and statistically robust manner.
To fill the gaps, this study aims to reveal how multi‐scale social distancing compliance in the USA varied geographically by determining stages in home‐dwelling time from a data‐driven perspective, using fine‐grained home‐dwelling time records from SafeGraph, and via a robust Bayesian inference approach. Specifically, the contributions of this work are summarized as follows:
We document the multi‐scale spatial disparity in social distancing compliance in the USA, revealed by the home‐dwelling time records collected from massive mobile devices.
We identify different social distancing stages by performing an automatic changepoint detection on U.S. home‐dwelling time records via Bayesian inference with weakly informative priors.
We investigate and reveal social distancing compliance in the USA from a multi‐scale perspective by exploring the spatial patterns of derived stage‐related variables.
We discuss policy compliance, spatial disparity of derived stage‐related variables, exposed inequity, and what policies can be suggested for the COVID‐19 pandemic and future epidemics.
2. HOME‐DWELLING TIME RECORDS
2.1. Data description
In this study, we collected home‐dwelling time records from SafeGraph (https://www.safegraph.com/), a commercial company that provides insights about physical places using aggregated anonymized location data derived from numerous cellphone applications. SafeGraph provides locational information using a panel of GPS points from 45 million anonymous mobile devices, accounting for about 10% of mobile devices in the USA. According to SafeGraph (2019), their sampling is highly representative given its high correlation (Pearson correlation coefficient of 0.97 at the U.S. county level) with the actual U.S. Census data in various demographic and socioeconomic dimensions. The home locations of device users are determined based on the common night‐time location of each mobile device over 6 weeks to Geohash‐7 granularity (~153 × ~153 m) (SafeGraph, 2020). Further, users’ home‐dwelling time is measured in minutes on a daily basis. To preserve users’ privacy, records are aggregated to the Census block group (CBG) level by calculating the median of daily home‐dwelling time for all available users within each CBG. Following Huang, Li, Lu, et al. (2020), the home‐dwelling time records retrieved in our study span January 1, 2020 to August 31, 2020, with a total of 244 days for 219,972 CBGs. To understand the dynamics of home‐dwelling time in the USA, we presented a heat map by plotting raw SafeGraph home‐dwelling time records from all CBGs in the USA (Figure 1), where high/low concentrations are marked as red/blue. The influence of social distancing policies (e.g., stay‐at‐home orders) on daily home‐dwelling time is obvious, evidenced by the considerable increase of home‐dwelling time following the U.S. National Emergency and the notable decrease in April 2020 when strict mitigation policies were gradually lifted. Figure 1 reveals a clear three‐stage pattern. Further, we derived prior distributions of parameters to be modeled, considering the characteristics of home‐dwelling time dynamics we observed from Figure 1 (details can be found in Section 3).
FIGURE 1.
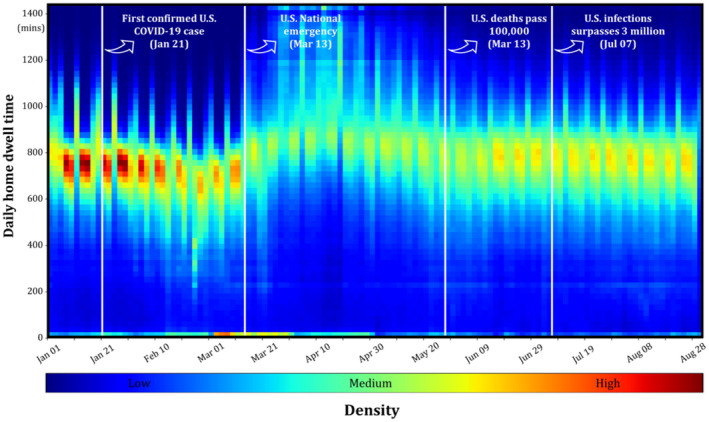
Heat map of raw SafeGraph home‐dwelling time records of 219,972 U.S. CBGs (modified from Huang, Li, Lu, et al., 2020). This heat map reveals the density of all available (day, home‐dwelling time) pairs within the investigated timeframe for all available CBGs in the USA. Important dates were retrieved from AJMC (https://www.ajmc.com/view/a‐timeline‐of‐covid19‐developments‐in‐2020)
2.2. Data aggregation
Despite the high representativeness of SafeGraph data, existing studies (e.g., Huang et al., 2022) have shown that the daily number of captured device users is insufficient for a certain amount of CBGs to form stable and credible time series as the foundation for the proposed Bayesian modeling. Efforts have been made to aggregate SafeGraph data to spatial units at higher geographical levels to mitigate this issue (Chiou & Tucker, 2020; Kang et al., 2020; Li et al., 2020). In our study, we aggregated the home‐dwelling time records at the CBG level to the U.S. Census Tracts, U.S. counties, U.S. states, and the USA as a whole, aiming to document the multi‐scale spatial disparity in social distancing compliance. For a spatial unit with a higher geographic level, we performed a weighting operation by averaging the CBG‐level home‐dwelling time weighted by the number of available devices within that spatial unit. For example, supposing a Census Tract contains two CBGs, CBG A (800 min from 600 devices) and CBG B (700 min from 400 devices), the home‐dwelling time for this Census Tract is 760 min . Such an aggregation approach is capable of providing reasonable estimations for coarser geographic scales by considering the heterogeneity of sample distributions.
3. METHODOLOGY
3.1. Bayesian inference concept
As a statistical inference method, Bayesian inference applies Bayes’ theorem (Bayes, 1958) to update the probability for a hypothesis when more evidence/information becomes available. The original Bayes’ theorem expresses the “posterior probability” (or conditional probability) of an event A after event B is observed in terms of the “prior probability” of A, the prior probability of B, and the posterior probability of B given A (Box & Tiao, 2011): . From a modeling perspective, we can replace B with observations and A with parameter set :
| (1) |
where denotes the set of prior distributions of parameter set before is observed (the priors). On certain occasions, is determined by , a group of hyperparameters [i.e., ]. denotes the posterior distribution of after taking into account the priors and . denotes the likelihood that suggests the distribution of conditional on .
3.2. Bayesian changepoint detection
Evolving from the basic Bayes’ theorem, Bayesian inference has been adopted to address changepoint detection tasks and has achieved great performance (Niculita, Skaf, & Jennions, 2014; Ray & Tsay, 2002; Tartakovsky & Moustakides, 2010), given its ability to objectively assess the uncertainties surrounding the changepoints, a significant advantage over a frequentist solution (Ruggieri, 2013). We assume that the observed stay‐at‐home records for a certain geographical region can be modeled by stationary Gaussian distributions parameterized by as mean and as standard deviation [i.e., , where changes given a series of changepoints ( in ]. In other words, we aim to fit a staging function to our observation . Supposing that a staging function with a total of states can well explain , parameter set contains mean values (i.e., {}), changepoints (i.e., ), and a :
| (2) |
We rewrite the model‐based Bayes’ theorem as below:
| (3) |
where denotes the distribution of observation . denotes a set of the prior distribution of all parameters to be estimated (the definitions of these priors are detailed in the next section). denotes the likelihood function that describes the probability of observing given our parameter set . denotes a set of the posterior distribution of all parameters after taking into account the priors and . We then formulate the likelihood function as:
| (4) |
Note that we assume can be modeled by a series of normal distributions, , , …. Thus, we can rewrite the likelihood function as:
| (5) |
3.3. Prior distribution assumption and model settings
The heat map of raw SafeGraph home‐dwelling time records (Figure 1) reveals a notable inverted “U‐shape” pattern, which suggests the potential existence of three stages along the timeline covered by the retrieved SafeGraph data. Supposing that we expect , a series of observed daily stay‐at‐home records at unit , to have two changepoints, respectively denoted as and , we model as follows:
| (6) |
where denotes the normal assumption that is parametrized by its mean and standard deviation .
Bayesian analyses require prior distributions, either uninformative, weakly informative, or informative ones, over unknown parameters. Prior distributions, indicating our prior knowledge of parameters to be modeled, affect the posterior distributions. In this study, we decided to implement weakly informative priors to facilitate models reaching reasonable posterior distributions without being excessively subjective. After the interpretation of Figure 1, we derived these parametric forms of the prior distributions for the model components:
| (7) |
where and , respectively, denote the continuous uniform and discrete uniform distributions that are bounded by the lower and upper limits. and are bounded by limits that represent the day count from January 1, 2020. , , , , and are characterized by parameters that represent home‐dwelling time in minutes.
Following Equation (5), we formulate the log‐likelihood function for the proposed Bayesian model:
| (8) |
where is piecewise on two changepoints to be modeled (i.e., and ):
| (9) |
3.4. Sampling mechanism
To perform posterior sampling, we used the Markov chain Monte Carlo (MCMC) sampling approach to enable samples to be obtained from successive states of a discrete‐time Markov chain (Geyer, 2011), which is designed to simulate samples that have a distribution arbitrarily close to the posterior distribution (Wang & Park, 2020). Two MCMC‐based algorithms were used: (1) Metropolis–Hastings (MH); and (2) No‐U‐Turn Sampler (NUTS). MH, a popular method for sampling discrete parameters, conducts controlled random walks over the parametric space to derive a sequence of random samples from a probability distribution where direct sampling is difficult (Martino & Elvira, 2014). Based on the gradient of the log posterior density, NUTS uses a recursive algorithm to build a set of likely candidate points that span a wide swath of the target distribution, achieving faster convergence than traditional sampling methods (Hoffman & Gelman, 2014). In this study, we conducted sampling using NUTS for variables with continuous prior assumptions, which includes , , , and . For parameters with discrete prior assumptions (i.e., and ), we adopted the MH sampling approach, given its non‐gradient sampling mechanism. Samples were obtained with 5,000 posterior draws.
3.5. Extra conditions
In this study, we hypothesize that home‐dwelling time records can be captured by the proposed three‐stage model (as observed in Figure 1). However, we acknowledge that not all geographic units feature such a pattern, especially for small geographic units like the Census Tracts, where a low number of mobile devices potentially leads to a certain level of randomness. In light of this issue, we included three additional conditions:
| (10) |
where denotes a cumulative normal distribution function. denotes the posterior distribution of the difference between and . denotes the posterior distribution of the difference between and . Similarly, denotes the posterior distribution of the difference between and . The observed three‐stage pattern stands if the conditions of , , and are all statistically true (with significant p values at ). The rationale of introducing the condition of a 10‐day gap between the two changepoints is that we aim to exclude time series with an unstable second stage detected by the proposed Bayesian model, presumably due to noise in the time series or biases in the sampling procedure. In this study, we set the significance as 0.05.
4. RESULTS
4.1. U.S. national level
Figure 2 presents the raw daily home‐dwelling time records with detected stage‐related variables for the U.S. national level. Two changepoints (i.e., and ) were identified, with the former corresponding to March 22, 2020 and the latter corresponding to May 17, 2020. The first changepoint () in home‐dwelling time appeared 9 days after the White House declared the National Emergency on March 13. After , home‐dwelling time in the USA maintained a high level (i.e., between and ), which lasted for a total of 56 days. The USA experienced a notable drop in home‐dwelling time starting from May 17 () when stay‐at‐home orders had been lifted (Moreland et al., 2020). The two identified changepoints separate the time series into three notable stages—Stage 1, Stage 2, and Stage 3—with distinctively different mean values of that stage (i.e., , , and ; see Figure 2). with a mean of 838.2 min is considerably higher than both with a mean of 638.7 min and with a mean of 673.7 min, revealing the generally strong and positive response to the COVID‐19 pandemic in the USA. Compared with , is 199.5 min higher, indicating that people in the USA spent around 3 hr 20 min more in Stage 2 than Stage 1. The sudden drop in home‐dwelling time after can be explained by the gradually loosened control measures from the “Opening Up America Again” guidelines (White House, 2020). Although is still higher than , their small difference reveals that society has largely returned to normal from a perspective of daily home‐dwelling duration.
FIGURE 2.
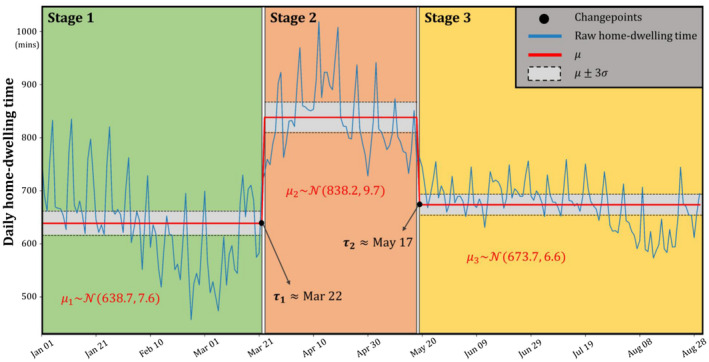
Daily home‐dwelling time records and detected stage‐related variables using the proposed Bayesian model for the U.S. national level
Figure 3 presents the posterior distribution (based on 5,000 posterior draws) of the parameters in the proposed Bayesian for home‐dwelling records in the USA as a whole. These parameters include stage means (i.e., , , and ; Figures 3a–c), changepoints (i.e., and ; Figures 3d and e), and standard deviation () (Figure 3f) in the general model setting of Equation (6). The results indicate that we provided reasonable priors to the proposed Bayesian model. Posteriors of , , still follow a normal distribution but with shifted means after considering the priors from our assumption and the home‐dwelling time records (i.e., the evidence). For changepoints, most posterior draws (the mode) of fall on March 22, which is the same as the median in its distribution. In comparison, the mode of (May 19) is different from its median (May 18). In this study, we chose the median values respectively from the posterior distribution of and as their optimal settings, following the rule of thumb of the optimal value selection from discrete distributions.
FIGURE 3.
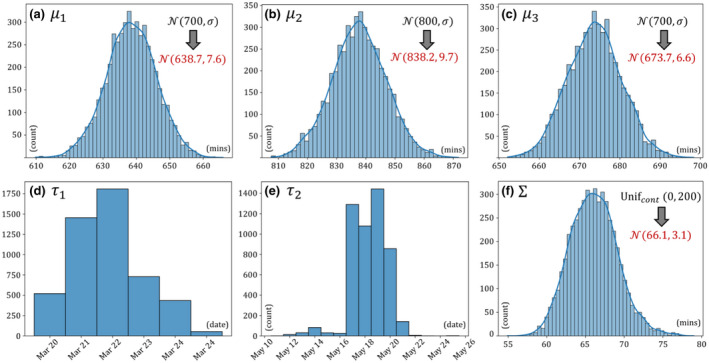
Posterior distribution of changepoints ( and ), stage mean values (, , and ), and standard deviation () in the general model setting [Equation (6)] for home‐dwelling records at the U.S. national level
4.2. U.S. state level
We applied the proposed Bayesian model to home‐dwelling time records for each U.S. state. Figure 4 presents the state‐level daily home‐dwelling time, derived stages, and stage‐related variables that include , , , , and . A summary of these variables can be found in Table B1 in Appendix B. The spatial distribution of stage‐related variables, together with , is presented in Figure A1 in Appendix A. The posterior distribution based on 5,000 posterior draws of , , , , and can be found respectively in Figures A1–A5 in Appendix A. In general, the impact of COVID‐19 on home‐dwelling time is evident, as all U.S. states saw a certain level of increase in home‐dwelling time, especially in March and April (Figure 4). The results reveal that the U.S. states present considerably similar (ranging from March 20 to March 30, 2020), indicating that state‐level responses reflected from the home‐dwelling time during the first wave do not differ significantly at the first changepoint, despite the varying issue dates of State of Emergency and stay‐at‐home orders. As an initial hotspot of COVID‐19 cases in the USA, Washington declared the first State of Emergency in the USA as early as February 29, 2020. However, the estimation from our Bayesian model suggests that of Washington is around March 22, 2020 (1 day before Washington's statewide stay‐at‐home order was issued), indicating that it was not until 22 days after the issuing of the State of Emergency that Washington started to present a statistical changepoint in home‐dwelling time. Despite the small differences in among these states, its spatial disparity is still noticeable, with California, Nevada, Utah, Illinois, and Missouri having the same and earliest (March 20, 2020) (Figure 1a). As for , Oklahoma, Mississippi, Texas, and Alabama present the top four earliest , suggesting their earlier return to normal compared to other states. In comparison, states that were heavily affected by the home‐dwelling policy—such as California, New York, and New Jersey—present the latest of May 19, 2020.
FIGURE 4.
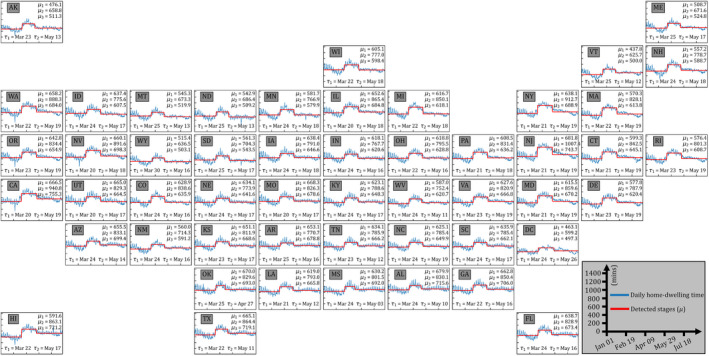
Daily home‐dwelling time, derived stages, and stage‐related variables (, , , , and ) from the proposed Bayesian model at the U.S. state level
We further derived the duration of Stage 2 by calculating (Figure 5a). A higher value of corresponds to a longer Stage 2. The results present notable spatial disparity of home‐dwelling time, revealing that Pacific states (e.g., California, Oregon, and Washington), Northeast/Mid‐Atlantic states (e.g., New York, Pennsylvania, and Virginia), and East North Central states (e.g., Wisconsin, Michigan, and Illinois) present relatively large values of , suggesting that Stage 2 in these states is considerably longer than that in other states. In comparison, Alabama is found with the shortest Stage 2, lasting only 33 days, followed by Mississippi with a Stage 2 lasting 40 days. We also derived the increase in home‐dwelling time when entering Stage 2 by calculating (Figure 5b). A higher value of suggests a more aggressive reaction to COVID‐19, evidenced by an intensive growth in daily home‐dwelling time at Stage 2. New Jersey, New York, and California stand out, as they are the top three states with the highest value of . New Jersey, for example, has a of 1,007.4 min, 325.6 min more compared to , presumably due to strict local social distancing policies. In contrast, Arkansas presents the lowest value of (117.6 min), followed by Wyoming (121.1 min) and Montana (128.0 min).
FIGURE 5.

(a) and (b) from the proposed Bayesian model at the U.S. state level (only conterminous U.S. states are presented)
4.3. U.S. county level
We further applied the proposed Bayesian model at the U.S. county level (only counties in the conterminous USA are involved) to reveal the staging patterns of home‐dwelling time records during the investigated temporal period. The county‐level analysis has the capability to reveal the hidden spatial heterogeneity that the preceding state‐level analysis fails to capture, thus providing valuable insights on the spatial differences in home‐dwelling time within and across states. Figure 6 presents daily home‐dwelling time and detected stage‐related variables for six selected U.S. counties that differ considerably in response: Hawaii County, Hawaii (Figure 6a); Wayne County, Georgia (Figure 6b); Pierce County, Washington (Figure 6c); Jefferson County, Arkansas (Figure 6d); New London County, Connecticut (Figure 6e); and Madera County, California (Figure 6f).
FIGURE 6.
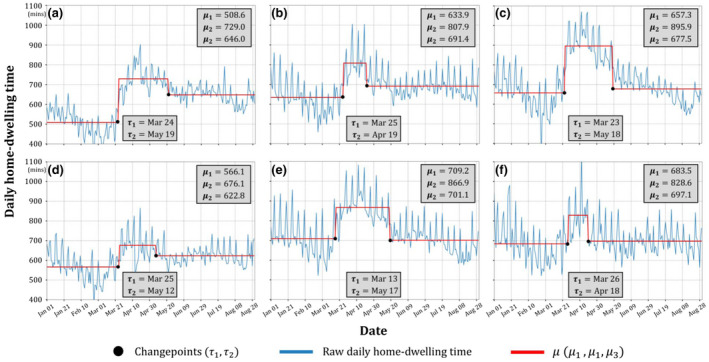
Daily home‐dwelling time records and detected stage‐related variables for selected U.S. counties: (a) Hawaii County, Hawaii; (b) Wayne County, Georgia; (c) Pierce County, Washington; (d) Jefferson County, Arkansas; (e) Utah County, Utah; (f) Adair County, Iowa
We investigated three specific interactions between stage‐related variables: (duration of Stage 2); (increase in home‐dwelling time when entering Stage 2 from Stage 1); and (decrease in home‐dwelling time comparing Stage 3 and Stage 1). To explore potential clustering spatial patterns, we calculated optimized Getis–Ord , an index that summarizes spatial patterns with statistical significance by exploring each feature within the context of neighboring features (Getis & Ord, 2010). The detailed calculation procedure of Getis–Ord is documented in Supporing Information Appendix C. Out of 3,108 counties in the conterminous USA, Bayesian‐derived stage‐related variables from 358 counties (accounting for 11.5%) fail to meet the extra conditions stated in Section 3.5, and these counties are not included in this analysis. Figure 7 presents the spatial patterns of the remaining counties in terms of (Figure 7a1), (Figure 7a2), (Figure 7a3), and the statistically significant hot/coldspots of (Figure 7b1), (Figure 7b2), and (Figure 7b3).
FIGURE 7.
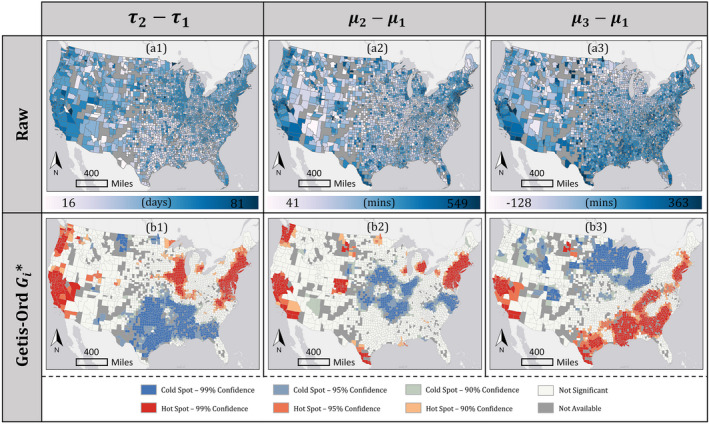
U.S. county‐level spatial patterns of (a1) , (a2) , (a3) and identified statistically significant hot/coldspots of (b1) , (b2) , (b3) . The calculation procedure of Geitis–Ord is detailed in Appendix C. The Z‐score distribution of is summarized at three significant levels: (99% confidence level), (95% confidence level), and (90% confidence level). Note that (a1), (a2), and (a3) are mapped with 10 classes categorized by Jenks natural breaks (Jenks, 1967)
For the duration of Stage 2 implied by , four hotspots with relatively long duration of Stage 2 are detected (Figure 7b1): (1) Mid‐Atlantic/East‐Coast region that contains the metropolitan areas of New York, Boston, Philadelphia, and D.C.; (2) Pacific Northwest region that contains the metropolitan areas of Portland and Seattle; (3) Lake Michage North that contains the metropolitan areas of Chicago and Milwaukee; and (4) Pacific West region that covers most parts of California. One extensive coldspot with a relatively short duration of Stage 2 is found in the West/East South Central region that covers Texas, Oklahoma, Arkansas, Louisiana, Mississippi, Alabama, Georgia, South Carolina (south part), and Tennessee (west part).
Similar hotspots are found for , which implies the intensity of increase in home‐dwelling time during the transition from Stage 1 to Stage 2 (Figure 7b2). For example, counties in California, as well as in metropolitan areas of New York, Boston, Philadelphia, D.C., Chicago, and Seattle, experience not only a long Stage 2 but also an intense increase in daily home‐dwelling time. A new hotspot (not identified in the hotspots of ) emerges in the metropolitan area of Denver, suggesting that the counties in Denver experienced a sharp increase in home‐dwelling time, but such increase only lasted for a limited duration. The coldspots of present different spatial patterns compared with those of , revealing the spatial disagreement between Stage 2 duration and the intensity of increase in home‐dwelling time during the stage transition from Stage 1 to Stage 2. A notable coldspot of (not identified in the coldspots of ) appears in the coastal areas of North Carolina and Virginia, suggesting that counties in these regions increased home‐dwelling time in a marginal manner during Stage 2, though such increases lasted for a while.
The hot/coldspots of , which suggest the recovery levels in home‐dwelling time comparing Stage 3 and Stage 1, are presented in Figure 7b3. A higher value of denotes less magnitude of recovery during the investigated period, while a lower value of denotes otherwise, with negative values suggesting even less home‐dwelling time in Stage 3 compared to the pre‐pandemic period. Different from Figure 7b1 and b2, no hotspot of is found for counties in metropolitan areas of Portland and Seattle, indicating their high recovery level despite their long‐lasting Stage 2, with a strong increase in home‐dwelling time. In comparison, the hotspots of remain notable for counties in California, metropolitan areas of New York, Boston, Philadelphia, and D.C. Similar hotspots can also be found in counties within the Deep South states, such as Mississippi, Alabama, Georgia, South Carolina, and Texas (south). In contrast to the observed lower recovery level in the south, a coldspot of stands out in the Great Lake region, revealing a considerably higher recovery level.
4.4. U.S. Census Tract level (Metro Atlanta as an example)
Taking the Atlanta–Sandy Springs–Alpharetta metropolitan statistical area (MSA), hereafter referred to as Metro Atlanta, as a pilot study area, we investigated how the derived stage‐related variables correlate with household income, one of the major factors responsible for the noticeable disparities in the exposure of many diseases (Anderson & Chu, 2007; Diez‐Roux, Link, & Northridge, 2000; Hopman, Allegranzi, & Mehtar, 2020). Metro Atlanta serves as an appropriate testbed due to the following reasons. As the 12th largest MSA in the USA, Metro Atlanta is the most populous metropolitan area in Georgia. Alongside its rapid growth, Metro Atlanta has shown the widening socioeconomic inequity underlying the uneven urban growth and development (Bullard, Johnson, & Torres, 1999; Huang, Li, Lu, et al., 2020). During the first wave of the COVID‐19 pandemic, Metro Atlanta exhibited spatially homogenous policy implementation, where the examination of the influence of household income on home‐dwelling time can be conducted under the condition of the same or similar regional mitigation measures.
Similar to the experiment at the U.S. county level, we investigated the same interactions between Bayesian‐derived stage‐related variables (i.e., , , and ). Out of 987 Census Tracts in Metro Atlanta, 126 (accounting for 12.8%) fail to meet the extra conditions detailed in Section 3.5. The spatial distribution of median household income (median hhinc), , , and in the study area can be found in Supporting Information Figure C1 in Appendix C. In general, the spatial patterns in Figure C1 imply a close relationship of median hhinc with , , and , evidenced by their similar distribution patterns, especially that between median hhinc and .
Figure 8 presents the scatterplots of median hhinc with (Figure 8a), (Figure 8b), and (Figure 8c) at the Census Tract level in Metro Atlanta. The relationship between median hhinc and follows a logarithmic correlation, suggesting that an increase in median household income tends to extend the duration of Stage 2 with diminishing marginal effects. Our logarithmic fit reveals their relationship to be (), indicating that a 10% increase in household income extends 1.319 days in Stage 2. The relationship between median hhinc and follows a strong positive linear correlation. A linear fit reveals (), suggesting that a $1,000 increase in household income translates to 1.8 min more daily home‐dwelling time when transitioning from Stage 1 to Stage 2. In comparison, median hhinc and follow a weak, low‐explanatory linear relationship: (), revealing the trivial contribution of to the recovery levels reflected in home‐dwelling time when comparing Stage 3 with Stage 1.
FIGURE 8.
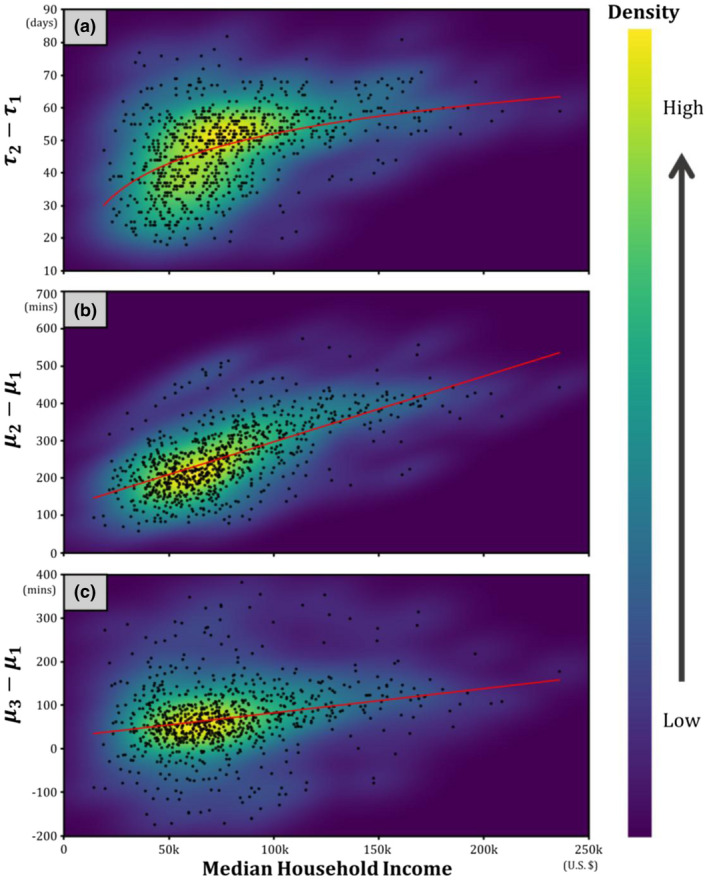
Scatterplot of median household income with (a) , (b) , (c) at the Census Tract level in the Atlanta Metropolitan area (Metro Atlanta)
5. DISCUSSION
5.1. What have we learnt?
In this study, we investigated social distancing stages using home‐dwelling time records aggregated at multi‐scales in the USA from a data‐driven perspective. Specifically, we adopted Bayesian inference with weakly informative priors as a data‐driven approach, aiming to reveal how stage‐related variables (i.e., changepoints and stage means) and their interactions vary spatiotemporally. Different from the existing effort with stage definition (e.g., “before the stay‐at‐home order,” “under the stay‐at‐home order,” “re‐opening”) from a purely policy‐driven perspective (Huang et al., 2022), our study contributes to the literature by proposing an automatic stage‐inferencing workflow that allows better exploration of the hidden patterns or confounders associated with policy implementation and policy adherence.
At the national level, our results show that home‐dwelling time increased significantly in the USA during the pandemic, which could be explained by the containment and closure policies implemented in the USA to restrain human mobility and gathering after the National Emergency declaration (March 13). Detailed information regarding state‐level stay‐at‐home orders can be found at https://www.usatoday.com/storytelling/coronavirus‐reopening‐america‐map/. By the first changepoint (τ1) on March 22, four states—including California, Illinois, New Jersey, and New York—had issued statewide mobility restrictions (Moreland et al., 2020). The other states also implemented various policies (e.g., school and workplace closures and restrictions on gatherings), though statewide restrictions had not been issued. With gradually strengthened policies, an increase in home‐dwelling time was observed in March and April at Stage 2. The second changepoint (τ2) appeared on May 17, 1 month after the White House released the “Opening Up America Again” guideline. By May 17, six states had lifted their statewide stay‐at‐home order, and many other states initiated phased opening strategies (Moreland et al., 2020). It is worth mentioning that the decreasing trend of home‐dwelling time started before the implementation of re‐opening policies. This might be explained by the quarantine fatigue observed in early April (Sun, Di, Sprigg, Tong, & Casal, 2020). Although home‐dwelling time decreased significantly from Stage 2 to Stage 3, the average home‐dwelling time at Stage 3 was still longer than that at Stage 1. This indicates that people spent more time at home after the lifting of containment and closure policies prior to the implementation of these policies. In addition to the remaining policies in certain states, panic effects caused by people's fear of being infected might have kept people from outdoor activities, especially with the increased COVID‐19 cases and deaths after the re‐opening (Kaufman, Whitaker, Mahendraratnam, Smith, & McClellan, 2020).
At the state level, our results reveal the spatial disparity across states. States with higher infection and death rates from COVID‐19 (e.g., Washington and New York) in the early stages of the pandemic were more likely to experience longer home‐dwelling time at Stage 2 compared with states having less COVID‐19 severity, presumably resulting from the strict policies implemented in these states. Additionally, a recent study indicates that workers from the sectors of information, finance/insurance, and professional/business services are more flexible over working from home compared to workers from the sectors of arts, entertainment and recreation, accommodation and food, and retail trade (Bick, Blandin, & Mertens, 2020). Thus, states with larger markets in sectors with the flexibility to work from home may experience extensive growth of home‐dwelling time at Stage 2 compared with other states. The state‐level economic and demographic structure could also contribute to the spatial variation of home‐dwelling time, as workers in middle age and/or with high educational levels and income are expected to be more likely to work from home (Bick et al., 2020).
The county‐level analysis further reveals the spatial heterogeneity of home‐dwelling time within and across states. There are obvious spatial variations among the western/eastern coastal regions, the Great Plain/South Central region, and the Great Lake region. The West Coast (e.g., California) and the East Coast (from Massachusetts to Virginia) have a longer duration of Stage 2 and a more notable increase of home‐dwelling time in Stage 2 and Stage 3, indicating the stronger adherence of stay‐at‐home policies by residents and their continuous tendency of home dwelling after the release of home‐dwelling policies. We observe spatial variations of home‐dwelling time within California, specifically, a less significant increase of home‐dwelling time from Stage 1 to Stage 2 in southern California (e.g., Barstow, Riverside, and San Diego) than that in northern California where high‐tech industries are located. The results reveal the heterogeneity of policy adherence under the same state policies, possibly explained by the different levels of policy stringency at the local level and degrees of urban governance and supervision (Vaid, McAdie, Kremer, Khanduja, & Bhandari, 2020). Similarly, notable spatial heterogeneity can be observed in the duration of home dwelling and the increase of home‐dwelling time within Michigan, Illinois, Wisconsin, and Indiana, where working routine has been recovered quickly after the lifting of home‐dwelling policy. Moreover, within the South and Southeast Central regions, it is interesting to observe Denver as the single spot in the Great Plains with a substantial increase of home‐dwelling time in Stage 2, though lasting for a limited period. This is possibly due to the high‐tech companies and innovative economy promoted by industrial transmission and development in Denver, which enable employees to work from home (Hathaway, 2013), whereas essential workers in relatively less developed counterparts of the Central region have to travel to work onsite. In addition, Texas has substantial variations in the increase of home‐dwelling time in Stage 2 (specifically, only south Texas is significant in such an increase), whereas Mississippi and Alabama retain a relatively higher level of home dwelling after the policy lifting. In sum, the county‐level variations of home dwelling reflect the varying degree of policy stringency and the local response and adherence to policy implementation, which are potentially subject to the local industrial and occupational structures, job types, and socioeconomic disparities.
While the national‐ and county‐level home‐dwelling time patterns indicate policy compliance and spatial disparities in response to the COVID‐19 pandemic, the Census Tract‐level evidence provides more details on the exposed inequity across the population. Taking Metro Atlanta as a pilot study, we illustrate that both the length of Stage 2 (i.e., τ2 − τ1) and the home‐dwelling time differential (i.e., μ2 − μ1) are positively associated with the median household income in a Census Tract. In other words, if a Census Tract has a higher median household income, its self‐quarantine period during the pandemic would tend to be longer, and the increase in home‐dwelling time would be greater. This indicates that people with higher incomes may be more protected by spending more time at home compared to the lower‐income population. The Census Tract‐level results echo previous studies, such as Huang et al. (2022), which also suggested that neighborhoods with lower household incomes or a larger share of racial minorities appeared to have shorter home‐dwelling time. Compared to the disadvantaged population groups, socioeconomically privileged people usually have more choices to work remotely, with a greater ability to access food and services without going out (Cetrulo, Guarascio, & Virgillito, 2020; Huang et al., 2022). In contrast, people with lower socioeconomic status may have to risk their health to secure their jobs and income by making more outdoor trips (Lou, Shen, & Niemeier, 2020). Subsequently, they would have a higher probability of being exposed and infected by COVID‐19, which would further harm their household's financial conditions. Thus, the pandemic might exacerbate social inequality, given that households in high‐income neighborhoods would be more resilient. The disparate exposure that disfavors low‐income populations can further compound other disadvantages, causing adverse health outcomes for vulnerable people. Mitigation measures need to recognize and account for the disparity in policy compliance and recovery, keeping the public value of social equity at the forefront of actions to support more effective readiness for future epidemics. It is imperative to reduce the immediate health effects and ensure equitable allocation of health care resources and the proper allocation of financial resources, such as subsidies, for more vulnerable populations.
Our multi‐scale analysis of home‐dwelling time based on the Bayesian inference method reveals the three‐stage pattern of home‐dwelling time in the reflection of the differences in policy stringency and local response and adherence to policy implementation. Our key findings summarized above align with some observations in a number of international studies. Similar to our finding that home‐dwelling policies tend to affect essential and low‐skilled workers more, such policies in Japan had more impact on female and low‐skilled workers who engaged in social and non‐flexible jobs (Kikuchi, Kitao, & Mikoshiba, 2021). Similar to the trend of home dwelling in the USA, a significant decrease in human mobility to public facilities and an increase in home‐dwelling time were also found in Australia (Wang, Liu, & Hu, 2020), South Korea (Kim, An, Min, Bitton, & Gawande, 2020), Italy, and other European countries (Flaxman et al., 2020).
5.2. Limitations and future directions
We need to acknowledge several limitations of this study and provide guidelines for future research. First, the raw SafeGraph home‐dwelling time records present a notable three‐stage pattern, leading to the model‐fitting strategy that involves two changepoints ( and and three stage means (,, and ). Despite the fact that home‐dwelling records in most geographical units in this study can be summarized by this pre‐conceptualized piecewise function, we acknowledge that certain geographical units, especially fine‐scale units such as Census Tracts, might not be constrained in such a way, given their great heterogeneity in urban/rural functionality. Thus, future efforts can be made to explore the possibility of hyper‐parameterizing changepoint numbers to further weaken the role of prior knowledge in model fitting.
Second, the weakly informative priors assumed in the Bayesian model lead to the targeted sampling patterns that facilitate model fitting. However, the pre‐conceptualized nature in these priors, to a certain degree, limits the sampling scope. Thus, efforts can be made to continuously weaken the informativeness of priors with an increasing number of posterior draws. In addition, the stage mean values serve as a simplified treatment of errors by neglecting the possibility of autocorrelation and heteroscedasticity to some degree (Kogan et al., 2021). Future efforts can be made to improve the analysis using sophisticated sampling strategies, autoregressive error parameters, and joint inferences to consider temporal autocorrelation and heteroscedasticity.
Third, the home‐dwelling time series we constructed spans January 1, 2020 to August 31, 2020. The intra‐annual seasonal variations in home‐dwelling time potentially pose challenges in differentiating the home‐dwelling stages induced by COVID‐19. Further efforts can be made to incorporate multi‐year records to reduce the impact of seasonality. When considering multi‐year records, however, attention should be paid to the comparability of cross‐year records, as additional uncertainty might be introduced due to the differences in representativeness, calculation methods, and data sources. In addition, future studies can expand the temporal coverage of the analytical timeframe to merge with the potential resurges and re‐introduction of social restriction policies.
Fourth, we adopted Bayesian inference in this study to derive home‐dwelling stages (from a probabilistic perspective). Although Bayesian probabilistic modeling has been recognized as a statistically robust stage detection method and has been widely adopted in a variety of domains (e.g., Beckage, Joseph, Belisle, Wolfson, & Platt, 2007; Shen & Liu, 2015; Zhao et al., 2019), the potential of other approaches, such as models based on the likelihood ratio (Keogh, Chu, Hart, & Pazzani, 2001), graphs (Chen & Zhang, 2015), and clustering (Tran, 2019), deserve further investigation. In addition, the Bayesian inference model we constructed follows an offline setting, as all samples have been received before the changepoints are inferred in a retrospective manner (Truong, Oudre, & Vayatis, 2020). We believe that future studies can explore the possibility of adopting online frameworks to better detect abrupt changes in home‐dwelling time (in real time or near real time) and investigate the driven forces behind them.
Finally, we investigated how derived stage‐related variables correlate with household income (one of the major economic factors) in Metro Atlanta (a city with widening socioeconomic inequity). Due to length limits, we did not provide detailed multi‐site comparative analyses nor investigate the contribution of other demographic and socioeconomic variables (e.g., race, ethnicity, gender, and work types) to the disparity in home‐dwelling stages. We encourage future efforts to be made in those directions.
6. CONCLUSIONS
In this study, we investigate stages in home‐dwelling time in the USA from a data‐driven perspective: a Bayesian inference approach with weakly informative priors. Specifically, we examine the multi‐scale geographic variation of stages in home‐dwelling time records, aiming to reveal the hidden patterns or confounders associated with the policy implementation and adherence. To our best knowledge, our work marks a pioneering effort to explore multi‐scale home‐dwelling patterns in the USA from a purely data‐driven perspective and in a statistically robust manner.
At the U.S. national level, two changepoints ( and ) are derived, with the former corresponding to March 22, 2020 (9 days after the White House declared the National Emergency on March 13) and the latter corresponding to May 17, 2020. The two identified changepoints separate the time series into three notable stages: Stage 1 (pre‐pandemic) with stage mean () of 638.7 min; Stage 2 (reaction) with stage mean () of 838.2 min; and Stage 3 (recovery) with stage mean () of 673.7 min. The small difference between and reveals that society has largely returned to normal after May 17 from a perspective of daily home‐dwelling duration. At the state level, our results reveal notable spatial disparity in home‐dwelling stage‐related variables across states, presumably resulting from various reasons that include the state's political partisanship, COVID‐19 severity, social distancing measures, re‐opening policies, and industry distributions. Pacific states, Northeast/Mid‐Atlantic states, and East North Central states present a longer Stage 2 compared to those in other states. Alabama is found with the shortest Stage 2 (33 days), followed by Mississippi (40 days). The top three states with the highest value of (increase in home‐dwelling time when transitioning from Stage 1 to Stage 2) are New Jersey (325.6 min), New York (274.6 min), and California (274.3 min). In contrast, Arkansas presents the lowest value of (117.6 min), followed by Wyoming (121.1 min) and Montana (128.0 min).
Our county‐level analysis further reveals the spatial heterogeneity of home‐dwelling time within and across states. Applying the optimized Getis–Ord spatial statistics, we reveal potential clustering spatial patterns of the interactions among stage‐related variables. Specifically, we observe notable spatial variations among the West/East Coast regions, the Great Plain/South Central region, and the Great Lake region. The West and East Coast have a longer duration of Stage 2 and a more notable increase of home‐dwelling time in Stage 2 and Stage 3, which suggests their stronger adherence to stay‐at‐home policies and their continuous tendency for home dwelling after the lifting of home‐dwelling policies. Taking Metro Atlanta as a pilot study, we observe that the length of Stage 2 (τ2 − τ1) and the increase in home‐dwelling time transitioning from Stage 1 to Stage 2 (μ2 − μ1) are positively associated with the median household income at the U.S. Census Tract level. The results suggest that Census Tracts with a higher median household income tend to have a longer self‐quarantine period with a more intensive increase in home‐dwelling time, revealing the luxury nature of stay‐at‐home policies and echoing many pieces of existing evidence.
When and to what extent to release a home‐dwelling policy and how to keep the effectiveness of a less restricted policy on virus control pose challenges for both politicians and healthcare systems in the USA and other countries when facing severe outbreaks. This study deepens our understanding of the multi‐scale spatial disparity in policy compliance using fine‐grained home‐dwelling records from a data‐driven perspective. The automatic identification of multi‐stage patterns of home‐dwelling time provides fundamental conceptual and methodological knowledge to evaluate policy effectiveness, and the Bayesian inference method used to optimize such identifications in our study can be applied to different geographic contexts and various waves along the pandemic timeline for more robust policy evaluation.
Supporting information
Supplementary Material
Huang, X. , Xu, Y. , Liu, R. , Wang, S. , Wang, S. , Zhang, M. , … Li, Z. (2022). Exploring the spatial disparity of home‐dwelling time patterns in the USA during the COVID‐19 pandemic via Bayesian inference. Transactions in GIS, 26, 1939–1961. 10.1111/tgis.12918
[Correction added on 24th March 2022, after first online publication: typo in author name corrected.]
DATA AVAILABILITY STATEMENT
The home‐dwelling records are derived from social distancing metrics that can be requested at https://www.safegraph.com/academics. Summarized daily home‐dwelling time and codes for Bayesian inference and mapping can be found at https://figshare.com/s/5b9c5f068ad4420b494a.
REFERENCES
- Anderson, G. F. , & Chu, E. (2007). Expanding priorities—confronting chronic disease in countries with low income. New England Journal of Medicine, 356(3), 209. 10.1056/NEJMp068182 [DOI] [PubMed] [Google Scholar]
- Badr, H. S. , Du, H. , Marshall, M. , Dong, E. , Squire, M. M. , & Gardner, L. M. (2020). Association between mobility patterns and COVID‐19 transmission in the USA: A mathematical modelling study. The Lancet Infectious Diseases, 20(11), 1247–1254. 10.1016/S1473-3099(20)30553-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baek, C.‐W. , McCrory, P. B. , Messer, T. , & Mui, P. (2020). Unemployment effects of stay at‐home orders: Evidence from high frequency claims data (IRLE Working Paper No. 101‐20). Berkeley, CA: University of California, Institute for Research on Labor and Employment. [Google Scholar]
- Banerjee, T. , Nayak, A. , & Zhao, H. (2021). A county‐level study of the effects of state‐mandated COVID‐19 lockdowns on urban and rural restaurant visits using consumers’ cell phone geo‐location data. Journal of Public Health, 1–10. 10.1007/s10389-020-01473-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bayes, F. R. S. (1958). An essay towards solving a problem in the doctrine of chances. Biometrika, 45(3–4), 296–315. 10.1093/biomet/45.3-4.296 [DOI] [PubMed] [Google Scholar]
- Beckage, B. , Joseph, L. , Belisle, P. , Wolfson, D. B. , & Platt, W. J. (2007). Bayesian change‐point analyses in ecology. New Phytologist, 174(2), 456–467. 10.1111/j.1469-8137.2007.01991.x [DOI] [PubMed] [Google Scholar]
- Bick, A. , Blandin, A. , & Mertens, K. (2020). Work from home after the COVID‐19 outbreak (Federal Reserve Bank of Dallas Research Department Working Papers). 10.24149/wp2017r1 [DOI] [Google Scholar]
- Box, G. E. , & Tiao, G. C. (2011). Bayesian inference in statistical analysis. New York, NY: John Wiley & Sons. [Google Scholar]
- Bullard, R. D. , Johnson, G. S. , & Torres, A. O. (1999). Sprawl Atlanta: Social equity dimensions of uneven growth and development. Atlanta, GA: Clark Atlanta University, Environmental Justice Resource Center. [Google Scholar]
- Cartenì, A. , Di Francesco, L. , & Martino, M. (2020). How mobility habits influenced the spread of the COVID‐19 pandemic: Results from the Italian case study. Science of the Total Environment, 741, 140489. 10.1016/j.scitotenv.2020.140489 [DOI] [PMC free article] [PubMed] [Google Scholar]
- CDC . (2021). COVID data tracker. Retrieved from https://covid.cdc.gov/covid‐data‐tracker/#cases_totalcases [Google Scholar]
- Cetrulo, A. , Guarascio, D. , & Virgillito, M. E. (2020). The privilege of working from home at the time of social distancing. Intereconomics, 55, 142–147. 10.1007/s10272-020-0891-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang, S. , Pierson, E. , Koh, P. W. , Gerardin, J. , Redbird, B. , Grusky, D. , & Leskovec, J. (2021). Mobility network models of COVID‐19 explain inequities and inform re‐opening. Nature, 589(7840), 82–87. 10.1038/s41586-020-2923-3 [DOI] [PubMed] [Google Scholar]
- Charoenwong, B. , Kwan, A. , & Pursiainen, V. (2020). Social connections with COVID19‐affected areas increase compliance with mobility restrictions. Science Advances, 6(47), eabc3054. 10.1126/sciadv.abc3054 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, H. , & Zhang, N. (2015). Graph‐based change‐point detection. Annals of Statistics, 43(1), 139–176. 10.1214/14-AOS1269 [DOI] [Google Scholar]
- Chernozhukov, V. , Kasahara, H. , & Schrimpf, P. (2021). Causal impact of masks, policies, behavior on early Covid‐19 pandemic in the US. Journal of Econometrics, 220(1), 23–62. 10.1016/j.jeconom.2020.09.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chiou, L. , & Tucker, C. (2020). Social distancing, internet access and inequality. Cambridge, MA: National Bureau of Economic Research. [Google Scholar]
- Czeisler, M. É. , Tynan, M. A. , Howard, M. E. , Honeycutt, S. , Fulmer, E. B. , Kidder, D. P. , … Czeisler, C. A. (2020). Public attitudes, behaviors, and beliefs related to COVID‐19, stay‐at‐home orders, nonessential business closures, and public health guidance—United States, New York City, and Los Angeles, May 5–12, 2020. Morbidity and Mortality Weekly Report, 69(24), 751. 10.15585/mmwr.mm6924e1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diez‐Roux, A. V. , Link, B. G. , & Northridge, M. E. (2000). A multilevel analysis of income inequality and cardiovascular disease risk factors. Social Science & Medicine, 50(5), 673–687. 10.1016/S0277-9536(99)00320-2 [DOI] [PubMed] [Google Scholar]
- Engle, S. , Stromme, J. , & Zhou, A. (2020). Staying at home: Mobility effects of Covid19. SSRN, Preprint. 10.2139/ssrn.3565703 [DOI] [Google Scholar]
- Flaxman, S. , Mishra, S. , Gandy, A. , Unwin, H. J. T. , Coupland, H. , Mellan, T. A. , Bhatt, S. (2020). Estimating the number of infections and the impact of non‐pharmaceutical interventions on COVID‐19 in European countries: Technical description update. Preprint, arXiv:2004.11342. [Google Scholar]
- Gao, S. , Rao, J. , Kang, Y. , Liang, Y. , & Kruse, J. (2020). Mapping county‐level mobility pattern changes in the United States in response to COVID19. SIGSPATIAL Special, 12(1), 16–26. 10.1145/3404820.3404824 [DOI] [Google Scholar]
- Gatto, M. , Bertuzzo, E. , Mari, L. , Miccoli, S. , Carraro, L. , Casagrandi, R. , & Rinaldo, A. (2020). Spread and dynamics of the COVID‐19 epidemic in Italy: Effects of emergency containment measures. Proceedings of the National Academy of Sciences of the United States of America, 117(19), 10484–10491. 10.1073/pnas.2004978117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Getis, A. , & Ord, J. K. (2010). The analysis of spatial association by use of distance statistics. In Anselin L., & Rey S. J. (Eds.), Perspectives on spatial data analysis (pp. 127–145). Berlin, Germany: Springer. [Google Scholar]
- Geyer, C. (2011). Introduction to Markov Chain Monte Carlo. In Brooks S., Gelman A., Jones G., & Meng X.‐L. (Eds.), Handbook of Markov Chain Monte Carlo (pp. 3–48). Boca Raton, FL: Chapman & Hall/CRC Press. [Google Scholar]
- Hathaway, I. (2013). Tech starts: High‐technology business formation and job creation in the United States. Kansas City, MO: Ewing Marion Kauffman Foundation. [Google Scholar]
- Hoeben, E. M. , Bernasco, W. , Suonperä Liebst, L. , Van Baak, C. , & Rosenkrantz Lindegaard, M. (2021). Social distancing compliance: A video observational analysis. PLoS One, 16(3), e0248221. 10.1371/journal.pone.0248221 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffman, M. D. , & Gelman, A. (2014). The No‐U‐Turn sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. Journal of Machine Learning Research, 15(1), 1593–1623. [Google Scholar]
- Hopman, J. , Allegranzi, B. , & Mehtar, S. (2020). Managing COVID‐19 in low‐ and middle‐income countries. Journal of the American Medical Association, 323(16), 1549–1550. 10.1001/jama.2020.4169 [DOI] [PubMed] [Google Scholar]
- Hu, S. , Xiong, C. , Yang, M. , Younes, H. , Luo, W. , & Zhang, L. (2021). A big‐data driven approach to analyzing and modeling human mobility trend under non‐pharmaceutical interventions during COVID‐19 pandemic. Transportation Research Part C: Emerging Technologies, 124, 102955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang, X. , Li, Z. , Jiang, Y. , Li, X. , & Porter, D. (2020). Twitter reveals human mobility dynamics during the COVID‐19 pandemic. PLoS One, 15(11), e0241957. 10.1371/journal.pone.0241957 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang, X. , Li, Z. , Jiang, Y. , Ye, X. , Deng, C. , Zhang, J. , & Li, X. (2021). The characteristics of multi‐source mobility datasets and how they reveal the luxury nature of social distancing in the US during the COVID‐19 pandemic. International Journal of Digital Earth, 14(4), 424–442. 10.1080/17538947.2021.1886358 [DOI] [Google Scholar]
- Huang, X. , Li, Z. , Lu, J. , Wang, S. , Wei, H. , & Chen, B. (2020). Time‐series clustering for home dwell time during COVID‐19: What can we learn from it? ISPRS International Journal of Geo‐Information, 9(11), 675. 10.3390/ijgi9110675 [DOI] [Google Scholar]
- Huang, X. , Lu, J. , Gao, S. , Wang, S. , Liu, Z. , & Wei, H. (2022). Staying at home is a privilege: Evidence from fine‐grained mobile phone location data in the U.S. during the COVID‐19 pandemic. Annals of the American Association of Geographers, 112(1), 285–305. [Google Scholar]
- Iio, K. , Guo, X. , Kong, X. , Rees, K. , & Bruce Wang, X. (2021). COVID‐19 and social distancing: Disparities in mobility adaptation between income groups. Transportation Research Interdisciplinary Perspectives, 10, 100333. 10.1016/j.trip.2021.100333 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenks, G. F. (1967). The data model concept in statistical mapping. International Yearbook of Cartography, 7, 186–190. [Google Scholar]
- Kang, Y. , Gao, S. , Liang, Y. , Li, M. , Rao, J. , & Kruse, J. (2020). Multiscale dynamic human mobility flow dataset in the US during the COVID‐19 epidemic. Scientific Data, 7(1), 390. 10.1038/s41597-020-00734-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufman, B. G. , Whitaker, R. , Mahendraratnam, N. , Smith, V. A. , & McClellan, M. B. (2020). Comparing associations of state reopening strategies with COVID‐19 burden. Journal of General Internal Medicine, 35(12), 3627–3634. 10.1007/s11606-020-06277-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keogh, E. , Chu, S. , Hart, D. , & Pazzani, M. (2001). An online algorithm for segmenting time series. Proceedings 2001 IEEE International Conference on Data Mining, San Jose, CA (pp. 289–296). IEEE: Piscataway, NJ. [Google Scholar]
- Kikuchi, S. , Kitao, S. , & Mikoshiba, M. (2021). Who suffers from the COVID‐19 shocks? Labor market heterogeneity and welfare consequences in Japan. Journal of the Japanese and International Economies, 59, 101117. 10.1016/j.jjie.2020.101117 [DOI] [Google Scholar]
- Kim, J. H. , An, J. A. R. , Min, P. K. , Bitton, A. , & Gawande, A. A. (2020). How South Korea responded to the COVID‐19 outbreak in Daegu. NEJM Catalyst Innovations in Care Delivery, 1(4), 1–14. 10.1056/CAT.20.0159 [DOI] [Google Scholar]
- Kogan, N. E. , Clemente, L. , Liautaud, P. , Kaashoek, J. , Link, N. B. , Nguyen, A. T. , … Santillana, M. (2021). An early warning approach to monitor COVID‐19 activity with multiple digital traces in near real time. Science Advances, 7(10), eabd6989. 10.1126/sciadv.abd6989 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kraemer, M. U. , Yang, C. H. , Gutierrez, B. , Wu, C. H. , Klein, B. , Pigott, D. M. , … Scarpino, S. V. (2020). The effect of human mobility and control measures on the COVID‐19 epidemic in China. Science, 368(6490), 493–497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee, M. , Zhao, J. , Sun, Q. , Pan, Y. , Zhou, W. , Xiong, C. , & Zhang, L. (2020). Human mobility trends during the early stage of the COVID‐19 pandemic in the United States. PLoS One, 15(11), e0241468. 10.1371/journal.pone.0241468 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, Z. , Huang, X. , Hu, T. , Ning, H. , Ye, X. & Li, X. (2020). ODT FLOW: A scalable platform for extracting, analyzing, and sharing multi‐source multi‐scale human mobility. Preprint, arXiv:2104.05040. [DOI] [PMC free article] [PubMed]
- Lou, J. , Shen, X. , & Niemeier, D. (2020). Are stay‐at‐home orders more difficult to follow for low‐income groups? Journal of Transport Geography, 89, 102894. 10.1016/j.jtrangeo.2020.102894 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martino, L. , & Elvira, V. (2014). Metropolis sampling. In Balakrishnan N., Colton T., Everitt B., Piegorsch W., Ruggeri F., & Teugels J. (Eds.), Wiley StatsRef: Statistics Reference Online (pp. 1–18). Chichester, UK: John Wiley & Sons. [Google Scholar]
- Moreland, A. , Herlihy, C. , Tynan, M. A. , Sunshine, G. , McCord, R. F. , Hilton, C. , … Popoola, A. (2020). Timing of state and territorial COVID‐19 stay‐at‐home orders and changes in population movement—United States, March 1–May 31, 2020. Morbidity and Mortality Weekly Report, 69(35), 1198. 10.15585/mmwr.mm6935a2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niculita, O. , Skaf, Z. , & Jennions, I. K. (2014). The application of Bayesian change point detection in UAV fuel systems. Procedia CIRP, 22, 115–121. 10.1016/j.procir.2014.07.119 [DOI] [Google Scholar]
- Nouvellet, P. , Bhatia, S. , Cori, A. , Ainslie, K. E. C. , Baguelin, M. , Bhatt, S. , … Donnelly, C. A. (2021). Reduction in mobility and COVID‐19 transmission. Nature Communications, 12(1), 1090. 10.1038/s41467-021-21358-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Painter, M. , & Qiu, T. (2020). Political beliefs affect compliance with Covid‐19 social distancing orders. Retrieved from https://voxeu.org/article/political‐beliefs‐and‐compliance‐social‐distancing‐orders 10.2139/ssrn.3569098 [DOI] [Google Scholar]
- Pan, Y. , Darzi, A. , Kabiri, A. , Zhao, G. , Luo, W. , Xiong, C. , & Zhang, L. (2020). Quantifying human mobility behaviour changes during the COVID‐19 outbreak in the United States. Scientific Reports, 10(1), 20742. 10.1038/s41598-020-77751-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raifman, J. , Nocka, K. , Jones, D. , Bor, J. , Lipson, S. , Jay, J. , … Galea, S. (2020). COVID‐19 US state policy database. Ann Arbor, MI: Inter‐university Consortium for Political and Social Research. [Google Scholar]
- Ray, B. K. , & Tsay, R. S. (2002). Bayesian methods for change‐point detection in long‐range dependent processes. Journal of Time Series Analysis, 23(6), 687–705. 10.1111/1467-9892.00286 [DOI] [Google Scholar]
- Ruggieri, E. (2013). A Bayesian approach to detecting change points in climatic records. International Journal of Climatology, 33(2), 520–528. 10.1002/joc.3447 [DOI] [Google Scholar]
- SafeGraph . (2019). What about bias in the SafeGraph dataset? Retrieved from https://www.safegraph.com/blog/what‐about‐bias‐in‐the‐safegraph‐dataset [Google Scholar]
- SafeGraph . (2020). Social distancing metrics. Retrieved from https://docs.safegraph.com/docs/social‐distancing‐metrics [Google Scholar]
- Shen, Y. , & Liu, X. (2015). Phenological changes of corn and soybeans over US by Bayesian change‐point model. Sustainability, 7(6), 6781–6803. 10.3390/su7066781 [DOI] [Google Scholar]
- Shim, E. , Tariq, A. , Choi, W. , Lee, Y. , & Chowell, G. (2020). Transmission potential and severity of COVID‐19 in South Korea. International Journal of Infectious Diseases, 93, 339–344. 10.1016/j.ijid.2020.03.031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun, Q. , Pan, Y. , Zhou, W. , Xiong, C. , & Zhang, L. (2020). Quantifying the influence of inter‐county mobility patterns on the COVID‐19 outbreak in the United States. Preprint, arXiv:2006.13860. [Google Scholar]
- Sun, Z. , Di, L. , Sprigg, W. , Tong, D. , & Casal, M. (2020). Community venue exposure risk estimator for the COVID‐19 pandemic. Health & Place, 66, 102450. 10.1016/j.healthplace.2020.102450 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tartakovsky, A. G. , & Moustakides, G. V. (2010). State‐of‐the‐art in Bayesian changepoint detection. Sequential Analysis, 29(2), 125–145. 10.1080/07474941003740997 [DOI] [Google Scholar]
- Tran, D. H. (2019). Automated change detection and reactive clustering in multivariate streaming data. In Proceedings of the 2019 IEEE‐RIVF International Conference on Computing and Communication Technologies, Da Nang, Vietnam (pp. 1–6). Piscataway, NJ: IEEE. [Google Scholar]
- Truong, C. , Oudre, L. , & Vayatis, N. (2020). Selective review of offline change point detection methods. Signal Processing, 167, 107299. 10.1016/j.sigpro.2019.107299 [DOI] [Google Scholar]
- Vaid, S. , McAdie, A. , Kremer, R. , Khanduja, V. , & Bhandari, M. (2020). Risk of a second wave of Covid‐19 infections: Using artificial intelligence to investigate stringency of physical distancing policies in North America. International Orthopaedics, 44(8), 1581–1589. 10.1007/s00264-020-04653-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Rooij, B. , de Bruijn, A. L. , Folmer, C. R. , Kooistra, E. , Kuiper, M. E. , Brownlee, M. , … Fine, A. (2020). Compliance with Covid‐19 mitigation measures in the United States. Preprint. https://psyarxiv.com/qymu3/ [Google Scholar]
- Wang, M. Y. , & Park, T. (2020). A brief tour of Bayesian sampling methods. In Tang N. (Ed.), Bayesian inference on complicated data (pp. 1–12). London, UK: Intech Open. [Google Scholar]
- Wang, S. , Liu, Y. , & Hu, T. (2020). Examining the change of human mobility adherent to social restriction policies and its effect on COVID‐19 cases in Australia. International Journal of Environmental Research and Public Health, 17(21), 7930. 10.3390/ijerph17217930 [DOI] [PMC free article] [PubMed] [Google Scholar]
- WHO . (2021). WHO‐Coronavirus disease (COVID‐19) dashboard. Retrieved from https://covid19.who.int/ [Google Scholar]
- White House . (2020). White House: Opening up America again. Retrieved from https://www.whitehouse.gov/openingamerica/ [Google Scholar]
- Yan, Y. , Malik, A. A. , Bayham, J. , Fenichel, E. P. , Couzens, C. , & Omer, S. B. (2021). Measuring voluntary and policy‐induced social distancing behavior during the COVID‐19 pandemic. Proceedings of the National Academy of Science of the United States of America, 118(16), e2008814118. 10.1073/pnas.2008814118 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao, K. , Wulder, M. A. , Hu, T. , Bright, R. , Wu, Q. , Qin, H. , … Brown, M. (2019). Detecting change‐point, trend, and seasonality in satellite time series data to track abrupt changes and nonlinear dynamics: A Bayesian ensemble algorithm. Remote Sensing of Environment, 232, 111181. 10.1016/j.rse.2019.04.034 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Material
Data Availability Statement
The home‐dwelling records are derived from social distancing metrics that can be requested at https://www.safegraph.com/academics. Summarized daily home‐dwelling time and codes for Bayesian inference and mapping can be found at https://figshare.com/s/5b9c5f068ad4420b494a.


