Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Jul 25;122(33):19171–19179. doi: 10.1021/acs.jpcc.8b04549

Adsorption Contraction Mechanics: Understanding Breathing Energetics in Isoreticular Metal–Organic Frameworks

Simon Krause †, Jack D Evans †,‡, Volodymyr Bon †, Irena Senkovska †, Sebastian Ehrling †, Ulrich Stoeck †, Pascal G Yot §, Paul Iacomi ∥, Philip Llewellyn ∥, Guillaume Maurin §, François-Xavier Coudert ‡, Stefan Kaskel †,*
PMCID: PMC9115760  PMID: 35601838

Abstract

graphic file with name jp8b04549_0007.jpg

A highly porous metal–organic framework DUT-48, isoreticular to DUT-49, is reported with a high surface area of 4560 m2·g–1 and methane storage capacity up to 0.27 g·g–1 (164 cm3·cm–3) at 6.5 MPa and 298 K. The flexibility of DUT-48 and DUT-49 under external and internal (adsorption-induced) pressure is analyzed and rationalized using a combination of advanced experimental and computational techniques. While both networks undergo a contraction by mechanical pressure, only DUT-49 shows adsorption-induced structural transitions and negative gas adsorption of n-butane and nitrogen. This adsorption behavior was analyzed by microcalorimetry measurements and molecular simulations to provide an explanation for the lack of adsorption-induced breathing in DUT-48. It was revealed that for DUT-48, a significantly lower adsorption enthalpy difference and a higher framework stiffness prevent adsorption-induced structural transitions and negative gas adsorption. The mechanical behavior of both DUT-48 and DUT-49 was further analyzed by mercury porosimetry experiments and molecular simulations. Both materials exhibit large volume changes under hydrostatic compression, demonstrating noteworthy potential as shock absorbers with unprecedented high work energies.

Introduction

Application of pressure to even the hardest materials, such as diamond,1 will generate changes in the structure. For some applications, pressure-induced structural transitions are an important prerequisite, exemplified in zirconia ceramics where crack propagation is stopped by incorporating a metastable phase which undergoes a phase transition to absorb energy.2 Moreover, where such transitions are large in magnitude and in a defined area and direction, they can be leveraged for novel shock absorbers.3 Amorphous materials often lack these properties because of their disordered structure. Alternatively, many ordered and crystalline materials show defined and large structural changes under the application of an external pressure; however, the prediction and tuning of the transitions remain challenging. Metal–organic frameworks (MOFs) are a class of crystalline materials with a wide spectrum of potential applications,4 in particular, for mechanics-related fields.5,6 The high porosity in MOFs allows for very large volume changes upon mechanical compression.

Many “softer” MOFs have shown distinct structural transitions with large changes in structure upon exposure to mechanical pressure7,8 but also temperature,9 irradiation,10 or to guest molecules.11−13 Several of these flexible MOFs are excellent candidates for mechanical shock absorbers.14−18 Under the application of hydrostatic pressure, MIL-53(Al)3 (MIL = Material of Institute Lavoisier) and MIL-47(V)17 can switch from a large pore to a contracted pore (cp) state. Because of this large change in unit cell volume (∼35%) combined with the high pressure required to induce the structural transition (∼120 MPa), MIL-47(V) is regarded as one of the best shock absorber materials. More recently, the fumarate version of MIL-53 in its Ga and Al forms has shown even higher mechanical energy absorption performances.3,16 Moreover, adsorption-induced stress, which acts similarly to internal pressure,19,20 can also cause contraction of MIL-53.21,22 Upon exposure to guest molecules such as water, methane, carbon dioxide, or xenon, the guest-free framework contracts at low pressures and expands again at higher pressures to its original state, filled with guest molecules. This transition which is also referred to as breathing can be also manipulated by functionalization of the terephthalate linker.23

An entirely new type of breathing transition in a mesoporous MOF has been recently observed in DUT-49 (DUT = Dresden University of Technology), which contracts from an open pore (op) structure to a cp form under adsorption-induced stress of methane, n-butane,24 or xenon.25 A novel aspect of this mesoporous breathing MOF is the passage through a metastable state during adsorption, causing a counterintuitive phenomenon called negative gas adsorption (NGA). With increasing gas pressure, DUT-49 releases previously adsorbed gas from its pore upon structural contraction in the cp state causing a negative step in the isotherm (∂Nads/∂P < 0). The NGA phenomenon implies that the material acts as a pressure amplifier, which is an interesting conceptually novel function of adsorbents. The structural transitions responsible for the NGA behavior have been extensively investigated by in situ diffraction and spectroscopic methods24 as well as theoretical calculations.26 However, the question of the molecular origins and construction principles of such pressure amplifying materials is still an open one. In particular, the development of rational concepts to further extend this class of materials requires a better understanding of their intrinsic mechanics for tuning NGA and thus mechanical energy storage in materials.

In this contribution, we report DUT-48 as a highly porous MOF isoreticular to DUT-49 with reduced ligand length (9,9′-(1,4-phenylene)bis(9H-carbazole-3,6-dicarboxylate), cpcdc) (Scheme 1). A series of experimental techniques including adsorption, microcalorimetry, and mercury intrusion were coupled to explore the guest and mechanically induced flexible behavior of DUT-48. An important finding is that both DUT-48 and DUT-49 materials can be termed as “flexible” MOFs because both materials undergo structural transformations under external pressure, showing potential as shock absorbing materials. However, the enhanced stiffness of DUT-48 caused by the shorter linker prevents adsorption-induced breathing. This difference in behavior was further interpreted and rationalized by a combination of force field and quantum-based molecular simulations.

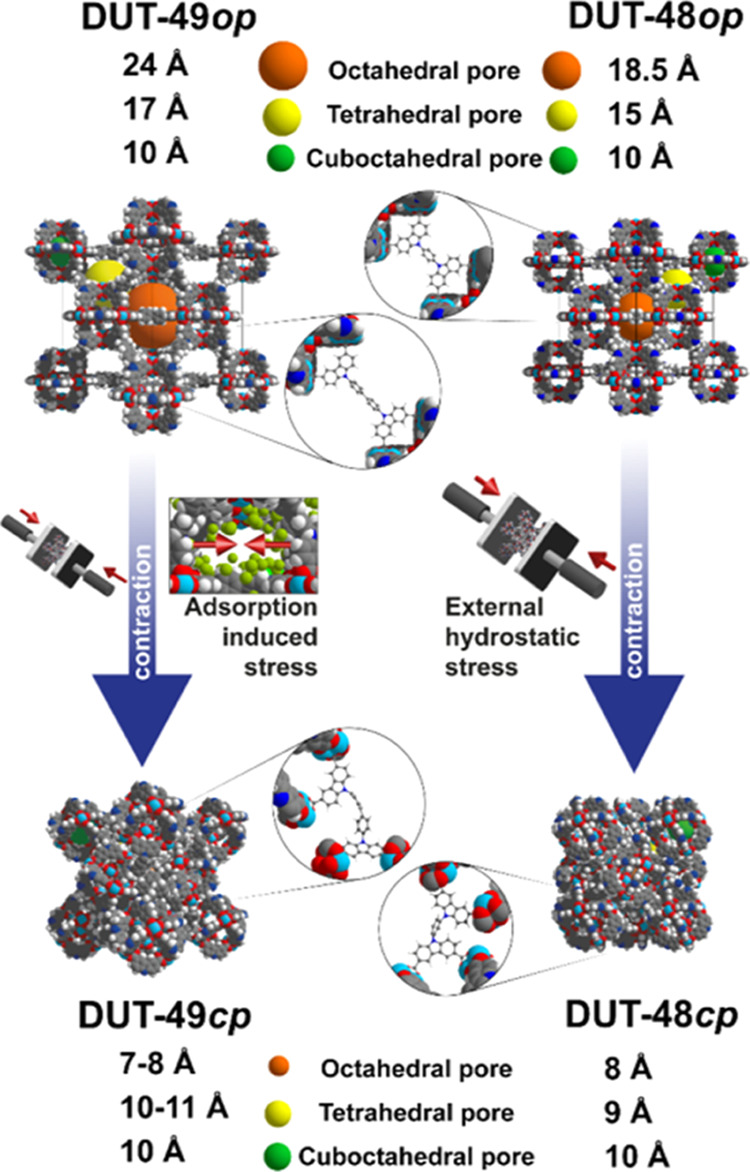
Scheme 1. Comparison of DUT-49op and DUT-48op Framework and Pore Size Including Magnified Illustration of Linker Molecules.

Scheme 1

Open in a new tab

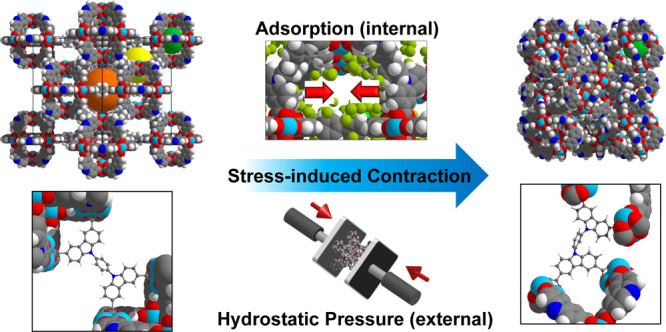
Structural contraction induced by either external hydrostatic compression or internal adsorption-induced stress to the contracted phases DUT-49cp and DUT-48cp

Experimental and Theoretical Methods

Synthesis of Organic Ligands and MOF Materials

The ligand (9,9′-([1,1′-biphenyl]-4,4′-diyl)bis(9H-carbazole-3,6-dicarboxylic acid)) (H4bbcdc) was synthesized according to a previously reported procedure.24 The ligand H4cpcdc was synthesized according to the procedure used for a similar carbazole-containing ligand.27 Both MOF materials were synthesized according to the previously mentioned procedures.24,28 Detailed synthesis procedures, activation of the MOF materials, and characterization are provided in the Supporting Information.

Gas Adsorption Experiments

Low-pressure adsorption experiments were performed on a BELSORP-max, high-pressure adsorption was performed on a BELSORP-HP instrument. Gases of purity 99.9% or higher were used. Detailed information about the adsorption measurements are provided in the Supporting Information.

Microcalorimetry Experiments

Physisorption isotherms and corresponding enthalpies were measured using a Tian-Calvet type microcalorimeter coupled with a home-made manometric gas dosing system.29 This apparatus allows for the simultaneous measurement of the adsorption isotherm and corresponding differential enthalpies. Further details are provided in the Supporting Information.

Intrusion Experiments

Mercury intrusion experiments were carried out in the range of pressure atm—415 MPa available with the Hg-porosimeter Micromeritics Autopore IV 9500. Details of sample preparation are provided in the Supporting Information.

Crystallography

A cubic single crystal of DUT-48 was placed into a glass capillary (d = 0.3 mm) with a small amount of the mother liqueur. The dataset was collected at BL14.2 beamline of the MX-facility at BESSY-II synchrotron, operated by Helmholtz-Zentrum Berlin für Materialien und Energie. Single crystal data for DUT-48: C34H20Cu2N2O10, 743.6 g mol–1, cubic, Fm3̅m, a = 40.490(5) Å, V = 66 381(23) Å3, Z = 24, ρcal = 0.444 g·cm–3, 3870 independent reflections observed, R1 = 0.0748 [I > 2σ(I)], wR2 = 0.2286 (all data) and GOF 1.121. These data can be obtained free of charge from the Cambridge Crystallographic Data Centre under entry CCDC-1827897 via www.ccdc.cam.ac.uk/data_request/cif. Additional experimental details can be obtained from the Supporting Information.

Simulation Details

The behavior and mechanical properties of the representative ligands were investigated for the corresponding acid via density functional theory (DFT) optimizations using the CRYSTAL14 software30 with localized TZVP basis sets31 and the hybrid exchange–correlation functional PBE0.32 Long-range dispersion corrections were included via the Grimme “D2” approach.33 Stress–strain curves were subsequently produced using the methodology described previously.26 Grand canonical Monte Carlo (GCMC) simulations were employed to simulate the adsorption and enthalpy of n-butane using the RASPA2.0 code.34 Frameworks were treated by the UFF forcefield,35 and n-butane was treated by the united-atom TraPPe force field.36

Molecular dynamics (MD) simulations used a modified MOF-FF force field37 recently adapted to lammps38 by Boyd et al.39 to describe the bonds, angles, dihedrals, and improper dihedrals present in the DUT-48 and DUT-49 frameworks. Further details can be found in the Supporting Information. Representative input files for molecular simulations are available online in our data repository at https://github.com/fxcoudert/citable-data.

Result and Discussion

The ligand H4cpcdc (Scheme 1) used for the synthesis of DUT-48 was obtained in a large-scale 5-step synthesis with high yield based on simple starting materials and 9H-carbazole (synthetic protocol in the Supporting Information). The ligand was used in a solvothermal reaction with Cu(NO3)2·3H2O in DMF or NMP to yield DUT-48 as blue powder. Zhou and co-workers have reported the synthesis of PCN-81, isomorphous to DUT-48 but crystallizing in the cubic space group Pa3̅, and PCN-82, bearing two additional methoxy groups on the linker and crystalizing in Fm3̅m.28 However, attempts to reproduce the reported structure of PCN-81 by replicating and also modifying the reaction conditions (see the Supporting Information) always yielded phase pure DUT-48, crystalizing in cubic space group Fm3̅m. From three different synthesis protocols, the reaction of H4cpcdc with Cu(NO3)2·3H2O in DMF with acetic acid as the modulator (for details see the Supporting Information) yielded the best result, and this was thus used for the further experiments. We note that the different synthesis protocols produce different particle sizes (Figures S19 and S20) which display different adsorption performances. The structure of DUT-48 was determined by synchrotron-based single crystal diffraction experiments (see Table S2). DUT-48 is isoreticular and isosymmetrical to DUT-49, while the linker is slightly buckled in PCN-81 (Figure S10). PCN-82 in contrast to PCN-81 retains its structure upon removal of solvent by freeze-drying and shows permanent porosity for gases.28 We hypothesize that freezing of the solvent, or partial evaporation, during the single-crystal characterization of PCN-82 produced a partial contraction to yield the difference in symmetry and ligand conformation.

To analyze the adsorption behavior of DUT-48, a well-established activation protocol for removal of solvent from the pores, involving supercritical CO2 drying, was applied.27,40 The resulting deep blue powder was activated additionally at 120 °C in dynamic vacuum (p < 10–3 mbar). Powder X-ray diffraction (PXRD) analysis showed structural preservation of DUT-48 upon activation. It is thermally stable up to 350 °C, similar to DUT-49, as determined by thermogravimetric analysis (Figure S11).

The pore volume and apparent Brunauer–Emmett–Teller (BET) area of DUT-48 were determined on the basis of a N2 adsorption isotherm at 77 K. A high BET area of 4560 m2·g–1 and a specific pore volume of 1.98 cm3·g–1 could be determined, which were higher than the values for isoreticular PCN-82 (4480 m2·g–1, 1.7 cm3·g–1)28 but lower compared to DUT-49 (5476 m2·g–1, 2.68 cm3·g–1)41 due to the reduced pore size.

The high BET area and specific pore volume motivated us to investigate the storage capacity of CH4, H2, and CO2 at high pressures. As expected, the maximum gravimetric excess uptake [CH4 0.23 g·g–1 (Figure S13), CO2 1.23 g·g–1 (Figure S14); H2 80 mg·g–1 (Figure S15)], as well as the pressure, at which the maximum capacity is reached (CH4 100 bar, CO2 45 bar; H2 50 bar) are lower for DUT-48 in comparison to DUT-49 because of the reduced porosity. The total CH4 adsorption capacity at 6.5 MPa and 25 °C is 164 cm3·cm–3 (0.27 g·g–1, Figure S15).

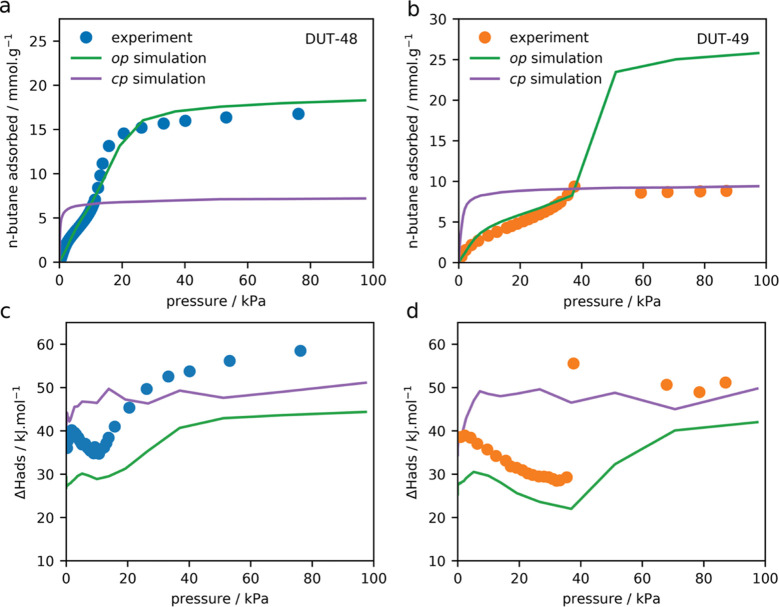
Neither the high-pressure adsorption experiments nor the N2 adsorption isotherm at 77 K showed hysteresis or unusual steps as indications for structural transitions similar to DUT-49 (Figure 1). From our previous studies of DUT-49, it is known that adsorption-induced transitions occur at temperatures close to the respective boiling point of the adsorbate. Nitrogen at 77 K was found to be a very sensitive adsorbate, only initiating structural transitions for DUT-49 crystals larger than 1–2 μm.42 Consequently, adsorption isotherms close to ambient temperature were recorded using n-butane at the respective boiling point of 273 K and also at 295 and 303 K (Figures 1 and 2). These conditions were previously found to induce a contraction from DUT-49op to DUT-49cp independent of particle size, which has been well studied by in situ PXRD in parallel to adsorption and derived from multiple steps, hysteresis, and spikes in the adsorption isotherms.24

Figure 1.

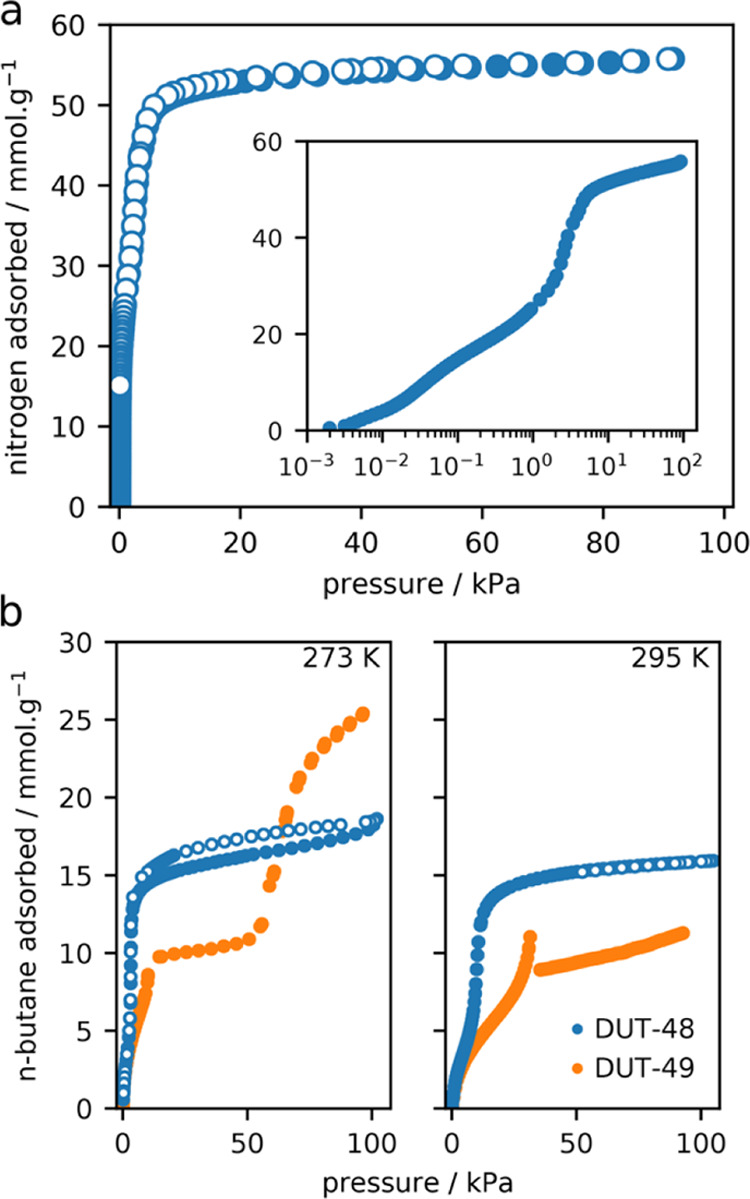
Figure 1

Open in a new tab

(a) Nitrogen adsorption isotherm at 77 K on DUT-48; inset: semilogarithmic. (b) n-Butane adsorption isotherm at 273 and 295 K. Isotherms of DUT-48 and DUT-49 are displayed in blue and orange circles, respectively. Adsorption and desorption are displayed as filled and open symbols, respectively.

Figure 2.

Figure 2

Open in a new tab

n-Butane adsorption isotherm of (a) DUT-48 and (b) DUT-49 at 303 K measured experimentally (circles) and predicted for op and cp phases by GCMC simulations (green and purple lines, respectively). Adsorption enthalpies for n-butane in (c) DUT-48 and (d) DUT-49 determined by calorimetry (circles), calculated by GCMC simulations for op (green line) and cp (purple line) structures.

In the case of DUT-48, adsorption of neither nitrogen nor n-butane induced a structural transition, illustrated by the lack of steps or hysteresis in the isotherms (Figure 1). PXRD measurements after the adsorption experiments showed no sign of structural transitions or decomposition of the pristine material (Figure S6), in contrast to DUT-49.

Analysis of Adsorption and Structure Thermodynamics

Upon contraction in DUT-49, the adsorption enthalpy for n-butane rises from 29.4 kJ·mol–1 for the op structure to over 50 kJ·mol–1 for the cp structure because of the reduction of porosity and increased gas–surface interactions.24 This increase in adsorption enthalpy which was calculated in our original study for DUT-49 as ΔΔH = 153 kJ·mol–1 per ligand compensates for the energy required for the endothermal structural transition that occurs upon NGA.24

To investigate the effect of a smaller pore structure, we monitored the pressure dependence of the adsorption enthalpies for n-butane at 303 K for both DUT-48 and DUT-49 (Figure 2).29 This provides access to experimental isosteric ΔHads of the cp phase in DUT-49 as well as the full profile for DUT-48. The experimentally obtained enthalpies match the values calculated with the van’t Hoff equation well (see the Supporting Information), indicating the validity of the data. A large increase in enthalpy is observed for DUT-49 after NGA because of the stronger interactions of n-butane with the microporous cp phase of DUT-49. However, we are unable to measure the enthalpies of adsorption for both the op and cp phases because the op and, especially, the cp phase are only experimentally present in a constrained pressure region. Thus, enthalpies of adsorption for op and cp phases of DUT-49 and DUT-48 were calculated for adsorption of n-butane using energy/particle fluctuations with GCMC methods (Figure 2). A representative model for a cp-phase of DUT-48 was generated from force-field-based MD simulations (additional details for the model of DUT-48cp are described later).

Simulated adsorption enthalpies track well with the experimental values, allowing for an accurate analysis of the adsorption enthalpies for all structures involved. There is a systematic underestimation of ΔHads by simulation by ca. 20%, as sampling the energetics of flexible n-butane is challenging by Monte Carlo methods—we note here that we used a readily available force field with no adjustment. The experimental ΔHads of DUT-49 shows a clear discontinuity after NGA with a significant increase in adsorption enthalpy. This change corresponds well to the disparate GCMC adsorption enthalpies calculated for the op and cp phases (43.7 and 21.6 kJ·mol–1, respectively). The cp phase of DUT-49 has a significantly higher adsorption enthalpy owing to the drastic reduction in pore size that leads to a significant increase of the host/guest interactions.

Contrastingly, the adsorption enthalpy of DUT-48 follows the behavior of the op phase corresponding to the behavior expected for a nanoporous material matching the profile predicted by GCMC simulations. This behavior can be characterized by an initial increase associated with cooperative adsorption at favorable adsorption sites in the smallest cubaoctahedral pores followed by a decrease once these pores are filled, and subsequently, upon similar cooperate adsorption in the larger pores, there is an increase. Notably, simulation reveals that this final increase occurs at lower pressure in DUT-48 than DUT-49 because of a smaller large pore size. The values obtained from in situ experiment and GCMC simulations are summarized in Table 1.

Table 1. Summary of ΔHads and ΔΔHads Values Determined by Microcalorimetry, Calculation Using Eq 1, and GCMC Simulations for op and cp Structures of DUT-48 and DUT-49 at 10 and 39 kPa, during n-Butane Adsorption at 303 Ka.

  microcalorimetry van’t Hoff (kJ·mol–1) GCMC
DUT-48op 34.6 34.8 27.3
DUT-48cp n.a. n.a. 45.0
DUT-49op 29.4 26.5 21.6
DUT-49cp 51 (±4) n.a. 43.7
ΔΔHads DUT-48 n.a. n.a. 81
ΔΔHads DUT-49 149 (±26) n.a. 153
Open in a new tab
a

van’t Hoff values were determined at loadings of 6.5 and 8.8 mmol·g–1, respectively. Uptakes for calculation of ΔΔHads were 110 and 166 molecules of n-butane per unit cell. ΔΔHads values are given per ligand with 24 ligands per unit cell.

The simulated adsorption enthalpy for the op and cp phases can be used to determine the energy gain, ΔΔHads (eq 1), for a transition from the op to cp phase.

graphic file with name jp8b04549_m001.jpg 1

In agreement with the previous study,24 we find ΔΔHads for n-butane and DUT-49 at ∼39 kPa and 303 K to be at around 150 kJ·mol–1 per ligand. In contrast, for DUT-48, at ∼10 kPa, the potential energy gain is around 80 kJ·mol–1, significantly lower than DUT-49.

In addition to understanding the thermodynamics of adsorption, we have applied molecular simulations to examine the thermodynamics of the DUT-48 framework itself. Total energies were calculated using several constant-volume (N, V, T) MD simulations, and free energies were calculated using thermodynamic integration.43 The resulting energy profiles show two minima for both DUT-49 and DUT-48 (Figure 3), as expected for bistable breathing MOFs.19 The minima at large volumes correspond to the observed crystal structure of the materials (op phase). The second minimum, at small cell volumes, owing to the conformational strain on the ligand is greater in energy than the op phase. Importantly, these simulations highlight that a cp phase for DUT-48 exists with a cell parameter of 32.8 Å, compared to 40.5 Å for the experimental op phase. The cp phase for DUT-48 is approximately 5 kJ·mol–1 per ligand higher in energy than for DUT-49. Additionally, the energy barrier for the op–cp transition is also greater.

Figure 3.

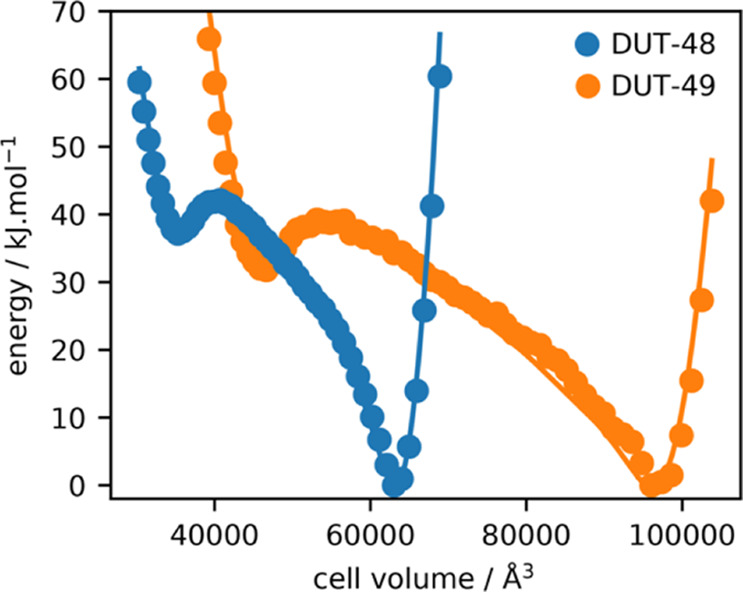
Figure 3

Open in a new tab

Profiles of free and internal energy (solid line and colored circles) obtained from (N, V, T) simulations as a function of unit-cell volume at 300 K. Energy is displayed per ligand.

The comprehensive thermodynamic analysis described here exposes two key differences between DUT-48 and DUT-49 that prevent DUT-48 from undergoing an adsorption-induced transition to a cp phase:

First, the differences in adsorption enthalpies (ΔΔHads) are significantly smaller than that is observed for DUT-49. Second, the proposed cp phase requires a greater unfavorable strain of the building units, resulting in a significantly higher energy state. Although the combination of these two factors results in the rigid adsorption profiles observed for DUT-48, we expect that these factors can be tuned using alternative ligands to produce a stimuli-responsive framework, thus providing the basis for further modification of DUT-49.

Analysis of Mechanical Stability

The adsorption-induced stress on the framework is limited by the extent of the host–guest interactions, as described above. As a result, the presented adsorption experiments for DUT-48 exhibit no structural contraction as the stress is not large enough to compensate for the energy required for a transition to the cp phase, the presence of which is indicated by the MD simulations. Thus, we further investigated the mechanical behavior of DUT-48 and DUT-49 in the absence of adsorbates to analyze if it is possible to contract DUT-48 by external stress, that is, by applying mechanical pressure.

Crystal structures of DUT-49, op, and cp feature a copper paddle wheel environment that is mostly undeformed in the cp structure.24,26 However, the ligand is significantly bent with deformation localized to the biphenyl unit, showing considerable similarity to the buckling behavior of macroscopic columns under load.44 DFT optimizations of the single isolated building unit with a series of fixed decreasing N-atom-to-N atom (N–N) distances has provided excellent insights into the mechanical force required to produce the op–cp transition in DUT-49. We have employed these simulations for the ligands used to form DUT-48 and DUT-49, and the resulting energy–strain curve was used to obtain the stress–strain profiles depicted in Figure 4. The bending of the ligands can be characterized by a “deflection” parameter, which is the N-centroid-N angle. The ligands exhibit two distinct regimes with the application of strain.

Figure 4.

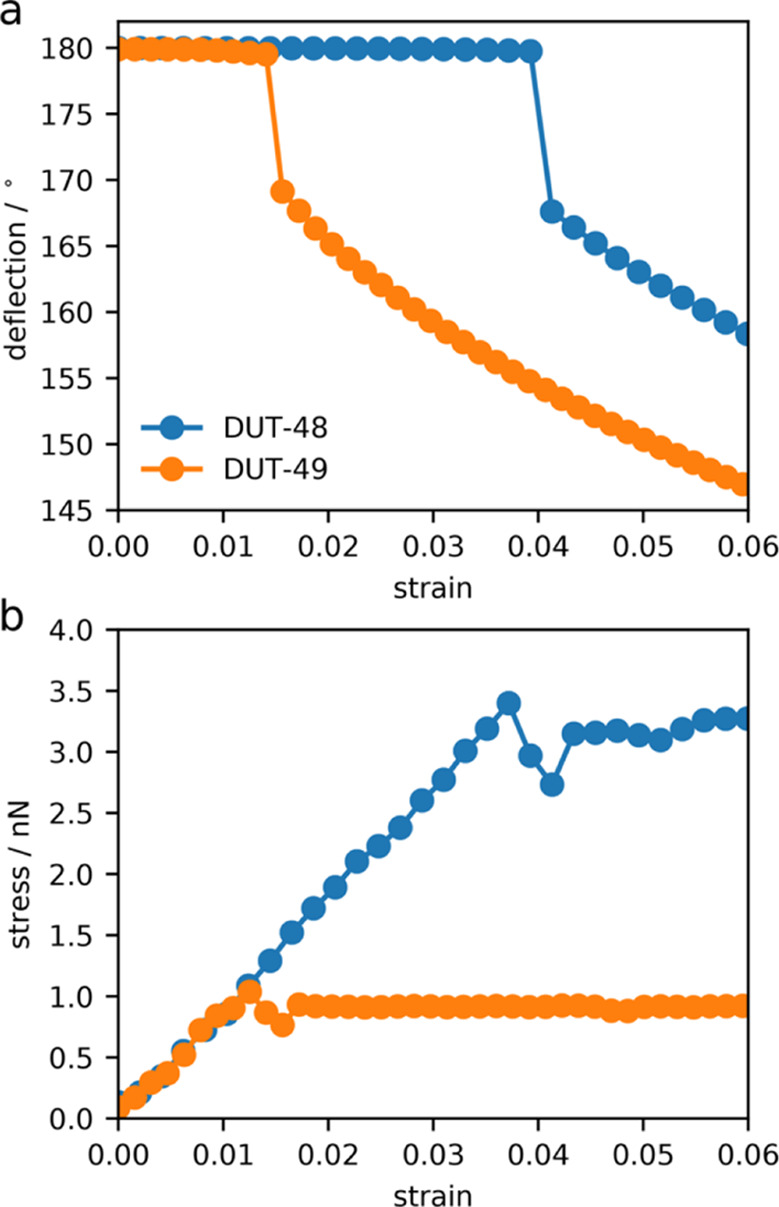
Figure 4

Open in a new tab

(a) Deflection angle for the ligands used to produce DUT-48 and DUT-49, defined as the N-centroid-N angle, for increasing strain. (b) Stress–strain curve of the ligands with increasing axial compression.

First, the elastic regime corresponds to small deformations, resulting in no deflection to the ligand. However, larger deformations produce a buckling phenomenon, resulting in a sudden large deflection of the ligand and distortions of other key bonds lengths and angles illustrated in the Supporting Information. We find here that the smaller ligand of DUT-48 requires almost three times the pressure to produce the buckling event than DUT-49. We note that this result is expected from Euler’s column formula where the stress required to produce buckling is inversely proportional to the length of the column.45 Nevertheless, these results pertain to only a single molecule. To investigate the response of the entire periodic lattice, we consult the constant-volume (N, V, T) MD simulations discussed previously (Figure 5).

Figure 5.

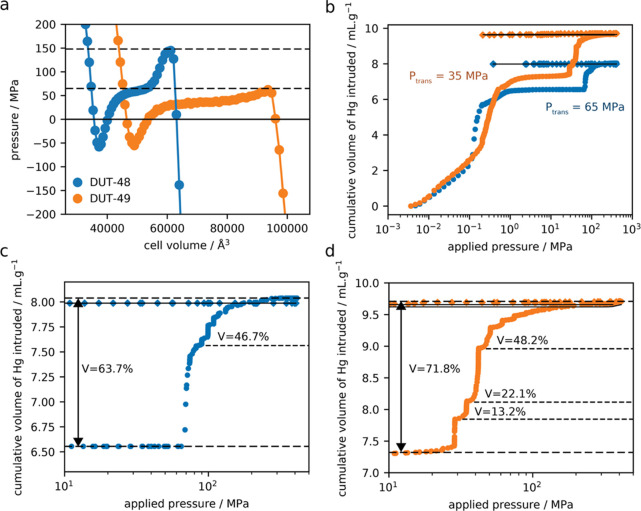
Figure 5

Open in a new tab

(a) Profiles of internal pressure for DUT-48 and DUT-49 obtained from (N, V, T) MD simulations as a function of unit cell volume at 300 K. The transition pressure for an op → cp transition is marked by a dotted line. (b) Cumulative volume of intruded mercury in two intrusion/extrusion cycles as a function of the applied pressure for the activated DUT-48 and DUT-49 (blue and orange, respectively). (c,d) Gradual volume variation of mercury intruded during the contraction show the difference in behavior for DUT-48 two steps (c) and DUT-49 three steps (d). Circles and diamonds correspond to the compression and decompression of the first cycle, respectively, and the black line to the compression–decompression curves of the second cycle.

Notably, the pressure profiles resulting from these simulations confirm the conclusions gained from the study of the adsorption case. DUT-48 requires a transition pressure of ∼150 MPa, significantly greater than that of DUT-49 (∼60 MPa). This transition pressure, while greater than DUT-49, is similar to other flexible frameworks and is achievable experimentally by applying hydrostatic pressure to provide an alternative pathway to adsorbate-induced op–cp transition.

The pressure-induced structural behavior of DUT-48 and DUT-49 was further explored by mercury intrusion which has been established to ensure application of pressure under hydrostatic conditions.8,17 In addition, Hg is a non-wetting fluid that is expected not to enter mesopores in the range of pressure [0–400 MPa] following the Washburn equation to enable the mechanical stability of the evacuated MOF framework. While this structural deformation is a very different mechanism to that attributed to adsorption, we hypothesize the response of the materials are similar. Figure 5b reports the evolution of the cumulative intruded mercury as a function of the applied pressure for two cycles of compression–decompression.

In both cases, the first part of the intrusion curve (<1 MPa) corresponds to the compaction of the powder and filling of the interparticular porosity. Subsequently, there is a second step corresponding to a total volume variation of ∼1.5 mL·g–1 and 2.3 mL·g–1 for DUT-48 and DUT-49, respectively. This is assigned to a contraction of the MOFs because the non-wetting Hg cannot penetrate the mesoporosity of both solids at this pressure. Thus, we assign this change in volume to the contraction of DUT-48 and DUT-49 at ∼65 and ∼35 MPa, respectively. Interestingly, Figure 5 shows a step-wise compression of the two solids. DUT-48 exhibits first increase of the mercury intruded volume associated with a unit cell contraction of ∼46.7%, followed by a stepped one leading to a total unit cell contraction of 63.7%. The compression of DUT-49 is even more progressive with the existence of three intermediate steps associated with a subsequent unit cell contraction of 13.2, 22.1, and 48.2% before reaching a total compression of 71.8% of the unit cell volume. These experimental findings support the predictions for both solids in terms of transition pressures (higher for DUT-48) and show slightly larger volume changes (similar for both MOFs) but within the margin of error of the method because a generic force field was used to describe the flexibility of the MOF architectures, and the pressure differences involved here are very small compared to the usual GPa scale of mechanical properties of stiff materials. The Hg intrusion measurements reveal that the structural transitions are irreversible once the applied pressure is released, and post mortem PXRD and scanning electron microscopy analysis (Figures S7–S9, S17 and S18) show amorphization and deformation of the crystals, suggesting that structural compression beyond the contracted phases occurs.

The so-observed pressure-induced behavior for the two solids corresponds to the scenario of a shock-absorber due to the irreversibility of the structural conversion.3,43 From the transition pressures and associated volume changes experimentally evidenced, we can derive work energies (W = P × ΔV) of 85 and 106 J·g–1 for DUT-48 and DUT-49, respectively. These performances are even more attractive than those of the best MOF materials reported so far for such an application (see Table 2).3,43,46

Table 2. Comparison of the Pressure-Induced Behaviors and the Energy Works Associated with the Structural Switching of Different MOF Materials Reported in the Literature.

MOF material behavior work (J·g–1) reference
silicate reversible nano-spring 11 (47)
ZIF-8–water 13.3 (48)
MIL53(Cr)–BDC 16 (8)
MIL-47(V)–BDC 33 (17)
MIL-53(Al)–FA 60 (16)
       
ZIF-4(Zn) irreversible nano-shock-absorber 4.4 (7)
MIL-53(Al)–BDC 7 (3)
MIL-53(Ga)–FA 9 (43)
DUT-48 85 this work
DUT-49 106 this work
Open in a new tab

Conclusions

In this study, we have synthesized and characterized DUT-48, a highly porous MOF isoreticular to DUT-49 with a reduced ligand length. DUT-48 can store up to 0.27 g·g–1 of methane at 6.5 MPa and 298 K because of its high BET area and pore volume. In contrast to DUT-49, DUT-48 does not undergo a structural transition upon adsorption of nitrogen or n-butane.

We have analyzed the adsorption energetics by microcalorimetry and GCMC simulations and determined that the adsorption energy gained by contraction of the pores in DUT-48 is not sufficient for compensating the energy required for this transition, thus preventing an adsorption-induced structural transition. As a result, neither guest-assisted structural contraction or NGA is observed in DUT-48. Furthermore, we have analyzed the mechanical behavior of DUT-48 and DUT-49 by MD and DFT simulations and found that it takes approximately three times the stress to contract DUT-48 which we relate to the shorter ligand length. In addition, this trend was confirmed by mercury intrusion experiments, showing that a higher pressure is required for DUT-48 (65 MPa) than DUT-49 (35 MPa) to induce a structural transition. Furthermore, the very high measured work energies of 85 and 106 J·g–1 for DUT-48 and DUT-49, respectively, highlight their outstanding potential as future shock-absorbers.

The presented findings provide fundamental insight into structural transition in DUT-49 type structures and importantly link external hydrostatic compression to the energetics of internal adsorption-induced contraction.

Acknowledgments

This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 742743). J.D.E. and F.-X.C. acknowledge PSL Research University for funding (project DEFORM, grant ANR-10-IDEX-0001-02), and HPC platforms were provided by a GENCI grant (A0030807069). P.I. and P.L. want to thank the European Union’s Horizon 2020 research and innovation programme for funding under the Marie Sklodowska-Curie grant agreement no. 641887 (project acronym: DEFNET). The authors thank the ANR/DFG Program FUN for financial support.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcc.8b04549.

  • Additional data and comprehensive experimental and simulation methodology (PDF)

Author Contributions

S.K. and J.D.E. contributed equally. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.

Supplementary Material

jp8b04549_si_001.pdf (4.3MB, pdf)

References

  1. Occelli F.; Loubeyre P.; LeToullec R. Properties of Diamond under Hydrostatic Pressures up to 140 GPa. Nat. Mater. 2003, 2, 151–154. 10.1038/nmat831. [DOI] [PubMed] [Google Scholar]
  2. Wang J.; Stevens R. Zirconia-toughened Alumina (ZTA) Ceramics. J. Mater. Sci. 1989, 24, 3421–3440. 10.1007/bf02385721. [DOI] [Google Scholar]
  3. Yot P. G.; Boudene Z.; Macia J.; Granier D.; Vanduyfhuys L.; Verstraelen T.; Van Speybroeck V.; Devic T.; Serre C.; Férey G.; et al. Metal-Organic Frameworks as Potential Shock Absorbers: The Case of the Highly Flexible MIL-53(Al). Chem. Commun. 2014, 50, 9462–9464. 10.1039/c4cc03853c. [DOI] [PubMed] [Google Scholar]
  4. Maurin G.; Serre C.; Cooper A.; Férey G. The New Age of MOFs and of Their Porous-related Solids. Chem. Soc. Rev. 2017, 46, 3104–3107. 10.1039/c7cs90049j. [DOI] [PubMed] [Google Scholar]
  5. Burtch N. C.; Heinen J.; Bennett T. D.; Dubbeldam D.; Allendorf M. D. Mechanical Properties in Metal-Organic Frameworks: Emerging Opportunities and Challenges for Device Functionality and Technological Applications. Adv. Mater. 2017, 1704124. 10.1002/adma.201704124. [DOI] [PubMed] [Google Scholar]
  6. Li W.; Henke S.; Cheetham A. K. Research Update: Mechanical properties of metal-organic frameworks - Influence of structure and chemical bonding. APL Mater. 2014, 2, 123902. 10.1063/1.4904966. [DOI] [Google Scholar]
  7. Henke S.; Wharmby M. T.; Kieslich G.; Hante I.; Schneemann A.; Wu Y.; Daisenberger D.; Cheetham A. K. Pore Closure in Zeolitic Imidazolate Frameworks under Mechanical Pressure. Chem. Sci. 2018, 9, 1654–1660. 10.1039/c7sc04952h. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Beurroies I.; Boulhout M.; Llewellyn P. L.; Kuchta B.; Férey G.; Serre C.; Denoyel R. Using Pressure to Provoke the Structural Transition of Metal-Organic Frameworks. Angew. Chem., Int. Ed. 2010, 49, 7526–7529. 10.1002/anie.201003048. [DOI] [PubMed] [Google Scholar]
  9. Liu Y.; Her J.-H.; Dailly A.; Ramirez-Cuesta A. J.; Neumann D. A.; Brown C. M. Reversible Structural Transition in MIL-53 with Large Temperature Hysteresis. J. Am. Chem. Soc. 2008, 130, 11813–11818. 10.1021/ja803669w. [DOI] [PubMed] [Google Scholar]
  10. Li H.; Hill M. R. Low-Energy CO2 Release from Metal-Organic Frameworks Triggered by External Stimuli. Acc. Chem. Res. 2017, 50, 778–786. 10.1021/acs.accounts.6b00591. [DOI] [PubMed] [Google Scholar]
  11. Schneemann A.; Bon V.; Schwedler I.; Senkovska I.; Kaskel S.; Fischer R. A. Flexible Metal-Organic Frameworks. Chem. Soc. Rev. 2014, 43, 6062–6096. 10.1039/c4cs00101j. [DOI] [PubMed] [Google Scholar]
  12. Chang Z.; Yang D.-H.; Xu J.; Hu T.-L.; Bu X.-H. Flexible Metal-Organic Frameworks: Recent Advances and Potential Applications. Adv. Mater. 2015, 27, 5432–5441. 10.1002/adma.201501523. [DOI] [PubMed] [Google Scholar]
  13. Vanduyfhuys L.; Rogge S. M. J.; Wieme J.; Vandenbrande S.; Maurin G.; Waroquier M.; Van Speybroeck V. Thermodynamic Insight into Stimuli-responsive Behaviour of Soft Porous Crystals. Nat. Commun. 2018, 9, 204. 10.1038/s41467-017-02666-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Su Z.; Miao Y.-R.; Zhang G.; Miller J. T.; Suslick K. S. Bond Breakage under Pressure in a Metal Organic Framework. Chem. Sci. 2017, 8, 8004–8011. 10.1039/c7sc03786d. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Öhrström L. Framework Chemistry Transforming our Perception of the Solid State. ACS Cent. Sci. 2017, 3, 528–530. 10.1021/acscentsci.7b00230. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Yot P. G.; Vanduyfhuys L.; Alvarez E.; Rodriguez J.; Itié J.-P.; Fabry P.; Guillou N.; Devic T.; Beurroies I.; Llewellyn P. L.; et al. Mechanical Energy Storage Performance of an Aluminum Fumarate Metal-Organic Framework. Chem. Sci. 2016, 7, 446–450. 10.1039/c5sc02794b. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Yot P. G.; Ma Q.; Haines J.; Yang Q.; Ghoufi A.; Devic T.; Serre C.; Dmitriev V.; Férey G.; Zhong C.; et al. Large Breathing of the MOF MIL-47(VIV) under Mechanical Pressure: A Joint Experimental-modelling Exploration. Chem. Sci. 2012, 3, 1100–1104. 10.1039/c2sc00745b. [DOI] [Google Scholar]
  18. Rodriguez J.; Beurroies I.; Loiseau T.; Denoyel R.; Llewellyn P. L. The Direct Heat Measurement of Mechanical Energy Storage Metal-Organic Frameworks. Angew. Chem., Int. Ed. 2015, 54, 4626–4630. 10.1002/anie.201411202. [DOI] [PubMed] [Google Scholar]
  19. Bousquet D.; Coudert F.-X.; Boutin A. Free Energy Landscapes for the Thermodynamic Understanding of Adsorption-induced Deformations and Structural Transitions in Porous Materials. J. Chem. Phys. 2012, 137, 044118. 10.1063/1.4738776. [DOI] [PubMed] [Google Scholar]
  20. Neimark A. V.; Coudert F.-X.; Triguero C.; Boutin A.; Fuchs A. H.; Beurroies I.; Denoyel R. Structural Transitions in MIL-53 (Cr): View from Outside and Inside. Langmuir 2011, 27, 4734–4741. 10.1021/la200094x. [DOI] [PubMed] [Google Scholar]
  21. Férey G.; Serre C. Large Breathing Effects in Three-dimensional Porous Hybrid Matter: Facts, Analyses, Rules and Consequences. Chem. Soc. Rev. 2009, 38, 1380–1399. 10.1039/b804302g. [DOI] [PubMed] [Google Scholar]
  22. Férey G.; Serre C.; Devic T.; Maurin G.; Jobic H.; Llewellyn P. L.; De Weireld G.; Vimont A.; Daturi M.; Chang J.-S. Why Hybrid Porous Solids Capture Greenhouse Gases?. Chem. Soc. Rev. 2011, 40, 550–562. 10.1039/c0cs00040j. [DOI] [PubMed] [Google Scholar]
  23. Yot P. G.; Yang K.; Guillerm V.; Ragon F.; Dmitriev V.; Parisiades P.; Elkaïm E.; Devic T.; Horcajada P.; Serre C.; et al. Impact of the Metal Centre and Functionalization on the Mechanical Behaviour of MIL-53 Metal-Organic Frameworks. Eur. J. Inorg. Chem. 2016, 4424–4429. 10.1002/ejic.201600263. [DOI] [Google Scholar]
  24. Krause S.; Bon V.; Senkovska I.; Stoeck U.; Wallacher D.; Többens D. M.; Zander S.; Pillai R. S.; Maurin G.; Coudert F.-X.; et al. A Pressure-amplifying Framework Material with Negative Gas Adsorption Transitions. Nature 2016, 532, 348–352. 10.1038/nature17430. [DOI] [PubMed] [Google Scholar]
  25. Schaber J.; Krause S.; Paasch S.; Senkovska I.; Bon V.; Többens D. M.; Wallacher D.; Kaskel S.; Brunner E. In Situ Monitoring of Unique Switching Transitions in the Pressure-Amplifying Flexible Framework Material DUT-49 by High-Pressure 129Xe NMR Spectroscopy. J. Phys. Chem. C 2017, 121, 5195–5200. 10.1021/acs.jpcc.7b01204. [DOI] [Google Scholar]
  26. Evans J. D.; Bocquet L.; Coudert F.-X. Origins of Negative Gas Adsorption. Chem 2016, 1, 873–886. 10.1016/j.chempr.2016.11.004. [DOI] [Google Scholar]
  27. Stoeck U.; Senkovska I.; Bon V.; Krause S.; Kaskel S. Assembly of Metal-Organic Polyhedra into Highly Porous Frameworks for Ethene Delivery. Chem. Commun. 2015, 51, 1046–1049. 10.1039/c4cc07920e. [DOI] [PubMed] [Google Scholar]
  28. Lu W.; Yuan D.; Makal T. A.; Wei Z.; Li J.-R.; Zhou H.-C. Highly Porous Metal-Organic Framework Sustained with 12-connected Nanoscopic Octahedra. Dalton Trans. 2013, 42, 1708–1714. 10.1039/c2dt32479b. [DOI] [PubMed] [Google Scholar]
  29. Llewellyn P. L.; Maurin G. Gas Adsorption Microcalorimetry and Modelling to Characterise Zeolites and Related Materials. C. R. Chim. 2005, 8, 283–302. 10.1016/j.crci.2004.11.004. [DOI] [Google Scholar]
  30. Dovesi R.; Orlando R.; Erba A.; Zicovich-Wilson C. M.; Civalleri B.; Casassa S.; Maschio L.; Ferrabone M.; De La Pierre M.; D’Arco P.; et al. CRYSTAL14: A program for theab initioinvestigation of crystalline solids. Int. J. Quantum Chem. 2014, 114, 1287–1317. 10.1002/qua.24658. [DOI] [Google Scholar]
  31. Peintinger M. F.; Oliveira D. V.; Bredow T. Consistent Gaussian Basis Sets of Triple-zeta Valence with Polarization Quality for Solid-state Calculations. J. Comput. Chem. 2013, 34, 451–459. 10.1002/jcc.23153. [DOI] [PubMed] [Google Scholar]
  32. Adamo C.; Barone V. Toward Reliable Density Functional Methods Without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158–6170. 10.1063/1.478522. [DOI] [Google Scholar]
  33. Grimme S. Semiempirical GGA-type Density Functional Constructed with a Long-range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]
  34. Dubbeldam D.; Calero S.; Ellis D. E.; Snurr R. Q. RASPA: Molecular Simulation Software for Adsorption and Diffusion in Flexible Nanoporous Materials. Mol. Simul. 2016, 42, 81–101. 10.1080/08927022.2015.1010082. [DOI] [Google Scholar]
  35. Rappe A. K.; Casewit C. J.; Colwell K. S.; Goddard W. A.; Skiff W. M. UFF, a Full Periodic Table Force Field for Molecular Mechanics and Molecular Dynamics Simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. 10.1021/ja00051a040. [DOI] [Google Scholar]
  36. Keasler S. J.; Charan S. M.; Wick C. D.; Economou I. G.; Siepmann J. I. Transferable Potentials for Phase Equilibria-United Atom Description of Five- and Six-Membered Cyclic Alkanes and Ethers. J. Phys. Chem. B 2012, 116, 11234–11246. 10.1021/jp302975c. [DOI] [PubMed] [Google Scholar]
  37. Bureekaew S.; Amirjalayer S.; Tafipolsky M.; Spickermann C.; Roy T. K.; Schmid R. MOF-FF - A flexible first-principles derived force field for metal-organic frameworks. Phys. Status Solidi B 2013, 250, 1128–1141. 10.1002/pssb.201248460. [DOI] [Google Scholar]
  38. Plimpton S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. 10.1006/jcph.1995.1039. [DOI] [Google Scholar]
  39. Boyd P. G.; Moosavi S. M.; Witman M.; Smit B. Force-Field Prediction of Materials Properties in Metal-Organic Frameworks. J. Phys. Chem. Lett. 2017, 8, 357–363. 10.1021/acs.jpclett.6b02532. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Grünker R.; Bon V.; Müller P.; Stoeck U.; Krause S.; Mueller U.; Senkovska I.; Kaskel S. A New Metal-Organic Framework with Ultra-high Surface Area. Chem. Commun. 2014, 50, 3450–3452. 10.1039/c4cc00113c. [DOI] [PubMed] [Google Scholar]
  41. Stoeck U.; Krause S.; Bon V.; Senkovska I.; Kaskel S. A Highly Porous Metal-Organic Framework, Constructed from a Cuboctahedral Super-molecular Building Block, with Exceptionally High Methane Uptake. Chem. Commun. 2012, 48, 10841–10843. 10.1039/c2cc34840c. [DOI] [PubMed] [Google Scholar]
  42. Krause S.; Bon V.; Senkovska I.; Többens D. M.; Wallacher D.; Pillai R. S.; Maurin G.; Kaskel S. The Effect of Crystallite Size on Pressure Amplification in Switchable Porous Solids. Nat. Commun. 2018, 9, 1573. 10.1038/s41467-018-03979-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Ramaswamy P.; Wieme J.; Alvarez E.; Vanduyfhuys L.; Itié J.-P.; Fabry P.; Van Speybroeck V.; Serre C.; Yot P. G.; Maurin G. Mechanical Properties of a Gallium Fumarate Metal-Organic Framework: A Joint Experimental-modelling Exploration. J. Mater. Chem. A 2017, 5, 11047–11054. 10.1039/c7ta01559c. [DOI] [Google Scholar]
  44. Eisley J. G.; Waas A. M.. Forces and Moments. Analysis of Structures; John Wiley & Sons, Ltd, 2011; pp 1–33. [Google Scholar]
  45. Shigley J. E.Shigley’s Mechanical Engineering Design; Tata McGraw-Hill Education, 2011. [Google Scholar]
  46. Ortiz G.; Nouali H.; Marichal C.; Chaplais G.; Patarin J. Energetic Performances of “ZIF-71-Aqueous Solution” Systems: A Perfect Shock-Absorber with Water. J. Phys. Chem. C 2014, 118, 21316–21322. 10.1021/jp505484x. [DOI] [Google Scholar]
  47. Tzanis L.; Nouali H.; Daou T. J.; Soulard M.; Patarin J. Influence of the Aqueous Medium on the Energetic Performances of Silicalite-1. Mater. Lett. 2014, 115, 229–232. 10.1016/j.matlet.2013.10.063. [DOI] [Google Scholar]
  48. Ortiz G.; Nouali H.; Marichal C.; Chaplais G.; Patarin J. Energetic performances of the metal-organic framework ZIF-8 obtained using high pressure water intrusion-extrusion experiments. Phys. Chem. Chem. Phys. 2013, 15, 4888–4891. 10.1039/c3cp00142c. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp8b04549_si_001.pdf (4.3MB, pdf)

Articles from The Journal of Physical Chemistry. C, Nanomaterials and Interfaces are provided here courtesy of American Chemical Society

RESOURCES