Abstract
The COVID-19 pandemic has led to exponential growth in COVID-19 medical waste (CMW) generation worldwide. This tremendous growth in CMW is a major transmission medium for COVID-19 virus and thus brings serious challenges to medical waste (MW) management. Designing an efficient and reliable CMW reverse supply chain in this situation can help to prevent epidemic spread. Nowadays, the assessment of CMW recycling channels has become a challenging mission for health-care institutions, especially in developing countries. It can be seen as a complex multi-criteria group decision-making (MCGDM) problem that requires the consideration of multiple conflicting tangible and intangible criteria. Nevertheless, few academics have been concerned about this issue. Moreover, current MCGDM methods have limited support for CMW recycling channel evaluation and they do not consider hospitals’ reverse supply chain strategy when evaluating. Thus, this study presents a novel MCGDM approach based on intuitionistic fuzzy sets (IFSs) and the VIKOR method for assessing the capacity of CWM recycling channels. According to the characteristics of CMW, processing flow and the TOE (Technology, Organization and Environment) theoretical framework, we established a new CMW recycling channel capacity evaluation index system which makes our proposed method more targeted and efficient. In the decision-making process, we integrate the best-worst method (BWM) and entropy to determine the decision makers (DMs) weighting in a more comprehensive way, considering both subjective and objective criteria, which was ignored by many MCGDM methods. A new aggregation operator called IFWA is proposed by us, considering the priority of DMs. Based on both the ranking of capacity and disposal charges, we then position the alternatives in the recycling channel priority index (RCPI) matrix constructed by us. According to this PCPI matrix and the reverse supply chain strategy of hospitals, a more reasonable CMW allocation strategy is determined and a more efficient CMW reverse supply chain is designed. Finally, a real case study from Wuhan was examined to illustrate the validation of our approach.
Keywords: COVID-19 medical waste allocation, MCGDM, COVID-19 medical waste recycling channel, Reverse supply chain strategy
1. Introduction
Since December 2019, the emergence of COVID-19 has attracted global attention and has enormously affected the world, threatening the health of the world population (Peng et al., 2020). This deadly virus has quickly spread to over 200 countries across the globe and has caused sudden panic among the public (Ahmadi et al., 2020). As of 22 April 2021, it wiped out millions of individuals worldwide, leaving behind 144,485,725 people infected by the unexpected disaster (Organization, 2021). With the sudden explosion of healthcare services demand, disposable personal protective equipment (PPE) has been swiftly consumed (WHO, 2020), which has resulted in an exponential increase in CMW production throughout the world (GW and LM, 2020, Tirkolaee et al., 2020, Yu et al., 2020, Zhao et al., 2021). Additionally, the high number of COVID-19-infected patients has also led to an explosion of CMW in healthcare establishments (Peng et al., 2020).
CMW is hazardous to both health and the environment (Das et al., 2021, Das et al., 2021). If it is not managed efficiently or disposed of in an environmentally sound manner, it could cause serious problems for patients, waste-related workers and the general public (Ahmadi et al., 2020, Ramteke and Sahu, 2020, Wang et al., 2020). Concretely, inefficient CMW management can accelerate the proliferation of COVID-19 and endanger the environment. Hence, the explosion of CMW creates a great challenge in MW management, especially in developing countries (Dharmaraj et al., 2021, GW and LM, 2020). Therefore, the issue of CMW management should be given as much attention as medical research; otherwise, all of the effort of the international community to fight against the COVID-19 pandemic will be invalidated (C. Chen et al., 2021). CMW recycling is one of the most efficient and feasible means to manage CMW and control the source of infection (Peng et al., 2020, Tirkolaee et al., 2020, Zhao et al., 2021). Dharmaraj et al. (2021) argued that CMW can be transformed into value added products such as oil, electricity, gas and char by means of pyrolysis, combustion, and other methods. Several notable examples involve incinerator ash from MW, which has been used for manufacturing Portland cement (Rowan & Laffey, 2021). Furthermore, many recycling channels use plastic medical waste, such as disposable gowns, syringes and personal protective equipment to generate valuable energy-producing products or use organic MW to obtain compost and bioenergy (Das et al., 2021, Das et al., 2021, Dharmaraj et al., 2021). In general, disposing of products at the end of their lifecycle when they might threaten the environment and the health of the public is called the reverse supply chain (Kargar et al., 2020). To this extent, the CMW recycling issue falls into the category of reverse supply chain management (Kargar et al., 2020, Yu et al., 2020). Hence, recycling the CMW and designing an efficient CMW reverse supply chain in this situation is quite urgent.
Because hospitals are the major source of CMW and are high-risk areas of the COVID-19 pandemic (Dharmaraj et al., 2021), the issue of designing a CMW reverse supply chain has become a major concern for its authority (Yazdani et al., 2020). However, most of these hospitals do not have enough handling time and space to contain and properly recycle CMW (Thakur & Ramesh, 2015). In their view, outsourcing the CMW disposal and recycling process is the best option, and the trend of outsourcing is increasing now (Thakur & Ramesh, 2015). To avoid the spread of the COVID-19 virus and to seek green development, hospitals prefer to cooperate with competent CMW recycling channels. However, this process is not easy for hospital authorities, because it is very difficult to evaluate the CMW recycling channels and allocate the CMW generated reasonably by considering multiple government regulations and cost effectiveness at the same time (Thakur & Ramesh, 2015).
In recent years, the issue of MW management has been explored by a great number of scholars, and many MCGDM methods have been introduced into this research area. However, most of the MCGDM methods proposed by the above scholars are used to address the assessment of MW management (Baghapour et al., 2018, Ouyang et al., 2021) and disposal alternatives (Manupati et al., 2021, Shi et al., 2017). Through the literature review, we found that there are still relatively few MCGDM articles on the evaluation of MW recycling channels and the existing relative literature still has some limitations: (1) The evaluation index system of CMW recycling channels is not sound enough. Due to the longer survival time and greater infectivity, CMW should not be disposed of as other common MW. However, there is no targeted and proper CMW recycling channel capacity evaluation index system in existing researches and the supporting role of the existing methods for assessing CMW recycling channels is limited. (2) Few scholars have considered the criteria weights and DM weights simultaneously when studying MCGDM problems. And when calculating the criteria weights, the majority of scholars tend to adopt a single subjective or objective method, ignoring their combination, which may cause the influence of several factors to be enhanced or weakened and then affect the result accuracy. (3) Scholars did not consider the enterprises’ reverse supply chain strategy when evaluating, which present challenges for hospitals to select CMW recycling channels. In reality, there are often differences in the reverse supply chain strategies of different healthcare organizations, which will affect their CMW recycling channel selection. The assessment result obtained by considering only the capacity without considering the reverse supply chain strategies are often not the most effective one.
Thus, there is an urgent need for a new decision-making method to help hospitals segment CMW recycling channels and achieve a more reasonable allocation of CMW. To fill the above research gap, we propose a hybrid MCGDM approach based on intuitionistic fuzzy sets (IFSs), which take the hospitals’ reverse supply chain strategies into account. It is a new analysis framework based on a new CMW recycling channel capacity evaluation index system, the VIKOR method and a proposed RCPI matrix for CMW recycling channel selection. Specially, according to the idea of combining subjective and objective issues at the same time, we integrate the best-worst method (BWM) and entropy to determine the decision makers (DMs) weighting in a more comprehensive way, considering both subjective and objective criteria, which was ignored by many MCGDM methods. Next, the aggregation operator IFWA is utilized to aggregate the individual judgements of DMs into an integrated weighting IF decision matrix. Based on both the ranking of capacity and disposal charges, we then position the alternatives in the recycling channel priority index (RCPI) matrix constructed by us. According to this PCPI matrix and the reverse supply chain strategy of the alternatives, a more reasonable CMW allocation strategy is determined.
The contributions and novelty of our study are threefold: (1) According to the characteristics of CMW, processing flow and the TOE theoretical framework, we established a new CMW recycling channel capacity evaluation criterion system which makes our proposed method more targeted and efficient. Specially, a targeted six-dimensional evaluation criterion system for CMW recycling channels is proposed. The evaluation criterion can comprehensively measure the capacity of CMW recycling channels from multiple aspects (Technology, Organization and Environment). (2) To address challenges of CMW recycling channel selection, we propose a novel decision-making framework based on a new CMW recycling channel capacity evaluation index system, IFSs, the VIKOR method and a proposed RCPI matrix. This framework incorporated the idea of customer segmentation into the MW recovery field to prioritize the CMW allocation process and take the hospitals’ reverse supply chain strategies into account. Based on the capacity and disposal charges, the CWM recycling channel alternatives are placed into a priority index matrix (RCPI) matrix constructed by us and are segmented into four types. According to this PCPI matrix and the reverse supply chain strategy of the alternatives, a more reasonable and referable decision framework for healthcare institutions to solve the problem of evaluating waste recycling channels and allocating CMW was established. (3) We propose a novel weighting method for our decision-making framework, which assigns weights both from criteria and DMs dimensions simultaneously, making our research results more accurate. Meanwhile, our integrated BWM-Entropy-VIKOR method objectively and subjectively considers the criteria of CMW recycling channels and determines the criteria weights jointly with the IF-BWM and IF-entropy weight methods criteria.
The remainder of this paper is arranged as follows: Section 2 is the related work. Section 3 proposes the assessment criteria for CMW recycling channels. Section 4 gives an introduction to the general procedure of the method proposed in this paper. A real case study from Wuhan is shown in Section 5 to illustrate our decision support framework. Section 6 compares this method with other methods, and finally, Section 7 presents some conclusions.
2. Related work
2.1. CMW(COVID-19 Medical Waste)
Generally, MW refers to potentially infectious waste generated from hospitals, mortuaries, blood banks, research centers, autopsy centers, laboratories and other facilities relating to medical procedures (Das et al., 2021, Das et al., 2021, Windfeld and Brooks, 2015, Xiao, 2018). It includes hazardous and non-hazardous waste such as sharps, chemical waste, pressurized containers, genotoxic waste, blood, pharmaceutical waste and healthcare devices (Das et al., 2021, Das et al., 2021). COVID-19 is caused by a newly discovered virus called SARS-CoV-2. Compared to other viruses, SARS-CoV-2 is more pathogenic and infectious. In addition, it has a longer survival time on hard surfaces (Dharmaraj et al., 2021). According to previous studies, the SARS-CoV-2 virus can survive on plastic or stainless objects for more than 48 h (Kampf et al., 2020). Hence, considering that more waste could carry this type of virus, the definition of CMW is expanded on the basis of MW (Dharmaraj et al., 2021, Nzediegwu and Chang, 2020). Nzediegwu and Chang (2020) argued that all of the waste related to medical staff, infected patients, and waste related workers during the COVID-19 pandemic should be classified as CMW (Nzediegwu & Chang, 2020), including but not limited to masks, medical gowns, and disposable cutlery. Then, CMW dramatically increased due to the expansion of the definition and the growth in the number of confirmed cases as well as their isolated close contacts.
In this paper, the CMW is classified as follows:
-
(1)
Hazardous CMW:
It can be divided into chemical CMW, infectious CMW, pathological CMW, radioactive CMW, sharps CMW as well as pharmaceutical CMW (Dharmaraj et al., 2021). Specifically, MW which contains some chemical substances is regarded as chemical CMW. In the COVID-19 period, the MW generated from personal protective equipment such as boots, gloves, masks and goggles was regarded as infectious CMW (Das et al., 2021, Das et al., 2021). Pathological CMW is typically a SARS-CoV-2-related sample of tissue in the laboratory. Radioactive CMW is the waste generated by health care facilities when performing radiological work. It is worthwhile to note that the radiopharmaceuticals stored in the patient's body are excreted in the urine and feces, which should also be regarded as radioactive CMW. Sharps CMW includes used ‘sharps’ such as needles, scalpels and infusion sets. Expired and contaminated pharmaceutical products are regarded as pharmaceutical CMW.
Although each type of hazardous CMW has different characteristics, they could lead to widespread transmission of the COVID-19 virus if not disposed of properly (Tripathi et al., 2020).
-
(2)
Non-hazardous CMW:
If the CMW generated in hospitals has not been in contact with hazardous CMW, it can be considered to be a non-hazardous CMW. Generally, a non-hazardous CMW is quite similar to a common domestic MW and thus can be disposed of by certain CMW recycling channels in a green way. Both asymptomatic patients and confirmed cases might generate a large amount of non-hazardous CMW during their daily life in hospitals, which poses potential and serious risks to the community and public. Some newspapers that use plastic packaging and food waste can be regarded as non-hazardous CMW (Manupati et al., 2021).
-
(3)
Other waste.
Test kits for COVID-19 can also be considered to be a special type of CMW. If not handled properly, these test kits could bring a COVID-19 breakout worldwide (G & L, 2020).
Based on scientific databases, there are many studies related to CMW (Dharmaraj et al., 2021, Nzediegwu and Chang, 2020), most of which are in the medical area. Alongside knowing the CMW and finding a proper disposal technique for it, when the COVID-19 pandemic outbreak occurred, assessing the CMW recycling channels and allocating CMW in a more reasonable way also became necessary.
2.2. Reverse supply chain MW management
Medical waste (MW) management is a complex process that includes MW collection, transport route identification, disposal site location, treatment technology selection and valuable energy recovery (Shi et al., 2017). In recent years, as public awareness in regard to green development implications has risen, the issue of MW management has received more academic attention worldwide. For example, Peng et al. (2020) emphasized the need for sound disposal of CMW and proposed various measures to manage CMW. Dharmaraj et al. (2021), after comparing various techniques used to treat CMW, proposed that pyrolysis could achieve recycling of CMW and is an efficient and environmentally friendly treatment technology for CMW management. We reviewed the literature on MW management in recent years and presented some of the studies in Table 2 . Table 2 clearly shows that the majority of existing research in the field of MW management is still conceptual and expository (Dharmaraj et al., 2021, Peng et al., 2020), and is devoted to the interpretation of the problems, necessities and concrete measures of waste management. However, many scholars have recognized the importance of the MCGDM approach to MW management efficiency. They attempted to introduce some MCGDM methods to the field of MW management for MW management optimization (see Table 3 ).
Table 2.
Literature Review of Medical Waste Management.
| Representative literature | Main Research Topics |
||||
|---|---|---|---|---|---|
| Conceptual and expository research | Operations research -based research on MW management optimization | Algorithm-based location-routing research for MW disposal facilities | Case study-based research on MW management | MCGDM-based research on MW management | |
| (Peng et al., 2020) | √ | ||||
| (Tirkolaee et al., 2020) | √ | ||||
| (Das et al., 2021, Das et al., 2021) | √ | ||||
| (Kargar et al., 2020) | √ | ||||
| (Dharmaraj et al., 2021) | √ | ||||
| (Chen et al., 2021) | √ | ||||
| (Mantzaras & Voudrias, 2017) | √ | ||||
| (Lee et al., 2016) | √ | ||||
| (Mishra, Rani, et al., 2020) | √ | ||||
| (Manupati et al., 2021) | √ | ||||
| This study | √ | ||||
Table 3.
Reviews representative MCGDM literature on MW disposal and recycling.
| Representative literature | linguistic set | Main Research Topics |
Method | |||
|---|---|---|---|---|---|---|
| Assessment of MW management and Disposal Alternatives | The Location of Medical Waste Disposal sites | Assessment of waste disposal facilities | Assessment of MW recycling channels | |||
| (Yazdani et al., 2020) | IRN | √ | IRN D’Bonferroni approach | |||
| (Mishra, Rani, et al., 2020) | IVIFSs | √ | COPRAS | |||
| (Wichapa & Khokhajaikiat, 2017) | TFNs | √ | FAHP | |||
| (Thakur & Ramesh, 2015) | GN | √ | Grey Theory | |||
| (Lee et al., 2016) | × | √ | AHP | |||
| (Mishra, Mardani, et al., 2020) | IFSs | √ | EDAS | |||
| (Shi et al., 2017) | IT2 FSs | √ | MABAC | |||
| (Manupati et al., 2021) | IFSs | √ | VIKOR | |||
| (Narayanamoorthy et al., 2020) | HFS | √ | MOOSRA | |||
| This study | IFSs | √ | VIKOR | |||
This review of the existing literature indicates that most scholars used the MCGDM approach for the assessment of MW management (Baghapour et al., 2018, Ouyang et al., 2021), MW treatment alternatives (Manupati et al., 2021, Shi et al., 2017) and the location of MW disposal sites (Tirkolaee et al., 2020). At present, there is a lack of effective reverse supply chain design for MW during pandemics. Because more than 200 countries are fighting the COVID-19 pandemic, there is an urgent need for such a CMW reverse supply chain network, to make it possible for the outbreak to be controlled in this direction. In fact, there have been many articles in the area of reverse supply chain waste management (Kargar et al., 2020, Yu et al., 2020). However, as the field of study narrows down, there are fewer studies on reverse supply chain optimization for MW.
In essence, the selection of appropriate CMW recycling channels can be seen as a sophisticated MCGDM problem that requires the consideration of many potential and conflicting evaluation criteria e.g., cost, capability, and environment. Unfortunately, very few scholars have proposed MCGDM methods for assessing MW recycling channels and there are many limitations in these methods. To the author's knowledge, in recent years, only Thakur and Ramesh (2015) included the assessment of MW disposal enterprises in the study of MCGDM, and proposed a developed MCGDM method for selecting MW disposal enterprises with grey theory. More specifically, the criteria systems used in the existing literature for assessing MW recycling channels are not comprehensive enough to consider economic, social and capacity factors. Moreover, most of them do not account for the differences in recycling fees for different types of MW by recycling channels. More importantly, due to the longer survival time and greater infectivity, the evaluation criteria systems for CMW recycling channels will be quite different from those for common MW. However, there is no targeted and proper CMW recycling channel capacity evaluation index system in existing researches. Thus, the supporting role of the existing MCGDM methods for assessing CMW recycling channels is limited.
In addition, scholars did not consider the enterprises’ reverse supply chain strategy when evaluating, which present challenges for hospitals to select CMW recycling channels. In reality, there are often differences in the reverse supply chain strategies of different healthcare organizations, which will affect their CMW recycling channel selection. The assessment result obtained by considering only the capacity without considering the reverse supply chain strategies are often not the most effective one. Meanwhile, no scholar has yet incorporated the idea of customer segmentation into the MW recovery field to prioritize CMW allocation by segmenting CMW recycling channels based on the MCGDM method. Hence, we constructed an RCPI matrix and proposed a developed MCGDM method to help healthcare institutions segment CMW recycling channels and achieve a more reasonable allocation of CWM.
2.3. MCGDM (Multi-Criteria Group Decision-Making)
From the above analysis, we find few studies on the assessment and selection of medical waste recycling channels. It is necessary for global healthcare institutions to adopt scientific and reasonable evaluation tools for assessing the performance of different MW recycling channels and allocating CMW in a more effective way. In essence, because both quantitative and qualitative factors should be considered, the MW recycling channel selection problem is an MCGDM problem (Mishra et al., 2020, Tremblay and Badri, 2018).
In recent decades, the MCGDM approach has been applied by many scholars in the field of waste management (Mardani et al., 2019, Torkayesh et al., 2021). However, Mardani et al. (2019) reported that most of these MCGDM methods used the conventional analytic hierarchy process (AHP) for decision making. Yazdani et al. (2020) argued that the BWM has advantages over the majority of conventional MCGDM techniques, such as the AHP and decision-making trial and evaluation laboratory (DEMATEL) for weight elicitation because it is simpler, requires less pairwise comparison data, and generates more reliable and consistent processing results. Thus, we use the BWM as a subjective method for determining the criteria weight in this study.
In practical situations, due to the uncertainty and complexity of decision-making issues and the vagueness of public recognition and feelings, decision makers have great difficulty in indicating their preference with crisp numerical values and accurately assessing how to convey the recognition and feelings of criteria and alternatives (Rani et al., 2019). Hence, decision makers tend to apply some linguistic sets to express their views and to assess the alternatives (Mishra et al., 2019, Rani et al., 2019). Recently, many scholars have attempted to employ the fuzzy set theory proposed by Zadeh (1965) to address the vagueness and uncertainty that can appear in MW management problems (Mardani et al., 2019, Mishra et al., 2020).
However, fuzzy sets (FSs) are represented only in terms of membership degrees, and they do not have the capability of expressing both pro- and con-decision-making information simultaneously. To address this problem, Atanassov (1986) developed intuitionistic fuzzy sets (IFSs), which were described by the membership degree (MD), non-membership degree (ND), and hesitation. IFSs have received more attention from researchers because of their ability to address ambiguity and have been discussed in many research areas, including but not limited to manufacturing (Dixit and Raj, 2018, Wu et al., 2019), sustainable supply chains (Amini et al., 2019, Mishra et al., 2019) and MW recycling (Mishra et al., 2020, Xiao, 2018). In recent years, several studies have been conducted to select suitable MW treatment techniques that have used IFS-based linguistic values to describe decision makers’ opinions. For example, Mishra, Mardani, et al. (2020) proposed a novel EDAS method based on IFSs called IF-EDAS to select the best MW disposal. Then in 2021, Manupati et al. (2021) proposed a fuzzy VIKOR method under intuitionistic fuzzy sets which was used to evaluate MW disposal techniques. Therefore, we choose the IFSs to address the ambiguity in the evaluation of CMW recycling channels.
The VIKOR method, an important MCGDM approach, was first proposed by S. Opricovic (1998) to solve discrete decision problems with conflicting and non-commensurable criteria. This MCGDM method is used to rank and select from several alternatives, and then obtain a compromise solution for the decision-making problem with conflicting criteria, which helps us to reach a reasonable decision (Serafim Opricovic & Tzeng, 2007). Compromise solutions are feasible solutions, which are the closest solutions to the ideal solutions. A compromise is a protocol established by mutual concessions (H.-C. Liu et al., 2013). One of the most important strengths of the VIKOR is that it introduces multi-criteria ranking indices under the specific measure of the ‘‘closeness’’ to the ideals (Serafim Opricovic & Tzeng, 2004), and the obtained compromise solution brings a maximum group utility to the ‘‘majority’’ while bringing a minimum individual regret to the ‘‘opponent’’. Due to the above characteristics and advantages, applications of the VIKOR method are becoming increasingly widespread. In our study, we applied the IF-VIKOR method, which was proposed for solving the multi-criteria optimization problem of complex systems, to obtain a compromised priority ranking of CMW recycling alternatives based on the established criterion for a recycling channel selection problem in CMW management.
In general, the solution process of MCGDM problems can be divided into two phases: the aggregation phase and the exploration phase (Chiclana et al., 1998). During the operation, in addition to the linguistic set selection and decision-making method determination, the remaining three most important steps are DM weight determination, criteria weight determination and aggregation operator selection. It is easy to know that the determination of weights runs through both the aggregation and exploration phases and could have a non-negligible impact on the final decision-making results. The aggregation operator influences the process of aggregating the individual decision matrixes into an integrated weighting decision matrix. Therefore, we propose a developed MCGDM method to evaluate the capability of CMW recycling channels by taking the calculation method of weights and the selection of the aggregation operator as breakthroughs. Table 4 reviews several representative studies on the calculation of DMs and criterion weights in MCGDM.
Table 4.
Literature review of weights calculation.
| Research field | Method | Main content | Typical references | |
|---|---|---|---|---|
| Computing the weights of DMs | Entropy | Entropy method is employed to compute the weights of DMs. | (Çalı & Balaman, 2019) (Albahri et al., 2021) (Tolga et al., 2020) |
|
| TOPSIS | The distance between each DM and the decision matrix is employed to obtain the weights of DMs. | (Daneshvar Rouyendegh et al., 2018) (Yue, 2011) |
||
| BWM | BWM method is employed to compute the type-2 fuzzy (TrIT2F) weights of DMs. | (Wan et al., 2021) | ||
| Computing the weights of criteria | Shapley values | The criteria weights are calculated in the form of Shapley values | (Mishra, Rani, et al., 2020) (Teng & Liu, 2021) |
|
| BWM |
BWM + LBWA | Proposed a new method to use BWM and LBWA to determine the weights of healthcare indicators and subsequently | (Torkayesh et al., 2021) | |
| BWM | The subjective weights of criterion are calculated by BWM method. | (Q. Wu et al., 2019) (Ishizaka & Resce, 2021) |
||
| Entropy | Entropy | Entropy method is employed to compute the weights of the criterion. | (Çalı & Balaman, 2019) (Albahri et al., 2021) |
|
| Deviation minimum method + Entropy | Proposed a new method to use deviation minimum method and entropy to determine the weights of healthcare indicators and subsequently. | (Ding et al., 2021) | ||
| Information entropy | The objective weights of criterion are calculated by IEW. | (Zhang et al., 2011) | ||
According to the above literature review, we found that there are still several limitations in the weight calculation process: (1) The determination of criteria weights and DM weights are two important steps in MCGDM, and their values have a large influence on the ranking results of the alternatives. Unfortunately, few scholars have considered these two types of weights simultaneously when studying MCGDM problems. (2) When calculating the criteria weights, the majority of scholars tend to adopt a single subjective or objective method, ignoring their combination. (3) Few scholars have studied the MCGDM problem when the weights of both the DMs and criteria are unknown.
To fill in the above research gaps, our study presented a developed VIKOR approach under intuitionistic fuzzy set (IFS) theory for assessing the capacity of CWM recycling channels. In the decision-making process, we proposed an optimum combination weighting method, which integrates the best-worst method (BWM) and IF-Entropy to compute the weights of criteria more comprehensively. In this way, both subjective and objective weight information were synthesized and a balance between the objective facts and DM opinions was achieved; therefore, the decision-making results became more accurate and rational. Moreover, the aggregation operator IFWA is utilized to aggregate the individual judgements of DMs into an integrated weighting IF decision matrix in our study. In addition, the DM weights are considered and obtained by using IF-Entropy. The key reason why we choose entropy to obtain the DM weight and criteria weights is that it avoids interference from multiple subjective factors and is very objective. Finally, the integrated BWM-Entropy-VIKOR method proposed by us is used to calculate the comprehensive assessment values of CMW recycling channels. The abbreviations used in this paper are shown Table 1.
Table 1.
Abbreviations used in this paper.
| Abbreviations | Full name |
|---|---|
| IRN | Interval rough numbers |
| MCGDM | Multi-criteria decision making |
| VIKOR | Vlse Kriterijumska Optimizacija I Kompromisno Resenje |
| CMW | COVID-19 medical waste |
| MW | Medical waste |
| IVIFSs | Interval-valued intuitionistic fuzzy sets |
| COPRAS | Complex proportional assessment |
| BWM | Best-worst method |
| LBWA | Level based weight assessment |
| FAHP | Fuzzy analytic hierarchy process |
| GN | Grey numbers |
| IFs | Intuitionistic fuzzy sets |
| EDAS | Evaluation based on Distance from Average Solution |
| MABAC | Multi-attributive border approximation area comparison |
| IT2 FSs | Interval type-2 fuzzy sets |
| MOOSRA | Multi-Objective Optimization on the basis of Simple Ratio Analysis |
| SOWIA | Subjective and Objective Weight Integrated Approach |
3. The evaluation criteria for COVID-19 medical waste recycling channels
Due to the longer survival time and greater infectivity, CMW should not be disposed of as other common MW. However, the evaluation index system of CMW recycling channels is not sound enough and there is no targeted and proper CMW recycling channel capacity evaluation index system in existing researches. Thus, in our study, we proposed criteria from six different dimensions to assess the capacity of CMW recycling and disposal channels, including the resilient response capability, rapid collection capability, scientific sorting capability, safe storage capacity, timely transportation capability, and harmless disposal capacity. It is a new evaluation index system targeted to CMW recycling channels. Actually, these six criteria are proposed according to previous studies, characteristics of CMW, processing flow and the TOE theoretical framework.
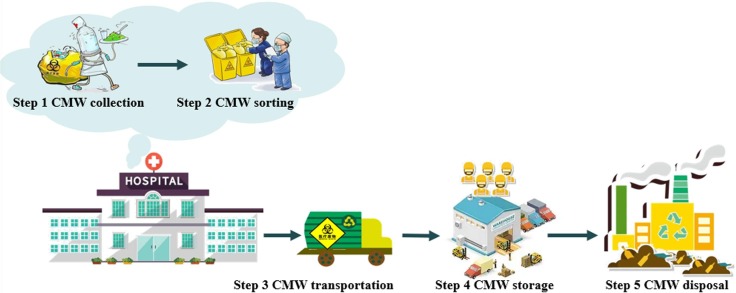
First, we divide the CMW recycling and disposal process conducted by recycling channels into five sequential steps, i.e., CMW collection, CMW sorting, CMW transportation, CMW storage, and CMW disposal, which can be seen more clearly in the Fig. 1 . We hope that the evaluation index system that we construct for CMW recycling channels is able to fully assess these five steps and ensure that they are carried out successfully. The conceptual framework of this paper can be seen in the Fig. 2 ).
Fig. 1.
The processing flow conducted by CMW recycling channels.
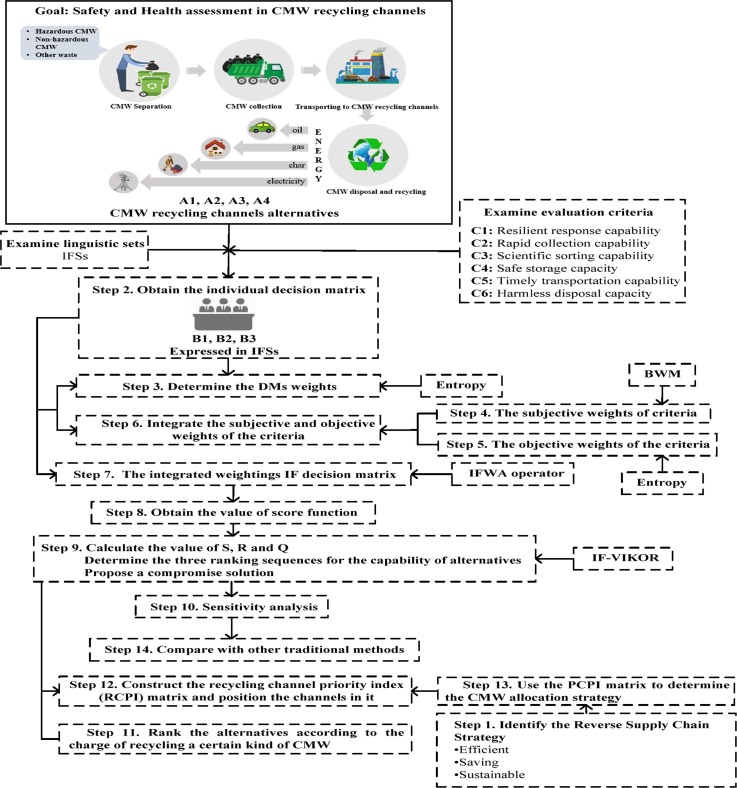
Fig. 2.
The conceptual framework of this paper.
Second, in order to make our CMW recycling channel capacity evaluation index system more targeted and effective, we sorted out the characteristics of the CMW mentioned in some relevant literature. The detailed CMW characteristics are list in Table 5 . We hope that the evaluation index system constructed by us can effectively assess the ability of the CMW recycling channels to address these CMW characteristics, including highly contagious, high pollutability, difficult to handle and long-term infectious.
Table 5.
Reviews representative literature on CMW characteristics.
| Representative literature | Highly contagious | High pollutability | Difficult to handle | Long-term infectious |
|---|---|---|---|---|
| (Thind et al., 2021) | √ | √ | √ | |
| (Peng et al., 2020) | √ | √ | √ | √ |
| (Das et al., 2021, Das et al., 2021) | √ | √ | √ | √ |
| (Thind et al., 2021) | √ | √ | ||
| (Dharmaraj et al., 2021) | √ | √ | √ | √ |
| (Chen et al., 2021) | √ | √ | √ |
Third, the new CMW recycling channels evaluation index system proposed by us is based on a TOE theoretical framework. Specifically, our integrated BWM-Entropy-VIKOR method is used to analyze the CMW recycling channel alternatives based on a set of technology-organization-environment (TOE) variables (rapid collection capability, scientific sorting capability, timely transportation capability, resilient response capability, safe storage capacity and harmless disposal capacity performance scores). In fact, these six criteria are proposed according to previous studies, characteristics of CMW, processing flow and the TOE theoretical framework.
We list a table of some relevant literature for statistics in Table 6 .
Table 6.
Reviews representative relevant literature.
| Representative literature | T(technology) |
O(organization) |
E(environment) |
|||
|---|---|---|---|---|---|---|
| Rapid collection capability | Scientific sorting capability | Timely transportation capability | Resilient response capability | Safe storage capacity | Harmless disposal capacity | |
| (Thind et al., 2021) | √ | √ | ||||
| (Yazdani et al., 2020) | √ | √ | √ | |||
| (Ekmekçioğlu et al., 2010) | √ | √ | ||||
| (Bahrani et al., 2016) | √ | √ | ||||
| (Das et al., 2021, Das et al., 2021) | √ | √ | √ | √ | √ | √ |
| (Arıkan et al., 2017) | √ | √ | ||||
| (Mishra, Rani, et al., 2020) | √ | √ | √ | √ | ||
| (Thakur & Ramesh, 1999) | √ | √ | ||||
The detailed information of the above six criteria are as follows:
3.1. Resilient response capability
Due to the uncertainty of the COVID-19 pandemic, CMW recycling channels should have resilient response capability. CMW recycling channels with resilient response capability are able to respond rapidly in the face of unforeseen circumstances. Concretely, when abrupt growth of infected patients appears in a healthcare institution, it will lead to the stock accumulation of various CMW. The amount of CMW could exceed the capacity of the recycling channels, but the CMW recycling channels with resilient response capabilities should take timely and effective measures to collect, transport, sort, store and dispose of the CWM. Because of the resilient response capability, CWM recycling channels in Wuhan successfully addressed the shortage of CMW disposal competence during the COVID-19 pandemic, which significantly reduced the risk of virus transmission (Tabish et al., 2020). Since the resilient response capability is the key factor in assessing the capacity of CMW recycling channels, it is urgent for scholars to propose a scientific evaluation approach that can help healthcare organizations to select the appropriate CMW recycling channels and achieve a reasonable distribution of CMW.
The problems to be solved by CMW recycling channels include the following: (1) Flexible selection for CMW disposal alternatives: disposal techniques should be selected or adopted based on the quantity, types and cost of CMW. (2) Temporary CMW treatment facilities: At present, the disposal facilities of CMW recycling channels are generally large-scale equipment with difficulties in movement and installation, lacking flexibility to adapt to the special disposal needs of massive highly infectious CMW suddenly generated during the COVID-19 pandemic. To improve the resilient response capability, CMW recycling channels should increase the number of movable temporary disposal facilities that are more suitable for emergency disposal of CMW. In Wuhan, the total capacity for local CMW disposal has been significantly improved depending on the emergency disposal facilities (Yang et al., 2021). As of April 10, 2020, only 30 t/d of the additional 215.6 t/d disposal capacity came from new centralized disposal facilities, with the remainder from emergency disposal facilities (Zhang et al., 2020). (3) Medical data system: A sophisticated medical data system should be implemented to support the prediction of CMW generation trends, thus guiding CMW management and promptly increasing the emergency response capacity of CMW recycling channels. (4) Emergency plans (Chen et al., 2021, Zhao et al., 2021): Emergency plans should be developed by CMW recycling channels to coordinate resources for disposal capacity throughout the broader region. Upon the outbreak of the COVID-19 pandemic, CMW can be transferred to recycling sites in surrounding cities as soon as possible to achieve joint prevention and control. (5)Temporary transportation facilities and temporary storage centres (Alshraideh et al., 2017): The generation of CMW is unpredictable, because the infection number is not stable (Yu et al., 2020). Therefore, temporary transportation facilities and temporary storage centres can help to manage CMW effectively and help to avoid transmission during the COVID-19 pandemic. CMW recycling channels must respond to the above problems.
3.2. Rapid collection capability
Considering that the SARS-CoV-2 virus can survive on hard surfaces for a long period of time (Kampf et al., 2020), CMW recycling channels should have rapid collection capability. As recently discovered, the COVID-19 virus can survive from several hours to several days, according to the substrate types and environmental conditions. Specifically, the survival times of SARS-CoV-2 following aerosolization on plastic objects, stainless steel, paper, and cardboard are 72 h, 48 h, 24 h, and 24 h, respectively (Kampf et al., 2020, van Doremalen et al., 2020). Therefore, delay in collection could lead to COVID-19 infection (Ramteke & Sahu, 2020). Many countries have introduced stringent regulations on the timing of CMW collection. For example, the Chinese government proposed that the temporary storage period of CMW in medical institutions cannot exceed 24–48 h (Das et al., 2021, Das et al., 2021, Nghiem et al., 2020, Peng et al., 2020). In Jordan, to prevent the further spread of the SARS-CoV-2 virus, CMW is required to be rapidly disposed of every day (Das et al., 2021, Das et al., 2021). To prevent the COVID-19 pandemic outbreak and respond to compulsory government regulations, CMW recycling channels should collect CMW rapidly (Nghiem et al., 2020).
3.3. Scientific soring capability
To ensure that the subsequent CMW disposal and recycling process can be carried out efficiently, CMW recycling channels should have scientific sorting capability. In this study, CMW is divided into three types: hazardous CMW, non-hazardous CMW and other CMW. Peng et al. (2020) also believed that the mixing of multiple CMW could create a potential risk due to the extremely high contagiousness of the SARS-CoV-2 virus. On the one hand, hazardous medical waste can cause the spread of the COVID-19 virus and serious pollution. If CMW is not scientifically segregated by recycling channels, ordinary medical waste will be mixed with hazardous medical waste, which will increase the risk of COVID-19 pandemic outbreaks (Dharmaraj et al., 2021). On the other hand, the appropriate treatment and recycling methods vary for each type of CMW. Currently, there are three types of techniques, namely, incineration and physical and chemical approaches, which are applied to the disposal of CMW. The COVID-19 pandemic brings multiple plastic CMW, which can be transformed into several valuable energy productions, such as oil, char and gas, through the pyrolysis process. Thus, scientific sorting allows for the recycling and reuse of plastic CMW, which not only effectively controls the spread of the epidemic but also improves the reverse supply chain of the medical resources. Windfeld and Brooks (2015) also argued that if we efficiently segregate recyclable MW from other hazardous MW, the amount of MW will be minimized significantly. In our view, scientific soring capability is one of the major criteria for evaluating the performance of CMW recycling channels.
3.4. Safe storage capacity
Because most CMW is extremely infectious, CMW recycling channels should have safe storage capacity (Chen et al., 2021). The exponential increase in CMW production makes the timely disposal of CMW quite difficult, and thus CMW often must be securely stored in some temporary warehouses designated by the CWM recycling channels. However, most CMW recycling channels might not have sufficient storage space, and as a result, multiple CMW must be stored in some non-designated sites, which could pose risks in terms of further COVID-19 breakouts. When the required storage area for CMW far exceeds the actual storage area that a CMW recycling channel can provide, this channel will be regarded as a storage capacity shortage. Thus, the CMW storage capacity of recycling channels should be developed to address the great challenge in CMW management. The security of CMW storage should also be taken seriously. Considering that the mixing of multiple CMW could create a potential risk, isolated storage can be seen as an effective measure in CMW management. Hence, CMW from fever clinics, isolation wards, observation wards, and nucleic acid testing labs must be stored isolated by recycling channels to avoid mixing them with common ward waste (Manupati et al., 2021). In addition to avoiding mixed storage of CMW, recycling channels should also pay attention to certain problems, as follows: (1) Adopt tight containment measures, (2) Display warning signs, (3) Set up special staff to manage CMW, (4) Strengthen the protection of staff, and (5) Strictly disinfect the stored CMW in a timely manner. In our view, safe storage capacity is expected to have an enormous impact on the existing CMW reverse supply chain and contribute to the control of the COVID-19 pandemic.
3.5. Timely transportation capacity
Because SARS-CoV-2 can exist on multiple materials for a long period of time, CMW recycling channels should also have timely transportation capability. There is a long transportation distance from health-care institutions to certain CMW recycling channels. Unlike the general MW, the CMW disposal process should be handled by specially trained staff and dedicated vehicles. If CMW is not delivered to the disposal site in time, there will be delays in the disposal and recycling of CMW, which could increase the risk of the spread of the virus (Nghiem et al., 2020, Peng et al., 2020). To address this challenge, a specific handover book should be set by the CMW recycling channel to record detailed information about the time, type and quantity between the internal and external transporters. The time of CMW transportation should be scheduled to avoid morning and evening peak hours, and the transportation routes should be scientifically planned rather than empirically determined. The performance of CMW transportation can be evaluated according to the transport route length, the incident rate of CMW freight vehicles and the punctuality rate of transportation (Chen et al., 2021).
3.6. Harmless disposal capacity
In recent years, eco-friendly waste disposal issues have been a keen concern for both academia and industry, and the goal of sustainable development is one of the major driving factors shaping MW reverse supply chains (Adeniran et al., 2017). For a CWM recycling channel, having harmless disposal capacity is a prerequisite and foundation for green development. However, improper management of CMW is common, and approximately two-thirds of CMW is currently handled in an unsafe manner (Patrício Silva et al., 2021). To date, CMW disposal channels around the world have attempted to use various technologies, such as landfills, shredding and incineration (Wang et al., 2020). During the COVID outbreak, these disposal methods caused several undesirable effects, and many health-deteriorating pollutants were emitted (Wang et al., 2020). However, “COVID” should not be an excuse for causing “Environmental Pollution“. Adopting alternative techniques can help to dispose of the CMW in a more proper way. In this regard, CMW can be used to generate energy and several value-added products. In our view, safety and green are the directions of modern supply chain development and are critical criteria for comprehensively assessing the capacity of CMW disposal channels. A qualified CMW recycling channel should take great responsibility for protecting the environment by disposing of CMW in a harmless way to gain a competitive edge.
4. Methodology
An integrated BWM-Entropy-VIKOR method under IFSs for assessing the capacity of CWM recycling channels is described in this section. The goal, alternative CMW recycling channels, evaluation criteria and linguistic terms should be determined by the DMs before our study. The conceptual framework of this paper is shown below.
In addition, the explanations of the notations involved in our study are listed in Table 7 .
Table 7.
Notations in our study.
| Notations | Definitions of notations |
|---|---|
| The set of alternatives; Ai represents alternative i; m alternatives | |
| The set of criteria; Cj represents alternative j; n criteria | |
| The set of DMs; represents DM k; p DMs | |
| Individual IF-decision matrix of | |
| The entropy value of | |
| The degree of divergence | |
| The weight of | |
| Set of DMs weights | |
| The preference of the most important criteria B over the criteria j | |
| Best-to-others vector | |
| Other-to-worst vector | |
| The preference of criteria j over the worst criteria W | |
| Minimum value of objective function | |
| The set of subjective criteria weights | |
| The entropy value of Cj | |
| The degree of divergence | |
| Objective weight of Cj | |
| The set of objective criterion weights | |
| The integrated weighting intuitionistic fuzzy decision matrix integrated wc and wd | |
| Score function | |
| The set of positive ideal solutions | |
| The set of negative ideal solutions | |
| Group utility value of alternative i | |
| Individual regret value of alternative i | |
| Trade-off evaluation value of alternative i | |
| The set of final criterion weights |
4.1. Determine the reverse supply chain strategy
The healthcare institution's strategy for allocating CMW, i.e., the priorities of different types of CMW recycling channel alternatives, must be aligned with its reverse supply chain strategy. Hence, it is the first logical step of our method and the most necessary initial step in developing a CMW allocation strategy. Here, we propose three reverse supply chain strategies:
-
1)
EFFICIENT REVERSE SUPPLY CHAIN STRATEGY
Healthcare institutions that adopt this strategy tend to seek efficient CMW recycling services. In other words, they prioritize options based on both the cost and strength and prefer to partner with a low-fee but competitive CMW recycling channel. When there is only a small difference in the strength of the two alternatives, this type of healthcare institution tends to choose the institution with lower fees.
-
2)
SAVING REVERSE SUPPLY CHAIN STRATEGY
Healthcare institutions that adopt this strategy tend to seek low-priced CMW recycling services. In other words, they prioritize options primarily on the basis of cost and prefer to partner with the CMW recycling agency that charges less. Due to the financial constraints on CMW disposal, these healthcare institutions can choose to sacrifice the capacity of recycling companies in exchange for lower disposal prices when necessary.
-
3)
SUSTAINABLE REVERSE SUPPLY CHAIN STRATEGY
Healthcare institutions that adopt this strategy tend to seek reliable and eco-friendly CMW recycling services. In other words, they prioritize options primarily on the basis of the capacity and pursue sustainable development. Most of these healthcare institutions are supported by the government and thus have ample funds for CMW disposal. Their sense of social responsibility is quite strong, and thus, they choose to sacrifice some of their interests for the safe disposal of CMW.
4.2. Ranking the alternatives’ capacity order on the basis of the hybrid VIKOR
-
1)
DETERMINE THE INDIVIDUAL DECISION MATRIX
Due to the complexity of evaluation and the vagueness of available information, DMs often show a certain degree of hesitation in the decision-making process. Unfortunately, traditional fuzzy sets have difficulty in expressing this degree of hesitation. To overcome this difficulty, Atanassov (1986) pioneered intuitionistic fuzzy sets (IFSs), which were described by membership degree (MD), non-membership degree (ND), and hesitation. In fact, with the introduction of IFs, Atanassov (1986) extended traditional fuzzy set theory and made it a powerful tool for addressing uncertainty. This section focuses on some definitions and algorithms of IFs.
Definition 4.1 (Atanassov, 1986) —
Let X be a nonempty set and an IFSA in X can be defined as.
(1) where
Here, and are membership and non-membership functions of an intuitionistic fuzzy set, respectively. and are degrees of membership and non-membership functions, respectively, satisfying.
Definition 4.2 (Atanassov, 1986) —
The intuitionistic index used to measure the degree of hesitation can be expressed as.
where. The IFS that consists of MD, ND can be expressed as (Zeshui & Yager, 2006). As a measure, a smaller hesitation means that the information we obtained is more reliable, and it facilitates us to model the uncertainty of IFSs.
Definition 4.3 (Zeshui & Yager, 2006) —
Let and be two IFSs of a given set.
Where
and;
and.
Let be a real number and, then the calculation rules of and are as follows:
(2)
(3)
(4)
(5)
- (5)
The Euclidean distance is as follows:
(6)
- (6)
The normalized Euclidean distance is the following:
(7) P decision makers evaluate each alternative according to each criterion based on the aforementioned IF theory and the linguistic terms, thus forming an individual decision matrix.
(8)
-
2)
DETERMINE THE WEIGHTS OF DMS
Bustince and Burillo (1996) extended the fuzzy nonprobability entropy formula proposed by De Luca and Termini (1972) to IFSs and stated that entropy can be referred to as intuitionistic fuzzy entropy (IF-entropy) when it satisfies the following conditions.
-
(1)
, if and only if r is a real number.
-
(2)
,when
-
(3)
when the fuzzy degree of is lower than that of.
-
(4)
Entropy has been widely used in various research areas, especially for the study of MCGDM issues. Generally, there are two types of weighting methods in MCGDM: the subjective weighting method and the objective weighting method. Entropy is a type of objective weighting method that is mainly used in cases where credible weights cannot be obtained by using subjective weighting methods. IF-Entropy represents the fuzzy degree of an IFS. A higher IF-Entropy implies a high degree of hesitation of the decision maker, and thus, a lower intuitive fuzzy entropy means that we obtain more accurate information. The higher the IF-Entropy of the assessment criteria is, the higher the ambiguity degree of the judgement information obtained, and the lower the weight that should be given (in contrast, the higher the weight that should be given). Moreover, the fuzzy degree of IF-Entropy considers the uncertainty and unknown degrees simultaneously, in which deviations between the membership degree and the non-membership degree represent the uncertainty degree while the hesitation degree represents the unknown degree. The calculation formula of IF-Entropy is (Vlachos & Sergiadis, 2007):
| (9) |
In our study, Eq. (10), (11), (12) are formulas for determining the DM weights by IF-Entropy for Rk, where Rk represents the individual IF-decision matrix of. Eq. (11) measures the IF-Entropy value of each criterion, where ;. If , then.
| (10) |
Eq. (11) is the formula for the divergence degree:
| (11) |
Based on Eq. (12), the weights of the DMs can be calculated by Eq. (12).
| (12) |
Then, a set of DMs weight can be obtained, where and .
-
3)
SUBJECTIVE WEIGHTING FOR CRITERIA
The BWM, a pairwise comparison-based approach, was proposed by Rezaei (2015). It uses linear mathematical models to compute the optimal criteria weight for multi-criteria problems. The steps of this method are explained as follows:
-
(1)
IDENTIFY AND DEFINE THE CRITERIA SET
A criteria set is identified by decision makers.
-
(2)
IDENTIFY THE BEST AND WORST CRITERION
DMs identify the best criterion and the worst criterion.
-
(3)
OBTAIN THE BEST-TO-OTHER VECTOR
DMs conduct a pairwise comparison between the best criteria and other criteria and then identify the preference of the best criterion over others on a 9-point scale. The obtained comparison results are indicated as the best-to-other vector:
| (13) |
where indicates the preference of the most important criterion B over criterion j;
-
(4)
OBTAIN THE OTHER-TO-WORST VECTOR
DMs conduct a pairwise comparison between the worst criteria and other criteria and then identify the preference of other criteria over the worst by a 9-point scale. The obtained comparison results are indicated as other-to-worst vectors:
| (14) |
where indicates the preference of criterion j over the worst criterion W;
-
(5)
CALCULATE THE SUBJECTIVE WEIGHTS OF CRITERIA
Optimal weights are computed for all criteria .
According to Eq. (15), the subjective criteria weights can be obtained. The set of subjective criterion weights is expressed by .
| (15) |
According to Eq. (19), the consistency ratio (CR) can be calculated by . The values of the corresponding consistency index (CI) for the BWM models are shown in Table 8 .
Table 8.
Consistency Index (CI).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|
| CI | 0 | 0.44 | 1.0 | 1.63 | 2.3 | 3.0 | 3.73 | 4.47 | 5.23 |
The closer the value of the consistency ratio is to 0, the better the consistency is, i.e., the more valid the obtained results are. The formula for calculating the consistency ratio is as follows (Rezaei, 2015):
| (16) |
The smaller the value of is, the smaller the value of CR, and the better consistency the vectors will have.
-
4)
OBJECTIVE WEIGHTING FOR CRITERIA
Based on the Eq. (9), Eq. (17) is obtained. After using Eq. (17), Eq. (18) and Eq. (19) to compute the group decision matrix R, we obtain the set of objective weights of criteria .
| (17) |
| (18) |
| (19) |
-
5)
INTEGRATE THE SUBJECTIVE AND OBJECTIVE WEIGHTS OF THE CRITERIA
Eq. (20) is used to combine the above subjective weights and objective weights and thus obtain the weight of Cj.
| (20) |
where represents the weight coordination coefficient. In our study, the subjective and objective weights of the criteria are assumed to be of equal importance, i.e., . After n calculations, the final set of criteria weights is obtained:.
-
6)
DETERMINE THE INTEGRATED WEIGHTING INTUITIONISTIC FUZZY DICISION MATRIX
According to Eq. (21) and Eq. (22), the IFWA operator is used to aggregate the decision matrix into an integrated weighting intuitionistic fuzzy decision matrix .
| (21) |
| (22) |
-
7)
OBTAIN THE VALUE OF THE SCORE FUNTION
In this paper, we use the score function given by Liu (2005). It is assumed that is an IF number; then, the value of the score function can be obtained by using Eq. (23).
| (23) |
If , then . If and are IF numbers, then.
If , then .
If , then .
-
8)
DETERMINE THE RANKING and THE COMPROMISE SOLUTION
TOPSIS and VIKOR are two typical multi-criteria compromise methods that are based on the idea of “closest to the ideal solution”. The major difference between these two methods is that the best solution obtained by the VIKOR method is closest to the ideal point, while the best solution obtained by the TOPSIS method is not always close to it. Moreover, the VIKOR method allows us to obtain trade-offs with priorities. The improvement of VIKOR by using IF numbers can address several fuzzy problems. By computing the positive ideal solution and negative ideal solution, the calculation method is shown in Eq. (24) and Eq. (25):
| (24) |
| (25) |
where T represents all criteria, i represents alternative i, and j represents the value of the scoring function of criterion j; i = 1, 2…, m, j = 1, 2…, n.
According to Eqs. (26), (27), (28), the values of , and can be obtained.
| (26) |
| (27) |
| (28) |
where , , , and is the weight for the strategy of the largest group utility while represents the weight for the individual regret. is set in this paper. We rank the alternatives according to the values of S, R and Q in ascending order. Then, we can obtain three ranking sequences. If the following two conditions are met, the alternative , which is ranked No. 1 by Q, can be regarded as the compromise solution (H.-C. Liu et al., 2013).
Condition(1). Acceptable advantage: , where is the alternative that is ranked No.1 by Q,.
Condition(2). Acceptable stability: The alternative must also be ranked No. 1 by R or/and S. The obtained compromise solution is stable in a decision-making process, which could be “voting by majority rule” (when v > 0.5 is needed), “by consensus” , or “with veto” .
Based on the ranking obtained, the capacity of CMW recycling channels is described on a number axis that ranges from low (L) to high (H), as shown in Fig. 3 .
Fig. 3.
Capacity of CMW recycling channels.
Based on the ranking of cost, the charges for CMW recycling are also described on a number axis that ranges from high (H) to low (L), as shown in Fig. 4 .
Fig. 4.
Charges for CMW recycling.
4.3. Ranking the alternative order on the basis of the RCPI matrix
-
1)
CONSTRUCT THE RECYCLING CHANNEL PRIORITY INDEX (RCPI) MATRIX AND POSITION THE CHANNELS IN IT
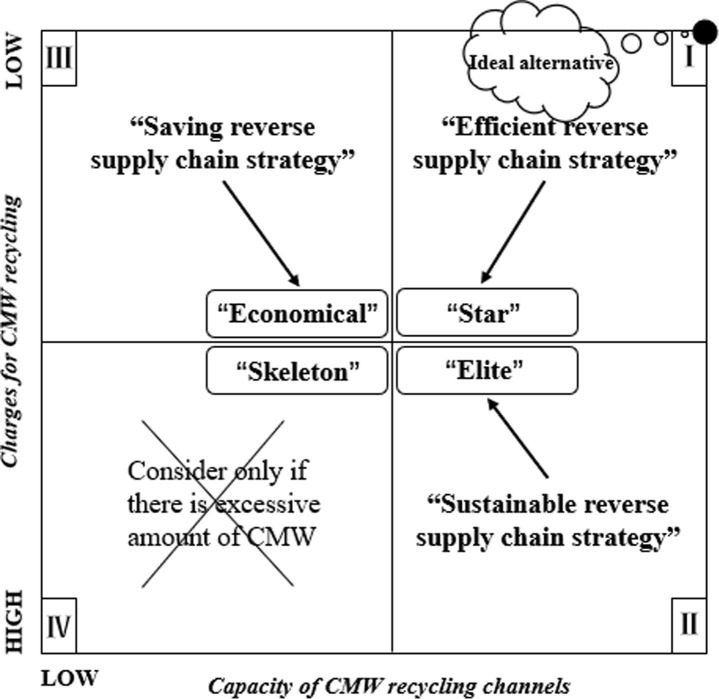
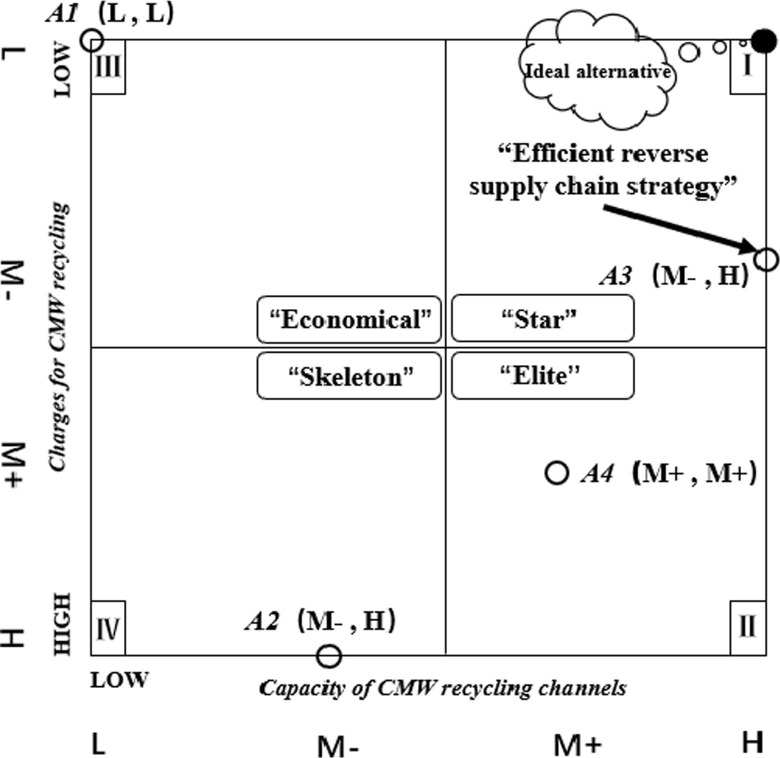
The recycling channel priority index (RCPI) matrix in Fig. 5 is a two-dimensional matrix with its horizontal axis denoting the capacity and its vertical axis denoting the charges.
Fig. 5.
Charges for CMW recycling.
The RCPI matrix is further divided into four quadrants, each representing a type of waste recycling channel. Specifically, based on the level of charges and capabilities, the alternatives in quadrants I, II, III and IV are named Star, Elite, Economical and Skeleton respectively.
For each CMW recycling channel of the healthcare institution, considering its capacity (Fig. 3) and charges (Fig. 4), the quadrant in the RCPI matrix to which the CMW recycling channel belongs and its precise location in that quadrant can be determined based on its capacity ranking (Fig. 3) and charge ranking (Fig. 4).
-
2)
USE RCPI MATRIX TO DETERMINE THE CMW ALLOCATION STRATEGY
Each type of CMW recycling channel is prioritized differently for healthcare institutions with different supply chain strategies. Thus, the RCPI matrix can help to formulate rational CMW allocation strategy strategies. The optimal CMW recycling channel type for each type of reverse supply chain strategy is listed in Table 9 .
Table 9.
Optimal recycling channel type for each supply chain strategies.
| Reverse supply chain strategy | Optimal CMW recycling channel type |
|---|---|
| Efficient reverse SC strategy | Star |
| Sustainable reverse SC strategy | Elite |
| Saving reverse SC strategy | Economical |
| × | Skeleton |
4.4. General steps in decision analysis
Step 1. Identify the Reverse Supply Chain (SC) Strategy.
Step 2. Obtain the individual decision matrix Rk.
Step 3. Determine the DM weights by entropy (Eqs. (10), (11), and (12)).
Step 4. Determine the subjective weights of criteria by BWM (Eqs. (13), (14), (16)), and model (15)).
Step 5. Determine the objective weights of the criteria by entropy (Eqs. (17), (18), and (19)).
Step 6. Integrate the subjective and objective weights of the criteria. ((Eq. (20)).
Step 7. Use the IFWA operator to determine the integrated weighting IF decision matrix.
Step 8. Obtain the value of the score function.
Step 9. Calculate the value of S, R and Q and determine the three ranking sequences for the capability of alternatives by IF-VIKOR and propose a compromise solution.
Step 10. Conduct the sensitivity analysis by analysing the effect of the parameter.
Step 11. Rank the alternatives according to the charge of recycling a certain type of CMW.
Step 12. Construct the recycling channel priority index (RCPI) matrix and position the channels in it.
Step 13. Use the PCPI matrix to determine the CMW allocation strategy.
Step 14. Compare with other traditional methods.
5. A real case study
In this section, a real case study conducted in Wuhan, China is presented to demonstrate the applicability and effectiveness of the proposed approach to CMW recycling channel evaluation and selection. There is a hospital that wants to allocate its CMW to recycling channels in a more reasonable way. Due to the ethical grounds of this study, the name of the above hospital cannot be disclosed. We obtained got the permission of the superintendent to collect data in the hospital and four CMW recycling channels. According to the survey, this hospital is a comprehensive medical institution that integrates clinical practice, teaching and research. It is also the designated hospital for medical treatment of public health emergencies in Wuhan. The average daily production of MW at this hospital during COVID-19 is approximately 2.1 tons, and the average daily production of CMW is approximately 150 kg. According to the hospital director, this hospital does not have the capacity to dispose of its daily generation of CMW independently. Therefore, CMW recycling channels are needed. To prevent the spread of the COVID virus within the hospital, a series of management measures for CMW were proposed. As far as we know, an area from the original storage room of general MW was separated to temporarily store the CMW. The CMW recycling company can collect CMW directly from it without any unnecessary intersection or contact. Furthermore, the funds for CMW disposal are limited in this hospital.
Based on preliminary surveys, four CMW recycling channels A = {A1, A2, A3, A4} are determined as alternatives. Some information on these channels is listed in Table 10 . Other detailed situations of these channels are listed as follows:
Table 10.
Partial information of the alternatives.
| Alternatives | Scale | Recycling charges for infectious CMW | Distance to the hospital |
|---|---|---|---|
| A1 | Large | Very cheap | Very long |
| A2 | Small | Very expensive | Short |
| A3 | Very large | Cheap | Very short |
| A4 | Very small | Expensive | Long |
A1: This company was established in 2016 and is headquartered in Wuhan, Hubei Province. With more than 260 employees, it is a high-tech enterprise in China and a member of the China Environmental Protection Association. It specializes in the research and development of technology for the environmentally sound treatment of medical waste, the manufacture of related treatment equipment and the recycling of medical waste. It is also a manufacturer and seller of harmless medical waste treatment equipment and an investment operator of harmless medical waste disposal projects.
A2: This company was founded in 2014 and its head office is located in Wuhan, Hubei Province. It provides municipal waste removal services, municipal waste treatment services, medical waste disposal services, municipal excreta treatment services, wastewater treatment services, and recycling and processing services for renewable resources. This company has built an advanced waste disposal system that uses technologies such as cloud computing, big data and blockchain. In addition, the enterprise has a special emergency storage warehouse for CMW.
A3: This company was founded in 2010 and its headquarters is located in Hefei, Anhui Province. It has undertaken large-scale projects such as domestic waste treatment in Wuhan City and centralized hazardous waste disposal in Hubei Province, and has rich experience in medical waste treatment. Its business scope covers sludge, industrial waste residue, municipal waste, hazardous waste, medical waste, chemical waste and other waste treatment fields.
A4:This company was founded in 2016 and its head office is located in Wuhan, Hubei Province. Its business scope covers medical waste collection, storage, treatment and recycling services. The company has an advantage in the road transportation of hazardous waste. In addition, the company attaches great importance to the recycling of CMW and has developed a set of contingency plans for CMW collection, sorting, transportation and recycling.
To assess the capacity of the CMW recycling channels, an expert committee was formed that consisted of three DMs, B1, B2 and B3. These experts were from various institutions, including a CMW disposal specialist, an industrial engineering professor, and an environment engineer. According to the literature regarding the assessment of waste recycling channels and views from DMs, resilient response capability, rapid collection capability, scientific sorting capability, safe storage capacity, timely transportation capability and harmless disposal capacity are identified as the assessment criteria.
To obtain the DMs’ judgement, several interviews were scheduled with these experts. In our first meeting, we presented our research framework and provided the objective information obtained already. Additionally, a questionnaire was prepared meticulously that covered the evaluation criteria of the CMW recycling channel alternatives. Then, the three DMs were asked to post their personal rating opinions of the CMW recycling channels with respect to every criterion by using certain linguistic values. Furthermore, the linguistic terms used were defined according to the questionnaires answered by all DMs. The linguistic terms for rating the alternatives are shown in Table 11 . In what follows, the integrated BWM-Entropy-VIKOR method and the PCPI matrix were used to segment the CMW recycling channels and allocate and determine CMW allocation options, which included the following steps:
Table 11.
Linguistic terms for rating the alternatives.
| Linguistic variables | Intuitionistic fuzzy numbers |
|---|---|
| Extremely good (EG)/extremely high (EH) | (1.00, 0.00, 0.00) |
| Very, very good (VVG)/very, very high (VVH) | (0.90, 0.10, 0.00) |
| Very good (VG)/very high (VH) | (0.80, 0.10, 0.10) |
| Good (G)/high (H) | (0.70, 0.20, 0.10) |
| Medium good (MG)/medium high (MH) | (0.60, 0.30, 0.10) |
| Fair (F)/medium (M) | (0.50, 0.40, 0.10) |
| Medium bad (MB)/medium low (ML) | (0.40, 0.50, 0.10) |
| Bad (B)/low (L) | (0.25, 0.60, 0.15) |
| Very bad (VB)/very low (VL) | (0.10, 0.75, 0.15) |
| Very, very bad (VVB)/very, very low (VVL) | (0.10, 0.90, 0.00) |
【Step 1】 Identify the reverse supply chain (SC) strategy.
Due to the large scale, adequate financial budget and eco-friendly disposal goal, the reverse SC strategy of this hospital is identified as “sustainable”.
【Step 2】 Obtain the individual decision matrix Rk. Determine the IFPR individual decision matrix Rk based on ratings provided by the DMs.
Based on the criteria and linguistic terms, evaluations of the four CMW recycling alternatives are provided by each DM. The individual assessment results are shown in Table 12 .
Table 12.
Importance of alternatives based on opinions of DMs.
| DMs | Alternative | Criteria |
|||||
|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | ||
| A1 | VG | G | F | MG | F | VG | |
| A2 | VVG | MG | F | MB | VVG | VG | |
| A3 | VG | MG | G | G | VG | VG | |
| A4 | G | VG | VG | VVG | G | F | |
| A1 | VVG | VG | G | G | MB | G | |
| A2 | VG | G | VG | F | F | VVG | |
| A3 | VVG | G | G | VG | VVG | VG | |
| A4 | VG | G | VVG | VG | VG | MG | |
| A1 | G | VG | G | G | G | VVG | |
| A2 | VG | G | G | G | VG | VG | |
| A3 | VVG | MG | G | G | F | G | |
| A4 | G | VG | VG | VG | F | G | |
Then, three individual decision matrixes can be obtained:
【Step 3】 Determine the DM weights by entropy according to Eqs. (10), (11), and (12).
In this step, we use the entropy to compute the weights of DMs. The entropy values are calculated by Eq. (10). The divergences are calculated by Eq. (11). Finally, the weights of the DMs are calculated by Eq. (12). The relevant results are shown in Table 13 .
Table 13.
The weights of DMs.
| E | 0.711 | 0.674 | 0.716 |
| d | 0.289 | 0.326 | 0.284 |
| 0.321 | 0.362 | 0.316 |
【Step 4】 Determine the subjective weights of the criteria by BWM.
In this section, eight experts from the health commission are invited to determine the best and worst criteria as well as the scores of the best-to-others and others-to-worst vectors. Based on these experts’ perspectives, C6 emerges out as the most important criteria whereas, C2 emerges as the least important criterion. Table 14, Table 15 represent the scores of the best-to-others and others-to-worst vectors, respectively. According to Eq. (13) and Eq. (14), we can obtain and .
Table 14.
Best-to-others vector.
| Best criteria | C1 | C2 | C3 | C4 | C5 | C6 |
|---|---|---|---|---|---|---|
| C6 | 3 | 9 | 7 | 6 | 4 | 1 |
Table 15.
Others-to-worst vector.
| Worst criteria | C1 | C2 | C3 | C4 | C5 | C6 |
|---|---|---|---|---|---|---|
| C2 | 4 | 1 | 5 | 6 | 3 | 8 |
Using Eq. (15), subjective criteria weights can be obtained as . The above results indicate that the harmless disposal capacity (C6) and the rapid collection capability (C2) are the best and worst criteria, respectively. According to Eqn. (16), the consistency degree can be computed as.
Due to the CR value (0.045), it is obvious that the obtained criteria weights have satisfactory consistency and a reliable level.
【Step 5】 Determine the objective weights of the criterion by IF-Entropy.
In this step, we use IF-Entropy again to compute the objective weights of the criterion. The entropy values are calculated by Eq. (22). The divergences are calculated by Eq. (23). Finally, the objective weights of the criterion are calculated by Eq. (24). The relevant results are shown in Table 16 .
Table 16.
Objective weights of the criterion.
| C1 | C2 | C3 | C4 | C5 | C6 | |
|---|---|---|---|---|---|---|
| E | 0.574 | 0.744 | 0.739 | 0.755 | 0.776 | 0.664 |
| d | 0.426 | 0.256 | 0.261 | 0.245 | 0.224 | 0.336 |
| 0.244 | 0.146 | 0.149 | 0.140 | 0.128 | 0.192 |
【Step 6】 Integrate the subjective and objective weights of the criteria by Eq. (20).
From the last two steps, the weights of the subjective and objective criteria are obtained as follows:
According to Eq. (20), the integrated weights can be calculated as follows:
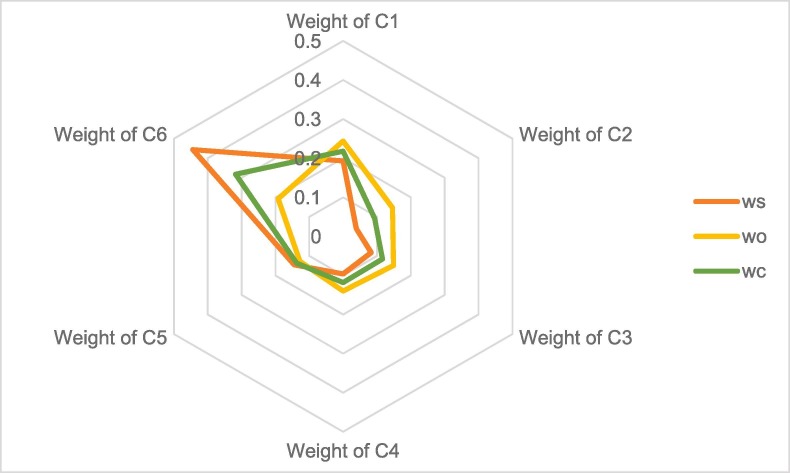
If we only use the objective weights or subjective weights as the weights of the criterion, the differences in the criteria weights obtained are shown in Fig. 6 . From this figure, it can be seen that if only subjective weights or objective weights are considered, some of the obtained criteria weights will be overestimated or underestimated, especially for C6 and C2. If both the objective and subjective weights are considered, the obtained criteria weights will be more reasonable.
Fig. 6.
Criterion weights by 3 wt calculation methods.
【Step 7】 Use the IFWA operator to determine the integrated weighting IF decision matrixes.
Eq. (21) and Eq. (22) are used to integrate the weights and decision matrix and obtain integrated weighting IF decision matrix, which is shown as follows:
【Step 8】 Obtain the value of the score function by Eq. (23).
By using Eq. (23), the score function values matrix can be obtained:
【Step 9】 Calculate the values of S, R and Q and determine the three ranking sequences for the capability of alternatives by IF-VIKOR.
The values , and (i = 1, 2…, m) are computed by Eqs. (26) - (28), and the relevant results are shown in Table 17 . Based on the obtained values of S, R and Q, the three rankings of the CMW recycling channel alternatives are shown in Table 18 .
Table 17.
The values of S, R and Q for all CMW recycling channel alternatives.
| Alternatives |
||||
|---|---|---|---|---|
| A1 | A2 | A3 | A4 | |
| S | 1.658 | 1.601 | 1.460 | 1.407 |
| R | 0.167 | 0.167 | 0.164 | 0.167 |
| Q | 1.000 | 0.888 | 0.105 | 0.500 |
Table 18.
The rankings of CMW recycling channel alternatives by S, R and Q.
| Alternatives |
||||
|---|---|---|---|---|
| A1 | A2 | A3 | A4 | |
| By S | 4 | 3 | 2 | 1 |
| By R | 2 | 2 | 1 | 2 |
| By Q | 4 | 3 | 1 | 2 |
From Table 10, the CMW recycling channel alternative A3 is the best in accordance with the values of Q. Moreover, Condition (1) and Condition (1) are satisfied: , and A3 is best ranked by R. Hence, the most suitable CMW recycling channel is A3 in this case. Considering that the values of R are similar, the rank by R is prone to error. It is worthwhile to note that A3 also outperforms A2 when sorted by R, which is consistent with the results when sorted by Q. Therefore, we take the sorting that corresponds to the value of Q as the prevailing sorting, i.e., A3 > A4 > A2 > A1.
【Step 10】 Conduct the sensitivity analysis by analysing the effect of the parameter v.
In the IF-VIKOR method, v represents the weight for the strategy of the largest group utility while 1-v represents the weight for the individual regret. We observe the change in ranking by changing the value of v. The related results are shown in Table 19 .
Table 19.
Influence of the parameter v on the ranking results.
|
v = 0.1 |
v = 0.2 |
v = 0.3 |
v = 0.4 |
|||||
|---|---|---|---|---|---|---|---|---|
| Q | order | Q | order | Q | order | Q | order | |
| A1 | 1.00 | 4 | 1.00 | 4 | 1.00 | 4 | 1.00 | 4 |
| A2 | 0.98 | 3 | 0.96 | 3 | 0.93 | 3 | 0.91 | 3 |
| A3 | 0.02 | 1 | 0.04 | 1 | 0.06 | 1 | 0.08 | 1 |
| A4 | 0.90 | 2 | 0.80 | 2 | 0.70 | 2 | 0.60 | 2 |
|
v = 0.5 |
v = 0.6 |
v = 0.7 |
v = 0.8 |
|||||
| Q | order | Q | order | Q | order | Q | order | |
| A1 | 1.00 | 4 | 1.00 | 4 | 1.00 | 4 | 1.00 | 4 |
| A2 | 0.89 | 3 | 0.87 | 3 | 0.84 | 3 | 0.82 | 3 |
| A3 | 0.10 | 1 | 0.13 | 1 | 0.15 | 1 | 0.17 | 1 |
| A4 | 0.50 | 2 | 0.40 | 2 | 0.30 | 2 | 0.20 | 2 |
From Table 19, it is obvious that different values of v from 0.1 to 0.8 will result in a different value of Q. However, the CMW recycling channel ranking always remains A3 > A4 > A2 > A1. Thus, the ranking results are always consistent when v changes.
【Step 11】 Rank the alternatives according to the charge of recycling a certain type of CMW.
We ranked the alternatives' recycling charges for infectious CMW, and the sorting result is: A2 > A4 > A3 > A1.
【Step 12】 Construct the recycling channel priority index (RCPI) matrix and position the channels in it.
The CMW recycling channel position in the RCPI Matrix is shown in Fig. 7 .
Fig. 7.
The CMW Recycling Channel Position in RCPI Matrix.
【Step 13】 Use the PCPI matrix to determine the CMW allocation strategy.
Because the reverse SC strategy of this hospital is “sustainable”, it is reasonable for the hospital to sacrifice some of their interests for the safe disposal of CMW. Thus, the optimal CMW recycling channel alternative of this case is A3.
6. Comparative analysis and discussion
6.1. Theoretical comparison and discussion
-
(1)
Compared with Several Classical Approaches
The existing traditional MCGDM methods can be classified into three types (Chai et al., 2013): (1) Compromise methods, including but not limited to TOPSIS, TODIM (an acronym in Portuguese for interactive and multi-criteria decision making) and VIKOR (vlse kriterijumska optimizacija i kompromisno resenje); (2) Multiple criteria utility techniques, including but not limited to AHP and BWM (the best-worst method); (3) Out ranking techniques, including but not limited to PROMETHEE (preference ranking organization method for enrichment evaluation) and ELECTRE (elimination and choice expressing reality); and (4) other techniques, including but not limited to DEMATEL (decision-making trial and evaluation laboratory). However, these traditional methods tend to ignore the weights of criteria or DMs, assuming that they are known. Neglecting the criteria or DM weight could influence the ranking results of the alternatives. To fill in this research gap, we proposed a novel VIKOR method that considers these two types of weights simultaneously. The comparison of the proposed method with the above traditional methods is shown in Table 20 .
-
(2)
Compared with Other Extended Approaches
Table 20.
The comparison of our method with other classical MCGDM methods.
| Characteristics | Multiple criteria utility techniques |
Out ranking techniques |
Compromise methods |
Other |
Our method | |||
|---|---|---|---|---|---|---|---|---|
| AHP | BWM | ELECTRE | PROMETHEE | TODIM | TOPSIS | DEMATEL | ||
| Weights of criteria | Yes | Yes | No | Yes | Yes | Yes | Yes | Yes |
| Weights of DMs | No | No | No | No | No | Yes | No | Yes |
| Ranking | Yes | No | Yes | Yes | Yes | Yes | No | Yes |
In addition to the above traditional MCGDM methods, in recent years, scholars have begun to integrate these traditional methods to propose novel integrated MCGDM methods, which can be divided into four categories (Chin et al., 2015): (1) subjective weighting approaches based on the subjective preferences of DMs; (2) objective weighting approaches on the basis of information from the criteria evaluation matrixes; and (3) hybrid weighting approaches, which generate weights by combining the subjective views of DMs and the objective criteria evaluation matrixes. Nevertheless, regardless of which of the above weighting methods is used, the final decision result is always a specific ranking, ignoring the influence of different corporate strategies. To some extent, the proposed recycling channel priority index (RCPI) matrix can address this problem well.
The major differences between the proposed method and the existing methods are as follows. First, our method objectively and subjectively considers the criteria and determines the criteria weights jointly with the IF-BWM and IF-entropy weight methods. It is simple and useful compared with the references (Liu et al., 2013, Qi et al., 2015). Second, the ranking results are no longer constant once calculated but change depending on the actual corporate strategy. In our method, the idea of customer segmentation is incorporated into the decision-making process. Based on the capacity and cost, the alternatives are placed into the RCPI matrix constructed by us and are segmented into four types. According to this PCPI matrix and the reverse supply chain strategy of the alternatives, a more reasonable and referable decision framework was established. The major differences between the proposed method and the existing methods are shown in Table 21 .
Table 21.
The discrepancy of the presented approach and the other three related approaches.
| Features | The existing MCGDM methods |
Our method | ||
|---|---|---|---|---|
| Subjective methods | Objective methods | Hybrid methods | ||
| Typical references | (Wang, 2005) (Shirland et al., 2003) |
(S. Liuiu et al., 2013) (Chen & Li, 2011) |
(Ding et al., 2021) (Chin et al., 2015) |
\ |
| Weight of DMs (Subjective/ Objective) |
Priori given (Subjective) |
Obtained from individual decision (Objective) |
Combination of objective and subjective decision (Subjective + Objective) |
Obtained by Entropy (Objective) |
| Weight of criteria (Subjective/ Objective) |
Subjective views of DMs (Subjective) |
Derived from the objective decision-making matrix (Objective) |
Comprehensively use the objective and subjective decision (Subjective + Objective) |
Jointly with IF-BWM and IF-Entropy weight method (Subjective + Objective) |
| Whether the ranking results vary with the corporate strategy or not | No | No | No | Yes |
| Whether the decision-making results provide a segmentation of alternatives or not | No | No | No | Yes |
6.2. Experimental comparison and discussion
-
(1)
Compared with Several Classical Approaches
As shown in Table 20, there are currently five classical MCGDM methods that can be used for ranking in addition to the VIKOR method, namely ELECTRE, PROMETHEE, TODIM, TOPSIS and AHP. However, among the above ranking methods, the scoring, weighting and aggregation methods of the AHP method are quite different from the others, and the ranking results obtained by this method are often different from those obtained by other ranking methods. Therefore, to retain consistency in the method-based comparisons, we considered four classical ranking methods viz., TODIM, TOPSIS, ELECTRE, and PROMETHEE in this paper. It is worthwhile to note that the linguist set, evaluation information, and weighting method are kept constant during the comparison process. The related results are presented in Table 22 .
Table 22.
Comparison of the results of computational experiments with articles.
| Method | Overall score value |
Ranking | |||
|---|---|---|---|---|---|
| A1 | A2 | A3 | A4 | ||
| Proposed Method | 1.00 | 0.89 | 0.11 | 0.50 | A3 > A4 > A2 > A1 |
| TODIM | 0 | 0.41 | 1 | 0.46 | A3 > A4 > A2 > A1 |
| TOPSIS | 0.53 | 0.69 | 0.64 | 0.30 | A2 > A3 > A1 > A4 |
| ELECTRE | −0.72 | −1.23 | 0.79 | 0.28 | A3 > A4 > A1 > A2 |
| PROMETHEE | −0.22 | 0.08 | 0.14 | 0.01 | A3 > A2 > A4 > A1 |
In addition, to determine the homogeneity of the developed method proposed in this paper with other traditional MCGDM methods, the Spearman correlation was calculated and is shown in Fig. 8 . The values of the Spearman correlation with maximum evaluation score rankings are given by 1.00, 0.80, 0.80,0.00 and 1.00. From Table 22 and Fig. 8, it is obtained that the ranking results of our method are highly consistent with other traditional MCGDM methods on IFSs. Specifically, the ranking results obtained by the TODIM method are in full agreement with the extended VIKOR method proposed in this paper, which proves the effectiveness of our method. At the same time, although there are some differences among the ranking results obtained by ELECTRE, PROMETHEE and our method, these differences are not significant and we can conclude that A3 is the strongest CMW recycling channel regardless of ELECTRE or PROMETHEE, which also proves the effectiveness of our proposed method. Although the ranking results obtained by the TOPSIS method are quite different from those of the other methods, the accuracy of the results obtained by this method is not as convincing as that of the extended VIKOR method, considering that the net dominance of the four scenarios obtained by TOPSIS is extremely similar.
Fig. 8.
The Spearman correlation.
Based on the capacity and disposal charges, the CWM recycling channel alternatives are placed into a priority index (RCPI) matrix constructed by us and are segmented into four types. Considering that the reverse supply chain strategy of the hospital in this case is “sustainable”, it is reasonable for this hospital to sacrifice some of its interests for the safe disposal of CMW. Thus, we argue that the optimal CMW recycling channel alternative of this case is A3. This decision result is more scientific and reliable than traditional MCGDM methods because it accounts for the influence of the reverse supply chain strategy on the ranking of alternatives.
Through our above discussion, it is obvious that our method established a more reasonable and referable decision framework for healthcare institutions to solve the problem of evaluating waste recycling channels and allocating CMW. By applying the integrated BWM-Entropy-VIKOR method and the RCPI matrix, we can achieve a more proper allocation of the CWM, which could lead to a better decision result.
-
(2)
Compared with Other Extended Approaches
In order to compared our proposed method with other extended approaches, the same case was reconducted through the methods of Zhang et al., Cheng et al., and Fei et al. Table 23 shows a comparison of the ranking results and the optimal choice under these different extended methods.
Table 23.
Comparison of Ranking Results and the Optimal Choice Obtained by Different Methods.
| Method in Reference | Method Introduction | Ranking | The optimal choice |
|---|---|---|---|
| Zhang et al. (2015) | Developed a heterogeneous MCGDM method based on the degree of deviation, the alternatives’ relative closeness and the TOPSIS method. | A4 > A3 > A2 > A1 | A4 |
| Cheng et al. (2017) | A solution to the HMCGDM problem of HAD considering distance measurement under the triangular fuzzy sets decision-making environment is proposed. | A4 > A3 > A2 > A1 | A4 |
| Fei et al. (2021) | A heterogeneous MCGDM method that takes into account the different backgrounds and preferences of DM is proposed. The process is based on DST and incorporates belief entropy. | A4 > A3 > A1 > A2 | A4 |
| Our Method | We propose a novel IFSs based MCGDM method, which considers the reverse supply chain strategy of the CMW recycling alternatives. | A3 > A4 > A2 > A1 | A3 |
As Table 21 shows, the proposed method, Zhang et al. (2015)’s method, Cheng et al. (2017)’s method and Fei et al. (2021)’s method obtained the similar ranking result, which means that in most cases, the results of our method are consistent with the results of previous methods. Specially, A3 and A4 are the priority ranges for choosing in several ranking results while A2 and A1 are alternatives with lower rankings. Differing from other method, we use IFSs for assessment and consider both subjective and objective issue, which can better reflect uncertainty and obtain more reasonable results. Moreover, the aggregation operator IFWA is utilized in our method to aggregate the individual judgements of DMs into an integrated weighting IF decision matrix, considering the priority of DMs.
With further analysis, it can be found that the optimal choice obtained by our method is quite different from others. We consider A3 as the best CMW recycling channel alternative while other three methods have the same result, A4. It is that we consider the reverse supply chain strategy of the hospital and the RCPI matrix, which lead to subtle differences between these optimal choices. Therefore, the effectiveness and superiority of our method are proven.
7. Conclusions
The explosion of CMW creates a great challenge in MW management, especially in developing countries. There is an urgent need for a new decision-making method to help hospitals segment CMW recycling channels and achieve a more reasonable allocation of CWMs. In this paper, we proposed an integrated BWM-Entropy-VIKOR method to evaluate the capacity of CMW recycling channels. We incorporated the idea of customer segmentation into the MW recovery field to prioritize the CMW allocation process. Based on the capacity and disposal charges, the CWM recycling channel alternatives are placed into a priority index (RCPI) matrix constructed by us and are segmented into four types. According to this PCPI matrix and the reverse supply chain strategy (efficient, saving or sustainable) of the alternatives, a more reasonable and referable decision framework for healthcare institutions to solve the problem of evaluating waste recycling channels and allocating CMW was established.
The contributions of our study involve three components: criteria (1) According to the characteristics of CMW, processing flow and the TOE theoretical framework, we established a new CMW recycling channel capacity evaluation criterion system which makes our proposed method more targeted and efficient. In terms of performance evaluation criteria, we proposed Specially, a targeted six-dimensional evaluation criterion system for CMW recycling channels with respect to the characteristics of CMW is proposed. The evaluation criterion can comprehensively measure the capacity of CMW recycling channels from multiple aspects (Technology, Organization and Environment). (2) To address challenges of CMW recycling channel selection, we propose a novel decision-making framework based on a new CMW recycling channel capacity evaluation index system, IFSs, the VIKOR method and a proposed RCPI matrix. This framework incorporated the idea of customer segmentation into the MW recovery field to prioritize the CMW allocation process and take the hospitals’ reverse supply chain strategies into account. Based on the capacity and disposal charges, the CWM recycling channel alternatives are placed into a priority index matrix (RCPI) matrix constructed by us and are segmented into four types. According to this PCPI matrix and the reverse supply chain strategy of the alternatives, a more reasonable and referable decision framework for healthcare institutions to solve the problem of evaluating waste recycling channels and allocating CMW was established. (3) We propose a novel weighting method for our decision-making framework, which assigns weights both from criteria and DMs dimensions simultaneously, making our research results more accurate. Meanwhile, our integrated BWM-Entropy-VIKOR method objectively and subjectively considers the criteria of CMW recycling channels and determines the criteria weights jointly with the IF-BWM and IF-entropy weight methods.
Although the integrated BWM-Entropy-VIKOR method approach is valuable and available, in our opinion, there are still several limitations and further study issues deserve to be explored based on this novel IF-VIKOR framework: (1) Our evaluation framework is limited to the selection of CMW recycling channels and CMW allocation strategy; thus, we can attempt to extend our framework to other areas, such as sustainable CMW disposal technique assessment, sustainable biomass crop assessment, CMW management assessment, and the location of CMW disposal sites. (2) The evaluation information of our method is only in IFS, and thus, further study can extend this VIKOR framework by selecting other linguistic sets, e.g., IT2 FSs, IVIFSs, dual hesitant fuzzy sets, probabilistic dual hesitant fuzzy sets, necessary and possible hesitant fuzzy sets, and others. Meanwhile, group consensus is a hot issue in current multi-criteria decision-making research (Sun et al., 2021, Wang et al., 2022, Wu et al., 2019, Wu et al., 2021). We could strengthen our research on this aspect in future work. (3) Due to the lack of effective integration with other theories and methods, our method still has large development space on usability. Hence, future work should attempt to combine the IF-VIKOR framework with other theories or approaches, including but not limited to prospect theory, SWARA, CRITIC, and the DEMATEL method. Moreover, our work can be expanded by applying several different MCGDM approaches, including but not limited to the WASPAS, COPRAS, ARAS, and TODIM methods, to evaluate the capacity of CMW recycling channels.
CRediT authorship contribution statement
Sen Liu: Conceptualization, Methodology, Formal analysis, Writing – original draft, Project administration, Funding acquisition. Jinxin Zhang: Methodology, Validation, Writing – original draft. Ben Niu: Writing – review & editing, Project administration, Funding acquisition. Ling Liu: Writing – review & editing, Funding acquisition. Xiaojun He: Validation.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
Acknowledgements
The authors would like to thank Shenzhen University Research Committee for technical support.
Ethical statement
The authors certify that this manuscript is original and has not been published and will not be submitted elsewhere for publication while being considered.
Funding statement
The work described in this paper was supported by The Natural Science Foundation of China (Grant No. 71862035, 71971143, 71862034); The Yunnan Fundamental Research Project under grant No. 2019FB085; Major Research Plan for National Natural Science Foundation of China (No. 91846301); Project of Guangdong Province Higher Vocational Colleges & Schools Pearl River Scholar Funded Scheme 2016; The 21th Yunnan Young and Middle-aged Academic and Technical Leaders Reserve Personnel Training Program under grant No. 2019HB030.
Data availability statement
All relevant data are within the paper.
References
- Adeniran A.E., Nubi A.T., Adelopo A.O. Solid waste generation and characterization in the University of Lagos for a sustainable waste management. Waste Management. 2017;67:3–10. doi: 10.1016/j.wasman.2017.05.002. [DOI] [PubMed] [Google Scholar]
- Ahmadi M., Sharifi A., Dorosti S., Jafarzadeh Ghoushchi S., Ghanbari N. Investigation of effective climatology parameters on COVID-19 outbreak in Iran. Science of The Total Environment. 2020;729 doi: 10.1016/j.scitotenv.2020.138705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Albahri A.S., Hamid R.A., Albahri O.S., Zaidan A.A. Detection-based prioritisation: Framework of multi-laboratory characteristics for asymptomatic COVID-19 carriers based on integrated Entropy–TOPSIS methods. Artificial Intelligence in Medicine. 2021;111 doi: 10.1016/j.artmed.2020.101983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fei L., Feng Y., Wang H. Modeling heterogeneous multi-attribute emergency decision-making with Dempster-Shafer theory. Computers & Industrial Engineering. 2021;161:107633. [Google Scholar]
- Ishizaka A., Resce G. Best-Worst PROMETHEE method for evaluating school performance in the OECD's PISA project. Socio-Economic Planning Sciences. 2021;73:100799. [Google Scholar]
- Alshraideh H., Qdais H. Stochastic modeling and optimization of medical waste collection in Northern Jordan. Journal of Material Cycles and Waste Management. 2017;19(2):743–753. [Google Scholar]
- Amini A., Alinezhad A., Yazdipoor F. A TOPSIS, VIKOR and DEA integrated evaluation method with belief structure under uncertainty to rank alternatives. International Journal of Advanced Operations Management. 2019;11:171–188. [Google Scholar]
- Arıkan E., Şimşit-Kalender Z.T., Vayvay Ö. Solid waste disposal methodology selection using multi-criteria decision making methods and an application in Turkey. Journal of Cleaner Production. 2017;142:403–412. [Google Scholar]
- Atanassov K.T. Intuitionistic fuzzy sets. Fuzzy Sets and Systems. 1986;20(1):87–96. [Google Scholar]
- Baghapour M.A., Shooshtarian M.R., Javaheri M.R., Dehghanifard S., Sefidkar R., Nobandegani A.F. A computer-based approach for data analyzing in hospital’s health-care waste management sector by developing an index using consensus-based fuzzy multi-criteria group decision-making models. International Journal of Medical Informatics. 2018;118:5–15. doi: 10.1016/j.ijmedinf.2018.07.001. [DOI] [PubMed] [Google Scholar]
- Bahrani S., Ebadi T., Ehsani H., Yousefi H., Maknoon R. Modeling landfill site selection by multi-criteria decision making and fuzzy functions in GIS, case study: Shabestar, Iran. Environmental Earth Sciences. 2016;75(4):1–14. [Google Scholar]
- Bustince H., Burillo P. Vague sets are intuitionistic fuzzy sets. Fuzzy Sets and Systems. 1996;79(3):403–405. [Google Scholar]
- Çalı S., Balaman Ş.Y. A novel outranking based multi criteria group decision making methodology integrating ELECTRE and VIKOR under intuitionistic fuzzy environment. Expert Systems with Applications. 2019;119:36–50. [Google Scholar]
- Chai J., Liu J.N.K., Ngai E.W.T. Application of decision-making techniques in supplier selection: A systematic review of literature. Expert Systems with Applications. 2013;40(10):3872–3885. [Google Scholar]
- Chen C., Chen J., Fang R., Ye F., Yang Z., Wang Z., Shi F., Tan W. What medical waste management system may cope With COVID-19 pandemic: Lessons from Wuhan. Resources Conservation and Recycling. 2021;170 doi: 10.1016/j.resconrec.2021.105600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen T.-Y., Li C.-H. Objective weights with intuitionistic fuzzy entropy measures and computational experiment analysis. Applied Soft Computing. 2011;11(8):5411–5423. [Google Scholar]
- Cheng J., Feng Y., Lin Z., Tan J. 基于异构公理设计的涡轮发电机关键部件抗振优化. Journal of Cleaner Production. 2017;141:1467–1477. [Google Scholar]
- Chiclana F., Herrera F., Herrera-Viedma E. Integrating three representation models in fuzzy multipurpose decision making based on fuzzy preference relations. Fuzzy Sets and Systems. 1998;97(1):33–48. [Google Scholar]
- Chin K.-S., Fu C., Wang Y. A method of determining attribute weights in evidential reasoning approach based on incompatibility among attributes. Computers & Industrial Engineering. 2015;87:150–162. [Google Scholar]
- Daneshvar Rouyendegh B., Yıldızbaşı A., Arıkan Ü. Using Intuitionistic Fuzzy TOPSIS in Site Selection of Wind Power Plants in Turkey. Advances in Fuzzy Systems. 2018;2018:1–14. [Google Scholar]
- Das A.K., Islam M.N., Billah M.M., Sarker A. COVID-19 pandemic and healthcare solid waste management strategy - A mini-review. Science of The Total Environment. 2021;778 doi: 10.1016/j.scitotenv.2021.146220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das A.K., Islam M.N., Billah M.M., Sarker A. COVID-19 pandemic and healthcare solid waste management strategy – A mini-review. Science of The Total Environment. 2021;778 doi: 10.1016/j.scitotenv.2021.146220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Luca A., Termini S. A definition of a nonprobabilistic entropy in the setting of fuzzy sets theory. Information and Control. 1972;20(4):301–312. [Google Scholar]
- Dharmaraj S., Ashokkumar V., Pandiyan R., Halimatul Munawaroh H.S., Chew K.W., Chen W.-H., Ngamcharussrivichai C. Pyrolysis: An effective technique for degradation of COVID-19 medical wastes. Chemosphere. 2021;275 doi: 10.1016/j.chemosphere.2021.130092. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- Ding Q., Wang Y.-M., Goh M. An extended TODIM approach for group emergency decision making based on bidirectional projection with hesitant triangular fuzzy sets. Computers & Industrial Engineering. 2021;151 doi: 10.1016/j.cie.2020.106959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dixit S., Raj T. Feasibility analysis of FMS in small and medium scale Indian industries with a hybrid approach using ISM and TOPSIS. International Journal of Advanced Operations Management. 2018;10(3):252–280. [Google Scholar]
- Ekmekçioğlu M., Kaya T., Kahraman C. Fuzzy multicriteria disposal method and site selection for municipal solid waste. Waste Management. 2010;30(8):1729–1736. doi: 10.1016/j.wasman.2010.02.031. [DOI] [PubMed] [Google Scholar]
- G, W. & L, M. (2020). The Hidden Risks of Medical Waste and the COVID-19 Pandemic. https://www.waste360.com/medical-waste/hidden-risks-medical-waste-and-covid-19-pandemic.
- Kampf G., Todt D., Pfaender S., Steinmann E. Persistence of coronaviruses on inanimate surfaces and their inactivation with biocidal agents. Journal of Hospital Infection. 2020;104(3):246–251. doi: 10.1016/j.jhin.2020.01.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kargar S., Paydar M.M., Safaei A.S. A reverse supply chain for medical waste: A case study in Babol healthcare sector. Waste Management. 2020;113:197–209. doi: 10.1016/j.wasman.2020.05.052. [DOI] [PubMed] [Google Scholar]
- Lee S., Vaccari M., Tudor T. Considerations for choosing appropriate healthcare waste management treatment technologies: A case study from an East Midlands NHS Trust, in England. Journal of Cleaner Production. 2016;135:139–147. [Google Scholar]
- Liu H.-C., Wu J., Li P. Assessment of health-care waste disposal methods using a VIKOR-based fuzzy multi-criteria decision making method. Waste Management. 2013;33(12):2744–2751. doi: 10.1016/j.wasman.2013.08.006. [DOI] [PubMed] [Google Scholar]
- Liu H.-W. 直觉模糊集之间和元素之间的新相似性度量. Mathematical and Computer Modelling. 2005;42(1):61–70. [Google Scholar]
- Liu S., Chan F.T.S., Ran W. Multi-attribute group decision-making with multi-granularity linguistic assessment information: An improved approach based on deviation and TOPSIS. Applied Mathematical Modelling. 2013;37(24):10129–10140. [Google Scholar]
- Mantzaras G., Voudrias E.A. An optimization model for collection, haul, transfer, treatment and disposal of infectious medical waste: Application to a Greek region. Waste Management. 2017;69:518–534. doi: 10.1016/j.wasman.2017.08.037. [DOI] [PubMed] [Google Scholar]
- Manupati V.K., Ramkumar M., Baba V., Agarwal A. Selection of the best healthcare waste disposal techniques during and post COVID-19 pandemic era. Journal of Cleaner Production. 2021;281 doi: 10.1016/j.jclepro.2020.125175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mardani A., Hooker R.E., Ozkul S., Yifan S., Nilashi M., Sabzi H.Z., Fei G.C. Application of decision making and fuzzy sets theory to evaluate the healthcare and medical problems: A review of three decades of research with recent developments. Expert Systems with Applications. 2019;137:202–231. [Google Scholar]
- Mishra A.R., Mardani A., Rani P., Zavadskas E.K. A novel EDAS approach on intuitionistic fuzzy set for assessment of health-care waste disposal technology using new parametric divergence measures. Journal of Cleaner Production. 2020;272 [Google Scholar]
- Mishra A.R., Rani P., Mardani A., Pardasani K.R., Govindan K., Alrasheedi M. Healthcare evaluation in hazardous waste recycling using novel interval-valued intuitionistic fuzzy information based on complex proportional assessment method. Computers & Industrial Engineering. 2020;139 [Google Scholar]
- Mishra A.R., Rani P., Pardasani K.R., Mardani A. A novel hesitant fuzzy WASPAS method for assessment of green supplier problem based on exponential information measures. Journal of Cleaner Production. 2019;238 [Google Scholar]
- Narayanamoorthy S., Annapoorani V., Kang D., Baleanu D., Jeon J., Kureethara J.V., Ramya L. A novel assessment of bio-medical waste disposal methods using integrating weighting approach and hesitant fuzzy MOOSRA. Journal of Cleaner Production. 2020;275 [Google Scholar]
- Nghiem L.D., Morgan B., Donner E., Short M.D. The COVID-19 pandemic: Considerations for the waste and wastewater services sector. Case Studies in Chemical and Environmental Engineering. 2020;1 doi: 10.1016/j.cscee.2020.100006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nzediegwu C., Chang S.X. Improper solid waste management increases potential for COVID-19 spread in developing countries. Resources, Conservation and Recycling. 2020;161 doi: 10.1016/j.resconrec.2020.104947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Opricovic S. Multicriteria optimization of civil engineering systems. Faculty of Civil Engineering. 1998;37:5–21. [Google Scholar]
- Opricovic S., Tzeng G.-H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. European Journal of Operational Research. 2004;156(2):445–455. [Google Scholar]
- Opricovic S., Tzeng G.-H. Extended VIKOR method in comparison with outranking methods. European Journal of Operational Research. 2007;178(2):514–529. [Google Scholar]
- Organization, W.H. (2021). WHO Coronavirus Disease (COVID-19) Dashboard. https://covid19.who.int/. (Accessed 22 April 2021).
- Ouyang L., Zhu Y., Zheng W., Yan L. An information fusion FMEA method to assess the risk of healthcare waste. Journal of Management Science and Engineering. 2021;6(1):111–124. [Google Scholar]
- Patrício Silva A.L., Prata J.C., Walker T.R., Duarte A.C., Ouyang W., Barcelò D., Rocha-Santos T. Increased plastic pollution due to COVID-19 pandemic: Challenges and recommendations. Chemical Engineering Journal. 2021;405 doi: 10.1016/j.cej.2020.126683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng J., Wu X., Wang R., Li C., Zhang Q., Wei D. Medical waste management practice during the 2019–2020 novel coronavirus pandemic: Experience in a general hospital. American Journal of Infection Control. 2020;48(8):918–921. doi: 10.1016/j.ajic.2020.05.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qi X., Liang C., Zhang J. Generalized cross-entropy based group decision making with unknown expert and attribute weights under interval-valued intuitionistic fuzzy environment. Computers & Industrial Engineering. 2015;79:52–64. [Google Scholar]
- Ramteke S., Sahu B.L. Novel coronavirus disease 2019 (COVID-19) pandemic: Considerations for the biomedical waste sector in India. Case Studies in Chemical and Environmental Engineering. 2020;2 doi: 10.1016/j.cscee.2020.100029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rani P., Mishra A.R., Pardasani K.R., Mardani A., Liao H., Streimikiene D. A novel VIKOR approach based on entropy and divergence measures of Pythagorean fuzzy sets to evaluate renewable energy technologies in India. Journal of Cleaner Production. 2019;238 [Google Scholar]
- Rezaei J. Best-worst multi-criteria decision-making method. Omega. 2015;53:49–57. [Google Scholar]
- Rowan N.J., Laffey J.G. Unlocking the surge in demand for personal and protective equipment (PPE) and improvised face coverings arising from coronavirus disease (COVID-19) pandemic – Implications for efficacy, re-use and sustainable waste management. Science of The Total Environment. 2021;752 doi: 10.1016/j.scitotenv.2020.142259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi H., Liu H.-C., Li P., Xu X.-G. An integrated decision making approach for assessing healthcare waste treatment technologies from a multiple stakeholder. Waste Management. 2017;59:508–517. doi: 10.1016/j.wasman.2016.11.016. [DOI] [PubMed] [Google Scholar]
- Shirland L.E., Jesse R.R., Thompson R.L., Iacovou C.L. Determining attribute weights using mathematical programming. Omega. 2003;31(6):423–437. [Google Scholar]
- Sun, Q., Wu, J., Chiclana, F., Fujita, H. & Herrera-Viedma, E. (2021). A dynamic feedback mechanism with attitudinal consensus threshold for minimum adjustment cost in group decision making. IEEE Transactions on Fuzzy Systems PP(99), 1-1.
- Tabish M., Khatoon A., Alkahtani S., Alkahtane A., Alghamdi J., Ahmed S., Mir S., Albasher G., Almeer R., Al-Sultan N., Aljarba N., Alqahtani W., Mohammed A.-Z., Nayak A., Hasnain M. Approaches for prevention and environmental management of novel COVID-19. Environmental Science and Pollution Research International. 2020 doi: 10.1007/s11356-020-10640-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teng F., Liu P. A large group decision-making method based on a generalized Shapley probabilistic linguistic Choquet average operator and the TODIM method. Computers & Industrial Engineering. 2021;151 [Google Scholar]
- Thakur V., Ramesh A. Selection of Waste Disposal Firms Using Grey Theory Based Multi-criteria Decision Making Technique. Procedia - Social and Behavioral Sciences. 2015;189:81–90. [Google Scholar]
- Thakur V., Ramesh A. Healthcare waste disposal strategy selection using grey-AHP approach. Benchmarking: An International Journal. 1999 [Google Scholar]
- Thind P.S., Sareen A., Singh D.D., Singh S., John S. Compromising situation of India’s bio-medical waste incineration units during pandemic outbreak of COVID-19: Associated environmental-health impacts and mitigation measures. Environmental Pollution. 2021;276 doi: 10.1016/j.envpol.2021.116621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tirkolaee E.B., Abbasian P., Weber G.W. Sustainable fuzzy multi-trip location-routing problem for medical waste management during the COVID-19 outbreak. Science of the Total Environment. 2020;10:143607. doi: 10.1016/j.scitotenv.2020.143607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tolga A.C., Parlak I.B., Castillo O. Finite-interval-valued Type-2 Gaussian fuzzy numbers applied to fuzzy TODIM in a healthcare problem. Engineering Applications of Artificial Intelligence. 2020;87 [Google Scholar]
- Torkayesh A.E., Pamucar D., Ecer F., Chatterjee P. An integrated BWM-LBWA-CoCoSo framework for evaluation of healthcare sectors in Eastern Europe. Socio-Economic Planning Sciences. 2021 [Google Scholar]
- Tremblay A., Badri A. Assessment of occupational health and safety performance evaluation tools: State of the art and challenges for small and medium-sized enterprises. Safety Science. 2018;101:260–267. [Google Scholar]
- Tripathi A., Tyagi V.K., Vivekanand V., Bose P., Suthar S. Challenges, opportunities and progress in solid waste management during COVID-19 pandemic. Case Studies in Chemical and Environmental Engineering. 2020;2 doi: 10.1016/j.cscee.2020.100060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Doremalen N., Bushmaker T., Morris D.H., Holbrook M.G., Gamble A., Williamson B.N., Tamin A., Harcourt J.L., Thornburg N.J., Gerber S.I., Lloyd-Smith J.O., de Wit E., Munster V.J. Aerosol and Surface Stability of SARS-CoV-2 as Compared with SARS-CoV-1. The New England Journal of Medicine. 2020;382(16):1564–1567. doi: 10.1056/NEJMc2004973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vlachos I.K., Sergiadis G.D. Intuitionistic fuzzy information – Applications to pattern recognition. Pattern Recognition Letters. 2007;28(2):197–206. [Google Scholar]
- Wan S.-P., Chen Z.-H., Dong J.-Y. An integrated interval type-2 fuzzy technique for democratic–autocratic multi-criteria decision making. Knowledge-Based Systems. 2021;214 [Google Scholar]
- Wang J., Shen J., Ye D., Yan X., Zhang Y., Yang W., Li X., Wang J., Zhang L., Pan L. Disinfection technology of hospital wastes and wastewater: Suggestions for disinfection strategy during coronavirus Disease 2019 (COVID-19) pandemic in China. Environmental Pollution. 2020;262 doi: 10.1016/j.envpol.2020.114665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang S., Wu J., Chiclana F., Sun Q., Herrera-Viedma E. Two stage feedback mechanism with different power structures for consensus in large-scale group decision-making. IEEE Transactions on Fuzzy Systems. 2022:1. [Google Scholar]
- Wang Y.-M. On fuzzy multiattribute decision-making models and methods with incomplete preference information. Fuzzy Sets and Systems. 2005;151(2):285–301. [Google Scholar]
- WHO. (2020). Shortage of Personal Protective Equipment Endangering Health Workers Worldwide. accessed 2020/5/11. https://www.who.int/news-room/detail/03-03-2020 accessed 2020/2025/2011.
- Wichapa N., Khokhajaikiat P. Solving multi-objective facility location problem using the fuzzy analytical hierarchy process and goal programming: A case study on infectious waste disposal centers. Operations Research Perspectives. 2017;4:39–48. [Google Scholar]
- Windfeld E.S., Brooks M.-S.-L. Medical waste management – A review. Journal of Environmental Management. 2015;163:98–108. doi: 10.1016/j.jenvman.2015.08.013. [DOI] [PubMed] [Google Scholar]
- Wu J., Sun Q., Fujita H., Chiclana F. An attitudinal consensus degree to control the feedback mechanism in group decision making with different adjustment cost. Knowledge-Based Systems. 2019;164:265–273. [Google Scholar]
- Wu, J., Wang, S., Chiclana, F., Herrera-Viedma, E.F. & Cybernetics, E. (2021). Two-fold personalized feedback mechanism for social network consensus by uninorm interval trust propagation. IEEE Transactions on Cybernetics PP(99), 1. [DOI] [PubMed]
- Wu Q., Zhou L., Chen Y., Chen H. An integrated approach to green supplier selection based on the interval type-2 fuzzy best-worst and extended VIKOR methods. Information Sciences. 2019;502:394–417. [Google Scholar]
- Xiao F. A novel multi-criteria decision making method for assessing health-care waste treatment technologies based on D numbers. Engineering Applications of Artificial Intelligence. 2018;71:216–225. [Google Scholar]
- Yang L., Yu X., Wu X., Wang J., Yan X., Jiang S., Chen Z. Emergency response to the explosive growth of health care wastes during COVID-19 pandemic in Wuhan, China. Resources, Conservation and Recycling. 2021;164 doi: 10.1016/j.resconrec.2020.105074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yazdani M., Tavana M., Pamučar D., Chatterjee P. A rough based multi-criteria evaluation method for healthcare waste disposal location decisions. Computers & Industrial Engineering. 2020;143 [Google Scholar]
- Yu H., Sun X., Solvang W., Zhao X. Reverse Logistics Network Design for Effective Management of Medical Waste in Epidemic Outbreaks: Insights from the Coronavirus Disease 2019 (COVID-19) Outbreak in Wuhan (China) International Journal of Environmental Research and Public Health. 2020;17:1770. doi: 10.3390/ijerph17051770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yue Z. Deriving decision maker’s weights based on distance measure for interval-valued intuitionistic fuzzy group decision making. Expert Systems with Applications. 2011;38(9):11665–11670. [Google Scholar]
- Zadeh L.A. Fuzzy sets. Information and Control. 1965;8(3):338–353. [Google Scholar]
- Zeshui X.U., Yager R.R. Some geometric aggregation operators based on intuitionistic fuzzy sets. International Journal of General Systems. 2006;35(4):417–433. [Google Scholar]
- Zhang H., Gu C.-L., Gu L.-W., Zhang Y. The evaluation of tourism destination competitiveness by TOPSIS & information entropy – A case in the Yangtze River Delta of China. Tourism Management. 2011;32(2):443–451. [Google Scholar]
- Zhang X., Xu Z., Wang H. Heterogeneous multiple criteria group decision making with incomplete weight information: A deviation modeling approach. Information Fusion. 2015;25:49–62. [Google Scholar]
- Zhang Z., Cheng L., Wang X., Lu R., Wei C., Lei M. Construction of Medical Waste Emergency Disposal System in China. Research of Environmental Sciences. 2020;33(7):1683–1690. [Google Scholar]
- Zhao H., Liu H., Wei G., Wang H., Zhu Y., Zhang R., Yang Y. Comparative life cycle assessment of emergency disposal scenarios for medical waste during the COVID-19 pandemic in China. Waste Management. 2021;126:388–399. doi: 10.1016/j.wasman.2021.03.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All relevant data are within the paper.