Hybrid modelling of biological systems: current progress and future prospects

Abstract

Integrated modelling of biological systems is becoming a necessity for constructing models containing the major biochemical processes of such systems in order to obtain a holistic understanding of their dynamics and to elucidate emergent behaviours. Hybrid modelling methods are crucial to achieve integrated modelling of biological systems. This paper reviews currently popular hybrid modelling methods, developed for systems biology, mainly revealing why they are proposed, how they are formed from single modelling formalisms and how to simulate them. By doing this, we identify future research requirements regarding hybrid approaches for further promoting integrated modelling of biological systems.

Introduction

Systems biology [1, 2] aims to study the interactions between the components of a biological system and how these interactions cause the behaviour of the system as a whole. Modelling and simulation play an essential role in achieving this goal. So far, many modelling formalisms have been proposed to represent biological systems from different perspectives. The diversity of biological phenomena and mechanisms result in the adoption of distinct modelling approaches, e.g. ordinary differential equations (ODEs) for describing deterministic systems and stochastic methods for representing systems with randomness. The degree of availability of kinetic data is another reason for people to explore different modelling formalisms. If kinetic data are sufficiently known, the quantitative (ODEs or stochastic) approaches could be appropriate options; otherwise, qualitative/uncertain methods such as Boolean networks or fuzzy logic may be adopted. Another important reason is due to the multi-disciplinarity of researchers [3], who tend to choose their favourite approaches. However, although we have seen many modelling formalisms, we are far from approaching the ultimate goal of systems biology, i.e. to study the behaviour of a system as a whole.

From its inception until now, the mainstream modelling work in this area has focused on fragments of biological systems, such as individual signalling networks, gene regulatory networks and metabolic networks, which however cannot give a complete view of the whole system. In order to obtain a holistic understanding of the cellular behaviour of the whole system, we need to integrate stepwise the fragments into a more comprehensive model which represents the system’s behaviour as an ensemble. Fortunately, with the rapid development of high-throughput experimental technologies such as genomics and proteomics and the increase of measurement data, hybrid integrated modelling of biological systems is becoming increasingly popular by offering a more and more complete picture of the whole system [4].

Historically, hybrid modelling of biological systems has mainly been motivated by the following observations.

• A biological system is inherently hybrid. The whole system can be generally thought of as a continuous model, but it may also comprise different kinds of discrete stochastic events, e.g. the gene regulation (e.g. activation or deactivation of genes) [5], the birth and death of species and the crossing of concentration thresholds of some species, all of which cause state switching [6]. For such biological phenomena, hybrid models that integrate discrete with continuous or stochastic with deterministic methods could be more appropriate.

• The availability of kinetic data usually differs for distinct components for most biological systems. In this case, quantitative and qualitative formalisms may have to be combined to form an integrated model [7].

• Different time scales inherent to biological systems also require hybrid modelling, i.e. components at different time scales may adopt distinct modelling formalisms, e.g. deterministic ones for large scales, but stochastic ones for small scales [8].

• The relief of the computational burden associated with simulation and analysis may be another reason for hybrid modelling, e.g. approximating stochastic dynamics by deterministic ODEs [9]. See [10] for a comparison of continuous, stochastic and hybrid simulation runtime using three biological models: break-repair, circadian oscillation and T7 phage. Taking the circadian oscillation as an example, the simulation time for the continuous, stochastic and hybrid models cost 0.197, 65342.273 and 53232.862 s, respectively, i.e. the hybrid simulation substantially decreases the computational burden due to stochastic simulation. Therefore, a hybrid model may provide a balance of accuracy and speed.

More recently hybrid modelling has attracted increasing attention, and a variety of hybrid methods have been proposed in the systems biology area. However, currently most hybrid modelling approaches and tools only integrate two single modelling formalisms, and thus only support the construction of integrated models for a few fragments of a biological system. Again, we are far from approaching the ultimate goal of systems biology: to construct comprehensive models of a biological system by considering its main biochemical processes, with each process being described by an appropriate modelling formalism. In the current situation, hybrid modelling is facing more and more challenges due to the wish for integrated modelling of biological systems.

In this paper, we review currently popular hybrid modelling methods developed for systems biology, mainly revealing why each hybrid method is proposed, how they are formed by different modelling formalisms and how they are simulated. Based on this survey and the analyses, we identify future prospects of hybrid approaches for achieving a new quality in integrated modelling of biological systems.

Considering that there are many different interpretations of the meaning of hybrid modelling, and a wide variety of hybrid approaches does exist in the literature, we set the boundary of our paper as follows. In this review we focus on dynamic modelling methods in which the behaviour of models can change with time. We also focus on those hybrid approaches that have been implemented by mainstream software tools in systems biology or have been used by other researchers. Hence, readers will be able to more easily understand which kinds of hybrid approaches are supported by these software tools; this in turn permits an informed decision regarding which tools are most appropriate for the scenarios they want to model. This paper basically aims to reach those readers who want to know how to use hybrid approaches and related tools in systems biology, but it may also be of interest for researchers devoted to developing new hybrid algorithms.

Modelling formalisms

In this section, we briefly review some widely used modelling formalisms (also called paradigms or methods) that usually contribute to the formation of hybrid approaches in systems biology. These formalisms can be roughly classified (see Figure 1) as: (1) basic modelling formalisms, including topology-based modelling, extended to constraint-based modelling (CBM), ODEs, continuous time Markov chain (CTMC) and logic modelling, extended to fuzzy logic; (2) higher modelling formalisms which can adopt basic formalisms as underlying semantics, including Petri nets (PNs) and rule-based modelling (RBM). That is, PN and RBM can adopt different semantics: purely qualitative, ODEs, CTMC or even a combination of them. For example, stochastic or continuous Petri nets (SPNs or CPNs) take the semantics of a CTMC or a set of ODEs, respectively.

Figure 1.

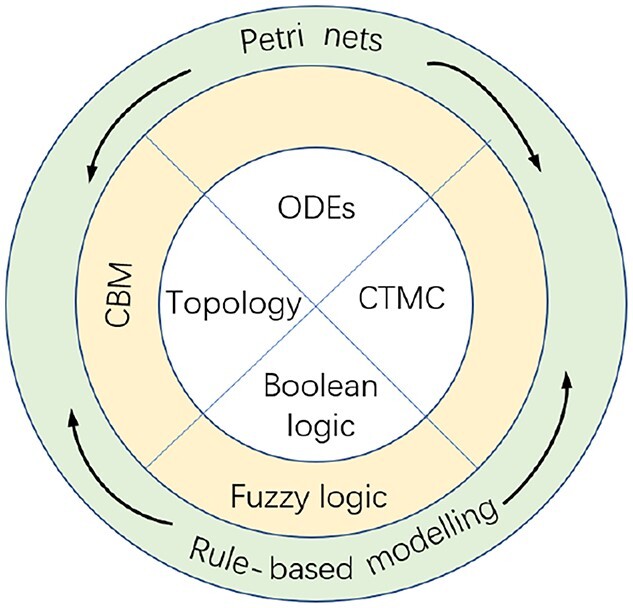
Popular modelling formalisms for biological systems. The inner circle comprises the four basic modelling formalisms: topology-based modelling, ordinary differential equations (ODEs), continuous time Markov chain (CTMC) and Boolean logic modelling. Further, topology-based modelling is extended to constraint-based modelling (CBM), and Boolean logic to fuzzy logic. The outer ring is labelled with higher modelling formalisms including Petri nets and rule-based modelling, which can adopt the basic formalisms as underlying semantics.

Topology-based modelling

The simplest mathematical abstraction of a biological network is the graph representation of its network topology as a purely qualitative model, from which the stoichiometric matrix is built and techniques of graph theory are used for analysing the biological network with measures such as degree distribution and clustering coefficient. For a review about topology-based modelling, refer to [11, 12].

Topology-based modelling has been widely applied to gene-based analyses, resulting in three families of methods: enrichment analysis, pathway topology-based and more recently mechanistic pathway activity (MPA) [13]. Enrichment analysis methods usually consider lists of genes without taking into account the functional relations among genes, whereas pathway topology-based methods do consider the relationships among genes. To analyse more precisely the functional consequences of the activity of pathways, MPA was proposed as a new paradigm. MPA methods aim to study the specific activities of internal elementary subpathways or circuits, of which the whole pathway is composed. They were first used for modelling signalling pathway activities and then generalized to construct integrated models by combining gene expression with metabolic modules. In order to achieve their results, they employ dedicated signal and flux propagation algorithms that iterate until the activity value of each node converges [14].

Ordinary differential equations

Differential equations describe the rates of change of continuous physical quantities, e.g. the species in biological systems. ODEs are one of the widely used deterministic modelling formalisms in systems biology [15] which have been applied to all kinds of biological networks. With ODEs, we can build a kinetic model for a biological network to be studied, for which we can use numerical simulation to thoroughly investigate its dynamic behaviour. Notably, there is a wealth of related simulation algorithms.

However, the use of ODEs for biological modelling has a main drawback – we need to know the mechanism of the system and we have to obtain sufficient kinetic data, which, however, may not be available in many cases. This hinders the construction of large-scale models as it is very cumbersome to gather all necessary kinetic parameters for the whole system. On the other hand, the computational burden of numerical simulation of a large number of ODEs, particularly if they are stiff, makes the analysis of a large model extremely expensive. Another disadvantage of ODEs for biological modelling is the lack of graphical representation. This issue has been addressed using the graphical representation of PNs for describing ODEs, i.e. CPNs [16]. The semantics of a CPN is thus equivalent to a set of ODEs. The family of differential equations also includes stochastic differential equations and partial differential equations (PDEs). The former can be used to model differential equation models with stochastic effects, while the latter offers spatial deterministic simulation capabilities.

Continuous time Markov chain

When constructing biological models where biochemical processes are characterized by interactions of molecular species of low numbers, stochasticity may have to be considered as the effect of randomness because the low numbers of molecules are not ignorable. One popular stochastic modelling method is the CTMC [17], which may be generated by, e.g. SPNs [18], and solved using stochastic simulation algorithms (SSAs) [19]. Stochastic simulation considers each chemical reaction as a random process and thus is more accurate than other deterministic simulation methods. The popular SSAs include Gillespie’s first reaction method and direct method [19], 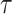-leap method [20], 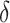-leap method [21] and Gibson–Bruck’s algorithm [22]. However, stochastic simulation is often computationally expensive as it may consume much runtime to accomplish the discrete and individual firing of all reactions.

Logic modelling

Logic modelling [23] was proposed to overcome the limitations of quantitative modelling imposed by the lack of kinetic data and thus precise kinetic parameters. Boolean networks [24] are among the simplest logic models, in which each variable, representing, e.g. the presence of a protein or the state of a gene, takes two values, 0 or 1, Boolean rules describe the state transition of a system, and Boolean logic is used to achieve the reasoning. Later, the variables in Boolean networks were extended to allow multiple values, which refines the description of the states and thus yields more precise behaviour of a system. Finally, fuzzy logic achieves continuous regulations of variables by extending their values to an interval [0,1] of belonging instead of two crisp values 0 and 1. Moreover, fuzzy logic allows the fusion of human-like reasoning into the construction of biological models, which offers a powerful way to incorporate biologists’ experience into a model [25].

Constraint-based modelling

CBM allows for rapid analysis of large networks under the steady-state assumption (i.e. no transient behaviour is analysed) by overcoming the limitations due to the lack of kinetic information required by kinetic models. One of the commonly used CBM approaches is flux balance analysis (FBA) [26, 27] for metabolic networks. With FBA, a metabolic network is first represented as a stoichiometric matrix in terms of the stoichiometric coefficients of each reaction, which imposes the mass balance constraints for the network. Together with the capability constraints imposed by the lower and upper bounds of reactions, the model describes an allowable solution space. Then an objective function is defined and solved by linear programming, producing a particular flux distribution. The merit of FBA is that it can be used to construct genome-scale metabolic networks and to analyse the flow of metabolites. But FBA does not consider kinetic parameters, and thus cannot analyse metabolite concentrations or transient behaviour. Typically, FBA cannot take into account regulatory effects.

Petri nets

A PN [28] is a bipartite graph consisting of two types of nodes, places and transitions, connected by directed arcs (also called edges). Places usually represent inactive objects like biological species. Places hold tokens which can describe quantities of species such as the number of molecules. Transitions represent actions or changes of objects like translation and transcription of species in the biological context. The execution of a PN is to randomly fire transitions that are enabled, which remove tokens from input places and add tokens to output places. PNs have been extended in many ways. For example, arcs have been enhanced to include read arcs, inhibitor arcs and marking-dependent arcs, the latter giving rise to self-modifying nets [29]. These merely qualitative Petri nets have been further extended to involve timing aspects, e.g. time Petri nets (TPNs) [30] associate transitions with deterministic time delays, SPNs with exponentially distributed random delays (stochastic rates) and CPNs with deterministic rates [16].

Orthogonal to these extensions are coloured Petri nets (ColPNs), which combine programming language concepts with PNs. PNs have been widely applied in systems biology to model different types of networks; see [31, 32] for reviews. Moreover, ColPNs and their extensions are suitable for spatial, multilevel and multiscale modelling of biological systems; see [33] for a review.

Rule-based modelling

RBM [34] uses notations similar to the chemical reaction equations to represent biological systems. Once a rule-based model is constructed, it can be interpreted as a set of ODEs if the state of species is considered as continuous concentrations, or as stochastic processes if the state of species is regarded as discrete numbers. Many variants of rule-based methods have been proposed, e.g. by allowing species with attributes or rules with reactant patterns [35]. Rule-based models offer an intuitive form that transparently represents biological networks. Analogue to RBM, Process Algebra [36] offers another popular modelling method to describe chemical reaction equations.

Spatial modelling

Space plays an important role in many phenomena where molecular mobility, e.g. diffusion of substrates or transport of molecules, has to be considered, especially in the integrated modelling scenario. The popular spatial modelling approaches can be classified into mesh-based, lattice-based, volume-based and off-lattice [37]. The widely used PDE approach is mesh-based, which realizes spatial modelling in a deterministic way. Cellular automata (CA) [38] is a lattice-based method, which runs on a lattice with a number of states that evolve in a discrete way. Each site on the lattice has single or multiple molecules. Other lattice-based methods include lattice gas CA [39]. The spatial Gillespie approach [40] evolved from SSAs is a volume-based method, where the whole volume is divided into a number of subvolumes. In each subvolume, all species are assumed to be uniformly distributed. Off-lattice methods, compared with lattice-based ones, offer a more realistic representation of spatial positions of cells, i.e. they do not need to be uniformly spaced on a fixed lattice [41]. As one of the off-lattice methods, agent-based modelling [42] considers a set of autonomous decision-making entities, called agents, which are located in space and individually sense the environment and make decisions based on a set of rules.

Artificial intelligence methods

The aforementioned modelling formalisms can be classified as classical theory-based (or physics-based) methods [43], in which a model usually represents causal relationships between inputs and outputs. With the arrival of big data, data-driven modelling has attracted much attention, where a model represents correlation relationships between one set of data and another set of data [43]. Data-driven modelling has many limitations, such as being incapable of representing causal relationships between inputs and outputs and of coping with changing circumstances. Data-driven modelling is usually achieved with artificial intelligence (AI) techniques, including data mining and machine learning. So far, AI techniques are mostly applied in bioinformatics, but they are starting to be applied in systems biology in various ways [44, 45], e.g. for identifying principal factors for constructing models, or building regression models to predict system behaviour. AI techniques such as neural networks (NNs) have also been applied to reconstruct gene regulatory networks from pseudo-time-series gene expression data [46].

Comparison of the formalisms

We have briefly reviewed some popular modelling formalisms that usually contribute to the formation of hybrid approaches. These modelling formalisms can be categorized in many ways, e.g. continuous and discrete, qualitative and quantitative, deterministic and stochastic [3, 47]. No single formalism covers all required features and thus each single formalism only partially fulfils the requirements of integrated modelling of biological systems. To better classify and clarify the different hybrid approaches that will be discussed below, we briefly summarize the features of each modelling formalism in Table 1.

Table 1.

Modelling formalisms and their features, discussed in Sections 2.1–2.9.

Category	Modelling	Simulation	Qualitative/	Continuous/	Deterministic/	Networks
	formalism	algorithm	quantitative	discrete	stochastic	supported
Topology-based modelling	Graph	N.A.	qualitative	discrete	N.A.	S, R, M
	Mechanistic pathway activity	signal and flux propagation	quantitative	continuous	deterministic	S, R, M
Deterministic modelling	Ordinary differential equations	Numerical integration	quantitative	continuous	deterministic	S, R, M
Stochastic modelling	Continuous time Markov Chain	Stochastic simulation algorithms	quantitative	discrete	stochastic	S, R, M
Logic modelling	Boolean networks	Discrete time simulation	qualitative	discrete	N.A.	R
	Fuzzy logic	Discrete time simulation	qualitative	continuous	deterministic	S, R, M
Constraint-based modelling	Flux balance analysis	Linear programming	quantitative	continuous	deterministic	M
Petri nets	Qualitative Petri nets	Discrete event simulation	qualitative	discrete	stochastic	S, R, M
	Continuous Petri nets	Numerical integration	quantitative	continuous	deterministic	S, R, M
	Stochastic Petri nets	Stochastic simulation algorithms	quantitative	discrete	stochastic	S, R, M
Rule-based modelling	Rule-based modelling	Depending on underlying semantics*	EITHER	EITHER	EITHER	S, R, M
Spatial modelling	Partial differential equations	Numerical integration	quantitative	continuous	deterministic	S, R, M
	Cellular automata	Discrete time simulation	EITHER	discrete	stochastic	S, R, M
	Spatial Gillespie	Spatial Stochastic simulation algorithms	quantitative	discrete	stochastic	S, R, M
Artificial intelligence methods	Neural networks, etc.	N.A.	EITHER	EITHER	N.A.	S, R, M

N.A. means not applicable. EITHER means either is applicable depending on the explanation about the constructed model. S, R and M refer to signalling, regulatory and metabolic networks, respectively. ^*The simulation algorithm that is adopted by rule-based modelling depends on the underlying semantics.

Hybrid modelling methods

A hybrid method refers to a combination of at least two distinct modelling formalisms, each properly characterizing a part of the system to be studied, by embracing complementarity of these formalisms. The complementarity of formalisms can be driven by several reasons, e.g. computational efficiency, data availability or the modellers’ individual preferences [48].

In this section, we review some popular hybrid modelling methods that may be suitable for addressing the future integrated modelling requirements for systems biology. For each class of hybrid methods, basically given chronologically ordered, we focus on clarifying why they are presented, how they are formed from single modelling formalisms and how to simulate them. Doing this will enable us to identify in the Discussion section future research requirements regarding hybrid approaches for promoting integrated modelling of biological systems.

Hybrid discrete/continuous methods (HDCMs)

In this class of hybrid discrete/continuous methods, some components of a biological system with continuous concentration changes are described using ODEs (events occur continuously and deterministically), while other components are represented as discrete quantities, where events occur according to deterministic time delays. This approach was motivated by the observation that ODEs can model well many biological phenomena, but cannot represent some mechanisms such as the switching and control of genes, which has to be modelled in a discrete way.

Hybrid functional Petri nets (HFPNs) [5] are one of the prominent methods falling into this category. HFPNs integrate discrete and continuous processes in one model with the unifying graphical representation as PNs (like a combination of TPNs and CPNs). In an HFPN, there are four types of nodes: continuous places/transitions and discrete places/transitions, and three kinds of arcs: standard, inhibitory and testing. A continuous transition has a property rate being a function of the marking of its corresponding preplaces. In contrast, a discrete transition has a property delay, which may be read as the time that a chemical reaction requires [49]. Continuous transitions fire continuously in terms of specified rates, which are processed with numerical ODEs solvers. Discrete transitions fire spontaneously when enabling conditions and firing delays are satisfied. The simulation procedure of an HFPN model is intuitive: integrating the ODEs for each continuous transition and firing each discrete transition according to the given firing rules and time constraints [5].

Initially, a software tool, called Genomic Object Net, was developed for representing and simulating HFPNs, which provided an editor and also a simulator for HFPNs with graphical user interface (GUI) support [5]. Later, Cell Illustrator [50] was developed to support the modelling and simulation of HFPNs with an easy-to-use user interface. Moreover, Cell Illustrator offers a rich library of icons for different biological elements and processes, which facilitates that biologists construct models with user-friendly icons of substrates and reactions. Cell Illustrator has been recognized as a useful hybrid modelling and simulation tool for biological networks for a long time due to the intuitive user interface, captivating icons of biological elements and simple simulation operations. However, the main drawbacks of this tool are obvious. It is commercial, which limits the wide application of this hybrid modelling tool. Moreover, Cell Illustrator does not support hierarchical modelling, which may be required to construct larger models. HFPNs have been used to construct and analyse models of different types of biochemical networks including gene regulatory networks, metabolic pathways and signalling pathways. For example, in the HFPN model of the phage genetic switch system [49], the switching mechanism of the 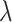phage is considered as a discrete component and the others as continuous ones. In the HFPN model of the glycolytic pathway and lac operon gene regulatory mechanism of Escherichia coli [5], the lac operon gene regulatory mechanism is modelled as a discrete component, where the switch of lac operon transcription is represented as a discrete transition with a fixed delay, while the glycolytic pathway is modelled as a continuous component. Moreover, [5] gave several other HFPN models of, e.g. the Fas-induced apoptosis and Drosophila circadian mechanism. See [51, 52] for some more sophisticated HFPN models.

Hybrid spatial/continuous methods (HSCMs) [41, 53, 54] make another large subclass of hybrid discrete/continuous methods (HDCMs). These methods usually couple spatial methods with ODEs or PDEs. The spatial methods represent in a discrete way each individual cell, the interactions between individual cells and between cells and their environment, while the continuous methods describe the biological reactions inside each individual cells. Take the hybrid CA/ODEs approach as an example. The simulation can be executed as follows. At each time step, inside each cell, the set of ODEs associated with this cell is integrated to obtain a new state; with the new state, each cell is updated in terms of discrete rules: remain, move or die. Repeat this computation until the termination condition is met. Other types of HSCMs can follow a similar simulation strategy. HSCMs have been applied in many scenarios, e.g. tumour or cancer modelling [54], or pattern formation [37].

A brief summary. HFPNs are a widely used graphical modelling method for constructing different types of biological networks, which are usually employed for intracellular modelling. HFPNs are in nature a quantitative method, which means accurate kinetic parameters are necessary to be obtained. Although HFPNs and Cell Illustrator are known to be a popular tool for constructing and analysing hybrid models of biological systems, their applications in fact are limited. The reasons for this may be mainly 2-fold. One is the commercial licensing of the Cell Illustrator tool, and the other is due to limitations of the HFPN method, e.g. it only allows discrete transitions to have fixed time delays. However, another HFPN tool called VANESA [55] could further promote the application of HFPNs due to its open-source release.

HSCMs are a group of methods belonging to the HDCMs class, which usually work in multilevel or multiscale scenarios. In these methods, the activities inside each individual cell (lower levels) are usually modelled as a continuous model, while the interactions between individual cells and between cells and their environment (upper levels) are modelled in a discrete way. Therefore, HFPNs and HSCMs aim at different biological modelling aspects. HSCMs also belong to another biological modelling branch of considerable size, spatial modelling, which mainly aim at multiscale modelling. Please note that many multiscale models are inherently hybrid, but this is not always the case (for a discussion see, e.g. [56]). There has been already a lot of work within this branch. Due to the space limit, we will not elaborate on HSCMs in this paper. The interested reader is referred to [41, 53, 54].

Hybrid stochastic/deterministic methods (HSDMs)

To alleviate the computational burden of stochastic simulation, a class of hybrid simulation methods has been proposed by combining stochastic and continuous simulation, with the latter being inherently deterministic. Some molecular species are considered as continuous quantities and the related reactions as deterministic processes, occurring continuously; this model component is described by ODEs. The molecular species represented as discrete quantities undergo stochastic events occurring in a discrete way. This class of hybrid simulation merges exact stochastic and deterministic algorithms, approximating stochasticity by considering the mean only. It improves the computational efficiency, while avoiding unacceptable result inaccuracy.

The hybrid simulation of HSDMs works as follows [10]. It first partitions the set of species into discrete and continuous ones and the reactions into stochastic and deterministic (continuous) ones. Then a system of ODEs is constructed for the deterministic regime. The system of ODEs is numerically integrated until a stochastic reaction is to occur, which is then fired. By repeating this procedure we obtain the simulation traces for the given simulation time.

The original hybrid simulation algorithm developed for this class was given in [9], discussing in detail how to derive a hybrid simulation algorithm based on Gillespie’s direct method. To improve the hybrid simulation efficiency, much research has been undertaken (see, e.g. [57, 58]). For a review of many hybrid simulation algorithms belonging to this class, see [59]. The implementation of hybrid simulation is usually a tough task as it requires to deal with ODE integration, stochastic simulation and interplay of both. Therefore, efficient software tools are necessary for aiding the development and execution of hybrid models.

Currently, there are three popular tools available for this class of hybrid simulation: COPASI [60], Virtual Cell [61] and Snoopy’s hybrid simulator [8]. COPASI does not provide graphical notations but uses tables to specify reactions and species of biological systems. It offers three hybrid algorithms: hybrid Runge–Kutta/Gibson–Bruck’s SSA (inefficient), hybrid LSODA/Gibson–Bruck’s SSA and hybrid RK-45/Gibson–Bruck’s SSA. In addition COPASI supports SBML models. Virtual cell also provides a module to construct and simulate hybrid models involving the RBM method and offers three hybrid algorithms: hybrid Gibson–Bruck’s SSA algorithm/Euler–Maruyama, hybrid Gibson–Bruck’s SSA algorithm/Milstein and hybrid adaptive Gibson–Bruck’s SSA algorithm/Milstein. Snoopy’s hybrid simulator exploits generalized hybrid Petri nets to describe a hybrid system. It does not provide a fixed combination of an ODE integrator and an SSA. Instead, it supports a flexible combination of popular stiff/non-stiff ODE solvers with Gillespie’s popular SSAs, and achieves performance gains by differentiating structural dependencies between the stochastic and deterministic subnets [62]. Snoopy’s hybrid simulator offers the hierarchical modelling capability and also a parameterized language, coloured hybrid Petri nets (CHPNs), to support the construction of large models.

All three tools are platform-independent and available free of charge. In summary, these three tools offer similar hybrid stochastic/deterministic simulation capabilities for analysing biological networks, where we consider events of lower frequency as stochastic ones and events of high frequency as deterministic ones.

For example, the Eukaryotic cell cycle control system contains some components (e.g. volume growth) which are better to be represented as deterministic processes, and also some reactions of low rates which are appropriate to be represented as stochastic processes. To address this issue, a hybrid SPN model was proposed [63], in which all reactions affecting mRNAs are represented as stochastic transitions, while such processes as volume growth are modelled as continuous transitions. Another similar hybrid model was also proposed for the Eukaryotic cell cycle in [64], which was simulated using the Haseltine and Rawlings approach given in [9]. Recently, Ahmadian et al. [65] proposed another hybrid stochastic model of the budding yeast cell cycle and simulated their model with the hybrid simulation algorithm given by [64]. Besides, some other hybrid models with HSDMs can be found, e.g. the hybrid model of the Yeast cell cycle based on multisite phosphorylation in [66], and the hybrid model of calcium dynamics inside a dendritic spine in [67].

A brief summary. In contrast to HDCMs in which each discrete reaction is associated with a fixed delay, HSDMs employ a random delay for each stochastic reaction and SSAs to simulate the stochastic components. In summary, there are many biological networks that are appropriately represented as hybrid stochastic/deterministic models due to their very nature. That is, this class of HSDMs may have a big potential to be widely used for the modelling of large biological networks.

Hybrid FBA-based methods (HFMs)

FBA has been successfully applied to study large-scale metabolic networks; however the steady-state assumption of this method makes it impossible to consider any dynamic behaviour of species. Moreover, it cannot be easily used for modelling integrated networks consisting of more than one type of networks such as both metabolic and signalling networks, which often involve multiple time scales.

To address these issues, many hybrid methods based on FBA have been proposed. For example, regulatory flux balance analysis (rFBA) [68] combines FBA with Boolean rules, where FBA is used for modelling metabolic networks and Boolean rules for representing regulatory networks. Thus, rFBA achieves the integrated modelling of both metabolic and regulatory networks in a qualitative manner.

Integrated FBA (iFBA) [69] further allows the combination of rFBA with ODEs, where ODEs are used for modelling specific subnetworks whose dynamic behaviour plays an essential role and their kinetic parameters are available. The simulation of iFBA takes the following steps. First, specify the initial conditions (states) for all the species. After that in parallel perform the following steps: calculate the regulatory protein states and gene and protein expression for the Boolean regulatory subnetwork; and solve the ODEs for the ODE subnetwork using an ODE numerical solver. Then determine the metabolic flux constraints and compute the flux distribution. Finally, update the conditions of all species. By repeating these steps, the analysis is done at each time step. The iFBA algorithm has been implemented in Matlab, which can be accessed freely, but (obviously) depends on Matlab. This algorithm has been used to explore an iFBA model of Escherichia coli consisting of a flux-balance-based central carbon metabolic network, a transcriptional regulatory component with Boolean networks, and an ODE-based detailed component of carbohydrate uptake control.

In addition, integrated dynamic FBA (idFBA) further considers metabolic, regulatory and signalling networks within one model [70] in a similar way to that of [69]. Both iFBA and idFBA methods offer a hybrid qualitative/quantitative way for analysing integrated biological networks.

Fisher et al. [71] further proposed a more powerful hybrid method called quasi steady state Petri nets (QSSPN) by combining FBA with a class of extended PNs, where FBA is used for modelling metabolic reactions and PNs for representing other molecular interactions such as signalling pathways and gene regulation. PNs, extended with inhibitor and read arcs and enjoying rich semantics such as deterministic firing in terms of numerical integration of ODEs and stochastic firing according to the Gillespie algorithm, greatly strengthen the modelling capabilities of dynamic networks. The simulation procedure of QSSPN is briefly described as follows. First, set the states of all species and initialize the simulation. Then set the bounds of fluxes in the quasi-steady state flux part of the model according to the state of the constraint places and further evaluate the objective function specified by a particular objective place with FBA. After that, deal with the PN part of the model by firing the deterministic, stochastic, delayed and scheduled transitions, respectively. Repeating these steps produces the traces of the QSSPN simulation. QSSPN is implemented as a command-line tool by extending the SurreyFBA software [72] and adding the simulation algorithm described above; Mac OSX and Linux binaries of the tool are offered for free. Besides, the PN models are built with Snoopy [73]. QSSPN has been used to construct a genome-scale metabolic network in human cell, using bile acid homeostasis in human hepatocytes as a case study. In this model PNs are used to represent different classes of molecular interactions. QSSPN as described in [71] is able to simulate genome-scale molecular interaction networks involving all classes of molecular interactions.

Later, MUFINS [74] was presented extending the QSSPN method and adding a GUI, which facilitates the construction and analysis of hybrid FBA models. MUFINS supports the integration of stochastic simulation, deterministic ODE simulation, parameter-free simulation [75] and FBA in a single software platform with GUI, offering multi-formalism functionality for modelling multiscale biological systems. Likewise, MUFINS is a free open-source software available under GNU GPL licence.

In a further development, Simone et al. [76] proposed another hybrid modelling framework by integrating FBA and PNs, in which PNs are used to model the dynamics of a system with the GreatSPN tool. The resulting model is then automatically transformed into a corresponding ODEs. The subsequent simulation runs on the hybrid FBA and ODEs model. A pancreatic ductal adenocarcinoma model has been developed to illustrate the approach.

A brief summary. Hybrid FBA-based methods make it possible to construct and analyse large-scale biological networks, which have gained increasing attentions these years. So far several such methods have proposed, some of them are discussed above. iFBA is an extended version of rFBA by modelling dynamic behaviour with ODEs, achieving a simple integration of metabolic, regulatory and signalling networks, but only allows for deterministic semantics. QSSPN further extends the hybrid modelling capability with the powerful PN formalism, allowing for the modelling of any kind of molecular interactions and both deterministic and stochastic simulation of dynamic behaviour. Moreover, MUFINS offers a GUI platform. Besides, note that rFBA is still a qualitative approach, but iFBA, idFBA and QSSPN contain both qualitative and quantitative components.

Hybrid logic/quantitative methods (HLQMs)

Modelling of biological systems often comes with challenges due to the lack of kinetic data or insufficient understanding of their internal mechanisms, which motivates researchers to investigate the use of qualitative logic methods, such as Boolean networks and fuzzy logic. By combining quantitative and logic methods, a new type of hybrid methods is obtained, which we call HLQMs. HLQMs model different components of a system with Boolean networks or fuzzy logic, complemented by a quantitative method, each component taking an appropriate formalism.

In this category, the integration of Boolean logic and ODEs consists of a simple hybrid method, which we call HBO. For example, Ryll et al. [77] presented a hybrid method linking Boolean models of signal transduction as well as gene regulation to ODE models of metabolic processes in their model of hormonal regulation of glucose homeostasis. They achieved the integration by converting the Boolean models into a set of logic-based ODEs and thus experimental data are needed for calibrating the newly added kinetic parameters due to the conversion.

Singhania et al. [78] gave a hybrid model of mammalian cell cycle regulation, in which Boolean logic is used to represent the activities of the regulatory proteins, while continuous differential equations describe cyclin levels. They simulate their model in two steps: creating complete ‘life histories’ for cells and finding the DNA and cyclin levels of each cell. During each step, they resolve the piecewise differential equations and compute the state transition for the Boolean model in a stochastic way.

Selvaggio et al. [79] proposed an HBO method for hierarchical models with different abstraction levels, in which they use ODEs to represent the bottom layer in a fine-grained manner and Boolean logic to represent the regulative interactions of higher layers in a coarse-grained fashion. They also applied their approach to simulating the pattern development of the Delta-Notch pathway. The hybrid simulation algorithm works as follows. They first threshold the internal variable 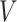of all the modules and generate a logic matrix. They then apply the logical rules on the logic matrix and obtain a dependent input of each module. By feeding the dependent and independent inputs, each module is integrated until the internal variable 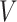crosses the quantization threshold. This process will be repeated until the break condition is met.

Compared with [77], the approaches of both [78] and [79] do not require recasting to a common description of ODEs and thus re-parameterization. These approaches are a good attempt to combine the pros of different modelling formalisms by overcoming the lack of quantitative information with a qualitative description that models activation and inhibition processes.

Another type of HLQMs is fuzzy hybrid functional Petri nets (FHFPNs) proposed by Windhager [80] based on HFPNs [5], in which an arc of an HFPN model can be associated with a fuzzy inference system (FIS). Thus, an FHFPN model consists of two parts: the FIS one and the HFPN model. That is, if a component of the system to be studied lacks measurement data, it can be modelled with FISs. Another hybrid method in this classification is the fuzzy ODE approach [81], in which the quantitative method takes the ODE formalism. Besides, fuzzy continuous Petri nets (FCPNs) [82, 83] have also been proposed, which are similar to the fuzzy ODE approach, where FCPNs are used to graphically describe a set of ODEs.

All these three approaches are similar in modelling a biological system by dividing a system into two parts: uncertain and certain, and thus modelling them using FISs and quantitative methods, respectively. The biggest merit of this class of methods is that they facilitate the integration of expert knowledge with quantitative models.

The simulation of FHFPNs or FCPNs takes a similar idea. (1) Initialize the simulation. (2) At each time step, perform the following two steps in parallel: numerically solving the quantitative part (usually a set of ODEs) of the model, and performing reasoning of each FIS in the model. (3) Update the concentration of each species by considering both computation steps. (4) Repeat the steps (2) and (3) until the simulation reaches the end time. For the construction and simulation of large HLQM models, Liu et al. developed a platform-independent FCPN tool which comes with a detailed user manual and some examples [83].

Windhager [80] discussed the modelling of common network motifs, such as feed-forward loop, negative feedback oscillator, positive feedback toggle switch and positive feedback one-way switch, using FHFPNs. He also applied FHFPNs to the modelling of green fluorescent protein (GFP) expression in a cell-free in vitro transcription/translation system. Bordon et al. used the fuzzy ODE approach to model a three-gene repressilator, where they represented the transcription rate of mRNA as an FIS and the other model parts as ODEs [81]. Liu et al. [83] modelled the Mercaptopurine metabolic pathway using FCPNs and used fuzzy NNs to learn fuzzy parameters of the model. These examples show that HLQMs are good at integrating experts’ knowledge with measurement data, to overcome to some degree the uncertain modelling challenges.

Besides these two aforementioned types of HLQMs, Liu et al. [7] proposed SPNs and CPNs with fuzzy kinetic parameters, where each kinetic parameter is either a crisp value or a fuzzy number if this parameter cannot be precisely estimated. To tackle even more complicated biological scenarios, Assaf et al. [84, 85] further proposed fuzzy hybrid PNs, and the coloured counterparts for these three fuzzy quantitative PN classes.

A brief summary. Currently, integrated modelling of biological systems is faced with the uncertainties due to the lack of kinetic data or insufficient knowledge about the mechanisms of biological systems. In this case, HLQMs offer a flexible way to integrate both quantitative data and qualitative knowledge within one model.

Spatial hybrid methods (SHMs)

Species perform their functions in space. Integrated modelling may have to consider the impact of space if there are diffusion or mobility of substrates. Current SHMs usually mean a combination of spatial stochastic and deterministic methods, which have been supported by several tools that will be discussed below.

SmartCell [86] developed its own graphical notation for constructing biological models, and offers an SHM by combining the deterministic ODE method with the stochastic next reaction/next subvolume method. A model built by SmartCell runs on a cell or part of a cell, being divided into a group of voxels. Three kinds of species movements in the cell can be defined: the diffusion inside a compartment, the diffusion between two compartments and the active transport between two compartments.

Virtual cell [87] employs a rule-based formalism to represent hybrid models and becomes an SHM [88] by combining the deterministic PDE method, solved by a finite volume method, and the stochastic method based on particles, solved by Smoldyn [89], a particle-based fixed time step Monte Carlo package. Virtual cell supports several ways, e.g. equation, image or mesh, to define a 1D, 2D or 3D geometry. This hybrid method has been applied to simulating a model of spontaneous emergence of cell polarity [88].

Besides, Snoopy uses CHPNs [8] to implement spatial hybrid modelling by combining CPNs and SPNs running on a lattice that is divided into 1D, 2D or 3D grids. This method has been used for constructing a dendritic spine model describing calcium dynamics [67], where the diffusion reactions are treated deterministically, and all others stochastically.

A brief summary. The three SHMs given above are different from each other in terms of model representation and simulation algorithms, which can be chosen in suitable scenarios. However, neither of these SHMs has obtained wide-spread use. The main reason could be the hard to obtain kinetic parameters, particularly in the spatial context. However, it will have to play a crucial role in the future integrated modelling of biological systems.

More complicated hybrid methods

In a cell, there exist a variety of molecular processes, such as molecular binding, enzymatic catalysis and molecular diffusion. To represent and analyse these physical and chemical processes, many simulation algorithms have been proposed. In order to consider multiple molecular processes in one model, usually more than one method has to be adopted.

To address this issue, Takahashi et al. [90] proposed a multi-algorithm, multi-timescale method for cell simulation, which depends on the design of a powerful meta-algorithm (which we call Takahashi’s method). The meta-algorithm contains three components: a data structure for model definition and execution, a driver algorithm that describes how interactions of sub-modules are handled and an algorithm for ODE integration. In their algorithm, a model is defined as a vector of state variables and a set of Steppers. A Stepper represents a computational unit of a model. According to Zeigler’s simulation framework [91], they defined three Stepper subclasses: DiscreteEventStepper, DiscreteTimeStepper and DifferentialStepper. They adopted a variant of the Runge–Kutta algorithm for ODE integration and the next reaction method for stochastic simulation. The simulation algorithm basically works as follows. (1) Initialize the simulator and obtain the dependencies of each Stepper. (2) Pick the Stepper 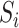that has the minimum scheduled time and update its local time. (3) Integrate each continuous variable. (4) Call transition functions, if is a discrete Stepper. (5) notifies the change of the variables to other Steppers. (6) Repeat the procedure until the simulation termination condition is reached. This algorithm has been implemented with the C++ language as part of E-Cell.

This meta-algorithm can be used to simulate a cell with different continuous and SSAs. The advantage of the meta-algorithm is that it uses Zeigler’s discrete and continuous simulation framework. Thus, it can efficiently integrate different simulation algorithms in one model with little intrusive modification to the algorithms themselves. More importantly, other algorithms can be easily added to this meta-algorithm.

Karr et al. [92] developed in 2012 the first whole-cell computational model of the life cycle of the human pathogen Mycoplasma genitalium, which consists of all of its molecular components and their interactions (which we call Karr’s model). In their work, they integrated 28 submodels into a unified model, each submodel adopting a specific modelling formalism (ODEs, FBA or Boolean logic) that may be different from others. In order to connect these submodels and simulate them as a whole, they made the following assumption: all the submodels are approximately independent on a small time scale less than 1 s. The simulation procedure they adopted is briefly described as follows. (1) Initialize the state variables of the cell. (2) At each time step, perform simulation independently for each submodel with the values of the state variables at the previous time step. (3) Update the values of the state variables of the cell. (4) Repeat these steps until either the cell divides or the simulation termination time is reached.

The distinguishing feature of the model is that it considers all the molecular components and their interactions of a cell and several modelling formalisms are combined to achieve this purpose. This provides a way to simulate a very complicated hybrid model. However, this approach has several drawbacks. Each submodel and its simulation algorithm was hardcoded together and implemented with Matlab. Thus, any modification of the model representation could affect the corresponding simulation algorithm. Moreover, such a model can hardly be understood and manipulated by any biologist.

A brief summary. The two approaches described above were proposed to model complicated biochemical processes inside a cell. The approach given by Takahashi et al. is a general method which can be applied to model any cell. In contrast, the second approach is only specific to the human pathogen Mycoplasma genitalium, which cannot be easily extended to model other types of cells.

Hybrid methods incorporating AI models

As mentioned above, the purpose of classical theory-based modelling is totally different from that of data-driven modelling. So far, AI techniques are usually employed to complement theory-based biological modelling, e.g. for selecting molecular features which are used as inputs of FBA models [93], aiding to generate constraint-based models by determining more precise flux boundaries [94], and analysing simulation results with AI techniques [94]. However, this kind of integration does not belong to the focus of our review of hybrid modelling methods, where we expect to see at least two modelling formalisms, each representing a part of a system.

At present, there are only a few genuine hybrid models, which actually combine theory-based modelling and AI techniques. For example, Khan et al. [46] presented a hybrid model by combining recurrent NNs and S-systems for the reconstruction of gene regulatory networks from pseudo-time-series gene expression data of Escherichia coli. Gerlee et al. [95] proposed a hybrid cellular automaton model of clonal evolution in cancer, in which the decision mechanism that determines the behaviour of a cell based on the cell genotype and its micro-environment is modelled with an artificial feed-forward NN. They also gave a detailed analysis and simulation procedure to explore the impact of the environment on the growth dynamics of the tumour. These are very early attempts to incorporate AI techniques into dynamic modelling of biological systems.

A brief summary. So far AI techniques are basically applied to aid the construction and analysis of biological models in the systems biology field by taking advantage of the special abilities of AI, e.g. classification, regression and clustering. This complementary power is very important for biological modelling by overcoming the disadvantages of classical theory-based modelling methods. However, strictly speaking, this integration is not within our hybrid definition. The genuine hybrid models combining theory-based modelling and AI techniques are very few by now, which is probably due to the nature of theory-based modelling and data-driven modelling. How to combine these two classes of methods to form a complementary modelling approach was discussed in detail in [43], which could be considered for the construction of biological models in the future. Besides, Camacho et al. [96] discussed in detail opportunities and challenges at the intersection of machine learning and network biology, which could also help to widen the application of machine learning in systems biology.

Comparison of the hybrid methods

We have reviewed popular hybrid modelling methods that were developed for systems biology, and provide a comparison in Table 2. These hybrid methods were proposed for different purposes and biological issues. Almost all hybrid methods only cover two modelling formalisms, each addressing one particular aspect of biological modelling, but not all aspects. Thus, they are hardly capable of constructing more complicated integrated models. Most hybrid methods contain two quantitative modelling formalisms, and thus are still quantitative methods, which means they are only applicable when kinetic data are available. Therefore, these quantitative hybrid methods cannot address the modelling issue that many components are not mechanistically well understood and lack measurement data. On the other hand, this issue could be addressed by hybrid methods combining qualitative and quantitative ones, e,g. those integrating Boolean rules or fuzzy logic. However, current applications of these hybrid methods are still very limited. In order to address all these issues, hybrid methods have to be greatly enhanced by allowing more modelling formalisms in one model, as, e.g. Karr et al. did in [92], and more sophisticated modelling tools need to be developed. Besides, AI techniques should be extensively explored w.r.t. their power to support the development of hybrid models by making use of their specific advantages, e.g. selecting the principle factors of models, estimating kinetic parameter values or narrowing the boundaries of parameter values.

Table 2.

A comparison of the hybrid methods discussed in Sections 3.1–3.7.

Category	Hybrid	Single methods	Type	Tool	Website
	method	contained
Hybrid discrete/	Hybrid functional Petri nets	TPNs (Discrete)+CPNs (ODEs)	QT	Cell Illustrator	http://www.cellillustrator.com
continuous method	Hybrid spatial/continuous methods	e.g. CA+ODEs or PDEs	QT		See Table 1 of [54] for a list of tools.
Hybrid stochastic/	Hybrid stochastic/	Table (SSAs+ODEs)	QT	COPASI	http://www.copasi.org
deterministic method	deterministic method	Rule-based (SSAs+ODEs)	QT	Virtual Cell	https://vcell.org/
		CPNs (ODEs)+SPNs (SSAs)	QT	Snoopy	https://www-dssz.informatik.tu-cottbus.de/DSSZ/Software/Snoopy
Hybrid FBA-based	Regulatory FBA	FBA+Boolean rules	QL	None	None
method	Integrated FBA	FBA+Boolean rules+ODEs	QL/QT	Matlab codes	https://simtk.org/projects/ifba
	Quasi steady state Petri nets	FBA+CPNs (ODEs)+SPNs (SSAs)	QT	QSSPN tool	http://sysbio3.fhms.surrey.ac.uk/qsspn/
				MUFINS	http://sysbio3.fhms.surrey.ac.uk/mufins/
Hybrid logic/	Hybrid Boolean logic/ODE method	ODEs+Boolean logic	QL/QT	Pseudocode	See [79].
quantitative method	Fuzzy hybrid functional Petri nets	CPNs (ODEs)+fuzzy logic	QL/QT	None	None
	Fuzzy continuous Petri nets	CPNs (ODEs)+fuzzy logic	QL/QT	FCPN tool	https://github.com/liufei2016/FCPN
Spatial hybrid method	SmartCell’s method	Spatial SSAs+ODEs	QT	SmartCell	http://software.crg.es/smartcell/
	Virtual Cell’s method	Particle simulation+PDEs	QT	VCell	https://vcell.org/
	Snoop’s method	Spatial SSAs+ODEs	QT	Snoopy	https://www-dssz.informatik.tu-cottbus.de/DSSZ/Software/Snoopy
Others	Takahashi’s method	ODEs+next reaction method	QT	E-Cell	http://www.e-cell.org/
	Karr’s model	ODEs+FBA+Boolean logic etc.	QL/QT	Matlab codes	https://simtk.org/projects/wholecell
Hybrid methods	Hybrid neural network/ODE method	NNs+ODEs	QT	None	None
incorporating AI models

QL and QT refer to qualitative and quantitative, respectively. None means not found.

Discussion

Integrated modelling of biological systems is required in many scenarios. In the systems biology field, comprehensive models for a cell, an organ or an organism [97] that incorporate all the relevant major processes have to be constructed by utilizing diverse and different sources of data as well as multiple modelling formalisms. This enables researcher to obtain a deeper understanding of the system dynamics, to identify limits of current knowledge and to elucidate emergent behaviour across multiple networks. In the synthetic biology field, the creation of a new biological system requires the assembly of different existing components. In order to support the analysis of the behaviour of the new system, a model needs to be constructed by integrating the models which describe the various components [23].

In the following text, we discuss how to enhance hybrid modelling research as a next step to more powerfully support the integrated modelling of biological systems.

A flexible multi-formalism modelling framework and powerful tool is indispensable. The next generation of hybrid biological models has to incorporate more than two formalisms, developed collaboratively by a group of people, just like in other fields such as manufacturing. In order to support different (experienced or not) modellers to adopt appropriate modelling formalisms for distinct components of a biological system, a flexible multi-formalism modelling framework and a corresponding powerful tool have to be developed, which at least enjoy the following features: (1) containing a number of popular modelling formalisms, e.g. those given in the second section; (2) offering friendly GUIs for model construction; (3) supporting the conversion among different modelling formalisms.

Modular development of hybrid biological models is becoming a necessity. To support the collaborative development of large hybrid models, the modularization of components will become necessary. This comes with several benefits. For example, it facilitates the management of components, e.g. easily adding new components, and deleting, updating or reusing existing components. With the rapid development of hybrid modelling techniques, reusability will become more and more imperative just like in many other engineering and software application areas [98, 99]. Moreover, each modular component can be developed independently and easily exploit distinct simulation algorithms.

A standard model format for hybrid modelling of biological systems is essential. Currently, SBML [100] is the widely used model format in the systems biology area. However, it does not support hybrid modelling comprising multiple popular modelling formalisms. Therefore, a new standard model format for hybrid modelling is necessary, which should be capable of addressing the following issues: (1) representing models developed with currently popular modelling formalisms, e.g. those given above, (2) representing multiple scales in time and space and (3) facilitating the information exchange among different modelling formalisms. In addition a unified exchange format among different modelling formalisms may have to be defined.

A powerful simulation engine that solves different types of modelling formalisms is needed. In order to support larger hybrid models, many different modelling formalisms have to be integrated into a single framework. To simulate such large models, a flexible and powerful simulation engine is necessary, which should be able to solve different types of models built with distinct formalisms. Such a simulation engine should enjoy the following features: (1) offering the simulation of models with popular modelling formalisms, (2) offering multiple time management mechanisms such as discrete event, discrete time and continuous time, (3) supporting a model to adopt different simulation algorithms without modifying the model representation and (4) supporting high-performance parallel simulation of hybrid models with, e.g. message passing interface [101] or GPU technologies.

Powerful analysis techniques for hybrid models should be developed. A hybrid model constructed with multiple modelling formalism usually cannot be directly analysed by those techniques applicable for each individual formalism. For example, model checking usually considers discrete transition systems like qualitative PNs. One strategy is to reuse the techniques of each formalism for the submodel developed with that formalism and then to analyse the interaction between submodels. However, this strategy cannot analyse the emergent behaviour of all the submodels as a whole. On the other hand, simulative model checking [102] is a promising technique, which could be used to analyse simulation traces from hybrid models after the simulation has been performed. However, this effectively performs a black-box analysis. In order to assure the correctness of the hybrid model, more powerful analysis techniques have to be developed, which should pay attention to analysing the interactions among submodels and the behaviour of the whole model.

Key Points

• Hybrid modelling methods are crucial to achieve integrated modelling of biological systems with the aim to construct comprehensive models of a biological system by considering its main biochemical processes.

• This paper reviews currently popular hybrid modelling methods, developed for systems biology, mainly revealing why they are proposed, how they are formed from single modelling formalisms, and how to simulate them.

• The paper concludes with identifying future research requirements regarding hybrid approaches for promoting integrated modelling of biological systems.

Author Biographies

Fei Liu is a Professor in the School of Software Engineering, South China University of Technology. His research interests are modelling and simulation, Petri nets and systems biology.

Monika Heiner is a Professor in the Department of Computer Science, Brandenburg University of Technology Cottbus-Senftenberg. Her research interests include modelling and analysis of technical as well as biochemical networks using qualitative and quantitative Petri nets, model checking and simulation techniques.

David Gilbert is a Professor in the Department of Computer Science, Brunel University London. His research interests include Bioinformatics, Systems Biology, Synthetic Biology, multiscale modelling, model checking and computational methods for the design of biological systems.

List of abbreviations

• CA: cellular automata

• CBM: constraint-based modelling

• CHPNs: coloured hybrid Petri nets

• ColPNs: coloured Petri nets

• CPNs: continuous Petri nets

• CTMC: continuous time Markov chain

• FBA: flux balance analysis

• FCPNs: fuzzy continuous Petri nets

• FHFPNs: fuzzy hybrid functional Petri nets

• FIS: fuzzy inference system

• GHPNs: generalized hybrid Petri nets

• HBO: hybrid Boolean logic/ODEs

• HDCM: hybrid discrete/continuous method

• HFM: hybrid FBA-based method

• HFPNs: hybrid functional Petri nets

• HLQM: hybrid logic/quantitative method

• HSCM: hybrid spatial/continuous method

• HSDM: hybrid stochastic/deterministic method

• iFBA: integrated FBA

• NN: neural network

• ODEs: ordinary differential equations

• PDEs: partial differential equations

• PNs: Petri nets

• QPNs: qualitative Petri nets

• RBM: rule-based modelling

• QSSPNs: quasi steady state Petri nets

• SHM: spatial hybrid method

• SPNs: stochastic Petri nets

• SSA: stochastic simulation algorithm

• TPNs: time Petri nets