Shape-programmable, deformation-locking, and self-sensing artificial muscle based on liquid crystal elastomer and low–melting point alloy

Abstract

An artificial muscle capable of shape programmability, deformation-locking capacity without needing continuous external energy, and self-sensing capability is highly desirable yet challenging in applications of reconfigurable antenna, deployable space structures, etc. Inspired by coupled behavior of the muscles, bones, and nerve system of mammals, a multifunctional artificial muscle based on polydopamine-coated liquid crystal elastomer (LCE) and low–melting point alloy (LMPA) in the form of a concentric tube/rod is proposed. Thereinto, the outer LCE is used for reversible contraction and recovery (i.e., muscle function); the inner LMPA in the resolidification state is adopted for deformation locking, and that in the melt state is adopted for angle variation monitoring by detecting resistance change (i.e., bones and nerve functions, respectively). The proposed artificial muscle demonstrates multiple performances, including controllable bending angle, position, and direction; deformation locking for supporting heavy objects; and real-time monitoring of angle variation, which also provides a straightforward and effective approach for designing soft devices.

Light-driven multifunctional artificial muscle has controllable deformation, deformation locking, and self-sensing abilities.

INTRODUCTION

Achievement of the integration of controllable actuation, deformation locking, large load-bearing capacity, self-sensing, and physical compatibility with human beings has long been a huge challenge in the robotics field (1–3). Numerous traditional hard robots, which are still dominant in practical applications (such as industrial, agricultural, and aerospace scenarios), can precisely control their motion by using high-precision sensors (4), bear large load by rigid structures (5), or lock themselves by locking devices (6). However, they probably increase their own redundancy or complexity due to motors, pulleys, bearings, gears, or belts and may bring security risk in the process of human-machine interaction due to undesirable effects of mechanism of inertia and friction. In contrast, several functions of soft robots, to a large extent, depend on materials (as opposed to—or in most cases rather than—electronics, sensors and controllers, and mechanical systems), which greatly improves the security of human-machine interaction (7–11). From this perspective, soft robots are complimentary to hard robots and may offer some unique advantages—such as better environmental adaptability, simple structure, and secure interaction—over their rigid counterparts. Moreover, they also offer tremendous application prospects [e.g., climbing robots (12–14), medical rehabilitation (7, 10), drug delivery (15–16), and so forth] and novel perspectives to circumvent or overcome certain weaknesses of hard robots.

Multiple soft robots capable of crawling (12), twisting (17), rolling (18), gripping (19), swimming (20), jumping (21), and flying (22) have been developed using pneumatic actuators, ionic polymer-metal composite actuators, shape-memory polymers, dielectric-elastomer actuators, and so on. However, in reconfigurable or programmable shape-morphing fields [e.g., reconfigurable antennas (23) and deployable space structures (24)], soft robots that can detect their flexible and controllable deformation in real time and maintain their desired working shapes under low to no energy consumption (i.e., simultaneously having controllable actuation, deformation locking, and self-sensing ability) have been anticipated, yet have rarely been reported. Low Young’s modulus and multiple degrees of freedom (DOFs) denote inherent properties of soft materials (e.g., elastomers, gels, and liquid crystals); therefore, the load-bearing capacity of soft robots is insufficient, and deformation is difficult to be controlled effectively, let alone shape locking.

The traditional hard robots have certain advantages (such as self-sensing, deformation locking, and large load-carrying capacity) owing to the closed-loop control that is conducive to deformation control and high-modulus materials with excellent shape retention (or deformation locking) and high bearing capacity. In recent studies, these advantages have been endowed to soft robots as well, in an attempt to overcome the shortcomings of soft materials (25–30). For instance, by injecting or mixing liquid metal into liquid crystal elastomer (LCE) (31–33) or integrating piezoresistive strain/pressure sensors into hydrogel (34), advantageous soft materials with desirable properties can be obtained. Moreover, this type of artificial muscle has the ability to sense its flexible deformation or adapt to its surroundings. By leveraging stiffness-tunable materials [e.g., magnetic shape-memory polymers (25) and multiphase organohydrogels (29)], the artificial muscle achieves dexterous shape morphing and manipulation under continuous external stimuli and sustains or locks its deformation to decrease continuous energy consumption in state of high stiffness. Much endeavor in overcoming the limitations of soft materials, in most cases, has been achieved by adding additional complex functional structures (28–30) (such as self-sensing and shape-locking structures) into one artificial muscle device, which unfortunately, to a large extent, sacrifices or weakens respective function or response speed, as well as increases fabrication cost.

Nature provides an alternative and straightforward inspiration where multiple living organisms, e.g., vertebrates or insects, have rigid structural frameworks along with soft materials (i.e., skeleton–muscle–nerve system), which endows them with sophisticated and agile movement, quick reaction or thinking, and unique body shape to adapt to unstructured environment in the real world. In particular, the muscles containing various nerves are attached to bones to form multifunctional organic whole, which perfectly realizes compatibility and coordination of various functions. In detail, the joints between bones provide more room for muscles to deform, and the deformation of muscles is more accurate and controllable under the feedback action of nerves. Moreover, the supporting function of bones can not only improve the load-bearing capacity of muscles but also reduce the energy cost of muscles during the period of relaxation. The functions of bones, muscles, and nerves cooperate well with each other, and even strengthen rather than weaken each function, to effectively perform a variety of physiological activities.

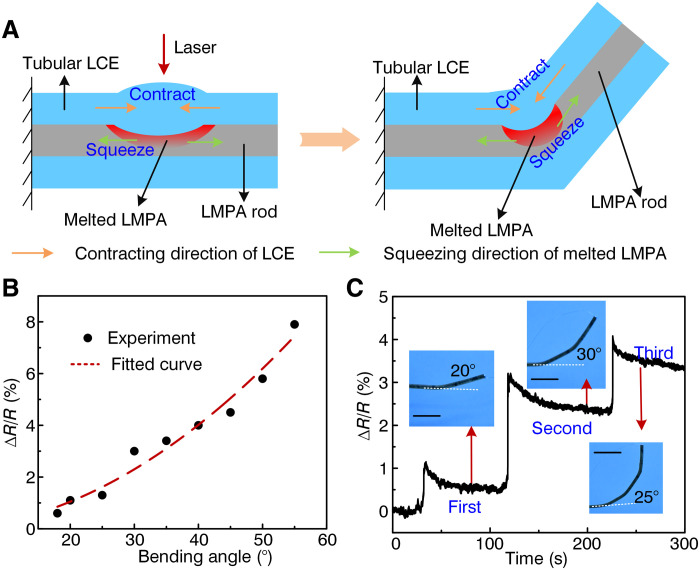
Inspired by this fascinating idea, in this study, a multifunctional artificial muscle with shape-programmable, deformation-locking, and self-sensing features based on LCE and low–melting point alloy (LMPA) is proposed in the form of a concentric tube/rod, as shown in Fig. 1A and fig. S1, where the outer LCE is used for reversible contraction and recovery, and the inner solid LMPA is adopted for shape locking, corresponding to the functions of muscles and bones. Meanwhile, the resistance change of the LMPA squeezed by the LCE is used for monitoring angle variation, and the melted section of LMPA under light stimuli provides more deformation space, corresponding to the functions of nerves and joints, respectively. In particular, a thin film of polydopamine (PDA) is coated on the surface of the LCE ring for achieving rapid photothermal conversion under light irradiation, triggering the contraction of the LCE, local melt of the LMPA, and following bending deformation after the temperature increases beyond the transformation temperature. At this time, the region of artificial muscle under light irradiation can be regarded as a universal joint that will not or only slightly limit the LCE deformation. Thus, the bending angle and direction of the artificial muscle can be adjusted by modifying the laser energy and irradiation direction, which allows convenient control in complex and unknown environments. The deformation-locking property is achieved by rapid resolidification of LMPA after the laser is turned off, which endows diverse shape-programmable or shape-reconfigurable artificial muscle with the high load-bearing capacity and low power consumption. The deformed status of artificial muscle can be monitored by testing the resistance change of the LMPA itself (rather than additional sensing structures), providing a simple approach for smart operation. Furthermore, a reconfigurable antenna is adopted as a typical application to demonstrate the flexible deformation and deformation locking characteristics of the proposed artificial muscle.

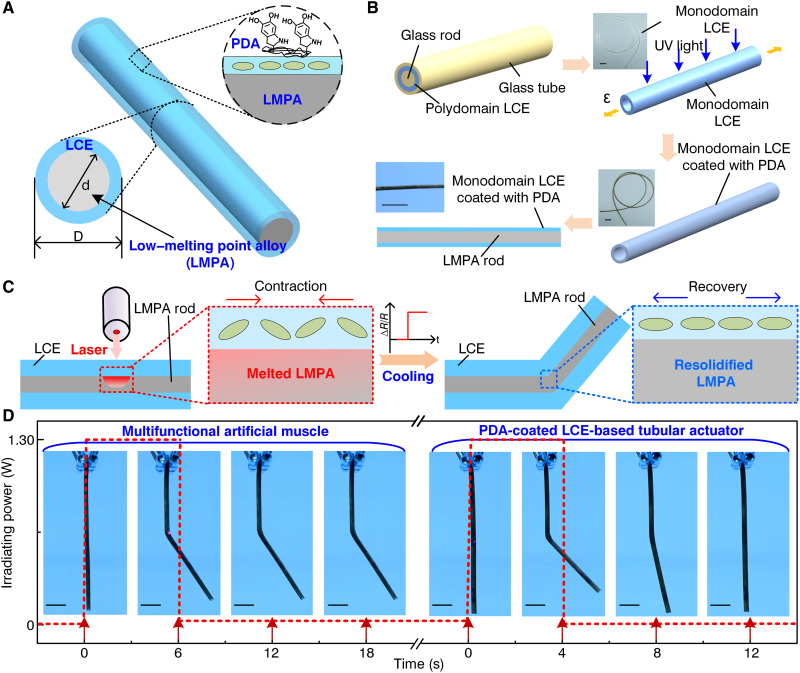
Fig. 1. Multifunctional artificial muscle composed of PDA-coated tubular LCE and LMPA rod.

(A) Multifunctional artificial muscle consisted of tubular LCE actuator coated with PDA and LMPA rod. (B) Fabrication steps of the multifunctional artificial muscle: Polydomain LCE was made in tubular and rod-shaped glass molds; monodomain LCE was obtained by stretching the polydomain LCE and photopolymerizing excess acrylate groups under the UV light; the PDA-coated LCE-based tubular actuator was formed by immersing the tubular LCE into dopamine/tris base buffer solution; multifunctional artificial muscle was obtained by embedding the LMPA rod into the PDA-coated LCE-based tubular actuator. Scale bars, 15 mm. (C) Working principle of the multifunctional artificial muscle under laser irradiation. (D) Angle variation of the multifunctional artificial muscle and PDA-coated LCE-based tubular actuator under laser irradiation of 1.3 W. Scale bars, 10 mm.

RESULTS

Manufacturing process and working principle

The fabrication process of proposed multifunctional artificial muscle coupled with soft (LCE) and hard (LMPA) materials is illustrated in Fig. 1B. Thereinto, rather than using one-step platinum-catalyzed hydrosilylation reaction of a divinyl mesogen with a tetrafunctional siloxane cross-linker proposed by Bergmann and Finkelmann (35), here, Michael addition reaction using amines or thiols was adopted to prepare LCE, which was also widely adopted by Yakacki et al. (36), Kotikian et al. (37), Gelebart et al. (38), Kuenstler et al. (39), etc. First, a loosely cross-linked hollow LCE (i.e., polydomain LCE) tube was fabricated via gelation in the glass tube and rod. After the gelation process, the loosely cross-linked hollow LCE tube was placed under a prestretch ratio (ε) of 500% to align the molecules along the length direction of the tube, and then the tube was cross-linked under the ultraviolet (UV) light (10 mW cm⁻²) for 10 min to form a nematic monodomain. To introduce the photothermal effect, the monodomain LCE tube was immersed in a dopamine/tris base buffer solution for approximately 24 hours, which resulted in the formation of a PDA layer on the surface via self-polymerization of dopamine. The PDA used in this study has excellent photostability and strong absorption characteristics in the near-infrared (NIR) region because the molar extinction coefficient of PDA nanoparticles is nearly 100 times higher than that of carbon nanotubes under the 808-nm NIR light (40, 41). Last, a multifunctional artificial muscle was fabricated by embedding a prefabricated LMPA rod into the PDA-coated LCE tube (the samples of tubular LCE, PDA-coated tubular LCE, and multifunctional artificial muscle are shown in fig. S2). The chemical component, fabrication process, and actuation performance of the LCE film are presented in fig. S3.

When one side of the fabricated artificial muscle was irradiated with a laser, the temperature escalated markedly because PDA led to instant transformation of light into heat in the irradiating region, thus triggering the nematic-to-isotropic transition of mesogens, i.e., macroscopic contraction of LCE and local melting of the LMPA. The high-temperature region of the LCE irradiated with the laser and the melting area of the LMPA were mainly concentrated on one side of the artificial muscle; therefore, the artificial muscle subsequently showed obvious bending deformation, instead of global contraction, when the unmelted LMPA could not bear a large difference in the contracting force between two sides of the artificial muscle at the irradiating region. After the laser was turned off, the LCE recovered to its monodomain state, and the alloy resolidified instantly, wherein the bending deformation was sustained by rapid resolidification of the LMPA, as demonstrated in Fig. 1C. Furthermore, the cross-sectional area of the LMPA rod at the local irradiating region got squeezed by the bending and thickening behavior of the LCE in the deformation process and triggered the change in the resistance, further inducing the sensing function.

For demonstrating the deformation behavior, comparative analysis of deformation between multifunctional artificial muscle and pure PDA-coated LCE-based tubular actuator was carried out, as shown in Fig. 1D. The multifunctional artificial muscle generated instantaneous bending deformation after about 6 s of laser irradiation (1.3 W). The bending deformation (bending angle of roughly 37°) was also immediately sustained after the laser was turned off at 6 s, which can also be observed in movie S1. In contrast, the PDA-coated LCE-based tubular actuator generated the maximum bending angle of 42° at 4 s under the irradiating power of 1.3 W and recovered to its initial straight state at 12 s after the laser was turned off at 4 s, as shown in movie S2. Therefore, the hard material of LMPA endows the proposed multifunctional artificial muscle with excellent deformation-locking property by rapid resolidification.

Characterization of bending deformation

To analyze the influence of light intensity on the value of bending angle, finite element analysis was performed by using the ABAQUS software. In the simulation, the heat source at the irradiating section was regarded as a Gaussian heat source, whose energy distribution is defined as follows (42)

$$q(x,y)=\frac{2\mathrm{\eta }P}{\mathrm{\pi }{w}^2}\text{exp}\{-2[\frac{{(x-\frac{a}{2})}^2+{(y-b)}^2}{w^2}\left]\right\}$$ (1)

where η is the absorption rate of the materials to the laser, p is the laser power, w is set as a radius of the laser spot, and a set (a/2, b) represents the two-dimensional (2D) coordinates of the laser spot center.

Harnessing a 2D temperature-displacement coupling model [the length (a) and diameter (b) of it were 30 and 2.4 mm, respectively], the temperature and stress distributions of the multifunctional artificial muscle were studied under different irradiating powers. More details about the heat boundary conditions of the multifunctional artificial muscle are given in fig. S4. Figure 2A illustrates that the bending angle reaches 49°, 44°, 39°, and 35° at the corresponding irradiating power of 2.0, 1.8, 1.6, and 1.4 W in the numerical simulations. The sizes of both the stress concentration area and high-temperature region (see fig. S5) also increased with the increase of the irradiating power. For a given irradiating power of 2.0 W, the revolution of stress and temperature distributions is demonstrated in movies S3 and S4, respectively. Specifically, the maximum heat-induced stress was maximum at the region close to the upper surface of the LCE and decayed with the thickness, triggering a large stress difference between the upper and lower surfaces of LCE. Moreover, the light-induced stress areas at the upper and lower LCE zones both increased with the increase of irradiating power. Furthermore, noteworthy, the compressive area of the LMPA coincided with the melting zone as presented in fig. S6 and increased with the irradiating power. On the basis of the results shown in fig. S6 and Fig. 2A, it could be inferred that large melting area, to a great extent, was helpful for unmelted LMPA to be compressed by the light-induced stress of the LCE, in particular, large stress at the laser irradiating position, which also provided more deformation space for the artificial muscle. Thus, large irradiating power was more likely to induce large stress in the LCE (i.e., large actuating stress) and a large compressive stress area (i.e., large melting area) in the LMPA, further triggering a large bending angle in the artificial muscle.

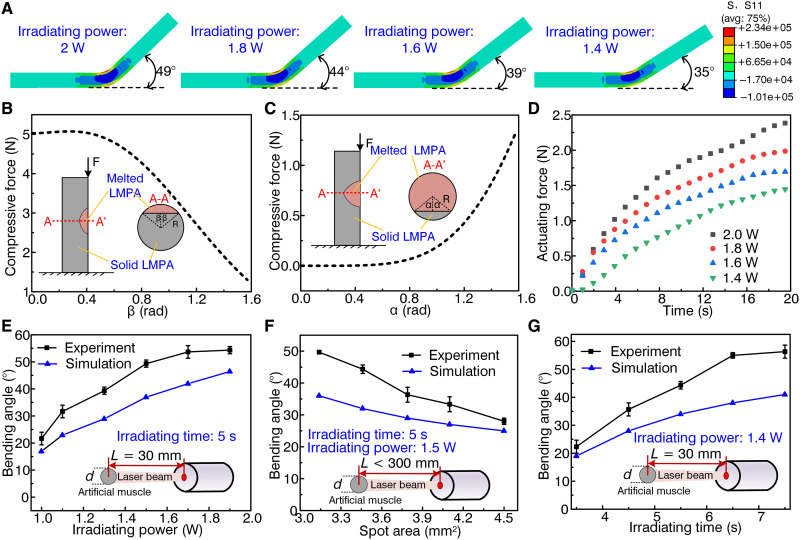
Fig. 2. Factors affecting bending deformation of the multifunctional artificial muscle.

(A) Stress distribution and bending angle of the multifunctional artificial muscle under different irradiating powers in the simulation. (B) Maximum compressive force (F) that the rod-like LMPA could bear when the laser heat locally melted a small part of the LMPA. Inset: Cross-section of LMPA. (C) Maximum compressive force (F) that the rod-like LMPA could bear when the laser heat locally melted a major part of the LMPA. Inset: Cross-section of LMPA. (D) Actuating force of the PDA-coated LCE-based tubular actuator under different irradiating powers. (E) Influence of irradiating power on the bending angle of the multifunctional artificial muscle (where L represents the irradiating distance). Inset: Illustration of laser beam applied on the surface of artificial muscle with the irradiating distance of 30 mm and irradiating time of 5 s. (F) Influence of spot area on the bending angle of the multifunctional artificial muscle (L represents the irradiating distance). Inset: Illustration of laser beam applied on the surface of artificial muscle with the irradiating power of 1.5 W and irradiating time of 5 s. (G) Influence of irradiating time on bending angle of multifunctional artificial muscle (where L represents the irradiating distance). Inset: Illustration of laser beam applied on the surface of artificial muscle with the irradiating power of 1.4 W and irradiating distance of 30 mm. In (E) to (G), three tests were conducted on samples for each data point, and the error bars present the SD of the three repeated data.

The numerical relationship between the melting area of the LMPA and the compressive force that produces bending deformation is illustrated in Fig. 2 (B and C), and the ideal theoretical models are shown in figs. S7 to S9 (noteworthy, the theoretical models were numerically analyzed under two conditions shown in Fig. 2, B and C, respectively). When the laser was irradiated on the tubular LCE surface, the contracting force (F′) of the LCE was generated along with a macroscopic shrinkage deformation, and the compressive force F was applied on the LMPA rod surface by static friction between the two surfaces. The relationship between the compressive force F and the melted area size of the LMPA rod at the irradiating region is given by

$${\mathrm{\sigma }}_L=\frac{F}{A}+\frac{M{y}_{\text{max}}}{I_x}\ge [{\mathrm{\sigma }}_L]$$ (2)

where σ_L denotes the LMPA strength, F is the compressive force to generate the bending deformation, A is the cross-sectional area of the unmelted LMPA rod, M is the bending moment of the LMPA rod, y_max is the distance between the cross-sectional centroid of the unmelted LMPA rod and the solid-liquid boundary, I_x is the cross-sectional moment of inertia of the unmelted LMPA rod, and [σ_L] is the allowable strength of the LMPA in this study (here, it was assumed that the allowable strength is equal to 2 MPa).

When the melting cross-sectional area of the LMPA is smaller than its unmelted area, the relationship between F and β is shown in Fig. 2B. In this case, it was assumed that the melted cross-sectional area of the LMPA denoted a bow-shaped structure, and the parameters of A, M, y_max, and I_x were calculated by $\mathrm{\pi }{R}^2-\frac{R^2(2\mathrm{\beta }-\text{sin}2\mathrm{\beta })}{2}$, $F(R+\frac{\frac{4}{3}R{\text{sin}}^3\mathrm{\beta }}{2\mathrm{\pi }-2\mathrm{\beta }+\text{sin}2\mathrm{\beta }})$, $R\text{cos}\mathrm{\beta }+\frac{\frac{4}{3}R{\text{sin}}^3\mathrm{\beta }}{2\mathrm{\pi }-2\mathrm{\beta }+\text{sin}2\mathrm{\beta }}$, and $\frac{(2\mathrm{\pi }-2\mathrm{\beta }+\text{sin}2\mathrm{\beta })[(2\mathrm{\beta }-\text{sin}2\mathrm{\beta })·\frac{9}{16}{R}^4(4\mathrm{\pi }-4\mathrm{\beta }+\text{sin}4\mathrm{\beta })+8R^4{\text{sin}}^6\mathrm{\beta }]-16\mathrm{\pi }{R}^4{\text{sin}}^6\mathrm{\beta }}{9(2\mathrm{\beta }-\text{sin}2\mathrm{\beta })(2\mathrm{\pi }-2\mathrm{\beta }+\text{sin}2\mathrm{\beta })}$, respectively, where R denotes the radius of the LMPA rod and β is the angle of a semicircle made by the melted bow-shaped LMPA.

According to Eq. 2, the value of F decreased from 5.02 to 1.3 N, with the increase in the angle of the semicircle β from 0 to 1.57 rad, which indicates that a small melting section of the LMPA typically required a large actuating force to generate bending deformation of a multifunctional artificial muscle. In particular, the artificial muscle would generate bending deformation when the actuating force of the LCE was larger than the value of F corresponding to β.

When the melting cross-sectional area of the LMPA is larger than the unmelted area at the irradiating section (i.e., another condition of the theoretical models), the relationship between F and α was obtained as demonstrated in Fig. 2C. In this case, it was assumed that the unmelted cross-sectional area of the LMPA was a bow-shaped structure. Therefore, the parameters A, M, y_max, and I_x were calculated by $\frac{R^2(2\mathrm{\alpha }-\text{sin}2\mathrm{\alpha })}{2}$, $F[\frac{4R{\text{sin}}^3\mathrm{\alpha }}{3(2\mathrm{\alpha }-\text{sin}2\mathrm{\alpha })}+R]$,$\frac{4R{\text{sin}}^3\mathrm{\alpha }}{3(2\mathrm{\alpha }-\text{sin}2\mathrm{\alpha })}-R\text{cos}\mathrm{\alpha }$, and $\frac{1}{4}{R}^4\mathrm{\alpha }+\frac{1}{2}{R}^4\text{cos}\mathrm{\alpha }{\text{sin}}^3\mathrm{\alpha }-\frac{1}{4}{R}^4\text{cos}\mathrm{\alpha }\text{sin}\mathrm{\alpha }-\frac{4R^4{\text{sin}}^6\mathrm{\alpha }}{9(\mathrm{\alpha }-\text{cos}\mathrm{\alpha }\text{sin}\mathrm{\alpha })}$ (43), respectively, where R represents the radius of the LMPA rod and α denotes the angle of a semicircle made by the unmelted bow-shaped LMPA.

According to Eq. 2, the compressive force F to generate the bending deformation increased from 0 to 1.3 N when the angle of semicircle α increased from 0 to 1.57 rad. In detail, when the actuating force of the LCE was larger than the value of F corresponding to α, the bending deformation occurred. It could also be observed that the smaller the section of unmelted LMPA, the smaller the value of F provided by the LCE.

In addition to the size of the LMPA melting area, the actuating force of the LCE is another notable factor that affects the deformation performance of an artificial muscle, as shown in Fig. 2D. For a fixed length of the PDA-coated LCE-based tubular actuator (inner diameter of 1.4 mm and outer diameter of 2.4 mm), the actuating force was tested under different irradiating powers ranging from 1.4 to 2.0 W for 20 s. For a specific irradiating power, the actuating force increased from zero to the maximum value within 20 s. With the increase in the laser power from 1.4 to 2.0 W, the maximum actuating force increased from 1.46 to 2.41 N. In addition to the irradiating power, increase in the irradiating time could also improve the actuating force, as shown in fig. S10. Furthermore, the actuating force cycle test was conducted under the irradiating power of 1.0 W, as presented in fig. S11. After the test cycles for 3600 s, the tubular LCE surface showed no noticeable scorch, thus illustrating the stable actuating property of the LCE. It was worth noting that if the PDA layer was too thick or the irradiating power was too high, the heat at the irradiating area would accumulate quickly, leading to the probability of generating smoking or scorch (figs. S12 and S13).

Specifically, bending angle of multifunctional artificial muscle is mainly governed by the laser power, spot area, and irradiating time, which was analyzed via experimental tests and simulations, as shown in Fig. 2 (E to G). First, the effect of irradiating power on bending angle was studied by fixing irradiating distance and irradiating time as demonstrated in the inset of Fig. 2E. The bending angle of the multifunctional artificial muscle progressively varied from 22° to 55° with the increase in the laser power from 1.0 to 1.9 W under an irradiating distance of 30 mm and irradiation time of 5 s. In the simulation, all other parameters (e.g., spot area and irradiating time) were kept unchangeable and only the laser irradiating power in Eq. 1 was increased from 1.0 to 1.9 W. The numerical values of bending angle also increased from 17° to 46.5° with the laser irradiating power, whose variation tendency was similar to that presented by experimental results.

Subsequently, the effect of the spot area on bending angle was studied by fixing the laser power (i.e., irradiating power) and irradiating time and by changing only the irradiating distance, as demonstrated in Fig. 2F. With the increase in the spot area from 3.14 to 4.5 mm² by increasing the irradiating distance from 30 to 300 mm, the bending angle decreased from 49.7° to 28° under the same laser power of 1.6 W and irradiation time of 5 s. Similarly, only the parameter of radius of the laser spot in Eq. 1 was changed in simulation. The bending angle progressively decreased from 36° to 25° with the increase in the spot area from 3.14 to 4.5 mm² in simulation, which is also in accordance with our experimental expectancy. Thus, other than changing the laser power, adjustment of the spot area that was governed by irradiating distance could also provide the desired bending angle for an artificial muscle. Noteworthy, we only discussed the case of spot area less than 4.5 mm² (i.e., the irradiating distance was below 300 mm) in the experiment. When the spot area was larger than 4.5 mm² (i.e., the diameter of laser spot was larger than the diameter of artificial muscle), more irradiating time or larger laser power was required to trigger the bending deformation of artificial muscle.

In addition to the irradiating power and spot area, the irradiating time is another significant factor that affects the bending angle. Figure 2G demonstrates that with the increase in the irradiating time from 3.5 to 7.5 s, the bending angle of the multifunctional artificial muscle progressively increased from 22° to 57° under the fixed irradiation distance of 30 mm and laser power of 1.4 W. Moreover, the bending angle also gradually increased from 19° to 41° by increasing the irradiating time from 3.5 to 7.5 s in simulation, which is also consistent with the variation tendency of bending angle in experiment. According to the experimental and simulation results, increasing the irradiation time can also trigger the increase of contraction area of LCE and melting area of LMPA, thus increasing the bending angle of multifunctional artificial muscle.

In the experiments of bending angle for artificial muscle, the irradiating power and spot area mainly affect the light intensity, further influencing the amount of heat absorbed by the artificial muscle under the same irradiating time. Moreover, longer irradiating time under the same laser power can also be conducive for artificial muscle to absorb more heat energy. Therefore, controlling how much heat is absorbed by artificial muscle is beneficial for the regulation of bending angle. In numerical simulations, by changing laser irradiating power, spot area, and irradiating time, respectively, the variation tendencies of bending angle are consistent with their experimental results. Yet, the values are not equal to experimental data, which may attribute to the discrepancy between the used parameters and actual values.

Flexible and controllable deformation, in particular, in the bending angle, direction, and position, can increase deformation possibility for a shape-programmable and shape-reconfigurable artificial muscle. Figure 3A exhibits that the bending angle could be adjusted by irradiating the same bending position from identical direction several times under the irradiating power of 1.4 W. The bending angle changed from 0 to 25° after the first irradiation on the artificial muscle surface, from 25° to 40° after the second irradiation, and from 40° to 50° after the third irradiation (see movie S5), which illustrates that a small bending angle was beneficial for accuracy adjustment and multiple irradiations were helpful to generate a large bending angle. After the first, second, and third laser irradiations, the increase in the bending angle was 25°, 15°, and 10°, respectively. The increase in the bending angle gradually decreased with the laser irradiation times, which could be mainly attributed to less contraction of the LCE after being irradiated several times.

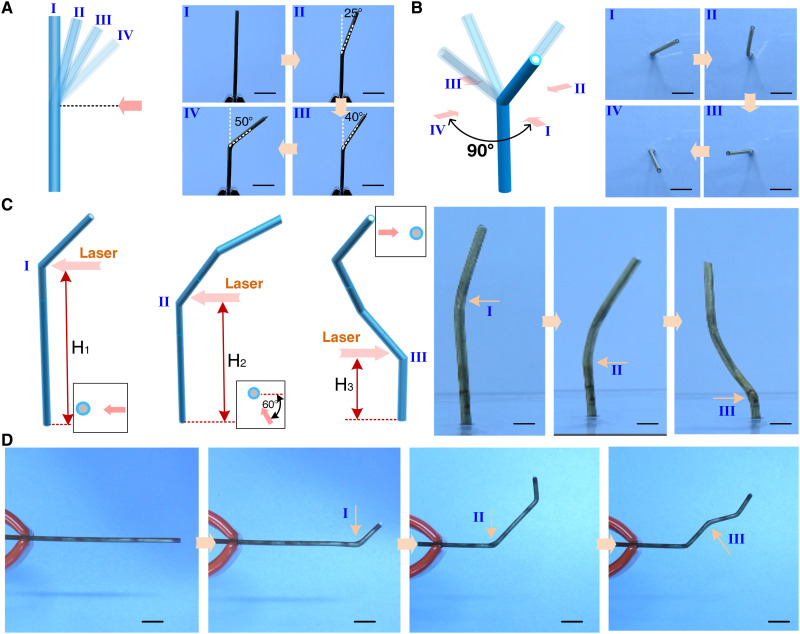
Fig. 3. Bending deformation of a multifunctional artificial muscle.

(A) Continuous adjustment of the bending angle of a multifunctional artificial muscle by irradiating the bending position from the same direction several times (I, II, III, and IV). Scale bars, 10 mm. (B) Different bending directions of the multifunctional artificial muscle obtained by adjusting the laser irradiating direction (I, II, III, and IV). Scale bars, 10 mm. (C) Multiple bending joints generated by irradiating the multifunctional artificial muscle at different positions (I, II, and III) and from different directions (0°, 60°, and 180°). Scale bars, 5 mm. (D) Shape change of the multifunctional artificial muscle by orderly applying the laser on different positions. In the experiment, one end of the multifunctional artificial muscle was clamped, and the other end was left free. Scale bars, 10 mm.

The bending direction of a multifunctional artificial muscle could also be changed by adjusting the laser irradiation direction, as shown in Fig. 3B. When the laser was sequentially irradiated at 90° apart on the surface of the multifunctional artificial muscle at the same height, bending direction of the artificial muscle changed continuously from I to IV (see movie S6). In the process of adjustment of bending direction, the value of the bending angle remained almost constant after four irradiations, which illustrated that changing the bending direction had little effect on the bending angle. In this study, the bending joint is regarded as a universal joint, and an artificial muscle can bend toward any direction by changing the laser irradiating direction.

Last, the multifunctional artificial muscle also has the feature of bending position selectivity, as shown in Fig. 3C. To verify its ability to have any number of bending positions, the LMPA rod was embedded into the PDA-coated LCE-based tubular actuator without prefabricating any bending position. The artificial muscle instantly generated bending deformation at all three positions when the laser was applied on the three positions in turn (see movie S7), wherein the distances between the laser beam and the ground at the three positions were H₁, H₂, and H₃, respectively, and the corresponding laser irradiation directions were 0°, 60°, and 180°, respectively. By selecting different irradiation heights, directions, and positions, more reconfigurable shapes could be generated. For instance, a “W” shape could be obtained by applying the laser on both sides of the artificial muscle, as shown in Fig. 3D and movie S8, which illustrates the potential of the proposed artificial muscle for shape programmability.

Characterization of rapid shape transformation and deformation locking

To evaluate the rapid shape transformation and deformation-locking performance of the artificial muscle, a test of irradiating the multifunctional artificial muscle from the topside and downside was performed under the irradiating power of 1.2 W, as shown in Fig. 4A. The specific dynamic process is demonstrated in movie S9. At 0.9 s, the laser was applied on the top surface of the multifunctional artificial muscle and turned off at 3.7 s. The artificial muscle started to generate large bending deformation at 3.5 s and maintained the maximum bending angle of 38° at 3.7 s. After an enduring time of 5.8 s, the laser irradiated the bending section of the artificial muscle from the downside at 9.5 s. The bending angle of artificial muscle instantly changed from 36° to −25° after the irradiation for about 3 s and finally sustained a value of −22° after the laser was turned off at 12.5 s, which also implied that the bending direction of artificial muscle could be adjusted even if the irradiation direction was 180° apart. To analyze the repeatability of bending deformation of the multifunctional artificial muscle, a laser spot with an irradiating power of 1.3 W was alternately applied on both sides of the artificial muscle. The five-cycle test results are shown in Fig. 4B, revealing that the upside and downside bending angles were approximately 45° and −35°, respectively, demonstrating the stable bending deformation capacity of multifunctional artificial muscle (manual operation probably led to slight angle inconsistency).

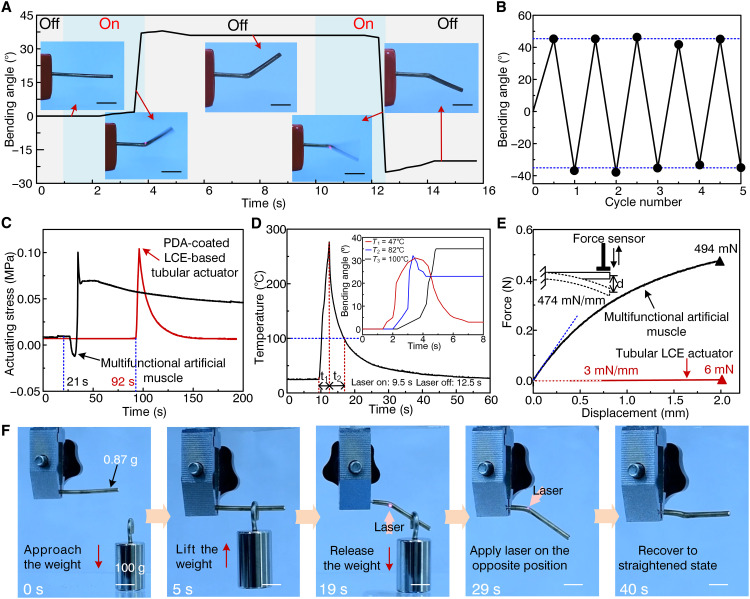
Fig. 4. Shape transformation and deformation locking of a multifunctional artificial muscle.

(A) Shape transformation and deformation locking of a multifunctional artificial muscle under the irradiating power of 1.2 W. Scale bars, 10 mm. (B) Repeatability of the multifunctional artificial muscle under the irradiating power of 1.3 W. (C) Actuating stress of the multifunctional artificial muscle and PDA-coated LCE-based tubular actuator under the irradiating power of 1.2 W. The laser was applied on the multifunctional artificial muscle and PDA-coated LCE-based tubular actuator at 21 and 92 s, respectively. (D) The highest temperature on the LCE surface as a function of time under the NIR laser irradiation of 1.6 W. Inset: Comparison of deformation locking of multifunctional artificial muscle with three different melting points (T₁, T₂, and T₃) and their law of variation for bending angle over time. (E) Bending stiffness and output force of the multifunctional artificial muscle and PDA-coated LCE-based tubular actuator. Inset: Schematic showing the test method of bending stiffness. (F) Time-lapse photographs of the pick-and-place operation of the multifunctional artificial muscle under the upward and downward bending deformations and transient laser irradiation from both directions. Scale bars, 10 mm. Laser power: 2.0 W. The weight of the multifunctional artificial muscle was 0.87 g, and the weight being lifted was 100 g.

Here, there is a difference on the upside and downside bending angles, which can be attributed to the actuating and recovering behavior of LCE. The initial state is different for bending upward and downward, corresponding to straight status with no stress difference of LCE between the top surface and bottom surface and bending status with a stress difference of LCE, respectively. In detail, the contracted LCE at irradiated area could not recover its original length even at room temperature due to deformation locking of multifunctional artificial muscle. Furthermore, we defined the speed of LCE recovering from contraction state to original state during the shape transformation process as recovery speed. If the recovery speed of LCE was smaller than the shape transformation speed of artificial muscle, the increase of bending angle would be restricted by the contracting LCE. In contrast, if the recovery speed of LCE was larger than the shape transformation speed of artificial muscle, the size of bending angle would hardly be restricted. According to the experimental results shown in Fig. 4 (A and B), the downward bending angle was smaller than the upward bending angle. The recovery speed of upside LCE, inferred here, was smaller than the downward bending speed of artificial muscle, which restricted the increase of downward bending angle. When artificial muscle bent upward, the recovery speed of LCE at the bottom side might be larger than the upward bending speed of artificial muscle due to small locking angle, leading to a larger bending angle.

Rapid melting and resolidification together constitute the main reason for the rapid shape transformation and deformation locking of an artificial muscle. By fixing two ends of an artificial muscle on a uniaxial testing machine, the rapid shape transformation and deformation locking mechanisms of the multifunctional artificial muscle and PDA-coated LCE-based tubular actuator were analyzed and compared from the perspective of stress, as shown in Fig. 4C. When the multifunctional artificial muscle was irradiated at 21 s and heated for a few seconds, its stress first suddenly decreased from 0.008 to −0.01 MPa and then increased to 0.1 MPa. The sudden decline in the tensile stress of the artificial muscle under a tension of 0.1 N could be mainly attributed to the melt of the LMPA rod, which resulted in a much smaller modulus that was conducive to promote deformation of the multifunctional artificial muscle. When the laser was powered off at 33 s, the actuating stress of the multifunctional artificial muscle began to decline from 0.1 MPa but did not recover to zero mainly because the rapidly resolidified LMPA limited the LCE recovery. In contrast, the actuating stress in the tubular LCE actuator suddenly increased to 0.1 MPa from zero when the laser was turned on at 92 s and then slowly decreased from its maximum value to zero when the laser irradiation was interrupted at 96 s. The comparative analysis of results indicates that the melt of the LMPA was the main reason for a sudden decrease in the tensile stress of the multifunctional artificial muscle from 0.008 to −0.01 MPa, and a rapid resolidification of the LMPA (i.e., deformation locking) prevented the actuating stress of the multifunctional artificial muscle from recovering to zero.

The rapid melting of LMPA mainly ascribes to the rapid photothermal conversion of PDA in the NIR region. When a laser beam with irradiating power of 2.0 W was applied on the surface of multifunctional artificial muscle (the melting point of LMPA was 100°C), the temperature, as shown in Fig. 4D, sharply increased from 24.9° to 276.5°C in 3 s after the laser irradiation was focused at 9.5 s, subsequently decreased to 100°C (the solidification point of the LMPA) in 4.3 s, and further decreased to 30°C in 35 s after the laser irradiation was removed at 12.5 s. If the irradiating time was defined as the heating time, i.e., t₁ shown in Fig. 4D, the heating time shortened with the increase of irradiating power (fig. S14), which also illustrates that high irradiating power was conducive to quick deformation of artificial muscle. Furthermore, if the time when the temperature decreased from the maximum to 100°C (the solidification point of LMPA) was defined as the cooling time (i.e., t₂ shown in Fig. 4D), the cooling time increased with the irradiating power, but its values were all below 4.3 s even if the multifunctional artificial muscle was exposed under larger irradiating power (fig. S15). The short cooling time, inferred here, mainly hinged on the rapid heat conduction between the irradiating and unirradiating sections of samples, besides thermal convection and radiation. The temperature difference of the solidification point (T_s) of LMPA and isotropic transition temperature (T_i) of the LCE, i.e., T_s − T_i, also mainly affect the deformation-locking performance of an artificial muscle, which is also presented in inset of Fig. 4D. In the test, the T_i of LCE adopted in this study was 78°C, which was obtained by the differential scanning calorimetry (DSC) measurement, as shown in fig. S16. The deformation-locking performance of the multifunctional artificial muscle was compared by embedding LMPA rods with different melting points (47°, 82°, and 100°C) into PDA-coated tubular LCE. It shows that the artificial muscle with the melting point of 100°C (i.e., high solidification point) easily hindered the angle recovery (movies S10 to S12). Otherwise, part deformation would be locked with T_s comparable to T_i, or even no deformation locking occurs as T_s < T_i. In detail, the temperature of melted LMPA had already lowered below solidification point when the LCE was still in contracting state, which was beneficial to deformation locking of multifunctional artificial muscle.

The deformation-locking performance also leads to high bending stiffness and large bearing capacity for multifunctional artificial muscle. As shown in the inset of Fig. 4E, the multifunctional artificial muscle and the PDA-coated LCE-based tubular actuator were horizontally fixed to the uniaxial testing machine, and the force sensor was moved down to press their free ends with a speed of 1 mm min⁻¹. As the bending stiffness denoted the slope of the load-displacement curve at a displacement of less than 1 mm (44), the stiffness values of the multifunctional artificial muscle and PDA-coated LCE-based tubular actuator reached 474 and 3 mN mm⁻¹, respectively. Thus, the stiffness of the multifunctional artificial muscle was nearly 158 times higher than that of the PDA-coated LCE-based tubular actuator. Compared with the previously reported stiffness-tunable actuators (28, 44–46), the multifunctional artificial muscle with the LMPA also exhibited a higher stiffness. The high stiffness endowed the multifunctional artificial muscle with a large load-bearing capacity. The load-bearing force of the multifunctional artificial muscle increased from 6 mN (i.e., the load-bearing force of PDA-coated LCE-based tubular actuator) to 494 mN, which is nearly an 82-fold increase. Comparative analysis of load-bearing capacity of the multifunctional artificial muscle and tubular LCE actuator under different diameters is presented in fig. S17, which reveals that a large diameter, in particular, embedded with the LMPA, could significantly improve the load-bearing capacity. Moreover, unlike the PDA-coated LCE-based tubular actuator, the multifunctional artificial muscle could lift a weight of 0.2 kg, thus illustrating that the LMPA rod obviously improved the load-bearing capacity of the multifunctional artificial muscle, as shown in fig. S18.

The bending stiffness values of the multifunctional artificial muscle and PDA-coated LCE-based tubular actuator were calculated by I₁ = πE₁D⁴/64 and I₂ = πE₂D⁴(1 − α⁴)/64, respectively, where E₁ denotes the modulus of the multifunctional artificial muscle, E₂ is the modulus of the tubular LCE, D is the external diameter of the multifunctional artificial muscle and tubular LCE, d is the inner diameter of the tubular actuator, and α is equal to d/D. In the tests, α was 0.58, which did not trigger the bending stiffness and bearing capacity to generate an order of magnitude change. Thus, the remaining parameters (i.e., E₁ and E₂) must greatly affect the stiffness and bearing capacity of the multifunctional artificial muscle and PDA-coated LCE-based tubular actuator. Therefore, their stress-strain relationships and Young’s moduli were studied, as shown in fig. S19. The results indicated that stress of the multifunctional artificial muscle linearly increased with strain, and its Young’s modulus could reach 4.2 GPa. In contrast, the stress of the PDA-coated LCE-based tubular actuator gradually increased with strain; however, its Young’s modulus was only 0.018 GPa. Therefore, introduction of the LMPA in the multifunctional artificial muscle markedly improved Young’s modulus, providing a nearly 233-fold increase.

To demonstrate the rapid shape transformation and deformation-locking features of the proposed multifunctional artificial muscle, the lifting and carrying experiments were performed by reversibly grasping a 100-g object. A series of pick-and-place operations performed by the multifunctional artificial muscle aided by a robot arm are presented in Fig. 4F. At the time of 0 s, the multifunctional artificial muscle of 0.87 g was in the original position. Then, the multifunctional artificial muscle approached the weight of 100 g and lifted it at 5 s, and no external energy was needed by the artificial muscle in the lifting process. When the multifunctional artificial muscle reached the target position at 19 s, it released the weight due to the exposure to laser irradiation for about 6 s. In the releasing process, the decrease in the unmelted section size of the LMPA reduced the bearing capacity of the multifunctional artificial muscle, resulting in a bending deformation under the function of a stress difference of the LCE. The multifunctional artificial muscle remained in the bending state after releasing the object and returned to its original position at 29 s. To recover its fully straightened state, laser irradiation was applied to the opposite position of the multifunctional artificial muscle, and the straightened state was achieved at 40 s. The entire process can be seen in movie S13. It seems that the recovery state was not identical to the initial state, which may be attributed to the slant irradiation of laser on the top surface. In practice, the multifunctional artificial muscle could recover to straight state from bending deformation by two laser beams alternately or by simultaneously irradiating the bending position, as presented in fig. S20 or movie S14. The results shown in Fig. 4F indicate that the proposed multifunctional artificial muscle could sustain its actuating state with zero-power consumption and requires laser irradiation for only several seconds to achieve rapid shape transformation between different bending states throughout the entire lifting and carrying process, which could be useful for low-power applications. Furthermore, the lifted weight (100 g) was about 115 times heavier than the weight of the multifunctional artificial muscle (0.87 g), which illustrates the excellent deformation-locking property and high load-bearing capacity of the proposed artificial muscle.

Characterization of sensing function

Theoretically, the resistance of the LMPA rod in the multifunctional artificial muscle is obtained by

$$R=\frac{\mathrm{\rho }L}{A}$$ (3)

where ρ is the electrical resistivity, L is the length of artificial muscle, and A is the cross-sectional area. According to Eq. 3, the size of cross-sectional area can significantly affect the resistance change of the LMPA rod if the changes in the electrical resistivity and length are ignored. The volume variations of the LCE and LMPA under light irradiation are shown in Fig. 5A. When the laser irradiated the surface of the multifunctional artificial muscle, the LCE at the irradiating region contracted along the length direction and thickened in the thickness direction (the thickness change of PDA-coated LCE film under laser irradiation is shown in fig. S21 or movie S15). Moreover, the LMPA under the LCE film began to melt when the temperature exceeded the melting point of 100°C of LMPA. Thus, the thickened LCE at the irradiated region would squeeze the melted alloy to both sides, triggering a decrease in the cross-sectional area of the LMPA rod. After the multifunctional artificial muscle generated bending deformation, the LCE at the irradiated section was still in a contractile state, and the melted LMPA instantly resolidified, thereby limiting the LCE recovery. Thus, the radius of the LMPA rod remained smaller than that in the original state, which caused an increase in the overall resistance of the multifunctional artificial muscle.

Fig. 5. Sensing function of the multifunctional artificial muscle.

(A) Schematic illustration of the multifunctional artificial muscle before and after bending deformation. (B) Response of ΔR/R to the different bending angles. Multiple samples with identical initial state in this test were irradiated under different irradiating powers. (C) Variation in resistance of one multifunctional artificial muscle sequentially irradiated at three different positions. Scale bars, 10 mm. In (B) and (C), one end of multifunctional artificial muscles was fixed, and the other end was free.

For the quantitative characterization of the change in resistance with the bending angle, we respectively irradiated multiple samples that had identical initial state (one end was fixed, and the other end was free) with different irradiating powers under the same irradiating distance. Figure 5B illustrates that the variation in resistance was about 1% when the bending angle reached 18° and further increased to 8% when the bending angle reached 55°. On the basis of the fitted curve, the resistance change increased with the bending angle, which indicated that the cross-sectional area of the LMPA rod at the bending section decreased with the bending angle. Therefore, the ability that the resistance change of the LMPA could reflect the bending angle value, similar to the nervous system in monitoring the motion signal, could be viewed as a sensing function of the proposed artificial muscle (measuring details can be seen in Materials and Methods).

To demonstrate the sensing function of the proposed multifunctional artificial muscle, a sample with a length of 50 mm and a diameter of 2.4 mm was prepared. Figure 5C demonstrates that when the laser was applied to the first position, the resistance increased by nearly 1.2% with the change in the bending angle by about 20°. However, the resistance decreased from 1.2% to 0.6% after the laser was turned off due to the decline in the electrical resistivity with the decrease in temperature. When the laser power was increased and the same irradiation distance and irradiation time were maintained at the second position, the bending angle reached about 30° when the resistance increased from 0.6 to 3.2%. The total resistance change was about 2.6% when the bending angle varied by about 30°, which is consistent with the law presented in Fig. 5B. When the laser power was reduced at the third position, the bending angle reached 25°, and the resistance increased by nearly 1.7%, i.e., from 2.4 to 4.1%. The bending angle value reflected by the resistance variation during the third irradiation coincided well with the bending angle corresponding to the resistance change presented in Fig. 5B. The resistance decline after the second and third irradiations could also be attributed to the decrease in the electrical resistivity of the LMPA with the decrease in temperature. According to the results of the three bending tests, the decline in resistance was no more than 1%, which illustrates that the cross-sectional area size, rather than the electrical resistivity, exhibited a significant effect on the resistance change. For comparison, resistance change of 30-mm-length LMPA rod heated by 2-mm-length hot plate was below 0.5% by changing temperature from 40° to 150°C with an interval of 10°C (fig. S22), which directly illustrated that resistance change of LMPA triggered by temperature was much smaller. Besides the fact that resistance could increase in the bending process and sustain its varying value during the deformation-locking process, it could also nearly recover to its original value along with the recovery of artificial muscle from locked-deformation state to original straight state (fig. S23). Thus, the dynamic deformation behavior of multifunctional artificial muscles can be monitored in real time by changes in electrical resistance.

Reconfigurable antenna equipped with multifunctional artificial muscle

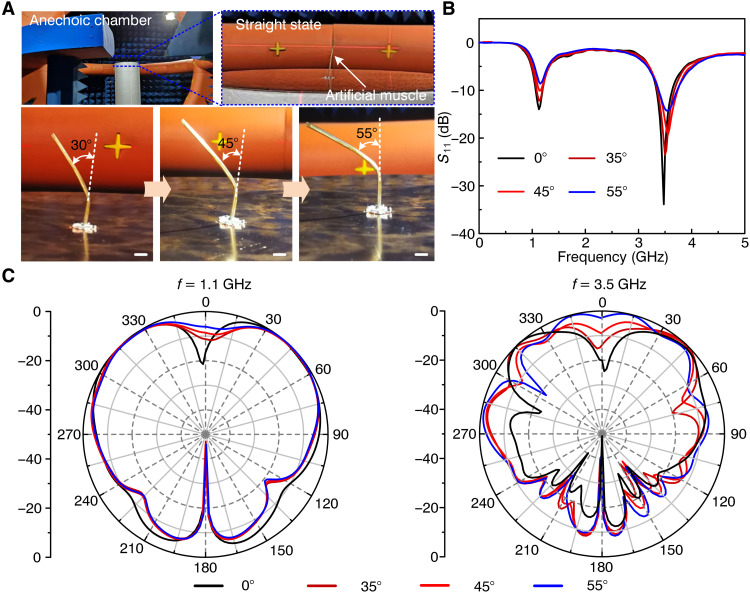
By using advantages of on-demand shape transformation and deformation locking, the application of the proposed multifunctional artificial muscle as a reconfigurable antenna was demonstrated. In this study, a length of 65 mm was adopted for the artificial muscle, and the irradiation height was approximately 25 mm. The multifunctional artificial muscle maintained its upright state before laser irradiation in the anechoic chamber. When the laser was applied on the artificial muscle surface, the bending angle was from 0° to 30° and further increased to 45° and 55° after the second and third irradiations, respectively, under the same irradiating power (1.6 W) and spot area (3.14 mm²). Different bending angles of the multifunctional artificial muscle are presented in Fig. 6A. For a 65-mm monopole antenna, the theoretical lower resonance was 1.15 GHz at 1/4 λ₁ (the wavelength at 1.15 GHz in the free space), and the higher resonance was 3.45 GHz at 3/4 λ₂ (the wavelength at 3.45 GHz in free space) in simulations. Figure 6B exhibits S₁₁ curves at different bending angles (S₁₁ refers to the ratio of the amplitude of the signal that reflects from port one to the amplitude of the incident signal on port one), which indicate that the monopole antenna had two resonances at 1.1 and 3.5 GHz, respectively. Deviations in the measurements and simulations were mainly due to the welding error and LCE covered on the antenna. The far-field pattern of the antenna tested in anechoic chamber indicated the energy radiation direction. The vertical polarization and far-field patterns in the xOz plane are shown in Fig. 6C, where it can be seen that the zero-point radiation was gradually eliminated at theta of zero with the increase in the bending angle from 0° to 55°. This result illustrated that this behavior did not lose the maximum gain of the antenna and was beneficial to antenna applications. Owing to the deformation locking provided by rapid resolidification of the LMPA, the reconfigured antenna could sustain any desired shapes without assistance from the external light field, which lowers the overall energy consumption in the working process. Moreover, owing to easy operation and regulation, a multifunctional artificial muscle as a remotely controlled and reconfigurable antenna is advantageous over the mechanically programmed antenna (23).

Fig. 6. Application of the multifunctional artificial muscle as a reconfigurable antenna:

(A) Different bending angles of the multifunctional artificial muscle after first, second, and third laser irradiations in anechoic chamber. Scale bars, 5 mm. (B) Experimental results of S₁₁ band of the reconfigurable antenna at different bending angles. Agilent AV3672E-S vector network analyzer (VNA) was used for S₁₁ measurements. (C) Vertical polarization and far-field patterns of the multifunctional artificial muscle as an antenna in the xOz plane.

DISCUSSION

Motivated by coupled behavioral characteristics of bones, muscles, and nerves of living animals, here, shape-programmable, deformation-locking, and self-sensing artificial muscle was constructed using the soft material (i.e., LCE) coupled with high-stiffness material (i.e., LMPA) in a concentric tube/rod form to overcome the disadvantages of pure soft materials. Here, the rigid component LMPA (equivalent of endoskeletons) mainly provides passive structural strength that pure soft materials do not have. In contrast, the pure soft materials made of LCE (equivalent of natural muscle) offer powerful actuating stress and secure physical compatibility. For the concentric structure of artificial muscle, the outer LCE with stress-strain behavior comparable to natural muscle is used for reversible contraction/recovery and the inner solid LMPA with high stiffness is adopted for shape locking; the resistance change of LMPA squeezed by LCE is used for monitoring angle variation, and the melted section of LMPA that lowers material stiffness under light stimuli provides more deformation space for LCE, corresponding to the function of muscles, bones, nerves, and joint, respectively. As a result, the proposed multifunctional artificial muscle simultaneously exhibits excellent shape-programmable, deformation-locking, and self-sensing properties, which is not only superior in low-power consumption, high load-bearing capacity, and deformation locking with respect to LCE-based artificial muscle (31, 39, 47–50) but also excellent in response time, sensing function, flexible shape programmability, and reconfigurability compared with LMPA-based artificial muscle (28, 30). To the best of our knowledge, an artificial muscle with these features has seldom been reported to date.

Previously reported LCE-based actuators obtained by injecting liquid metal into tubular LCE (31, 33) or dispersing liquid metal into LCE (32) perform excellent actuation or sensing functions, yet they are still far from satisfactory with respect to their load-bearing capacity, low-power consumption, and deformation locking. Moreover, by changing temperature to adjust stiffness of materials (25, 29), the materials can sustain high stiffness and deformation under low temperature and flexibly deform under high temperature; however, they lack feedback function to surroundings and quick response. Nonetheless, the proposed multifunctional artificial muscle simultaneously has shape-programmable, deformation-locking, and self-sensing capabilities by phase transition of LMPA, reversible deformation of LCE, and their volume changes. Thus, the artificial muscle can generate reconfigurable deformation without prefabricating structures, sustain different shapes without energy consumption, and aid in sensing the deformation size without extra integrating sensors; thus it may have the potential to be used in reconfigurable deformation along with self-perception and low power. In particular, the proposed artificial muscle, acting as reconfigurable antennas, can not only easily reconfigure its electromagnetic performance (e.g., frequency of operation, polarization, and radiation pattern) via its reconfigurable structures such as the shape-morphing antennas based on LCE (51), liquid metal (52), or shape-memory polymer (53) but also demonstrate its unique character, i.e., sustain its different working shapes without consuming any energy.

Rigid structural material embedded in artificial muscle can effectively reduce the DOF of soft material, further lowering the possibility of uncontrollable deformation for artificial muscle. Moreover, the local melt of LMPA lowers the local stiffness of artificial muscle and only allows for the differentiated shrinking of LCE along the length direction of fiber, resulting in following bending deformation of artificial muscle. Further, the magnitude of deformation can be controlled precisely by adjusting the size of melting area of LMPA and actuating force of LCE via light intensity. Thereinto, the actuating force of LCE can not only be changed by irradiating power (Fig. 2D) and irradiating time (fig. S10) but also be significantly affected by prestretching of LCE, which was also deeply discussed in our previous studies (50, 54). Simulation studies and numerical models were investigated to observe the temperature and stress distributions and to analyze the controllable deformation of the proposed multifunctional artificial muscle, respectively. According to the experimental results, the bending angle of the multifunctional artificial muscle could not only be controlled by modifying the irradiating power, irradiating distance, and irradiation time but also be effectively adjusted by multiple irradiations. Furthermore, the proposed multifunctional artificial muscle without prefabricated structures can have any number of bendable joints and can be adjusted in any direction, which is suitable for tasks requiring frequent reconfiguration. Thus, flexible and controllable deformation, in particular, in the bending angle, direction, and position, endows the artificial muscle with more shape programmability and reconfigurability possibilities.

Rapid shape transformation and deformation locking of a multifunctional artificial muscle are realized by rapid local melt and resolidification of LMPA at the irradiating area, which also simultaneously leads to high stiffness, high load-bearing capacity, and low power consumption. Furthermore, a proof of concept of the proposed multifunctional artificial muscle as a robot for lifting and carrying, assisted by a robot arm, is presented. The results indicate that artificial muscle can bear 115 times its own weight, which (the ratio between the weights of the object and the artificial muscle) is higher than most of soft artificial muscle with flexible deformation and rapid response studied to date (29, 55). Last, a reconfigurable antenna was also designed and fabricated to demonstrate the controllable deformation, deformation locking, and low power features, which is also slightly similar to the muscles of some mollusks in a catch state (they lock the shells without consuming energy) (56). Compared with other various stimuli-responsive artificial muscles, the proposed artificial muscle without prefabricated structures can sustain programmable and reconfigurable shapes without requiring continuous external energy, which has also been rarely reported in previous studies.

The interaction of LCE and LMPA under laser irradiation not only endows artificial muscle with controllable deformation and deformation locking but also triggers the resistance change of LMPA, i.e., sensing function, which is superior to those by introducing additional sensing structures (11, 27, 57, 58). The sensing function of proposed multifunctional artificial muscle could be used to monitor the size of bending angle via resistance change, which is helpful to controllably adjust the bending angle. Owing to the sensing function on bending angle and predetermined irradiation direction, the specific sensing mechanisms have the potential to be further extended to more complex deformation modes, such as multiangle adjustment at one position and multiple point bending upward or downward, as shown in Fig. 3. Here, noteworthy, the artificial muscle mainly monitors the bending angle rather than the bending direction or position (undeniably, more attention will be paid to intelligent artificial muscle with more sensing functions in our future study). Benefiting from the development of various novel materials and artificial intelligence, similar multifunctional artificial muscle, mainly the one coupled with more human-like functions, i.e., all-in-one material, is expected to have better physical compatibility and actuating performance to fuse with machines and humans, which, to a certain degree, may extend the application in soft grippers, haptic displays, medical care, etc.

However, so far, hard robots are still dominant compared with soft robots in their respective fields of application. Nonetheless, by introducing hard material into soft material, the proposed multifunctional artificial muscle, which is similar to vertebrates or insects having rigid structural frameworks along with soft materials, would be a promising system integrating benefits of both, which may blur the application boundaries between soft and hard robots and escalate the development of soft robots. For instance, hard robot (e.g., conventional industrial arms) may be far from optimal while considering safety and dependability during its operation in anthropic environments, whose noncollaborative factors can be mainly mitigated by overincreasing of various sensors or controllers, which, however, usually corresponds to a complexity of construction. Inspired by biomimetic rather than classical machine-tool design, soft robots, even with open-loop control, demonstrate good compatibility with biological materials and humans due to their soft and compliant nature and ability to perform uncertain works, which is also regarded as an advantage for soft robot without the need for precise control. However, confronted with the situation using compensated input to determine output, closed-loop control may be more suitable for implemented systems to generate more accurate and robust actuation, which also lays the groundwork for intelligent autonomous system. Moreover, more endeavors or attempts such as machine learning techniques are also adopted from previous work to enhance the controllability of soft robot by various sensors (59, 60). In our experiment, the hard material of LMPA restricts many uncertain deformations of soft material (i.e., LCE); therefore, the controllability of bending angle of multifunctional artificial muscle can be improved to a certain extent by controlling the local melting size of LMPA and contracting force of LCE rather than adopting complex controlling technologies. In contrast, using a single servo motor and deformable tubular material can also improve security to a certain extent during human-machine interaction. However, referring to sensing and deformation locking, it may need more mechanical parts for the controllable deformation. Furthermore, it is also difficult to generate reconfigurable or complex deformation for limited strings, as those shown in Fig. 3. The artificial muscle proposed here can generate reconfigurable deformation without prefabricating structures, sustain different shapes without energy consumption, and aid in sensing the size of deformation without extra integrating sensors, opening up a new avenue for smart artificial muscles.

MATERIALS AND METHODS

Materials

1,4-Bis-[4-(3-acryloyloxypropyloxy) benzoyloxy]-2-methylbenzene (RM257; 99%; Xi’an Caijing Opto-electrical Science & Technology Co. Ltd.), (2-hydroxyethoxy)-2-methylpropiophenone (HHMP; 98%; TCI, Shanghai), 2,2′-(ethylenedioxy) diethanethiol (EDDET; 95%; TCI, Shanghai), pentaerythritol tetrakis (3-mercaptopropionate) (PETMP; 95%, TCI, Shanghai), dipropylamine (DPA; 98%; TCI, Shanghai), PDA hydrochloride (PDA; 99%; Alfa Aesar, Beijing), and tris base (99.8 to 100.1%; Alfa Aesar, Beijing) were used in this study. All the chemicals were used as purchased without further purification. Components (percentage) of the LMPA with a melting point of 47°C are as follows: lead (22.6%), tin (8.3%), bismuth (44.7%), cadmium (5.3%), and indium (19.1%). Components (percentage) of the LMPA with a melting point of 82°C are as follows: lead (43%), bismuth (50%), and cadmium (7%). Components (percentage) of the LMPA with a melting point of 100°C are as follows: lead (30%), tin (18%), and bismuth (52%).

Fabrication of tubular LCE

RM257 (11.5 g, 19.54 mmol) and toluene (3.565 g) were mixed in a beaker and heated in an oven at 85°C for about 20 min. Then, the HHMP photoinitiator (0.074 g, 0.33 mmol) was added to the beaker. After the mixture became clear again, PETMP (0.083 g, 1.69 mmol) and EDDET (2.477 g, 13.59 mmol) were mixed together and subsequently added to the abovementioned mixture. The catalyst PDA (0.036 g, 0.36 mmol) was later poured into the same beaker. The solution was stirred for about 3 min, degassed in a vacuum chamber for about 5 min, and then poured into the glass tube and rod molds. Next, the molds were placed in a dark environment for 24 hours. In the subsequent step, the cured tubular LCE was placed in the oven at 85°C for 12 hours to evaporate the solvent. After the tubular LCE was cooled down to room temperature, it appeared opaque and retained the polydomain state. Last, a monodomain tubular LCE was obtained by stretching the tubular to five times its original length under the 365-nm UV irradiation (10 mW cm⁻²) for 10 min.

DSC measurement of tubular LCE

The DSC curve of the tubular LCE was obtained using DSC1 machine (Mettler-Toledo, Switzerland) in the nitrogen atmosphere. The samples (~10 mg) were loaded into a standard aluminum DSC pan. The heating scanning rate was 10°C min⁻¹ in the temperature range between −50° and 150°C.

Fabrication of PDA-coated tubular LCE

Dopamine hydrochloride (0.2 g, 1.05 mmol) and tris base (0.1 g, 0.83 mmol) were dissolved in water (100 ml). The pH of the tris base buffer solution was 8.5, and it was measured using a pH strip (Hydrion test paper, pH 1.0 to 11.0, Micro Essential Laboratory). The monodomain LCE tubes were immersed in the solution and stirred for 24 hours. The pH of the buffer solution barely changed; the resulting PDA-coated LCE tubes were washed three times with deionized water and then air-dried.

Fabrication of multifunctional artificial muscle (PDA-coated LCE tube embedded with LMPA rod)

Melted LMPA was poured into a tubular mold. Once solidified, the LMPA rod was taken out of the mold. Last, the multifunctional artificial muscle was assembled by embedding the LMPA rod into the PDA-coated LCE-based tube.

Finite element simulation of multifunctional artificial muscle

To better comprehend the deformation-locking phenomenon of a multifunctional artificial muscle, the temperature and stress distributions in the multifunctional artificial muscle under different laser irradiating powers were studied by harnessing the ABAQUS software version 6.14 (Dassault Systèmes Simulia Corp., USA). The density, specific heat, and thermal conductivity were set to 1200 kg m⁻³, 1700 J kg⁻¹ °C⁻¹, and 0.6 W m⁻¹ K⁻¹, respectively, for LCE and 9750 kg m⁻³, 350 J kg⁻¹ °C⁻¹, and 3.5 W m⁻¹ K⁻¹, respectively, for LMPA (table S1). The values of Young’s modulus and Poisson’s ratio of the LCE and LMPA are listed in tables S2 and S3, respectively. The trilayered structure was modeled using a four-node bilinear plane stress quadrilateral element (ABAQUS element type CPS4R).

Stress-strain tests of multifunctional artificial muscle and PDA-coated tubular LCE

The artificial muscle (outside diameter: 2.4 mm) and PDA-coated tubular LCE (outside diameter: 2.4 mm; inner diameter: 1.4 mm) were vertically fixed on the uniaxial testing machine (Perfect International Instruments Co. Ltd., Dongguan, China). The stress of both samples was obtained with the load cell (PT-2KG) of the uniaxial testing machine under the same drawing speed of 1 mm min⁻¹. On the basis of the force-displacement data and geometries of the samples, the stress-strain curves of multifunctional artificial muscle and PDA-coated tubular LCE were obtained. If it was assumed that the slope of the curves at the origin of coordinates was Young’s modulus, the Young’s modulus of multifunctional artificial muscle and PDA-coated tubular LCE could be calculated. The corresponding results are presented in fig. S19.

Characterization of the actuating force of multifunctional artificial muscle and PDA-coated tubular LCE

Two ends of artificial muscle (outside diameter: 2.4 mm) and PDA-coated tubular LCE (outside diameter: 2.4 mm; inner diameter: 1.4 mm) were, respectively, preloaded with load (0.1 N) on the uniaxial testing machine (Perfect International Instruments Co. Ltd., Dongguan, China). Then, NIR laser irradiation (semiconductor laser with a wavelength of 808 nm and maximum laser power of 2.0 W; Xi’an Lei Ze Electronic Technology Co. Ltd.) was applied on the middle of the specimens, and the actuation stress was recorded with the load cell (PT-2KG) of the machine. On the basis of the actuating force data and geometries of specimens, the curves of the actuating force with time could be obtained, as shown in Fig. 4C.

Temperature and deformation characterization of multifunctional artificial muscle under laser irradiation

One end of multifunctional artificial muscle was horizontally or vertically fastened on a clamp, and the other end was free. When the artificial muscle generated bending deformation, the laser applied on its surface was turned off. The deformation videos were obtained using the digital camera (Nikon, D7500) and analyzed by using ImageJ software. The blue background of movies and photographs is just a stylistic choice. The surface temperature of multifunctional artificial muscle was measured by thermal imaging technique (FLIR T630).

Force/displacement measurement of multifunctional artificial muscle and PDA-coated tubular LCE

One end of the multifunctional artificial muscle (outside diameter: 2.4 mm; length: 30 mm) and PDA-coated LCE-based tubular actuator (outside diameter: 2.4 mm; inner diameter: 1.4 mm; length: 30 mm) was horizontally fixed to the uniaxial testing machine (Perfect International Instruments Co. Ltd., Dongguan, China), and the other end was pressed with a load cell (PT-2KG) with a speed of 1 mm min⁻¹. Thus, the force-displacement curves were recorded with the load cell. The bending stiffness could be obtained if the slope of force/displacement curve was used to define the samples’ stiffness (44), and the corresponding results are shown in Fig. 4E.

Sensing performance test of multifunctional artificial muscle

One end of multifunctional artificial muscle (length, 50 mm) was horizontally fixed with a clamp, and the other end was free. Further, the free and fixed ends were connected to the precision source/measure unit (Keysight B2912A) with a silver wire (diameter, 100 μm) to obtain the resistance of multifunctional artificial muscle. Thereinto, the minimum measurement resolution of precision source/measure unit was 10 fA/100 nV. The measuring device is shown in fig. S24. Here, multiple samples with identical initial state were used to study the resistance change under different bending angles by irradiating the middle position of their surfaces. The measuring results are presented in Fig. 5B. Moreover, the resistance test of same sample was also conducted by orderly irradiating different positions to explore the relationship between resistance change and bending angle, which is shown in Fig. 5C.

The test of multifunctional artificial muscle as a reconfigurable antenna

The artificial muscle with different bending angles was tested using Satimo antenna measurement system (EMT-24) in anechoic chamber. Different configurations with different bending angles are shown in Fig. 6C. Furthermore, an Agilent AV3672E-S vector network analyzer (VNA) was used for S₁₁ measurement, as shown in Fig. 6B.

Supplementary Materials

This PDF file includes:

Sections S1 to S5

Figs. S1 to S24

Tables S1 to S3

References

Other Supplementary Material for this manuscript includes the following:

Movies S1 to S15