Abstract
Some physical properties of hexahalometallate K2XBr6(X = Se, Pt) were computed in the zinc blend structure using GGA-PBESOL. The cell constant of K2SeBr6 and K2PtBr6 is consistent to the experiment value quoted in the literature, where the error is 0.95% and 1%. K2SeBr6 and K2PtBr6 present covalent bonding, high anisotropy and are ductile. The elastic constants of K2SeBr6 and K2PtBr6 are significantly smaller due to their larger reticular distances, lower Coulomb forces and then they are soft and damage tolerant. The interatomic separation is greater in K2SeBr6 than in K2PtBr6, hence the Coulomb interaction in K2PtBr6 is greater than that of K2SeBr6. The internal coordinate of Br atom in K2PtBr6 is lower than that of the same atom in K2SeBr6, and this can be explained by the fact that it is inversely proportional to the atom radius of Se and Pt. There are two major plasmonic processes, with intensities 3.7 and 1.35 located around 53.5 nm and 72.8 nm for K2SeBr6 and K2PtBr6.
Subject terms: Materials science, Physics
Introduction
Progress in experiment and theory, coupled with computational model is accelerating the discovery of new materials with useful physical parameters. The cubic antifluorite class K2XBr6(X = Pt, Se) have received increased interest since they exhibit structural phase transitions at lower temperatures. The family of hexahalometallate attracts researchers due to their light-absorbing materials in photovoltaic applications. The hexahalometallate double perovskites K2XBr6(X = Pt, Se) crystallize in the cubic antifluorite K2PtCl6 structure. They have the stoichiometric formula X2MA6, where X, M and A are alkaline metal, polyvalent or heavy transition metal and halogen. The K atom in K2XBr6 (X = Pt, Se) of the three-dimensional structure is bonded to twelve equivalents Br atoms to form KBr12 cuboctahedra. The faces contain six equivalents KBr12 cuboctahedra and four equivalents PtBr6 (SeBr6) octahedral. Studies conducted by other researchers, it is stated that, the investigation on elastic constants and compressibility of K2XBr6(X = Pt, Se) has carried out experimentally by N. Wruk et al. using Brillouin scattering and ultrasonic wave velocity measurements1. The study conducted by Walter Abriel and Mary Anne White on K2SeBr6 by x‐ray powder diffraction in the temperature range 10 K to 290 K, and heat capacity measurements indicates three phases for K2SeBr6, K2PtCl6 cubic structure, Rb2TeI6 tetragonal structure and K2TeBr6 monoclinic structure2. The phase-transition temperatures of hexahalometallate material K2PtBr6 (K2SeBr6) have been studied experimentally and found to be 209 K, 221 K and 249 K1 (78 K, 105 K, 137 K, 143 K and 169 K1). K2XBr6(X = Pt, Se) hexahalometallate materials show a suitable energy gap, sufficient absorption, low reflectivity, weaker cost and therefore adequate performance for photovoltaic applications3–7. Our study confirms the characteristics of mentioned materials above, which have a band gap range of (0.98 eV to 2.25 eV), an absorption coefficient of 237,311 cm-1 (211,556 cm-1) and reflectivity of (0.1–0.3%) in the extreme ultraviolet light. The band gap range (1–2.25 eV) and the absorption of extreme ultraviolet light make K2SeBr6 and K2PtBr6 as absorber materials in solar cells. These compounds are poor reflector and can be used as an anti-reflection coating material.
The aim of this work is the use of GGA-PBESOL and HSE hybrid approximations to obtain adequate structural, elastic and optoelectronic properties of K2XBr6 (X = Pt, Se). The paper is organized such as the calculation scheme is detailed in the second part. The exposure and discussion of obtained results are reported in the third section. This work is concluded by an conclusion in the last part.
Calculation scheme
Calculations were carried out using the DFT framework as implemented in the CASTEP code8. The valence states of K2XBr6(X = Se, Pt) are K: 4s1, Se: 4p4, Pt: 5d9 and Br: 4p5. An ultra soft pseudo-potential type Vanderbilt9 describes the interaction of valence electrons and ions cores. The GGA-PBESOL of Perdew et al.10 is adopted for the non-local correlation exchange effect. The best convergence of the computed structures and energies requires the use of cut-off energy of 630 eV. The irreducible Brillouin zone was sampled up to 8 × 8 × 8 k-grid on the Monkhorst–Pack scheme11. The tolerance of geometry optimization were a difference of total energy 5 × 10−6 eV/atom, a maximum ionic Hellmann–Feynman force 10–2 eV/Å, maximum stress 2 × 10–2 eV/Å3 and ionic displacement of 5 × 10–4 Å. The calculation of the optical parameters requires the use of uniform distribution of 20 × 20 × 20 k-points. The self-consistent calculations converge if the total energy is minimal. The structural parameters were estimated using the minimization technique of Broyden-Fletcher-Goldfarb-Shanno (BFGS)12, which provide a fast way to find the lowest energy structure. The basic idea behind the hybrid functionals is to mix exchange energies calculated in an exact (Hartree–Fock-like) manner with those obtained from DFT methods in order to improve performance. The accuracy of the electronic properties predicted by density functional theory depends on the used exchange–correlation functional. Non-local hybrid functionals gives more accurate results than semi-local functionals. The non-local Hartree–Fock exchange is an integral part of the hybrid functionals implemented in the FLAPW mehod13. The non-local exchange in HSE enlarges the elements of the optical transition matrix and leads to better accuracy of HSE in calculating electronic properties. Omitting the non-local exchange in the transition operator for HSE leads to errors. The importance of non-local correction in the velocity gauge has been widely discussed for non-local pseudo potentials14,15. The neglect of the non-local term in the velocity gauge leads to inaccuracy, especially for transitions that involve localized d electrons16,17. The non-locality of the potential comes from the fact that the electron Hamiltonian is replaced by an approximate Hamiltonian in the independent electron approximation with an effective potential, which reintroduces the electron–electron interactions in the Kohn–Sham equations.
Results and discussion
Structure and morphology
The crystal structure of K2PtBr6 is illustrated in Fig. 1. The location of atoms is such that (Se, Pt) atom is placed at the center of the octahedron formed by the four atoms of Br. The K atoms occupy interstitial sites. The antifluorite class K2XBr6(X = Se, Pt) adopt the cubic structure with space group Fm3m at ambient conditions. The occupied Wyckoff sites for K, (Se, Pt) and Br atoms are ± (1/4, 1/4, 1/4) a0, (0, 0, 0) a0 and ± (x, 0, 0) a0, ± (0, x, 0) a0 , ± (0, 0, x) a0. The lattice constant, bulk modulus and its pressure derivative of K2XBr6(X = Se, Pt) are listed in Table 1. The cell constant of K2SeBr6 and K2PtBr6 is consistent to the experimental value quoted in the literature1,2, where the error is 0.95% and 1%. The bulk modulus calculated for K2SeBr6 and K2PtBr6 using the fit scheme P(V/V0) as reported in Fig. 2 is in good agreement with available experimental data1. The interatomic distances dX-Br, dK-Br and dBr-Br in K2SeBr6 (K2PtBr6) at equilibrium are 2.5681 Ǻ, 3.6769 Ǻ and 3.6319 Ǻ (2.4703 Ǻ, 3.6306 Ǻ and 3.4936 Ǻ). It should be pointed that, bond lengths reported for K2SeBr6 are in good agreement with those found in the literature dSe-Br = 2.555 Ǻ, dPt-Br = 2.50 Ǻ, dK-Br = 3.685 Ǻ and dBr-Br = 3.613 Ǻ2. Figure 3 shows the effect of pressure on dK-Br, dBr-Br and dBr-X (X = Se, Pt) bond lengths in K2SeBr6 and K2PtBr6. The bond lengths in K2SeBr6 are large than those in K2PtBr6; hence, the Coulomb interaction in K2PtBr6 is greater than that in K2SeBr6, which can be explained by the fact that the distances are inversely proportional to the lattice constant. Also, the distance dBr-Se is greater than that of dBr-Pt. All bond lengths decrease monotonously when the pressure increases. Figure 4 displays the effect of pressure on the internal coordinate of Br atom in K2SeBr6 and K2PtBr6. The internal coordinate of Br atom in K2PtBr6 is lower than that of the same atom in K2SeBr6, and this is explained by the fact that it is inversely proportional to the atom radius of Se (1.15 Ǻ) and Pt (1.35 Ǻ).
Figure 1.
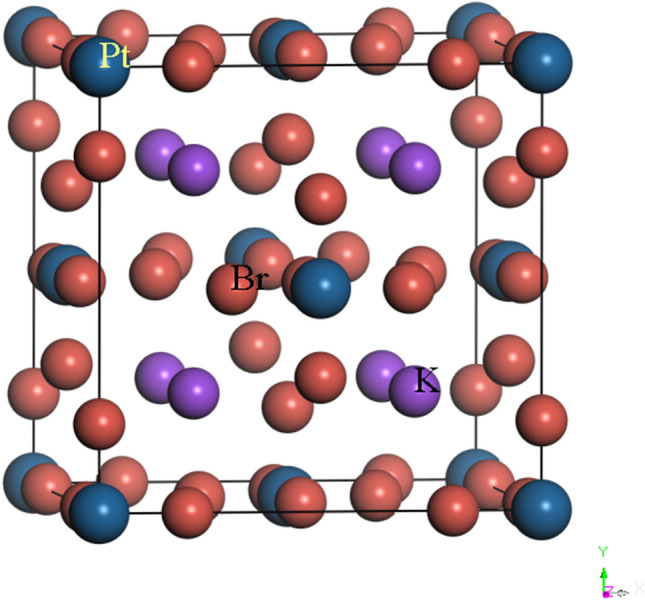
The crystal structure of K2PtBr6.
Table 1.
The lattice constant, bulk modulus and its pressure derivative and elastic moduli of K2XBr6(X = Se, Pt).
| K2SeBr6 | K2PtBr6 | |||||
|---|---|---|---|---|---|---|
| This Work | Experiment | Other | This Work | Experiment | Other | |
| A (Å ) | 10.2653 | 10.363 1 | 10.3995 | 10.293 1 | ||
| x | 0.24065 | 0.24695 | ||||
| *B0 (GPa) | 15.35 | 16.70 1 | 15.43 | 15.20 1 | ||
| B’ | 6.15 | 7.20 | ||||
| C11 (GPa) | 15.49 | 23.20 1 | 22.27 | 21.60 1 | ||
| C12 (GPa) | 11.95 | 13.50 1 | 8.97 | 12.0 1 | ||
| C44 (GPa) | 7.08 | 9.30 1 | 5.95 | 8.50 1 | ||
| **B0 (GPa) | 13.13 | 13.40 | ||||
Figure 2.
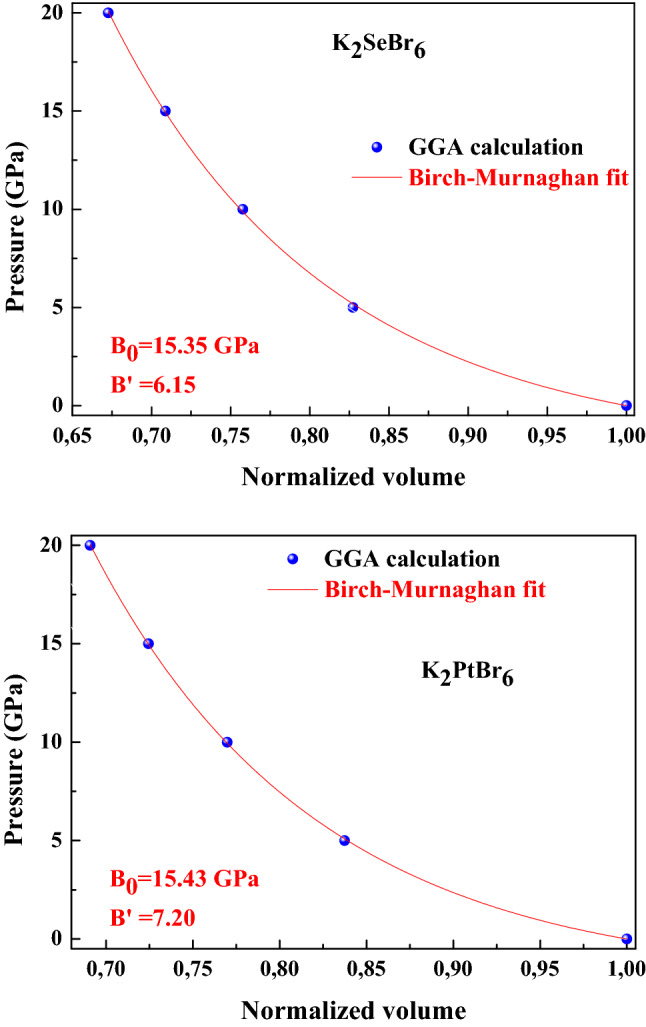
The pressure effect on normalized volume in K2SeBr6 and K2PtBr6.
Figure 3.
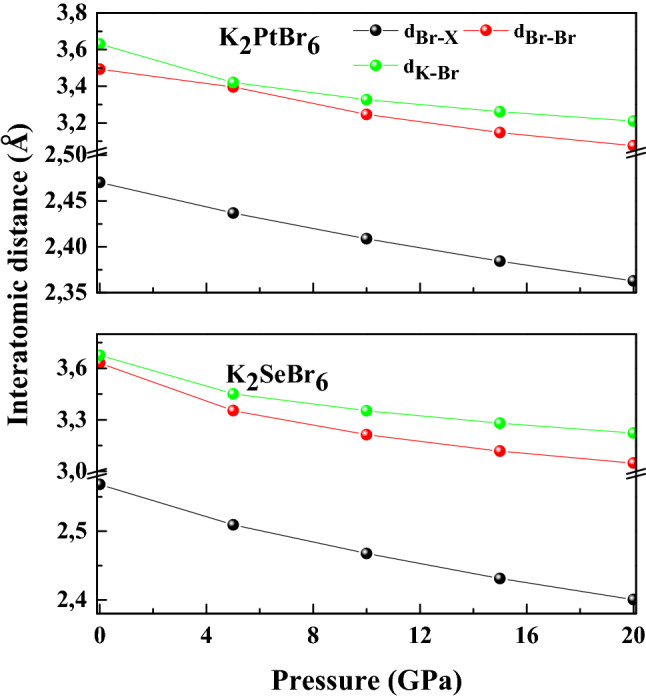
Effect of pressure on bond lengths dK-Br, dBr-Br and dBr-X(X=Se, Pt) in K2SeBr6 and K2PtBr6.
Figure 4.
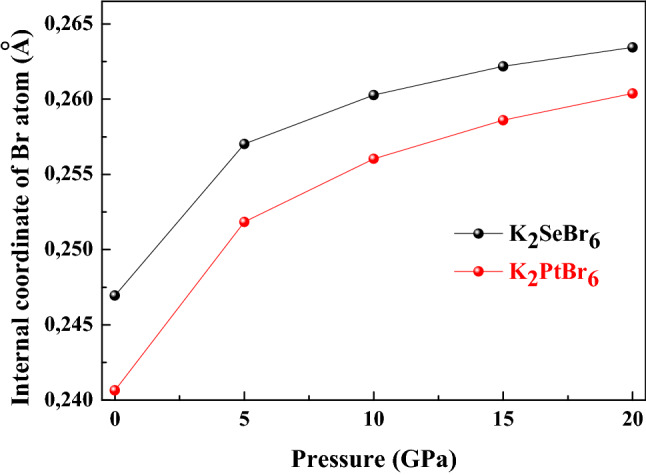
The pressure effect on internal coordinate of Br atom in K2SeBr6 and K2PtBr6.
Elastic constants and related parameters
The knowledge of elastic constants is essential for a better theoretical understanding of the properties of materials that are determined by the phonons density of states and the electron–phonon interaction processes. The three independent elastic constants C11, C12 and C44 require for their elastic characterization. The elastic moduli of K2XBr6(X = Se, Pt) computed at equilibrium using GGA-PBESOL are reported in Table 1. No theoretical value is reported in the literature, then our computation is prediction. The elastic constants of K2SeBr6 and K2PtBr6 are significantly small because of their quite large reticular distances, low Colombian forces, so they are quite soft and tolerant to damage. This result is qualitatively explained in these two materials by their binding forces, which are mainly ionic. It was noted that C11, C12 and C44 agree reasonably with their experiment values1. The elastic stability of K2SeBr6 and K2PtBr6 was defined taking into account the Born’s criteria, from which the following conditions must be satisfied for zinc blend structure18:
| 1 |
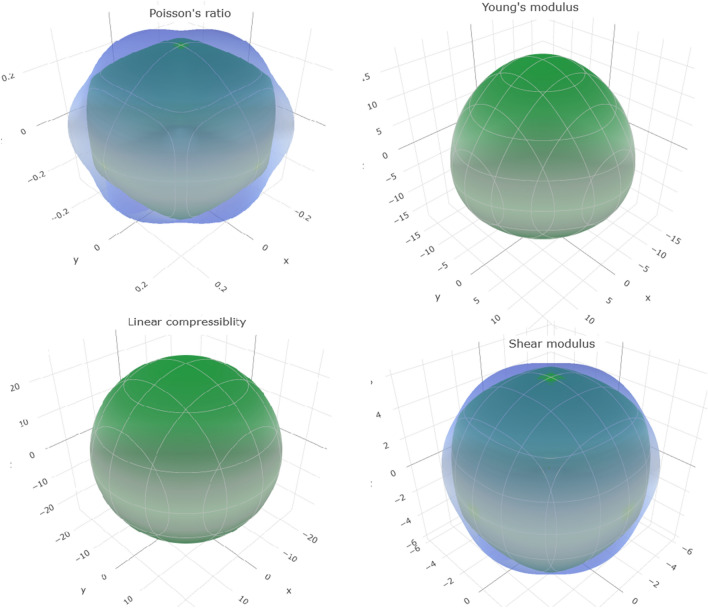
The bulk modulus calculated from the elastic constants is identical to that deduced from equation of state fitting P(V/V0). This makes our results as reliable. Figure 5 visualizes the dependence on pressure of K2XBr6(X = Se, Pt) elastic moduli. It is observed that the elastic values of GGA-PBESOL increase as a function of the applied pressure, from zero to 20 GPa. These compounds show weaker elastic constants, which explain their lower hardness. The bulk modulus, shear modulus, Young’s modulus, Poisson’s ratio, the universal anisotropy and BH/GH ratio for isotropic polycrystalline materials of K2XBr6(X = Pt, Se) using theVoigt-Reuss-Hill approximation19–21 are reported in Table 2. The values of the Poisson coefficient between 0.25 and 0.5 are associated with the interatomic forces of central types and covalent bonding character. The nature of the bonds in a compound is described by the factor σ, either ionic-covalent (0.16 ≤ σ ≤ 0.30) in K2PtBr6 (0.29) and metallic (σ ≥ 0.33) in K2SeBr6 (0.35). The Pugh’s criterion (BH/GH) and universal anisotropy indicate that K2XBr6(X = Pt, Se) are ductile and anisotropic. The extreme values of Young’s modulus, linear compressibility, shear modulus and Poisson’s ratio for K2XBr6(X = Pt, Se) are listed in Table 3. These values prove the isotropic linear compressibility and confirm the anisotropy of the other parameters and the anisotropy is more pronounced in K2SeBr6. We represent in Fig. 6 using ELATE software22 the effect of orientation on mechanical parameters for K2PtBr6. Young’s modulus, shear modulus and Poisson's ratio are anisotropic, while linear compressibility is isotropic.
Figure 5.
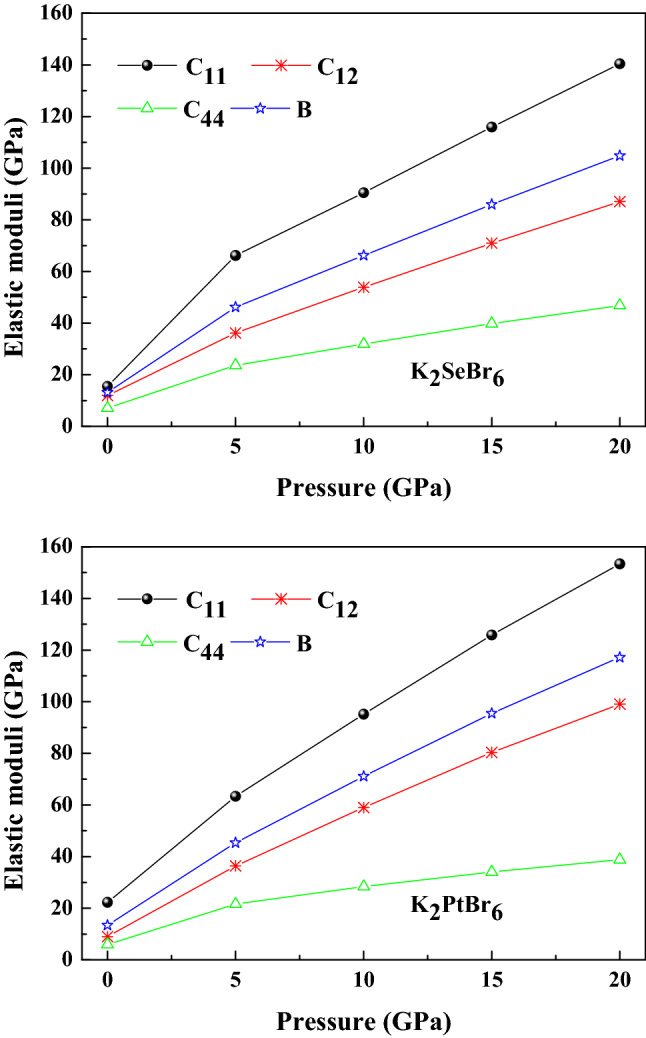
Elastic moduli of K2SeBr6 and K2PtBr6.
Table 2.
The extreme values of Young’s modulus (GPa), linear compressibility (GPa), shear modulus (GPa) and Poisson’s ratio for K2XBr6(X = Pt, Se).
| Material | Young’smodulus | Linear compressibility | Shear modulus | Poisson’s ratio | ||||
|---|---|---|---|---|---|---|---|---|
| Emin | Emax | βmin | βmax | Gmin | Gmax | σ min | σ max | |
| K2SeBr6 | 5.0801 | 18.014 | 25.374 | 25.374 | 1.7694 | 7.0839 | 0.22305 | 0.94375 |
| K2PtBr6 | 15.565 | 17.117 | 24.857 | 24.857 | 5.9567 | 6.6484 | 0.26729 | 0.33683 |
Table 3.
The bulk modulus, shear modulus, Young’s modulus, Poisson’s ratio, anisotropy factorand BH/GHratio for K2XBr6(X = Pt, Se).
| Material | B (GPa) | (GPa) | EH (GPa) |
σH | AU | BH/GH | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| BV | BR | BH | GV | GR | GH | |||||
| K2SeBr6 | 13.137 | 13.137 | 13.137 | 4.9581 | 3.2179 | 4.088 | 11.111 | 0.35903 | 2.70401 | 3.21 |
| K2PtBr6 | 13.41 | 13.41 | 13.41 | 6.2334 | 6.2154 | 6.2244 | 16.171 | 0.29902 | 0.0145 | 2.15 |
Figure 6.
The orientation effect on Poisson's ratio, Young's modulus, linear compressibility and shear modulus in K2PtBr6.
Band structure and states densities
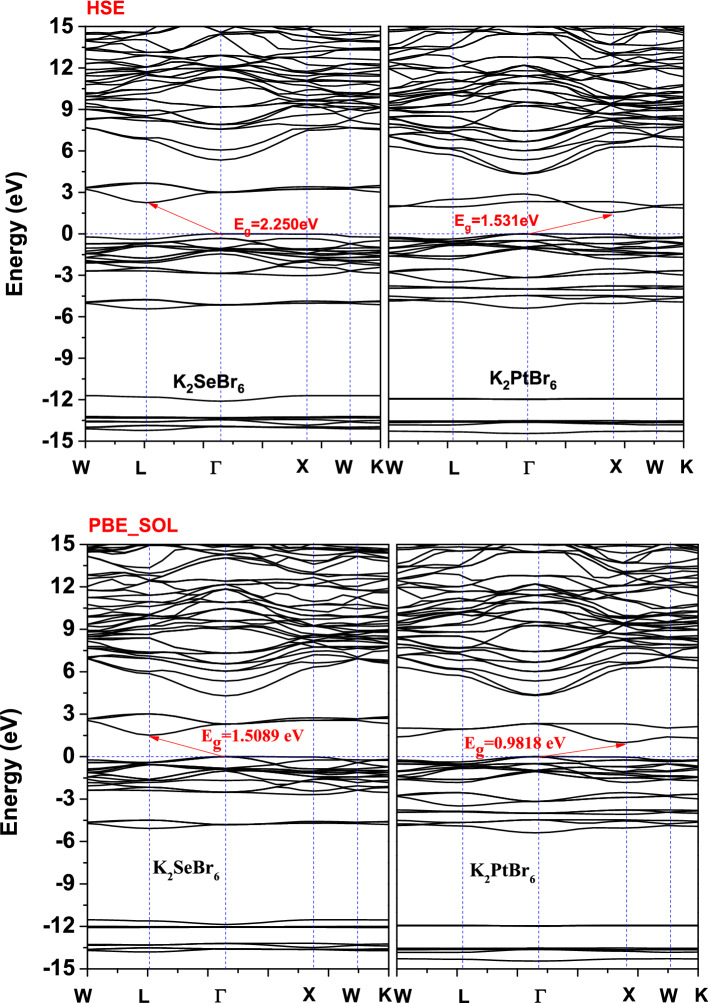
Understanding the band structure and estimating band gap of K2XBr6(X = Pt, Se), we use both GGA (PBE-SOL) and HSE hybrid functional as shown in Fig. 7. The calculations were conducted on K2XBr6(X = Pt, Se), by neglecting the presence of the K-state in the (Pt, Se) site. The electronic band structure of K2SeBr6 and k2PtBr6 were computed using the equilibrium lattice constant. The bottom of the conduction band is at Γ point for K2SeBr6 and k2PtBr6. The top of the valence band is at L and X points in K2SeBr6 and k2PtBr6 compounds, which indicate an indirect band gap Γ-L (Γ-X) of 1.5089 eV and 2.250 eV (0.9818 eV and 1.531 eV) for K2SeBr6 (k2PtBr6). No experimental and theoretical value are present in the literature, and then our results are predictions. Note that the HSE approximation gives a value close to the experimental one. We report the various band gaps at equilibrium lattice constant for K2SeBr6 and k2PtBr6 using GGA and HSE in Table 4. By varying the applied pressure between 0 and 20 GPa, the fundamental band gap as shown in Fig. 8 decreases. K2PtBr6 becomes metallic at a pressure of 15 GPa. We visualize the plots of PDOS and TDOS of K2SeBr6 and K2PtBr6 in Fig. 9. The top of valence band region is − 2.86 eV to EF (− 2 eV to EF) for K2SeBr6 (k2PtBr6). The electronic contribution in this region is due mainly to Br: p orbital in K2SeBr6 and K2PtBr6. The first conduction band of K2SeBr6 (K2PtBr6) starts at 1.68 eV (4 eV), then the transitions occur between Br: p and K: p sites. It is noted that the Pt site does not participate in the electronic contribution at the conduction and valence bands.
Figure 7.
Band structures of K2XBr6(X = Pt, Se) in zinc blend structure performed with GGA (PBE-SOL) and HSE hybrid.
Table 4.
The various band gaps at zero pressure for K2SeBr6 and K2PtBr6.
| Material | EΓ-Γ | EΓ-X | EΓ-L | EX-X | EL-L |
|---|---|---|---|---|---|
| K2PBr6 | |||||
| E0 (eV) | 2.323 | 0.98 | 1.88 | 1.14 | 2.31 |
| α × 10–2 (eV/GPa) | − 9.94 | ||||
| β × 10–3 (eV/GPa2) | 2.8 | ||||
| K2SeBr6 | |||||
| E0 (eV) | 2.29 | 2.56 | 1.5 | 2.58 | 1.902 |
| α × 10–2 (eV/GPa) | − 7.09 | ||||
| β × 10–3 (eV/GPa2) | 1.56 |
Figure 8.
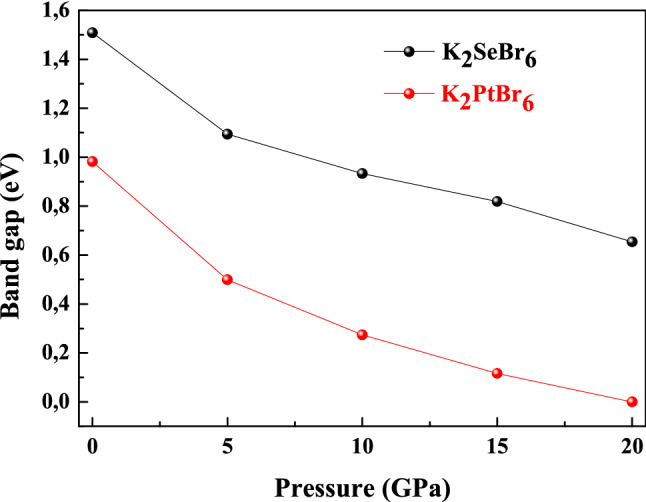
Fundamental band gap of K2XBr6(X = Pt, Se) with GGA (PBE-SOL) and HSE hybrid.
Figure 9.
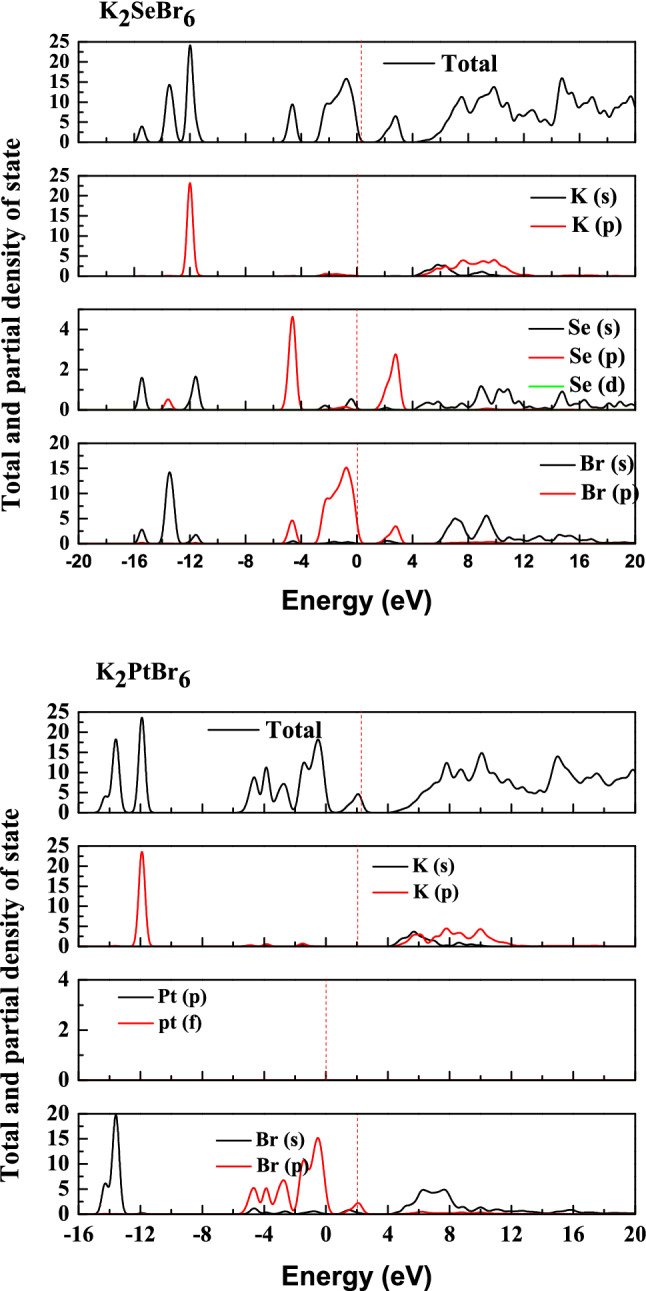
Total and partial density of states for K2SeBr6 and K2PtBr6.
Optical properties
The real dielectric constant is a measure of polarization, while the imaginary part is a measure of the dielectric losses. The complex dielectric function is the sum of real and imaginary parts.
The optical quantities such as reflectivity, absorption, loss function and refractive index depend on the structure of the material. These parameters cited above are isotropic in a material with cubic structure. The reflectivity of any material is calculated by dielectric function through the equation:
| 2 |
We display the plots of reflectivity, absorption and loss function as a function of wavelength for K2SeBr6 and K2PtBr6 in Fig. 10. The reflectivity is a measure of the ability of a material to reflect radiation. The reflectivity of K2SeBr6 and K2PtBr6 starts at wavelength around 60 nm and reaches several peaks of maxima (0.23) and minima (0.05) in the field of extreme ultraviolet light. In practice, the roughness, uniformity of thickness, inter diffusion, oxidation and thermal stability limit the reflectivity. We observe various absorption peaks in extreme ultraviolet light. These peaks are due to the electronic transitions from the top of the valence band to the bottom of the conduction band. The maximum absorption is between 234,720 cm-1 and 229,405 cm-1 at wavelength range 56 nm to 105 nm for K2SeBr6 and K2PtBr6. Indeed, K2SeBr6 and K2PtBr6 have a narrow gap and absorb extreme ultraviolet light and consequently, they are candidates in the fields of photo catalysis and photovoltaic. The loss function is calculated through the equation:
| 3 |
Figure 10.
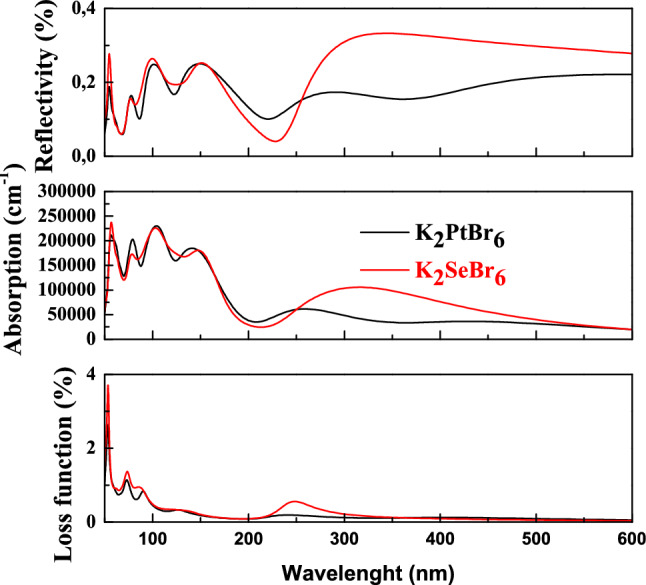
The reflectivity, absorption and loss function in K2SeBr6 and K2PtBr6.
The loss function demonstrates the existence of two major plasmonic processes, with intensity 3.7 and 1.35 located around 53.5 nm and 72.8 nm. There is no loss in the ultra violet and visible light domains. We present in Fig. 11 the refractive index of K2SeBr6 and K2PtBr6 as a function of energy. The static refractive index is 2.583 (2.407) for K2SeBr6 (K2PtBr6). It reaches a series of maxima 3.106 (2.678) and minima 0.383 (0.485) between 1.7 eV and 23 eV for K2SeBr6 (K2PtBr6). It is reported that an experimental refractive index 2.15 and 2.11 for K2SeBr6 and K2PtBr6 calculated by N. Wruk et al.1. The refractive index is given as:
| 4 |
Figure 11.
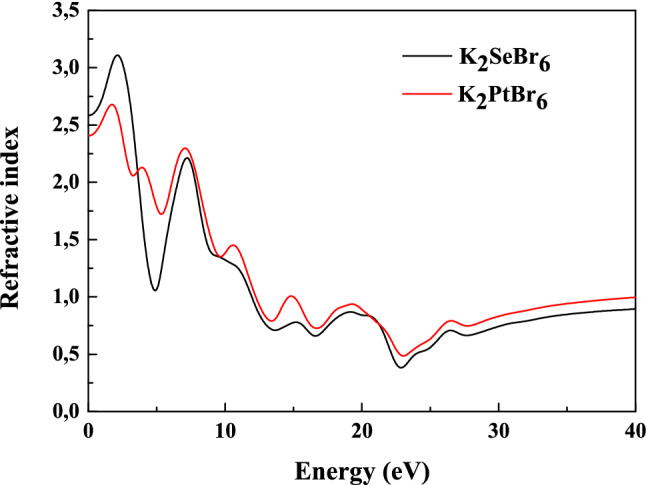
The refractive index in K2SeBr6 and K2PtBr6.
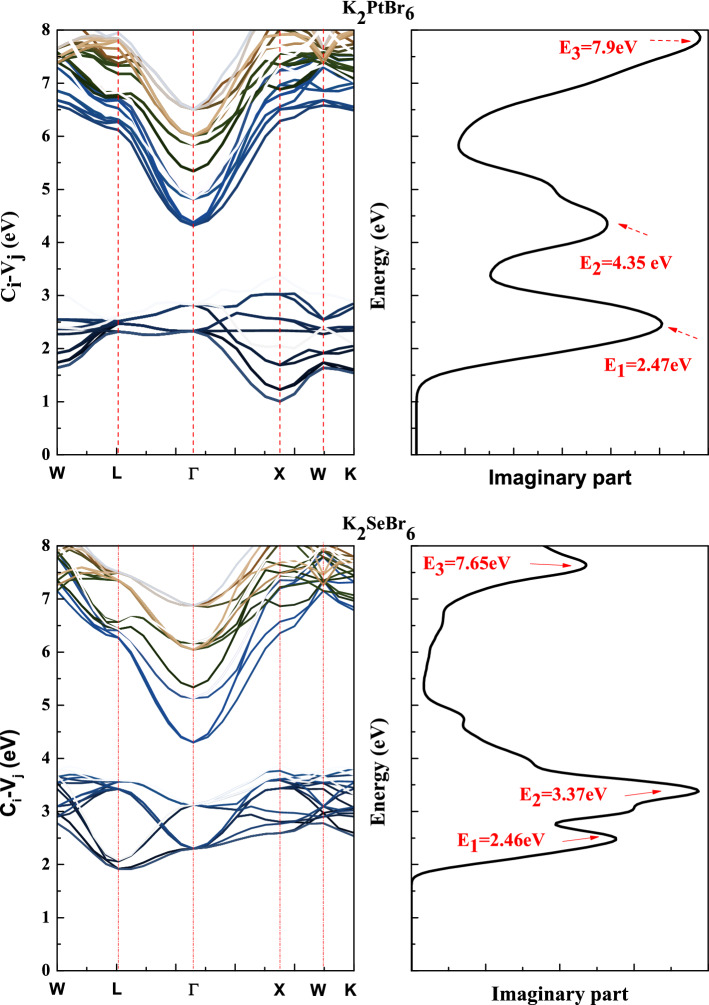
The refractive index is more important when photons move through the material and when bonds between atoms are covalent. The static refractive index enhanced with the expansion of the electronic cloud and the increase in density on the structure. The general trend is that the decrease in reflectivity results from the increase in absorption and the decrease in refractive index. The plots of imaginary part and for K2SeBr6(X = Se, Pt) are reported in Fig. 12 (right and left panel). The imaginary part and optical transitions are connected to the absorption coefficient. The main contribution to the optical transitions from six top valence bands to seven lower conduction bands for K2SeBr6(X = Se, Pt) are reported in Table 5. The isotropic optical parameters of K2SeBr6 and K2PtBr6 makes them as windows and lenses. The band gap range (1–2.25 eV) and absorption of extreme ultraviolet light make K2SeBr6 and K2PtBr6 as absorber materials.
Figure 12.
The imaginary part and transition energy in K2SeBr6 and K2PtBr6.
Table 5.
The main contribution to the optical transitions for K2SeBr6(X = Se, Pt).
| Peaks | W → L | L → Γ | Γ → X | X →W | W → K |
|---|---|---|---|---|---|
| K2PtBr6 | |||||
| E = 2.47 eV |
V5 → C2, V3 → C2 V4 →C1, V6 → C1 |
V5 → C1 | V3 → C2 | ||
| E = 4.35 eV |
V3 → C3, V1 → C4, V1 → C3 |
||||
| E = 7.9 eV |
V3 → C4, V4 → C4 V5 → C4 |
V6 → C7, V6 → C5 V5 → C7, V5 → C6 |
V6 → C7, V5 → C7 V6 → C6, V3 → C6 V3 → C5, V1 → C6 |
||
| E = 7.47 eV | V6 → C7 |
V6 → C7, V4 → C7 V3 → C7 |
|||
| K2SeBr6 | |||||
| E = 2.46 eV | V1 → C1, V6 → C1, V3 → C1 |
V5 → C1, V1 → C2 V3 → C3 |
V1 → C1 | ||
| E = 3.35 eV |
V3 → C3, V5 → C1, V1 → C3, V3 → C3 |
V5 → C2, V3 → C6, V3 → C4 |
V6 → C1 | V3 → C2 | |
| E = 7.65 eV |
V5 → C3, V6 → C6 V6 → C7, V4 → C6 V5 → C7 |
V6 → C7, V6 → C5 V5 → C7, V6 → C4 | V6 → C7, V3 → C7 V6 → C5, V2 → C7 V6 → C5 | V6 → C4, V5 → C2 | |
Conclusion
Employing a plane-wave pseudo-potential using the DFT framework, within the generalized gradient approximation, we studied the structural, mechanical and optoelectronic parameters of K2PtBr6 and K2SeBr6 hexahalometallate materials. The bulk modulus of K2SeBr6 and K2PtBr6 agrees well with experiment value where the error is 8% and 1.4%. The elastic constants of K2SeBr6 and K2PtBr6 are significantly smaller, then they are fairly soft and damage tolerant. An electronic study shows that K2PtBr6 is indirect band gap semiconductor and becomes metallic at a pressure of 15 GPa. The partial density of states indicates that the valence electrons are transferred from Br: p state to K: p site. The band gap size, optical absorption and reflectivity make K2SeBr6 and K2PtBr6 as candidate absorbers. The static refractive index increases with the expansion of the electronic cloud and the increase in density on the structure. The general trend is that the decrease in reflectivity results from the increase in absorption and the decrease in refractive index. There is no loss in the ultra violet and visible light domains. The compounds are poor reflector and can be used as an anti-reflection coating material.
Acknowledgements
We would like to thank Taif University Research Supporting Project number (TURSP-2020/63), Taif University, Taif, Saudi Arabia.
Author contributions
Manuscript title: Fundamental properties of hexahalometallate single crystals K2XBr6(X= Se, Pt): Ab initio study. All authors who have made substantial contributions to the work reported in the manuscript . the role of each author in the paper. • Conceptualization , Data curation, Formal analysis: a-c • Investigation, Methodology, Project administration, Resources: c - e • Software, Supervision, Validation, Visualization, Writing - original draft, Writing - review editing: c, f. This statement is approved by all the authors.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Wruk N, Pelzl J, Saundersn GA, Hailing T. J. Phys. Chem. Solids. 1985;46(11):1235–1242. doi: 10.1016/0022-3697(85)90125-8. [DOI] [Google Scholar]
- 2.Abriel W, White MA. J. Chem. Phys. 1990;93:8321. doi: 10.1063/1.459315. [DOI] [Google Scholar]
- 3.Eperon GE, Paterno GM, Suttonn RJ, Zampetti A, Haghighirad AA, Cacialli F, Snaith HJ. J. Mater. Chem. A. 2015;3(39):19688–19695. doi: 10.1039/C5TA06398A. [DOI] [Google Scholar]
- 4.Green MA, Ho-Baillie A, Snaith HJ. Nat. Photonics. 2014;8(7):506–514. doi: 10.1038/nphoton.2014.134. [DOI] [Google Scholar]
- 5.Kojima A, Teshima K, Shirai Y, Miyasaka T. J. Am. Chem. Soc. 2009;131:6050–6051. doi: 10.1021/ja809598r. [DOI] [PubMed] [Google Scholar]
- 6.Yin WJ, Shi T, Yan Y. Adv. Mater. 2014;26:4653–4658. doi: 10.1002/adma.201306281. [DOI] [PubMed] [Google Scholar]
- 7.Huang X, Paudel TR, Dowben PA, Dong S, Tsymbal EY. Phys. Rev. B. 2016;94:195309. doi: 10.1103/PhysRevB.94.195309. [DOI] [Google Scholar]
- 8.Clark SJ, Segall MD, Pickard CJ, Hasnip PJ, Probert MIJ, Payne KRMC. Zeitschrift Fur Kristallographie. 2005;220:567–570. doi: 10.1524/zkri.220.5.567.65075. [DOI] [Google Scholar]
- 9.Vanderbilt D. Phys. Rev. B. 1990;41:7892. doi: 10.1103/PhysRevB.41.7892. [DOI] [PubMed] [Google Scholar]
- 10.Perdew JP, Burke K, Ernzerhof M. Phys. Rev. Lett. 1996;77:3865. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 11.Monkhorst HJ, Pack JD. Phys. Rev. B. 1976;13:5188. doi: 10.1103/PhysRevB.13.5188. [DOI] [Google Scholar]
- 12.Fischer TH, Almlof J. J. Phys. Chem. 1992;96:9768. doi: 10.1021/j100203a036. [DOI] [Google Scholar]
- 13.Marti D, Dupertuis M-A, Deveaud B. General theory for the interference of two-photon and one-photon processes in semiconductor heterostructures. Ann. Phys. 2005;316:234. doi: 10.1016/j.aop.2004.09.015. [DOI] [Google Scholar]
- 14.Pickard CJ, Payne MC. Second-order kp perturbation theory with Vanderbilt pseudopotentials and plane waves. Phys. Rev. B. 2000;62:4383. doi: 10.1103/PhysRevB.62.4383. [DOI] [Google Scholar]
- 15.GajdoS M, Hummer K, Kresse G, Furthmüller J, Bechstedt F. Linear optical properties in the projector-augmented wave methodology. Phys. Rev. B. 2006;73:045112. doi: 10.1103/PhysRevB.73.045112. [DOI] [Google Scholar]
- 16.Magdalena Laurien, Oleg Rubel, Cond-mat. mtrl-sci (2021).
- 17.Read AJ, Needs RJ. Calculation of optical matrix elements with nonlocal pseudopotentials. Phys. Rev. B. 1991;44:13071. doi: 10.1103/PhysRevB.44.13071. [DOI] [PubMed] [Google Scholar]
- 18.Sinko GV, Smirnov NA. J. Phys.: Condens. Matter. 2002;14:6989. [Google Scholar]
- 19.Voigt W. Lehrbuch der Kristallphysik. Teubner; 1928. [Google Scholar]
- 20.Reuss A, Angew Z. Math. Mech. 1929;9:49–58. [Google Scholar]
- 21.Hill R. Proc. Phys. Soc. London A. 1952;65:349. doi: 10.1088/0370-1298/65/5/307. [DOI] [Google Scholar]
- 22.Gaillac R, Pullumbi P, Coudert F-X. ELATE: an open-source online application for adnalysis and visualization of elastic tensors. J. Phys. Condens. Matter. 2016;28:275201. doi: 10.1088/0953-8984/28/27/275201. [DOI] [PubMed] [Google Scholar]