Genetic architecture of 11 major psychiatric disorders at biobehavioral, functional genomic, and molecular genetic levels of analysis

Abstract

We interrogate the joint genetic architecture of 11 major psychiatric disorders at biobehavioral, functional genomic, and molecular genetic levels of analysis. We identify four broad factors (Neurodevelopmental, Compulsive, Psychotic, and Internalizing) that underlie genetic correlations among the disorders, and test whether these factors adequately explain their genetic correlations with biobehavioral traits. We introduce Stratified Genomic Structural Equation Modeling, which we use to identify gene sets that disproportionately contribute to genetic risk sharing. This includes protein-truncating variant–intolerant genes expressed in excitatory and GABAergic brain cells that are enriched for genetic overlap across disorders with psychotic features. Multivariate association analyses detect 152 (20 novel) independent loci that act on the individual factors and identify nine loci that act heterogeneously across disorders within a factor. Despite moderate-to-high genetic correlations across all 11 disorders, we find little utility of a single dimension of genetic risk across psychiatric disorders either at the level of biobehavioral correlates or at the level of individual variants.

Psychiatric disorders aggregate both within individuals and within families. Offspring of parents with psychiatric illness are at higher risk for developing a broad range of psychiatric disorders, not just the specific parental disorder^1-3. Moreover, approximately half of individuals with a psychiatric illness will concurrently meet criteria for a second disorder⁴. Comorbidity is the norm, rather than the exception. Factor analyses that have modeled these comorbidity patterns consistently identify a transdiagnostic p-factor representing general risk across psychiatric disorders, along with several intermediate factors representing more specific clusters of psychiatric risk (e.g., psychotic disorders, mood disorders)^5-7. Modern genomics has built on these findings to begin to elucidate the genetic basis for shared risk across disorders^8,9, with new statistical tools paired with genome-wide association study (GWAS) data being used to identify variants associated with multiple disorders^10,11. Most recently, Lee et al.¹² identified three major dimensions of genetic risk sharing (Neurodevelopmental, Compulsive and Psychotic) across eight psychiatric disorders, raising the possibility that key mechanisms of individual disorder risk may operate through these more general factors. Importantly, however, neither phenotypic comorbidity nor genetic correlations among disorders are by themselves sufficient to establish the etiological, diagnostic, or therapeutic utility of the identified factors.

Here we apply Genomic Structural Equation Modelling (Genomic SEM)¹³ to GWAS data to examine the genetic architecture of 11 major psychiatric disorders (average total sample size per disorder = 156,771 participants; range = 9,725–802,939) across biobehavioral, functional genomic, and molecular genetic levels of analysis. Genomic SEM is able to investigate the multivariate genetic architecture across disorders that were not measured in the same sample, thereby offering novel insights across the diagnostic spectrum. We begin by estimating several potential genomic factor models and identify four broad factors that index shared genetic liability within and across constellations of disorders. We then evaluate the utility of these factors using a multi-step approach. First, we test the extent to which the factors adequately explain the patterns of genetic correlation between psychiatric disorders and a wide range of external biobehavioral traits. Second, we introduce Stratified Genomic SEM, which we apply to identify gene sets and categories (e.g., protein-truncating variant–intolerant genes, low minor allele frequency (MAF) SNPs) for which genetic risk sharing across subclusters of disorders, as indexed by each of the factors, and genetic differentiation, as indexed by disorder-specific residuals, is enriched. Finally, we capitalize on Genomic SEM for multivariate GWAS to identify loci that confer risk to multiple disorders via the factors, along with loci that operate heterogeneously across disorders within a given factor. Collectively, these results offer key insights into the shared and disorder-specific mechanisms of genetic risk for psychiatric disease.

Results

Genomic factor analysis across 11 psychiatric traits.

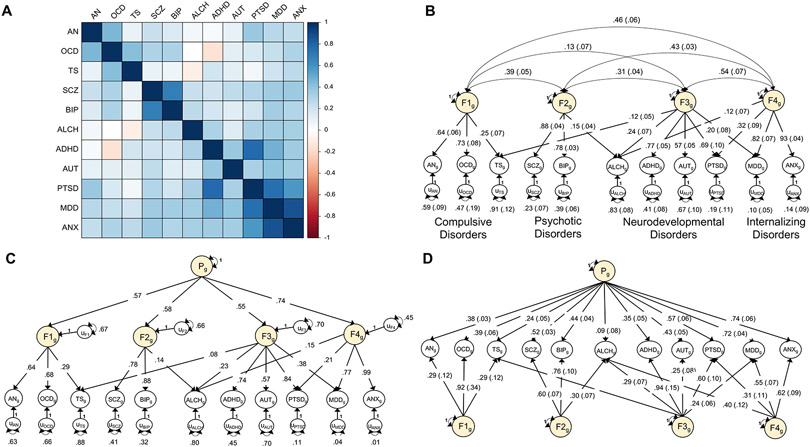
We curated the most recent European ancestry GWAS summary data for 11 major psychiatric disorders: attention-deficit/hyperactivity disorder (ADHD)¹⁴, problematic alcohol use (ALCH)¹⁵, anorexia nervosa (AN)¹⁶, autism spectrum disorder (AUT)¹⁷, anxiety disorders (ANX)^18,19, bipolar disorder (BIP)²⁰, major depressive disorder (MDD)^21,22, obsessive compulsive disorder (OCD)²³, post-traumatic stress disorder (PTSD)^24,25, schizophrenia (SCZ)²⁶, and Tourette syndrome (TS)²⁷ (Table 1 and Supplementary Table 1). A heatmap of genetic correlations estimated using LD Score regression (LDSC)⁸ indicates pervasive overlap across the 11 disorders, with more pronounced clustering observed among certain constellations of disorders (Fig. 1a and Supplementary Table 2).

Table 1 ∣.

Contributing univariate GWAS

Contributing univariate GWAS	Population prevalence	Cases / Controls	SNP- heritability (SE)	Mean χ2(1)	LDSC univariate intercept	Independent hits (LD with Q hits)	LD with factor hits (LD with Q hits)	Unique from factor hits (LD with Q hits)
AN	.009	16,992 / 55,525	.138 (.010)	1.297	1.020	8 (0)	1 (0)	7 (0)
OCD	.02	2,688 / 7,037	.265 (.019)	1.062	0.993	0 (0)	0 (0)	0 (0)
TS	.007	4,819 / 9,488	.207 (.026)	1.123	1.014	1 (0)	0 (0)	1 (0)
SCZ	.01	53,386 / 77,258	.208 (.005)	2.118	1.077	179 (2)	89 (2)	90 (0)
BIP	.01	20,352 / 31,358	.202 (.009)	1.396	1.020	16 (0)	9 (0)	7 (0)
ALCH	.12	176,024	.060 (.040)	1.199	0.994	6 (3)	2 (1)	4 (2)
ADHD	.087	24,116 / 91,557	.250 (.025)	1.221	0.969	6 (0)	3 (0)	3 (0)
AUT	.02	18,382 / 27,969	.133 (.011)	1.198	1.008	3 (1)	0 (0)	3 (1)
PTSD	.068	12,255 / 26,338	.264 (.008)	1.119	0.991	0 (0)	0 (0)	0 (0)
MDD	.21	249,227 / 553,712	.087 (.014)	1.957	1.024	109 (0)	43 (0)	66 (0)
ANX	.311	30,993 / 69,883	.294 (.003)	1.194	0.998	2 (0)	2 (0)	0 (0)

Independent hits were defined using a pruning window of 250 kb and r² < 0.1. Hits are considered in LD if their LD was r² > 0.10 or within a 250-kb window of one another. Reported population prevalences were used for the liability scale conversion. We note that, for the five traits (ALCH, ADHD, PTSD, MDD, and ANX) for which the finalized univariate summary statistics were produced by applying Genomic SEM to meta-analyze two summary statistics of the same or similar phenotypes, the liability scale conversion was used for the univariate meta-analysis only. The meta-analyzed outcome for these five traits was subsequently treated as continuous in all downstream analyses as these then reflected summary statistics for a latent factor defined by the two-indicators in the prior, meta-analytic stage. Values in parentheses indicate whether any of the hits were in LD with hits for factor-specific Q_SNP hits from the respective model. To facilitate comparison across mean χ² values reported in each row, all χ² statistics with df > 1 were converted to were converted to χ²(1) statistics before taking their means. For all GWAS analyses, we correct for multiple testing by employing the field standard significance threshold of P < 5 × 10⁻⁸.

Figure 1 ∣. Multivariate genetic architecture of 11 psychiatric disorders.

a, Genetic correlations estimated using LDSC. b, Standardized results for the correlated factors. c, Standardized results from the hierarchical factor model. d, Standardized results from the bifactor model. The genetic components of disorders and common genetic factors of disorders are inferred variables that are represented as circles. Regression relationships between variables are depicted as one-headed arrows pointing from the independent variables to the dependent variables. Covariance relationships between variables are represented as two-headed arrows linking the variables. (Residual) variances of a variable are represented as a two-headed arrow connecting the variable to itself; for simplicity, residuals of the indicators are not depicted for the bifactor model. ADHD, attention-deficit/hyperactivity disorder; OCD, obsessive-compulsive disorder; TS, Tourette syndrome; PTSD, post-traumatic stress disorder; AN, anorexia nervosa; AUT, autism spectrum disorder; ALCH, problematic alcohol use; ANX, anxiety; MDD, major depressive disorder; BIP, bipolar disorder; SCZ, schizophrenia.

We formally modeled this genetic covariance structure in Genomic SEM¹³, finding that a four correlated factors model fit the data well (Fig. 1b). Factor 1 consists of disorders characterized largely by compulsive behaviors (AN, OCD, TS). Factor 2 is characterized by disorders that may have psychotic features (SCZ, BIP). Factor 3 is characterized primarily by childhood-onset neurodevelopmental disorders (ADHD, AUT). Factor 4 is characterized by internalizing disorders (ANX, MDD). In line with prior evidence for a higher-order transdiagnostic “p-factor”^5-7, we find that a hierarchical model also fit the genetic covariance structure well (Fig. 1c). We retained these two models—the four correlated factors model and the hierarchical factor model—to examine the utility of the genomic factors at biobehavioral, functional genomic, and molecular levels of analysis. We discuss a post-hoc bifactor model (Fig. 1d) at the end of the Results section.

Psychiatric genetics factors and biobehavioral traits.

We examined patterns of correlations across the psychiatric factors and 49 biobehavioral traits²⁸, 101 metrics of brain morphology²⁹, and circadian activity across 24 hours³⁰. Results for brain morphology are presented in Supplementary Figures 3 and 4 and Supplementary Table 4, as none of these associations were significant at a Bonferroni-corrected threshold for 174 tests (P < 2.87 × 10⁻⁴). To evaluate the extent to which external traits operated through a given factor, we calculated χ²difference tests comparing a model in which the trait predicted the factor only to one in which it predicted the individual disorders of a given factor (or the first-order factors in the case of analyses using the p-factor model; Supplementary Fig. 5). We term the χ²difference across these two models the Q_trait heterogeneity index (Fig. 2). A significant Q_trait index indicates that the pattern of associations between the individual disorders and the external trait is not well accounted for by the factor.

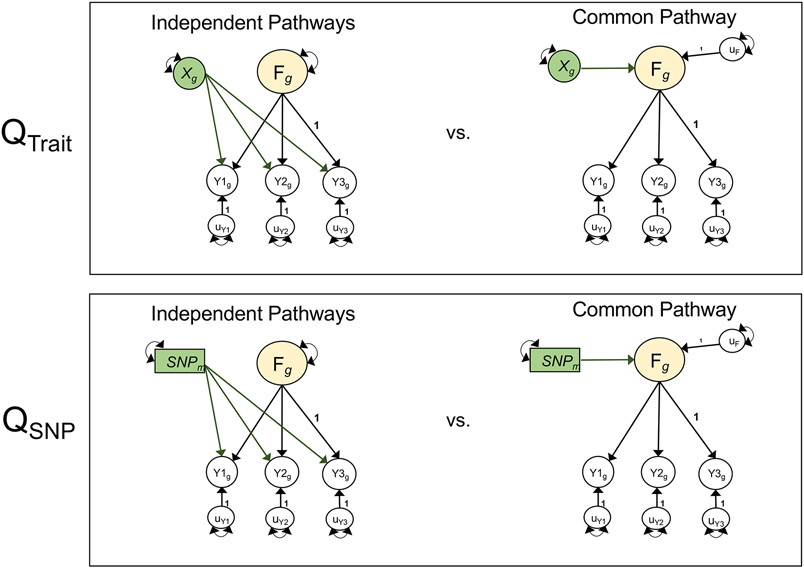
Figure 2 ∣. Model comparisons for producing Q metrics.

Unstandardized path diagrams for common pathway (right) and independent pathways (left) models used to compute the Genomic SEM heterogeneity statistics for associations with external traits (Q_Trait, top) and individual SNPs (Q_SNP, bottom). In this example, F is a common genetic factor of the genetic components of three GWAS phenotypes (Y₁-Y₃). Observed variables are represented as squares, and latent variables are represented as circles. The genetic component of each phenotype is represented with a circle as the genetic component is a latent variable that is not directly measured, but is inferred using LDSC. SNPs are directly measured, and are therefore represented as squares. Single-headed arrows are regression relations, and double-headed arrows are variances. Paths labeled 1 are fixed to 1 for model identification purposes. All unlabeled paths represent freely estimated model parameters. Q represents the decrement in model fit of the common pathway model relative to the more restrictive independent pathways model. Q is a χ² distributed test statistic with k − 1 degrees of freedom, representing the difference between the k SNP-phenotype or Trait-phenotype b coefficients in the independent pathways model and the 1 SNP-factor or Trait-factor b coefficient in the common pathway model. Q is estimated here using a χ² difference test across the common and independent pathways models; this is statistically equivalent to the 2-step procedure outlined in the original Genomic SEM¹³ publication for calculating Q_SNP. Q_Trait indexes whether the pattern of genetic associations between the genetic component of an external trait (depicted as X_g) and the individual disorders is well accounted for by a given factor. Q_SNP indexes whether the associations between an individaul SNP (depicted as SNP_m) and the individual dissorders is well accounted for by the factor. For simplicity, we depict a stylized representation containing only one factor and three disorders. The full models used to derive Q_Trait and Q_SNP for the empirical analyses reported in this paper are presented in Supplementary Figures 5 and 38.

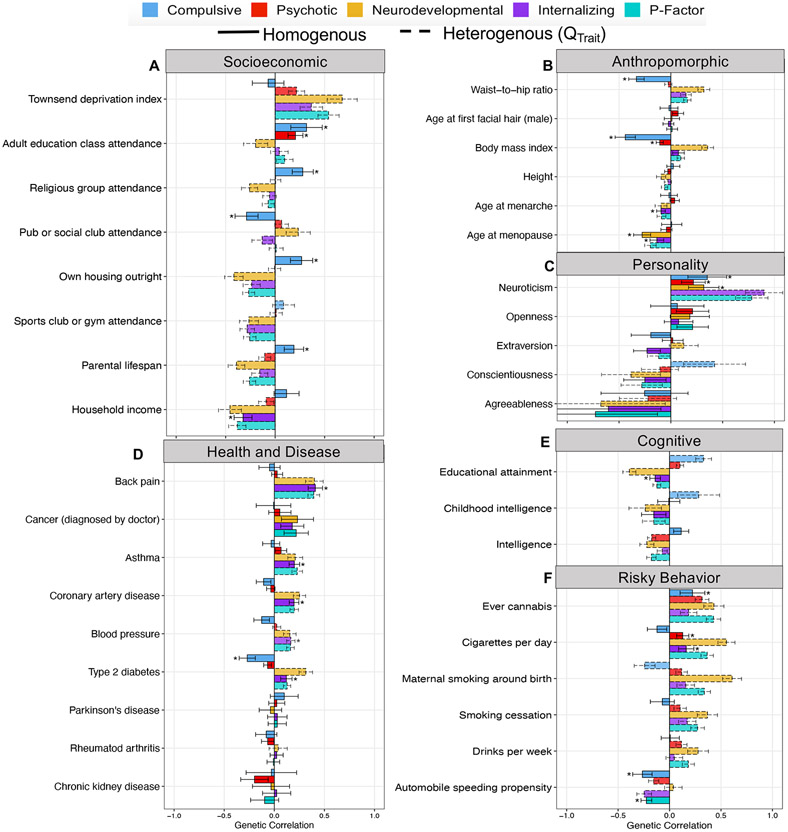
Using a Bonferroni correction for 174 tests, 7/49 correlations with biobehavioral traits were significant for Q_trait for the Compulsive factor, 18/49 for the Psychotic factor, 39/49 for the Neurodevelopmental factor, 17/49 for the Internalizing factor, and 38/49 for the p-factor (Fig. 3 and Supplementary Table 5). Excluding genetic correlations significant for Q_trait, and using the same Bonferroni correction, 17 genetic correlations were significant for the Compulsive factor, 12 for the Psychotic factor, five for the Neurodevelopmental factor, 20 for the Internalizing factor, and three for the p-factor. We provide a more detailed assessment of significant correlations in the Supplementary Note.

Figure 3 ∣. Genetic correlations with complex traits across psychiatric factors.

a-f, Panels depict point estimates for genetic correlations with complex traits of interest for the four psychiatric factors from the correlated factors model and the second-order, p-factor from the hierarchical model. Genetic correlations are shown for socioeconomic (a), anthropromorphic (b), personality (c), health and disease (d), cognitive (e), and risky behavior outcomes (f). Bars depicted with a dashed outline were significant at a Bonferroni-corrected threshold for model comparisons indicating heterogeneity across the factor indicators in their genetic correlations with the outside trait. Error bars are +/− 1.96 SE. Bars depicted with an asterisk above produced a genetic correlation that was significant at a Bonferroni-corrected threshold and were not significantly heterogeneous. The total effective sample size for the factors was: Compulsive factor (n = 19,108), Psychotic factor (n = 87,138), Neurodevelopmental factor (n = 55,932), Internalizing factor (n = 455,340), and hierarchical p-factor (n = 667,343). Sample sizes for the complex traits are reported in Supplementary Table 5.

Atypical patterns of physical movement throughout the 24-hour cycle may reflect disturbances in basic homeostatic processes that confer transdiagnostic psychiatric risk³¹. Using accelerometer data from UK Biobank³⁰, we examined genetic correlations between the individual psychiatric traits and factors and physical movement across a 24-hour period (Fig. 4 and Supplementary Table 6). One correlation was significant for Q_trait for the Compulsive factor, two for the Psychotic factor, 12 for the Neurodevelopmental factor, seven for the Internalizing factor, and 18 for the p-factor. Excluding significant Q_trait correlations, eight correlations were significant for the Compulsive factor, four for the Psychotic factor, one for the Neurodevelopmental factor, six for the Internalizing factor, and two for the p-factor.

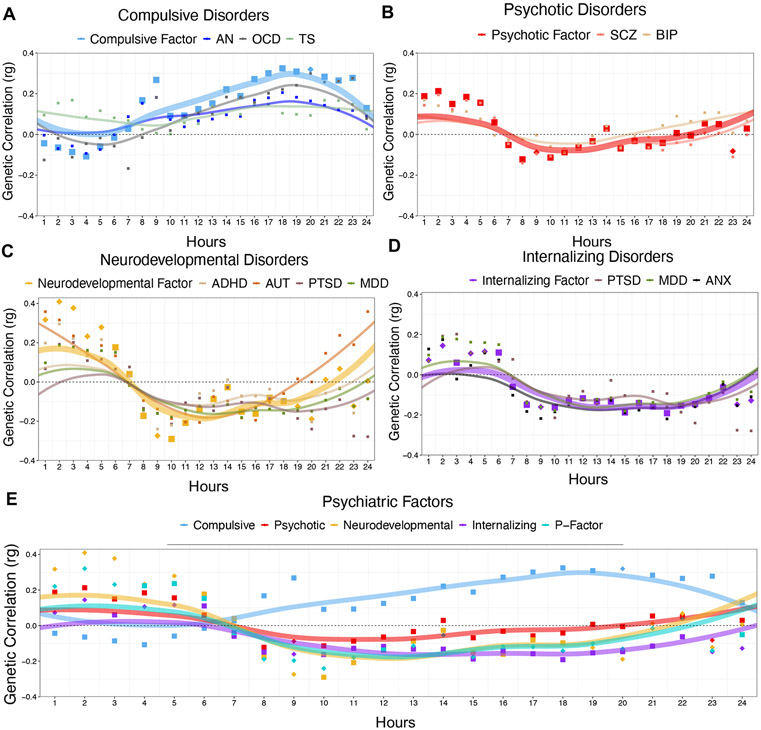
Figure 4 ∣. Genetic correlations with accelerometer data across psychiatric disorders and factors.

a-e, Panels depicts genetic correlations between accelerometer-based average total hourly movement within the 24-hour day beginning at midnight (n ~ 95,000) and each psychiatric disorder, along with the respective psychiatric factor, for the compulsive disorders (a), psychotic disorders (b), neurodevelopmental disorders (c), internalizing disorders (d), and psychiatric factors (e). Across all panels, the psychiatric factors are depicted with larger points and lines. For the psychiatric factors, points depicted as diamonds were significant at a Bonferroni-corrected threshold for model comparisons indicating heterogeneity across the factor indicators in their genetic correlations with that particular time point. As it loaded on three different factors (see Fig. 1), ALCH was not as assigned to a panel above. Lines represent loess regression lines estimated in ggplot2.

Compulsive disorders were positively genetically correlated with physical movement throughout the daylight hours and into the evening. Psychotic disorders were positively genetically correlated with excess movement in the early morning hours. The pattern of associations deviated from the factor structure largely in the daylight and evening hours, with larger positive genetic correlations observed for BIP. Genetic correlations with movement throughout the day were heterogeneous across disorders that load on the Neurodevelopmental disorders factor. Internalizing disorders were negatively genetically correlated with movement throughout the daylight and earlier evening hours.

Stratified Genomic SEM.

Overview and validation via simulation.

We developed Stratified Genomic SEM to allow the basic principles of Genomic SEM to be applied to genetic covariance matrices estimated within different gene sets and categories (Methods). These gene sets and categories, collectively referred to as annotations, can be constructed based on a variety of sources, such as collateral gene expression data obtained from single-cell RNA sequencing. Such an analysis goes beyond methods such as Stratified LDSC (S-LDSC)³² that estimate enrichment of heritability for particular traits within functional annotations. Rather, Stratified Genomic SEM utilizes a multivariate framework to ask whether shared and unique genetic signal across a set of traits is enriched within particular annotations. Enrichment is defined as the ratio of the proportion of genome-wide risk sharing indexed by the annotation to that annotation’s size as a proportion of the genome (Methods). The null, corresponding to no enrichment, is a ratio of 1.0, with values above 1.0 indicating enriched signal within a functional annotation.

In order to validate the key statistical properties of Stratified Genomic SEM, we began by simulating genetically correlated phenotypes that were enriched in six annotations. We then show that our multivariate extension of S-LDSC produces accurate estimates of stratified genetic covariance along with unbiased standard errors (Supplementary Figs. 8-10 and Supplementary Tables 7-9). Finally, we demonstrate that these stratified genetic covariance matrices can be used as input to Stratified Genomic SEM to produce unbiased factor loadings and unbiased standard errors (Supplementary Fig. 11).

Genetic enrichment of psychiatric factors.

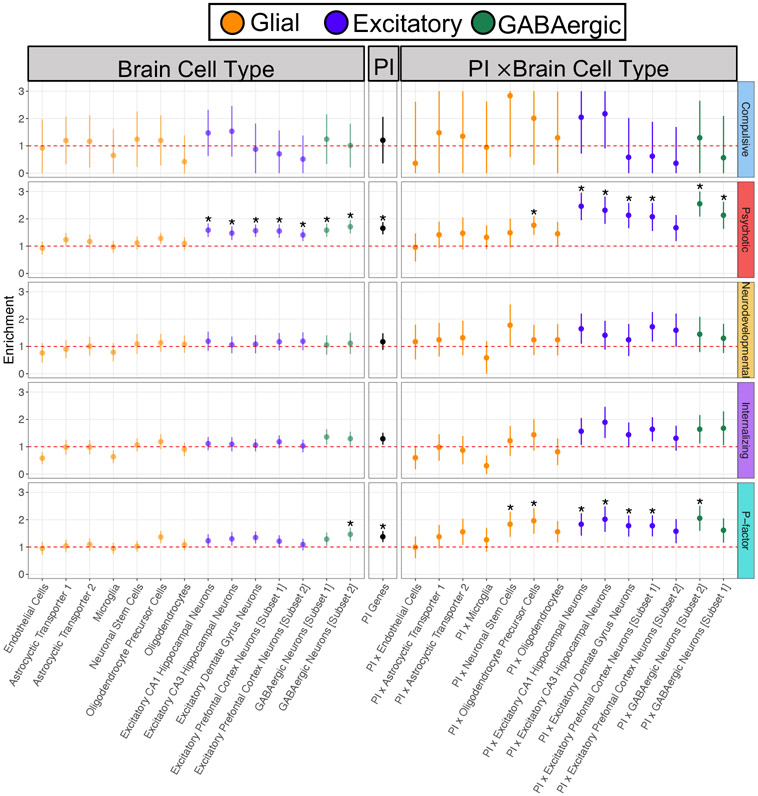
We fit Stratified Genomic SEM models to examine whether the degree of risk sharing and differentiation is enriched across disorders. In total, enrichment analyses were based on 168 binary annotations. This included 29 annotations created to examine the interaction between expression patterns for protein-truncating variant (PTV)–intolerant (PI) genes (obtained from the Genome Aggregation Database; gnomAD³³) and human brain cells in the hippocampus and prefrontal cortex (obtained from GTEx³⁴). Using a Bonferroni correction for 168 tests, we identify 40 annotations significantly enriched for the Psychotic disorders factor, one annotation (conserved primate) for the Neurodevelopmental disorders factor, four annotations for the Internalizing disorders factor, and 38 annotations for the p-factor (Supplementary Table 10 and Supplementary Figs. 12-18).

PI results revealed that these annotations were particularly enriched for the Psychotic disorders factor, with 5 out of the 10 most significantly enriched gene sets falling in this category (Fig. 5). The most enriched annotations for the Neurodevelopmental and Internalizing disorders factors were fetal female brain DNase and fetal male brain H3K4me1, respectively. For specific tissues, brain regions were generally enriched, as was also observed for other complex traits³⁵, but were most enriched for the Psychotic disorders factor. Genetic sharing across disorders, as estimated by a higher order p-factor, was enriched in conserved annotations, and enrichment increased from low to high MAF alleles (Supplementary Figs. 19-24).

Figure 5 ∣. Genetic enrichment of factors for brain cell, PI, and PI × brain cell annotations.

Figure depicts enrichment of the four factors from correlated factors model and the second-order, p-factor from the hierarchical factor model for the brain cell genes, protein-truncating variant (PTV)–intolerant (PI) genes, and PI × brain cell gene annotations. Enrichment is indexed by the ratio of the proportion of genome-wide relative risk sharing indexed by the annotation to that annotation’s size as a proportion of the genome. The red dashed line reflects the null ratio of 1.0, corresponding to no enrichment. Ratios greater than 1.0 indicate enrichment of shared signal, whereas ratios less than 1.0 indicate depletion of shared signal. Error bars depict 95% confidence intervals. Points depicted with an asterisk were significantly enriched at a Bonferroni-corrected threshold. To maintain equal scaling purposes across all panels, error bars are capped at 3 and 0 for the Compulsive disorders factor; no annotations were significant for this factor.

We went on to examine enrichment of residual (i.e., unique) variance for the individual disorders in the correlated factors model and the residuals of the psychiatric factors in the hierarchical model (Supplementary Table 10). Results for the individual disorders revealed 17 significant residual enrichment estimates at a Bonferroni-corrected threshold. This included 13 significant estimates for various disorders within evolutionarily conserved annotations (e.g., conserved primate), along with significant enrichment unique to MDD for coding regions and the PI × excitatory dentate gyrus neurons annotation.

Multivariate GWAS.

Simulations.

We conducted a series of simulations to further validate the calibration of Genomic SEM for multivariate GWAS in the specific context of the analyses presented here. For each simulation, we used Genomic SEM to estimate factor-specific SNP effects and factor-specific indices of heterogeneity, as indexed by Q_SNP¹³. Q_SNP indexes violation of the null hypothesis that the SNP acts on the individual disorders entirely via the factor on which they load (Fig. 2; see Methods). As expected, simulation results revealed that the power to detect multivariate SNP effects and Q_SNP decreased and increased, respectively, as population SNP effects increasingly deviated from those implied by the factor structure (Supplementary Figs. 25-28 and Supplementary Table 11). These simulations additionally illustrated that that SNP effects on factors, as estimated with Genomic SEM, are not simply the reflection of the most high-powered univariate GWAS that defines the factor, that there is null signal when the population of SNP effects is set to 0, and that power for Q_SNP is particularly high when there are directionally discordant SNP effects across the factor indicators.

We present additional results benchmarking Genomic SEM against existing methods— Multi-trait Analysis of GWAS (MTAG)³⁶, Model Averaging Genome-wide Association Meta-analysis (MA-GWAMA), and N-weighted Multivariate GWAMA (N-GWAMA)³⁷—in the Supplementary Note. In addition, we examined the performance of multivariate GWAS in Genomic SEM when specified as an unstructured model that computes an omnibus index of association across all 11 disorders. Unstructured model results were obtained by comparing a maximally complex model in which the SNP is allowed to have direct regression relations with each of the 11 disorders against a null model in which the SNP is associated with none of the disorders. This is in contrast to the multivariate GWAS specified as a factor model discussed initially that estimates SNP effects on the factors, as this defines a structure of the relationship between the SNP and the 11 disorders. Briefly, we find the unstructured model is particularly well suited when the aim is to identify an exhaustive set of SNPs relevant to psychiatric risk, but does little to elucidate the specific patterning of associations. In contrast, the factor model allows us to systematically probe the genetic underpinnings of convergence and divergence across clusters of psychiatric disorders.

Empirical results.

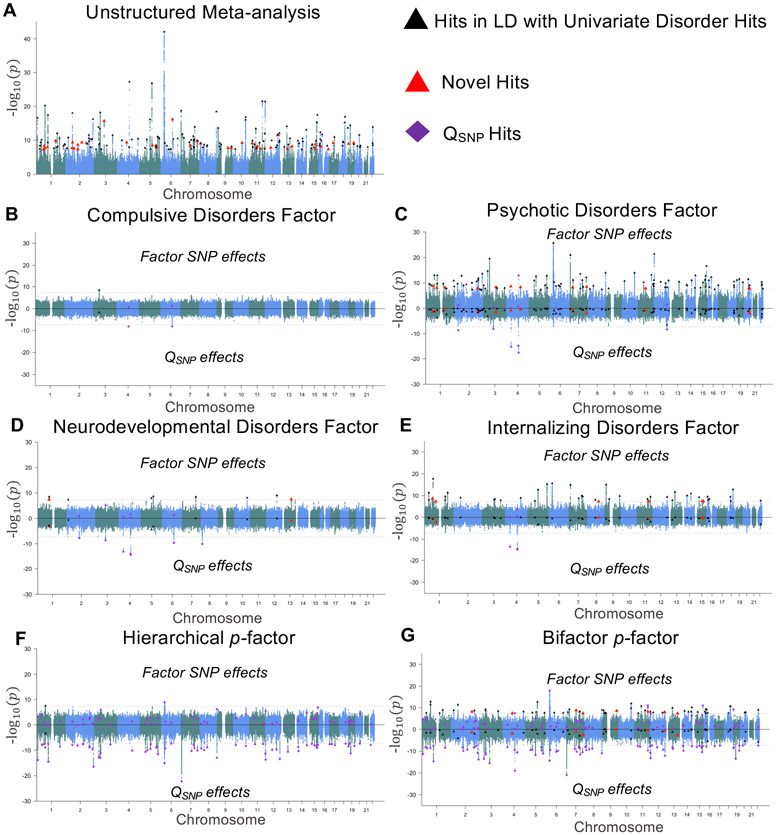
Using the 4,775,763 SNPs present across the 11 disorders, the unstructured multivariate GWAS identified 184 associated loci at a conventional genome-wide significance threshold (P < 5 × 10⁻⁸)³⁸, 39 of which were not in LD with any of the univariate associations (see Fig. 6 for Miami plots, Supplementary Fig. 32 for QQ-plots, and Supplementary Table 12 for individual hits).

Figure 6 ∣. Miami plots for psychiatric factors.

a, Results from an unstructured meta-analysis of the 11 psychiatric traits. b-e, Results from the correlated factors model for the Compulsive disorders factor (Factor 1; b), Psychotic disorders factor (Factor 2; c), Neurodevelopmental disorders factor (Factor 3; d), and Internalizing disorders factor (Factor 4; e). f, Results of the SNP effect on the second-order p-factor from the hierarchical model. g, Results from a model in which the SNP predicted the p-factor from a bifactor model. The top half of the plots depict the −log₁₀(P) values for SNP effects on the factor; the bottom half depicts the log₁₀(P) values for the factor-specific Q_SNP effects. As the omnibus meta-analysis does not impose a structure on the patterning of SNP-disorder associations, it does not have a Q_SNP statistic. The gray dashed line marks the threshold for genome-wide significance (P < 5 × 10⁻⁸). Black triangles denote independent factor hits that were in LD with hits for one of the univariate indicators and were not in LD with factor-specific Q_SNP hits. Large red triangles denote novel loci that were not in LD with any of the univariate GWAS or factor-specific Q_SNP hits. Purple diamonds denote Q_SNP hits.

We went on to perform the structured multivariate GWAS analyses using two factor models: the correlated factors model (with Factors 1-4 as the GWAS target) and the hierarchical factor model (with the higher order p-factor as the GWAS target; Fig. 6, Supplementary Fig. 32 for QQ-plots, and Supplementary Fig. 33 for bar plots of individual variants estimated as genome-wide significant). We also estimate Q_SNP specific to each factor used as a GWAS target (see Methods for details).

We identified one hit for the Compulsive disorders factor, a locus also associated with AN¹⁶ (Supplementary Tables 14 and 15). We identified two loci for the Compulsive disorders factor-specific Q_SNP statistic (Supplementary Table 16), including a locus (rs1906252) with strong opposing effects on AN and TS. We identified 108 hits for the Psychotic disorders factor, 96 of which were in LD with previously reported associations for BIP and SCZ (Supplementary Table 17), and 12 of which were novel relative to the contributing univariate GWASs. The Psychotic disorders factor-specific Q_SNP statistic revealed six hits, three of which were in LD with hits for ALCH (Supplementary Table 19), including a locus in the well-described Alcohol Dehydrogenase 1B (ADH1B) gene that was significant for factor-specific Q_SNP for all four factors.

We identified nine hits for the Neurodevelopmental disorders factor (Supplementary Table 20), three of which were in LD with hits for ADHD or MDD, and two of which were novel relative to the contributing univariate GWASs. There were seven hits for the Neurodevelopmental Q_SNP statistic, many of which appeared to be specific to AUT (Supplementary Table 22). We identified 44 independent hits for the Internalizing disorders factor, six of which were unique of hits from the contributing univariate GWASs (Supplementary Table 23). Three loci were identified for the Internalizing factor-specific Q_SNP statistic, all three of which were in LD with hits for ALCH (Supplementary Table 25). We note that the discrepancy in the number of univariate MDD hits (109) relative to the number of Internalizing factor hits (44) can be attributed to a combination of signal specific to MDD and splitting the MDD signal across two factors (Supplementary Fig. 38).

Nine hits from the correlated factors model were in LD across the factors, and one hit was in LD with a Q_SNP hit. In total, our structured GWAS discovered 152 independent loci that are likely to operate broadly within constellations of phenotypes, 20 of which were novel relative to the univariate traits. We identify nine independent Q_SNP hits that do not conform to the identified factor structure (Table 2), a third of which appeared to operate through pathways unique to ALCH.

Table 2 ∣.

Summary of multivariate GWAS results

Multivariate GWAS target	Effective n	Mean χ2(1)	LDSC univariate intercept	Independent hits (LD with Q hits)	LD with univariate trait hits (LD with Q hits)	Unique from univariate trait hits (LD with Q hits)
Multivariate GWAS
Factor 1 (Compulsive)	19,108	1.209	0.973	1 (0)	1 (0)	0 (0)
Factor 2 (Psychotic)	87,138	1.869	0.975	108 (1)	96 (1)	12 (0)
Factor 3 (Neurodevelopmental)	55,932	1.301	1.022	9 (0)	7 (0)	2 (0)
Factor 4 (Internalizing)	455,340	1.635	0.997	44 (0)	38 (0)	6 (0)
Total hits across Factors 1-4	-	-	-	153 (1)	133 (1)	20 (0)
Hierarchical p factor	667,343	1.795	0.955	2 (1)	2 (1)	0 (0)
Bifactor p factor	666,557	1.985	0.982	66 (8)	58 (8)	8 (0)
Unstructured meta-analysis	-	2.216	0.883	184	145 (−)	39 (−)
Heterogeneity index (QSNP)
Factor 1 (Compulsive) QSNP	-	1.113	1.001	2	1	1
Factor 2 (Psychotic) QSNP	-	1.251	0.994	6	4	2
Factor 3 (Neurodevelopmental) QSNP	-	1.246	0.980	7	4	3
Factor 4 (Internalizing) QSNP	-	1.142	0.977	3	3	0
Total QSNP hits across Factors 1-4	-	-	-	9	5	4
Hierarchical p factor QSNP	-	1.667	0.928	69	58	11
Bifactor p factor QSNP	-	1.645	0.936	76	59	17

Independent hits were defined using a pruning window of 250 kb and r² < 0.1. Hits are considered in LD if their LD was r² > 0.10 or within a 250-kb window of one another. Values in parentheses indicate whether any of the hits were in LD with hits for factor-specific Q_SNP hits from the respective model. Factor-specific Q_SNP indexes whether a particular SNP is unlikely to operate through the identified factor structure, as will often be the case when a SNP effect is highly specific to an individual disorder. To facilitate comparison across mean χ² values reported in each row, all χ² statistics with df > 1 (i.e. those for Q_SNP and those for the unstructured multivariate GWAS) were converted to χ²(1) statistics before taking their means. For all GWAS analyses, we correct for multiple testing by employing the field standard significance threshold of P < 5 × 10⁻⁸.

We identified only two genome-wide hits for the higher-order p-factor, both of which were in LD with univariate hits for MDD and SCZ (Supplementary Table 26), and have been described in multiple external GWAS of psychiatric traits (Supplementary Table 27). The p-factor was characterized by the highest level of heterogeneity, with 69 loci identified for Q_SNP (Supplementary Table 28), 49 of which were in LD with hits on the four psychiatric factors from the correlated factors model. Despite few hits for p, its considerable mean χ² (1.795) may be attributable to the aggregation of heterogeneous signal across factors 1-4 in the hierarchical factor GWAS.

In a post-hoc analysis, we specified the p-factor in the context of a bifactor model^5,6 in which the p-factor and four domain-specific factors are orthogonal to one another and directly predict the 11 disorders (Fig. 1d). In contrast to the hierarchical model, the bifactor model allows for direct associations between p and the 11 disorders. We identified 66 independent hits on the bifactor p-factor, including the two hits for the hierarchical p-factor (Supplementary Table 29). Among these 66 hits, 38 were in LD with hits from the correlated factors model, eight were novel relative to univariate hits, and seven were novel relative to both univariate and correlated factors hits. We identified 76 Q_SNP hits, 50 of which were in LD with hierarchical p, Q_SNP hits (Supplementary Table 31). Although the bifactor specification of p produced more factor hits than did the hierarchical specification, the pattern of results with respect to the large number of Q_SNP hits and high overall mean χ² of Q_SNP was similar, and the LDSC genetic correlation across these two specifications of p was > 0.99. Collectively, these results indicate low utility of either specification of the p-factor at the level of individual genetic variants.

Estimating causal effects of problematic alcohol use.

One third of the Q_SNP discoveries from the correlated factors model appeared to operate through pathways unique to ALCH. This motivated an examination of the causal effects of ALCH on the disorders and factors using a form of multi-trait Mendelian randomization (MR) within the Genomic SEM framework. We ran two types of MR models: one using the Q_SNP variant in the ADH1B gene as a single instrumental variable for ALCH, and a second multi-variant MR approach using eight loci identified from an independent ALCH discovery GWAS as instrumental variables³⁹. The multi-variant approach allowed for additional effects of the loci on other disorders or factors where appropriate (Supplementary Note). Results from the ADH1B and multi-variant Genomic SEM-MR approaches tentatively supported a causal effect of ALCH on MDD and BIP (Supplementary Note and Supplementary Figs. 39 and 40). In these models, ALCH loadings on factors 2-4 were no longer significant, but the remaining disorders continued to load significantly on their respective factors. Multiple causation by ALCH is thus insufficient to fully account for widespread genetic overlap observed across disorders.

Discussion

We used Genomic SEM to identify four broad factors (Neurodevelopmental, Compulsive, Psychotic, and Internalizing) that provide a reasonable model of the genetic correlations among 11 major psychiatric disorders. We find that the Compulsive, Psychotic, and Internalizing factors are generally effective at describing the genetic relationships between psychiatric disorders at biobehavioral, functional genomic, and molecular levels of analysis. At the biobehavioral level, the pattern of associations with external correlates was informative with respect to the shared and distinct characteristics across the disorders. For example, the accelerometer results displayed both divergent patterns of findings across the factors and convergent patterns for the disorders within a factor. This provides evidence for both the validity and the utility of the genetic factor model for characterizing genetic associations with basic aspects of everyday functioning that may be, at face, relatively distal from the biological mechanisms of the disorders themselves. Results were less consistent with respect to the utility of a Neurodevelopmental disorders factor. For example, the Neurodevelopmental disorders factor exhibited much higher degrees of heterogeneity with respect to relationships with external correlates and with respect to effects of individual variants, a finding that seemed to be largely driven by divergent patterns for AUT.

Although the genetic correlations among the 11 disorders were somewhat consistent with the concept of a general p-factor, a hierarchical factor model that specified such a p-factor was found to offer limited biological insight, obscuring patterns of genetic correlations with external biobehavioral traits, enrichment within specific biological annotations, and associations with individual variants. Compared to the hierarchical model, a bifactor model identified a larger number of GWAS hits for p, but continued to exhibit a great deal of SNP-level heterogeneity. Given that a p-factor was found to be insufficient for accounting for patterns of multivariate associations at biobehavioral and variant levels of analysis, the question arises: what processes give rise to the moderate genetic correlations observed among the four, first-order factors? One possibility is that genetic correlations among the four factors originate from shared biology underlying pairwise combinations of factors and not from any biology that is shared across all factors. Similarly, genetic correlations among the factors themselves may reflect combinations of shared biology among subsets of disorders spanning factors that are not shared across all disorders within the corresponding factors.

In some circumstances, genetic correlations across disorders may arise from direct, potentially mutual, causation between the factor or disorder-specific liabilities and one another⁴⁰ or reflect causation directly between the symptoms of different disorders⁴¹. Based on significant locus-specific violations of the four factor model at loci relevant to ALCH, we incorporated MR into Genomic SEM models, with both single and multi-variant MR indicating causal effects of ALCH on MDD and BIP.

In order to identify gene sets and categories in which shared and unique genetic signal for multiple disorders is disproportionally localized, we developed and validated both a multivariate extension of S-LDSC and Stratified Genomic SEM. In line with prior findings linking SCZ and BIP to excitatory hippocampal CA1^42,43 and CA3^44,45 neurons and GABAergic neurons^46,47, we observe that the intersection between PI genes and genes expressed in both excitatory and GABAergic neurons explained an outsized proportion of the genetic variance in the Psychotic disorders factor. These results converge with considerable evidence from prior univariate work in indicating shared risk pathways for SCZ and BIP. Enrichment of variance unique to MDD, rather than shared across internalizing disorders, in excitatory dentate gyrus (DG) neurons is consistent with prior findings on the anti-depressive effects of DG stimulation in mouse models⁴⁸ and the observation that anti-depressants increase neurogenesis in this region⁴⁹.

We provide a more detailed account of limitations in the Supplementary Note, but highlight limitations particularly relevant to future work here. Summary statistics from well-powered GWASs spanning the wide range of psychiatric disorders investigated here were only consistently available for individuals of European ancestry. A major priority for continued work in this area will be to increase the diversity of populations for which psychiatric GWAS are available. Recently developed methods for the stratified analysis of genetic correlations across ancestral populations will be invaluable for the analysis of such data⁵⁰. Moreover, our results may have been influenced by the phenotyping and case-ascertainment methods used. Cai et al.⁵¹ have specifically reported that psychiatric phenotypes derived using minimal phenotyping (defined as “individuals’ self-reported symptoms, help seeking, diagnoses or medication”) may produce GWAS signals of low specificity. Although our sensitivity analyses suggested minimal differences when excluding GWAS that used self-report cohorts, this issue should continue to be explored in future work. It will also be informative for future research to examine further the effect of heterogeneity in how samples are ascertained and disorders are assessed on genetic relationships among disorders⁵².

The current analyses revealed four correlated psychiatric factors that account for extensive genetic overlap across disorders. We elucidate the composition of these factors by demonstrating patterns of correlations with external biobehavioral traits, develop and apply Stratified Genomic SEM to identify classes of genes that explain disproportionate levels of genetic risk sharing and uniqueness, and distinguish pleiotropic loci with directionally concordant effects on the individual factors from those acting heterogeneously across disorders within a factor. Our results offer critical insights into shared and disorder specific mechanisms of genetic risk and suggest possible avenues for revising a psychiatric nosology currently defined largely by clinical observation. Evidence derived from multivariate genetic analysis, alongside evidence at other levels of explanation (e.g., cognitive neuroscience, environmental stressors), could guide the development of novel treatments and revision of established diagnostic taxonomies.

Methods

The section directly below gives an overview of Genomic SEM followed by the validation and application of the novel method introduced here, Stratified Genomic SEM. The Supplementary Note provides additional details about the curation of the psychiatric phenotypes, model fitting procedure, results excluding self-report GWAS, comparison to prior results from the second iteration of results from the PGC cross-disorder group (i.e., CDG2)¹², genetic correlations with external traits, interpretation and estimation of the Q metrics (Q_Trait and Q_SNP), multivariate GWAS simulations, multivariate MR analyses, S-LDSC results, quality control procedures, and an extended account of the limitations outlined in the Discussion.

Overview of Genomic SEM.

Genomic SEM is a two-stage Structural Equation Modelling approach. In the first stage, a genetic covariance matrix (S) and its associated sampling covariance matrix (V_S) are estimated with a multivariate version of LD Score regression (LDSC). S consists of heritabilities on the diagonal and genetic covariances (co-heritabilities) on the off-diagonal. V consists of squared standard errors of S on the diagonal and sampling covariances on the off-diagonal, which capture dependencies between estimating errors that will arise in situations such as participant sample overlap across GWAS phenotypes. In the second stage, a structural equation model is fit to S by optimizing a fit function that minimizes the discrepancy between the model-implied genetic covariance matrix (Σ(θ)) and S, weighted by the elements within V. We use the diagonally weighted least squares (WLS) fit function described in Grotzinger et al.¹³:

$$F_{{}_{WLS}}(\theta )={\left(s-\sigma (\theta )\right)}^{\prime }{D}_{{}_S}^{-1}\left(s-\sigma (\theta )\right)$$

where S and Σ(θ) have been half-vectorized to produce s and σ(θ), respectively, and D_S is V_S with its off-diagonal elements set to 0. The sampling covariance matrix of the stage 2, Genomic SEM parameter estimates (V_θ) are obtained using a sandwich correction described in Grotzinger et al.¹³:

$$V_{{}_{\theta }}={\left(\widehat{\Delta }{}^{\prime }{\Gamma }^{-1}\widehat{\Delta }\right)}^{-1}\widehat{\Delta }{}^{\prime }{\Gamma }^{-1}{V}_{{}_S}{\Gamma }^{-1}\widehat{\Delta }{\left(\widehat{\Delta }{}^{\prime }{\Gamma }^{-1}\widehat{\Delta }\right)}^{-1}$$

where $\widehat{\Delta }$ is the matrix of model derivatives evaluated at the parameter estimates, Γ is the stage 2 weight matrix, D_S, and V_S is the sampling covariance matrix of S. Validation of Genomic SEM in Grotzinger et al.¹³ demonstrated that the framework produces unbiased standard errors, appropriately accounts for sample overlap in multivariate GWAS, and produces accurate point estimates for different population generating models. In addition, polygenic scores derived from Genomic SEM summary statistics were found to better predict the individual traits that define the factor than polygenic scores constructed from the summary statistics for the individual traits. As part of the current analyses, we sought to further validate Genomic SEM via a series of simulations based directly on the factor structure identified here and additionally benchmark Genomic SEM against existing multivariate methods.

Overview of Stratified Genomic SEM.

Stratified Genomic SEM extends the overall Genomic SEM framework by allowing potentially different structural equation models to be fit to genetic covariance matrices estimated in different gene sets and categories. These gene sets and categories, collectively referred to as annotations, can be constructed based on a variety of sources, such as collateral gene expression data obtained from single-cell RNA sequencing. We develop a multivariate extension of Stratified LD Score Regression (S-LDSC)³² below to estimate these annotation-specific genetic covariance matrices and their associated sampling covariance matrices. We describe two types of annotation-specific genetic covariance matrices, S₀ and Sτ. S₀ contains estimates of genetic covariance within a specific annotation without controlling for overlap with other annotations. In other words, it is composed of the zero-order coefficients implied by the multivariate S-LDSC model. Sτ contains estimates of genetic covariance controlling for annotation overlap. In other words, it is composed of multiple regression coefficients estimated by the multivariate S-LDSC model. The distinction between S₀ and Sτ directly parallels the distinction made in univariate S-LDSC³² between overall heritability explained by an annotation and the incremental contribution of an annotation to heritability beyond all other annotations considered. Note that the estimates required to populate elements of an overall genome-wide S matrix can be produced either from the zero-order annotation that includes all SNPs or by aggregating parameters corresponding to each annotation from the multivariate S-LDSC model used to estimate Sτ.

Below, we validate via simulation that Stratified Genomic SEM produces unbiased model parameter estimates and standard errors, and that model fit indices appropriately favor the population generating model within a given annotation. There is a wide array of research questions that can be asked using Stratified Genomic SEM. In this paper, we examine genetic enrichment of variance in psychiatric genetic factors across a broad range of annotations.

Multivariate Stratified LDSC.

Under a multivariate extension of the S-LDSC model, the expected value of the product of z statistics for each pairwise combination of phenotypes for SNP j equals:

$$E\left[z_{1j}{z}_{2j}\right]=\sqrt{N_1{N}_2}\sum _c{\tau }_c\frac{\ell (j,c)}{M_c}+\frac{\rho N_s}{\sqrt{N_1{N}_2}}+a$$

where N_i is the sample size for study i, c indexes a genomic annotation, M_c is the number of SNPs in annotation c, ℓ(j,c) is the LD score of SNP j with respect to annotation c (that is, the sum of squared LD this SNP has with all SNPs in the annotation), τ_c is a vector of free parameters used to compute the conditional contribution to heritability or coheritability (genetic covariance) in annotation c, N_s is the number of individuals included in both GWAS samples, ρ is the phenotypic correlation within the overlapping samples, and a is a term representing unmeasured sources of confounding such as shared population stratification across GWASs⁵³. The inclusion of the term M_c in the above equation produces LD scores ($\frac{\ell (j,c)}{M_c}$) that are scaled relative to the size of the respective annotations, thereby allowing τ_c to be interpreted on the same scale as genome-wide estimates of heritability and coheritability, rather than on a per SNP scale. Note that when the z statistics for the same phenotype is double entered on the left hand side of the above equation, such that E[z_1j z_2j] becomes $E\left[{\chi }_j^2\right]$, the equation reduces to the univariate S-LDSC model⁸.

Following Finucane et al.³², the multivariate S-LDSC model is estimated by regressing the product of z statistics against the annotation-specific LD scores using a weighted regression model (see online supplement of Finucane et al.³² for a description of how weights are calculated). Standard errors and dependencies among estimation errors (i.e., sampling covariances) are estimated using a multivariate block jackknife. As sample overlap creates a dependency between z statistics for the two traits, thus increasing their products, the S-LDSC intercept (ρN_s/√(N₁N₂) + a) is affected, but the regression slope is unaffected, and the estimates of partitioned genetic covariance and their standard errors are not biased.

Derivation of S_τ and S₀.

S_τ,c is a matrix containing estimates of genetic variance and covariance in annotation c, controlling for overlap with other annotations. It is composed of multiple regression coefficients, τ_c, estimated directly with the multivariate S-LDSC model by populating each of its cells with the corresponding τ estimate from the multivariate S-LDSC model.

S_0,c is a matrix containing estimates of genetic covariance in annotation c, without controlling for overlap with other annotations. The elements ζ_c composing S_0,c can be derived from the τ_c estimates from the multivariate S-LDSC model in combination with knowledge of annotation overlap. Thus, the zero-order contribution of target annotation t to heritability or co-heritability is written as:

$${\zeta }_t=\sum _c\left(\frac{\mid C_c\cap C_t\mid }{\mid C_c\mid }\right){\tau }_c$$

where ∣C_c ∩ C_t∣ is the number of SNPs in annotation c that are also in target annotation t, and ∣C_c∣ is the total number of SNPs in annotation c (alternatively expressed as M_c), such that $\left(\frac{\mid C_c\cap C_t\mid }{\mid C_c\mid }\right)$ reflects the proportion of SNPs in annotatio c that are also in target annotation t. This proportion is used to weight the term τ_c for each annotation in deriving the zero-order contribution of target annotation t to heritability or coheritability.

When the multivariate S-LDSC model is correct, Sτ is expected to produce unbiased estimates of the conditional contribution of an annotation to genetic covariance, after controlling for the effects of variants in all other annotation (i.e., accounting for the fact that variants can reside in multiple annotations). In comparison, S₀ is expected to produce unbiased estimates of the total contribution of all genetic variants in an annotation to genetic covariance (i.e., irrespective of its overlap with the other annotations). S₀ has two desirable properties. First, its estimate is not as directly contingent on which other annotations are included in the multivariate S-LDSC model. Second, because it does not decompose contributions of an annotation into those that are shared vs. unique of other annotations, it is expected to produce more stable estimates at small and moderate sample sizes. For this reason, the empirical Stratified Genomic SEM analyses reported here employ S₀ matrices, and should be interpreted accordingly.

Simulations of stratified genetic covariance.

Simulation procedure.

Using raw, individual-level genotype data simulation, we sought to validate the point estimates and standard errors (SEs) produced by Stratified Genomic SEM. We compare results for S₀ and Sτ. We began by generating 100 sets of 45, 100% heritable phenotypes (“orthogonal genotypes”) using the GCTA package⁵⁴. Each 100% heritable phenotype was specified to have 10,000 randomly selected causal variants from within a particular annotation. These phenotypes were paired with genotypic data for 100,000 randomly selected, unrelated individuals of European descent from UK Biobank data for the 1,209,498 SNPs present in HapMap3.

The simulated genotypes were used to construct six different factor structures for six causal annotations. All orthogonal genotypes were scaled M = 0, SD = 1. For three of the causal annotations (DHS Peaks, H3K27ac, and PromoterUSC), seven genotypes for each annotation were used to construct six new correlated genotypes, each as the weighted linear combination of a domain-specific genetic factor and a general genetic factor, which was constructed from the seventh genotype. For the remaining three causal annotations (FetalDHS, H3K9ac, and TFBS), eight genotypes for each annotation were used to construct two sets of three correlated genotypes for two correlated general genetic factors, constructed from the seventh and eighth genotypes. A set of six “total” genotypes was created by summing a factor indicator genotype from each of the six causal annotations. As each genotype within each annotation was specified to have 10,000 causal SNPs, the “total” genotypes created as the sum of six annotations had 60,000 causal SNPs in the population generating model.

Phenotypes were subsequently constructed as the weighted linear combination of one of the six “total” genotypes and domain-specific environmental factors (randomly sampled from a normal distribution with M = 0, SD = 1). Heritabilities for phenotypes 1-6 were all set to $h_k^2=60\%$, such that the weights for the genotypes were $\sqrt{h_k^2}$ and the weights for the environmental factors were $\sqrt{(1-h_k^2)}$. Each of the 600 phenotypes (100 sets of 6 phenotypes) was then analyzed as a univariate GWAS in PLINK⁵⁵ to produce univariate GWAS summary statistics. The summary statistics were then munged, and Stratified Genomic SEM using the 1000 Genomes Phase 3 BaselineLD Version 2.2 model was used to construct 100 sets of 6 × 6 stratified zero-order genetic covariance matrices (S₀), τ covariance matrices (Sτ), and their corresponding sampling covariance matrices (V_S0 and V_Sτ).

Validating S₀ and V_S0.

For the zero-order genetic covariance matrix, we would expect the annotation including all SNPs—i.e. the genome-wide annotation—to reflect the weighted linear combination of the generating covariance matrices specified for the six causal annotations, with weights equal to the proportion of all SNPs contained in each of the corresponding causal annotations. For each of the six causal annotations, we expect the zero-order covariance matrix for the corresponding annotation to be a linear combination of that annotation’s population-generating matrix and the remaining annotations’ population-generating matrices weighted by the proportion of SNPs overlapping across the annotations. To test these expectations, we created average observed covariance matrices across the 100 simulations for the genome-wide annotation and six causal annotations. The estimated S₀ genome-wide covariance matrix approximately reflected an additive mixture of the six population generating covariance matrices, and was estimated with minimal bias (absolute value of mean discrepancy = 0.004; Supplementary Fig. 8). In addition, the observed covariance matrices for each of the causal annotations were minimally biased relative to the generating population (Supplementary Table 7).

In order to evaluate the accuracy of the SEs, we analyzed the ratio of the mean SE estimate across the 100 simulations over the empirical SE (calculated as the standard deviation of the parameter estimates across the 100 simulations). A value above 1 for this ratio indicates conservative SE estimates. This ratio was calculated within each of the annotations and for each cell of the covariance matrix. The average ratio across annotations and cells of the covariance matrix was 1.030 (see Supplementary Fig. 9 for distribution across all annotations and Supplementary Table 7 for ratio within causal annotations). Thus, we have produced a SE estimate for stratified heritability and covariance that performs as expected. In fact, our estimates are very slightly conservative as the mean SE was slightly larger than the empirical SE. Moreover, the average z statistic for heritability and covariance estimates within the causal annotations were all highly significant, suggesting more than adequate power under the conditions of the current simulation.

Validating Sτ and V_Sτ.

The expectation for the genetic S_τ covariance matrices is that the observed covariance matrices will reflect the generating model within only that annotation. Indeed, the causal annotations closely matched their respective population generating covariance matrices and bias was minimal (Supplementary Fig. 10 and Supplementary Table 7). We then analyzed the ratio of the mean SE estimate across the 100 runs over the empirical SE (calculated as the standard deviation of the parameter estimates across the 100 runs). The average ratio of SE estimates was 1.014 across all annotations (Supplementary Fig. 9) and, importantly, was also close to 1 for the causal annotations. Results for 4,459 of the total 5,300 covariance matrices produced negative heritability estimates. This included some of the causal annotations (Supplementary Table 30), but was largely true for the non-causal annotations. Negative heritability estimates are unsurprising for the non-causal annotations as their population generating effect is 0. The z statistics for the S_τ heritabilities and covariances were, on average, smaller relative to the S₀ covariance matrices. This is to be expected as the S₀ covariance matrices include power gained from variance shared with overlapping annotations.

The S_τ covariance matrices for the causal annotations were then used as input for Genomic SEM models. The two types of population generating models—a common factor and correlated factors model—were run for each annotation. For all causal annotations, Genomic SEM estimates closely matched the parameters specified in the generating population (Supplementary Table 8 and Supplementary Fig. 11). In addition, the ratio of the mean model SEs over the empirical SEs was near 1. Model fit statistics (CFI, AIC, and model χ²) also generally favored the generating model for a particular annotation (Supplementary Table 9). This was least true for the H3K27ac annotation. This is unsurprising as the population-generating model for the H3K27ac annotation—a correlated factors model with a factor correlation of 0.7—most closely matched the competing common factor model. Collectively, these results indicate that Stratified Genomic SEM produces unbiased parameter estimates and standard errors for S₀ and S_τ, that S_τ shows specificity to the causal annotations of interest, and that model fit indices generally favor the appropriate model.

Estimating genetic enrichment of model parameters.

We can examine whether the proportional contribution of an annotation to a given genome-wide parameter in Stratified Genomic SEM is different than would be expected on the basis of the relative size of that annotation, so long as the parameter is scaled comparably across all annotations considered⁵⁶. This is formalized by testing the null hypothesis,

$$\left(\frac{{\theta }_c}{\theta }\right)=\left(\frac{M_c}{M}\right),$$

where θ_c is the parameter estimate in annotation c, as estimated from a Genomic SEM model applied to S_0,c; θ is the genome-wide parameter estimate, as estimated from a Genomic SEM model applied to the genome-wide S matrix derived via aggregating the conditional contributions of all annotations included in the multivariate S-LDSC model; M_c is the number of SNPs in annotation c; and M is the total number of SNPs used to computed the LD-scores. This formula can be rearranged to produce a ratio of ratios (the so-called enrichment ratio) that indexes the magnitude of enrichment:

$$\frac{\left(\frac{{\theta }_c}{\theta }\right)}{\left(\frac{M_c}{M}\right)},$$

with a value of 1.0 corresponding to the null of no enrichment, values greater than 1.0 corresponding to enrichment (overrepresentation of signal in the annotation relative to its size), and values below 1.0 corresponding to depletion (underrepresentation of signal in the annotation relative to its size).

In the current application, we are interested in enrichment of genetic signal shared across subclusters of disorders and disorder-specific signal, as indexed by a factor model that allows the estimates of factor variances and disorder-specific uniquenesses, respectively, to vary across annotations, while holding all factor loadings invariant across annotations. We use a two-step model-fitting procedure to estimate the enrichment ratio in order to directly obtain an estimate of its SE. In Step 1, we estimate the factor loadings needed to scale the total genome-wide variances of the factors to 1.0. This is achieved by fitting a model to the genome-wide S-LDSC matrix in which unit variance identification is used. In Step 2, the loading estimates from the prior Step 1 model are fixed and the factor variance is freely estimated separately in each annotation using the S_0,c matrices. Thus, the estimated factor variances in Step 2 are scaled proportionally relative to the genome-wide factor variance (i.e., the numerator of the enrichment ratio). This estimate and its SE are subsequently divided by the proportion of SNPs in the corresponding annotation (i.e., the denominator of the enrichment ratio). For clarification, we note that genome-wide enrichment across all SNPs is exactly equal to 1. That is, for Step 2, if the genome-wide S-LDSC matrix is used as input, this produces a parameter estimate of 1, which is then divided by a proportion of 1.0, which reflects the ratio of M/M (i.e., all SNPs over all SNPs).

Selection and creation of annotations.

In order to construct the genome-wide S-LDSC matrix, and estimate stratified genetic covariance, we utilized pre-computed annotation files provided by the original S-LDSC authors³². In line with recommendations, we utilized all annotations from the most recent 1000 Genomes Phase 3 BaselineLD Version 2.2⁵⁷ that includes a total of 97 annotations ranging from coding, UTR, promoter, and flanking window annotations. For tissue specific histone marks, we included annotations constructed based on data from the Roadmap Epigenetics Project⁵⁸ for narrowly defined peaks for DNase hypersensitivity, H3K27ac, H3K4me1, H3K4me3, H3K9ac, and H3K36me3 chromatin. For tissue-specific gene expression, we include annotations constructed based on RNA sequencing data from human tissues from Genotype-Tissue Expression (GTEx)⁵⁹ and for annotations constructed from human, mouse, and rat microarray experiments from the Franke Lab (i.e., DEPICT)⁶⁰. For both tissue-specific histone/chromatin marks and gene expression, we utilized only brain and endocrine relevant regions in addition to 5 randomly selected control regions from each (i.e., 10 controls total).

We also created 29 annotations to examine the interaction between protein-truncating variant (PTV)–intolerant (PI) genes and human brain cells. PI genes were obtained from the Genome Aggregation Database (gnomAD), and ascertained using the probability of loss-of-function intolerance (pLI) metric. We selected genes with pLI > 0.9, producing a list of 3,063 genes³³. Human brain cell gene sets were based on single-nucleus RNA-seq (sNuc-seq) data generated GTEx project brain tissues in the hippocampus and prefrontal cortex³⁴. Excluding sporadic genes and genes with low expression, for the 14 cell types we selected the top 1,600 (~15%) differentially expressed genes in each cell type, which likely cover all genes that are important for a specific cell type. PI × human brain cell gene sets contained the intersection of genes that are PTV-intolerant and each human brain cell gene set. Annotations were created using a 100-kb window and LD information from the European subsample of 1000 Genomes Phase 3.

We do not estimate enrichment of psychiatric factors for continuous or flanking window annotations, yielding a total of 168 binary annotations across the baseline model, gene expression, histone marks, PI, and brain cell annotations. For a Bonferroni correction < 0.05, this corresponds to P < 2.98 × 10⁻⁴. We note that continuous and flanking window annotations were retained for construction of the genome-wide, S-LDSC matrix.

Appendix

Consortia

iPSYCH

Jakob Grove^9-12, Manuel Mattheisen^10,17,19-22, Anders D. Børglum^9-11, and Ole Mors^9,23

Tourette Syndrome and Obsessive Compulsive Disorder Working Group of the Psychiatric Genetics Consortium

Manuel Mattheisen^10,17,19-22

Bipolar Disorder Working Group of the Psychiatric Genetics Consortium

Cathryn M. Lewis^7,8, Andrew M. McIntosh⁶, Jakob Grove^9-12, Manuel Mattheisen^10,17,19-22, Anders D. Børglum^9-11, Ole Mors^9,23, Gerome Breen^7,8, Phil H. Lee^24,25, and Jordan W. Smoller^24,25

Major Depressive Disorder Working Group of the Psychiatric Genetics Consortium

Mark J. Adams⁶, Cathryn M. Lewis^7,8, Andrew M. McIntosh⁶, Jakob Grove^9-12, Manuel Mattheisen^10,17,19-22, Anders D. Børglum^9-11, Ole Mors^9,23, Gerome Breen^7,8, Kenneth S. Kendler²⁶, Jordan W. Smoller^24,25, and Michel G. Nivard^4,28

Schizophrenia Working Group of the Psychiatric Genetics Consortium

Andrew M. McIntosh⁶, Sandra M. Meier^10,20, Manuel Mattheisen^10,17,19-22, Anders D. Børglum^9-11, Ole Mors^9,23, Phil H. Lee^24,25, Kenneth S. Kendler²⁶, and Jordan W. Smoller^24,25

Data Availability

The data that support the findings of this study are all publicly available or can be requested for access. Specific download links for various datasets are directly below.

Summary statistics for data from the PGC can be downloaded or requested here: https://www.med.unc.edu/pgc/download-results/

Summary statistics for the Anxiety phenotype in UKB (TotANX_OR) can be downloaded here: https://drive.google.com/drive/folders/1fguHvz7l2G45sbMI9h_veQun4aXNTy1v

23andMe summary statistics are made available through 23andMe to qualified researchers under an agreement with 23andMe that protects the privacy of 23andMe participants. Please visit research.23andme.com/collaborate/#publication for more information.

Summary statistics for the volume-based neuroimaging phenotypes were downloaded from: https://github.com/BIG-S2/GWAS

Summary statistics for the health and well-being complex trait correlations can be downloaded from: https://atlas.ctglab.nl/

Summary statistics for the circadian rhythm correlations across 24-hours can be downloaded from: https://cnsgenomics.com/software/gcta/#DataResource

Data from gnomAD used to identify PI genes for creation of annotations can be downloaded here: https://storage.googleapis.com/gnomad-public/release/2.1.1/constraint/gnomad.v2.1.1.lof_metrics.by_gene.txt.bgz

Gene count data per cell for creation of annotations were obtained from: https://storage.googleapis.com/gtex_additional_datasets/single_cell_data/GTEx_droncseq_hip_pcf.tar

Data which map individual cells to cell types (e.g. neuron, astrocyte etc.) were obtained from: https://static-content.springer.com/esm/art%3A10.1038%2Fnmeth.4407/MediaObjects/41592_2017_BFnmeth4407_MOESM10_ESM.xlsx

Links to the LD-scores, reference panel data, and the code used to produce the current results can all be found at: https://github.com/MichelNivard/GenomicSEM/wiki

Links to the BaselineLD v2.2 annotations can be found here: https://data.broadinstitute.org/alkesgroup/LDSCORE/