Analyzing and reconciling colocalization and transcriptome-wide association studies from the perspective of inferential reproducibility

Summary

Transcriptome-wide association studies and colocalization analysis are popular computational approaches for integrating genetic-association data from molecular and complex traits. They show the unique ability to go beyond variant-level genetic-association evidence and implicate critical functional units, e.g., genes, in disease etiology. However, in practice, when the two approaches are applied to the same molecular and complex-trait data, the inference results can be markedly different. This paper systematically investigates the inferential reproducibility between the two approaches through theoretical derivation, numerical experiments, and analyses of four complex trait GWAS and GTEx eQTL data. We identify two classes of inconsistent inference results. We find that the first class of inconsistent results (i.e., genes with strong colocalization but weak transcriptome-wide association study [TWAS] signals) might suggest an interesting biological phenomenon, i.e., horizontal pleiotropy; thus, the two approaches are truly complementary. The inconsistency in the second class (i.e., genes with weak colocalization but strong TWAS signals) can be understood and effectively reconciled. To this end, we propose a computational approach for locus-level colocalization analysis. We demonstrate that the joint TWAS and locus-level colocalization analysis improves specificity and sensitivity for implicating biologically relevant genes.

Introduction

With the rapid advancements of sequencing technologies, genetic association analyses have been routinely performed and have made significant contributions to insights into the roles of genetic variants in complex diseases. As a result of recent expansions in the large-scale joint genotyping and phenotyping of molecular traits, integrative genetic analysis has emerged as a tool for studying the biological basis of complex diseases. Integrative analyses have the unique ability to allow interpretation of genetic associations beyond individual mutations and link complex diseases to functional genomic units, e.g., genes, metabolites, and proteins.^{1, 2, 3} Discoveries from integrative genetic analyses have enabled the discovery of novel drug targets,⁴ and hence improved treatments for diseases.

In this paper, our discussions focus on two prevailing types of integrative genetic analyses: transcriptome-wide association studies (TWASs) and colocalization analysis. Both approaches are widely applied to integrating results from expression quantitative-trait loci (eQTL) mapping and complex-traits genome-wide association studies (GWASs). They have shown promise in nominating potential causal genes for complex diseases.^5,6 The analytical goal of a TWAS is to test associations between a complex trait of interest and genetically predicted gene expression levels (that are constructed from eQTL information).^{7, 8, 9, 10} More broadly, it connects to the causal inference framework of instrumental variable analysis: given an established TWAS association, the causal effect from a target gene to the complex trait can be estimated.^{10, 11, 12} Nevertheless, our discussions focus on the testing stage, which we refer to as TWAS scanning henceforth. Colocalization analysis aims to identify overlapping causal genetic variants for both molecular (e.g., gene expression) and complex traits.^{13, 14, 15, 16} A colocalized genetic variant in a particular cis-gene region implies that a single mutation is responsible for variations in both molecular and complex traits, thus establishing an intuitive link between the traits. A more detailed review of both approaches is provided in the material and methods section.

Our primary motivation was to investigate the consistency and inconsistency patterns between the inference results from a TWAS scan and those from a colocalization analysis in practical settings. Such patterns are examples of inferential reproducibility—one of the three modes defined in the lexicon of reproducibility by Goodman et al..¹⁷ Narrowly speaking, inferential reproducibility refers to the consistency of inference results when different analytical approaches are applied to the same data. In practice, both a TWAS scan and a colocalization analysis are often applied to the same eQTL and GWAS data combinations. However, the implicated genes and the number of discoveries from the two analyses are often markedly different, making biological interpretation and the design of follow-up studies challenging. Thus, a systematic investigation is warranted to help us dissect and understand these practical differences.

Under the settings of inferential reproducibility, the overlapping findings from all approaches are often considered conceptual replications for individual methods and have enhanced validity. The emphasis of the inferential reproducibility analysis is typically placed on the difference sets. We focus on examining the implicated genes reported only by either colocalization or TWAS analysis in our specific application context. Unlike its method reproducibility and results reproducibility counterparts, inferential reproducibility does not expect or even encourage all methods to yield identical results. On the contrary, the differences driven by different analytical and operational assumptions are largely anticipated.^17,18 The goal of the inferential reproducibility analysis is to quantify, understand, and interpret these differences properly. The aim of our study is to provide insights into how different analytical and operating assumptions of the computational procedures, combined with specific data characteristics, lead to different gene nominations. Specifically, we show that the inconsistent results in these integrative genetic analyses have distinct characteristics: in one scenario (i.e., for strong TWAS but weak colocalization signals), they can be reconciled; in the other (i.e., for weak TWAS but strong colocalization signals), they are truly complementary.

On the basis of our analysis of inferential reproducibility and to better facilitate connecting the reconcilable set of genes implicated by the two integrative analysis approaches, we propose a novel locus-level method of colocalization analysis derived from the same probabilistic modeling framework of fastENLOC. In contrast to the existing locus-level colocalization methods in the literature, e.g., RTC,¹⁹ JLIM,²⁰ our method carefully constructs the candidate loci selected for analysis from the state-of-the-art Bayesian multi-SNP fine-mapping algorithms, and the inference results show much-improved resolution and specificity. Thus, as an approach complementary to variant-level colocalization, it can overcome some of the latter’s intrinsic power limitations stemming from the currently available data.¹⁶ This method is implemented in the software package fastENLOC v2.0 (web resources).

Material and methods

Overview of TWAS scanning and variant-level colocalization analysis

This section provides an overview of TWAS scanning and variant-level colocalization analyses. There are multiple implementations for each integrative approach. Here, we emphasize the commonality among different implementations and refer the readers to the cited publications for their differences.

TWAS scanning

TWAS scanning aims to identify genes whose genetically predicted expression levels are associated with a complex trait studied in a GWAS. Most available approaches assume a linear prediction model for gene expression levels; this model is trained with the available eQTL datasets. Different TWAS scanning approaches apply different supervised learning algorithms to train the prediction model. For example, PrediXcan⁷ utilizes the shrinkage method, elastic net; TWAS-Fusion⁸ and PTWAS¹⁰ adopt Bayesian prediction and model-averaging approaches, respectively. The fully trained prediction model can be applied to GWAS datasets and impute the gene expressions on the basis of only the corresponding genotype information. Finally, association testing is performed between the observed complex-trait phenotype and the imputed expression phenotypes in a separate GWAS dataset. Particularly, under the assumption of a linear-prediction model, the association testing procedure can be effectively carried out with only summary-level GWAS statistics.

Existing literature has explicitly connected TWAS scanning to the testing procedure in instrumental-variable analysis and Mendelian randomization.^8,10,12 Particularly, a multi-SNP prediction of gene expressions is viewed as a composite instrumental variable (i.e., a weighted sum of genotypes from potential eQTL SNPs). A prediction model involving a single genetic variant can be straightforwardly derived according to the principles of either supervised learning or instrumental variable analysis (see section 1 of the supplemental methods), which is similar to, but more powerful than, the existing SMR⁹ method.

Variant-level colocalization analysis

Variant-level colocalization analysis aims to identify the overlapping of causal eQTL and GWAS SNPs. Most existing variant-level colocalization methods take the Bayesian probabilistic modeling approach to effectively account for the inevitable uncertainty in determining causal genetic variants.^{13, 14, 15, 16} They also take advantage of fine-mapping results obtained from individual analysis of each trait to achieve improved accuracy. The colocalization probabilities for individual SNPs (i.e., SNP-level colocalization probabilities, or SCPs) can be unimpressive, especially when a few SNPs are in high linkage disequilibrium (LD). The aforementioned methods all report a regional-level colocalization probability (RCP) to represent the probability that a genomic region harbors a single colocalized variant.

Variant-level colcoalization analysis is known to have limited power given the available GWAS and molecular QTL data. Two classes of false-negative (FN) errors are commonly encountered in practice.¹⁶ Specifically, the class I FNs refer to the cases where the genetic-association analyses for individual traits fail to identify at least one genuine association at a colocalized site. The class II FNs are caused by inaccurate quantification of association evidence at the individual variant level: even if both associations are identified for a locus, the probabilistic characterization of the assumed causal variants might lead to weak evidence for variant-level colocalization. The extensive class II FNs in the analysis of real data motivate us to propose a locus-level approach to colocalization analysis in this paper.

Evaluating inferential reproducibility between TWAS scanning and colocalization analysis

TWAS scanning and colocalization analysis can be applied to the same molecular QTL and GWAS datasets, which form the basis for evaluating the inferential reproducibility of these methods. For this evaluation, we select four complex traits, including standing heights from the UK Biobank, coronary artery disease (CAD) status from the CARDioGRAM Consortium, and high-density lipoprotein (HDL) and low-density lipoprotein (LDL) measurements from the Global Lipids Genetic Consortium (GLGC). These four traits are representative of a range of quantitative and discrete complex traits measured at organismal and molecular levels.

We performed TWAS scanning and variant-level colocalization analyses for the selected GWAS traits by using the multi-tissue eQTL data from the GTEx project (v8). To enable direct comparisons, we applied the integrative approaches, PTWAS for TWAS scanning and fastENLOC for colocalization analysis, by using the same set of cis-eQTL annotations derived from the multi-SNP fine-mapping analysis method, DAP-G.¹⁵ Our main motivation for these selections was to minimize the procedural differences in eQTL and GWAS data pre-processing. Thus, we could focus on the important analytical factors that lead to differences in inferential results. Our main results also extend to other TWAS-scanning and colocalization-analysis methods.

Our comparison focuses on the gene-level quantification for each trait-tissue-gene combination. The PTWASscanning reports a correlation testing p value for each target trait-tissue-gene combination. In the colocalization analysis, fastENLOC computes a regional colocalization probability (RCP) for an independent GWAS hit and an independent eQTL signal of a target gene in a specific tissue. We subsequently computed a gene-level variant colocalization probability (GRCP) by considering all available independent eQTL signals for the target gene in the corresponding tissue, i.e.,

$${\text{GRCP}}_{G_t}=1-\prod _{r\in G_t}\left(1-{\text{RCP}}_r\right),$$ (Equation 1)

where the set G_t represents the set of independent eQTL signals within the cis-region of the target gene-tissue pair. The GRCP represents the probability that the target gene harbors at least one colocalized causal variant for a trait-tissue-gene combination.

Processing of GTEx eQTL and complex-trait GWAS data

We used the multi-tissue eQTL data generated from the GTEx project (v8) in our real-data analysis. The data were processed and analyzed by the GTEx consortium. The pre-processing and analysis protocols are documented by the GTEx Consortium.¹ For evaluating inferential reproducibility, we particularly focus on the cis-eQTL fine-mapping results generated by the software package DAP-G;²¹ these results are publicly available at the GTEx portal and were re-formatted for PTWAS scanning and fastENLOC without further processing.

The summary statistics from the four selected complex-trait GWASs (HDL and LDL from the GLGC consortium; standing height from the UK Biobank; and coronary artery disease from the CARDioGRAM consortium) are also publicly available. We used the single-SNP-association Z scores for the four traits harmonized by the GTEx project.¹ The main purpose of the harmonization procedure is to match common SNPs between the SNPs interrogated in the GWAS and those from the GTEx project. More specifically, if a GTEx SNP is missing from the corresponding GWAS, its GWAS Z score is imputed with the software package impG.²² The harmonized Z scores are subsequently used in PTWAS scanning and fastENLOC analyses.

Probabilistic colocalization analysis at the locus level

We propose a locus-level colocalization analysis method to (1) remedy the weakness that exists in variant-level colocalization analysis as a result of the extensive class II false negatives; and (2) provide an effective analytical tool for reconciling TWAS and colocalization analysis. The motivation will be elucidated in the results section.

The overall goal of the proposed computational method is to quantify the probability of a genomic locus harboring both a causal molecular QTL and a causal GWAS variant. We define such a probability as the locus-level colocalization probability (LCP). LCP differs from RCP: RCP quantifies the probability of a genomic region containing a single colocalized variant, whereas LCP accounts for additional possible events that distinct causal variants for different traits coexist in the same locus. Thus, it follows that LCP ≥ RCP for any given loci.

The key to the proposed approach is the specification of candidate colocalization loci. The computation is based on the same probabilistic generative model used in the variant-level colocalization analysis.

Specification of candidate colocalization loci

Our implementation defines a candidate colocalization locus by the intersected signal clusters (or credible sets) from the target molecular and complex traits. Signal clusters are generated from Bayesian multi-SNP fine-mapping analysis of genetic-association data. A signal cluster is constructed from an identified set of LD SNPs representing the same underlying association signal for a given trait. Member SNPs in a signal cluster satisfy both the redundancy condition and the LD condition (also known as the purity condition in some implementations). The redundancy condition indicates that members of the same signal cluster can be used to represent the same underlying association signal almost interchangeably, with only slight quantitative differences (in model likelihood/posterior probabilities).²³ The LD condition requires that all member SNPs are in high LD. The construction of signal clusters is similar to the widely used conditional analysis in genetic-association studies. By these two conditions and under certain statistical assumptions of statistical fine-mapping analysis, it follows that at most one variant within a signal cluster represents the true association signal. Available fine-mapping algorithms that can produce necessary signal clusters or credible sets include SuSIE,²³ FINEMAP,²⁴ and DAP-G.¹⁵

The candidate loci constructed from signal clusters are also practically small and typically include only a few SNPs in LD. For example, the fine-mapping of the GTEx whole-blood eQTLs by DAP-G yields 113,318 signal clusters with coverage probability ≥0.95 (i.e., the 95% Bayesian credible sets). On average, each signal cluster contains only 16 SNPs (median = 8) with the minimum pairwise R² > 0.5.

Computation of locus-level colocalization probability

Let Y_e and Y_g denote the genotype and phenotype data combinations for the molecular and the complex traits of interest, respectively. Consider p overlapping SNPs in a candidate colocalization locus. Let β_i and α_i denote the genetic effects of SNP i for the complex and molecular traits, respectively. The latent binary association status of all member SNPs in the locus for the complex trait is represented by a p-binary vector, γ, where γ_i = 1(β_i ≠ 0). Similarly, we use p-vector d to denote the latent association status for the molecular trait, where d_i = 1(α_i ≠ 0).

Let Γ_k and D_k denote the sets of configurations of γ and d values with exactly k independent association signals for the corresponding traits, respectively. By the construction of the candidate locus, it follows that

$$\text{Pr}\left(\mathit{\gamma }\in {\text{Γ}}_k|{\mathit{Y}}_g\right)=0\text{ and Pr}\left(\mathit{d}\in D_k|{\mathit{Y}}_e\right)=0,\forall k\ge 2.$$ (Equation 2)

Thus, the problem of locus-level colocalization then can be framed as evaluating the posterior probability, $\text{Pr}\left(\mathit{\gamma }\in {\text{Γ}}_1,\mathit{d}\in D_1|{\mathit{Y}}_g,{\mathit{Y}}_e\right)$. If we assume the molecular and complex trait data are collected from two non-overlapping sets of samples, it follows that

$$\text{Pr}\left(\mathit{\gamma }\in {\text{Γ}}_1,\mathit{d}\in D_1|{\mathit{Y}}_g,{\mathit{Y}}_e\right)=\text{Pr}\left(\mathit{\gamma }\in {\text{Γ}}_1|\mathit{d}\in D_1,{\mathit{Y}}_g\right)\text{Pr}\left(\mathit{d}\in D_1|{\mathit{Y}}_e\right)$$ (Equation 3)

Next, we show that both required probabilities can be deduced from the variant-level colocalization model detailed in Wen et al. and Hukku et al.^15,16

It follows from Equation 2 that

$$\text{Pr}\left(\mathit{d}\in D_1|{\mathit{Y}}_e\right)=\sum _{i=1}^p\text{Pr}\left(d_i=1|{\mathit{Y}}_e\right),$$ (Equation 4)

where $\text{Pr}\left(d_i=1|{\mathit{Y}}_e\right)$ denotes the posterior inclusion probability (PIP) for member SNP i computed from the fine-mapping analysis of the molecular QTLs.

The computation of $\text{Pr}\left(\mathit{\gamma }\in {\text{Γ}}_1|\mathit{d}\in D_1,{\mathit{Y}}_g\right)$ can be formulated as a problem of fine-mapping GWAS hits with informative molecular QTL priors.²¹ More specifically, the variant-level priors,

$$\begin{array}{l}{\pi }_{\text{ne}}:=\text{Pr}\left({\gamma }_i=1|d_i=0\right)\\ {\pi }_{\text{e}}:=\text{Pr}\left({\gamma }_i=1|d_i=1\right)\end{array}$$ (Equation 5)

can be estimated by a multiple imputation (MI) procedure described in Hukku et al.¹⁵ Thus, one can compute the prior required for the locus-level colocalization analysis by considering all compatible configurations of γ and d values, i.e.,

$$\begin{gathered} \text{Pr}\left(\mathit{\gamma }\in {\text{Γ}}_1|\mathit{d}\in D_1\right) \\ =\left(\begin{array}{l}p\\ 1\end{array}\right){\left(1-{\pi }_{\text{ne}}\right)}^{p-1}{\pi }_{\text{e}}+2\left(\begin{array}{l}p\\ 2\end{array}\right){\left(1-{\pi }_{\text{ne}}\right)}^{p-2}\left(1-{\pi }_{\text{e}}\right){\pi }_{\text{ne}} \\ =p{\left(1-{\pi }_{\text{ne}}\right)}^{p-2}\left[{\pi }_{\text{e}}\left(1-{\pi }_{\text{ne}}\right)+\left(p-1\right){\pi }_{\text{ne}}\left(1-{\pi }_{\text{e}}\right)\right]. \end{gathered}$$ (Equation 6)

Similarly,

$$\text{Pr}\left(\mathit{\gamma }=0|\mathit{d}\in D_1\right)=p{\left(1-{\pi }_{\text{ne}}\right)}^{p-1}\left(1-{\pi }_{\text{e}}\right).$$ (Equation 7)

As in the variant-level colocalization analysis, the PIPs of GWAS SNPs are assumed to be available from Bayesian fine-mapping methods based on an exchangeable and eQTL non-informative prior, $\text{Pr}\left({\gamma }_i=1\right):=\pi$, which can also be estimated by the average of all GWAS PIPs.¹⁵ For this eQTL non-informative prior, the induced prior probabilities for the locus of interest are given by

$$\begin{array}{l}\text{Pr}\left(\mathit{\gamma }\in {\text{Γ}}_1\right)=p\pi {\left(1-\pi \right)}^{p-1}\\ \text{Pr}\left(\mathit{\gamma }=0\right)={\left(1-\pi \right)}^{p-1}\end{array}$$ (Equation 8)

It again follows from Equation 2 that

$$\text{Pr}\left(\mathit{\gamma }\in {\text{Γ}}_1|{\mathit{Y}}_g\right)=\sum _{i=1}^p\text{Pr}\left({\gamma }_i=1|{\mathit{Y}}_g\right).$$ (Equation 9)

The marginal likelihood defined by the Bayes factor, $\text{BF}=\frac{P\left({\mathit{Y}}_g\right|\mathit{\gamma }\in {\text{Γ}}_1)}{P\left({\mathit{Y}}_g\right|\mathit{\gamma }=0)}$, can be obtained from

$$\text{BF}=\frac{\text{Pr}\left(\mathit{\gamma }\in {\text{Γ}}_1|{\mathit{Y}}_g\right)}{1-\text{Pr}\left(\mathit{\gamma }\in {\text{Γ}}_1|{\mathit{Y}}_g\right)}\frac{\left(1-\pi \right)}{\pi p}.$$ (Equation 10)

Put together, by Equations 2, 6, (7), and (10), and the Bayes theorem,

$$\text{Pr}\left(\mathit{\gamma }\in {\text{Γ}}_1|\mathit{d}\in D_1,{\mathit{Y}}_g\right)=\frac{\text{Pr}\left(\mathit{\gamma }\in {\text{Γ}}_1|\mathit{d}\in D_1\right)\text{BF}}{\text{Pr}\left(\mathit{\gamma }=0|\mathit{d}\in D_1\right)+\text{Pr}\left(\mathit{\gamma }\in {\text{Γ}}_1|\mathit{d}\in D_1\right)\text{BF}}$$ (Equation 11)

Thus, the desired locus-level colocalization probability, $\text{Pr}\left(\mathit{\gamma }\in {\text{Γ}}_1,\mathit{d}\in D_1|{\mathit{Y}}_g,{\mathit{Y}}_e\right)$, can be computed by Equation 3.

Finally, for each gene, we define a gene-level colocalization probability (GLCP) by

$${\text{GLCP}}_{G_t}=1-\prod _{l\in G_t}\left(1-{\text{LCP}}_l\right).$$ (Equation 12)

Results

Comparing findings from TWAS scanning and colocalization analysis

We performed TWAS scanning and variant-level colocalization for the four selected GWAS traits and the eQTL data from 49 GTEx tissues. A correlation testing p value from PTWAS and a GRCP from fastENLOC are computed for each trait-tissue-gene combination.

We compute the Spearman’s rank correlation between the -log10 PTWAS p values and the corresponding GRCPs among all examined genes in each trait-tissue pair. Across the 196 trait-tissue pairs, the two measures are only modestly correlated (mean = 0.223 and median = 0.085). Despite their correlations’ being significantly different from 0 in all trait-tissue pairs, TWAS scanning and colocalization analyses show a high degree of discordance in ranking important genes (Figure S1).

Next, we inspected the overlapping between noteworthy genes implicated by the two approaches (i.e., the set of conceptually replicated genes). Following previous investigations,^1,5,6,25 we consider that a gene is noteworthy in the colocalization analysis if its GRCP exceeds the probability threshold of 0.50 for a given trait-tissue pair. In the TWAS analysis, a gene is deemed noteworthy if it is rejected at the FDR 5% level in a trait-tissue pair (FDR controls are performed via the qvalue method based on the PTWAS p values). The full results of this analysis are summarized in Table 1. Marginally, the TWAS analysis implicates many more noteworthy genes than the colocalization analysis does (128,130 vs. 2,337) across 49 × 4 = 196 trait-tissue pairs. Among the two sets, there is an overlap of 2,054 genes, corresponding to 88% of the noteworthy colocalization genes and 1.6% of the noteworthy TWAS genes, respectively. This finding suggests that most colocalization genes also show strong evidence of TWAS associations, whereas the vast majority of TWAS genes generally lack strong evidence for variant-level colocalizations.

Table 1.

Noteworthy findings in joint analysis of GTEx eQTL and four GWAS traits by different analysis approaches

Complex trait	Analysis approach
	TWAS	VCa	LCb	TWAS + VC	TWAS + LC
Height	116,396	1,674	5,387	1,524	4,701
CAD	2,500	612	1,013	486	762
HDL	4,996	35	652	30	448
LDL	4,238	16	464	14	344
Total	128,130	2,337	7,516	2,054	6,255

For TWAS scanning, the noteworthy genes are identified at a 5% FDR level in each trait-tissue pair; for VC and LC analysis, the noteworthy genes are those with GRCP and GLCP values ≥ 0.50, respectively.

^aVariant-level colocalization analysis.

^bLocus-level colocalization analysis.

To better understand the discrepancy between the TWAS and colocalization analysis, we subsequently investigated the two difference sets of the noteworthy genes in greater detail.

Strong colocalization and weak TWAS signals

There are 283 trait-tissue-gene combinations that show strong variant-level colocalization but weak TWAS association evidence. A small subset of these findings can be attributed to the threshold effect of TWAS analysis. That is, if we re-define noteworthy TWAS genes by (slightly) relaxing the FDR control level, these combinations will be re-classified in the overlapping set. However, the majority of the combinations in this set show compatibility with the null hypothesis of the TWAS scan, suggesting that genetically predicted gene expression levels are uncorrelated with complex traits of interest. Upon further inspection, we find that most of these instances can be explained by the phenomenon known as “horizontal pleiotropy.”

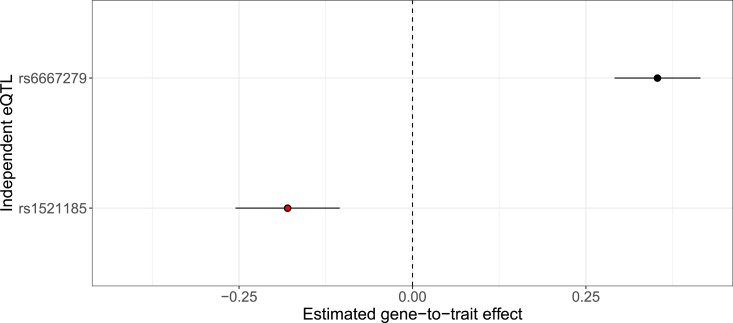
To illustrate, we take one of the extreme examples in the CAD GWAS. Two independent eQTLs are confidently identified (with posterior probabilities >0.92) in TDRKH (MIM: 609501) (Ensembl: ENSG00000182134) from the GTEx artery tibial tissue samples. One of the eQTL signals, represented by 10 tightly linked SNPs, also shows strong colocalization evidence, with GRCP = 0.92. In contrast, the predicted gene expression, constructed primarily from these two independent eQTL signals, shows little correlation with GWAS CAD status; the resulting p value is = 0.98. A detailed instrumental variable (IV) analysis, implemented in the PTWAS estimation procedure, reveals that the two independent eQTLs indicate opposite gene-to-trait effects on the GWAS trait (Figure 1): one implies that increased gene expression levels increase CAD risk, whereas the other suggests that increased expression levels decrease the risk. When the two eQTLs are combined to predict gene expressions, the overall gene effect on the disease implicated by the predicted expression levels is “canceled out.” The extreme level of heterogeneity estimated for gene-to-trait effects by independent instruments indicates that the vertical pleiotropy represented by variant → gene → trait is highly unlikely in this case.

Figure 1.

Estimated gene-to-trait effects on CAD by two independent eQTL SNPs of TDRKH explain its strong colocalization but weak TWAS signals

The eQTL fine-mapping analysis of TDRKH with GTEx tibial artery tissue samples identifies two independent strong eQTLs (SPIPs $>0.9$) represented by the lead SNPs rs6667279 and rs1521185, respectively. The second eQTL signal, represented by rs1521185 (highlighted in red), also shows strong variant-level colocalization, with RCP = 0.92. The figure shows estimated gene-to-trait effects when the two lead independent eQTL SNPs are used as instruments. Specifically, the first instrument shows that increased gene expression is associated with increased CAD risk, whereas the colocalized instrument predicts the opposite. As a result, the gene expression predicted on the basis of combining the two SNPs shows no evidence of association with CAD risk (PTWAS-scan p value = 0.98).

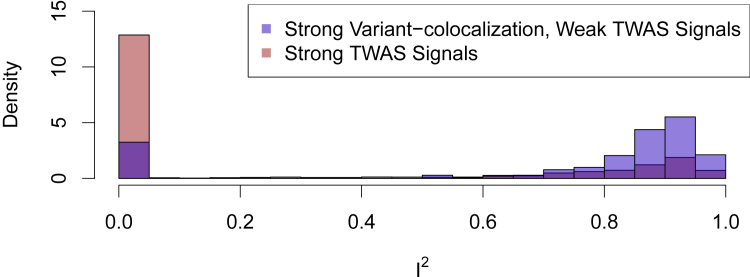
Among the 283 identified combinations, the overwhelming majority of the genes contain multiple independent eQTLs. We quantify the heterogeneity of the inferred gene-to-trait effects by using all available independent eQTLs for each combination and computing an I² value.¹⁰ (An I² value ranges from 0 to 1, where values close to 1 indicate extreme heterogeneity.) For example, the I² value for TDRKH illustrated above is 0.95. The distribution of I² values from this set is shown in Figure 2. The mean I² value is 0.73 (median = 0.88), clearly indicating that the majority of cases in this category suggest horizontal, instead of vertical, pleiotropy. In comparison, the set of genes implicated by both TWAS scanning and colocalization analyses have much lower I² values on average (mean = 0.28; median = 0.00).

Figure 2.

Histogram of I² statistics for genes with strong variant-level colocalization but weak TWAS signals

The I² statistic represents the level of heterogeneity in estimated gene-to-trait effects from independent eQTLs. Large I² values (i.e., I²→1) indicate that vertical pleiotropy is unlikely. The figure shows that genes with strong variant-level colocalization but weak TWAS signals are more likely to have high I² values than those with strong TWAS signals. That is, the phenomenon illustrated in Figure 1 can be common in this set of genes. The peak at I² = 0 for this set mostly represent the genes whose TWAS-scan p value approach but do not exceed the pre-defined FDR significance level.

In summary, we find that most instances in this difference set of implicated genes represent a scenario where the two integrative-analysis approaches can be complementary. Additionally, most implicated genes in this set are unlikely to be direct causal genes for the complex traits, and their relevance to the complex traits could potentially be explained by the phenomenon of horizontal pleiotropy.

Strong TWAS and weak colocalization signals

Strong TWAS and weak colocalization signals account for most discrepancies between colocalization and TWAS analyses. This phenomenon is largely anticipated by different hypotheses employed by the two approaches. A straightforward analytical derivation shows that discovering a TWAS signal does not imply the existence of variant-level colocalization. Instead, the necessary conditions that drive TWAS signals are much relaxed and can be precisely summarized in the following proposition.

Assuming linear prediction and association models and provided that a target gene’s genotype-predicted gene-expression level is correlated with a complex trait of interest, there is at least one inferred eQTL of the target gene in linkage disequilibrium with a causal GWAS variant. (Proposition 1)

Proof: Let sets E and G denote the collections of inferred eQTLs (of the target gene) and the causal GWAS hits, respectively. According to the linear-model assumption, the genotype-predicted gene expression (${\hat{y}}_e$) can be written as

$${\hat{y}}_e={\hat{\mu }}_e+\sum _{i\in E}{\hat{\beta }}_i{g}_i,$$ (Equation 13)

where g_i represents the genotype of SNP i and ${\hat{\beta }}_i$ is the estimated eQTL effect for prediction. Without loss of generality, assume the complex trait of interest (y_c) is quantitative and its genetic association can be described by the following linear model, i.e.,

$$y_c={\mu }_c+\sum _{j\in G}{\alpha }_j{g}_j+e,e\sim \text{N}\left(0,{\sigma }^2\right),$$

where e and σ² represent the residual error and its variance, respectively, and α_j denotes the genetic effect of SNP j to the complex trait.

A TWAS scan procedure examines the correlation between ${\hat{y}}_e$ and y_c and tests the null hypothesis, $H_0:Corr\left({\hat{y}}_e,y_c\right)=0$. It follows that

$$\text{Corr}\left({\hat{y}}_e,y_c\right)\propto \sum _{i\in E,j\in G}{\alpha }_j{\hat{\beta }}_i\text{Cov}\left(g_i,g_j\right)$$ (Equation 14)

Therefore,

$$\text{Corr}\left({\hat{y}}_e,y_c\right)\ne 0\Rightarrow \exists \text{ a pair of }\left(i,j\right),\text{ such that }{\alpha }_j{\hat{\beta }}_i\text{Cov}\left(g_i,g_j\right)\ne 0.$$

Note that this simple proposition states a necessary but not sufficient condition for the existence of TWAS signals. Specifically, the TWAS signal is driven by the sum of all non-zero ${\alpha }_j{\hat{\beta }}_i\text{Cov}\left(g_i,g_j\right)$ pairs. As illustrated in the previous section, it is statistically possible that multiple terms with different signs can cancel each other out. Additionally, the linearity of the prediction-model assumption covers almost all popular TWAS approaches, but it can be relaxed to allow non-linear prediction functions. In the expanded prediction function family, Equation 13 becomes a first-order approximation.

The proposition also implies a direct connection between the TWAS scan and variant-level colocalization analysis. By definition, a variant-level colocalization signal satisfies the condition ${\alpha }_j{\hat{\beta }}_i\text{Cov}\left(g_i,g_j\right)\ne 0$ for some i = j. A colocalized genetic variant of both molecular and complex traits should also drive a TWAS signal in the absence of the cancellation phenomenon. This corollary explains our observation that most genes implicated by the colocalization analysis are also implicated by the TWAS scan.

Next, by assuming the absence of allelic heterogeneity for the target gene, we consider the scenario whereby only a single term in Equation 14 drives a TWAS signal. It becomes apparent that the strength of a TWAS signal reflects the joint effect of ${\alpha }_j,{\hat{\beta }}_i$, and the LD between the two variants (i and j). It further implies that even when the LD between a causal eQTL and a GWAS hit is weak, relatively strong genetic effects, α_j and/or β_i, can compensate for the strength of the resulting TWAS signal. This result seemingly explains a common pattern in practical TWAS scan results: noteworthy signals tend to cluster around some of the strongest GWAS hits. Mancuso et al.¹¹ also discussed a similar pattern of clustered TWAS signals due to LD. However, our derivation does not need to assume any true causal relationship between genes and the complex trait of interest (i.e., the phenomenon can exist without any causal genes).

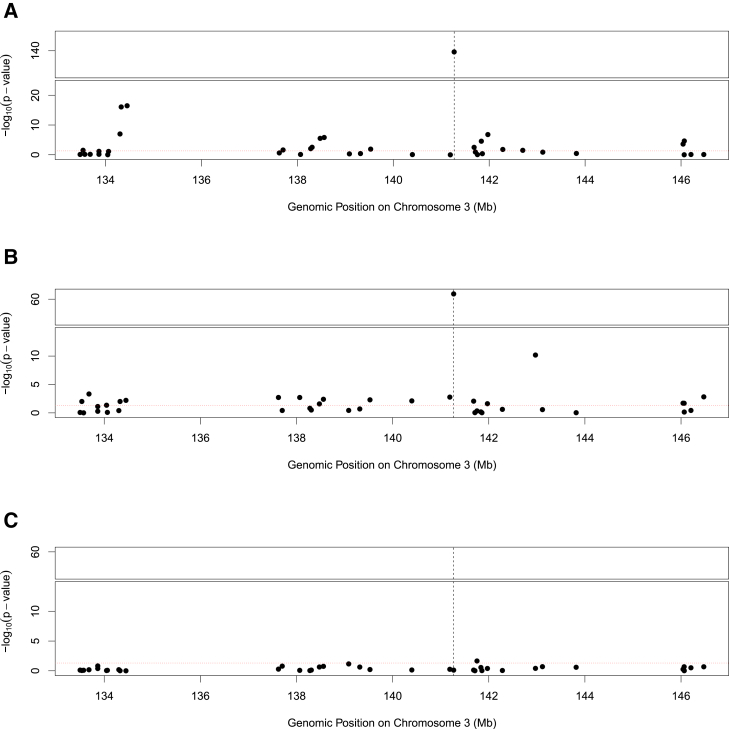
Figure 3 shows a particular instance from the TWAS scan of a height GWAS (UK Biobank) and GTEx skeletal-muscle genes, where a cluster of TWAS signals are centered around one of the most significant GWAS hits on chromosome 3 (rs2871960) identified in the UK Biobank data. The eQTL analysis of the GTEx data suggests that the putative causal GWAS SNP is probably not a causal eQTL.

Figure 3.

Simulation illustrating LD-hitchhiking effects in TWAS scan

(A) Panel A shows an observed cluster of significant TWAS-scan genes from UK Biobank standing-height data. The signals are centered around ZBTB38 (MIM: 612218) (Ensembl ID: ENSG00000177311), whose position is labeled by the dotted vertical line. Each point on the figure represents a TWAS-scan p value of a neighboring gene.

(B) A similar cluster pattern can be replicated from a simulated dataset, which is generated under the assumption of a single causal variant within ZBTB38.

(C) The significant TWAS-scan cluster disappears once the genotypes of the sole causal SNP are regressed out from the simulated phenotype data. The horizontal red line indicates the nominal 0.05 significance level in all three panels. The simulation experiment illustrates that the significant TWAS-scan findings can be attributed to the LD-hitchhiking effects.

We conducted simulations to demonstrate that this single GWAS signal (p value = 2.4 × 10⁻²⁵⁶) drives the entire cluster of TWAS signals at this locus. We utilized the real eQTL genotype and phenotype data from GTEx for 39 neighboring genes at this locus and independently simulated the phenotype data of a complex trait; we assumed that rs2871960 was the only causal SNP. (The details of the simulation setting are provided in section 2.1 of the supplemental methods.) The PTWAS scan of the simulated data replicates the pattern observed in the real data; a third of neighboring genes show significant TWAS associations. To confirm that the sole GWAS association induces all TWAS signals, we repeated the analysis with the residuals of simulated complex trait phenotype by regressing out the genotypes of SNP rs2871960 (Figure 3). The results of the alternative TWAS scanning approach, SMR, display an identical pattern (Table S3).

Although the LD-hitchhiking TWAS signals are not false positives from the perspective of statistical associations, the abundance of signals of these sorts should caution the biological interpretations. For example, it would be a mistake to regard all LD-hitchhiking TWAS signals as independent candidates of causal genes for the trait of interest. On this point, we are in full agreement with Mancuso et al.¹¹ that TWAS results need to be further processed, better understood, and carefully reported.

In summary, our statistical analysis reveals some main characteristics of TWAS signals, which do not require variant-level colocalization and tend to be correlated. These characteristics help explain the difference set of strong TWAS but weak colocalization signals. Regarding this difference set of implicated genes, we find that the two approaches can be reconciled by (1) re-defining the standard for colocalization (i.e., adjusting colocalization analysis); and (2) removing non-independent findings from TWAS-scan reporting (i.e., adjusting TWAS scanning).

Locus-level colocalization: A reconciliation

The proposed approach to locus-level colocalization analysis has some desired properties that can reconcile the results of the TWAS scan and colocalization analysis, especially for the set of genes showing strong TWAS but weak variant-level colocalization signals.

From the perspective of variant-level colocalization analysis, the lack of statistical power is a primary limiting factor in the analysis of current molecular and complex-trait data. Many authors^26,27 have shown that it is often difficult, if not impossible, to pinpoint the causal genetic associations in current molecular QTL mapping studies. Furthermore, with a limited sample size, the lead SNPs, whether quantified by Bayesian or frequentist approaches, are often not the true causal SNPs. In many cases, we are relatively certain of a genuine association signal among a group of tightly linked variants (e.g., variants within a signal cluster) but uncertain about the exact variants. Hukku et al.¹⁶ show that such uncertainty causes a large class of false-negative findings (i.e., class II FNs) in variant-level colocalization analysis. Their simulation studies based on realistic settings show more class II FNs than the identified true findings. To address this fundamental limitation, the proposed locus-level colocalization analysis identifies the co-existence of casual eQTLs and GWAS hits at a slightly coarser resolution. The key rationale is that even when locus-level colocalizations do not show strong evidence of variant-level colocalizations in the current data, they might very well prove to be class II FNs in future experiments with improved statistical power.

From the perspective of the TWAS scan, the critical issue for reconciliation is to filter out redundant representations due to LD and report only independent and biologically relevant signals. One possible solution is to require causal SNPs for molecular and complex traits colocalized at a small enough genomic region, such that not only is Cov(g_i,g_j) in Equation 14 automatically constrained, but the interpretation of the TWAS signal also becomes natural. This idea is not new. Many authors^16,25,28 have proposed using variant-level colocalizations as a prerequisite for following up on TWAS scan results. These proposals are also supported by a class of probabilistic generative models that connect TWAS scanning and colocalization analysis (Section 2.2 of the supplemental methods). Here, we relax the colocalization standard and consider the limited practical power in identifying variant-level colocalizations.

To interpret significant results of TWAS scanning by using the locus-level colocalization analysis, we require that the GLCPs (defined in the Equation 12) of candidate causal genes exceed a threshold (pre-defined or by FDR control).

Simulation study

We designed and conducted simulation experiments to benchmark the proposed locus-level colocalization analysis by comparing it to variant-level colocalization and TWAS-scan analyses. We took the real individual-level genotype data from 838 individuals in the GTEx covering 22 distinct LD regions. Specifically, we selected random segments of 50 consecutive common SNPs (with minor-allele frequency > 0.1) from each of the 22 autosomes. Treating the 1,100 selected SNPs as a single cis region of a target gene, we randomly selected two SNPs to simulate the gene expression levels and two SNPs to simulate a quantitative trait by using a set of linear models (see details in the material and methods section). This design ensured modest to strong realistic LD patterns within each LD region but weak LD between different regions (Figures S2 and S3). We generated 5,000 datasets where all four causal SNPs were located in distinct LD regions (i.e., no variant or locus-level colocalizations). Additionally, we simulated 2,500 datasets with one causal eQTL and one causal GWAS hit colocalized at a single variant, and the remaining causal eQTL and the remaining causal GWAS SNP reside in two different LD regions. This particular simulation scheme can be re-formulated by a structural equation model (SEM) commonly assumed by TWAS scanning and Mendelian randomization (Section 2.2 of the supplemental methods). Thus, the simulated datasets are also suitable for TWAS scanning. By this design, we intended to avoid LD-hitchhiking effects, such that the TWAS results would be more concordant with the locus-level colocalization findings.

We analyzed the simulated datasets by using TWAS scanning and variant- and locus-level colocalization methods. We applied three approaches to TWAS scans: PTWAS, PrediXcan,⁷ and the improved SMR approach (a single-SNP TWAS method described in section 1 of the supplemental methods). For the variant- and locus-level colocalization analyses, we used the algorithms implemented in the software package fastENLOC.

We considered a finding to be a true positive one if a simulated gene harboring a colocalized signal was identified at 5% FDR level, and we considered a finding to be a false positive one if a gene where causal variants reside in distinct LD segments passed the same significance threshold for FDR control. The results by the three different integrative-analysis approaches are summarized in Table 2 and Figure 4.

Table 2.

Comparison of power and realized FDR in simulation study

Method	Power	FDR
Locus-level colocalization	0.70 (1739/2500)	0.01 (14/1753)
SNP-level colocalization	0.43 (1067/2500)	0.00 (0/1067)
PTWAS	0.67 (1684/2500)	0.20a (418/2012)
PrediXcan	0.55 (1384/2500)	0.16a (260/1644)
SMR	0.45 (1119/2500)	0.21a (299/1418)

^aRealized FDR exceeds the control level (5%).

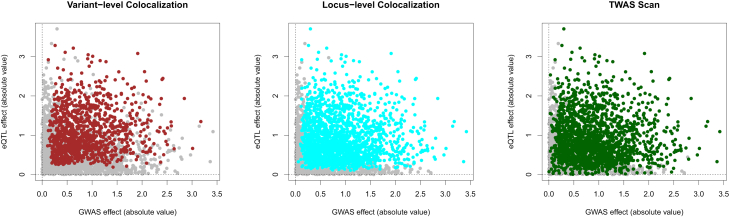
Figure 4.

Comparing sensitivity of different integrative-analysis approaches in simulations

The bi-plots represent the eQTL and GWAS effects of the colocalized variant in 2,500 simulated datasets. The highlighted points in each plot indicate the true positive discoveries by the corresponding methods at the 5% FDR level. The power increment of the locus-level colocalization method over the variant-level colocalization method is visually clear.

The variant-level colocalization analysis forms a conservative baseline for comparison. It reports no false-positive findings but the lowest power. Following the methods of Hukku et al.,¹⁶ we further assigned all the false-negative findings to one of two distinct classes. For a colocalized signal, a class I false negative (FN) refers to a failure to identify the association signal for at least one trait within a genomic segment; a class II FN refers to a failure to quantify the variant-level colocalization probability despite both association signals’ being localized within the same segment. We estimate that 47.4% of FNs (or 679 instances) in variant-level colocalization analysis fall into the category of class II. Our results indicate that the proposed locus-level colocalization analysis effectively rescues those class II FNs without greatly increasing false-positive findings: 95.2% of the original class II FNs are now identified by the locus-level colocalization analysis. There is no loss of true variant-level colocalization findings because LCP is always no less than the corresponding RCP (Figure 4).

The multivariate PTWAS-scan approach reports the most findings (2,102) across all examined methods by a large margin. However, despite our best efforts in assembling the artificial genomic region, a significant proportion of the TWAS-scan findings (19.9%) are results of weak LDs between distinct eQTL and GWAS variants located in different segments. Specifically, we found that the maximum R² values between a causal eQTL and a causal GWAS hit a range from 6 × 10⁻⁴ to 0.148 (mean = 0.027) within this set. A detailed inspection confirms that the true expectations of gene expression levels (computed by the true genetic association model of gene expressions) are indeed significantly correlated with the simulated phenotypes. We emphasize that these findings are only considered false positives by the standard of colocalization analysis or the intended structural equation model. In summary, the extremely low level of LD required to drive a TWAS signal can be surprising, but this phenomenon is well explained and anticipated by Proposition 1 (i.e., the strong genetic effects of eQTLs and/or GWAS hits can compensate weak LDs). Interpreting the (biological) relevance of this set of genes can be difficult because such associations should only be characterized as accidental. The joint analysis based on filtering TWAS scan results with locus-level colocalization analysis results is proven to be effective at removing these accidental association signals. The filtered TWAS discovery set maintains reasonably good power (61%) and is much easier to interpret.

Re-analysis of GTEx and GWAS data via locus-level colocalizations

Finally, we re-analyzed the four complex-traits GWAS and the GTEx eQTL data by using the proposed locus-level colocalization approach. We again ensured that all examined methods utilized identical input information. Detailed comparisons between PTWAS, variant-, and locus-level colocalization analyses are provided in Table 1. Across 196 trait-tissue pairs, the locus-level colocalization identifies 7,516 genes with GLCP >0.50, representing a 2.2-fold increase of discoveries than the variant-level colocalization analysis. A remarkable 83% of the high-GLCP genes overlap with the significant PTWAS genes. We considered this set of 6,255 PTWAS genes filtered by locus-level colocalization analysis to be high-priority genes for further validation.

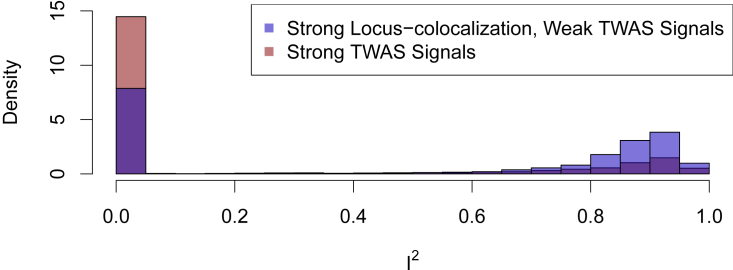
We first inspected the set of 1,261 genes that showed high GLCP but did not pass FDR control at 5% level in a PTWAS scan analysis. Similar to the weak TWAS and strong colocalization signals implicated by variant-level colocalization analysis, this set of genes also shows excessive heterogeneity in estimated gene-to-trait effects across multiple independent eQTL signals (Figure 5), suggesting potential horizontal pleiotropy. Figure 5 also indicates an increase of genes whose PTWAS signals are close but do not pass the FDR control threshold.

Figure 5.

Histogram of I² statistics for genes with strong locus-level colocalization but weak TWAS signals

The figure indicates that genes with strong locus-level colocalization but weak TWAS signals are more likely to have high I² values than those with strong TWAS signals. This phenomenon is similar to findings for genes with strong variant-level colocalization but weak TWAS signals, indicating that both sets of genes are most likely enriched with cases of horizontal pleiotropy.

In the set of 6,255 PTWAS significant genes filtered by the locus-level colocalization analysis, we find many discoveries have documented biological relevance to the corresponding complex traits in the literature. We first investigate the Online Mendelian Inheritance in Man (OMIM)²⁹ database to find associated genes. For this investigation, we select phenotype OMIM IDs mapped to any of our four traits and subsequently identify all confirmed gene associations with those phenotypes. In total, we extract 12 validated genes from the OMIM across the 4 analyzed complex traits, with 6 in our result by the joint PTWAS and locus-level colocalization analysis (Table S1). It is worth noting that the joint SNP-level colocalization and PTWAS analysis only identifies one out of 12 genes.

An illustrative example is LPL (MIM:609708) (Ensembl id: ENSG00000175445) with HDL. Within the adipose subcutaneous tissue, there is a very strong TWAS signal (p value = 9.7 × 10⁻¹³⁵) and substantial evidence for locus-level colocalization (GLCP = 0.97). Meanwhile, the GRCP for this gene is only 0.07, reinforcing the added utility of locus-level colocalization.

Additionally, we utilized one of the largest gene-disease association repositories, DisGeNET,³⁰ to inspect the biological relevance of CAD-associated genes implicated by the proposed joint analysis. DisGeNET comprehensively integrates and ranks multiple types of reliable gene-disease association evidence from a catalog of source databases. We pulled out a list of 65 high-confidence CAD-relevant genes whose DisGenNET scores are greater than the built-in default selection threshold of 0.3. The PTWAS scanning identified 510 unique genes across 49 tissues in our integrative analyses. A subset of 172 unique genes passed the additional filtering of the locus-level colocalization analysis. We found that 23 of the 172 genes appear in the DisGenNET CAD gene list (Table S2). In comparison, the remaining 338 genes that lack locus-level colocalization evidence only contribute seven additional hits on the DisGenNET CAD list. A Fisher exact test indicates that the enrichment of CAD-relevant genes implicated by the proposed joint analysis is statistically highly significant in contrast to the stand-alone TWASscanning (p value = 8.8 × 10⁻⁷). Compared to the joint analysis of TWAS and variant-level colocalization analysis (which flags 17 DisGenNET genes from 117 implicated unique genes), the proposed method represents a 35% increase in confirmed discoveries, while having a similar level of signal enrichment.

Discussion

This paper systematically investigates two prevailing methods of integrative genetic analysis, TWAS scanning and colocalization analysis, and focuses on understanding and reconciling their inferential differences in practical settings. From the perspective of inferential reproducibility, we identify multiple statistical and biological factors that yield different sets of implicated genes. In one scenario (i.e., strong colocalization but weak TWAS signals), we find that most genes in the specific difference set show interesting characteristics requiring further biological investigations, indicating that the two approaches are complementary. In the other scenario (i.e., strong TWAS but weak colocalization signals), we find that the differences can be effectively reconciled. Subsequently, we propose and implement a new locus-level colocalization analysis method to bridge the two types of analyses. We illustrate that the proposed joint-analysis approach can produce a rich list of biologically relevant “conceptual replications” for downstream investigations and validations.

Variant-level colocalization analysis utilizes a conceptually rigorous and superior standard for examining the overlapping of causal association signals at the finest resolution. It exhibits the highest specificity among the existing integrative-analysis approaches. The most noticeable drawback is its limited sensitivity given currently available data.¹⁶ The issue is originated from the difficulty in quantifying variant-level association evidence and uncertainty in the presence of LD.^26,27 Although future data with more precise phenotyping (e.g., single-cell expression data) and/or a larger sample size will certainly improve the power of variant-level colocalization analysis, the intrinsic difficulty due to complex LD patterns might not be fully resolved. We trade off the rigid conceptual standard of variant-level colocalizations for improved sensitivity in the proposed locus-level colocalization analysis. This is mostly motivated by a series of realistic simulation studies presented in Hukku et al.¹⁶ and this paper, where the ratios of class II false negatives versus reported findings (which contain few false-positive errors) are often strikingly high (i.e., ∼1:1).

We acknowledge that locus-level colocalization analyses are conceptually not new. For example, RTC¹⁹ and JLIM²⁰ are two representatives of general-sense locus-level colocalization methods in the literature. However, we observe at least three distinct advantages of the proposed approach over the existing methods. First, we define target loci through the fine-mapping output of signal clusters, which harbor very limited but highly relevant candidate genetic variants. In comparison, existing approaches often analyze genomic regions at 100kb scales.^9,19,20 (We have attempted to apply these existing methods to our simulated data but failed to obtain results, mostly because of conflicts in the locus definition.) As expected, the precise locus definition provided by the proposed approach results in high specificity, which is comparable to variant-level colocalization analysis, as shown in our real-data analysis. It is worth emphasizing that the high-resolution feature of the proposed method makes it feasible to reconcile its results with the TWAS results. Second, the proposed approach takes full advantage of (Bayesian) multi-SNP fine-mapping analysis of molecular and GWAS data and yield more precise colocalization results with appropriate uncertainty quantification. In comparison, most existing methods rely on single-SNP-association testing results and often fail to account for widespread allelic heterogeneity in molecular traits. Third, the proposed method performs explicit enrichment estimation, which utilizes the prior information that molecular QTLs are most likely enriched in GWAS hits. The enrichment estimate is subsequently incorporated to allow computation of locus-level colocalization probabilities through an empirical Bayes framework and improve statistical power. This feature, inherited from the variant-level colocalization analysis,^16,31 is not presented in any existing locus-level colocalization methods.

The empirical comparison of TWAS scanning and colocalization analyses helps us identify statistical factors that differentiate the two sets of results. One of this work’s most important take-away messages is that the results of TWAS scans are unlikely to be independent and probably need further processing. At a certain level, PTWAS scanning is analogous to single-variant testing in the common practice of genetic-association analysis, where the community standard is not stopping at reporting significant individual variants but summarizing the testing results and grouping linked variants to flag independent causal variant-harboring loci.

Our proposal to apply locus-level colocalization to screen and filter the results of TWAS scanning follows the similar strategy established in PhenomeXcan,²⁵ which is proven to be effective at identifying biologically relevant potential causal genes. Given the increased sensitivity of locus-level versus variant-level colocalization analysis, the improvement in the performance of such a strategy is logically expected. We note that the software FOCUS utilizes an alternative and statistically elegant strategy (analogous to the multi-variant fine-mapping in genetic-association analysis) to parse correlated findings from TWAS scans and identify potential causal genes. This strategy can be highly effective if the assumption of a causal gene in the genomic region of interest is met. In comparison, our proposed strategy does not require such an assumption but relies on the biological implication from colocalizations and hence offers some added robustness in inference. We illustrate the differences between the proposed method and the FOCUS by using the LD-hitchhiking simulation data (Section 3 of the supplemental methods). In practice, the two strategies can be complementary and applied simultaneously. Additionally, we note that many authors^{8, 9, 10,12} have connected TWAS analysis to Mendelian randomization (MR) and instrumental variable (IV) analyses and point out that the scan procedure is equivalent to the testing procedure in MR and IV analyses. We strongly agree that additional estimation and heterogeneity-diagnostic procedures from the MR and IV analyses can be further applied to validate the causality of implicated genes in combination with the proposed joint analysis. Particularly, the set of consistent findings identified from both the TWAS scan and colocalization analyses form a strong set of causal candidate genes for the downstream validation and analysis. Finally, the proposed joint analysis can also be used for identifying cases of horizontal pleiotropy. We note that horizontal pleiotropy is a general statistical term for the alternative to a direct causal path linking genetic variants, molecular traits, and complex traits (i.e., vertical pleiotropy). Various biological mechanisms can lead to the observed phenomenon of horizontal pleiotropy. These findings can be critical to uncovering the full molecular mechanisms underlying complex diseases and deserve attention from the community.

Much of this work is motivated by a desire to understand the inferential reproducibility between TWAS scanning and colocalization analysis. Unlike the other types of reproducibility, namely, methods and results reproducibility, inconsistency in conclusions from different analytical methods is anticipated in the analysis of inferential reproducibility.¹⁷ Furthermore, the primary aim is to identify analytical assumptions and factors driving inferential differences and understand the extent of inconsistency between methods. These factors are particularly important for practitioners who aim to design analysis schemes with all available tools. As demonstrated in this paper, inferential reproducibility is fundamentally different from inferential errors/mistakes. It should be treated with care and, most importantly, in a context-dependent manner.

Published: May 5, 2022

Web resources

• •Data analysis and simulation code, https://github.com/xqwen/TWAS_vs_coloc
• •fastENLOC, https://github.com/xqwen/fastenloc
• •Harmonized GWAS summary statistics for standing height, HDL, LDL, and CAD, https://tinyurl.com/mr2636yy
• •Multi-tissue eQTL data from the GTEx project, https://www.gtexportal.org/home/
• •Online Mendelian Inheritance in Man, http://www.omim.org
• •PTWAS, https://github.com/xqwen/ptwas

Supplemental information

Table S1. Full list of genes from our data with validated associations in OMIM for all four examined traits (HDL, LDL, CAD, height)

We provide the PTWAS p value, GLCP, and GSCP from our analysis for each trait-gene-tissue combination, and we highlight all entries that appear in our filtered list of genes and that are significant in both TWAS and GLCP.

Table S2. Full list of genes from our data with validated associations in DisGeNET for CAD

We provide the PTWAS p value, GLCP, and GSCP from our analysis for each gene-tissue combination, and we highlight all entries that appear in our filtered list of genes and that are significant in both TWAS and GLCP.

Table S3. Full results from our simulations inspecting the LD-hitchhiking effect

We show the TWAS p value (both PTWAS and SMR) for each of the 39 examined genes, before and after the one causal GWAS SNP is regressed out.

Data and code availability

All real and simulated data used in this paper are publicly available (see web resources). The locus-level colocalization method is implemented in the software package fastENLOC v2.0, which is freely available at https://github.com/xqwen/fastenloc. The Github repository https://github.com/xqwen/TWAS_vs_coloc contains the necessary code and scripts for reproducing the analyses and simulations described in the paper.