Integrating mechanism-based modeling with biomedical imaging to build practical digital twins for clinical oncology

Chengyue Wu; Guillermo Lorenzo; David A Hormuth, II; Ernesto A B F Lima; Kalina P Slavkova; Julie C DiCarlo; John Virostko; Caleb M Phillips; Debra Patt; Caroline Chung; Thomas E Yankeelov

doi:10.1063/5.0086789

. 2022 May 17;3(2):021304. doi: 10.1063/5.0086789

Integrating mechanism-based modeling with biomedical imaging to build practical digital twins for clinical oncology

Chengyue Wu ^1,^a), Guillermo Lorenzo ^1,2,^1,2, David A Hormuth II ^1,3,^1,3, Ernesto A B F Lima ^1,4,^1,4, Kalina P Slavkova ⁵, Julie C DiCarlo ^1,3,^1,3, John Virostko ^3,6,7,^3,6,7,^3,6,7, Caleb M Phillips ¹, Debra Patt ⁸, Caroline Chung ⁹, Thomas E Yankeelov ^{1,3,6,7,10,11,}^{1,3,6,7,10,11,}^{1,3,6,7,10,11,}^{1,3,6,7,10,11,}^{1,3,6,7,10,11,}^{1,3,6,7,10,11}

PMCID: PMC9119003 PMID: 35602761

Abstract

Digital twins employ mathematical and computational models to virtually represent a physical object (e.g., planes and human organs), predict the behavior of the object, and enable decision-making to optimize the future behavior of the object. While digital twins have been widely used in engineering for decades, their applications to oncology are only just emerging. Due to advances in experimental techniques quantitatively characterizing cancer, as well as advances in the mathematical and computational sciences, the notion of building and applying digital twins to understand tumor dynamics and personalize the care of cancer patients has been increasingly appreciated. In this review, we present the opportunities and challenges of applying digital twins in clinical oncology, with a particular focus on integrating medical imaging with mechanism-based, tissue-scale mathematical modeling. Specifically, we first introduce the general digital twin framework and then illustrate existing applications of image-guided digital twins in healthcare. Next, we detail both the imaging and modeling techniques that provide practical opportunities to build patient-specific digital twins for oncology. We then describe the current challenges and limitations in developing image-guided, mechanism-based digital twins for oncology along with potential solutions. We conclude by outlining five fundamental questions that can serve as a roadmap when designing and building a practical digital twin for oncology and attempt to provide answers for a specific application to brain cancer. We hope that this contribution provides motivation for the imaging science, oncology, and computational communities to develop practical digital twin technologies to improve the care of patients battling cancer.

I. INTRODUCTION

A. Definitions of digital twins

1. Conceptual and practical definition of a digital twin

In 2010, NASA published a formal definition of a digital twin as an “integrated multi-physics, multi-scale, probabilistic simulation of a vehicle or system that uses the best available physical models, sensor updates, fleet history, etc., to mirror the life of its flying twin.”¹ Though specialized to aeronautics, this definition reflects the status of a digital twin as a natural extension of simulation and optimization. More recently, digital twins connote the coupling of quantitative sensing techniques capable of acquiring large datasets with realistic mathematical models that characterize key components of the spatial and temporal dynamics of the phenomena under investigation. Thus, digital twins have moved simulation beyond replicating a physical device and are now used to test components, diagnose issues, and optimize operations.² These developments have brought digital twins out of the realm of science fiction and into real-world application in fields as varied as manufacturing, aeronautics, public utilities, and—the subject of this article—oncology.

2. Mathematical definition of a digital twin

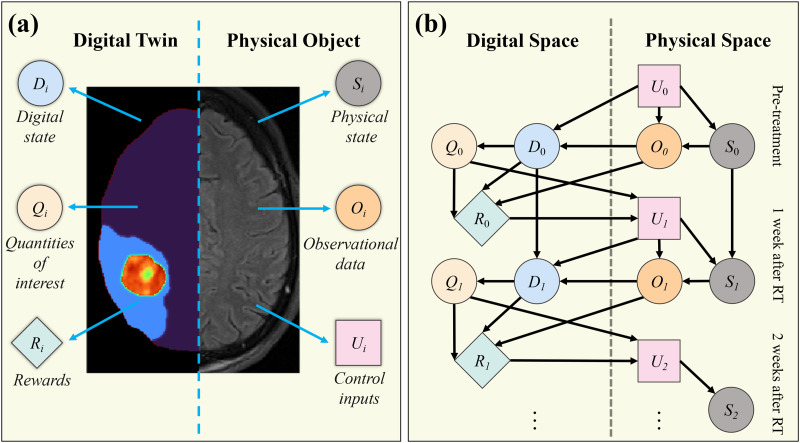
A digital twin is a mathematical model (or a collection of models) that provides a virtual representation of a specific physical object and predicts its behavior at future time points.³ Accurate predictions allow a tailored decision-making process for which actions could be applied to the target object to optimize either its behaviors or outcomes from an intervention. The general framework for building a digital twin of a particular object can be mathematically abstracted from six major components⁴ [see Fig. 1(a)]:

(1)
Physical state (S): the parameterized state of the physical object
(2)
Observational data (O): the available information describing the state of the physical object
(3)
Control inputs (U): the actions or decisions that influence the physical object
(4)
Digital state (D): the parameters and model inputs that define the computational models comprising the digital twin
(5)
Quantities of interest (Q): the model outputs, or quantities estimated via model outputs, describing the physical object
(6)
Rewards (R): the quantification of overall performance of the object-twin system.

Based on these six elements, a dynamic decision network can be established [see Fig. 1(b)]. Initially, experiments (U₀) are applied to the target physical object to obtain observational data (O₀), which represent the physical state (S₀). Then, the digital state (D₀) is constructed by leveraging these data to calibrate or assign the model parameters and define the digital twin geometry. The models constituting the digital twin can be statistical, mechanism-based, or a hybrid of the two. (The term “mechanism-based” refers to the property that each term or parameter included in the model represents a specific biological or physical mechanism.) The models specified by D₀ will output the predictions of the behaviors of the physical object [i.e., the quantities of interest (Q₀)]. Finally, based on Q₀, the predicted outcomes can be evaluated and quantified as rewards (R₀). For example, in oncology, rewards may be overall survival, drug toxicity, and quality of life. Furthermore, as guided by Q₀ and R₀, decisions (U₁) are made on what adjustments should be applied to the physical object and what additional experiments should be performed to monitor the changes of the physical state (S₁). As more data (O₁) are acquired, the digital state can be updated as D₁, as well as its outputs Q₁ and R₁. This iterative procedure can continue over time to optimize the behaviors of the physical object.

3. Examples of digital twins

The use of digital twins rapidly expanded beyond NASA's initial efforts into a variety of fields. For example, the automotive industry was an early adopter of digital twins, using them to guide vehicle design, test precondition safety systems in adverse conditions, monitor vehicle use, and streamline service visits. In fact, some automobile manufacturers now generate a digital twin for every car sold.⁵ In this setting, a myriad of sensors on each vehicle continuously monitor data from the various components and stream these data to digital twins at the factory. If these data indicate that the vehicle needs maintenance, the driver can be alerted, or the issue can be corrected remotely by a software update. Similar implementations of digital twins have occurred across the transportation industry including planes and trains. The utility sector has also made use of digital twins to monitor electric grids, wind power farms, and wastewater plants in an attempt to save energy and predict faults.⁶ In fact, digital twins are said to be bringing a “Fourth Industrial Revolution” as “smart factories” with embedded sensors can monitor the manufacturing process and synchronize with a digital twin to optimize processes, make decisions about production control, and predict maintenance and failure of components.⁷ Most recently, digital twins have begun to be applied in healthcare and medicine.⁸ By employing medical imaging data, image-guided digital twins have been used to address problems in cardiology,^3,9 diabetes,¹⁰ and oncology.¹¹ All these applications have a common goal of improving treatment outcomes for individual patients by building patient-specific models that can predict disease progression and treatment response.

B. Rationale for digital twins in clinical oncology

1. How clinical trials determine therapeutic regimens

The conventional approach for determining therapeutic regimens in oncology, as well as other diseases, is through the clinical trial process. A clinical trial is an investigation performed on human subjects for the purpose of assessing the safety or efficacy of a specific intervention. The treatment(s) being tested may be pharmacological agents, medical devices, or novel surgical procedures or interventions. Clinical trials typically employ a three-phased approach. In oncology, phase I studies seek to identify side effects and dose-limiting toxicities using a dose-escalation paradigm. If phase I studies demonstrate safety and acceptable toxicity, the efficacy of the treatment is evaluated in subsequent phase II studies. Randomized phase II and III studies frequently compare the investigational intervention against the current standard-of-care intervention. Phase II studies are smaller than phase III studies and are focused on establishing efficacy while continuing to evaluate safety. Phase III trials tend to be much larger, involve many sites, and are designed to obtain data to characterize whether the investigational intervention is more effective and safer than the intervention of the control arm. It is these data that are typically submitted with a new drug application to the Food and Drug Administration (FDA) in the United States or similar regulatory bodies.

For every treatment that has been approved after a successful phase III trial, there are copious examples of interventions that have failed in clinical trials. In fact, fewer than 10% of drugs in phase I studies will be approved, while approximately 25% of phase II and 60% of phase III drugs will be approved.¹² Despite the large number of studies undertaken for successful drugs to reach patients, clinical trials are also plagued by scarcity in terms of the number of patients enrolled in each study, the number of treatments that can be compared simultaneously, and the range of doses that can be evaluated in any one trial. Thus, the cost of performing trials on drugs that fail, combined with the cost of performing clinical trials with the necessary rigor to prevent bias, adds to incredibly high clinical research costs; the budget for a single oncology study in the U.S. is estimated to be $79 × 10⁶, including an average per-patient cost of $59 500.¹³ Recruitment is also a challenge: only 3% of adult cancer patients enroll in clinical trials, with lower enrollment from elderly and minority groups.¹⁴ These low accrual rates prolong study duration and have led to early closure or failure of many clinical trials¹⁵ and the imbalance of representative populations enrolled into clinical trials may introduce bias and limit the generalizability of the study findings. An interesting exception is clinical trials for pediatric cancers, in which more than 50% of patients enroll in clinical trials.^16,17

Given the high cost and challenges of recruiting the required number of patients, it is difficult to overstate the importance of designing more expedient methods for accepting or rejecting candidate treatments as early as possible, as well as for determining which patients could benefit from candidate treatments to guide efficient patient recruitment. While designing better in vitro and preclinical models certainly helps, these systems may fail to mimic the complexity of human studies.¹⁸ An in silico approach that is capable of faithfully representing an individual's biology and interactions with various interventional strategies would not only dramatically reduce the cost of clinical trials but also improve the efficiency of identifying promising drugs in a substantially shorter timeframe.

Aside from the high cost and challenges of patient recruitment, clinical trials (as well as other population-based approaches) have an intrinsic limitation of not being able to capture the unique biological features characterizing the tumors of individual patients, and this can lead to sub-optimal outcomes. Clinical trials can only control for a certain number of variables to ensure that the study enrollment is feasible, which leaves many other variables that may influence the response of patients. For example, other medications patients may be taking, comorbid illnesses that may have not been accounted for in the study design but may influence toxicity, etc. Most phase I studies are done in patients who have been heavily pretreated, which may influence individual patient responses. Furthermore, different combinations of multiple therapies and the timing and sequencing of treatment delivery may influence the outcome; but given the enormous number of therapeutic options it is simply impossible for clinical trials to experimentally evaluate all the possible interventions that might be appropriate for a particular cancer. As additional therapeutic targets and treatment options are continuously evolving,^19–21 the determination of proper treatments for a specific patient becomes increasingly complex.

2. How digital twins can hasten the arrival of patient-specific oncology care

Digital twins provide a practical framework to glean additional insights from current population-based approaches while filling the unmet needs of patient-specific oncology care. Specifically, prognoses (i.e., the expected course of the disease) are currently determined from the statistical summary of population data including the age and gender of the individual, the type and subtype of cancer, the stage of disease at diagnosis, and the molecular profile of the tumor.²² In contrast, digital twins can hasten the arrival of a truly personalized prognosis by serving to establish the pathophysiology of an individual patient's disease, so that the survival of an individual patient can be specifically predicted, rather than extrapolated from a population.

The ability to make accurate patient-specific predictions would not only improve prognosis, but would also identify mechanistic reasons for different responses to treatment across patients and provide guidance on how to personalize the intervention for individual patients. Determining the optimal choice of treatment(s), including the combination, dose, sequence, and timing of therapies, is extremely complex, and a comprehensive evaluation of all options by traditional clinical trials or experiments is impossible. In contrast, as the dynamic decision network in Sec. I A 2 illustrates [Fig. 1(b)], a digital twin constrained by the observational data from an individual patient can systematically explore many possible treatments in silico and therefore present a compelling strategy to optimize the patient's outcome.^23–26 Currently, complex treatment decisions for individual patients are often addressed at tumor boards attended by physicians and scientists from many different specialties who provide recommendations based on their pooled experience, expertise, and biases. In comparison, digital twins can provide a decision-making framework to quantify and integrate additional patient care factors including the clinicians' experience and expertise as well as the patients' perspective on the quality of life, to develop a personally optimized therapeutic strategy.²⁷

More recently, there have been efforts to develop methods to generate quantifiable predictions of tumor dynamics for individual patients with the goal of accurately diagnosing the disease, predicting response, and establishing optimal treatment options.^28–31 While these studies were not specifically presented as digital twins, the goals, challenges, and techniques are closely related to those required to develop digital twins and thus provide a unified foundation for establishing more comprehensive digital twins for oncology. The potential of digital twins to hasten the arrival of personalized precision cancer care has been increasingly appreciated.^32–34 In fact, multiple studies have demonstrated successful prototypes of digital twins across several scales.^35–40 A practical digital twin needs to balance the complexity of computational models with the availability of data to achieve a particular clinical goal. In this review, we focus on digital twins that employ clinical imaging data and discuss why this is a promising direction, what models and data can be used to build this type of digital twin, and what problems they can address. We also present some of the technical details on how to construct these digital twins.

C. Integrating quantitative imaging and mechanism-based mathematical modeling

The point of view we espouse for constructing practical digital twins in oncology relies on advanced biomedical imaging and mathematical models designed to employ such data.⁴¹ Importantly, the central role of medical imaging in screening, diagnosing, staging, guiding therapy, monitoring, and evaluating response presents itself as an important source of patient-specific measures of tumor growth and response.⁴² Additionally, medical imaging provides noninvasive, serial observations of the spatiotemporal variations in the physical state of the patient, which can be employed as the observational data of a patient's digital twin. We^{11,29,43–46} and others^47–51 have demonstrated that mathematical models can be initialized and personalized by medical imaging data collected from patients. Once personalized, the image-guided mathematical model parameters serve as a digital representation of that patient's tumor where treatment can be optimized and response can be forecasted. Early efforts by Swanson et al.⁵² relied on anatomical or structural imaging, which report on the location and extent of the disease to estimate tumor-specific parameters of proliferation and invasion in patients with glioblastoma. The approach by Swanson et al. has evolved over the years to produce an informative “days gained”⁵³ metric of treatment efficacy where real or hypothetical patient outcomes are compared to an untreated “virtual control” (i.e., digital twin). More recently, advanced quantitative imaging techniques are capable of reporting on the heterogeneity in tumor biology and are now being employed in image-guided mathematical models. For example, in Weis et al.,⁴³ longitudinal maps of tumor cellularity—as estimated by diffusion-weighted (DW-) magnetic resonance imaging (MRI)—collected before and after the first cycle of neoadjuvant systemic therapy (NAT) in patients with breast cancer were used to calibrate a mechanically coupled, reaction–diffusion equation to identify patient-specific and spatially varying net-proliferation rates and tumor cell diffusion. These rates were then used to run the mathematical model forward in time to predict response at the conclusion of NAT. Jarrett et al.²⁹ extended this effort by incorporating longitudinal dynamic contrast-enhanced (DCE-) MRI to quantify tissue perfusion and approximate the delivery of chemotherapy. By leveraging quantitative MRI to estimate both tumor cellularity and tissue perfusion, Jarrett et al.²⁹ were able to employ digital twins to identify alternative therapeutic regimens that were hypothesized to outperform the standard-of-care for each individual patient. This initial effort into developing a digital twin in breast cancer demonstrates the utility, and potentially paradigm-shifting power, of using advanced quantitative imaging measures to personalize and construct digital twins in oncology.

D. Outline for the remainder of the manuscript

We attempt to provide an up-to-date review of the opportunities, established techniques, and challenges of developing digital twins for oncology that are built upon the integration of quantitative biomedical imaging and mechanism-based mathematical modeling. In Sec. II, we describe the state-of-the-art of image-guided digital twins in multiple fields of healthcare, specifically highlighting the milestones in cardiovascular simulation, convection-enhanced drug delivery, and virtual reality for surgery. In Sec. III, we detail the techniques required to make practical image-guided digital twins for oncology a reality. Specifically, we discuss (1) the clinically available imaging techniques that provide a quantitative characterization of cancer, (2) the current mechanism-based models that capture the salient features of tumor development, tumor response, and the underlying pathological processes, and (3) how the imaging data are integrated into the mathematical models. In Sec. IV, we discuss how artificial intelligence (AI) and big data can assist the development of mechanism-based digital twins for cancer. In Sec. V, we explicitly list and discuss the current barriers to success for image-guided digital twins in oncology, including limitations in what biological mechanisms can be included in tissue-scale models, available data, and computational techniques required for model implementation, calibration, selection, updating, and evaluation. Finally, in Sec. VI, we illustrate the process of developing an image-based, mechanism-based digital twin for oncology, with a specific application to brain cancer.

II. IMAGE-GUIDED DIGITAL TWINS IN HEALTHCARE

There have been substantial efforts to develop image-guided digital twins for various diseases, each with the common goal of improving treatment outcomes for individual patients. By summarizing several previous examples of digital twins in other fields of medicine, we see the potential for employing digital twins in clinical oncology.

A. Simulation of cardiovascular disease and their treatments

Patient-specific simulation of cardiovascular disease constitutes one of the most developed applications of digital twins in healthcare. The mathematical and computational modeling of cardiovascular pathologies has been systematically investigated for several decades and has led to practical tools for guiding interventions.^4,54,55 Indeed, some cardiovascular modeling tools are already commercially available. For example, HeartFlow analysis and HeartFlow planner (HeartFlow^®, Inc, Redwood city, CA) are FDA-approved software for assisting in diagnosis, risk prognosis, and surgical planning for coronary artery disease.^56,57 HeartFlow analysis produces a personalized, color-coded 3D rendering of the patient's coronary arteries based on x-ray computed tomography (CT) scans, providing physicians detailed information about the location and severity of stenoses (i.e., narrowing or blockage of coronary arteries which can lead to heart failure). In particular, the software calculates the pressure field within the diseased arteries and the resulting “fractional flow reserve,” which is commonly used to determine the risk level for a patient.⁵⁸ Furthermore, HeartFlow planner allows physicians to interactively explore different intervention scenarios, virtually modifying each identified stenosis to see the potential impact on blood flow. Nevertheless, there are more challenges in cardiac modeling attracting great interest, including, for example, the incorporation of models and data across multiple spatial and temporal scales,^3,59–63 as well as more complete analyses of cardiac electrophysiology, mechanics, and hemodynamics.^9,60,64–66 Additionally, there are several efforts to develop open-source software environments^60,67,68 to make cutting-edge cardiovascular modeling techniques (e.g., image analysis, mesh generation, numerical solvers, and visualization) accessible to a wide audience, including researchers, clinicians, and students.

B. Planning convection-enhanced drug delivery for brain diseases

Another healthcare application that substantially benefits from digital twins is convection-enhanced delivery (CED) of therapeutics for brain diseases, including high-grade tumors, Parkinson's disease, and Alzheimer's disease.^69–71 CED involves the direct infusion of drugs into the brain via implanted catheters. This technique allows drugs that do not cross the blood–brain barrier to be delivered in therapeutic concentrations throughout large volumes of brain tissue, while minimizing systemic exposure.⁶⁹ Preclinical and clinical efforts over the last two decades, however, indicate that the success of CED treatments is intimately connected to the proper placement of catheters as well as infusion rate.⁷² Suboptimal administration of CED may result in undesirable consequences (e.g., reflux along catheters and leakage into the cerebrospinal fluid or bloodstream), which can increase the risk of off-target side effects.^69,73 Thus, an accurate prediction of the spatiotemporal distribution of the delivered therapeutics is necessary to maximize the successful application of a given therapy.^72,74 This necessarily requires digital twins of individual patients to provide detailed computational modeling of the physiological properties, the specific drugs delivered, and the design of the catheters employed for administration of the treatments.^69,72–75

As a commercial tool widely used in clinical trials,^76–78 iPlan^® Flow (BrainLab AG, Feldkirchen, Germany) is FDA-approved software designed to support patient-specific optimization of CED for brain diseases. iPlan uses MRI data to simulate the distribution of drugs infused into the brain and then uses this simulation to guide the placement of intra-cranial catheters.⁷⁹ There are additional efforts to address existing challenges in the simulation of CED. For example, iPlan flow uses an algorithm that calculates the backflow along catheters assuming a constant diameter of catheter tip design.⁸⁰ However, studies have indicated that catheters with a stepped design can prevent severe reflux.^75,76 To address this issue, Rosenbluth et al. modified the calculation of backflow along the catheter to account for the effect of the step in the catheter tip.⁸¹ Another existing challenge is that the relationship between model parameters and the available imaging measurements can be different for different CED therapies. To begin to address this limitation, Woodall et al. developed a new mechanism-based model guided by multi-modality images (MRI, x-ray CT, and single-photon emission computed tomography) to predict the distribution of radioactive, Rhenium-186 nanoliposomes delivered via CED.⁴⁴

C. Virtual reality and digital twins for surgical planning

Virtual, mixed, and augmented reality (VR) enable users to visualize objects in a computational environment, upon which devices are developed to enable manual interaction between users and the computational environment. Emerging VR technology seeks to import the sensed motions of the user in the physical world into the computational environment, and in feedback, to create an experience of touch by applying forces or vibrations to the user. These haptic technologies have seen increasing use in planning complex surgeries as well as in training physicians in techniques that are not frequently performed.^82–88 Recently, the integration of digital twins with VR technology has been regarded as a promising framework to personalize surgical planning. Specifically, digital twins provide patient-specific anatomy extracted from medical images and personalized models of tissue mechanics and interactions with surgical instrumentation, enabling patient-specific simulations in VR implementation.^3,84,89 Together, these technologies enable surgeons to systematically explore individual patients' anatomy in 3D to plan the surgical procedure, guide intraoperative decision-making, and gain practice before the actual surgery.^{54,57,84,87,89–92}

The potential of integrating VR with digital twins to assist in personalizing surgical procedures has been increasingly appreciated in medicine. For example, a commercial platform called ImmersiveView^® Surgical Plan (ImmersiveTouch^TM, Chicago, Illinois) is designed to generate 3D replicas from patient scans (including CT, MRI, and 3D angiography), allowing surgeons to study and collaborate on surgical tactics. Using a headset, surgeons can perform multiple reality-emulating procedures (e.g., drawing, measuring, and cutting) on the digital twin representing patient-specific anatomy. While this system is currently used at several academic medical centers, extensive prospective studies that quantitatively determine the utility of digital twins for surgical planning and decision-making are still required before these emerging technologies are available for widespread clinical use.^3,84 A central challenge in developing reliable digital twins for surgery is the construction of realistic models that adequately capture in vivo tissue deformation due to interaction with surgical instrumentation.^89,91–94 Also, the constructed models need to be reliably parameterized with imaging and clinical measurements.^3,92,94 Current efforts also seek to provide accurate and fast registration of the patient's anatomy during the intervention to refine the feedback (i.e., experience of touch) from the digital twin to the surgeon.^85,87,91,93

III. MAKING IMAGE-GUIDED DIGITAL TWINS PRACTICAL FOR CLINICAL ONCOLOGY

While practical, rigorous, commercialized digital twins do not currently exist for clinical oncology, there have been many efforts seeking to integrate biological data with computational models in cancer biology and oncology.^34,35 In recent years, there have been tremendous developments in methods to quantitatively describe tumor growth from the cell scale^95–97 to the tissue scale.^36,98,99 In particular, the data required for tissue scale models, which describe phenomena that are of direct clinical interest, can now be directly and routinely measured. Specifically, much effort has been invested in developing tissue-scale models for (1) identifying pathophysiological characteristics of tumors,^46,100 (2) predicting spatiotemporal changes of tumor size, shape, tumor cell density, and response to administrated therapies,^36,98,99 and (3) identifying and optimizing treatment options on a patient-specific basis.^11,29 Moreover, modeling at the tissue scale can be informed by medical imaging data, such as x-ray CT, MRI, and positron emission tomography (PET), which are clinically available and can provide longitudinal in vivo measurements of cancers.^101,102 Thus, in this section, we focus on the measurements available from current clinical imaging techniques and how such data can be integrated into tissue-scale mechanism-based models to construct digital twins (see Fig. 2 for an overview).

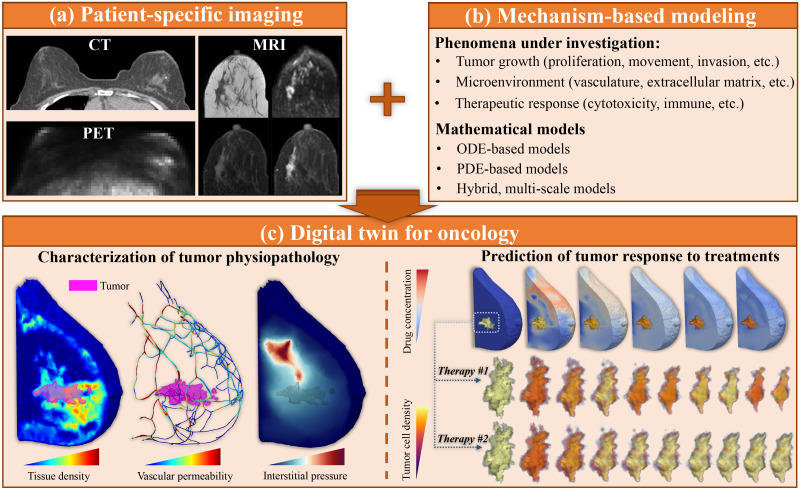
FIG. 2. — Integrating clinical imaging and mechanism-based modeling to build patient-specific digital twins for oncology. Panel (a) illustrates three of the primary imaging modalities in clinical oncology (for the specific example of breast cancer): CT, MRI, and PET. From left to right, and then top to bottom, the MRI data include T₁-weighted images, diffusion weighted MRI, and pre-contrast and post-contrast DCE-MRI.¹⁰³ The PET scan employs the radiotracer fluorodeoxyglucose (FDG) and was downloaded from the QIN-breast collection of the Cancer Imaging Archive.^104–106 Panel (b) lists several of the key, mechanism-based modeling methods for cancer, as well as some of the phenomena investigated with the models. Integrating panels (a) and (b), a digital twin for a specific application in oncology can be established, as illustrated in panel (c) for the treatment for breast cancer with NAT. Specifically, imaging data can provide a detailed characterization of (for example) morphology, tissue cell density, vascular permeability, and interstitial pressure.⁴⁶ Mechanism-based models can then be personalized with such data to make patient-specific predictions of the outcomes of a range of treatment plans. For example, as shown in panel (c), the digital twin can predict the spatiotemporal distribution of delivered therapies, and tumor response to a specific therapeutic plan (i.e., therapy No. 1 causes the tumor volume to shrink by 67.64%, while therapy No. 2 only reduces the tumor volume by 31.29%).

A. Clinical imaging techniques

Biomedical imaging plays a fundamental role in clinical oncology as it provides data to assist in tumor detection, staging, treatment planning, assessment of treatment response, and post-treatment monitoring. The primary biomedical imaging modalities include CT, MRI, and PET [see Fig. 2(a) for examples]. These techniques use different physical mechanisms to noninvasively generate three-dimensional images inside the body. For example, CT scans use rotating x-ray sources to generate multiple projection images that can be reconstructed to form 2D cross-sectional images, MRI employs magnetic fields to generate three-dimensional images of any orientation inside the body, and PET imaging involves the injection of a radioactive material preferentially accumulates in specific regions that can be determined by reconstruction techniques similar to x-ray CT.^107–109 CT and MRI measurements of tumor size are commonly used to assess the treatment response using the Response Evaluation Criteria in Solid Tumors (RECIST)¹¹⁰ which partitions patients into one of four categories (complete response, partial response, stable disease, and progressive disease) based on changes in the longest dimension of their tumor(s) between visits. By employing different methods of image acquisition and processing, these three modalities can probe an array of biological features regarding tumor and surrounding tissue.⁴²

X-ray CT, MRI, and PET are all capable of providing quantitative biomarkers of the underlying physiological, cellular, and molecular characteristics of cancer.¹¹¹ For example, contrast-enhanced CT and MRI can be used to quantify vascular perfusion and permeability.^{103,112–114} Diffusion-weighted MRI measures the motion of water in tissue and provides a surrogate of cellularity, which has proven to be useful in assessing and predicting the response of a tumor to therapy.^115–118 Other MRI techniques under development for tumor imaging include MR spectroscopy which assays the biochemical milieu of the tumor¹¹⁹ and MR elastography which measures tissue stiffness.¹²⁰ PET imaging allows for comparative assessment of glucose metabolism via the tracer fluorodeoxyglucose (¹⁸FDG-PET).^121,122 PET has also been employed to measure hypoxia, apoptosis, and the density of various cell surface receptors.¹²³ The tracer fluoromisonidazole (¹⁸F-FMISO PET) is used primarily for imaging hypoxia,^124,125 and the tracer fluoroethyltyrosine (¹⁸F-FET PET) is used for imaging metabolic activity.^126,127 Simultaneous acquisition of PET with CT or MRI can further increase the utility of the data by providing better anatomical referencing and spatial localization of the PET functional data.^128,129 By assessing complementary aspects of tumors, biomedical imaging can characterize many important aspects of tumor pathophysiology at multiple timepoints in 3D, thereby providing measurements that are both accessible and powerful for constructing realistic, clinically relevant digital twins.

B. Mechanism-based mathematical modeling

The standard-of-care in oncology relies on the treating physician to integrate the individual patient's clinical and imaging information with the statistical analysis of population-level data acquired from both clinical trials and medical practice.^130,131 Features observed at the population level, however, frequently obscure important characteristics of the individual to the point that the population-level features may not be relevant to the individual patient. In contrast, mathematical models—built upon established biology, chemistry, and physics—can accurately (and practically) characterize the fundamental mechanisms underlying cancer growth and therapeutic response. Such advances toward a mechanistic understanding of the disease provide opportunities to better use individual patient's data to inform their optimal treatment plan.

The behavior and interaction of tumor cells with, for example, healthy cells, immune cells, and vasculature can be described through the language of ordinary differential equations (ODEs), which describe the change in the quantity of species over time, or partial differential equations (PDEs), which describe the change in the quantity of species over both time and space^{35,36,99,132–134} [Fig. 2(b)]. There have been many recent developments in these mechanism-based models^36,45 with promising results for reproducing and forecasting the growth and treatment response of tumors of the brain,^30,135–139 breast,^29,140 prostate,^31,141,142 head and neck,¹⁴³ pancreas,^144,145 and kidney.¹⁴⁶ These models often begin by characterizing the change in the total number of tumor cells or in the tumor volume over time. But they can be further extended to account for other important phenomena, including the evolving mechanical properties of the tissue during tumor growth or the dynamics of the availability of nutrients and therapeutics.

To develop clinically actionable digital twins using mechanism-based models, it is essential that these models are constructed upon clear mathematical relationships connecting patient data with model inputs (e.g., initial conditions and parameters) and outputs (e.g., model variables or other quantities of interest that are readily calculated from model variables).^3,11,36 To this end, ODE models of tumor growth and treatment response often describe the temporal change in tumor volume, total tumor cell number, or other clinically relevant biomarkers (e.g., serum prostate specific antigen in prostate cancer).^{31,142,143,147} ODE models are attractive because they can incorporate not only imaging data, but also multi-dimensional omics data (e.g., genomic, proteomic, transcriptomic, and metabolomic¹⁴⁸), which makes such models a practical paradigm for accounting for multi-scale mechanisms. For example, intracellular signaling pathways and metabolic networks are commonly represented by coupled ODEs describing the temporal dynamics of entire signaling pathways.^{136,137,149–151} Inter-cellular interactions and transformations, such as communication between tumor-immune cells, and epithelial-mesenchymal transition, can also be represented by ODEs.^152,153 Another key advantage of ODE models is that, in general, they can be solved using well-established algorithms that are straightforward to implement and require a minimal computational cost. However, they are not able to provide a spatially resolved prediction of tumor growth or therapeutic delivery, which may limit their utility in building digital twins for some decision-making processes requiring local tumor information (e.g., biopsy, surgery, or radiotherapy planning).

This limitation is overcome by PDE models, which often extend ODE formulations to incorporate the movement of the modeled species and their interaction(s) with spatially varying tissue properties.^{35,36,99,132–134,138} Tumor cell movement is often modeled via a diffusion term which can be randomly defined or informed by tissue type,⁵² mechanical properties,¹⁵⁴ or tissue anisotropy.¹⁵⁵ These models can return spatially resolved estimates of tumor quantities that are readily comparable to clinical imaging measurements, such as tumor morphology, cell density, vasculature networks, and perfusion (see Sec. III B below). Additionally, by integrating certain PDE model variables over a region of interest it is possible to estimate the scalar quantities of interest usually employed in ODE models (e.g., tumor volume). However, to solve and parameterize PDE models it is necessary to employ more advanced numerical methods, which are usually more computationally intensive.^132,138

C. Linking imaging and mechanism-based modeling to enable digital twins practical for oncology

After reviewing the information presented in Secs. III A and III B, we hope that the reader finds it natural to employ quantitative imaging techniques to populate mechanism-based mathematical models that describe the biophysical dynamics of tumors and their response to treatment [as shown in Fig. 2(c)]. Recalling the digital twin framework introduced in Sec. I A 2 (and Fig. 1), imaging provides the observational data to establish the digital state of a model, thereby linking the physical objects [i.e., tumor(s) of an individual patient] to their digital twins. Importantly, as imaging data are resolved in 3D (or 4D) at voxel locations, image-guided digital twins have the inherent advantage to naturally and explicitly incorporate the spatiotemporal heterogeneity of the tissue and tumor. For instance, tumor cell density is a typical quantity-of-interest in tissue-scale PDE models and can be estimated from the apparent diffusion coefficient (ADC) maps extracted from DW-MRI,^{11,29,43,45,156} where these ADC maps provide an initial condition for the models. T₁- and T₂-weighted MRI data enable the acquisition of high-resolution images to segment the host tissue and determine the tumor geometry,^{11,29,135,139,141} which define the computational domains of PDE models. Additionally, the pharmacokinetic analysis of contrast-enhanced CT or MRI data can identify local vasculature, quantify tumor-induced angiogenesis, and estimate hemodynamics as well as therapeutic transport within the tumor-bearing tissue,^29,45,46,157 all of which can be used to inform model parameters. Combinations of quantitative imaging data can also be used to characterize local intratumoral heterogeneity¹⁵⁸ that may indicate critically different prognosis and/or therapeutic response.^159–161 The characterization of heterogeneity from imaging data could initialize multiple intratumoral species in a mechanism-based model. Additionally, different PET modalities can also estimate tumor cell density (FET-PET),¹³⁹ characterize hypoxia-mediated radiation-induced tumor cell death (¹⁸F-FMISO PET),¹⁶² estimate tumor cell proliferation (¹⁸FDG-PET),¹⁴⁴ and report on cell surface receptor expression.¹⁶³

Beyond model initialization, all the imaging measurements discussed in the last paragraph can be performed longitudinally to enable parameter identification, model validation, physical tumor monitoring, and data assimilation. For instance, by comparing the DW-MRI and DCE-MRI measurements from multiple time points (e.g., pretreatment and after a few cycles of treatment administration), parameters that are difficult to initialize (e.g., the spatially resolved proliferation rate of tumor cells) can be calibrated on a patient-specific basis.^29,99 The follow-up measurements of tumor cell density by DW-MRI during or after treatment, as well as the derived metrics of clinical interest (e.g., tumor volume and longest axis), can also be compared to the corresponding predictions to validate realized digital twins.²⁹ Additionally, contrast-enhanced CT or MRI acquired over the course of treatment to monitor the change of tumor-associated vasculature can lead to a more accurate estimation of the therapy delivery and distribution.¹⁶⁴ All these procedures allow for refining the digital state (see Fig. 1) and improving the prediction of the quantities of interest of the digital twins which, in principle, could contribute to optimizing patient-specific interventions.

The collection of imaging data can also be guided by and benefit from the outputs of digital twins. Indeed, one application of digital twins in cancer is to guide the management of control inputs (see Fig. 1) for the individual patient, based on the predicted tumor response given by the patient data-constrained models. The control inputs can span not only treatment options but also data collection including, for example, imaging studies, biopsies, and blood tests. Specifically, a digital twin validated to accurately predict tumor progression and treatment response in an individual patient can assist in deciding the frequency of follow-up imaging examinations. Hence, patients who are predicted to have a less favorable response to the selected treatment could be advised to anticipate additional follow-up imaging examinations, so that early plans can be made for alternative interventions if deemed appropriate. Conversely, patients who are predicted to have a more favorable response to treatment could be advised to schedule fewer follow-up examinations, addressing the concerns of overdiagnosis and overtreatment.¹⁶⁵ This latter issue is especially important for slow-growing tumors like those frequently found in certain prostate^166,167 and breast cancer.^168,169 Additionally, the uncertainty of a model's prediction would increase with the duration of time forecasted past the last data acquisition point. Thus, uncertainty quantification¹⁷⁰ of the digital twin's status would improve guidance on when the current prediction is reliable and when additional imaging data should be collected to maintain a sufficiently high level of confidence in predictions.

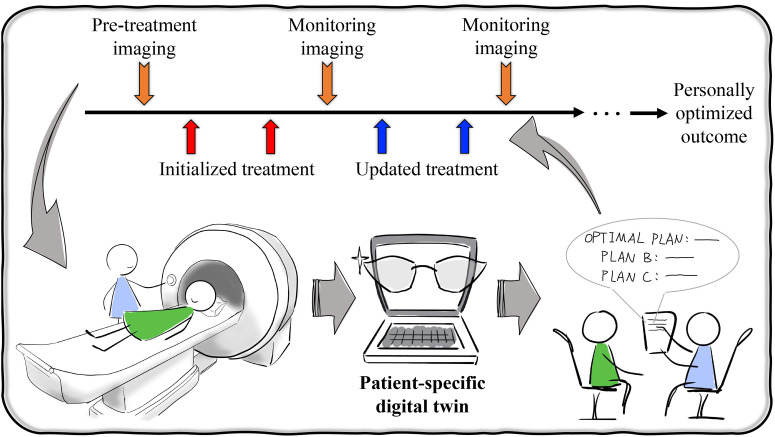
We here provide a motivating illustration (Fig. 3) on how a digital twin, realized via imaging data, could be practically linked to personalize a neoadjuvant systemic therapy (NAT) regimen for a breast cancer patient. Consider a woman who has recently been diagnosed with locally advanced breast cancer. As the current standard-of-care, NAT would be recommended for her to minimize the tumor burden before surgery and to improve her long-term outcomes.¹⁷¹ Unfortunately, nearly 50% of HER2+, 67.4% of triple-negative, and 90.7% of HR+/HER2- breast cancer patients who receive standard NAT show residual tumors at surgery,¹⁷² which is correlated with poor long-term outcomes. A major challenge to improving outcome for these patient populations is to optimally tailor the treatment plan for each individual patient. Currently, a patient's treatment plan is determined by a multidisciplinary team that includes not only the medical oncologist, but also the patient's surgeon, radiologist, and possibly a radiation oncologist.¹⁷³ In many instances, the treatment plan is largely determined by the experience and expertise of the patient's treating oncologists²⁷ and, for the most part, restricted to a few fixed, standard protocols as guided by the National Comprehensive Cancer Network.¹³⁰ If, however, a mechanism-based digital twin was available, it could be used as a platform to systematically test a large number of potential therapeutic protocols and predict their effects on tumor response. The results of such predictions could then be rank-ordered by the anticipated outcome. Selection of a plan would be made after discussion between the patient and treating oncologist covering the range of predicted outcomes and potential toxicities, so that the patient understands the decision-making process before beginning the personalized regimen. After the first few cycles of treatment, the patient would return for a subset of repeat imaging and clinical exams at the appropriate pre-determined frequency to update the digital twin. The updated twin would then provide a higher-confidence prediction of tumor response. This would allow for dramatically earlier modifications to the treatment protocol than what is currently available. Refining the therapeutic approach might even occur multiple times over the course of treatment. In this way, a digital twin would significantly hasten the arrival of personalized neoadjuvant therapy for breast cancer, thereby almost certainly improving outcomes. Of course, while this example focused on the NAT of breast cancer, such a framework would apply more generally to any disease site.

IV. ROLE OF ARTIFICIAL INTELLIGENCE AND BIG DATA

Complementary to the mechanism-based modeling approaches described above are the statistical-based artificial intelligence (AI) methods.¹⁷⁴ In this section, we briefly introduce the AI/Big data paradigm commonly seen in healthcare (Sec. IV A) and discuss its role in assisting the development of image-guided, mechanism-based digital twins (Sec. IV B).

A. Summary of the AI/big data paradigm

AI is, broadly, the ability of machines to perform independent tasks without human intervention. Machine learning (ML) is a subset of AI, which is defined as a general-purpose method of AI that identifies relationships from data without the need to define these relationships a priori.¹⁷⁵ Neural networks are a tool within ML whose architecture is based on the neuronal structure of the human brain. The basic computational unit in the neural network is called a node or neuron, which takes one or more weighted inputs, uses a transfer function to combine the inputs, and provides an output. The nodes are grouped in layers, which are the core architectural blocks of a neural network. One layer is a collection of “nodes” operating together at a specific depth within a neural network. Nodes from separate layers are linked together with a certain strength, also termed a “weight.”¹⁷⁶ The output of neurons in one layer activates downstream nodes via nonlinear activation functions.¹⁷⁷ Convolutional neural networks (CNNs) take this a step further by convolving the output of preceding layers using filters of tunable size.¹⁷⁷ Deep neural networks (DNNs)—advanced from the conventional three-layer CNNs—are NNs with multiple layers that exploit the hierarchical structure of real-world data, where each processing layer progressively builds upon the output of the preceding layer.¹⁷⁸ This multi-layer abstraction makes DNNs especially useful for image reconstruction and classification.

There are two common forms of DNNs: trained (supervised) and un-trained (unsupervised).¹⁷⁹ Supervised methods involve exposing DNNs to large amounts of labeled “training” data,^174,180 where parameters in the DNN are iteratively adjusted to minimize the error between the DNN output and the ground truth. For example, when diagnosing brain cancer from MRI, a training dataset could be built with a large collection of T₁-weighted brain MRI scans including both healthy and pathological cases. The network would be trained to separate the scans that contain a pathology from those that are healthy using ground-truth labels provided by a radiologist. In unsupervised methods, however, there are no ground-truth labels with which the network can be trained.¹⁷⁴ Instead, the structure of the DNN itself imposes constraints on the structure of the output.^179,181

There are advantages and disadvantages with both trained and un-trained networks. The primary issue with trained methods is the potential lack of sufficiently large training datasets that adequately span all possible biological features for a specific problem.¹⁷⁴ If a training dataset does not span all such features, there is the risk of the network not recognizing novel features outside the scope presented in the training datasets.¹⁸² For example, Elmarakeby et al. developed a deep neural architecture called P-NET (pathway-aware multi-layered hierarchical network) to predict cancer state in prostate cancer patients based on genomic pathways.¹⁸³ This P-NET required over 3000 biological pathways from patient data for training. While the method performed better than other deep learning methods, its training and tuning heavily relied on the quantity and quality of the annotated patient data. Untrained methods, on the other hand, are not limited by data availability; however, their accuracy is usually slightly outperformed by trained methods.^182,184

It is important to note the inherent limitation of AI methods: since they often do not incorporate the underlying physical mechanisms describing the phenomenon under investigation, AI methods alone cannot explain the correlations observed within the data. This may lead to a limited understanding of the phenomena under investigation, but the AI methods may identify patterns and relationships that trigger a worthwhile investigation for underlying mechanisms. The rapid growth of AI methods has shown promise for achieving widespread deployment of deep learning in precision medicine, especially when integrated with mechanism-based models.^174,185

B. AI/big data to assist in the implementation of mechanism-based digital twins

AI and big data have proven capable of aiding in the practical implementation of digital twins built on mechanism-based models in healthcare.¹⁸⁶ Specifically, employing AI to enable fast and accurate data arrangement, parameter identification, and evaluation of mechanism-based models are known as hybrid AI-mechanistic technologies. For example, with the rise of technologies like wearable devices, it becomes increasingly feasible to collect large amounts of biometric data from an individual patient. These data would enable oncologists to monitor patients outside of the walls of the clinic, thereby facilitating decision-making about the choice of therapies and overall patient management.¹⁸⁷ At the same time, however, the management of these biometric data also becomes increasingly challenging.¹⁸⁸ AI methods provide a level of autonomy in data storage, management, and updating for the maintenance of digital twins.^28,189 Specifically, in the context of system health monitoring, AI technologies have been developed to monitor patient health status and to recommend healthcare actions.^{188,190–192} This approach, which is known as “condition-based maintenance,” manifests the utility of AI in patient monitoring and data management to support the implementation of digital twins for healthcare.

Another opportunity for AI methods to assist mechanism-based digital twins is to increase the spatial and temporal resolution of medical images, which would improve the accuracy with which a digital twin can be realized. Both supervised and unsupervised methods of training DNNs have dramatically improved the spatial and temporal resolution at which quantitative imaging data can be reconstructed. For example, Cohen et al. developed a DNN applied to the MR fingerprinting technique, which achieved a reconstruction of high spatial resolution T₁ and T₂ maps 300 and 5000 times faster, respectively, than the conventional dictionary-matching methods.¹⁹³ This increase in resolution provides access to a more refined domain on which to perform calculations, more accurate segmentation of important anatomical features,¹⁹⁴ and more refined parametric maps of tissue properties.¹⁹⁵

AI technologies are also attracting attention in computational science as they can enable the solution and calibration of complex mechanism-based models in practical time frames, which are of great importance in building digital twins to support real-time clinical decision-making.³ For example, Brunet et al. developed an approach combining a mechanism-based model with DNN to learn complex elastic tissue deformations and, hence, non-rigidly register patient-specific organ geometries in real-time for augmented reality during liver surgery.⁸⁷ Raissi et al. presented a mechanism-informed deep-learning framework that encodes the Navier–Stokes equations into neural networks to directly extract velocity and pressure fields from longitudinal images of flow phenomena.¹⁹⁶ The authors further showed that this hybrid approach could estimate quantitative hemodynamics in patient-specific intracranial aneurysms. Moreover, Zhang et al. utilized a neural network representation of a complex structural constitutive model accounting for detailed tissue features to efficiently calculate the mechanical response of heart valves.⁶³ These successes in other areas of medicine provide motivation for the extension of these hybrid AI-mechanistic technologies to oncology.

Hybrid approaches combining AI and mechanism-based models are also a promising strategy for integrating multi-scale, multi-modal datasets within the digital twins.¹⁹⁷ For example, the hybrid model for glioblastoma growth proposed by Gaw et al., which integrated imaging and histopathological biopsy data, showed superior predictive performance than either the mechanistic or machine learning components of the hybrid method alone.¹⁹⁸ The authors also showed that the mechanism-based model is the feature providing the greatest contribution to the hybrid model forecasts. Hybrid strategies combining mechanistic modeling and AI approaches can also be exploited to investigate the genetic markers supporting each mechanism of a biophysical model, which provides an opportunity to integrate omics data with macroscopic observations within digital twins. For instance, Nicolo et al. combined an ML analysis with a mechanistic model to estimate the time to post-surgery detection of distant metastatic recurrence of early-stage breast cancer to find correlations of this relapse metric and the underlying model mechanisms with a panel of diagnostic clinicopathological features.¹⁹⁹ In the context of digital twins, these patient-specific clinicopathological data, such as gene expression panels, could therefore be leveraged to estimate individualized mechanistic parameters, such as proliferation rate, mobility, invasion, and reaction to targeted therapies.

AI techniques have also been leveraged to characterize parameter uncertainty and solve inverse problems for poorly-constrained parameters within mechanism-based models. For instance, Ardizzone et al. performed a mathematical analysis on how an invertible neural network can be used for determining the posterior distribution of a parameter of interest given a dataset of relevant measurements.²⁰⁰ Another example from Wang et al. is a theory guided neural network that outputs quantities of interest from inputted stochastic parameters and is closely coupled with the Monte Carlo method for evaluating parameter uncertainty simultaneously. The utility of such a method lies in its superior computation of uncertainty compared with simulated implementations.²⁰¹

While there have been strong early signals of the benefits of integrating AI and big data with mechanism-based modeling to enable digital twin technologies, there are a number of ongoing challenges to overcome in order to achieve clinical impact. One fundamental challenge is the potential inaccessibility of sufficiently large training datasets needed for any modeling approach that relies (at least in part) on AI methods to generate models with adequate generalizability across given anatomy or disease in clinical practice. Techniques known as data augmentation have been investigated to enlarge existing medical imaging datasets of limited size and to balance the proportion of healthy and pathological cases within a given dataset.²⁰² These techniques show promise for addressing the limitation of insufficient training datasets; however, data augmentation techniques (in general), rely on synthesizing new data by extrapolating from existing data, which may have a concern of overfitting in training the AI models. Furthermore, such methods would not be able to account for important features not found in the base data sets and may further augment biases in the original dataset. For supervised methods, big data remains a necessity to expose AI algorithms to all possible physiological features so that the resulting analysis obtained from AI algorithms achieves diagnostic-quality accuracy and precision.¹⁷⁹ The quality of annotations and the imaging data themselves can also impact the efficiency of training and performance of the supervised models. Another limitation is whether AI software could be extensively deployed,^28,192 regarding both generalizability and feasibility of the techniques, such that clinics around the world could reliably leverage AI-based digital twins. Finally, there remains the fundamental concern that using big data inherently means straying away from patient-specific care as it relies on properties of large populations of patients which may obscure subtle, patient-specific differences.

V. BARRIERS TO SUCCESS OF IMAGE-GUIDED MECHANISM-BASED DIGITAL TWINS FOR CLINICAL ONCOLOGY

Any developing field inherently has a set of fundamental barriers that must be overcome to realize the promise of the effort. In this section, we describe the major barriers to successfully applying image-guided digital twins in clinical oncology, and discuss current efforts and potential methods to address the challenges.

A. Limitations of realistic mathematical models

Despite the utility of mathematical and computational models, all models are based on simplifications and assumptions of the key system components under investigation.²⁰³ Mathematical models of cancer have been constructed for over a century and they vary tremendously in complexity depending on the phenomena they attempt to characterize. Cancer initiation, growth, expansion, and invasion depend on phenomena at multiple spatial and temporal scales, and this presents additional challenges in establishing proper mathematical models.^204–207 Large-scale cancer behaviors (e.g., growth, invasion, and therapy response) depend on small-scale characteristics (e.g., cancer cell genotypes, phenotypes, populations, and cell–cell or cell–environment interactions).^208,209 Tissue mechanical properties such as stiffness can facilitate signaling pathways at the subcellular scale that dictate cell death and proliferation and affect tumor size, shape, and interactions with the surrounding tissues.^210–212 One of the challenges when developing a practical model is how to establish the connections between phenomena at different scales and, subsequently, how to calibrate model parameters from partial data on these processes. See Ref. 205 for a comprehensive discussion on the open challenges associated with multi-scale modeling.

Instead of incorporating all phenomena at all spatial and temporal scales, the level of complexity (i.e., the number of processes described) of the digital twin should be chosen according to the goals of the problem under investigation.²¹³ In particular, it is imperative to determine which quantities-of-interest are central to understanding the phenomena. These might be clinical endpoints (e.g., overall survival, time to progression, or distinguishing complete response, partial response, stable disease, and progressive disease) or detailed measurements of tumor development and its interaction with the microenvironment (e.g., tumor cell counts, proliferation rate, accumulation of delivered therapy in tumor or other tissues). Based on the selected endpoints, the proper models that contain the appropriate quantities-of-interest can be constructed. For digital twins based on biomedical imaging, the governing models are necessarily designed to incorporate observables that are accessible in the clinical setting; therefore, they are most frequently operating at the tissue scale. However, the accuracy of tissue-scale modeling may be limited for some applications (e.g., immunotherapy response) due to the lack of description of finer-scale biological processes. Thus, efforts have been made to integrate image-guided, tissue-scale models with finer-scale biological processes.^{206,207,214,215} For example, Rahman et al. linked a PDE-based tissue-scale model, an agent-based cellular-scale model, and an ODE-based subcellular-scale model.²¹⁴ In this approach, a fully coupling bridging algorithm was designed to achieve communication across the scales via passing parameters and solutions. In particular, the pathway activities solved at the subcellular scale are transferred into the cellular-scale model to inform cell proliferation at the cellular scale which is then imported into the tissue-scale model. The density of tumor cells solved at the tissue scale is then fed back into the cellular-scale model, while the distribution of nutrients solved at the tissue scale is fed back into the subcellular-scale model. A practical consideration for such multi-scale digital twins is the limited availability of the appropriate multi-scale data.^34,35

B. Limitations of available data

A fundamental limitation in constructing and applying clinically meaningful digital twins in oncology is the currently limited access to the necessary data types. Existing digital twins in healthcare frequently make use of highly resolved spatial data collected via anatomical imaging, or highly resolved temporal data collected via wearable devices reporting on, for example, an individual's blood pressure, oxygen saturation, and temperature. These data, however, are of limited specificity for mechanism-based modeling of phenomena as complex as tumor growth and response to therapy.

Currently, image-guided digital twins rely on the clinical, in vivo measurement of cancer-relevant data obtained from the biomedical imaging modalities discussed above in Sec. III A. Biomedical imaging, though, has several limitations including, perhaps most importantly, the limited assessment frequency for each patient due to logistics, expense, and burden to the patient. Patients must travel to imaging centers for each measurement, and the imaging center may operate at a patient volume which can make it complicated for patients to schedule several exams that fit their constraints. Measurements thus typically happen at only a limited number of time points. Though portable, lower-cost imaging scanners have the potential to acquire data more frequently,²¹⁶ even if continuous monitoring is not possible. In addition to the limited assessment frequency, there are also limits imposed by the spatial resolution of biomedical imaging where each voxel is at the scale of millions of cancer cells. Advances in imaging hardware and acquisition techniques are improving the available spatial resolution while maintaining sufficient signal to characterize fine details.²¹⁷ Moreover, the common imaging modalities interrogate only a limited subset of the relevant cancer biology. Still, new nuclear imaging probes are being developed to assay tumor receptors and targets, such as the recently approved tracer for imaging prostate cancer metastases.²¹⁸ Magnetic particle imaging is based on the use of superparamagnetic iron oxide nanoparticles as a tracer to perform cell tracking and vascular imaging.²¹⁹ Although still limited to pre-clinical use, magnetic particle imaging was recently demonstrated to track the movement and persistence of T cells in solid tumors in a mouse model of brain cancer for adoptive immunotherapy.²²⁰ These developments are important because the currently available methods of imaging response to immunotherapy are quite limited.²²¹

As discussed in Sec. V A, image-guided digital twins may also be integrated with multi-scale models to enhance their ability to capture more detailed tumor characteristics and processes. However, this integration requires the appropriate (quantitative) data from multiple temporal and spatial scales.³⁵ At the subcellular scale, mathematical models describing signaling pathways, metabolic networks, and the evolution of cell populations can be informed by analysis of biopsy specimens including (for example) quantitative polymerase chain reaction, whole-genome sequencing, RNA sequencing, and flow cytometry.^222–224 At the cellular scale, models representing cell–cell or cell–microenvironment interactions can also be informed by analysis of tissue samples including (for example) immunohistochemical staining and microscopic techniques.^225–227 Unfortunately, the availability of such data for individual patients is currently limited and much effort is required to promote the acquisition and management of such in the clinical setting. Furthermore, such data suffer from sparse sampling in both the spatial and temporal domains. Thus, the body of work that currently integrates multi-scale data into predictive, biology-based mathematical models is currently limited.³⁴

C. Limitations of computational techniques

Central to the computational implementation of an image-guided digital twin is the construction of a geometric model of the tumor-bearing organ frequently based on anatomical imaging (e.g., x-ray CT and MRI).^8,228 This geometric model can be directly used for clinical assessment, but it also defines the computational domain in which the PDEs are solved within the digital twin framework.^8,132,228 Thus, the method selected to solve the model needs to handle the image-informed geometric representation of the tumor and host organ. The finite difference method (FDM) and the finite element method (FEM) have traditionally been used for this purpose.¹³² However, both methods may suffer from geometric discretization issues that can compromise prediction accuracy and that may limit their use within digital twins. In brief, the FDM relies on capturing complex organ border anatomies by introducing enough grid points (i.e., spatial points where the PDEs are solved over time). While the standard unstructured FEM meshes used to approximate complex anatomic geometries are inherently susceptible to discretization errors (i.e., mismatches between the real geometry and the approximated geometry provided by the finite-element mesh).¹³² Alternatively, Isogeometric Analysis (IGA) is a recent generalization of classical FEM that leverages highly continuous functional spaces from computer-aided geometric design (e.g., B-splines, non-uniform rational B-splines, T-splines, hierarchical splines), which accommodate the representation of exact geometries and ultimately lead to superior accuracy.^132,229,230 Furthermore, image-guided mechanism-based models of solid tumor growth and therapeutic response may be more amenable to FEM or IGA immersed-boundary methods.^{132,231–234} These computational strategies rely on a background mesh, which exactly represents the voxel imaging space and a level set function, which identifies the organ domain on where PDEs are actually solved. Thus, immersed-boundary methods eliminate the need to explicitly discretize the complex tumor-bearing organ anatomy, but they may require ancillary techniques to impose certain boundary conditions accurately and efficiently (e.g., Nitsche method^235,236).

Personalized mechanism-based model calibration, parameter update, model selection, and in silico therapeutic optimization are also common tasks in the construction and normal operation of digital twins in clinical oncology.¹³² These tasks require repeatedly solving the mechanism-based model, which can result in a prohibitive computational cost. Furthermore, a robust digital twin implementation requires the provision of accurate real-time predictive feedback, which further increases the expensive computational cost. To overcome this limitation, the hybrid AI-mechanistic approaches constructed as neural networks encoding mechanism-based models are promising to facilitate rapid (and accurate) model evaluations (see Sec. IV B).^{63,87,196,237,238} Importantly, the challenging demand on the computational cost can be met by properly using high-performance computing techniques involving parallelization to solve, select, or average the models in the digital twin, while accounting for data uncertainties, model inadequacies, and new data availability. The most common approaches are MPI (Message Passing Interface), which splits the computational tasks among several computers connected in a cluster (each one being a node); OpenMP (Open Multi-Processing),^239–241 which can further parallelize each task among the CPUs (Central Processing Units) on a node; and, most recently, solving the model using a GPU (Graphics Processing Unit),^240,242,243 which divides the tasks among the processing units present in video cards.

D. Limitations of model selection, validation, and uncertainty quantification

Beyond leveraging efficient computational strategies, the selection of which model to use within a digital twin is also a crucial decision. As discussed above in Secs. III B and V A, a variety of models may be available to describe a particular phenomenon of interest.^132,244 Model selection can be carried out over a pool of feasible alternatives via the Akaike information criterion,²⁴⁵ Bayesian information criterion,²⁴⁵ model plausibility,²⁴⁶ or other information criteria.²⁴⁵ These techniques identify the best model among the considered alternatives according to different metrics (e.g., model complexity assessed via the number of model parameters, quality of fit, or model likelihood given the data) and then use the selected model to make predictions about the modeled system.^{134,244,247,248} Another possibility is to rank the models according to their performance and average their predictions.^99,249 In this case, the weight of each model can deal with data uncertainties and model inadequacies either following the frequentist approach, where the probability of an event can be predicted by observing a large dataset,^203,250 or the Bayesian approach, which does not require a large dataset and where prior information on parameters guides the posterior distribution of model parameters.²⁰⁴

Once a model is developed and calibrated, its predictive capability needs to be assessed through model validation, whereby a model prediction is compared against new data to evaluate its accuracy.^203,251 To assess the validity of the model, one must select a metric to compute the error between the model prediction and data. If the error is below the desired tolerance, the model is deemed valid. As discussed in Ref. 251, the validation can only provide supporting evidence of the model's predictive capability. It is important to realize that the limited availability of the appropriate data directly influences the ability to quantitatively validate the model under investigation. If one doesn't have access to the data types that characterize the different spatial and temporal scales and model constituents, then quantitatively characterizing the accuracy of the predictions is challenging. In such a situation, a staggered validation approach can be explored.²⁵² For example, in Refs. 252 and 253, the authors designed a sequence of four experiments with increasing complexity where they systematically calibrated the rates of apoptosis, proliferation, and necrosis, as well as cell mobility. The mechanisms represented by the model were isolated and respectively validated by being compared to the data acquired from corresponding experiments.

The development of digital twins for clinical oncology is a challenging endeavor not only due to the limitations described previously but also because of the presence of uncertainties. Uncertainties in the observational data, model selection, and model parameters result in uncertainties in the predicted quantities of interest.¹³⁴ In data acquisition, the uncertainties arise from experimental measurement error, different measurement tools with a unique spatial and temporal resolution, and errors introduced during data processing (e.g., cell counting, image segmentation, and registration). In model selection, the uncertainties come from the underlying model assumptions and the numerical methods used to solve the mathematical models (e.g., due to discretization and numerical approximation errors). In developing a digital twin, some simplifications will inevitably be made, leading to the model prediction being an approximation of reality and, consequentially, increasing model uncertainties. The final source of uncertainty is in the values of the model parameters. As the tumor environment is highly heterogeneous, with not only inter- but also intra-patient heterogeneity, and with the inherent stochasticity of tumor growth, the uncertainties in model parameters represent the variability of these parameters. All these uncertainties must be considered during model calibration and when interpreting the predictions of the model to increase the reliability of the model results.²⁵⁰ Nevertheless, it is worthwhile to point out that a realistic expectation of the performance of digital twins is not to provide perfect, zero-uncertainty predictions. Instead, a digital twin with certain uncertainties but controlled and quantified is a leap forward compared to the cumulative, unquantified uncertainty in current standard-of-care approaches; it can substantially enhance the current clinical practice.

VI. FIVE QUESTIONS TO ANSWER FOR A PRACTICAL APPLICATION (A BLUEPRINT)

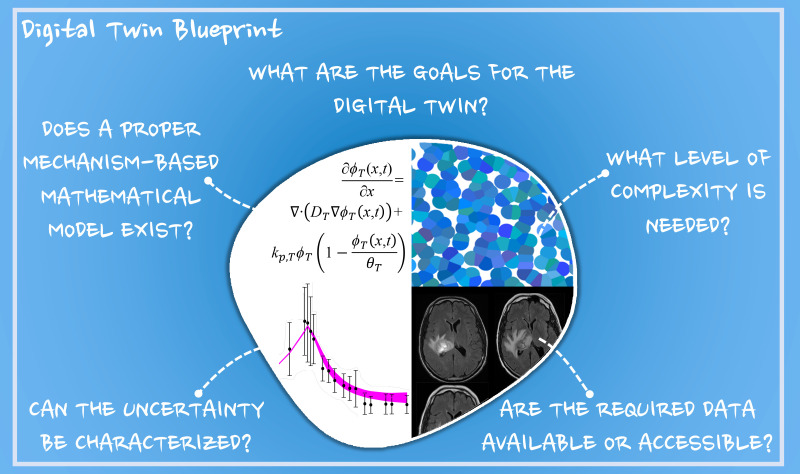
Thus far we have presented the utility of digital twins in healthcare, promising effort and perspectives in image-guided mechanism-based modeling in oncology, roles for big data and AI, and technical barriers to a successful implementation of digital twins in clinical oncology. Still, the question remains on how to practically develop a digital twin framework for specific applications in clinical oncology. Toward this end, we provide a specific example of adaptive radiotherapy for high-grade gliomas and identify five questions that can serve as a blueprint for building a digital twin for any specific applications in oncology (see Fig. 4). Surgery, followed by radiotherapy combined with concurrent and adjuvant chemotherapy is the standard treatment approach for patients with high-grade gliomas to target residual and infiltrative tumors.²⁵⁴ Response to radiotherapy is highly dependent on the ability to target the tumor and on the tumor cells' sensitivity to radiation, which is influenced by multiple factors including tumor physiology, phenotypic behavior, and genetic status.^255,256 Adaptive radiotherapy, consisting of anticipatory adjustments in the radiotherapy treatment, can target subregions of disease that are likely to progress during the course of therapy. A digital twin framework can be applied in this setting to assist in identifying patients that will benefit from adaptive treatment over the standard-of-care dose and schedule. Establishing a digital twin for this application can be achieved by answering five questions:

(1)
What are the goals for the digital twin?
(2)
What level of complexity is needed?
(3)
Does a proper mechanism-based mathematical model exist?
(4)
Are the required data available or accessible?
(5)
Can the uncertainty be characterized?

FIG. 4. — Questions to answer for building a practical digital twin for oncology: a blueprint. When building a practical digital twin, five guiding (related) questions need to be answered. First, it must be decided “what are the goals for the digital twin?,” and these goals need to be kept in mind throughout the entire development. It should then be determined “what level of complexity is needed?” to adequately describe the phenomenon under investigation, which is intimately connected to the answer to the first question. The next step is to determine “whether a proper mechanism-based mathematical model exists” for the problem at hand and “whether the required data are available or accessible” to inform all components of the model. These last three questions are closely related and need to be answered with direct collaboration between experimentalists, clinicians, and mathematical modelers. Furthermore, given the inherent limitations in both data measurement and mathematical modeling, it is important to “characterize the uncertainty” of both so that the confidence intervals on any predictions made by the digital twin can be explicitly computed.

While our discussion in this section will be framed around this specific application, it should be clear that this framework can be applied generically to other settings; for example, personalizing neoadjuvant systemic therapy of locally advanced breast cancer,²⁹ planning immediate radical treatment vs active surveillance to avoid overtreatment of prostate cancer,²⁵⁷ optimizing the combination of checkpoint inhibitor drugs of metastatic melanoma.²⁵⁸ We also note that although the blueprint is presented as five individual questions, the questions are closely related and should be considered simultaneously in practice.

A. What are the goals for the digital twin?

Using the framework of the digital twin defined in Sec. I A 2 [Fig. 1(a)], the first decision that we need to make is what the control inputs are for the digital twin (i.e., the goals of building the digital twin)? This question additionally requires identifying what the quantities of interest and rewards are to achieve those goals. This question must be answered prior to all the subsequent questions in the proposed blueprint, and they must be kept in mind throughout the development of the digital twin. In the context of building a digital twin for adaptive radiotherapy in high-grade gliomas, the goal is to guide the optimization of the treatment dose, schedule, and examination frequency for an individual patient.²⁵⁹ Thus, the control inputs to be adapted include the radiotherapy protocol (i.e., the target location and the dose given by each administration of radiotherapy, and the frequency of radiation doses) and the planning of additional tests (e.g., imaging, blood work). To achieve this adaption, the rewards need to reflect both the overall survival and neurotoxicity. For example, the rewards can be defined as the time between the end of radiotherapy and the progression of the disease given constraints on the total cumulative radiation dose, so that the optimization of the radiotherapy protocol would maximize the rewards. Moreover, the choice of target control inputs and associated rewards can affect the choice of quantities of interest. For example, if the goal is to optimize both the target location and dosage of radiation, the digital twin needs to be designed to output quantities that represent the effect of the change in the radiation target location, such as spatially resolved maps of tumor cell density and local response to radiotherapy. Conversely, if the goal is only to optimize the radiation dosage, a digital twin which outputs the scalar value of tumor volume or total cellularity achieved at the conclusion of the radiation plan might be sufficient. This consideration would affect the answers to downstream questions, such as questions related to the model complexity, which will be discussed in Secs. VI B and VI E.

B. What level of complexity is needed?

As discussed in Sec. V, the level of complexity informs which scales (i.e., subcellular, cellular, microenvironmental, and tissue scales) must be resolved in both the modeling and imaging components. In the context of radiotherapy in high-grade glioma, to optimize the therapeutic outcome, the digital twin must provide a robust representation of the dynamics of tumor response to a radiotherapy protocol, which is inherently a multi-scale process. Radiotherapy causes DNA damage, but the sensitivity to radiotherapy is dependent on not only each individual cell's proliferation and genetic variability but also the oxygenation and vascularization of the local tissue.^260,261 To develop a realistic understanding of a patient-specific response to radiotherapy, all scales included in the model must be informed through patient-specific data. However, a complete characterization of multi-scale phenomena is often infeasible from an experimental/clinical perspective, and therefore the level of complexity in the digital twin must be linked to the quantities that can be reasonably measured and evaluated within the system. This should be addressed on a case-by-case basis. For example, to account for the effect of vascularization and oxygenation on the efficacy of radiotherapy, it must be determined if resolving the effect of the capillaries (i.e., events at the microenvironmental scale) is required, or if characterizing the bulk averaged effect of the vasculature (i.e., events at the tissue scale) is sufficient. While both effects can be described mathematically,²⁶² if the appropriate data are not available to calibrate the mathematical formulation, the digital twin cannot be properly personalized.

C. Does a proper mechanism-based mathematical model exist?

The next question to address is if a mechanism-based model exists for the phenomena under investigation at the desired level of complexity. For radiotherapy of high-grade gliomas, models from the cellular to the tissue scales have been developed and shown to be successful in predicting response.^98,162 At the cellular scale, the linear-quadratic model for cell death due to radiotherapy has been utilized for decades.^263,264 While this model was phenomenologically derived, it has been successful at predicting the surviving fraction of cells at an end point following radiation and determining fractionated radiotherapy plans.²⁶⁵ At the tissue scale, the linear-quadratic model for cell death has been used within reaction-diffusion models of tumor growth (with or without vasculature) to predict response to radiotherapy both in the pre-clinical and clinical settings.^30,266,267 Recent work by Liu et al.²⁶⁸ has introduced a dynamic death rate in ODE tumor growth models that characterizes both the effects of early and late cell death due to radiotherapy throughout the time course (as opposed to just a pre-selected end point). This approach, and others,^147,269,270 allow for radiation therapy to include a spectrum of cell responses and not simply a binary classification of survival or cell death. Efforts to bridge the gap between the cell and tissue scales have resulted in multi-scale models of glioma that are based on conservation laws, that incorporate molecular factors that cause phenotypic transitions of individual cells, and that introduce mutational events that result in biologically relevant sub-clones (e.g., cells with higher epidermal growth factor receptor density express more aggressive behavior).^271–273 Other multi-scale efforts have included signaling pathways,²⁷⁴ angiogenesis,^207,275 and invasion.²⁷⁶

D. Are the required data available or accessible?

As digital twins are designed to represent real-world phenomena, it is important to not only have realistic models, but also have relevant data available, including input data for informing the parameters that define the digital twin and end point data for evaluating and refining to maintain the accuracy and robustness of the digital twin. For the example of building a patient-specific radiotherapy plan for high-grade gliomas, imaging is a fundamental component, which typically involves acquiring images before and following treatment for diagnosis, monitoring, and prognosis.^277,278 Imaging is also routinely used to help guide treatment targeting, positioning, and adaptation.^279,280 Importantly, there are many publicly accessible radiological datasets of brain cancer (see, for example, the Cancer Imaging Archive,²⁸¹ and the Multimodal Brain Tumor Image Segmentation Benchmark²⁸²) which can help augment the study-specific data that may be acquired. Most importantly, establishing digital twins requires close collaboration between experimentalists, clinicians, and modelers with a consensus goal (as identified in Sec. VI A). For example, to build a digital twin for high-grade gliomas, a set of pretreatment images is required to provide the initial conditions of tumor properties (e.g., cellularity, vascularity, and anatomical landmarks). Additionally, to personalize patient-specific response to the radiotherapy, at least one session of follow-up imaging is required to calibrate the parameters in the digital twin. Furthermore, if multiple imaging sessions were performed to longitudinally monitor the patient's response, the digital twin would benefit from continuous refinement to preserve an accurate prediction of the planned radiotherapy. For example, we have recently extended our previous model of response to radiation therapy³⁰ to include advanced quantitative MRI data collected weekly during radiotherapy.²⁸³ This data acquisition protocol provides an adequate source of data to initialize and longitudinally calibrate digital twins of tumor growth and response prior to the conclusion of radiotherapy. While weekly or more frequent MRI assessment is not currently part of the standard-of-care, the recent advent of MRI-guided linear accelerators²⁸⁴ may facilitate daily acquisitions of anatomical and functional imaging data, which makes it increasingly feasible to access large amounts of relevant imaging data for building glioma-based digital twins.

E. Can the uncertainty be characterized?

There are multiple sources of uncertainty that need to be quantified to provide a reliable digital twin. First, data uncertainty comes from sparsely and inconsistently sampled data in time and space, imprecise imaging, and post-processing procedures. Specifically in the context of glioma, the images are commonly collected at a spatial resolution ranging from one to a few mm³. The quality of brain MR images, depending on the choice of imaging protocol, the acquisition and reconstruction techniques, and the day-to-day setup, could introduce noise or artifacts.¹¹¹ Furthermore, image-based segmentation of brain tumors present additional uncertainty due to the limitations of segmentation methods, image quality, the intrinsic intratumoral heterogeneity, and the effects of therapeutic interventions on the imaging features.^285,286 For example, the primary regions of high-grade gliomas show elevated intensity in the contrast-enhanced T₁-weighted MRI, which generally demonstrates increased cell density and vascularization. However, high-grade gliomas are infiltrative and may invade surrounding tissue to generate regions with a low cell density. These regions do not show increased intensity in the contrast-enhanced T₁-weighted MRI, but they do in the T₂-FLAIR (Fluid Attenuated Inversion Recovery) MRI; this makes it challenging to accurately differentiate invasive tumor from edema and/or inflammation.²⁸² Additionally, specific processing of imaging data (e.g., calculation of ADC maps from DW-MRI) and the data-driven parameter calibration^132,138,287 may further contribute to uncertainty.

Model uncertainties can arise from the assumptions and simplifications in the mathematical formulation of models. In the context of glioma modeling questions that arise include the following:

(1)
Should the mechanical interactions between the tumor and brain tissue, as well as between the brain and the surrounding skull be considered?
(2)
Should white and gray matter be assigned different tissue mechanical properties?
(3)
Which types of cells should be included in the model?
(4)
Should the formation of new blood vessels be included?
(5)
Should a global parameterization or spatially-resolved parameter maps be used?

Each question has multiple possible answers, which may require new assumptions or new modeling hypotheses that will affect the uncertainty in the selected model and its predictions. Additionally, the numerical methods leveraged to solve the developed model will also affect uncertainty through errors in geometric discretization and approximation of the solution to the differential equations.

The most challenging aspect is that these uncertainties accumulate (i.e., the total uncertainty in the scenario is the sum of the data, model, and numerical uncertainties) and affect the predictive accuracy of the model. Thus, it is important to select a method that can characterize these uncertainties. The Bayesian framework addresses this endeavor and propagates the error to the probability distribution of the model parameters and outcomes.²⁰³ Hence, instead of relying on deterministic estimates of the parameters, one can randomly draw from the probability distributions of the model parameters and solve the forward problem for each sample to obtain the corresponding probability distributions of the quantities of interest, which enable the estimation of their uncertainties.^134,248,252

VII. SUMMARY

Digital twin technology provides a promising and practical methodology to achieve precision care on a patient-specific basis in oncology. As one of the most practical approaches, image-guided mechanism-based digital twins integrate clinically available imaging techniques that provide quantitative, observational data of patients with mechanism-based mathematical models to understand and forecast the dynamics of tumor growth and treatment response. These digital twins can potentially improve the accuracy of diagnosis and prognosis, as well as provide opportunities to personally optimize treatment. The practical application of digital twins will benefit from the development of more realistic mechanism-based mathematical models, experimental techniques to observe multi-scale tumor dynamics at an improved spatial and temporal resolution, and more advanced numerical techniques for rapid and accurate model calibration and model selection and uncertainty quantification. Establishing a patient-specific digital twin is a goal-oriented task, which requires collaborative efforts between experimentalists, clinicians, and mathematical modelers. We hope this review serves to motivate more discussion of, collaboration on, and development of digital twins for oncological application, including necessary improvements in data capture to support the development and deployment of digital twins, as they are essential to hastening the arrival of truly personalized care for cancer patients.

ACKNOWLEDGMENTS

We thank the National Institutes of Health for funding through Nos. NCI U01CA142565, U01CA174706, U01CA253540, R01CA240589, and U24CA226110. We thank the Cancer Prevention and Research Institute of Texas for support through CPRIT RR160005. T.E.Y. is a CPRIT Scholar in Cancer Research. G.L. acknowledges funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie Grant Agreement No. 838786.

AUTHOR DECLARATIONS

Conflict of Interest

The authors have no conflicts to disclose.

DATA AVAILABILITY

Data sharing is not applicable to this article as no new data were created or analyzed in this study.

References

1. Shafto M., Conroy M., Doyle R., Glaessgen E., Kemp C., LeMoigne J., and Wang L., “ Modeling, simulation, information technology & processing roadmap,” Technical Report, National Aeronautics and Space Administration (2012), Vol. 32, pp. 1–38; available at https://www.nasa.gov/pdf/501321main_TA11-MSITP-DRAFT-Nov2010-A1.pdf. [Google Scholar]
2. Rosen R., Von Wichert G., Lo G., and Bettenhausen K. D., “ About the importance of autonomy and digital twins for the future of manufacturing,” Ifac Papersonline 48, 567–572 (2015). 10.1016/j.ifacol.2015.06.141 [DOI] [Google Scholar]
3. Niederer S. A., Sacks M. S., Girolami M., and Willcox K., “ Scaling digital twins from the artisanal to the industrial,” Nat. Comput. Sci. 1, 313–320 (2021). 10.1038/s43588-021-00072-5 [DOI] [PubMed] [Google Scholar]
4. Kapteyn M. G., Pretorius J. V., and Willcox K. E., “ A probabilistic graphical model foundation for enabling predictive digital twins at scale,” Nat. Comput. Sci. 1, 337–347 (2021). 10.1038/s43588-021-00069-0 [DOI] [PubMed] [Google Scholar]
5. Schleich B., Anwer N., Mathieu L., and Wartzack S., “ Shaping the digital twin for design and production engineering,” CIRP Ann. 66, 141–144 (2017). 10.1016/j.cirp.2017.04.040 [DOI] [Google Scholar]
6. Tao F., Zhang H., Liu A., and Nee A. Y., “ Digital twin in industry: State-of-the-art,” IEEE Trans. Ind. Inf. 15, 2405–2415 (2019). 10.1109/TII.2018.2873186 [DOI] [Google Scholar]
7. Negri E., Fumagalli L., and Macchi M., “ A review of the roles of digital twin in CPS-based production systems,” in 27th International Conference on Flexible Automation and Intelligent Manufacturing, FAIM, edited by Pellicciari M. and Peruzzini M. ( Elsevier, 2017), pp. 939–948. [Google Scholar]
8. Rasheed A., San O., and Kvamsdal T., “ Digital twin: Values, challenges and enablers from a modeling perspective,” IEEE Access 8, 21980–22012 (2020). 10.1109/ACCESS.2020.2970143 [DOI] [Google Scholar]
9. Peirlinck M., Costabal F. S., Yao J., Guccione J. M., Tripathy S., Wang Y., Ozturk D., Segars P., Morrison T. M., Levine S., and Kuhl E., “ Precision medicine in human heart modeling,” Biomech. Model. Mechanobiol. 20, 803–831 (2021). 10.1007/s10237-021-01421-z [DOI] [PMC free article] [PubMed] [Google Scholar]
10. Shamanna P., Saboo B., Damodharan S., Mohammed J., Mohamed M., Poon T., Kleinman N., and Thajudeen M., “ Reducing HbA1c in type 2 diabetes using digital twin technology-enabled precision nutrition: A retrospective analysis,” Diabetes Ther. 11, 2703–2714 (2020). 10.1007/s13300-020-00931-w [DOI] [PMC free article] [PubMed] [Google Scholar]
11. Hormuth D. A., Jarrett A. M., Lorenzo G., Lima E. A., Wu C., Chung C., Patt D., and Yankeelov T. E., “ Math, magnets, and medicine: Enabling personalized oncology,” Expert Rev. Precis. Med. Drug Dev. 6, 79–81 (2021). 10.1080/23808993.2021.1878023 [DOI] [PMC free article] [PubMed] [Google Scholar]
12. Dowden H. and Munro J., “ Trends in clinical success rates and therapeutic focus,” Nat. Rev. Drug Discov. 18, 495–496 (2019). 10.1038/d41573-019-00074-z [DOI] [PubMed] [Google Scholar]
13.BTP Practice, “ Biopharmaceutical industry‐sponsored clinical trials: Impact on state economies,” Technical Report (2015); available at http://phrma-docs.phrma.org/sites/default/files/pdf/biopharmaceutical-industry-sponsored-clinical-trials-impact-on-state-economies.pdf.
14. Umutyan A., Chiechi C., Beckett L. A., Paterniti D. A., Turrell C., Gandara D. R., Davis S. W., Wun T., M. S. Chen, Jr. , and Lara P. N., Jr., “ Overcoming barriers to cancer clinical trial accrual: Impact of a mass media campaign,” Cancer 112, 212–219 (2008). 10.1002/cncr.23170 [DOI] [PubMed] [Google Scholar]
15. Haidich A. B. and Ioannidis J. P., “ Effect of early patient enrollment on the time to completion and publication of randomized controlled trials,” Am. J. Epidemiol. 154, 873–880 (2001). 10.1093/aje/154.9.873 [DOI] [PubMed] [Google Scholar]
16. Unger J. M., Cook E., Tai E., and Bleyer A., “ The role of clinical trial participation in cancer research: Barriers, evidence, and strategies,” Am. Soc. Clin. Oncol. Educ. Book 36, 185–198 (2016). 10.1200/EDBK_156686 [DOI] [PMC free article] [PubMed] [Google Scholar]
17. Hunger S. P., Lu X., Devidas M., Camitta B. M., Gaynon P. S., Winick N. J., Reaman G. H., and Carroll W. L., “ Improved survival for children and adolescents with acute lymphoblastic leukemia between 1990 and 2005: A report from the children's oncology group,” J. Clin. Oncol. 30(14), 1663 (2012). 10.1200/JCO.2011.37.8018 [DOI] [PMC free article] [PubMed] [Google Scholar]
18. Pan E., Bogumil D., Cortessis V., Yu S., and Nieva J., “ A systematic review of the efficacy of preclinical models of lung cancer drugs,” Front. Oncol. 10, 591 (2020). 10.3389/fonc.2020.00591 [DOI] [PMC free article] [PubMed] [Google Scholar]
19. Tam C. S., Opat S., D'Sa S., Jurczak W., Lee H. P., Cull G., Owen R. G., Marlton P., Wahlin B. E., Sanz R. G., and McCarthy H., “ A randomized phase 3 trial of zanubrutinib vs ibrutinib in symptomatic Waldenström macroglobulinemia: The ASPEN study,” Blood 136(18), 2038–2050 (2020). 10.1182/blood.2020006844 [DOI] [PMC free article] [PubMed] [Google Scholar]
20. Schmid P., Cortés J., Dent R., Pusztai L., McArthur H. L., Kuemmel S., Bergh J., Denkert C., Park Y. H., Hui R., and Harbeck N., “ KEYNOTE-522: Phase III study of pembrolizumab (pembro)+ chemotherapy (chemo) vs placebo (pbo)+ chemo as neoadjuvant treatment, followed by pembro vs pbo as adjuvant treatment for early triple-negative breast cancer (TNBC),” Ann. Oncol. 30, v853–v854 (2019). 10.1093/annonc/mdz394.003 [DOI] [Google Scholar]
21. Chien A. J., Tripathy D., Albain K. S., Symmans W. F., Rugo H. S., Melisko M. E., Wallace A. M., Schwab R., Helsten T., Forero-Torres A., and Stringer-Reasor E., “ MK-2206 and standard neoadjuvant chemotherapy improves response in patients with human epidermal growth factor receptor 2–positive and/or hormone receptor–negative breast cancers in the I-SPY 2 trial,” J. Clin. Oncol. 38, 1059–1069 (2020). 10.1200/JCO.19.01027 [DOI] [PMC free article] [PubMed] [Google Scholar]
22. Ludwig J. A. and Weinstein J. N., “ Biomarkers in cancer staging, prognosis and treatment selection,” Nat. Rev. Cancer 5, 845–856 (2005). 10.1038/nrc1739 [DOI] [PubMed] [Google Scholar]
23. Jarrett A. M., Faghihi D., Hormuth D. A., Lima E. A., Virostko J., Biros G., Patt D., and Yankeelov T. E., “ Optimal control theory for personalized therapeutic regimens in oncology: Background, history, challenges, and opportunities,” J. Clin. Med. 9, 1314 (2020). 10.3390/jcm9051314 [DOI] [PMC free article] [PubMed] [Google Scholar]
24. Colli P., Gomez H., Lorenzo G., Marinoschi G., Reali A., and Rocca E., “ Optimal control of cytotoxic and antiangiogenic therapies on prostate cancer growth,” Math. Models Methods Appl. Sci. 14, 1–50 (2021). 10.1142/S0218202521500299 [DOI] [Google Scholar]
25. Angaroni F., Graudenzi A., Rossignolo M., Maspero D., Calarco T., Piazza R., Montangero S., and Antoniotti M., “ An optimal control framework for the automated design of personalized cancer treatments,” Front. Bioeng. Biotechnol. 8, 523 (2020). 10.3389/fbioe.2020.00523 [DOI] [PMC free article] [PubMed] [Google Scholar]
26. Poels K. E., Schoenfeld A. J., Makhnin A., Tobi Y., Wang Y., Frisco-Cabanos H., Chakrabarti S., Shi M., Napoli C., McDonald T. O., and Tan W., “ Identification of optimal dosing schedules of dacomitinib and osimertinib for a phase I/II trial in advanced EGFR-mutant non-small cell lung cancer,” Nat. Commun. 12, 3697 (2021). 10.1038/s41467-021-23912-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
27. Pasetto S., Gatenby R. A., and Enderling H., “ Bayesian framework to augment tumor board decision making,” JCO Clin. Cancer Inf. 5, 508–517 (2021). 10.1200/CCI.20.00085 [DOI] [PMC free article] [PubMed] [Google Scholar]
28. Booyse W., Wilke D. N., and Heyns S., “ Deep digital twins for detection, diagnostics and prognostics,” Mech. Syst. Signal Process. 140, 106612 (2020). 10.1016/j.ymssp.2019.106612 [DOI] [Google Scholar]
29. Jarrett A. M., Hormuth I. D., Wu C., Kazerouni A. S., Ekrut D. A., Virostko J., Sorace A. G., DiCarlo J. C., Kowalski J., Patt D., and Goodgame B., “ Evaluating patient-specific neoadjuvant regimens for breast cancer via a mathematical model constrained by quantitative magnetic resonance imaging data,” Neoplasia 22, 820–830 (2020). 10.1016/j.neo.2020.10.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
30. Hormuth D. A. II, Al Feghali K. A., Elliott A. M., Yankeelov T. E., and Chung C., “ Image-based personalization of computational models for predicting response of high-grade glioma to chemoradiation,” Sci. Rep. 11, 8520 (2021). 10.1038/s41598-021-87887-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
31. Brady-Nicholls R., Nagy J. D., Gerke T. A., Zhang T., Wang A. Z., Zhang J., Gatenby R. A., and Enderling H., “ Prostate-specific antigen dynamics predict individual responses to intermittent androgen deprivation,” Nat. Commun. 11, 1750 (2020). 10.1038/s41467-020-15424-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
32. Stahlberg E., Hanlon S. E., Ellingson S., Kovatch P., Borkon L., and Hollingsworth P., in Seventh Computational Approaches for Cancer Workshop (CAFCW21), St. Louis, Missouri, 2021. [Google Scholar]
33.IMAG, “ NCI-DOE collaboration 2020 virtual ideas lab: Toward building a cancer patient ‘digital twin’,” in Virtual Meeting, July 6–10 (2020). [Google Scholar]
34. Hernandez-Boussard T., Macklin P., Greenspan E. J., Gryshuk A. L., Stahlberg E., Syeda-Mahmood T., and Shmulevich I., “ Digital twins for predictive oncology will be a paradigm shift for precision cancer care,” Nat. Med. 27, 2065–2066 (2021). 10.1038/s41591-021-01558-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
35. Kazerouni A. S., Gadde M., Gardner A., Hormuth D. A. II, Jarrett A. M., Johnson K. E., Lima E. A. B. F., Lorenzo G., Phillips C., Brock A., and Yankeelov T. E., “ Integrating quantitative assays with biologically-based mathematical modeling for predictive oncology,” Iscience 23, 101807 (2020). 10.1016/j.isci.2020.101807 [DOI] [PMC free article] [PubMed] [Google Scholar]
36. Rockne R. C., Hawkins-Daarud A., Swanson K. R., Sluka J. P., Glazier J. A., Macklin P., Hormuth I. D., Jarrett A. M., Lima E. A., Oden J. T., and Biros G., “ The 2019 mathematical oncology roadmap,” Phys. Biol. 16, 041005 (2019). 10.1088/1478-3975/ab1a09 [DOI] [PMC free article] [PubMed] [Google Scholar]
37. Dogra P., Butner J. D., Chuang Y. L., Caserta S., Goel S., Brinker C. J., Cristini V., and Wang Z., “ Mathematical modeling in cancer nanomedicine: A review,” Biomed. Microdev. 21, 40 (2019). 10.1007/s10544-019-0380-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
38. Hamis S., Powathil G. G., and Chaplain M. A., “ Blackboard to bedside: A mathematical modeling bottom-up approach toward personalized cancer treatments,” JCO Clin. Cancer Inf. 3, 1–11 (2019). 10.1200/CCI.18.00068 [DOI] [PubMed] [Google Scholar]
39. Metzcar J., Wang Y., Heiland R., and Macklin P., “ A review of cell-based computational modeling in cancer biology,” JCO Clin. Cancer Inf. 3, 1–3 (2019). 10.1200/CCI.18.00069 [DOI] [PMC free article] [PubMed] [Google Scholar]
40. Sun X. and Hu B., “ Mathematical modeling and computational prediction of cancer drug resistance,” Briefings Bioinf. 19, 1382–1399 (2018). 10.1093/bib/bbx065 [DOI] [PMC free article] [PubMed] [Google Scholar]
41. Yankeelov T. E., Quaranta V., Evans K. J., and Rericha E. C., “ Toward a science of tumor forecasting for clinical oncology,” Cancer Res. 75(6), 918–923 (2015). 10.1158/0008-5472.CAN-14-2233 [DOI] [PMC free article] [PubMed] [Google Scholar]
42. Yankeelov T. E., Mankoff D. A., Schwartz L. H., Lieberman F. S., Buatti J. M., Mountz J. M., Erickson B. J., Fennessy F. M., Huang W., Kalpathy-Cramer J., and Wahl R. L., “ Quantitative imaging in cancer clinical trials,” Clin. Cancer Res. 22, 284–290 (2016). 10.1158/1078-0432.CCR-14-3336 [DOI] [PMC free article] [PubMed] [Google Scholar]
43. Weis J. A., Miga M. I., Arlinghaus L. R., Li X., Chakravarthy A. B., Abramson V., Farley J., and Yankeelov T. E., “ A mechanically coupled reaction-diffusion model for predicting the response of breast tumors to neoadjuvant chemotherapy,” Phys. Med. Biol. 58, 5851–5866 (2013). 10.1088/0031-9155/58/17/5851 [DOI] [PMC free article] [PubMed] [Google Scholar]
44. Woodall R., Hormuth I. D., Wu C., Abdelmalik M., Phillips W. T., Bao A., Hughes T. J. R., Brenner A. J., and Yankeelov T. E., “ Patient specific, imaging-informed modeling of rhenium-186 nanoliposome delivery via convection-enhanced delivery in glioblastoma multiforme,” Biomed. Phys. Eng. Express 7, 45012 (2021). 10.1088/2057-1976/ac02a6 [DOI] [PMC free article] [PubMed] [Google Scholar]
45. Yankeelov T. E., Atuegwu N., Hormuth D. A., Weis J. A., Barnes S. L., Miga M. I., Rericha E. C., and Quaranta V., “ Clinically relevant modeling of tumor growth and treatment response,” Sci. Transl. Med. 5, 187ps9 (2013). 10.1126/scitranslmed.3005686 [DOI] [PMC free article] [PubMed] [Google Scholar]
46. Wu C., Hormuth D. A., Oliver T. A., Pineda F., Lorenzo G., Karczmar G. S., Moser R. D., and Yankeelov T. E., “ Patient-specific characterization of breast cancer hemodynamics using image-guided computational fluid dynamics,” IEEE Trans. Med. Imaging 39, 2760–2771 (2020). 10.1109/TMI.2020.2975375 [DOI] [PMC free article] [PubMed] [Google Scholar]
47. Baldock A., Rockne R., Boone A., Neal M., Bridge C., Guyman L., Mrugala M., Rockhill J., Swanson K. R., Trister A. D., and Hawkins-Daarud A., “ From patient-specific mathematical neuro-oncology to precision medicine,” Front. Oncol. 3, 62 (2013). 10.3389/fonc.2013.00062 [DOI] [PMC free article] [PubMed] [Google Scholar]
48. Whitmire P., Rickertsen C. R., Hawkins-Daarud A., Carrasco E., Lorence J., De Leon G., Curtin L., Bayless S., Clark-Swanson K., Peeri N. C., and Corpuz C., “ Sex-specific impact of patterns of imageable tumor growth on survival of primary glioblastoma patients,” BMC Cancer 20, 447 (2020). 10.1186/s12885-020-06816-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
49. Scheufele K., Subramanian S., and Biros G., “ Fully automatic calibration of tumor-growth models using a single mpMRI scan,” IEEE Trans. Med. Imaging 40, 193–204 (2021). 10.1109/TMI.2020.3024264 [DOI] [PMC free article] [PubMed] [Google Scholar]
50. Lê M., Delingette H., Kalpathy-Cramer J., Gerstner E. R., Batchelor T., Unkelbach J., and Ayache N., “ MRI based Bayesian personalization of a tumor growth model,” IEEE Trans. Med. Imaging 35, 2329–2339 (2016). 10.1109/TMI.2016.2561098 [DOI] [PubMed] [Google Scholar]
51. Lipková J., Angelikopoulos P., Wu S., Alberts E., Wiestler B., Diehl C., Preibisch C., Pyka T., Combs S. E., Hadjidoukas P., and Van Leemput K., “ Personalized radiotherapy design for glioblastoma: Integrating mathematical tumor models, multimodal scans, and Bayesian inference,” IEEE Trans. Med. Imaging 38, 1875–1884 (2019). 10.1109/TMI.2019.2902044 [DOI] [PMC free article] [PubMed] [Google Scholar]
52. Swanson K. R., Alvord E. C., and Murray J. D., “ A quantitative model for differential motility of gliomas in grey and white matter,” Cell Proliferation 33, 317–329 (2000). 10.1046/j.1365-2184.2000.00177.x [DOI] [PMC free article] [PubMed] [Google Scholar]
53. Neal M. L., Trister A. D., Cloke T., Sodt R., Ahn S., Baldock A. L., Bridge C. A., Lai A., Cloughesy T. F., Mrugala M. M., and Rockhill J. K., “ Discriminating survival outcomes in patients with glioblastoma using a simulation-based, patient-specific response metric,” PLoS One 8, e51951 (2013). 10.1371/journal.pone.0051951 [DOI] [PMC free article] [PubMed] [Google Scholar]
54. Romarowski R. M., Conti M., Morganti S., Grassi V., Marrocco-Trischitta M. M., Trimarchi S., and Auricchio F., “ Computational simulation of TEVAR in the ascending aorta for optimal endograft selection: A patient-specific case study,” Comput. Biol. Med. 103, 140–147 (2018). 10.1016/j.compbiomed.2018.10.014 [DOI] [PubMed] [Google Scholar]
55. Corral-Acero J., Margara F., Marciniak M., Rodero C., Loncaric F., Feng Y., Gilbert A., Fernandes J. F., Bukhari H. A., Wajdan A., and Martinez M. V., “ The ‘digital twin’ to enable the vision of precision cardiology,” Eur. Heart J. 41, 4556–4564 (2020). 10.1093/eurheartj/ehaa159 [DOI] [PMC free article] [PubMed] [Google Scholar]
56. Taylor C. A., Fonte T. A., and Min J. K., “ Computational fluid dynamics applied to cardiac computed tomography for noninvasive quantification of fractional flow reserve: Scientific basis,” J. Am. Coll. Cardiol. 61(22), 2233–2241 (2013). 10.1016/j.jacc.2012.11.083 [DOI] [PubMed] [Google Scholar]
57. Sankaran S., Lesage D., Tombropoulos R., Xiao N., Kim H. J., Spain D., Schaap M., and Taylor C. A., “ Physics driven real-time blood flow simulations,” Comput. Methods Appl. Mech. Eng. 364, 112963 (2020). 10.1016/j.cma.2020.112963 [DOI] [Google Scholar]
58. De Bruyne B. and Sarma J., “ Fractional flow reserve: A review,” Heart 94(7), 949–959 (2008). 10.1136/hrt.2007.122838 [DOI] [PubMed] [Google Scholar]
59. Sankaran S., Moghadam M. E., Kahn A. M., Tseng E. E., Guccione J. M., and Marsden A. L., “ Patient-specific multiscale modeling of blood flow for coronary artery bypass graft surgery,” Ann. Biomed. Eng. 40(10), 2228–2242 (2012). 10.1007/s10439-012-0579-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
60. Baillargeon B., Rebelo N., Fox D. D., Taylor R. L., and Kuhl E., “ The living heart project: A robust and integrative simulator for human heart function,” Eur. J. Mech.-A/Solids 48, 38–47 (2014). 10.1016/j.euromechsol.2014.04.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
61. Kayvanpour E., Mansi T., Sedaghat-Hamedani F., Amr A., Neumann D., Georgescu B., Seegerer P., Kamen A., Haas J., Frese K. S., and Irawati M., “ Towards personalized cardiology: Multi-scale modeling of the failing heart,” PLoS One 10(7), e0134869 (2015). 10.1371/journal.pone.0134869 [DOI] [PMC free article] [PubMed] [Google Scholar]
62. Liu J., Yang W., Lan I. S., and Marsden A. L., “ Fluid-structure interaction modeling of blood flow in the pulmonary arteries using the unified continuum and variational multiscale formulation,” Mech. Res. Commun. 107, 103556 (2020). 10.1016/j.mechrescom.2020.103556 [DOI] [PMC free article] [PubMed] [Google Scholar]
63. Zhang W., Rossini G., Kamensky D., Bui‐Thanh T., and Sacks M. S., “ Isogeometric finite element‐based simulation of the aortic heart valve: Integration of neural network structural material model and structural tensor fiber architecture representations,” Int. J. Numer. Methods Biomed. Eng. 37, e3438 (2021). 10.1002/cnm.3438 [DOI] [PMC free article] [PubMed] [Google Scholar]
64. Clayton R. H., Bernus O., Cherry E. M., Dierckx H., Fenton F. H., Mirabella L., Panfilov A. V., Sachse F. B., Seemann G., and Zhang H., “ Models of cardiac tissue electrophysiology: Progress, challenges and open questions,” Prog. Biophys. Mol. Biol. 104(1–3), 22–48 (2011). 10.1016/j.pbiomolbio.2010.05.008 [DOI] [PubMed] [Google Scholar]
65. Zhou L., Bar-Cohen Y., Peck R. A., Chirikian G. V., Harwin B., Chmait R. H., Pruetz J. D., Silka M. J., and Loeb G. E., “ Analytical modeling for computing lead stress in a novel epicardial micropacemaker,” Cardiovasc. Eng. Technol. 8(1), 96–105 (2017). 10.1007/s13239-017-0292-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
66. Sahli Costabal F., Yao J., and Kuhl E., “ Predicting drug-induced arrhythmias by multiscale modeling,” Int. J. Numer. Methods Biomed. Eng. 34(5), e2964 (2018). 10.1002/cnm.2964 [DOI] [PubMed] [Google Scholar]
67. Arthurs C. J., Khlebnikov R., Melville A., Marčan M., Gomez A., Dillon-Murphy D., Cuomo F., Silva Vieira M., Schollenberger J., Lynch S. R., and Tossas-Betancourt C., “ CRIMSON: An open-source software framework for cardiovascular integrated modelling and simulation,” PLOS Comput. Biol. 17, e1008881 (2021). 10.1371/journal.pcbi.1008881 [DOI] [PMC free article] [PubMed] [Google Scholar]
68. Updegrove A., Wilson N. M., Merkow J., Lan H., Marsden A. L., and Shadden S. C., “ SimVascular: An open source pipeline for cardiovascular simulation,” Ann. Biomed. Eng. 45(3), 525–541 (2017). 10.1007/s10439-016-1762-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
69. Barua N. U., Gill S. S., and Love S., “ Convection‐enhanced drug delivery to the brain: Therapeutic potential and neuropathological considerations,” Brain Pathol. 24, 117–127 (2014). 10.1111/bpa.12082 [DOI] [PMC free article] [PubMed] [Google Scholar]
70. Lam M. F., Thomas M. G., and Lind C. R., “ Neurosurgical convection-enhanced delivery of treatments for Parkinson's disease,” J. Clin. Neurosci. 18(9), 1163–1167 (2011). 10.1016/j.jocn.2011.01.012 [DOI] [PubMed] [Google Scholar]
71. Saito R. and Tominaga T., “ Convection-enhanced delivery of therapeutics for malignant gliomas.” Neurol. Med.-Chir. 57, 8–16 (2016). 10.2176/nmc.ra.2016-0071 [DOI] [PMC free article] [PubMed] [Google Scholar]
72. Jahangiri A., Chin A. T., Flanigan P. M., Chen R., Bankiewicz K., and Aghi M. K., “ Convection-enhanced delivery in glioblastoma: A review of preclinical and clinical studies,” J. Neurosurg. 126, 191–200 (2017). 10.3171/2016.1.JNS151591 [DOI] [PMC free article] [PubMed] [Google Scholar]
73. Debinski W. and Tatter S. B., “ Convection-enhanced delivery for the treatment of brain tumors,” Expert Rev. Neurother. 9, 1519–1527 (2009). 10.1586/ern.09.99 [DOI] [PMC free article] [PubMed] [Google Scholar]
74. Phillips W. T., Bao A., Brenner A. J., and Goins B. A., “ Image-guided interventional therapy for cancer with radiotherapeutic nanoparticles,” Adv. Drug Delivery Rev. 76, 39–59 (2014). 10.1016/j.addr.2014.07.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
75. Krauze M. T., Saito R., Noble C., Tamas M., Bringas J., Park J. W., Berger M. S., and Bankiewicz K., “ Reflux-free cannula for convection-enhanced high-speed delivery of therapeutic agents,” J. Neurosurg. 103, 923–929 (2005). 10.3171/jns.2005.103.5.0923 [DOI] [PMC free article] [PubMed] [Google Scholar]
76. Bao A., Phillips W., Brenner A., Floyd J., Gorzell B., Cooper A., Martinez R., Salman U., and Goins B., “ First-in-human study of 186Re-nanoliposomes (186RNL) delivered intra-tumorally by convection-enhanced delivery for treatment of recurrent glioblastoma: Safety, image biodistribution, and radiation dosimetry,” J. Nucl. Med. 58(supplement 1), 599 (2017); available at https://jnm.snmjournals.org/content/58/supplement_1/599. [Google Scholar]
77. Wembacher-Schroeder E., Kerstein N., Bander E. D., Pandit-Taskar N., Thomson R., and Souweidane M. M., “ Evaluation of a patient-specific algorithm for predicting distribution for convection-enhanced drug delivery into the brainstem of patients with diffuse intrinsic pontine glioma,” J. Neurosurg. 1, 1–9 (2021). 10.3171/2020.11.PEDS20571 [DOI] [PubMed] [Google Scholar]
78. Morgenstern P. F., Zhou Z., Wembacher-Schröder E., Cina V., Tsiouris A. J., and Souweidane M. M., “ Clinical tolerance of corticospinal tracts in convection-enhanced delivery to the brainstem,” J. Neurosurg. 131(6), 1812–1818 (2018). 10.3171/2018.6.JNS18854 [DOI] [PubMed] [Google Scholar]
79. Sampson J. H., Raghavan R., Brady M. L., Provenzale J. M., Herndon J. E., Croteau D., Friedman A. H., Reardon D. A., Coleman R. E., Wong T., and Bigner D. D., “ Clinical utility of a patient-specific algorithm for simulating intracerebral drug infusions,” Neuro-oncology 9, 343–353 (2007). 10.1215/15228517-2007-007 [DOI] [PMC free article] [PubMed] [Google Scholar]
80. Morrison P. F., Chen M. Y., Chadwick R. S., Lonser R. R., and Oldfield E. H., “ Focal delivery during direct infusion to brain: Role of flow rate, catheter diameter, and tissue mechanics,” Am. J. Physiol. 277(4), 21518–21229 (1999). 10.1152/ajpregu.1999.277.4.R1218 [DOI] [PubMed] [Google Scholar]
81. Rosenbluth K. H., Eschermann J. F., Mittermeyer G., Thomson R., Mittermeyer S., and Bankiewicz K. S., “ Analysis of a simulation algorithm for direct brain drug delivery,” Neuroimage 59, 2423–2429 (2012). 10.1016/j.neuroimage.2011.08.107 [DOI] [PMC free article] [PubMed] [Google Scholar]
82. McCloy R. and Stone R., “ Virtual reality in surgery,” BMJ 323, 912–915 (2001). 10.1136/bmj.323.7318.912 [DOI] [PMC free article] [PubMed] [Google Scholar]
83. Badash I., Burtt K., Solorzano C. A., and Carey J. N., “ Innovations in surgery simulation: A review of past, current and future techniques,” Ann. Transl. Med. 4(23), 453 (2016). 10.21037/atm.2016.12.24 [DOI] [PMC free article] [PubMed] [Google Scholar]
84. Devoto L., Muscroft S., and Chand M., “ Highly accurate, patient-specific, 3-dimensional mixed-reality model creation for surgical training and decision-making,” JAMA Surg. 154(10), 968–969 (2019). 10.1001/jamasurg.2019.2546 [DOI] [PubMed] [Google Scholar]
85. Laaki H., Miche Y., and Tammi K., “ Prototyping a digital twin for real time remote control over mobile networks: Application of remote surgery,” IEEE Access 7, 20325–20336 (2019). 10.1109/ACCESS.2019.2897018 [DOI] [Google Scholar]
86. Ryu W. H., Dharampal N., Mostafa A. E., Sharlin E., Kopp G., Jacobs W. B., Hurlbert R. J., Chan S., and Sutherland G. R., “ Systematic review of patient-specific surgical simulation: Toward advancing medical education,” J. Surg. Educ. 74(6), 1028–1038 (2017). 10.1016/j.jsurg.2017.05.018 [DOI] [PubMed] [Google Scholar]
87. Brunet J. N., Mendizabal A., Petit A., Golse N., Vibert E., and Cotin S., “ Physics-based deep neural network for augmented reality during liver surgery,” in International Conference on Medical Image Computing and Computer-Assisted Intervention ( Springer, Cham, 2019), pp. 137–145. [Google Scholar]
88. Tepper O. M., Rudy H. L., Lefkowitz A., Weimer K. A., Marks S. M., Stern C. S., and Garfein E. S., “ Mixed reality with HoloLens: Where virtual reality meets augmented reality in the operating room,” Plast. Reconstr. Surg. 140(5), 1066–1070 (2017). 10.1097/PRS.0000000000003802 [DOI] [PubMed] [Google Scholar]
89. Ahmed H. and Devoto L., “ The potential of a digital twin in surgery,” Surg. Innovation 28, 509 (2020). 10.1177/1553350620975896 [DOI] [PMC free article] [PubMed] [Google Scholar]
90. Cevidanes L. H., Tucker S., Styner M., Kim H., Chapuis J., Reyes M., Proffit W., Turvey T., and Jaskolka M., “ Three-dimensional surgical simulation,” Am. J. Orthod. Dentofacial Orthop. 138(3), 361–371 (2010). 10.1016/j.ajodo.2009.08.026 [DOI] [PMC free article] [PubMed] [Google Scholar]
91. Fang C., Zhang P., and Qi X., “ Digital and intelligent liver surgery in the new era: Prospects and dilemmas,” EBioMedicine 41, 693–701 (2019). 10.1016/j.ebiom.2019.02.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
92. de Zélicourt D. A. and Kurtcuoglu V., “ Patient-specific surgical planning, where do we stand? The example of the Fontan procedure,” Ann. Biomed. Eng. 44(1), 174–186 (2016). 10.1007/s10439-015-1381-9 [DOI] [PubMed] [Google Scholar]
93. Malone H. R., Syed O. N., Downes M. S., D'Ambrosio A. L., Quest D. O., and Kaiser M. G., “ Simulation in neurosurgery: A review of computer-based simulation environments and their surgical applications,” Neurosurgery 67(4), 1105–1116 (2010). 10.1227/NEU.0b013e3181ee46d0 [DOI] [PubMed] [Google Scholar]
94. Misra S., Ramesh K. T., and Okamura A. M., “ Modeling of tool-tissue interactions for computer-based surgical simulation: A literature review,” Presence 17(5), 463 (2008). 10.1162/pres.17.5.463 [DOI] [PMC free article] [PubMed] [Google Scholar]
95. Bouhaddou M., Barrette A. M., Stern A. D., Koch R. J., DiStefano M. S., Riesel E. A., Santos L. C., Tan A. L., Mertz A. E., and Birtwistle M. R., “ A mechanistic pan-cancer pathway model informed by multi-omics data interprets stochastic cell fate responses to drugs and mitogens,” PLoS Comput. Biol. 14(3), e1005985 (2018). 10.1371/journal.pcbi.1005985 [DOI] [PMC free article] [PubMed] [Google Scholar]
96. Gruber M., Bozic I., Leshchiner I., Livitz D., Stevenson K., Rassenti L., Rosebrock D., Taylor-Weiner A., Olive O., Goyetche R., and Fernandes S. M., “ Growth dynamics in naturally progressing chronic lymphocytic leukaemia,” Nature 570(7762), 474–479 (2019). 10.1038/s41586-019-1252-x [DOI] [PMC free article] [PubMed] [Google Scholar]
97. Chowell D., Napier J., Gupta R., Anderson K. S., Maley C. C., and Sayres M. A., “ Modeling the subclonal evolution of cancer cell populations,” Cancer Res. 78(3), 830–839 (2018). 10.1158/0008-5472.CAN-17-1229 [DOI] [PMC free article] [PubMed] [Google Scholar]
98. Hormuth D. A., Jarrett A. M., Feng X., and Yankeelov T. E., “ Calibrating a predictive model of tumor growth and angiogenesis with quantitative MRI,” Ann. Biomed. Eng. 47, 1539–1551 (2019). 10.1007/s10439-019-02262-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
99. Hormuth D. A., Jarrett A. M., Davis T., and Yankeelov T. E., “ Towards an image-informed mathematical model of in vivo response to fractionated radiation therapy,” Cancers 13, 1765 (2021). 10.3390/cancers13081765 [DOI] [PMC free article] [PubMed] [Google Scholar]
100. Padhani A. R., Liu G., Mu-Koh D., Chenevert T. L., Thoeny H. C., Takahara T., Dzik-Jurasz A., Ross B. D., Van Cauteren M., Collins D., and Hammoud D. A., “ Diffusion-weighted magnetic resonance imaging as a cancer biomarker: Consensus and recommendations,” Neoplasia 11, 102–125 (2009). 10.1593/neo.81328 [DOI] [PMC free article] [PubMed] [Google Scholar]
101. Yankeelov T. E., Pickens D. R., and Price R. R., Quantitative MRI in Cancer ( Taylor & Francis, 2011). [Google Scholar]
102. Castell F. and Cook G. J. R., “ Quantitative techniques in 18FDG PET scanning in oncology,” Br. J. Cancer 98, 1597–1601 (2008). 10.1038/sj.bjc.6604330 [DOI] [PMC free article] [PubMed] [Google Scholar]
103. Wu C., Pineda F., Hormuth D. A., Karczmar G. S., and Yankeelov T. E., “ Quantitative analysis of vascular properties derived from ultrafast DCE-MRI to discriminate malignant and benign breast tumors,” Magn. Reson. Med. 81, 2147–2160 (2019). 10.1002/mrm.27529 [DOI] [PMC free article] [PubMed] [Google Scholar]
104. Li X., Abramson R. G., Arlinghaus L. R., Chakravarthy A. B., Abramson V. G., Sanders M., and Yankeelov T. E. (2016). “ Data from QIN-breast,” Cancer Imaging Archive. 10.7937/K9/TCIA.2016.21JUebH0 [DOI] [Google Scholar]
105. Li X., Abramson R. G., Arlinghaus L. R., Kang H., Chakravarthy A. B., Abramson V. G., Farley J., Mayer I. A., Kelley M. C., Meszoely I. M., Means-Powell J., Grau A. M., Sanders M., and Yankeelov T. E., “ Multiparametric magnetic resonance imaging for predicting pathological response after the first cycle of neoadjuvant chemotherapy in breast cancer,” Invest. Radiol. 50(4), 195–204 (2015). 10.1097/RLI.0000000000000100 [DOI] [PMC free article] [PubMed] [Google Scholar]
106. Clark K., Vendt B., Smith K., Freymann J., Kirby J., Koppel P., Moore S., Phillips S., Maffitt D., Pringle M., Tarbox L., and Prior F., “ The cancer imaging archive (TCIA): Maintaining and operating a public information repository,” J. Digital Imaging 26(6), 1045–1057 (2013). 10.1007/s10278-013-9622-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
107. Macovski A., Medical Imaging Systems ( Prentice-Hall, 1983). [Google Scholar]
108.Clinical PET and PET/CT: Principles and Applications, edited by Kim E. E., Lee M. C., Inoue T., and Wong W. H. ( Springer Science & Business Media, 2012). [Google Scholar]
109. Nishimura D. G., Principles of Magnetic Resonance Imaging ( Stanford University, 2010). [Google Scholar]
110. Eisenhauer E. A., Therasse P., Bogaerts J., Schwartz L. H., Sargent D., Ford R., Dancey J., Arbuck S., Gwyther S., Mooney M., and Rubinstein L., “ New response evaluation criteria in solid tumours: Revised RECIST guideline (version 1.1),” Eur. J. Cancer 45, 228–247 (2009). 10.1016/j.ejca.2008.10.026 [DOI] [PubMed] [Google Scholar]
111. Hormuth D. A., Sorace A. G., Virostko J., Abramson R. G., Bhujwalla Z. M., Enriquez‐Navas P., Gillies R., Hazle J. D., Mason R. P., Quarles C. C., and Weis J. A., “ Translating preclinical MRI methods to clinical oncology,” J. Magn. Reson. Imaging 50, 1377–1392 (2019). 10.1002/jmri.26731 [DOI] [PMC free article] [PubMed] [Google Scholar]
112. Yankeelov T. E. and Gore J. C., “ Dynamic contrast enhanced magnetic resonance imaging in oncology: Theory, data acquisition, analysis, and examples,” Curr. Med. Imaging Rev. 3, 91–107 (2009). 10.2174/157340507780619179 [DOI] [PMC free article] [PubMed] [Google Scholar]
113. Pineda F. D., Medved M., Wang S., Fan X., Schacht D. V., Sennett C., Oto A., Newstead G. M., Abe H., and Karczmar G. S., “ Ultrafast bilateral DCE-MRI of the breast with conventional fourier sampling: Preliminary evaluation of semi-quantitative analysis,” Acad. Radiol. 23(9), 1137–1144 (2016). 10.1016/j.acra.2016.04.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
114. Onishi N., Kataoka M., Kanao S., Sagawa H., Iima M., Nickel M. D., Toi M., and Togashi K., “ Ultrafast dynamic contrast-enhanced MRI of the breast using compressed sensing: Breast cancer diagnosis based on separate visualization of breast arteries and veins,” J. Magn. Reson. Imaging 47(1), 97–104 (2018). 10.1002/jmri.25747 [DOI] [PubMed] [Google Scholar]
115. Chenevert T. L., Stegman L. D., Taylor J. M., Robertson P. L., Greenberg H. S., Rehemtulla A., and Ross B. D., “ Diffusion magnetic resonance imaging: An early surrogate marker of therapeutic efficacy in brain tumors,” J. Natl. Cancer Inst. 92, 2029–2036 (2000). 10.1093/jnci/92.24.2029 [DOI] [PubMed] [Google Scholar]
116. van Houdt P. J., Yang Y., and van der Heide U. A., “ Quantitative magnetic resonance imaging for biological image-guided adaptive radiotherapy,” Front. Oncol. 10, 615643 (2021). 10.3389/fonc.2020.615643 [DOI] [PMC free article] [PubMed] [Google Scholar]
117. Partridge S. C., Nissan N., Rahbar H., Kitsch A. E., and Sigmund E. E., “ Diffusion-weighted breast MRI: Clinical applications and emerging techniques,” J. Magn. Reson. Imaging 45(2), 337–355 (2017). 10.1002/jmri.25479 [DOI] [PMC free article] [PubMed] [Google Scholar]
118. Partridge S. C., Zhang Z., Newitt D. C., Gibbs J. E., Chenevert T. L., Rosen M. A., Bolan P. J., Marques H. S., Romanoff J., Cimino L., Joe B. N., Umphrey H. R., Ojeda-Fournier H., Dogan B., Oh K., Abe H., Drukteinis J. S., Esserman L. J., and Hylton N. M., “ Diffusion-weighted MRI findings predict pathologic response in neoadjuvant treatment of breast cancer: The ACRIN 6698 multicenter trial,” Radiology 289(3), 618–627 (2018). 10.1148/radiol.2018180273 [DOI] [PMC free article] [PubMed] [Google Scholar]
119. Horská A. and Barker P. B., “ Imaging of brain tumors: MR spectroscopy and metabolic imaging,” Neuroimaging Clin. 20(3), 293–310 (2010). 10.1016/j.nic.2010.04.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
120. Pepin K. M., Ehman R. L., and McGee K. P., “ Magnetic resonance elastography (MRE) in cancer: Technique, analysis, and applications,” Prog. Nucl. Magn. Reson. Spectrosc. 90, 32–48 (2015). 10.1016/j.pnmrs.2015.06.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
121. Wahl R. L., Jacene H., Kasamon Y., and Lodge M. A., “ From RECIST to PERCIST: Evolving considerations for PET response criteria in solid tumors,” J. Nucl. Med. 50, 122S–150S (2009). 10.2967/jnumed.108.057307 [DOI] [PMC free article] [PubMed] [Google Scholar]
122. Pinker K., Riedl C., and Weber W. A., “ Evaluating tumor response with FDG PET: Updates on PERCIST, comparison with EORTC criteria and clues to future developments,” Eur. J. Nucl. Med. Mol. Imaging 44(Suppl 1), 55–66 (2017). 10.1007/s00259-017-3687-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
123. Farwell M. D., Pryma D. A., and Mankoff D. A., “ PET/CT imaging in cancer: Current applications and future directions,” Cancer 120, 3433–3445 (2014). 10.1002/cncr.28860 [DOI] [PubMed] [Google Scholar]
124. Carmona-Bozo J. C., Manavaki R., Woitek R., Torheim T., Baxter G. C., Caracò C., Provenzano E., Graves M. J., Fryer T. D., Patterson A. J., and Gilbert F. J., “ Hypoxia and perfusion in breast cancer: Simultaneous assessment using PET/MR imaging,” Eur. Radiol. 31(1), 333–344 (2021). 10.1007/s00330-020-07067-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
125. Muzi M., Peterson L. M., O'Sullivan J. N., Fink J. R., Rajendran J. G., McLaughlin L. J., Muzi J. P., Mankoff D. A., and Krohn K. A., “ ¹⁸F-fluoromisonidazole quantification of hypoxia in human cancer patients using image-derived blood surrogate tissue reference regions,” J. Nucl. Med. 56(8), 1223–1228 (2015). 10.2967/jnumed.115.158717 [DOI] [PMC free article] [PubMed] [Google Scholar]
126. Holzgreve A., Brendel M., Gu S., Carlsen J., Mille E., Böning G., Mastrella G., Unterrainer M., Gildehaus F. J., Rominger A., Bartenstein P., Kälin R. E., Glass R., and Albert N. L., “ Monitoring of tumor growth with [18F]-FET PET in a mouse model of glioblastoma: SUV measurements and volumetric approaches,” Front. Neurosci. 10, 260 (2016). 10.3389/fnins.2016.00260 [DOI] [PMC free article] [PubMed] [Google Scholar]
127. Pöpperl G., Kreth F. W., Mehrkens J. H., Herms J., Seelos K., Koch W., Gildehaus F. J., Kretzschmar H. A., Tonn J. C., and Tatsch K., “ FET PET for the evaluation of untreated gliomas: Correlation of FET uptake and uptake kinetics with tumour grading,” Eur. J. Nucl. Med. Mol. Imaging 34(12), 1933–1942 (2007). 10.1007/s00259-007-0534-y [DOI] [PubMed] [Google Scholar]
128. Karls S., Shah H., and Jacene H., “ PET/CT for lymphoma post-therapy response assessment in other lymphomas, response assessment for autologous stem cell transplant, and lymphoma follow-up,” Semin. Nucl. Med. 48(1), 37–49 (2018). 10.1053/j.semnuclmed.2017.09.004 [DOI] [PubMed] [Google Scholar]
129. Ehman E. C., Johnson G. B., Villanueva-Meyer J. E., Cha S., Leynes A. P., Larson P. E. Z., and Hope T. A., “ PET/MRI: Where might it replace PET/CT?,” J. Magn. Reson. Imaging 46(5), 1247–1262 (2017). 10.1002/jmri.25711 [DOI] [PMC free article] [PubMed] [Google Scholar]
130. Waks A. G. and Winer E. P., “ Breast cancer treatment: A review,” JAMA 321, 288–300 (2019). 10.1001/jama.2018.19323 [DOI] [PubMed] [Google Scholar]
131. Litwin M. S. and Tan H. J., “ The diagnosis and treatment of prostate cancer: A review,” JAMA 317, 2532–2542 (2017). 10.1001/jama.2017.7248 [DOI] [PubMed] [Google Scholar]
132. Lorenzo G., Hormuth I. D., Jarrett A. M., Lima E. A., Subramanian S., “ Biros G., Oden J. T., Hughes T. J., and Yankeelov T. E., Quantitative in vivo imaging to enable tumor forecasting and treatment optimization,” arXiv:2102.12602 (2021).
133. Karolak A., Markov D. A., McCawley L. J., and Rejniak K. A., “ Towards personalized computational oncology: From spatial models of tumour spheroids, to organoids, to tissues,” J. R. Soc. Interface 15, 20170703 (2018). 10.1098/rsif.2017.0703 [DOI] [PMC free article] [PubMed] [Google Scholar]
134. Lima E. A. B. F., Oden J. T., Wohlmuth B., Shahmoradi A., Hormuth I. D., Yankeelov T. E., Scarabosio L., and Horger T., “ Selection and validation of predictive models of radiation effects on tumor growth based on noninvasive imaging data,” Comput. Methods Appl. Mech. Eng. 327, 277–305 (2017). 10.1016/j.cma.2017.08.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
135. Wang C. H., Rockhill J. K., Mrugala M., Peacock D. L., Lai A., Jusenius K., Wardlaw J. M., Cloughesy T., Spence A. M., Rockne R., and Alvord E. C., “ Prognostic significance of growth kinetics in newly diagnosed glioblastomas revealed by combining serial imaging with a novel biomathematical model,” Cancer Res. 69, 9133–9140 (2009). 10.1158/0008-5472.CAN-08-3863 [DOI] [PMC free article] [PubMed] [Google Scholar]
136. Fey D., Halasz M., Dreidax D., Kennedy S. P., Hastings J. F., Rauch N., Munoz A. G., Pilkington R., Fischer M., Westermann F., and Kolch W., “ Signaling pathway models as biomarkers: Patient-specific simulations of JNK activity predict the survival of neuroblastoma patients,” Sci. Signaling 8, ra130 (2015). 10.1126/scisignal.aab0990 [DOI] [PubMed] [Google Scholar]
137. Tuncbag N., Milani P., Pokorny J. L., Johnson H., Sio T. T., Dalin S., Iyekegbe D. O., White F. M., Sarkaria J. N., and Fraenkel E., “ Network modeling identifies patient-specific pathways in glioblastoma,” Sci. Rep. 6, 28668 (2016). 10.1038/srep28668 [DOI] [PMC free article] [PubMed] [Google Scholar]
138. Mang A., Bakas S., Subramanian S., Davatzikos C., and Biros G., “ Integrated biophysical modeling and image analysis: Application to neuro-oncology,” Annu. Rev. Biomed. Eng. 22, 309–341 (2020). 10.1146/annurev-bioeng-062117-121105 [DOI] [PMC free article] [PubMed] [Google Scholar]
139. Tunc B., Hormuth D., Biros G., and Yankeelov T. E., “ Modeling of glioma growth with mass effect by longitudinal magnetic resonance imaging,” IEEE Trans. Biomed. Eng. 68(12), 3713–3724 (2021). 10.1109/TBME.2021.3085523 [DOI] [PMC free article] [PubMed] [Google Scholar]
140. Vavourakis V., Eiben B., Hipwell J. H., Williams N. R., Keshtgar M., and Hawkes D. J., “ Multiscale mechano-biological finite element modelling of oncoplastic breast surgery—numerical study towards surgical planning and cosmetic outcome prediction,” PLoS One 11, e0159766 (2016). 10.1371/journal.pone.0159766 [DOI] [PMC free article] [PubMed] [Google Scholar]
141. Lorenzo G., Hughes T. J., Dominguez-Frojan P., Reali A., and Gomez H., “ Computer simulations suggest that prostate enlargement due to benign prostatic hyperplasia mechanically impedes prostate cancer growth,” Proc. Natl. Acad. Sci. 116, 1152–1161 (2019). 10.1073/pnas.1815735116 [DOI] [PMC free article] [PubMed] [Google Scholar]
142. Lorenzo G., Pérez-García V. M., Mariño A., Pérez-Romasanta L. A., Reali A., and Gomez H., “ Mechanistic modelling of prostate-specific antigen dynamics shows potential for personalized prediction of radiation therapy outcome,” J. R. Soc. Interface 16, 20190195 (2019). 10.1098/rsif.2019.0195 [DOI] [PMC free article] [PubMed] [Google Scholar]
143. Zahid M. U., Mohsin N., Mohamed A. S., Caudell J. J., Harrison L. B., Fuller C. D., Moros E. G., and Enderling H., “ Forecasting individual patient response to radiotherapy in head and neck cancer with a dynamic carrying capacity model,” Int. J. Radiat. Oncol. Biol. Phys. 111(3), 693–704 (2021). 10.1016/j.ijrobp.2021.05.132 [DOI] [PMC free article] [PubMed] [Google Scholar]
144. Wong K. C., Summers R. M., Kebebew E., and Yao J., “ Pancreatic tumor growth prediction with elastic-growth decomposition, image-derived motion, and FDM-FEM coupling,” IEEE Trans. Med. Imaging 36, 111–123 (2016). 10.1109/TMI.2016.2597313 [DOI] [PMC free article] [PubMed] [Google Scholar]
145. Liu Y., Sadowski S. M., Weisbrod A. B., Kebebew E., Summers R. M., and Yao J., “ Patient specific tumor growth prediction using multimodal images,” Med. Image Anal. 18, 555–566 (2014). 10.1016/j.media.2014.02.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
146. Chen X., Summers R. M., and Yao J., “ Kidney tumor growth prediction by coupling reaction-diffusion and biomechanical model,” IEEE Trans. Biomed. Eng. 60, 169–173 (2012). 10.1109/TBME.2012.2222027 [DOI] [PMC free article] [PubMed] [Google Scholar]
147. Glazar D. J., Grass G. D., Arrington J. A., Forsyth P. A., Raghunand N., Yu H. H., Sahebjam S., and Enderling H., “ Tumor volume dynamics as an early biomarker for patient-specific evolution of resistance and progression in recurrent high-grade glioma,” J. Clin. Med. 9, 2019 (2020). 10.3390/jcm9072019 [DOI] [PMC free article] [PubMed] [Google Scholar]
148. Kaur P., Singh A., and Chana I., “ Computational techniques and tools for omics data analysis: State-of-the-art, challenges, and future directions,” Arch. Comput. Methods Eng. 28, 4595–4631 (2021). 10.1007/s11831-021-09547-0 [DOI] [Google Scholar]
149. Falco M. M., Peña-Chilet M., Loucera C., Hidalgo M. R., and Dopazo J., “ Mechanistic models of signaling pathways deconvolute the glioblastoma single-cell functional landscape,” NAR Cancer 2, zcaa011 (2020). 10.1093/narcan/zcaa011 [DOI] [PMC free article] [PubMed] [Google Scholar]
150. Ebata K., Yamashiro S., Iida K., and Okada M., “ Building patient‐specific models for receptor tyrosine kinase signaling networks,” FEBS J. 289(1), 90–101 (2021). 10.1111/febs.15831 [DOI] [PubMed] [Google Scholar]
151. Klipp E. and Liebermeister W., “ Mathematical modeling of intracellular signaling pathways,” BMC Neurosci. 7, S10 (2006). 10.1186/1471-2202-7-S1-S10 [DOI] [PMC free article] [PubMed] [Google Scholar]
152. Mahlbacher G. E., Reihmer K. C., and Frieboes H. B., “ Mathematical modeling of tumor-immune cell interactions,” J. Theor. Biol. 469, 47–60 (2019). 10.1016/j.jtbi.2019.03.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
153. Jolly M. K., Tripathi S. C., Somarelli J. A., Hanash S. M., and Levine H., “ Epithelial/mesenchymal plasticity: How have quantitative mathematical models helped improve our understanding?,” Mol. Oncol. 11, 739–754 (2017). 10.1002/1878-0261.12084 [DOI] [PMC free article] [PubMed] [Google Scholar]
154. Weis J. A., Miga M. I., Arlinghaus L. R., Li X., Abramson V., Chakravarthy A. B., Pendyala P., and Yankeelov T. E., “ Predicting the response of breast cancer to neoadjuvant therapy using a mechanically coupled reaction–diffusion model,” Cancer Res. 75(22), 4697–4707 (2015). 10.1158/0008-5472.CAN-14-2945 [DOI] [PMC free article] [PubMed] [Google Scholar]
155. Jbabdi S., Mandonnet E., Duffau H., Capelle L., Swanson K. R., Pélégrini‐Issac M., Guillevin R., and Benali H., “ Simulation of anisotropic growth of low‐grade gliomas using diffusion tensor imaging,” Magn. Reson. Med. 54(3), 616–624 (2005). 10.1002/mrm.20625 [DOI] [PubMed] [Google Scholar]
156. Atuegwu N. C., Arlinghaus L. R., Li X., Welch E. B., Chakravarthy B. A., Gore J. C., and Yankeelov T. E., “ Integration of diffusion-weighted MRI data and a simple mathematical model to predict breast tumor cellularity during neoadjuvant chemotherapy,” Magn. Reson. Med. 66, 1689–1696 (2011). 10.1002/mrm.23203 [DOI] [PMC free article] [PubMed] [Google Scholar]
157. Zhu W., Kato Y., and Artemov D., “ Heterogeneity of tumor vasculature and antiangiogenic intervention: Insights from MR angiography and DCE-MRI,” PLoS One 9(1), e86583 (2014). 10.1371/journal.pone.0086583 [DOI] [PMC free article] [PubMed] [Google Scholar]
158. Gatenby R. A., Grove O., and Gillies R. J., “ Quantitative imaging in cancer evolution and ecology,” Radiology 269(1), 8–14 (2013). 10.1148/radiol.13122697 [DOI] [PMC free article] [PubMed] [Google Scholar]
159. Syed A. K., Whisenant J. G., Barnes S. L., Sorace A. G., and Yankeelov T. E., “ Multiparametric analysis of longitudinal quantitative MRI data to identify distinct tumor habitats in preclinical models of breast cancer,” Cancers 12, 1682 (2020). 10.3390/cancers12061682 [DOI] [PMC free article] [PubMed] [Google Scholar]
160. Roque T., Risser L., Kersemans V., Smart S., Allen D., Kinchesh P., Gilchrist S., Gomes A. L., Schnabel J. A., and Chappell M. A., “ A DCE-MRI driven 3-D reaction-diffusion model of solid tumor growth,” IEEE Trans. Med. Imaging 37, 724–732 (2017). 10.1109/TMI.2017.2779811 [DOI] [PubMed] [Google Scholar]
161. Chang Y. C., Ackerstaff E., Tschudi Y., Jimenez B., Foltz W., Fisher C., Lilge L., Cho H., Carlin S., Gillies R. J., and Balagurunathan Y., “ Delineation of tumor habitats based on dynamic contrast enhanced MRI,” Sci. Rep. 7, 9746 (2017). 10.1038/s41598-017-09932-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
162. Rockne R. C., Trister A. D., Jacobs J., Hawkins-Daarud A. J., Neal M. L., Hendrickson K., Mrugala M. M., Rockhill J. K., Kinahan P., Krohn K. A., and Swanson K. R., “ A patient-specific computational model of hypoxia-modulated radiation resistance in glioblastoma using 18F-FMISO-PET,” J. R. Soc. Interface 12, 20141174 (2015). 10.1098/rsif.2014.1174 [DOI] [PMC free article] [PubMed] [Google Scholar]
163. Jarrett A. M., Hormuth D. A., Adhikarla V., Sahoo P., Abler D., Tumyan L., Schmolze D., Mortimer J., Rockne R. C., and Yankeelov T. E., “ Towards integration of ⁶⁴Cu-DOTA-trastuzumab PET-CT and MRI with mathematical modeling to predict response to neoadjuvant therapy in HER2 + breast cancer,” Sci. Rep. 10, 20518 (2020). 10.1038/s41598-020-77397-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
164. Wu C., Hormuth D. A., Pineda F., Karczmar G. S., and Yankeelov T. E., “ Towards patient-specific optimization of neoadjuvant treatment protocols for breast cancer based on image-guided fluid dynamics,” IEEE Trans. Biomed. Eng. (published online 2022). 10.1109/TBME.2022.3168402 [DOI] [PMC free article] [PubMed] [Google Scholar]
165. Esserman L. J., Thompson I. M., Reid B., Nelson P., Ransohoff D. F., Welch H. G., Hwang S., Berry D. A., Kinzler K. W., Black W. C., and Bissell M., “ Addressing overdiagnosis and overtreatment in cancer: A prescription for change,” Lancet Oncol. 15(6), e234–e242 (2014). 10.1016/S1470-2045(13)70598-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
166. Loeb S., Bjurlin M. A., Nicholson J., Tammela T. L., Penson D. F., Carter H. B., Carroll P., and Etzioni R., “ Overdiagnosis and overtreatment of prostate cancer,” Eur. Urol. 65(6), 1046–1055 (2014). 10.1016/j.eururo.2013.12.062 [DOI] [PMC free article] [PubMed] [Google Scholar]
167. Eklund M., Jäderling F., Discacciati A., Bergman M., Annerstedt M., Aly M., Glaessgen A., Carlsson S., Grönberg H., and Nordström T., “ MRI-targeted or standard biopsy in prostate cancer screening,” N. Engl. J. Med. 385(10), 908–920 (2021). 10.1056/NEJMoa2100852 [DOI] [PubMed] [Google Scholar]
168. Co M., “ Ductal carcinoma in situ of the breasts: Over‐diagnosis, over‐treatment and a decade of lost direction,” Precis. Med. Sci. 9(1), 4–8 (2020). 10.1002/prm2.12008 [DOI] [Google Scholar]
169. Van Luijt P. A., Heijnsdijk E. A., Fracheboud J., Overbeek L. I., Broeders M. J., Wesseling J., den Heeten G. J., and de Koning H. J., “ The distribution of ductal carcinoma in situ (DCIS) grade in 4232 women and its impact on overdiagnosis in breast cancer screening,” Breast Cancer Res. 18(1), 47 (2016). 10.1186/s13058-016-0705-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
170. Hawkins-Daarud A., Prudhomme S., van der Zee K. G., and Oden J. T., “ Bayesian calibration, validation, and uncertainty quantification of diffuse interface models of tumor growth,” J. Math. Biol. 67(6), 1457–1485 (2013). 10.1007/s00285-012-0595-9 [DOI] [PubMed] [Google Scholar]
171. Liedtke C., Mazouni C., Hess K. R., André F., Tordai A., Mejia J. A., Symmans W. F., Gonzalez-Angulo A. M., Hennessy B., Green M., and Cristofanilli M., “ Response to neoadjuvant therapy and long-term survival in patients with triple-negative breast cancer,” J. Clin. Oncol. 26, 1275–1281 (2008). 10.1200/JCO.2007.14.4147 [DOI] [PubMed] [Google Scholar]
172. Spring L. M., Fell G., Arfe A., Sharma C., Greenup R., Reynolds K. L., Smith B. L., Alexander B., Moy B., Isakoff S. J., and Parmigiani G., “ Pathological complete response after neoadjuvant chemotherapy and impact on breast cancer recurrence and survival: A comprehensive meta-analysis,” Clin. Cancer Res. 26, 2838 (2020). 10.1158/1078-0432.CCR-19-3492 [DOI] [PMC free article] [PubMed] [Google Scholar]
173. Korde L. A., Somerfield M. R., Carey L. A., Crews J. R., Denduluri N., Hwang E. S., Khan S. A., Loibl S., Morris E. A., Perez A., and Regan M. M., “ Neoadjuvant chemotherapy, endocrine therapy, and targeted therapy for breast cancer: ASCO guideline,” J. Clin. Oncol. 39(13), 1485–1505 (2021). 10.1200/JCO.20.03399 [DOI] [PMC free article] [PubMed] [Google Scholar]
174. Castiglioni I., Rundo L., Codari M., Di Leo G., Salvatore C., Interlenghi M., Gallivanone F., Cozzi A., D'Amico N. C., and Sardanelli F., “ AI applications to medical images: From machine learning to deep learning,” Phys. Med. 83, 9–24 (2021). 10.1016/j.ejmp.2021.02.006 [DOI] [PubMed] [Google Scholar]
175. Murphy K. P., Machine Learning: A Probabilistic Perspective ( MIT Press, 2012). [Google Scholar]
176. Guresen E. and Kayakutlu G., “ Definition of artificial neural networks with comparison to other networks,” Procedia Comput. Sci. 3, 426–433 (2011). 10.1016/j.procs.2010.12.071 [DOI] [Google Scholar]
177. Schmidhuber J., “ Deep learning in neural networks: An overview,” Neural Networks 61, 85–117 (2015). 10.1016/j.neunet.2014.09.003 [DOI] [PubMed] [Google Scholar]
178. LeCun Y., Bengio Y., and Hinton G., “ Deep learning,” Nature 521, 436–444 (2015). 10.1038/nature14539 [DOI] [PubMed] [Google Scholar]
179. Darestani M. and Heckel R., “ Can un-trained neural networks compete with trained neural networks at image reconstruction?,” arXiv:2007.02471 (2020).
180. Miotto R., Wang F., Wang S., Jiang X., and Dudley J. T., “ Deep learning for healthcare: Review, opportunities and challenges,” Briefings Bioinf. 19, 1236–1246 (2018). 10.1093/bib/bbx044 [DOI] [PMC free article] [PubMed] [Google Scholar]
181. Ulyanov D., Vedaldi A., and Lempitsky V., “ Deep image prior,” Int. J. Comput. Vis. 128, 1867–1888 (2020). 10.1007/s11263-020-01303-4 [DOI] [Google Scholar]
182. Wang T., Lei Y., Fu Y., Wynne J. F., Curran W. J., Liu T., and Yang X., “ A review on medical imaging synthesis using deep learning and its clinical applications,” J. Appl. Clin. Med. Phys. 22, 11–36 (2020). 10.1002/acm2.13121 [DOI] [PMC free article] [PubMed] [Google Scholar]
183. Elmarakeby H. A., Hwang J., Arafeh R., Crowdis J., Gang S., Liu D., AlDubayan S. H., Salari K., Kregel S., Richter C., and Arnoff T. E., “ Biologically informed deep neural network for prostate cancer discovery,” Nature 598, 348–352 (2021). 10.1038/s41586-021-03922-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
184. Darestani M. Z. and Heckel R., “ Accelerated MRI with un-trained neural networks,” IEEE Trans. Comput. Imaging 7, 724–733 (2021). 10.1109/TCI.2021.3097596 [DOI] [Google Scholar]
185. Kaissis G. A., Makowski M. R., Rückert D., and Braren R. F., “ Secure, privacy-preserving and federated machine learning in medical imaging,” Nat. Mach. Intell. 2, 305–311 (2020). 10.1038/s42256-020-0186-1 [DOI] [Google Scholar]
186. Björnsson B., Borrebaeck C., Elander N., Gasslander T., Gawel D. R., Gustafsson M., Jörnsten R., Lee E. J., Li X., Lilja S., and Martínez-Enguita D., “ Digital twins to personalize medicine,” Genome Med. 12, 1–4 (2020). 10.1186/s13073-019-0701-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
187. Izmailova E. S. and Wood W. A., “ Biometric monitoring technologies in cancer: The past, present, and future,” JCO Clin. Cancer Inf. 5, 728–733 (2021). 10.1200/CCI.21.00019 [DOI] [PubMed] [Google Scholar]
188. Ahmadi-Assalemi G., Al-Khateeb H., Maple C., Epiphaniou G., Alhaboby Z. A., Alkaabi S., and Alhaboby D., “ Digital twins for precision healthcare,” in Cyber Defence in the Age of AI, Smart Societies and Augmented Humanity, edited by Jahankhani H., Kendzierskyj S., Chelvachandran N., and Ibarra J. ( Springer Nature Switzerland AG, Cham, Switzerland, 2020), pp. 133–158. [Google Scholar]
189. Croatti A., Gabellini M., Montagna S., and Ricci A., “ On the integration of agents and digital twins in healthcare,” J. Med. Syst. 44, 161 (2020). 10.1007/s10916-020-01623-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
190. Ash D., Gold G., Seiver A., and Hayes-Rosh B., “ Guaranteeing real-time response with limited resources,” Artif. Intell. Med. 5, 49–66 (1995). 10.1016/0933-3657(93)90005-N [DOI] [PubMed] [Google Scholar]
191. Jardine A. K. S., Lin D., and Banjevic D., “ A review on machinery diagnostics and prognostics implementing condition-based maintenance,” Mech. Syst. Signal Process. 20, 1483–1510 (2006). 10.1016/j.ymssp.2005.09.012 [DOI] [Google Scholar]
192. Khan S. and Yairi T., “ A review on the applications of deep learning in system health management,” Mech. Syst. Signal Process. 107, 241–265 (2019). 10.1016/j.ymssp.2017.11.024 [DOI] [Google Scholar]
193. Cohen O., Zhu B., and Rosen M. S., “ MR fingerprinting deep reconstruction network (DRONE),” Magn. Reson. Med. 80(3), 885–894 (2018). 10.1002/mrm.27198 [DOI] [PMC free article] [PubMed] [Google Scholar]
194. Ronneberger O., Fischer P., and Brox T., “ U-net: Convolutional networks for biomedical image segmentation,” in International Conference on Medical Image Computing and Computer-Assisted Intervention ( Springer, Cham, 2015), pp. 234–241. [Google Scholar]
195. Li Y., Wang Y., Qi H., Hu Z., Chen Z., Yang R., Qiao H., Sun J., Wang T., Zhao X., and Guo H., “ Deep learning–enhanced T₁ mapping with spatial-temporal and physical constraint,” Magn. Reson. Med. 86, 1647–1661 (2021). 10.1002/mrm.28793 [DOI] [PubMed] [Google Scholar]
196. Raissi M., Yazdani A., and Karniadakis G. E., “ Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations,” Science 367, 1026–1030 (2020). 10.1126/science.aaw4741 [DOI] [PMC free article] [PubMed] [Google Scholar]
197. Alber M., Tepole A. B., Cannon W. R., De S., Dura-Bernal S., Garikipati K., Karniadakis G., Lytton W. W., Perdikaris P., Petzold L., and Kuhl E., “ Integrating machine learning and multiscale modeling—perspectives, challenges, and opportunities in the biological, biomedical, and behavioral sciences,” npj Digital Med. 2, 115 (2019). 10.1038/s41746-019-0193-y [DOI] [PMC free article] [PubMed] [Google Scholar]
198. Gaw N., Hawkins-Daarud A., Hu L. S., Yoon H., Wang L., Xu Y., Jackson P. R., Singleton K. W., Baxter L. C., Eschbacher J., and Gonzales A., “ Integration of machine learning and mechanistic models accurately predicts variation in cell density of glioblastoma using multiparametric MRI,” Sci. Rep. 9, 10063 (2019). 10.1038/s41598-019-46296-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
199. Nicolò C., Périer C., Prague M., Bellera C., MacGrogan G., Saut O., and Benzekry S., “ Machine learning and mechanistic modeling for prediction of metastatic relapse in early-stage breast cancer,” JCO Clin. Cancer Inf. 4, 259–274 (2020). 10.1200/CCI.19.00133 [DOI] [PubMed] [Google Scholar]
200. Ardizzone L., Kruse J., Wirkert S., Rahner D., Pellegrini E. W., Klessen R. S., Maier-Hein L., Rother C., and Köthe U., “ Analyzing inverse problems with invertible neural networks,” arXiv:1808.04730v3 (2018).
201. Wang N., Chang H., and Zhang D., “ Efficient uncertainty quantification for dynamic subsurface flow with surrogate by theory-guided neural network,” Comput. Methods Appl. Mech. Eng. 373(1), 113492 (2021). 10.1016/j.cma.2020.113492 [DOI] [Google Scholar]
202. Hussain Z., Gimenez F., Yi D., and Rubin D., “ Differential data augmentation techniques for medical imaging classification tasks,” in AMIA Annual Symposium Proceedings ( American Medical Informatics Association, 2017), p. 979. [PMC free article] [PubMed] [Google Scholar]
203. Oden J. T., Babuška I., and Faghihi D., “ Predictive computational science: Computer predictions in the presence of uncertainty,” in Encyclopedia of Computational Mechanics, 2nd ed. ( Wiley, 2017), pp. 1–26. [Google Scholar]
204. Oden J. T., Lima E. A., Almeida R. C., Feng Y., Rylander M. N., Fuentes D., Faghihi D., Rahman M. M., DeWitt M., Gadde M., and Zhou J. C., “ Toward predictive multiscale modeling of vascular tumor growth,” Arch. Comput. Methods Eng. 23, 735–779 (2016). 10.1007/s11831-015-9156-x [DOI] [Google Scholar]
205. Fletcher A. and Osborne J., “ Seven challenges in the multiscale modelling of multicellular tissues,” WIREs Mech. Dis. 14, e1527 (2020). 10.1002/wsbm.1527 [DOI] [PMC free article] [PubMed] [Google Scholar]
206. Zangooei M. H. and Habibi J., “ Hybrid multiscale modeling and prediction of cancer cell behavior,” PLoS One 12, e0183810 (2017). 10.1371/journal.pone.0183810 [DOI] [PMC free article] [PubMed] [Google Scholar]
207. Phillips C. M., Lima E. A., Woodall R. T., Brock A., and Yankeelov T. E., “ A hybrid model of tumor growth and angiogenesis: In silico experiments,” PLoS One 15, e0231137 (2020). 10.1371/journal.pone.0231137 [DOI] [PMC free article] [PubMed] [Google Scholar]
208. Hanahan D. and Weinberg R. A., “ Hallmarks of cancer: The next generation,” Cell 144(5), 646–674 (2011). 10.1016/j.cell.2011.02.013 [DOI] [PubMed] [Google Scholar]
209. Hanahan D. and Coussens L. M., “ Accessories to the crime: Functions of cells recruited to the tumor microenvironment,” Cancer Cell 21(3), 309–322 (2012). 10.1016/j.ccr.2012.02.022 [DOI] [PubMed] [Google Scholar]
210. Guimarães C. F., Gasperini L., Marques A. P., and Reis R. L., “ The stiffness of living tissues and its implications for tissue engineering,” Nat. Rev. Mater. 5, 351–370 (2020). 10.1038/s41578-019-0169-1 [DOI] [Google Scholar]
211. Bader D. L. and Knight M. M., “ Biomechanical analysis of structural deformation in living cells,” Med. Biol. Eng. Comput. 46, 951 (2008). 10.1007/s11517-008-0381-4 [DOI] [PubMed] [Google Scholar]
212. Miller C. and Davidson L., “ The interplay between cell signalling and mechanics in developmental processes,” Nat. Rev. Genet. 14, 733–744 (2013). 10.1038/nrg3513 [DOI] [PMC free article] [PubMed] [Google Scholar]
213. Hammes-Schiffer S. and Galli G., “ Integration of theory and experiment in the modelling of heterogeneous electrocatalysis,” Nat. Energy 6, 700–705 (2021). 10.1038/s41560-021-00827-4 [DOI] [Google Scholar]
214. Rahman M. M., Feng Y., Yankeelov T. E., and Oden J. T., “ A fully coupled space–time multiscale modeling framework for predicting tumor growth,” Comput. Methods Appl. Mech. Eng. 320, 261–286 (2017). 10.1016/j.cma.2017.03.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
215. Jarrett A. M., Bloom M. J., Godfrey W., Syed A. K., Ekrut D. A., Ehrlich L. I., Yankeelov T. E., and Sorace A. G., “ Mathematical modelling of trastuzumab-induced immune response in an in vivo murine model of HER2+ breast cancer,” Math. Med. Biol. 36, 381–410 (2019). 10.1093/imammb/dqy014 [DOI] [PMC free article] [PubMed] [Google Scholar]
216. Sheth K. N., Mazurek M. H., Yuen M. M., Cahn B. A., Shah J. T., Ward A., Kim J. A., Gilmore E. J., Falcone G. J., Petersen N., and Gobeske K. T., “ Assessment of brain injury using portable, low-field magnetic resonance imaging at the bedside of critically ill patients,” JAMA Neurol. 78, 41–47 (2021). 10.1001/jamaneurol.2020.3263 [DOI] [PMC free article] [PubMed] [Google Scholar]
217. Edlow B. L., Mareyam A., Horn A., Polimeni J. R., Witzel T., Tisdall M. D., Augustinack J. C., Stockmann J. P., Diamond B. R., Stevens A., and Tirrell L. S., “ 7 Tesla MRI of the ex vivo human brain at 100 micron resolution,” Sci. Data 6, 244 (2019). 10.1038/s41597-019-0254-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
218. Sterzing F., Kratochwil C., Fiedler H., Katayama S., Habl G., Kopka K., Afshar-Oromieh A., Debus J., Haberkorn U., and Giesel F. L., “ 68 Ga-PSMA-11 PET/CT: A new technique with high potential for the radiotherapeutic management of prostate cancer patients,” Eur. J. Nucl. Med. Mol. Imaging 43, 34–41 (2016). 10.1007/s00259-015-3188-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
219. Zhou X. Y., Tay Z. W., Chandrasekharan P., Elaine Y. Y., Hensley D. W., Orendorff R., Jeffris K. E., Mai D., Zheng B., Goodwill P. W., and Conolly S. M., “ Magnetic particle imaging for radiation-free, sensitive and high-contrast vascular imaging and cell tracking,” Curr. Opin. Chem. Biol. 45, 131–138 (2018). 10.1016/j.cbpa.2018.04.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
220. Rivera-Rodriguez A., Hoang-Minh L. B., Chiu-Lam A., Sarna N., Marrero-Morales L., Mitchell D. A., and Rinaldi-Ramos C. M., “ Tracking adoptive T cell immunotherapy using magnetic particle imaging,” Nanotheranostics 5, 431–444 (2021). 10.7150/ntno.55165 [DOI] [PMC free article] [PubMed] [Google Scholar]
221. Nishino M., Hatabu H., and Hodi F. S., “ Imaging of cancer immunotherapy: Current approaches and future directions,” Radiology 290, 9–22 (2019). 10.1148/radiol.2018181349 [DOI] [PMC free article] [PubMed] [Google Scholar]
222. Alvarez-Garcia V., Bartos C., Keraite I., Trivedi U., Brennan P. M., Kersaudy-Kerhoas M., Gharbi K., Oikonomidou O., and Leslie N. R., “ A simple and robust real-time qPCR method for the detection of PIK3CA mutations,” Sci. Rep. 8, 4290 (2018). 10.1038/s41598-018-22473-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
223. Becht E., McInnes L., Healy J., Dutertre C. A., Kwok I. W., Ng L. G., Ginhoux F., and Newell E. W., “ Dimensionality reduction for visualizing single-cell data using UMAP,” Nat. Biotechnol. 37(1), 38–44 (2019). 10.1038/nbt.4314 [DOI] [PubMed] [Google Scholar]
224. Pisco A. O., Brock A., Zhou J., Moor A., Mojtahedi M., Jackson D., and Huang S., “ Non-Darwinian dynamics in therapy-induced cancer drug resistance,” Nat. Commun. 4, 2467 (2013). 10.1038/ncomms3467 [DOI] [PMC free article] [PubMed] [Google Scholar]
225. Heindl A., Nawaz S., and Yuan Y., “ Mapping spatial heterogeneity in the tumor microenvironment: A new era for digital pathology,” Lab. Invest. 95, 377–384 (2015). 10.1038/labinvest.2014.155 [DOI] [PubMed] [Google Scholar]
226. Rejniak K. A., Wang S. E., Bryce N. S., Chang H., Parvin B., Jourquin J., Estrada L., Gray J. W., Arteaga C. L., Weaver A. M., and Quaranta V., “ Linking changes in epithelial morphogenesis to cancer mutations using computational modeling,” PLoS Comput. Biol. 6, e1000900 (2010). 10.1371/journal.pcbi.1000900 [DOI] [PMC free article] [PubMed] [Google Scholar]
227. Gurcan M. N., Boucheron L. E., Can A., Madabhushi A., Rajpoot N. M., and Yener B., “ Histopathological image analysis: A review,” IEEE Rev. Biomed. Eng. 2, 147–171 (2009). 10.1109/RBME.2009.2034865 [DOI] [PMC free article] [PubMed] [Google Scholar]
228. Erol T., Mendi A. F., and Dogan D., “ The digital twin revolution in healthcare,” in Proceedings of the 4th International Symposium on Multidisciplinary Studies and Innovative Technologies, ISMSIT, Istanbul, Turkey (IEEE, 2020), pp. 1–7. 10.1109/ISMSIT50672.2020.9255249 [DOI] [Google Scholar]
229. Cottrell J. A., Hughes T. J. R., and Bazilevs Y., Isogeometric Analysis: Toward Integration of CAD and FEA ( John Wiley & Sons, 2009). [Google Scholar]
230. Lorenzo G., Scott M. A., Tew K., Hughes T. J. R., and Gomez H., “ Hierarchically refined and coarsened splines for moving interface problems, with particular application to phase-field models of prostate tumor growth,” Comput. Methods Appl. Mech. Eng. 319, 515–548 (2017). 10.1016/j.cma.2017.03.009 [DOI] [Google Scholar]
231. D¨uster A., Parvizian J., Yang Z., and Rank E., “ The finite cell method for three-dimensional problems of solid mechanics,” Comput. Methods Appl. Mech. Eng. 197(45–48), 3768–3782 (2008). 10.1016/j.cma.2008.02.036 [DOI] [Google Scholar]
232. Parvizian J., D¨uster A., and Rank E., “ Finite cell method: H- and p-extension for embedded domain problems in solid mechanics,” Comput. Mech. 41(1), 121–133 (2007). 10.1007/s00466-007-0173-y [DOI] [Google Scholar]
233. Schillinger D. and Ruess M., “ The finite cell method: A review in the context of higher-order structural analysis of CAD and image-based geometric models,” Arch. Comput. Methods Eng. 22(3), 391–455 (2015). 10.1007/s11831-014-9115-y [DOI] [Google Scholar]
234. Burman E., Claus S., Hansbo P., Larson M. G., and Massing A., “ CutFEM: Discretizing geometry and partial differential equations,” Int. J. Numer. Methods Eng. 104(7), 472–501 (2015). 10.1002/nme.4823 [DOI] [Google Scholar]
235. Hansbo A. and Hansbo P., “ An unfitted finite element method, based on Nitsche's method, for elliptic interface problems,” Comput. Methods Appl. Mech. Eng. 191, 5537–5552 (2002). 10.1016/S0045-7825(02)00524-8 [DOI] [Google Scholar]
236. Embar A., Dolbow J., and Harari I., “ Imposing Dirichlet boundary conditions with Nitsche's method and spline-based finite elements,” Int. J. Numer. Methods Eng. 83, 877–898 (2010). 10.1002/nme.2863 [DOI] [Google Scholar]
237. Raissi M., Perdikaris P., and Karniadakis G. E., “ Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations,” J. Comput. Phys. 378, 686–707 (2019). 10.1016/j.jcp.2018.10.045 [DOI] [Google Scholar]
238. Haghighat E., Raissi M., Moure A., Gomez H., and Juanes R., “ A physics-informed deep learning framework for inversion and surrogate modeling in solid mechanics,” Comput. Methods Appl. Mech. Eng. 379, 113741 (2021). 10.1016/j.cma.2021.113741 [DOI] [Google Scholar]
239. Reshetova G., Vladimir C., and Tatyana K., “ Numerical experiments with digital twins of core samples for estimating effective elastic parameters,” in Supercomputing ( Springer International Publishing, Cham, 2019), pp. 290–301. [Google Scholar]
240. Cheverda V., Lisitsa V., Protasov M., Reshetova G., Glinsky B., Chernykh I., Merzlikina A., Volyanskaya V., Petrov D., Melnik A., and Shilikov V., “ Digital twins of multiscale 3D heterogeneous geological objects: 3D simulations and seismic imaging of faults, fractures and caves,” J. Phys. 1392, 12051 (2019). 10.1088/1742-6596/1392/1/012051 [DOI] [Google Scholar]
241. Hirschvogel M., Jagschies L., Maier A., Wildhirt S. M., and Gee M. W., “ An in silico twin for epicardial augmentation of the failing heart,” Int. J. Numer. Methods Biomed. Eng. 35, e3233 (2019). 10.1002/cnm.3233 [DOI] [PubMed] [Google Scholar]
242. Yoders J., “ Nvidia partners with Bentley on digital twin modeling,” Eng. News Rec. 286, 103 (2021); available at https://www.enr.com/articles/51786-nvidia-and-bentley-partner-on-digital-twin-modeling-and-simulation-environment. [Google Scholar]
243. Kłusek A., Łoś M., Paszyński M., and Dzwinel W., “ Efficient model of tumor dynamics simulated in multi-GPU environment,” Int. J. High Perform. Comput. Appl. 33, 489–506 (2019). 10.1177/1094342018816772 [DOI] [Google Scholar]
244. da Costa J. M. J., Orlande H. R. B., and da Silva W. B., “ Model selection and parameter estimation in tumor growth models using approximate Bayesian computation-ABC,” Comput. Appl. Math. 37, 2795–2815 (2018). 10.1007/s40314-017-0479-0 [DOI] [Google Scholar]
245. Konishi S. and Kitagawa G., Information Criteria and Statistical Modeling, 1st ed. ( Springer Science & Business Media, 2008). [Google Scholar]
246. Jeffreys H., The Theory of Probability, 3rd ed. ( Oxford University Press, 1998). [Google Scholar]
247. Hormuth D. A. II, Jarrett A. M., Lima E. A. B. F., McKenna M. T., Fuentes D. T., and Yankeelov T. E., “ Mechanism-based modeling of tumor growth and treatment response constrained by multiparametric imaging data,” JCO Clin. Cancer Inf. 3, 1–10 (2019). 10.1200/CCI.18.00055 [DOI] [PMC free article] [PubMed] [Google Scholar]
248. Lima E. A. B. F., Oden J. T., Hormuth D. A., Yankeelov T. E., and Almeida R. C., “ Selection, calibration, and validation of models of tumor growth,” Math. Models Methods Appl. Sci. 26, 2341–2368 (2016). 10.1142/S021820251650055X [DOI] [PMC free article] [PubMed] [Google Scholar]
249. Dzwinel W., Kłusek A., and Paszyński M., “ A concept of a prognostic system for personalized anti-tumor therapy based on supermodeling,” Procedia Comput. Sci. 108, 1832–1841 (2017). 10.1016/j.procs.2017.05.013 [DOI] [Google Scholar]
250. Gargalo C. L., de Las Heras S. C., Jones M. N., Udugama I., Mansouri S. S., Krühne U., and Gernaey K. V., “ Towards the development of digital twins for the bio-manufacturing industry,” in Digital Twins, Advances in Biochemical Engineering/Biotechnology, edited by Herwig C., Pörtner R., and Möller J. ( Springer, Cham, 2020), pp. 1–34. [DOI] [PubMed] [Google Scholar]
251. Schroeder B. B., Hund L., and Kittinger R. S., “ The need for credibility guidance for analyses quantifying margin and uncertainty,” in Model Validation and Uncertainty Quantification ( Springer, Cham, 2020), Vol. 3, pp 11–23. [Google Scholar]
252. Lima E. A., Ghousifam N., Ozkan A., Oden J. T., Shahmoradi A., Rylander M. N., Wohlmuth B., and Yankeelov T. E., “ Calibration of multi-parameter models of avascular tumor growth using time resolved microscopy data,” Sci. Rep. 8, 14558 (2018). 10.1038/s41598-018-32347-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
253. Phillips C., Lima E. A., Gadde M., Jarrett A. M., Rylander M. N., and Yankeelov T. E., “ Towards integration of time-resolved confocal microscopy of a 3D in vitro microfluidic platform with a hybrid multiscale model of tumor angiogenesis,” bioRxiv (2021). 10.1101/2021.09.29.462293 [DOI] [PMC free article] [PubMed] [Google Scholar]
254. Stupp R., Mason W. P., Van Den Bent M. J., Weller M., Fisher B., Taphoorn M. J., Belanger K., Brandes A. A., Marosi C., Bogdahn U., and Curschmann J., “ Radiotherapy plus concomitant and adjuvant temozolomide for glioblastoma,” N. Engl. J. Med. 352(10), 987–996 (2005). 10.1056/NEJMoa043330 [DOI] [PubMed] [Google Scholar]
255. Tang L., Wei F., Wu Y., He Y., Shi L., Xiong F., Gong Z., Guo C., Li X., Deng H., and Cao K., “ Role of metabolism in cancer cell radioresistance and radiosensitization methods,” J. Exp. Clin. Cancer Res. 37(1), 87 (2018). 10.1186/s13046-018-0758-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
256. Jing X., Yang F., Shao C., Wei K., Xie M., Shen H., and Shu Y., “ Role of hypoxia in cancer therapy by regulating the tumor microenvironment,” Mol. Cancer 18(1), 157 (2019). 10.1186/s12943-019-1089-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
257. Vickers A. J., “ Effects of magnetic resonance imaging targeting on overdiagnosis and overtreatment of prostate cancer,” Eur. Urol. 80(5), 567–572 (2021). 10.1016/j.eururo.2021.06.026 [DOI] [PMC free article] [PubMed] [Google Scholar]
258. Khair D. O., Bax H. J., Mele S., Crescioli S., Pellizzari G., Khiabany A., Nakamura M., Harris R. J., French E., Hoffmann R. M., and Williams I. P., “ Combining immune checkpoint inhibitors: Established and emerging targets and strategies to improve outcomes in melanoma,” Front. Immunol. 10, 453 (2019). 10.3389/fimmu.2019.00453 [DOI] [PMC free article] [PubMed] [Google Scholar]
259. Yan D., “ Adaptive radiotherapy: Merging principle into clinical practice,” Semin. Radiat. Oncol. 20(2), 79–83 (2010). 10.1016/j.semradonc.2009.11.001 [DOI] [PubMed] [Google Scholar]
260. Rockwell S., Dobrucki I. T., Kim E. Y., Marrison S. T., and Vu V. T., “ Hypoxia and radiation therapy: Past history, ongoing research, and future promise,” Curr. Mol. Med. 9(4), 442–458 (2009). 10.2174/156652409788167087 [DOI] [PMC free article] [PubMed] [Google Scholar]
261. Potiron V. A., Abderrahmani R., Clément-Colmou K., Marionneau-Lambot S., Oullier T., Paris F., and Supiot S., “ Improved functionality of the vasculature during conventionally fractionated radiation therapy of prostate cancer,” PLoS One 8(12), e84076 (2013). 10.1371/journal.pone.0084076 [DOI] [PMC free article] [PubMed] [Google Scholar]
262. Hormuth D. A., Phillips C. M., Wu C., Lima E. A., Lorenzo G., Jha P. K., Jarrett A. M., Oden J. T., and Yankeelov T. E., “ Biologically-based mathematical modeling of tumor vasculature and angiogenesis via time-resolved imaging data,” Cancers 13, 3008 (2021). 10.3390/cancers13123008 [DOI] [PMC free article] [PubMed] [Google Scholar]
263. McMahon S. J., “ The linear quadratic model: Usage, interpretation and challenges,” Phys. Med. Biol. 64(1), 01TR01 (2018). 10.1088/1361-6560/aaf26a [DOI] [PubMed] [Google Scholar]
264. Jones L., Hoban P., and Metcalfe P., “ The use of the linear quadratic model in radiotherapy: A review,” Australas. Phys. Eng. Sci. Med. 24(3), 132–146 (2001). 10.1007/BF03178355 [DOI] [PubMed] [Google Scholar]
265. Brenner D. J., “ The linear-quadratic model is an appropriate methodology for determining isoeffective doses at large doses per fraction,” Semin. Radiat. Oncol. 18(4), 234–239 (2008). 10.1016/j.semradonc.2008.04.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
266. Hormuth I. D., Weis J. A., Barnes S. L., Miga M. I., Rericha E. C., Quaranta V., and Yankeelov T. E., “ Predicting in vivo glioma growth with the reaction diffusion equation constrained by quantitative magnetic resonance imaging data,” Phys. Biol. 12, 46006 (2015). 10.1088/1478-3975/12/4/046006 [DOI] [PMC free article] [PubMed] [Google Scholar]
267. Hormuth D. A., Jarrett A. M., and Yankeelov T. E., “ Forecasting tumor and vasculature response dynamics to radiation therapy via image based mathematical modeling,” Radiat. Oncol. 15, 1–4 (2020). 10.1186/s13014-019-1446-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
268. Liu J., Hormuth D. A., Davis T., Yang J., McKenna M. T., Jarrett A. M., Enderling H., Brock A., and Yankeelov T. E., “ A time-resolved experimental–mathematical model for predicting the response of glioma cells to single-dose radiation therapy,” Integr. Biol. 13(7), 167–183 (2021). 10.1093/intbio/zyab010 [DOI] [PMC free article] [PubMed] [Google Scholar]
269. Brüningk S. C., Rivens I., Box C., Oelfke U., and ter Haar G., “ 3D tumour spheroids for the prediction of the effects of radiation and hyperthermia treatments,” Sci. Rep. 10(1), 1653 (2020). 10.1038/s41598-020-58569-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
270. Sunassee E. D., Tan D., Ji N., Brady R., Moros E. G., Caudell J. J., Yartsev S., and Enderling H., “ Proliferation saturation index in an adaptive Bayesian approach to predict patient-specific radiotherapy responses,” Int. J. Radiat. Biol. 95, 1421 (2019). 10.1080/09553002.2019.1589013 [DOI] [PMC free article] [PubMed] [Google Scholar]
271. Zhang L., Strouthos C. G., Wang Z., and Deisboeck T. S., “ Simulating brain tumor heterogeneity with a multiscale agent-based model: Linking molecular signatures, phenotypes and expansion rate,” Math. Comput. Model. 49(1–2), 307–319 (2009). 10.1016/j.mcm.2008.05.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
272. Frieboes H. B., Lowengrub J. S., Wise S., Zheng X., Macklin P., Bearer E. L., and Cristini V., “ Computer simulation of glioma growth and morphology,” Neuroimage 37, S59–S70 (2007). 10.1016/j.neuroimage.2007.03.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
273. Alfonso J. C., Talkenberger K., Seifert M., Klink B., Hawkins-Daarud A., Swanson K. R., Hatzikirou H., and Deutsch A., “ The biology and mathematical modelling of glioma invasion: A review,” J. R. Soc. Interface 14(136), 20170490 (2017). 10.1098/rsif.2017.0490 [DOI] [PMC free article] [PubMed] [Google Scholar]
274. Rocha H. L., Almeida R. C., Lima E. A. B. F., Resende A. C. M., Oden J. T., and Yankeelov T. E., “ A hybrid three-scale model of tumor growth,” Math. Models Methods Appl. Sci. 28, 61–93 (2018). 10.1142/S0218202518500021 [DOI] [PMC free article] [PubMed] [Google Scholar]
275. Perfahl H., Byrne H. M., Chen T., Estrella V., Alarcón T., Lapin A., Gatenby R. A., Gillies R. J., Lloyd M. C., Maini P. K., and Reuss M., “ Multiscale modelling of vascular tumour growth in 3D: The roles of domain size and boundary conditions,” PLoS One 6(4), e14790 (2011). 10.1371/journal.pone.0014790 [DOI] [PMC free article] [PubMed] [Google Scholar]
276. Anderson A. R., “ A hybrid mathematical model of solid tumour invasion: The importance of cell adhesion,” Math. Med. Biol. 22(2), 163–186 (2005). 10.1093/imammb/dqi005 [DOI] [PubMed] [Google Scholar]
277. Mabray M. C., R. F. Barajas, Jr. , and Cha S., “ Modern brain tumor imaging,” Brain Tumor Res. Treat. 3(1), 8–23 (2015). 10.14791/btrt.2015.3.1.8 [DOI] [PMC free article] [PubMed] [Google Scholar]
278. Jones K. M., Michel K. A., Bankson J. A., Fuller C. D., Klopp A. H., and Venkatesan A. M., “ Emerging magnetic resonance imaging technologies for radiation therapy planning and response assessment,” Int. J. Radiat. Oncol. Biol. Phys. 101(5), 1046–1056 (2018). 10.1016/j.ijrobp.2018.03.028 [DOI] [PMC free article] [PubMed] [Google Scholar]
279. Jaffray D., Kupelian P., Djemil T., and Macklis R. M., “ Review of image-guided radiation therapy,” Expert Rev. Anticancer Ther. 7(1), 89–103 (2007). 10.1586/14737140.7.1.89 [DOI] [PubMed] [Google Scholar]
280. Lagendijk J. J. W., Raaymakers B. W., and van Vulpen M., “ The magnetic resonance imaging–linac system,” Semin. Radiat. Oncol. 24(3), 207–209 (2014). 10.1016/j.semradonc.2014.02.009 [DOI] [PubMed] [Google Scholar]
281. Scarpace L., Mikkelsen T., Cha S., Rao S., Tekchandani S., Gutman D., Saltz J. H., Erickson B. J., Pedano N., Flanders A. E., Barnholtz-Sloan J., Ostrom Q., Barboriak D., and Pierce L. J. (2016). “ Radiology data from the cancer genome atlas glioblastoma multiforme [TCGA-GBM] collection [data set],” Cancer Imaging Archive. 10.7937/K9/TCIA.2016.RNYFUYE9. [DOI] [Google Scholar]
282. Menze B. H., Jakab A., Bauer S., Kalpathy-Cramer J., Farahani K., Kirby J., Burren Y., Porz N., Slotboom J., Wiest R., Lanczi L., Gerstner E., Weber M. A., Arbel T., Avants B. B., Ayache N., Buendia P., Collins D. L., Cordier N. et al. , “ The multimodal brain tumor image segmentation benchmark (BRATS),” IEEE Trans. Medical Imaging 34(10), 1993–2024 (2015). 10.1109/TMI.2014.2377694 [DOI] [PMC free article] [PubMed] [Google Scholar]
283. Farhat M., Hormuth D., Langshaw H., Elliott A., Landry L., and Yankeelov T., “ Computational models forecasting response of high-grade glioma during adaptive radiation therapy,” in RSNA 2021 Annual Meeting, Chicago, IL (Radiological Society of North America, 2021), p. 12311. [Google Scholar]
284. Pathmanathan A. U., van As N. J., Kerkmeijer L. G. W., Christodouleas J., Lawton C. A. F., Vesprini D., van der Heide U. A., Frank S. J., Nill S., Oelfke U., van Herk M., Li X. A., Mittauer K., Ritter M., Choudhury A., and Tree A. C., “ Magnetic resonance imaging-guided adaptive radiation therapy: A game changer for prostate treatment?,” Int. J. Radiat. Oncol. Biol. Phys. 100(2), 361–373 (2018). 10.1016/j.ijrobp.2017.10.020 [DOI] [PubMed] [Google Scholar]
285. Ellingson B. M., Bendszus M., Boxerman J., Barboriak D., Erickson B. J., Smits M., Nelson S. J., Gerstner E., Alexander B., Goldmacher G., and Wick W., “ Consensus recommendations for a standardized brain tumor imaging protocol in clinical trials,” Neuro-oncology 17(9), 1188–1198 (2015). 10.1093/neuonc/nov095 [DOI] [PMC free article] [PubMed] [Google Scholar]
286. Kaufmann T. J., Smits M., Boxerman J., Huang R., Barboriak D. P., Weller M., Chung C., Tsien C., Brown P. D., Shankar L., and Galanis E., “ Consensus recommendations for a standardized brain tumor imaging protocol for clinical trials in brain metastases,” Neuro-oncology 22(6), 757–772 (2020). 10.1093/neuonc/noaa030 [DOI] [PMC free article] [PubMed] [Google Scholar]
287. Hormuth D. A., SL I. I., Weis J. A., Miga M. I., and Yankeelov T. E., “ Mechanically coupled reaction-diffusion model to predict glioma growth: Methodological details,” Methods Mol. Biol. 1711, 225 (2018). 10.1007/978-1-4939-7493-1_11 [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Availability Statement

Data sharing is not applicable to this article as no new data were created or analyzed in this study.

[c1] 1. Shafto M., Conroy M., Doyle R., Glaessgen E., Kemp C., LeMoigne J., and Wang L., “ Modeling, simulation, information technology & processing roadmap,” Technical Report, National Aeronautics and Space Administration (2012), Vol. 32, pp. 1–38; available at https://www.nasa.gov/pdf/501321main_TA11-MSITP-DRAFT-Nov2010-A1.pdf. [Google Scholar]

[c2] 2. Rosen R., Von Wichert G., Lo G., and Bettenhausen K. D., “ About the importance of autonomy and digital twins for the future of manufacturing,” Ifac Papersonline 48, 567–572 (2015). 10.1016/j.ifacol.2015.06.141 [DOI] [Google Scholar]

[c3] 3. Niederer S. A., Sacks M. S., Girolami M., and Willcox K., “ Scaling digital twins from the artisanal to the industrial,” Nat. Comput. Sci. 1, 313–320 (2021). 10.1038/s43588-021-00072-5 [DOI] [PubMed] [Google Scholar]

[c4] 4. Kapteyn M. G., Pretorius J. V., and Willcox K. E., “ A probabilistic graphical model foundation for enabling predictive digital twins at scale,” Nat. Comput. Sci. 1, 337–347 (2021). 10.1038/s43588-021-00069-0 [DOI] [PubMed] [Google Scholar]

[c5] 5. Schleich B., Anwer N., Mathieu L., and Wartzack S., “ Shaping the digital twin for design and production engineering,” CIRP Ann. 66, 141–144 (2017). 10.1016/j.cirp.2017.04.040 [DOI] [Google Scholar]

[c6] 6. Tao F., Zhang H., Liu A., and Nee A. Y., “ Digital twin in industry: State-of-the-art,” IEEE Trans. Ind. Inf. 15, 2405–2415 (2019). 10.1109/TII.2018.2873186 [DOI] [Google Scholar]

[c7] 7. Negri E., Fumagalli L., and Macchi M., “ A review of the roles of digital twin in CPS-based production systems,” in 27th International Conference on Flexible Automation and Intelligent Manufacturing, FAIM, edited by Pellicciari M. and Peruzzini M. ( Elsevier, 2017), pp. 939–948. [Google Scholar]

[c8] 8. Rasheed A., San O., and Kvamsdal T., “ Digital twin: Values, challenges and enablers from a modeling perspective,” IEEE Access 8, 21980–22012 (2020). 10.1109/ACCESS.2020.2970143 [DOI] [Google Scholar]

[c9] 9. Peirlinck M., Costabal F. S., Yao J., Guccione J. M., Tripathy S., Wang Y., Ozturk D., Segars P., Morrison T. M., Levine S., and Kuhl E., “ Precision medicine in human heart modeling,” Biomech. Model. Mechanobiol. 20, 803–831 (2021). 10.1007/s10237-021-01421-z [DOI] [PMC free article] [PubMed] [Google Scholar]

[c10] 10. Shamanna P., Saboo B., Damodharan S., Mohammed J., Mohamed M., Poon T., Kleinman N., and Thajudeen M., “ Reducing HbA1c in type 2 diabetes using digital twin technology-enabled precision nutrition: A retrospective analysis,” Diabetes Ther. 11, 2703–2714 (2020). 10.1007/s13300-020-00931-w [DOI] [PMC free article] [PubMed] [Google Scholar]

[c11] 11. Hormuth D. A., Jarrett A. M., Lorenzo G., Lima E. A., Wu C., Chung C., Patt D., and Yankeelov T. E., “ Math, magnets, and medicine: Enabling personalized oncology,” Expert Rev. Precis. Med. Drug Dev. 6, 79–81 (2021). 10.1080/23808993.2021.1878023 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c12] 12. Dowden H. and Munro J., “ Trends in clinical success rates and therapeutic focus,” Nat. Rev. Drug Discov. 18, 495–496 (2019). 10.1038/d41573-019-00074-z [DOI] [PubMed] [Google Scholar]

[c13] 13.BTP Practice, “ Biopharmaceutical industry‐sponsored clinical trials: Impact on state economies,” Technical Report (2015); available at http://phrma-docs.phrma.org/sites/default/files/pdf/biopharmaceutical-industry-sponsored-clinical-trials-impact-on-state-economies.pdf.

[c14] 14. Umutyan A., Chiechi C., Beckett L. A., Paterniti D. A., Turrell C., Gandara D. R., Davis S. W., Wun T., M. S. Chen, Jr. , and Lara P. N., Jr., “ Overcoming barriers to cancer clinical trial accrual: Impact of a mass media campaign,” Cancer 112, 212–219 (2008). 10.1002/cncr.23170 [DOI] [PubMed] [Google Scholar]

[c15] 15. Haidich A. B. and Ioannidis J. P., “ Effect of early patient enrollment on the time to completion and publication of randomized controlled trials,” Am. J. Epidemiol. 154, 873–880 (2001). 10.1093/aje/154.9.873 [DOI] [PubMed] [Google Scholar]

[c16] 16. Unger J. M., Cook E., Tai E., and Bleyer A., “ The role of clinical trial participation in cancer research: Barriers, evidence, and strategies,” Am. Soc. Clin. Oncol. Educ. Book 36, 185–198 (2016). 10.1200/EDBK_156686 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c17] 17. Hunger S. P., Lu X., Devidas M., Camitta B. M., Gaynon P. S., Winick N. J., Reaman G. H., and Carroll W. L., “ Improved survival for children and adolescents with acute lymphoblastic leukemia between 1990 and 2005: A report from the children's oncology group,” J. Clin. Oncol. 30(14), 1663 (2012). 10.1200/JCO.2011.37.8018 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c18] 18. Pan E., Bogumil D., Cortessis V., Yu S., and Nieva J., “ A systematic review of the efficacy of preclinical models of lung cancer drugs,” Front. Oncol. 10, 591 (2020). 10.3389/fonc.2020.00591 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c19] 19. Tam C. S., Opat S., D'Sa S., Jurczak W., Lee H. P., Cull G., Owen R. G., Marlton P., Wahlin B. E., Sanz R. G., and McCarthy H., “ A randomized phase 3 trial of zanubrutinib vs ibrutinib in symptomatic Waldenström macroglobulinemia: The ASPEN study,” Blood 136(18), 2038–2050 (2020). 10.1182/blood.2020006844 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c20] 20. Schmid P., Cortés J., Dent R., Pusztai L., McArthur H. L., Kuemmel S., Bergh J., Denkert C., Park Y. H., Hui R., and Harbeck N., “ KEYNOTE-522: Phase III study of pembrolizumab (pembro)+ chemotherapy (chemo) vs placebo (pbo)+ chemo as neoadjuvant treatment, followed by pembro vs pbo as adjuvant treatment for early triple-negative breast cancer (TNBC),” Ann. Oncol. 30, v853–v854 (2019). 10.1093/annonc/mdz394.003 [DOI] [Google Scholar]

[c21] 21. Chien A. J., Tripathy D., Albain K. S., Symmans W. F., Rugo H. S., Melisko M. E., Wallace A. M., Schwab R., Helsten T., Forero-Torres A., and Stringer-Reasor E., “ MK-2206 and standard neoadjuvant chemotherapy improves response in patients with human epidermal growth factor receptor 2–positive and/or hormone receptor–negative breast cancers in the I-SPY 2 trial,” J. Clin. Oncol. 38, 1059–1069 (2020). 10.1200/JCO.19.01027 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c22] 22. Ludwig J. A. and Weinstein J. N., “ Biomarkers in cancer staging, prognosis and treatment selection,” Nat. Rev. Cancer 5, 845–856 (2005). 10.1038/nrc1739 [DOI] [PubMed] [Google Scholar]

[c23] 23. Jarrett A. M., Faghihi D., Hormuth D. A., Lima E. A., Virostko J., Biros G., Patt D., and Yankeelov T. E., “ Optimal control theory for personalized therapeutic regimens in oncology: Background, history, challenges, and opportunities,” J. Clin. Med. 9, 1314 (2020). 10.3390/jcm9051314 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c24] 24. Colli P., Gomez H., Lorenzo G., Marinoschi G., Reali A., and Rocca E., “ Optimal control of cytotoxic and antiangiogenic therapies on prostate cancer growth,” Math. Models Methods Appl. Sci. 14, 1–50 (2021). 10.1142/S0218202521500299 [DOI] [Google Scholar]

[c25] 25. Angaroni F., Graudenzi A., Rossignolo M., Maspero D., Calarco T., Piazza R., Montangero S., and Antoniotti M., “ An optimal control framework for the automated design of personalized cancer treatments,” Front. Bioeng. Biotechnol. 8, 523 (2020). 10.3389/fbioe.2020.00523 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c26] 26. Poels K. E., Schoenfeld A. J., Makhnin A., Tobi Y., Wang Y., Frisco-Cabanos H., Chakrabarti S., Shi M., Napoli C., McDonald T. O., and Tan W., “ Identification of optimal dosing schedules of dacomitinib and osimertinib for a phase I/II trial in advanced EGFR-mutant non-small cell lung cancer,” Nat. Commun. 12, 3697 (2021). 10.1038/s41467-021-23912-4 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c27] 27. Pasetto S., Gatenby R. A., and Enderling H., “ Bayesian framework to augment tumor board decision making,” JCO Clin. Cancer Inf. 5, 508–517 (2021). 10.1200/CCI.20.00085 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c28] 28. Booyse W., Wilke D. N., and Heyns S., “ Deep digital twins for detection, diagnostics and prognostics,” Mech. Syst. Signal Process. 140, 106612 (2020). 10.1016/j.ymssp.2019.106612 [DOI] [Google Scholar]

[c29] 29. Jarrett A. M., Hormuth I. D., Wu C., Kazerouni A. S., Ekrut D. A., Virostko J., Sorace A. G., DiCarlo J. C., Kowalski J., Patt D., and Goodgame B., “ Evaluating patient-specific neoadjuvant regimens for breast cancer via a mathematical model constrained by quantitative magnetic resonance imaging data,” Neoplasia 22, 820–830 (2020). 10.1016/j.neo.2020.10.011 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c30] 30. Hormuth D. A. II, Al Feghali K. A., Elliott A. M., Yankeelov T. E., and Chung C., “ Image-based personalization of computational models for predicting response of high-grade glioma to chemoradiation,” Sci. Rep. 11, 8520 (2021). 10.1038/s41598-021-87887-4 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c31] 31. Brady-Nicholls R., Nagy J. D., Gerke T. A., Zhang T., Wang A. Z., Zhang J., Gatenby R. A., and Enderling H., “ Prostate-specific antigen dynamics predict individual responses to intermittent androgen deprivation,” Nat. Commun. 11, 1750 (2020). 10.1038/s41467-020-15424-4 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c32] 32. Stahlberg E., Hanlon S. E., Ellingson S., Kovatch P., Borkon L., and Hollingsworth P., in Seventh Computational Approaches for Cancer Workshop (CAFCW21), St. Louis, Missouri, 2021. [Google Scholar]

[c33] 33.IMAG, “ NCI-DOE collaboration 2020 virtual ideas lab: Toward building a cancer patient ‘digital twin’,” in Virtual Meeting, July 6–10 (2020). [Google Scholar]

[c34] 34. Hernandez-Boussard T., Macklin P., Greenspan E. J., Gryshuk A. L., Stahlberg E., Syeda-Mahmood T., and Shmulevich I., “ Digital twins for predictive oncology will be a paradigm shift for precision cancer care,” Nat. Med. 27, 2065–2066 (2021). 10.1038/s41591-021-01558-5 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c35] 35. Kazerouni A. S., Gadde M., Gardner A., Hormuth D. A. II, Jarrett A. M., Johnson K. E., Lima E. A. B. F., Lorenzo G., Phillips C., Brock A., and Yankeelov T. E., “ Integrating quantitative assays with biologically-based mathematical modeling for predictive oncology,” Iscience 23, 101807 (2020). 10.1016/j.isci.2020.101807 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c36] 36. Rockne R. C., Hawkins-Daarud A., Swanson K. R., Sluka J. P., Glazier J. A., Macklin P., Hormuth I. D., Jarrett A. M., Lima E. A., Oden J. T., and Biros G., “ The 2019 mathematical oncology roadmap,” Phys. Biol. 16, 041005 (2019). 10.1088/1478-3975/ab1a09 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c37] 37. Dogra P., Butner J. D., Chuang Y. L., Caserta S., Goel S., Brinker C. J., Cristini V., and Wang Z., “ Mathematical modeling in cancer nanomedicine: A review,” Biomed. Microdev. 21, 40 (2019). 10.1007/s10544-019-0380-2 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c38] 38. Hamis S., Powathil G. G., and Chaplain M. A., “ Blackboard to bedside: A mathematical modeling bottom-up approach toward personalized cancer treatments,” JCO Clin. Cancer Inf. 3, 1–11 (2019). 10.1200/CCI.18.00068 [DOI] [PubMed] [Google Scholar]

[c39] 39. Metzcar J., Wang Y., Heiland R., and Macklin P., “ A review of cell-based computational modeling in cancer biology,” JCO Clin. Cancer Inf. 3, 1–3 (2019). 10.1200/CCI.18.00069 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c40] 40. Sun X. and Hu B., “ Mathematical modeling and computational prediction of cancer drug resistance,” Briefings Bioinf. 19, 1382–1399 (2018). 10.1093/bib/bbx065 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c41] 41. Yankeelov T. E., Quaranta V., Evans K. J., and Rericha E. C., “ Toward a science of tumor forecasting for clinical oncology,” Cancer Res. 75(6), 918–923 (2015). 10.1158/0008-5472.CAN-14-2233 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c42] 42. Yankeelov T. E., Mankoff D. A., Schwartz L. H., Lieberman F. S., Buatti J. M., Mountz J. M., Erickson B. J., Fennessy F. M., Huang W., Kalpathy-Cramer J., and Wahl R. L., “ Quantitative imaging in cancer clinical trials,” Clin. Cancer Res. 22, 284–290 (2016). 10.1158/1078-0432.CCR-14-3336 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c43] 43. Weis J. A., Miga M. I., Arlinghaus L. R., Li X., Chakravarthy A. B., Abramson V., Farley J., and Yankeelov T. E., “ A mechanically coupled reaction-diffusion model for predicting the response of breast tumors to neoadjuvant chemotherapy,” Phys. Med. Biol. 58, 5851–5866 (2013). 10.1088/0031-9155/58/17/5851 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c44] 44. Woodall R., Hormuth I. D., Wu C., Abdelmalik M., Phillips W. T., Bao A., Hughes T. J. R., Brenner A. J., and Yankeelov T. E., “ Patient specific, imaging-informed modeling of rhenium-186 nanoliposome delivery via convection-enhanced delivery in glioblastoma multiforme,” Biomed. Phys. Eng. Express 7, 45012 (2021). 10.1088/2057-1976/ac02a6 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c45] 45. Yankeelov T. E., Atuegwu N., Hormuth D. A., Weis J. A., Barnes S. L., Miga M. I., Rericha E. C., and Quaranta V., “ Clinically relevant modeling of tumor growth and treatment response,” Sci. Transl. Med. 5, 187ps9 (2013). 10.1126/scitranslmed.3005686 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c46] 46. Wu C., Hormuth D. A., Oliver T. A., Pineda F., Lorenzo G., Karczmar G. S., Moser R. D., and Yankeelov T. E., “ Patient-specific characterization of breast cancer hemodynamics using image-guided computational fluid dynamics,” IEEE Trans. Med. Imaging 39, 2760–2771 (2020). 10.1109/TMI.2020.2975375 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c47] 47. Baldock A., Rockne R., Boone A., Neal M., Bridge C., Guyman L., Mrugala M., Rockhill J., Swanson K. R., Trister A. D., and Hawkins-Daarud A., “ From patient-specific mathematical neuro-oncology to precision medicine,” Front. Oncol. 3, 62 (2013). 10.3389/fonc.2013.00062 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c48] 48. Whitmire P., Rickertsen C. R., Hawkins-Daarud A., Carrasco E., Lorence J., De Leon G., Curtin L., Bayless S., Clark-Swanson K., Peeri N. C., and Corpuz C., “ Sex-specific impact of patterns of imageable tumor growth on survival of primary glioblastoma patients,” BMC Cancer 20, 447 (2020). 10.1186/s12885-020-06816-2 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c49] 49. Scheufele K., Subramanian S., and Biros G., “ Fully automatic calibration of tumor-growth models using a single mpMRI scan,” IEEE Trans. Med. Imaging 40, 193–204 (2021). 10.1109/TMI.2020.3024264 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c50] 50. Lê M., Delingette H., Kalpathy-Cramer J., Gerstner E. R., Batchelor T., Unkelbach J., and Ayache N., “ MRI based Bayesian personalization of a tumor growth model,” IEEE Trans. Med. Imaging 35, 2329–2339 (2016). 10.1109/TMI.2016.2561098 [DOI] [PubMed] [Google Scholar]

[c51] 51. Lipková J., Angelikopoulos P., Wu S., Alberts E., Wiestler B., Diehl C., Preibisch C., Pyka T., Combs S. E., Hadjidoukas P., and Van Leemput K., “ Personalized radiotherapy design for glioblastoma: Integrating mathematical tumor models, multimodal scans, and Bayesian inference,” IEEE Trans. Med. Imaging 38, 1875–1884 (2019). 10.1109/TMI.2019.2902044 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c52] 52. Swanson K. R., Alvord E. C., and Murray J. D., “ A quantitative model for differential motility of gliomas in grey and white matter,” Cell Proliferation 33, 317–329 (2000). 10.1046/j.1365-2184.2000.00177.x [DOI] [PMC free article] [PubMed] [Google Scholar]

[c53] 53. Neal M. L., Trister A. D., Cloke T., Sodt R., Ahn S., Baldock A. L., Bridge C. A., Lai A., Cloughesy T. F., Mrugala M. M., and Rockhill J. K., “ Discriminating survival outcomes in patients with glioblastoma using a simulation-based, patient-specific response metric,” PLoS One 8, e51951 (2013). 10.1371/journal.pone.0051951 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c54] 54. Romarowski R. M., Conti M., Morganti S., Grassi V., Marrocco-Trischitta M. M., Trimarchi S., and Auricchio F., “ Computational simulation of TEVAR in the ascending aorta for optimal endograft selection: A patient-specific case study,” Comput. Biol. Med. 103, 140–147 (2018). 10.1016/j.compbiomed.2018.10.014 [DOI] [PubMed] [Google Scholar]

[c55] 55. Corral-Acero J., Margara F., Marciniak M., Rodero C., Loncaric F., Feng Y., Gilbert A., Fernandes J. F., Bukhari H. A., Wajdan A., and Martinez M. V., “ The ‘digital twin’ to enable the vision of precision cardiology,” Eur. Heart J. 41, 4556–4564 (2020). 10.1093/eurheartj/ehaa159 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c56] 56. Taylor C. A., Fonte T. A., and Min J. K., “ Computational fluid dynamics applied to cardiac computed tomography for noninvasive quantification of fractional flow reserve: Scientific basis,” J. Am. Coll. Cardiol. 61(22), 2233–2241 (2013). 10.1016/j.jacc.2012.11.083 [DOI] [PubMed] [Google Scholar]

[c57] 57. Sankaran S., Lesage D., Tombropoulos R., Xiao N., Kim H. J., Spain D., Schaap M., and Taylor C. A., “ Physics driven real-time blood flow simulations,” Comput. Methods Appl. Mech. Eng. 364, 112963 (2020). 10.1016/j.cma.2020.112963 [DOI] [Google Scholar]

[c58] 58. De Bruyne B. and Sarma J., “ Fractional flow reserve: A review,” Heart 94(7), 949–959 (2008). 10.1136/hrt.2007.122838 [DOI] [PubMed] [Google Scholar]

[c59] 59. Sankaran S., Moghadam M. E., Kahn A. M., Tseng E. E., Guccione J. M., and Marsden A. L., “ Patient-specific multiscale modeling of blood flow for coronary artery bypass graft surgery,” Ann. Biomed. Eng. 40(10), 2228–2242 (2012). 10.1007/s10439-012-0579-3 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c60] 60. Baillargeon B., Rebelo N., Fox D. D., Taylor R. L., and Kuhl E., “ The living heart project: A robust and integrative simulator for human heart function,” Eur. J. Mech.-A/Solids 48, 38–47 (2014). 10.1016/j.euromechsol.2014.04.001 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c61] 61. Kayvanpour E., Mansi T., Sedaghat-Hamedani F., Amr A., Neumann D., Georgescu B., Seegerer P., Kamen A., Haas J., Frese K. S., and Irawati M., “ Towards personalized cardiology: Multi-scale modeling of the failing heart,” PLoS One 10(7), e0134869 (2015). 10.1371/journal.pone.0134869 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c62] 62. Liu J., Yang W., Lan I. S., and Marsden A. L., “ Fluid-structure interaction modeling of blood flow in the pulmonary arteries using the unified continuum and variational multiscale formulation,” Mech. Res. Commun. 107, 103556 (2020). 10.1016/j.mechrescom.2020.103556 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c63] 63. Zhang W., Rossini G., Kamensky D., Bui‐Thanh T., and Sacks M. S., “ Isogeometric finite element‐based simulation of the aortic heart valve: Integration of neural network structural material model and structural tensor fiber architecture representations,” Int. J. Numer. Methods Biomed. Eng. 37, e3438 (2021). 10.1002/cnm.3438 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c64] 64. Clayton R. H., Bernus O., Cherry E. M., Dierckx H., Fenton F. H., Mirabella L., Panfilov A. V., Sachse F. B., Seemann G., and Zhang H., “ Models of cardiac tissue electrophysiology: Progress, challenges and open questions,” Prog. Biophys. Mol. Biol. 104(1–3), 22–48 (2011). 10.1016/j.pbiomolbio.2010.05.008 [DOI] [PubMed] [Google Scholar]

[c65] 65. Zhou L., Bar-Cohen Y., Peck R. A., Chirikian G. V., Harwin B., Chmait R. H., Pruetz J. D., Silka M. J., and Loeb G. E., “ Analytical modeling for computing lead stress in a novel epicardial micropacemaker,” Cardiovasc. Eng. Technol. 8(1), 96–105 (2017). 10.1007/s13239-017-0292-3 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c66] 66. Sahli Costabal F., Yao J., and Kuhl E., “ Predicting drug-induced arrhythmias by multiscale modeling,” Int. J. Numer. Methods Biomed. Eng. 34(5), e2964 (2018). 10.1002/cnm.2964 [DOI] [PubMed] [Google Scholar]

[c67] 67. Arthurs C. J., Khlebnikov R., Melville A., Marčan M., Gomez A., Dillon-Murphy D., Cuomo F., Silva Vieira M., Schollenberger J., Lynch S. R., and Tossas-Betancourt C., “ CRIMSON: An open-source software framework for cardiovascular integrated modelling and simulation,” PLOS Comput. Biol. 17, e1008881 (2021). 10.1371/journal.pcbi.1008881 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c68] 68. Updegrove A., Wilson N. M., Merkow J., Lan H., Marsden A. L., and Shadden S. C., “ SimVascular: An open source pipeline for cardiovascular simulation,” Ann. Biomed. Eng. 45(3), 525–541 (2017). 10.1007/s10439-016-1762-8 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c69] 69. Barua N. U., Gill S. S., and Love S., “ Convection‐enhanced drug delivery to the brain: Therapeutic potential and neuropathological considerations,” Brain Pathol. 24, 117–127 (2014). 10.1111/bpa.12082 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c70] 70. Lam M. F., Thomas M. G., and Lind C. R., “ Neurosurgical convection-enhanced delivery of treatments for Parkinson's disease,” J. Clin. Neurosci. 18(9), 1163–1167 (2011). 10.1016/j.jocn.2011.01.012 [DOI] [PubMed] [Google Scholar]

[c71] 71. Saito R. and Tominaga T., “ Convection-enhanced delivery of therapeutics for malignant gliomas.” Neurol. Med.-Chir. 57, 8–16 (2016). 10.2176/nmc.ra.2016-0071 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c72] 72. Jahangiri A., Chin A. T., Flanigan P. M., Chen R., Bankiewicz K., and Aghi M. K., “ Convection-enhanced delivery in glioblastoma: A review of preclinical and clinical studies,” J. Neurosurg. 126, 191–200 (2017). 10.3171/2016.1.JNS151591 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c73] 73. Debinski W. and Tatter S. B., “ Convection-enhanced delivery for the treatment of brain tumors,” Expert Rev. Neurother. 9, 1519–1527 (2009). 10.1586/ern.09.99 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c74] 74. Phillips W. T., Bao A., Brenner A. J., and Goins B. A., “ Image-guided interventional therapy for cancer with radiotherapeutic nanoparticles,” Adv. Drug Delivery Rev. 76, 39–59 (2014). 10.1016/j.addr.2014.07.001 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c75] 75. Krauze M. T., Saito R., Noble C., Tamas M., Bringas J., Park J. W., Berger M. S., and Bankiewicz K., “ Reflux-free cannula for convection-enhanced high-speed delivery of therapeutic agents,” J. Neurosurg. 103, 923–929 (2005). 10.3171/jns.2005.103.5.0923 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c76] 76. Bao A., Phillips W., Brenner A., Floyd J., Gorzell B., Cooper A., Martinez R., Salman U., and Goins B., “ First-in-human study of 186Re-nanoliposomes (186RNL) delivered intra-tumorally by convection-enhanced delivery for treatment of recurrent glioblastoma: Safety, image biodistribution, and radiation dosimetry,” J. Nucl. Med. 58(supplement 1), 599 (2017); available at https://jnm.snmjournals.org/content/58/supplement_1/599. [Google Scholar]

[c77] 77. Wembacher-Schroeder E., Kerstein N., Bander E. D., Pandit-Taskar N., Thomson R., and Souweidane M. M., “ Evaluation of a patient-specific algorithm for predicting distribution for convection-enhanced drug delivery into the brainstem of patients with diffuse intrinsic pontine glioma,” J. Neurosurg. 1, 1–9 (2021). 10.3171/2020.11.PEDS20571 [DOI] [PubMed] [Google Scholar]

[c78] 78. Morgenstern P. F., Zhou Z., Wembacher-Schröder E., Cina V., Tsiouris A. J., and Souweidane M. M., “ Clinical tolerance of corticospinal tracts in convection-enhanced delivery to the brainstem,” J. Neurosurg. 131(6), 1812–1818 (2018). 10.3171/2018.6.JNS18854 [DOI] [PubMed] [Google Scholar]

[c79] 79. Sampson J. H., Raghavan R., Brady M. L., Provenzale J. M., Herndon J. E., Croteau D., Friedman A. H., Reardon D. A., Coleman R. E., Wong T., and Bigner D. D., “ Clinical utility of a patient-specific algorithm for simulating intracerebral drug infusions,” Neuro-oncology 9, 343–353 (2007). 10.1215/15228517-2007-007 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c80] 80. Morrison P. F., Chen M. Y., Chadwick R. S., Lonser R. R., and Oldfield E. H., “ Focal delivery during direct infusion to brain: Role of flow rate, catheter diameter, and tissue mechanics,” Am. J. Physiol. 277(4), 21518–21229 (1999). 10.1152/ajpregu.1999.277.4.R1218 [DOI] [PubMed] [Google Scholar]

[c81] 81. Rosenbluth K. H., Eschermann J. F., Mittermeyer G., Thomson R., Mittermeyer S., and Bankiewicz K. S., “ Analysis of a simulation algorithm for direct brain drug delivery,” Neuroimage 59, 2423–2429 (2012). 10.1016/j.neuroimage.2011.08.107 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c82] 82. McCloy R. and Stone R., “ Virtual reality in surgery,” BMJ 323, 912–915 (2001). 10.1136/bmj.323.7318.912 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c83] 83. Badash I., Burtt K., Solorzano C. A., and Carey J. N., “ Innovations in surgery simulation: A review of past, current and future techniques,” Ann. Transl. Med. 4(23), 453 (2016). 10.21037/atm.2016.12.24 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c84] 84. Devoto L., Muscroft S., and Chand M., “ Highly accurate, patient-specific, 3-dimensional mixed-reality model creation for surgical training and decision-making,” JAMA Surg. 154(10), 968–969 (2019). 10.1001/jamasurg.2019.2546 [DOI] [PubMed] [Google Scholar]

[c85] 85. Laaki H., Miche Y., and Tammi K., “ Prototyping a digital twin for real time remote control over mobile networks: Application of remote surgery,” IEEE Access 7, 20325–20336 (2019). 10.1109/ACCESS.2019.2897018 [DOI] [Google Scholar]

[c86] 86. Ryu W. H., Dharampal N., Mostafa A. E., Sharlin E., Kopp G., Jacobs W. B., Hurlbert R. J., Chan S., and Sutherland G. R., “ Systematic review of patient-specific surgical simulation: Toward advancing medical education,” J. Surg. Educ. 74(6), 1028–1038 (2017). 10.1016/j.jsurg.2017.05.018 [DOI] [PubMed] [Google Scholar]

[c87] 87. Brunet J. N., Mendizabal A., Petit A., Golse N., Vibert E., and Cotin S., “ Physics-based deep neural network for augmented reality during liver surgery,” in International Conference on Medical Image Computing and Computer-Assisted Intervention ( Springer, Cham, 2019), pp. 137–145. [Google Scholar]

[c88] 88. Tepper O. M., Rudy H. L., Lefkowitz A., Weimer K. A., Marks S. M., Stern C. S., and Garfein E. S., “ Mixed reality with HoloLens: Where virtual reality meets augmented reality in the operating room,” Plast. Reconstr. Surg. 140(5), 1066–1070 (2017). 10.1097/PRS.0000000000003802 [DOI] [PubMed] [Google Scholar]

[c89] 89. Ahmed H. and Devoto L., “ The potential of a digital twin in surgery,” Surg. Innovation 28, 509 (2020). 10.1177/1553350620975896 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c90] 90. Cevidanes L. H., Tucker S., Styner M., Kim H., Chapuis J., Reyes M., Proffit W., Turvey T., and Jaskolka M., “ Three-dimensional surgical simulation,” Am. J. Orthod. Dentofacial Orthop. 138(3), 361–371 (2010). 10.1016/j.ajodo.2009.08.026 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c91] 91. Fang C., Zhang P., and Qi X., “ Digital and intelligent liver surgery in the new era: Prospects and dilemmas,” EBioMedicine 41, 693–701 (2019). 10.1016/j.ebiom.2019.02.017 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c92] 92. de Zélicourt D. A. and Kurtcuoglu V., “ Patient-specific surgical planning, where do we stand? The example of the Fontan procedure,” Ann. Biomed. Eng. 44(1), 174–186 (2016). 10.1007/s10439-015-1381-9 [DOI] [PubMed] [Google Scholar]

[c93] 93. Malone H. R., Syed O. N., Downes M. S., D'Ambrosio A. L., Quest D. O., and Kaiser M. G., “ Simulation in neurosurgery: A review of computer-based simulation environments and their surgical applications,” Neurosurgery 67(4), 1105–1116 (2010). 10.1227/NEU.0b013e3181ee46d0 [DOI] [PubMed] [Google Scholar]

[c94] 94. Misra S., Ramesh K. T., and Okamura A. M., “ Modeling of tool-tissue interactions for computer-based surgical simulation: A literature review,” Presence 17(5), 463 (2008). 10.1162/pres.17.5.463 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c95] 95. Bouhaddou M., Barrette A. M., Stern A. D., Koch R. J., DiStefano M. S., Riesel E. A., Santos L. C., Tan A. L., Mertz A. E., and Birtwistle M. R., “ A mechanistic pan-cancer pathway model informed by multi-omics data interprets stochastic cell fate responses to drugs and mitogens,” PLoS Comput. Biol. 14(3), e1005985 (2018). 10.1371/journal.pcbi.1005985 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c96] 96. Gruber M., Bozic I., Leshchiner I., Livitz D., Stevenson K., Rassenti L., Rosebrock D., Taylor-Weiner A., Olive O., Goyetche R., and Fernandes S. M., “ Growth dynamics in naturally progressing chronic lymphocytic leukaemia,” Nature 570(7762), 474–479 (2019). 10.1038/s41586-019-1252-x [DOI] [PMC free article] [PubMed] [Google Scholar]

[c97] 97. Chowell D., Napier J., Gupta R., Anderson K. S., Maley C. C., and Sayres M. A., “ Modeling the subclonal evolution of cancer cell populations,” Cancer Res. 78(3), 830–839 (2018). 10.1158/0008-5472.CAN-17-1229 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c98] 98. Hormuth D. A., Jarrett A. M., Feng X., and Yankeelov T. E., “ Calibrating a predictive model of tumor growth and angiogenesis with quantitative MRI,” Ann. Biomed. Eng. 47, 1539–1551 (2019). 10.1007/s10439-019-02262-9 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c99] 99. Hormuth D. A., Jarrett A. M., Davis T., and Yankeelov T. E., “ Towards an image-informed mathematical model of in vivo response to fractionated radiation therapy,” Cancers 13, 1765 (2021). 10.3390/cancers13081765 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c100] 100. Padhani A. R., Liu G., Mu-Koh D., Chenevert T. L., Thoeny H. C., Takahara T., Dzik-Jurasz A., Ross B. D., Van Cauteren M., Collins D., and Hammoud D. A., “ Diffusion-weighted magnetic resonance imaging as a cancer biomarker: Consensus and recommendations,” Neoplasia 11, 102–125 (2009). 10.1593/neo.81328 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c101] 101. Yankeelov T. E., Pickens D. R., and Price R. R., Quantitative MRI in Cancer ( Taylor & Francis, 2011). [Google Scholar]

[c102] 102. Castell F. and Cook G. J. R., “ Quantitative techniques in 18FDG PET scanning in oncology,” Br. J. Cancer 98, 1597–1601 (2008). 10.1038/sj.bjc.6604330 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c103] 103. Wu C., Pineda F., Hormuth D. A., Karczmar G. S., and Yankeelov T. E., “ Quantitative analysis of vascular properties derived from ultrafast DCE-MRI to discriminate malignant and benign breast tumors,” Magn. Reson. Med. 81, 2147–2160 (2019). 10.1002/mrm.27529 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c104] 104. Li X., Abramson R. G., Arlinghaus L. R., Chakravarthy A. B., Abramson V. G., Sanders M., and Yankeelov T. E. (2016). “ Data from QIN-breast,” Cancer Imaging Archive. 10.7937/K9/TCIA.2016.21JUebH0 [DOI] [Google Scholar]

[c105] 105. Li X., Abramson R. G., Arlinghaus L. R., Kang H., Chakravarthy A. B., Abramson V. G., Farley J., Mayer I. A., Kelley M. C., Meszoely I. M., Means-Powell J., Grau A. M., Sanders M., and Yankeelov T. E., “ Multiparametric magnetic resonance imaging for predicting pathological response after the first cycle of neoadjuvant chemotherapy in breast cancer,” Invest. Radiol. 50(4), 195–204 (2015). 10.1097/RLI.0000000000000100 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c106] 106. Clark K., Vendt B., Smith K., Freymann J., Kirby J., Koppel P., Moore S., Phillips S., Maffitt D., Pringle M., Tarbox L., and Prior F., “ The cancer imaging archive (TCIA): Maintaining and operating a public information repository,” J. Digital Imaging 26(6), 1045–1057 (2013). 10.1007/s10278-013-9622-7 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c107] 107. Macovski A., Medical Imaging Systems ( Prentice-Hall, 1983). [Google Scholar]

[c108] 108.Clinical PET and PET/CT: Principles and Applications, edited by Kim E. E., Lee M. C., Inoue T., and Wong W. H. ( Springer Science & Business Media, 2012). [Google Scholar]

[c109] 109. Nishimura D. G., Principles of Magnetic Resonance Imaging ( Stanford University, 2010). [Google Scholar]

[c110] 110. Eisenhauer E. A., Therasse P., Bogaerts J., Schwartz L. H., Sargent D., Ford R., Dancey J., Arbuck S., Gwyther S., Mooney M., and Rubinstein L., “ New response evaluation criteria in solid tumours: Revised RECIST guideline (version 1.1),” Eur. J. Cancer 45, 228–247 (2009). 10.1016/j.ejca.2008.10.026 [DOI] [PubMed] [Google Scholar]

[c111] 111. Hormuth D. A., Sorace A. G., Virostko J., Abramson R. G., Bhujwalla Z. M., Enriquez‐Navas P., Gillies R., Hazle J. D., Mason R. P., Quarles C. C., and Weis J. A., “ Translating preclinical MRI methods to clinical oncology,” J. Magn. Reson. Imaging 50, 1377–1392 (2019). 10.1002/jmri.26731 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c112] 112. Yankeelov T. E. and Gore J. C., “ Dynamic contrast enhanced magnetic resonance imaging in oncology: Theory, data acquisition, analysis, and examples,” Curr. Med. Imaging Rev. 3, 91–107 (2009). 10.2174/157340507780619179 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c113] 113. Pineda F. D., Medved M., Wang S., Fan X., Schacht D. V., Sennett C., Oto A., Newstead G. M., Abe H., and Karczmar G. S., “ Ultrafast bilateral DCE-MRI of the breast with conventional fourier sampling: Preliminary evaluation of semi-quantitative analysis,” Acad. Radiol. 23(9), 1137–1144 (2016). 10.1016/j.acra.2016.04.008 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c114] 114. Onishi N., Kataoka M., Kanao S., Sagawa H., Iima M., Nickel M. D., Toi M., and Togashi K., “ Ultrafast dynamic contrast-enhanced MRI of the breast using compressed sensing: Breast cancer diagnosis based on separate visualization of breast arteries and veins,” J. Magn. Reson. Imaging 47(1), 97–104 (2018). 10.1002/jmri.25747 [DOI] [PubMed] [Google Scholar]

[c115] 115. Chenevert T. L., Stegman L. D., Taylor J. M., Robertson P. L., Greenberg H. S., Rehemtulla A., and Ross B. D., “ Diffusion magnetic resonance imaging: An early surrogate marker of therapeutic efficacy in brain tumors,” J. Natl. Cancer Inst. 92, 2029–2036 (2000). 10.1093/jnci/92.24.2029 [DOI] [PubMed] [Google Scholar]

[c116] 116. van Houdt P. J., Yang Y., and van der Heide U. A., “ Quantitative magnetic resonance imaging for biological image-guided adaptive radiotherapy,” Front. Oncol. 10, 615643 (2021). 10.3389/fonc.2020.615643 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c117] 117. Partridge S. C., Nissan N., Rahbar H., Kitsch A. E., and Sigmund E. E., “ Diffusion-weighted breast MRI: Clinical applications and emerging techniques,” J. Magn. Reson. Imaging 45(2), 337–355 (2017). 10.1002/jmri.25479 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c118] 118. Partridge S. C., Zhang Z., Newitt D. C., Gibbs J. E., Chenevert T. L., Rosen M. A., Bolan P. J., Marques H. S., Romanoff J., Cimino L., Joe B. N., Umphrey H. R., Ojeda-Fournier H., Dogan B., Oh K., Abe H., Drukteinis J. S., Esserman L. J., and Hylton N. M., “ Diffusion-weighted MRI findings predict pathologic response in neoadjuvant treatment of breast cancer: The ACRIN 6698 multicenter trial,” Radiology 289(3), 618–627 (2018). 10.1148/radiol.2018180273 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c119] 119. Horská A. and Barker P. B., “ Imaging of brain tumors: MR spectroscopy and metabolic imaging,” Neuroimaging Clin. 20(3), 293–310 (2010). 10.1016/j.nic.2010.04.003 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c120] 120. Pepin K. M., Ehman R. L., and McGee K. P., “ Magnetic resonance elastography (MRE) in cancer: Technique, analysis, and applications,” Prog. Nucl. Magn. Reson. Spectrosc. 90, 32–48 (2015). 10.1016/j.pnmrs.2015.06.001 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c121] 121. Wahl R. L., Jacene H., Kasamon Y., and Lodge M. A., “ From RECIST to PERCIST: Evolving considerations for PET response criteria in solid tumors,” J. Nucl. Med. 50, 122S–150S (2009). 10.2967/jnumed.108.057307 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c122] 122. Pinker K., Riedl C., and Weber W. A., “ Evaluating tumor response with FDG PET: Updates on PERCIST, comparison with EORTC criteria and clues to future developments,” Eur. J. Nucl. Med. Mol. Imaging 44(Suppl 1), 55–66 (2017). 10.1007/s00259-017-3687-3 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c123] 123. Farwell M. D., Pryma D. A., and Mankoff D. A., “ PET/CT imaging in cancer: Current applications and future directions,” Cancer 120, 3433–3445 (2014). 10.1002/cncr.28860 [DOI] [PubMed] [Google Scholar]

[c124] 124. Carmona-Bozo J. C., Manavaki R., Woitek R., Torheim T., Baxter G. C., Caracò C., Provenzano E., Graves M. J., Fryer T. D., Patterson A. J., and Gilbert F. J., “ Hypoxia and perfusion in breast cancer: Simultaneous assessment using PET/MR imaging,” Eur. Radiol. 31(1), 333–344 (2021). 10.1007/s00330-020-07067-2 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c125] 125. Muzi M., Peterson L. M., O'Sullivan J. N., Fink J. R., Rajendran J. G., McLaughlin L. J., Muzi J. P., Mankoff D. A., and Krohn K. A., “ ¹⁸F-fluoromisonidazole quantification of hypoxia in human cancer patients using image-derived blood surrogate tissue reference regions,” J. Nucl. Med. 56(8), 1223–1228 (2015). 10.2967/jnumed.115.158717 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c126] 126. Holzgreve A., Brendel M., Gu S., Carlsen J., Mille E., Böning G., Mastrella G., Unterrainer M., Gildehaus F. J., Rominger A., Bartenstein P., Kälin R. E., Glass R., and Albert N. L., “ Monitoring of tumor growth with [18F]-FET PET in a mouse model of glioblastoma: SUV measurements and volumetric approaches,” Front. Neurosci. 10, 260 (2016). 10.3389/fnins.2016.00260 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c127] 127. Pöpperl G., Kreth F. W., Mehrkens J. H., Herms J., Seelos K., Koch W., Gildehaus F. J., Kretzschmar H. A., Tonn J. C., and Tatsch K., “ FET PET for the evaluation of untreated gliomas: Correlation of FET uptake and uptake kinetics with tumour grading,” Eur. J. Nucl. Med. Mol. Imaging 34(12), 1933–1942 (2007). 10.1007/s00259-007-0534-y [DOI] [PubMed] [Google Scholar]

[c128] 128. Karls S., Shah H., and Jacene H., “ PET/CT for lymphoma post-therapy response assessment in other lymphomas, response assessment for autologous stem cell transplant, and lymphoma follow-up,” Semin. Nucl. Med. 48(1), 37–49 (2018). 10.1053/j.semnuclmed.2017.09.004 [DOI] [PubMed] [Google Scholar]

[c129] 129. Ehman E. C., Johnson G. B., Villanueva-Meyer J. E., Cha S., Leynes A. P., Larson P. E. Z., and Hope T. A., “ PET/MRI: Where might it replace PET/CT?,” J. Magn. Reson. Imaging 46(5), 1247–1262 (2017). 10.1002/jmri.25711 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c130] 130. Waks A. G. and Winer E. P., “ Breast cancer treatment: A review,” JAMA 321, 288–300 (2019). 10.1001/jama.2018.19323 [DOI] [PubMed] [Google Scholar]

[c131] 131. Litwin M. S. and Tan H. J., “ The diagnosis and treatment of prostate cancer: A review,” JAMA 317, 2532–2542 (2017). 10.1001/jama.2017.7248 [DOI] [PubMed] [Google Scholar]

[c132] 132. Lorenzo G., Hormuth I. D., Jarrett A. M., Lima E. A., Subramanian S., “ Biros G., Oden J. T., Hughes T. J., and Yankeelov T. E., Quantitative in vivo imaging to enable tumor forecasting and treatment optimization,” arXiv:2102.12602 (2021).

[c133] 133. Karolak A., Markov D. A., McCawley L. J., and Rejniak K. A., “ Towards personalized computational oncology: From spatial models of tumour spheroids, to organoids, to tissues,” J. R. Soc. Interface 15, 20170703 (2018). 10.1098/rsif.2017.0703 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c134] 134. Lima E. A. B. F., Oden J. T., Wohlmuth B., Shahmoradi A., Hormuth I. D., Yankeelov T. E., Scarabosio L., and Horger T., “ Selection and validation of predictive models of radiation effects on tumor growth based on noninvasive imaging data,” Comput. Methods Appl. Mech. Eng. 327, 277–305 (2017). 10.1016/j.cma.2017.08.009 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c135] 135. Wang C. H., Rockhill J. K., Mrugala M., Peacock D. L., Lai A., Jusenius K., Wardlaw J. M., Cloughesy T., Spence A. M., Rockne R., and Alvord E. C., “ Prognostic significance of growth kinetics in newly diagnosed glioblastomas revealed by combining serial imaging with a novel biomathematical model,” Cancer Res. 69, 9133–9140 (2009). 10.1158/0008-5472.CAN-08-3863 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c136] 136. Fey D., Halasz M., Dreidax D., Kennedy S. P., Hastings J. F., Rauch N., Munoz A. G., Pilkington R., Fischer M., Westermann F., and Kolch W., “ Signaling pathway models as biomarkers: Patient-specific simulations of JNK activity predict the survival of neuroblastoma patients,” Sci. Signaling 8, ra130 (2015). 10.1126/scisignal.aab0990 [DOI] [PubMed] [Google Scholar]

[c137] 137. Tuncbag N., Milani P., Pokorny J. L., Johnson H., Sio T. T., Dalin S., Iyekegbe D. O., White F. M., Sarkaria J. N., and Fraenkel E., “ Network modeling identifies patient-specific pathways in glioblastoma,” Sci. Rep. 6, 28668 (2016). 10.1038/srep28668 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c138] 138. Mang A., Bakas S., Subramanian S., Davatzikos C., and Biros G., “ Integrated biophysical modeling and image analysis: Application to neuro-oncology,” Annu. Rev. Biomed. Eng. 22, 309–341 (2020). 10.1146/annurev-bioeng-062117-121105 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c139] 139. Tunc B., Hormuth D., Biros G., and Yankeelov T. E., “ Modeling of glioma growth with mass effect by longitudinal magnetic resonance imaging,” IEEE Trans. Biomed. Eng. 68(12), 3713–3724 (2021). 10.1109/TBME.2021.3085523 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c140] 140. Vavourakis V., Eiben B., Hipwell J. H., Williams N. R., Keshtgar M., and Hawkes D. J., “ Multiscale mechano-biological finite element modelling of oncoplastic breast surgery—numerical study towards surgical planning and cosmetic outcome prediction,” PLoS One 11, e0159766 (2016). 10.1371/journal.pone.0159766 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c141] 141. Lorenzo G., Hughes T. J., Dominguez-Frojan P., Reali A., and Gomez H., “ Computer simulations suggest that prostate enlargement due to benign prostatic hyperplasia mechanically impedes prostate cancer growth,” Proc. Natl. Acad. Sci. 116, 1152–1161 (2019). 10.1073/pnas.1815735116 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c142] 142. Lorenzo G., Pérez-García V. M., Mariño A., Pérez-Romasanta L. A., Reali A., and Gomez H., “ Mechanistic modelling of prostate-specific antigen dynamics shows potential for personalized prediction of radiation therapy outcome,” J. R. Soc. Interface 16, 20190195 (2019). 10.1098/rsif.2019.0195 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c143] 143. Zahid M. U., Mohsin N., Mohamed A. S., Caudell J. J., Harrison L. B., Fuller C. D., Moros E. G., and Enderling H., “ Forecasting individual patient response to radiotherapy in head and neck cancer with a dynamic carrying capacity model,” Int. J. Radiat. Oncol. Biol. Phys. 111(3), 693–704 (2021). 10.1016/j.ijrobp.2021.05.132 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c144] 144. Wong K. C., Summers R. M., Kebebew E., and Yao J., “ Pancreatic tumor growth prediction with elastic-growth decomposition, image-derived motion, and FDM-FEM coupling,” IEEE Trans. Med. Imaging 36, 111–123 (2016). 10.1109/TMI.2016.2597313 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c145] 145. Liu Y., Sadowski S. M., Weisbrod A. B., Kebebew E., Summers R. M., and Yao J., “ Patient specific tumor growth prediction using multimodal images,” Med. Image Anal. 18, 555–566 (2014). 10.1016/j.media.2014.02.005 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c146] 146. Chen X., Summers R. M., and Yao J., “ Kidney tumor growth prediction by coupling reaction-diffusion and biomechanical model,” IEEE Trans. Biomed. Eng. 60, 169–173 (2012). 10.1109/TBME.2012.2222027 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c147] 147. Glazar D. J., Grass G. D., Arrington J. A., Forsyth P. A., Raghunand N., Yu H. H., Sahebjam S., and Enderling H., “ Tumor volume dynamics as an early biomarker for patient-specific evolution of resistance and progression in recurrent high-grade glioma,” J. Clin. Med. 9, 2019 (2020). 10.3390/jcm9072019 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c148] 148. Kaur P., Singh A., and Chana I., “ Computational techniques and tools for omics data analysis: State-of-the-art, challenges, and future directions,” Arch. Comput. Methods Eng. 28, 4595–4631 (2021). 10.1007/s11831-021-09547-0 [DOI] [Google Scholar]

[c149] 149. Falco M. M., Peña-Chilet M., Loucera C., Hidalgo M. R., and Dopazo J., “ Mechanistic models of signaling pathways deconvolute the glioblastoma single-cell functional landscape,” NAR Cancer 2, zcaa011 (2020). 10.1093/narcan/zcaa011 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c150] 150. Ebata K., Yamashiro S., Iida K., and Okada M., “ Building patient‐specific models for receptor tyrosine kinase signaling networks,” FEBS J. 289(1), 90–101 (2021). 10.1111/febs.15831 [DOI] [PubMed] [Google Scholar]

[c151] 151. Klipp E. and Liebermeister W., “ Mathematical modeling of intracellular signaling pathways,” BMC Neurosci. 7, S10 (2006). 10.1186/1471-2202-7-S1-S10 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c152] 152. Mahlbacher G. E., Reihmer K. C., and Frieboes H. B., “ Mathematical modeling of tumor-immune cell interactions,” J. Theor. Biol. 469, 47–60 (2019). 10.1016/j.jtbi.2019.03.002 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c153] 153. Jolly M. K., Tripathi S. C., Somarelli J. A., Hanash S. M., and Levine H., “ Epithelial/mesenchymal plasticity: How have quantitative mathematical models helped improve our understanding?,” Mol. Oncol. 11, 739–754 (2017). 10.1002/1878-0261.12084 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c154] 154. Weis J. A., Miga M. I., Arlinghaus L. R., Li X., Abramson V., Chakravarthy A. B., Pendyala P., and Yankeelov T. E., “ Predicting the response of breast cancer to neoadjuvant therapy using a mechanically coupled reaction–diffusion model,” Cancer Res. 75(22), 4697–4707 (2015). 10.1158/0008-5472.CAN-14-2945 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c155] 155. Jbabdi S., Mandonnet E., Duffau H., Capelle L., Swanson K. R., Pélégrini‐Issac M., Guillevin R., and Benali H., “ Simulation of anisotropic growth of low‐grade gliomas using diffusion tensor imaging,” Magn. Reson. Med. 54(3), 616–624 (2005). 10.1002/mrm.20625 [DOI] [PubMed] [Google Scholar]

[c156] 156. Atuegwu N. C., Arlinghaus L. R., Li X., Welch E. B., Chakravarthy B. A., Gore J. C., and Yankeelov T. E., “ Integration of diffusion-weighted MRI data and a simple mathematical model to predict breast tumor cellularity during neoadjuvant chemotherapy,” Magn. Reson. Med. 66, 1689–1696 (2011). 10.1002/mrm.23203 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c157] 157. Zhu W., Kato Y., and Artemov D., “ Heterogeneity of tumor vasculature and antiangiogenic intervention: Insights from MR angiography and DCE-MRI,” PLoS One 9(1), e86583 (2014). 10.1371/journal.pone.0086583 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c158] 158. Gatenby R. A., Grove O., and Gillies R. J., “ Quantitative imaging in cancer evolution and ecology,” Radiology 269(1), 8–14 (2013). 10.1148/radiol.13122697 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c159] 159. Syed A. K., Whisenant J. G., Barnes S. L., Sorace A. G., and Yankeelov T. E., “ Multiparametric analysis of longitudinal quantitative MRI data to identify distinct tumor habitats in preclinical models of breast cancer,” Cancers 12, 1682 (2020). 10.3390/cancers12061682 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c160] 160. Roque T., Risser L., Kersemans V., Smart S., Allen D., Kinchesh P., Gilchrist S., Gomes A. L., Schnabel J. A., and Chappell M. A., “ A DCE-MRI driven 3-D reaction-diffusion model of solid tumor growth,” IEEE Trans. Med. Imaging 37, 724–732 (2017). 10.1109/TMI.2017.2779811 [DOI] [PubMed] [Google Scholar]

[c161] 161. Chang Y. C., Ackerstaff E., Tschudi Y., Jimenez B., Foltz W., Fisher C., Lilge L., Cho H., Carlin S., Gillies R. J., and Balagurunathan Y., “ Delineation of tumor habitats based on dynamic contrast enhanced MRI,” Sci. Rep. 7, 9746 (2017). 10.1038/s41598-017-09932-5 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c162] 162. Rockne R. C., Trister A. D., Jacobs J., Hawkins-Daarud A. J., Neal M. L., Hendrickson K., Mrugala M. M., Rockhill J. K., Kinahan P., Krohn K. A., and Swanson K. R., “ A patient-specific computational model of hypoxia-modulated radiation resistance in glioblastoma using 18F-FMISO-PET,” J. R. Soc. Interface 12, 20141174 (2015). 10.1098/rsif.2014.1174 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c163] 163. Jarrett A. M., Hormuth D. A., Adhikarla V., Sahoo P., Abler D., Tumyan L., Schmolze D., Mortimer J., Rockne R. C., and Yankeelov T. E., “ Towards integration of ⁶⁴Cu-DOTA-trastuzumab PET-CT and MRI with mathematical modeling to predict response to neoadjuvant therapy in HER2 + breast cancer,” Sci. Rep. 10, 20518 (2020). 10.1038/s41598-020-77397-0 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c164] 164. Wu C., Hormuth D. A., Pineda F., Karczmar G. S., and Yankeelov T. E., “ Towards patient-specific optimization of neoadjuvant treatment protocols for breast cancer based on image-guided fluid dynamics,” IEEE Trans. Biomed. Eng. (published online 2022). 10.1109/TBME.2022.3168402 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c165] 165. Esserman L. J., Thompson I. M., Reid B., Nelson P., Ransohoff D. F., Welch H. G., Hwang S., Berry D. A., Kinzler K. W., Black W. C., and Bissell M., “ Addressing overdiagnosis and overtreatment in cancer: A prescription for change,” Lancet Oncol. 15(6), e234–e242 (2014). 10.1016/S1470-2045(13)70598-9 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c166] 166. Loeb S., Bjurlin M. A., Nicholson J., Tammela T. L., Penson D. F., Carter H. B., Carroll P., and Etzioni R., “ Overdiagnosis and overtreatment of prostate cancer,” Eur. Urol. 65(6), 1046–1055 (2014). 10.1016/j.eururo.2013.12.062 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c167] 167. Eklund M., Jäderling F., Discacciati A., Bergman M., Annerstedt M., Aly M., Glaessgen A., Carlsson S., Grönberg H., and Nordström T., “ MRI-targeted or standard biopsy in prostate cancer screening,” N. Engl. J. Med. 385(10), 908–920 (2021). 10.1056/NEJMoa2100852 [DOI] [PubMed] [Google Scholar]

[c168] 168. Co M., “ Ductal carcinoma in situ of the breasts: Over‐diagnosis, over‐treatment and a decade of lost direction,” Precis. Med. Sci. 9(1), 4–8 (2020). 10.1002/prm2.12008 [DOI] [Google Scholar]

[c169] 169. Van Luijt P. A., Heijnsdijk E. A., Fracheboud J., Overbeek L. I., Broeders M. J., Wesseling J., den Heeten G. J., and de Koning H. J., “ The distribution of ductal carcinoma in situ (DCIS) grade in 4232 women and its impact on overdiagnosis in breast cancer screening,” Breast Cancer Res. 18(1), 47 (2016). 10.1186/s13058-016-0705-5 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c170] 170. Hawkins-Daarud A., Prudhomme S., van der Zee K. G., and Oden J. T., “ Bayesian calibration, validation, and uncertainty quantification of diffuse interface models of tumor growth,” J. Math. Biol. 67(6), 1457–1485 (2013). 10.1007/s00285-012-0595-9 [DOI] [PubMed] [Google Scholar]

[c171] 171. Liedtke C., Mazouni C., Hess K. R., André F., Tordai A., Mejia J. A., Symmans W. F., Gonzalez-Angulo A. M., Hennessy B., Green M., and Cristofanilli M., “ Response to neoadjuvant therapy and long-term survival in patients with triple-negative breast cancer,” J. Clin. Oncol. 26, 1275–1281 (2008). 10.1200/JCO.2007.14.4147 [DOI] [PubMed] [Google Scholar]

[c172] 172. Spring L. M., Fell G., Arfe A., Sharma C., Greenup R., Reynolds K. L., Smith B. L., Alexander B., Moy B., Isakoff S. J., and Parmigiani G., “ Pathological complete response after neoadjuvant chemotherapy and impact on breast cancer recurrence and survival: A comprehensive meta-analysis,” Clin. Cancer Res. 26, 2838 (2020). 10.1158/1078-0432.CCR-19-3492 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c173] 173. Korde L. A., Somerfield M. R., Carey L. A., Crews J. R., Denduluri N., Hwang E. S., Khan S. A., Loibl S., Morris E. A., Perez A., and Regan M. M., “ Neoadjuvant chemotherapy, endocrine therapy, and targeted therapy for breast cancer: ASCO guideline,” J. Clin. Oncol. 39(13), 1485–1505 (2021). 10.1200/JCO.20.03399 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c174] 174. Castiglioni I., Rundo L., Codari M., Di Leo G., Salvatore C., Interlenghi M., Gallivanone F., Cozzi A., D'Amico N. C., and Sardanelli F., “ AI applications to medical images: From machine learning to deep learning,” Phys. Med. 83, 9–24 (2021). 10.1016/j.ejmp.2021.02.006 [DOI] [PubMed] [Google Scholar]

[c175] 175. Murphy K. P., Machine Learning: A Probabilistic Perspective ( MIT Press, 2012). [Google Scholar]

[c176] 176. Guresen E. and Kayakutlu G., “ Definition of artificial neural networks with comparison to other networks,” Procedia Comput. Sci. 3, 426–433 (2011). 10.1016/j.procs.2010.12.071 [DOI] [Google Scholar]

[c177] 177. Schmidhuber J., “ Deep learning in neural networks: An overview,” Neural Networks 61, 85–117 (2015). 10.1016/j.neunet.2014.09.003 [DOI] [PubMed] [Google Scholar]

[c178] 178. LeCun Y., Bengio Y., and Hinton G., “ Deep learning,” Nature 521, 436–444 (2015). 10.1038/nature14539 [DOI] [PubMed] [Google Scholar]

[c179] 179. Darestani M. and Heckel R., “ Can un-trained neural networks compete with trained neural networks at image reconstruction?,” arXiv:2007.02471 (2020).

[c180] 180. Miotto R., Wang F., Wang S., Jiang X., and Dudley J. T., “ Deep learning for healthcare: Review, opportunities and challenges,” Briefings Bioinf. 19, 1236–1246 (2018). 10.1093/bib/bbx044 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c181] 181. Ulyanov D., Vedaldi A., and Lempitsky V., “ Deep image prior,” Int. J. Comput. Vis. 128, 1867–1888 (2020). 10.1007/s11263-020-01303-4 [DOI] [Google Scholar]

[c182] 182. Wang T., Lei Y., Fu Y., Wynne J. F., Curran W. J., Liu T., and Yang X., “ A review on medical imaging synthesis using deep learning and its clinical applications,” J. Appl. Clin. Med. Phys. 22, 11–36 (2020). 10.1002/acm2.13121 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c183] 183. Elmarakeby H. A., Hwang J., Arafeh R., Crowdis J., Gang S., Liu D., AlDubayan S. H., Salari K., Kregel S., Richter C., and Arnoff T. E., “ Biologically informed deep neural network for prostate cancer discovery,” Nature 598, 348–352 (2021). 10.1038/s41586-021-03922-4 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c184] 184. Darestani M. Z. and Heckel R., “ Accelerated MRI with un-trained neural networks,” IEEE Trans. Comput. Imaging 7, 724–733 (2021). 10.1109/TCI.2021.3097596 [DOI] [Google Scholar]

[c185] 185. Kaissis G. A., Makowski M. R., Rückert D., and Braren R. F., “ Secure, privacy-preserving and federated machine learning in medical imaging,” Nat. Mach. Intell. 2, 305–311 (2020). 10.1038/s42256-020-0186-1 [DOI] [Google Scholar]

[c186] 186. Björnsson B., Borrebaeck C., Elander N., Gasslander T., Gawel D. R., Gustafsson M., Jörnsten R., Lee E. J., Li X., Lilja S., and Martínez-Enguita D., “ Digital twins to personalize medicine,” Genome Med. 12, 1–4 (2020). 10.1186/s13073-019-0701-3 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c187] 187. Izmailova E. S. and Wood W. A., “ Biometric monitoring technologies in cancer: The past, present, and future,” JCO Clin. Cancer Inf. 5, 728–733 (2021). 10.1200/CCI.21.00019 [DOI] [PubMed] [Google Scholar]

[c188] 188. Ahmadi-Assalemi G., Al-Khateeb H., Maple C., Epiphaniou G., Alhaboby Z. A., Alkaabi S., and Alhaboby D., “ Digital twins for precision healthcare,” in Cyber Defence in the Age of AI, Smart Societies and Augmented Humanity, edited by Jahankhani H., Kendzierskyj S., Chelvachandran N., and Ibarra J. ( Springer Nature Switzerland AG, Cham, Switzerland, 2020), pp. 133–158. [Google Scholar]

[c189] 189. Croatti A., Gabellini M., Montagna S., and Ricci A., “ On the integration of agents and digital twins in healthcare,” J. Med. Syst. 44, 161 (2020). 10.1007/s10916-020-01623-5 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c190] 190. Ash D., Gold G., Seiver A., and Hayes-Rosh B., “ Guaranteeing real-time response with limited resources,” Artif. Intell. Med. 5, 49–66 (1995). 10.1016/0933-3657(93)90005-N [DOI] [PubMed] [Google Scholar]

[c191] 191. Jardine A. K. S., Lin D., and Banjevic D., “ A review on machinery diagnostics and prognostics implementing condition-based maintenance,” Mech. Syst. Signal Process. 20, 1483–1510 (2006). 10.1016/j.ymssp.2005.09.012 [DOI] [Google Scholar]

[c192] 192. Khan S. and Yairi T., “ A review on the applications of deep learning in system health management,” Mech. Syst. Signal Process. 107, 241–265 (2019). 10.1016/j.ymssp.2017.11.024 [DOI] [Google Scholar]

[c193] 193. Cohen O., Zhu B., and Rosen M. S., “ MR fingerprinting deep reconstruction network (DRONE),” Magn. Reson. Med. 80(3), 885–894 (2018). 10.1002/mrm.27198 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c194] 194. Ronneberger O., Fischer P., and Brox T., “ U-net: Convolutional networks for biomedical image segmentation,” in International Conference on Medical Image Computing and Computer-Assisted Intervention ( Springer, Cham, 2015), pp. 234–241. [Google Scholar]

[c195] 195. Li Y., Wang Y., Qi H., Hu Z., Chen Z., Yang R., Qiao H., Sun J., Wang T., Zhao X., and Guo H., “ Deep learning–enhanced T₁ mapping with spatial-temporal and physical constraint,” Magn. Reson. Med. 86, 1647–1661 (2021). 10.1002/mrm.28793 [DOI] [PubMed] [Google Scholar]

[c196] 196. Raissi M., Yazdani A., and Karniadakis G. E., “ Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations,” Science 367, 1026–1030 (2020). 10.1126/science.aaw4741 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c197] 197. Alber M., Tepole A. B., Cannon W. R., De S., Dura-Bernal S., Garikipati K., Karniadakis G., Lytton W. W., Perdikaris P., Petzold L., and Kuhl E., “ Integrating machine learning and multiscale modeling—perspectives, challenges, and opportunities in the biological, biomedical, and behavioral sciences,” npj Digital Med. 2, 115 (2019). 10.1038/s41746-019-0193-y [DOI] [PMC free article] [PubMed] [Google Scholar]

[c198] 198. Gaw N., Hawkins-Daarud A., Hu L. S., Yoon H., Wang L., Xu Y., Jackson P. R., Singleton K. W., Baxter L. C., Eschbacher J., and Gonzales A., “ Integration of machine learning and mechanistic models accurately predicts variation in cell density of glioblastoma using multiparametric MRI,” Sci. Rep. 9, 10063 (2019). 10.1038/s41598-019-46296-4 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c199] 199. Nicolò C., Périer C., Prague M., Bellera C., MacGrogan G., Saut O., and Benzekry S., “ Machine learning and mechanistic modeling for prediction of metastatic relapse in early-stage breast cancer,” JCO Clin. Cancer Inf. 4, 259–274 (2020). 10.1200/CCI.19.00133 [DOI] [PubMed] [Google Scholar]

[c200] 200. Ardizzone L., Kruse J., Wirkert S., Rahner D., Pellegrini E. W., Klessen R. S., Maier-Hein L., Rother C., and Köthe U., “ Analyzing inverse problems with invertible neural networks,” arXiv:1808.04730v3 (2018).

[c201] 201. Wang N., Chang H., and Zhang D., “ Efficient uncertainty quantification for dynamic subsurface flow with surrogate by theory-guided neural network,” Comput. Methods Appl. Mech. Eng. 373(1), 113492 (2021). 10.1016/j.cma.2020.113492 [DOI] [Google Scholar]

[c202] 202. Hussain Z., Gimenez F., Yi D., and Rubin D., “ Differential data augmentation techniques for medical imaging classification tasks,” in AMIA Annual Symposium Proceedings ( American Medical Informatics Association, 2017), p. 979. [PMC free article] [PubMed] [Google Scholar]

[c203] 203. Oden J. T., Babuška I., and Faghihi D., “ Predictive computational science: Computer predictions in the presence of uncertainty,” in Encyclopedia of Computational Mechanics, 2nd ed. ( Wiley, 2017), pp. 1–26. [Google Scholar]

[c204] 204. Oden J. T., Lima E. A., Almeida R. C., Feng Y., Rylander M. N., Fuentes D., Faghihi D., Rahman M. M., DeWitt M., Gadde M., and Zhou J. C., “ Toward predictive multiscale modeling of vascular tumor growth,” Arch. Comput. Methods Eng. 23, 735–779 (2016). 10.1007/s11831-015-9156-x [DOI] [Google Scholar]

[c205] 205. Fletcher A. and Osborne J., “ Seven challenges in the multiscale modelling of multicellular tissues,” WIREs Mech. Dis. 14, e1527 (2020). 10.1002/wsbm.1527 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c206] 206. Zangooei M. H. and Habibi J., “ Hybrid multiscale modeling and prediction of cancer cell behavior,” PLoS One 12, e0183810 (2017). 10.1371/journal.pone.0183810 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c207] 207. Phillips C. M., Lima E. A., Woodall R. T., Brock A., and Yankeelov T. E., “ A hybrid model of tumor growth and angiogenesis: In silico experiments,” PLoS One 15, e0231137 (2020). 10.1371/journal.pone.0231137 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c208] 208. Hanahan D. and Weinberg R. A., “ Hallmarks of cancer: The next generation,” Cell 144(5), 646–674 (2011). 10.1016/j.cell.2011.02.013 [DOI] [PubMed] [Google Scholar]

[c209] 209. Hanahan D. and Coussens L. M., “ Accessories to the crime: Functions of cells recruited to the tumor microenvironment,” Cancer Cell 21(3), 309–322 (2012). 10.1016/j.ccr.2012.02.022 [DOI] [PubMed] [Google Scholar]

[c210] 210. Guimarães C. F., Gasperini L., Marques A. P., and Reis R. L., “ The stiffness of living tissues and its implications for tissue engineering,” Nat. Rev. Mater. 5, 351–370 (2020). 10.1038/s41578-019-0169-1 [DOI] [Google Scholar]

[c211] 211. Bader D. L. and Knight M. M., “ Biomechanical analysis of structural deformation in living cells,” Med. Biol. Eng. Comput. 46, 951 (2008). 10.1007/s11517-008-0381-4 [DOI] [PubMed] [Google Scholar]

[c212] 212. Miller C. and Davidson L., “ The interplay between cell signalling and mechanics in developmental processes,” Nat. Rev. Genet. 14, 733–744 (2013). 10.1038/nrg3513 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c213] 213. Hammes-Schiffer S. and Galli G., “ Integration of theory and experiment in the modelling of heterogeneous electrocatalysis,” Nat. Energy 6, 700–705 (2021). 10.1038/s41560-021-00827-4 [DOI] [Google Scholar]

[c214] 214. Rahman M. M., Feng Y., Yankeelov T. E., and Oden J. T., “ A fully coupled space–time multiscale modeling framework for predicting tumor growth,” Comput. Methods Appl. Mech. Eng. 320, 261–286 (2017). 10.1016/j.cma.2017.03.021 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c215] 215. Jarrett A. M., Bloom M. J., Godfrey W., Syed A. K., Ekrut D. A., Ehrlich L. I., Yankeelov T. E., and Sorace A. G., “ Mathematical modelling of trastuzumab-induced immune response in an in vivo murine model of HER2+ breast cancer,” Math. Med. Biol. 36, 381–410 (2019). 10.1093/imammb/dqy014 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c216] 216. Sheth K. N., Mazurek M. H., Yuen M. M., Cahn B. A., Shah J. T., Ward A., Kim J. A., Gilmore E. J., Falcone G. J., Petersen N., and Gobeske K. T., “ Assessment of brain injury using portable, low-field magnetic resonance imaging at the bedside of critically ill patients,” JAMA Neurol. 78, 41–47 (2021). 10.1001/jamaneurol.2020.3263 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c217] 217. Edlow B. L., Mareyam A., Horn A., Polimeni J. R., Witzel T., Tisdall M. D., Augustinack J. C., Stockmann J. P., Diamond B. R., Stevens A., and Tirrell L. S., “ 7 Tesla MRI of the ex vivo human brain at 100 micron resolution,” Sci. Data 6, 244 (2019). 10.1038/s41597-019-0254-8 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c218] 218. Sterzing F., Kratochwil C., Fiedler H., Katayama S., Habl G., Kopka K., Afshar-Oromieh A., Debus J., Haberkorn U., and Giesel F. L., “ 68 Ga-PSMA-11 PET/CT: A new technique with high potential for the radiotherapeutic management of prostate cancer patients,” Eur. J. Nucl. Med. Mol. Imaging 43, 34–41 (2016). 10.1007/s00259-015-3188-1 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c219] 219. Zhou X. Y., Tay Z. W., Chandrasekharan P., Elaine Y. Y., Hensley D. W., Orendorff R., Jeffris K. E., Mai D., Zheng B., Goodwill P. W., and Conolly S. M., “ Magnetic particle imaging for radiation-free, sensitive and high-contrast vascular imaging and cell tracking,” Curr. Opin. Chem. Biol. 45, 131–138 (2018). 10.1016/j.cbpa.2018.04.014 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c220] 220. Rivera-Rodriguez A., Hoang-Minh L. B., Chiu-Lam A., Sarna N., Marrero-Morales L., Mitchell D. A., and Rinaldi-Ramos C. M., “ Tracking adoptive T cell immunotherapy using magnetic particle imaging,” Nanotheranostics 5, 431–444 (2021). 10.7150/ntno.55165 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c221] 221. Nishino M., Hatabu H., and Hodi F. S., “ Imaging of cancer immunotherapy: Current approaches and future directions,” Radiology 290, 9–22 (2019). 10.1148/radiol.2018181349 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c222] 222. Alvarez-Garcia V., Bartos C., Keraite I., Trivedi U., Brennan P. M., Kersaudy-Kerhoas M., Gharbi K., Oikonomidou O., and Leslie N. R., “ A simple and robust real-time qPCR method for the detection of PIK3CA mutations,” Sci. Rep. 8, 4290 (2018). 10.1038/s41598-018-22473-9 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c223] 223. Becht E., McInnes L., Healy J., Dutertre C. A., Kwok I. W., Ng L. G., Ginhoux F., and Newell E. W., “ Dimensionality reduction for visualizing single-cell data using UMAP,” Nat. Biotechnol. 37(1), 38–44 (2019). 10.1038/nbt.4314 [DOI] [PubMed] [Google Scholar]

[c224] 224. Pisco A. O., Brock A., Zhou J., Moor A., Mojtahedi M., Jackson D., and Huang S., “ Non-Darwinian dynamics in therapy-induced cancer drug resistance,” Nat. Commun. 4, 2467 (2013). 10.1038/ncomms3467 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c225] 225. Heindl A., Nawaz S., and Yuan Y., “ Mapping spatial heterogeneity in the tumor microenvironment: A new era for digital pathology,” Lab. Invest. 95, 377–384 (2015). 10.1038/labinvest.2014.155 [DOI] [PubMed] [Google Scholar]

[c226] 226. Rejniak K. A., Wang S. E., Bryce N. S., Chang H., Parvin B., Jourquin J., Estrada L., Gray J. W., Arteaga C. L., Weaver A. M., and Quaranta V., “ Linking changes in epithelial morphogenesis to cancer mutations using computational modeling,” PLoS Comput. Biol. 6, e1000900 (2010). 10.1371/journal.pcbi.1000900 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c227] 227. Gurcan M. N., Boucheron L. E., Can A., Madabhushi A., Rajpoot N. M., and Yener B., “ Histopathological image analysis: A review,” IEEE Rev. Biomed. Eng. 2, 147–171 (2009). 10.1109/RBME.2009.2034865 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c228] 228. Erol T., Mendi A. F., and Dogan D., “ The digital twin revolution in healthcare,” in Proceedings of the 4th International Symposium on Multidisciplinary Studies and Innovative Technologies, ISMSIT, Istanbul, Turkey (IEEE, 2020), pp. 1–7. 10.1109/ISMSIT50672.2020.9255249 [DOI] [Google Scholar]

[c229] 229. Cottrell J. A., Hughes T. J. R., and Bazilevs Y., Isogeometric Analysis: Toward Integration of CAD and FEA ( John Wiley & Sons, 2009). [Google Scholar]

[c230] 230. Lorenzo G., Scott M. A., Tew K., Hughes T. J. R., and Gomez H., “ Hierarchically refined and coarsened splines for moving interface problems, with particular application to phase-field models of prostate tumor growth,” Comput. Methods Appl. Mech. Eng. 319, 515–548 (2017). 10.1016/j.cma.2017.03.009 [DOI] [Google Scholar]

[c231] 231. D¨uster A., Parvizian J., Yang Z., and Rank E., “ The finite cell method for three-dimensional problems of solid mechanics,” Comput. Methods Appl. Mech. Eng. 197(45–48), 3768–3782 (2008). 10.1016/j.cma.2008.02.036 [DOI] [Google Scholar]

[c232] 232. Parvizian J., D¨uster A., and Rank E., “ Finite cell method: H- and p-extension for embedded domain problems in solid mechanics,” Comput. Mech. 41(1), 121–133 (2007). 10.1007/s00466-007-0173-y [DOI] [Google Scholar]

[c233] 233. Schillinger D. and Ruess M., “ The finite cell method: A review in the context of higher-order structural analysis of CAD and image-based geometric models,” Arch. Comput. Methods Eng. 22(3), 391–455 (2015). 10.1007/s11831-014-9115-y [DOI] [Google Scholar]

[c234] 234. Burman E., Claus S., Hansbo P., Larson M. G., and Massing A., “ CutFEM: Discretizing geometry and partial differential equations,” Int. J. Numer. Methods Eng. 104(7), 472–501 (2015). 10.1002/nme.4823 [DOI] [Google Scholar]

[c235] 235. Hansbo A. and Hansbo P., “ An unfitted finite element method, based on Nitsche's method, for elliptic interface problems,” Comput. Methods Appl. Mech. Eng. 191, 5537–5552 (2002). 10.1016/S0045-7825(02)00524-8 [DOI] [Google Scholar]

[c236] 236. Embar A., Dolbow J., and Harari I., “ Imposing Dirichlet boundary conditions with Nitsche's method and spline-based finite elements,” Int. J. Numer. Methods Eng. 83, 877–898 (2010). 10.1002/nme.2863 [DOI] [Google Scholar]

[c237] 237. Raissi M., Perdikaris P., and Karniadakis G. E., “ Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations,” J. Comput. Phys. 378, 686–707 (2019). 10.1016/j.jcp.2018.10.045 [DOI] [Google Scholar]

[c238] 238. Haghighat E., Raissi M., Moure A., Gomez H., and Juanes R., “ A physics-informed deep learning framework for inversion and surrogate modeling in solid mechanics,” Comput. Methods Appl. Mech. Eng. 379, 113741 (2021). 10.1016/j.cma.2021.113741 [DOI] [Google Scholar]

[c239] 239. Reshetova G., Vladimir C., and Tatyana K., “ Numerical experiments with digital twins of core samples for estimating effective elastic parameters,” in Supercomputing ( Springer International Publishing, Cham, 2019), pp. 290–301. [Google Scholar]

[c240] 240. Cheverda V., Lisitsa V., Protasov M., Reshetova G., Glinsky B., Chernykh I., Merzlikina A., Volyanskaya V., Petrov D., Melnik A., and Shilikov V., “ Digital twins of multiscale 3D heterogeneous geological objects: 3D simulations and seismic imaging of faults, fractures and caves,” J. Phys. 1392, 12051 (2019). 10.1088/1742-6596/1392/1/012051 [DOI] [Google Scholar]

[c241] 241. Hirschvogel M., Jagschies L., Maier A., Wildhirt S. M., and Gee M. W., “ An in silico twin for epicardial augmentation of the failing heart,” Int. J. Numer. Methods Biomed. Eng. 35, e3233 (2019). 10.1002/cnm.3233 [DOI] [PubMed] [Google Scholar]

[c242] 242. Yoders J., “ Nvidia partners with Bentley on digital twin modeling,” Eng. News Rec. 286, 103 (2021); available at https://www.enr.com/articles/51786-nvidia-and-bentley-partner-on-digital-twin-modeling-and-simulation-environment. [Google Scholar]

[c243] 243. Kłusek A., Łoś M., Paszyński M., and Dzwinel W., “ Efficient model of tumor dynamics simulated in multi-GPU environment,” Int. J. High Perform. Comput. Appl. 33, 489–506 (2019). 10.1177/1094342018816772 [DOI] [Google Scholar]

[c244] 244. da Costa J. M. J., Orlande H. R. B., and da Silva W. B., “ Model selection and parameter estimation in tumor growth models using approximate Bayesian computation-ABC,” Comput. Appl. Math. 37, 2795–2815 (2018). 10.1007/s40314-017-0479-0 [DOI] [Google Scholar]

[c245] 245. Konishi S. and Kitagawa G., Information Criteria and Statistical Modeling, 1st ed. ( Springer Science & Business Media, 2008). [Google Scholar]

[c246] 246. Jeffreys H., The Theory of Probability, 3rd ed. ( Oxford University Press, 1998). [Google Scholar]

[c247] 247. Hormuth D. A. II, Jarrett A. M., Lima E. A. B. F., McKenna M. T., Fuentes D. T., and Yankeelov T. E., “ Mechanism-based modeling of tumor growth and treatment response constrained by multiparametric imaging data,” JCO Clin. Cancer Inf. 3, 1–10 (2019). 10.1200/CCI.18.00055 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c248] 248. Lima E. A. B. F., Oden J. T., Hormuth D. A., Yankeelov T. E., and Almeida R. C., “ Selection, calibration, and validation of models of tumor growth,” Math. Models Methods Appl. Sci. 26, 2341–2368 (2016). 10.1142/S021820251650055X [DOI] [PMC free article] [PubMed] [Google Scholar]

[c249] 249. Dzwinel W., Kłusek A., and Paszyński M., “ A concept of a prognostic system for personalized anti-tumor therapy based on supermodeling,” Procedia Comput. Sci. 108, 1832–1841 (2017). 10.1016/j.procs.2017.05.013 [DOI] [Google Scholar]

[c250] 250. Gargalo C. L., de Las Heras S. C., Jones M. N., Udugama I., Mansouri S. S., Krühne U., and Gernaey K. V., “ Towards the development of digital twins for the bio-manufacturing industry,” in Digital Twins, Advances in Biochemical Engineering/Biotechnology, edited by Herwig C., Pörtner R., and Möller J. ( Springer, Cham, 2020), pp. 1–34. [DOI] [PubMed] [Google Scholar]

[c251] 251. Schroeder B. B., Hund L., and Kittinger R. S., “ The need for credibility guidance for analyses quantifying margin and uncertainty,” in Model Validation and Uncertainty Quantification ( Springer, Cham, 2020), Vol. 3, pp 11–23. [Google Scholar]

[c252] 252. Lima E. A., Ghousifam N., Ozkan A., Oden J. T., Shahmoradi A., Rylander M. N., Wohlmuth B., and Yankeelov T. E., “ Calibration of multi-parameter models of avascular tumor growth using time resolved microscopy data,” Sci. Rep. 8, 14558 (2018). 10.1038/s41598-018-32347-9 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c253] 253. Phillips C., Lima E. A., Gadde M., Jarrett A. M., Rylander M. N., and Yankeelov T. E., “ Towards integration of time-resolved confocal microscopy of a 3D in vitro microfluidic platform with a hybrid multiscale model of tumor angiogenesis,” bioRxiv (2021). 10.1101/2021.09.29.462293 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c254] 254. Stupp R., Mason W. P., Van Den Bent M. J., Weller M., Fisher B., Taphoorn M. J., Belanger K., Brandes A. A., Marosi C., Bogdahn U., and Curschmann J., “ Radiotherapy plus concomitant and adjuvant temozolomide for glioblastoma,” N. Engl. J. Med. 352(10), 987–996 (2005). 10.1056/NEJMoa043330 [DOI] [PubMed] [Google Scholar]

[c255] 255. Tang L., Wei F., Wu Y., He Y., Shi L., Xiong F., Gong Z., Guo C., Li X., Deng H., and Cao K., “ Role of metabolism in cancer cell radioresistance and radiosensitization methods,” J. Exp. Clin. Cancer Res. 37(1), 87 (2018). 10.1186/s13046-018-0758-7 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c256] 256. Jing X., Yang F., Shao C., Wei K., Xie M., Shen H., and Shu Y., “ Role of hypoxia in cancer therapy by regulating the tumor microenvironment,” Mol. Cancer 18(1), 157 (2019). 10.1186/s12943-019-1089-9 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c257] 257. Vickers A. J., “ Effects of magnetic resonance imaging targeting on overdiagnosis and overtreatment of prostate cancer,” Eur. Urol. 80(5), 567–572 (2021). 10.1016/j.eururo.2021.06.026 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c258] 258. Khair D. O., Bax H. J., Mele S., Crescioli S., Pellizzari G., Khiabany A., Nakamura M., Harris R. J., French E., Hoffmann R. M., and Williams I. P., “ Combining immune checkpoint inhibitors: Established and emerging targets and strategies to improve outcomes in melanoma,” Front. Immunol. 10, 453 (2019). 10.3389/fimmu.2019.00453 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c259] 259. Yan D., “ Adaptive radiotherapy: Merging principle into clinical practice,” Semin. Radiat. Oncol. 20(2), 79–83 (2010). 10.1016/j.semradonc.2009.11.001 [DOI] [PubMed] [Google Scholar]

[c260] 260. Rockwell S., Dobrucki I. T., Kim E. Y., Marrison S. T., and Vu V. T., “ Hypoxia and radiation therapy: Past history, ongoing research, and future promise,” Curr. Mol. Med. 9(4), 442–458 (2009). 10.2174/156652409788167087 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c261] 261. Potiron V. A., Abderrahmani R., Clément-Colmou K., Marionneau-Lambot S., Oullier T., Paris F., and Supiot S., “ Improved functionality of the vasculature during conventionally fractionated radiation therapy of prostate cancer,” PLoS One 8(12), e84076 (2013). 10.1371/journal.pone.0084076 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c262] 262. Hormuth D. A., Phillips C. M., Wu C., Lima E. A., Lorenzo G., Jha P. K., Jarrett A. M., Oden J. T., and Yankeelov T. E., “ Biologically-based mathematical modeling of tumor vasculature and angiogenesis via time-resolved imaging data,” Cancers 13, 3008 (2021). 10.3390/cancers13123008 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c263] 263. McMahon S. J., “ The linear quadratic model: Usage, interpretation and challenges,” Phys. Med. Biol. 64(1), 01TR01 (2018). 10.1088/1361-6560/aaf26a [DOI] [PubMed] [Google Scholar]

[c264] 264. Jones L., Hoban P., and Metcalfe P., “ The use of the linear quadratic model in radiotherapy: A review,” Australas. Phys. Eng. Sci. Med. 24(3), 132–146 (2001). 10.1007/BF03178355 [DOI] [PubMed] [Google Scholar]

[c265] 265. Brenner D. J., “ The linear-quadratic model is an appropriate methodology for determining isoeffective doses at large doses per fraction,” Semin. Radiat. Oncol. 18(4), 234–239 (2008). 10.1016/j.semradonc.2008.04.004 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c266] 266. Hormuth I. D., Weis J. A., Barnes S. L., Miga M. I., Rericha E. C., Quaranta V., and Yankeelov T. E., “ Predicting in vivo glioma growth with the reaction diffusion equation constrained by quantitative magnetic resonance imaging data,” Phys. Biol. 12, 46006 (2015). 10.1088/1478-3975/12/4/046006 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c267] 267. Hormuth D. A., Jarrett A. M., and Yankeelov T. E., “ Forecasting tumor and vasculature response dynamics to radiation therapy via image based mathematical modeling,” Radiat. Oncol. 15, 1–4 (2020). 10.1186/s13014-019-1446-2 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c268] 268. Liu J., Hormuth D. A., Davis T., Yang J., McKenna M. T., Jarrett A. M., Enderling H., Brock A., and Yankeelov T. E., “ A time-resolved experimental–mathematical model for predicting the response of glioma cells to single-dose radiation therapy,” Integr. Biol. 13(7), 167–183 (2021). 10.1093/intbio/zyab010 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c269] 269. Brüningk S. C., Rivens I., Box C., Oelfke U., and ter Haar G., “ 3D tumour spheroids for the prediction of the effects of radiation and hyperthermia treatments,” Sci. Rep. 10(1), 1653 (2020). 10.1038/s41598-020-58569-4 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c270] 270. Sunassee E. D., Tan D., Ji N., Brady R., Moros E. G., Caudell J. J., Yartsev S., and Enderling H., “ Proliferation saturation index in an adaptive Bayesian approach to predict patient-specific radiotherapy responses,” Int. J. Radiat. Biol. 95, 1421 (2019). 10.1080/09553002.2019.1589013 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c271] 271. Zhang L., Strouthos C. G., Wang Z., and Deisboeck T. S., “ Simulating brain tumor heterogeneity with a multiscale agent-based model: Linking molecular signatures, phenotypes and expansion rate,” Math. Comput. Model. 49(1–2), 307–319 (2009). 10.1016/j.mcm.2008.05.011 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c272] 272. Frieboes H. B., Lowengrub J. S., Wise S., Zheng X., Macklin P., Bearer E. L., and Cristini V., “ Computer simulation of glioma growth and morphology,” Neuroimage 37, S59–S70 (2007). 10.1016/j.neuroimage.2007.03.008 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c273] 273. Alfonso J. C., Talkenberger K., Seifert M., Klink B., Hawkins-Daarud A., Swanson K. R., Hatzikirou H., and Deutsch A., “ The biology and mathematical modelling of glioma invasion: A review,” J. R. Soc. Interface 14(136), 20170490 (2017). 10.1098/rsif.2017.0490 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c274] 274. Rocha H. L., Almeida R. C., Lima E. A. B. F., Resende A. C. M., Oden J. T., and Yankeelov T. E., “ A hybrid three-scale model of tumor growth,” Math. Models Methods Appl. Sci. 28, 61–93 (2018). 10.1142/S0218202518500021 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c275] 275. Perfahl H., Byrne H. M., Chen T., Estrella V., Alarcón T., Lapin A., Gatenby R. A., Gillies R. J., Lloyd M. C., Maini P. K., and Reuss M., “ Multiscale modelling of vascular tumour growth in 3D: The roles of domain size and boundary conditions,” PLoS One 6(4), e14790 (2011). 10.1371/journal.pone.0014790 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c276] 276. Anderson A. R., “ A hybrid mathematical model of solid tumour invasion: The importance of cell adhesion,” Math. Med. Biol. 22(2), 163–186 (2005). 10.1093/imammb/dqi005 [DOI] [PubMed] [Google Scholar]

[c277] 277. Mabray M. C., R. F. Barajas, Jr. , and Cha S., “ Modern brain tumor imaging,” Brain Tumor Res. Treat. 3(1), 8–23 (2015). 10.14791/btrt.2015.3.1.8 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c278] 278. Jones K. M., Michel K. A., Bankson J. A., Fuller C. D., Klopp A. H., and Venkatesan A. M., “ Emerging magnetic resonance imaging technologies for radiation therapy planning and response assessment,” Int. J. Radiat. Oncol. Biol. Phys. 101(5), 1046–1056 (2018). 10.1016/j.ijrobp.2018.03.028 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c279] 279. Jaffray D., Kupelian P., Djemil T., and Macklis R. M., “ Review of image-guided radiation therapy,” Expert Rev. Anticancer Ther. 7(1), 89–103 (2007). 10.1586/14737140.7.1.89 [DOI] [PubMed] [Google Scholar]

[c280] 280. Lagendijk J. J. W., Raaymakers B. W., and van Vulpen M., “ The magnetic resonance imaging–linac system,” Semin. Radiat. Oncol. 24(3), 207–209 (2014). 10.1016/j.semradonc.2014.02.009 [DOI] [PubMed] [Google Scholar]

[c281] 281. Scarpace L., Mikkelsen T., Cha S., Rao S., Tekchandani S., Gutman D., Saltz J. H., Erickson B. J., Pedano N., Flanders A. E., Barnholtz-Sloan J., Ostrom Q., Barboriak D., and Pierce L. J. (2016). “ Radiology data from the cancer genome atlas glioblastoma multiforme [TCGA-GBM] collection [data set],” Cancer Imaging Archive. 10.7937/K9/TCIA.2016.RNYFUYE9. [DOI] [Google Scholar]

[c282] 282. Menze B. H., Jakab A., Bauer S., Kalpathy-Cramer J., Farahani K., Kirby J., Burren Y., Porz N., Slotboom J., Wiest R., Lanczi L., Gerstner E., Weber M. A., Arbel T., Avants B. B., Ayache N., Buendia P., Collins D. L., Cordier N. et al. , “ The multimodal brain tumor image segmentation benchmark (BRATS),” IEEE Trans. Medical Imaging 34(10), 1993–2024 (2015). 10.1109/TMI.2014.2377694 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c283] 283. Farhat M., Hormuth D., Langshaw H., Elliott A., Landry L., and Yankeelov T., “ Computational models forecasting response of high-grade glioma during adaptive radiation therapy,” in RSNA 2021 Annual Meeting, Chicago, IL (Radiological Society of North America, 2021), p. 12311. [Google Scholar]

[c284] 284. Pathmanathan A. U., van As N. J., Kerkmeijer L. G. W., Christodouleas J., Lawton C. A. F., Vesprini D., van der Heide U. A., Frank S. J., Nill S., Oelfke U., van Herk M., Li X. A., Mittauer K., Ritter M., Choudhury A., and Tree A. C., “ Magnetic resonance imaging-guided adaptive radiation therapy: A game changer for prostate treatment?,” Int. J. Radiat. Oncol. Biol. Phys. 100(2), 361–373 (2018). 10.1016/j.ijrobp.2017.10.020 [DOI] [PubMed] [Google Scholar]

[c285] 285. Ellingson B. M., Bendszus M., Boxerman J., Barboriak D., Erickson B. J., Smits M., Nelson S. J., Gerstner E., Alexander B., Goldmacher G., and Wick W., “ Consensus recommendations for a standardized brain tumor imaging protocol in clinical trials,” Neuro-oncology 17(9), 1188–1198 (2015). 10.1093/neuonc/nov095 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c286] 286. Kaufmann T. J., Smits M., Boxerman J., Huang R., Barboriak D. P., Weller M., Chung C., Tsien C., Brown P. D., Shankar L., and Galanis E., “ Consensus recommendations for a standardized brain tumor imaging protocol for clinical trials in brain metastases,” Neuro-oncology 22(6), 757–772 (2020). 10.1093/neuonc/noaa030 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c287] 287. Hormuth D. A., SL I. I., Weis J. A., Miga M. I., and Yankeelov T. E., “ Mechanically coupled reaction-diffusion model to predict glioma growth: Methodological details,” Methods Mol. Biol. 1711, 225 (2018). 10.1007/978-1-4939-7493-1_11 [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Integrating mechanism-based modeling with biomedical imaging to build practical digital twins for clinical oncology

Chengyue Wu

Guillermo Lorenzo

David A Hormuth II

Ernesto A B F Lima

Kalina P Slavkova

Julie C DiCarlo

John Virostko

Caleb M Phillips

Debra Patt

Caroline Chung

Thomas E Yankeelov

Abstract

I. INTRODUCTION

A. Definitions of digital twins

1. Conceptual and practical definition of a digital twin

2. Mathematical definition of a digital twin

FIG. 1.

3. Examples of digital twins

B. Rationale for digital twins in clinical oncology

1. How clinical trials determine therapeutic regimens

2. How digital twins can hasten the arrival of patient-specific oncology care

C. Integrating quantitative imaging and mechanism-based mathematical modeling

D. Outline for the remainder of the manuscript

II. IMAGE-GUIDED DIGITAL TWINS IN HEALTHCARE

A. Simulation of cardiovascular disease and their treatments

B. Planning convection-enhanced drug delivery for brain diseases

C. Virtual reality and digital twins for surgical planning

III. MAKING IMAGE-GUIDED DIGITAL TWINS PRACTICAL FOR CLINICAL ONCOLOGY

FIG. 2.

A. Clinical imaging techniques

B. Mechanism-based mathematical modeling

C. Linking imaging and mechanism-based modeling to enable digital twins practical for oncology

FIG. 3.

IV. ROLE OF ARTIFICIAL INTELLIGENCE AND BIG DATA

A. Summary of the AI/big data paradigm

B. AI/big data to assist in the implementation of mechanism-based digital twins

V. BARRIERS TO SUCCESS OF IMAGE-GUIDED MECHANISM-BASED DIGITAL TWINS FOR CLINICAL ONCOLOGY

A. Limitations of realistic mathematical models

B. Limitations of available data

C. Limitations of computational techniques

D. Limitations of model selection, validation, and uncertainty quantification

VI. FIVE QUESTIONS TO ANSWER FOR A PRACTICAL APPLICATION (A BLUEPRINT)

FIG. 4.

A. What are the goals for the digital twin?

B. What level of complexity is needed?

C. Does a proper mechanism-based mathematical model exist?

D. Are the required data available or accessible?

E. Can the uncertainty be characterized?

VII. SUMMARY

ACKNOWLEDGMENTS

AUTHOR DECLARATIONS

Conflict of Interest

DATA AVAILABILITY

References

Associated Data

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases