Orientation-specific long-term neural adaptation of the visual system in keratoconus

Abstract

Eyes with the corneal ectasia keratoconus have performed better than expected (e.g. visual acuity) given their elevated levels of higher-order aberrations that cause rotationally asymmetric retinal blur. Adapted neural processing has been suggested as an explanation but has not been measured across multiple meridional orientations. Using a custom Maxwellian-view laser interferometer to bypass ocular optics, sinusoidal grating neural contrast sensitivity was measured in six eyes (three subjects) with keratoconus and four typical eyes (two subjects) at six spatial frequencies and eight orientations using a two-interval forced-choice paradigm. Total measurement duration was 24 to 28 hours per subject. Neural contrast sensitivity functions of typical eyes agreed with literature and generally showed the oblique effect on a linear-scale and rotational symmetry on a log-scale (rotational symmetry was quantified as the ratio of the minor and major radii of an ellipse fit to all orientations within each spatial frequency; typical eye mean 0.93, median 0.93; where a circle = 1). Mean sensitivities of eyes with keratoconus were 20% to 60% lower (at lower and higher spatial frequencies respectively) than typical eyes. Orientation-specific neural contrast sensitivity functions in keratoconus showed substantial rotational asymmetry (ellipse radii ratio: mean 0.84; median 0.86) and large meridional reductions. The visual image quality metric VSX was used with a permutation test to combine the asymmetric optical aberrations of the eyes with keratoconus and their measured asymmetric neural functions, which illustrated how the neural sensitivities generally mitigated the detrimental effects of the optics.

1. Introduction

Visual performance is most broadly a combination of ocular optics (responsible for retinal image formation) and neural visual processing (responsible for detecting and interpreting the retinal image into a visual percept). It has been shown that foveal (Mon-Williams, Tresilian, Strang, Kochhar, & Wann, 1998; Murray et al., 2010; Pesudovs & Brennan, 1993; Sawides, de Gracia, Dorronsoro, Webster, & Marcos, 2011; Sawides et al., 2010; Webster, Georgeson, & Webster, 2002) and peripheral (Zheleznyak, Barbot, Ghosh, & Yoon, 2016) optics can impact visual neural processing. Moreover, it has been inferred that the neural processing of an adult visual system is calibrated to its habitual optical aberrations (Artal et al., 2003, 2004; Sabesan & Yoon, 2010; Vinas, Sawides, De Gracia, & Marcos, 2012) and that the calibration is adaptable to changes in the optics (Sabesan, Barbot, & Yoon, 2017; Vinas et al., 2012).

When investigating the interactions of optical and neural aspects of vision, it is informative to study eyes with the cornea ectasia keratoconus. These eyes habitually experience elevated levels of higher-order aberrations that cause rotationally-asymmetric blurring of the retinal image (Kosaki et al., 2007; Pantanelli, MacRae, Jeong, & Yoon, 2007), which is not correctable with conventional (sphere and cylinder) ophthalmic corrections (Choi, Wee, Lee, & Kim, 2007; Marsack, Parker, Pesudovs, Donnelly III, & Applegate, 2007; Marsack et al., 2014; Negishi, Kumanomido, Utsumi, & Tsubota, 2007). Additionally, disease onset is typically during adolescence (Belin, Duncan, Ambrosio Jr, & Gomes, 2015), so the visual systems of these individuals have typical visual experiences throughout the sensitive and critical periods of development.

Some eyes with keratoconus have performed better than what would be expected from their highly aberrated optics (Hastings et al., 2019; Michael, Guevara, de la Paz, Alvarez de Toledo, & Barraquer, 2011), and adapted neural processing has been suggested as an explanation (Michael et al., 2011; Sabesan & Yoon, 2010). However, in those cases, neural processing was not measured and directly compared with typical eyes, but rather indirectly inferred from manipulations of the ocular optics and comparisons of total performance (not bypassing optics). We sought to examine interactions between measures of the optics and neural processing in eyes with keratoconus.

When the neural processing of eyes with keratoconus has been isolated (bypassing the optics), it has generally only been measured using a grating contrast sensitivity task in one meridian (Kawara & Ohzu, 1977; Kayazawa, Yamamoto, & Itoi, 1981), or using a psychophysical method that prevented stratification of orientations (Rouger, Benard, Gatinel, & Legras, 2010; Sabesan et al., 2017). An exception is Hrdina et al. (2018) who measured grating contrast sensitivity along two meridians in three eyes with keratoconus and corroborated the importance of meridional differences that have been demonstrated when (albeit to a much lesser degree) the optics of typical eyes are asymmetric (Murray et al., 2010). Short-term orientation-specific adaptation has also been demonstrated in typical eyes (Haak, Fast, Bao, Lee, & Engel, 2014; Zhang, Bao, Kwon, He, & Engel, 2009).

The limitation of the abovementioned keratoconus studies to probe neural processing at multiple spatial frequencies and multiple orientations stems from the arduous nature of the task, which is compounded in duration and difficulty by the disease. However, a functional measure of neural sensitivity along multiple visual meridians is necessary to reveal adaptive and synergistic neural processing with the rotationally-asymmetric optics.

One such potential synergistic process may be driven by a desire of the nervous system to minimize the long-term cost of adaptation (Haak et al., 2014; Radhakrishnan, Dorronsoro, Sawides, Webster, & Marcos, 2015) to orientation-specific blur (contrast loss). This long-term change in sensitivity is distinct from short-term adaptation that boosts neural performance in blurred meridians but which fades within one day of constant adaptation (Haak et al., 2014). While adaptation periods of four hours have been considered “prolonged”, “long-term” (Kwon, Legge, Fang, Cheong, & He, 2009), or “intermediate timescales” (Zhang et al., 2009), eyes with keratoconus are valuable in being truly chronically adapted to asymmetric optics – especially in individuals that are clinically ineligible for rigid contact lenses and habitually dependent on spectacles.

Therefore, here we (1) contribute to the literature of the neural processing of eyes with keratoconus by measuring orientation-specific neural contrast sensitivity functions and (2) investigate whether synergy between the optical and neural components of these eyes could serve to benefit overall visual performance. Neural contrast sensitivity is measured by bypassing the ocular optics and directly stimulating the retina using ophthalmic laser interferometry, while comprehensive descriptions of the ocular optics are obtained from wavefront sensing, and the two measurements are combined using a visual image quality metric.

2. Materials and methods

2.1. Subjects

This study adhered to the tenets of the declaration of Helsinki. Prior to data collection, the purpose and methods were explained to each subject and written informed consent approved by the University of Houston Institutional Review Board was signed.

Six eyes with keratoconus (three subjects, aged 44, 30, and 36) participated; disease severity (Belin et al., 2015) evaluated using the Topometric/KC Staging software on the Pentacam HR (Oculus Inc, Arlington, WA) is described in Table 1. Four typically-sighted myopic eyes without keratoconus (two subjects, aged 35 and 33) completed all orientations as controls. Total experiment duration was 24 to 28 hours per subject, divided between eight to twelve sessions on different days depending on subject fatigue and availability. Three additional typically-sighted subjects performed neural contrast sensitivity measurements (Section 2.3) in one eye at one orientation. Exclusion criteria for all subjects included systemic conditions that could have ocular consequences as well as any history of ocular surgery, trauma, or pathology other than keratoconus.

Table 1.

Disease severities (Belin et al., 2015) of the eyes with keratoconus, where 0 is normal and >4 is the most severe. All typically-sighted eyes were graded as 0 across dimensions A, B, and C.

	(A) Anterior corneal radius of curvature	(B) Posterior corneal radius of curvature	(C) Thinnest pachymetry
KC1 Right	1.9	2.6	1.4
KC1 Left	1.6	2.4	1.8
KC2 Right	2.8	>4.0	0.4
KC2 Left	2.8	>4.0	0.6
KC3 Right	2.3	>4.0	3.1
KC3 Left	>4.0	>4.0	>4.0

2.2. Wavefront error

Subjects were fit with a dental impression bite-bar that aligned them across wavefront error and interferometry measurements. Wavefront error was measured at 840 nm in a darkened room without mydriasis using a COAS HD wavefront sensor (Johnson and Johnson Vision, Santa Ana, CA), which output a normalized Zernike expansion reported at 555 nm. Three measurements were recorded at the beginning and three at the end of the experiment. The means of each set of measurements differed by less than the standard deviation of each set, so both sets were pooled and averaged (per Zernike term) after being scaled down (Schwiegerling, 2002) to a common pupil size. No mydriatic was used due to the long duration of the data collection. A common 5 mm pupil diameter was possible across all measurements of KC2, KC3, and all typical subjects. Subject KC1 had relatively small scotopic pupils and the maximum common pupil diameter across all their measurements was 4 mm.

2.3. Ophthalmic laser interferometry

2.3.1. System

Sinusoidal interference fringes were generated using an amplitude-division Maxwellian-view ophthalmic interferometer similar to that of Williams (1985a, 1985b), and Coletta and Sharma (1995). A floating, vibration-damped optical table helped isolate the system from vibrations that could reduce interference fringe stability. The dental impression bite-bar was mounted to a separate three-axis translation stage adjacent to the optical table.

Monochromatic light from a 543 nm helium-neon laser (Research Electro Optics, Boulder, CO) was divided into two beams with a 50/50 beam-splitter cube. Each beam was (square-wave) flickered at 500 Hz by an acousto-optic modulator (AOM) using a Rigol DG1022 function generator (Rigol Technologies, Beaverton, OR), a two-channel fixed frequency driver (Brimrose Corp, Sparks, MD), and a custom MATLAB interface (The Mathworks Inc, Natick, MA). Contrast of the interference fringe was controlled by varying the relative phase of the AOM flicker. When the two beams flickered in phase, they arrived at the retina at the same time and produced maximum contrast. When the beams were perfectly out of phase, they did not temporally overlap on the retina, resulting in a zero contrast uniform field (500 Hz flicker is much higher the human critical fusion frequency). This technique allows modulation of contrast while maintaining constant retinal illuminance (Coletta & Sharma, 1995; Williams, 1985a, 1985b).

After the beams were recombined (50/50 pellicle) they passed through a dove prism, which was electronically rotated (NanoPZ-Util v1.0.2, Newport Corp, Irvine, CA) and controlled the orientation of the fringes with better than 0.25° resolution. Calibration experiments verified that rotating the coherent beams in this manner did not alter contrast, spatial frequency, or power.

Spatial frequency of the interference fringes is proportional to the separation of the point foci of the beams in the focal plane of the Maxwellian-view lens (Westheimer, 1960). The separation of point foci was controlled by adjusting two mirrors equipped with micrometers to displace each beam equally and oppositely from the center of the entrance pupil to minimize the role of the Stiles-Crawford effect. An aperture on the surface of the Maxwellian-view lens limited the interference pattern to a circular 10° diameter patch.

Incoherent light of 540 nm was superimposed on the coherent beams (50/50 pellicle), as has been done before (Campbell & Green, 1965; Coletta & Sharma, 1995; Williams, 1985a, 1985b), to reduce the prominence of spatial noise (speckle) in the coherent beams. The power of the coherent and incoherent beams were individually measured (Bass, 1995) using a Newport 1936-C power meter (Newport Corp, Irvine, CA) and neutral density filters were inserted into the beams such that the proportions of coherent and incoherent light were equalized; resulting in a 50% coherence fraction (Coletta & Sharma, 1995; Williams, 1985b). The incoherent light extended slightly (less than 0.5°) in all directions beyond the perimeter of the 10° coherent patch. The 543 and 540 nm lights are very near to the peak sensitivity of foveal cones (555 nm) and neutral density filters were added before the Maxwellian-view lens such that the resultant retinal illuminance (Bass, 1995; Wyszecki & Stiles, 2000) was 15 td, which was continuously visible and comfortable for prolonged viewing. This is comparable to studies that used a similar wavelength laser (Atchison, Schmid, & Pritchard, 2006; Coletta & Sharma, 1995).

Subjects were initially positioned with the pupil plane of the eye at the focal length of the Maxwellian-view lens. To reduce the detrimental effects of floaters and tear film debris, subjects were adjusted axially to the position where floaters were (subjectively) least noticeable. In agreement with literature (Coletta & Sharma, 1995; Williams, 1985a, 1985b), this typically positioned the Maxwellian-view foci closer to the corneal plane – this has a negligible effect on spatial frequency at the retina (Thibos, 1990; Williams, 1985a) and is convenient for eyes with keratoconus because the ectatic cornea is the primary source of higher-order aberrations.

Intensity profiles of the resultant stimulus (sinusoidal interference patterns combined with incoherent light) were measured using a Lasercam HR camera and BeamView 32-bit software (v 4.8.1; Coherent Inc, Santa Clara, CA) levelled with the optical table and the bite-bar mount. The stimulus reached the camera via the 50/50 pellicle that introduced the incoherent light and, therefore, was equivalent to that viewed by the subject. Via Fourier analysis, Michelson contrast was calculated, and spatial frequency evaluated with a resolution of 0.27 cycles per degree. The crosshair function in the BeamView software was used to align the gratings to the desired orientation. Although the laser was warmed-up prior to any measurements, calculating contrast at each visit in this way allowed compensations of any subtle variability in laser intensity across visits.

2.3.2. Psychophysical method

All subjects performed interferometry without correction. The degree to which the orientation-specific neural contrast sensitivity function of eyes with keratoconus might be asymmetric was unknown and, because orientation-specific channels of the visual system have been estimated (McMahon & Macleod, 2003) as spanning 22.5°, neural contrast sensitivity was evaluated for six spatial frequencies (2, 4, 8, 16, 22.5, and 32 cycles per degree) at eight orientations (0° (horizontal), 22.5°, 45°, 67.5°, 90°, 112.5°, 135°, and 157.5°) in a random order.

Measurement of each spatial frequency and orientation combination began with a method of adjustment, which started at zero phase offset and the subject increased the phase offset (decreasing contrast) until the grating was just barely perceptible. This was followed by a two-interval forced choice paradigm of seven randomized constant stimulus levels. Pilot data indicated control subjects and those with keratoconus underestimated their thresholds subjectively, that is, the method of adjustment threshold was consistently higher contrast than the forced choice method (Vaegan & Halliday, 1982; Higgins, Jaffe, Caruso, & deMonasterio, 1988). Consequently, two levels of constant stimuli were higher contrast (easier to see) and four were lower contrast (more difficult to see) than the method of adjustment threshold, spaced in 0.4 log unit contrast step multiples of that adjustment threshold; the seventh constant stimulus was the method of adjustment threshold. Stimuli were flashed for 0.5 sec each and separated by 1 sec. Each flash was accompanied by an audible tone. Subjects pressed one of two keys to indicate whether they perceived the stimulus in the first or second interval, after which they pressed the same key again to queue the next stimulus. No feedback was provided regarding correctness of the response. Each constant stimulus was displayed sixteen times. Stimulus generation and subject responses were controlled and recorded in MATLAB.

Eyes with more advanced keratoconus struggled to perform the adjustment of some high spatial frequencies. In these cases, the subject was told which orientation was being tested and the constant stimuli started at maximum contrast and decreased in 0.4 log unit multiple steps.

Constant stimulus trials for the 48 unique spatial frequency and orientation combinations were counterbalanced into two “runs” to offset learning effects (Gaito, 1961). Method of adjustment and half the constant stimulus trials (run 1) were performed on the subject’s preferred eye first, which was measured first to facilitate more effective training (Section 2.3.3) and understanding of the task. Thereafter, half of the trials (run 1) were performed on the second eye; each eye followed a unique random order. The second half of trials (run 2) were then performed in reverse order (opposite to run 1) on the second eye, after which the second half of trials (run 2) for the first eye were performed in reverse order. Thus, the last spatial frequency and orientation measured, was the same as the first combination completed.

2.3.3. Training

At the first visit, subjects underwent training that familiarized them with correct positioning and alignment in the system, fixation of the stimulus, and use of the keypad. Subjects KC2 and KC3 were unfamiliar with psychophysical concepts and methods. The concept of refining a method of adjustment threshold was explained and demonstrated. Subject KC1 and all control subjects were experienced with visual psychophysics and had experienced interferometry during construction and calibration of the system. Training also included measurements for all 8 orientations at 8 cycles per degree (amounting to 8 method of adjustment and 448 forced choice trials) – these data were not included in the analyses; 8 cycles per degree was tested again as part of the randomized order.

To acclimate the subject to the stimulus every time spatial frequency was changed, subjects performed an initial method of adjustment and forced choice series (56 trials) for that spatial frequency at a vertical (90°) orientation – these data were also not included in the final analyses.

2.3.4. Data analyses

After the first half of measurements had been performed on an eye (run 1), interim data were fit with Gumbel psychometric functions (Kingdom & Prins, 2010) in MATLAB using the Palamedes (Prins & Kingdom, 2018) toolbox. The function is defined as:

$$P{F}_{Gumbel}\left(x,\alpha ,\beta \right)=1-exp\left(-{10}^{\beta \left(x-\alpha \right)}\right)$$ (1)

where

$$x\in \left(-\infty ,+\infty \right),\alpha \left(thershold\right)\in \left(-\infty ,+\infty \right),\beta \left(slope\right)\in \left(0,+\infty \right)$$

Each spatial frequency and orientation combination for each eye was inspected and if a subject had set the adjustment threshold such that they saw or missed most forced choice stimuli, stimuli (contrast levels) were added such that they spanned the range from 50% (guess rate) to 100% correct when the second half of data were collected. Contrast levels that were added in run 2 were repeated within that run such that they were also evaluated 16 times in total. Forced choice data from the two runs at the same spatial frequency and orientation were then pooled and fit with psychometric functions. On average, approximately 150 forced choice trials were performed for each spatial frequency and orientation combination. All psychometric functions were fit using maximum likelihood methods, assuming a lapse rate of 1% (0.01) and guess rate of 50% (0.5). Detailed description of the likelihood function used by the Palamedes toolbox can be found in Section 4.3.3.1 (page 86) of Kingdom and Prins (Kingdom & Prins, 2010).

2.4. Visual image quality metric

An elegant method of combining comprehensive optical measures (such as wavefront error) with measures of neural processing (such as neural contrast sensitivity) is by using a visual image quality metric, such as the visual Strehl ratio (VSX) (Thibos, Hong, Bradley, & Applegate, 2004). Change in the common (base 10) logarithm of VSX has been well correlated with changes in visual performance (Schoneveld, Pesudovs, & Coster, 2009) particularly with visual acuity (Ravikumar, Sarver, & Applegate, 2012). VSX has been shown predictive of subjective best focus (Marsack, Thibos, & Applegate, 2004; Martin, Vasudevan, Himebaugh, Bradley, & Thibos, 2011; Thibos et al., 2004) and used to predict (Hastings, Marsack, Nguyen, Cheng, & Applegate, 2017; Ravikumar, Benoit, Marsack, & Anderson, 2019) and evaluate (Hastings, Marsack, Thibos, & Applegate, 2018; Hastings, Zanayed, Nguyen, Applegate, & Marsack, 2020) ophthalmic corrections across modalities (Hastings et al., 2019).

VSX is calculated as the ratio of the volume of the two-dimensional point spread function (PSF) of an eye (determined from wavefront error at a specific pupil size (Goodman, 1996)) to the volume of a diffraction-limited PSF, where both PSFs are first weighted by the inverse Fourier transform of a neural contrast sensitivity function. Historically, the PSF of an eye was paired with a representative neural function from Campbell and Green (1965); instead, here we paired the PSF of each eye with the measured neural contrast sensitivity function of that eye.

Prior to use in VSX, neural contrast sensitivities at the six spatial frequencies (independently along each of the eight orientations) were fit with a double exponential function (Movshon & Kiorpes, 1988; Wensveen, Smith, Hung, & Harwerth, 2011), defined as

$$k_{ncs}{\left(w{k}_{sf}\right)}^{\alpha }\exp \left(-\beta f{k}_{sf}\right)$$ (2)

where f is spatial frequency, α and β affect the slopes of the low and high frequency portions of the fit respectfully, and k_sf and k_ncs control the positions along the spatial frequency and neural contrast sensitivity axes respectively. Two-dimensional radial interpolation between the functions for all eight orientations was then performed in MATLAB and the two-dimensional neural contrast sensitivity function was loaded into the metric calculation.

Using VSX, two analyses were performed to investigate the combined interactions of the measured optical and neural components. First, the PSF of the habitual wavefront error of each eye was weighted with the inverse Fourier transform of the two-dimensional neural contrast sensitivity function of that eye. This was done nine separate times where, in each case, the relative structure of the neural weighting function was maintained and was rotated relative to the PSF by a multiple of 22.5°, effectively ranging from 0° (habitual alignment) to 180° rotation. Across all rotations, a constant denominator was used in the metric (López-Gil et al., 2013; Sreenivasan, Aslakson, Kornaus, & Thibos, 2013). This rotation analysis is conceptually analogous to that of Artal et al. (2003, 2004). While they rotated the aberration structure of an eye and presumed the new retinal image to be processed by stable neural architecture, we rotated the measured neural contrast sensitivity function and held the optical PSF constant.

Second, a permutation test was performed where all possible ordered arrangements of the eight neural contrast sensitivity orientations were generated – this resulted in 40,320 (or 8!) conditions per eye. Each of the generated neural functions underwent a two-dimensional inverse Fourier transform and was used to weight the habitual optical PSF. The habitually aligned (measured) neural contrast sensitivity function was then ranked (as a percentile) among the 40,320 possible conditions.

3. Results

Sensitivities determined from Gumbel (log-Weibull) functions are reported because they provided maximum log-likelihood fit (Kingdom & Prins, 2010) in all typical eyes and for most spatial frequencies in eyes with keratoconus (better than cumulative normal or logistic functions that were also evaluated by Palamedes (Prins & Kingdom, 2018)). Gumbel functions are appropriate in principle because of the logarithmic manner that the visual system processes contrast (decelerating transducer function) (Kingdom & Prins, 2010). Results are compared with a model of neural contrast sensitivity calculated at the same retinal illuminance, which was shown representative of most neural contrast sensitivity literature of typical eyes (Hastings, Marsack, Thibos, & Applegate, 2020).

3.1. Typically-sighted (control) eyes

Neural contrast sensitivity functions of seven typically-sighted eyes (Section 2.1) measured using horizontally-orientated gratings were equivalent or slightly better than the reference model from literature defined for the same retinal illuminance (Fig. 1). This is a familiar method of plotting contrast sensitivity; readers might be less familiar with the polar representations of neural contrast sensitivity used for orientation-specific measurements, so Fig. 2. provides explanation for the figures that follow.

Fig. 1.

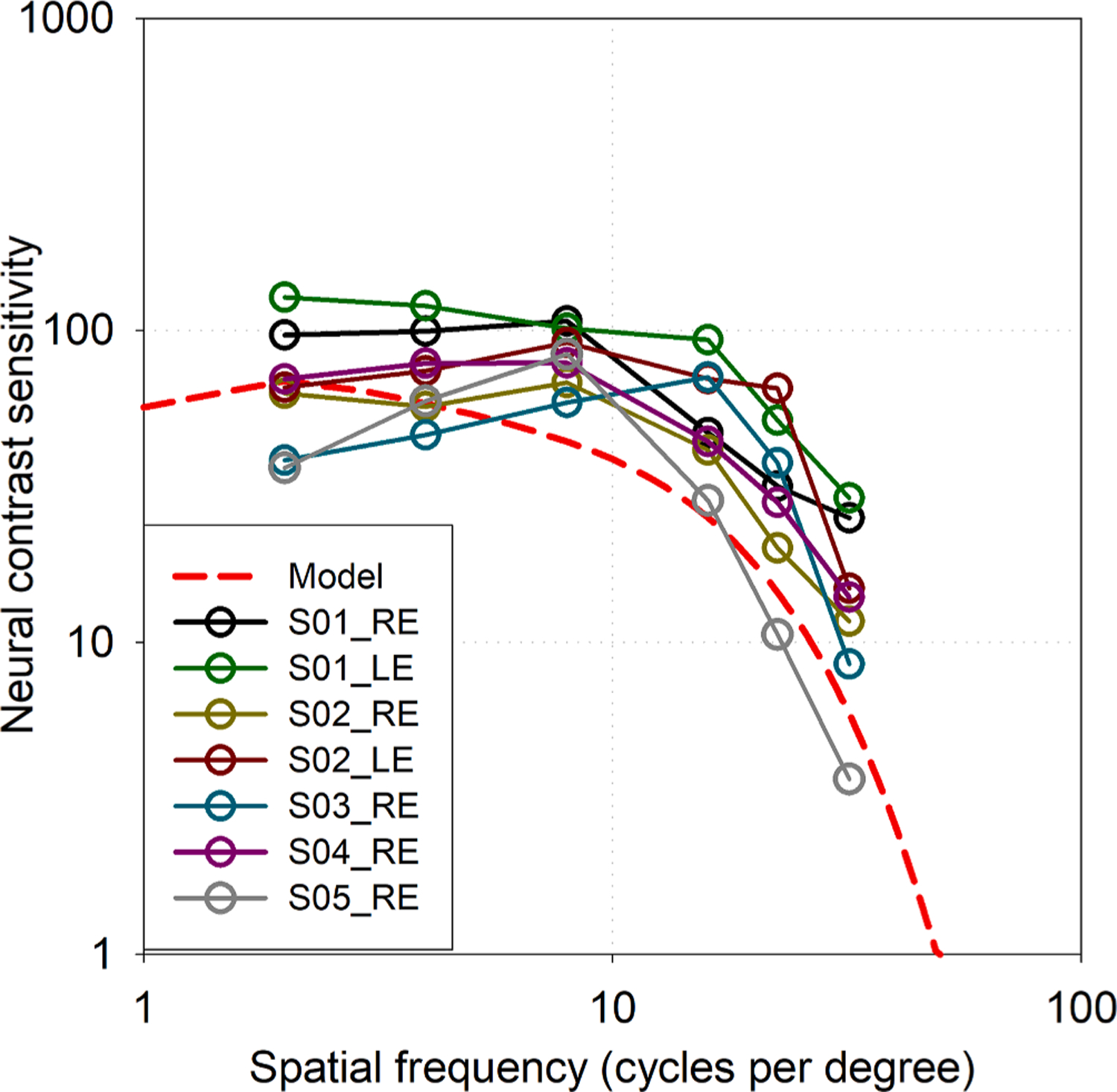
Neural contrast sensitivity of seven typically-sighted eyes measured at six spatial frequencies with horizontally-oriented gratings. Solid lines merely aid in tracking data from each individual. The dashed line is a representative model from literature of neural contrast sensitivity in typical eyes at the same retinal illuminance (Hastings et al., 2020).

Fig. 2.

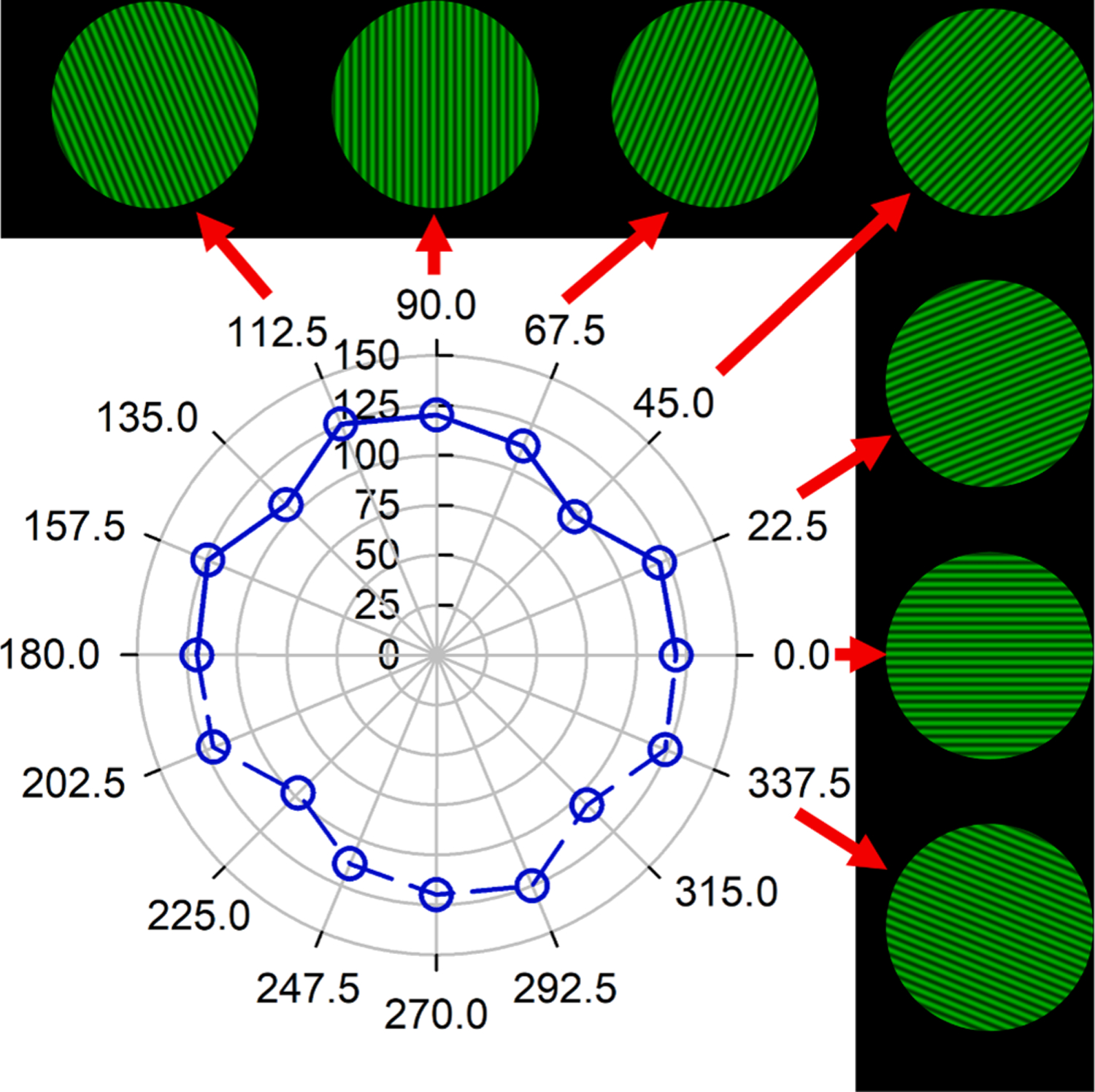
Explanation of the polar representation of orientation-specific (angular axis) neural contrast sensitivity (radial axis). In subsequent plots the angular labels are omitted for neatness. Grating orientation co-ordinates are labelled as perceived (subject-view, not clinician-view; illustrated by computer-simulated images here) and are the same for right and left eyes. Neural contrast sensitivity was measured at eight grating orientations connected by solid lines: 0° (horizontal), 22.5°, 45°, 67.5°, 90°, 112.5°, 135°, and 157.5°. Because grating targets have an azimuthal frequency of 1, a grating at a particular orientation is equivalent to one rotated through 180° (e.g. 90° is equivalent to 270°). In subsequent plots, neural contrast sensitivities are reflected and plotted through 360° to more easily appreciate rotational symmetries or elongations. Data shown here correspond to Fig. 3A, 4 cycles per degree, linear scale.

Four typical eyes completed measurements at all eight orientations; logarithmic and linear neural contrast sensitivities are plotted per spatial frequency in polar form for a representative eye (the left eye of S01) in Fig. 3A. This eye was chosen because it had 2.75 D of refractive astigmatism that was habitually well-corrected. Consequently, note the general rotational symmetry of the logarithmic sensitivities as well as the oblique effect (better sensitivity in cardinal than oblique meridians) (Campbell, Kulikowski, & Levinson, 1966; Mitchell, Freeman, & Westheimer, 1967) present in the linear sensitivities.

Fig. 3.

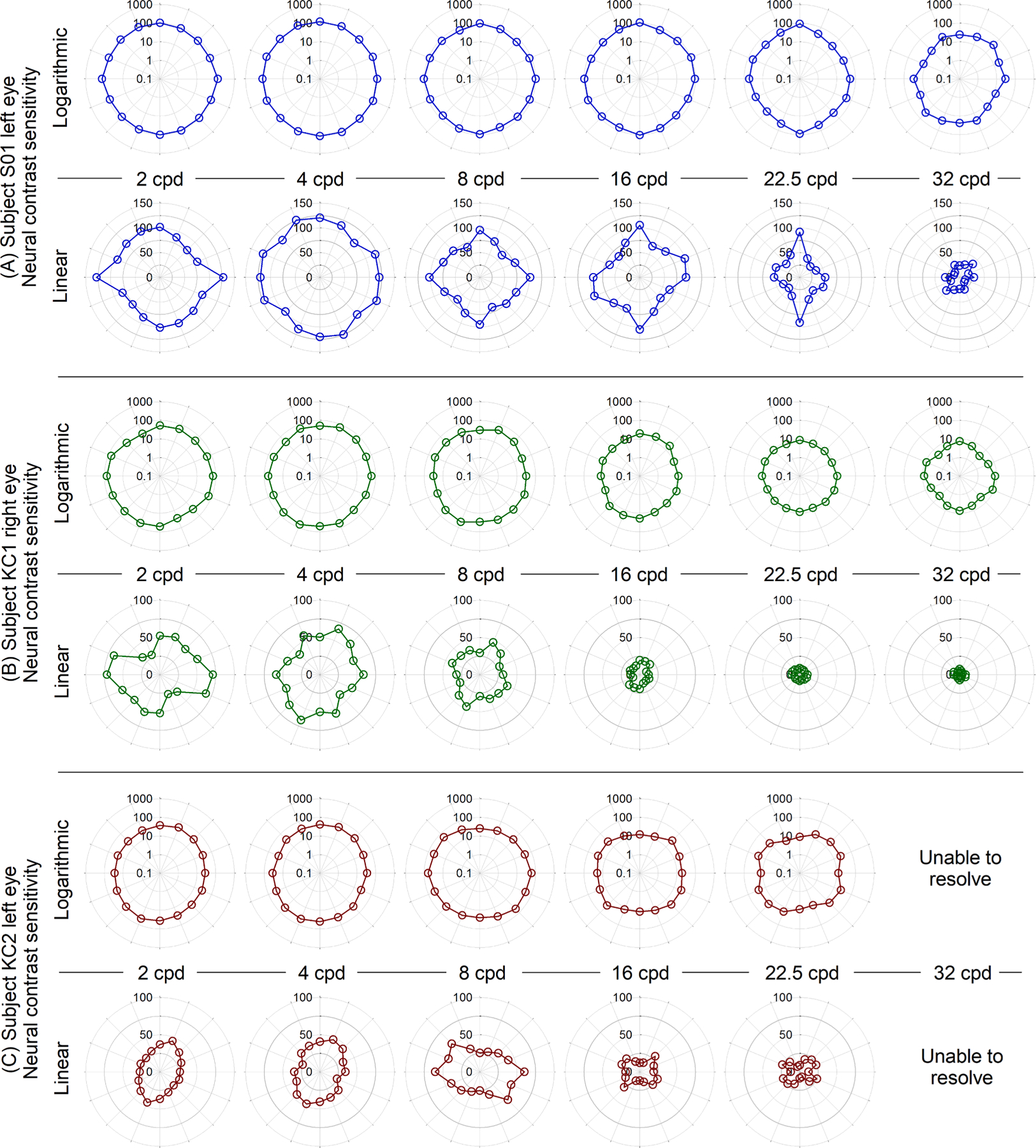
Neural contrast sensitivities at six spatial frequencies and eight orientations for (A) typically-sighted left eye of S01 that had 2.75 D of habitually well-corrected refractive astigmatism, (B) one of the mildest (right eye of KC1) and (C) one of the most severe keratoconus disease severities (left eye of KC2). (A) is representative of the typical eyes in that sensitivities were generally rotationally symmetric on a logarithmic scale, and a linear scale revealed the oblique effect. Note, linear scales in (B) and (C) differ from those in (A). Sensitivities of the eyes with keratoconus were worse than typical and did not show rotational or cardinal symmetry. The left eye of KC2 (C) was unable to resolve gratings at 32 cycles per degree. Angular scale increments are omitted for neatness but follow conventions defined in Fig. 2.

The polar plots of logarithmic neural contrast sensitivity (Fig. 3) were used for two additional analyses: First, the area enclosed by neural contrast sensitivities at all orientations (of each given spatial frequency) was calculated. This is analogous to the metric of area under the logarithmic contrast sensitivity function (Applegate, Hilmantel, & Howland, 1997). The logarithmic sensitivities through all 360° were converted from polar to rectangular co-ordinates and input into the polyarea MATLAB function, which essentially connects adjacent points with straight lines and calculates the area enclosed by the resultant polygon.

Second, to more quantitatively evaluate rotational symmetry, an ellipse was fit using a least-squares method to the polar representations (Fig. 3) of logarithmic neural contrast sensitivity. Rotational symmetry was quantified as the ratio of the minor and major diameters of those best-fit ellipses, where the ratio for a circle equals 1 and the lower the number (less than 1), the greater the asymmetry. This method was preferred over other circularity analyses that merely returned an RMS error because the orientation of greatest elongation (major axis orientation) was useful in examining correlations (Section 3.3). Across all spatial frequencies and all typical eyes, the mean ± SD of this rotational-symmetry metric was 0.93 ± 0.04 (median 0.93) (arbitrary units).

3.2. Eyes with keratoconus

Because the subjects with keratoconus were habitually wearing spectacles, they were adapted to elevated levels of higher-order aberration, ranging from 2.5× to above 6× the age- and pupil size-matched norms of typical eyes (Applegate, Donnelly III, Marsack, Koenig, & Pesudovs, 2007).

The six eyes with keratoconus displayed substantially different neural contrast sensitivities to the typical eyes. Sensitivities were worse than those of typical eyes and, even when plotted on logarithmic scales, sensitivities at most spatial frequencies were considerably cardinally- and rotationally-asymmetric. Neural contrast sensitivities for one of the mildest (right eye of subject KC1) and one of the most severe (left eye of subject KC2) disease severities are shown in Fig. 3B and C respectively. The left eye of subject KC2 was unable to see 32 cycles per degree (the subject reported not seeing many of the 32 cycles per degree constant stimuli, and all data were around the 50% guess rate). The responses of this eye to other spatial frequencies were reliable and it was the impression of the investigators that the subject was attentive, motivated, and trying their best.

The most basic summative comparison between the neural contrast sensitivity of typical eyes and those with keratoconus is to radially average (across all orientations per spatial frequency) and pool the eyes within each of the groups (Fig. 4A). While this precludes orientation-specific interpretations (such as those possible from Fig. 3), these plots distill 80 neural contrast sensitivity functions into one figure (32 typical and 48 keratoconus). Eyes with keratoconus were between 20% (lowest spatial frequencies) and 60% (highest spatial frequencies) worse than typical eyes (only the four typical eyes that completed all orientations were pooled here). Because some eyes with severe keratoconus were unable to resolve very high spatial frequencies (two and four eyes at 22.5 and 32 cycles per degree (cpd respectively), light green traces omit those eyes, while dark green include them with a sensitivity of zero.

Fig. 4.

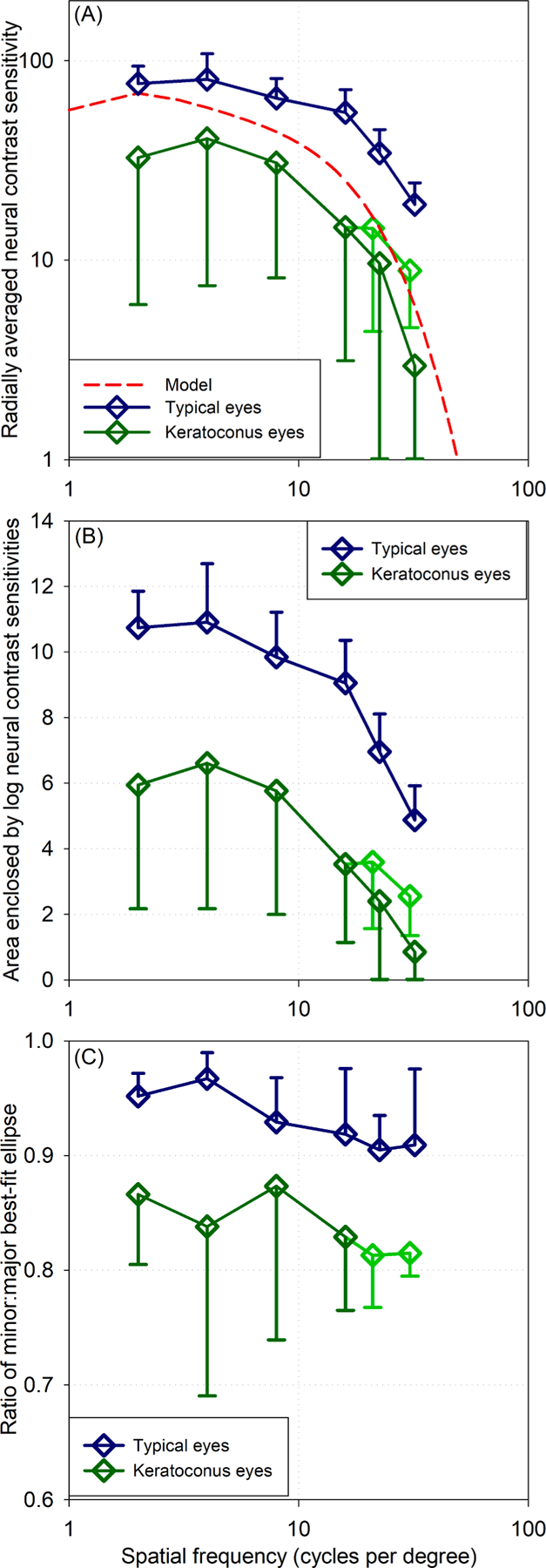
Comparison of neural contrast sensitivities of eyes with keratoconus and those of typical eyes. Error bars are ±1 SD. The four typical eyes that completed all orientations are pooled here. Light green traces omit eyes with severe keratoconus that could not resolve high spatial frequencies; dark green traces include those eyes with sensitivity of zero. (A) Radially averaged (across all orientations, hence the variability in eyes with keratoconus) mean neural contrast sensitivity. (B) Areas enclosed within polar representations (e.g. Fig. 3) of logarithmic neural contrast sensitivities through 360°. (C) Rotational symmetry of polar representations of neural contrast sensitivity expressed as the ratio of minor and major diameters of a best fit ellipse to the data (where a circle = 1 and the lower the value, the greater the asymmetry).

Areas enclosed by logarithmic neural contrast sensitivities as well as rotational symmetry were evaluated as was done for typical eyes. The areas of eyes with keratoconus were substantially smaller than those of typical eyes across all spatial frequencies (Fig. 4B). Rotational asymmetry generally worsened (Fig. 4C) with increasing spatial frequency and, at all spatial frequencies, neural contrast sensitivities of eyes with keratoconus were less rotationally symmetric (mean SD ± 0.84 ± 0.08; median 0.86) than typical eyes.

3.3. Synergy of asymmetric neural sensitivity with asymmetric optics

Relationships between the neural contrast sensitivity and optics of eyes with keratoconus can be investigated in many ways. For instance, at high spatial frequencies, the orientation of maximum elongation for the polar plots of neural contrast sensitivity correlated well with the orientation of residual coma through the habitual correction: for 16 cpd R² = 0.924, and for 22.5 cpd R² = 0.740 (coma orientation was calculated from Zernike terms C7 and C8). This is not surprising because coma is the dominant aberration in keratoconus (Kosaki et al., 2007; Pantanelli et al., 2007). However, despite being mathematically independent, individual aberration terms interact visually (Applegate, Marsack, Ramos, & Sarver, 2003; Applegate, Sarver, & Khemsara, 2002; Hu, Ravikumar, Hastings, & Marsack, 2020) and we prefer to emphasize methods such as visual image quality metrics (VSX), that account for the total visual interaction of all aberrations, rather than individual aberration terms.

It was first necessary to show that the mathematical rotation of the neural weighting function of VSX (inverse Fourier transform of a measured neural contrast sensitivity function) did not alter the shape or volume of the function. Indeed, although discretely resampled over a square grid by MATLAB, the difference due to rotation was always less than 0.75% of the weighting function volume (mean ± SD difference 0.44 ± 0.18%; median 0.43%).

Fig. 5 plots VSX results when the neural weighting function was rotated in 22.5° increments relative to the PSF, normalized to the case where the two functions were habitually aligned. Because both the neural functions and PSFs of typical eyes were more rotationally symmetric, rotating one relative to the other did not have a significant effect on the metric value. In contrast, most of the eyes with keratoconus showed substantial decreases in visual image quality (VSX) – some nearly a 20% decrease – when the neural function was rotated from its habitual orientation (and maintained the same relative shape).

Fig. 5.

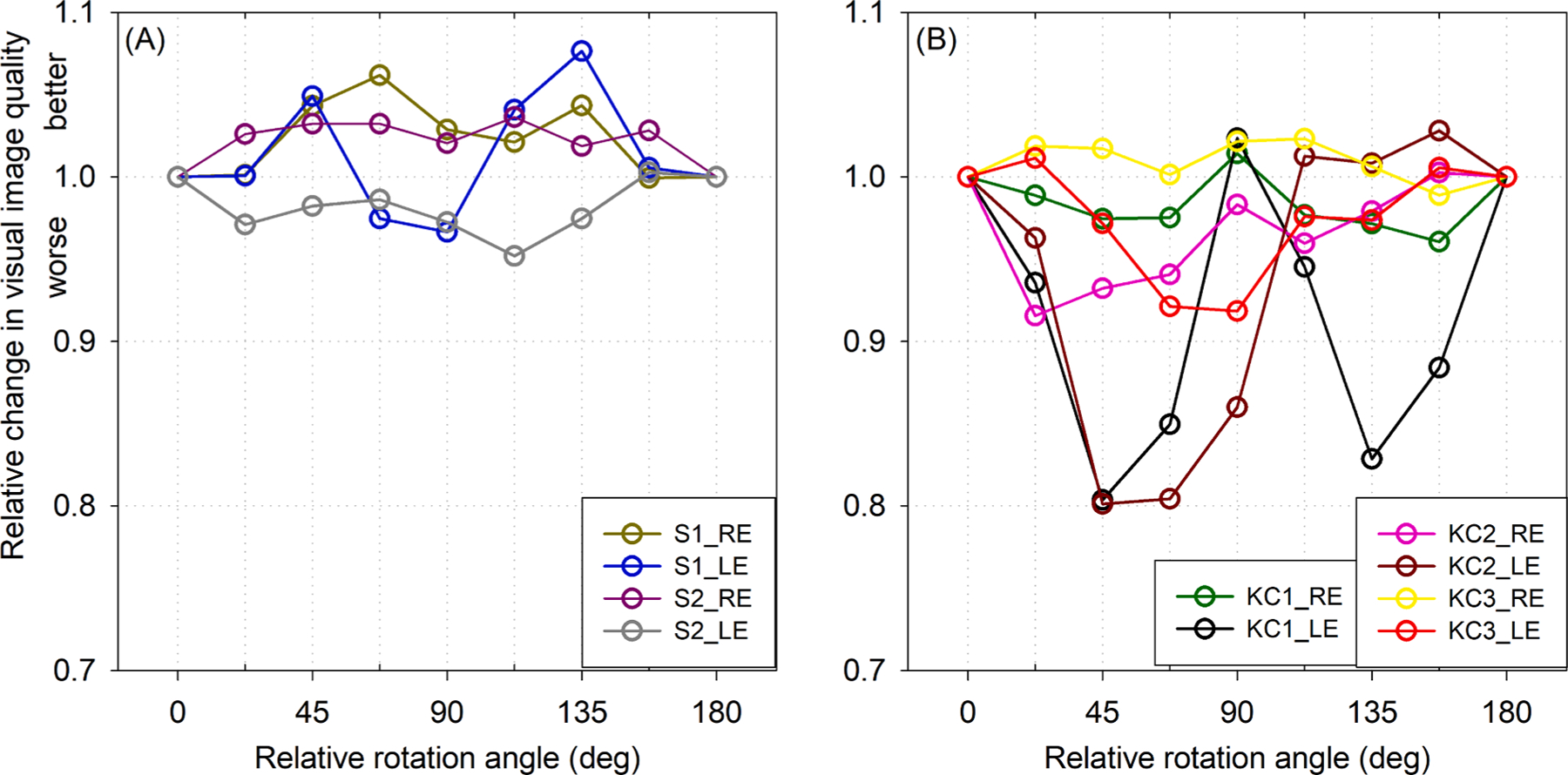
Relative change in visual image quality (VSX) with rotation of the measured neural function relative to the PSF, normalized to the habitually aligned orientation (0° and 180°). (A) Being more rotationally symmetric, neural weighting functions and PSFs of typical eyes were less affected by rotation of one relative to the other. (B) Most eyes with keratoconus (KC) showed substantial decreases in visual image quality when the neural function was rotated relative to the PSF. This suggests the asymmetric neural sensitivities of eyes with keratoconus are beneficially tuned relative to their asymmetric optics.

The VSX value associated with the habitually aligned (measured) neural contrast sensitivity function for each eye was ranked as a percentile of the 40,320 possible permutations of that neural function. If the measured neural function synergized with the optical PSF to provide the best visual image quality out of all possible permutations, the symbol (Fig. 6) would be plotted at 100; analogously, ranking at the 80th percentile means that 20% of the 40,320 permutations were better than the habitually aligned case and 80% were worse. The habitual neural contrast sensitivity functions for five of the six eyes with keratoconus synergized with the optics such that they ranked highly (generally around or above the 80th percentile) out of all permutations. In contrast, the habitual neural functions of most typical eyes seemed less specifically tuned to their optics and ranked much lower among all the possible permutations.

Fig. 6.

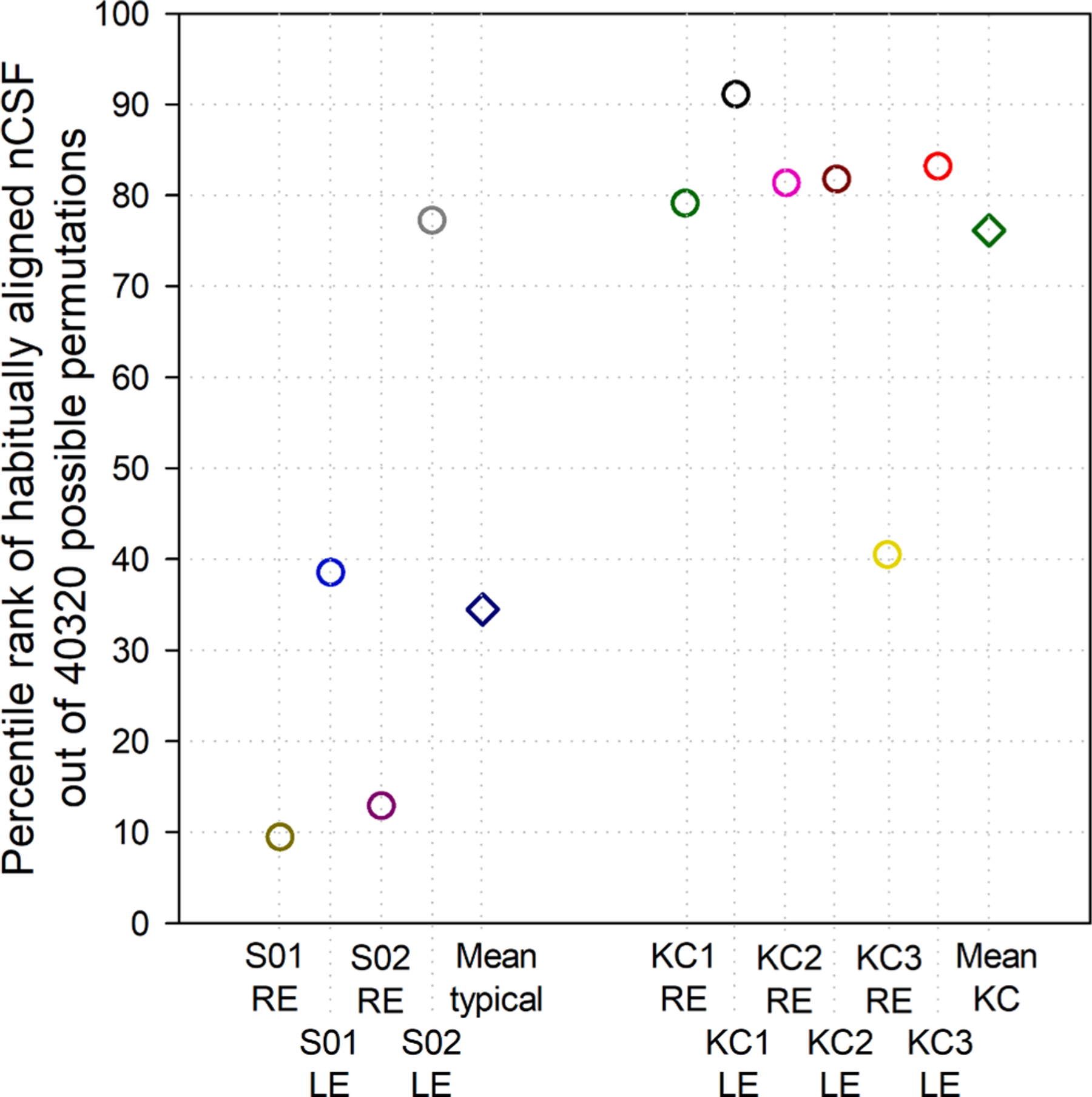
Percentile rank of VSX calculated using the habitually aligned (measured) neural contrast sensitivity function (nCSF) out of 40,320 possible permutations for each eye. For five of the six eyes with keratoconus (KC), the habitual nCSF was quite favorably suited to the optical PSF and ranked highly (around or above the 80th percentile). In contrast, the habitual neural functions of most typical eyes seemed less specifically tuned to their optics and ranked much lower out of all possible permutations.

4. Discussion

We sought to measure orientation-specific neural contrast sensitivities in eyes with keratoconus that habitually experienced rotationally asymmetric retinal image blur, and to investigate whether the characteristics of those neural sensitivities ultimately benefited the visual system in the presence of that habitual optical blur.

4.1. Methodology

The method of constant stimuli was employed, rather than a potentially more efficient predictive paradigm, because we could not assume that the eyes with keratoconus would follow the predefined parameters and priors of typical eyes. This decision was vindicated by how the sensitivities of eyes with keratoconus differed from those of typical eyes. Different parameters for predictive models have been defined, for instance, for the peripheral contrast sensitivity function of typical eyes (Rosen, Lundstrom, Venkataraman, Winter, & Unsbo, 2014), however making such modifications for keratoconus would imply existence of a normative function for keratoconus. This is challenging because of the spectrum of disease severities across individuals and the possible progression of an individual’s severity over time.

The habitual visual demands and environment of each subject were not factored into the interpretation of the neural contrast sensitivities because these are difficult to accurately gauge. Stimulation (or neglect) of particular spatial frequency and orientation channels during routine visual tasks or by the visual environment could influence performance. It has also been suggested that the brain is able to switch between different states of neural adaptation (Yehezkel, Sagi, Sterkin, Belkin, & Polat, 2010). For these reasons, we tried to only provide sufficient training so as to perform the task reliably. Excessive training would have added to the already substantial duration, but also might have masked any habitual tuning of the neural sensitivities by stimulating spatial frequency and orientation channels that were not habitually used. This has been shown possible with lengthy perceptual learning in keratoconus (Sabesan et al., 2017).

4.2. Typical eyes

Typical eyes were included to serve as controls and generally performed as expected. Performance of seven eyes with horizontal gratings was equivalent to, or better than, a model that unified most previous literature. The slightly better performance found here might be due to a more sophisticated design of the interferometry system. Indeed, the design of the system was based on Williams (1985a), who reported better performance than all other literature with which they compared.

Polar analyses of typical eyes agreed qualitatively with the sparse reports of neural contrast sensitivity at multiple orientations (Campbell et al., 1966; Mitchell et al., 1967); numerous differences (such as, in wavelength, retinal illuminance, and psychophysical paradigm) preclude quantitative comparisons. The example in Fig. 3A was selected because it was the only typical eye with substantial (habitually well-corrected) astigmatism (Vinas et al., 2012). While it was generally representative of the logarithmic rotational symmetry and linear oblique effect of the typical eyes, it also illustrated the tendency for contrast sensitivities to be generally symmetric at lower spatial frequencies and become increasingly asymmetric with increasing spatial frequency) (Cottaris, Jiang, Ding, Wandell, & Brainard, 2019).

4.3. Eyes with keratoconus

A goal of this study was to explore orientation-specific neural contrast sensitivities of eyes with keratoconus. As discussed in Section 4.1, establishing normative values of these measures for this population is challenging given the spectrum of aberrations and disease severities as well as the length and difficulty of the experimental task.

A few studies have used laser interferometry to measure neural contrast sensitivities along one meridian in eyes with keratoconus. Again, despite differences in methodology, the presented results agree qualitatively with the irregular (or notched) performance and reduced high spatial frequency sensitivities reported for one subject in Fig. 4 of Kayazawa et al. (1981) and two subjects in Fig. 14 of Kawara and Ohzu (1977). Studies using adaptive optics (Hrdina et al., 2018; Sabesan et al., 2017) made similar observations (in three and two eyes respectively), which they termed neural insufficiency, meaning, a loss of high spatial frequency performance caused by insufficient stimulation of those spatial frequency channels due to poor habitual optics. Under the assumption that these eyes experienced typical visual development, this study agrees with those ideas; that the visual neural system in keratoconus experiences an acquired deficit due to elevated residual levels of aberrations that habitually deteriorate the retinal image. As such, this adolescent and adult plasticity is distinct from the developmental causes attributed to meridional amblyopia in typical eyes (Mitchell, Freeman, Millodot, & Haegerstrom, 1973).

Combining the four analyses presented of neural contrast sensitivity in eyes with keratoconus (Figs. 3–6), one infers that these visual systems appear to emphasize neural processing in orientations that benefit vision while limiting neural sensitivity in meridians of poorer optical quality. One potential explanation for this process may be an attempt by the nervous systems to minimize the long-term cost of adaptation (Haak et al., 2014; Radhakrishnan et al., 2015) to orientation-specific blur (contrast loss). However, these visual systems seem unable to assign more neural resources to a particular meridian than in typical eyes, or to reallocate “unused” resources from one orientation to another. If this were possible, the areas enclosed by polar plots of neural contrast sensitivity would have been comparable across typical eyes and those with keratoconus, but this was not the case. Similarly, radially-averaged sensitivities were generally lower in keratoconus. This ceiling of malleability could be the result of experiencing typical visual development or a physiological limitation. The visual systems of the eyes with keratoconus seem to be able to attenuate sensitivity in certain meridians, thereby relatively accentuating others, however, these relative accentuations do not afford the visual system any absolute meridional super-ability over typical eyes.

4.4. Optical and neural synergy

Although we did not measure visual performance with the various combinations of the PSF and rotated or generated (permutation) neural weighting functions, we estimated visual performance using a surrogate visual image quality metric that has been well correlated with visual performance in typical eyes (Section 2.4) as well as those with keratoconus (Ravikumar, Marsack, Bedell, Shi, & Applegate, 2013; Schoneveld et al., 2009).

Using VSX, Figs. 5 and 6 suggest that the asymmetric neural functions of eyes with keratoconus mitigate the detrimental effects of their asymmetric optics, emphasizing meridians that are better in focus and being less sensitive to meridians with greater blur, which ultimately benefits visual image quality. This mitigation of poor optics is illustrated in Fig. 7. where (A) an optical PSF, (B) a neural-PSF (the inverse Fourier transform of the measured two-dimensional neural contrast sensitivity function), and (C) a weighted PSF (the inner product of (A) and (B); the numerator of the VSX metric) are shown for the right eye of subject KC01. The tuning of neural sensitivity to the aberration structure of eyes with keratoconus might help explain why the measured performance of these eyes can be better than would be predicted from their optical aberrations (Hastings et al., 2019).

Fig. 7.

Mitigation of detrimental effects of asymmetric optics by asymmetric neural sensitivities (please also see online animation). (A) Optical PSF (generated from wavefront error) (Goodman, 1996), (B) neural-PSF (inverse Fourier transform of the measured neural contrast sensitivity function), and (C) weighted PSF (inner product of (A) and (B); the numerator of VSX) for the right eye of subject KC1. Red arrows indicate directions with substantial optical blur in (A); these correspond to (darker) regions of lower sensitivity in (B). Conversely, (lighter) regions of greater sensitivity in (B), correspond to directions with less optical blur in (A); these are indicated by green arrows. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

4.5. Challenges and limitations

While the neural processing of the visual system is complex and has been modelled in great detail (Watson & Ahumada, 2005, 2008), the conceptually simpler measurement of neural contrast sensitivity has been a common summative functional measure of visual neural processing and captures beneficial behavioral effects such as fixational eye movements. Unfortunately, measurement of neural contrast sensitivity at multiple spatial frequencies and grating orientations is arduous and unlikely to be adopted clinically.

Laser interferometry has been a popular method of bypassing the optical components of an eye and stimulating the retina directly. While it has advantages over other methods, such as being unaffected by diffraction, which affects adaptive optics measurements, it is not possible to quantitatively evaluate residual aberrations with interferometry, which is possible with adaptive optics. Qualitatively, subjects with keratoconus reported the gratings to appear crisp and undistorted, which was unlike their best-corrected habitual percepts. Additionally, the myopia and astigmatism (and higher-order aberrations) of the control subjects were effectively bypassed by the system. Subjects were always aware of the orientation of the gratings (either through correct self-identification or after being told by the investigators), therefore no feedback was sought during the method of constant stimuli regarding the perceived orientation or spatial frequency. Thus, subject responses indicate the detection rather than the identification of the grating targets.

It remains to be investigated whether the directional attenuations in contrast (modulation) sensitivity observed here could serve to mitigate detrimental effects of poor phase transfer in those meridians. This is challenging to investigate with grating targets, which are insensitive to phase shifts, and remains for future investigation – even the discrimination of relative spatial phase using compound gratings has been shown to be driven by local contrast discrimination and not phase per se (Badcock, 1984).

Throughout this work, the assumption was made that at some point, the neural processing of eyes with keratoconus resembled that of typical eyes. To the best of our knowledge, there is no literature longitudinally characterizing individuals before the onset of keratoconus, through clinical disease diagnosis and progression. This remains an ambition of future work. Nevertheless, the assumption seems reasonable given that high spatial frequency performance has been restored in eyes with keratoconus using intensive perceptual learning (Sabesan et al., 2017), while similar learning in typical eyes did not cause much improvement (Rossi & Roorda, 2010). Whether such improvements could also accrue passively after prolonged stimulation by individualized wavefront-guided corrections (Hastings et al., 2019) also remains to be investigated.

Finally, the synergistic relations of optical and neural components were demonstrated here using a single PSF for each eye. Accommodative posture and pupil size can both alter the PSF (by changing the underlying aberration structure of the eye) and, by extension, can change the adapting retinal blur. That said, aberration changes during accommodation have been shown to be small relative to habitually uncorrected aberrations in typical eyes (Cheng et al., 2004). Given that habitually uncorrected aberrations (originating primarily from the anterior and posterior corneal surfaces) are much larger in eyes with keratoconus, we believe that different accommodated postures should have a comparatively minor effect on the characteristics of the PSF. Although physiological pupil constriction and dilation are not always concentric, at habitual physiological pupil diameters (which are greater than 2 mm (Watson & Yellott, 2012), where diffraction does not dominate the PSF), a change in pupil size predominantly scales all aberrations proportionally and should not markedly change the orientation or shape of the PSF. Thus, while being an instantaneous measure of a dynamic property, we believe the PSFs used here were reasonable characterizations of the habitual ocular optics.

5. Conclusions

Orientation-specific neural contrast sensitivity functions were measured using ophthalmic laser interferometry in eyes with keratoconus and typical control eyes. The eyes with keratoconus showed lower and less cardinally- and rotationally-symmetric sensitivities than typical eyes, especially at higher spatial frequencies. The asymmetries of the neural processing related beneficially to visual image quality, that is, they helped mitigate the detrimental effects of the asymmetric optical aberrations of the eyes with keratoconus.