Estimating the Causal Effect of Treatment Regimes for Organ Transplantation

Summary.

Patients awaiting cadaveric organ transplantation face a difficult decision if offered a low-quality organ: accept the organ or remain on the waiting list and hope a better organ is offered in the future. A dynamic treatment regime (DTR) for transplantation is a rule that determines whether a patient should decline an offered organ. Existing methods can estimate the effect of DTRs on survival outcomes, but these were developed for applications where treatment is abundantly available. For transplantation, organ availability is limited, and existing methods can only estimate the effect of a DTR assuming a single patient follows the DTR. We show for transplantation that the effect of a DTR depends on whether other patients follow the DTR. To estimate the anticipated survival if the entire population awaiting transplantation were to adopt a DTR, we develop a novel inverse probability weighted estimator (IPCW) which re-weights patients based on the probability of following their transplant history in the counterfactual world in which all patients follow the DTR of interest. We estimate this counterfactual probability using hot deck imputation to fill in data that is not observed for patients who are artificially censored by IPCW once they no longer follow the DTR of interest. We show via simulation that our proposed method has good finite-sample properties, and we apply our method to a lung transplantation observational registry.

1. Introduction

Determining an optimal rule or regime that dictates when a patient should start treatment is an important step in personalizing medicine (Cain et al., 2010). However, determining when a patient should undergo organ transplantation is challenging because the availability and the quality of cadaveric organs on any particular day are random and complex processes.

Because the number of people awaiting all solid organ transplants exceeds the number of available organs in the United States, the United Network for Organ Sharing (UNOS) maintains a national list used to orderly offer available cadaveric organs to potential recipients. For lung transplantation, for example, cadaveric lungs are offered based on the blood type of the donor and recipient, location, and the lung allocation score (LAS), a composite score of over a dozen patient characteristic that quantifies both patients’ risk of death on the waiting list and their anticipated survival benefit from lung transplantation (Egan and Kotloff, 2005). Importantly, although the order in which organs are offered is deterministic, who actually receives the offered organ is random as patients may decline the offer (see Colvin-Adams et al. (2012) for a description of the lung allocation policy).

Poor quality of the organ is one reason patients may decline an offer. For example, patients transplanted with a lung from donors over age 50 or with a history of smoking generally have poorer post-transplant survival than patients who received lungs from younger, healthier patients (Reyes et al., 2010). Although accepting low-quality lungs may lead to poor post-transplant prognosis, declining offered lungs and remaining on the waiting list is not without risk: the LAS system effectively allocates lungs to patients most in need, but it does not guarantee that a patient who declines an organ will be offered another if her condition deteriorates. The challenge is to weigh the potential survival benefit to be gained by forgoing a low-quality organ in favor of waiting for a high-quality organ against the risk that the patient may die before being offered a high-quality organ.

One way to improve a patient’s anticipated survival time is to use available observational data to estimate the anticipated survival if the patient were to adopt a particular strategy, or dynamic treatment regime (DTR), that dictates which organs should be avoided. Formally, a treatment regime is a function that maps a patient’s treatment and covariate history to an action to be taken (Moodie et al., 2007). Organ transplantation is an example of a multi-stage treatment regime because each time the patient is offered an organ, she must decide whether to accept it. For lung transplantation, one potential treatment regime for a patient would be “for any viable lung transplantation that is offered, decline the transplantation if the donor was ≥50 years old and the recipient’s LAS <50, otherwise accept the organ.” This regime is dynamic in the sense that it depends on the time-evolving characteristics (LAS) of the potential recipient.

Several statistical methods have been proposed to estimate the effect of complying with different DTRs on survival, both within the context of organ transplantation and in other therapeutic areas. The parametric G-formula has been proposed to estimate the counterfactual distribution of various outcomes if patients were to follow a particular DTR by developing a series of models for the waiting list and organ allocation process (e.g., patient arrivals to the waiting list, longitudinal changes in patient acuity and death while on the waiting list, organ arrivals and their quality, organ allocation, and post-transplant survival. See Robins and Hernán (2008) for a detailed exposition of parametric G-formula). This is the approach used in the Thoracic Simulated Allocation Model (Scientific Registry of Transplant Recipients, 2015) used by UNOS to evaluate different allocation policies However, this approach requires developing and correctly specifying a multitude of statistical models to obtain consistent estimators of the counterfactual survival.

Other approaches have sought to avoid modeling the entire waiting list and allocation process. Schaubel et al. (2006) introduced a sequential stratification method to test whether patients awaiting kidney transplantation should accept kidneys from expanded criteria donors versus remaining on the waiting list and possibly receiving a kidney from a traditional donor in the future (see also Schaubel et al. (2009)). This method can be easily applied to compare the effect of accepting versus declining other marginal organs. However, the approach does not permit direct comparisons of different rules for declining an available organ (e.g., declining all organs from donors over 50 years of age versus declining all organs from donors over 40 years of age). Other methods include inverse probability of compliance weighted (IPCW) Kaplan–Meier and Cox proportional hazards models (Hernán and Robins, 2006; Hernán et al., 2006; Cole and Hernán, 2008; Cain and Cole, 2009; Cain et al., 2010; Orellana et al., 2010). In these methods, a patient’s follow-up time is considered only while she is “compliant” with a regime of interest. When a patient becomes non-compliant with the regime, her follow-up time is artificially censored. Observations are weighted according to the inverse of probability of compliance to correct for the potential selection bias introduced by the artificial censoring (Hernán et al., 2006).

In organ transplantation, the anticipated survival for a given DTR depends on the quality and availability of organs, and these depend on the strategies that other patients follow to accept or decline an organ. This is conceptually similar, although not identical, to the “spillover” (Rubin, 1980) effect described in other contexts. The effect of an intervention that “spills over” is not limited to the individual who receives the intervention; this creates interference between subjects where the potential outcomes of one subject are affected by the treatment allocation another subject receives. An important limitation of sequential stratification and IPCW methods in transplantation applications is that they estimate the anticipated survival if a randomly selected patient were to follow a treatment regime, and all other patients made no changes to their behavior. This may be of great interest to particular patients, but it may have less public health relevance. A policy dictating that certain organs should be avoided would change the dynamics of the waiting list. For example, because patients would decline organs, the size of the waiting list may increase, thus reducing each patients probability of getting a transplant. A meaningful analysis would, therefore, estimate the causal effect of a treatment strategy on survival if the entire population of patients were to follow the strategy.

We demonstrate how we can estimate the causal effect of following a DTR, assuming that all patients are following the DTR of interest, by re-weighting patients based on the probability of following their transplant history in the counterfactual world in which all patients follow the DTR of interest. We investigate the finite-sample properties of our proposed estimators with a simulation study, and we demonstrate the method using lung transplantation data from UNOS.

2. Statistical Framework

To aid the reader, we have included a summary of the notation used throughout the manuscript in Web Appendix A.

2.1. Potential Outcomes

Consider a hypothetical population of patients eligible for organ transplantation. Let T*(∞) denote the survival time from listing (i.e., entry on the waiting list) if the patient, possibly contrary to fact, were to never receive a transplanted organ. Define T*(b, q) as a random patient’s counterfactual survival time from listing if the patient were to receive an organ b days after listing with organ characteristics $\mathit{q}\in \mathcal{Q}$, where $\mathcal{Q}$ is the set of all donor characteristics. Define X*(b) to be the covariates collected b days after listing for a random patient if she had remained untransplanted including whether or not the patient had previously died prior to time b. Throughout, we use the overbar notation to denote history, so that ${\overline{\mathit{X}}}^{\ast }(b)$ is the history of time-dependent covariates through b days after listing. Assume that X*(b) contains all the information that will be used to accept or decline organs or order patients on the waiting list in any counterfactual scenarios considered below. Because, we do not observe T*(b, q) for all possible b and q, these are known as potential outcomes. Let the set of potential outcomes for the ith patient be ${\mathcal{P}}_i=\{T_i^{\ast }(\infty ),T_i^{\ast }(b,\mathit{q}),{\mathit{X}}^{\ast }(b)\forall b\le T_i^{\ast }(\infty ),\mathit{q}\in \mathcal{Q})$.

Inferring the distribution of T*(b, q) is not of primary interest, because there may not be an organ offered to a particular patient b days after listing with characteristics q. Formally, define a transplant regime for whether or not to accept an organ b days after entering the waiting list as a function g which maps from ${\overline{\mathit{X}}}^{\ast }(b)$ and q to an indicator for whether or not the patient should decline an offered organ. We further elaborate of the regimes of interest in Section 2.3.

The quality and the availability of organs will vary depending on the rules other patients use to accept or decline organs and the order in which cadaveric organs are offered to potential recipients (i.e., the allocation rules). Therefore, when (or if) a patient receives a transplant while following regime g is random and depends on the regimes other patients use to accept or decline organs. We refer to this as “transplant regime spillover.” With this in mind, define T^(g,g′) to be the time a randomly selected patient would have lived if she followed regime g for declining offered organs and all other patients follow regime g′. Note that, in principle, each patient could follow a different regime, but for simplicity we only consider the scenario in which all other patients follow a common regime g′. We make precise what we mean by “all other patients follow regime g′” in Section 2.3. Finally, for the purposes of this article, we assume the allocation rules are the ones currently used and do not change and, therefore, do not index outcomes by the allocation rules used.

The goal of this analysis is to estimate Pr{T^(g,g′) ≥ t} for a given g, $g^{\prime }\in \mathcal{G}$, where $\mathcal{G}$ is the set of all possible treatment regimes. The distribution of T^(g,g′) is a mixture distribution of well-defined counterfactual survival times. If we let B^(g,g′) and Q^(g,g′) be, respectively, the random time from listing until organ transplantation and vector of organ characteristics for a random subject if she followed regime g for declining offered organs and all other patients follow regime g′, then f_T^(g,g′)(t), the density of T^(g,g′), is equal to

$$\begin{gathered} \sum _{\overline{\mathit{x}}(t)}{f}_{T^{\ast }(\infty )\mid {\overline{\mathit{X}}}^{\ast }(t)}\{t\mid \overline{\mathit{x}}(t)\}\left[\prod _{s=1}^{t}1-\sum _q{\rho }^{(g,g^{\prime })}\{s,\mathit{q}\mid \overline{\mathit{x}}(s)\}\right]f_{{\overline{\mathit{X}}}^{\ast }(t)}\{\overline{\mathit{x}}(t)\} \\ +\sum _{b=1}^t\sum _q\sum _{\overline{\mathit{x}}(b)}{f}_{T^{\ast }(b,q)\mid {\overline{\mathit{X}}}^{\ast }(b)}\{t\mid \overline{\mathit{x}}(b)\}\left[\prod _{s=1}^{b-1}1-\sum _q{\rho }^{(g,g^{\prime })}\{s,\mathit{q}\mid \overline{\mathit{x}}(s)\}\right] \\ \times {\rho }^{(g,g^{\prime })}\{b,\mathit{q}\mid \overline{\mathit{x}}(b)\}{f}_{{\overline{\mathit{X}}}^{\ast }(b)}\{\overline{\mathit{x}}(b)\}, \end{gathered}$$ (1)

where $f_{T^{\ast }(b,q)\mid {\overline{\mathit{X}}}^{\ast }(b)}$ is the conditional density of T*(b, q) given ${\overline{\mathit{X}}}^{\ast }(b)$, $f_{\overline{{\mathit{X}}^{\ast }}(t)}$ is the density of time-dependent covariates, and ${\rho }^{(g,g^{\prime })}\{b,\mathit{q}\mid \overline{\mathit{x}}(b)\}$ is the probability a patient receives a transplant b days after listing with organ characteristics q given she is untransplanted b−1 days after listing with covariate history $\overline{\mathit{x}}(b)$, and given that she follows regime g while all others follow regime g′. In the preceding, for simplicity of exposition, we have assumed that the organ and patient characteristics are discrete, but equation (1) is easily generalized to allow for continuous characteristics. The first term in equation (1) gives the conditional distribution of the survival time assuming the subject remains untransplanted weighted by the likelihood of remaining untransplanted given covariates. The second term gives the survival distribution given a subject was transplanted b days after listing with characteristics q weighted by the probability of being transplanted then with those characteristics.

The derivation of the density of T^(g,g′) given in equation (1) is similar to the density of following a probabilistic DTR given in Murphy et al. (2001). However, the key difference is that the probability of initiating treatment depends on the treatment regime other patients follow. “Spillover” typically refers to situations in which the distribution of well-defined potential outcomes depends on the treatment assignment of others, which is not the case here. However, we refer to this as transplant regime spillover.

2.2. Observed Data

Assume that we observe a cohort of n patients listed for organ transplantation over a period of p days. Let T_i be the observed time from entering the waiting list to death for the ith patient, and X_ij be the vector of covariates collected on the ith patient on the jth study day, j = 1, …, p, including whether or not the subject was eligible (i.e., active on the waiting list) for transplantation. We assume that after transplantation no additional covariate information is collected. For the purposes of this analysis, we will assume that death information and transplant information are recorded daily as they are in the UNOS registry and that the temporal ordering of events on a given day is (1) time-dependent covariates are updated, (2) organs are assigned to patients and are transplanted, and then (3) patients die. Define N_ij = I(L_i + T_i = j) and Y_ij = I(L_i + T_i ≥ j) to be the indicators for whether or not the ith patient died on the jth day of the study and whether the ith patient was at risk for death on the jth day of the study, respectively, where L_i is the day of the study subject i entered the waiting list. In this study, because we use national death registries to monitor patients’ vital statuses, all patients are followed until death or study day p so that N_ij and Y_ij are observed (i.e., not subject to right-censoring) for all patients for j = 1, …, p.

Let S_j be the number of organs available for transplant on the jth day of the study, let Q_jk be the characteristics of the kth organ transplanted on the jth day, and let A_ijk be the indicator for whether or not the ith person received the kth organ on study day j. Define the filtration E_ijk = { (A_ilm, Q_lm, X_il)_{l=1,…,j−1;m=1,…,Sl} , X_ij, S_j, (A_ijm, Q_jm)_{m=1,…,k−1} , Q_jk, }. That is, E_ijk is the collection of all information on the ith subject at the time of the kth transplant on the jth day but excluding whether the ith patient actually receives the kth organ. Similarly define E_·jk to be the collection of information on all subjects i = 1, … , n prior to assigning the kth organ on the jth study day.

Given the data in the observational registry, one can determine the order in which patients were offered the organ. Let R_ijk be the rank of the ith patient on the waiting list for the kth organ on the jth day of the study, and assume smaller R_ijk indicates higher rank, that is, R_ijk < R_{i′ jk} implies that patient i will be offered the kth organ before patient i′. Let $O_{ijk}={\prod }_{i^{\prime }:R_{i^{\prime }jk}<R_{ijk}}1-A_{i^{\prime }jk}$ be the indicator that the ith subject is offered the kth organ on the jth day.

2.3. Transplant Regimes

Because transplantation involves many logistical and clinical considerations (e.g., crossmatching, physical examination of the organ anatomy), it is not practical to dictate that a patient/physician must accept an offered organ. For the same reason, we do not attempt to infer the distribution of survival times under a regime that dictates when a patient should receive an organ, for example, “receive a transplant the first day LAS > 50,” because an organ may not be available on that particular day. Instead, we are interested in transplant regimes that dictate whether or not an available organ should be declined based on the organ quality and patient characteristics. We colloquially refer to these organs as “low-quality” organs. Let D_ijk (g, E_ijk) be an indicator for whether or not the kth organ on day j should be avoided by patient i under regime g based on the organ and patient characteristics. To be precise, if the ith patient is “following” or “compliant with” regime g, then the probability of accepting the organ is ${\pi }_{ijk}^{A(g)}(E_{ijk})={\pi }_{ijk}^{A(\varnothing )}(E_{ijk})\left\{1-D_{ijk}(g,E_{ijk})\right\}$, where ${\pi }_{ijk}^{A(\varnothing )}(E_{ijk})$ is the probability of accepting the organ if no changes are made to her organ acceptance policy. We will frequently refer to the transplant regime where patients make no changes to their propensity to accept or decline organs, that is, they accept or decline organs with the same probability that they accept or decline organs in the observed data. We refer to this regime as ∅.

Similarly, let ${\pi }_{ijk}^{O(g,g^{\prime })}(E_{\cdot jk})$ denote the conditional probability given the observed data that the ith patient is offered the kth organ on day j given that she is following regime g and all other patients are following regime g′. Note that ${\pi }_{ijk}^{O(g,g^{\prime })}(E_{\cdot jk})$ is the probability that all patients who would have ranked higher than the ith decline the organ in the counterfactual world in which they are all following regime g′. Finally, let ${\pi }_{ijk}^{(g,g^{\prime })}(a_{ijk},E_{\cdot jk})$ be the probability that ith person receives and does not receive if a_ijk = 1 and a_ijk = 0, respectively, the kth available organ on the jth day given all the observed information up until the time of assigning that organ, assuming the ith patient is following regime g and all other patients are following regime g′. Note that

$$\begin{gathered} {\pi }_{ijk}^{(g,g^{\prime })}(a_{ijk},E_{\cdot jk})=a_{ijk}{\pi }_{ijk}^{A(g)}(E_{ijk}){\pi }_{ijk}^{O(g,g^{\prime })}(E_{\cdot jk}) \\ +(1-a_{ijk})\{1-{\pi }_{ijk}^{A(g)}(E_{ijk}){\pi }_{ijk}^{O(g,g^{\prime })}(E_{\cdot jk})\}. \end{gathered}$$ (2)

Similarly, define ${\overline{\pi }}_{ij}^{(g,g^{\prime })}({\overline{a}}_{ij},{\overline{E}}_{\cdot j{S}_j})={\prod }_{m=1}^j{\prod }_{k=1}^{S_m}{\pi }_{imk}^{(g,g^{\prime })}(a_{imk},E_{\cdot mk})$, the probability that the ith patient has her treatment history through study day j given that she is following regime g and all other patients follow regime g′.

2.4. Identifying Assumptions

To estimate the causal effect of a treatment regime on the survival probability t days after entering the waiting list, we must make the following assumptions to relate the observed data to the distribution of the potential outcomes (Robins and Hernán, 2008).

We assume that $1-{\pi }_{ijk}^{A(g)}(E_{\cdot jk})>0\forall i,j,k$. That is, there is some non-zero probability that a patient will remain compliant with a particular regime g of the form discussed in Section 2.3. This is known as the positivity assumption.

We make the so-called sequential ignorability or no unmeasured confounders assumption that the probability of receiving an organ at any time depends only on the observed data up until that time and not additionally on any potential outcomes. This assumption implies A_ijk is conditionally independent of $\mathcal{P}$ given E_·jk for all i = 1, …, n, j = 1, …, p, and k = 1, …, S_j, where $\mathcal{P}=({\mathcal{P}}_1,\dots ,{\mathcal{P}}_n)$.

We assume that $T_i=T_i^{\ast }(t,\mathit{q})$ if ${\sum }_{k=1}^{S_{L_i+t}}{A}_{i,L_i+t,k}=1$ and ${\sum }_{k=1}^{S_{L_i+t}}{A}_{i,L_i+t,k}{\mathit{Q}}_{L_i+t,k}=\mathit{q}$, and similarly $T_i=T_i^{\ast }(\infty )$ if ${\sum }_{m=1}^p{\sum }_{k=1}^{S_m}{A}_{imk}=0$. This assumption is referred to as the consistency assumption.

Finally, we assume that the availability and the characteristics of cadaveric organs and when patients enter the waiting list does not depend on the characteristics of the patients on the waiting list or the regimes that patients use to accept or decline organs. We refer to this as the waiting list stability assumption.

3. Class of Estimators

To estimate S_r (g, g′), the survival probability r days after entering the waiting list for a random patient who follows regime g while all other patients follow regime g′, we first estimate ${\lambda }_t^{(g,g^{\prime })}$, the discrete-time hazard of death t days after entering the waiting list, t = 1, …, r, for a randomly selected patient if she were to following regime g and all other patients followed regime g′. Assuming for now that ${\overline{\pi }}_{ij}^{(\varnothing ,\varnothing )}({\overline{A}}_{ij},{\overline{E}}_{\cdot j{S}_j})$ and ${\overline{\pi }}_{ij}^{(g,g^{\prime })}({\overline{A}}_{ij},{\overline{E}}_{\cdot j{S}_j})$ are known, we can estimate ${\lambda }_t^{(g,g^{\prime })}$ by solving the estimating equation

$$\sum _{j=1}^p\sum _{i=1}^n\frac{{\overline{\pi }}_{ij}^{(g,g^{\prime })}({\overline{A}}_{ij},{\overline{E}}_{\cdot j{S}_j})}{{\overline{\pi }}_{ij}^{(\varnothing ,\varnothing )}({\overline{A}}_{ij},{\overline{E}}_{\cdot j{S}_j})}\left\{N_{ij}-Y_{ij}{\lambda }_t^{(g,g^{\prime })}\right\}I(j-L_i=t)=0,$$ (3)

where we remind the reader that j indexes the study day but t indexes the day since listing. The vector of estimated discrete-time hazards ${\widehat{\lambda }}^{(g,g^{\prime })}={\left\{{\widehat{\lambda }}_1^{(g,g^{\prime })},\dots ,{\widehat{\lambda }}_r^{(g,g^{\prime })}\right\}}^T$ is the solution to the corresponding r-dimensional estimating equation. The survival probability $S_r^{(g,g^{\prime })}$ can easily be estimated as ${\widehat{S}}_r^{(g,g^{\prime })}={\prod }_{t\le r}\left\{1-{\widehat{\lambda }}_t^{(g,g^{\prime })}\right\}$, which is equivalent to a weighted Kaplan–Meier survival estimator. Note that the IPCWs, $\frac{{\overline{\pi }}_{ij}^{(g,g^{\prime })}({\overline{A}}_{ij},{\overline{E}}_{\cdot j{S}_j})}{{\overline{\pi }}_{ij}^{(\varnothing ,\varnothing )}({\overline{A}}_{ij},{\overline{E}}_{\cdot j{S}_j})}$, are a ratio of the probability of observing the transplant history under regime g while all others follow regime g′ to the probability of the observed treatment history for the ith patient. The purpose of the numerator of these weights is not stabilization (i.e., reduction in variance). Instead the numerator of the weights allows us to estimate a different causal survival distribution; one which corresponds to the regime other subjects on the waiting list adopt. This estimator could be adapted using inverse probability of censoring weights if we considered an outcome other than overall survival in which subjects may be lost to follow-up; we discuss this in the Web Appendix B.

We have implicitly argued that the estimating function is not the sum of independent observations, because individuals’ actions on the waiting list impact others. However, if we are willing to assume that the waiting list “turns over” after m individuals (i.e., none of the same individuals remain on the waiting list after m have been added, a reasonable assumption for this acutely ill population), then, we prove in Web Appendix B under standard regularity conditions (DasGupta, 2008), ${\widehat{\lambda }}^{(g,g^{\prime })}$ is a consistent and asymptotically normal estimator for λ^{(g, g′)} as n → ∞.

3.1. Estimating the Denominator of the Inverse Probability Weights

In most applications, the numerator and denominator of the weights are unknown and must be estimated. We discussed in Section 2.3 that the probability a particular patient is offered an organ depends on the probability that all others who rank higher on the waiting list decline the organ. The denominator of the weights, however, is just the probability of observed treatment history assuming all patients follow regime ∅ (the regime in which all patients make no change in their propensity to accept or decline organs). To estimate this probability, we only require a model for the probability that patients accept organs given that they are offered based on the observed data. Although many models are possible, a natural model for accepting an organ given the organ is offered is the logistic model

$${\pi }_{ijk}^{A(\varnothing )}(E_{ijk};\phi )={\left\{1+e^{-\left({\phi }_0+{\phi }_1^T{\overline{\mathit{X}}}_{ij}+{\phi }_2^T{\overline{\mathit{X}}}_{ij}{\mathit{Q}}_{jk}+{\phi }_3^T{\mathit{Q}}_{jk}\right)}\right\}}^{-1},$$ (4)

where ${\overline{\mathit{X}}}_{ij}{\mathit{Q}}_{jk}$ is a vector of donor-patient interaction characteristics. The estimated coefficient vector $\widehat{\phi }=({\widehat{\phi }}_0,{\widehat{\phi }}_1^T,{\widehat{\phi }}_2^T,{\widehat{\phi }}_3^T{)}^T$ can now be used to estimate ${\pi }_{ijk}^{A(g)}(E_{ijk};\phi )$ and ${\pi }_{ijk}^{O(\varnothing ,\varnothing )}(E_{\cdot jk};\phi )={\prod }_{i:R_{i^{\prime }jk}<R_{ijk}}\{(1-{\pi }_{i^{\prime }jk}^{A(\varnothing )}(E_{i^{\prime }jk};\phi )$ in equation (2) to estimate the denominator of the weights in equation (3), that is, ${\overline{\pi }}_{ij}^{(\varnothing ,\varnothing )}\left({\overline{A}}_{ij},{\overline{E}}_{\cdot j{S}_j}\right)$.

3.2. Estimating the Numerator of the Inverse Probability Weights

To estimate S_r(g, ∅), estimating the numerator of the weights is straightforward. In this case, ${\pi }_{ijk}^{(g,\varnothing )}(a_{ijk},E_{jk})=a_{ijk}{\pi }_{ijk}^{A(g)}(E_{ijk}){\pi }_{ijk}^{O(g,\varnothing )}(E_{\cdot jk})+(1-a_{ijk})\left\{1-{\pi }_{ijk}^{A(g)}(E_{ijk}){\pi }_{ijk}^{O(g,\varnothing )}(E_{\cdot jk})\right\}$. Although we wrote ${\pi }_{ijk}^{O(g,\varnothing )}$ for consistent notation, note that if subject i is compliant with regime g through study day j, then ${\pi }_{ijk}^{O(g,\varnothing )}(E_{\cdot jk})={\pi }_{ijk}^{O(\varnothing ,\varnothing )}(E_{\cdot jk})$ (the conditional probability of being offered an organ depends on the actions of other patients, all of whom are following regime ∅) which can be is easily estimated as described above. Similarly, ${\widehat{\pi }}_{ijk}^{A(g)}(E_{ijk})={\pi }_{ijk}^{A(\varnothing )}(E_{ijk};\widehat{\phi })\left\{1-D_{ijk}(g,E_{ijk})\right\}$.

When g′ ≠ ∅, estimating the numerator of the weights is more challenging. Although estimating ${\pi }_{ijk}^{A(g)}$ using Model 4 is straightforward, if all patients are following regime g′, we can no longer use ${\prod }_{i:R_{i^{\prime }jk}<R_{ijk}}\{(1-{\pi }_{i^{\prime }jk}^{A(g^{\prime })}(E_{i^{\prime }jk};\widehat{\phi })\}$ to estimate the probability of being offered an organ, because the number of patients on the waiting list and their characteristics at the time the organ is offered would be different than in the observed data. That is, in the counterfactual world in which patients follow regime g′ the ordering of patients to be offered an available organ would be different from the rank, R_ijk, in the observed data.

Note that ${\pi }_{ijk}^{O(g,g^{\prime })}(E_{\cdot jk})=E\{{\pi }_{ijk}^{O(g,g^{\prime })}(E_{\cdot jk}^{(g,g^{\prime })},E_{\cdot jk})\mid E_{\cdot jk}\}=E\{{\pi }_{ijk}^{O(g,g^{\prime })}(E_{\cdot jk}^{(g,g^{\prime })})\mid E_{\cdot jk}\}$, where $E_{\cdot jk}^{(g,g^{\prime })}$ is the data we would have observed up to the allocation of the kth organ on the jth day had all patients followed regime g′ and the ith patient followed regime g, and ${\pi }_{ijk}^{O(g,g^{\prime })}(E_{\cdot jk}^{(g,g^{\prime })})$ is the probability the ith subject is offered the kth organ on the jth day given the counterfactual data. Note that given $E_{\cdot jk}^{(g,g^{\prime })}$, calculation of the probability of being offered an organ is straightforward and would follow a similar approach to that outlined for the observed data.

However, analytically evaluating the outer expectation is challenging. Therefore, we propose to estimate this quantity using Monte Carlo integration/summation. To do so, we must be able to simulate $E_{\cdot jk}^{(g,g^{\prime })}$ given the observed data E_·jk. We describe how one can simulate such a hypothetical dataset with minimal assumptions.

Given E_·jk, patient and organ arrival times and their characteristics are fixed. To allocate organs, we assume that if in the observed data O_ijk = 0 (i.e., we do not know whether or not the ith subject would have accepted the kth organ on the jth day) patients accept offered organs in the hypothetical dataset with probability $\left\{1-D_{ijk}(g,E_{ijk}^{(g,g^{\prime })})\right\}\times {\pi }_{ijk}^{A(\varnothing )}(E_{ijk}^{(g,g^{\prime })})$ for the ith subject and with probability $\left\{1-D_{ijk}(g^{\prime },E_{ijk}^{(g,g^{\prime })})\right\}{\pi }_{ijk}^{A(\varnothing )}(E_{ijk}^{(g,g^{\prime })})$ for all others. If in the observed data the patient was offered the organ, then in the hypothetical dataset the patient accepts the organ with probability 1 if A_ijk = 1 and with probability 0 if A_ijk = 0 (i.e., if in the observed data we know a patient accepted or declined an organ than this is preserved in the simulated dataset).

Similarly, because we condition on E_·jk, patients in the simulated dataset begin with the same covariate trajectory as in the observed dataset. However, it is possible for a subject in the observed dataset to remain on the waiting list in the simulated dataset longer than in the observed one. In such a case, we need to simulate their covariate trajectory until death or transplant. Rather than postulate a parametric model for X_ij given ${\overline{\mathit{X}}}_{i{j}^{\prime }}$, ${\overline{A}}_{i{j}^{\prime }{S}_{j^{\prime }}}=0$ (for j′ < j), we use hot deck imputation. When discussing the imputation, we avoid the “donor-recipient” verbiage common in the literature (for example, see Andridge and Little (2010)), because that can obviously create confusion here. We refer to an individual whose values are to be filled in as the “borrower” and the pool of potential patients whose values could be used as the “lenders.”

If the ith patient was transplanted on the jth day in the observed data, the data for the eligible lenders is the set

$$\begin{gathered} ([\{{\mathit{X}}_{i^{\prime }{j}^{\prime }},{\mathit{X}}_{i^{\prime }(j^{\prime }+1)},\dots \},\left\{(A_{i^{\prime }{j}^{\prime }k}{)}_{k=1,\dots ,S_{j^{\prime }}},(A_{i^{\prime }(j^{\prime }+1),k}{)}_{k=1,\dots ,S_{(j^{\prime }+1)}},\dots \right\}\phantom{]}\phantom{)}, \\ \phantom{(}{\phantom{[}{T}_{i^{\prime }}]}_{i^{\prime }\ne i}:j-L_i=j^{\prime }-L_{i^{\prime }},), \end{gathered}$$

that is, the potential data are the covariate history, transplantation history, and death time for each lender, taken from the time where the lender had been on the waiting list for as long as the borrower, but not necessarily concurrently. The lender can be selected as the patient whose X_i′ minimizes (X_ij − X_{i′ j′})^T (X_ij − X_{i′ j′}) or some other distance metric for multi-dimensional covariates (including past history of patient covariates). The borrower’s information from time j is replaced by the lender’s data beginning at time j′. If the lender received a transplant, the process may be repeated.

Typically, in Monte Carlo integration one would simulate several datasets and average the integrand across them to estimate ${\pi }_{ijk}^{O(g,g^{\prime })}(E_{\cdot jk})$. However, in this application, simulating such a dataset can be computationally intensive when combined with resampling methods for standard error estimation, and we have found that simulating a single dataset to estimate ${\pi }_{ijk}^{O(g,g^{\prime })}(E_{\cdot jk})$ for all i, j, and k is sufficient. Note that to estimate ${\pi }_{ijk}^{O(g,g^{\prime })}(E_{\cdot jk})$ we do not need to simulate post-transplant outcomes.

Because estimating the numerator of the weights is a complicated function of the observed data, we recommend estimating the standard error of ${\widehat{S}}_r^{(g,g^{\prime })}$ using the nonparametric bootstrap (Efron, 1979).

4. Defining Lower Quality Organs

In some applications the definition of a “low-quality” organ may be defined a priori. For example, we may define an organ as low-quality if the donor has smoked more than 20 pack-years. Here, however, we consider treatment regimes of the type “decline all organs in the lowest d percentile of donor quality.” In this scenario we define “low-quality” as a continuous measure depending on donor and donor-recipient interaction characteristics, and we estimate those combinations of characteristics that lead to poorer survival. We can then estimate the anticipated survival if a patient were to avoid organs below a certain threshold of the donor quality score. We assume that, given ${\overline{\mathit{X}}}^{\ast }(b)$, the distribution of $T^{\ast }(b,\mathit{q})-b$ (the potential residual lifetime after transplantation) follows a discrete-time proportional hazards model. That is, $\text{Pr}\left\{T^{\ast }(b,\mathit{q})-b=t\right\}={\lambda }_t^{PT}\text{exp}\left\{{\xi }_1^T{\overline{\mathit{X}}}^{\ast }(b)+{\xi }_2^T\mathit{Q}+{\xi }_3^T{\overline{\mathit{X}}}^{\ast }(b)\mathit{Q}\right\}$, where ${\lambda }_t^{PT}$ is the baseline post-transplantation discrete-time hazard of death t days after transplantation. We can estimate $\xi ={\left({\xi }_1^T,{\xi }_2^T,{\xi }_3^T\right)}^T$ using the observed data. For an organ with characteristics q and a potential recipient with characteristics ${\overline{\mathit{X}}}^{\ast }(b)$, we define the organ quality score as $-\left\{{\xi }_2^T\mathit{Q}+{\xi }_3^T{\overline{X}}^{\ast }(b)\mathit{Q}\right\}$. We may now define a low-quality organ as one that is below a threshold h, that is $D_{ijk}(g,E_{ijk})=I\left[-\left\{{\xi }_2^T\mathit{Q}+{\xi }_3^T{\overline{\mathit{X}}}^{\ast }(j-L_i)\mathit{Q}\right\}<h\right]$. For example, because we assume that each of organ is of different quality for each patient due to patient-donor interaction characteristics, we can define the collection of potential donor scores for the ith participant as ${\mathcal{Q}}_i=\left({\left[-\left\{{\xi }_2^T{\mathit{Q}}_{jk}+{\xi }_3^T{\overline{X}}^{\ast }(j-L_i){\mathit{Q}}_{jk}\right\}\right]}_{j=1,\dots ,p,k=1,\dots ,S_j}\right)$. The threshold h_i for the ith patient can be defined as a quantile of ${\mathcal{Q}}_i$.

5. Simulation Study

We designed a simulation study to test the small-sample performance of the proposed estimators. Patients entered the waiting list and organs arrived according to independent Poisson processes with rate parameters 0.5 and 0.32, respectively. Participants were assigned a time-dependent scalar covariate X_ij representing disease severity, with higher scores indicating a greater hazard of death on the waiting list and a greater need for transplantation. For each subject, we generated b_i0 ~ N(−1, 1) and $b_{i1}\sim N\left(\frac{1}{365},\frac{1}{(4.365{)}^2}\right)$. For study day j and a subject who arrived to the waiting list on day L_i, we let $X_{ij}=b_{i0}+b_{i1}\cdot \lfloor \frac{j-L_i}{30}\rfloor \cdot 30$, where ⌊·⌋ is the floor function, so that covariate values were updated every 30 days. Patients and organs were randomly assigned an ABO blood-type based on the probability observed in the analysis in Section 6. Each organ was assigned a binary indicator variable for “low-quality” with probability 0.5. For each organ arrival on study day j, the waiting list ranking was based on patient-donor blood-type match (exact match and then compatible) and then by the X_ij value similar to the ordering for cadaveric lungs. Patients accepted the organ with probability {1 + e^{(−φ₀−x_ijφ₁)}}⁻¹ with φ₀ = −2.5 and φ₁ = 0.25. In the results reported, here, we analyzed data collected over a 10 year observational period during which the waiting list had reached a steady state.

We estimated the survival distribution assuming a randomly selected patient follows the treatment regime g = decline all low-quality organs while (a) all other subjects followed their current propensity to accept or decline an offered organ (followed regime ∅), or (b) all other subjects follow regime g. In addition to the IPCW estimators proposed in Section 3 to estimate $S_t^{(g,\varnothing )}$ and $S_t^{(g,g)}$ we considered an ad hoc estimator, ${\widehat{S}}_t^{(NC)}$, that censors individuals at the time of non-compliance from the regime g but does not use any weights. This is not a consistent estimator for any causal effect of interest; we include this ad hoc estimator as it is used commonly in practice. For each estimator, we report results for 1000 Monte Carlo datasets. We estimated the standard error of the estimators using 100 bootstrap re-sampled datasets.

$S_t^{(g,\varnothing )}$ and $S_t^{(g,g)}$, the true survival probabilities t days after entering the waiting list for following regime g, are not available in closed form. Therefore, the survival curves were estimated via Monte Carlo simulation. To estimate $S_t^{(g,\varnothing )}$, for each simulated dataset, we randomly selected one observation and forced it to decline all low-quality organs, whereas high-quality organs were accepted with probability {1 + e^{(−φ₀−x_ijφ₁)}}⁻¹. Similarly, to estimate $S_t^{(g,g)}$, for each Monte Carlo dataset, we forced all individuals to decline all low-quality organs. The Monte Carlo datasets were independent of the ones to evaluate the proposed estimators.

Table 1 shows the true survival probabilities, the bias of the estimators, and coverage probabilities of 95% Wald-type confidence intervals for four time points. Although ${\widehat{S}}_t^{(NC)}$ is a convenient and frequently used estimator, it does not consistently estimate any causal effect of interest, and the bias is large for all time points for both causal estimands. For all time points, $S_t^{(g,\varnothing )}$ is greater than $S_t^{(g,g)}$, indicating that in this example, the causal estimand varies based on the question of interest. Importantly, ${\widehat{S}}_t^{(g,\varnothing )}$ and ${\widehat{S}}_t^{(g,g)}$ are not interchangeable: the mean of each estimator is close to its target, but ${\widehat{S}}_t^{(g,\varnothing )}$ is a substantially biased estimator for $S_t^{(g,g)}$, and ${\widehat{S}}_t^{(g,g)}$ is a substantially biased estimator for $S_t^{(g,\varnothing )}$. The simulation results demonstrate the good performance of the estimators, but, perhaps more importantly, they highlight the danger of a naive analysis that fails to carefully specify the target of estimation: an analyst attempting to estimate $S_t^{(g,g)}$ by using the more common estimator ${\widehat{S}}_t^{(g,\varnothing )}$ may draw erroneous conclusions.

Table 1.

Bias and Coverage Probabilities (CP) of 95% CIs from simulation. $S_t^{(g,\varnothing )}$ and $S_t^{(g,g)}$ are the simulated true survival probabilities t days after entering the waiting list for following regime g assuming either no other patients follow g or all other patients follow g, respectively. Their estimators are ${\widehat{S}}_t^{(g,\varnothing )}$ and ${\widehat{S}}_t^{(g,g)}$. ${\widehat{S}}^{(NC)}$ is a naive estimator that censors patients at non-compliance, but does not use weights.

			Estimator bias			CP
Target	t	True survival	${\widehat{S}}^{(NC)}$	${\widehat{S}}^{(g,\varnothing )}$	${\widehat{S}}^{(g,g)}$	${\widehat{S}}^{(g,\varnothing )}$	${\widehat{S}}^{(g,g)}$
$S_t^{(g,\varnothing )}$	180	0.785	0.010	−0.006	−0.018	0.954	0.735
	360	0.636	0.029	−0.000	−0.036	0.966	0.519
	540	0.533	0.039	0.003	−0.056	0.954	0.269
	720	0.463	0.045	0.004	−0.073	0.951	0.152
$S_t^{(g,g)}$	180	0.770	0.024	0.009	−0.003	0.882	0.967
	360	0.599	0.066	0.037	0.001	0.333	0.978
	540	0.471	0.101	0.065	0.006	0.045	0.972
	720	0.382	0.125	0.084	0.007	0.014	0.960

6. Application to UNOS Data

We illustrate our method with data from the UNOS national registry of lung transplants and use the continuous measure of lung quality described in Section 4. The observational period included transplants between May 4, 2005 and September 30, 2011.

We estimated ξ, the coefficients for the lung quality model, following the approach in Section 4. To be eligible for inclusion in the analysis of the lung quality score, patients must have been older than 18, not received a previous lung transplant, and not listed for simultaneous heart transplant. A total of 9091 patients contributed to the lung quality model. With these patients, we modeled post-transplant survival with recipient, donor, and recipient-donor interaction characteristics as predictors. These included recipient age, donor-patient age difference, an indicator for donor age >50, LAS at time of transplant (LAS-T), an indicator for donor history of diabetes, patient native disease group, transplant type (single vs. double lung), an indicator for patient being on life support at time of transplant, donor race, donor-patient height difference, recipient body mass index, an indicator for donor history of smoking ≥20 pack-years, and rank on the waiting list. The rank was meant to capture the declining viability of the organ for transplantation after numerous declines. Restricted cubic spline (RCS) basis functions with four knot points were used for continuous covariates to model nonlinear associations with the log hazard. We selected variables using grouped lasso with 5-fold cross validation, with the result that all variables were retained. Web Appendix C shows estimated coefficients from the model (Web Table S1), plots illustrating the effect on survival of variables modeled with RCS (Web Figure S1), and survival plots showing the effect of donor quality on post-transplant survival (Web Figure S2). We estimated the organ quality for each potential recipient for each possible donor in the dataset, and the distribution of these scores was used to define the qth percentile for each patient. The intraclass correlation coefficient for the estimated donor quality scores was 0.153, indicating most of the variability in donor quality scores is attributable to differences among the donors.

To compare treatment regimes based on donor quality, inclusion criteria were the same as above except that we now included both transplanted and non-transplanted patients. The total number of patients was 13,039. As predictors in the logistic regression model for the probability of accepting we included patient age, current LAS, time on the waiting list, native disease, patient-donor height difference, an indicator for donor smoking ≥20 pack-years, and an indicator for donor age ≥50 and its interaction with the patient age. As before, we used RCSs to allow for a nonlinear association with the log odds of accepting a donor organ. Estimated coefficients from the model and illustrations of the RCS coefficients are shown in Web Appendix C, Web Table S2 and Web Figure S2, respectively. We created the simulated dataset used in estimating the numerator of the IPCWs as described in Section 3.2. For the ith patient transplanted on the jth day, the lender i′ was selected as arg min (∣LAS_ij − LAS_{i′ j′}∣ : j − L_i = j′ − L_i′). If patient i′ later received a transplant, the process was repeated until the ith patient’s LAS trajectory was imputed through time of death with no transplantation. Because LAS was the only time-varying covariate considered in the organ acceptance model, no other variables aside from LAS were imputed.

We considered treatment regimes of the form “decline all donor organs below the pth percentile of donor quality scores if LAS is below M; if LAS ≥ M, any donor organ is acceptable,” where p and M can vary. LAS ranges from 0 to 100 (median LAS-T 38.79; 25th and 75th percentiles: 34.23, 47.27) with greater score indicating greater patient acuity and anticipated benefit for transplant. Examining these regimes allows us to investigate the effect of avoiding low quality organs while the patient is less acute. Importantly, we considered scenarios in which either a single patient adopts, or all patients adopt, the treatment regimes to investigate the effect of “transplant regime spillover.”

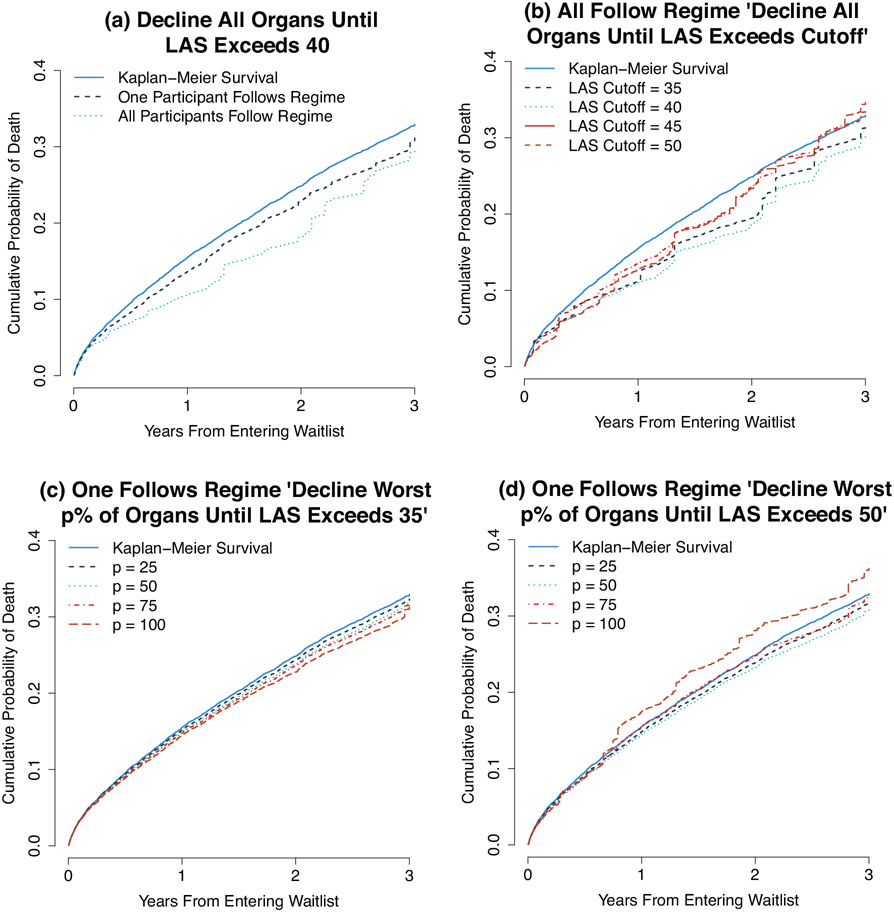
We illustrate the estimators with four scenarios. For each, we compare the estimates to the estimated survival if no subjects were to alter their propensity to accept an organ using the Kaplan–Meier estimator where all patients have a weight of 1. The results are shown in Figure 1 and in Table 2, with standard errors estimated using the bootstrap. Plot (a) shows that the estimated survival distribution for the treatment regime “decline all organs when the LAS is less than 40” is different depending on whether all patients follow the regime or only the single individual does. In both cases, the regime may offer a survival benefit, but the benefit is increased if all patients follow the regime rather than if only a single individual does. The survival benefits for both cases are statistically significant at 1 and 2 years of follow-up, but not at 3 years. The survival benefit for a single random patient who adopts the regime only comes from avoiding transplantation, a procedure with significant peri-operative mortality while the patient is less acute. But if all patients adopt the regime, this prevents relatively healthy patients (ones who are unlikely to die soon on the waiting list) from receiving cadaveric organs and ensures that more organs are available for the most acute patients.

Figure 1.

Anticipated cumulative probability of death while following the treatment regime “decline worst p% of organs until LAS exceeds M.” This figure appears in color in the electronic version of this article.

Table 2.

Difference from Un-weighted Kaplan–Meier Survival(S.E.) in probability of death for following the treatment regime. Negative numbers indicate a decreased cumulative probability of death. All regimes have the form “Decline organs while LAS < LAS threshold.” Estimates differ based on whether we assume one patient follows the regime or all patients follow the regime. The columns indicate which organs should be declined, the LAS threshold, and whether one or all patients are assumed to follow the regime.

Plot	Which organs to decline	LAS threshold	Who follows	1 year	2 years	3 years
(a)	All	40	One	−1.8%(0.26)	−2.0%(0.82)	−1.8%(1.22)
	All	40	All	−4.5%(1.00)	−6.3%(1.75)	−2.8%(2.88)
(b)	All	35	All	−4.3%(1.40)	−5.4%(2.01)	−1.4%(3.08)
	All	40	All	−4.5%(1.00)	−6.3%(1.75)	−2.8%(2.88)
	All	45	All	−1.9%(1.61)	−1.3%(2.51)	0.7%(3.13)
	All	50	All	−2.7%(1.48)	−1.5%(2.37)	1.7%(3.59)
(c)	Worst 25%	35	One	−0.3%(0.07)	−0.6%(0.11)	−0.6%(0.14)
	Worst 50%	35	One	−0.5%(0.09)	−1.0%(0.15)	−1.0%(0.27)
	Worst 75%	35	One	−0.7%(0.12)	−1.3%(0.19)	−1.2%(0.43)
	All	35	One	−1.0%(0.17)	−2.1%(0.28)	−1.7%(0.90)
(d)	Worst 25%	50	One	−0.7%(0.15)	−1.0%(0.21)	−1.2%(0.32)
	Worst 50%	50	One	−1.0%(0.24)	−1.6%(0.37)	−2.0%(0.58)
	Worst 75%	50	One	−0.1%(0.67)	−0.1%(0.88)	−0.2%(1.61)
	All	50	One	2.0%(1.70)	3.2%(2.20)	3.3%(2.68)

Plot (b) shows the anticipated survival when all patients follow the regime with p fixed at 100 (i.e., regimes in which patients declined all organs) and M varying from 35 to 50 in increments of 5. At lower values of M, there is an anticipated survival benefit. That is, patients with less acuity may benefit from delaying organ transplant until their LAS increases, a finding consistent with previous research which found no anticipated survival benefit for those transplanted at low LAS (Vock et al., 2013, 2017). However, as M increases above 40, the anticipated survival declines by 3 years of follow-up. Web Table S3 in Web Appendix C shows the estimated proportion of donor lungs that would be declined and the estimated mean time until transplantation for treatment regimes considered in plot (b).

Plots (c) and (d) demonstrate that the effect of an organ quality threshold depends on the LAS threshold M. Plot (c) shows that for M at 35, as p increases (i.e., declining a greater number of organs) the survival benefit increases. That is, patients with relatively low LAS may be best served by avoiding all organ transplants, even high-quality organs. In plot (d), we consider the same scenario but with M = 50. Here, there is a modest survival benefit until p = 100, at which point the anticipated survival is worse than with the Kaplan–Meier estimate. Here, it appears that patient with high LAS scores may gain a modest survival benefit by declining the worst organs, but declining all organs has a negative impact on survival. The small difference in expected survival among different regimes with different organ quality thresholds is consistent with previous work demonstrating the poor predictive ability of many donor factors on post-transplant survival (Reyes et al., 2010; Chaney et al., 2014).

7. Discussion

We demonstrated how we can approach the problem of testing treatment regimes when treatment is available stochastically and when the effect of the treatment regime depends on whether other patients follow the proposed regime. Specifically, we introduced a novel IPCW-based estimator developed to test the efficacy of a treatment regime when either only a single individual uses a strategy versus the efficacy when the entire population uses a strategy. We restricted our attention to the extreme cases where either only one patient or all patients adopt a strategy, but the estimator can be used for intermediate cases using simple modifications to the method. Web Appendix D shows results for the case where 50% of patients adopt a treatment regime. Furthermore, our analysis only considered survival which is only one component of patient well-being. The effect of these regimes considered here may be different if we considered a composite endpoint which incorporated quality of life measures.

The method relies heavily on correctly specifying the model for patients’ probability of accepting organs. However, the method is attractive because many other processes need not be modeled at all to obtain reasonable estimates of the anticipated survival for following different regimes. In contrast to commonly used methods, we need not specify models for the stochastic organ arrival process, patient additions to the waiting list, the distribution of patient characteristics over time, survival on the waiting list in the absence of transplantation, or for post-transplant survival, as is the case for the thoracic simulated allocation model.

Although the method was developed in the context of treatment regimes for accepting organ transplants, an area in which data are publicly available, the method is relevant for many other to other applications. We could, for example, use the proposed method to develop strategies on how to prioritize operating rooms in a hospital, provided that we have access to an observational dataset and can devise a means to estimate the probability of observing treatment history in the observed data and in the counterfactual world.

The results of the simulation and the application demonstrate the care an analyst must use in specifying the target of estimation when attempting to estimate the efficacy of a treatment regime when individuals are competing for treatment. In particular, we demonstrated that substantively different conclusions on the effectiveness of a policy for declining cadaveric organs can be reached depending on whether or not others on the waiting list adopt the same policy. We did not make any attempt in this manuscript to identify an optimal treatment regime that would be of the greatest benefit to an individual, or a (possibly different) treatment regime that would be of the greatest benefit to the population. We plan to address this issue in future work.