The hyoid as a sound conducting apparatus in laryngeally echolocating bats

Abstract

The morphology of the stylohyal‐tympanic bone articulation found in laryngeally echolocating bats is highly indicative of a function associated with signal production. One untested hypothesis is that this morphology allows the transfer of a sound signal from the larynx to the tympanic bones (auditory bulla) via the hyoid apparatus during signal production by the larynx. We used µCT data and finite element analysis to model the propagation of sound through the hyoid chain into the tympanic bones to test this hypothesis. We modeled sound pressure (dB) wave propagation from the basihyal to the tympanic bones, vibratory behavior (m) of the stylohyal—tympanic bone unit, and the stylohyal and tympanic bones when the stylohyal bone is allowed to pivot on the tympanic bone. Sound pressure wave propagation was modeled using the harmonic acoustics solver in ANSYS and vibratory behavior was modeled using coupled modal and harmonic response analyses in ANSYS. For both analyses (harmonic acoustics and harmonic response), the input excitation on the basihyal and thyrohyals was modeled as the estimated pressure (Pa) imposed by the collision of the vibrating thyroid cartilage of the larynx against these bones during signal production. Our models support the hypothesis that this stereotypical hyoid morphology found in laryngeally echolocating bats can transfer sound to the auditory bullae at an amplitude that is likely heard for the species Artibeus jamaicensis and Rhinolophus pusillus.

We modeled sound propagation from the larynx, through the hyoid apparatus, and into the tympanic bones in two species of layngeally echolocating bat. We found that in both species, this apparatus could be used to convey outgoing echolocation signals to ear.

1. INTRODUCTION

The echolocation signals produced by extant bats are either formed by the larynx or the tongue, with laryngeal echolocation being the more common and derived form (Simmons et al., 1979). Laryngeally echolocating bats exhibit many adaptations associated with the production and reception of sophisticated call sequences. For example, echolocation is coupled with laryngeal cartilage that is structurally reinforced through extensive calcification or ossification, presumably in response to the increased mechanical demands during vocalization (Carter, 2020; Carter & Adams, 2014; Denny, 1976; Griffiths, 1978; Suthers, 2004). Additionally, the cochleae of laryngeally echolocating bats have enlarged basal turns relative to other mammals and internal adaptations that increase the stiffness of the basilar membrane, thereby increasing sensitivity to the higher frequencies associated with echolocation signals (Kössl & Vater, 1995; Vater & Kössl, 2011). A trait that appears ubiquitous among laryngeal echolocators is an articulation formed by the attachment of the stylohyal to the tympanic bone of the auditory bulla via a flattened paddle‐like expansion that wraps around the bulla (Veselka et al., 2010). This flattened cranial end of the stylohyal is at the distal end of the hyoid chain which is composed of the thyrohyals, basihyal, hypohyals, ceratohyals, and stylohyals (Figure 1).

FIGURE 1.

Volume rendered µCT scans of Artibeus jamaicensis (b and d) and Rhinolophus pusillus (a and c) showing basihyal and fused thyrohyals (green), hypohyals (purple), ceratohyals (pink), stylohyals (blue), and tympanic (grey) bone. Intervening cartilaginous segments are white. The calcified larynx of the R. pusillus is indicated in orange, while the only part of the larynx that is calcified in A. jamaicensis is the cricoid (Carter 2020) and is not shown here. Points of view are from cranial (a), ventral (b), and lateral (c and d) aspects

The unique morphology of a stylohyal and auditory bulla articulation not found in other mammals suggests an adaptation novel to bats due to their highly derived laryngeal echolocation ability. As laryngeally echolocating bats exhibit such stereotypical cochlear and hyoid morphology, this adaptive morphology has been used to infer the presence of echolocation in fossil bats. For example, the oldest complete bat fossil, Onychonycteris finneyi, which dates to the late early Eocene, exhibits what appears to be an intermediate form, having cochleae with smaller basal turns and a stylohyal with a “tiny knob” at the cranial end rather than a flat plate. Simmons et al. (2008) argued this fossil represented a species that could not echolocate due to the smaller cochleae, whereas Veselka et al. (2010) noted that its stylohyal morphology, albeit less derived than extant species, permits the possibility of echolocation. Veselka et al. (2010) concede that the position of the stylohyal relative to the tympanic bone within the fossil may also be due to the crushed state of the fossil.

Although various hypotheses have been suggested as to the functional anatomy of the hyoid apparatus in laryngeally echolocating bats, to our knowledge, none have been explicitly tested. These hypotheses include providing mechanical support to the larynx, anchoring the prominent laryngeal muscles via a hyoid apparatus bound to the auditory bulla, or mechanical coupling of the larynx to the auditory bulla for the purpose of sound propagation between them (Veselka et al., 2010). Arguably, the latter would be beneficial for several reasons: (1) to register the outgoing vocalization from the larynx with the brain for phase comparison with the returning echo and therefore providing neural separation of the signals, (2) allow for the perception and possible correction of changes in vocalization structure between the larynx and the mouth or nostrils, and (3) transmit sound into the middle ear and triggering/modulating the reflex mechanism that dampens vibration of the ear ossicles, thereby preventing self‐deafening during echolocation signal emission (Veselka et al., 2010). A fourth hypothesis, presented by Wittrock (2010), suggests that the tympanic and/or stylohyal bones could act as a local oscillator through “ringing” (resonance) caused by the outgoing signal and therefore allow mixing of the outgoing signal and returning echo. This mixing could provide a beat note due to alternating constructive and destructive interference between the incoming signal and the local oscillator. This heterodyne detection system would be particularly useful for high duty cycle echolocators that make use of Doppler shifts. All four of these hypotheses would support selection for more efficient propagation of laryngeal vocalizations from the basihyal to the tympanic bones and resonance of the stylohyal and/or tympanic bones at certain frequencies.

In the present paper, we used μCT data and finite element analysis (FEA) to model two different mechanical components of sound in the hyoid apparatus from two different species of laryngeally echolocating bat. The first component of sound we modeled was the mechanical pressure wave (sequential compressions and refractions of particles that make up the bone/cartilage) generated in the basihyal via a sinusoidal/periodic pressure applied to the dorso‐medial surface of the basihyal and medial surfaces of the thyrohyals (henceforth collectively referred to as the laryngeal surface of the hyoid apparatus) and the subsequent propagation of the pressure wave through the hyoid apparatus chain and into the tympanic bone (measured in dB SPL). The sinusoidal pressure applied to the laryngeal surface of the hyoid apparatus represents the pressure applied due to impact of the vibrating larynx against the hyoid during echolocation signal production. Based on µCT images on the necks of bats (Carter, 2020; Veselka et al., 2010), the laryngeal surface of the hyoid apparatus is in close proximity to the thyroid cartilage of the larynx and therefore this contact/collision was assumed to have no significant amounts of intervening soft tissue/damping. This sinusoidal pressure/impact is considered the excitation input and was modeled across the range of frequencies associated with the echolocation signals from both species. Second, we modeled vibration of the hyoid apparatus and tympanic bones (measured in displacement, m) in response to the excitation input across the same frequency range. We modeled these vibratory behaviors on a hyoid apparatus with varying degrees of constraint on the basihyal to assess the role that hyoid musculature contraction plays in affecting the vibratory response of the hyoid to the excitation input. As the middle ear of laryngeally echolocating bats is highly efficient in transmitting the frequencies of sounds associated with echolocation from the tympanic membrane to the cochlea, even the very small displacements of the tympanic membrane due to high frequency sound are heard. For example, in laryngeally echolocating bats, a sound of 100 dB (SPL ref 20 µPa, all reports of sound pressure level hence forth are referenced to 20 µPa) at 100 kHz causes a tympanic membrane displacement at the umbo of the malleus of only 2.9e‐10 m (Manly et al., 1972; Neuweiler, 2000; Wilson & Bruns, 1983). Therefore, a displacement of the umbo of the malleus by 2.9e‐10 m is all that it takes for a bat to hear a 100 kHz sound at 100 dB. Furthermore, bats can hear the frequencies associated with echolocation below 20 dB, with some hearing them at or below 0 dB (see Heffner et al., 2013 for review). Therefore, in forming our hypotheses, we considered any vibration displacement amplitude at the site of tympanic membrane attachment onto the tympanic bone, of more than 2.9e‐11 m (therefore within an order of magnitude of the 2.9e‐10 m displacement) to be physiologically relevant when assessing the results of our models. As we could not visualize the tympanic membrane in our scans and therefore include it in our models, we used the location of its attachment onto the tympanic bone as a proxy in generating the displacement data. In this scenario, the tympanic bone and membrane would vibrate together and activate the ossicular chain and therefore represent a form of bone conducted (BC) hearing. We also considered a sound pressure level of 20 dB or larger to be physiologically relevant.

For both species, we hypothesized that an excitation input at the frequencies and amplitude associated with the echolocation signals will result in pressure wave propagation from the laryngeal surface, along the hyoid chain, and into the tympanic bone. The predicted outcome that will support this first hypothesis is that the amplitude of the sound pressure wave arriving in the tympanic bone will be at or above 20 dB for both species. Second, we hypothesized that areas of the tympanic bone associated with tympanic membrane attachment and, in one species, the cranial ends of the hyoid apparatus (stylohyal), will vibrate at levels considered physiologically relevant in response to an excitation input at the frequencies associated with echolocation. The predicted outcome that will support this second hypothesis is a displacement of the medial edge (inner rim) of the tympanic bone of 2.9e‐11 m or more in the x‐axis (orthogonal to the plane of the tympanic membrane) at frequencies close to those associated with the echolocation of each species. Finally, we hypothesized that by constraining the basihyal by varying degrees, the vibratory behavior of the tympanic and stylohyal bones will differ (as indicated by different magnitudes of displacement and frequency at which they occur) depending on the level of constraint applied in each analysis. We predicted that by increasing constraint on the basihyal, the vibratory peaks, of the tympanic bone rim and cranial end of the stylohyal, which indicate larger displacements or resonance, will be shifted in frequency but also decreased in amplitude.

2. METHODS

2.1. Specimens, computed tomography, and segmentation

In order to create the geometry needed for each FE model, we used µCT scans of Artibeus jamaicensis (Phyllostomidae) and Rhinolophus pusillus (Rhinolophidae). Although both species use nasally‐, rather than orally‐emitted echolocation, each employs a different form of laryngeal echolocation and hyoid morphology (Figure 1) (Pedersen & Müller, 2013). Rhinolophus pusillus uses constant frequency, high duty cycle echolocation (sequences of intermittent calls where >50% of time is occupied with sound [Fenton et al., 2012]) with the dominant/information carrying harmonic averaging around 105 kHz in nonflying individuals (Jiang et al., 2010). Bats from the genus Rhinolophus emit echolocation calls as loud as 123 dB at 10 cm (Waters & Jones, 1995). Artibeus jamaicensis uses broad bandwidth frequency modulated, low duty cycle echolocation (sequences of intermittent calls where <10% of the time is occupied by sound [Fenton et al., 2012]) with the dominant harmonic sweeping down from approximately 78 to 54 kHz and contains a maximum power around 62 kHz (Carter et al. 2014). While historically being considered a “whispering” bat (Neuweiler, 2000), A. jamaicensis has more recently been documented emitting echolocation calls as loud as 110 dB at 10 cm (Brinkløv et al., 2009). In addition, as we were unable to use contrast‐enhanced scans (due to relying on museum collections for specimens) to visualize less dense connective tissue, we compared these two species because both have hyoid apparatus largely consisting of a bony chain separated by what we assumed were small cartilaginous joints (Figure 1). While these assumed small segments of cartilage appear as empty spaces on the traditional µCT scans, the hyoid apparatus of bats and indeed many mammals is described as a bony chain linked with segments of cartilage (Currey, 2006; Griffiths et al., 1992; Romankowowa, 1963; Sprague, 1943).

The A. jamaicensis specimen came from a captive colony kept at the University of Northern Colorado, Greeley, USA and was euthanized and stored in 70% ethanol for an unrelated study. Care of this captive colony has been outlined previously (see Carter & Adams, 2014). The R. pusillus specimen resides in the mammal collections of the American Museum of Natural History (AMNH#56973) and is fluid preserved (ethanol). The A. jamaicensis specimen was removed from the ethanol and imaged on a Scanco µCT 50 (Scanco Medical) at the Vanderbilt Center for Small Animal Imaging, Vanderbilt University, Nashville, TN, USA. These image data were generated using a 0.75 s exposure, with an angular separation 0.18°, through 360° of rotation with an X‐ray tube voltage set at 70 kV with a 200 µA anode current and using a 0.55 mm thick aluminum filter. This resulted in an isotropic voxel size of 11.4 µm. The data were reconstructed using the associated Scanco image processing algorithms. The R. pusillus specimen was removed from the ethanol and imaged on a GE Phoenix v|tome|x s240 with a 2 s exposure, with an angular separation of 0.24°, through 360° of rotation with X‐ray tube voltage set at 140 kV and anode current at 140 µA. This resulted in an isotropic voxel size of 19.6 µm. The data were reconstructed with Datos|x 2 reconstruction software (General Electric Company) using a proprietary graphics processing unit‐based reconstruction technique.

The scans were viewed and segmented in Dragonfly (Object Research Systems). We created separate segmentations for most bones of the hyoid apparatus (thyrohyal—basihyal [fused], hypohyal, ceratohyal, and stylohyal) and left and right tympanic bones using the automatic threshold function. Our bone segmentations included internal cavities wherever present. To create segmentations of the cartilaginous segments, we used the inverse threshold function to highlight and select the pixels that make up the void between each boney segment (Figure 1). Using the detailed diagrams from Sprague (1943) and relying on the position of the adjacent bones in the scans, we defined the borders of these cartilaginous pieces and expanded them to overlap slightly with the ends of the bones for later editing. Segmentations were converted into digital mesh (facet) bodies and exported from Dragonfly as.stl files and individually imported into the computer‐aided design (CAD) software, Fusion 360 (Autodesk), and later SpaceClaim (SpaceClaim) for further geometry refinement.

2.2. Geometry refinement

Post processing of mesh (facet) bodies generated from μCT data involved reducing facet number, smoothing, and closing gaps within Fusion 360 which was important to create watertight facet bodies that would translate well into solid body models necessary for our FEA. Reducing and smoothing facets also allowed for more reasonable FEA computation time. The R. pusillus model was reduced from 479,901 to 164,188 facets, and the A. jamaicensis model was reduced from 1,298,776 to 281,092 facets. The initial discrepancy in the number of facets between models was expected and attributed to differences in scan resolution and hyoid dimensions. After reducing facet number, we performed one iteration of smoothing and closed any holes present with the remove and fill function in Fusion 360. Once watertight meshes were achieved for all the bones from both models, they were assembled by inserting each edited boney and cartilaginous mesh into a single file and exported as.stl files for further processing with SpaceClaim. Within SpaceClaim, each model was edited using the shrink‐wrap tool which ensured that the size and distribution of surface facets was uniform (significantly reducing FEA computation time). Since the cartilaginous bodies were segmented with a slight overlap with the ends of the adjacent bone, we used the Boolean cut function to remove the overlapping part of the cartilage which produced cartilaginous pieces that perfectly matched the shape of the adjacent bone and therefore ensured the cartilage and adjacent ends of bones were flush. Moreover, this provided clean contact surfaces between cartilage and bone for our FE models. Lastly, the facet bodies were converted into solid bodies, saved as a SpaceClaim file, and loaded into the FEA software ANSYS (ANSYS). The 3D models used to build our FE models are available on Data Dryad (datadryad.org, https://doi.org/10.5061/dryad.3ffbg79k8).

2.3. FE modeling, harmonic acoustics (sound pressure wave)

ANSYS provides several analyses to model different aspects of sound propagation, including a harmonic acoustics analysis and a coupled modal and harmonic response analysis. The harmonic acoustics analysis models the propagation of a mechanical sound pressure wave (sequential compressions and refractions of particles through materials) and assumes no structural vibration/resonance. The coupled modal and harmonic response analysis calculates the natural frequencies of the model to analyze its structural response in the form of vibration to an excitation input. Each of these analyses models a different aspect of sound (vibration and pressure wave propagation) and therefore tests a different hypothesis. Using the harmonic acoustics solver to model sound wave propagation, we loaded our geometries and assigned material properties to the pieces of cartilage and bone. Bone and cartilage were assumed to be isotropic elastic materials (Dumont et al., 2005) with material properties gleaned from the literature (Table 1). The scans of each bat revealed no spongy bone in A. jamaicensis and only small traces in the basihyal of R. pusillus; thus, all bone except the tympanic bones (auditory bulla) were assigned cortical bone material properties. We assigned the tympanic bones material properties that made them more brittle and denser than cortical bone (Currey, 2006). This was done as parts of the tympanic rings appeared denser than the stylohyal bones in certain slices, however, the higher values we used are not typical of most terrestrial mammals but rather are found in whales. These tympanic bone material properties provided harmonic acoustics models with more transmission loss, making it less likely that we overestimated the ability of the hyoid apparatus to transmit sound via pressure waves. ANSYS automatically generated the contacts between bodies that were touching, and all contacts were assigned as bonded (no separation or sliding between bodies). For each model/species, we ran two harmonic acoustics analyses: one with an input excitation as a sinusoidal pressure of 6.3 Pa which is equivalent to 110 dB, and the other with a sinusoidal input excitation of 63.2 Pa which is equivalent to 130 dB. The excitation input for each model/species was scoped onto the laryngeal surface (Figure 2), with the pressure vector normal to the surface of the model and was set to sweep from 0 to 150 kHz. These pressures represent the impact of the vibrating larynx on the fused basihyal and thyrohyals during echolocation signal production and are based on sound pressure level of echolocation signal (dB SPL). These two input sound pressure intensities were chosen as they differ by an order of magnitude and are assumed to be rough approximations of echolocation signal intensity at the larynx. As the hyoid and tympanic bones are surrounded by muscle, we included appropriate sound energy absorption coefficients (ratio of absorbed energy to incident energy) on all external surfaces of the hyoid apparatus and tympanic bones (Table 2). The surface of the tympanic bone that faces the middle ear was considered to be in contact with air. As the harmonic acoustics solver is only modeling the propagation of a pressure wave, there is no need to model any attachment points to external structures (e.g. skull). We selected sound pressure (dB) outputs scoped to the entire model (providing sound pressure level contour plots over the entire model) and a frequency response of sound pressure level scoped to a facet on each tympanic bone (Figure 3). Each facet on the tympanic bone was located on the same place on the left and right tympanic bones, on the surface where the stylohyal lies against the tympanic bone. This frequency response provided the amplitude of the sound pressure wave (dB) reaching these points for the different frequencies (0–150 kHz) modeled. We meshed the harmonic acoustics models with a fine mesh so that we had more than six quadratic elements per wavelength which is necessary to accurately run harmonic acoustics analyses. This meshing resulted in 227,487 10‐noded tetrahedron elements with 407,096 nodes for the A. jamaicensis model and 283,048 10‐noded tetrahedron elements with 498,127 nodes for the R. pusillus model.

TABLE 1.

Material properties of the tissues used in all FE models from Currey (2006)

Property	Cartilage	Muscle	Cortical bone	Tympanic bone
Young's modulus (GPa)	0.1	—	20.0	31.3
Density (kg/m3)	1100	1200	2000	2400
Speed of sound (m/s)	1640	1588	2660	3512
Poisson's ratio	0.4	—	0.3	0.3

FIGURE 2.

(a) Artibeus jamaicensis and (b) Rhinolophus pusillus show the dorsal aspects of the FE model geometry with the laryngeal surface (area of sinusoidal excitation input) shaded in red. (c) A. jamaicensis and (d) R. pusillus show the medial aspects of the FE model geometry with the area where vibratory data were collected shaded in blue. The orange dot in (c) indicates the location of the facet where vibratory data were collected at the end of the stylohyal in A. jamaicensis. (e) and (f) show the lateral aspect of the FE model geometry for A. jamaicensis with the bonded area between the stylohyal and tympanic bones shaded in green. (e) Shows the scenario where the entire interface between the stylohyal and tympanic bones is bonded and (f) shows the scenario where there is a pivot‐like articulation between them

TABLE 2.

Absorption coefficients (1—reflection coefficient) of sound energy between tissues. Calculated using the reflection coefficient = ([Z ₁ − Z ₂]/[Z ₁ + Z ₂])², where Z (acoustic impedance) = density (kg/m³) × speed of sound (m/s)

	Air	Muscle	Tympanic bone
Cartilage	—	0.99	—
Cortical bone	—	0.62	0.93
Tympanic bone	0.0	0.6	—

FIGURE 3.

Sagittal slices through the tympanic bone, stylohyal bone, skull bones, and cochlea in Rhinolophus pusillus (a and b) and Artibeus jamaicensis (c and d). Blue circles indicate the locations from where sound pressure level (dB) data were collected in our acoustic models

2.4. FE modeling, harmonic response (vibration and resonance)

To model the vibratory response of a free and constrained hyoid apparatus, we used the mode‐superposition method which uses the natural frequencies and mode shapes from the modal analysis to characterize the dynamic response (vibration) of a structure to transient, or steady harmonic excitations, but does not model pressure waves. Because the articulation of the stylohyal with the tympanic bone appears different in the scans between the two species (Figure 3), we modeled two different types of connection in the A. jamaicensis versus one in the R. pusillus model. As the stylohyal appears fused to the tympanic bone in scans of R. pusillus, we bonded the two bones together across the entire articulating interface, forming a stylohyal—tympanic bone unit that would vibrate as a single body. This fusion between the stylohyal and tympanic bones was also found for other high duty cycle species (Veselka et al., 2010). In A. jamaicensis, the stylohyal bone is separated from the tympanic bone by a small gap across most of the paddle‐shaped cranial end (Figure 3). However, as the stylohyal meets the tympanic bone more proximally, a small segment of the stylohyal appears fused to the tympanic bone. As we were unsure of the exact nature of this connection and the mobility of the bones relative to each other, we modeled it in two different ways in this species. The first was a bonded connection across the entire articulating interface of both bones, forming a stylohyal—tympanic bone unit like in R. pusillus, and the second was with only a small area of the stylohyal bonded to the tympanic bone (Figure 2). This second scenario created a pivot‐like arrangement whereby the cranial end of the stylohyal was free to move slightly in all three axes around its attachment point on the tympanic bone. In both species, the tympanic bones that compose the auditory bulla show no evidence of fusion to the associated skull bones but rather are separated from the skull by small spaces in the scans (Figure 3). We therefore modeled the joint between the tympanic bone and the rest of the skull as an attachment that allowed slight rotational movement in all three axes but no separation. We did this by fixing one facet on the surface of the tympanic that contacts the skull (Figure 4). We also fixed single facets on the ends of the thyrohyal bones to simulate attachment to the thyroid cartilage of the larynx via thyrohyal cartilage. All other contacts between bones and cartilage in the hyoid chain were defined as bonded.

FIGURE 4.

Fixed support boundary conditions for the harmonic response analyses for Artibeus jamaicensis (a–c) and Rhinolophus pusillus (d–f). The green triangles (a and d) indicate the location of the fixed support attaching the tympanic bones the skull. The red triangles (b–f) indicate the location of the fixed support attaching the thryohyal bones to thyrohyal cartilage (which attaches to the thyroid cartilage of the larynx). The black triangle (c and f) indicates the location of the fixed point used to constrain the basihyal at one point. The black and yellow triangles indicate the locations of the fixed supports used to constrain the basihyal at three points. The black, yellow, and blue triangles indicate the locations of the fixed supports used to constrain the basihyal at five points. Elements of the volume rendered models are color coded as follows: basihyal and fused thyrohyals (green), hypohyals (purple), ceratohyals (pink), stylohyals (blue), tympanic bones (grey), cartilaginous segments (white)

To model muscular constraints on the basihyal, we fixed either a single point on the center of the ventral surface of the body, three points in a vertical line on the center of the ventral surface of the basihyal, or five points arranged in a diamond on the ventral surface of the basihyal (Figure 4). Not only did this provide situations with varying basihyal mobility but also reflects the attachment points for some of the hyoid musculature in echolocating bats. For example, the geniohyoideus inserts onto the center of the ventral surface the basihyal (Griffiths, 1982, 1994; Griffiths et al. 1992) and is represented in our models by the single point and/or three vertical point constraints. Several muscles have attachments that spread more laterally onto the ventral surface of the basihyal, either directly onto the bone via their own tendons (hyoglossus, madibulo‐hyoid, and stylo‐hyoideus) or through the tendons of other muscles (e.g., sterno‐hyoideus). In our models, these attachments are represented by the diamond‐shaped five‐point constraint (Griffiths, 1982, 1994; Griffiths et al. 1992). A sinusoidal pressure of 63.2 Pa (130 dB) was scoped to the laryngeal surface of the R. pusillus model and a sinusoidal pressure of 6.32 Pa (dB 110) was scoped to the laryngeal surface of the A. jamaicensis model (Figure 2). The pressure vectors of these inputs were normal to the surface of the models. As most oscillatory systems dissipate energy due to frictional forces, we assigned a damping coefficient of 0.02 (Dodge et al., 2012) to all our harmonic response (vibration) analyses. Harmonic response models were meshed to the same resolution parameters as the previous harmonic acoustics models. We selected displacement (m) as an output variable scoped to the entire model, providing animations of the entire model and associated resonant mode shapes. We also generated a frequency response of maximum displacement scoped to an area along the medial rim of the tympanic bone (i.e., the amount of displacement felt by the points that move the most at all frequencies) and to a single facet on the tip of the cranial end of the stylohyal bones (A. jamaicensis), providing quantitative data on displacement of these tips in all three axes at the different frequencies (0–150 kHz) modeled (Figure 2).

3. RESULTS

3.1. Harmonic acoustics (sound pressure wave)

For both species, harmonic acoustics analyses suggest that a sound pressure wave above 20 dB in amplitude reaches the tympanic bone for frequencies associated with echolocation (Figures 5 and 6). Specifically, in the A. jamaicensis hyoid model, at the frequencies associated with echolocation (50–80 kHz) in this species, sound pressure waves in the tympanic bone had amplitudes from 70 to 55 dB for the 130 dB input and between 47 and 35 dB for the 110 dB input. For the R. pusillus model, at the frequencies associated with echolocation (100–110 kHz) in this species, sound pressure waves in the tympanic bone had amplitudes from 68 to 66 dB for the 130 dB input and between 48 and 46 dB for the 110 dB input.

FIGURE 5.

Contour plots of sound pressure level (dB) for Rhinolophus pusillus (a) at 105 kHz and Artibeus jamaicensis (b) at 63 kHz. Input pressures on laryngeal surfaces of the hyoid apparatus are 63 Pa (130 dB) for Rhinolophus pusillus and 6.3 Pa (110 dB) for A. jamaicensis

FIGURE 6.

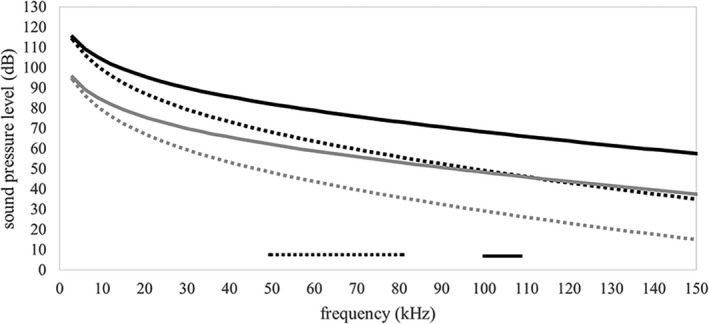
Frequency response curves for sound pressure level (dB) measured from facets on the left and right tympanic bones where the cranial end of the stylohyal articulates. Data points represent the average sound pressure level measured between tympanic bones (left and right) at a particular frequency. Black curves represent data from models with a 63 Pa (130 dB) input excitation and gray curves represent data from models with a 6.3 Pa (110 dB) input excitation. Solid black and gray curves are from Rhinolophus pusillus and dotted black and grey lines are from Artibeus jamaicensis. The solid and dotted bars along the horizontal axis indicate echolocation frequency ranges for each species, A. jamaicensis (dotted) and R. pusillus (solid)

3.2. Harmonic response (vibration and resonance)

When modeled as a bony unit, the harmonic analyses suggested that vibration of the stylohyal—tympanic bone unit could also transmit sound from the larynx to tympanic bones in these two species. For both species, there are large vibratory displacements at certain frequencies (resonance peaks), measured from around the tympanic bone rim on the geometry that exceed the assigned 2.9e‐11 m displacement. Specifically, the unconstrained hyoid of both species (Figures 7a and 8a) exhibited many peaks across a wide range of frequencies that reached the 2.9e‐11 m displacement threshold. When we constrained the hyoid at one point, fewer resonant peaks reached the 2.9e‐11 m displacement threshold in A. jamaicensis, however there was a peak in the x‐axis (orthogonal to the tympanic anulus) that just breached the 2.9 e‐11 m threshold at 58 kHz, which overlapped with the echolocation frequency range (50–80 kHz) of this species (Figure 7b). When we constrained one point on the R. pusillus basihyal, many resonant peaks reached the 2.9e‐11 m displacement threshold, including a peak in the x‐axis (orthogonal to the tympanic anulus) with a maximum displacement of 5.27e‐11 m at 101 kHz which is also within the echolocation frequency range (100–110 kHz) of this species (Figure 8b). Constraining three and five points on the basihyal of the A. jamaicensis model resulted in only one resonant peak just reaching the 2.9e‐11 m threshold at 5.5 kHz (Figure 7c), which is unlikely to be associated with echolocation. Constraining three points on the basihyal of the R. pusillus model resulted in three resonant peaks reaching the 2.9e‐11 m threshold at frequencies lower than the 100–110 kHz dominant harmonic range (Figure 8c). However, there is a peak in the x‐axis between 50 and 60 kHz, which falls within the nondominant/information carrying harmonic frequency range. Surprisingly, constraining five points on the basihyal of the R. pusillus model resulted in a resonant peak just reaching the threshold of 2.9e‐11 m at 101 kHz (Figure 8d).

FIGURE 7.

Frequency response curves in all three axes (x—solid black, y—solid gray, z—dotted black) for maximum tympanic ring displacement (m) in Artibeus jamaicensis with the stylohyal and tympanic bones fused together across the entire interface. The x‐axis (solid black line) is orthogonal to the tympanic ring and therefore orthogonal to the plane of the tympanic membrane; the y‐axis is along the occipito‐rostral plane and the z‐axis is along the dorso‐ventral plane. The 2.9e‐11 m displacement threshold is indicated by the thick horizontal black line and the echolocation frequency range is indicated by the black bar along the horizontal axis. Data are from an unconstrained basihyal (a), basihyal constrained at one point (b), basihyal constrained at three points (c), and basihyal constrained at five points (d)

FIGURE 8.

Frequency response curves in all three axes (x—solid black, y—solid grey, z—dotted black) for maximum tympanic ring displacement (m) in Rhinolophus pusillus with the stylohyal and tympanic bones fused together across the entire interface. The x‐axis (solid black line) is orthogonal to the tympanic ring and therefore orthogonal to the plane of the tympanic membrane; the y‐axis is along the occipito‐rostral plane and the z‐axis is along the dorso‐ventral plane. The 2.9e‐11 mm displacement threshold is indicated by the thick horizontal black line and the echolocation frequency range is indicated by the black bar along the horizontal axis. Data are from an unconstrained basihyal (a), basihyal constrained at one point (b), basihyal constrained at three points (c), and basihyal constrained at five points (d)

In A. jamaicensis, when the cranial end of the stylohyal bone is allowed to pivot on the tympanic bone, the vibratory behavior of both the cranial end of the stylohyal bone and the tympanic ring were similar to the vibratory behavior of the stylohyal—tympanic bone unit (Figures 9 and 10). Most notably, when the basihyal was constrained at one point, the cranial end of the stylohyal had a prominent resonant peak in the x‐axis of 1.53e‐10 m of displacement at 65 kHz (Figure 9b), and the tympanic ring had a peak overlapping exactly with the echolocation frequency range of A. jamaicensis (Figure 10b).

FIGURE 9.

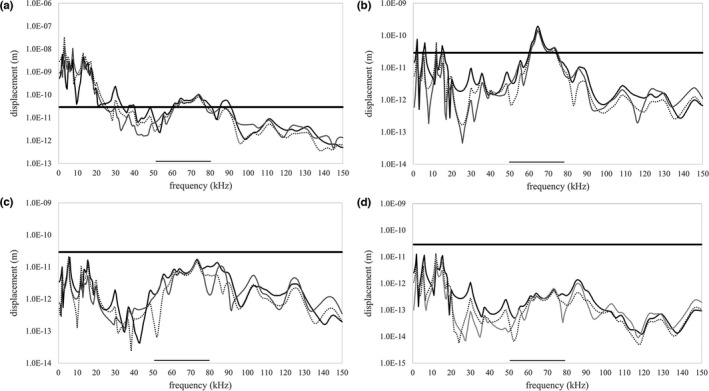
Frequency response curves in all three axes (x—solid black, y—solid grey, z—dotted black) for maximum displacement (m) of the cranial end of the stylohyal in Artibeus jamaicensis with the stylohyal and tympanic bones articulated with a pivot‐like connection. The x‐axis (solid black line) is orthogonal to the tympanic ring and therefore orthogonal to the plane of the tympanic membrane; the y‐axis is along the occipito‐rostral plane and the z‐axis is along the dorso‐ventral plane. The 2.9e‐11 mm displacement threshold is indicated by the thick horizontal black line and the echolocation frequency range is indicated by the black bar along the horizontal axis. Data are from an unconstrained basihyal (a), basihyal constrained at one point (b), basihyal constrained at three points (c), and basihyal constrained at five points (d)

FIGURE 10.

Frequency response curves in all three axes (x—solid black, y—solid grey, z—dotted black) for maximum tympanic ring displacement (m) in Artibeus jamaicensis with the stylohyal and tympanic bones articulated with a pivot‐like connection. The x‐axis (solid black line) is orthogonal to the tympanic ring and therefore orthogonal to the plane of the tympanic membrane; the y‐axis is along the occipito‐rostral plane and the z‐axis is along the dorso‐ventral plane. The 2.9e‐11 mm displacement threshold is indicated by the thick horizontal black line and the echolocation frequency range is indicated by the black bar along the horizontal axis. Data are from an unconstrained basihyal (a), basihyal constrained at one point (b), basihyal constrained at three points (c), and basihyal constrained at five points (d)

4. DISCUSSION

We found support for the hypothesis that a sound pressure wave could be transmitted from the basihyal along the hyoid chain and into the tympanic bone at an amplitude that is physiologically relevant. There is a large body of evidence that suggests that bats have middle ears, cochleae, and central nervous systems extremely sensitive to the frequencies at which they echolocate (see Neuweiler, 2000 for review). Most bats studied so far can hear the frequencies associated with their echolocation system below 20 dB, with some hearing them at or below 0 dB. This hearing sensitivity suggests that the sound pressure wave arriving at the tympanic bones in our FE models falls well within the range that bats can hear. It should be noted that the expected downward sweep in amplitude with increasing frequency of the sound pressure wave in Figure 6 is due to higher frequency pressure waves attenuating more than lower frequency waves as they travel though a medium and is represented by a frequency dependent dissipation term in the equations that govern the harmonic acoustics model. The material property of bone and cartilage that defines how much sound energy in the form of pressure waves would leave the hyoid apparatus and pass into the surrounding soft tissues, is the acoustic impedance (Z) (Z = density × speed of sound) (Table 2) (Currey, 2006). Acoustic impedance is the resistance to a traveling sound pressure wave through a material and the more similar the acoustic impedance of two materials, the more sound energy that passes between them or the higher the absorption coefficient (ratio of absorbed energy to incident energy). This means less sound energy passes between bone and soft tissue (with more being reflected back into the bone) than between cartilage or fascia and soft tissue. Additionally, as we modeled the tympanic bones as more dense than cortical stylohyal bones, more sound energy is reflected into stylohyal bones than if we had modeled them with the same density. Given the relationship between acoustic impedance and the absorption coefficient, a hyoid apparatus that is made up mostly of bone will lose less sound to the surrounding tissue than one with large cartilaginous or fascial segments. If this form of sound transfer (pressure waves) were the dominant way in which bats transferred a signal from the larynx to the ear, one would expect highly ossified hyoid apparatus in all laryngeally echolocating species. However, there are many laryngeally echolocating bat species that exhibit a hyoid apparatus where boney elements have been replaced with cartilage or fascia (Sprague, 1943), suggesting that other factors are at play in the selection of hyoid morphology that functions to transmit sound. This may include the transmission of the sound signal as a vibratory displacement (m) rather than a sound pressure wave (dB).

Our models also support this hypothesis that vibration, particularly resonance, of the stylohyal—tympanic bone unit could be used to effectively transmit sound from the larynx to the ear in laryngeally echolocating bats. The amplitude of displacement during resonance suggests that a stylohyal—tympanic bone unit and/or the cranial ends of the stylohyal bones vibrate to a degree that could be effectively transmitted through the ear ossicles and into the cochlea. The level of displacement of the stylohyal—tympanic bone unit in our models is largely due to the relative mobility of the auditory bulla against the rest of the skull. This morphology, where the auditory bulla is not fused to the skull but instead free to move, is documented in many mammal groups, including bats (van der Klaauw, 1931; Moore, 1981), and we feel it provides the mobility needed to transmit sound in the form of vibratory displacement. Our models also supported the hypothesis that by constraining the basihyal, the vibratory behavior of the stylohyal—tympanic bone unit and/or cranial ends of the stylohyal can be changed. This change takes the form of shifting the resonant peaks in the frequency domain while also affecting the amplitude of resonant peaks. Generally, more constraint of the basihyal resulted in decreased amplitude of resonant vibration. The A. jamaicensis model functioned best in transmitting sound via resonant vibration when minimally constrained (unconstrained and one point of constraint) and had close overlap of the resonant frequencies and echolocation signal frequencies with one point of constraint. Surprisingly, the R. pusillus hyoid—tympanic bone unit still resonated at a level that we considered physiologically relevant when constrained with five points. These vibratory data suggest that if bats are using resonant vibration to transmit sound through the hyoid apparatus, then fine scale control of the complex musculature associated with the hyoid apparatus in bats (Griffiths, 1982, 1994; Griffiths et al.1992) would be needed. This control could be used to ensure resonant peaks at the frequencies associated with echolocation while simultaneously preventing too much damping of the system. While our models show that sound pressure waves and resonant vibration reach the tympanic bones via the hyoid apparatus, they do not show the subsequent movement of sound into the cochlea. Both forms of sound we modeled would likely be heard through a form of BC hearing (see Stenfelt & Goode, 2005 for review). Bone conducted hearing involves a few different potential routes that sound can take into the cochlea, and most involve vibration of skull bones and subsequent sensation in the cochlea. These include sound radiated into the external ear canal from skull bones which puts the tympanic membrane into motion, middle ear ossicle inertia, inertia of the cochlear fluids, compression of the cochlea walls, and pressure transmission from cerebrospinal fluid. Considering the results from our models, the most likely scenario is one where the tympanic bone vibrates and either sets the middle ear ossicles into motion or transmits vibrations into the surrounding skull bones and cochlea. Given that many of the resonant peaks in our harmonic response analysis are in the axis orthogonal to the plane of the tympanic annulus and membrane, and that the malleus is also fused to the tympanic bone in bats, these displacements would likely put the middle ear ossicles into motion. Although not documented in bats, the tympanic ring as a vibratory unit of hearing has been documented in cetaceans and sirenia (Fleischer, 1980). The transfer of the sound pressure waves (dB) from the tympanic bone into the cochlea could also take a route through the three middle ear ossicles via the tympano‐mallear fusion and result in a pressure wave in the cochlear fluid that causes basilar membrane displacement. This could occur through excitation of the tympanic and other ear bones into vibratory resonance by the arriving pressure waves and/or the transfer of the pressure waves through the ear ossicles into the cochlea.

There are no published data on the material properties of the bones and cartilage that make up the bat hyoid apparatus, thus we had to rely on data published from other bones and cartilage for other mammal species. Currey (2006) provides an in‐depth analysis and discussion of the mechanical properties of bones and cartilage, and we feel that the material properties used in our models come close to approximating how the hyoid responds to an excitation associated with echolocation signal production. It should be noted that along with increased reflectance of pressure waves back into the stylohyal bones, the denser tympanic bones of our models will exhibit resonant peaks shifted towards lower frequencies than if we had modeled them with the same density as the cortical bone we assigned to the bones of the hyoid apparatus. Furthermore, the musculature that encases much of the hyoid apparatus was not built into our models for simplicity's sake. We included sound pressure wave absorption coefficients across all external surfaces (Table 2) and an overall damping coefficient that accounts for loss of oscillatory energy to the surrounding soft tissue through friction. Although not likely to exactly match the in vivo environment in which the hyoid apparatus functions in bats, we are confident these parameters approximate the energy loss of the system to the surrounding tissue. It should also be noted that in some cases the peaks in the harmonic response analyses only just breach the somewhat arbitrary 2.9e‐11 m displacement threshold and given the assumptions in material properties and damping coefficient, interpreting those peaks as functional should be cautioned. Indeed, by changing variables in the model, those peaks that previously just breached the threshold may fall below it and be deemed nonfunctional. Similarly, the choice of 2.9e‐11 m displacement as our threshold could have been too conservative—meaning we are incorrectly discounting some of the peaks that fall below 2.9e‐11 m as nonfunctional. Conversely, our choice of a 2.9e‐11 m displacement threshold could be too generous, resulting in functionality being incorrectly assigned to certain peaks. Given these necessary assumptions, it is important to note that the absolute values derived from our models probably do not exactly represent what is happening in echolocating bats. Rather, we should use these models to understand patterns of sound propagation through the hyoid apparatus, including a potential form of BC hearing in which the tympanic bone acts as a vibratory unit. Furthermore, the resonance peaks in the vibration data of the tympanic bones that we observed in our models could provide the mechanism whereby the outgoing signal can be mixed with the incoming echo, forming a beat note in a heterodyne detection system (Wittrock, 2010). Viewed in this light, our analyses still provide support for the hypothesis that sound can be transmitted through the hyoid apparatus from larynx to the tympanic bulla, providing evidence for a possible function of the stereotypical hyoid morphology found in laryngeally echolocating bats.

Although stylohyal morphology and its articulation with the tympanic bone show high similarity between different families of laryngeally echolocating bats (Carter, 2020; Sprague, 1943; Veselka et al., 2010), there is variation in the morphology of the more proximal elements of the anterior cornu of hyoid apparatus. For example, there is a tendency towards reduction of the hypohyal in length, with this reduction reaching its extreme in Eptesicus, Minipterus, and Kerivoula, where it is present as a slender fascial attachment of the anterior cornu to the basihyal (Sprague, 1943). In this reduced scenario, the efficient propagation of sound pressure waves (dB) through this slender fascial attachment seems unlikely, however it could still play a role in transmitting a vibration from the basihyal into the stylohyal and tympanic bones. Another aspect of this system that exhibits structural variation between bat species, is the degree to which the larynx is reinforced through mineralization (Carter, 2020). High duty cycle bats (R. pusillus) exhibit the most mineralization, including extensive thyroid cartilage calcification. The low duty cycle phyllostomids (A. jamaicensis) exhibit the least, with only the cricoid cartilage being calcified. While we did not build these differences into our models, one might predict that the R. pusillus thyroid cartilage would deform less (due to more mineralized reinforcement) upon impact with the laryngeal surface of the hyoid and therefore be more efficient in the transfer of kinetic energy into the basihyal. Related to this, is the effect that the intensity of the input signal on the laryngeal surface of the hyoid apparatus has on the amplitude of the signal arriving at the ear. As signal loss through damping or absorption appears to be the main obstacle to the hyoid transmitting sound effectively, bat species with relatively intense echolocation calls (input signals) would likely have signals with greater amplitudes arriving at the ear via the hyoid. Finally, while there is no stylohyal – tympanic bone articulation in the tongue clicking echolocators from the genus Rousettus (Pteropodidae) like that found in laryngeally echolocating bats, there is a short fascial attachment between the tympanohyal and the stylohyal. Like the fascial hypohyal in the genera Eptesicus, Minipterus, and Kerivoula, this attachment could provide a route for vibration from the basihyal, through the anterior cornu and into the tympanic bones. As the basihyal also serves as an attachment site for the muscles of the tongue, the hyoid morphology in Rousettus bats could allow for echolocation sound transmission from the site of signal production (tongue) to the ear during signal emission. Of course, all of these hypotheses require further FE modeling and provide productive areas for future research.

Snipes, C.C.G. & Carter, R.T. (2022) The hyoid as a sound conducting apparatus in laryngeally echolocating bats. Journal of Anatomy, 240, 1020–1033. Available from: 10.1111/joa.13615

DATA AVAILABILITY STATEMENT

The 3D models used to build our FE models are available on Data Dryad (datadryad.org, https://doi.org/10.5061/dryad.3ffbg79k8).