Assessing the contribution of rare variants to complex trait heritability from whole genome sequence data

Abstract

Analyses of data from genome-wide association studies on unrelated individuals have shown that for human traits and disease, approximately one-third to two-thirds of heritability is captured by common SNPs. However, it is not known whether the remaining heritability is due to the imperfect tagging of causal variants by common SNPs, in particular if the causal variants are rare. Here we estimated heritability for height and body mass index (BMI) from whole-genome sequence data on 25,465 unrelated individuals of European ancestry. The estimated heritability was 0.68 (SE 0.10) for height and 0.30 (SE 0.10) for BMI. Low-MAF variants in low linkage disequilibrium (LD) with neighbouring variants were enriched for heritability, to a greater extent for protein-altering variants, consistent with negative selection thereon. Our results imply that rare variants, in particular those in regions of low LD, are a major source of the still missing heritability of complex traits and disease.

Introduction

Natural selection shapes the joint distribution of effect size and allele frequency of genetic variants for complex traits in populations, including that of common disease in humans, and determines the amount of additive genetic variation in outbred populations¹. Traditionally, additive genetic variation, and its ratio to total phenotypic variation (narrow-sense heritability) is estimated using resemblance between relatives, by equating the expected proportion of genotypes shared identical-by-descent with the observed phenotypic correlation between relatives^1,2. Such methods are powerful but blind with respect to genetic architecture. In the last decade, experimental designs that use observed genotypes at many loci in the genome have facilitated the mapping of genetic variants associated with complex traits. In particular, genome-wide association studies (GWAS) in humans have discovered thousands of variants associated with complex traits and diseases³. GWAS to date have mainly relied on arrays of common SNPs that are in LD with underlying causal variants. Despite their success in mapping trait-associated variants and detecting evidence for negative selection^4,5, the proportion of phenotypic variance captured by all common SNPs, i.e., the SNP-based heritability ($h_{\mathit{SNP}}^2$), is significantly less than the estimates of pedigree heritability ($h_{\mathit{ped}}^2$)^6,7. Using SNP genotypes imputed from a fully sequenced reference panel recovers additional additive variance^8,9, but there is still a gap between SNP-based and pedigree heritability estimates. The most plausible hypotheses for this discrepancy are that causal variants are not well tagged (or imputed) by common SNPs because they are rare and that pedigree heritability is over-estimated due to confounding of common environmental effects or non-additive genetic variation^7,10,11.

Understanding the sources of the still missing heritability and achieving a better quantification of the genetic architecture of complex traits is important for experimental designs to map additional trait loci, for precision medicine and to understand the association between specific traits and fitness. Here we address the hypothesis that the still missing heritability is to a large extent due to rare variants not sufficiently tagged by common SNPs, by estimating additive genetic variance for height and body mass index (BMI) from whole genome sequence (WGS) data on a large sample of 25,465 unrelated individuals from the Trans-Omics for Precision Medicine (TOPMed) program¹².

Results

Heritability estimates of height and BMI using WGS data

Data overview and quality control

We used a dataset of 66,790 genomes (Supplementary Table 1) from which we selected a subset of 25,465 genomes (Supplementary Table 2) with European ancestry by performing a two-step principal component analysis (PCA) on common and rare variants, using the 1000 Genomes¹³ and the Human Genome Diversity Panel¹⁴ as the reference panels (Online Methods; Supplementary Figure 1, Supplementary Figure 2). We further removed outlier individuals based on their heterozygosity by grouping variants with similar minor allele frequency (MAF) and linkage disequilibrium (LD) characteristics (Online Methods, Supplementary Figure 3, Supplementary Figure 4). After stringent quality control (QC), we retained 33.7M (out of 950M sequenced) variants, including 31.3M SNPs and 2.4M insertion-deletions (indels). We analysed variants observed at least 5 times in our dataset, which corresponds to a MAF threshold of 0.0001. The available phenotypes, height and BMI, were pre-adjusted for age and standardized to a mean of 0 and a variance of 1 in each sex and cohort group (Online methods, Supplementary Figure 5). We also analysed both traits with a rank-based inverse normal transformation (height_RINT and BMI_RINT) after adjusting for age and sex (Supplementary Note 1, Supplementary Figure 6).

First, we used common variants known to be associated with height and BMI in European samples to test the consistency of predictive power of polygenic scores for each trait within each cohort, and the prediction results were consistent with those reported previously¹⁵ and those in the UK Biobank (UKB) (Online Methods, Supplementary Figure 7). Then, to verify that we could replicate prior estimates of $h_{\mathit{SNP}}^2$ based on common SNPs, we selected ~992k HapMap 3 (HM3)¹⁶ SNPs from the sequence variants and estimated $h_{\mathit{SNP}}^2$ for height and BMI using the residual maximum likelihood analysis (GREML) approach implemented in GCTA¹⁷. We estimated an $h_{\mathit{SNP}}^2$ of 0.48 (SE 0.02) for height and 0.24 (SE 0.02) for BMI, again consistent with previous estimates^6,18. To mimic a SNP-array plus imputation strategy, we imputed sequence variants in common with those available on three commonly used arrays to the Haplotype Reference Consortium (HRC) reference panels¹⁹ (Supplementary Figure 8) and estimated heritability by stratifying the imputed variants according to MAF and LD using the GREML-LDMS approach⁸ implemented in GCTA (Online Methods, Supplementary Table 3 and Supplementary Table 4). We followed recommendations from Evans et al.²⁰ for the LD annotation and therefore used SNP-specific LD metrics rather than segment-based metrics used in Yang et al.⁸ (Online Methods, Supplementary Figure 9, and Supplementary Note 1). Estimates obtained using this imputation strategy are hereafter referred to as $h_{G+\mathit{IMP}}^2$. Estimates were in the range of 0.50-0.56 (SE 0.06-0.07) for height and 0.16-0.21 (SE 0.07) for BMI (Figure 1). When replacing the imputed SNPs with their sequenced genotypes, the estimates of $h_{G+\mathit{IMP}(\mathit{WGS})}^2$ consistently increased (Supplementary Figure 10) with most of the differences coming from the variants with 0.0001 < MAF < 0.001 in the low-LD group, where imputation accuracy was the lowest. Overall, we largely replicate results from previous studies for common or imputed variants.

Figure 1:

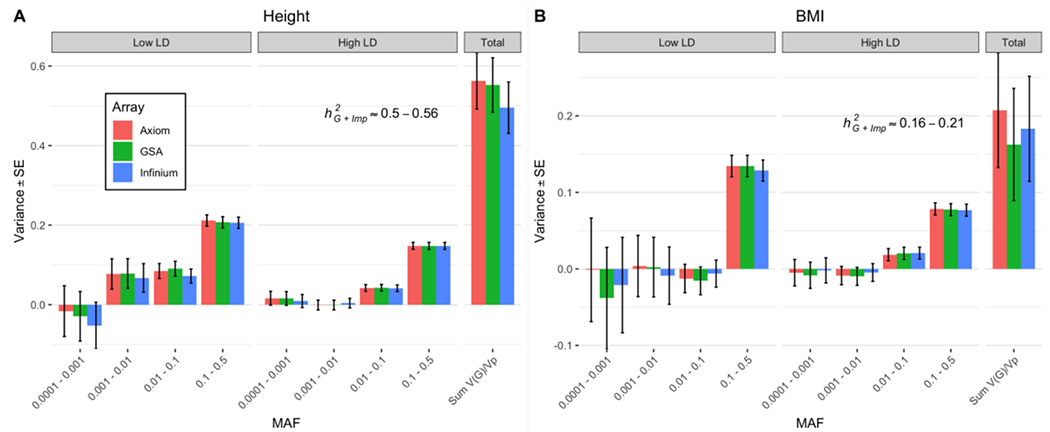
GREML-LDMS estimates with 8 bins (2 LD bins for each of the 4 MAF bins) correcting for 20 PCs (calculated from LD-pruned HM3 SNPs) after imputing SNPs from Illumina InfiniumCore24, GSA 24 and Affymetrix Axiom arrays using Haplotype Reference Consortium reference panels for N=25,465 samples. (A) Estimates of $h_{G+\mathit{IMP}}^2$ for height are between 0.50-0.56 (SE 0.06-0.07). (B) Estimates for BMI are between 0.16-0.21 (SE 0.07). The large SEs of the estimates for variants with MAF between 0.0001 to 0.001 can be explained by the large number of imputed variants in this MAF bin because the sampling variance of a SNP-based heritability estimate is proportional to the effective number of independent variants ³⁷. Between ~19.0M and ~20.0M variants in total are included in the analysis. The number of variants in each of the 4 MAF bins (twice the number in each LD bin) can be found in Supplementary Figure 8.

Estimation of trait heritability from WGS data

Having established that results from common or imputed variants were consistent with expectation, we then used all sequence variants with MAF > 0.0001 to estimate and partition additive genetic variance. We grouped variants according to MAF and LD (Supplementary Table 5, Supplementary Figure 11), using the GREML-LDMS partitioning method^8,20 with a median-based LD grouping strategy (Online Methods). Estimates of heritability based on WGS data ($h_{\mathit{WGS}}^2$) were consistently larger than $h_{G+\mathit{IMP}}^2$. When correcting for the first 20 principal components (PCs) computed from HM3 SNPs, we found $h_{\mathit{WGS}}^2$ ~0.70 (SE 0.09) for height and ~0.29 (SE 0.09) for BMI (Supplementary Figure 12). The estimates for height are close to the pedigree estimates of 0.7-0.8 while this is not the case for BMI at 0.4-0.6, respectively^7,21. We discuss below how much these results might be inflated by uncorrected population stratification.

The difference between $h_{\mathit{WGS}}^2$ and $h_{G+\mathit{IMP}}^2$ is predominantly explained by rare variants, in particular those in low LD with nearby variants. For the variants with MAF < 0.1, 0.31 of the phenotypic variance for height was accounted for by variants in the low-LD group but only 0.03 of the variance by variants in the high-LD group. For BMI, 0.05 of the phenotypic variance is accounted for by variants in the low-LD group and 0.03 from the ones in the high-LD group. Importantly, the large contribution of rare variants with low LD metrics could only be detected using WGS data as these variants are not present on SNP arrays and their imputation is not sufficiently accurate²². For both traits, our results confirm evidence for negative selection^4,5 (Supplementary Figure 13).

Impact of rare variant stratification

We conducted several analyses to attempt to quantify the contribution of any uncaptured population stratification to our estimates that is associated with rare variants. We fitted PCs in a linear model to investigate their contribution to phenotypic variance (Supplementary Note 3, Supplementary Figure 14), used UKB WES birthplace coordinates as a fixed covariate (Supplementary Note 3, Supplementary Figure 15), compared both datasets (Supplementary Note 3, Supplementary Figure 16) and investigated the effect of highly localized environmental effects (Supplementary Note 2, Supplementary Figures 17 to 22). Consistent with previous simulation studies using GWAS and polygenic scores^23,24, we found that very large, localized effects (effect size of 2 standard deviations) lead to an upward bias in the estimate of genetic variance attributed to rare variants but no bias was observed under realistic scenarios. We then quantified the number of PCs that are necessary to correct for population stratification within each MAF/LD bin using a correlation based approach. By further dividing SNP groupings based on their location on either the odd- or even-numbered chromosomes, we computed two sets of PCs for each LD/MAF bin (Online methods). Any variance explained by fitting a PC from one set of chromosomes on the other set would capture inter-chromosomal correlations, an indication of population stratification in the absence of relatedness. We did not have additional geographic information (e.g., place of birth or current residence) to directly quantify how much this strategy can detect and correct for the effect of spatial substructure in the TOPMed dataset, and again used UKB data where such spatial information is available. We estimated the number of relevant PCs to account for population stratification by quantifying the inter-chromosomal correlations, (Supplementary Figure 23). By using birth coordinates and PCs of the UKB samples, we could visualise the stratification on a map (Supplementary Figure 24) and quantify it using Moran’s index of spatial autocorrelation (Supplementary Figure 25). From these analyses on the UKB data we concluded that our approach to discover which PCs are necessary to account for population stratification is appropriate. After performing the same analysis on TOPMed samples, we identified 48 PCs across the 8 MAF/LD bins that could fully account for population stratification between sets of chromosomes. We then used those PCs computed from independent variants in the GREML-LDMS analyses, which decreased estimates of $h_{\mathit{WGS}}^2$ from 0.70 (SE 0.09) to 0.60 (SE 0.09) and from 0.29 (SE 0.10) to 0.23 (SE 0.10) for height and BMI respectively (Supplementary Figure 12), suggesting the presence of population stratification effects not captured by the 20 common variants PCs used in the analysis above. Importantly, biases in heritability estimates due to uncorrected population stratification do not match the actual proportion of trait variance that it explains. Finally, we repeated the GREML-LDMS analyses fitting 160 PCs (i.e., 20 PCs computed from each of the 8 MAF/LD bins) and observed very similar estimates to fitting only the 48 PCs identified from the inter-chromosomal correlations, indicating that population stratification has been accounted for when using the 48 PCs.

Impact of LD annotation

To further check the robustness of our results, we compared GREML-LDMS estimates by selecting a larger set of variants (Supplementary Note 1, Supplementary Figure 26, Supplementary Figure 27). We also tested a different estimator of relatedness (Supplementary Note 3, Supplementary Figures 28 to 30). Further, we tested how performing QC based on GRM elements was affecting heritability estimates (Supplementary Note 1, Supplementary Figures 31 to 33). These analyses indicated that the QC steps performed were ensuring the robustness of our heritability estimates. We also investigated the impact of LD annotations. We first used in-sample or out-sample LD/MAF from the UK10K dataset²⁵ and observed consistent heritability estimates suggesting that our inference from TOPMed annotation is not biased by using MAF and LD stratification from another dataset (Supplementary Note 1, Supplementary Figure 34). We then investigated the effect of LD partitioning and found that dividing each MAF bin into 3 or 4 LD bins could appropriately capture LD heterogeneity for rare variants MAF groupings, increasing the $h_{\mathit{WGS}}^2$ to 0.67 – 0.68 (SE 0.10) for height and 0.28 – 0.32 (SE 0.10) for BMI (Figure 2), with 48 PCs fitted as fixed covariates (Supplementary Note 1, Supplementary Figures 35 to 37).

Figure 2:

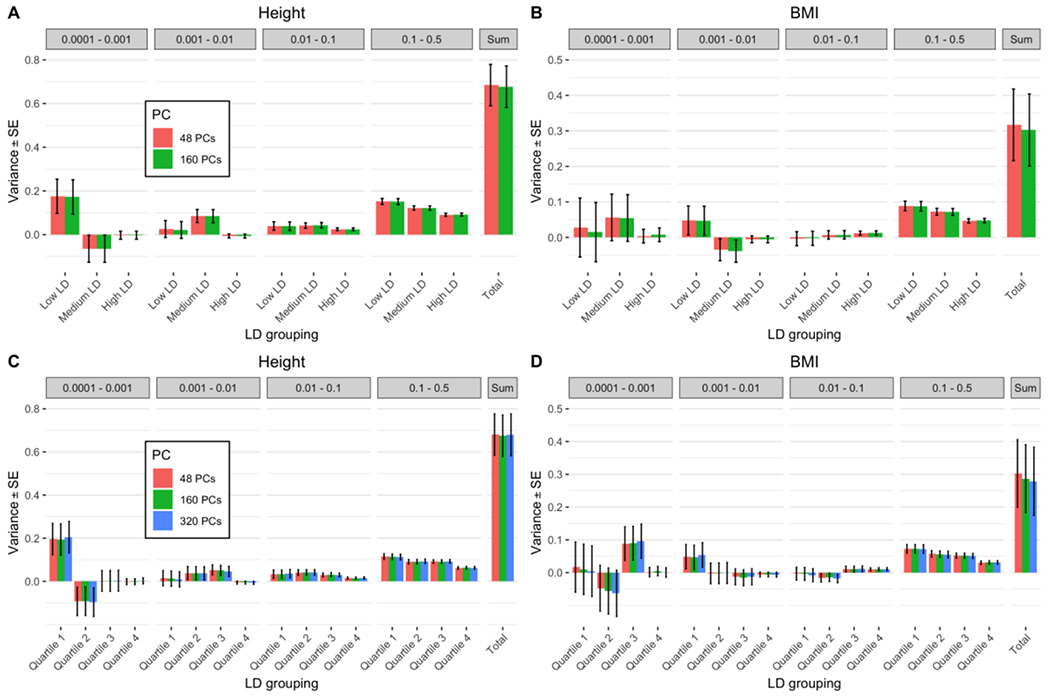
GREML-LDMS of height and BMI for N=25,465 samples using 3 or 4 LD groups for each MAF bin correcting for 48/160/320 PCs computed from WGS variants. Each variant was allocated in a tertile or a quartile according to its LD score. (A) Estimates using 3 LD bins for height: 0.68 (SE 0.09 – 0.10). (B) Estimates using 3 LD bins for BMI: 0.30 – 0.32 (SE 0.10). (C) Estimates using 4 LD bins for height: 0.67 – 0.68 (SE 0.10). (D) Estimates using 4 LD bins for BMI: 0.28 – 0.30 (SE 0.10).

Functional annotation

Having estimated and partitioned additive genetic variance from WGS data and investigated the robustness of the estimates, we then explored whether the variance could further be partitioned by functional genomic annotations. To investigate the specific contribution of low-LD variants with MAF < 0.1 to heritability, we partitioned the low-MAF and low-LD variants bins further according to the putative effect of a variant on protein coding using SnpEff²⁶. The protein-altering group comprises loss of function and non-synonymous variants whereas the remaining variant set comprises synonymous, regulatory or non-coding variants (Online methods, Supplementary Table 8). The proportion of protein-altering variants was different across the LD and MAF groups, with an increase in low MAF bins (Supplementary Figure 11), consistent with purifying selection on this class of variants⁵. Overall, we considered a total number of 11 groups (2 bins for variants with MAF > 0.1 and 3 MAF bins for variants with MAF < 0.1; each MAF bin is further split into 3 groups: low LD protein-altering, low LD non-protein-altering and high LD). When running a GREML-LDMS analysis with these 11 bins fitting the 48 PCs, the total estimates remained similar for height 0.61 (SE 0.09) and slightly increased for BMI 0.24 (SE 0.10), although these estimates are biased downward owing to the use of only 2 LD bins (further splitting by LD and variant effect would lead to fitting too many random effects in the analysis). Interestingly, the average variance explained per variant was larger for bins with protein-altering variants (low-LD) compared to bins with non-protein-altering variants (low-LD) or high-LD variants (Figure 3).

Figure 3:

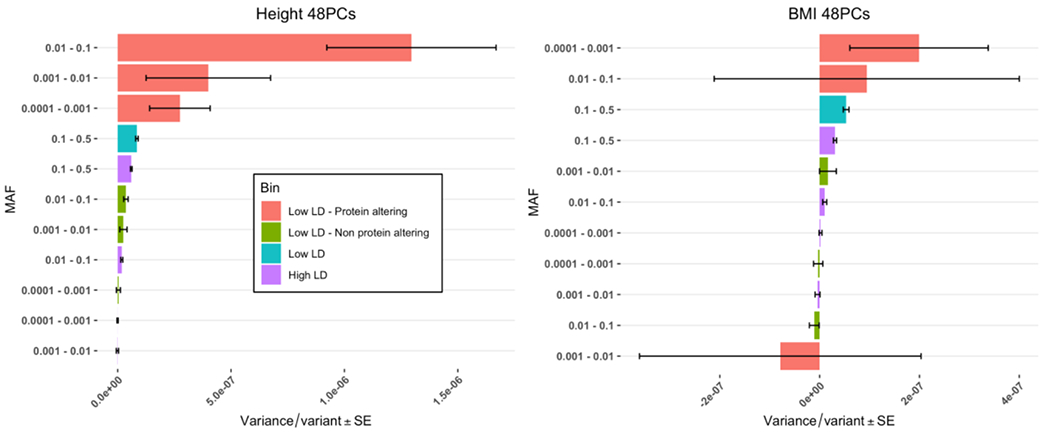
Variance explained per variant (the estimate of genetic variance divided by the number of variants in each bin) from GREML-LDMS with the low-LD and low-MAF (< 0.1) variants partitioned into 2 distinct categories according to the SnpEff putative effect of the variant (protein-altering or non-protein-altering), correcting for 48 PCs from WGS variants for N=25,465 samples. There is a total of 11 genetic components in this analysis. There is an apparent enrichment of heritability in the protein-altering groupings (low LD) over non-protein-altering (low LD) or high LD variants for height (A) as well as for BMI, although the standard errors for this trait are large (B).

Discussion

We have used a dataset with both WGS data and phenotypes to estimate the heritability of height and BMI captured by rare and common variants sequenced in a sample of 25,465 unrelated individuals from the TOPMed consortium. Our estimates largely but not fully recover the heritability estimated from pedigree data, in particular for height and less so for BMI. We observed an additional variance detected over and above SNP arrays or imputation due to rare variants, in particular rare protein-altering variants in low LD with other genomic variants.

To assess the robustness of these results, we conducted several follow-up analyses. We estimated the variance explained by correcting for a large number of principal components (up to 160) which may minimize any bias due to population stratification. We used a LD and MAF reference from another European ancestry dataset with whole genome sequences (Supplementary Note 1), and furthermore investigated the robustness of our estimates with alternative LD partitioning. All three analyses confirmed the validity of our estimates as additional variance is systematically detected from rare variants not previously tagged by imputation methods. We also estimated heritability for height and BMI using another GRM estimator and confirmed the robustness of our statistical framework. Moreover, comparing $h_{\mathit{WGS}}^2$ with $h_{G+\mathit{IMP}}^2$ allowed us to demonstrate that most of the heritability due to very rare variants (0.0001 < MAF < 0.001) was missing when using imputed data but revealed by using WGS data. We evaluated the loss of information on variance component estimates due to imputation compared to a similar variant coverage of WGS data and found negligible differences in the estimates of genetic variance. We investigated further the enrichment in heritability for different types of variants (high or low impact on the protein) and showed that for low-LD variants with MAF < 0.1, non-synonymous and protein-altering variants are more enriched for trait heritability than synonymous or non-coding variants, as shown in previous studies^27,28.

By investigating the variance explained by principal components from one chromosome set onto the other, we identified inter-chromosomal correlations among rare variants, indicating residual stratification in the sample. Inter-chromosomal correlation for rare variants is to be expected as it has been shown that recent population growth resulted in an excess of rare variants in European populations^29,30, and our analyses show that PCs derived from common variants only are insufficient to account for it. We used the UKB WES dataset to detect and quantify such a stratification in a sample independent of the TOPMed. Although we would expect a larger stratification in TOPMed than in the UKB samples, the similar inter-chromosomal correlation patterns show that we can capture it through fitting PCs as fixed effects in a GREML-LDMS analysis. The concordance of the GREML-LDMS estimates fitting either 48 PCs identified through the chromosome analysis or a larger number of PCs (e.g., 160, 20 PCs per bin) indicates that population stratification can be accounted for by a set of selected PCs. Population stratification could bias estimates of heritability if it is correlated with environmental effects. Estimated variance explained by rare variants could be inflated by large localized environmental effects, and such biases could be alleviated but not fully accounted for by fitting a limited number of PCs (Supplementary Note 2). Regression of the phenotypes on PCs accounted for little variance explained even when fitting a large number of PCs calculated from rare variants, but linear combinations of SNPs (i.e., PCs) may not be able to capture geographically localized effects, which may be non-linear in PCs. Similarly, there is no bias due to environmental effect associated with birthplace spatial coordinates using the UKB exome data. Nevertheless, the absence of any such effect in the UKB does not provide direct evidence of its absence in the TOPMed sample.

One potential bias seems to be related to extreme values in the diagonal elements of the rare variants GRMs. When removing individuals with high diagonal values, we saw an increase in $h_{\mathit{WGS}}^2$ estimate to levels that recover most of the remaining missing heritability, with a large contribution from the low-LD rare variants. This was not observed when removing individuals based on their off-diagonal elements. Differences between individuals in their diagonal values can reflect inbreeding, population structure, sequencing artefacts and sampling variance. IBD segments from different ancestries could also lead to an inflation of diagonal values of rare variants GRMs (Supplementary Note 3, Supplementary Figures 38 to 41). For common variants, the contribution to the estimate of genetic variance from differences in diagonal values is dwarfed by that from the off-diagonals, but this is not the case for rare variants (Supplementary Figure 42). Large diagonal values would bias the estimates downwards if they are not correlated with increased genetic variance. Further work is needed to fully understand the causes and consequences of the variance of diagonal values in GRMs estimated from rare variants.

Height is known to drive positive assortative mating in the population³¹, which implies that the genetic variance in the current population is larger than that in a randomly mating population². Although the difference between the true heritabilities in randomly and assortatively mating populations is typically small, recent findings using SNP array data have shown that estimates from GREML can be biased upwardly for traits undergoing assortative mating, and that it approaches the random mating heritability only for very large sample sizes³². We do not know how much our estimates from WGS data on height are biased because of assortative mating.

The experimental design to estimate trait heritability that is least biased by assumptions is to use sibling pairs and their realized identity-by-descent relationships estimated from marker data³³. Recently, Kemper et al. reported an estimate of 0.81 (SE 0.10) for the heritability of height in the current population using this design³⁴. Our GREML estimates for height accounting for population stratification are in the range of 0.60 to 0.70. Therefore, even if we consider the largest estimates then there is still a gap between those and the within-family estimate of heritability. One explanation for this discrepancy could be sampling variance, since our estimation errors are about 0.09 – 0.10 and that from Kemper et al. is even larger. On the other hand, while our research shows a large role of low-LD rare (0.0001 to 0.01) variants, variants with MAF<0.0001 (including singletons³⁵, which were ignored in our study), and structural variants, which are not well-captured by short-read WGS data, could contribute to trait variance and explain the apparent still-missing heritability. In addition, we only studied the autosome, and would expect the X chromosome to contribute a small amount of genetic variation. Finally, the current human genome assembly is known to contain gaps³⁶, which will lead to an under-estimation of genetic variance from WGS data but not in pedigree designs. A complete human genome, larger sample size for both the sibling and WGS population designs are needed to resolve these outstanding questions.

Our results lead to a number of important QC and analysis considerations when estimating and partitioning genetic variance from single-ancestry WGS data. Stringent quality control should be performed at multiple levels, including variant- and individual-level genotype QC by selecting high quality variants and rejecting individuals with outlying genome-wide heterozygosity; population stratification QC, by selecting individuals from the targeted ancestry using multiple rounds of global ancestry projections; and common variant trait association QC, by validating that prediction accuracy and SNP-based heritability are consistent with prior reports on the same trait, ideally in the same ancestry. Individual and pairwise sample QC could also be performed by estimating identity-by-descent segments and on properties of genomic relationship matrices. Finally, for the actual analysis it is important to fit a sufficient number of principal components estimated from both common and rare variants, and to stratify variants in as many LD, MAF and functional annotation strata as the sample size allows.

Our estimates of heritability from WGS data have standard error of about 9-10%. Since standard errors are approximately inversely proportional to sample size³⁷, doubling the sample size to 50,000 would narrow errors to ~5% and would allow further and more precise partitioning of genetic variance. Until now the question of the contribution from rare variants to the missing heritability could only be investigated through imputing genotypes from WGS reference panels that was subject to imperfect tagging. Our results quantify this contribution and allows for recovery of some of the remaining missing heritability. It would be interesting to further partition the genome (by variant type, predicted variant deleteriousness³⁸ and more LD/MAF groupings), but standard errors of the estimates would be too large given our current sample size. Similarly, with a larger sample size, contribution to the heritability from assortative mating could be quantified³⁹. The contribution of rare variants to narrow-sense heritability, larger than expected under a neutral model, also reinforces previous observations that height- and BMI-associated variants have been under negative selection^4,5,8, although population expansion could also lead to an increase in heritability from rare variants⁴⁰. Once again, a larger sample size would allow us to draw stronger conclusions on the selective pressure on the genetic variants associated with the two traits. Additionally, the TOPMed samples come from multiple cohorts across the US are potentially subject to multiple and diverse non-genetic effects. Some cohorts of the TOPMed program are ascertained towards diseases correlated with high BMI values. Having case-control cohorts as part of the larger analysis might affect the robustness of the estimates. Finally, our sample for analysis was restricted to a single ancestry. Since genetic architecture and heritability are per definition population specific, future analyses using data from other ancestries will reveal how generalisable our results are.

Our results have important implications for the still missing heritability of many traits and diseases⁷. Indeed, the ratio of SNP to pedigree heritability for diseases is lower than for height and BMI, leading to potentially more discovery from rare variants contributing to diseases using WGS data. Our results are also important for polygenic scores as using WGS data could, in principle, lead to predictors with larger prediction accuracy for many polygenic diseases. With the cost for sequencing still much higher than array genotyping, large scale WGS data acquisition is currently limited to national initiatives such as the TOPMed and other programs but is bound to expand in the next decade. Large cohorts of genotyping array data will still prove useful for gene discovery or predictions of common diseases and should complement WGS data for a broader understanding of genetic architecture. In the future, WGS programs for specific diseases on large cohorts could lead to a large increase of low MAF variants identified. Sample sizes required to detect such variants from genome-wide association studies using sequence data are of the same order of magnitude as current well-powered GWAS on common variants, i.e., hundreds of thousands to millions of individuals.

Online Methods

Data collection

In this study, we used Whole-Genome Sequence (WGS) data from the Trans-Omics for Precision Medicine (TOPMed) Program. The TOPMed program collects WGS data from different studies and centers, in the United States and elsewhere, in partnership with the National Heart, Lung, and Blood Institute (NHLBI, see URLs). The “freeze 8” version of the data includes 140,306 samples containing ~920M SNPs and indels in the called variants files (as BCF, binary variant call format). These variants have been called using genome assembly GRCh38 as human genome reference (see URLs for methods). Data were downloaded from dbGap using the ASCP 3.91.168954 software. Participant consent was obtained for each of the 20 studies (Supplementary Table 1, Supplementary Table 2) containing Europeans samples in the freeze 8 as well as the associated phenotypes for height and BMI. Ethics approval to conduct the study was obtained from the University of Queensland Human Research Ethics Committee (EC00457).

Quality control

We selected freeze 8 samples with height and BMI phenotypes available (N=66,790). After removing individuals under 18 years old, we had 64,930 adults left. For each sex within each of the 20 different studies included in this analysis (each cohort), we regressed the height and BMI according to their age and kept the residuals. Moreover, to remove differences in mean and standard deviation between sexes and among cohorts, we standardized the residuals by the standard deviation of each sex and cohort. The standardized residuals on height and BMI of each gender group of each cohort followed a distribution with a mean of 0 and variance of 1 (Supplementary Figure 5). We also applied a rank-based inverse normal transformation on the height and BMI (Height_RINT and BMI_RINT) after adjustment for age and sex. On the genotypes, we performed a multi-step quality control. We first selected the samples with phenotypes available (N=66,790) and retained only the high-quality variants that passed a SVM classifier. The SVM classifier was trained using variants present on genotyping arrays labelled as positive controls, and variants with many Mendelian inconsistencies labelled as negative controls. We then excluded variants with genotypes missingness rate > 0.05, Hardy-Weinberg equilibrium test P value <1 × 10⁻⁶, or with a minor allele frequency < 0.0001 using PLINK v1.9 (see URLs¹). To select samples of European ancestry, we performed a similar QC on the 2,504 samples of the 1000 Genomes Project (with a MAF threshold of 0.004, to account for the difference in sample size between datasets). On the 1000 Genomes genotypes, we used different parameters to select two sets of independent variants for common (M=1,495,743, MAF range of 0.01 to 0.5, window size of 50kb and R² threshold of 0.1) and rare variants (M=1,512,042, MAF range of 0.004 to 0.01, window size of 100kb and R² threshold of 0.05). We computed 20 principal components on the 1000 Genomes samples using common and rare variants and then used the variants loadings to project TOPMed samples on the PCs (with respectively 579,015 and 1,268,148 variants matching) (Supplementary Figure 1).

TOPMed samples were classified as of European ancestry if their Euclidean distance, based on the first 4 PCs computed from common variants weighted by their respective eigenvalues, to the cluster of the 1000 Genomes samples of European ancestry was lower than 3 SD of the within-cluster distance (N=37,212 samples left). We then performed similar filtering on the first 4 PCs computed rare variants, which removed extra 274 samples (N=36,938). To further remove ancestral outliers not captured by PCs, we used global ancestry estimates in the TOPMed samples. These were inferred using RFMix^2,3 from 639,958 autosomal SNPs on 938 individuals (grouped in 7 super-populations) from the Human Genome Diversity Panel. We removed 2,900 individuals with inferred global ancestry more than 3 standard deviations away from the mean of European, East-Asian, African and North-American populations (Supplementary Figure 2).

For the remaining 34,038 individuals, we built a genetic relatedness matrix using variants on HM3 reference panels with a MAF > 0.01 and removed one of each pair of individuals with estimated genetic relatedness > 0.05, resulting in 28,755 unrelated individuals.

The last QC step was to remove individuals showing an excess of heterozygosity after we noticed individuals showing short IBD segments from different ancestries but having a high impact on the off-diagonal elements of the GRM for the rare variant bins (see Supplementary Note 3 and Supplementary Figures 38 to 41). As described above, we stratified the variants by MAF and LD into 8 bins and computed the sample heterozygosity using the variants in each bin. To obtain a uniform distribution of heterozygosity across MAF range, we performed 4 rounds of filtering, removing samples 3 standard deviations away from the mean heterozygosity of the samples within each MAF and LD bin (Supplementary Figure 4).

At the end of all the quality control steps, we retained 25,465 unrelated individuals of European ancestry and 33.7 million variants (MAF and LD distributions of the variants are shown in Supplementary Figure 11). We also computed a 2^nd dataset with the same samples but using all the genotyped variants with a MAF > 0.0001 (not only the SVM-filtered high-quality ones). We maintained SNP QC for each step of the QC process and also recomputed the LD score with the final samples.

Polygenic scores from common variants

To perform joint genotype-phenotype QC, we constructed a polygenic score (PGS) for each trait using trait-associated variants identified in the UKB. We performed GWAS of height and BMI in N=400,831 European ancestry participants of the UKB using fastGWA⁴. We then selected 1362 and 452 independent (LD r² < 0.01) genome-wide significant SNPs (P < 5×10⁻⁸) to calculate PGS of height and BMI, respectively, of which 1360 and 449 SNPs were matched to our TOPMed data. For each phenotype, we regressed the standardized phenotype on the mean-centred PGS and computed the regression slope and the variance explained by the predictor (Supplementary Figure 7). To make a direct comparison with a non-TOPMed dataset we performed the same analysis using a hold-out sample of 14,587 UKB participants independent of our GWAS discovery set. The regression of the predicted trait on its PGS gave a slope of ~0.90 for height and ~0.83 for BMI, with a corresponding variance explained of 0.25 and 0.04, respectively.

Statistical framework of the GREML analysis

The GREML analysis is based on the idea to fit the effects of all the variants as random effects in a mixed linear model (MLM),

$$\mathit{Y}=\mathit{X}\mathit{B}+\mathit{g}+\mathit{\epsilon }$$

where XB is a vector of fixed effects such as age, sex and in our case the principal components of each subset of variants, g is an n x 1 vector of the total genetic effects captured by all the sequenced variants of all the individuals (with n being the sample size) and ε is a vector of residuals effects. From MLM, g follows a distribution $\mathit{g}~N(0,\mathit{A}{\sigma }_g^2)$ where A is a GRM interpreted as the genetic relationship between individuals. We estimate ${\sigma }_g^2$ using the REML algorithm⁵.

The genetic relationship between individuals j and k (A_jk) was estimated by the following equation:

$$A_{jk}=\frac{\underset{i=1}{\overset{N}{{{\displaystyle \sum }}^{\text{}}}}\left(x_{ij}-2p_i\right)\left(x_{ik}-2p_i\right)}{2\underset{i=1}{\overset{N}{{{\displaystyle \sum }}^{\text{}}}}{p}_i\left(1-p_i\right)}$$

where x_ij (x_ij takes value in 0,1 or 2) is the minor allele count for SNP i in individual j, N is the number of variants, and p is the sample minor allele frequency.

We refer to this method of estimating pairwise relationships as the ratio of total SNP covariance and the total SNP heterozygosity over loci, also called the ratio of averages^6,7. By using the sample allele frequencies, A_jk does not represent a measure of kinship between two individuals, although the GRM should be highly correlated with the kinship matrix if we were to have full and accurate pedigree data on the entire sample ⁶.We calculated multiple GRMs based on subsets of SNPs (stratified by MAF, LD, annotations, etc) and fit them as random effects according to a more general model:

$$\mathit{Y}=\mathit{X}\mathit{B}+\sum _{i=1}^r{\mathit{g}}_i+\mathit{\epsilon }$$

where the phenotypic variance ${\sigma }_P^2$ is the sum of the residual variance and the variance of each of the i^th genetic factor (each with a corresponding GRM).

To compare the methods to calculate the genetic relationship between individuals j and k we also used an estimator where the ratio is the SNP covariance divided by SNP heterozygosity (the average of ratios) from the following equation:

$$A_{jk}=\frac{1}{N}\sum _{i=1}^N\frac{\left(x_{ij}-2p_i\right)\left(x_{ik}-2p_i\right)}{2p_i\left(1-p_i\right)}$$

It has been shown previously that this estimator is less accurate than the ratio of average estimator when there is some degree of relatedness among samples⁶.

Proportion of genetic variation captured by imputation

Previous REML estimates based on rare variants were conducted by imputing SNP chip data on a reference panel such as 1000 Genomes⁸. To check the consistency of our dataset with previous estimates, we mimicked SNP chip data by selecting SNPs in our dataset present on Illumina InfiniumCore24 v1.2, GSA 24 V3.0 and Affymetrix UKB Axiom arrays. We downloaded the list of SNPs of these arrays, the UCSC to Ensembl reference and the GRCh37 reference. With those, we selected subsets of the SNPs in common between the TOPMed dataset and each of the SNP arrays. After this merging and cleaning process, we retained the majority of the SNPs present on each array (Supplementary Table 3). We then imputed our dataset on the Michigan imputation server⁹. Imputation was performed in multiple stages. Prior to imputation, each SNP coordinate was lifted from hg38 to hg19. Then each chromosome was phased against Europeans from HRC.r1.1⁹ reference using EAGLE2 2.4¹⁰. In a second stage, data were imputed using Minimac 4. On the imputed datasets, we removed variants with imputation info score < 0.3, missingness rate > 0.05, Hardy-Weinberg equilibrium test P-value <1 × 10⁻⁶, or MAF < 0.0001 and individuals with missingness rate > 0.05. After imputation and filtering, we had between ~19 and 20M SNPs left in each imputed dataset (Supplementary Table 4 and Supplementary Figure 8). In each imputed dataset, we stratified SNPs into 4 MAF bins (0.0001 < MAF < 0. 001, 0.001 < MAF < 0.01, 0.01 < MAF < 0.1, 0.1 < MAF < 0.5). For each of the 22 autosomes, we calculated the LD score of each variant with the others on a sliding window of 10Mb using GCTA software⁵. We performed two types of LD binning, selecting variants based on their individual LD scores or on their segment-based LD scores (segment length=200Kb) (Supplementary Figure 9). Each of the 4 MAF bins was divided into 2 more bins, one for variants with LD scores above the median value of the variants in the bin (high LD bin) and one for variants with LD score below median (low LD bin) (Supplementary Table 5). We then used GCTA to perform a GREML-LDMS analysis with the first 20 PCs calculated using HM3 SNPs from the WGS dataset fitted as fixed effects and the variants in the 8 MAF and LD bins as 8 random-effect components (Figure 1).

To assess the influence of imputation errors on variance estimates, we selected, for the dataset imputed from the SNPs on the Axiom array, the SNPs that were available in both the imputed UKB data and the TOPMed WGS data. We had 17.9M SNPs in both the TOPMed and the imputed datasets. In each of these pairwise datasets (a set from the TOPMed WGS and another set from the imputed UKB), we partitioned SNPs in 8 bins, according to their MAF and LD scores, similarly to the analysis above. We then ran a GREML-LDMS analysis on height and BMI in each dataset with either 20 principal components calculated from HM3 SNPs or 160 PCs (20 PCs computed from each of the 8 MAF/LD bins) fitted as fixed covariates.

GREML estimates from WGS data

Before estimating the proportion of phenotypic variance due to additive genetic factors from WGS data we initially wanted to check for consistency with previous studies and performed a single-component GREML analysis (GREML-SC approach) in GCTA using HM3 SNPs with 20 PCs. We calculated the PCs from LD-pruned SNPs and fitted them as fixed effects in the GREML-SC analysis. Note that we chose the GREML-LDMS analysis to estimate heritability of height and BMI when using the entire dataset for the following reasons. It has previously been shown⁸ that a GREML-SC approach can give a biased estimate of h² if causal variants have a different MAF spectrum from the variants used in the GREML analysis. Moreover, if two variants in the same GRM have different LD properties, this can also lead to biased estimates of heritability. We performed a GREML-LDMS analysis using 4 MAF bin (0.0001 < MAF < 0. 001, 0.001 < MAF < 0.01, 0.01 < MAF < 0.1 and 0.1 < MAF < 0.5) and 2 LD bins. Similar to what was done using data imputed from array SNPs, we defined 8 bins by splitting each of the 4 MAF bin into two LD bins (Supplementary Figure 12). Within each of these 8 bins, we calculated 20 PCs that we fitted together as fixed covariates to correct for population stratification (160 PCs in total). To investigate how low-quality variants would bias estimates, we also conducted an analysis including the variants that did not pass a support vector machine (SVM) classifier or additional filters on excess of heterozygosity and Mendelian discordancy.

To investigate the robustness of the assumptions on the relationship between MAF and effect size, we ran a GREML-LDMS analysis on the previously defined 8 MAF and LD bins using either the ratio of averages over loci or the average over loci of ratios methods to compute the GRMs (Supplementary Figure 30). To investigate the relationship between LD and effect size, we also divided each MAF bin into 3 (low, medium and high LD) or 4 LD bins (quartiles) with a similar number of variants and calculated the GRMs using the ratio of averages method. We ran a GREML-LDMS analysis using the 12 or 16 GRMs (Figure 2, Supplementary Figure 36). For each model, we calculated the corresponding AIC using the log-likelihood and the number of fixed and random effects fitted in the model (Supplementary Figure 37).

On the 25,465 individuals left after the QC process, we also applied a more stringent relatedness threshold of 0.025, which further removed 1,255 samples with estimated relatedness from HM3 SNPs between 0.025 and 0.05. We performed GREML-LDMS on height and BMI using 4 MAF and 2/3/4 LD bins fitting 48 PCs as fixed effects.

Enrichment analysis using the variant effect consequence

Using SnpEff annotations¹¹ and the LD and MAF bins defined from the GREML-LDMS analysis on the WGS data mentioned above, we further separated the low-LD variants in each of the 0.0001 < MAF < 0.001, 0.001 < MAF < 0.01 and 0.01 < MAF < 0.1 bins into 2 bins according to their predicted variant effects. The SnpEff variant effect annotations were divided into 4 categories according to their predicted effects on gene expression and protein translation. The 4 categories are based on the Sequence Ontology terms used in functional annotations (Supplementary Table 8). Putative effects on proteins can be “High” (protein truncating variants, frameshift variants, stop gained, and stop lost etc), “Moderate” (mostly non-synonymous variants), “Low” (mostly synonymous variants) or “Modifier” (mostly intronic and upstream or downstream regulatory variants). We merged variants having “High” and “Moderate” impacts in a “Protein-altering” bin and variants having “Low” and “Modifier” impacts in a “Non-protein-altering” bin. We then ran a GREML-LDMS analysis with 11 GRMs, fitting the 48 PCs shown to well capture the effect of population stratification (Figure 3) as fixed covariates. To compute the variance explained per SNP, we divided the estimate of variance explained for each bin by the number of variants in the bin. The standard error was obtained by dividing the standard error of the estimated variance explained for the bin by the number of variants in the bin.

Investigation of the influence of spatial coordinates on GREML estimates using whole-exome sequence (WES) data from the UKB

We used the spatial coordinates in the UKB to evaluate the influence of local spatial stratification on GREML estimates. Based on a GRM derived from HM3 SNPs in the UKB, we selected a set of 35,867 unrelated individuals of European ancestry with WES data available. These individuals also had phenotypical data, including age, sex, height, BMI, assessment center and north / east birth coordinates. For each sex, we regressed height and BMI against age and then standardized the residuals to a mean of 0 and variance of 1. We also performed a RINT for both height and BMI. We imputed the missing north and east birth coordinates (UKB data field 129 and 130) using the average birth coordinates of the samples from the same assessment center and scaled each coordinate to fall into 0 to 1 range. Quality control on the genotype data were excluding variants with genotypes missingness rate >0.05, Hardy-Weinberg equilibrium test P value < 1 × 10⁻⁶, or with a minor allele count > 3 (similar MAF than the TOPMed dataset) and excluding individuals with sample missingness rate > 0.05. We had 2,075,174 variants left in the dataset. We removed HM3 SNPs duplicated with the imputed dataset from SNP array and calculated 14 GRMs based on individual LD and MAF properties of the variants. We ran a GREML-LDMS fitting 14 GRMs from exome variants and a GRM from HM3 SNPs imputed from SNP array. We fitted as fixed covariates 20 PCs computed from HM3 variants. To evaluate the effect of local spatial stratification, we also fitted the east and north birth coordinates on top of the PCs.

We compared our estimates with TOPMed by selecting variants found in both the TOPMed WGS and UKB WES datasets. We kept ~678k variants observed in both datasets, filtered out the ones showing a deviation from Hardy-Weinberg with a Fisher’s exact test p-value < 0.05 (Bonferroni corrected) and then grouped them into ~130K common ones (MAF > 0.01) and ~548k rare ones (0.0001 < MAF < 0.01). We calculated 4 GRMs (MAF- and LD-stratified) for each of the TOPMed and UKB Exome datasets and ran a GREML-LDMS analysis fitting 20 PCs calculated from their respective HM3 SNPs.

Rare variants population stratification

To evaluate the effect of population stratification, we separated the UKB Exome dataset into whether a variant was on odd or even chromosomes. For each of these two sets of variants, we stratified them by MAF and LD into 14 bins, pruned them for LD in each bin using different criteria (window size and LD r² threshold of 50 and 0.1 respectively for common variants and of 2000 and 0.01 respectively, for rare variants), and used the pruned variants to compute 150 PCs in each bin. We then evaluated the population stratification by looking at the adjusted R² of fitting each PC from a set of chromosomes against all the PCs from the other chromosomes in each MAF/LD bin. For each PC, by taking the mean of the two R² computed on a chromosome set on the other and vice versa, we obtained an average R² of inter-chromosomal correlations for each MAF/LD bin (Supplementary Figure 23). For each individual, we computed across all MAF/LD bins, $P{C}_{i:1>50}^{odd-Even}=P{C}_i^{Odd}\ast P{C}_i^{Even}$ as the product of the PCs of odd and even chromosomes. After centering and scaling, we applied the RINT transformation to smoothen outliers and plotted this PC interaction term for each individual according to their birth coordinates (Supplementary Figure 24). With this PC interaction term, we computed Moran’s I as a measure of spatial autocorrelation (Supplementary Figure 25). We repeated the same procedure (computing PCs using LD-pruned SNPs from odd and even chromosomes) for the TOPMed individuals (Supplementary Figure 23). For the adjusted R² that measures inter-chromosomal correlations, we used a segmented regression to find the optimal number of PCs to be fitted in the GREML-LDMS analysis to account for population stratification.

Influence of outlier samples on heritability estimates

To investigate the influence of outlier samples/pairs on the heritability estimates, we investigated ways to filter outlier individuals other than the QC step on heterozygosity. We also noticed a strong relationship between the proportion of African ancestry and the diagonal values of the GRM constructed from variants in the MAF range of 0.0001 to 0.001 in the high-LD bins (Supplementary Note 3, Supplementary Figure 43). To investigate the influence of extreme values across the GRMs, we removed extreme values from the GRMs computed on unrelated individuals of European ancestry (N=28,755). We removed samples based either on the GRM diagonals, off-diagonals or both. For the filtering based on diagonals, we removed samples with diagonal values smaller than 0.7 or larger than 1.3 across any of the 8 WGS GRMs, i.e., corresponding to approximatively the mean of the 3 standard deviations thresholds from each rare-variants GRM (Supplementary Table 6). This step removed 3,426 individuals, with the extreme values mostly coming from the rare variants GRMs in the high-LD groups. For the filtering based on off-diagonals, we selected a value of 0.1 across all GRMs as a cut-off to remove one of each pair of individuals with large off-diagonal values. This threshold was selected as a compromise to maximise the number of samples left in the analysis while investigating the effect of large off-diagonal values. It is of note that the pairs with large off-diagonal values were all found in the rare variants GRMs in the high-LD bins, which is partly because we have pruned individuals for relatedness based on the GRM derived from HM3 SNPs. This process removed additional 2,061 individuals. Finally, we also filtered samples based on both their diagonal and off-diagonals (pair > 0.1) GRM values (4,526 samples removed in total).

Data Availability

The individual-level genotype and phenotype TOPMed data used in this manuscript are available through dbGaP. The dbGaP accession numbers for all TOPMed studies referenced in this paper are listed in Supplementary Table 1. The genotypic data is under restricted access. This research was conducted under TOPMed proposal ID 3235. Individual-level genotype and phenotype data for the UKB is available through formal application (http://www.ukbiobank.ac.uk). The UK10K data is accessible at https://www.uk10k.org/. The 1000 Genomes genotype data are available at https://www.internationalgenome.org.

Code Availability

No custom code was used for this study. GRM computation, LD score calculations, PC projections and GREML analyses were performed using GCTA 1.92.4 (https://cnsgenomics.com/software/gcta/#Download). WGS analyses followed the steps described here: https://cnsgenomics.com/software/gcta/#GREMLinWGSorimputeddata. Plink 1.9 (https://www.cog-genomics.org/plink/1.9/) and 2.0 were used in this study (https://www.cog-genomics.org/plink/2.0/). R 3.4.1 (https://www.r-project.org/) and Tidyverse packages (https://www.tidyverse.org/) were used to generate figures and additional analyses. KING 2.2.6 was used for IBD calculations (https://www.kingrelatedness.com/). All the parameters used for analyses are described in the Methods sections.

Statistics and reproducibility

No statistical method was used to predetermine sample size. All box plots depict the first and third quartiles as the lower and upper bounds, respectively. The whiskers represent 1.5 × the interquartile range (IQR) and the center depicts the median. All statistical tests used are defined in the figure legends. We excluded UKB and TOPMed participants of non-European ancestries as described in Methods. Quality control criteria were applied to genetic variants. We did not use any study design that required randomization or blinding.