HIGHLIGHTS
-
•
Starting testing programs early is effective in reducing the infection spread.
-
•
Starting testing programs early also leads to less self-isolation in total.
-
•
Higher symptomatic isolation compliance is favored if early testing is unavailable.
-
•
Delay in the start of testing results in extra testing capacity to make up.
Keywords: Infectious disease, diagnostic testing, compliance with self-isolation, simulation, mathematical modeling
Abstract
Introduction
Diagnostic tests can play an important role in reducing the transmission of infectious respiratory diseases, particularly during a pandemic. The potential benefit of diagnostic testing depends on at least 4 factors: (1) how soon testing becomes available after the beginning of the pandemic and (2) at what capacity; (3) compliance with isolation after testing positive; and (4) compliance with isolation when experiencing symptoms, even in the absence of testing.
Methods
To understand the interplay between these factors and provide further insight into policy decisions for future pandemics, we developed a compartmental model and simulated numerous scenarios using the dynamics of COVID-19 as a case study.
Results
Our results quantified the significant benefits of early start of testing and high compliance with isolation. Early start of testing, even with low testing capacity over time, could significantly slow down the disease spread if compliance with isolation is high. By contrast, when the start of testing was delayed, the benefit of testing on reducing infection spread was limited, even when testing capacity was high; the additional testing capacity required increased superlinearly for each day of delay to achieve a similar infection attack rate as in starting testing earlier.
Conclusions
Our study highlighted the importance of the early start of testing and public health messaging to promote isolation compliance when needed for an ongoing effective response to COVID-19 and future pandemics.
Graphical Abstract

INTRODUCTION
The impact of pandemics on health and society has been significant throughout history and continues to grow.1 For example, coronavirus disease 2019 (COVID-19) has caused >5.57 million deaths worldwide (as of January 20, 2022).2 To control the spread of infectious diseases, governments and public health agencies rely on nonpharmaceutical interventions, such as physical distancing, and pharmaceutical interventions, such as vaccines or therapeutics. Widespread and frequent diagnostic testing can help to contain infection spread when the individuals who test positive comply with isolation,3, 4, 5 which significantly reduces disease transmission.6,7 However, it takes time to start implementing testing programs owing to the challenges associated with the development and distribution of testing kits, the collection of patient samples, and the limited laboratory capacity available for testing.8 For example, although the Centers for Disease Control and Prevention confirmed the first COVID-19 case in the U.S. on January 20, 2020,9 the total number of specimens tested daily for COVID-19 in the U.S. remained below 1,000 until March 4, 2020,10 whereas the number of confirmed cases reached 1,234 on March 15, 2020.11 Moreover, it is estimated that only 1 in 4 COVID-19 infections were reported.12 The impact of testing also depends on the individuals’ compliance with isolation protocols after receiving a positive test result or when experiencing symptoms (even in the absence of testing). In practice, there is high variability in self-isolation compliance across different settings. According to surveys, estimates of compliance with isolation across different communities worldwide ranged from 18% to 95%13, 14, 15, 16 and from 40% to 95% in the U.S.17,18 An individual's compliance with isolation depends on many factors, for example, the availability of financial support during isolation and/or the presence of symptoms.19,20
The effectiveness of diagnostic testing during an infectious disease outbreak depends on at least the following 4 factors: (1) how soon testing becomes available since the beginning of the pandemic and (2) at what capacity, (3) compliance with isolation after testing positive, and (4) compliance with isolation when experiencing symptoms. To understand the impact of these factors and their interactions on health outcomes, we developed a compartmental model21 to simulate the transmission dynamics under various levels of diagnostic testing capacity and compliance with 2 types of isolation: (1) post-testing isolation, where an individual self-isolates after receiving a positive test result, and (2) symptomatic isolation, where an individual self-isolates when experiencing symptoms in the absence of a diagnostic test. The compliance rate refers to the fraction of individuals who comply with post-testing or symptomatic isolation, respectively. Across different scenarios, we estimated and compared the infection attack rate (IAR) and isolation percentage (IP), that is, the percentage of the population who self-isolated at some point during the pandemic. Furthermore, we quantified the impact of the start day of testing (relative to Day 1, when the first case occurred) on the spread of the disease and identified the amount of additional testing capacity required to maintain an IAR similar to that of an equivalent scenario with an earlier start day of testing.
Compartmental models,21 including basic and extended Susceptible–Infected–Recovered (SIR) models, have been widely used in modeling the progression and spread of infectious diseases,22,23 the impact of behaviors,24 and interventions such as lockdowns or vaccines.25, 26, 27, 28 Complementing and extending previous work (e.g., Agusto et al.29 and Anand and colleagues30), the compartmental model proposed in this work explores the impact of the complex interactions between the testing start day, the dynamically changing daily diagnostic testing capacity, and the population behaviors (i.e., compliance with self-isolation) on health outcomes to help inform decisions regarding effective deployment of interventions.
METHODS
Model Description
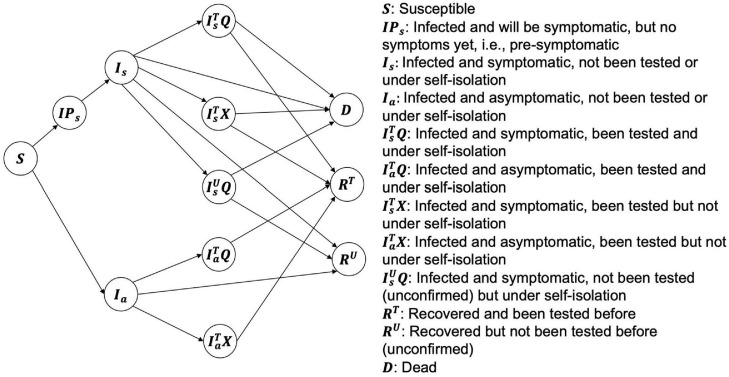
The compartmental model21 (an extended SIR model) developed in this study consists of 12 states, which fall under 4 main groups: (1) : susceptible; (2) : infected (including , presymptomatic; , symptomatic; , asymptomatic), (3) : recovered (, recovered and diagnosed with a test; , recovered but have not been diagnosed owing to the absence of testing), and (4) : dead. Figure 1 shows the definitions of the states and transitions between the states. In addition to and individuals who are infected were further divided into 5 groups (), considering (1) whether they are symptomatic () or asymptomatic (), (2) whether they have been diagnosed with testing () or have not been tested (i.e., unconfirmed) (), and (3) whether they are isolated/quarantined () or not ( after being diagnosed by a positive test. For example, refers to the group of infected individuals who are asymptomatic (), diagnosed with a positive test (), but not under isolation (). Equations 1–12 in Methods of the Supplemental Materials describe the dynamics of the model in detail, taking account of both testing availability and self-isolation compliance.
Figure 1.
Simplified diagram of the extended SIR model incorporating compliance with post-testing isolation and symptomatic isolation.
SIR, Susceptible–Infected–Recovered.
Letting and denote the compliance rates of post-testing (with or without symptoms) and symptomatic (without testing) isolation, respectively, that is, the proportion of diagnosed (with a positive test) or symptomatic (but not tested/diagnosed) patients who self-isolate, we assumed that the compliance rate of post-testing isolation for symptomatic (patients is greater than that for asymptomatic patients (, that is, , and the compliance rate of post-testing isolation for symptomatic patients (is greater than the compliance rate of symptomatic isolation, that is, . The parameter represents the proportion of infections that were symptomatic, with an estimate of .31 Appendix Table 1 presents the parameters and their values/ranges.32, 33, 34, 35 Note that owing to nonpharmaceutical interventions, which contribute to the reductions in the basic reproduction number,36 we assumed that the transmission rates, and , linearly decrease during the first 4 months after the identification of the first case and then stabilize.
When there was limited testing capacity, we assumed that symptomatic individuals were prioritized for diagnostic testing; if the capacity was sufficient to test all symptomatic individuals, the remaining capacity would be uniformly distributed among all other individuals who have not been diagnosed before. We assumed that the available testing capacity increased linearly daily.
Using the model described earlier, we simulated a cohort of 500,000 individuals for a 1-year time horizon and estimated the number of infections and isolations. The cohort size was selected on the basis of the rough median population of the largest 100 cities in the U.S. For example, the population in Atlanta was estimated to be 498,715 in 2020.37 The simulations were initialized with 1 infected and symptomatic individual on Day 1. The simulation was coded using the statistical software R,38 and the package deSolve was used to solve the differential equations.39
Simulation Scenarios
We simulated various scenarios to investigate the impact of testing start day and testing capacity as well as compliance with isolation on IAR and other metrics. The simulated scenarios are shown in Table 1, where each scenario is defined by the start day of testing, capacity (daily testing capacity increments), post-testing isolation compliance rates (symptomatic and asymptomatic), and symptomatic isolation (without testing) compliance rate. We referred to testing start days of 30, 45, and 60 as early, moderate, and late, respectively. We referred to daily testing capacity increments of 100, 500, and 1,000 as low, medium, and high capacity, respectively. In each scenario, the post-testing isolation compliance rate for (1) symptomatic patients was 0.95 or 0.80, labeled as high and low, respectively, and (2) asymptomatic patients was 0.90, 0.50, or 0.10, labeled as high, medium, and low, respectively. Therefore, we used a pair of labels to denote the post-testing isolation compliance rate combinations for symptomatic and asymptomatic patients, as shown in Table 1. For example, (high, high) represents that the post-testing isolation compliance rates for both symptomatic and asymptomatic patients are high, that is, . Moreover, we considered 2 levels of compliance with symptomatic isolation, that is, and , which were labeled as high and low, respectively. To emphasize the impact of testing and the corresponding post-testing isolation compliance, we fixed the symptomatic isolation compliance rate in the main body to be high (.
Table 1.
Simulation Scenarios
| Model parameters | Labels | Values |
|---|---|---|
| Testing start day () | ||
| Early | ||
| Moderate | ||
| Late | ||
| Capacity (capacity on day ) | ||
| Low | ||
| Medium | ||
| High | ||
| Post-testing isolation compliance rates () | ||
| (High, high) | (0.95, 0.90) | |
| (High, moderate) | (0.95, 0.50) | |
| (High, low) | (0.95, 0.10) | |
| (Low, moderate) | (0.80, 0.50) | |
| (Low, low) | (0.80, 0.10) | |
| Symptomatic isolation compliance rate () | ||
| High | 0.8 | |
| Low | 0.5 |
Note: The post-testing isolation compliance rate represents the proportion of individuals who isolate themselves after receiving a positive testing diagnosis, and the symptomatic isolation compliance rate represents the proportion of individuals who isolate themselves after starting to experience symptoms (and before diagnosis).
In the baseline scenario, there was no testing or self-isolation. The intervention scenarios included testing, post-testing isolation, and symptomatic isolation, assuming that symptomatic isolation started on Day 45 and that post-testing isolation started when testing capacity became available.
As summarized in Table 1, 90 intervention scenarios covering a wide range of settings and parameter values were tested in the simulations. The following 4 scenarios, where testing started on Day 45, were considered as benchmark scenarios when investigating the impact of delaying the testing start day and/or lowering post-testing self-isolation compliance:
-
1.
Scenario SI: low capacity; (high, high) post-testing isolation compliance (); high symptomatic compliance ();
-
2.
Scenario SII: low capacity; (high, high) post-testing isolation compliance (); low symptomatic compliance ();
-
3.
Scenario SIII: high capacity; (high, high) post-testing isolation compliance (); high symptomatic compliance (); and
-
4.
Scenario SIV: high capacity; (high, high) post-testing isolation compliance (); low symptomatic compliance ().
Outcome Metrics
To assess the impact of testing capacity and isolation compliance in different scenarios, we evaluated the following:
-
1.
IAR: percentage of the population infected during the time horizon;
-
2.
IP: percentage of the population who isolated either owing to a positive diagnostic test result or owing to symptoms; and
-
3.
Capacity counterbalance factor (). Consider one of the scenarios from Scenarios SI, SII, SIII, and SIV, denoted by , as the benchmark scenario. is with capacity , testing start day , and (high, high) post-testing isolation compliance rates that lead to an IAR of . Consider a modified scenario, denoted by , which is similar to except that the testing start day is delayed to and/or post-testing isolation compliance rates are lower; in , a higher capacity , where 1 will be needed to keep the IAR (approximately) at as in . We refer to as the capacity counterbalance factor.
IAR assesses the public health impact; IP serves as a proxy for assessing the potential social and economic impact40 of the disease, and reveals the tradeoff between testing start date/post-testing isolation compliance and testing capacity.
RESULTS
In the baseline scenario, there is no testing or self-isolation. The resultant IAR is 69.43% and IP is 0.00%.
Table 2 depicts the IAR and IP under various intervention scenarios and shows the tradeoffs between testing start day, capacity, and compliance with isolation when the symptomatic isolation compliance is high (). Additional results with low symptomatic isolation compliance () were summarized in Appendix Table 2. Earlier start of testing, higher testing capacity, and higher self-isolation compliance rates decrease the IAR. Among these factors, the start time of testing significantly impacts the IAR; hence, the results for IAR and IP are summarized on the basis of different testing start days. When fixing the testing start day and capacity, we observed that (high, high) post-testing isolation compliance leads to the lowest IAR, whereas (low, low) post-testing isolation compliance leads to the highest IAR.
Table 2.
IAR and IP in Various Scenarios When Symptomatic Isolation Compliance Is High (w=80%)
| Testing start day | Capacity | Post-testing isolation compliance rates () |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (High, high), % | (High, moderate), % | (High, low), % | (How, moderate), % | (Low, low), % | (High, high), % | (High, moderate), % | (High, low), % | (Low, moderate), % | (Low, low), % | ||
| IAR | IP | ||||||||||
| Early | |||||||||||
| Low | 2.42 | 2.43 | 2.44 | 3.75 | 3.76 | 1.19 | 1.19 | 1.19 | 1.77 | 1.77 | |
| Medium | 1.94 | 1.98 | 2.01 | 3.16 | 3.23 | 0.98 | 0.99 | 0.99 | 1.53 | 1.53 | |
| High | 1.88 | 1.94 | 2.01 | 3.09 | 3.21 | 0.97 | 0.98 | 0.99 | 1.52 | 1.53 | |
| Moderate | |||||||||||
| Low | 15.19 | 15.20 | 15.21 | 15.95 | 15.97 | 6.54 | 6.53 | 6.53 | 6.77 | 6.76 | |
| Medium | 13.15 | 13.20 | 13.26 | 14.19 | 14.26 | 5.86 | 5.84 | 5.83 | 6.18 | 6.17 | |
| High | 12.45 | 12.55 | 12.67 | 13.60 | 13.73 | 5.65 | 5.63 | 5.61 | 6.01 | 5.98 | |
| Late | |||||||||||
| Low | 19.21 | 19.21 | 19.21 | 19.45 | 19.45 | 7.78 | 7.78 | 7.77 | 7.82 | 7.82 | |
| Medium | 18.75 | 18.76 | 18.78 | 19.05 | 19.07 | 7.68 | 7.67 | 7.66 | 7.74 | 7.73 | |
| High | 18.60 | 18.63 | 18.66 | 18.93 | 18.97 | 7.67 | 7.65 | 7.64 | 7.72 | 7.71 | |
IAR, infection attack rate; IP, isolation percentage.
With an early testing start day, even low capacity can maintain a low IAR. Specifically, with (high, high) post-testing isolation compliance, the IAR is as low as 2.42%; with (high, low) post-testing isolation compliance, the IAR is 2.44%; and with (low, low) post-testing isolation compliance, the IAR is 3.76%. The IP under early versus late start of testing is also lower. With high testing capacity, the (high, high) post-testing isolation compliance leads to an IAR of 1.88% and an IP of 0.97%.
With moderate testing start day, both IAR and IP significantly increase compared with those of early start: under high capacity, the IAR and IP under (high, high) post-testing isolation compliance are 12.45% and 5.65%, respectively; under low capacity and (low, low) post-testing isolation compliance, the IAR and IP are 15.97% and 6.76%, respectively.
With late testing start day, both IAR and IP significantly increase compared with those of early or moderate start: under (high, high) post-testing isolation compliance, the IAR is as high as 19.21%, 18.75%, and 18.60% with low, medium, and high capacity, respectively. The IP exceeds 7.64% for all scenarios with late start of testing. However, with late start of testing, if the symptomatic isolation compliance is low, the IAR will be at least 28.20%.
Table 3 shows the results on capacity counterbalance factors required under various modified scenarios to achieve an IAR similar to that in Scenario SI (i.e., ). For example, when post-testing isolation compliance rates are (high, high), delaying the start of testing for 5 days (i.e., versus requires a capacity counterbalance factor of 13, that is, That is, to maintain the IAR, the daily testing capacity increments need to be 1,300, compared with 100 in Scenario SI. When there is no delay in the start of testing, that is, 45, but compliance with post-testing isolation of symptomatic patients is (low, low) in a modified scenario (versus [high, high] in Scenario SI as ), then the capacity counterbalance factor is 2, that is, the testing capacity should be doubled in the modified scenario to maintain an IAR similar to that in Scenario SI.
Table 3.
Capacity Counterbalance Factors in Modified Scenarios () to Maintain an IAR Similar to That in the Benchmark Scenario When Is Scenario SI
| Testing start day | Post-testing isolation compliance rates |
||||
|---|---|---|---|---|---|
| (High, high) | (High, moderate) | (High, low) | (Low, moderate) | (Low, low) | |
| Day 45 | 1.0 | 2.0 | 2.0 | 2.0 | 2.0 |
| Day 46 | 2.0 | 2.0 | 2.0 | 3.0 | 4.0 |
| Day 47 | 2.0 | 3.0 | 3.0 | 5.0 | 6.0 |
| Day 48 | 4.0 | 4.0 | 4.0 | 11.0 | 14.0 |
| Day 49 | 6.0 | 7.0 | 7.0 | 30.0 | 213.0 |
| Day 50 | 13.0 | 17.0 | 26.0 | 116.0 | ― |
| Day 51 | 35.0 | 69.0 | ― | 534.0 | ― |
| Day 52 | 121.0 | 431.0 | ― | ― | ― |
| Day 53 | 420.0 | ― | ― | ― | ― |
| Day 54 | 3,247.0 | ― | ― | ― | ― |
IAR, infection attack rate.
Appendix Table 3 shows the results regarding the capacity counterbalance factors under Scenarios SII, SIII, and SIV, where the testing capacity is higher and/or where the symptomatic isolation compliance is lower than in Scenario SI. Similarly, the delay in testing starting day significantly increases the required capacity to maintain an IAR similar to that in Scenario SII/SIII/SIV.
DISCUSSION
Diagnostic testing plays a significant role in controlling the spread of infectious diseases by enabling the early detection of infected individuals, encouraging self-isolation, and reducing transmission.6,41, 42, 43 The effectiveness of testing in preventing or controlling an outbreak depends on when (how early) testing becomes available, how quickly the testing capacity ramps up, and the willingness of individuals to self-isolate (i.e., compliance) when they test positive or have symptoms. The IAR and the IP, that is, the proportion of the population who self-isolate either owing to symptoms or a positive test result, are 2 metrics used in this study to assess the public health and social impact of testing programs. Moreover, we introduced the capacity counterbalance factor metric to assess the tradeoff between testing start date/post-testing isolation compliance and testing capacity.
The results of this study suggest that starting testing early with a lower capacity is more effective in reducing the infection spread than starting late with a higher capacity, especially when the individuals who tested positive have high compliance with self-isolation (each column in Table 2 shows results for a particular compliance rate). Moreover, early start of testing with higher testing capacity leads to lower IP in general, even when the compliance is high. When an early start of testing is not possible, improving compliance with symptomatic isolation is important in reducing the spread of the disease.
When the start of testing is delayed, the additional capacity required (capacity counterbalance factor) grows superlinearly to achieve an IAR similar to that in Scenario SI. The results highlight the importance of complying with post-testing isolation, especially for symptomatic patients. Let us consider small delay scenarios (the start of testing is delayed by <4 days, compared with Scenario SI, where the testing start day is 45). Comparing these small delay scenarios, when fixing the testing start day, a decrease in post-testing isolation compliance of asymptomatic patients () does not significantly increase the capacity counterbalance factor, because the testing capacity is low, and thus, during the first 4 days after testing starts, symptomatic patients would be prioritized for testing. However, a decrease in post-testing isolation compliance of the symptomatic patients () significantly increases the capacity counterbalance factor; for example, when the start of testing is delayed to day 49, under (high, medium) post-testing compliance, compared with under (low, medium) post-testing compliance.
Although the importance of early testing has been acknowledged,44 to the best of our knowledge, this study is the first that considers the complex interplay between multiple factors to evaluate the impact of testing and self-isolation on public health outcomes. The results of this study highlight the benefits of the early start of testing and high compliance with isolation. In practice, the testing capacity may not be sufficient to meet the demand,45 especially during the initial stages of the infection spread, and compliance with self-isolation may be low, even in the presence of symptoms. For example, 65%‒90% of working adults reported going to work when they had cold/influenza symptoms6,42,46 owing to a variety of reasons such as high work load, not wanting to use or limited sick time, and perceived pressure or fear of judgment.46,47 The results of this study show that low compliance with self-isolation can significantly increase the IAR, underscoring the importance of reducing barriers to self-isolation, which in turn could increase self-isolation compliance and reduce infectious disease spread. To improve public health outcomes and reduce the social and economic impact of the diseases spread, it is important to communicate the importance of self-isolation through public health campaigns and community-based organizations, as well as to encourage or require businesses, at a systems level, with legal requirements to remove (perceived) penalties or increase incentives for their employees to self-isolate when needed.
The extended SIR model assumes homogenous mixing of the population and is not able to account for demographic- 23 or geographic-dependent information, for example, as in agent-based models.33,48 In this computational study, the testing capacity linearly increased over time, whereas in practice, the capacity increase might follow different patterns. Other factors, such as the willingness to test or compliance with other interventions, would also impact health outcomes. In some cases, there might be correlations among some of these factors, for example, people who are willing to self-isolate might also be more likely to get tested or follow other interventions and recommendations. Exploring these additional complex interactions is an important direction for future research. Despite these limitations owing to modeling assumptions and parameter values, the model proposed in this study can capture the salient characteristics of disease spread dynamics considering the complex interplay between multiple factors related to diagnostic testing and self-isolation.
CONCLUSIONS
In this study, we developed and used an extended SIR model to analyze the impact of diagnostic testing availability (including the start day and capacity of testing programs), compliance with post-testing isolation, and compliance with symptomatic isolation on the disease spread. We quantified the significant advantages and effectiveness of early start of testing and high compliance with self-isolation. Investments in the early start of testing programs and public health education on self-isolation can lower the IAR substantially.
CREDIT AUTHOR STATEMENT
Zhuoting Yu: Conceptualization, Methodology, Software, Validation, Formal analysis, Writing - Original Draft, Visualization. Pinar Keskinocak: Conceptualization, Methodology, Validation, Formal analysis, Writing - Review and Editing, Visualization, Supervision, Project administration. Lauren N. Steimle: Conceptualization, Methodology, Validation, Formal analysis, Writing - Review and Editing, Visualization, Supervision. Inci Yildirim: Conceptualization, Writing - Review and Editing, Supervision.
Declarations of interest
None.
ACKNOWLEDGMENTS
The authors thank the anonymous referees for their valuable suggestions for improving this article.
This does not necessarily represent the views of the Centers for Disease Control and Prevention and Council of States and Territorial Epidemiologists.
This research has been supported in part by the RADx-UP NIH/NIDDK grant (P30DK111024-05S1) and by the Cooperative Agreement Number NU38OT000297 from the Centers for Disease Control and Prevention and Council of States and Territorial Epidemiologists. This research was also supported in part by the William W. George endowment and the following benefactors at Georgia Tech: Andrea Laliberte, Joseph C. Mello, Richard Rick E. and Charlene Zalesky, and Claudia and Paul Raines.
Footnotes
Supplementary material associated with this article can be found at doi:10.1016/j.focus.2022. 100006.
Appendix. Supplementary materials
REFERENCES
- 1.Jamison DT, Gelband H, Horton S, et al. Disease control priorities, third edition. volume 9: improving health and reducing poverty. Washington, DC: The World Bank. https://openknowledge.worldbank.org/handle/10986/28877. Published 2017. Accessed April 1, 2021.
- 2.Dong E, Du H, Gardner L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect Dis. 2020;20(5):533–534. doi: 10.1016/S1473-3099(20)30120-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Cutler DM, Summers LH. The COVID-19 pandemic and the $16 trillion virus. JAMA. 2020;324(15):1495–1496. doi: 10.1001/jama.2020.19759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.WHO Director-General's opening remarks at the media briefing on COVID-19 - 16 March 2020.https://www.who.int/director-general/speeches/detail/who-director-general-s-opening-remarks-at-the-media-briefing-on-covid-19---16-march-2020. Published March 16, 2020. Accessed April 1, 2021.
- 5.National Institutes of Health . National Institutes of Health; Bethesda, MD: September 4, 2020. Why COVID-19 testing is the key to getting back to normal.https://www.nia.nih.gov/news/why-covid-19-testing-key-getting-back-normal Accessed July 22, 2021. [Google Scholar]
- 6.Kucharski AJ, Klepac P, Conlan AJK, et al. Effectiveness of isolation, testing, contact tracing, and physical distancing on reducing transmission of SARS-CoV-2 in different settings: a mathematical modelling study. Lancet Infect Dis. 2020;20(10):1151–1160. doi: 10.1016/S1473-3099(20)30457-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.WHO . WHO; Geneva, Switzerland: 2020. WHO Director-General’s opening remarks at the media briefing on COVID-19 –11 March 2020.https://www.who.int/director-general/speeches/detail/who-director-general-s-opening-remarks-at-the-media-briefing-on-covid-19---11-march-2020 Published March 11, 2020. Accessed June 1, 2021. [Google Scholar]
- 8.Davis K. Harvard University; Cambridge, MA: May 18, 2020. Better late than never: COVID-19 testing across the United States.https://sitn.hms.harvard.edu/flash/2020/covid-19-testing/ Accessed July 22, 2021. [Google Scholar]
- 9.Holshue ML, DeBolt C, Lindquist S, et al. First case of 2019 novel coronavirus in the United States. N Engl J Med. 2020;382(10):929–936. doi: 10.1056/NEJMoa2001191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Previous U.S. viral testing data, August 27, 2020. Centers for Disease Control and Prevention. https://www.cdc.gov/coronavirus/2019-ncov/cases-updates/previous-testing-in-us.html. Updated August 27, 2020. Accessed January 1, 2021.
- 11.Centers for Disease Control and Prevention; August 27, 2020. Previous U.S. case data.https://www.cdc.gov/coronavirus/2019-ncov/covid-data/previouscases.html Accessed April 1, 2022. [Google Scholar]
- 12.Centers for Disease Control and Prevention; November 16, 2021. Estimated COVID-19 burden.https://www.cdc.gov/coronavirus/2019-ncov/cases-updates/burden.html Accessed March 1, 2022. [Google Scholar]
- 13.Domenghino A, Aschmann HE, Ballouz T, et al. Mental health of individuals infected with SARS-CoV-2 during mandated isolation and compliance with recommendations - a population-based cohort study. PLoS One. 2022;17(3) doi: 10.1371/journal.pone.0264655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.National Institute for Public Health and the Environment of Netherlands . National Institute for Public Health and the Environment of Netherlands; BA Bilthoven, The Netherlands: June 16, 2020. Many people willing to isolate at home in case of positive COVID-19 test.https://www.rivm.nl/en/news/many-people-willing-to-isolate-at-home-in-case-of-positive-covid-19-test Accessed August 1, 2020. [Google Scholar]
- 15.Patel J, Fernandes G, Sridhar D. How can we improve self-isolation and quarantine for covid-19? BMJ. 2021;372:n625. doi: 10.1136/bmj.n625. [DOI] [PubMed] [Google Scholar]
- 16.Smith LE, Amlȏt R, Lambert H, et al. Factors associated with adherence to self-isolation and lockdown measures in the UK: a cross-sectional survey. Public Health. 2020;187:41–52. doi: 10.1016/j.puhe.2020.07.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kerr CC, Mistry D, Stuart RM, et al. Controlling COVID-19 via test-trace-quarantine. Nat Commun. 2021;12(1):2993. doi: 10.1038/s41467-021-23276-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Vatovec C, Hanley JC. Survey of awareness, attitudes, and compliance with COVID-19 measures among Vermont residents. PLoS One. 2022;17(3) doi: 10.1371/journal.pone.0265014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bodas M, Peleg K. Self-isolation compliance in the COVID-19 era influenced by compensation: findings from a recent survey in Israel public attitudes COVID-19 outbreak self-isolation across sectional study adult population of Israel. Health Aff (Millwood) 2020;39(6):936–941. doi: 10.1377/hlthaff.2020.00382. [DOI] [PubMed] [Google Scholar]
- 20.Cevik M, Baral SD, Crozier A, Cassell JA. Support for self-isolation is critical in Covid-19 response. BMJ. 2021;372:n224. doi: 10.1136/bmj.n224. [DOI] [PubMed] [Google Scholar]
- 21.Tolles J, Luong T. Modeling epidemics with compartmental models. JAMA. 2020;323(24):2515–2516. doi: 10.1001/jama.2020.8420. [DOI] [PubMed] [Google Scholar]
- 22.Lin Q, Zhao S, Gao D, et al. A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and governmental action. Int J Infect Dis. 2020;93:211–216. doi: 10.1016/j.ijid.2020.02.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ram V, Schaposnik LP. A modified age-structured SIR model for COVID-19 type viruses. Sci Rep. 2021;11(1):15194. doi: 10.1038/s41598-021-94609-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Dashtbali M, Mirzaie M. A compartmental model that predicts the effect of social distancing and vaccination on controlling COVID-19. Sci Rep. 2021;11(1):8191. doi: 10.1038/s41598-021-86873-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Fujimoto AB, Keskinocak P, Yildirim I. Significance of SARS-CoV-2 specific antibody testing during COVID-19 vaccine allocation. Vaccine. 2021;39(35):5055–5063. doi: 10.1016/j.vaccine.2021.06.067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kim D, Keskinoca P, Pekgün, P, Yildirim I. The balancing role of distribution speed against varying efficacy levels of COVID-19 vaccines under variants. Sci Rep. 2022;12(1):7493. doi: 10.1038/s41598-022-11060-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kim D, Pekgün P, Yildirim I, Keskinocak P. Resource allocation for different types of vaccines against COVID-19: tradeoffs and synergies between efficacy and reach. Vaccine. 2021;39(47):6876–6882. doi: 10.1016/j.vaccine.2021.10.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Sharov KS. Creating and applying SIR modified compartmental model for calculation of COVID-19 lockdown efficiency. Chaos Solitons Fractals. 2020;141 doi: 10.1016/j.chaos.2020.110295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Agusto FB, Erovenko IV, Fulk A, et al. To isolate or not to isolate: the impact of changing behavior on COVID-19 transmission. BMC Public Health. 2022;22(1):138. doi: 10.1186/s12889-021-12275-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Anand N, Sabarinath A, Geetha S, Somanath S. Predicting the spread of COVID-19 using SIR model augmented to incorporate quarantine and testing. Trans Indian Natl Acad Eng. 2020;5(2):141–148. doi: 10.1007/s41403-020-00151-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.COVID-19 pandemic planning scenarios, December 2020, Centers for Disease Control and Prevention.https://www.cdc.gov/coronavirus/2019-ncov/hcp/planning-scenarios.html#five-scenarios. Updated March 19, 2021. Accessed January 1, 2021.
- 32.Giordano G, Blanchini F, Bruno R, et al. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat Med. 2020;26(6):855–860. doi: 10.1038/s41591-020-0883-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Keskinocak P, Oruc BE, Baxter A, Asplund J, Serban N. The impact of social distancing on COVID19 spread: State of Georgia case study. PLoS One. 2020;15(10) doi: 10.1371/journal.pone.0239798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Prem K, Liu Y, Russell TW, et al. The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China: a modelling study. Lancet Public Health. 2020;5(5):e261–e270. doi: 10.1016/S2468-2667(20)30073-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Weitz JS, Park SW, Eksin C, Dushoff J. Awareness-driven behavior changes can shift the shape of epidemics away from peaks and toward plateaus, shoulders, and oscillations. Proc Natl Acad Sci U S A. 2020;117(51):32764–32771. doi: 10.1073/pnas.2009911117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Davies NG, Kucharski AJ, Eggo RM, Gimma A, Edmunds WJ. Effects of non-pharmaceutical interventions on COVID-19 cases, deaths, and demand for hospital services in the UK: a modelling study. Lancet Public Health. 2020;5(7):e375–e385. doi: 10.1016/S2468-2667(20)30133-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.QuickFacts - Atlanta city, Georgia, July 1, 2021, United States Census Bureau.https://www.census.gov/quickfacts/atlantacitygeorgia. Accessed April 1, 2022.
- 38.Core Team R. R Foundation for Statistical Computing; Vienna, Austria.: 2019. R: A Language and Environment for Statistical Computing.https://cran.r-project.org/ [Google Scholar]
- 39.Soetaert K, Petzoldt T, Setzer RW. Solving differential equations in R: package deSolve. J Stat Softw. 2010;33(9):1–25. doi: 10.18637/jss.v033.i09. [DOI] [Google Scholar]
- 40.Anderson RM, Heesterbeek H, Klinkenberg D, Hollingsworth TD. How will country-based mitigation measures influence the course of the COVID-19 epidemic? Lancet. 2020;395(10228):931–934. doi: 10.1016/S0140-6736(20)30567-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Monjur MR, Hassan MZ. Early phases of COVID-19 management in a low-income country: Bangladesh. Infect Control Hosp Epidemiol. 2020;41(9):1116–1117. doi: 10.1017/ice.2020.147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Peto J. Covid-19 mass testing facilities could end the epidemic rapidly. BMJ. 2020;368:m1163. doi: 10.1136/bmj.m1163. [DOI] [PubMed] [Google Scholar]
- 43.Sharfstein JM, Becker SJ, Mello MM. Diagnostic testing for the novel coronavirus. JAMA. 2020;323(15):1437–1438. doi: 10.1001/jama.2020.3864. [DOI] [PubMed] [Google Scholar]
- 44.Goldstein ND, Burstyn I. On the importance of early testing even when imperfect in a pandemic such as COVID-19. Glob Epidemiol. 2020;2 doi: 10.1016/j.gloepi.2020.100031. 100031–100031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lieberman-Cribbin W, Tuminello S, Flores RM, Taioli E. Disparities in COVID-19 testing and positivity in New York City. Am J Prev Med. 2020;59(3):326–332. doi: 10.1016/j.amepre.2020.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Faulkner B. Nearly a quarter of employees fear boss’ judgement for calling in sick. AXA. June 29, 2015 https://www.axa.co.uk/newsroom/media-releases/2015/nearly-a-quarter-of-employees-fear-bosses-judgement-for-calling-in-sick/ Accessed April 1, 2021. [Google Scholar]
- 47.Claire Cain Miller SK, Sanger-Katz M. Avoiding coronavirus may be a luxury some workers can't afford. The New York Times. March 1, 2020 https://www.nytimes.com/2020/03/01/upshot/coronavirus-sick-days-service-workers.html Accessed April 1, 2021. [Google Scholar]
- 48.Baxter A, Oruc BE, Asplund J, Keskinocak P, Serban N. Evaluating scenarios for school reopening under COVID19. BMC Public Health. 2022;22(1):496. doi: 10.1186/s12889-022-12910-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.