Abstract
Objective:
Diffuse correlation spectroscopy (DCS) is an optical technique that allows for the non-invasive measurement of blood flow. Recent work has shown that utilizing longer wavelengths beyond the traditional NIR range provides a significant improvement to signal-to-noise ratio (SNR). However, current detectors both sensitive to longer wavelengths and suitable for clinical applications (InGaAs/InP SPADs) suffer from suboptimal afterpulsing and dark noise characteristics. To overcome these barriers, we introduce a cross correlation method to more accurately recover blood flow information using InGaAs/InP SPADs.
Methods:
Two InGaAs/InP SPAD detectors were used for during in vitro and in vivo DCS measurements. Cross correlation of the photon streams from each detector was performed to calculate the correlation function. Detector operating parameters were varied to determine parameters which maximized measurement SNR. State-space modeling was performed to determine the detector characteristics at each operating point.
Results:
Evaluation of detector characteristics was performed across the range of operating conditions. Modeling the effects of the detector noise on the correlation function provided a method to correct the distortion of the correlation curve, yielding accurate recovery of flow information as confirmed by a reference detector.
Conclusion:
Through a combination of cross-correlation of the signals from two detectors, model-based characterization of detector response, and optimization of detector operating parameters, the method allows for the accurate estimation of the true blood flow index. Significance: This work presents a method by which DCS can be performed at longer NIR wavelengths with existing detector technology, taking advantage of the increased SNR.
Keywords: Fluid flow measurement, Infrared detectors Biomedical applications of optical radiation, Semiconductor device modeling
I. Introduction
Diffuse correlation spectroscopy (DCS) is an established optical technique that allows for the non-invasive measurement of tissue blood flow by analyzing the temporal correlation of the intensity of multiply scattered light [1]. DCS has shown to be effective in monitoring blood flow in many clinical and research environments, including monitoring of cerebral blood flow at the bedside [2]–[4] and characterization of breast cancer legions as malignant or benign [5], [6]. To improve sensitivity to the target tissue; which is typically below dermal layers, layers of subcutaneous fat, and bone, depending on the measurement location; larger source detector separations are used, reducing measurement SNR. Several approaches building on the traditional DCS technique have been proposed to address this challenge, including heterodyne detection [7]–[10], time resolved detection [11]–[14], ultrasound tagging of light [15], [16], and multi-speckle detection [17], [18]. In addition, recent developments in the literature [19]–[22] have shown the effectiveness of moving to wavelengths beyond the traditional NIR range (650 – 850 nm) due to reduced optical attenuation relative to the traditional NIR range, increased safe exposure limits as defined by the ANSI standard, an increased number of photons per unit energy, and a slower autocorrelation decay due to lower scattering at the longer wavelength. Based on previous calculations and in vivo results [19], [22], approximately 10 times more photons will find their way to the detectors using 1064 nm wavelength compared to the traditional NIR range, allowing for the use of longer source-detector separations to improve sensitivity to deeper blood flows while maintaining a similar signal-to-noise ratio (SNR), with an added benefit of measuring a slower decorrelation rate, improving the fitting of the curve. These benefits are difficult to fully realize in practice due to shortcomings in the characteristics of detectors sensitive to light at 1064 nm. Single photon detectors at 1064 nm include superconducting nanowire single-photon detectors (SNSPD) and InGaAs/InP single photon avalanche diodes (SPADs). SNSPDs have superior detection characteristics (e.g., high photon detection efficiency, low dark count rate, no afterpulsing) but their low portability and high cost limit their suitability for clinical applications. InGaAs/InP SPADs, while portable and suitable for a clinical environment, have poor noise characteristics, including relatively high dark count rate (DCR) and excessive afterpulsing [23], [24]. An afterpulse is generated when electrons from a previous avalanche become trapped in the detector material and subsequently trigger another avalanche when the detector is rebiased. Advances in detector hardware provide future solutions to reduce afterpulsing [25], though current strategies to mitigate their effects include using detector hold off times in the range of tens of microseconds to allow trapped charges to diffuse out [26]. This strategy presents a challenge for DCS, where the long hold off time (>10μs) can obscure the signal fluctuations that occur on the order of several microseconds. To move closer to a DCS setup for measurements at 1064 nm that is suitable for clinical applications, we propose to use cross-correlation of optical signals from two InGaAs/InP SPAD detectors to correct for the shortcomings of the InGaAs/InP SPADs. The use of cross-correlation, taking advantage of the Hanbury Brown Twiss effect [27], reduces the artifacts in the intensity autocorrelation function by allowing for photon interarrival times shorter than the hold off time and removing the relationship between an afterpulse and its inciting count, though the presence of the afterpulsing counts in the detector streams still represents a source of correlated noise. Afterpulsing counts can extend the correlation present in the intensity signal to longer delay times, leading to an artificial slowing of the autocorrelation decay. In this work we show that this disruption can be accounted for, both through the optimization of the operating parameters of the detectors (temperature, excess bias voltage, and hold-off time) as well as modeling the effects of these afterpulse trains on the correlation function. By addressing these challenges, DCS systems using sources beyond the traditional NIR range can be built with suitable portability for many applications.
II. Materials and methods
A. Diffuse correlation spectroscopy
Diffuse correlation spectroscopy relates the observed temporal fluctuations of light intensity to the motion of optical scatterers in the tissue. The rate of decay of the temporal intensity autocorrelation function, g2(τ), is first related to the temporal electric field autocorrelation function, g1(τ), by the Siegert relation [28], given as
| (1) |
where β is the coherence factor of the measurement that is dependent upon the measurement geometry, number of modes collected, coherence of the laser source, and presence of noise counts. The electric field autocorrelation function can be calculated as a weighted sum of electric field autocorrelation functions along individual pathlengths, , over the pathlength distribution for the measurement given as,
| (2) |
where n is the index of refraction of the sample, k0 is the wavenumber of the light in vacuum, μs’ is the reduced scattering coefficient, ⟨Δr2(τ)⟩ is the mean squared displacement at time delay τ, and s is the pathlength of the photon. Blood flow in the tissue is described by the blood flow index (BFi), which is related to the mean squared displacement of the scatterers (e.g., red blood cells) by the following expression, ⟨Δr2(τ)⟩ = α6Dbτ = BFiτ, where α is the fraction of scattering events that happen at moving scatters and Db is the apparent diffusion coefficient. In this study, data are fit using the correlation diffusion equation for a homogenous, semi-infinite slab. Though blood flow at a macroscopic level does not appear to be diffusive, shear-induced diffusion of red blood cells in blood vessels has been investigated as the dominant source of the diffusive nature of experimentally measured flows [29]–[31], though other flow models have been proposed to describe the measured flow dynamics [32], [33].
B. Hardware
We used a custom built DCS system consisting of a 1064 nm laser source, two InGaAs/InP SPADs (PDM-IR fiber-pigtailed, Micro Photon Devices), and a custom FPGA-based software correlator board, described previously[34]. For the continuous wave (CW) DCS experiments, a long coherence length laser at 1064 nm (RFLM-125–0-1064, NP Photonics) was used. For the gated measurements, a custom-built pulsed laser at 1064 nm was used, generating pulses with a full width half maximum of 250 ps at a repetition rate of 25 MHz. In both the CW and pulsed experiments, 100 mW of incident power over a spot size larger than 1 mm was used, conforming to the ANSI standard for the maximal permissible exposure for skin. Light from the sample was collected using a 6.2 μm diameter fiber (1060 HI) and sent to both detectors using a 50/50 fused fiber coupler (TW1064R5F2A, Thorlabs). A reference measurement was made using a superconducting nanowire detector (SNSPD) (Quantum Opus) tuned for maximum efficiency at 1064 nm (~85–90%) for comparison. For the CW experiments, the InGaAs/InP detectors were set to free running mode. For gated experiments, a gate width of 5 ns was used to capture the entire temporal point spread function (TPSF), leading to measurements of the DCS autocorrelation that are effectively CW. In all cases, reference detectors were run in a free running mode.
C. Detector characterization experiments
To optimize the operating parameters of the InGaAs/InP detectors, we characterized the detector performance in both CW and gated mode. An intralipid solution with a reduced scattering coefficient (μs’) of 6 cm−1 and an absorption coefficient (μa) of 0.14 cm−1 at 1064 nm was measured at a source-detector separation of 1.2 cm, while the detectors’ temperature, excess bias voltage, and hold off time were varied. Detector settings were optimized based on the SNR of the plateau of g2(τ) at short time lags (SNR = ⟨g2(10−6 s to 10−5 s) – 1⟩/STD(g2(10−6 s to 10−5 s)). The intralipid sample was measured for 60 s at each detector setting, and autocorrelation functions were calculated at a rate of 0.1 Hz. The range of the operating parameters can be seen below in Table I. In-vivo experiments were performed using the gated mode only. Measurements of the forehead were done at a source-detector separation of 1 cm. An elastic band was placed over the probe, and pressure was applied to the probe by tightening the tension in the band. A baseline of 60s was first acquired, followed by 60s of tourniquet tightening and 60s of recovery. Autocorrelation functions were calculated at 0.25 Hz, and a 12s-long moving average was applied to remove residual cardiac pulsation present in the fitted BFi. The protocol was repeated 3 times, and the results were averaged. This study was reviewed and approved by the Mass General Brigham Institutional Review Board (#2019P003074; approved February 05, 2021).
TABLE I.
Detector operating parameters
| Free running | Gated | |
|---|---|---|
|
| ||
| Excess bias | 2.0 V, 2.5 V, 3.0 V, 3.5 V, 4.0 V | 2.0 V, 4.0 V, 6.0 V, |
| voltage | 7.0 V | |
| Hold off time | 10 μs, 20 μs, 30 μs, 40 μs, 50 μs | 5 μs, 10 μs, 20 μs |
| Temperature | 225 K, 229 K, 233 K | |
D. Detector modeling
As seen in the results section below, the use of cross-correlation successfully removes large artifacts related to the afterpulsing and hold off time, making these InGaAs/Inp detectors usable for DCS measurements. Still the presence of afterpulsing counts results in a distortion of the correlation function that needs to be addressed. To remove the remaining distortion of the correlation function (i.e. the slower decay) after the calculation of the cross-correlation, we model the operation of each individual SPAD in a state-space representation. By discretizing time into bins set by the clock frequency of the correlator board (150 MHz), we can describe the state of the detector at all times though the following model, seen below in Fig. 1.
Fig. 1.
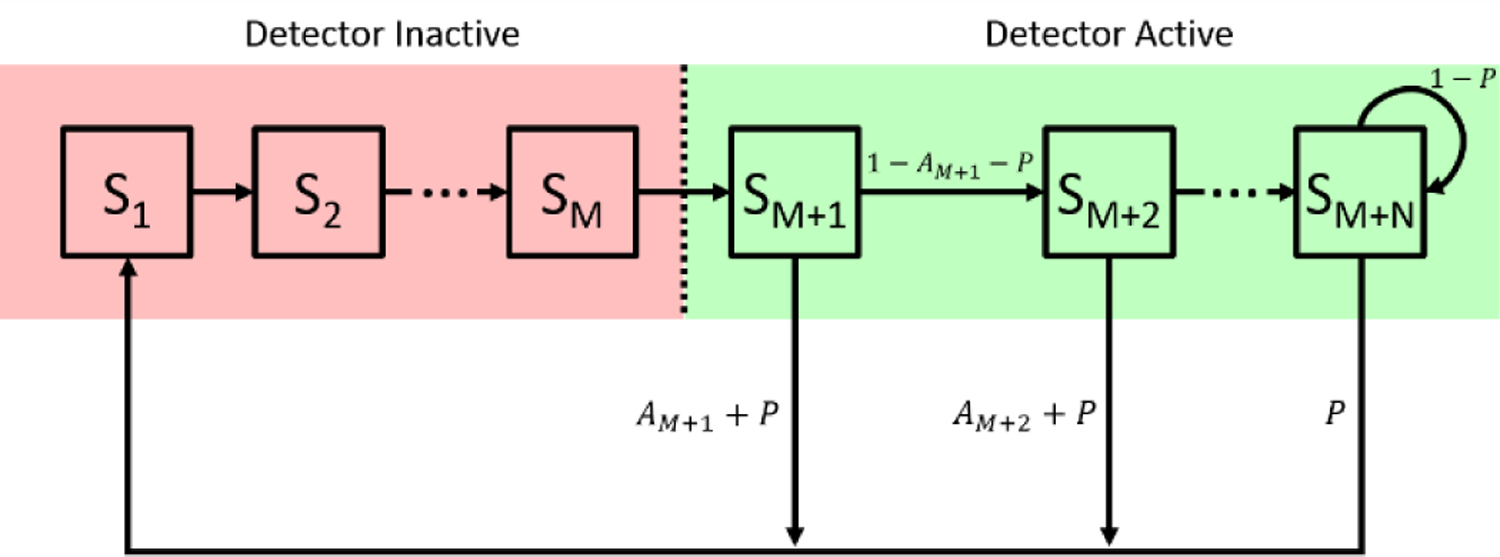
State space model used to represent a detector module. Detector states are labeled with respect to their position relative to the detection state S1, with the same numbering given for their state transition probabilities, which are labeled near the arrow indicating the state transition.
The detector operates in two phases, inactive and active. The length of the inactive period, the hold off time, is set in terms of M clock cycles. Each state, Si, represents the detector at a particular number of clock cycles after the detector has entered the hold off time. Following the activation of the detector at state Sm+1, the detector can detect a photon that is either a true count, a (thermal) dark count, or an afterpulse. Upon a detection event, the simulated detector is quenched during the state transition between the detection state and state S1, and the simulated detection electronics register that the photon has arrived during state S1. In this model, the probability of detecting a signal photon or registering a dark count event are lumped into the probability p. The probability of detecting an afterpulsing count is given for each active state as Ai. Based on previous literature, the probability of afterpulsing is modeled as a power law decay, given as , where AP0 is the effective afterpulsing count rate during the first active state, fs is the sampling frequency used for the simulation, and α is the power coefficient [24]. To determine how many active states, N, need to be considered, we impose that P>>Am+n such that an afterpulse would be extremely unlikely beyond that state in comparison to the signal photon or dark count detection.
We propose to use this model to understand both the steady state and dynamic performance of the detector to determine the detector characteristics (P, AP0, and α) governing the state transition probabilities. With qi being the probability of being in a particular state, Si, for the detector in the steady state, we can derive the equations to describe the distribution of probability throughout the states. As we are dealing with probabilities, all should sum to 1, as given below in (3),
| (3) |
To investigate the steady state response of the detector, we impose the assumption that the probability of entering a state Si is equal to the probability of leaving the state. We can express the steady state probability for each state, qi, in terms of the probability of the detector being in the previous state, qi-1, and the associated state transition probabilities. For the inactive states, the state transition probability to go from one state to the next is equal to one, which gives the relation q1 = q2 =...= qM+1. For the active states, we can define the probability of entering the state as the probability of being in the previous state multiplied by the probability of not detecting a photon in that state, while the probability of exiting the state is equal to one. Balancing the probability of entering and exiting the state gives the relation qi = qi–1(1 – Ai–1 – P). For the last state, Sm+n, the use of the recurrence relation gives a different probability of exiting the state. The probability of entering the state will be the same as previously described for other active states, but the probability of exiting the state is given as the probability of being in state Sm+n, qM+N, multiplied by the probability of detecting a real photon or a dark count, P. Balancing these probabilities gives the following relation, . The description of these steady state probabilities is summarized in (4). Here, we use the recurrence relation at state Sm+n to simplify the description of the model when the afterpulsing probability, Am+n, is effectively equal to zero. If instead we used an infinite number of active states after Sm+n, we could continue to express the probability of being in the series of states as qM+N+m = RM+N+m–1(1 – P), where m is the number of states past state Sm+n. If we then express the total probability of being in this series of states we would have the relation , which reduces to . Then using the relation for active states with afterpulsing, we can calculate the probability of being in state Sm+n by taking the probability of being in state Sm+n-1 multiplied by the state transition probability, 1-Am+n-1-P. This description gives the same total probability for the states without afterpulsing as the model containing the recurrence relation.
| (4) |
The relationships defined in (3) and (4) allow for the expression of the total probability in terms of the probability of being in the first inactive state, q1. This is useful because it allows for the estimation of the probability of being in the state that reports simulated photon detections. By cascading the relations expressed in (4), and plugging into (3) gives (5),
| (5) |
Based on the above expression, the average count rate for a measurement with a given set of P, AP0, and α can be expressed as q1*fs. This can be seen by expressing q1 in terms of the probability of entering the state, equal to , which is equal to the probability of detecting a photon during a particular state residence time, given as 1/fs. Then by multiplying by the sampling rate of the simulation, fs, we can estimate the count rate of the simulation in terms of counts per second. While there is not a unique mapping of measured count rate to detector characteristics, by comparing the estimated count rate from the steady state analysis and the count rate of the measurements, the set of appropriate detector characteristics can be narrowed, reducing the search size in the variable space.
To explore the dynamic properties of the detector response, we consider a time series of the detection state, given as q1[n]. In the previous section we defined the probability of being in a state Si in the detector steady state condition as qi. In the next section, to allow for dynamics of the detector, we describe the probability of being in a state Si at a particular time index in terms of clock cycles, n, as qi[n]. The form of the discrete time autocorrelation for the system is given as . To simplify the calculation of the autocorrelation, we modify the model by adding a known detection at n=0 in the form of a Knonecker delta. By arbitrarily setting n=0 when q1=1, the autocorrelation of the signal will be equal to the expected probability of being state S1 at a time lag of k. To determine this, we can describe the probability of being in state Si at a certain time by a set of difference equations, given below in (6) and (7).
| (6) |
| (7) |
Equation 6 describes the transition from detecting a photon in the active period of the detector to the detection state, and (7) describes the transition of probability through the states in terms of the probability of being in the detection state, S1, at some previous point in time. Like in the steady state analysis, we can see a recurrence relationship that occurs in the final active state. To solve this system of equations for q1[n], we first take the z-transform of the above equations, given below in (8) and (9).
| (8) |
| (9) |
Plugging in the expressions from (9) into (8) yields the following solution for Q1(z),
| (10) |
where the coefficients of ai and bj can be expressed as;
| (11) |
| (12) |
Finally, by taking the inverse z-transform of Q1(z), we are left with the estimated autocorrelation of the detector for a given set of properties (P, AP0, and α) to compare to the measured autocorrelation. We fit for the properties by minimizing a loss function of the form, , where g2[k] is the measured autocorrelation function, is the estimated autocorrelation function calculated as , R is a regularization term that is based on the estimated count rate of the measurement, and λ is the scaling factor for the regularization term. Below an empirically chosen relative difference, dr, in count rate, R = 0. Above the relative difference threshold, detector characteristics are penalized and the regularization term takes the form, , where CR is the measured count rate, is the estimated count rate calculated as . For this work the relative difference threshold was set to 0.1.
With this model in place, we can characterize the performance of the detector during the different operating conditions in the terms discussed above. To then determine the effects of the detector characteristics on the cross-correlation function and the fitted BFi, we develop a model which generates synthetic data to allow for estimates of corrections to the measured BFi. To generate these synthetic data, we first define the three types of photon detection events (real photon detections arising from the back scattered light, afterpulsing counts, and thermal dark counts). To simulate the real intensity signal, I[n], white noise is convolved with the electric field autocorrelation function, g1(τ), corresponding to the estimated optical properties of the sample (μa, μs’, index of refraction), the wavelength of light (λ), the source-detector separation (ρ), and the effective Db value. The signal is then normalized such that . This corresponds to an intensity signal where the coherence factor, β, is equal to 1, indicating we are measuring the fluctuation of a single speckle. In practice for the reflectance geometry, β is limited to 0.5, as two independent polarizations are captured by the single mode fiber.
To account for this, we generate two instances of I[n] and add the two together. We then convert the generated intensity signal to a probability of photon detection within a certain time bin, n, given as , where Ps[n] is the probability of detecting a signal photon in bin n, CR is the count rate of the measurement in counts per second, and fs is the sampling rate of the simulation. To simulate the afterpulsing of the detector, the afterpulsing parameters estimated from the real measurement are used describe the probability of detection, equal to , where n0 is the time bin when the last photon was detected. The dark counts are estimated as a uniform probability across all time bins n, equal to , where DCR is the dark count rate in counts per second. The total probability for photon detection during a particular time bin is given as P [n] = PS [n] + PAP [n – n0] + PDCR. Random numbers, R[n], are sampled from a uniform distribution spanning from 0 to 1 for each time bin in order until P[n]>R[n], indicating a photon detection event. The timestamp of the detected event is saved and the detector is then set to the “inactive state” by skipping the next M time bins, corresponding to the hold off time. This process is repeated until a sufficient number of photon detection events are recorded to generate the intensity autocorrelation function, g2(τ). To simulate the use of cross-correlation, the model is run again using the same intensity signal, as though another detector is being used. The seed of the RNG was reset at the beginning of each set of simulations to ensure the observations of the speckle signal for each detector were unique. This model is shown pictorially in Fig. 2. Simulated g2(τ)’s calculated by cross-correlation are then simulated for a range of Db values to determine the calibration curve to convert the apparent Db to true Db. This calibration is dependent only on the detector characteristics and applicable across all samples, with the caveat that the distortion of the correlation curve is dependent upon the measurement count rate, as is explored in further sections. To ensure accurate recovery of BFi from the experimental data, calibration curves are generated for each calculated g2(τ) to account for possible differences in measurement count rate.
Fig. 2.
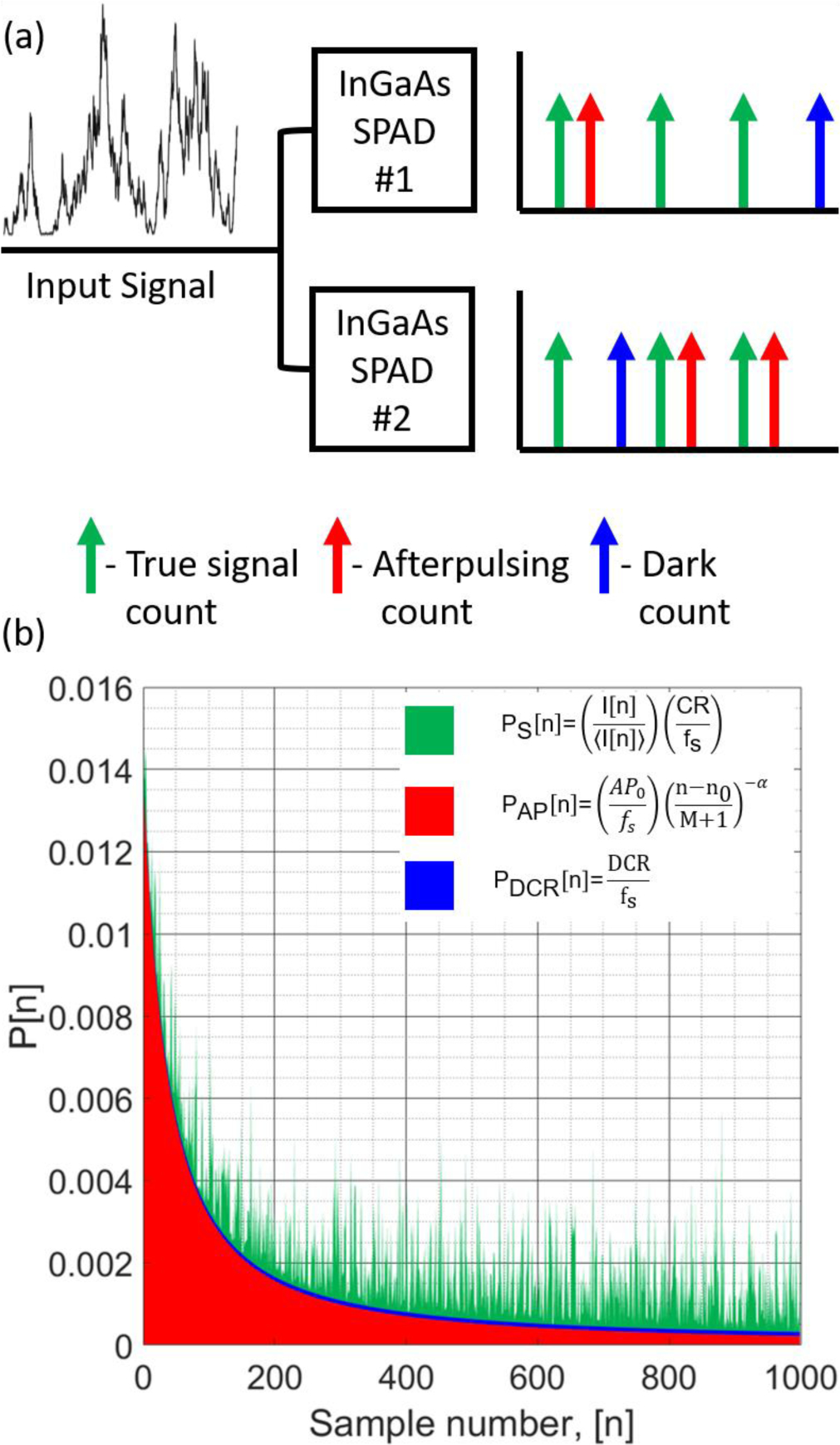
(a) Pictorial model description for the synthetic data model. The photon counts collected by the simulated detectors are shown with different types of counts color coded to their descriptions. (b) An example of the probabilities for the detection of each type of count is shown color coded in the same way as in (a). Inputs to the model, including the count rate of the back scattered light, DCR of the detector, and afterpulsing probabilities (P=10 kcps, AP0=140 kcps, and α=1.37), are used to determine the probabilities.
III. Results and discussion
A. Comparison of autocorrelation and cross-correlation
To show the effects on g2(τ) caused by calculating either the autocorrelation of the summed detector streams or the cross-correlation of the detector streams, we plot the correlation functions against the reference measurement correlation function taken by the SNSPD from the CW intralipid phantom measurements in Fig. 3(a) and Fig. 3(b). The obvious artifacts present in the autocorrelation, including the peaking behavior and oscillations that can be attributed to the afterpulsing of the detector as well as the step function drop at the hold off time, would likely prevent accurate characterization of the BFi. The cross-correlation curve is relatively clean, with the major features present in the autocorrelation now absent, as seen in Fig. 3(a). When compared to the reference measurement in Fig. 3(b), it can be seen that the decorrelation of the InGaAs/InP detectors is slowed, the possibility of which was discussed in the sections above due to the presence of afterpulsing counts remaining in the detector streams. This effect is not limited to the cross-correlation calculation, as the can be seen in Fig. 3(b). Although the major slowing factor of the autocorrelation is the afterpulsing tail, even at long lags where afterpulsing should be resolved (τ > 1 ms), the autocorrelation still decays slower than the reference measurement. To show the effects of the slowing, BFi values are fit from cross-correlation functions calculated from each of the detector setting manipulations and plotted as a box plot in Fig. 3(c). The BFi fit from the InGaAs/InP detectors can be seen to be ~30% lower than the reference measurement. The large error in the accuracy of the absolute value provides the motivation for the use of the models described in the methods section. Even though a large discrepancy in BFi is present at this stage, the use of cross-correlation removes the bulk of the artifacts present when the autocorrelation is calculated, and provides promising results.
Fig. 3.
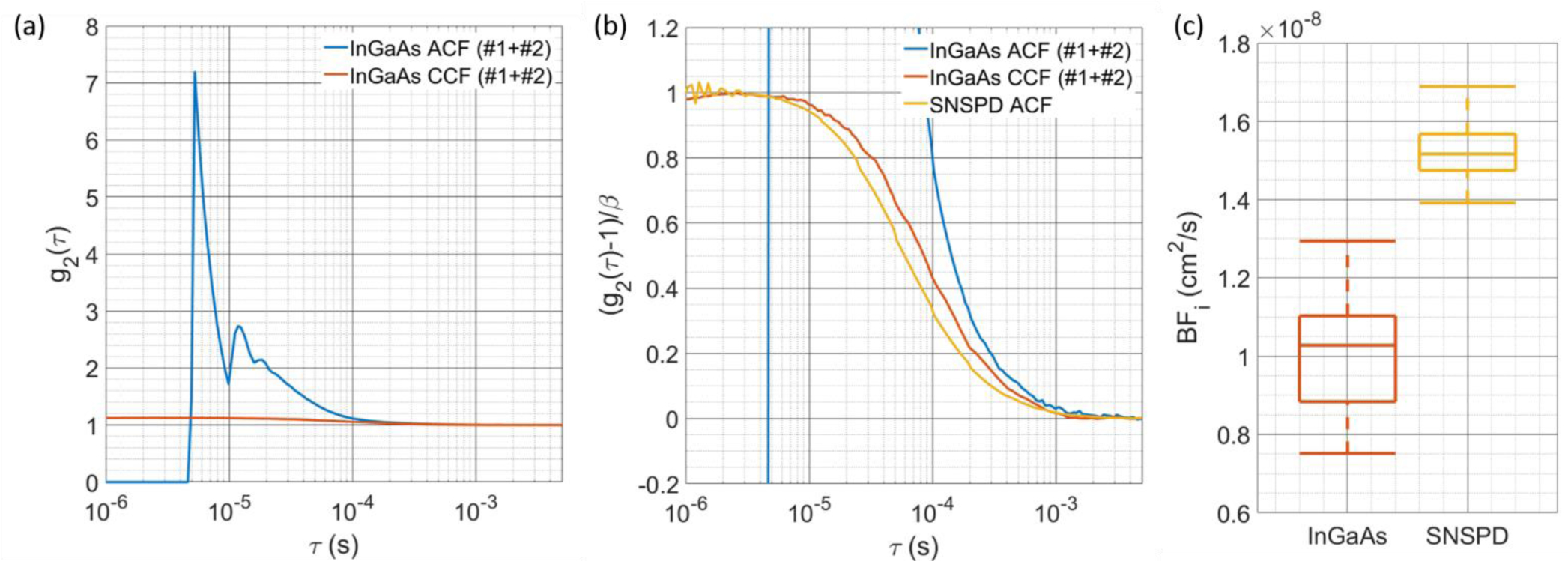
(a) Comparison of the g2(τ) calculated with autocorrelation of the combined counts of both detectors and the cross-correlation between the counts of each detector. The large artifacts due to afterpulsing are present in the autocorrelation calculation, though cross-correlation can be seen to remove the artifacts and extend the g2 to times below the hold-off time. (b) The comparison between the SNSPD autocorrelation, InGaAs/InP autocorrelation, and InGaAs/InP cross correlation shows that the cross-correlation is not completely without distortion, showing a slower decay. Quantification of this decay is shown in (c), where BFi is fit from g2(τ)’s calculated from measurements at different operating conditions. The consistently lower BFi is likely due to the “extension” of correlation by afterpulsing counts.
B. Estimation of detector characteristics at different operating conditions
The first step to correcting the BFi estimated from the cross-correlation g2(τ) is the determination of the detector characteristics (P, AP0, and α) corresponding to each operating condition (excess bias voltage, hold off time, and temperature). An example of the fitted autocorrelation curves from each individual SPAD can be seen below in Fig. 4(a). Here we plot the average of 5 modeled autocorrelation functions generated by multi-starting the optimization with plus and minus a standard deviation in the shading. We can see from this figure that the model provides an autocorrelation function that matches the shape of the afterpulsing corrupted correlation function. Further, we can also appreciate the differences in the correlation curve for the detectors that are being operated in the same conditions, indicating a fair amount of variable performance (P = [8.53, 5.71] kcps, AP0 = [175.9, 160.7] kcps, α = [1.79, 2.10], for detectors 1 and 2, respectively). To demonstrate that the fitted parameters of the model are consistent with the expected results for these SPAD detectors, e.g. increasing the excess bias voltage will increase the dark count and afterpulsing, we plot the estimated detector characteristics (P, AP0, and α) for one of the detectors operated in free running mode at a single temperature in Fig. 4(c), 4(d), and 4(e) and at a single excess bias voltage in Fig. 4(f), 4(g), and 4(h). The estimated detector characteristics match intuition, with afterpulsing probability increasing with increasing bias voltage and decreasing hold off time. The decay rate of the afterpulsing doesn’t show consistent behavior with bias voltage, though as was expected, the increasing magnitude of the parameter with increasing hold off time indicates a faster decay of the afterpulsing. For the background count rate, we see consistent increases in the probability of detection with increasing bias voltage, but the relationship with the hold off time is less clear. Though we would expect the probability of detection in the active state to be equal across the different hold off times, for shorter hold offs, the estimated parameter is lower than for the longer hold off times, where for hold off times >30 μs, the curves overlap, seen in Fig. 4(d) and 4(g). We believe these results may be due to the relatively extreme afterpulsing that is present in the short hold off time operating conditions. We also see results that are consistent with expectation as the temperature of the SPAD is varied. We see decreases in the afterpulsing rate with increased temperature as well as having an increase in the count rate. The decay rate of the afterpulsing again shows a relatively inconsistent behavior with the change in detector operating parameter, though with increasing hold off time, the rate of the afterpulsing decay increases. These results provide evidence that the detector characteristics can be determined across a range of operating conditions. Finally, by using the fitted detector characteristics, we can correct the BFi derived from the cross-correlation and show that the BFi estimated from all free running conditions explored match well with the BFi derived from the reference measurements, shown in Fig. 4(b).
Fig. 4.
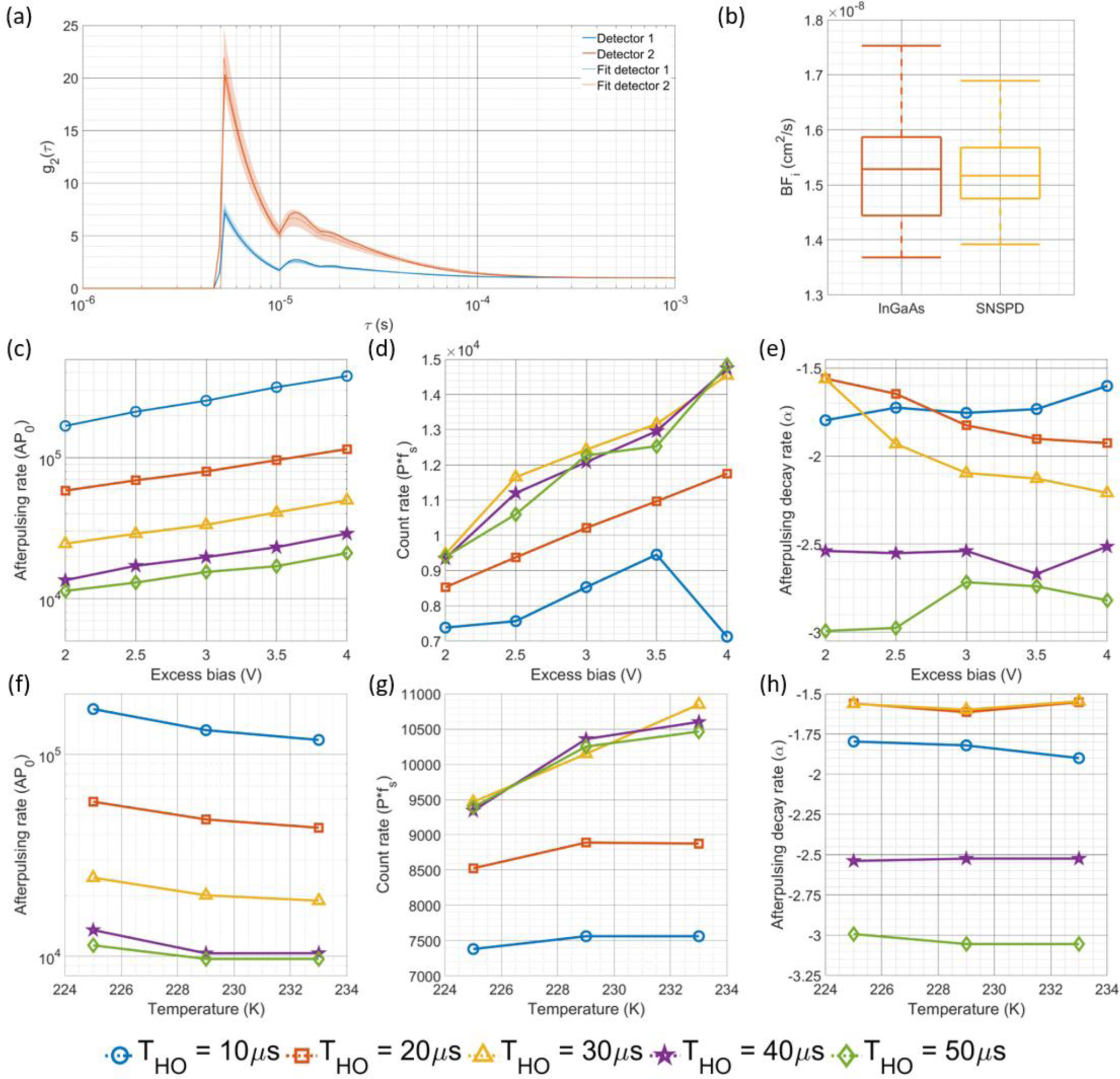
(a) Comparison of the autocorrelation calculated from the individual detector counts and their respective estimated autocorrelations fit using the detector model for a single set of detector operating parameters (Excess bias = 2.5 V, Hold off time = 10 μs, Temperature = 229 K). (b) Using the fitted properties, the BFi derived from the cross-correlation is corrected to account for the slowing of the correlation decay caused by the afterpulsing, and can be seen to match the BFi derived from the reference measurement. Fitting the correlation curves with the state space model allows for estimation of the afterpulsing probability at hold off time, shown in (c) and (f), measured count rate, shown in (d) and (g), and afterpulsing decay rate, shown in (e) and (h). The plots in (c), (d), and (e) are shown for a fixed temperature of 225K, and for the plots in (f), (g), and (h), the excess bias voltage is fixed at 2.0 V. The fit values for these parameters generally follow the intuition surrounding how altering the operating parameters (excess bias voltage, hold off time, and temperature) should affect the detector characteristics (P, AP0, and α). Based on the count rate estimation shown in (d), at extremely high afterpulsing rates/detector non-linearity conditions like those for the shorter hold off time condition, the estimation of count rate might be inaccurate, as shown in the difference between the 10 and 20 μs hold off time vs. the rest of the measurements.
C. Signal-to-noise ratio at different operating conditions
For the selection of optimal operating parameters, we use the SNR of the plateau of the measured cross-correlation g2(τ). Below we compare surface plots for the CW operation (Fig. 5(a)) and gated operation (Fig. 5(b)) for the SNR of the plateau of g2(τ) as a function of the hold off time and excess bias voltage and temperature. For both sets of results, we calculate g2(τ) at a frequency of 0.1 Hz from the intralipid phantom data. To simplify the plotting of the results, we collapse the data along the temperature axis and plot the SNR results for the CW and gated operation in Fig. 5(c) and 5(d), respectively. From these results, it is readily evident that gated operation, even when measurements are not time resolved, allow for much greater SNR, likely due to the reduction in the duty cycle of the dark count rate and the possibility of having afterpulses. Another beneficial feature of gated operation is the increase in SNR with increasing bias voltage, indicating that the increases in detection efficiency are not being overwhelmed by increases in the noise counts, as we theorize is the case for CW operation. Based on the results of these experiments, only gated operation was used for the in vivo experiments, with the SNR of the CW measurement not being high enough. While the SNR of the curve seems sufficient to fit for BFi, the combination of the higher sampling rate and the increase in the variability of fitted BFi after correction imposes the need for a slightly higher SNR than is traditionally required to make measurements. The settings used for the in vivo experiments were determined to be a temperature of 225K, an excess bias of 7V and a hold off time of 5 μs.
Fig. 5.
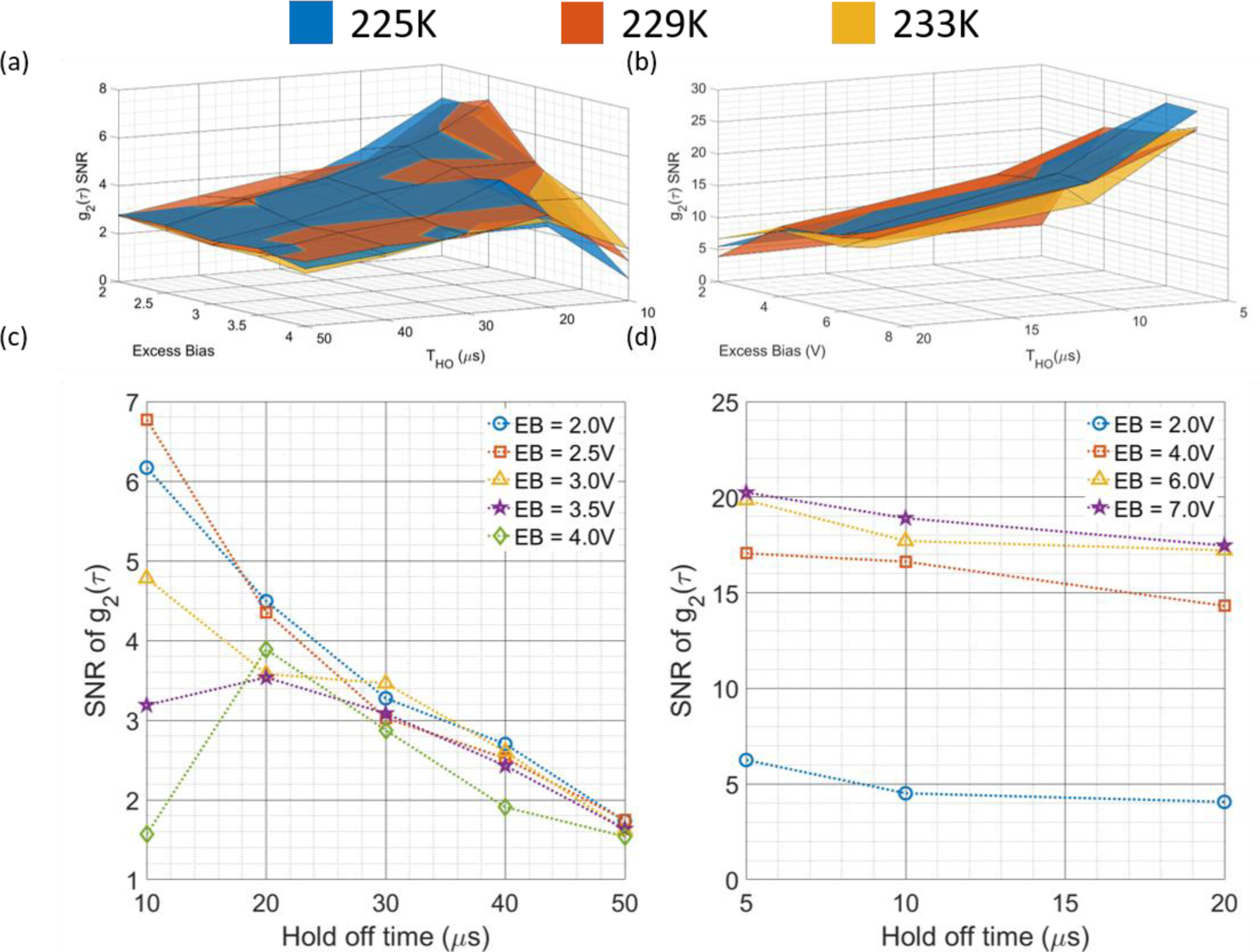
The comparisons of the SNR of the g2(τ) curves as a function of the three operating parameters (excess bias voltage, hold off time, and temperature) are shown in (a) for the CW operation and (b) for the gated operation. To increase readability, the results present in (a) and (b) are averaged by the temperature, and presented in (c) and (d), respectively. It can be seen that for CW operation, a high bias voltage does not improve SNR, indicating that the noise counts grow faster than the increase in signal counts mediated by an increase in detection efficiency. For gated operation, the lower duty cycle allows for a reduction in dark counts, and the increase in detection efficiency is better realized, as indicated by the increased SNR at higher bias voltage. In general, across these measurements, increases in the hold off time are detrimental to SNR as they reduce the duty cycle of the detector and limit the number of back scattered photons that can be detected.
D. In vivo tourniquet tightening experiment and correction of the measured BFi
With the optimal operating conditions determined for these detectors, measurements of in vivo blood flow were taken. The time trace of BFi fit from the reference detector, naively fit BFi from the InGaAs/InP detector cross-correlation, and model corrected BFi from the InGaAs/InP detector cross-correlation can be seen in Fig. 6(a). In these experiments, the hyperemia peak observed at the release of the tourniquet was relatively blunted, though this could be due to the appropriateness of the model used to fit the data at a relatively short source-detector separation [35] or the relatively small reduction in blood flow (~30%) caused by the tourniquet. Relative changes in BFi normalized to the baseline period show similarity between detectors (not plotted here), though as is seen in the next section, the relationship between the true BFi and the apparent BFi is nonlinear, which could complicate the use of relative BFi. To correct for the offset in absolute BFi, we apply the synthetic data model to determine the relationship between the estimated BFi and true BFi for the set of detector characteristics determined by fitting the individual detector autocorrelation function. Seen below in Fig. 6(b), we show a scatterplot of BFi values fit from the reference measurement g2(τ) and the InGaAs/InP cross-correlation g2(τ). For the uncorrected data, the BFi is significantly lower, with the discrepancy becoming more severe for higher values of true BFi. Following correction, the data falls along the line of unity, and accurate BFi estimates can be made using the afterpulsing corrupted g2(τ).
Fig. 6.
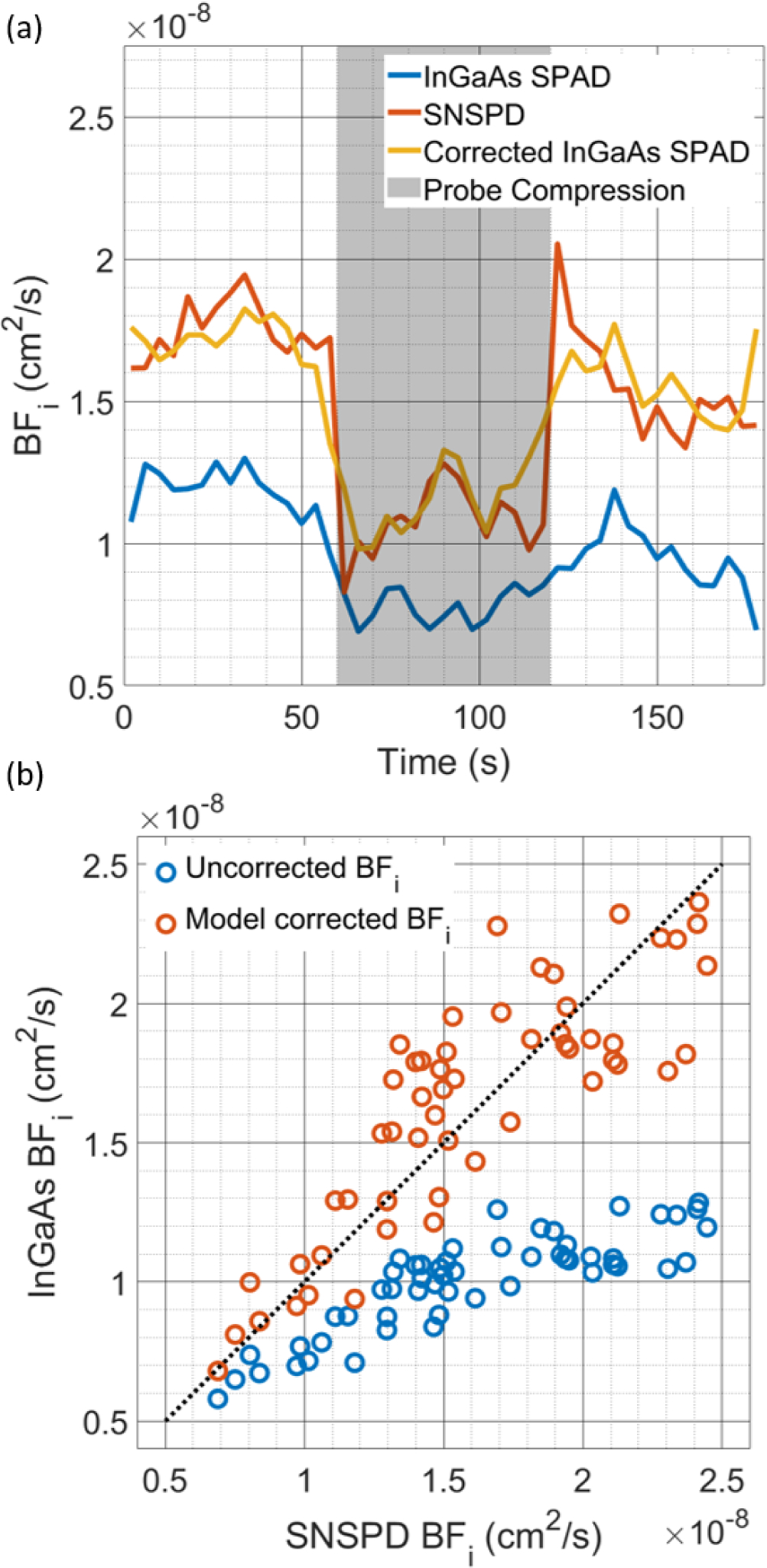
(a) Comparison of the time course of fitted BFi during the probe compression protocol. The effect of the afterpulsing on the BFi is seen in the lower BFi fitted for the uncorrected data, but following correction, the InGaAs/InP detector cross-correlation gives very similar results to that of the SNSPD. (b) Comparison of the BFi fitted from the SNSPD and InGaAs/InP measurements with and without the correction by the model. Large systematic errors can be seen in the estimate of BFi without correction, but the model allows the extraction of accurate BFi values. Due to the compression of the dynamic range of the autocorrelation decay at higher BFi values, the variability of the BFi estimates after correction can be seen to increase with the degree of the discrepancy between the true BFi and the naively fit BFi.
E. Estimating BFi distortion for a more realistic source-detector separation optimizing for cerebral sensitivity
In this work, all InGaAs/InP SPAD measurements were made at relatively short source-detector separations (~1 cm) due to the photon detection efficiency of these particular modules, which are currently optimized to be most sensitive to light around 1500 nm [36]. While we were limited to the short separation range in this work due to detector fiber coupling inefficiencies, we can still estimate the performance of a SPAD with comparable afterpulsing as though measurements were made at longer separations. Based on previous in vivo measurements of photon counts at a long source-detector separation taken with an SNSPD detector and normalizing that count rate by the detector efficiency of the free space version of this InGaAs/InP SPAD (~40% @ 1064nm), we estimate we should collect between 5 kcps and 50 kcps. Plugging these estimated count rates into the synthetic data model yields the results seen below in Fig. 7(a) and 7(b), comparing the true BFi and the BFi estimated from the naively fit autocorrelation function. The BFi underestimation strongly depends on count rate, and for the low count rates explored below, the degree of slowing matches the slowing seen in the in-vivo results where the count rate was 8.5 kcps total between the two detectors. Comparing to the results presented above in Fig. 6(b), the distortion to the recovered BFi is greater with the faster decorrelation seen at the longer source-detector separation, though with count rates >10 kcps the relationship between true BFi and recovered BFi does not “saturate” in a physiologic range of blood flow index, and by applying our distortion correction model, will make the recovery of the blood flow index possible.
Fig. 7:
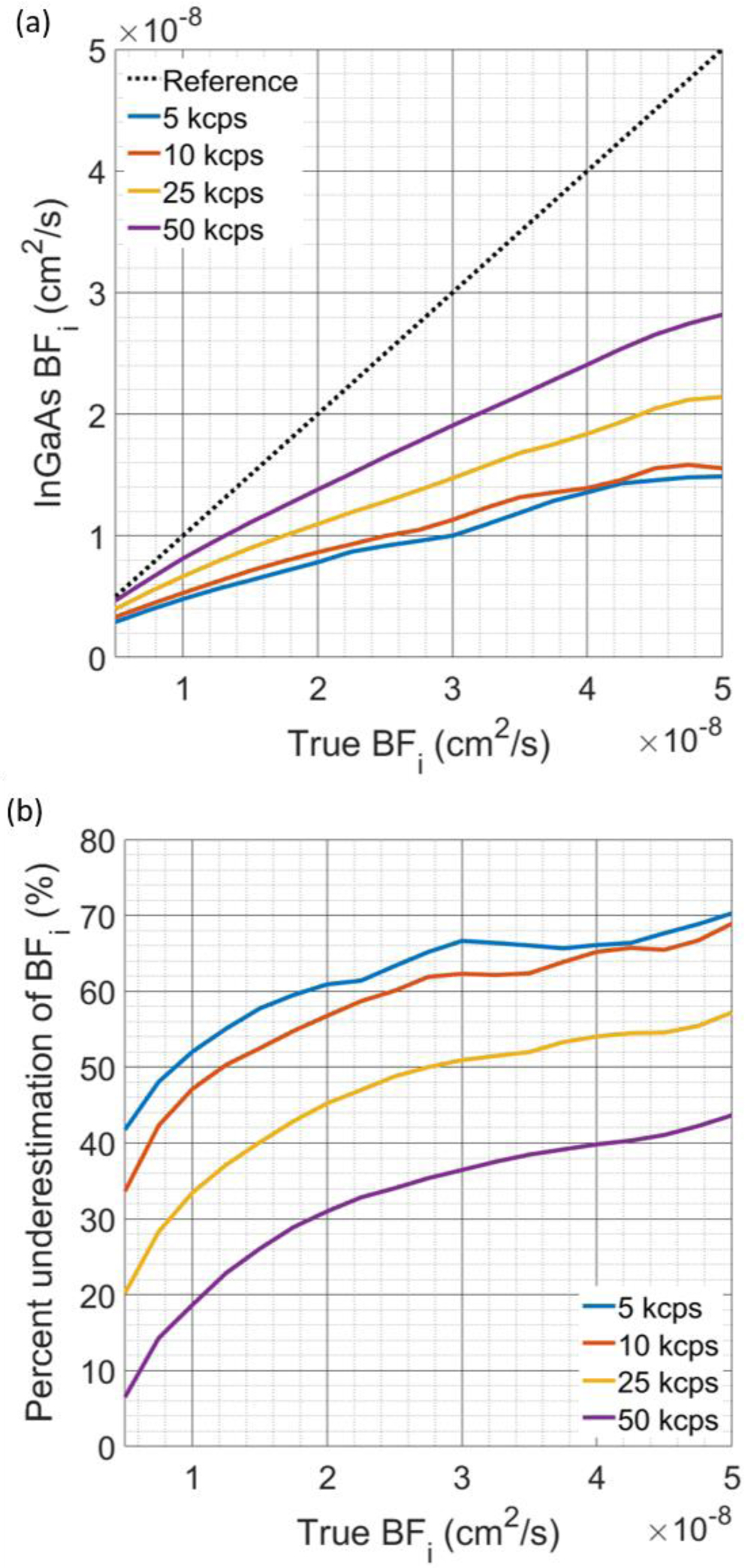
(a) Comparison of the recovered BFi from g2(τ) curves generated by the synthetic data model. The detector characteristics for each detector used for these simulations were AP0 = [180, 140] kcps, DCR = [0.25, 0.25] kcps, and α = [1.37, 1.54], as fit from the measurements made at the operating conditions used for the in vivo experiments. At low count rates, the BFi recovered from the curves shows more severe underestimation, seen in both (a) and (b), though with a higher photon count rate, the degree of underestimation is improved. The relationship shown provides a rationale for the relative BFi matching well between the InGaAs/InP measurement and the reference measurement, as these measurements were made over a relatively small range of BFi values. With an increase in the range of BFi made during a particular measurement, this accuracy would likely be degraded, as the relationship between InGaAs/InP derived BFi and true BFi is nonlinear.
IV. Conclusion
Here we have detailed a set of methods to correct the inherent shortcomings of InGaAs/InP sPAD detectors when applied to diffuse correlation spectroscopy. Through a combination of detector cross-correlation and appropriate modeling, distortions of the correlation function can be accounted for and accurate BFi values can be measured. To start we show that using cross-correlation, InGaAs/InP detectors become usable for DCs despite the strong AP and long holdoff time. A residual afterpulsing artifact is still present at low count rate, and we provided a detector modeling approach to remove the systematic bias from BFi values derived from the cross-correlation data. We showed that accurate characterization of detector effects was possible across a range of operating parameters. Although here we assume a power law model for the afterpulsing, inclusion of different types of models for afterpulsing, as have been explored in the literature [37], is easily possible by swapping the function dependence of Ai. The use of these models also seems to give results similar to those made through time-correlated single photon counting experiments without the need for the required instrumentation, which could be a benefit in detector characterization [38]. In general, for detectors with this profile of afterpulsing and detection efficiency, we find that operating the detector in gated mode with a high excess bias voltage provides the best performance, allowing for in vivo measurements to be made. We believe the application of this analysis can open the door for higher sNR DCs measurements made at longer wavelengths.
Acknowledgment
The authors would like to thank Micro Photon Devices and Nick Bertone for enabling this study by lending the two InGaAs/InP modules used to perform these experiments. Conflict of interest: The authors have patents on the NIRS and DCS technologies. MAF has a financial interest in 149 Medical, Inc., a company developing DCS technology for assessing and monitoring cerebral blood flow in newborn infants. MAF’s interests were reviewed and are managed by Massachusetts General Hospital and Partners HealthCare in accordance with their conflict of interest policies. Any opinions, findings, conclusions, or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the Assistant Secretary of Defense for Research and Engineering.
This work was supported in part by the U.S. National Institutes of Health under Grants R21EB028626–01, U01EB028660–02, F31NS118753–01, T32EB001680–16.
Contributor Information
Mitchell B. Robinson, Harvard-MIT Program in Health Sciences and Technology, Massachusetts Institute of Technology, Cambridge, MA 02139 USA
Marco Renna, Athinoula A. Martinos Center for Biomedical Imaging, Department of Radiology, Massachusetts General Hospital and Harvard Medical School..
Nisan N. Ozana, Athinoula A. Martinos Center for Biomedical Imaging, Department of Radiology, Massachusetts General Hospital and Harvard Medical School.
Adriano Peruch, Athinoula A. Martinos Center for Biomedical Imaging, Department of Radiology, Massachusetts General Hospital and Harvard Medical School..
Sava Sakadžić, Athinoula A. Martinos Center for Biomedical Imaging, Department of Radiology, Massachusetts General Hospital and Harvard Medical School..
Megan L. Blackwell, Massachusetts Institute of Technology Lincoln Laboratory.
Jonathan M. Richardson, Massachusetts Institute of Technology Lincoln Laboratory.
Brian F. Aull, Massachusetts Institute of Technology Lincoln Laboratory.
Stefan A. Carp, Athinoula A. Martinos Center for Biomedical Imaging, Department of Radiology, Massachusetts General Hospital and Harvard Medical School.
Maria Angela Franceschini, Athinoula A. Martinos Center for Biomedical Imaging, Department of Radiology, Massachusetts General Hospital and Harvard Medical School..
References
- [1].Boas DA and Yodh AG, “Spatially varying dynamical properties of turbid media probed with diffusing temporal light correlation,” J. Opt. Soc. Am. A, vol. 14, no. 1, p. 192, Jan. 1997, doi: 10.1364/JOSAA.14.000192. [DOI] [Google Scholar]
- [2].Shang Y, Li T, and Yu G, “Clinical applications of near-infrared diffuse correlation spectroscopy and tomography for tissue blood flow monitoring and imaging,” Physiological Measurement, vol. 38, no. 4. NIH Public Access, pp. R1–R26, 2017. doi: 10.1088/1361-6579/aa60b7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Parthasarathy AB et al. , “Dynamic autoregulation of cerebral blood flow measured non-invasively with fast diffuse correlation spectroscopy.,” J. Cereb. Blood Flow Metab, vol. 38, no. 2, pp. 230–240, Feb. 2018, doi: 10.1177/0271678X17747833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Busch DR et al. , “Detection of Brain Hypoxia Based on Noninvasive Optical Monitoring of Cerebral Blood Flow with Diffuse Correlation Spectroscopy,” Neurocrit. Care, vol. 30, no. 1, pp. 72–80, Feb. 2019, doi: 10.1007/s12028-018-0573-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Yazdi HS et al. , “Mapping breast cancer blood flow index, composition, and metabolism in a human subject using combined diffuse optical spectroscopic imaging and diffuse correlation spectroscopy,” J. Biomed. Opt, vol. 22, no. 4, p. 045003, Apr. 2017, doi: 10.1117/1.jbo.22.4.045003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Durduran T et al. , “Diffuse optical measurement of blood flow in breast tumors,” Opt. Lett, vol. 30, no. 21, p. 2915, Nov. 2005, doi: 10.1364/ol.30.002915. [DOI] [PubMed] [Google Scholar]
- [7].Zhou W et al. , “Highly parallel, interferometric diffusing wave spectroscopy for monitoring cerebral blood flow dynamics,” Optica, vol. 5, no. 5, p. 518, May 2018, doi: 10.1364/OPTICA.5.000518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].James E and Powell S, “Fourier domain diffuse correlation spectroscopy with heterodyne holographic detection,” Biomed. Opt. Express, vol. 11, no. 11, p. 6755, Nov. 2020, doi: 10.1364/boe.400525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Nakaji H, “Diffusing wave spectroscopy with heterodyne detection,” 10451537, Feb. 03, 2017. Accessed: Jul. 18, 2018. [Online]. Available: http://appft.uspto.gov/netacgi/nph-Parser?Sect1=PTO2&Sect2=HITOFF&p=1&u=%2Fnetahtml%2FPTO%2Fsearch-bool.html&r=1&f=G&l=50&co1=AND&d=PG01&s1=20170227445&OS=20170227445&RS=20170227445 [Google Scholar]
- [10].Robinson MB et al. , “Interferometric diffuse correlation spectroscopy improves measurements at long source–detector separation and low photon count rate,” J. Biomed. Opt, vol. 25, no. 09, p. 097004, Sep. 2020, doi: 10.1117/1.JBO.25.9.097004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Kholiqov O et al. , “Time-of-flight resolved light field fluctuations reveal deep human tissue physiology,” Nat. Commun, vol. 11, no. 1, p. 391, 2020, doi: 10.1038/s41467-019-14228-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Tamborini D et al. , “Portable System for Time-Domain Diffuse Correlation Spectroscopy,” IEEE Trans. Biomed. Eng, vol. 66, no. 11, pp. 3014–3025, Nov. 2019, doi: 10.1109/TBME.2019.2899762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Pagliazzi M et al. , “Time domain diffuse correlation spectroscopy with a high coherence pulsed source: in vivo and phantom results,” Biomed. Opt. Express, vol. 8, no. 11, p. 5311, Nov. 2017, doi: 10.1364/boe.8.005311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Samaei S et al. , “Time-domain diffuse correlation spectroscopy (TD-DCS) for noninvasive, depth-dependent blood flow quantification in human tissue in vivo,” Sci. Reports 2021 111, vol. 11, no. 1, pp. 1–10, Jan. 2021, doi: 10.1038/s41598-021-81448-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Tsalach A et al. , “Depth selective acousto-optic flow measurement.,” Biomed. Opt. Express, vol. 6, no. 12, pp. 4871–86, Dec. 2015, doi: 10.1364/BOE.6.004871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Robinson MB et al. , “Characterization of continuous wave ultrasound for acousto-optic modulated diffuse correlation spectroscopy (AOM-DCS),” Biomed. Opt. Express, vol. 11, no. 6, p. 3071, Jun. 2020, doi: 10.1364/boe.390322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Sie EJ et al. , “High-sensitivity multispeckle diffuse correlation spectroscopy,” 10.1117/1.NPh.7.3.035010, vol. 7, no. 3, p. 035010, Sep. 2020, doi: . [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Liu W et al. , “Fast and sensitive diffuse correlation spectroscopy with highly parallelized single photon detection,” APL Photonics, vol. 6, no. 2, p. 026106, Feb. 2021, doi: 10.1063/5.0031225. [DOI] [Google Scholar]
- [19].Carp SA et al. , “Diffuse correlation spectroscopy measurements of blood flow using 1064 nm light,” J. Biomed. Opt, vol. 25, no. 09, pp. 97003–97004, Sep. 2020, doi: 10.1117/1.JBO.25.9.097003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Colombo L et al. , “In vivo time-domain diffuse correlation spectroscopy above the water absorption peak,” Opt. Lett, vol. 45, no. 13, p. 3377, Jul. 2020, doi: 10.1364/ol.392355. [DOI] [PubMed] [Google Scholar]
- [21].Blackwell M et al. , “Novel detector solutions for diffuse correlation spectroscopy at 1064 nm (Conference Presentation),” in Dynamics and Fluctuations in Biomedical Photonics XVII, Mar. 2020, vol. 11239, p. 12. doi: 10.1117/12.2545178. [Google Scholar]
- [22].Ozana N et al. , “Superconducting nanowire single-photon sensing of cerebral blood flow,” 10.1117/1.NPh.8.3.035006, vol. 8, no. 3, p. 035006, Aug. 2021, doi: . [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Restelli A, Bienfang JC, and Migdall AL, “Time-domain measurements of afterpulsing in InGaAs/InP SPAD gated with sub-nanosecond pulses,” in Journal of Modern Optics, 2012, vol. 59, no. 17, pp. 1465–1471. doi: 10.1080/09500340.2012.687463. [DOI] [Google Scholar]
- [24].Itzler MA, Jiang X, and Entwistle M, “Power law temporal dependence of InGaAs/InP SPAD afterpulsing,” J. Mod. Opt, vol. 59, no. 17, pp. 1472–1480, Oct. 2012, doi: 10.1080/09500340.2012.698659. [DOI] [Google Scholar]
- [25].Zhang J et al. , “Advances in InGaAs/InP single-photon detector systems for quantum communication,” Light Sci. Appl, vol. 4, no. 5, p. 286, May 2015, doi: 10.1038/lsa.2015.59. [DOI] [Google Scholar]
- [26].Jiang X et al. , “InGaAsP-InP avalanche photodiodes for single photon detection,” IEEE J. Sel. Top. Quantum Electron, vol. 13, no. 4, pp. 895–904, Jul. 2007, doi: 10.1109/JSTQE.2007.903001. [DOI] [Google Scholar]
- [27].BROWN RH and TWISS RQ, “Correlation between Photons in two Coherent Beams of Light,” Nat. 1956 1774497, vol. 177, no. 4497, pp. 27–29, 1956, doi: 10.1038/177027A0. [DOI] [Google Scholar]
- [28].Siegert AJF, On the fluctuations in signals returned by many independently moving scatterers. Radiation Laboratory, Massachusetts Institute of Technology, 1943. [Google Scholar]
- [29].Carp SA et al. , “Due to intravascular multiple sequential scattering, Diffuse Correlation Spectroscopy of tissue primarily measures relative red blood cell motion within vessels,” Biomed. Opt. Express, vol. 2, no. 7, p. 2047, Jul. 2011, doi: 10.1364/boe.2.002047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Boas DA et al. , “Establishing the diffuse correlation spectroscopy signal relationship with blood flow,” Neurophotonics, vol. 3, no. 3, p. 031412, Jul. 2016, doi: 10.1117/1.nph.3.3.031412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Sakadžic S et al. , “Theoretical model of blood flow measurement by diffuse correlation spectroscopy,” J. Biomed. Opt, vol. 22, no. 2, p. 27006, Feb. 2017, doi: 10.1117/1.JBO.22.2.027006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Du Le VN and Srinivasan VJ, “Beyond diffuse correlations: deciphering random flow in time-of-flight resolved light dynamics,” Opt. Express, vol. 28, no. 8, p. 11191, Apr. 2020, doi: 10.1364/oe.385202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Verdecchia K et al. , “Assessment of the best flow model to characterize diffuse correlation spectroscopy data acquired directly on the brain.,” Biomed. Opt. Express, vol. 6, no. 11, pp. 4288–301, Nov. 2015, doi: 10.1364/BOE.6.004288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Farzam P et al. , “Fast diffuse correlation spectroscopy (DCS) for non-invasive measurement of intracranial pressure (ICP)(Conference Presentation),” in Clinical and Translational Neurophotonics, 2017, vol. 10050, p. 100500U. [Google Scholar]
- [35].Samaei S et al. , “Time-domain diffuse correlation spectroscopy (TD-DCS) for noninvasive, depth-dependent blood flow quantification in human tissue in vivo,” Sci. Rep, vol. 11, no. 1, p. 1817, Dec. 2021, doi: 10.1038/s41598-021-81448-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].“Micro Photon Devices - PDM-IR.” http://www.micro-photon-devices.com/Products/SPAD-by-Wavelength/900nm-1700nm/PDM-IR (accessed Mar. 05, 2021).
- [37].Ziarkash AW et al. , “Comparative study of afterpulsing behavior and models in single photon counting avalanche photo diode detectors,” Sci. Rep, vol. 8, no. 1, pp. 1–8, Dec. 2018, doi: 10.1038/s41598-018-23398-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Tosi A et al. , “Low-noise, low-jitter, high detection efficiency InGaAs/InP single-photon avalanche diode,” IEEE J. Sel. Top. Quantum Electron, vol. 20, no. 6, pp. 192–197, Nov. 2014, doi: 10.1109/JSTQE.2014.2328440. [DOI] [Google Scholar]


